Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2021 Nov 1.
Published in final edited form as: Ultrasound Med Biol. 2020 Aug 6;46(11):3080–3087. doi: 10.1016/j.ultrasmedbio.2020.07.006

Ultrasound Attenuation Estimation in Harmonic Imaging for Robust Fatty Liver Detection

Ping Gong 1, Chenyun Zhou 1,2, Pengfei Song 1,3,4, Chengwu Huang 1, U-Wai Lok 1, Shanshan Tang 1, Kymberly Watt 5, Matthew Callstrom 1, Shigao Chen 1,*
PMCID: PMC7534411  NIHMSID: NIHMS1620010  PMID: 32773254

Abstract

Accurate detection of liver steatosis is important for liver disease management. Ultrasound attenuation coefficient estimation (ACE) has great potential in quantifying liver fat content. The commonly-used ACE methods (e.g., spectral shift methods, reference phantom methods) assumed linear tissue response to ultrasound and were developed in fundamental imaging. However, fundamental imaging may be vulnerable to reverberation clutters introduced by body wall. The clutters superimposed on liver echoes may bias the attenuation estimation. Here we propose to apply a new ACE technique, reference frequency method (RFM), in harmonic imaging to mitigate the reverberation bias. The accuracy of harmonic RFM was validated through phantom study. In a pilot patient study, harmonic RFM provided more robust in-vivo performance as compared to fundamental RFM, demonstrating the potential of ACE in harmonic imaging.

Keywords: Fatty liver detection, ultrasound attenuation estimation, harmonic imaging

Introduction

Fatty liver, or hepatosteatosis, is characterized histologically by triglyceride accumulation within the cytoplasm of hepatocytes and refers to fat accumulation in the liver exceeding 5%−10% by weight (Obika and Noguchi 2012). When hepatosteatosis is present in the absence of excessive alcohol consumption, it is termed Nonalcoholic Fatty Liver Disease (NAFLD). NAFLD is the most common liver disorder in Western countries, affecting 17–46% of adults (Marchesini et al. 2016). Between 75 million and 100 million individuals in the United States are estimated to have NAFLD (Rinella 2015). About 20–30% of subjects with NAFLD will develop a more severe form called nonalcoholic steatohepatitis (NASH), which may result in liver fibrosis and progress to cirrhosis, liver failure, or hepatocellular carcinoma (Machado and Cortez-Pinto 2013). Therefore, detection of NAFLD is important for diagnosis of NASH at early stage for timely intervention to improve long term outcome. Liver biopsy is the gold standard for diagnosis and staging of NAFLD (Machado and Cortez-Pinto 2013). However, the invasiveness of liver biopsy makes it unsuitable for screening and frequent follow-ups. Noninvasive alternatives such as B-mode ultrasound and CT have low sensitivity for liver steatosis (Dasarathy et al. 2009, Lawrence et al. 2012). Proton density fat fraction (PDFF) acquired with Magnetic Resonance Imaging (MRI) is a standardized and objective measure of mobile proton density proportion attributable to fat in the liver which has been shown to have high fat measurement accuracy in phantoms, human liver samples, animal and human studies (Kinner et al. 2016). The imaging time and cost have also been considerably reduced with abbreviated sequences (Canellas et al. 2019). However, MRI has limited availability worldwide with more restrictions and contraindications, and thus limiting its use in clinical practice. Therefore, low-cost, widely accessible, and accurate liver steatosis staging biomarkers are in urgent need. It has been reported that the elevated fat content in the liver is associated with increased ultrasound attenuation, and several studies have shown feasibility of ultrasound attenuation in steatosis staging using Fibroscan’s Controlled Attenuation Parameter (CAP) (Taylor al. 1986, Lin et al. 1988, Lu et al. 1999, Sasso et al. 2010, Karlas et al. 2017). However, CAP is not compatible with clinical ultrasound scanners and requires an expensive stand-alone device, which could limit its accessibility. In addition, measurements are made blindly without B-mode imaging guidance, and thus are susceptible to bias caused by major vessels within the liver. Consequently, attenuation coefficient estimation (ACE) technologies that are compatible with clinical ultrasound scanners would have high clinical significance.

At present, the two commonly used ACE methods in ultrasound array imaging systems are the spectral shift method (Kuc and Li 1985, Bigelow et al. 2008, Samimi and Varghese 2015) and the reference phantom-based methods (Kuc and Schwartz 1979, Kuc 1980, Parker and Waag 1983, Parker et al. 1988, Yao et al. 1990, Kim and Varghese 2008, Coila and Lavarello 2018). The spectral shift method estimates the attenuation coefficient through the downshift of the ultrasound center frequency with increasing depth (Kim and Varghese 2008). For the reference phantom-based methods (Kuc and Schwartz 1979, Kuc 1980, Parker and Waag 1983, Parker et al. 1988, Yao et al. 1990, Kim and Varghese 2008, Samimi and Varghese 2016), a well-calibrated phantom is needed to normalize system-dependent effects such as focusing, diffraction, and time gain compensation (TGC). To our knowledge, the above ACE methods were developed and implemented under fundamental imaging mode so that they were vulnerable to the reverberation clutters introduced by the body wall. The clutter signals superimposed on liver echoes may bias attenuation estimation in liver, especially for patients with large Body Mass Index (BMI). In contrast, harmonic imaging can effectively mitigate the reverberation issue compared to fundamental mode, which makes it the default mode for abdominal scanning in many commercial ultrasound scanners (Krishnan et al. 2017). The reduction of reverberation clutters in harmonic imaging may lead to more accurate ACE measurements of liver.

Recently, we developed a novel system-independent attenuation coefficient estimation technique based on spectra normalization, which is referred to as reference frequency method (RFM). This technique does not require a reference phantom for normalization. The power of each frequency component is normalized by the power of an adjacent frequency component in the spectrum to cancel system-dependent effects such as focusing and TGC (Gong et al. 2019). In this paper, we propose to apply RFM in harmonic imaging (RFM-HI) for more robust ACE in liver. The accuracy of RFM-HI was first validated with a calibrated tissue-mimicking phantom. The feasibility of in-vivo RFM-HI was tested on 20 patients who underwent clinically-indicated MRI of liver. The acquired attenuation estimates were correlated with MRI-PDFF to evaluate the performance of RFM-HI.

Materials and Methods

Theory

In ultrasound harmonic imaging, the power spectrum of the backscattered signals S(fi, z) can be modeled as a function of backscatter location and the frequency of ultrasound (Yao et al. 1990, Nam et al. 2011)

S(fi,z)=G(fi)⋅TGC(z)⋅D(fi,z)⋅H(fi,z)⋅BSC(fi)⋅A(fi,z), (1)

where G(fi) accounts for the transmit and receive transducer responses at frequency fi (i is the frequency component within second harmonic bandwidth); TGC(z) is the time gain compensation (TGC), which varies as a function of depth z; D(fi, z) is the combined effects of focusing, beamforming, and diffraction; H(fi, z) accounts for the harmonic generation during ultrasound propagation; BSC(fi) is the backscatter coefficient which is assumed to be uniform in the local region of interest (ROI); and A(fi, z) is the frequency-dependent attenuation defined as (Yao et al. 1990, Nam et al. 2011):

A(fi,Zk)=exp(−4afizk), (2)

where a is the frequency-dependent ultrasound attenuation coefficient. A(fi, z) is also assumed to be uniform in the ROI and has linear frequency dependency.

In RFM, we assume that the differences of beamforming and diffraction effects between two adjacent frequency components (i.e., fi and fi−1) are negligible as D(fi, z) = D(fi−1, z). Then the power spectra can be normalized by calculating the power ratio (Rs(fi, z)) between adjacent frequency components S(fi, zk) and S(fi−1, zk) to cancel TGC and diffraction as

Rs(fi,z)=s(fi,z)s(fi−1,z)=G(fi)G(fi−1)⋅TGC(z)TGC(z)⋅D(fi,z)D(fi−1,z)⋅H(fi,z)H(fi−1,z)⋅BSC(fi)BSC(fi−1)⋅A(fi,z)A(fi−1,z)=G(fi)G(fi−1)⋅H(fi,z)H(fi−1,z)⋅BSC(fi)BSC(fi−1)⋅A(fi,z)A(fi−1,z) (3)

We assume that the differences of harmonic generation effects between two adjacent frequency components are also negligible as H(fi, z) = H(fi−1, z), then we get

RS(fi,Z)=G(fi)G(fi−1)⋅BSC(fi)BSC(fi−1)⋅A(fi,z)A(fi−1,z) (4)

After taking the natural logarithm on both sides of Eq. (4), we obtain the following linear relationship between frequency power ratio (ln[Rs(fi, z)) and imaging depth (z):

ln[RS(fi,z)]=−4a(fi−fi−1)z+ln[G(fi)G(fi−1)⋅BSC(fi)BSC(fi−1)] (5)

Then the attenuation coefficient can be estimated from the slope of the decay trend of frequency power ratio with respect to each second harmonic frequency component.

ai= slope −4(fi−fi−1)z (6)

Multiple frequency power ratios can be averaged within the second harmonic frequency bandwidth to facilitate more robust attenuation estimation.

Tissue-mimicking Phantom Validation

The proposed RFM-HI was first validated on a tissue-mimicking phantom calibrated using 2D ultrasound attenuation imaging (ATI) function on a commercial ultrasound scanner, Aplio i800 (Canon Medical Systems, Tochigi, Japan). ATI acquisitions were performed using the curved array i8CX1 (1 – 8 MHz) following regular acquisition procedures (Jeon et al. 2019). The median attenuation coefficient measured from the phantom was 0.57 dB/cm/MHz from five repeated valid measurements (R2 ≥ 0.90, interquartile range/median <30%) (Jeon et al. 2019). Harmonic RFM data of the calibrated phantom were acquired with a General Electric LOGIQ E9 (LE9) system (General Electric Healthcare, Wauwatosa, WI) with conventional line-by-line focused beam scanning and a curved array transducer C1–6D (1 – 6 MHz, General Electric Healthcare, Wauwatosa, WI). For LE9 harmonic imaging, 100 A-lines were acquired with focal depth set at 6.5 cm. The imaging frame rate was 20 Hz. The center frequency of the transmit pulse was around 2 MHz. IQ data obtained from the calibrated phantom were stored using the RF Capture module available on LE9 and then offline-processed for attenuation estimation. The IQ post-processing method was similar to that described in (Gong et al. 2019). Briefly, a region of interest (ROI) was selected on the beamformed IQ image which was set axially around 2 – 10 cm with 40 lateral A-lines for the phantom study. The selected ROI was divided into 20-wavelength-long data blocks along the axial direction with 90% overlaps (the wavelength was calculated regarding to the second harmonic center frequency, i.e., 4 MHz). Each A-line segment in a given data block was first zero-padded and then Fourier transformed to obtain a single power spectrum. The power spectra of all A-line segments in the given data block were averaged laterally to obtain the mean power spectrum at a certain depth. The frequency power ratio between adjacent frequencies was calculated using Eq. (3). Multiple frequency power ratio (ln[Rs(fi, z)) with respect to each second harmonic frequency component (fi) were averaged within the frequency bandwidth of 3.2 – 4.5 MHz to provide a mean frequency power ratio. At last, linear regression was applied on the linearly decaying portion of the mean frequency power ratio curve for attenuation estimation.

In-vivo Liver Test

For clinical validation, the proposed method was tested on twenty patients, who underwent clinically-indicated magnetic resonance imaging (MRI) of liver (nine males, eleven females; age: 56±10years; body mass indices: 32.4 ±6.3 kg/m2). The study was approved by Institutional Review Board (IRB) of Mayo Clinic. A written informed consent was obtained at the time of enrollment of each participant. All patients were fasted for over 6 hours before scanning. Proton density fat fraction (PDFF) acquired with MRI was used as reference standard (Kinner et al. 2016). The PDFF was measured with MRI scanner GE Optima 450 (General Electric Healthcare, Wauwatosa, WI) using IDEAL IQ sequence. The in-vivo liver ultrasound scans were performed on the same day of MRI-PDFF, using the same GE-LE9 system and C1–6D probe as in phantom study. All other imaging parameters were the same as described above. Other than harmonic imaging, RFM in fundamental imaging (RFM-FI) was also performed for the twenty patients for comparison. For LE9 fundamental mode, 127 A-lines were acquired with the same focal depth at 6.5cm as in HI. The imaging frame rate was 28 Hz with pulse center frequency at around 3 MHz. The frequency range used for RFM-FI was 2.5 – 3.5 MHz.

Construction of 2D Attenuation Coefficient Maps for In-vivo Livers

For in-vivo ACE under both fundamental and harmonic imaging modes, an approximately 5 × 5-cm region of interest (ROI) was first selected for attenuation evaluation at around 4 – 10 cm depth. Laterally, the ROI was positioned in the most uniform liver parenchyma area from the liver right lobe B-mode images. Rib shadow, major vascular structures or cysts were avoided during the ROI selection (Taylor et al. 1986). The selected ROI was then divided into multiple 3 × 3-cm sub-ROIs, with 70% overlap in both lateral and axial directions. ACE analysis was performed within each sub-ROI, following the above steps. The estimated attenuation value was assigned to each pixel inside the corresponding sub-ROI. Then the sub-ROI was translated in both lateral and axial direction to repeat the same ACE process until it covered the entire ROI. The local attenuation coefficient of each pixel was calculated as the average of the all estimated attenuation values obtained from all sub-ROIs covering that pixel. The degree of attenuation was color-coded to form the 2D-ACE map which overlaid on the corresponding B-mode regions. The mean attenuation value of the 2D-ACE map was calculated and displayed in unit of dB/cm/MHz for each measurement. The median attenuation value from the 10 consecutive measurements was used as the final attenuation estimation for each patient. At last, the final attenuation measurements from all patients under fundamental and harmonic imaging were correlated with clinically-indicated MRI-PDFF to evaluate the performance of proposed ACE method under both imaging modes.

Results

Figure 1 shows the mean frequency power curve and mean frequency power ratio curve after taking natural logarithm. Linear regression was applied on the linearly decaying portion of the mean frequency power ratio curve (i.e., 4–10 cm in Figure 1b) and an attenuation coefficient of 0.59 dB/cm/MHz was estimated from the decay slope. The process was repeated on 5 measurements and a mean attenuation coefficient of 0.59 dB/cm/MHz was achieved with a standard deviation of 0.03 dB/cm/MHz. Comparing these five RFM-HI phantom measurements with Toshiba Calibrations, no significant difference was detected using two-tailed t test at a significance level of 5%. Phantom study validated that accurate ACE values can be obtained using RFM under harmonic imaging mode. Note that RFM-HI could not obtain the linear decay trend in the near field of frequency power ratio curve (i.e., < 4cm depth) and this will be discussed in detail in the Discussion section.

Figure 1.

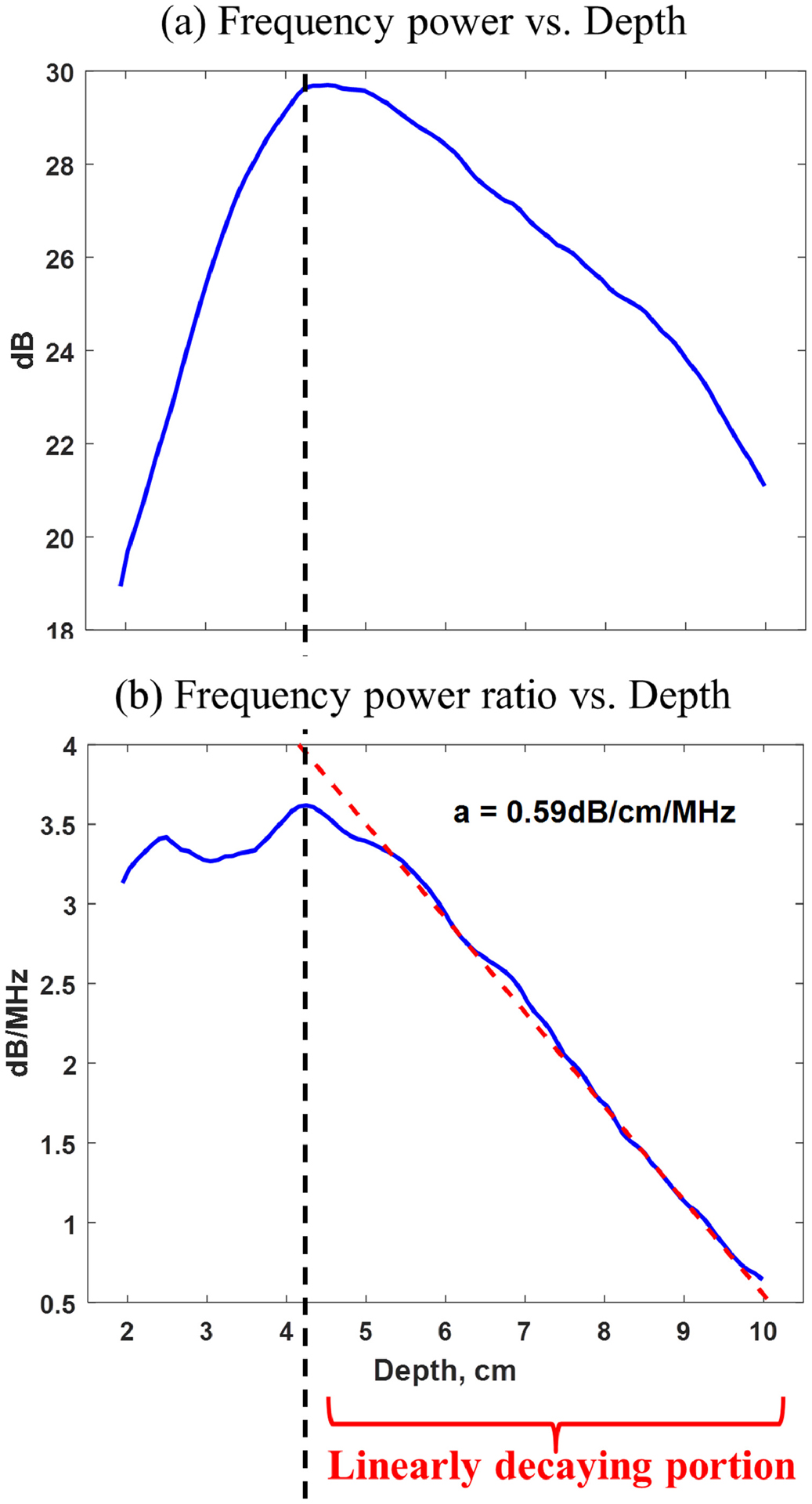
Figure 1.

Open in a new tab

(a) Mean frequency power curve versus depth; (b) Mean frequency power ratio curve versus depth. Linear regression was applied at larger depth of the mean frequency power ratio curve (i.e., 4–10 cm) and an attenuation coefficient of 0.59 dB/cm/MHz was estimated from the decay slope.

Figure 2 shows the representative 2D-ACE maps acquired under both fundamental and harmonic imaging modes from three patients with different MRI-PDFF values. In these cases, RFM-FI and RFM-HI provided similar ACE performances, which both agreed well with the MRI-PDFF, demonstrating the feasibility of RFM in harmonic imaging for in-vivo. The demographic data of all twenty patients are shown in Table 1, including the mean ROI sizes, body wall thicknesses, and median attenuation values from the 10 consecutive measurements under RFM-FI and RFM-HI. The correlation plots of MRI-PDFF versus median ACE estimations are shown in Figure 3. Harmonic RFM shows improved correlation with PDFF values (coefficient of determination, R=0.91, p<0.05), as compared to that in fundamental RFM (R=0.68, p<0.05). A significant difference was detected between these two correlation coefficients using Fisher’s Z-transformation (p<0.05). The improvement demonstrated the robustness and potential of the RFM in harmonic imaging.

Figure 2.

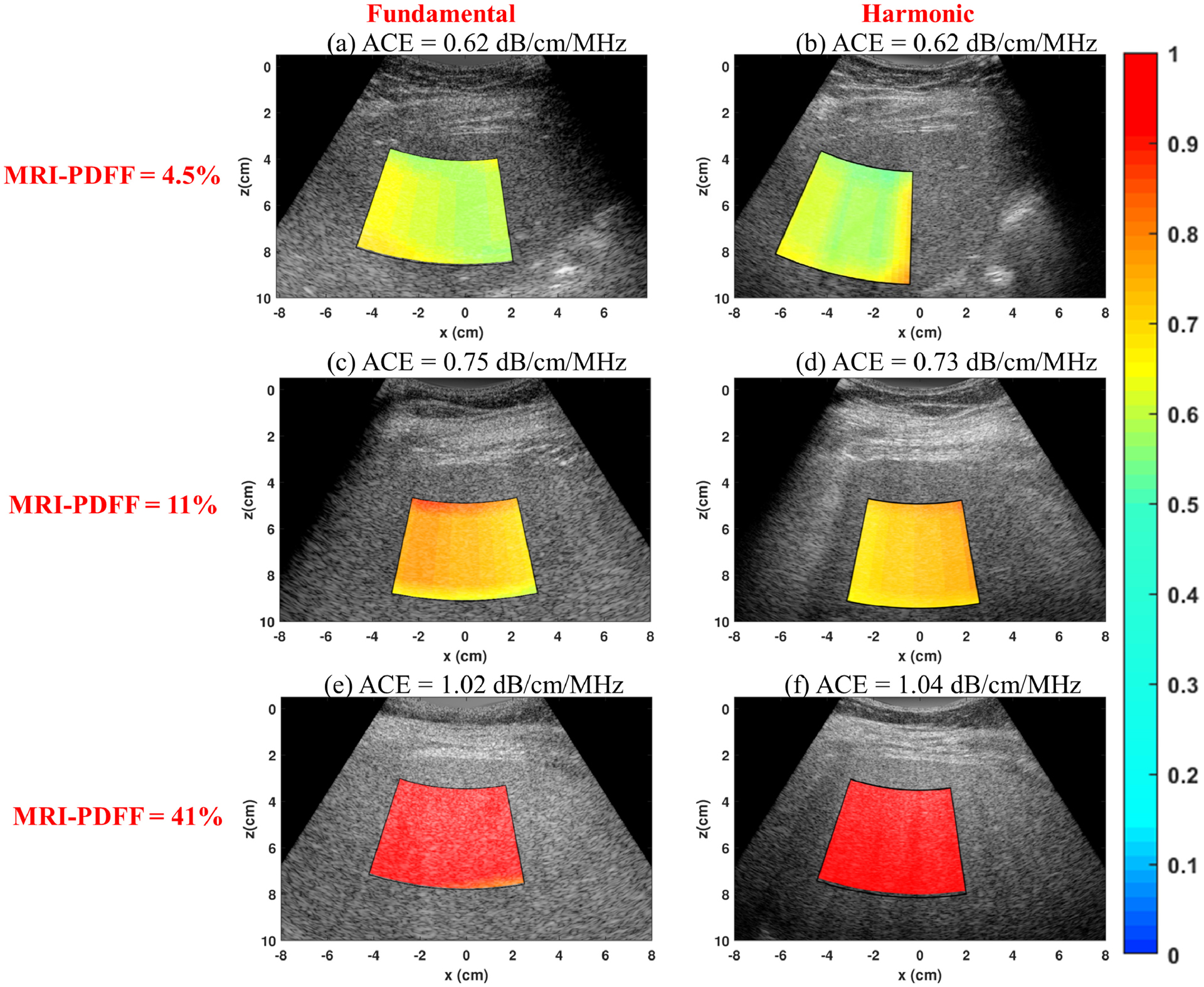
Figure 2.

Open in a new tab

Representative 2D attenuation coefficient maps acquired under both fundamental and harmonic imaging modes from three patients with different proton density fat fraction (PDFF). (a) Fundamental Reference Frequency Method (RFM) image acquired from a patient with PDFF of 4.5%; (b) Harmonic RFM image acquired from a patient with PDFF of 4.5%; (c) Fundamental RFM image acquired from a patient with PDFF of 11%; (d) Harmonic RFM image acquired from a patient with PDFF of 11%; (e) Fundamental RFM image acquired from a patient with PDFF of 41%; (f) Harmonic RFM image acquired from a patient with PDFF of 41%.

Table I.

Patient Demography

Patient No. Sex BMI Age MRI-PDFF ROI size (cm) (lateral×axial) Body wall thickness (cm) ACE-(Fund) ACE-(HI)
1 male 29.2 39 9% 5.5×5.1 2.8 0.64±0.047 0.64±0.029
2 female 34.27 53 15% 5.8×5.3 2.8 0.43±0.027 0.67±0.009
3 female 25.97 57 43% 6.4×4.8 2.2 1.05±0.019 1.01±0.044
4 male 39.21 71 14% 6.0×5.0 2.9 0.75±0.039 0.80±0.032
5 female 38.36 53 3.00% 5.7×4.9 3.2 0.34±0.029 0.55±0.039
6 female 31.29 53 4.50% 5.4×5.4 2.2 0.64±0.024 0.63±0.054
7 male 29.69 47 21% 5.4×6.0 2.0 0.83±0.020 0.89±0.043
8 male 34.92 44 8.50% 5.9×5.4 2.5 0.58±0.034 0.67±0.022
9 male 38.55 51 11% 5.7×5.1 3.3 0.74±0.011 0.74±0.059
10 female 22.7 64 16% 5.9×4.6 2.2 0.61±0.031 0.74±0.021
11 female 27.5 66 8.50% 5.8×5.0 3.1 0.61±0.030 0.72±0.021
12 female 27.82 54 22.50% 5.7×5.2 2.1 0.58±0.056 0.81±0.029
13 female 36.96 42 19% 6.0×5.3 2.5 0.46±0.029 0.74±0.030
14 male 27.85 72 6.50% 6.0×5.5 1.9 0.74±0.028 0.67±0.034
15 male 50.7 61 5% 6.1×5.4 3.5 0.23±0.016 0.53±0.028
16 female 31.49 60 2.50% 5.7×5.4 2.6 0.51±0.057 0.45±0.045
17 male 28.5 63 10.50% 5.7×5.8 2.3 0.64±0.035 0.70±0.037
18 female 33.05 47 8% 5.6×5.6 2.9 0.58±0.051 0.63±0.046
19 male 32.8 50 2.50% 5.5×5.6 2.2 0.51±0.050 0.55±0.036
20 female 27.3 73 31% 5.9×5.0 2.5 0.87±0.051 0.90±0.027
Open in a new tab

Abbreviations: BMI = Body Mass Index; MRI-PDFF = Magnetic resonance imaging proton density fat fraction. ACE = Attenuation coefficient estimation.

Figure 3.

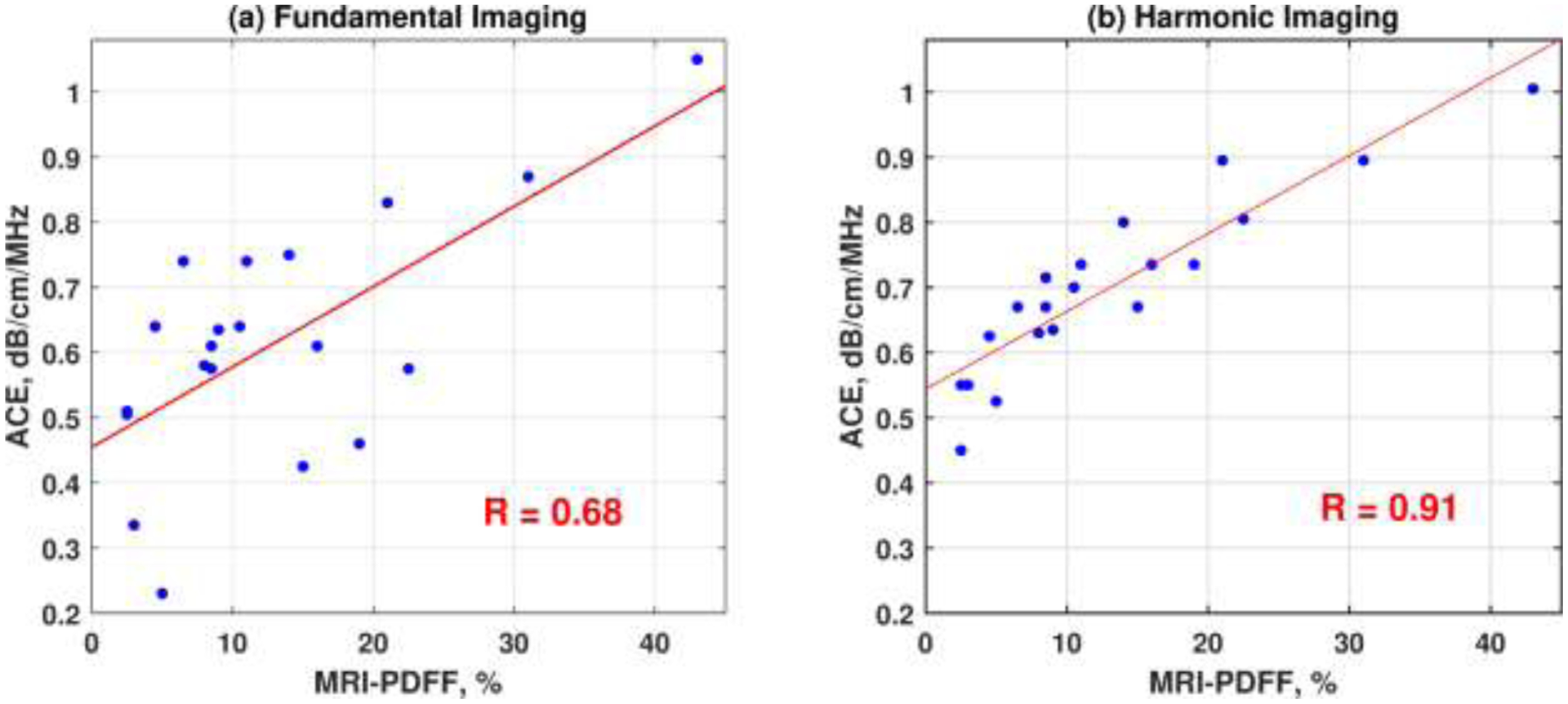
Figure 3.

Open in a new tab

Correlation plots of estimated ultrasound attenuation coefficients versus proton density fat fraction (PDFF) measured with Magnetic Resonance Imaging (MRI) of the eleven patients acquired under both (a) fundamental and (b) harmonic ultrasound imaging.

Discussion

This paper described the process of applying a newly developed system-independent attenuation coefficient estimation technique, reference frequency method (RFM), in harmonic imaging. In this study, we assumed that the differences of harmonic generation between adjacent frequencies can be cancelled out during spectra normalization. The assumption was first validated by a phantom study. We noticed that such assumption was valid and accurate attenuation value could be achieved at larger imaging depth (i.e., >4 cm in Figure 1b) rather than at smaller depth (i.e., <4 cm). This may be because in harmonic imaging, the change of backscattered signal magnitude with depth is a competition between harmonic generation and ultrasound attenuation. At smaller depth region, the generation of second harmonic tended to dominate the magnitude change, leading to violation of the assumption. The second harmonic energy accumulated as ultrasound propagated into the medium and the harmonic echo magnitude slowly built up until it reached the peak. Afterwards, the echo magnitude started to decay at larger depth where ultrasound attenuation played a more significant role (i.e. attenuation dominating region) and the assumption became valid. Correspondingly, the frequency power ratio curve was linearly attenuated in similar depth region and accurate attenuation value could be achieved. We admit that this is a limitation that RFM-HI was unable to provide accurate ACE in the near field where harmonic generation dominated. However, this may not be a critical issue since the first few centimeters of abdominal ultrasound image usually consists of body walls (see Figure 2) which are not suitable for analysis. In addition, the general size of normal human livers are around 13–15 cm in depth in ultrasound image (Riestra-Candelaria, et al. 2016). Consequently, the depth range in harmonic imaging should still be sufficient for ACE. In this study, the attenuation dominating region was experimental determined in phantom to be 4 cm and beyond in depth, which was generally also applicable for patient imaging. Notice that, in Figure 2e and 2f, the ROI was placed in the depth range between 3 and 7 cm. This is because the liver fat content for this patient was very high (PDFF = 43%), leading to high ACE values (>1dB/cm/MHz). Consequently, attenuation started to dominate at a shallower depth in this case as compared to other patients. To avoid noise contamination for signals in deeper imaging regions, the ROI location was shifted upwards by 1 cm to ensure sufficient SNR. Nevertheless, the sweet spot for robust ACE in harmonic imaging generally is around 4 – 10 cm depths where attenuation dominates and SNR is sufficiently high. In future studies, quality control factors such as linear coefficient of determination can be applied to automatically determine the starting point of the linear decay portion on frequency power ratio curve, and thus maximize the available depth range for ACE.

The clinical feasibility of the RFM-HI was demonstrated by a pilot clinical study with twenty patients. Harmonic RFM-HI provided more robust attenuation estimations and better correlation with the MRI-PDFF as compared to fundamental RFM. One possible reason for the enhanced ACE performance in harmonic imaging may be attributed to the suppression of reverberation clutters originated from the body wall. Figure 4 shows fundamental and harmonic ultrasound images of water below a pork belly sample (the pork belly was warmed up to 37°C before imaging). Ideally, the water should have no echoes. However, the fundamental image presented severe reverberation clutters from the pork belly in water (Figure 4a). In practice, such clutters from body wall may superimpose on liver echoes and bias the estimated attenuation values. In the pilot study, the patient body wall thickness showed a strong and significant correlation with patient BMI (r = 0.72, p < 0.05). Therefore, the reverberation issue may exacerbate for the high BMI patients, usually the high-risk group for hepatosteatosis (the mean BMI for patients in the study was 32.4±6.3 kg/m2) (Loomis, Kabadi et al. 2016). As a result, the reliability and accuracy of fundamental ACE may be hindered for these high BMI patients: the residual of each estimated attenuation value with respect to the linear regression line in Figure 3a were calculated as a metric to evaluate the robustness of RFM-FI; A moderate correlation was detected between the fundamental residues and patient BMI (r = 0.66, p < 0.05). However, no significant correlation was detected between the residues in RFM-HI and patient BMI (r = 0.22, p = 0.35). This may be because harmonic imaging can suppress reverberation clutters more effectively than fundamental imaging (see Figure 4). Consequently, harmonic imaging may play a more important role for high BMI patients when reverberation clutter is high. More extensive clinical studies with larger patient sample sizes are needed in the future to assess the full capability of RFM in harmonic imaging for fatty liver screening and monitoring. The reverberation artifacts in fundamental imaging may be reduced by rotating the probe to increase the angle between transducer surface and liver capsule during ultrasound scanning as suggested in (Dahl and Sheth 2014). However, this may increase the scanning difficulty and introduce rib shadowing effects or coupling issues.

Figure 4.

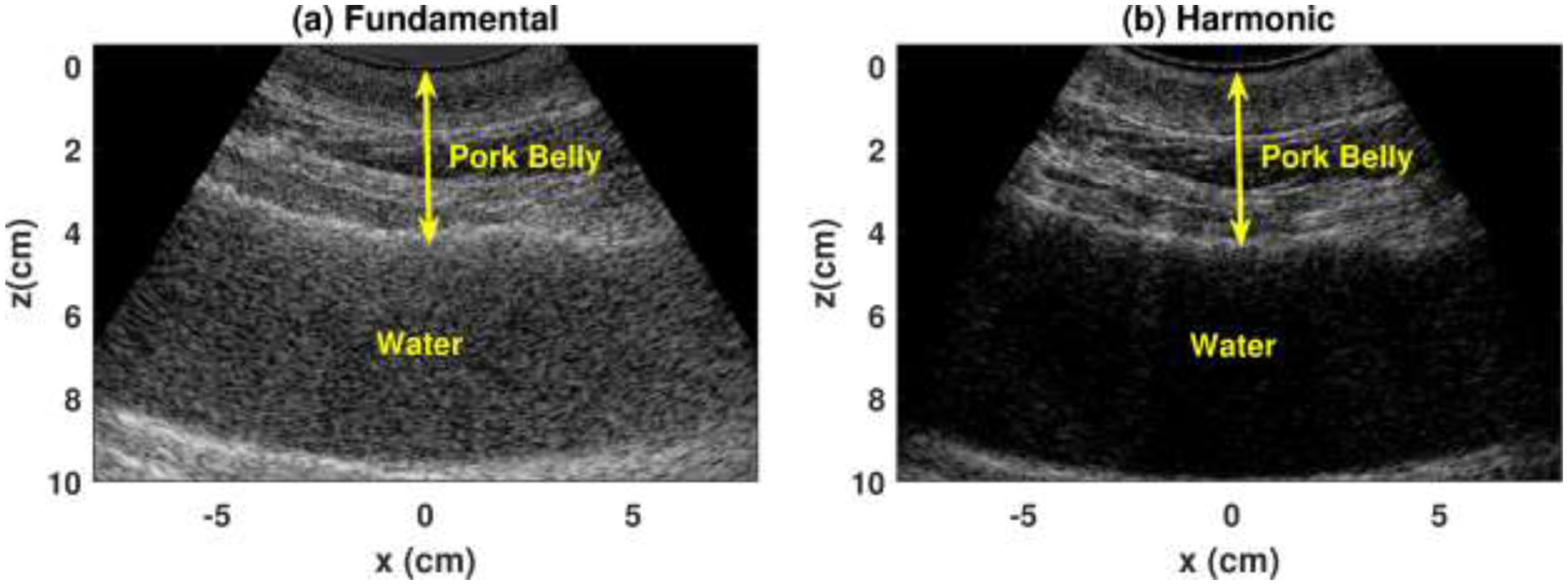
Figure 4.

Open in a new tab

Ultrasound images of water below a pork belly in (a) fundamental and (b) harmonic mode.

As mentioned above, one concern of RFM-HI is the ultrasound penetration. With new single crystal transducers and scanner hardware, penetration of ultrasound imaging has improved significantly. The high BMI values of the pilot patient study also reveal the feasibility of harmonic RFM in difficult-to-image patients. Moreover, extensive studies have been performed to improve the signal-to-noise ratio (SNR) of ultrasound images, such as using multi-focuses or multiple transmit beams (Tong et al. 2014). The delay-encoded harmonic imaging technique as described in (Gong et al. 2017) could also be considered to mitigate the penetration issue and facilitate reliable ACE with harmonic imaging. The robustness of the proposed harmonic RFM technique is expected to be further improved after combination with these SNR-improving techniques. In addition, noise cancellation strategies can also be investigated to further suppress the noise influence on harmonic RFM analysis (Huang et al. 2019).

The ROI size used in the study is relatively large (mean ROI size for all patients enrolled in the study: 5.3cm [min: 4.6cm, max: 6.0cm] × 5.8cm [min: 5.4cm, max: 6.4cm]). The ROI size selection was a tradeoff among ACE resolution, measurement accuracy and computational cost. From this study, a general ROI size can be suggested as 5 – 6 cm in both lateral and axial dimensions, which offered a robust solution to estimate mean attenuation coefficient of relatively uniform tissues such as liver parenchyma. However, RFM may not be suitable to detect local attenuation variations for heterogeneous tissues. This may be partly due to the low transmit frequencies of curved arrays, which has larger wavelength and thus requires large sub-ROI for ACE. For measuring and monitoring ACE in other tissues, such as breast, a linear array probe with higher transmit frequencies can be used for smaller sub-ROI to detect local ACE changes.

The acquisition and post-processing time for RFM was a little longer as compared to the ATI real time examination. The time it took for RFM IQ data storage using the RF Capture module on LE9 system and IQ data off-line processing on a HP EliteDesk 800 G4 computer using Matlab R2018b software were around 2 seconds and 1 second, respectively. However, the ACE process for each sub-ROI is independent, which makes it amendable to parallel programming. Therefore, further optimization can be performed to speed up the RFM process for easier clinical application.

Conclusion

In this paper, we proposed to apply a new reference-phantom-free ACE method, reference frequency method (RFM), in harmonic imaging. Harmonic RFM provided accurate and more robust attenuation estimation in phantom and in in-vivo liver studies as compared to fundamental RFM. The enhancement demonstrated the feasibility and potential of harmonic RFM in liver steatosis detection, especially for large BMI patients.

Acknowledgement

The authors are grateful to Ms. Jill Weston for her efforts in patient recruitment. The study was partially supported by the National Institute of Diabetes and Digestive and Kidney Diseases under Award Numbers R21DK121943 and R01DK106957.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Bigelow TA, McFarlin BL, O’Brien WD, Oelze ML. In vivo ultrasonic attenuation slope estimates for detecting cervical ripening in rats: Preliminary results. J Acoust Soc Am. 2008;123(3):1794–800. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Canellas R, Rosenkrantz AB, Taouli B, Sala E, Saini S, Pedrosa I, Wang ZJ, Sahani DV. Abbreviated MRI Protocols for the Abdomen. Radiographics. 2019;39(3): 744–758. [DOI] [PubMed] [Google Scholar]
  3. Coila AL, Lavarello R. Regularized spectral log difference technique for ultrasonic attenuation imaging. IEEE Trans Ultrason Ferroelectr Freq Control. 2018;65(3):378–89. [DOI] [PubMed] [Google Scholar]
  4. Dahl JJ, Sheth NM. Reverberation clutter from subcutaneous tissue layers: Simulation and in vivo demonstrations. Ultrasound Med Biol. 2014;40(4): 714–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Dasarathy S, Dasarathy J, Khiyami A, Joseph R, Lopez R, McCullough AJ. Validity of real time ultrasound in the diagnosis of hepatic steatosis: a prospective study. J Hepatol. 2009;51(6):1061–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Gong P, Song P, Chen S. Delay-Encoded Harmonic Imaging (DE-HI) in Multiplane-Wave Compounding. IEEE Trans Med Imaging. 2017;36(4):952–9. [DOI] [PubMed] [Google Scholar]
  7. Gong P, Song P, Huang C, Trzasko J, Chen S. System-independent ultrasound attenuation coefficient estimation using spectra normalization. IEEE Trans Ultrason Ferroelectr Freq Control. 2019;66(5):867–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Huang C, Song P, Gong P, Trzasko JD, Manduca A, Chen S. Debiasing-based Noise Suppression for Ultrafast Ultrasound Microvessel Imaging. IEEE Trans Ultrason Ferroelectr Freq Control. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Jeon SK, Lee JM, Joo I, Yoon JH, Lee DH, Lee JY, Han JK. Prospective Evaluation of Hepatic Steatosis Using Ultrasound Attenuation Imaging in Patients with Chronic Liver Disease with Magnetic Resonance Imaging Proton Density Fat Fraction as the Reference Standard. Ultrasound Med Biol. 2019;45(6):1407–16. [DOI] [PubMed] [Google Scholar]
  10. Karlas T, Petroff D, Sasso M, Fan JG, Mi YQ, de Ledinghen V, Kumar M, Lupsor-Platon M, Han KH, Cardoso AC, Ferraioli G, Chan WK, Wong VW, Myers RP, Chayama K, Friedrich-Rust M, Beaugrand M, Shen F, Hiriart JB, Sarin SK, Badea R, Jung KS, Marcellin P, Filice C, Mahadeva S, Wong GL, Crotty P, Masaki K, Bojunga J, Bedossa P, Keim V, Wiegand J. Individual patient data meta-analysis of controlled attenuation parameter (CAP) technology for assessing steatosis. J Hepatol. 2017;66(5):1022–30. [DOI] [PubMed] [Google Scholar]
  11. Kim H, Varghese T. Hybrid Spectral Domain Method For Attenuation Slope Estimation. Ultrasound Med Biol. 2008;34(11):1808–19. [DOI] [PubMed] [Google Scholar]
  12. Kinner S, Reeder SB, Yokoo T. Quantitative Imaging Biomarkers of NAFLD. Digest Dis Sci. 2016;61(5):1337–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Krishnan KB, Nagaraj N, Singhal N, Thapar S, Yadav K. A Two-Parameter Model for Ultrasonic Tissue Characterization with Harmonic Imaging. arXiv preprint arXiv:171203495. 2017. [Google Scholar]
  14. Kuc R Clinical application of an ultrasound attenuation coefficient estimation technique for liver pathology characterization. IEEE Trans Biomed Eng. 1980(6):312–9. [DOI] [PubMed] [Google Scholar]
  15. Kuc R, Li H. Reduced-order Autoregressive Modeling for Center-frequency Estimation. Ultrason Imaging. 1985;7(3):244–51. [DOI] [PubMed] [Google Scholar]
  16. Kuc R, Schwartz M. Estimating the acoustic attenuation coefficient slope for liver from reflected ultrasound signals. IEEE Trans Sonics Ultrason. 1979;26(5):353–61. [Google Scholar]
  17. Lawrence DA, Oliva IB, Israel GM. Detection of hepatic steatosis on contrast-enhanced CT images: diagnostic accuracy of identification of areas of presumed focal fatty sparing. AJR Am J Roentgenol. 2012;199(1):44–7. [DOI] [PubMed] [Google Scholar]
  18. Lin T, Ophir J, Potter G. Correlation of Ultrasonic-Attenuation with Pathologic Fat and Fibrosis in Liver-disease. Ultrason Imaging. 1988;10(1):59–59. [DOI] [PubMed] [Google Scholar]
  19. Loomis AK, Kabadi S, Preiss D, Hyde C, Bonato V, St. Louis M, Desai J, Gill JM, Welsh P, Waterworth D, Sattar N. Body mass index and risk of nonalcoholic fatty liver disease: two electronic health record prospective studies. The Journal of Clinical Endocrinology & Metabolism. 2016;101(3):945–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. L Lu ZF, Zagzebski JA, Lee FT. Ultrasound backscatter and attenuation in human liver with diffuse disease. Ultrasound Med Biol. 1999;25(7):1047–54. [DOI] [PubMed] [Google Scholar]
  21. Machado MV, Cortez-Pinto H. Non-invasive diagnosis of non-alcoholic fatty liver disease. A critical appraisal. J Hepatol. 2013;58(5):1007–19. [DOI] [PubMed] [Google Scholar]
  22. Marchesini G, Day CP, Dufour JF, Canbay A, Nobili V, Ratziu V, Tilg H, Roden M, Gastaldelli A, Yki-Jarvinen H, Schick F, Vettor R, Fruhbeck G, Mathus-Vliegen L. EASL-EASD-EASO Clinical Practice Guidelines for the management of non-alcoholic fatty liver disease. J Hepatol. 2016;64(6):1388–402. [DOI] [PubMed] [Google Scholar]
  23. Nam K, Zagzebski JA, Hally TJ. Simultaneous Backscatter And Attenuation Estimation Using A Least Squares Method With Constraints. Ultrasound Med Biol. 2011;37(12):2096–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Obika M, Noguchi H. Diagnosis and Evaluation of Nonalcoholic Fatty Liver Disease. Exp Diabetes Res. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Parker KJ, Lerner RM, Waag RC. Comparison of techniques for in vivo attenuation measurements. IEEE Trans Biomed Eng. 1988;35(12):1064–8. [DOI] [PubMed] [Google Scholar]
  26. Parker KJ, Waag RC. Measurement of ultrasonic attenuation within regions selected from B-scan images. IEEE Trans Biomed Eng. 1983(8):431–7. [DOI] [PubMed] [Google Scholar]
  27. Riestra-Candelaria BL, Rodríguez-Mojica W, Vázquez-Quiñones LE, Jorge JC. Ultrasound accuracy of liver length measurement with cadaveric specimens. J Diagn Med Sonogr. 2016;32(1):12–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Rinella ME. Nonalcoholic Fatty Liver Disease A Systematic Review. Jama-J Am Med Assoc. 2015;313(22):2263–73. [DOI] [PubMed] [Google Scholar]
  29. Samimi K, Varghese T. Performance Evaluation of the Spectral Centroid Downshift Method for Attenuation Estimation. IEEE Trans Ultrason Ferroelectr Freq Control. 2015;62(5):871–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Samimi K, Varghese T. Optimum Diffraction-Corrected Frequency-Shift Estimator of the Ultrasonic Attenuation Coefficient. IEEE Trans Ultrason Ferroelectr Freq Control. 2016;63(5):691–702. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Sasso M, Beaugrand M, de Ledinghen V, Douvin C, Marcellin P, Poupon R, Sandrin L, Miette V. Controlled Attenuation Parameter (CAP): A Novel VCTE (TM) Guided Ultrasonic Attenuation Measurement For The Evaluation of Hepatic Steatosis: Preliminary Study and Validation in A Cohort of Patients With Chronic Liver Disease From Various Causes. Ultrasound Med Biol. 2010;36(11):1825–35. [DOI] [PubMed] [Google Scholar]
  32. Taylor KJW, Riely CA, Hammers L, Flax S, Weltin G, Garciatsao G, Conn HO, Kuc R, Barwick KW. Quantitative US Attenuation in Normal Liver and in Patients with Diffuse Liver-Disease - Importance of Fat. Radiology. 1986;160(1):65–71. [DOI] [PubMed] [Google Scholar]
  33. Tong L, Ramalli A, Jasaityte R, Tortoli P, D’Hooge J. Multi-Transmit Beam Forming for Fast Cardiac Imaging-Experimental Validation and In Vivo Application. IEEE Trans Med Imaging. 2014;33(6):1205–19. [DOI] [PubMed] [Google Scholar]
  34. Yao LX, Zagzebski JA, Madsen EL. Backscatter Coefficient Measurements Using a Reference Phantom to Extract Depth-Dependent Instrumentation Factors. Ultrason Imaging. 1990;12(1):58–70. [DOI] [PubMed] [Google Scholar]

RESOURCES