Abstract
Husk has multiple functions such as protecting ears from diseases, infection, and dehydration during development. Additionally, husks comprised of fewer, shorter, thinner, and narrower layers allow faster moisture evaporation of kernels prior to harvest. Intensive studies have been conducted to identify appropriate husk architecture by understanding the genetic basis of related traits, including husk length, husk layer number, husk thickness, and husk width. However, marker-assisted selection is inefficient because the identified quantitative trait loci and associated genetic loci could only explain a small proportion of total phenotypic variation. Genomic selection (GS) has been used successfully on many species including maize on other traits. Thus, the potential of using GS for husk traits to directly identify superior inbred lines, without knowing the specific underlying genetic loci, is well worth exploring. In this study, we compared four GS models on a maize association population with 498 inbred lines belonging to four subpopulations, including 27 lines in stiff stalk, 67 lines in non-stiff stalk, 193 lines in tropical-subtropical, and 211 lines in mixture subpopulations. Genomic Best Linear Unbiased Prediction with principal components as cofactor, performed the best and was selected to examine the impact of interaction between sampling proportions and subpopulations. We found that predictions on inbred lines in a subpopulation were benefited from excluding individuals from other subpopulations for training if the training population within the subpopulation was large enough. Husk thickness exhibited the highest prediction accuracy among all husk traits. These results gave strategic insight to improve husk architecture.
Keywords: genomic selection, husk, population structure, prediction accuracy, maize, gBLUP, marker assisted selection, breeding, rrBLUP, GAPIT, GenPred, Genomic, Prediction, Shared data resources
The husk is a leaf-like tissue covering the outside of a maize ear. Similar to rice and coconut husks (Ali 2011; Ding et al. 2012; Johar et al. 2012), maize husks recycle anthocyanins and provide fiber for secondary uses such as bioethanol production(Li et al. 2008; Jalil et al. 2012; Ekhuemelo and Tor 2013). More specifically, the maize husk performs three major physiological functions. First, the husk performs limited photosynthesis to provide carbon with a C4-like pathway(Pengelly et al. 2011; Wang et al. 2013). Second, the husk protects the ear from pest damage and pathogen infection(Barry et al. 1986; Warfield and Davis 1996; Demissie et al. 2008). Particularly, in subtropical or tropical areas, ear rot is a serious issue during maize ear development (Renfro and Ullstrup 1976; Afolabi et al. 2007). Tight-husked maize is more resistant to ear rot than loose-husked maize(Warfield and Davis 1996). Third, the husk prevents moisture from penetrating the maize ear before harvest time(Sweeney et al. 1994). After physiological maturation of maize kernels, the husk is the main pathway for kernel dehydration. In temperate areas, the timing of mechanical harvest requires fast dehydration of maize during colder weather(Hicks et al. 1976). Thus, appropriate husk architecture is essential to both ear development and kernel dehydration prior to harvest.
Although much morphological and genetic research of the maize husk has been conducted during the past decades, molecular breeding studies of husk traits are still in their infancy. Husk development initiates from the lateral meristem(Wang et al. 2013). The main traits that influence the level of husk function are husk length (HL), layer number (HN), thickness (HT) and width (HW). HN typically ranges from 6 to 19 in hybrids and inbreds(Brewbaker and Kim 1979). HN is highly correlated to tassel branch number(Brewbaker 2015). The variance in husk traits is large across both natural populations and recombinant inbred lines (RIL) (Brewbaker and Kim 1979; Zhou et al. 2016a; Cui et al. 2016, 2018). The husk traits are genetically controlled by multiple genes. In our recent study(Cui et al. 2018), we dissected the genetic architecture of HL, HN, and HW across three RIL populations. We detected a total of 21 quantitative trait loci (QTL) associated with the three husk traits. In most cases, the associations included one or two large-effect QTL plus many small-effect QTL. In another previous study in a maize association inbred population, we detected 63 single nucleotide polymorphisms (SNPs) by genome-wide association study(GWAS) that were significantly associated with HL, HN, HT, and HW (P < 1.04×10−5)(Cui et al. 2016). However, none of these SNPs passed the classic, standard threshold of α = 0.01 after Bonferroni correction(Holm 1979). Similarly, another GWAS of HN and husk weight did not find any associated loci under the same threshold(Zhou et al. 2016a). Based on the evidence above, husk traits are complex and governed by many genes, most with small effects which are hard to detect through GWAS. Consequently, molecular breeding using traditional marker-assisted selection (MAS) is inefficient for these polygenic, complex traits because MAS works best with QTL that have large or moderate effects(Collard and Mackill 2008; Hayes et al. 2009).
Genomic selection (GS) was developed in 1990s (Bernardo 1994) based on mixed linear model and expanded to Bayesian framework in 2000s (Meuwissen et al. 2001). Genotyping cost reduction due to newly developed molecular technologies made GS more affordable for breeding(Zhang et al. 2007; VanRaden 2008). GS is efficient in improving polygenic traits controlled by small-effect genetic loci, such as animal body size(VanRaden et al. 2009; Chesnais et al. 2016; Mehrban et al. 2017) and plant yield(Crossa et al. 2013, 2014). GS incorporates all marker effects across the whole genome to evaluate genomic estimated breeding values (GEBVs). With a training set that includes both genotypic and phenotypic data, a prediction model is “trained” to calculate GEBVs for the validation set (also called the testing set). GS was introduced in 1994 in format of the genomic Best Linear Unbiased Prediction (gBLUP) and maize was used for the demonstration. One study in a bi-parental maize population found that estimates of stover and grain yield using GS were 14–50% higher than with MAS(Massman et al. 2013). Another study in a multi-parental maize population found that GS achieved genetic gains of ∼2% for grain yield with two rapid cycles per year(Zhang et al. 2017a).
Prediction accuracy, defined as the correlation between the observed and predicted breeding values, is commonly used to assess the efficiency of GS(Combs and Bernardo 2013).Prediction accuracy in plant breeding is dependent on statistical models used(Heffner et al. 2009; Ogutu et al. 2011; Spindel et al. 2015), training population size(Heffner et al. 2011), the relationship between the training and testing populations(Ly et al. 2013), marker density(Zhang et al. 2017b), rate of linkage disequilibrium decay(Calus and Veerkamp 2007), and trait heritability(Dong et al. 2018). Trait heritability can be defined as broad-sense or narrow-sense. Broad-sense heritability includes all genetic contributions, including additive, dominant, and epistatic effects. Narrow-sense heritability includes only additive effects, which is more important for breeding with selection based on additive effects(Holland et al. 2010).
Population structure is also considered an essential factor influencing prediction accuracy(Ly et al. 2013; Guo et al. 2014). Several strategies have been compared to handle population structure in GS. One cassava study evaluated prediction accuracy by comparing cross-validation with close relatives (CV-CR) to cross-validation without close relatives (Ly et al. 2013). In a similar comparison on a maize association panel, three strategies were evaluated: within subpopulations, across subpopulations, and combined subpopulations(Guo et al. 2014). The closer genetic relationship among individuals of CV-CR and individuals within subpopulations have closer genetic relationships led to higher prediction accuracy.
Maize has a strong population structure, typically classified as Stiff Stalk (SS), Non-Stiff Stalk (NSS), Tropical-SubTropical (TST), and MIXED (MIXED) subpopulations. Our objectives are 1) to demonstrate that MAS is less favorite for prediction on husk traits, 2) to model population structure appropriately to increase prediction accuracy, and 3) to investigate the interactions between training population size and subpopulations. The results are expected to provide the inside to improve husk traits through GS, especially to make a strategic plan for selecting traits and establishing training populations across subpopulations.
Materials And Methods
Plant materials and husk trait observations
The maize association panel used in this study is comprised of 508 inbred lines, which were collected from tropical, subtropical, and temperate germplasms(Yang et al. 2011; Li et al. 2012). Due to germination issues, only 498 lines were measured in this experiment. These inbred lines were categorized into four subpopulations based on origins: 27 SS lines, 67 NSS lines, 193 TST lines, and remaining 211 MIXED lines. Detailed information about this panel is listed in supplemental material (Table S4).
All the lines were planted as single row plots with three replications using a randomized complete block design in two locations in China: Sanya (SY) city of Hainan (HN) province in southern China in 2013 and Beijing (BJ) city in northern China in 2014. All plants were grown under open-pollination conditions. Four traits, HN, HL, HT, and HW, were measured at the maturity stage from at least six well-pollinated plants in each row in both locations. HN was counted from the first (outer) layer of each husk to the last layer (inner). HL was measured on the third layer of each husk (counting from the outside to inside). HW was measured at the midpoint of the third layer of each husk. HT was measured as total thickness by punching a disc from the interior to the exterior of all husk layers. Husk phenotype data are listed in supplemental material (Table S4). Detailed husk measurement information is provided in the previous study (Cui et al. 2016). Mean trait values of all replications were calculated across all environments. We used mean values instead of BLUPs for two reasons. One is that mean values and BLUPs are similar in balanced data. The other is to avoid contamination of using information from testing population. (Dong et al. 2018).
Genotypic markers
Genotypic markers for the 508 lines were downloaded from the website of www.maizego.org/Resources, with the download link: https://pan.baidu.com/s/1mhR1L1Y#list/path=%2F. The genetic markers came from four genotyping platforms: the Illumina Maize SNP50 array, RNA sequencing, reduced genome sequencing (GBS), and the Affymetrix Axiom Maize 600K array. It took three steps to merge all SNP markers for each platform. First, Yang et al. (2014)(Yang et al. 2014) combined the 56,110 SNPs from the SNP array and the 556,809 SNPs from RNA sequencing(Fu et al. 2013), using identity by descent based projection and the k-nearest neighbor algorithm. Second, Liu et al. (2017)(Liu et al. 2017) conducted SNP allele calling by GBS and the 600K SNP array. The missing genotypes were imputed by Beagle v4.0(Browning and Browning 2007). Third, quality control was applied to remove SNPs with minor allele frequencies below 5%. The final dataset was composed of ∼1.25 M SNPs.
Estimates of heritability, genomic breeding values, and genomic selection
The four husk traits were analyzed one at a time for each environment and their mean values across environments separately in a fixed and random effects mixed linear model. The first three principal components (PCs) derived from all markers were fitted as fixed effects. The additive genetic effects of individuals and the residuals were fitted as random effects. The statistical model is as follows:
| (1) |
where y is a vector (n*1) of observations, and n is the number of lines; μ is the overall mean; β is a vector (p*1) of fixed effects; u is a vector (n*1) of random effects representing additive genetic effects of individuals; X is a design matrix (n*p) for fixed effects, so p equals 3 when the first three PCs were used as cofactors; Z is a design matrix (n*n) for random line effects, so Z is the identity matrix; and ε is the residuals. The random effects followed normal distributions: u ∼ N(0, Kσu2) and ε ∼ N(0, Iσe2), where I is the identity matrix and K is the additive relationship matrix (n*n) derived from all the markers using Zhang algorithm in GAPIT(Lipka et al. 2012). σu2 is the variance of individual additive genetic effects, and σe2 is the variance of residuals. The estimation of u is the estimated genomic breeding values. The proportion of σu2 over the total variance (σu2 + σe2) was defined as the estimate of heritability. The analyses was conducted by using the R software packages, GAPIT(Lipka et al. 2012; Tang et al. 2016). The phenotypes and genotypes of all individuals were used in the analyses to estimate heritabilities and genomic breeding values. The model was also used as genomic selection with the whole population divided into training and testing populations.
Model selection
Four models were evaluated for accuracy of prediction. The evaluations were conducted by randomly sampling 20% of whole population as testing population and the rest as training population. The first model is a MAS. GWAS were conducted in the training population using BLINK, a software implemented in C language (Huang et al. 2018). The top ten most significant associated SNPs, named as quantitative trait nucleotide (QTNs) were used to predict the breeding values for the individuals in the testing population(Guo et al. 2011); The second model is a fixed effect model containing the first three PCs derived from all SNPs. The effects of the PCs were estimated in the training population. The estimated effects were used to predict the breeding values of individuals in the testing population. The third model is a random effect mixed model containing the additive genetic effect of the individuals with variance structure defined by the kinship matrix derived from all SNPs. All individuals in both training and testing populations were included in the analyses. However, the phenotypes of the individuals from the testing population were masked by setting them as “NA”. Breeding values were estimated for all individuals. This model is commonly referred as genomic Best Linear Unbiased Prediction (gBLUP). The fourth model is a combination of the second and third in the format of fixed and random effects mixed linear model. The analyses of gBLUP were conducted using R package “rrBLUP v4.5”(Endelman 2011). Pearson correlation coefficient was calculated between observed and predicted phenotypes. The random sampling was replicated 20 times.
Assessment of gBLUP accuracy
The objective of the assessment was to evaluate the impact of training population size and relationship between training and testing populations on prediction accuracy using gBLUP model. Cross validations were performed under three scenarios: 1) Subpopulations ignored, where 10–90% of individuals from the whole population were randomly selected as the testing population, with the remaining individuals as the training population; 2) prediction within subpopulations, where 10–90% of one subpopulation were randomly selected treated as the testing set, with the remaining individuals of this same subpopulation as the training population; and 3) prediction across subpopulations, where 10–90% of individuals from one subpopulation were randomly selected as the testing population, with the remaining individuals of this subpopulation and the other subpopulations as the training population. Prediction accuracy was calculated as the Pearson correlation coefficient between predicted values and true values of the testing population. Sampling were repeated 100 times for each scenario.
Data availability
All phenotypic data and results data are included within the manuscript in supplementary. The genotypes (∼1.25M) used in this study are all publicly available at the website of Jianbing Yan (http://www.maizego.org/Resources.html), or through the direct download link (https://pan.baidu.com/s/1mhR1L1Y#list/path=%2F). Supplemental material available at figshare: https://doi.org/10.25387/g3.11829177.
Results
Husk trait heritability and phenotypic correlation
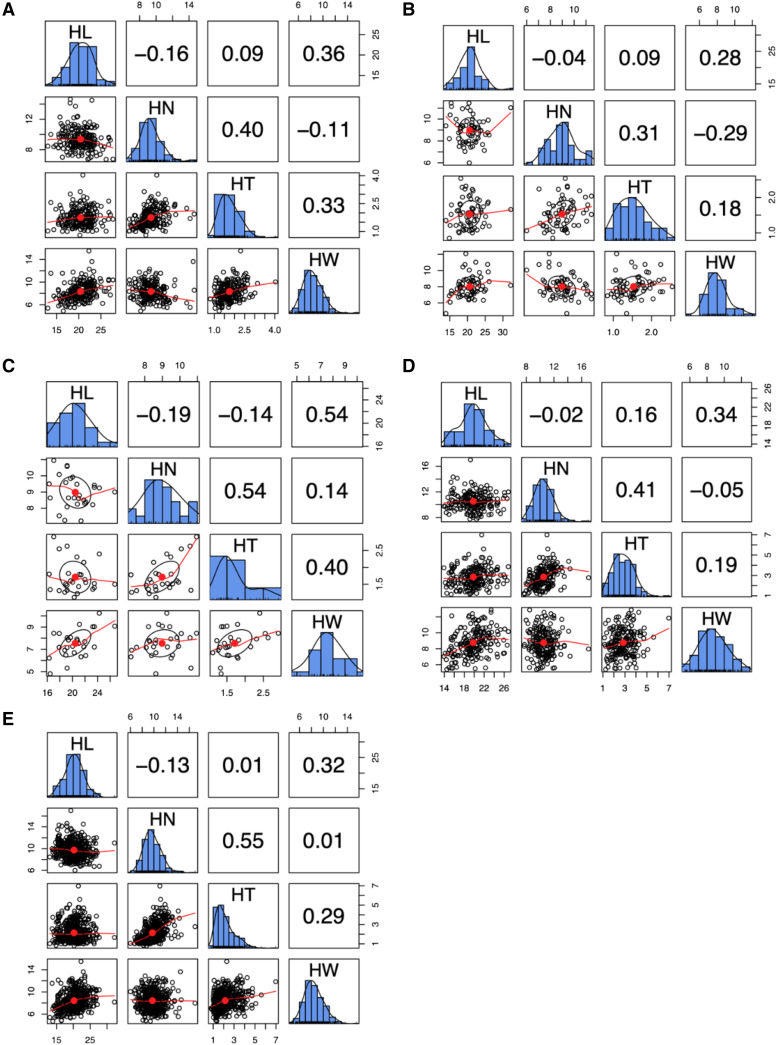
All husk traits in the whole association populations or each subpopulation showed continuous and approximately normal distributions (Figure 1). In each subpopulation, HN and HT showed the highest correlation and the second were HL and HW. Within subpopulation, the highest correlation (r = 0.54) appeared in SS between HN and HT. The Estimated genomic breeding values followed the same trend (Figure S1).
Figure 1.
Phenotypic correlation and frequency distributions of four husk traits in different subpopulations. (A) Admixed (MIXED) subpopulation. (B) Non-stiff stalk (NSS) subpopulation. (C) Stiff stalk (SS) subpopulation. (D) Tropical-subtropical (TST) subpopulation. (E) Whole association panel. The husk traits are husk length (HL), husk layer number (HN), husk thickness (HT), and husk width (HW). The unit of measure is cm for HL, HT, and HW.The plots on the diagonal line exhibit the phenotypic distribution of the mean value for each husk trait. Displayed below the diagonal line, are the scatter plots for mean value of each two husk traits; displayed above the diagonal line are Pearson correlation coefficients. The red line and red dot represent the lowest regression fitting curve and the correlation ellipse, respectively.
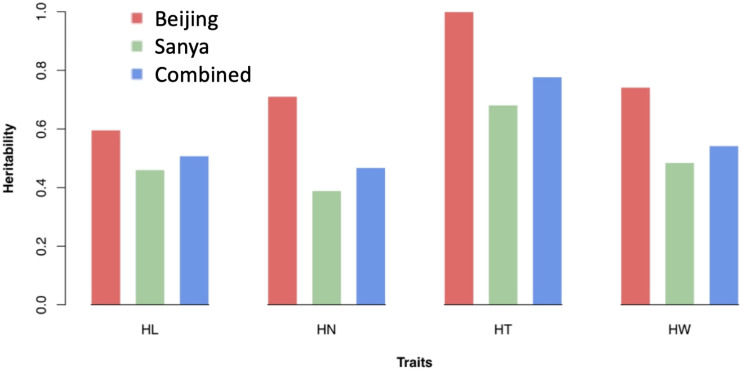
The narrow-sense heritability of husk traits was evaluated in two different locations separately and combined. In addition to residual effects, random effects are the individual total additive genetic effects with variance structure defined by an additive relationship matrix. All the husk traits showed higher heritability in Beijing than Sanya (Figure 2). The heritability of husk traits in Beijing ranged from 0.60 (HL) to 0.99 (HT). The heritability of husk traits in Sanya ranged from 0.39 (HN) to 0.68 (HT). The heritability of the combined locations ranged from 0.47 (HN) to 0.78 (HT). At each location, HT exhibited the highest heritability, ranging from 0.68 to 0.99.
Figure 2.
Heritability estimates of husk traits in two locations and combined. HL = husk length, HN = husk layer number, HT = husk thickness, and HW = husk width.
Model selection
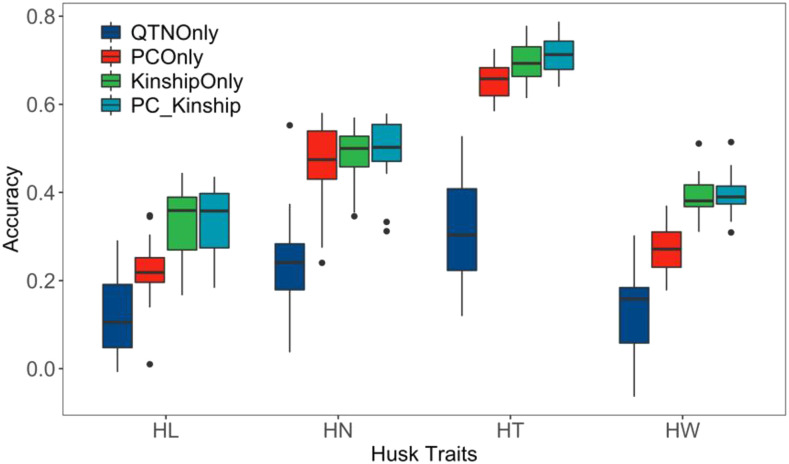
The association panel of 498 inbred lines has a strong population structure with four subpopulations. It was reasonable to have concerns if major associated SNPs or principal components would be close to sophisticated models such as gBLUP. Four models were compared: 1) MAS with the top ten associated SNPs; 2) PCs only; 3) Kinship only, and 4) PCs + Kinship. The results suggested MAS was far less accurate. PCs only were not as good as models with kinship. Kinship with PCs performed better than kinship across traits. The exception was HL, where the two models were similar (Figure 3). The results suggested that incorporating population structure only was not enough for prediction.
Figure 3.
Comparison among four models to predict four husk traits. The comparisons were conducted in a population with 498 maize inbred lines by randomly sampling 20% of whole population as testing population and the rest as training population. The sampling was conducted 20 times. The models include 1) MAS using the top ten associated markers (QTNs) only; 2) Using PCs only; 3) Using kinship only; and 4) Using both PCs and kinship.
Cross-validation by random sampling across whole population
We randomly masked 10–90% of all lines as the testing population (inference) and treated the remaining lines as the training population (reference, or validation). Prediction accuracy was computed as the Pearson correlation coefficient between the predicted and the observed phenotypes in the testing population using the instant method(Zhou et al. 2016b).
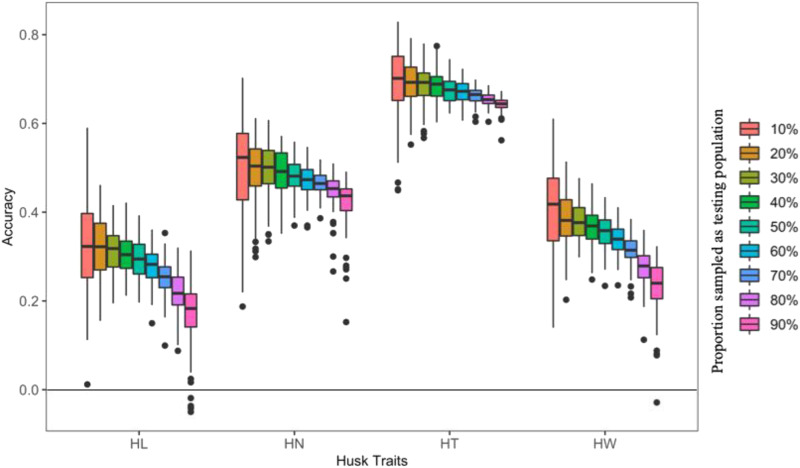
HT and HL exhibited the highest and lowest prediction accuracy, respectively (Figure 4 and Table S1). In order from highest to lowest, the prediction accuracies for the four traits were HT > HN > HW > HL. In general, prediction accuracy declined as the proportion of inference increased for each husk trait. For HT, however, this decline was minimal, only decrease 7.3% from the highest and to the lowest. This may be because its heritability was higher in each environment compared to the other traits.
Figure 4.
Accuracies to predict proportion of inbreds using the rest as training population. There are 498 maize inbred lines in total. Part of the lines (10–90%) were randomly sampled as the testing population and the rest as the training population. The sampling was conducted 100 times. HL = husk length, HN = husk layer number, HT = husk thickness, and HW = husk width.
Cross validation within subpopulations
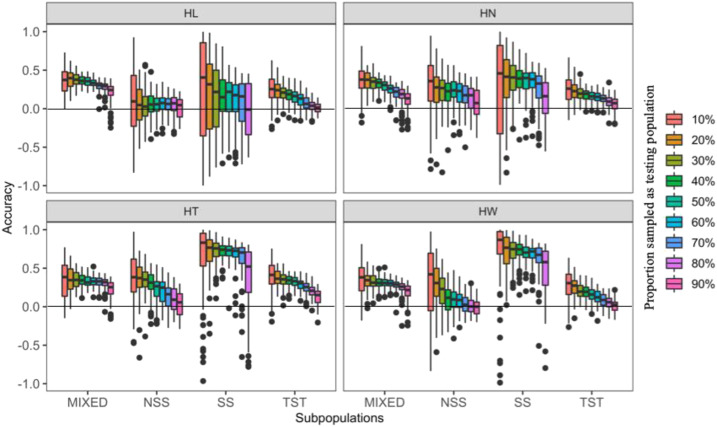
The degree of prediction accuracy in GS is related to the relationship between the training sets and the testing sets (Guo et al., 2014; Ly et al., 2013). GS within subpopulations that have closely related individuals will result in higher prediction accuracies than GS within randomly selected lines. Thus, to further estimate and compare prediction accuracies, we masked varying proportions (10–90%) of lines from a particular subpopulation into the testing population and treated the remaining lines within the same subpopulation as the training population (Figure 5 and Table S2). For example, the 10% proportion of inference within MIXED subpopulation represents sampling 10% lines from this subpopulation as testing population and remaining 90% lines from this subpopulation were treated as training population.
Figure 5.
Prediction accuracies for four husk traits within subpopulations. There are 67 inbred lines in non-stiff stalk (NSS), 27 in stiff stalk (SS), 193 in ropical-subtropical (TST) and 211 in admixed (MIXED). Within each subpopulation, certain proportions (10–90%) of inbred lines were sampled as testing population and the rest lines within the subpopulation as the training population. The sampling was replicated 100 times. Husk traits: HL = husk length, HN = husk layer number, HT = husk thickness, and HW = husk width.
In the MIXED subpopulation, we found little difference in prediction accuracy among the husk traits using 10–50% of the inference population. In order from highest to lowest, the prediction accuracies for the four traits were HL > HN > HW > HT. In the NSS subpopulation, the order of prediction accuracies was HT > HW > HN > HL. In SS, HT and HW exhibited the higher levels of prediction accuracies compared to HN and HL, across all proportions used for the inference population. In TST, the highest prediction accuracies occurred with HT (≤ 0.394). For the other three traits, prediction accuracies from highest to lowest were HW > HL > HN.
Cross validation across subpopulations
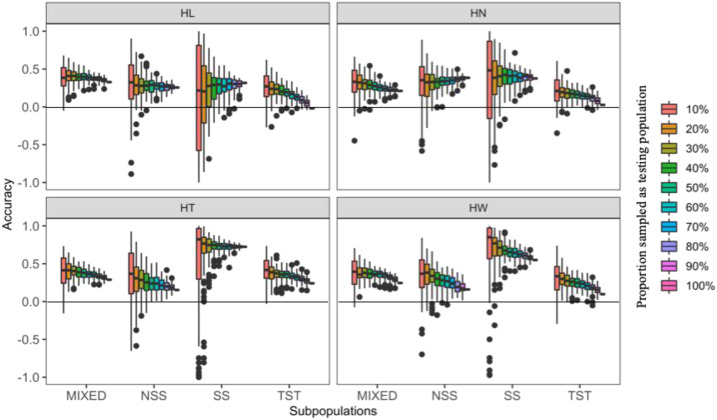
We also assessed prediction accuracy by masking varying proportions (10–100%) of the lines from each of the four subpopulations into the testing population and treating the remaining lines as the training population (Figure 6 and Table S3). For example, the 10% proportion of inference within MIXED subpopulation represents sampling 10% lines from this subpopulation as testing population and remaining 90% lines from MIXED subpopulation plus all the lines from other three subpopulations were treated as training population.
Figure 6.
Prediction accuracies for husk traits across subpopulations. There are 67 inbred lines in non-stiff stalk (NSS), 27 in stiff stalk (SS), 193 in tropical-subtropical (TST) and 211 in admixed (MIXED). For each subpopulation, certain proportions (10–90%) of inbred lines were sampled as testing population and the rest, including the lines from other subpopulations, as the training population. The sampling was replicated 100 times. Husk traits: HL = husk length, HN = husk layer number, HT = husk thickness, and HW = husk width.
In the MIXED subpopulation, prediction accuracy varied little among husk traits. In order from highest to lowest, the prediction accuracies for the four husk traits were HL > HT > HW > HN. In the NSS subpopulation, from highest to lowest, prediction accuracies were HW > HN > HT > HL. In the SS subpopulation, HT exhibited the highest prediction accuracy (≥0.718); the other three traits ordered as HW > HN > HL. In the TST subpopulation, HT exhibited the highest prediction accuracy; the order of prediction accuracies for the other traits was HW > HL > HN. For HL, the highest prediction accuracy occurred in MIXED. For the other three husk traits, their highest prediction accuracies occurred in SS.
Discussion
Heritability plays the key role for GS
Heritability is variously dependent on the genetic architecture of a trait. For example, in plants, flowering traits that are controlled by several major QTL have high heritabilities and yield traits that are controlled by multiple small-effect genetic loci have low heritabilities(Dicenta et al. 1993; Crossa et al. 2010; Heffner et al. 2011). In turn, trait heritability affects GS prediction accuracy(Zhang et al. 2017b). For example, GS with traits of higher heritability always results in a higher prediction accuracy compared to traits of lower heritability(Jannink et al. 2010). In our study, HT had the highest heritability across both planting locations and among all husk traits. On the contrary, HL had the lowest heritability in Beijing and the second lowest in Sanya. For the other two husk traits, GS prediction accuracy was better for HN than HW.
Benefit of using other subpopulations depends on training population size
Kinship among individuals is critical for GS. To have a high prediction accuracy, individuals in the testing population must have closely related individuals in the training population. Population structure can be the major factor affecting kinship. For example, in a previous study with maize and rice diversity panels, population structure explained 33% and 7.5% of the genomic variation, respectively(Guo et al. 2014). Individuals within subpopulations are more related than individuals among the subpopulations. For such reason, closely related individuals within the same subpopulation structure were split across training and testing populations(Ly et al. 2013; Spindel et al. 2015).
Our association panel was clustered into four subpopulations, MIXED, NSS, SS, and TST based on origins. Population study using 1,536 SNPs suggested that TST had the largest distance with the rest, especially SS, on the first principal component which explained 18.2% of total genetic variation. The second principal component (6.9% variance explained) separates SS from NSS with MIXED in the middle among other three with majority between TST and NSS (Yang et al. 2011). We conducted two sampling schemes in cross validation to evaluate the relationship between GS prediction accuracy and the relatedness between training and testing populations. One sampling scheme was to evaluate how one subpopulation was influenced by other subpopulations (Guo et al. 2014). The other was to evaluate how a subpopulation performed without using other subpopulations (Ly et al. 2013; Guo et al. 2014). In both schemes, the SS subpopulation showed the highest prediction accuracies across all husk traits, except HL.
For a subpopulation, prediction accuracies were higher when training populations were large and sampled with the same subpopulation than introducing extra lines from other subpopulations. For examples, HT in SS had prediction accuracy of 0.634 with 90% of lines as training population. The prediction accuracy dropped to 0.542 when all lines from other subpopulations joined to the training population; HT in NSS had prediction accuracy of 0.394 with 90% of lines as training population. The prediction accuracy dropped to 0.321 when all lines from other subpopulations joined to the training population.
However, when the numbers of lines in the training population were small, introducing lines from other subpopulations was beneficial. For examples, HT in SS had prediction accuracy of 0.358 with 20% of lines as training population. The prediction accuracy increased to 0.724 when all lines from other subpopulations joined to the training population; HT in NSS had prediction accuracy of 0.088 with 20% of lines as training population. The prediction accuracy increased to 0.202 when all lines from other subpopulations joined to the training population.
Implication to breeding on husk traits
Determining the most suitable husk traits for breeding improvements in maize depends primarily on planting location, especially climatic conditions. For example, in temperate areas such as north China, appropriate husk traits would include a shorter length, a lower number of layers, a thinner cross-section (thickness), and a narrower width, all features conducive to fast kernel dehydration during mechanical harvest. According to GEBVs of husk traits (supplemental material Table S4 and S5) and the relationships between husk traits and PCs (Figure S2), TST lines are unfavorite due to high values on HT and HN for temperate areas. SS, NSS, and MIXED lines are in favorite.
In contrast, in tropical and subtropical areas, such as southern China, appropriate husk traits would include greater length, number of layers, thickness, and width. Together, these characteristics are suitable for protection against pest damage and pathogen infection, which are more prevalent and intense in tropical and subtropical areas(Renfro and Ullstrup 1976; Afolabi et al. 2007). Most lines in the TST subpopulation should be appropriate choices for breeding improvements in tropical and subtropical areas.
Trait wise, the most predictable husk trait in our GS study was HT. Consistent with its high heritability in all locations, HT exhibited the highest prediction accuracies within and among most subpopulations. Thus, to improve husk traits by GS in maize breeding selection programs, we recommend beginning with HT.
Conclusions
The four husk traits had moderate to high heritabilities with HT at the top. The higher heritability, the higher accuracy of genomic prediction. Among four GS models, gBLUP with PCs has the highest prediction accuracies, followed by gBLUP without PCs, PCs only. With the best model of gBLUP with PCs, including individuals of external subpopulations, would help to predict individuals in a subpopulation when the training individual within the subpopulation was not large. Otherwise, the inclusion of the individuals of external subpopulation decreased prediction accuracy. HT was recommended as the first husk trait for breeding using GS.
Acknowledgments
This project was partially supported by The National Transgenic Major Program of China (2019ZX08010-004), National Natural Science Foundation of China (31771880), Natural Science Guidance Foundation of Liaoning Province(2019-ZD-0723), the USDA National Institute of Food and Agriculture (Hatch project 1014919, Award #s 2016-68004-24770, 2018-70005-28792, and 2019-67013-29171), National Science Foundation (Award number DBI 1661348), the National Natural Science Foundation of China (31901434), and the Washington Grain Commission (Endowment and Award #s 126593 and 134574). The authors are grateful to X. Yang (China Agricultural University) for providing seeds of 508-line association panel. The authors thank Dr. Linda R. Klein for valuable writing advice and editing the manuscript.
Footnotes
Supplemental material available at figshare: https://doi.org/10.25387/g3.11829177.
Communicating editor: P. Brown
Literature Cited
- Afolabi C. G., Ojiambo P. S., Ekpo E. J. A., Menkir A., and Bandyopadhyay R., 2007. Evaluation of Maize Inbred Lines for Resistance to Fusarium Ear Rot and Fumonisin Accumulation in Grain in Tropical Africa. Plant Dis. 91: 279–286. 10.1094/PDIS-91-3-0279 [DOI] [PubMed] [Google Scholar]
- Ali M., 2011. Coconut fibre: A versatile material and its applications in engineering. J. Civ. Eng. Constr. Technol. 2: 189–197. [Google Scholar]
- Barry D., Lillehoj E. B., Widstrom N. W., McMillan W. W., Zuber M. S. et al. , 1986. Effect of Husk Tightness and Insect (Lepidoptera) Infestation on Aflatoxin Contamination of Preharvest Maize. Environ. Entomol. 15: 1116–1118. 10.1093/ee/15.6.1116 [DOI] [Google Scholar]
- Bernardo R., 1994. Prediction of maize single-cross performance using RFLPs and information from related hybrids. Crop Sci. 34: 20–25. 10.2135/cropsci1994.0011183X003400010003x [DOI] [Google Scholar]
- Brewbaker J. L., 2015. Diversity and genetics of tassel branch numbers in maize. Crop Sci. 55: 65–78. 10.2135/cropsci2014.03.0248 [DOI] [Google Scholar]
- Brewbaker J. L., and Kim S. K., 1979. Inheritance of husk numbers and ear insect damage in maize. Crop Sci. 19: 32–36. 10.2135/cropsci1979.0011183X001900010008x [DOI] [Google Scholar]
- Browning S. R., and Browning B. L., 2007. Rapid and accurate haplotype phasing and missing-Data inference for whole-genome association studies by use of localized haplotype clustering. Am. J. Hum. Genet. 81: 1084–1097. 10.1086/521987 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calus M. P., and Veerkamp R. F., 2007. Accuracy of breeding values when using and ignoring the polygenic effect in genomic breeding value estimation with a marker density of one SNP per cM. J. Anim. Breed. Genet. 124: 362–368. 10.1111/j.1439-0388.2007.00691.x [DOI] [PubMed] [Google Scholar]
- Chesnais J. P., Cooper T. A., Wiggans G. R., Sargolzaei M., Pryce J. E. et al. , 2016. Using genomics to enhance selection of novel traits in North American dairy cattle. J. Dairy Sci. 99: 2413–2427. 10.3168/jds.2015-9970 [DOI] [PubMed] [Google Scholar]
- Collard B. C., and Mackill D. J., 2008. Marker-assisted selection: an approach for precision plant breeding in the twenty-first century. Philos. Trans. R. Soc. B Biol. Sci. 363: 557–572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Combs E., and Bernardo R., 2013. Accuracy of genomewide selection for different traits with constant population size, heritability, and number of markers. Plant Genome 6: 1–7. 10.3835/plantgenome2012.11.0030 [DOI] [Google Scholar]
- Crossa J., Beyene Y., Kassa S., Pérez P., Hickey J. M. et al. , 2013. Genomic Prediction in Maize Breeding Populations with Genotyping-by-Sequencing. G3 (Bethesda) 3: 1903–1926. 10.1534/g3.113.008227 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossa J., De Los Campos G., Pérez P., Gianola D., Burgueño J. et al. , 2010. Prediction of genetic values of quantitative traits in plant breeding using pedigree and molecular markers. Genetics 186: 713–724. 10.1534/genetics.110.118521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossa J., Pérez P., Hickey J., Burgueño J., Ornella L. et al. , 2014. Genomic prediction in CIMMYT maize and wheat breeding programs. Heredity 112: 48–60. 10.1038/hdy.2013.16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui Z., Luo J., Qi C., Ruan Y., Li J. et al. , 2016. Genome-wide association study (GWAS) reveals the genetic architecture of four husk traits in maize. BMC Genomics 17: 946 10.1186/s12864-016-3229-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui Z., Xia A., Zhang A., Luo J., Yang X. et al. , 2018. Linkage mapping combined with association analysis reveals QTL and candidate genes for three husk traits in maize. Theor. Appl. Genet. 131: 2131–2144. 10.1007/s00122-018-3142-2 [DOI] [PubMed] [Google Scholar]
- Demissie G., Tefera T., and Tadesse A., 2008. Importance of husk covering on field infestation of maize by Sitophilus zeamais Motsch (Coleoptera: Curculionidea) at Bako, Western Ethiopia. Afr. J. Biotechnol. 7: 3777–3782. [Google Scholar]
- Dicenta F., Garcia J. E., and Carbonell E. A., 1993. Heritability of flowering, productivity and maturity in almond. J. Hortic. Sci. 68: 113–120. 10.1080/00221589.1993.11516334 [DOI] [Google Scholar]
- Ding T. Y., Hii S. L., and Ong L., 2012. Comparision of pretreatment strategies for conversion of coconut husk fiber to fermentable sugars. BioResources 7: 1540–1547. 10.15376/biores.7.2.1540-1547 [DOI] [Google Scholar]
- Dong H., Wang R., Yuan Y., Anderson J., Pumphrey M. O. et al. , 2018. Evaluation of the Potential for Genomic Selection to Improve Spring Wheat Resistance to Fusarium Head Blight in the Pacific Northwest. Front. Plant Sci. 9: 911 10.3389/fpls.2018.00911 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ekhuemelo D. O., and Tor K., 2013. Assessment of fibre characteristics and suitability of maize husk and stalk for pulp and paper production. J. Res. For. Wildl. Environ. 5: 41–49. [Google Scholar]
- Endelman J. B., 2011. Ridge regression and other kernels for genomic selection in the R package rrBLUP. Plant Genome 4: 250–255. 10.3835/plantgenome2011.08.0024 [DOI] [Google Scholar]
- Fu J., Cheng Y., Linghu J., Yang X., Kang L. et al. , 2013. RNA sequencing reveals the complex regulatory network in the maize kernel. Nat. Commun. 4: 2832 10.1038/ncomms3832 [DOI] [PubMed] [Google Scholar]
- Guo Z., Tucker D. M., Basten C. J., Gandhi H., Ersoz E. et al. , 2014. The impact of population structure on genomic prediction in stratified populations. Theor. Appl. Genet. 127: 749–762. 10.1007/s00122-013-2255-x [DOI] [PubMed] [Google Scholar]
- Guo G., Zhou Z., Wang Y., Zhao K., Zhu L. et al. , 2011. Canine hip dysplasia is predictable by genotyping. Osteoarthritis Cartilage 19: 420–429. 10.1016/j.joca.2010.12.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes B. J., Bowman P. J., Chamberlain A. J., and Goddard M. E., 2009. Invited review: Genomic selection in dairy cattle: Progress and challenges. J. Dairy Sci. 92: 433–443. 10.3168/jds.2008-1646 [DOI] [PubMed] [Google Scholar]
- Heffner E. L., Jannink J.-L., Iwata H., Souza E., and Sorrells M. E., 2011. Genomic selection accuracy for grain quality traits in biparental wheat populations. Crop Sci. 51: 2597–2606. 10.2135/cropsci2011.05.0253 [DOI] [Google Scholar]
- Heffner E. L., Sorrells M. E., and Jannink J., 2009. Genomic Selection for Crop Improvement. Crop Sci. 49: 1–12. 10.2135/cropsci2008.08.0512 [DOI] [Google Scholar]
- Hicks D. R., Geadelmann G. L., and Peterson R. H., 1976. Drying Rates of Frosted Maturing Maize1. Agron. J. 68: 452–455. 10.2134/agronj1976.00021962006800030004x [DOI] [Google Scholar]
- Holland J. B., Nyquist W. E., and Cervantes-Martínez C. T., 2010. Estimating and Interpreting Heritability for Plant Breeding: An Update, pp. 9–112 in Plant Breeding Reviews, John Wiley & Sons, Inc., Oxford, UK. [Google Scholar]
- Holm S., 1979. A simple sequentially rejective multiple test procedure. Scand. J. Stat. 6: 65–70. [Google Scholar]
- Huang M., Liu X., Zhou Y., Summers R. M., and Zhang Z., 2018. BLINK: A package for the next level of Genome-Wide association studies with both individuals and markers in the millions. Gigascience 8: giy154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jalil A. A., Triwahyono S., Yaakob M. R., Azmi Z. Z. A., Sapawe N. et al. , 2012. Utilization of bivalve shell-treated Zea mays L. (maize) husk leaf as a low-cost biosorbent for enhanced adsorption of malachite green. Bioresour. Technol. 120: 218–224. 10.1016/j.biortech.2012.06.066 [DOI] [PubMed] [Google Scholar]
- Jannink J. L., Lorenz A. J., and Iwata H., 2010. Genomic selection in plant breeding: from theory to practice. Brief. Funct. Genomics 9: 166–177. 10.1093/bfgp/elq001 [DOI] [PubMed] [Google Scholar]
- Johar N., Ahmad I., and Dufresne A., 2012. Extraction, preparation and characterization of cellulose fibres and nanocrystals from rice husk. Ind. Crops Prod. 37: 93–99. 10.1016/j.indcrop.2011.12.016 [DOI] [Google Scholar]
- Li C.-Y., Kim H.-W., Won S., Min H.-K., Park K.-J. et al. , 2008. Corn Husk as a Potential Source of Anthocyanins. J. Agric. Food Chem. 56: 11413–11416. 10.1021/jf802201c [DOI] [PubMed] [Google Scholar]
- Li Q., Yang X., Xu S., Cai Y., Zhang D. et al. , 2012. Genome-wide association studies identified three independent polymorphisms associated with α-tocopherol content in maize kernels. PLoS One 7: e36807 10.1371/journal.pone.0036807 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipka A. E., Tian F., Wang Q., Peiffer J., Li M. et al. , 2012. GAPIT: genome association and prediction integrated tool. Bioinformatics 28: 2397–2399. 10.1093/bioinformatics/bts444 [DOI] [PubMed] [Google Scholar]
- Liu H., Luo X., Niu L., Xiao Y., Chen L. et al. , 2017. Distant eQTLs and Non-coding Sequences Play Critical Roles in Regulating Gene Expression and Quantitative Trait Variation in Maize. Mol. Plant 10: 414–426. 10.1016/j.molp.2016.06.016 [DOI] [PubMed] [Google Scholar]
- Ly D., Hamblin M., Rabbi I., Melaku G., Bakare M. et al. , 2013. Relatedness and Genotype × Environment Interaction Affect Prediction Accuracies in Genomic Selection: A Study in Cassava. Crop Sci. 53: 1312–1325. 10.2135/cropsci2012.11.0653 [DOI] [Google Scholar]
- Massman J. M., Jung H. J. G., and Bernardo R., 2013. Genomewide selection vs. marker-assisted recurrent selection to improve grain yield and stover-quality traits for cellulosic ethanol in maize. Crop Sci. 53: 58–66. 10.2135/cropsci2012.02.0112 [DOI] [Google Scholar]
- Mehrban H., Lee D. H., Moradi M. H., IlCho C., and Naserkheil M., 2017. Predictive performance of genomic selection methods for carcass traits in Hanwoo beef cattle: impacts of the genetic architecture. Genet. Sel. Evol. 49: 1 10.1186/s12711-016-0283-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen T. H. E., Hayes B. J., and Goddard M. E., 2001. Prediction of total genetic value using genome-wide dense marker maps. Genetics 157: 1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogutu J. O., Piepho H.-P., and Schulz-Streeck T., 2011. A comparison of random forests, boosting and support vector machines for genomic selection. BMC Proc. 5: S11 10.1186/1753-6561-5-S3-S11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pengelly J. J. L., Kwasny S., Bala S., Evans J. R., Voznesenskaya E. V. et al. , 2011. Functional Analysis of Corn Husk Photosynthesis. Plant Physiol. 156: 503–513. 10.1104/pp.111.176495 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renfro B. L., and Ullstrup A. J., 1976. A Comparison of Maize Diseases in Temperate and in Tropical Environments. PANS 22: 491–498. 10.1080/09670877609414339 [DOI] [Google Scholar]
- Spindel J., Begum H., Akdemir D., Virk P., Collard B. et al. , 2015. Genomic Selection and Association Mapping in Rice (Oryza sativa): Effect of Trait Genetic Architecture, Training Population Composition, Marker Number and Statistical Model on Accuracy of Rice Genomic Selection in Elite, Tropical Rice Breeding Lines. PLoS Genet. 11: e1004982 10.1371/journal.pgen.1004982 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sweeney P. M., St. Martin S. K., and Clucas C. P., 1994. Indirect Inbred Selection to Reduce Grain Moisture in Maize Hybrids. Crop Sci. 34: 391 10.2135/cropsci1994.0011183X003400020016x [DOI] [Google Scholar]
- Tang Y., Liu X., Wang J., Li M., Wang Q. et al. , 2016. GAPIT Version 2: An Enhanced Integrated Tool for Genomic Association and Prediction. Plant genome 9: 1–9. 10.3835/plantgenome2015.11.0120 [DOI] [PubMed] [Google Scholar]
- VanRaden P. M., 2008. Efficient methods to compute genomic predictions. J. Dairy Sci. 91: 4414–4423. 10.3168/jds.2007-0980 [DOI] [PubMed] [Google Scholar]
- VanRaden P. M., Van Tassell C. P., Wiggans G. R., Sonstegard T. S., Schnabel R. D. et al. , 2009. Invited review: reliability of genomic predictions for North American Holstein bulls. J. Dairy Sci. 92: 16–24. 10.3168/jds.2008-1514 [DOI] [PubMed] [Google Scholar]
- Wang P., Kelly S., Fouracre J. P., and Langdale J. A., 2013. Genome-wide transcript analysis of early maize leaf development reveals gene cohorts associated with the differentiation of C 4 Kranz anatomy. Plant J. 75: 656–670. 10.1111/tpj.12229 [DOI] [PubMed] [Google Scholar]
- Warfield C. Y., and Davis R. M., 1996. Importance of the husk covering on the susceptibility of corn hybrids to Fusarium ear rot. Plant Dis. 80: 208 10.1094/PD-80-0208 [DOI] [Google Scholar]
- Yang X., Gao S., Xu S., Zhang Z., Prasanna B. M. et al. , 2011. Characterization of a global germplasm collection and its potential utilization for analysis of complex quantitative traits in maize. Mol. Breed. 28: 511–526. 10.1007/s11032-010-9500-7 [DOI] [Google Scholar]
- Yang N., Lu Y., Yang X., Huang J., Zhou Y. et al. , 2014. Genome Wide Association Studies Using a New Nonparametric Model Reveal the Genetic Architecture of 17 Agronomic Traits in an Enlarged Maize Association Panel. PLoS Genet. 10: e1004573 10.1371/journal.pgen.1004573 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X., Pérez-Rodríguez P., Burgueño J., Olsen M., Buckler E. et al. , 2017a Rapid Cycling Genomic Selection in a Multiparental Tropical Maize Population. G3 (Bethesda) 7: 2315–2326. 10.1534/g3.117.043141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z., Todhunter R. J., Buckler E. S., and Van Vleck L. D., 2007. Technical note: Use of marker-based relationships with multiple-trait derivative-free restricted maximal likelihood. J. Anim. Sci. 85: 881–885. 10.2527/jas.2006-656 [DOI] [PubMed] [Google Scholar]
- Zhang A., Wang H., Beyene Y., Semagn K., Liu Y. et al. , 2017b Effect of Trait Heritability, Training Population Size and Marker Density on Genomic Prediction Accuracy Estimation in 22 bi-parental Tropical Maize Populations. Front. Plant Sci. 8: 1916 10.3389/fpls.2017.01916 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou G., Hao D., Chen G., Lu H., Shi M. et al. , 2016a Genome-wide association study of the husk number and weight in maize (Zea mays L.). Euphytica 210: 195–205. 10.1007/s10681-016-1698-y [DOI] [Google Scholar]
- Zhou Y., Isabel Vales M., Wang A., and Zhang Z., 2016b Systematic bias of correlation coefficient may explain negative accuracy of genomic prediction. Brief. Bioinform. 5: 744. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All phenotypic data and results data are included within the manuscript in supplementary. The genotypes (∼1.25M) used in this study are all publicly available at the website of Jianbing Yan (http://www.maizego.org/Resources.html), or through the direct download link (https://pan.baidu.com/s/1mhR1L1Y#list/path=%2F). Supplemental material available at figshare: https://doi.org/10.25387/g3.11829177.