Beyond Deterministic Models in Drug Discovery and Development

Abstract

The model-informed drug discovery and development paradigm is now well established among the pharmaceutical industry and regulatory agencies. This success has been mainly due to the ability of pharmacometrics to bring together different modeling strategies, such as population pharmacokinetics/pharmacodynamics (PK/PD) and systems biology/pharmacology. However, there are promising quantitative approaches that are still seldom used by pharmacometricians and that deserve consideration. One such case is the stochastic modeling approach, which can be important when modeling small populations because random events can have a huge impact on these systems. In this review, we aim to raise awareness of stochastic models and how to combine them with existing modeling techniques, with the ultimate goal of making future drug–disease models more versatile and realistic.

Highlights

• Nonlinear mixed-effect modeling is currently the most successful methodology used to characterize the PK/PD data from different individuals.

• Stochastic modeling approaches deserve consideration for use in model-informed drug discovery and development because events occurring at random can have important repercussions on disease progression and treatment effects, especially when population size is small.

• Stochastic models can also help in the refinement of the original structural PK/PD model.

• Deterministic systems have a greater mathematical simplicity, are computationally less demanding, and parameter estimation is well established with a large existing toolkit to help with model fitting and simulation.

• Coronavirus disease 2019 is the most recent application where researchers are building such models to describe the spread of this disease in the population.

Mathematical Modeling and Simulation in Drug Development and Patient Management

Current drug discovery and development is a long and complex process associated with a high attrition rate, resulting in an unacceptable cost–benefit ratio for the drug industry. This fact motivated the emergence of a strategic initiative by the US Food and Drug Administration (FDA) in 2004, the Critical Path Initiative, with six broad topic areas, one of which was devoted to promote mathematics, statistics, and computational analysis within the drug development and regulatory review process [1]. This represented the first step towards the current Model-Informed Drug Discovery and Development (MID3) paradigm that nowadays includes the disciplines of pharmacometrics (see Glossary) and systems pharmacology (PSP). From a high-level perspective, PSP involves integrating and quantitatively linking all types of information, methodologies and tools associated with the development of mechanistic models of biological/physiological processes, and pharmacology that can help in our understanding and prediction of drug response in patients. The value of MID3 approaches in decision-making is evidenced by the large number of related publications, recent examples of which can be found in [2., 3., 4., 5.]. In these examples, the reliability and explanatory power of the models depend predominantly on the level of detail included and the assumptions on which they are based. A combination of strategies is often the best way to proceed. Especially in pharmacometrics, quantifying the mean tendency of a population using ordinary differential equations (ODEs) is the most common procedure, but also finding ways of modeling the variance of the data, which may be the result of extrinsic random events and/or sampling errors. This is the case of nonlinear mixed-effects (NLME) models (more commonly known as population PK/PD models), extensively used by the pharmaceutical industry and regulatory agencies to analyze experimental and clinical data, allowing the optimization of trial designs and proposing dosing paradigms to maximize treatment efficacy.

In general, the mathematical models defined in PSP are deterministic; that is, the trajectory of the model components is fully determined by the parameter values and initial conditions of the system and no changes can occur in the absence of external perturbations. However, disease progression and real pharmacological processes are always subject to stochastic effects, such as mutation acquisition leading to cancerous cells or to drug resistance [6,7], patient withdrawal from a clinical trial, or the initial transmission of infectious diseases [8]. Such events occurring at random can have important repercussions for disease progression and treatment effects especially when the population size is small; in addition, ignoring these phenomena may affect the estimation of PK/PD parameters and derived conclusions. Stochastic models are able to capture this phenomenon by assuming that the dynamics of the system is partly driven by random fluctuations. However, those models come at a price; they are generally computationally more demanding and more arduous to fit to experimental data.

Our main goal with this review is to encourage the PSP community to consider the stochastic strategy between the methodologies that are part of MID3 to evaluate their potential use in clinical trial design and patient management. To this end, we first provide an overall description of the deterministic and stochastic approaches (more extended for the case of the stochastic models because they are less applied in the pharmacology arena) and the main differences regarding: (i) model structure; (ii) simulation process; and (iii) data fitting. Then, we provide the most significant examples found in literature for each approach and finish with a section dedicated to nonlinear mixed-effects models and proposals to combine the different modeling perspectives.

Differences between Deterministic and Stochastic Modeling Approaches

Model Structure

The structure of a model mathematically describes the relationship between the variables in a system. This relationship can be based on different formalisms ranging from qualitative strategies to quantitative approaches. Here, we focus on the latter.

Quantitative models can be further divided into deterministic and stochastic systems. Deterministic models are often described by a system of ODEs. Here, the output of the model is fully determined by the parameter values and the initial conditions of the system, and no randomness is assumed to be present. Thus, the outcome of a deterministic model is unique and attempts to represent the average behavior of the system, which in many cases is a suitable representation of real biological processes.

However, there are two key limitations in deterministic models: (i) they do not account for uncertainty in model dynamics; and (ii) they are trapped in constant steady states that are not necessarily steady when considering stochasticity. The first limitation can pose a practical problem because biochemical processes are always exposed to stochastic effects and are intrinsically heterogeneous, meaning that proper data fitting to a deterministic model requires some interpretation of real stochasticity. The second issue refers to the ability for randomness to produce spontaneous transitions, causing a system to switch from one stable state to another. In fact, some models posit that this ability of stochastic systems is fundamental to cell plasticity [9,10] and, hence, it could be an important feature to consider for understanding cancer progression [11,12].

Stochastic processes assume that the dynamics of the system in every individual is partly driven by random fluctuations (also known as process/system noise) and, hence, the same set of parameter values and initial conditions can lead to different outcomes of the system. This approach considers that each biological/pharmacological process is a random event that can take place with a certain probability related to the properties of the components within the biological system. Thus, the evolution of the system over time is dependent on a series of consecutive probabilistic events. Consequently, the stochastic approach requires background in probability theory. The master equation [13] is one fundamental mathematical description of this approach and it is obtained as a probability distribution for all the events that can occur during a very short time interval (see Box 1 for an example). As can also be appreciated in the birth–death process from Box 1, many deterministic models represent the average behavior of all possible stochastic evolutions; that is, the differential equations of deterministic modeling can be nearly equivalent to the differential equation that describes the time evolution of the mean of stochastic processes.

Box 1. Deterministic Model.

Consider a cell population n where each cell gives birth to an offspring according to a constant birth rate β or dies according to a certain death rate δ. Assuming that the population grows exponentially, then the ODE governing the exponential growth of the population can be defined using Equation I:

$$\frac{\mathit{dn}}{\mathit{dt}}=\left(\beta -\delta \right)·n$$ [I]

The analytical solution of Equation I is: n(t) = n ₀ · e ^(β−δ)·t. This curve is fully determined by the birth and death rates and the initial condition of the population n ₀: if the birth rate exceeds the death rate, β > δ, then the population size exponentially increases, but when β < δ, it exponentially decreases toward zero.

Stochastic Model

To consider the stochastic version of the birth–death process, we need to define the master equation of the system as a probability distribution for all the events that can occur during the time interval (t,t + Δt). Assume that the time interval Δt is short enough so that only one of the following cases can exclusively occur: (i) a new cell is born with probability βΔt; (ii) the cell dies with probability δΔt; and (iii) the cell neither gives birth nor dies with probability 1 – βΔt – δΔt. Now we need to calculate the probability distribution Pn(t), that is, the probability that the population size (the total number of cells in this case) is n at time t, which is the sum of the probabilities of all the mutually exclusive events explained earlier and is given by Equation II:

$$\mathit{Pn}\left(t+\mathrm{\Delta }t\right)=\mathit{Pn}\left(t\right)\left(1–\mathit{\beta n}\mathrm{\Delta }t–\mathit{\delta n}\mathrm{\Delta }t\right)+\mathit{Pn}–1\left(t\right)\beta \left(n–1\right)\mathrm{\Delta }t+\mathit{Pn}+1\left(t\right)\delta \left(n+1\right)\mathrm{\Delta }t$$ [II]

By letting Δt → 0, we obtain the master equation of the birth-death process (Equation III):

$$\frac{d{P}_n\left(t\right)}{\mathit{dt}}=\mathrm{\beta }·\left(\mathrm{n}–1\right)·\mathrm{Pn}–1\left(\mathrm{t}\right)+\mathrm{\delta }·\left(\mathrm{n}+1\right)·\mathrm{Pn}+1\left(\mathrm{t}\right)–\left(\mathrm{\beta }+\mathrm{\delta }\right)·\mathrm{n}·\mathrm{Pn}\left(\mathrm{t}\right)\text{for}\mathrm{n}\ge 1$$ [III]

Equation III allows us to compute the average and variance population size values by solving the first and second moments of the master equation using Equations [IV], [V]:

$$\text{Average}:⧽n⧽=n_0·e^{\left(\beta -\delta \right)·t}$$ [IV]

$$\text{Variance}:\mathit{Var}\left[n\right]=n_0·\frac{\beta +\delta }{\beta -\delta }·e^{\left(\beta -\delta \right)·t}·\left(e^{\left(\beta -\delta \right)·t}-1\right)$$ [V]

We note that the analytic equation obtained for the average of the stochastic process is the same as the analytic equation resulting from the deterministic model, although this is not necessarily the case for all stochastic models. Another aspect to highlight is the dependence on time of the variance equation, which makes the variance of the process to increase over time when β – δ > 0.

Alt-text: Box 1

Model Simulation

Unfortunately, the analytical solution of a master equation is often intractable, especially if a large number of components are involved. Instead of attempting to directly solve for the probability of being in every state at a given time, numerical simulations attempt to sample many trajectories of the stochastic system to gather enough information about the probabilistic properties. The most common algorithm of this form is the Gillespie stochastic simulation algorithm (Gillespie SSA), which provides exact simulations of possible trajectories of the master equation by using standard Monte Carlo techniques that make random choices as the simulation progresses [14]. However, the computational cost can be high for large biological systems because: (i) simulations must be repeated many times to reveal the complete range of behaviors of the system; and (ii) every reaction event is individually simulated at each iteration of the algorithm.

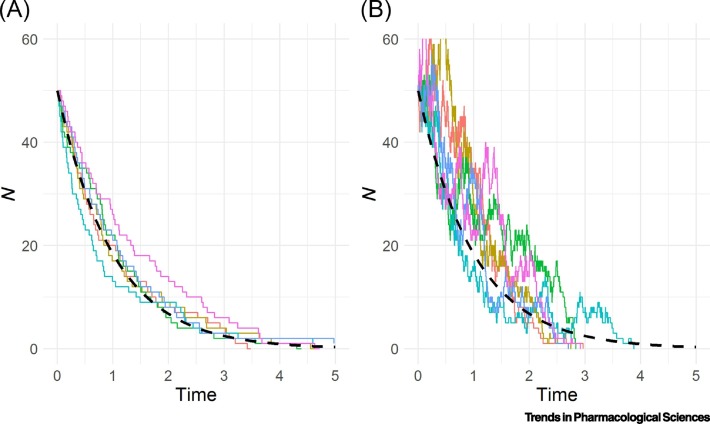
In Figure 1 , the use of Gillespie SSA to compute six stochastic realizations of the birth–death process described in Box 1 is shown, together with the deterministic solution for two different birth and death rate value combinations. While related, stochastic and ODE simulations can show differences in behavior. First, in deterministic models, the number of cells never reaches zero, but simply tends to zero as time goes to infinity. However, in the stochastic simulations, the cells go extinct and there is considerable randomness associated with the time when this occurs. The possibility that the population of cells can die out is an important feature of stochastic models opposed to deterministic ones. Another point of divergence is that the stochastic process depends explicitly on both the birth rate and the death rate, and not just on the net growth rate (β − δ), as in the case of the deterministic model. As can be seen in Figure 1, the shape of the curve is governed by the result of β − δ, but the variance of the process is also controlled by β + δ (see the equations in Box 1), thus Figure 1B shows a greater degree of noise than the Figure 1A. Table 1 provides a summary of the main differences between deterministic and stochastic approaches.

Figure 1.

Six Realizations of a Stochastic Linear Birth-Death Process (Solid Lines) Together with the Continuous Deterministic Solution (Dashed Line) Corresponding to an Exponential Function for Two Different Birth (β) and Death (δ) Rate Combinations.

Each combination has β – δ = –1 (arbitrary units) and an initial number of cells of 50 [(A) β = 0 and δ = 1; (B) β = 4 and δ = 5]. N represents the total number of cells/molecules. The stochastic realizations were computed using a self-coded stochastic simulation algorithm.

Table 1.

Main Differences between the Deterministic and Stochastic Approach

Character	Deterministic	Stochastic
Model structure	Defined by analytic or ODEs	Defined by a master equation or SDEs
Uncertainty in model dynamics?	No, dynamics is fully determined by parameter values and initial conditions	Yes, the same set of parameter values and initial conditions can lead to different results
Describes	Average behavior of components in a biological system	Stochastic effects that appear in biological systems
Unique outcome?	Yes	No
Variance of process	Variability can be introduced as random effects in model parameters	Is inherent to the system
Population may become extinct in mass action models?	No	Yes
Rate constants	Quantify the rate of specific biological processes/reactions	Might be interpreted as the probability that a biological process/reaction occurs in a very small time interval
Model simulation	ODE solver	•Gillespie or Stochastic Simulation Algorithm: exact method. Requires a probabilistic method involving repeated generation of random numbers •Tau-leaping: approximate and discrete-valued simulation method •SDE solver: continuous approximation
Existing toolkit for parameter estimation and simulation	Large	Small
Computational expense	In general, computationally less demanding than for stochastic models	High
Examples	•Exponential and logistic growth model (see analytic equation from Figure 1 in the main text) •Susceptible–infected–recovered (SIR) model [33]	•Branching process and Moran process (see Box 2 in the main text) •Stochastic SIR models [8,54]

In SSAs, discrete particle (molecules, cells, etc.) counts are considered rather than continuous concentrations. Since the fluctuations/noise in the system only increase by the square root of the particle number, as this number increases, the system becomes seemingly more deterministic because stochastic fluctuations become negligible. Therefore, when the initial number of particles is high, using ODEs instead of stochastic processes will give very approximate results with a smaller computational cost, because simulations of deterministic systems are easily performed with the high number of numerical ODE solvers available. Re-interpreting the model from discrete numbers of molecules to real concentration values gives rise to the Langevin equation, an example of stochastic differential equation (SDE), which uses a Gaussian additive noise term and which approximates the underlying random behavior of the model while being a continuous-valued simulation like an ODE. Again, taking the limit as the number of molecules going to infinity on the SDE representation recovers the classical mass-action kinetics of ODE model behavior [15].

Some stochastic simulation software tools exist for easier computation of these processes, including StochSS [16], GillesPy [17], or COPASI [18], but numerous published studies of stochastic process simulation in biomedicine are still accomplished using self-coded algorithms in programming languages such as C++ due to the fast computing time needed. Recent advances in this field have greatly reduced the computational complexity; the sorting direct method [19], composition-rejection SSA [20], and rejection-based SSA (RSSA) [21] tend to be orders of magnitude faster than the traditional Gillespie SSA [22]. These more efficient methodologies, along with the first adaptive methods for stiff stochastic differential equations, are implemented in newer Julia-based stochastic simulation software tools, such as DifferentialEquations.jl [23].

Model Fitting

A model needs to be capable of describing the experimental data. Values of model parameters are generally obtained using estimation techniques aimed at searching the model that minimizes the difference between the observations and the predictions. Extensive research has been done on numerical ODE solvers and advanced algorithms that allow for a straightforward estimation of parameters from deterministic models thanks to the development of easy-to-use tools [24]. Stochastic models introduce additional challenges due to their intrinsic stochasticity and, therefore, there is a lack of tools for easily finding parameter estimates for such models. Although a few frameworks, such as StochSS, exist to help users to automatically complete this task, many studies found in literature treat the system as deterministic instead of stochastic when estimating the parameters of the model to be able to use common procedures, such as maximum likelihood estimation [25]. In those cases, the estimates of the parameter obtained through the deterministic formulation may be plugged back into the stochastic model for the simulation of the stochastic process [26]. A word of caution should be given for this practice since ignoring stochastic phenomena in the modeling may affect the estimation of model parameters and the derived conclusions. Furthermore, in deterministic models such as ODEs, small perturbations in the solution can cause the system to converge to a separate steady state. Such lack of robustness would lead to many trajectories in stochastic systems not matching the data, thus assigning a low likelihood to that set of parameters. Thus, stochastic modeling can help with the convergence of parameter estimation because it reduces the number of local minima [27]. A formal discussion about the theory behind parameter estimation algorithms in stochastic systems is beyond the scope of this review.

Even when estimating parameters in deterministic systems, the data will not fit perfectly to the prediction of a model because there could be assay errors or because the model might not be completely accurate. This discrepancy is usually accounted for by a residual error term (i.e., measurement noise). However, only defining this source of uncertainty might not be enough when modeling the data of different individuals. To account for a variation component in addition to the residual error, a NLME approach can be adopted, which uses deterministic models to characterize the dynamics of the systems and a stochastic strategy to add random effects to model parameters. This methodology is discussed later.

Applications of the Two Modeling Approaches

Tumor growth inhibition models, frequently used to analyze the effect of anticancer agents in oncology, are examples of deterministic models [28., 29., 30., 31.]. In these models, tumors are often assumed to grow exponentially or following the so-called logistic curves or Gompertz law [32] and the change in tumor size is generally explained by the cell growth minus tumor shrinkage due to drug effects. Infectious diseases can be modeled by the popular susceptible–infected–recovered (SIR) model [33], which study the spread of viruses by classifying individuals as susceptible to the disease, infected, and recovered. Sizes in these classes change depending on the fatality of the virus and the resources used to combat it. Variants of these models have been proposed to model the spread of Coronavirus Disease 2019 (COVID-19) [34,35].

Those deterministic models provide good approximations of the growth of large populations, but for small populations, it is important to analyze their inherent randomness because these populations can go extinct due to random fluctuations, even in cases where the birth rate of the population is greater than the death rate, something that is impossible when considering deterministic models. That is why many authors have focused on the calculation of the probability of extinction of a population [36., 37., 38.]. For the birth–death process described in Box 1, the probability of extinction of the cell population at time t is given by Equation 1 (see [39] for a more exhaustive mathematical explanation):

$$P\left(n\left(t\right)=0\right)={\left(\frac{-\delta ·e^{\left(\delta -\beta \right)·t}+\delta }{-\delta ·e^{\left(\delta -\beta \right)·t}+\beta }\right)}^{n_0}$$ [1]

From Equation 1, we can see that, when t→∞ and β < δ,the probability of extinction will be 1 but when t→∞ and β > δ, the probability of extinction becomes $P\left(n\left(t\right)=0\right)\sim {\left(\frac{\delta }{\beta }\right)}^{n_0}$, which means that, for a small population size n ₀,we can obtain a probability of extinction of the process that is different from 0. This property introduces the possibility of a complete cure of the patient if the tumor cells become extinct because of the anticancer treatment. This can also be extrapolated to infectious diseases, where estimation of the basic reproduction number [40] is crucial because it determines the threshold between disease extinction and outbreak.

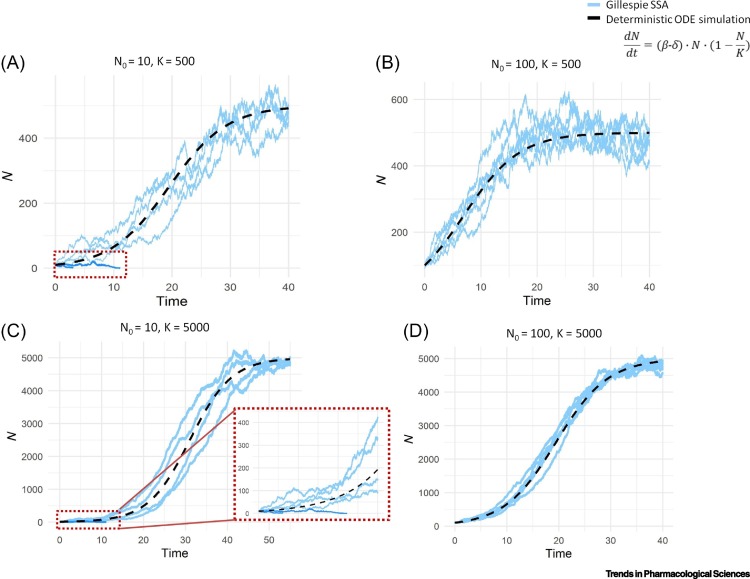
Another important characteristic of stochastic models is that the same initial conditions and parameter values can lead to different steady states of the system. For example, in [38], the authors propose a stochastic mathematical model for the analysis of adoptive cell transfer immunotherapy against melanoma skin cancer where the treatment comprises the injection of T cells that recognize a melanocyte-specific antigen and are able to kill differentiated melanoma cell types. Given that the number of T cells injected is low, the stochastic effects exerted by these cells can be significant because, due to random fluctuations, the injected T cells can die out, which leads to the growth of the differentiated melanoma cells. This behavior would not be seen in the deterministic version of the same model because the immune cells would never die due to stochasticity and explains why some patients respond to therapy while others do not. The same behavior can be observed in the logistic growth model simulated in Figure 2 : when choosing a small initial population of cells, the SSA show two different steady-state values for the model, one around the carrying capacity (K) and the other one in zero, because, due to stochasticity, some of these cell populations could become extinct. However, when choosing a larger initial population, even randomness is included, the number of cells never reaches zero. Fluctuations also become less meaningful when the value of K increases, since the noise increases by the square root of cell the number and, therefore, for long periods of time, it fluctuates on a scale of $\sqrt{K}$. This model behavior could be useful to characterize the minimal residual disease (MRD) and how it can develop into the complete cure of the patient or into a relapse, as demonstrated in [41], where the authors showed how random events in MRD may affect the patient's fate. This work may aid clinicians in choosing treatment strategies that reduce the risk of relapse.

Figure 2.

Logistic Growth Model.

Six realizations of a stochastic logistic growth model (continuous blue lines) together with the deterministic solution (black dashed line). N represents a population of cells/molecules, with an initial value N₀, β is the birth rate value (1.2 arbitrary units in this example), δ is the death rate (equal to 1), and K is the carrying capacity [equal to 500 in (A,B) and 5000 in (C,D)].

Stochastic models have been widely used to model clonal evolution in growing tumors and the evolution of resistance to anticancer drugs, which occurs when an initially sensitive tumor no longer responds to treatment due to randomly generated (epi)genetic alterations in cancer cells [6,42., 43., 44.]. Here, discrete stochastic models describe cell growth and mutation acquisition by defining probabilistic reaction rates of the respective events in the form of a Markov process. Some of the most popular models in this context include branching processes [45., 46., 47.], and Moran processes [48] (Box 2 ). One example is research where the PK of erlotinib was linked to the growth kinetics of drug-sensitive and drug-resistant nonsmall-cell lung cancer cell lines and a branching process was used to explore the dynamics of these cells and the resistance to the treatment [49,50]. Another example is the extension of the Moran process shown in [51], where a new type of individual can become advantageous only if it manages to change environmental factors. These models have been widely used to identify optimal dosing regimens that minimize the total number of cancer cells or the probability of developing resistance [49,50,52].

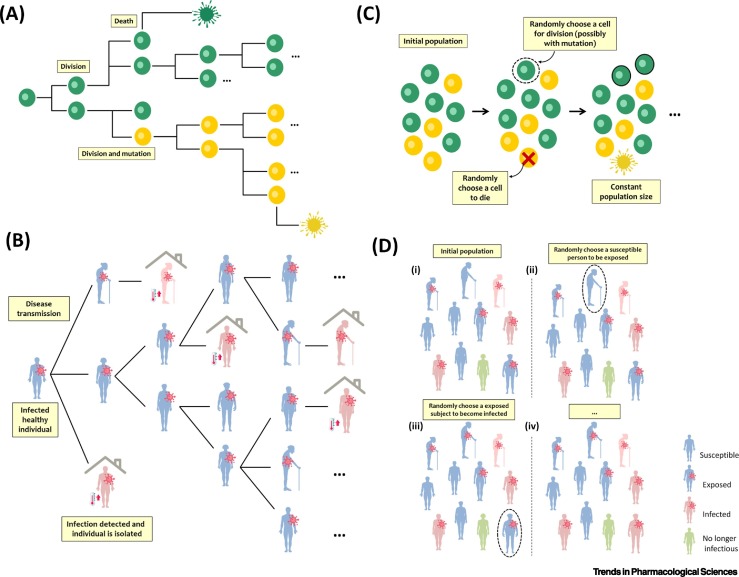
Box 2. Branching Process.

Branching processes are a class of stochastic models that describe the growth and composition of populations by stochastically reproducing individuals of the same or different type [46]. Multitype branching processes are convenient for modeling clonal evolution of cancer cells because new (epi)genetic alterations emerge as random events during cell division and give rise to tumor subclones with different fitness than their ancestors. Here, each cell is fully described by the cell-intrinsic birth, mutation, and death rates (Figure IA). Apart from simulating the growth of heterogeneous cancer cell populations, the distinctive characteristic of these models compared with deterministic approaches is that they allow the probability of developing resistance at any time after treatment initiation to be determined [72].

Branching processes can also be used to model infectious disease spread (Figure IB), where each subject infects a random number of individuals according to some probability distribution. Here, giving birth corresponds to infecting someone and death corresponds to actual death, recovery, or isolation (no longer infectious). The offspring mean in these models correspond to the basic reproduction number, which determines the average number of infections caused by a single individual in a fully susceptible population and is a key factor in determining how fast an infection will spread in a population.

Moran Process

The Moran process, named after the Australian statistician Pat Moran, is a widely used stochastic model in population genetics [48]. In this model, the total population size is fixed and stable coexistence of different cell types is impossible. At each time step, a cell is chosen to divide at random, but proportional to fitness. The chosen cell produces a daughter cell that replaces another randomly chosen cell that dies. Thus, the total number of cells remains strictly constant (Figure IC). This model can be useful not only to describe cancer initiation since the total number of precancer cells tends to be stable, but also as an attempt to include spatial considerations into the stochastic process of selection and mutation [51,73]. Stochastic SIR models can also be thought as a special case of Moran process, because the population size is always constant, but the number of susceptible, infectious, and recovered individuals varies depending on the transmission and recovery rates defined (Figure ID).

Alt-text: Box 2

Another interest area is the use of stochastic processes to model infectious disease transmission [53]. Here, it is vital to take stochasticity into account in the initial epidemic growth because chance can have the most important role when the number of infectives is small. Indeed, contamination is a highly random process that depends on different aspects: the number of contacts between individuals; the transmission rate of the virus; and for how long patients remain contagious. Figure IB shows the two-type branching process described in [54] to characterize the growth of two subpopulations with COVID-19: contaminated but healthy individuals who do not know that they are infected, and detected cases that, once they are discovered, are isolated from the population and stop spreading the virus. Separating the population into two groups is a great simplification of reality and, therefore, the authors of [8] classified individuals into four categories: susceptible; exposed; infectious; and no longer infectious (Figure ID). They defined a more complex contact structure, a stochastic transmission rate, and calculated the risk that introduced infections would establish in a new population. The incorporation of a new treatment in these models could provoke a decrease in the infection rate or an increase in the recovery rate.

Figure I.

Schematic Representation of Branching and Moran Processes.

(A) Schematic representation of a two-type branching process for modeling clonal evolution of cancer cells where new (epi)genetic alterations emerge as random events during cell division and give rise to tumor subclones with fitness (birth and death rates) different from that of their ancestors. (B) Schematic representation of a two-type branching process to characterize infectious disease transmission. Here, contaminated but healthy individuals (blue color) infect a random number of individuals. Infected cases can be detected (red color) and isolated from the population to stop spreading the virus. (C) Schematic showing a Moran process to describe clonal evolution where total population size is fixed. At each time step, a randomly chosen cell divides and the daughter cell replaces another cell that dies. Hence, the total number of cells remains constant. (D) Schematic representation of a stochastic SEIR (susceptible, exposed, infected, and no longer infectious) model where population size is always constant, but the number of individuals in each group varies depending on the transmission and recovery rates defined. (A) and (C) are based on the figure from [74].

Nonlinear Mixed-Effects Models

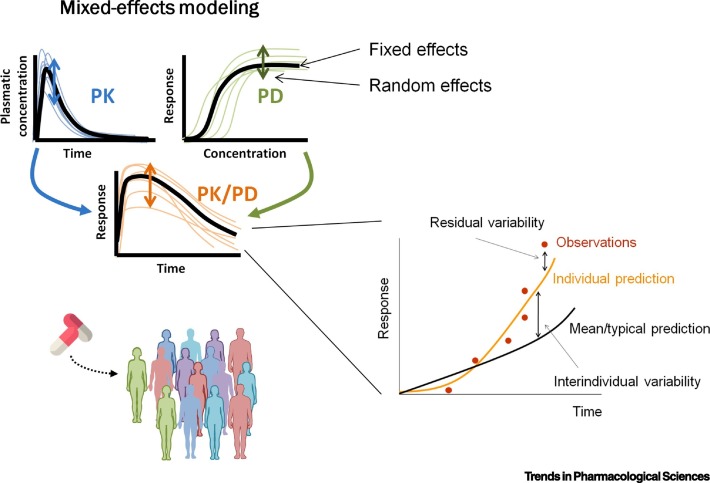
NLME modeling is the gold-standard methodology for the analysis of longitudinal PK/PD data, because it provides a reasonable approximation of the dynamics of the drug in the body and its effects [55., 56., 57.]. NLME models characterize the individuals by a common deterministic model known as the structural model and a statistical model that allows for model parameters to vary within the population. The term ‘mixed-effects’ refers to the presence of both fixed effects that describe the typical parameter values of the population and random effects that handle the variability of the model. In general, there are two sources of random variability; variability assigned to model parameters and residual variability (RV) to account for the differences between the individual prediction of the model and the measured observation. Unexplained parameter variability can be further divided into interindividual variability and between-occasion variability. Figure 3 graphically represents these basic concepts.

Figure 3.

Basic Scheme of the Main Principles of the Mixed-Effects Modeling Approach, the Gold-Standard Methodology in Pharmacometrics.

Fixed effects represent the parameter values that characterize the mean description of the population and random effects handle the unexplained variability of the model. This methodology describes not only the mean/typical behavior of the population, but also the individual profiles of each patient. Interindividual variability describes the difference between the population and individual profiles, whereas residual variability accounts for the differences between the individual predictions and the measured observations.

In the NLME approach, the structural model is generally defined by an algebraic or ordinary differential equation. Even if some randomness in model parameters is involved, this methodology does not allow for uncertainty in the dynamics of the model. Therefore, this stochasticity must not be confused with the stochastic models explained earlier. The stochastic component of NLME models is needed to describe the randomness involved in the measurements of the population but, given an initial condition and the parameter values for every individual, the output of the model will always be the same. The currently most popular tools to estimate parameters in NLME modeling are NONMEMi, MONOLIXii, and Staniii.

This structural model could be replaced with a stochastic model to introduce stochasticity in the dynamics of the model itself. NLME models based on SDEs extend the first-stage model of the hierarchical structure by decomposing the residual variability into measurement noise accounting for uncorrelated errors (assay sensitivity, sampling errors, etc.) and system noise accounting for model misspecifications or true random physiological fluctuations [58,59]. Thus, here three levels of random effects are included. One example of the application of SDEs into PK/PD modeling is work by Mazuka et al. [58], who evaluated the use of SDEs to characterize the absorption properties of single oral dose of metformin. The authors suggested a state equation for the absorption rate parameter of the drug that fluctuates randomly, which managed to better capture the absorption phase of the concentration profiles. Tracking the temporal dynamics of the absorption rate parameter allowed the refinement of the original structural model by using a Weibull function that described the extended release absorption rate. For more applications in PK/PD modeling, see [60].

Bridging the Gap

Up to this point, deterministic and stochastic models can be thought of as distinct modeling paradigms. However, we argue that these approaches are not mutually exclusive and could be combined to create models where components can be deterministic or stochastic.

For instance, NLME models are best suited for modeling extrinsic variability; that is, variability coming from different subjects. The rest of the unexplained intraindividual/intrinsic variability is then modeled using a normally distributed error term. Stochastic models could help to decipher part of this unexplained intrinsic variability by allowing the simulation of processes that can happen at random in every individual and, hence, help in differentiating between real source of errors during measurement collection and errors due to model misspecifications.

We have repeatedly highlighted that stochastic models have been proven to be important to characterize the effects made by small populations (e.g., to analyze the evolution of the minimal residual disease or adoptive cell transfer immunotherapy, or to model the initial infectious disease transmissions). It can be also useful to model in vitro experiments because drug effects are complex and probabilistic at the single-cell level. Genetically identical cells differ widely in their responsiveness to drugs even in a uniform environment due to stochasticity in gene expression levels or other biochemical phenomena [61]. Thus, applying single-cell assays and quantitative modeling to determine which of the observed phenomena arise from processes that are inevitably stochastic, and which ones are explained by the presence of special subpopulation of cells (characterized by covariate models) could be important for the evaluation of different treatments [62] and can possibly explain large amounts of what was previously unknown variability.

However, research efforts that incorporate stochastic phenomena at higher than the single-cell level are rarely found and there is almost no experience in the application of those models to guide clinical trial design or patient management. Some examples of the implementation of SDEs in NONMEM already exist where the absorption or elimination rate constant have been defined as stochastic processes and the extended Kalman filter has been coupled for parameter estimation [63., 64., 65.]. This same method has also been implemented in R [66] and Matlab [67] for estimation of insulin secretion rates. We have also mentioned the use of branching processes for optimal dose regimen identification [52]. However, the use of Gillespie SSA or related more advanced methodologies is rarely seen in combination with population PK/PD models, mainly due to a lack of tools to perform such integration easily. Pumasiv, a Julia-based pharmacometric modeling platform that builds on top of DifferentialEquations.jl, tries to overcome this limitation by allowing these models (SDEs, SSAs, and such mixtures with delay differential equations and stochastic delay differential equations) to be the dynamics of nonlinear mixed-effect, physiologically based PK, or quantitative systems pharmacology (QSP) models. While Pumas is still in its alpha version, this wider array of models will enable pharmacometricians to start exploring effects that were previously inaccessible.

Concluding Remarks

Here, we have raised awareness of stochastic models and how to combine them with existing modeling techniques with the ultimate goal of making future models more versatile and useful. While there are still many aspects that need to be improved, we believe that the activity of combining models could become a major part of PSP in near future, in which different processes could be modeled independently and then integrated in the simulation process through variable transformation and synchronization (see Outstanding Questions). QSP represents a perfect example where different modeling strategies coming from systems biology and pharmacometrics have been merged [68]. Although many advances have been made in this research area over the past decadev [2,69., 70., 71.], the use of stochastic models in QSP is infrequent. However, with recent advances in adaptive stochastic simulation techniques, this area is ripe for pharmacometric modelers to uncover the effects of stochastic models and utilize their inherent randomness to improve the prediction of disease progression and drug effects.

Outstanding Questions.

What are the best practices for integrating models built using different strategies?

Would stochastic model dynamics be considered more often in model-informed drug discovery and development?

Will more straightforward stochastic modeling tools be developed?

Would the activity of combining modeling approaches become a major part of pharmacometrics and systems pharmacology in the near future?

Alt-text: Outstanding Questions

Glossary

Adoptive cell transfer

immunotherapy based on the isolation of immune cells from patients with a tumor, expanded in vitro and readministered to mediate a tumor-specific response.

Basic reproduction number

average number of infections caused by a single individual in a full susceptible population.

Gillespie stochastic simulation algorithm

a general method for numerically simulating stochastic processes that involves repeated generation of random numbers.

Gompertz growth

growth models used for modeling tumors growing in a confined space with limited nutrients, where ultimate depletion of nutrients will eventually slow tumor growth.

Logistic model

growth model the net growth rate of which decreases with increasing tumor size, such that the number of cells is given by an increasing curve that converges on a maximum size.

Markov process

stochastic process in which the conditional probability distribution over all future events depends only on the present state and not on its earlier history.

Master equation

system of ordinary differential equations that describe the temporal evolution of the probability distribution of each state in a particular stochastic system.

Maximum likelihood estimation

procedure that determines values for the parameters of a model by maximizing the likelihood that the process described by the model produces the data that are actually observed.

Minimal residual disease (MRD)

describes the small number of cancer cells that remains in the body after cancer treatment.

Moments of a statistical distribution

numerical characteristic that describes the shape of a probability distribution. The first moment refers to the expected value or mean of the distribution and the second moment indicates the variance.

Pharmacodynamics (PD)

combination of all processes that relate drug concentrations at the site of action with the therapeutic effect of the drug.

Pharmacokinetics (PK)

combination of all processes (absorption, distribution, metabolism, and excretion) that describe the concentration–time profile of a drug in the body.

Pharmacometrics

science of developing and applying mathematical and statistical methods to characterize, understand, and predict the PK/PD behavior of a drug.

Stochastic differential equations (SDEs)

differential equations the coefficients of which are random numbers or random functions of the independent variable.

Systems pharmacology (PSP)

multiscale discipline that focuses on the combination of the interactions among multiple levels of biological organization (molecules, cells, tissues, organs, etc.) and basic principles of PK/PD as a means to describe and predict therapeutic and adverse drug effects at the whole-organism level.

Resources

ⁱhttps://iconplc.com/innovation/nonmem/ⁱⁱhttp://lixoft.com/products/monolix/ⁱⁱⁱhttps://mc-stan.org/^ivhttps://pumas.ai/^vhttps://www.nigms.nih.gov/Training/Documents/SystemsPharmaWPSorger2011.pdf