Confluence of Timing and Reward Biases in Perceptual Decision-Making Dynamics

Abstract

Although the decisions of our daily lives often occur in the context of temporal and reward structures, the impact of such regularities on decision-making strategy is poorly understood. Here, to explore how temporal and reward context modulate strategy, we trained 2 male rhesus monkeys to perform a novel perceptual decision-making task with asymmetric rewards and time-varying evidence reliability. To model the choice and response time patterns, we developed a computational framework for fitting generalized drift-diffusion models, which flexibly accommodate diverse evidence accumulation strategies. We found that a dynamic urgency signal and leaky integration, in combination with two independent forms of reward biases, best capture behavior. We also tested how temporal structure influences urgency by systematically manipulating the temporal structure of sensory evidence, and found that the time course of urgency was affected by temporal context. Overall, our approach identified key components of cognitive mechanisms for incorporating temporal and reward structure into decisions.

SIGNIFICANCE STATEMENT In everyday life, decisions are influenced by many factors, including reward structures and stimulus timing. While reward and timing have been characterized in isolation, ecologically valid decision-making involves a multiplicity of factors acting simultaneously. This raises questions about whether the same decision-making strategy is used when these two factors are concurrently manipulated. To address these questions, we trained rhesus monkeys to perform a novel decision-making task with both reward asymmetry and temporal uncertainty. In order to understand their strategy and hint at its neural mechanisms, we used the new generalized drift diffusion modeling framework to model both reward and timing mechanisms. We found two of each reward and timing mechanisms are necessary to explain our data.

Introduction

In an uncertain and dynamic environment, humans and other animals detect temporal regularities in the environment and use them to inform decision-making (Woodrow, 1914; Rosenbaum and Collyer, 1998; Behrens et al., 2007; Los, 2010; Farashahi et al., 2017). Even in relatively simple perceptual tasks, the timing and accuracy of decisions are sensitive to the temporal statistics of stimuli (Grosjean et al., 2001). Understanding how such regularities are reflected in the response times (RTs) during perceptual tasks is, therefore, important for testing models of decision-making processes and their underlying neural mechanisms (Luce, 1986).

One paradigm for studying perceptual decision-making computations and their neural correlates is to present dynamic sensory evidence over time (Newsome et al., 1989; Roitman and Shadlen, 2002). Evidence accumulation has been proposed as a leading strategy under this paradigm, formalized using the drift-diffusion model (DDM) (Ratcliff, 1978; Ratcliff et al., 2016). In the DDM, a dynamic decision variable integrates evidence over time, and a decision is reached when this variable crosses a bound. An open question is how evidence accumulation is dynamically modulated by temporal uncertainty or stimulus expectation. Such dynamic modulation is important for integrating relevant information while ignoring irrelevant information. Uncertainty in information onset time creates a need to modulate the integration process over time. For example, beginning integration before relevant information is available causes noise to be unnecessarily integrated, reducing accuracy (Laming, 1979; Grosjean et al., 2001). It is unknown how these timing factors should be implemented within a DDM framework. Time-varying bounds (Hanks et al., 2014; Murphy et al., 2016) and gain modulation (Ditterich, 2006b; Cisek et al., 2009) have improved predictive ability for RT patterns, but have not been used to explain uncertainty in stimulus onset time.

In addition to sensory evidence and temporal expectation, decisions should incorporate differences in value among the options. Reward bias has long been an active topic of research (Laming, 1968; Ratcliff, 1985; Feng et al., 2009; Rorie et al., 2010; Mulder et al., 2012), with more recent attention to its connections to timing (Lauwereyns et al., 2002; Gao et al., 2011; Hanks et al., 2011; Drugowitsch et al., 2012; Nagano-Saito et al., 2012; Voskuilen et al., 2016). While these asymmetries have previously been incorporated into the DDM framework (Edwards, 1965; Laming, 1968; Ratcliff, 1985; Ratcliff and McKoon, 2008; Mulder et al., 2012), the strategies through which sensory, value, and timing information are combined to form a decision are still poorly understood.

To investigate these issues, we developed a novel behavioral paradigm in which evidence onset is temporally uncertain. Therefore, the temporal structure of evidence could be strategically exploited during decision-making. By simultaneously manipulating reward differences between options, we also examined whether and how time-varying evidence interacts with temporal strategies to produce reward bias. We trained monkeys to perform this task, and found that the animals exploited the temporal structure of the evidence and adjusted decision timing to reduce evidence onset uncertainty.

To model the decision-making behavior, we fit generalized DDMs (GDDMs) to choice and RT behavior. GDDMs encompass both the DDM and nonintegrative models as special cases (Cisek et al., 2009; Thura et al., 2012). We found that a GDDM with timing and reward processes can quantitatively capture the animal's behavior as determined by its RT distribution. Temporal modulation of the integration process can be implemented through an urgency signal, which varies across time. Such an urgency signal can flexibly adjust the animal's behavior as task timing demands change. In addition, capturing reward-related behavioral effects required two mechanisms: one dependent on the integration process and the other independent of integration. Overall, our findings suggest that evidence accumulation in perceptual decision-making can be flexibly modulated by temporal and reward expectation, and that GDDMs capture these phenomena.

Materials and Methods

Experimental design

Animal preparation

Two male rhesus macaque monkeys (Q and P, identified as Monkey 1 and Monkey 2, respectively: body weight, 10.5-11.0 kg) were used. The animal was seated in a primate chair with its head fixed, and eye position was monitored with a high-speed eye tracker (ET49, Thomas Recording). All procedures used in this study were approved by the Institutional Animal Care and Use Committee at Yale University, and conformed to the Public Health Service Policy on Human Care and Use of Laboratory Animals and Guide for the Care and Use of Laboratory Animals.

Behavioral tasks

Animals were trained to perform a color matching task, in which the onset time of the sample was systematically manipulated by varying the duration of noninformative stimulus (presample) that preceded the sample. Two versions of the task were used. First, in the color matching task with asymmetric reward (see Fig. 1a), either large or small magnitude of reward was randomly assigned for identifying the correct color of the sample at a given trial. Presample duration was randomly selected from three discrete values at each trial. Second, in the color matching task with timing blocks (see Fig. 1b), two sets of presample intervals were used and presented in alternating blocks of trials (i.e., short- and long-presample blocks). In each block, presample duration was randomly selected from three discrete values. The magnitude of reward was the same for all correct choices. Animals were first trained for the task with timing blocks and then for the task with asymmetric reward. RT was measured from the time of target fixation.

Figure 1.

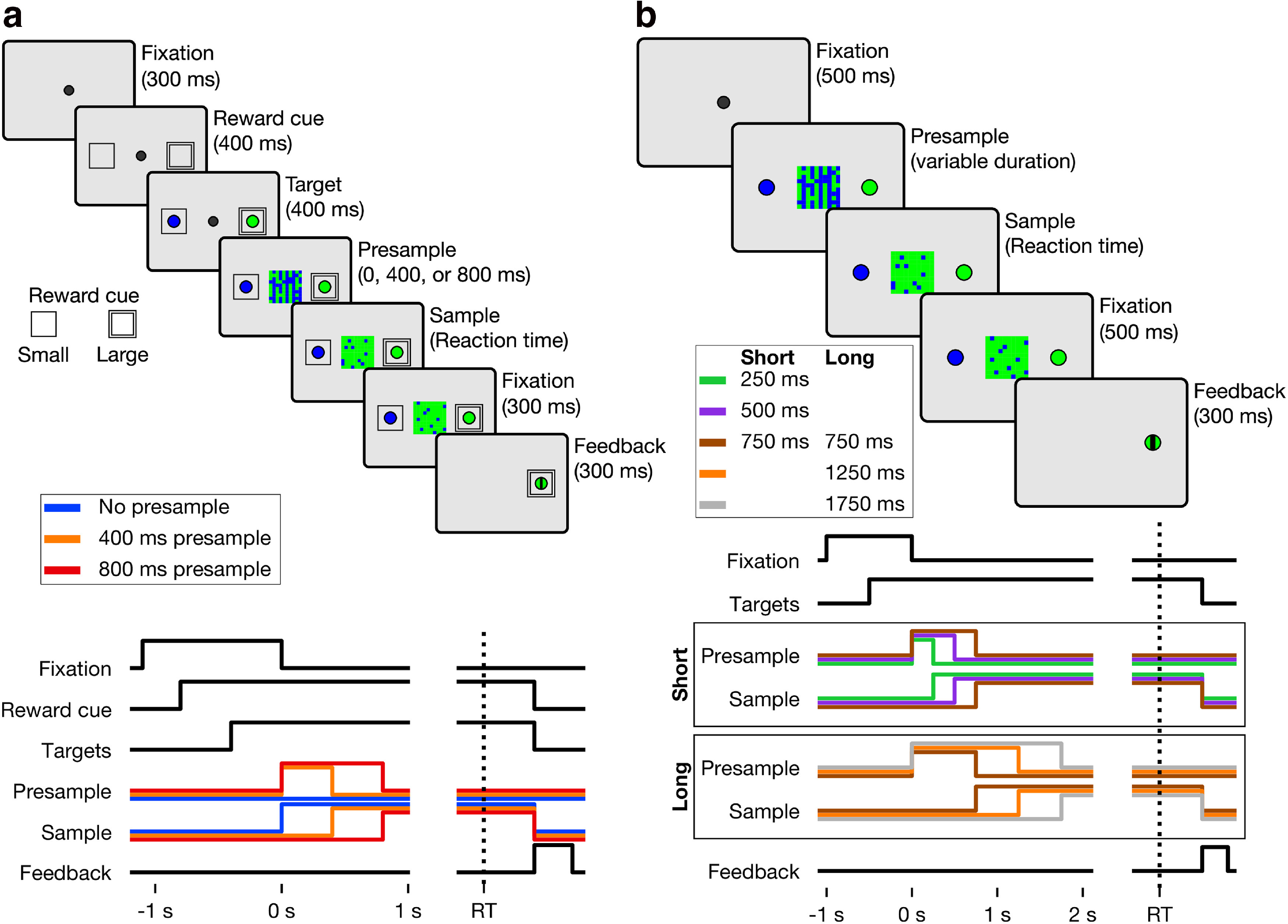
Behavioral task. a, Color matching task with asymmetric reward. Top, For each task, the temporal sequence of trial events. Inset, Reward cues indicating a large or small reward. Bottom, Timeline indicating the presence of various task elements on the screen, with presample and sample lines for each condition represented by the line color. b, Color matching task with timing blocks. Similar format to a. The timeline of task events is split by presample duration.

Color matching task with asymmetric reward

Each trial began when the animal fixated a central square (white, 0.6° × 0.6° in visual angle) (see Fig. 1a). After the 0.3 s fixation period, cues indicating magnitudes of reward available from two alternative choices were presented at the potential locations of saccade targets. Two sets of reward cues were used: in addition to those shown in Figure 1a, for some sessions, a circle was used for the large-reward target and a diamond for the small-reward target. Two nested squares in thin gray lines (or a circle) and a single square in thicker white lines (or a 45°-angled square) indicated larger and smaller reward, respectively. The ratio of reward magnitude was 2:3 and 1:4 for Monkeys 1 and 2, respectively. Following the reward-cue period (0.4 s), a green disk was presented inside one of the two reward cues and a blue disk appeared within the other, serving as targets for choice saccade. After 0.4 s of target period, a checkered square with equal numbers of green and blue pixels (20 × 20; 1.63° × 1.63° in visual angle), or presample, was presented replacing the central fixation target. In addition, green and blue pixels were dynamically redistributed to random positions at a rate of 20 Hz. After a variable interval (0, 0.4, 0.8 s), the presample was replaced by the sample, which was identical to the presample, except that it contained green and blue pixels in different proportions. Presample duration was randomly sampled from the three intervals with equal probability. The animal was allowed to shift its gaze toward one of the peripheral target at any time after the onset of the sample and was rewarded only when it correctly chose the target with the same color as the majority of the pixels in the sample. Choices made during presample were punished by an immediate end of the trial followed by a 2 s timeout. Three levels of color coherence were used for the sample (6%, 20%, 40% for Monkey 1; 4%, 14%, 26% of pixels for Monkey 2), each with equal probability. In ∼5% of the trials, the presample never changed to a sample, meaning the coherence of each color was 50% and there was no correct choice. On these trials, a reward was delivered with 50% probability regardless of the monkey's choice. After 0.3 s of fixation on the chosen target, feedback was provided for 0.3 s with a horizontal or vertical bar superimposed on the chosen target, indicating erroneous or correct choice, respectively. Reward was delivered only for correct choices. Color coherence, location of saccade target with correct color, presample duration, and location of large-reward cue were pseudo-randomly selected for each trial. Monkey 1 performed 30,868 trials across 50 sessions, and Monkey 2 performed 23,695 trials across 29 sessions.

Color matching task with timing blocks

The sequence of trial events was the same as in the color matching task with asymmetry (see Fig. 1b), except that fixation and saccade targets were presented simultaneously without the reward cue, and the durations of the presample varied between blocks. Presample duration for the majority of the trials (60%) in the short- and long-presample block was 0.5 and 1.25 s, respectively. In the remaining trials, the presample was terminated with equal probability (20%) either earlier (0.25 and 0.75 s for short- and long-presample blocks, respectively) or later (0.75 and 1.75 s for short- and long-presample blocks, respectively) than the most frequent presample durations. Choices made during the presample were penalized by subsequent 5 s timeout. Three levels of color coherence were used for the sample (8%, 20%, and 40% for both monkeys), each with equal probability. Short- and long-presample blocks alternated within a given session and the order of the two types of block was randomized across sessions. Monkey 1 performed 12,773 trials across 10 sessions, and Monkey 2 performed 10,777 trials across 10 sessions.

Training procedure

Animals were initially trained for the color matching task without presample. Once the performance reached learning criteria (e.g., probability of correct choice ≥0.75 [≥0.5] for high [low] coherence sample), the presample of variable duration was introduced. A premature choice during the presample was explicitly signaled by immediate removal of all stimuli on the screen, including the presample, followed by a timeout. Animals were first trained on the color matching task with timing blocks with short- and long-presample blocks in separate sessions, and then two types of blocks were combined within a session. After the behavioral dataset was collected for the color matching task with timing blocks, training for asymmetric reward began by introducing two different magnitudes of reward as well as reward cues around saccade targets. After introducing the asymmetric reward, we did not impose any additional performance criteria to punish animals' reward bias. Training of the animals followed a common strategy used in previous human studies. Namely, the temporal structure and contingencies of the task were learned under the easy condition, with difficult conditions being gradually introduced, and distinct types of feedback were provided for incorrect and premature choices (Devine et al., 2019). There was no significant change in incorrect responses to high-coherence small-reward trials across sessions (Kendall-Mann trend test p > 0.05 for both monkeys).

Statistical analysis

Behavioral analyses

In analyzing animals' behavior, we measured RT relative to the presample onset. When we refer to the RT relative to the onset of the sample, this is explicitly referred to as sample RT.

A linear model was fit to examine the dependence of RT on task parameters as follows:

as well as sample-aligned RT on task parameters as follows:

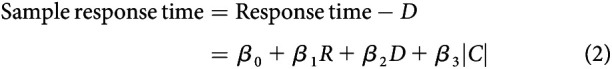Here, R is reward magnitude, where 1 indicates that the large-reward target was the correct response and 0 that the small-reward target was correct; D is presample duration in units of seconds; and $\left|C\right|$ is unsigned coherence, where 1 corresponds to a solid color patch and 0 to an equal ratio of each color. We define RT relative to the onset of the presample, rather than the sample, given that the transition from presample to sample was not explicitly cued. Coherence takes values ≥0. All notation is described in Table 1.

Table 1.

Summary of notation^a

Notation	Definition
Task variables
D	Presample duration in ms
C	Coherence strength from −1 to 1; C > 0 indicates large-reward target correct
R	1 = large-reward target correct; 0 = small-reward target correct
B	1 = long-presample block; 0 = short-presample block
Parameters
s	Signal-to-noise ratio (s > 0)
$\ell$	Leak magnitude, 0 = perfect integration; ∞ = no integration ($\ell \ge 0$)
tnd	Non-decision time ($t_{nd}\ge 0$)
μ	Drift rate (DDM only) ($\mu \ge 0$)
σ	Noise (DDM only) (σ > 0)
pL	The probability of a lapse ($p_L\ge 0$)
λ	Decay rate of lapse trials (symmetric) (λ > 0)
t1	Onset time of increase in urgency ($t_1\ge 0$)
σ0	Urgency at time t = 0 (${\sigma }_0>0$)
$m_{\sigma }$	Slope of linear ramp in gain function (mσ ∈ ℝ)
τB	Decay rate of exponential decrease in bounds (${\tau }_B>0$)
x0	Starting position of decision variable (x0 ∈ ℝ)
m	Increase in leak baseline over time (m ∈ ℝ)
me	Momentary bias in sensory evidence (DDM only) (me ∈ ℝ)
pmap	Probability of a mapping error given the threshold was crossed for the small-reward target (p ≥ 0)
λhr	Decay of lapse probability toward the large-reward target (replaces λ) (λhr ≥ 0)
λlr	The decay rate of lapse trials toward the small-reward target (replaces λ) (λlr ≥ 0)
Miscellaneous
x	Decision variable
$\Gamma (t)$	Gain function
$\Theta (t)$	Decision bound
I	Indicator function
W	Wiener process
G	1 = correct trial; 0 = error trial
βi	Regression coefficients
τ	The leak time constant, defined as $\frac{1}{\ell }$

^aAll mathematical notation used in equations and models.

To examine second-order interaction terms, a second model was fit as follows:

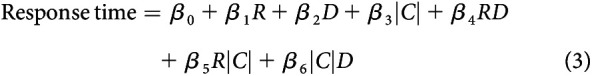Similarly, a logistic regression model was fit to understand how the task parameters influenced the monkey's decision to choose the correct target as follows:

where variables are as defined above. Likewise, a second model was fit which contained second-order interaction terms as follows:

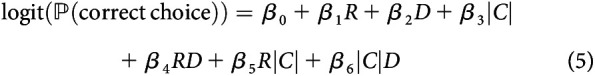Trials with zero coherence were excluded from these regression analyses.

Likewise, RT was examined for the color match task with timing blocks using the linear model as follows:

where B is the block, coded as 0 for the short-presample block and 1 for long-presample, and other terms are as specified above. Accuracy was likewise analyzed with the logistic regression model as follows:

DDM with reward mechanisms

The DDM is governed by a decision variable x. The evolution of x in our reward-biased DDM model, similar to that of Fan et al. (2018) and Gesiarz et al. (2019), is described as follows:

where the following parameters were fit to data: μ is signal strength; σ is noise level; and m_e is momentary sensory evidence bias.

Additional terms in the model are as follows: W, a Wiener process with standard deviation 1; C, the color coherence; and $I_{t>D}$, an indicator function for the presample on the current trial. I_t>D = 0 if t is in the presample, and I_t>D = 1 otherwise.

We specify that x has initial condition given by parameter x = x₀ at t = 0 s to capture reward bias. We use the convention that positive values of x indicate choices toward the large-reward target; thus, positive coherence indicates motion toward the large-reward target and negative coherence away from it. When $\left|{\displaystyle {\int }_0^t\text{d}}x\right|\ge 1$, a decision to choose left or right is made based on the sign of x. Since the parameter σ is fit to data, integration bounds are fixed at 1 to prevent over parameterization. The RTs generated by this model were increased by the non-decision time t_nd.

Since our fitting procedure is based on maximum likelihood, rare trials in which the choice appears unrelated to the stimulus (lapses) may have a large impact on the fitted parameters. Normally, this is addressed with a uniform distribution mixture model, whereby the probability of any given RT is some fixed value plus the distribution generated by the DDM (Ratcliff and Tuerlinckx, 2002). This solves the problem of fitting to likelihood but does so in a way that imposes an unnatural hazard function. Ideally, this mixture distribution should have a flat hazard rate. Thus, for the purposes of model fitting, we fit a mixture model between the drift-diffusion process and an exponentially distributed lapse rate with rate parameter λ. This is given by the following:

where there is a p_L probability of any given trial being a lapse trial, and t is the RT. While we fit both the p_L and λ parameters to data, results were unchanged when we fixed these parameters at constant values (data not shown).

Thus, overall, this model contained seven parameters: three to capture the basic DDM process (μ, σ, and t_nd), two for the mixture model (p_L and λ), and two to capture the reward mechanisms (x₀ and m_e).

GDDM

Like the DDM, the GDDM is governed by the evolution of a decision variable x. The instantaneous value of x is described by:

where the parameters that could potentially be fit by simulations are as follows:

• $\ell$: The leak parameter, constrained to $\ell \ge 0$ because a negative $\ell$ would correspond to unstable integration. Its inverse is the leak time constant.

• x₀: The initial position of the integrator, and the location to which the leaky integrator decays. This was constrained to be $x_0\ge 0$. By default, it was fixed to x₀ = 0.

• m: The change in the leaky integrator baseline over time. By default this was fixed at m = 0.

• Γ(t): The sensory gain, a function of time. By default, $\Gamma (t)={\sigma }_0$.

• s: The signal-to-noise ratio, constrained to s ≥ 0. This is analogous to the ratio $\mu /\sigma$ in the DDM.

• $\Theta (t)$: The decision bound. When $\left|{\displaystyle {\int }_0^t\text{d}}x\right|\ge \Theta (t)$, a decision to choose left or right is made based on the sign of x. Since noise is allowed to vary, integration bounds are subject to the constraint Θ(0) = 1 to prevent overfitting. In the absence of collapsing bounds, this fixes the bounds to be equal to ±1, the default.

Additional terms in this equation are defined as follows:

• W: White noise (i.e. a Wiener process).

• C: Coherence. We use the convention that positive values of x indicate choices toward the large-reward target; thus, positive coherence indicates motion toward the large-reward target and negative coherence away from it.

• I_t>D, An indicator function for the presample on the current trial. I_t>D = 0 if we are in the presample, and I_t>D = 1 otherwise.

As above, we fit a mixture model between the drift-diffusion process and an exponentially distributed lapse rate with rate λ, with a p_L probability of any given trial being a lapse trial. This is given by the following:

Overall, in the simplest possible case where all parameters are set to their defaults (thereby indicating that no reward or timing effects are included in the model), the model includes six parameters: three to capture the basic DDM process (s, σ₀, and t_nd), two for the mixture model (p_L and λ), and one to capture leaky integration ($\ell$). Reward and timing mechanisms added to the model increased the number of parameters as explained below.

Reward mechanisms

Within the GDDM framework, we designed reward mechanisms for the model according to our hypothesized cognitive mechanisms.

Initial bias

The total evidence necessary to reach a decision might be lower for the large-reward target than for the small-reward target. This is equivalent to changing the starting position of integration. Because our model deals with leaky integration, we furthermore impose that the leak decays to this position instead of to zero. This adds one parameter to the model: the magnitude of the baseline shift x₀.

Time-dependent bias

The total evidence necessary to reach a decision might be initially the same for the large- and small-reward targets, but a bias may develop toward the large-reward target over the small-reward target that increases linearly over time. Without leak, this is equivalent to a constant bias on the drift rate (i.e., a continuous integration of a constant). Because our model deals with leaky integration, such a bias would instead change the point to which the leaky integrator decays. Thus, we model this bias by temporally modulating the position to which the leaky integrator decays. This adds one parameter to the model: the slope of the increase in large-reward bias m.

Mapping error

After integrating to the bound, with some probability, small-reward choices may be mapped to a response toward the large-reward target. Equivalently, some percentage of small-reward choices might be assigned to be large-reward instead. This is different from a standard lapse in that it always applies in the direction of the large-reward target. This mechanism was first described in discrete evidence paradigms (Erlich et al., 2015; Hanks et al., 2015). This mechanism adds one parameter to the model: the probability of making a mapping error on any given trial p_map.

Mapping error was implemented by modifying RT histograms obtained from the simulations. For a simulated probability density function $f(x|R=r,C=c,G=g,D=p)$, where R is large versus small reward, C is coherence, G is correct or error trial, and D is the presample duration, we compute the final density $f\prime (x)$ using f(x). For the mapping error, this was calculated as follows:

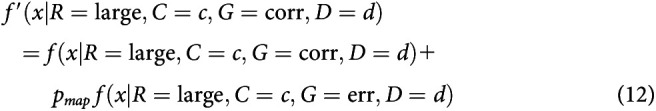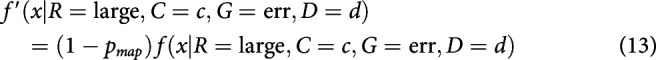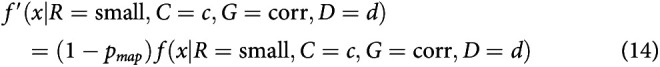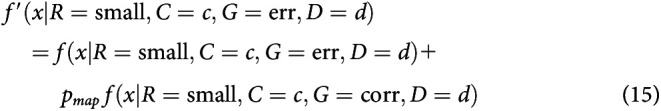Lapse rate bias

The lapse rate, assumed to be exponentially distributed, may have been higher in the direction of the large-reward target compared with the small-reward target. This is given for large- and small-reward targets respectively by the following:

This mechanism has three parameters: the lapse rates for both large- and small-reward targets λ_hr and λ_lr, and the probability of any given trial being a lapsed trial p_L. Models that include this mechanism do not include unbiased lapse rate, as it is redundant. Since the unbiased lapse rate uses two parameters, this mechanism adds one net parameter to the model.

Timing mechanisms

Similarly, we designed timing mechanisms to capture the ideas of urgency signals. Two types of urgency signal have been previously described in the literature: a “gain function,” which scales evidence and noise uniformly throughout the course of the trial (Gold and Shadlen, 2001; Ditterich, 2006b; Cisek et al., 2009); and “collapsing bounds,” which cause the decision bounds to become less stringent as the trial progresses (Drugowitsch et al., 2012; Hanks et al., 2014; Murphy et al., 2016).

Collapsing bounds

Collapsing bounds can be used to implement an urgency signal of various forms. While much debate has focused on the correct form of the bounds (Hawkins et al., 2015a; Malhotra et al., 2018), we use an exponentially collapsing bound for simplicity. This mechanism adds one parameter to the model: the time constant of the exponential collapse τ_B. It is implemented as follows:

This form satisfies the imposed boundary condition Θ(0) = 1.

Delayed collapsing bounds

This implements an exponentially decreasing bound as an urgency signal similarly to collapsing bounds, except that the bounds do not begin to collapse until late in the trial. This mechanism adds two parameters to the model: the time before the bounds begin to collapse t₁ and the rate of collapse τ_B. This is implemented as follows:

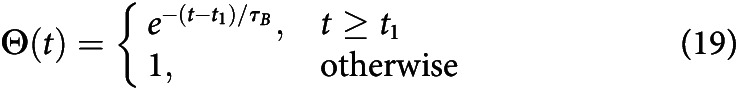These also satisfies the boundary condition Θ(0) = 1 for all t₁ ≥ 0. This shared similarities with other forms of collapsing bounds (Hawkins et al., 2015a; Zylberberg et al., 2016).

Linear gain

A gain function can also be used to implement an urgency signal. It scales both the evidence and the noise simultaneously to preserve signal-to-noise ratio. This mechanism adds one parameter to the model: the rate at which gain increases $m_{\sigma }$. It is implemented as follows:

Delayed gain

The delayed gain function implements an urgency signal similarly to linear gain, but it does not begin to increase the grain until part way into the trial. This mechanism adds two parameters to the model: the time at which the value begins to ramp t₁ and the slope of the ramp $m_{\sigma }$. It is implemented as follows:

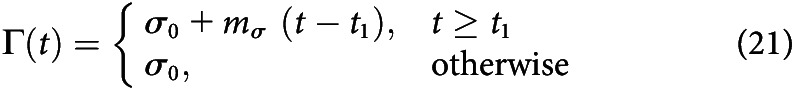Simulations without leak

Simulations without leak were performed by setting $\ell =0$.

Fitting method

As we fit models with many parameters, we must be careful about the methods used for parameter estimation. One common approach in the field is to fit the parameters of the DDM based only on the probability of a correct response and the mean RT for correct trials. This uses only a very small subset of the data, using only two summary statistics, and is thus insufficient for fitting complex models. A second approach, which is commonly used when fitting complex models, is to simulate individual trajectories of the decision variable, and then perform tests on the quadrants of the simulated values to determine whether there is a match. While this approach utilizes more data than the previously discussed method, it still uses only summary statistics of the data. More critically, this simulation process is very slow, and hence does not permit efficiently fitting the model to data. These two approaches are principally used to overcome limitations in simulating and fitting these models, namely, that a full RT distribution is not always available. Our approach simulates the stochastic differential equations by numerically solving the Fokker-Planck equations so that we may use likelihood-based methods on the entire RT distribution for estimating parameters. This allows all data to be used through a robust statistical framework.

RT distributions simulated directly from the Fokker-Planck equation often use the forward Euler method, an easy-to-implement method for solving stochastic differential equations. The forward Euler method mandates the use of very small time steps and a coarse decision variable discretization to maintain numerical stability. In practice, this means that simulations that achieve a reasonable margin of error are prohibitively time-consuming for fitting parameters.

To circumvent this, we instead solve the Fokker-Planck equation using the Crank-Nicolson method (for the fixed-bound conditions) or the backward Euler method (for the collapsing bound conditions). These methods do not require small time steps to achieve low margin of error. As a result, we are able to fit parameters using the results of these numerical solutions. Simulations were performed using the PyDDM package (Shinn et al., 2020) using a time step of 5 ms and decision variable discretization of 0.005. Correctness of the implementation was verified using specialized techniques (Shinn, 2020). The models in this paper, in conjunction with an interactive viewer, are available at https://pyddm.readthedocs.io/en/latest/cookbook/papers/shinn2020.html.

Optimization routine

Fitting is performed by minimizing the negative log-likelihood function. For low-dimensional models, parameters may be optimized using a variety of local search methods, and these tend to give similar results. To increase the speed of convergence, many of these methods will estimate the gradient. However, for high-dimensional models, local search methods are often unable to minimize the log-likelihood function for two reasons. First, in high dimensions, the gradient will often flatten, making it difficult for these methods to operate. In practice, they fail to converge to a local minimum. Second, there may be multiple local minima, and these search methods cannot distinguish between a local and a global minimum. On way of addressing this is to perform the search several times with different initial conditions and select the best one, such as basin hopping (Wales and Doye, 1997). However, this relies on the fact that there are few local minima. Alternatively, this can be solved using a dedicated method for global optimization, such as differential evolution (Storn and Price, 1997).

Because we were simultaneously fitting up to 16 parameters, using an appropriate optimization routine was critical. Through the Scipy package (Virtanen et al., 2020), we tried the L-BFGS-B method (a local search method that approximates the gradient), the Nelder-Mead simplex method (a local search method that does not use the gradient) (Gao and Han, 2012), basin hopping, and differential evolution. Of these, only differential evolution both converged and gave consistent measurements across resets. Thus, we used differential evolution for parameter optimization.

Cross-validation procedure

Once obtaining a fit, there are many different processes that may be used for evaluating the fit of a model to protect against overfitting. There are two types of overfitting that are important to consider for complex models, such as ours, with many parameters. First, overfitting may occur because the model mechanism is complicated; thus, the parameters of the model may fit to noise within the data. Second, overfitting may be the result of the modeler testing many potential model mechanisms and choosing the best mechanism. Simple models with few parameters may only be concerned with the first of these, but models with complicated mechanisms must guard against both types of overfitting.

Many papers simply evaluate the best fit and report these values. This does not protect against either overfitting the parameters or overfitting the model mechanism. A more sophisticated approach is to use a measure, such as AIC or Bayesian information criterion (BIC), which takes the model complexity into account when comparing two competing models. However, these metrics judge model complexity exclusively by the number of parameters, and this has been shown to be a poor metric for evaluating model complexity because of differences in parameter expressivity (Myung et al., 2000; Piantadosi, 2018). BIC places a stronger penalty on model complexity than AIC. Additionally, this only helps with overfitting the parameter values and does not prevent overfitting of the model mechanism.

A better approach is to use k-fold cross-validation, which will properly penalize complex models over simple models by ensuring that the parameters are not overfit. While better than AIC and BIC, k-fold cross-validation still does not protect against overfitting the model mechanism. In order to test for this using k-fold cross-validation, we would need to perform k-fold cross-validation within a separate independent test set only after models are finalized. However, because the test would be completely independent, there is no conceptual advantage to performing k-fold cross-validation within the test dataset. Furthermore, k-fold cross-validation requires refitting the model separately to each subset of the data. Because of the long execution time of our model, it is not practical to repeat this fit several times for each model.

For complex models, the best way to prevent overfitting is to use held-out data, which are not analyzed or otherwise examined in any way until the final model has been constructed and the conclusions of the model have been determined. Therefore, to ensure robustness and protect against both types of overfitting, we split the dataset into two halves: an “exploration” dataset and a “validation” dataset. All analyses and model fitting were performed only on the exploration data using BIC for comparing models. The validation trials were not fit to the model or otherwise examined until all analyses for the present manuscript were complete. After unmasking the validation trials, no additional analyses were performed, no additional results were added to the manuscript, and no existing results were removed. For a more robust analysis, we evaluate models on the validation dataset using the held-out log-likelihood (HOLL), that is, the likelihood under the held-out (validation) data when parameters were fit using the exploration dataset (see Figs. 2, 3, 6, 7). All quantitative and qualitative results found using BIC were unchanged when using HOLL with the validation dataset; in particular, the regression model analyses were unchanged, and there were minimal changes in the GDDM model fits. The difference between the rank order validation HOLL and rank order exploration BIC for the 78 GDDMs was at most 2 in both monkeys for all models with log likelihood falling within 1000 of the best model, and a total of zero models in Monkey 1 and 8 models in Monkey 2 had a rank difference >5. Thus, multiple model comparison approaches in different subsets of the data converged on the same results.

Figure 2.

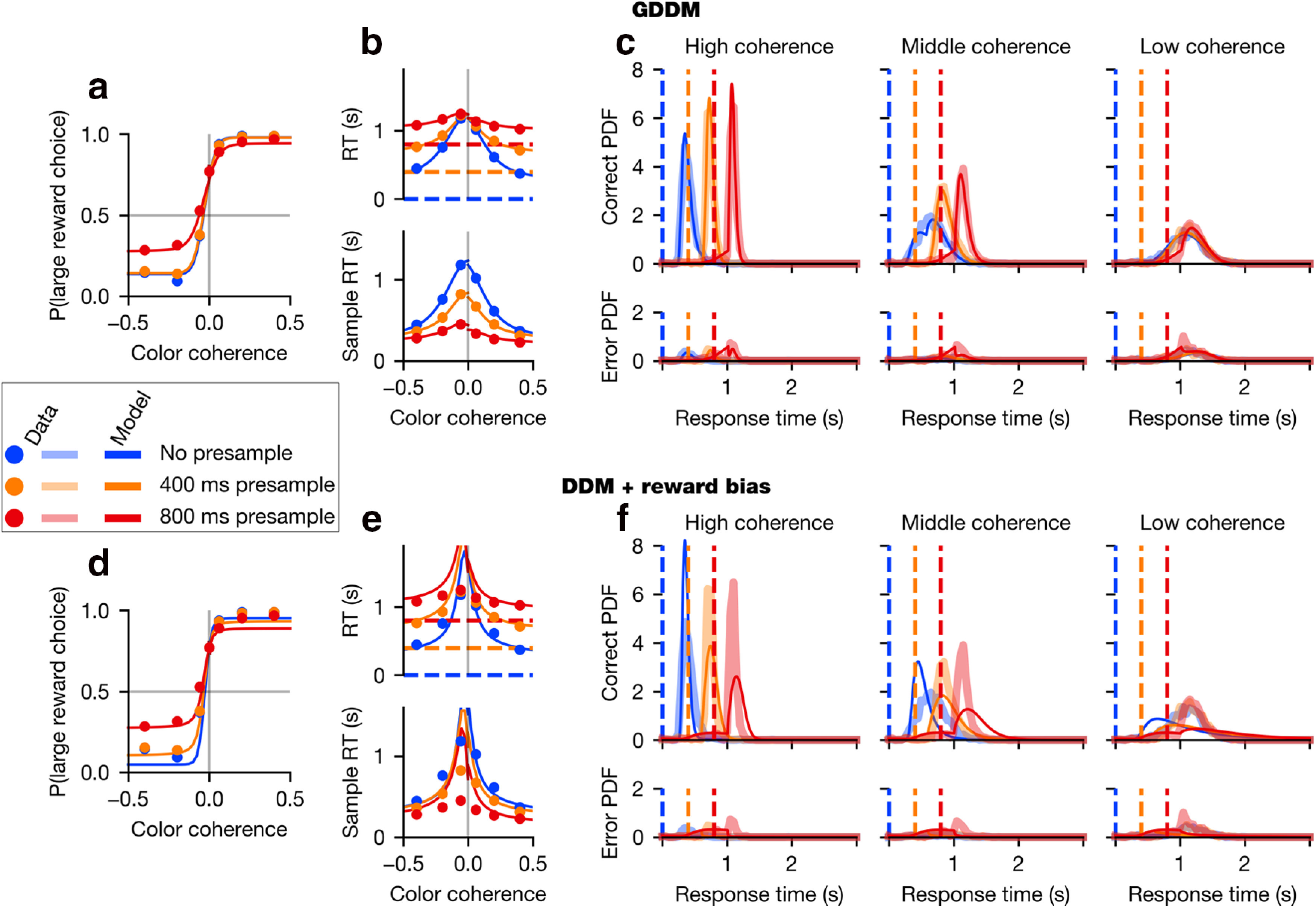
Monkey 1 data and model performance. Psychometric (a, d) and chronometric (b, e) functions, as well as RT histograms (c, f), are plotted for the validation data of Monkey 1. Data are plotted for each coherence value as dots in the behavioral function (a, b, d, e) and as thick translucent lines in the probability distributions (c, f). “Sample RT” indicates the RT minus the presample duration. Overlaid in as a thin solid line is the model fit for the best-fit (a–c) GDDM with collapsing bounds described in “Modeling strategies during perceptual decision-making” or (d–f) DDM with reward mechanisms described in “Violation of time-invariant evidence accumulation”. Parameters were fit to the exploration data in each case. Error bars for 95% CI are hidden beneath the markers.

Figure 3.

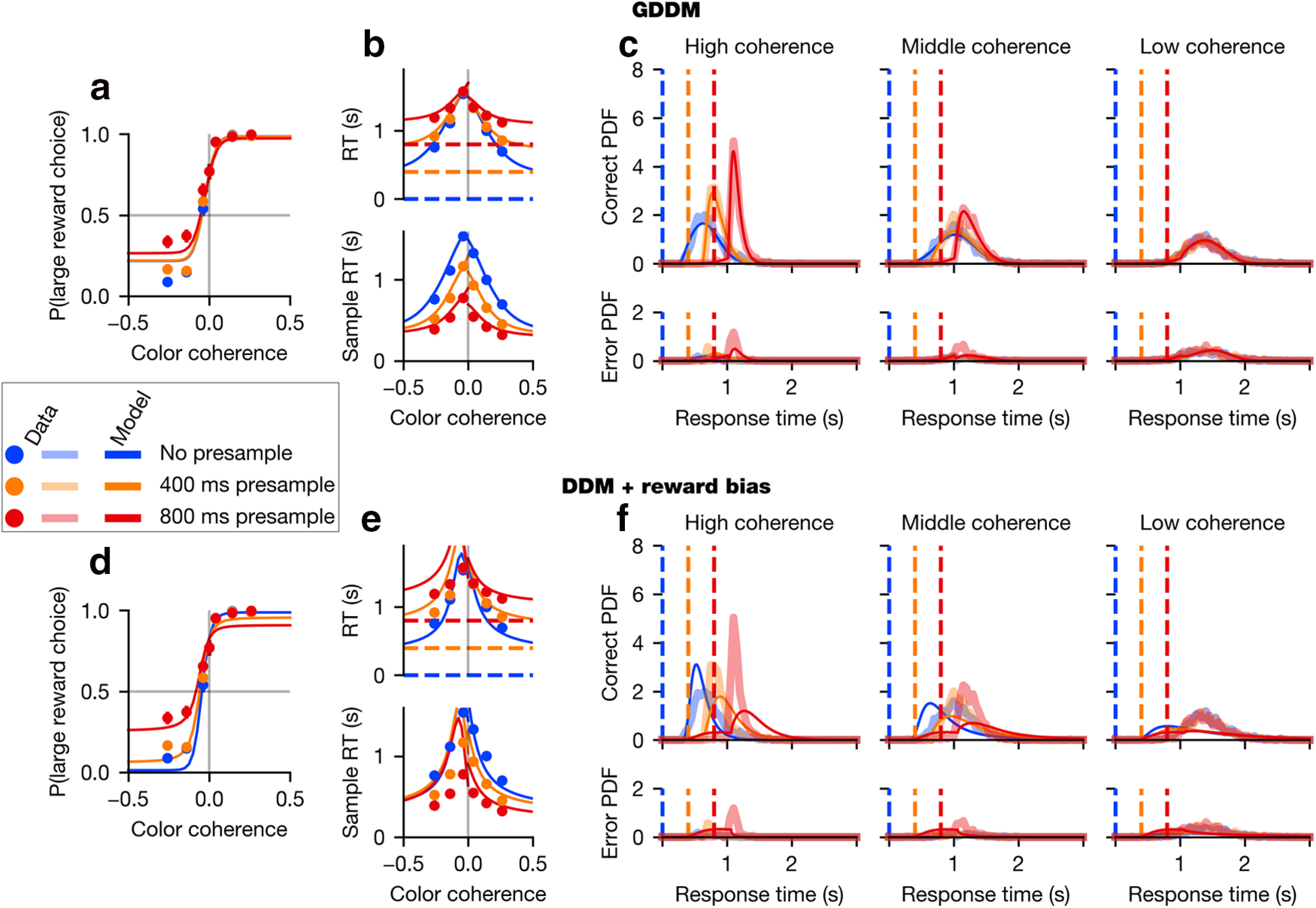
Monkey 2 data and model performance (a–f). Format similar to Figure 2, but with data from Monkey 2. Plotted is the validation data, whereas model parameters were fit to the exploration data.

Figure 6.

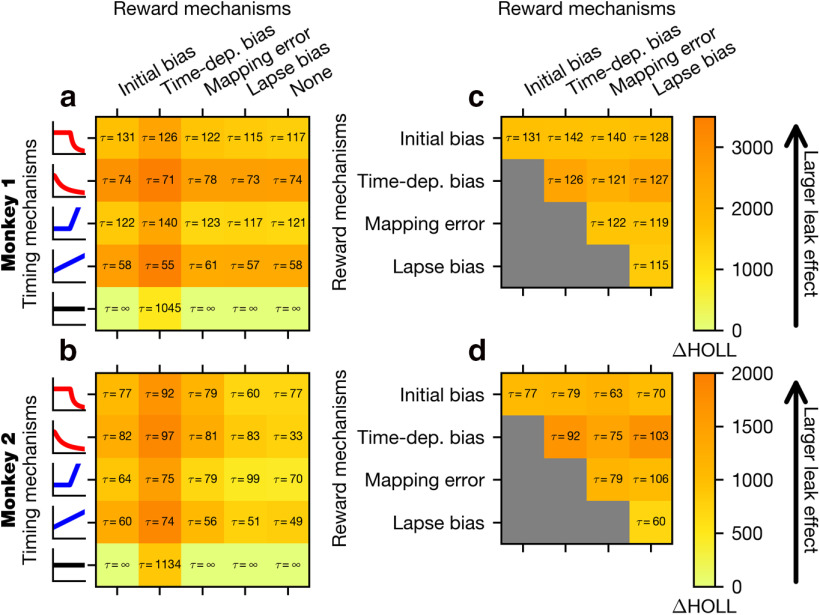
Leaky integration improves model fit nonuniformly. All models shown in Figure 6 were subsequently fit to the exploration data with leaky integration disabled. The difference in HOLL on the validation data is shown, with larger ΔHOLL indicating a larger effect of leaky integration. As in Figure 6, models involving one reward mechanism and one urgency signal (a, b) as well as models involving two timing mechanisms in conjunction with the delayed collapse urgency signal (c, d) were examined for Monkey 1 (a, c) and Monkey 2 (b, d). Overlaid are leaky integration time constants in units of milliseconds for each model.

Figure 7.

Impact of parameters on RT and choice. A positive perturbation was made to each model parameter from the best-fit delayed collapsing bounds model for Monkey 1. As a representative increase, perturbations were chosen such that the model's HOLL decreased by 2000. a, Direction of perturbation. For each parameter, the change in mean RT (x axis) and accuracy (y axis) are plotted, and then normalized to lie on the unit circle to aid in visualization. Top left, Increases in accuracy and decreases in RT. Bottom left, Decreases in accuracy and increases in RT. b–d, Absolute perturbations for different presample durations and coherence levels. The mean RT and accuracy of the best fit delayed collapsing bounds model are plotted as points for each presample and coherence condition, averaged across reward magnitude. Color hue represents presample duration, and saturation indicates color coherence. Arrows indicate the perturbed model's speed and accuracy. Points with a black circle represent small arrows with lengths <10% of the plot size.

We did not perform this validation procedure on the task with timing blocks, as sample size was limited. Nevertheless, all models were developed on data from the task with asymmetric reward before being applied to data from the task with timing blocks.

Software accessibility

Software is available at https://github.com/murraylab/PyDDM.

Results

Behavioral task

Two rhesus monkeys were trained to perform a two-alternative forced choice, color matching task (Fig. 1a). In each trial, a central square patch was presented consisting of a 20 × 20 grid of green and blue pixels that rearranged randomly at 20 Hz. Stimulus presentation was divided into two consecutive periods containing an uninformative “presample” and informative “sample.” The animal indicated its choice by shifting its gaze to one of two flanking choice targets, one green and one blue. The trial was rewarded via juice delivery if the selected target color corresponded to the majority color of pixels in the sample. Task difficulty was manipulated by parametrically varying the proportion of pixels of each color in the sample, which we refer to as color coherence. Animals were allowed to direct their gaze to a choice target any time after the onset of the sample. In addition, reward cues were displayed surrounding the saccade targets, which indicated whether a large or small reward would be delivered for a correct response to the corresponding target. These reward cues were randomly assigned to a target on each trial. Zero coherence corresponds to a 50/50 mixture of blue and green pixels, and coherence of ±1 corresponds to a solid color. By convention, we define coherence relative to large- and small-reward targets, where a coherence of 1 or −1 corresponds to all pixels being the color of the large-reward or small-reward target, respectively.

Temporal uncertainty in the sensory evidence was introduced by varying the duration of the uninformative presample. No explicit cue was presented to indicate this transition from presample to sample. During the presample period, the color coherence was zero; and at the transition to the sample, the coherence switched to the particular value chosen for that trial. The presample duration was selected randomly from three possible time intervals (0, 0.4, or 0.8 s) with equal probability. A premature choice was punished by a 2 s timeout. In a separate experiment described below, we manipulated the set of presample durations (Fig. 1b).

Effect of task parameters on behavior

We predicted that all three primary task variables (coherence, presample duration, and reward location) would lead to systematic changes in the animal's behavior as measured by the RT distributions. In this study, RT was measured from the onset of the presample, since the transition from presample to sample was not explicitly cued. To test the impact of these three task variables on the animal's performance, we used multiple-regression models to predict RT and accuracy in individual trials using these three task variables (see Materials and Methods).

We found that all three task variables had a significant influence on RT (p < 0.05 for both animals, Eq. 1), sample-aligned RT (p < 0.05 for both animals, Eq. 2), and accuracy (p < 0.05 for both animals, Eq. 4). Higher absolute coherences decreased the RT and increased accuracy, meaning that animals responded faster (Figs. 2b, 3b) and more accurately (Figs. 2a, 3a) on easier trials. Likewise, responses directed toward the large-reward target were faster than those directed at the small-reward target (Figs. 2b, 3b). Furthermore, responses were faster and more accurate on trials with shorter presample durations (Figs. 2a,b, 3a,b).

We next examined whether these task variables modulated RT and accuracy independently. We found that both accuracy (p < 0.05 for both animals, Eq. 3) and RT (p < 0.05 for both animals, Eq. 5) were significantly modulated by the interaction between absolute coherence and presample duration. This interaction's effect on RT can be seen in the chronometric function (Figs. 2b, 3b) by observing that, for low-coherence trials, RT aligned to the presample is approximately equal regardless of the presample duration. In other words, despite the fact that there is 800 ms of additional sensory evidence presented to the animal during the 0 ms presample trials compared with the 800 ms presample trials, the RT is similar in both cases. Such similarity in RT is reflected in the overlap in the RT distribution in low-coherence trials for all presample durations (Figs. 2c, 3c). By contrast, for middle- or high-coherence trials, the RT shows a larger effect of coherence.

In summary, we find that coherence, presample duration, and large-reward location not only modulated RT and accuracy independently, but the interaction between coherence and presample duration influences choice and RT. To gain insights into the underlying mechanisms, we first tested whether a DDM that incorporated these task variables could provide a parsimonious account for the observed behaviors.

Violation of time-invariant evidence accumulation

The DDM is one of the simplest models that formalizes evidence integration for two alternative choices (Luce, 1986; Bogacz et al., 2006; Ratcliff et al., 2016). Recently, studies have shown that reward bias in psychometric functions can be accounted for by two separate mechanisms (Fan et al., 2018; Gesiarz et al., 2019). First, the initial bias shifts the starting position of the decision variable in the direction of the large-reward target (Edwards, 1965; Laming, 1968; Ratcliff, 1985). Second, a time-dependent bias allows a constant evidence signal to be continuously added to the integrator in the direction of the large-reward choice (Ashby, 1983; Ratcliff, 1985; Mulder et al., 2012). These two types of reward biases have been shown to be effective in reproducing choice bias (Voss et al., 2004; Diederich and Busemeyer, 2006; Ratcliff and McKoon, 2008; van Ravenzwaaij et al., 2012).

We thus took this combined reward-biased DDM (Fan et al., 2018; Gesiarz et al., 2019) as a point of departure to gain further insights and understanding of our data. In this extended seven parameter model (see Materials and Methods, Eq. 8), the weight on evidence is constant over time, as are the bounds. We fit this model by maximizing likelihood using the method of differential evolution (Storn and Price, 1997). Parameters of the fitted model are shown in Table 2. Full parameters for all models tested are provided in Extended data Tables 2-1 and 2-2.

Table 2.

Model parameters^a

Task	Reward	Reward	Time	Time	Time	Time	Reward	Reward
Model	GDDM	GDDM	GDDM	GDDM	GDDM	GDDM	DDM	DDM
Monkey	1	2	1	1	2	2	1	2
Block	—	—	Short	Long	Short	Long	—	—
s	9.32	6.52	11.25	11.25	12.11	12.11	—	—
σ0	1.03	1.16	1.62	1.62	1.40	1.40	—	—
tnd	0.22	0.21	0.20	0.20	0.22	0.22	0.27	0.21
$\ell$	7.14	15.82	22.67	22.67	9.81	9.81	—	—
τB	1.19	0.70	0.35	0.35	0.47	0.47	—	—
t1	0.36	0.09	0.00	0.21	0.20	0.73	—	—
x0	0.09	0.05	—	—	—	—	−0.16	−0.04
pmap	0.12	0.21	—	—	—	—	—	—
pL	0.04	0.03	0.03	0.03	0.04	0.04	0.03	0.10
λ	1.02	0.12	0.47	0.47	1.47	1.47	0.48	0.95
μ	—	—	—	—	—	—	2.90	6.27
σ	—	—	—	—	—	—	0.77	0.76
me	—	—	—	—	—	—	0.60	0.43

^aParameters for each displayed model. Reward, Color matching task with asymmetric reward; Time, Color matching task with timing blocks.

Table 2-1

Parameters for all models fit to data from the color matching task with asymmetric reward. Download Table 2-1, CSV file ^{(92.7KB, csv)} .

Table 2-2

Parameters for all models fit to data from the color matching task with timing blocks. Download Table 2-2, CSV file ^{(92.7KB, csv)} .

While the DDM with combined reward bias correctly predicted that the large-reward target would be chosen with a higher probability and a shorter RT than the small-reward target, overall this model could not fit other major features of the choice and RT data as measured by the psychometric (Figs. 2d, 3d) and chronometric functions (Figs. 2e, 3e) as well as the RT distributions (Figs. 2f, 3f). First, it failed to reproduce the overlapping RT distributions across different durations of presample for low-coherence samples (Figs. 2f, 3f). This model, like DDM models in general, predicts that RT should depend on the amount of evidence which has been integrated. However, the overlapping RT distributions indicate a minimal effect of evidence integrated during the early part of the trial compared with evidence later in the trial.

Second, the model failed to produce the characteristic shapes of RT distributions in the data. In both the data and the model, color coherence and sample time jointly influenced the shape of the RT distribution. However, the distribution of the actual RT data became more symmetric as color coherence decreased, whereas the distribution of RT in the model remained skewed similarly in all conditions (Figs. 2f, 3f, top panels).

Finally, the model failed to fit the time course of errors induced by the strong reward bias. During the task, errors during high-coherence stimuli were made almost exclusively because animals tended to choose the large-reward target when the evidence supported the small-reward choice (Figs. 2d, 3d). Therefore, errors during the high-coherence sample particularly reflect animals' strong bias toward large-reward target, and the error rate tended to sharply increase immediately after the sample onset (Figs. 2f, 3f, bottom panels). By contrast, the DDM predicted that fewer errors must follow the onset of the sample, as more evidence supporting correct choice becomes available after sample onset. These results collectively suggest that animals' behavior during the task used in our study cannot be fully explained by a time-invariant evidence integration strategy in conjunction with simple extensions to incorporate reward bias.

Modeling the effects of temporal and reward structures on behavior

The above results suggest that relatively simple modifications of the DDM are insufficient in that they cannot accurately reproduce the RT distribution. This is especially true of their ability to model the evolution of reward effects over time under temporally uncertain conditions. Therefore, we extended the DDM framework to create a GDDM for testing potential mechanisms to account for animals' behavior in our task. Compared with the DDM, GDDM allows the time-varying modulation of evidence accumulation, urgency, and reward bias, as summarized below.

Mechanisms for modulating the time scale of evidence integration

While the simple DDM assumes perfect integration in which the integrated evidence does not decay over time, we consider the possibility that animals might integrate evidence at a relatively short time scale so that the integrated evidence primarily reflects the most recent evidence (Brown and Holmes, 2001; Usher and McClelland, 2001; Brown et al., 2005; Cisek et al., 2009; Feng et al., 2009; Ossmy et al., 2013; Veliz-Cuba et al., 2016). Therefore, the GDDM included a “leak” parameter that determines the time constant of the decay in decision variable.

Mechanisms of time-varying urgency

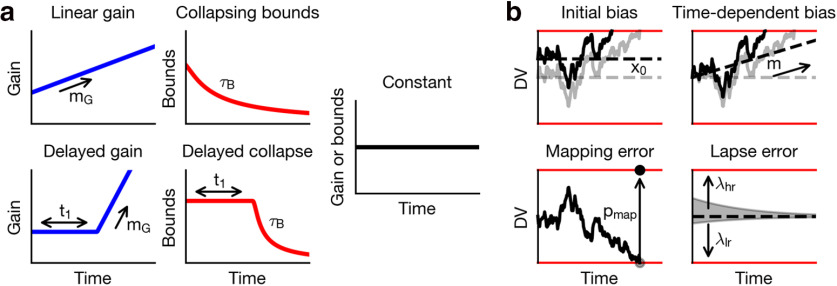
An urgency signal can be characterized across two dimensions: its type and its form. Here, we considered collapsing decision bounds and an increasing gain of the momentary sensory evidence as two alternative means to modulate the evidence accumulation process. In addition, the urgency signal was implemented as a linearly increasing gain function (“linear gain,” Fig. 4a) or a gradually decreasing bound (“collapsing bounds,” Fig. 4a). The limiting cases, where the slope of the gain function is zero or the time constant of the collapsing bound is infinite, correspond to time-independent urgency, or equivalently to the lack of explicit urgency in the simple DDM (“constant,” Fig. 4a). To allow for an effect of task structure on urgency, the delayed urgency signal introduced a delay before the linear increase in the gain function (“delayed gain,” Fig. 4a) or exponential collapse of the bounds (“delayed collapse,” Fig. 4a). We hypothesized that this delay parameter would be tuned by the temporal uncertainty of the behavioral task.

Figure 4.

GDDM components. Our GDDM included extensions related to timing and reward. a, We modeled timing using two types of urgency signals. We implemented a gain function and collapsing bounds, each with and without a time delay. Constant gain and constant bounds indicate the absence of an urgency signal. Red represents bounds. Blue represents gain functions. b, Reward mechanisms are shown with example decision variable trajectories for each mechanism. Initial bias: the integrator starts biased toward the large-reward target, and the leaky integrator decays back to this starting position instead of to the origin. Time-dependent bias: there is a gradual increase in baseline evidence toward the large-reward target over time. Mapping error: once a decision is reached, the monkey chooses the opposite target on a percentage of trials. Lapse error: there is a higher, exponentially distributed probability of making an evidence-independent choice to the large-reward target at any given point throughout the trial, contrasted to equal probabilities in the absence of this mechanism.

Mechanisms of reward bias

We found that animals' bias toward the large-reward choice increased as the sample was presented at a more predictable time, particularly for higher coherence samples (Figs. 2a, 3a). We considered two classes of mechanism: one in which reward directly influences the integration process and the other in which the reward bias is implemented outside the integration process. Similar to how the DDM was extended to incorporate reward bias, the effect of reward on the integration process can be modeled by an “initial bias,” which maintains a fixed magnitude throughout the trial, or a “time-dependent bias,” which increases in magnitude throughout the trial (Fan et al., 2018; Gesiarz et al., 2019) (Figs. 2d-f, 3d-f, 4b). We also considered two additional types of reward bias, which are outside the integration process. First, the animal may be biased in its categorical choice at the end of evidence accumulation (Erlich et al., 2015; Hanks et al., 2015). Namely, when the decision variable reaches the bound, animals may, with some probability, mistakenly produce a motor response toward the large-reward choice, even if they correctly reached the bound for small-reward choice (“mapping error,” Fig. 4b). In other words, the mapping error increased responses toward the large-reward target and decreased responses toward the small-reward target, and it induced errors in the small-reward condition, which had the same RT distribution as the correct responses to the small-reward target. This is consistent with experimental data, which show that the animal erroneously chose the large-reward target in a sizable fraction of trials, even at the strongest coherence condition, but rarely erroneously chose the small-reward target (Figs. 2a, 3a). Second, we also considered that a small number of responses may be generated randomly anytime during the integration process (“lapse trials”). The responses on these lapse trials may be also biased toward the large-reward choice (Simen et al., 2009; Noorbaloochi et al., 2015), which can be implemented by an asymmetric lapse rate for the large- and small-reward choices, Fig. 4b) (Yartsev et al., 2018). In contrast to the mapping error, which took the form of a simulated RT distribution and applied only to the errors in the small-reward condition and correct responses in the large-reward condition, the lapse bias took the form of an exponential distribution and applied similarly to both conditions, albeit asymmetrically.

Modeling strategies during perceptual decision-making

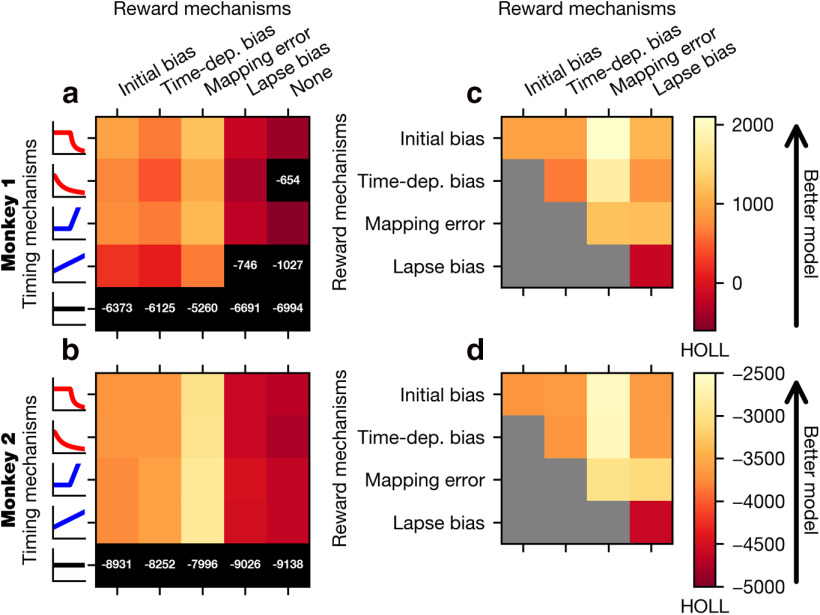
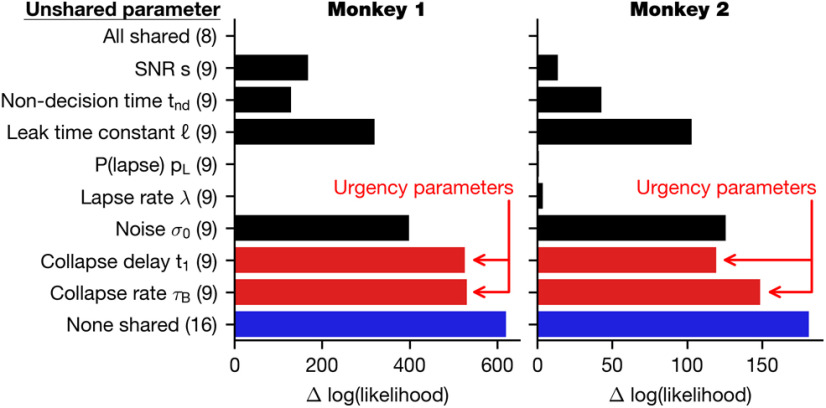
We fit the GDDM to the choice and RT behavior for each animal and evaluated model fit with HOLL. Overall, models with time-varying urgency performed remarkably better than ones with constant urgency, such as the simple DDM (Fig. 5a,b). When combined with each of several different reward bias mechanisms, models with delayed urgency best explained the data for Monkey 1, whereas models with nondelayed and delayed urgency performed similarly well for Monkey 2. Both the delayed gain function and the delayed collapsing bounds performed similarly well, suggesting that the type of urgency signal does not matter as much as the delay in the increased urgency. Despite some individual differences, these results suggest that the animal's strategic adaptation to the temporal structure of sensory evidence can be well accounted for by a time-varying urgency.

Figure 5.

Fit of potential GDDM models. Various models were fit to the exploration data from Monkey 1 (a, c) or Monkey 2 (b, d) and subsequently evaluated with HOLL on the validation data. Color represents the HOLL of the model, with higher values indicating a better fit. a, b, Models were constructed by selecting one urgency signal (Fig. 4b) and one reward mechanism (Fig. 4a). Models with HOLL outside the range of the color bar are shown in black with their corresponding overlaid HOLL value. c, d, Models were constructed using the delayed collapse urgency signal in conjunction with one or two reward mechanisms (Fig. 4a). Models with only one reward mechanism appear on the diagonal. All models used leaky integration.

Regarding reward bias mechanisms, we first compared GDDMs with only one of the four reward bias mechanisms, and found that the models with mapping error performed best. This suggests that asymmetric rewards affected the animal's choice through an integration-independent mechanism (Fig. 5a,b). Moreover, models with a time-dependent bias did not perform better than those with initial bias, suggesting that the reward bias mechanisms need not depend on time to explain the observed effects. We next asked whether these bias mechanisms could be combined to further improve model fit. In conjunction with a delayed collapsing bounds urgency signal and leaky integration, we tested all combinations of two reward bias mechanisms, and found that adding initial bias to the mapping error mechanism consistently improved the model fit for both monkeys more than any other mechanism, such as time-dependent bias or lapse bias (Fig. 5c,d). While initial bias and time-dependent bias both performed well individually and with mapping error, the combination of initial bias with time-dependent bias was no better than initial bias or time-dependent bias alone (Fig. 5c,d). These results suggest that both integration-dependent mechanisms, such as initial bias and time-dependent bias, and integration-independent mechanisms, such as mapping error, are needed to explain animals' reward bias.

We next examined the role of leak in evidence accumulation in the GDDM. For our best-fit delayed collapsing bounds model, the time constant was 140 ms for Monkey 1 and 63 ms for Monkey 2. We found that, given urgency mechanisms, the estimated time scale of integration was consistently short (<150 ms) across all the tested models (Fig. 6). Model comparison showed that adding a leak parameter to each model improved model fit for all the models, except the simple DDM (Fig. 6), for which the best-fitting leak time constant was often infinity. A time constant of infinity implies that unstable integration may have been more effective for this model. Notably, the models with nondelayed urgency and the models implementing time-dependent bias mechanism showed particularly large improvement with the addition of the leak parameter (Fig. 6a,b). This result suggests that the leaky integration might improve these models by providing a mechanism to disregard early uncertain evidence, a property that can also be represented through a delayed urgency signal. However, the fact that the leak parameter also produced substantial improvement in delayed urgency models suggests that the short time scale of integration itself is an important feature.

To determine whether Monkey 2's short time constant could be explained more simply by a nonintegrative strategy, we explored the performance of the model while fixing Monkey 2's time constant at 20 ms. When the parameters of the best fitting model were used in conjunction with this shorter leak time constant, the HOLL decreased from −2601 to −34,864. When refitting all other parameters, HOLL was −9319, which is still worse than not including leak at all (Fig. 6d). Thus, the short time constant of leaky integration cannot be explained by a nonintegrative strategy.

The best-fit delayed collapsing bounds model captured behavior quite well (Figs. 2a–c, 3a–c). It fit the psychometric and chronometric functions and exhibited major features of choice and RT data that cannot be accounted for by simple DDM with integration-based reward mechanisms alone (Figs. 2d–f, 3d–f). In particular, the best-fit delayed collapsing bounds model dramatically improves the quantitative and qualitative fit to the RT distributions, compared with the simpler model (Figs. 2c,f, 3c,f). This model provided the best fit of all models considered here for Monkey 1, and nearly the best fit for Monkey 2, for which a slightly higher likelihood can be obtained through the use of the delayed gain function as an urgency signal (Fig. 4). Fitted parameters are shown in Table 2.

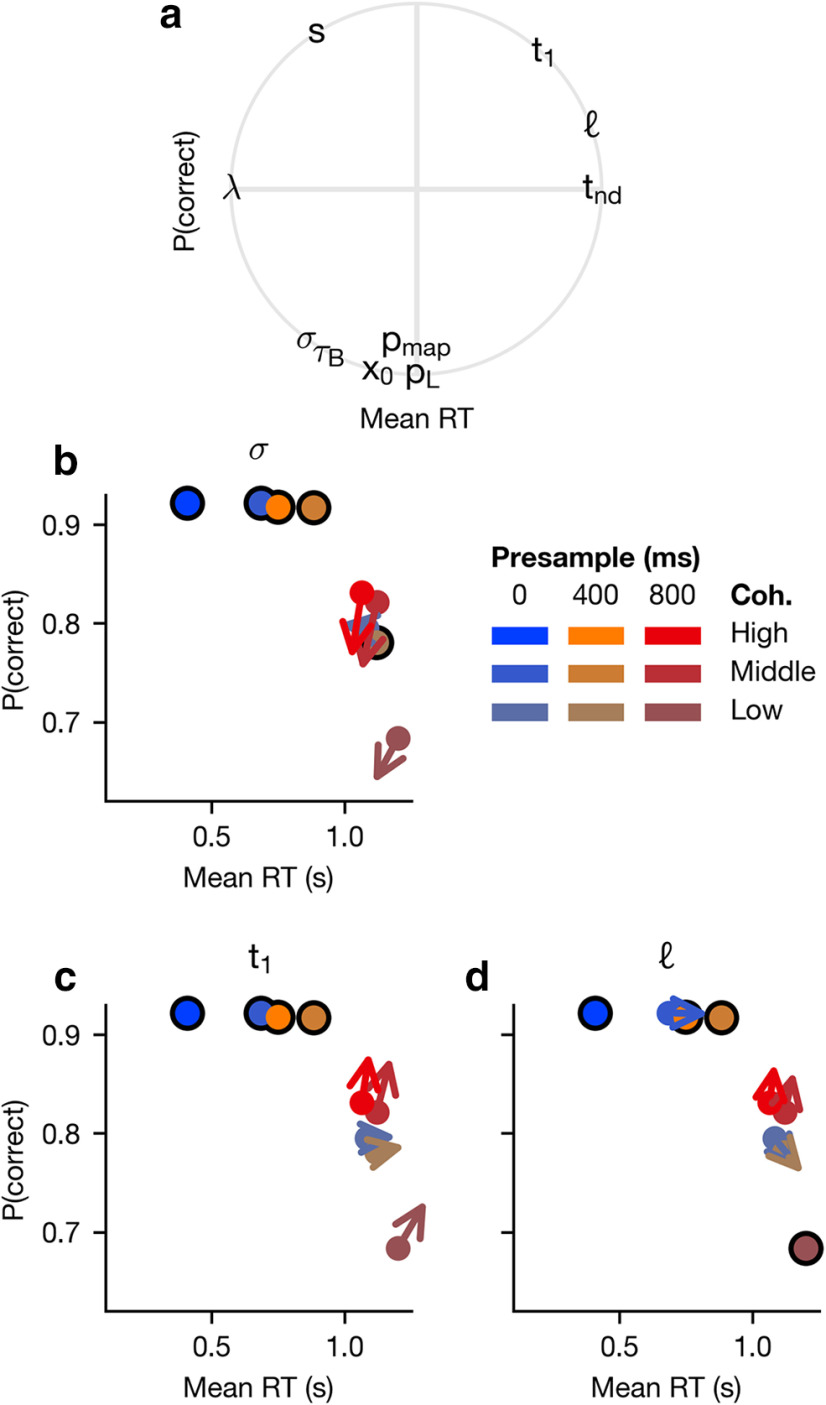
In order to examine how each of these parameters influenced the speed-accuracy trade-off (Fig. 7), we perturbed each of the parameters and examined the changes in RT and accuracy. Each perturbation was increased by an arbitrary amount to visualize the effect of each parameter. We found that only the signal-to-noise ratio parameter(s) can both decrease the mean RT and increase the accuracy, whereas the other parameters shift the trade-off by changing speed, accuracy, or both (Fig. 7a). This also shows that the mapping error parameter p_map and the lapse probability p_L change the probability of a correct response without changing mean RT, whereas the non-decision time t_nd and the lapse rate shape parameter λ change mean RT without changing the probability of a correct response. All other parameters improve either mean RT or the probability of a correct response at the expense of the other. To determine whether these effects were consistent across presample durations and coherence levels, we examined three critical parameters individually: the noise level (σ), the delay of the collapsing bounds (t₁), and the leak constant ($\ell$). We found that each of these three parameters has consistent effects across presample durations and coherences (Fig. 7b–d).

As mentioned above, the RT distributions in our data during the low-coherence sample overlap with one another for all presample durations, and this could not be captured by the simple DDM with reward bias, which uniformly integrates sensory evidence (Figs. 2d–f, 3d–f). By contrast, the best delayed collapsing bounds GDDM correctly predicts overlapping RT distributions as well as the RT-accuracy relationship for low-coherence samples (Figs. 2a–c, 3a–c). When evidence is weak, delayed urgency combined with a short time scale of integration implies that the decision is most likely to be driven not by the total evidence, but rather by the later evidence close to the maximum presample duration used (0.8 s), that is, when the uncertainty about stimulus onset is resolved.

Finally, the best-fit delayed collapsing bounds GDDM fit the time course of errors frequently occurring after the onset of the high-coherence sample. This pattern of errors is inconsistent with one of the basic tenets of the DDM that stronger sensory evidence for one alternative makes the subject more likely to choose that alternative. To the contrary, our result shows that, in the presence of asymmetric rewards, strong evidence for one alternative can paradoxically make the subject more likely to choose the other alternative. The apparently dynamic reward bias that increases with presample duration is mostly captured by the mapping error mechanism, indicating a failure of mapping the decision variable to motor output correctly.

Manipulating temporal expectation changes strategy

Thus far, our findings suggest a set of mechanisms in the GDDM to quantitatively capture the behavioral choice and RT patterns. The two temporal features in this model, leaky integration and a delayed urgency signal, hint that the temporal structure of the task may drive their properties. By manipulating the task's structure, we tested whether the urgency signal could be flexibly influenced by temporal context within a single experimental session.

We investigated this question using a variant of the task in the same monkeys (Fig. 1b). In this new task, the duration of temporal uncertainty was manipulated by varying the set of alternative presample durations between different blocks of trials within a session. In the “short-presample” blocks, there was a 0.5 s presample in a majority of the trials (60%); in the remaining 40% of trials, the sample arrived either earlier (0.25 s) or later (0.75 s) with 20% probability each. Similarly, in the “long-presample” block, 60% of trials had a presample of duration 1.25 s, and 20% each had 0.75 s and 1.75 s (Fig. 1b). Accordingly, 20% of trials in each block had a 0.75 s presample, which corresponded to the longest presample duration in the short-presample block and the shortest presample duration in the long-presample block. No reward bias was imposed in this modified version of the task, so a correct response to either target elicited an identical reward.

This task was used to test whether temporal context can modify the urgency mechanisms of the fitted GDDM. Under a pure DDM framework, the RT distribution for the 0.75 s presample should be the same in both blocks. However, if temporal context influenced behavior, the RTs for the 0.75 s presample in the short-presample block would be on average shorter than those in the long-presample block.

We first performed a linear regression analysis to determine the effect of coherence, presample duration, and block on RT and accuracy (see Materials and Methods). As expected, we found higher coherences and shorter presample durations both decreased RT (p < 0.05; Eq. 6) and increased accuracy (p < 0.05; Eq. 7). More importantly, we also found a significant effect of the block regressor, in that trials presented during the long-presample blocks had significantly longer RT (p < 0.05; Eq. 6) and higher accuracy (p < 0.05; Eq. 7) compared with the short-presample blocks.

To examine more mechanistically how the animals altered their decision-making strategies, we fit the best-fit delayed collapsing bounds GDDM chosen for the first task, including a leaky delayed collapsing bound, to the second task. Fitted parameters are shown in Table 2. Mechanisms for reward bias were removed given the lack of reward asymmetry in the present task. This model provided an excellent fit to the psychometric and chronometric functions as well as the probability distribution (Fig. 8).

Figure 8.

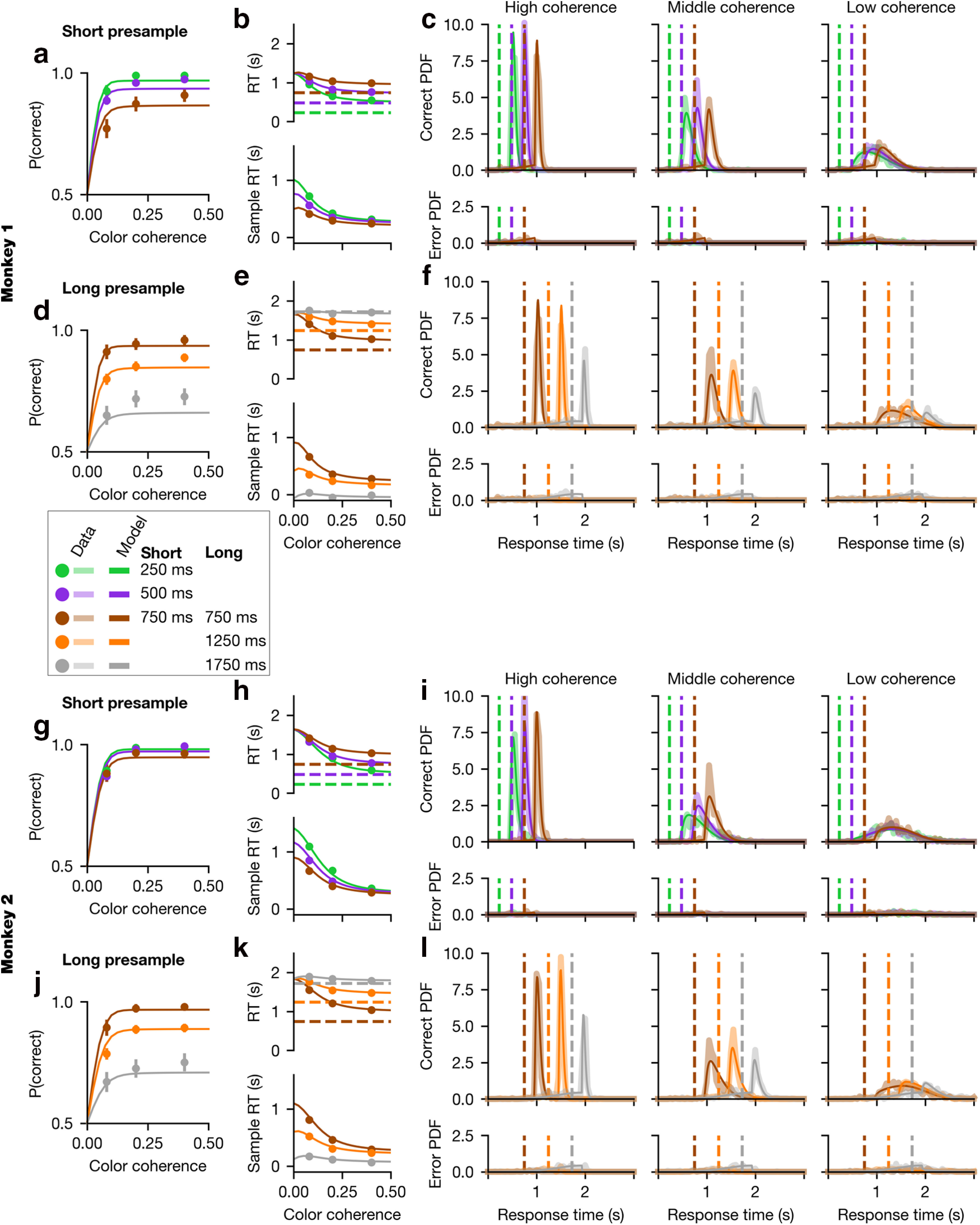
Model fit to timing dataset. Psychometric functions (a, d, g, j), chronometric functions (b, e, h, k), and RT histograms (c, f, i, l) are shown for short-presample (a–c, g–i) and long-presample (d–f, j–l) blocks for Monkey 1 (a–f) and Monkey 2 (g, h–l). Data are represented by dots in the behavioral functions and thick translucent lines in the probability distributions. “Sample RT” indicates the RT minus the presample duration. Overlaid as a thin solid line is a GDDM, including delayed collapsing bounds and a leaky integrator with a separate “collapse delay” t₁ parameter for short- and long-presample blocks. Error bars for 95% CI are hidden beneath the markers.

To investigate which model parameters could best explain the difference between blocks, we allowed individual parameters in this model to differ for the two blocks and assessed the log-likelihood in each case. For comparison, we also fit a 16 parameter model in which all of the parameters were allowed to vary between blocks, and an 8 parameter model, which fixed all parameters to be the same for both blocks.

We then examined the difference in HOLL when each parameter was fit separately for each block compared with shared between the blocks, as well as when all parameters or no parameters are shared. We found that the 16 parameter model fit the data better than models in which only a single parameter was allowed to vary between the short and long blocks. Nevertheless, changes in the urgency signal alone were sufficient to explain most of this improvement in model fit (Fig. 9). For example, in Figure 8, the model that allows the “collapse delay” t₁ parameter to vary is shown. This demonstrates that the timing of the urgency signal mediates a critical aspect of the monkey's change in strategy between different temporal contexts.

Figure 9.

Urgency signal captures changes between presample blocks. An 8 parameter GDDM with a delayed collapse urgency signal and leaky integration was fit to data from the color matching task with timing blocks. The block type (either long- or short-presample) was incorporated into the model by allowing one parameter at a time to vary between blocks, forming a 9 parameter model, and then refitting all parameters of the new model to the data. For comparison, we also fit the 16 parameter model where we allowed all parameters to differ between blocks (blue). The improvement in log likelihood for each model is shown, as well as the total number of parameters of the model in parentheses. Left, Monkey 1. Right, Monkey 2. Red represents parameters related to the urgency signal.

Urgency timing can implement a speed-accuracy trade-off

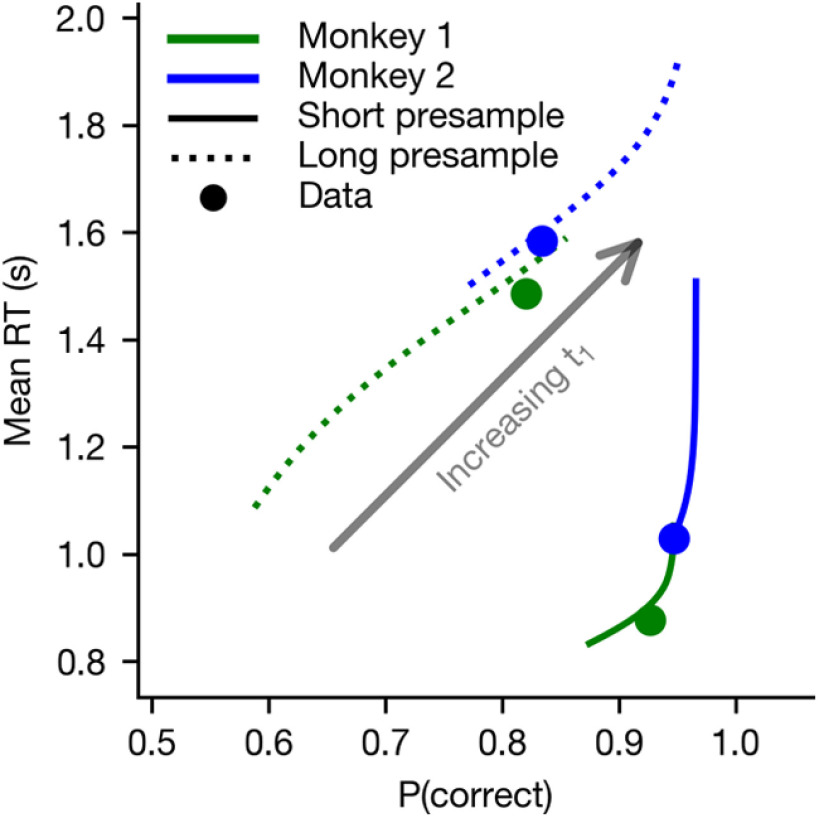
The above results showed that context-dependent changes in the timing of the urgency signal can account for the changes in behavior related to temporal uncertainty. In theory, the animal could increase accuracy by simply delaying the onset of the increase in urgency signal for the longest possible duration (1750 ms) on every trial, which would minimize the effect of integrating noise. However, this would come at the cost of long RT. Conversely, the animal could reduce RT by beginning to increase urgency immediately at the beginning of the trial, but at the cost of lower accuracy. Therefore, the onset of the urgency signal can mediate a speed-accuracy trade-off, with longer onset delays favoring accuracy and shorter onset delays favoring speed.

To examine this quantitatively, we systematically varied the “collapse delay” t₁ (Fig. 4b) from 0 ms to 1000 ms, separately for long- and short-presample blocks, to observe how this parameter modulated the speed-accuracy trade-off in the GDDM, with all other parameters shared (Fig. 10). This analysis confirmed that changes to the urgency signal influence the speed-accuracy trade-off. Furthermore, modulation of the urgency signal governed a nearly continuous range of potential speed-accuracy tradeoffs across both animals, despite differences in other estimated parameter values. Both animals' speed-accuracy trade-off fell along this continuum. This demonstrates that strategic modulation of speed-accuracy trade-off can be accomplished using changes to only the urgency signal, and suggests that urgency may be critical for timing-related decision strategies.

Figure 10.

Urgency signal mediates a speed-accuracy trade-off. A GDDM with a delayed collapse urgency signal and leaky integration was fit to each monkey's RT data in the color matching task with timing blocks. Using these parameters, the “collapse delay t₁” parameter was varied systematically across the linearly spaced values from 0 to 1, representing the hypothetical case in which the subject could control this parameter while leaving the other parameters fixed. For each value, the mean RT and probability of a correct response were plotted for the long-presample (dotted lines) and short-presample (solid lines) blocks. Filled dots represent the actual parameters.

Discussion

In this study, we found that perceptual decision-making is driven by temporal modulation of evidence accumulation via a dynamic urgency signal. We also showed that reward bias in animals' choice can be accounted for by separate integration-dependent and integration-independent mechanisms.

Temporal uncertainty and decision-making

An internal urgency to commit to a decision has long been hypothesized to modulate the speed and accuracy of perceptual decision-making (Reddi and Carpenter, 2000). In computational models of decision-making, urgency has typically been implemented either by a collapsing bound or gain modulation of sensory evidence (Ditterich, 2006a,b; Churchland et al., 2008; Forstmann et al., 2008, 2010; Ratcliff and McKoon, 2008; Cisek et al., 2009; Drugowitsch et al., 2012; Hanks et al., 2014; Murphy et al., 2016). In models with collapsing bounds, an evidence-independent, time-varying signal is combined with the accumulators with fixed weight on evidence, while the gain function multiplicatively modulates the evidence with time-varying weight. However, the nature of time-varying mechanisms has been controversial (Hawkins et al., 2015a,b; Voskuilen et al., 2016). In our study, we varied the uncertainty about evidence onset over time during the stimulus presentation to probe the time-varying mechanisms. We found that the urgency signals with a task-relevant delay performed better than urgency signals without such a delay. Using an array of computational models, we showed that an urgency signal provides a flexible mechanism by which temporal information can be incorporated into the decision.

The neural mechanisms of urgency have been widely studied (Hanks et al., 2014; Thura and Cisek, 2014; Braunlich and Seger, 2016; van Maanen et al., 2016; Thura and Cisek, 2017). Our behavioral model allows for a direct comparison with neutrally derived urgency signals (e.g., from neuronal recordings in frontal eye fields or lateral intraparietal area). Consistent with our delayed urgency signal, we predict a nonlinear neural urgency signal which remains relatively flat during initial stimulus presentation and then begins to increase throughout the course of the trial.

Recently, several studies have found, using dynamically fluctuating sensory evidence, that subjects can adjust the gain or weight on the evidence across time during the trial, depending on the temporal statistics of evidence (Cheadle et al., 2014; Levi et al., 2018). In these prior studies, however, subjects were not allowed to freely choose the timing of their response, so it was not possible to determine whether, and how, the subject's strategy reflected a speed-accuracy trade-off. In the present study, we adopted an RT paradigm and explicitly showed that animals voluntarily adjusted the timing of their decision to reduce uncertainty about evidence through task-specific, time-varying urgency. In this study, we did not explore the potential optimality of this strategy, and this presents an interesting opportunity for future investigation (Drugowitsch et al., 2012, 2014).

Time-varying stimuli were also used to test the time scale of evidence integration (Bronfman et al., 2016). Whereas the traditional DDM assumes a perfect integrator, recent studies have raised possibility that evidence integration may be leaky, as the accuracy of the decision does not necessarily increase with integration time (Usher and McClelland, 2001; Zariwala et al., 2013; Tsetsos et al., 2015; Farashahi et al., 2018). Moreover, when evidence dynamically changes during the course of a trial, models with leaky integration, or even instantaneous evidence, can fit the data well, as shown in the present study (Cisek et al., 2009; Thura et al., 2012; Thura and Cisek, 2014; Bronfman et al., 2016). In addition to leaky integration, bounded integration has also been proposed as a mechanism to account for the apparent failure to use the full stream of stimulus information (Kiani et al., 2008).

Our use of a dynamic urgency signal can be seen as a generalization of the idea that integration must begin at a single point in time (Teichert et al., 2016). Recently, integration onset was examined by (Devine et al., 2019), who tested human subjects on a perceptual decision-making paradigm with multiple presample durations, a single-sample coherence level, and no reward bias. Based on behavioral and EEG data, they proposed that under temporal uncertainty, integration begins approximately at the time of the earliest sample onset. However, their analyses did not fit a model of decision-making processes to test against alternative mechanisms. By contrast, we find strong evidence that our subjects used the temporal statistics of the task to modulate the evidence accumulation process. Applying our model comparison framework in other task paradigms can test the generality of these strategies.

A monotonically increasing gain function provides a straightforward mechanism to weight late evidence more than early evidence. Although the collapsing bounds mechanism does not by itself weight late evidence more than early evidence, the interplay between time-varying urgency and leaky integration may provide a mechanism for weighting of late evidence over early evidence. For example, in fixed-duration paradigms, a leaky integrator can effectively weight late evidence more than early evidence (Lam et al., 2017; Levi et al., 2018). We found that leaky integration improved fit in all models but played a larger role for simpler urgency signals than for the best-fitting delayed urgency signals, suggesting that leaky integration may capture a component of behavior related to the delay in urgency increase. While our results imply that both leaky integration and a delayed urgency signal are necessary, the ability of a time-varying urgency signal to reduce the relative benefit of adding leaky integration to the model demonstrates the flexibility of the urgency signal.

Asymmetric rewards and decision-making

Asymmetry in reward or prior probability of the correct target can induce a bias to targets with a higher expected value (Lauwereyns et al., 2002; Voss et al., 2004; Diederich and Busemeyer, 2006; Ratcliff and McKoon, 2008; Feng et al., 2009; Rorie et al., 2010; Teichert and Ferrera, 2010; Mulder et al., 2012). Several studies have indicated that reward bias in perceptual decision-making could be well accounted for by an integration-dependent mechanism in which reward is modeled either as constant evidence (i.e., initial bias) or momentary evidence (i.e., time-dependent bias) (Feng et al., 2009; Rorie et al., 2010; Fan et al., 2018; Gesiarz et al., 2019). These mechanisms are attractive because they have well-known neural correlates (Lauwereyns et al., 2002; Rorie et al., 2010; Afacan-Seref et al., 2018; Doi et al., 2020). In our task, even a combination of these two reward mechanisms could not fit our data in the absence of an urgency signal or leaky integration. Likewise, recent studies have reported that, under time pressure, reward bias might be produced by integration-independent mechanisms, such as a ramping signal to select the high-reward choice that races with the process of evidence integration (Simen et al., 2009; Noorbaloochi et al., 2015; Afacan-Seref et al., 2018). However, this possibility was not consistent with our data either. This discrepancy might be because of the fact that previous studies have seldom tested the possible role of urgency in modulating the balance between evidence and bias when determining choice. Although reward bias increasing with time following the onset of an informative sensory stimulus could imply a time-varying bias mechanism, our results showed that such a time-varying bias is not necessary to explain our data.

Because our model showed an initial bias, we anticipate this bias should be represented in neural activity before the onset of evidence, such as in baseline activity of decision related neurons biased toward the high-reward choice. Prior studies found baseline neural activity tuned to reward bias in monkeys and humans (Rorie et al., 2010; Summerfield and Koechlin, 2010; Doi et al., 2020). As described in Results, in our model the combination of initial bias and leaky integration produces an offset in the decision variable baseline toward the high-reward choice. The success of mapping error in fitting our data also provide links to prior work, which showed that deactivation of the mouse frontal orienting fields led to similar error patterns (Erlich et al., 2015). Overall, our results suggest that temporal and reward structures play an important role in perceptual decision-making. In addition, models within the GDDM framework can effectively describe the contribution of temporal and reward related factors during decision-making and play an important role in investigating the neural mechanisms of decision-making.

As investigators explore complicated behavioral tasks and computational models, it is important to use methods of model-fitting, which are specialized for complex, high-dimensional models. In this study, we fit each model to the entire RT distributions of correct and error choices using maximum likelihood, and were able to provide qualitatively good fits to both the psychometric function and the RT distribution. By contrast, much prior work has fit models directly to the psychometric and chronometric functions, producing excellent fits to these reduced behavioral functions with a potentially poor fit to the RT distributions. Indeed, we found that evaluating and providing model fits to the entire probability distribution are highly informative for differentiating different models and mechanisms. This methodology is imperative for simulating and fitting complex models. Our methodological innovations will therefore allow for increased complexity in experimental design to test a broad range of hypotheses about the mechanisms of decision-making.