Abstract
Images formed by individual Shack-Hartmann wavefront sensor lenslets are displaced proportionally to the average wavefront slope over their aperture. This principle fails when the lenslet illumination is non-uniform. Here we demonstrate that the resulting error is proportional to the linear component of the illumination intensity, the quadratic wavefront component, and the lenslet size. For illustrative purposes, we compare the error due to centered Gaussian illumination decaying by 30% at the pupil edge against the error due to assuming the wavefront at the lenslet center being equal to the wavefront average across each lenslet. When testing up to ninth-order Zernike polynomial wavefronts and simulating nine lenslets across the pupil, the maximum centroid errors due to non-uniform illumination and sampling are 1.4% and 21%, respectively, and 0.5% and 6.7% when considering 25 lenslets across the pupil in the absence of other sources of error.
The Shack-Hartmann wavefront sensor (SHWS) [1,2] is widely used in astronomy [3,4], microscopy [5–7], refractive surgery [8], and metrology [9], among other applications. Its principle, based on geometrical optics, is simple, wherein a test beam is sampled by an array of lenslets, each of which creates an image onto a pixelated sensor. According to geometrical optics, each of these images displaces from a nominal position proportionally to the average wavefront gradient over the corresponding lenslet. Diffraction theory, however, indicates that this image centroid shift also depends on the variation of the intensity across each lenslet [10–13] and therefore, ignoring non-uniform illumination results in centroid error.
When the pixelated sensor of a SHWS is at the geometrical focus of the lenslet array [10,11], the angular displacement of a lenslet image centroid along the x-axis, ϱx under the Fresnel (parabolic) approximation of the Huygens-Fresnel principle is given by
| (1) |
where I(x, y) and W(x, y) are the intensity profile and wavefront at the lenslet, respectively, and the integrations are performed over the lenslet area. When the intensity can be considered uniform across the lenslet, that is, I(x, y) ≈ I0, Eq. (1) reduces to the well-known SHWS principle,
| (2) |
with A being the lenslet area. However, there are situations in which the intensity variation across each lenslet is non-negligible, for example, in ophthalmic wavefront sensing [14–19], or when using light emerging from a single mode optical fiber [20]. Let us now explore this scenario by modeling the intensity and wavefront variations over a single lenslet as second-order polynomials. For simplicity, we will perform the calculations in one dimension, assuming a SHWS lenslet of diameter D, centered on the origin of coordinates. Using Eq. (1), we then have that the centroid of the lenslet image at the pixelated sensor can be approximated as
| (3) |
After calculating the derivative, rearranging terms and performing the integrals noting that due to symmetry the integral of odd powers of x cancel out, this reduces to
| (4) |
This approximate formula shows that a linear variation of the intensity across the lenslet alone does not affect the image centroid; a quadratic wavefront term is also required. This can be better appreciated by defining the error due to non-uniform illumination as
| (5) |
which, under the approximations that lead to Eq. (4), takes the form
| (6) |
This error is proportional to the lenslet area D and non-zero only when the intensity has a linear component, and the wavefront has a quadratic component.
Let us now illustrate the magnitude of the centroid error due to Gaussian illumination of the SHWS pupil with a 30% drop in intensity from the center to its edge and wavefronts with the shape of Zernike polynomials up to the ninth order. Such an intensity variation is found, for example, in the human eye (Stiles-Crawford effect [15]), when using a single-mode optical fiber as an illumination source [21]. We assume the intensity profile is of the form , with r being the normalized radial coordinate [14]. Numerical integration methods of symbolic functions in Matlab (Mathworks, Inc., Natick, Massachusetts) were used to calculate the error due to a non-uniform intensity profile, which we define as the difference between Eqs. (1) and (2) and the sampling error which we define as the difference between the wavefront slope at the lenslet center and the average across the lenslet assuming uniform intensity for comparison (see Figs. 1 and 2). The calculations were repeated for nine and 25 lenslets across the SHWS pupil, ignoring all other source of errors, including detector pixelation, lenslet crosstalk, finite number of photons, and digitization noise.
Fig. 1.
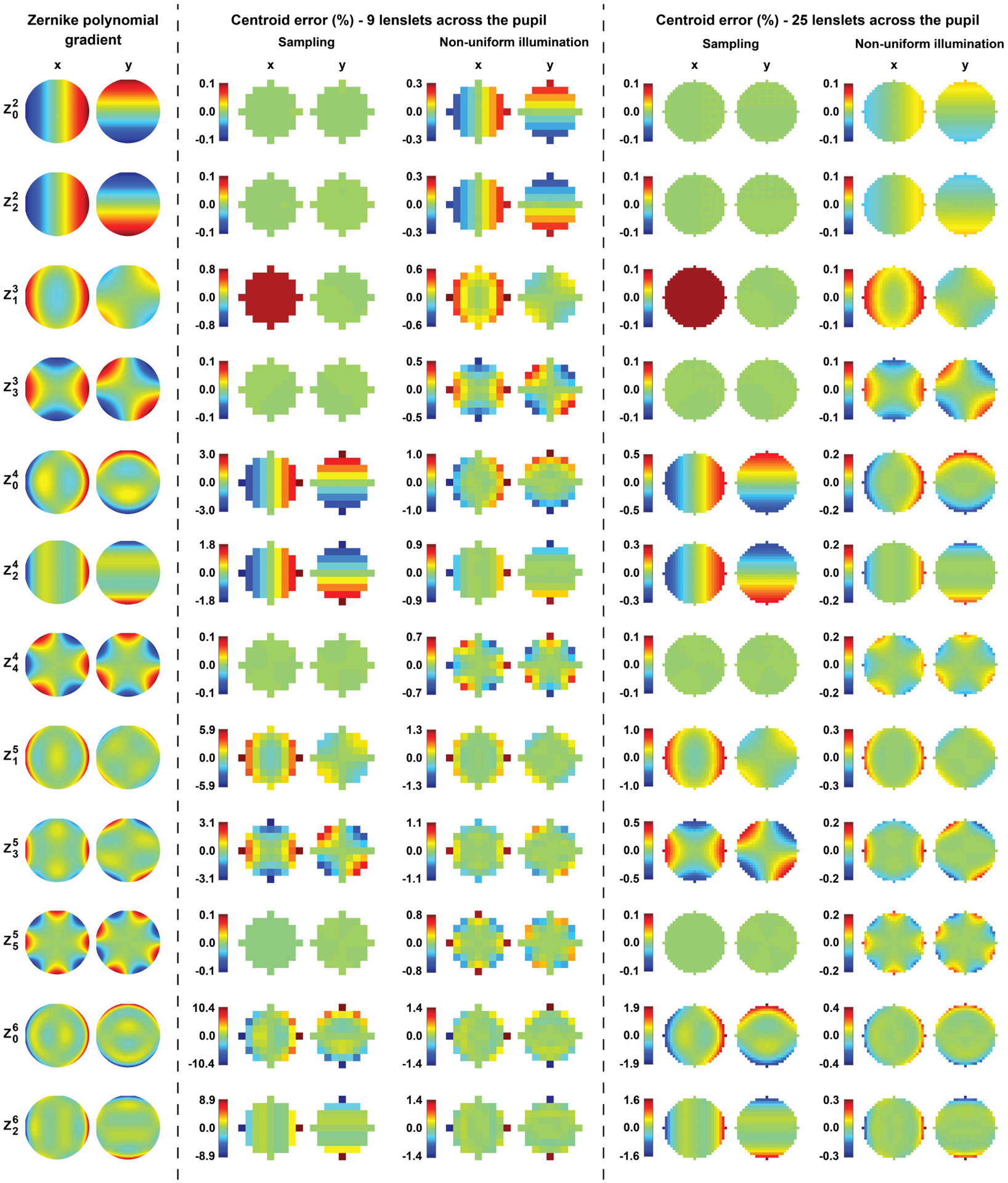
Slopes of Zernike polynomials ( to ) over the unit circle (first two columns), normalized to their peak values. The following columns show the theoretical centroid errors that would be seen in a SHWS due to the finite lenslet size (sampling) and non-uniform lenslet intensity profile, when using either nine or 25 lenslets across the diameter of a circular pupil. Some polynomials have been excluded due to symmetry.
Fig. 2.
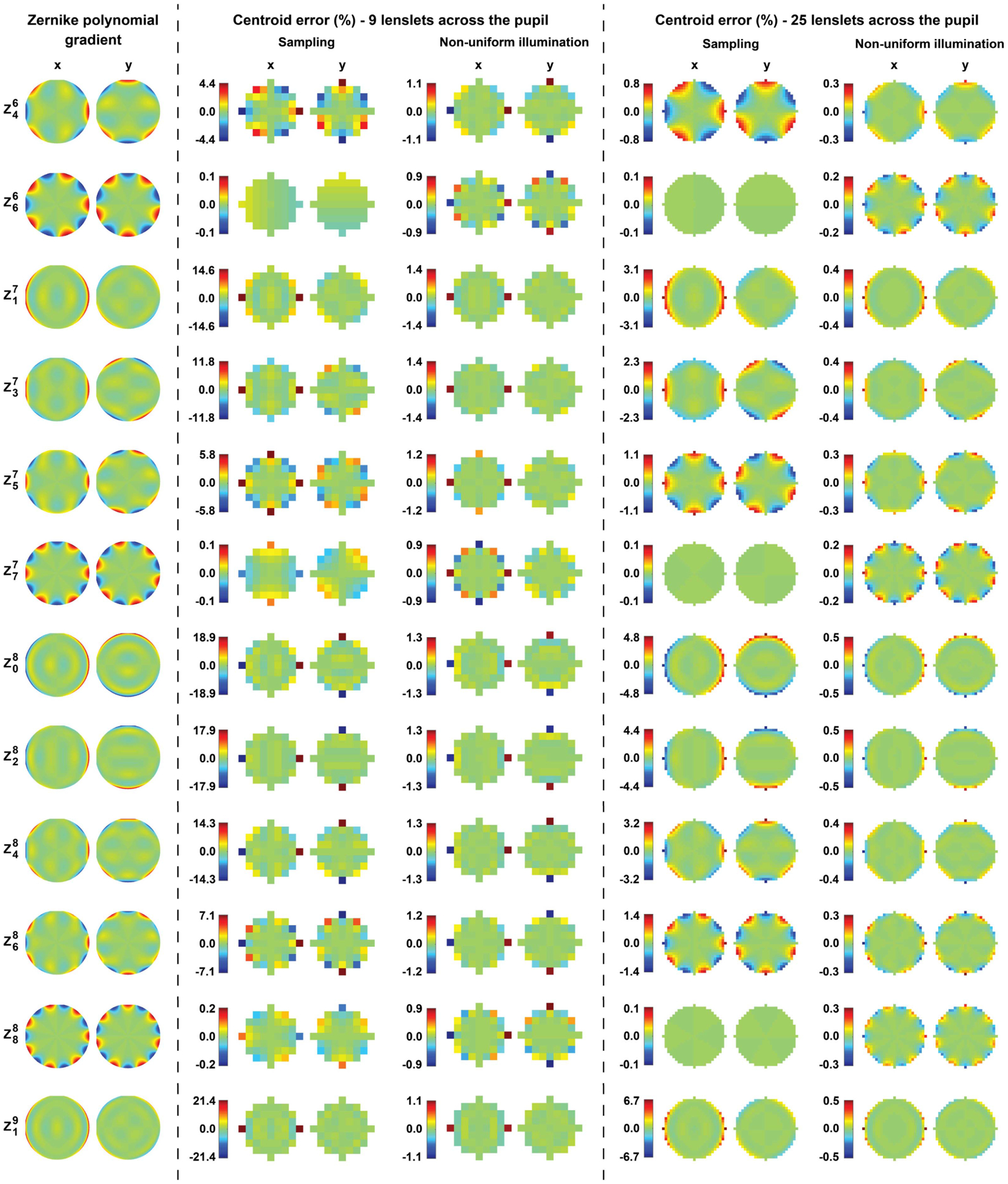
Slopes of Zernike polynomials ( to ) over the unit circle (first two columns), normalized to their peak values. The following columns show the theoretical centroid errors that would be seen in a SHWS due to the finite lenslet size (sampling) and non-uniform lenslet intensity profile, when using either nine or 25 lenslets across the diameter of a circular pupil. Some polynomials have been excluded due to symmetry.
For these simulated scenarios, the maximum centroid error due to sampling and non-uniform illumination (see Figs. 1 and 2) was as high as 21% and 1.4%, respectively, for nine lenslets across the pupil, and 6.7% and 0.5% for 25 lenslets across the pupil. As predicted by Eq. (6), the error due to non-uniform illumination is reduced proportionally to the lenslet area, with the largest centroid error for all simulated polynomials always occurring at the pupil edge. Interestingly, a large sampling error is not necessarily accompanied by a large non-uniform illumination error, even though both are related to the non-linear terms of the wavefront.
In summary, the centroid error due to non-uniform illumination in the SHWS is approximately proportional to the lenslet area, the linear variation of the intensity across the lenslet and the quadratic term of the wavefront. Therefore, this error can be mitigated by increasing the number of lenslets across the pupil, reducing the lenslet fill factor, or flattening the intensity profile at the SHWS pupil through apodization. Apodization can be achieved through the use of optical filters such as those demonstrated in vision science [22,23] or spatial light modulators. In the latter case, the transmission of such a device could be adjusted in real time using intensity profiles derived from the total or peak intensity of the SHWS lenslet images, provided the intensity pattern does not change substantially between consecutive SHWS images.
Funding.
National Eye Institute (P30EY026877, R01EY025231, R01EY028287, U01EY025477); Research to Prevent Blindness (Departmental Award).
REFERENCES
- 1.Shack RV and Platt BC, in Spring Meeting of the Optical Society of America (Optical Society of America, 1971). [Google Scholar]
- 2.Platt BC and Shack R, J. Refract. Surg 17, S573 (2001). [DOI] [PubMed] [Google Scholar]
- 3.Wizinowich PL, Le Mignant D, Bouchez AH, Campbell RD, Chin JCY, Contos AR, van Dam MA, Hartman SK, Johansson EM, Lafon RE, Lewis H, Stomski PJ, and Summers DM, Publ. Astron. Soc. Pac 118, 297 (2006). [Google Scholar]
- 4.Hardy JW, Adaptive Optics for Astronomical Telescopes (Oxford University, 1998), Vol. 16. [Google Scholar]
- 5.Booth MJ, Phil. Trans. R. Soc. A 365, 2829 (2007). [DOI] [PubMed] [Google Scholar]
- 6.Roorda A, Romero-Borja F, Donnelly W III, Queener H, Hebert T, and Campbell M, Opt. Express 10, 405 (2002). [DOI] [PubMed] [Google Scholar]
- 7.Dubra A, Sulai Y, Norris JL, Cooper RF, Dubis AM, Williams DR, and Carroll J, Biomed. Opt. Express 2, 1864 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mrochen M, Kaemmerer M, and Seiler T, J. Cataract Refract. Surg 27, 201 (2001). [DOI] [PubMed] [Google Scholar]
- 9.Dörband B, Müller H, and Gross H, Handbook of Optical Systems, Volume 5: Metrology of Optical Components and Systems (Wiley, 2012), Vol. 5. [Google Scholar]
- 10.Bara S, J. Opt. Soc. Am. A 20, 2237 (2003). [DOI] [PubMed] [Google Scholar]
- 11.Akondi V and Dubra A, Opt. Lett 44, 4151 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Robert C, Conan JM, Michau V, Fusco T, and Vedrenne N, J. Opt. Soc. Am. A 23, 613 (2006). [DOI] [PubMed] [Google Scholar]
- 13.Barchers JD, Fried DL, and Link DJ, Appl. Opt 41, 1012 (2002). [DOI] [PubMed] [Google Scholar]
- 14.Gao W, Jonnal RS, Cense B, Kocaoglu OP, Wang Q, and Miller DT, Opt. Express 17, 23085 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Stiles Walter S, Crawford BH, and Parsons John H, Proc. R. Soc. London B 112, 428 (1933). [Google Scholar]
- 16.Metcalf H, J. Opt. Soc. Am 55, 72 (1965). [Google Scholar]
- 17.Vohnsen B, Carmichael A, Sharmin N, Qaysi S, and Valente D, J. Vis 17(12):18 (2017). [DOI] [PubMed] [Google Scholar]
- 18.Marcos S, Diaz-Santana L, Llorente L, and Dainty C, J. Opt. Soc. Am. A 19, 1063 (2002). [DOI] [PubMed] [Google Scholar]
- 19.Westheimer G, J. Physiol 192, 309 (1967). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ma X, Mu J, Rao C, Yang J, Rao X, and Tian Y, Opt. Express 22, 15589 (2014). [DOI] [PubMed] [Google Scholar]
- 21.Ghatak A and Thyagarajan K, Introduction to Fiber Optics (Cambridge University, 1998). [Google Scholar]
- 22.Dalimier E, Dainty C, and Barbur JL, J. Mod. Opt 55, 791 (2008). [Google Scholar]
- 23.Wilson BJ, Decker KE, and Roorda A, J. Opt. Soc. Am. A 19, 833 (2002). [DOI] [PubMed] [Google Scholar]


