Transient indicators of tipping points in infectious diseases

Abstract

The majority of known early warning indicators of critical transitions rely on asymptotic resilience and critical slowing down. In continuous systems, critical slowing down is mathematically described by a decrease in magnitude of the dominant eigenvalue of the Jacobian matrix on the approach to a critical transition. Here, we show that measures of transient dynamics, specifically, reactivity and the maximum of the amplification envelope, also change systematically as a bifurcation is approached in an important class of models for epidemics of infectious diseases. Furthermore, we introduce indicators designed to detect trends in these measures and find that they reliably classify time series of case notifications simulated from stochastic models according to levels of vaccine uptake. Greater attention should be focused on the potential for systems to exhibit transient amplification of perturbations as a critical threshold is approached, and should be considered when searching for generic leading indicators of tipping points. Awareness of this phenomenon will enrich understanding of the dynamics of complex systems on the verge of a critical transition.

1. Introduction

Anticipating abrupt shifts in system state that are caused by gradual directional change in system conditions (critical transitions or ‘tipping points’) is a key issue for the natural and social sciences [1], including climate science [2,3], ecology [4–8], finance [9] and epidemiology [10–12]. In the situation where the change in an exogenous forcing variable is slow relative to the characteristic speed of the internal variables, the tipping point may be described mathematically as a bifurcation. As a bifurcation is approached, the system exhibits critical slowing down, i.e. its return rate to a stable equilibrium state following a perturbation decreases [13,14]. The long-term return rate to a stable equilibrium (sometimes called ‘asymptotic resilience’ [15,16]) is approximated by the dominant eigenvalue of the Jacobian matrix of the model representing the system. Prior to a bifurcation, the real part of the dominant eigenvalue approaches zero in continuous-time models (equivalently, the magnitude of the dominant eigenvalue approaches unity in discrete-time models).

Commonly used early warning signals for tipping points such as autocorrelation [17], variance [18] and the power spectrum [19,20] in one dimension are all functions of asymptotic resilience [21,22]. However, in systems that are non-normal, i.e. systems in which the eigenvectors of the Jacobian matrix obtained from linear stability analysis about a stable equilibrium are non-orthogonal [23,24], return to equilibrium can be dominated by long transients rather than the asymptotic return rate [23,25,26]. In normal systems, using asymptotic resilience as a measure of return rate is appropriate because trajectories quickly follow the direction of the dominant (slow) eigenvector and therefore move towards equilibrium [24,26]. In non-normal systems (termed ‘reactive’ by Neubert & Caswell [16]), if eigenvectors are nearly parallel to each other, then trajectories can initially be pulled in the direction of faster subdominant eigenvectors, away from the stable equilibrium [24], and towards an alternative equilibrium. Indeed, many systems in ecology and epidemiology are characterized by a non-normal Jacobian matrix [24,27,28]. Non-normal dynamics, characterized by extended and amplified transient behaviour, are common close to bifurcations and when there is a difference in timescales [29,30]. For example, in infectious disease systems, non-normality arises due to the difference in timescales between vital dynamics of the population and disease transmission [31,32]. In food webs, long transients arise due to timescale differences in predator–prey and consumer–resource interactions [27,30,33–35]. Until now, it has not been clear how the tendency for perturbations to amplify or go away from equilibrium in reactive systems could be harnessed as an early warning signal of a critical transition.

Neubert & Caswell [16] introduced two measures of transient dynamics, reactivity and amplification envelope. Both metrics can be calculated using the Jacobian matrix about a stable equilibrium. Reactivity provides an estimate of the potential for instantaneous growth of perturbations, and the maximum of the amplification envelope (maximum amplification) quantifies the relative maximum magnitude that a perturbation can transiently attain. Measures of transient dynamics offer a complementary alternative to resilience-based indicators for quantification of a system’s response to perturbations prior to a critical transition, and may be especially useful for reactive systems. The performance of transience statistics as an early warning system has not yet been assessed. To address this gap, we use vaccine-preventable infectious diseases as case studies for systems near criticality that have detectable transient behaviour [36,37]. Developing methods for monitoring reemergence of childhood immunizing diseases that can be used by decision makers is important for emergency preparedness [11,12,38,39], and tools that use signals in transient behaviour of time-series data could be especially helpful.

We study measles and pertussis as prototypical examples of childhood immunizing diseases with potential for re-emergence while causing significant morbidity and mortality [40,41]. Firstly, measles and pertussis have very high transmission potential (represented by very similar basic reproduction numbers) but differ in their infectious periods, and in this respect, represent ends of a spectrum. Given the historical importance of these infectious diseases and the availability of long-term incidence data, they have been the subject of intense scrutiny, with numerous efforts to explain their epidemiological dynamics using mechanistic transmission models. This body of work has highlighted the role played by seasonality [42,43], nonlinearity and stochasticity [44–47], contact patterns [48,49] and immunity [50–52] in shaping infectious disease dynamics. Secondly, measles and pertussis systems exhibit a separation of timescales. Outbreaks are often abrupt, and are followed by low disease prevalence over longer timescales. Thirdly, measles and pertussis have resurged in a number of developed countries [41,53–57]. Two dominant hypotheses for the resurgence are long-term declines in vaccine uptake [58] and very slowly waning immunity [52]. Changes in vaccine uptake or immunity are a slow driver of resurgence dynamics of childhood immunizing diseases (relative to the timescales of transmission and infection), inducing the crossing of a critical re-emergence threshold. Fourthly, infectious disease systems can undergo critical transitions [11]. Criticality in infectious disease models occurs at the point where the basic reproduction number R₀—the number of secondary infected cases arising from a single infected case in a susceptible population—is equal to unity. If the basic reproduction number of a disease exceeds unity, then the disease may be endemic; alternatively, if R₀ < 1, it will eventually die out. In deterministic compartmental susceptible–infectious–recovered (SIR) models of immunizing pathogens, a transcritical bifurcation occurs at the critical point. For these four reasons, measles and pertussis systems provide a useful case study for exploring how changes in transient behaviour can serve as an early warning signal prior to a critical transition [11].

Here, we show that reactivity and maximum amplification increase prior to the transcritical bifurcation of an SIR model with host demography and vaccination in both directions. Small perturbations to the endemic and disease-free equilibria of these systems potentially may grow in magnitude as the transcritical bifurcation is approached, i.e. when the disease is on the verge of elimination. This phenomenon has not been previously noted for compartmental disease models (but see Hosack et al. [32], which proposed reactivity as an index for transient increases in prevalence of infected hosts of a vector-borne disease). We show that reactivity depends on asymptotic resilience for these systems, and can be a reliable indicator of a critical transition resulting from directional changes in host immunity level. Next, we demonstrate these results in measles and pertussis time series. We show that increase in reactivity and maximum amplification prior to a critical transition predicted by theory is detectable in stochastic simulations of measles and pertussis models. Our demonstration that diagnostic changes in transient properties accompany the approach to a critical threshold may be important for health policy, including preparedness for temporary resurgence and forecasting. Furthermore, from a scientific perspective, our work indicates transient dynamics of complex multi-timescaled systems may be targeted for developing novel indicators of tipping points.

2. Methods

2.1. Model

We study the short-term response of the following model. Denoting the number of susceptible, infected and recovered individuals in a population of size N by S(t), I(t) and R(t), respectively, the standard SIR model with host demography and vaccination is given by

$$\begin{array}{cc}& \frac{\text{d}S}{\text{d}t}=\mu N(1-p)-\frac{\beta SI}{N}-\mu S,\\ & \frac{\text{d}I}{\text{d}t}=\frac{\beta SI}{N}-(\gamma +\mu )I\\ \text{and}& \frac{\text{d}R}{\text{d}t}=\mu Np+\gamma I-\mu R,\end{array}\}$$ 2.1

where μ is the per capita mortality rate, β is the transmission coefficient, p is the fraction of individuals vaccinated at birth and γ is the per capita recovery rate [59,60]. The per capita birth rate is equal to the per capita mortality rate to keep the population size S(t) + I(t) + R(t) = N constant. Setting p = 0 recovers the SIR model without vaccination. The basic reproduction number R₀ for the SIR model in the absence of vaccination is β/(γ + μ). If p > 0, the effective reproduction number is R₀(1 − p). System (2.1) has two steady states, the disease-free equilibrium, (N(1 − p), 0, Np) and the endemic equilibrium (N/R₀, μN(R₀(1 − p) − 1)/β, N [1 − 1/R₀ − μ(R₀ (1 − p) − 1)/β]). The system exhibits a transcritical bifurcation, i.e. the disease-free equilibrium and the endemic equilibrium meet and exchange stability at p* = 1 − 1/R₀. If p < p* the endemic equilibrium is locally asymptotically stable and if p > p* the disease-free equilibrium is locally asymptotically stable. Thus, p* is the critical proportion of new recruits to the population (births) that must be vaccinated to achieve elimination of the infection. Therefore, the mathematical description of elimination is the occurrence of a transcritical bifurcation, with the fraction vaccinated p as the bifurcation parameter. Similarly, emergence of disease due to reduction of immunity levels also corresponds to a transcritical bifurcation of the SIR model.

Since the population size is constant, we reduce system (2.1) to a system of two equations,

$$\begin{array}{cc}& \frac{\text{d}S}{\text{d}t}=\mu N(1-p)-\frac{\beta SI}{N}-\mu S\\ \text{and}& \frac{\text{d}I}{\text{d}t}=\frac{\beta SI}{N}-(\gamma +\mu )I.\end{array}\}$$ 2.2

To investigate the dynamics of perturbations from a stable equilibrium $(\overline{S},\overline{I})$ (depending on the value of vaccine uptake, either the endemic equilibrium or the disease-free equilibrium can be stable), linearizing system (2.2) about a stable equilibrium yields the matrix equation,

$$\frac{\text{d}z(t)}{\text{d}t}=\mathbf{J}z(t),z(0)=z_0,$$ 2.3

where J is the Jacobian matrix evaluated at the stable equilibrium $(\overline{S},\overline{I})$ of system (2.2), $z(t)=(S(t)-\overline{S},I(t)-\overline{I})$ is a 2 × 1 perturbation vector and $z_0=(S(0)-\overline{S},I(0)-\overline{I})$ is the initial perturbation from the equilibrium $(\overline{S},\overline{I})$. The solution of the linearized system (2.3) may be written as

$$z(t)=z_0\exp (\mathbf{J}t),$$ 2.4

where exp (Jt) is the matrix exponential.

2.2. Analytical measures of transient growth

Transient growth of a perturbation is an increase in the magnitude of a perturbation in the phase space, away from the stable equilibrium, as time increases. In a normal system (where the eigenvectors of a Jacobian matrix are orthogonal), the dominant eigenvalue λ₁ of the Jacobian matrix accurately describes how the magnitudes of perturbations from the equilibrium change with time [16,24]. However, if the Jacobian matrix is non-normal, asymptotic resilience may not always govern the system’s response to pulse perturbations [16,23,26]. Particularly, if the Jacobian matrix is non-normal, perturbations can temporarily move away from equilibrium (amplify) before they eventually decay at rate −Re λ₁.

A measure of short-term transient growth is reactivity [16], denoted by ν, which is the maximum instantaneous growth rate of a perturbation (in the limit t → 0 in continuous time)

$$\nu =\underset{\parallel z(0)\parallel \ne 0}{max}\left(\frac{1}{\parallel z(t)\parallel }\frac{\text{d}\parallel z(t)\parallel }{\text{d}t}\right){|}_{t=0},$$ 2.5

where || · || denotes the l₂-norm (Euclidean vector norm). The reactivity of each equilibrium of system (2.2) is the dominant eigenvalue of the Hermitian part of the Jacobian matrix, H(J) = (J + J^T)/2, where J^T is the transpose of J [16,23]. Reactivity is a rate, and therefore its units are per unit time. If ν is positive, the equilibrium is reactive, i.e. some (but not necessarily all) perturbations can exhibit transient growth away from the equilibrium. The magnitude of positive reactivity indicates a system’s potential to exhibit transient growth of perturbations.

To examine how reactivity changes as the transcritical bifurcation is approached from both directions in the SIR model (2.2) we calculated analytical expressions for reactivity of the endemic equilibrium (R₀(1 − p) > 1, elimination scenario) and for reactivity of the disease-free equilibrium (R₀(1 − p) < 1, emergence scenario). Table 1 shows the Jacobian matrices, Hermitian matrices, eigenvalues and reactivity expressions for both scenarios, as well as equations for the shorthand variables x = R₀ (1 − p) and Γ = γ + μ.

Table 1.

Matrices and expressions. We use shorthand variables Γ = γ + μ and x = R₀(1 − p) to denote rate of transfer out of the infectious class and effective reproduction number, respectively. Note x < 1 if p > p* and x > 1 if p < p*; 1 − x > 0 if x < 1 and x − 1 > 0 if x > 1. Subscript d indicates disease-free equilibrium; subscript e indicates endemic equilibrium.

endemic Jacobian Je	asymptotic resilience −Re λ1	oscillation frequency Im λ1
$\left(\begin{array}{cc}-\mu x& -\mathit{\Gamma }\\ \mu (x-1)& 0\end{array}\right)$	$\frac{\mu x}{2}$	$\sqrt{-{(\mu x)}^2/4+\mathit{\Gamma }\mu (x-1)}$

Hermitian H(Je)	reactivity νe
$\left(\begin{array}{cc}-\mu x& -\frac{1}{2}(\mathit{\Gamma }-\mu (x-1))\\ -\frac{1}{2}(\mathit{\Gamma }-\mu (x-1))& 0\end{array}\right)$	$-\frac{\mu x}{2}+\frac{1}{2}\sqrt{{(-\mu x)}^2+{(\mathit{\Gamma }-\mu (x-1))}^2}$

disease-free Jacobian Jd	asymptotic resilience −λ1	eigenvalues
$\left(\begin{array}{cc}-\mu & -\mathit{\Gamma }x\\ 0& -\mathit{\Gamma }(1-x)\end{array}\right)$	min (μ, Γ(1 − x))	−μ, −Γ(1 − x)

Hermitian H(Jd)	reactivity νd
$\left(\begin{array}{cc}-\mu & -\mathit{\Gamma }x/2\\ -\mathit{\Gamma }x/2& -\mathit{\Gamma }(1-x)\end{array}\right)$	$\frac{-\mu -\mathit{\Gamma }(1-x)}{2}+\frac{1}{2}\sqrt{{(-\mu -\mathit{\Gamma }(1-x))}^2-4\mu \mathit{\Gamma }(1-x)+{(\mathit{\Gamma }x)}^2}$

Another useful measure of short-term transient growth is the maximum of the amplification envelope, defined as the maximum possible amplification that a perturbation to the steady state may achieve relative to the initial displacement from equilibrium [16],

$$\rho (t)=\underset{\parallel z_0\parallel \ne 0}{max}\frac{\parallel z(t)\parallel }{\parallel z_0\parallel }=\underset{\parallel z_0\parallel \ne 0}{max}\frac{\parallel z_0\exp (\mathbf{J}t)\parallel }{\parallel z_0\parallel }=\parallel |\exp (\mathbf{J}t)\parallel |,$$ 2.6

where $\parallel |$ · $\parallel |$ denotes the matrix norm induced by the l₂ norm. The matrix norm of the matrix exponential exp (Jt) is the largest singular value obtained from the singular value decomposition of the matrix exponential at each time t ≥ 0, and so must be calculated numerically. A perturbation is amplified relative to an initial perturbation z₀ from the steady state if the ratio ||z(t)||/||z₀|| is greater than unity. Since the amplification envelope maximizes this ratio over all initial perturbations from the steady state, it yields a ‘worst case’ estimate for amplification of perturbations [16]. Note that because the amplification envelope is a ratio, its maximum (which we term maximum amplification) is dimensionless. To determine how transient amplification of perturbations changes as the critical threshold of the SIR model is approached from both directions, we calculated maximum amplification for measles and pertussis as a function of vaccine uptake using Wolfram Mathematica 10.4.

2.3. Data and study design

Our purpose in studying transient dynamics in models is to develop methods to provide insight into biological data. Next, we describe specific examples of datasets that we consider to be good candidates for an analysis based on transient indicators.

As a specific example of an infectious disease whose potential for emergence is of interest, we consider measles in the USA in the 2010s. For specific examples of two outbreaks to compare, we consider the outbreak originating in California in December 2014 described by Zipprich et al. [61] and the outbreak originating in Minnesota in April 2017 described by Hall et al. [62]. The available data for these outbreaks are the number of confirmed cases by the date of rash onset (figure 1). Different outbreak settings are likely to vary in how close they are to the point of emergence due to differences in contact rates and vaccination coverage.

Figure 1.

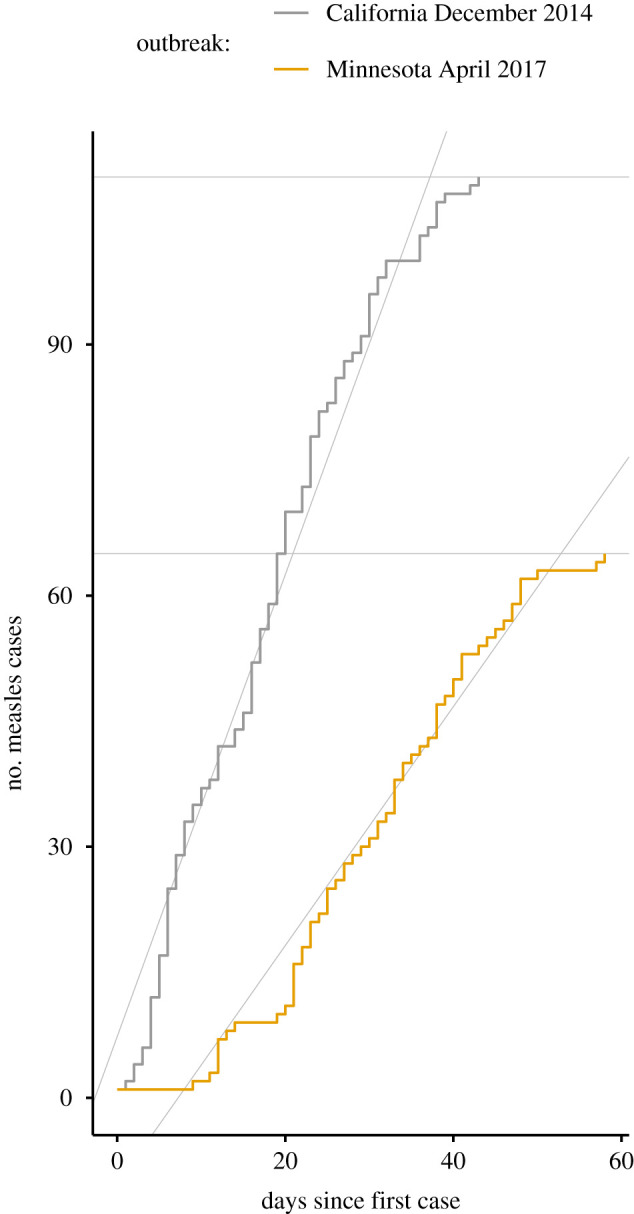
Two historical outbreaks with very different values of transient indicators. The maximum amplification indicator may be read from the height of the cumulative case count. The reactivity indicator is calculated from the slope of the least-squares line. These indicators have higher values in the California outbreak.

As a specific example of infectious disease whose potential for elimination is of interest, we consider pertussis in the USA in the period of 1938–1956. The available data consist of weekly reports of the number of cases of pertussis in each US state, which have been provided in a digital format by Van Panhuis et al. [63]. Pertussis may have moved closer to elimination in this period due to the rollout and increased coverage of whole-cell pertussis vaccines [64]. We prepared the time series for analysis following a similar procedure to Magpantay & Rohani [65], linearly interpolating missing data and excluding all data from states with a rate of missingness above 50%. State counts were added together to create a single US pertussis time series (figure 2a). Our pre-processing code is publicly available online [66].

Figure 2.

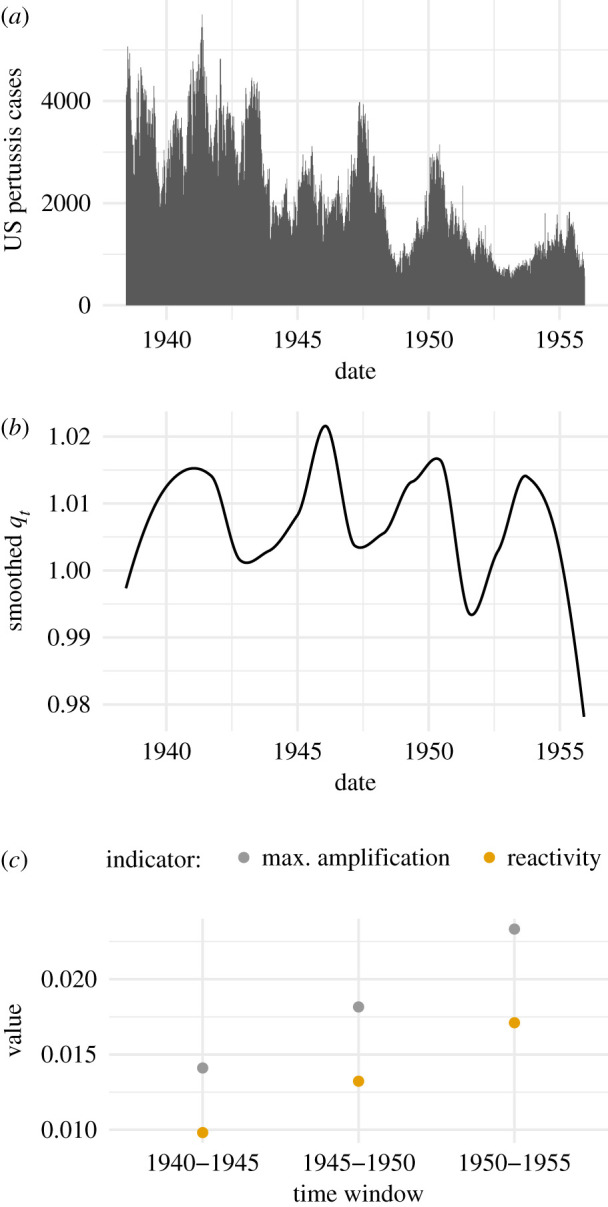
Transient indicators calculated from historical pertussis case reports increased over the period 1940–1955. (a) National level weekly total of pertussis case notifications for most states in the United States. (b) Estimated smoother of q_t (2.12). This smoother is proportional to the number of susceptibles, which our transient indicators target. (c) Both transient indicators increase in each successive 5-year window, which may be a consequence of increasing use of an effective vaccine.

To allow for the performance of the statistical methods that we develop below to be systematically studied, we simulated additional datasets having the same structure as these example empirical datasets. In the emergence scenario, the population immunity level of a locally eliminated disease decreases and we evaluate the ability of indicators to identify that the disease is closer to the point of emergence. In the elimination scenario, population immunity to an endemic disease jumps higher due to vaccination and we evaluate the ability of transient indicators to determine whether the system has moved closer to the point of elimination. A similar pair of scenarios was considered by O’Regan & Drake [10], but, given that the subject of the present work is transient dynamics, our scenarios occur over much shorter timescales. A detailed description of the simulation models may be found in the electronic supplementary material.

2.4. Indicators

2.4.1. Emergence

The direct output of our simulation model, a time series of cases per day, does not permit the direct calculation of reactivity and the maximum amplification according to their definitions. In particular, the part in the definitions about being the maximum over all possible perturbations seems impractical for the calculation of an indicator based on the observation of a single perturbation. However, even from a single observed perturbation it is possible to calculate indicators that are directly related to the reactivity and the maximum of the amplification envelope. The mathematical link between these two pairs of indicators is the behaviour of the eigenvectors of the linearized model (2.3). The derivation of these indicators is available in the electronic supplementary material.

Our specific formulae for calculating these indicators from the time series of cases of each outbreak are as follows. Let

$$n_t=\sum _{i=1}^t{C}_i,$$ 2.7

where C_t denotes the number of cases in day t. Thus n_t denotes the cumulative number of cases up to and including week t. The slope of the least-squares regression of n_t on t follows:

$${\tilde{\nu }}_d=\frac{\sum _{t=1}^{t_{\max }}(n_t-{\overline{n}}_t)(t-\overline{t})}{\sum _{t=1}^{t_{\max }}{(t-\overline{t})}^2},$$ 2.8

where the overbar denotes the sample mean and t_max denotes the index of the last observation in the time series. Equation (2.8) is a standard estimator for the slope of a straight line. Its use is justified by the approximate linearity of the cumulative number of cases over time in both the empirical (figure 1) and simulated (electronic supplementary material, figure S1) data. Strong departures from linearity in a dataset may indicate model violation, and the justification for the methods we describe here should be re-evaluated in light of likely causes of nonlinearity before they are applied. This ${\tilde{\nu }}_d$ variable serves as our reactivity indicator for the emergence scenarios, and the maximum amplification indicator is simply

$${\tilde{\rho }}_d=max(n_t).$$ 2.9

To allow comparison of our transient indicators with some previously studied generic indicators [1] derived from asymptotic dynamics, we also computed the mean, variance and lag-1 autocorrelation for each outbreak time series.

2.4.2. Elimination

In the elimination scenario, analysis of the eigenvectors of the linearized model (2.3) again provides a rationale for the use of practical indicators of reactivity and maximum amplification. In this case, the eigenvectors are complex, and the modulus of each element determines the relative amplitude of the S and I variables in damped oscillation around the equilibrium. Figure 3 illustrates that, for parameters typical of childhood diseases (i.e. x < Γ, μ ≪ 1, [59]) the relative amplitude of the S variable is many times that of the I variable. Therefore, transient growth of the norm of $(S-\overline{S},I-\overline{I})$ and maximum amplification must be dominated by the S component. Given that we know that S is a sine wave with decaying amplitude, our approach then is to use an estimate of the rate at which S first crosses the equilibrium as our reactivity indicator and an estimate of the amplitude of S in its first cycle as our maximum amplification indicator.

Figure 3.

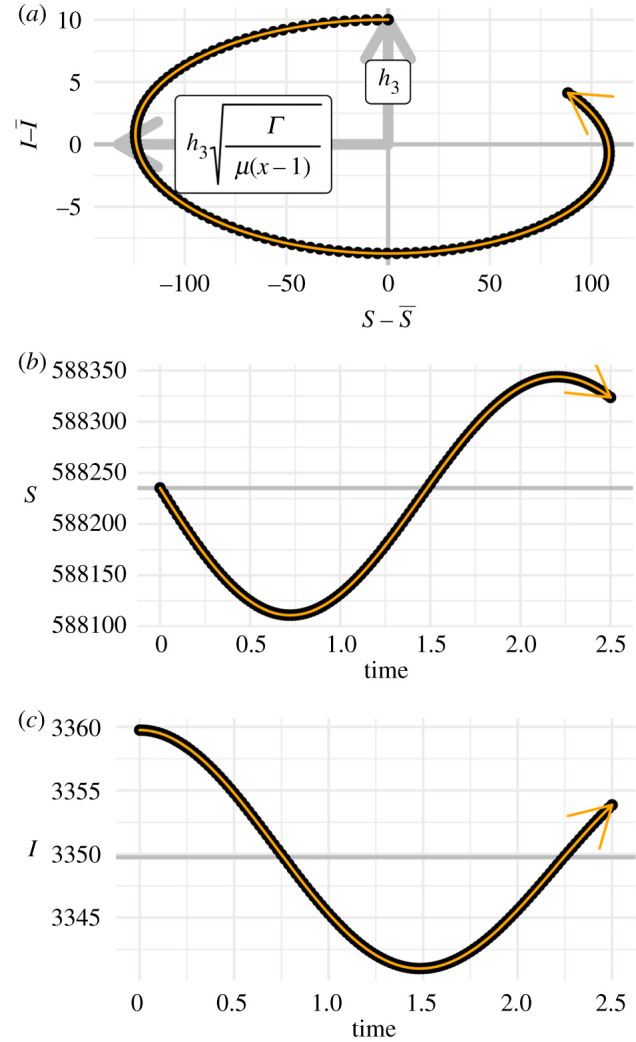
Near a stable endemic equilibrium $(\overline{S},\overline{I})$, transient growth of a perturbation is dominated by growth in $S-\overline{S}$. (a) The grey arrows point to bounds around the inward spiral of the perturbations to the equilibrium. The relative size of the bounds is determined by the relative sizes of the components of the eigenvectors of the Jacobian matrix, J_e in table 1. For this example, we used the values of the measles parameters in electronic supplementary material, table S2 and p = 8/17. These arrows are labelled with formulae for the modulus, in which h₃ is a normalization constant. These formulae indicate that the large relative amplitude of the S component of the spiral may be expected for typical parameterizations of our model. The black points are weekly samples from an example trajectory calculated with the same parameters as the grey arrows, and the orange path indicates the direction of time. (b,c) Plots of the dynamics of individual variables. The horizontal grey reference lines indicate the equilibrium values $\overline{S}$ and $\overline{I}$.

This approach requires us to estimate S, which is not observed in our model. Actually, since we are interested in trends in these indicators rather than in absolute values, it suffices for us to estimate a time series that is proportional to S. We do so by using the following relationships:

$$E(C_t)={\int }_{t-1}^t\gamma I(t)\hspace{0.17em}\text{d}t=\gamma {\tilde{I}}_t$$ 2.10

and

$$\begin{array}{rl}E(C_{t+l})& \approx {\int }_{t-1}^t\beta S(t)I(t)/[S(t)+I(t)+R(t)]\hspace{0.17em}\text{d}t\\ & \approx \beta {\tilde{S}}_t{\tilde{I}}_t/{\int }_{t-1}^t[S(t)+I(t)+R(t)]\hspace{0.17em}\text{d}t,\end{array}$$ 2.11

where the number of recovery events (cases) in week t is denoted by C_t and the overtilde denotes the integrated value of a random variable over the week indicated in the variable’s subscript. Equation (2.10) comes from integrating the transition rate of the recovery event in electronic supplementary material, table S1 over the course of week t. The approximation (2.11) is based on firstly assuming that individuals who are recovering in week t were on average infected about l weeks prior. A further approximation is then made that the integral over the transition rate of the transmission event in electronic supplementary material, table S1 may be separated into integrals over component factors. We now introduce the estimator q as

$$q_t=\frac{C_{t+l}}{C_t}\propto {\tilde{S}}_t.$$ 2.12

For l, we use the whole number of weeks that is closest to the infectious period of the disease (l = 2 for measles and 3 for pertussis).

The q_t calculated using (2.12) are noisy estimates and thus we next smooth them using the loess function in R [67], setting the span parameter to 0.4. We chose this span subjectively to balance responsiveness to changes in S in our simulations and the elimination of noise. We used the same value for our analysis of empirical pertussis data, which corresponds to a greater degree of smoothing given the longer length of the time series. We justified this choice by reasoning that the empirical data was subject to more observation noise than was present in our simulations and because the smoothed time series (figure 2b) seemed responsive to the dominant multi-year cycles in cases. Figure 2b also illustrates that the smoother tended to take on extreme values at the ends of the time series. We therefore excluded the first and last 1–2 years of the smoothed time series from the following steps of calculating the indicators.

The smoothed time series of q_t is centred by subtracting the mean to generate a times series of approximate norms, which we denote o_t. The series o_t is first-differenced and divided by the time step size to calculate a time series of approximate growth rates of the norm of the deviations, which we denote m_t. The solution (2.4) has the form of a vector of linear combinations of exponential functions, where the eigenvalues are the coefficient of time in the exponents. In this scenario, the two eigenvalues are complex conjugates and using Euler’s formula the exponential function may be written in terms of sinusoidal functions. The Harmonic Addition Theorem [68] then implies that small deviations in S decay as damped sinusoidal waves. For such deviations, the growth rate of S is near-maximal when the deviations are near-zero. Thus, as a reactivity estimate, we average |m_t| over all t such that |o_t| is within a small fraction ε of the range of o_t. Specifically, we use ε = 0.05. In summary, we have

$${\tilde{\nu }}_e=\text{mean}(|m_t|)\text{for }t\text{ such that }|o_t|<0.05\times [\text{max}(o_t)-\text{min}(o_t)].$$ 2.13

In our simulations, o_t and a value of ${\tilde{\nu }}_e$ were calculated separately for 5-year windows before and after the step change in vaccine uptake, yielding two reactivity indicators for each simulation. Likewise, we obtain two maximum amplification indicators ${\tilde{\rho }}_e$ according to

$${\tilde{\rho }}_e=\text{max}(o_t)-\text{min}(o_t).$$ 2.14

We use periods of 5 years based on the fact that the cycles of cases in our empirical and simulated data are typically 3–5 years long and inclusion of a complete cycle ensures that the extreme values of o_t are available as inputs for equations (2.13) and (2.14). In the empirical pertussis time series (figure 2a), we do not know when any large changes in vaccination occurred but expect that such changes occurred one or more times, so we simply divide the data evenly into three 5-year windows.

As with the emergence scenarios, we computed the mean, variance, and lag-1 autocorrelation on the cases time series of each window to allow the performance of these transient indicators to be compared with previously studied generic indicators. However, we use the negative mean as an indicator for elimination because we expect cases to decrease with vaccination.

3. Results

3.1. Emergence

3.1.1. Analytical results

The eigenvalues of the disease-free equilibrium are real but just one depends on vaccine uptake p (table 1), namely −Γ(1 − x). Although this eigenvalue has greater magnitude than μ for p > 1 − γ/β, it is clearly the eigenvalue that is more informative of vaccine uptake. Only very close to the emergence threshold does this eigenvalue have smaller magnitude than μ, suggesting that signatures of critical slowing down might remain hidden to methods that seek to detect it through asymptotic resilience [69,70]. Moreover, this informative eigenvalue of the disease-free equilibrium is greater for measles than pertussis. Thus, for the same levels of vaccine uptake, subcritical pertussis systems are predicted to take longer to go to equilibrium than measles systems.

The disease-free reactivity ν_d is typically positive because the determinant and trace of H(J_d) will both be negative provided x < 1 and γ ≫ μ, which is typical for childhood immunizing diseases [59], since γ and μ are the reciprocals of the infectious period and human lifespan, respectively. The disease-free reactivity, ν_d, depends on the eigenvalue −Γ(1 − x), and consequently increases with p as the threshold p* is approached from the right (electronic supplementary material).

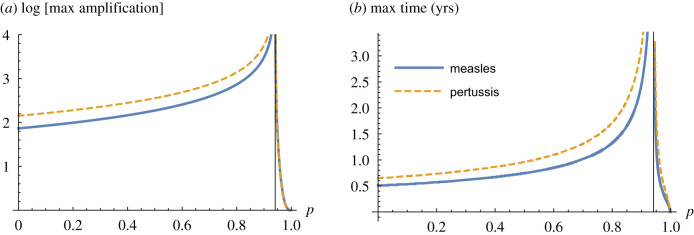
For our measles and pertussis models, the magnitude of maximum transient amplification and the timing of its occurrence increase as the system moves closer to emergence (figure 4).The measles dynamics exhibit greater magnitudes of transient amplification compared with pertussis and the timing of the maximum amplification for pertussis transients is more delayed relative to measles. In summary, our models for measles and pertussis differ in their transient dynamics in spite of having equivalent asymptotic resilience.

Figure 4.

Maximum amplification (peak of the amplification envelope, (a)) and time of maximum amplification (b) increase as vaccine uptake p approaches the critical threshold from left and right. The vertical line indicates the critical threshold p* = 1 − 1/R₀.

3.1.2. Data analysis results

To determine which of the two empirical measles outbreaks in figure 1 occurred in populations closer to the point of emergence, we calculated values of transient indicators for each outbreak using equations (2.8) and (2.9). The California outbreak had a reactivity indicator value of 2.76 susceptibles per day and a maximum amplification indicator value of 110 susceptibles. The Minnesota outbreak had a reactivity indicator value of 1.43 susceptibles per day and a maximum amplification indicator value of 65 susceptibles. Thus the transient indicators suggest that the California outbreak’s population was closer to the point of emergence.

To evaluate the performance of our transient indicators in absolute terms and relative to previously studied indicators for infectious disease, we calculated indicators on simulated outbreaks in which the vaccination rate of the populations varied. Electronic supplementary material, figure S4 shows the distribution of all indicators for each of the parameter settings in our simulations. For these simulations, the distribution of the indicators for measles and pertussis parameters was essentially the same. The transient indicators behaved as predicted by the deterministic analysis in §3.1.1 in that outbreaks from simulations with lower levels of vaccine uptake had higher values of the indicators.

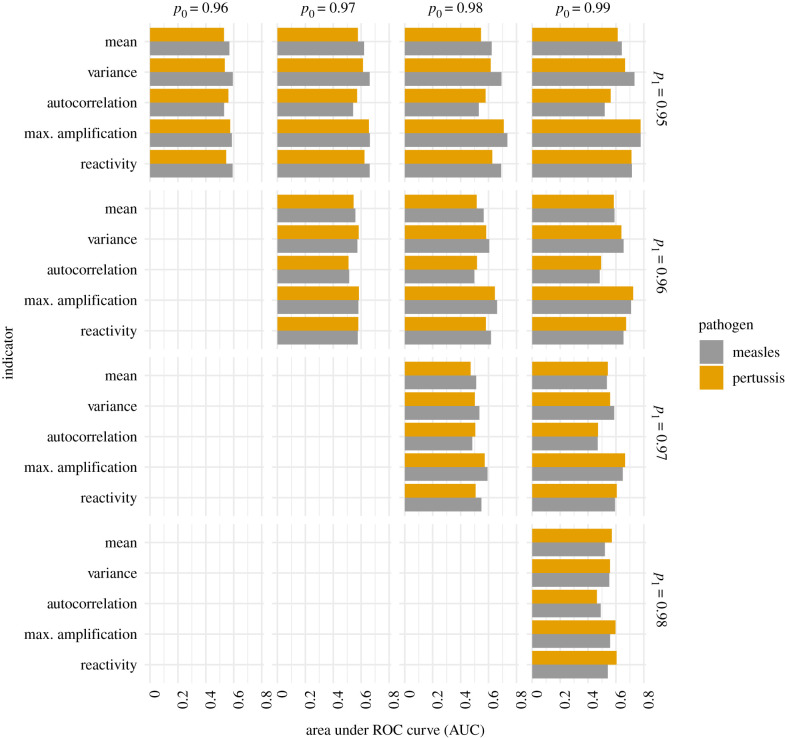
To evaluate the use of the indicators for classifying data by vaccination rate, we calculated AUC for distributions from all pairs of vaccine uptake for each indicator. Although, classification performance was poor for small differences in vaccine uptake, for the largest difference in vaccine uptake both of the transient indicators had AUCs above 0.6 (figure 5). Maximum amplification had an AUC which grew faster than all of the other indicators and it approached 0.8 for the largest difference in vaccine uptake. In sum, transient indicators can provide a reasonable approach to monitoring how close a disease is to emergence.

Figure 5.

Indicators of emergence were typically higher in outbreaks where vaccine uptakes were closer to the threshold of disease emergence, but this result was sensitive to the difference in vaccine uptake between the pair of outbreaks analysed. That is, the AUC was about 0.5 for all indicators for differences of 0.01 but AUC increased as this difference increases. Maximum amplification, an indicator based on transient dynamics, achieved the highest AUCs. These AUCs were calculated from the pairs of distributions in electronic supplementary material, figure S4. Panel labels across the top give the vaccine uptake p₀ that is higher within a pair; those along the right side give the vaccine uptake p₁ that is closer to the emergence threshold. The emergence threshold was p ≈ 0.94.

3.2. Elimination

3.2.1. Analytical results

The eigenvalues of the endemic equilibrium are complex conjugates, and therefore the real part indicates the speed of the approach to equilibrium (asymptotic resilience) and the magnitude of the imaginary part yields the period of damped transient oscillations to equilibrium. Asymptotic resilience of the endemic equilibrium is independent of recovery rate, and thus it is the same for measles and pertussis systems. However, the oscillatory period of perturbations of the endemic equilibrium depends on recovery rate, which would be one way to distinguish between them. Pertussis oscillations have slightly longer periods than measles oscillations (figure 6), indicating that pertussis perturbations move more slowly. Thus, for the same levels of vaccine uptake, supercritical pertussis systems take longer to relax to equilibrium than measles systems.

Figure 6.

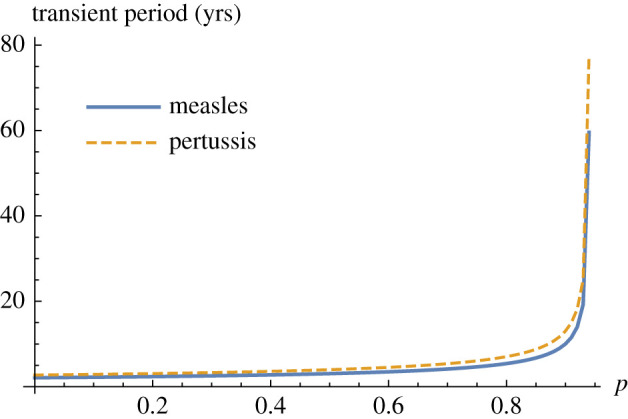
Period of transients given approximately by 2π/|Im(λ_1,2)|. Oscillation frequency |Im λ_1,2| declines as vaccine uptake p increases. Parameters used are in electronic supplementary material, table S2.

The reactivity of the endemic steady states of model (2.2) is positive since the trace and the determinant of H(J_e) are negative. The endemic reactivity, ν_e, is a function of asymptotic resilience (table 1), and is an increasing function of vaccine uptake p in the typical case that R₀ (1 − p) < Γ/μ + 1 (electronic supplementary material). As resilience decreases with p, reactivity increases, thereby signalling the critical slowing down of the system prior to the bifurcation. The maximum of the amplification envelope responds to progress toward elimination in the same way as it responds to movement towards emergence. That is, the magnitude of maximum transient amplification and the timing of its occurrence increase as the system moves closer to elimination (figure 4).

3.2.2. Data analysis results

To determine whether progress towards elimination of pertussis occurred in the USA during the period 1940–1955 (figure 2a), we calculated values of transient indicators in successive 5-year windows of the time series using equations (2.13) and (2.14). Values of both indicators increased in each successive window (figure 2c), suggesting sustained progress toward elimination throughout the period.

To evaluate the performance of our transient indicators in absolute terms and relative to previously studied indicators for infectious disease, we calculated indicators on simulated outbreaks in which the vaccine uptake of the populations jumped upwards. Electronic supplementary material, figure S5 shows the distribution of the difference in value of the indicators between windows before and after the jump in vaccine uptake for each of the parameter settings in our simulations. The transient indicators behaved as predicted by the deterministic analysis in §3.2.1 in that the difference of the indicators shifted to the right with the size of the step in vaccine uptake.

To evaluate the use of differences in indicators for identifying differences in vaccine uptake, we calculated AUC using distributions of differences in indicators between windows when no change occurred in vaccine uptake as a null distribution and distributions for each of the jumps in vaccine uptake as a test distribution. In contrast to the results of our emergence simulations, we found that all indicators had AUCs above 0.6 for all changes in vaccination rate (figure 7). The negative mean, in fact, always had an AUC of 1. The transient indicators of maximum amplification and reactivity had similar AUCs which generally exceeded those of the other indicators for both measles and pertussis parameters. In sum, transient indicators can provide a reasonable approach to monitoring progress towards elimination.

Figure 7.

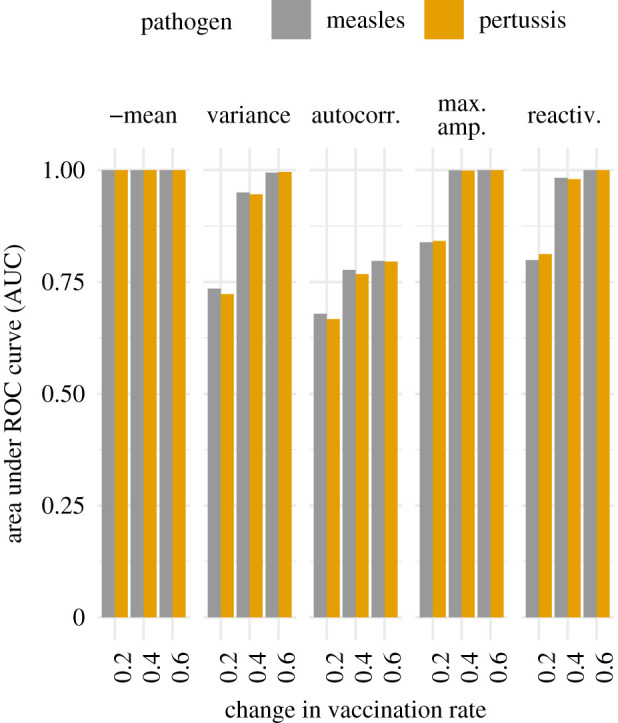
Indicators of progress towards elimination typically increased following a jump in the vaccine uptake for an endemic disease, especially for larger jumps. That is, the AUCs were above 0.5 for all indicators for all changes in the vaccine uptake p, and the AUCs less than 1 increased with the size of the change. The indicators based on transient dynamics, maximum amplification and reactivity, had higher AUCs than the other indicators, with the exception of the negative mean.

4. Discussion

In this paper, we have provided the first demonstration of transient indicators of tipping points. We have shown theoretically that short-term responses of immunizing disease systems, characterized by reactivity and the maximum of the amplification envelope, can change systematically as a tipping point is approached. The theory performs robustly when tested on measles and pertussis time series and stochastic simulations of vaccine-preventable diseases, indicating that measurements of transient dynamics may be a useful addition to the tipping-point-detection toolbox and may serve as a promising avenue for future research. Moreover, the transient indicators developed here could be used to forecast re-emergence of vaccine-preventable diseases through analysing epidemiological incidence data. Our work shows that transient indicators provide an additional approach for predicting resurgence that can be used in tandem with resilience-based indicators.

Our emergence scenario is intended to be broadly representative of infrequently reported notifiable diseases, such as diseases that have been eliminated locally and diseases that occur in small outbreaks following an infrequent transmission from another species. Our elimination scenario is intended to be representative of a commonly reported notifiable disease for which a major change in the extent of vaccine use occurs. In both of these scenarios, our indicators have major advantages over more generic methods of estimating reactivity. Our SIR-specific indicators exploit the structure of the SIR Jacobian matrix, unlike generic methods that estimate the Jacobian as an intermediate step to the estimation of reactivity, Neubert et al. [71], for example. This need for additional estimation likely makes the generic approach less efficient, and potentially highly unreliable for short time series such as the ones in our simulation study. Moreover, observation of all of the system’s state variables is needed. Such observations were not included in our scenarios because they are rarely available in practice. Although the use of state-space reconstruction methods may allow for this problem to be addressed, it seems that using indicators such as ours that rely on commonly employed modelling assumptions may be preferable. For the simulation study in this work, we found our reactivity indicators to produce higher AUCs than we were able to obtain with a straightforward application of the method of Neubert et al. [71]. Our application of transient indicators to stochastic simulations of vaccine-preventable diseases has indicated that transient indicators can perform at least as well as standard early warning signals based on critical slowing down (figures 5 and 7).

Our analysis sheds light on the mechanisms driving post-vaccination-era dynamics of measles and pertussis. In the supercritical situation, pertussis has slower dynamics than measles, although asymptotic resilience is the same for both diseases. In oscillatory systems, an estimate for the period of oscillations is needed in addition to resilience to assess the tendency for the system to switch dynamical state. Our pertussis models had longer periods of transient oscillations than our measles models (table 1 and figure 6) and transient growth of perturbations from equilibrium can last longer in the pertussis models and reach a greater magnitude prior to bifurcation (figure 4). Nevertheless, both systems exhibit a detectable change in transient dynamics before elimination and emergence, and performance of transient-based indicators was similar for both systems in our simulations (figures 5 and 7).

The use of transient indicators has some limitations. First, they can only be used if non-normal dynamics are suspected. This is easily checked by computing reactivity using methods developed in Neubert & Caswell [16] and Caswell & Neubert [27], as non-normality is confirmed by positive reactivity. If it is established that reactivity increases as a parameter moves toward a bifurcation point, a system-specific indicator could be developed to detect changes in transient dynamics. Transient indicators take advantage of the fact that non-normal dynamics are a general and widespread phenomenon; these dynamics appear in systems with multiple timescales. Therefore, transient dynamics may be effectively targeted for indicator development in a wide variety of systems.

In conclusion, we have shown that transient dynamics can change systematically prior to a bifurcation. In the vicinity of the critical vaccination threshold in immunizing disease systems, increased short-term growth and increased maximum size of perturbations may be expected. Measurement of such characteristics may be useful for detection of impending tipping points more generally. In particular, changes in reactivity could be a promising leading indicator of a tipping point in a variety of systems, not just infectious disease systems, because reactivity is likely to change systematically within non-normal dynamical systems [23,27,35].

Data accessibility

R and Mathematica files associated with this manuscript are available in a Zenodo web archive [66].

Authors' contributions

S.M.O. and E.B.O. contributed equally to the study. S.M.O., E.B.O., P.R. and J.M.D. conceived the main ideas. S.M.O. designed and performed mathematical analysis. E.B.O. designed and performed simulations and statistical analysis. All authors participated in the interpretation of results, drafting of the manuscript, gave final approval for publication and agree to be held accountable for the work performed therein.

Competing interests

We declare we have no competing interest.

Funding

Research reported here was supported by the National Institute of General Medical Sciences of the National Institutes of Health under award no. U01GM110744. The content is solely the responsibility of the authors and does not necessarily reflect the official views of the National Institutes of Health. This research was supported by a grant from the National Science Foundation, ADVANCE Institutional Transformation grant (award no. HRD-1409799).