Abstract
The lymphatic system transports lymph from the interstitial space back to the great veins via a series of orchestrated contractions of chains of lymphangions. Biomechanical models of lymph transport, validated with ex vivo or in vivo experimental results, have proved useful in revealing novel insight into lymphatic pumping; however, a need remains to characterize the contributions of vasoregulatory compounds in these modelling tools. Nitric oxide (NO) is a key mediator of lymphatic pumping. We quantified the active contractile and passive biaxial biomechanical response of rat tail collecting lymphatics and changes in the contractile response to the exogenous NO administration and integrated these findings into a biomechanical model. The passive mechanical response was characterized with a three-fibre family model. Nonlinear regression and non-parametric bootstrapping were used to identify best-fit material parameters to passive cylindrical biaxial mechanical data, assessing uniqueness and parameter confidence intervals; this model yielded a good fit (R2 = 0.90). Exogenous delivery of NO via sodium nitroprusside (SNP) elicited a dose-dependent suppression of contractions; the amplitude of contractions decreased by 30% and the contraction frequency decreased by 70%. Contractile function was characterized with a modified Rachev–Hayashi model, introducing a parameter that is related to SNP concentration; the model provided a good fit (R2 = 0.89) to changes in contractile responses to varying concentrations of SNP. These results demonstrated the significant role of NO in lymphatic pumping and provide a predictive biomechanical model to integrate the combined effect of mechanical loading and NO on lymphatic contractility and mechanical response.
Keywords: nitric oxide, structure and function relationships, lymphatic muscle, constitutive models
1. Introduction
The lymphatic system is composed of a hierarchical network of lymphatic vessels to transport lymph from the interstitial space back to the great veins [1]. The lymphatic network plays a key role in tissues haemostasis, transport of macromolecules and dietary fat and immune cell surveillance [2]. Once lymph is formed, the network of lymphatic capillaries (initial lymphatics) absorb lymph; collecting lymphatic vessels unidirectionally transport lymph from the initial lymphatics to the great veins [1,3]. The primary lymphatic valve prevents the leakage of absorbed lymph back to the interstitium [4]. Collecting lymphatic vessels (lymphangions) actively transport lymph via a series of orchestrated contractions, via specialized lymphatic muscle cell contraction and secondary lymphatic valves that ensure unidirectional flow of lymph against an adverse pressure gradient [4,5].
The lymphatic system can adjust its contractile function in response to mechanical and biochemical stimuli. Circumferential mechanical stretch due to transmural pressure is a modulator of lymphatic contractility; e.g. the frequency of contractions changes in response to pressure and the active tension changes with stretch for lymphatic vessels [6–8]. We have used the rat tail to show that collecting lymphatic vessels experience axial prestretch in vivo and to show that axial stretch is a regulator of lymphatic contractility in an ex vivo setting [9]. Further, small molecules such as nitric oxide (NO), histamine and endothelin-1 (ET-1) can regulate lymphatic contractility [10–15]. Changes in endothelial-derived NO via altered wall shear stress on the lymphatic endothelium or NO production from iNOS-expressing immune cells surrounding lymphatic vessels have been reported [10,16–19]. Collecting lymphatic vessels experience different flow patterns such as no-flow, slow-flow or even retrograde flow due to the phasic contractions of individual lymphangions, and opening/closing of secondary valves which likely regulate NO expression and availability [20,21].
The combination of ex vivo and in vivo studies and computational modelling has emerged as a useful tool to better understand lymphatic function. Several groups have developed mathematical models, validated with experimental observations, to study pumping of collecting lymphatic vessels [22–33]. These computational models have provided insight into lymphatic pumping in the context of optimal working conditions [34,35]. Our group previously developed a computational model to characterize the passive and active mechanics of the rat thoracic duct, with material parameters identified by fitting model parameters to passive and active (contractile) experimental data from cylindrical biaxial data via nonlinear regression [24]. Further, an algorithm was developed to use this framework, coupled with a valve model, to perform parametric studies of lymphatic growth and remodelling under altered mechanical loading conditions [25,36]. We have recently used the rat tail to study the intrinsic pumping function of collecting lymphatic vessels, in vivo [36,37]. In an in vivo setting, we also showed that the lymphatic pumping pressure (i.e. the maximum pressure that can be achieved along a lymphatic chain to maintain flow) increases along the length of the lymphatic chain and decreases when exogenous NO is administered; these results were characterized well using our previously reported mathematical modelling framework [36].
Given the complexity and regional heterogeneity of the lymphatic system [1,6,38], accurate characterization of specific lymphatic beds is crucial to integrate findings across different experimental models. Further, while our previous model provided a framework for integrating changes in contractile function, functional dependencies between model parameters and vasoregulatory molecules (e.g. NO, or ET-1) have not been experimentally validated. Thus, the purpose of this paper is to characterize pressure-dependent and NO-dependent modulation of rat tail lymphatic contractility via ex vivo experiments and to quantify mathematical modelling parameters to accurately capture these experimental observations. Sodium nitroprusside (SNP), an exogenous NO donor, was delivered in a dose-dependent manner to rat tail collecting lymphatics ex vivo, under controlled pressure and axial stretch, and vessel contractility was quantified. Passive cylindrical biaxial mechanical testing was performed to quantify the passive biomechanical response. Motivated by our previous multiphoton observation of collagen fibres in rat tail lymphatic vessels [9], a three-fibre family constitutive model (longitudinally and diagonally organized collagen fibres) was used to estimate the passive mechanical response. A modified Rachev–Hayashi model was used to characterize the active contractile function of rat tail lymphatic vessels and their respective changes due to the administration of SNP doses. Taken together, this paper presents findings at the interface of lymphatic physiology and biomechanical modelling to experimentally quantify and mathematically characterize the biomechanical behaviour and contractile function of rat tail collecting lymphatic vessels in response to both mechanical (i.e. pressure and stretch) and biochemical (i.e. exogenous NO) stimuli.
2. Material and methods
2.1. Vessel isolation and cannulation procedure
All animal experiments were approved by the Georgia Institute of Technology Institutional Animal Care and Use Committee (IACUC) and were performed in accordance with the principles outlined in the National Institutes of Health Guide for the Care and Use of Laboratory Animals. Segments of collecting lymphatic vessels (containing approx. 1–2 valves) from male Sprague Dawley rats (300–350 g) were isolated, immediately placed in Dulbecco's phosphate-buffered saline (DPBS, Corning), and the surrounding fat and connective tissues were carefully removed. Once vessels were cleaned, vessels were mounted on opposing cannulae in a custom-designed vessel chamber [24]. A custom LabVIEW program was used to control transmural pressure via a syringe pump (Harvard Apparatus, Inc.) and pressure sensors (1psi SSC series, Honeywell, Inc.). Linear actuators and XYZ stages (Newport Precision Instruments, LTA series, and M-461 series) were used to precisely control axial stretch, , where is the loaded length and L is the unloaded length of the isolated vessel between the two mounting sutures. Using an inverted microscope (2.5× magnification) and a digital camera (Allied Vision Technologies, Marlin F-033B), the active and passive response of vessels to controlled transmural pressures and axial stretches were captured and saved for further analysis. Axial force was measured using a 50 mN force transducer (Aurora Scientific, Model 400A). Each vessel was harvested from a different animal.
2.2. Exogenous NO and contractile function
Vessels were equilibrated for 60 min to establish stable contractions, while bathed in Dulbecco's modified Eagle's medium/nutrient mixture F-12 (DMEM/F-12), supplemented with penicillin–streptomycin (1 : 100, pH = 7.4 at 37°C) at constant transmural pressure (3 mm Hg) and axial stretch (λz = 1.10). SNP doses (10−7, 10−6, 10−5, 10−4 M) were then administrated in 5 min increments at each dose (n = 4). After SNP studies, the bathing solution was exchanged with a Ca2+-free PBS solution (Corning® phosphate-buffered saline, 1X without calcium and magnesium, PH 7.4 ± 0.1) containing 3 mM EDTA to assess the passive vessel diameter [24,39]. All experiments were performed at constant pressure (3 mm Hg) and λz = 1.10. A custom-written LabView program was used for post-processing of images recorded during the protocol to generate diameter tracings versus time. From these diameter tracings, end-systolic diameter (ESD), end-diastolic diameter (EDD) and contraction frequency (FREQ) were measured and contractile amplitude (AMP), ejection fraction (EF), fractional pump flow (FPF), were calculated as
| 2.1 |
| 2.2 |
| 2.3 |
Further, to obtain the SNP dose–response curve, changes in the above parameters and a change in lymphatic tone (tone) were calculated as follows:
| 2.4 |
| 2.5 |
| 2.6 |
| 2.7 |
where EDDcalcium-free indicates the EDD when the vessel is placed in a calcium-free bath at the same pressure. The subscript ‘basal’ represents the parameters for each vessel before the administration of SNP.
2.3. Cylindrical biaxial mechanical testing
A second set of vessels (n = 5) were isolated, cleaned, mounted on our custom vessel chamber, allowed to equilibrate and placed in Ca2+-free PBS solution for passive cylindrical biaxial mechanical testing [24,39]. All vessels were preconditioned by three inflation–deflation cycles from 0 to 10 mm Hg at λz = 1.10. Three inflation–deflation cycles from 0 to 10 mm Hg were conducted at each axial stretch λz = 1.10, 1.20 and 1.30.
2.4. Constitutive modelling
We modelled the passive rat tail collecting lymphatic vessels as long, straight, thin-walled cylinders in the framework of finite elasticity and incorporated the active (contractile) stress as
| 2.8 |
where is the ‘total’ Cauchy stress tensor, is the passive contribution to the Cauchy stress borne by the passive structural elements of the vessel wall (e.g. collagen, elastin, the passive contribution of lymphatic muscle cells) and is the active contribution of the Cauchy stress that arises due to lymphatic muscle cell contraction. In this theoretical framework, equilibrium requires that
| 2.9 |
where and are circumferential and axial components of the total Cauchy stress, respectively, P is the transmural pressure, r is the luminal radius, h is the wall thickness and f is the measured axial force. In the framework of finite elasticity, passive Cauchy stress is
| 2.10 |
where p is a Lagrange multiplier that enforces incompressibility, I is the identity tensor, F is the deformation gradient, is the right Cauchy–Green strain tensor and is a scalar-valued function representing the stored energy for elastic deformations. For inflation and extension of a materially symmetric thin-walled tube, , where the three stretch ratios are, and and (h, r, ℓ) and (H, R, L) are thickness, radius, and length for loaded, and unloaded vessel, respectively. We observed that collagen fibres in the rat tail lymphatic vessels are distributed preferentially in the axial direction [9]; thus, we chose a three-family stored energy function
| 2.11 |
where c, and are the material parameters, IC is the first invariant of the right Cauchy–Green strain tensor ()), is the stretch of the ith fibre family where is the fibre angle (see [40,41] for details). For this three-fibre family model, we let (axial direction) and (two symmetric diagonal fibre families), where is a structural parameter, solved via nonlinear regression along with c, and . Further, to ensure material symmetry, we let and .
To model the active contractile force generated by lymphatic muscle cells, we modify a model proposed by Caulk et al. [24] to incorporate the effect of SNP doses on the contractile force generation. We let the active contractile response contribute to the circumferential Cauchy stress; i.e. , where
| 2.12 |
and
| 2.13 |
where Tact is a scaling parameter, is the circumferential stretch, and are the stretches at which the active force is maximum and minimum, respectively, parameter is the maximum dilation to SNP, IC50 (inhibitory concentration, 50%) is the dose associated with 50% of the maximal dilation. The parameters λM and λ0 were prescribed as the maximum stretch achieved during the passive testing (λM = 1.85) and the minimum circumferential stretch (λ0 = 0.85) during the active testing. Tact changes from a minimum value (basal value) at the end diastole to a maximum value at the end systole during contractions, where a is a parameter.
2.5. Parameter estimation and bootstrapping
Since the lymphatic system shows regional heterogeneity it is crucial to have robust parameter estimation to identify biomechanical properties that yield unique parameter sets with known confidence intervals for each parameter [6,42]. To determine best-fit parameters, nonlinear regression using function lsqnonlin in MATLAB 2018b (MathWorks, Inc.) was used to identify the material and structural parameters (c, , , , and ) that minimized the following objective function
where the superscript th indicates a theoretical (model predicted) value, the superscript exp denotes an experimental value and overbar indicates the mean values across all data points for a given vessel. Since the objective function is the residual sum of squares to the total sum of squares, the coefficient of determination for each specimen is R2 = 1 − error. Data were transformed to a log-space as this is beneficial to provide a good fit for both low and high values of circumferential and axial stresses.
We used a non-parametric bootstrapping technique to assess the uniqueness of the fitted parameter sets and estimate the confidence interval of nonlinear regression. The details of the bootstrap technique for parameter estimation can be found in [43–45]. In brief, to apply the bootstrap technique to biaxial data, resampling with replacement was used to generate bootstrap replicants that have the same number of observations as the original data; each datum has the same probability to be chosen. To estimate 95% confidence intervals, we used the bias-corrected and accelerated percentile method (the BCa intervals) which is a second-order accurate interval that corrects for bias and skewness of bootstrap estimates. Bootstrap replicants greater than or equal to 1000 typically provide an accurate estimate [43]. The function bootci in Matlab 2018b (MathWorks, Inc.) was used to generate 2000 bootstrap sample sets; for each set model parameters were determined via nonlinear regression and the average and 95% confidence intervals of the 2000 sets of parameters were determined. The mathematical details of the BCa correction can be found in [46,47].
2.6. Statistics
To determine the statistical significance between control and experimental groups, a one-way ANOVA in conjunction with Tukey's post hoc correction was used to make multiple comparisons. Prism 5 (GraphPad Software) was used to perform all statistical analyses with statistical significance defined as p < 0.05 and results were reported as means (±s.e.m.).
3. Results
3.1. Passive and active biomechanical properties
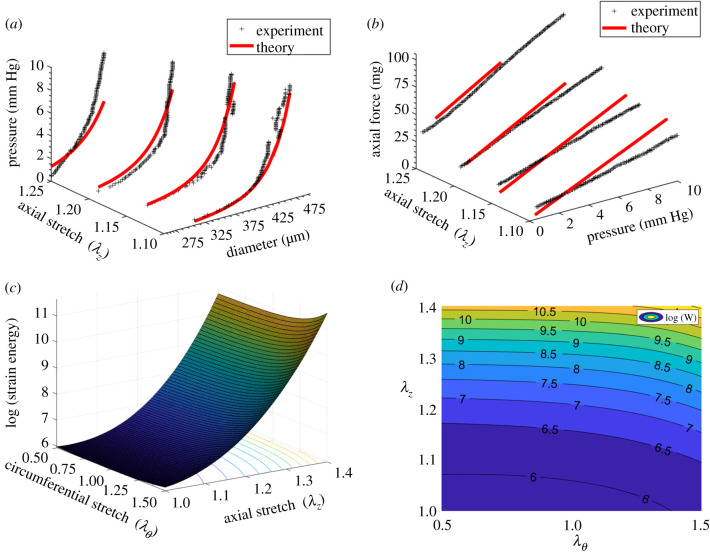
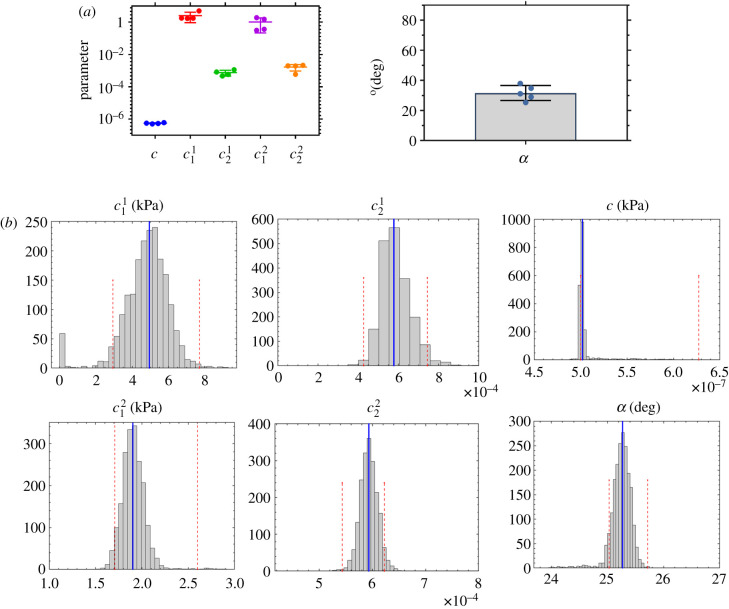
The three-fibre family constitutive model yielded a good fit (R2 = 0.90 ± 0.03) for the rat tail lymphatic vessels (figure 1 and table 1, using the geometric parameters in table 2). Supporting the previous experimental observation, our modelling results indicate that a three-fibre family model was sufficient to provide a good fit of biaxial data [9]. Based on the estimated parameters, the axial fibre family and two symmetric diagonal fibre families significantly contribute to the load-bearing function of lymphatic vessels; however, the isotropic term (namely, ) had a much smaller contribution; i.e. and (figure 2a and table 1). The confidence intervals for the fitted material parameters suggest that these parameter sets are unique and repeatable (figure 2b). Note that we also considered a four-fibre family model, following previous studies [24,40], adding a fourth fibre-family circumferential direction; however, the addition of a fourth fibre family did not improve the descriptive capability of the constitutive model and yielded multiple distinct parameter sets and much larger confidence intervals, suggesting non-uniqueness of the four-fibre family model for characterizing these tissues (results not shown).
Figure 1.
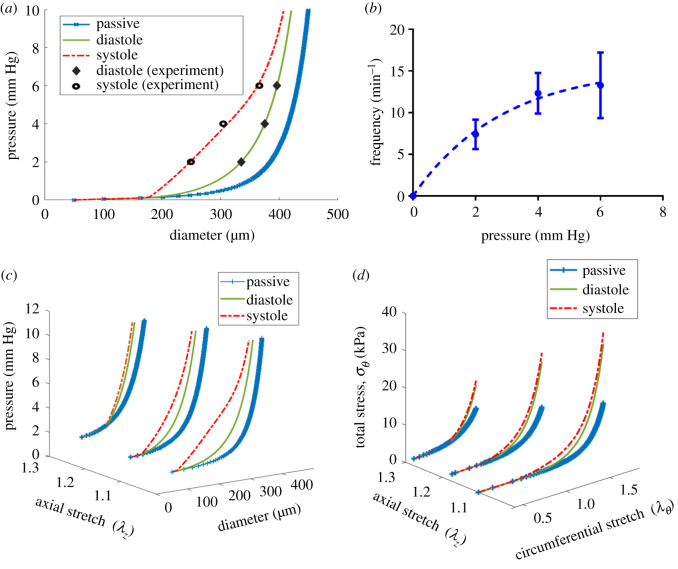
A representative plot of experimental biaxial testing and respective fitting results using a three-fibre family constitutive model including pressure–diameter measurements at different axial stretches and their respective theoretical values (a), axial force–pressure measurements at different axial stretches and their respective theoretical values (b), the stored strain energy calculated based on the estimated parameters (c) and a two-dimensional iso-contour representation of strain energy as a functional of circumferential and axial stretches (d). As shown in (c,d) the strain energy is sensitive to axial stretch and circumferential stretch indicating a stiffening response (increased stored energy), especially for axial stretch above 20% . The black plus symbols indicate experimental data and the red solid lines denote theoretical values based on the best-fit values (sample 1 in table 1).
Table 1.
Passive material parameter estimations respective confidence intervals for rat tail lymphatic vessels using a three-fibre family constitutive model. The objective function for the optimization was defined as Error = 1 − R2 value, calculated based on the biaxial data and estimated parameters. The best-fit values along with the bootstrapped confidence intervals are presented for each specimen. The estimated parameters and associated R2-values exhibit consistency indicating reasonable fits.
| specimen | elastic fibre | axial collagen |
diagonal collagen |
R2 | ||||
|---|---|---|---|---|---|---|---|---|
| c (kPa) | (kPa) | (kPa) | (degrees) | |||||
| 1 | best fit | 5.02 × 10−7 | 4.94 | 5.78 × 10−4 | 1.90 | 5.93 × 10−4 | 25.3 | 0.926 |
| BCa interval | 5.00 × 10−7 | 2.93 | 4.27 × 10−4 | 1.71 | 5.43 × 10−4 | 25.0 | ||
| 6.27 × 10−7 | 7.71 | 7.44 × 10−4 | 2.60 | 6.23 × 10−4 | 25.7 | |||
| 2 | best fit | 6.03 × 10−7 | 1.69 | 1.15 × 10−3 | 0.314 | 1.99 × 10−3 | 31.1 | 0.918 |
| BCa interval | 5.31 × 10−7 | 1.20 | 7.11 × 10−4 | 0.196 | 1.87 × 10−3 | 30.9 | ||
| 9.95 × 10−7 | 7.50 | 1.25 × 10−3 | 0.406 | 2.16 × 10−3 | 31.3 | |||
| 3 | best fit | 5.66 × 10−7 | 1.74 | 8.30 × 10−4 | 1.50 | 2.12 × 10−3 | 34.9 | 0.877 |
| BCa interval | 3.75 × 10−7 | 0.123 | 1.92 × 10−4 | 0.115 | 3.29 × 10−10 | 34.4 | ||
| 9.31 × 10−7 | 16.2 | 1.89 × 10−3 | 8.94 | 4.70 × 10−3 | 66.7 | |||
| 4 | best fit | 5.41 × 10−7 | 1.78 | 4.67 × 10−4 | 0.367 | 1.95 × 10−3 | 37.9 | 0.912 |
| BCa interval | 5.10 × 10−7 | 1.13 | 3.29 × 10−4 | 0.291 | 1.85 × 10−3 | 37.7 | ||
| 7.78 × 10−7 | 2.32 | 5.71 × 10−4 | 0.412 | 2.03 × 10−3 | 38.0 | |||
| 5 | best fit | 5.00 × 10−7 | 0.118 | 2.99 × 10−3 | 1.98 | 1.10 × 10−3 | 29.0 | 0.861 |
| BCa interval | 4.69 × 10−7 | 0.00 | 1.30 × 10−3 | 0.094 | 2.67 × 10−4 | 29.0 | ||
| 1.00 × 10−6 | 2.49 | 1.56 × 10−2 | 4.46 | 2.68 × 10−3 | 29.0 | |||
| average | 5.43 × 10−7 | 2.05 | 1.20 × 10−3 | 1.21 | 1.55 × 10−3 | 31.6 | 0.899 | |
| s.e. | 4.41 × 10−8 | 1.76 | 1.03 × 10−3 | 0.817 | 6.70 × 10−4 | 4.9 | 0.028 | |
Table 2.
Structural parameters associated with the unloaded geometry for rat tail lymphatic vessels presented in table 1. The diameter, thickness and length were estimated based on images obtained using an inverted microscope 2.5×–10× and analysed using the LabView and ImageJ.
| specimen | length (mm) | diameter (µm) | thickness (µm) | thickness/diameter ratio |
|---|---|---|---|---|
| 1 | 2.76 | 252 | 19 | 0.08 |
| 2 | 3.40 | 231 | 11 | 0.05 |
| 3 | 2.64 | 252 | 25 | 0.10 |
| 4 | 2.65 | 315 | 24 | 0.08 |
| 5 | 2.03 | 206 | 20 | 0.10 |
| average | 2.70 | 251 | 19.9 | 0.08 |
| s.e. | 0.48 | 40.4 | 5.6 | 0.02 |
Figure 2.
Material properties based on the fitted experimental biaxial data from rat tail lymphatic vessels (n = 5) using a three-fibre constitutive model including best-fit values of model parameters (a), and a representative estimation of respective confidence intervals using bootstrap technique showing the results of 2000 bootstrapping along with the best-fit values (blue line) and the BCa confidence intervals for each parameter (red dashed lines) based on the specimen 1 in table 1 (b).
3.2. Effect of transmural pressure on lymphatic contractility
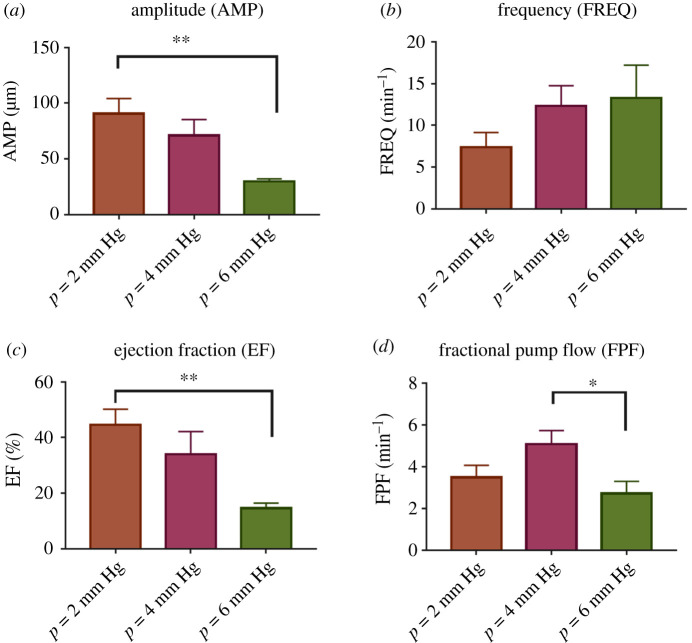
As has been shown in other tissue beds, rat tail lymphatics exhibit a functional contractile response to changes in pressure. The amplitude of contraction decreased from 90.7 ± 13.6 µm to 29.9 ± 2.3 µm as the pressure increased from 2 to 6 mm Hg (figure 3a). Similarly, the ejection fraction decreased 67% (from 44.6% ± 5.6% to 14.7 ± 1.7%) as pressure increased from 2 to 6 mm Hg (figure 3b, n = 5). By contrast, although not statistically significant, the mean frequency of contractions nominally increased by 40% (from 7.4 ± 1.8 min−1 to 13.3 ± 3.9 min−1, figure 3c) as the pressure increased from 2 to 6 mm Hg. Consequently, the fractional pump flow decreased 47% (from 5.1 ± 0.6 min−1 to 2.7 ± 0.6 min−1 figure 3d).
Figure 3.
Effect of transmural pressure on the contractile function of rat tail lymphatic vessels. The contractile metrics were plotted as a function of transmural pressure (n = 5), including the amplitude of contractions (AMP; a), frequency of contractions (FREQ; b), ejection fraction (EF; c), fractional pump flow (FPF; d). The axial stretch was approximately 10% for all experiments. All data are presented as mean (±s.e.m.) and statistical significance was tested via ANOVA with Tukey's post hoc tests (*p < 0.05, **p < 0.005).
3.3. Exogenous NO inhibits lymphatic contractility in a dose-dependent manner
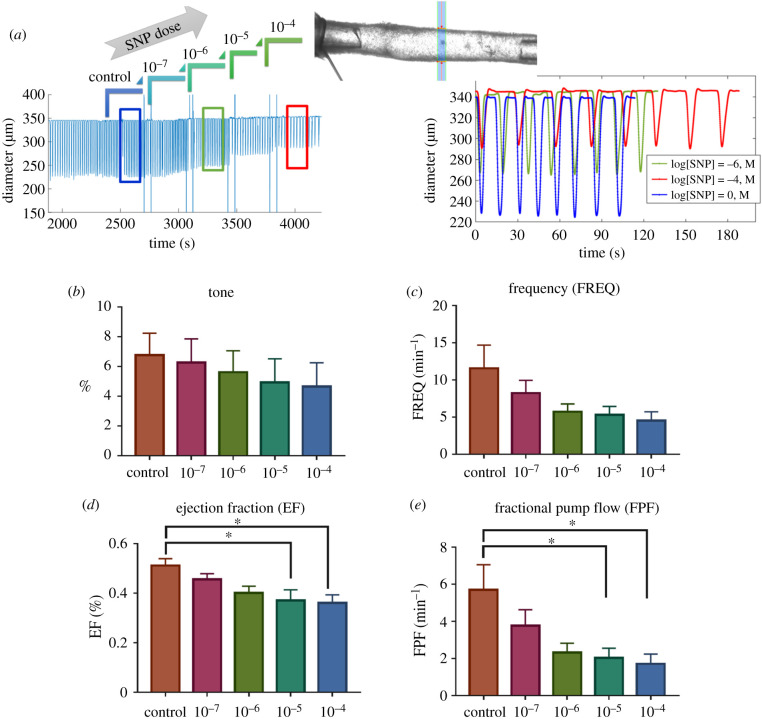
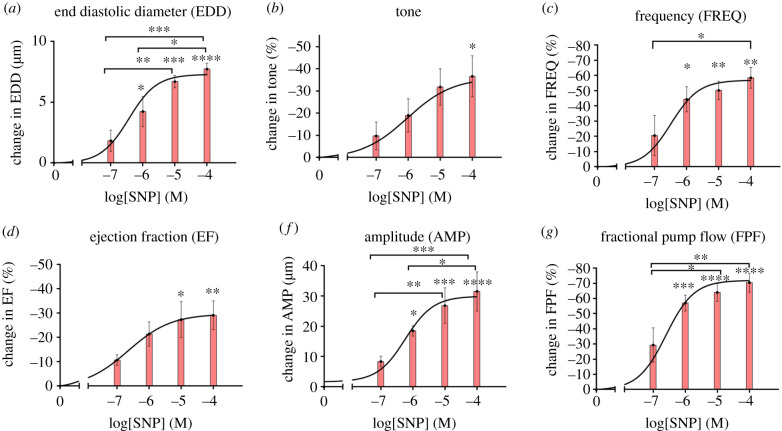
A representative isolated lymphatic vessel from rat tail, along with the respective diameter tracing in response to the administration of SNP doses (10−7, 10−6, 10−5, 10−4 M) to the bath are shown in figure 4a. The contractile activity of the isolated vessels in response to the administration of SNP doses was quantified (figures 4 and 5). The mean lymphatic tone decreased by 36.6% (from 6.8 ± 1.5% to 4.6 ± 1.6%, no statistical significance) equivalent to approximately 8 μm increase in the diastolic diameter (figures 4b and 5b). The frequency of contractions decreased almost 60% (from 11.6 ± 3.1 min−1 to 4.5 ± 1.2 min−1, no statistical significance) at the highest dose; however, the maximum reduction occurred from 10−7 (M) to 10−8 (M), (figures 4c and 5c). Similar trends were observed for the ejection fraction and amplitude of contraction, however, the maximum reduction was around 30%. The ejection fraction decreased 31.4% (from 0.52 ± 0.03 to 0.36 ± 0.03) (figures 4d and 5d) equivalent to approximately 32 um decrease in the contraction amplitude (figure 5e). Consequently, the fractional pump flow decreased with increase in the SNP concentration up to approximately 70% from 5.7 ± 1.3 (min−1) to 1.7 ± 0.5 (min−1) (figures 4e and 5f).
Figure 4.
Effect of exogenous NO on contractile function of isolated vessels from rat tail via SNP administration at different doses. A representative of diameter tracing from an isolated vessel experiment where different doses of SNP were administrated (a). Changes in contractile parameters were plotted as a function of NO doses, including change in basal tone (tone; b), frequency of contractions (FREQ; b), ejection fraction (EF; c), fractional pump flow (FPF; d). The pressure was set to 3 mm Hg and the axial stretch was approximately 10% for all experiments. All data are presented as mean ± s.e.m. (n = 4) and statistical significance was tested via ANOVA with Tukey's post hoc tests (*p < 0.05).
Figure 5.
Per cent change in contractile metrics (from figure 4) in response to different SNP doses including per cent change in end-diastolic diameter (AMP; a), per cent change in basal tone (tone; b), per cent change in frequency of contractions (FREQ; c), per cent change in amplitude of contractions (AMP; d) per cent change in ejection fraction (EF; e), per cent change in fractional pump flow (FPF; f). All data are presented as mean ± s.e.m. (n = 4) and statistical significance was tested via ANOVA and Tukey's post hoc tests (*p < 0.05, **p < 0.005, etc.). The statistical significances were tested to compare changes with respect to control values (zero SNP dose) as well as multiple comparisons between different doses.
3.4. Constitutive modelling of active contractile function and its response to NO
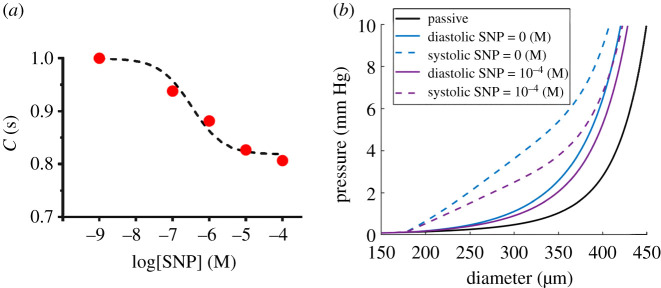
As shown by Caulk et al. [24], diastolic tension increase with increased pressure and hence the diastolic value for Tact is a function of pressure. We used the average tone (tone = 7.6% at 3 mm Hg, figure 4b) to fit a linear relationship between the diastolic Tact and transmural pressure (, and P (mm Hg) is basal pressure). Similarly, the average ejection fractions (44.6% at 2 mm Hg, 34% at 4 mm Hg, 14.7% at 6 mm Hg, figure 3c) were used to obtain systolic Tact . Modelling results including systolic, diastolic and passive diameter–pressure curves, along with respective experimental data, are shown in figure 6a. In addition, a nonlinear regression and was used to fit the frequency data (figure 6b). Pressure–diameter curves showed that increased axial stretch from 10% to 30% resulted in reduced systolic diameter and consequently the ejection fraction decreased from approximately 45% to less than 1% (figure 6c). Further, respective stress–strain curves showed the total circumferential stress decreased with increased axial stretch (figure 6d). Similarly, in order to model the effect of SNP on active stress, changes in contractile data due to SNP doses (figure 5b,d) were used to fit a dose–response curve (figure 7a). The parameter f(SNP) was calculated at each dose and nonlinear regression was used to fit a dose–response curve, yielding bSNP = 0.8 and (R2 = 0.9) The results suggested that the half-maximal effective concentration is approximately 10−6 (M) which caused an approximately 20% change in active stress generation resulted in an approximately 30% reduction in diastolic and systolic diameters (figure 7b).
Figure 6.
Modelling active contractile function of rat tail lymphatics based on the passive biomechanical data and active contractile data. The pressure–diameter curves for passive behaviour including passive, diastolic and systolic curves were plotted for three different values of axial stretch (a) and fitting results of contraction frequency in response to the transmural pressure (b). The passive parameters were obtained based on the constitutive model (equations ((2.8)–(2.11))) using the fitted parameters from sample 1 in table 1, and active diastolic and systolic curves were computed based on the active-tension model, equation (2.12) where parameter Tact was determined to be Tsys = Tdia + 1.6498 (kPa) at systole and Tdia = 0.87 × P(mm Hg) at diastole, estimated based on an algorithm to fit the contractile data for three pressures of 2, 4 and 6 mm Hg at 10% stretch in figure 3. An exponential equation using nonlinear regression (FREQ = 15.51 × (1 − exp(−0.3493 × Pressure), R2 = 0.52) was used to fit experimental data. The pressure–diameter curves for passive behaviour including passive, diastolic and systolic curves were plotted for three different values of axial stretch (c) and the respective computed total circumferential stresses were plotted as a function of circumferential and axial stretches (d).
Figure 7.
Modelling the effect of SNP on the active contractile behaviour of rat tail lymphatic vessels. A dose–response curve using a dose-dependent equation fits the correction factor (equation (2.12)) modelling the decrease in active contractile stress (C(SNP) = 0.80 + 0.2/(1 + 10^(log(SNP) + 6.42)), R2 = 0.98) due to SNP administration (a). Modelling results show the maximal changes in systolic and diastolic diameters in response to a 20% decrease of active stress at the maximum SNP dose (SNP = 10−4 (M)) (b).
4. Discussion
4.1. Robust three-fibre family model fit experimental data well and yielded unique parameter sets
To gain a better understanding of lymphatic transport in the context of lymphatic physiology and pathophysiology, it is essential to develop a basic knowledge of lymphatic vessel mechanics. Ohhashi et al. [48] showed that lymphatic vessels from the bovine mesentery manifest a nonlinear relationship between pressure and diameter, being very distensible at lower pressures and less distensible at larger pressures. More recent studies report similar findings in the rat mesentery [49], rat thoracic duct [24] and human pelvic vessels [50]. Based on the passive pressure–diameter relationship in the rat mesentery, the normal operating pressure is estimated to be between 0 and 5 cm H2O (approx. 3.7 mm Hg), a range in which the vessel is very distensible [49]. Our group performed biaxial testing on the lymphatic vessel from rat thoracic duct and showed that the nonlinear transitional response is a function of the axial stretch and pressure [24]. We showed that at the lower axial stretch the transition occurs at low pressures (less than 5 cm H2O, less than 3.7 mm Hg); however, the pressure–diameter relationship in the rat thoracic duct transitions to a linear shape at an axial stretch above 60%. Similar trends are observed for the human pelvic lymphatic vessels with some variations [50]. Our biaxial characterization of passive biomechanical properties of rat tail collecting lymphatic vessel is qualitatively similar to those of rat mesentery and thoracic duct; however, rat tail lymphatic vessels experience lower levels of the axial stretch and, for values above 30%, the vessel becomes stiff and the passive diameter does not notably change over physiological ranges of transmural pressure. The axial forces in the rat tail lymphatic vessel can reach approximately 1 mN at 25% stretch (p = 10 mm Hg) compared to approximately 1 mN at 50% stretch (p = 10 mm Hg) for the rat thoracic duct [24]. Similarly, the human pelvic lymphatic vessel is very sensitive to the axial stretch (approx. 1 mN at 20% stretch versus ∼4 mN at 30% stretch, p = 5 cm H2O approx. 3.7 mm Hg) [50].
We fit the passive biaxial data using a three-fibre family constitutive framework, originally adapted from Holzapfel et al. [41]. The estimated parameters for the axial and diagonal collagen fibres implies the axial fibre family plays a significant role in the load-bearing function. The significance of axial stretch in passive behaviour of lymphatic vessels is in agreement with our recent quantification of collagen fibre orientation in the rat tail lymphatic, where the vessels have a predominant organization of collagen fibres in the axial direction and experience axial prestretch of approximately 20% in situ [9]. Non-parametric bootstrapping, used to assess the uniqueness of the fitted parameter sets and to obtain the confidence intervals of estimated parameters, showed that the three-fibre family model yielded a unique set of material parameters. Our results suggest that a three-fibre family along with the bootstrapping technique can be a useful tool not only to establish a descriptive framework to study the regional heterogeneity in the material properties of lymphatic vessels but also to study changes in those properties in pathological scenarios.
4.2. Lymphatic pumping characteristics show regional variability
The effect of the transmural pressure on the modulation of lymphatic contractility has been very well-documented. Gashev et al. [42] characterized the regional heterogeneity of contractility in the rat mesentery, rat thoracic duct, rat neck and rat hindlimb lymphatics. In the rat mesentery, rat neck, rat hindlimb the frequency continuously increases with incremental increases in pressure, while the rat thoracic duct shows a peak in the mid-pressure range and the frequency decreases for higher pressures. The rat neck lymphatic vessels showed the highest frequency while the thoracic duct showed the lowest frequency. By contrast, the rat mesentery and rat thoracic duct have the highest ejection fraction while the rat neck has the smallest ejection fraction values. Consequently, the rat mesentery showed the highest, and the thoracic duct the lowest, values of fractional pump flow. Further, a peak is observed in the fractional pump flow for all the lymphatic vessel from all regions. Our characterization of rat tail lymphatic contractility, suggests that the changes in frequency response are similar to those of the rat mesentery; however, the ejection fractions are slightly smaller and are closer to those of thoracic duct. Ultimately, the fractional pump flow from the rat tail, which represents the overall pumping, is similar to the rat mesentery.
The regional heterogeneity in lymphatic function suggests that some vessels mainly serve as a pump (e.g. mesenteric and tail lymphatics) where a high pumping capacity is needed, and some mainly function as a conduit (e.g. thoracic duct) where minimal pumping is required [6,42]. This idea is also supported by the shear-flow sensitivity response in lymphatic vessels, where a significant shear-inhibition is observed in the lymphatic vessels from rat thoracic duct [51,52]. Gashev et al. [42] has previously reported the differences in contractile metrics for other tissues beds such as mesentery, thoracic duct, cervical and femoral lymphatics. The values of maximum ejection fractions were 0.21 ± 0.03 for cervical lymphatics (neck), 0.24 ± 0.05 for femoral lymphatics (hindlimb) 0.43 ± 0.04 for thoracic duct (at approx. 2.2 mm Hg) and 0.64 ± 0.04 for mesenteric lymphatics (at approx. 3.7 mm Hg). Further elevation in pressure resulted in a significance decrease in the ejection fraction values for all these vessels. Absolute values of contraction frequencies at approximately 2.2 mm Hg were 16.1 ± 2.6 min−1 for cervical lymphatics; 12.7 ± 1.5 min−1 for femoral lymphatics 5.0 ± 0.5 min−1 for thoracic duct; and 12.4 ± 1.8 min−1 for mesenteric lymphatics at approximately 3.7 mm Hg. An increase in pressure resulted in a significant increase in contraction frequency for all these vessels except for the thoracic duct, for which frequency declined. Our results suggest that the collecting lymphatic vessels from the rat tail exhibit strong pumping capability similar to the rat mesentery. Functionally, the rat tail lymphatics are afferent (pre-nodal), where there is no lymph node upstream to the vessels. Hence, the strong contractility can be justified by their major pumping role in the tail tissue.
4.3. The physiological importance of NO and its inhibitory effect on lymphatic function
NO is believed to be a key regulator in the modulation of lymphatic contractile function [42,53–57]. There are several sources of NO in lymphatic systems including (i) production of NO via LECs (eNOS pathway) due to shear stress (ii) production of NO via inducible NO synthase (iNOS pathway) in immune cells or lymphatic SMCs surrounding lymphatics (iii) production via nerve tissues (nNOS pathway) in prevascular tissues [10,19,56,58]. The mechanism of NO is believed to be involved in the production of the cGMP pathway that leads to the relaxation of muscle cells [59–64]. Based on microelectrode and immunohistochemical studies, it has been suggested that NO is produced in response to flow in both the valvular and tubular region of a lymphangion [13,17,65]. There is evidence that contractile metrics such as amplitude and frequency of contractions are attenuated in response to NO synthesis due to imposed flow [52]. Similarly, inhibition of NO synthase has shown that contractions enhance under basal conditions thus eliminating the inhibitory effect of imposed flow on contractions [8,10,66]. It is widely accepted that the effect of NO can be context-specific. For example, a high concentration of NO is believed to suppress amplitude and frequency of contractions; however, a low concentration of NO is thought to enhance contractions by increasing amplitude at the expense of frequency reduction [10,13,17,18,57,58,67]. By contrast, comparing the in situ measurements of lymphatic function in NO-deficient (eNOS−/–) mice, to the temporary inhibition of NO synthesis (via blockers infusion) have shown that diastolic diameter decreases but overall pump function is maintained with NO inhibition [19]. Gasheva et al. [10] have studied the active contractions of rat thoracic duct after NO synthase blockade with abluminal administration of L-NAME. They showed that NO released in response to shear stress/flow maintains higher contraction amplitude especially at lower pressures (e.g. approx. 20% for control group versus approx. 7% for L-NAME at 3 cm H2O). However, contraction frequency increased with the NO blockade and fractional pump flow did not significantly change. In addition, the tone index was approximately 160% higher after the NO blockade (approx. 13%) suggesting that the decreased tone due to NO is a regulatory mechanism to improve diastolic filling and provides higher amplitude of contractions.
As mentioned earlier, inducible NO (via iNOS) can be another significant source of NO; however, the studies in this area are very limited [19]. It has been shown that NO released by endothelium with acetylcholine (ACh) stimulation inhibits spontaneous contractions of lymphatic vessels. Modelling approaches have been used to investigate the regulatory mechanism of NO on lymphatic contractility [34]. Kunert et al. [34] presented a model describing two complementary feedback mechanisms to modulate lymphatic contractions involving: (i) a contraction triggered by Ca+2 rise due to a stretch (ii) a shear-mediated response to inhibit contractions via NO production. Specifically, this model predicts that NO is essential for the phasic contractions and without NO production phasic contractions are completely abolished; however, the modelling results have been questioned based on ex vivo studies of NO synthesis blockade showing spontaneous contractions develop and even improve in the absence of endothelial-derived NO [18]. In addition, entrainment of lymphatic contractions to flow can still be achieved when NO is blocked [51].
Although studies on NO synthase have advanced our knowledge of lymphatic contractility, the effect of exogenous NO is perhaps less well studied. Hence, we used SNP to deliver exogenous NO to the isolated lymphatic vessels at different doses. Our findings support the idea that the effect of NO is dose-dependent and the administration of higher doses of NO can suppress all aspects of contractility. Our experimental findings show exogenous NO has an inhibitory effect on lymphatic contractions; however, there is a dose–response relationship and higher doses of NO cannot completely abolish contractions. Interestingly, we showed that exogenous NO decreased the amplitude of contractions; however, the predominant effect was on the frequency of contractions. The results are supported by the observation that both endothelial-derived and exogenous NO decrease pacemaking activity of lymphatic muscle cells [68]. Specifically, it has been shown that the amplitude and frequency of spontaneous transient depolarization of lymphatic muscle cells diminish with SNP [51]. Further, we showed that exogenous NO reduced pumping up to 70% but it is not able to completely abolish contractions. The reduction in contraction frequency is almost twice the reduction in tone and amplitude. The results suggest the exogenous NO diminishes pacemaking activity in line with the established effect of SNP on the reduction of spontaneous transient depolarization frequency and amplitude in lymphatic SMCs [18,53,69]. The findings also suggest that overproduction of NO production beyond the physiological range, (e.g. NO production from iNOS-expressing cells located surrounding lymphatic vessels in inflammatory scenarios [70]) can inhibit lymphatic contractions, a possible mechanism that may lead to the lymphatic dysfunction in pathological scenarios.
Mechanisms involved in sensing the shear stress are not well established, however, it is well known that the production of NO by endothelial cells (eNOs signalling pathway) occurs in response to shear sensation. Since endogenous NO production has physiological relevance, most studies have focused on endogenous sources of NO. The effect of endothelial-derived NO on lymphatic contractility is also well documented via pharmacological inhibition and genetic deletion of the eNOS pathway. The genetic deletion of eNOS suggests that all aspects of lymphatic contractility are inhibited in a dose-dependent manner, while the pharmacological inhibition approach suggests that the relaxation and decreased contractile frequency due to NO provide stronger contractions, ultimately to enhance lymphatic pumping function [10,18]. Although exogenous pathways are not well established, it has been suggested that the exogenous NO inhibits lymphatic pumping [36,53,68,71–73]. For example, NO can be produced by exogenous sources such as NO production by myeloid cells (iNOS signalling pathway) in inflammatory scenarios.
We showed that the administration of exogenous NO suppresses all aspects of lymphatic contractility in a dose-dependent way. Further, we have recently shown that axial stretch is a modulator of lymphatic contractility and an increase in axial stretch of approximately 30% significantly reduces lymphatic contractility (less than 10%). The constitutive framework and estimated parameters support the significance of axial stretch in lymphatic function. Specifically, our modelling results suggest that a slight increase in axial stretch can significantly reduce total mechanical stress and stretch in the circumferential direction. In addition, the modelling results predict that the decrease in the circumferential stretch due to an increased axial stretch significantly reduces lymphatic muscle force production. Ultimately, the constitutive framework and specific experimental data for the rat tail lymphatic vessel pave the way for the future experimental and computational studies both in the context of lymphatic physiology and pathophysiology. In particular, the recent results from rat tail lymphatics suggest that the rat tail is a promising option to develop animal models of lymphatic dysfunction. Specifically, the study of lymphatic remodelling due to surgical interventions in the context of lymphatic pathologies such as lymphoedema or other inflammatory scenarios remains an exciting area for future studies. The presented specific experimental data along with the constitutive framework provide a basis for such studies.
In closure, this work characterized the contractile function of lymphatic vessels in response to altered mechanical stimuli and exogenous NO stimulus via ex vivo experiments on the isolated rat tail collecting lymphatic vessels. The computational model captures well the observed changes in contractile function to changes in both mechanical load and NO; such a model will prove useful in the understanding of lymphatic transport in the context of lymphatic physiology and pathophysiology.
Acknowledgements
We gratefully acknowledge that this work was funded by a grant from the American Heart Association (17PRE33670828) and the National Institutes of Health (R01-HL113061).
Ethics
All animal experiments were approved by the Georgia Institute of Technology Institutional Animal Care and Use Committee (IACUC) and were performed in accordance with the principles outlined in the National Institutes of Health Guide for the Care and Use of Laboratory Animals.
Data accessibility
This article has no additional data.
Authors' contributions
M.S.R. conducted all experiments, wrote all of the modelling and data analysis code, helped conceive the experimental design and helped draft the manuscript. J.B.D. and R.L.G. helped conceive of the overall experimental questions and experimental design and critically revised the manuscript. All authors gave final approval for publication and agree to be held accountable for the work performed therein.
Competing interests
We declare we have no competing interests.
Funding
This work was funded by the American Heart Association (grant no. 17PRE33670828) and the National Institutes of Health (grant no. R01-HL113061).
References
- 1.Zawieja DC. 2009. Contractile physiology of lymphatics. Lymphat. Res. Biol. 7, 87–96. ( 10.1089/lrb.2009.0007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Breslin JW, Yang Y, Scallan JP, Sweat RS, Adderley SP, Murfee WL. 2018. Lymphatic vessel network structure and physiology. Compr Physiol. 9, 207–299. ( 10.1002/cphy.c180015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chakraborty S, Davis MJ, Muthuchamy M. 2015. Emerging trends in the pathophysiology of lymphatic contractile function. Semin. Cell Dev. Biol. 38, 55–66. ( 10.1016/j.semcdb.2015.01.005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Davis MJ, Rahbar E, Gashev AA, Zawieja DC, Moore JE Jr. 2011. Determinants of valve gating in collecting lymphatic vessels from rat mesentery. Am. J. Physiol. Circ. Physiol. 301, H48–H60. ( 10.1152/ajpheart.00133.2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Muthuchamy M, Zawieja D. 2008. Molecular regulation of lymphatic contractility. Ann. N.Y. Acad. Sci. 1131, 89–99. ( 10.1196/annals.1413.008) [DOI] [PubMed] [Google Scholar]
- 6.Gashev AA, Zhang R-Z, Muthuchamy M, Zawieja DC, Davis MJ. 2012. Regional heterogeneity of length–tension relationships in rat lymph vessels. Lymphat. Res. Biol. 10, 14–19. ( 10.1089/lrb.2011.0013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhang R, Gashev AA, Zawieja DC, Lane MM, Davis MJ. 2007. Length-dependence of lymphatic phasic contractile activity under isometric and isobaric conditions. Microcirculation 14, 613–625. ( 10.1080/10739680701436160) [DOI] [PubMed] [Google Scholar]
- 8.Gashev AA. 2002. Physiologic aspects of lymphatic contractile function: current perspectives. Ann. N.Y. Acad. Sci. 979, 178–187; discussion 188–196 ( 10.1111/j.1749-6632.2002.tb04878.x) [DOI] [PubMed] [Google Scholar]
- 9.Razavi MS, Leonard-Duke J, Hardie B, Dixon JB, Gleason RL. 2020. Axial stretch regulates rat tail collecting lymphatic vessel contractions. Sci. Rep. 10, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gasheva OY, Zawieja DC, Gashev AA. 2006. Contraction-initiated NO-dependent lymphatic relaxation: a self-regulatory mechanism in rat thoracic duct. J. Physiol. 575, 821–832. ( 10.1113/jphysiol.2006.115212) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bakker EN, Sipkema P. 1997. Components of acetylcholine-induced dilation in isolated rat arterioles. Am. J. Physiol. 273, H1848–H1853. [DOI] [PubMed] [Google Scholar]
- 12.Nizamutdinova IT, Maejima D, Nagai T, Meininger CJ, Gashev AA. 2017. Histamine as an endothelium-derived relaxing factor in aged mesenteric lymphatic vessels. Lymphat. Res. Biol. 15, 136–145. ( 10.1089/lrb.2016.0062) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bohlen HG, Wang W, Gashev A, Gasheva O, Zawieja D. 2009. Phasic contractions of rat mesenteric lymphatics increase basal and phasic nitric oxide generation in vivo. Am. J. Physiol. Heart Circ. Physiol. 297, H1319–H1328. ( 10.1152/ajpheart.00039.2009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.von der Weid PY. 1998. ATP-sensitive K+ channels in smooth muscle cells of guinea-pig mesenteric lymphatics: role in nitric oxide and beta-adrenoceptor agonist-induced hyperpolarizations. Br. J. Pharmacol. 125, 17–22. ( 10.1038/sj.bjp.0702026) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Imtiaz MS, Zhao J, Hosaka K, von der Weid P-Y, Crowe M, van Helden DF. 2007. Pacemaking through Ca2+ stores interacting as coupled oscillators via membrane depolarization. Biophys. J. 92, 3843–3861. ( 10.1526/biophysj.106.095687) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gashev AA, Zawieja DC. 2010. Hydrodynamic regulation of lymphatic transport and the impact of aging. Pathophysiol. Off. J. Int. Soc. Pathophysiol. 17, 277–287. ( 10.1016/j.pathophys.2009.09.002) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bohlen HG, Gasheva OY, Zawieja DC. 2011. Nitric oxide formation by lymphatic bulb and valves is a major regulatory component of lymphatic pumping. Am. J. Physiol. Heart Circ. Physiol. 301, H1897–H1906. ( 10.1152/ajpheart.00260.2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Scallan JP, Davis MJ. 2013. Genetic removal of basal nitric oxide enhances contractile activity in isolated murine collecting lymphatic vessels. J. Physiol. 591, 2139–2156. ( 10.1113/jphysiol.2012.250662) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Liao S, et al. 2011. Impaired lymphatic contraction associated with immunosuppression. Proc. Natl Acad. Sci. USA 108, 18 784–18 789. ( 10.1073/pnas.1116152108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dixon JB, Greiner ST, Gashev AA, Cote GL, Moore JE, Zawieja DC. 2006. Lymph flow, shear stress, and lymphocyte velocity in rat mesenteric prenodal lymphatics. Microcirculation 13, 597–610. ( 10.1080/10739680600893909) [DOI] [PubMed] [Google Scholar]
- 21.Dixon JB, Gashev AA, Zawieja DC, Moore JE, Coté GL. 2007. Image correlation algorithm for measuring lymphocyte velocity and diameter changes in contracting microlymphatics. Ann. Biomed. Eng. 35, 387–396. ( 10.1007/s10439-006-9225-2) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bertram CD, Macaskill C, Davis MJ, Moore JE Jr. 2014. Development of a model of a multi-lymphangion lymphatic vessel incorporating realistic and measured parameter values. Biomech. Model. Mechanobiol. 13, 401–416. ( 10.1007/s10237-013-0505-0) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bertram CD, Macaskill C, Moore JE. 2011. Simulation of a chain of collapsible contracting lymphangions with progressive valve closure. J. Biomech. Eng. 133, 011008 ( 10.1115/1.4002799) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Caulk AW, Nepiyushchikh ZV, Shaw R, Dixon JB, Gleason RL. 2015. Quantification of the passive and active biaxial mechanical behaviour and microstructural organization of rat thoracic ducts. J. R. Soc. Interface 12, 20150280 ( 10.1098/rsif.2015.0280) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Caulk AW, Dixon JB, Gleason RL. 2016. A lumped parameter model of mechanically mediated acute and long-term adaptations of contractility and geometry in lymphatics for characterization of lymphedema. Biomech. Model. Mechanobiol. 15, 1601–1618. ( 10.1007/s10237-016-0785-2) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jamalian S, Bertram CD, Richardson WJ, Moore JE. 2013. Parameter sensitivity analysis of a lumped-parameter model of a chain of lymphangions in series. Am. J. Physiol. Heart Circ. Physiol. 305, H1709–H1717. ( 10.1152/ajpheart.00403.2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jamalian S, Jafarnejad M, Zawieja SD, Bertram CD, Gashev AA, Zawieja DC, Davis MJ, Moore JE. 2017. Demonstration and analysis of the suction effect for pumping lymph from tissue beds at subatmospheric pressure. Sci. Rep. 7, Article number 12080 ( 10.1038/s41598-017-11599-x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bertram CD, Macaskill C, Davis MJ, Moore JE. 2016. Consequences of intravascular lymphatic valve properties: a study of contraction timing in a multi-lymphangion model. Am. J. Physiol. Heart Circ. Physiol. 310, H847–H860. ( 10.1152/ajpheart.00669.2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jamalian S, Davis MJ, Zawieja DC, Moore JE. 2016. Network scale modeling of lymph transport and its effective pumping parameters. PLoS ONE 11, e0148384 ( 10.1371/journal.pone.0148384) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kunert C, Baish JW, Liao S, Padera TP, Munn LL. 2015. Mechanobiological oscillators control lymph flow -- revised. Nature 115, 10 938–10 943. ( 10.1073/pnas.1508330112) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Baish JW, Kunert C, Padera TP, Munn LL. 2016. Synchronization and random triggering of lymphatic vessel contractions. PLoS Comput. Biol. 12, e1005231 ( 10.1371/journal.pcbi.1005231) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Margaris KN, Black RA. 2012. Modelling the lymphatic system: challenges and opportunities. J. R. Soc. Interface 9, 601–612. ( 10.1098/rsif.2011.0751) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Grande KJ, Cochran RP, Reinhall PG, Kunzelma KS. 1998. Stress variations in the human aortic root and valve: the role of anatomic asymmetry. Ann. Biomed. Eng. 26, 534–545. ( 10.1114/1.122) [DOI] [PubMed] [Google Scholar]
- 34.Kunert C, Baish JW, Liao S, Padera TP, Munn LL. 2015. Reply to Davis: nitric oxide regulates lymphatic contractions. Proc. Natl Acad. Sci. USA 113, E106 ( 10.1073/pnas.1522233113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Davis MJ. 2015. Is nitric oxide important for the diastolic phase of the lymphatic contraction/relaxation cycle? Proc. Natl Acad. Sci. USA 113, E105 ( 10.1073/pnas.1521707113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Razavi MS, Nelson TS, Nepiyushchikh Z, Gleason RL, Dixon JB. 2017. The relationship between lymphangion chain length and maximum pressure generation established through in vivo imaging and computational modeling. Am. J. Physiol. Circ. Physiol. 313, H1249–H1260. ( 10.1152/ajpheart.00003.2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kassis T, Kohan AB, Weiler MJ, Nipper ME, Cornelius R, Tso P, Dixon JB. 2012. A dual-channel in-situ optical imaging system for quantifying lipid uptake and lymphatic pump function. J. Biomed. Opt. 17, 086005 ( 10.1117/1.JBO.17.8.086005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Swartz MA. 2001. The physiology of the lymphatic system. Adv. Drug Deliv. Rev. 50, 3–20. ( 10.1016/S0169-409X(01)00150-8) [DOI] [PubMed] [Google Scholar]
- 39.Scallan JP, Wolpers JH, Davis MJ. 2013. Constriction of isolated collecting lymphatic vessels in response to acute increases in downstream pressure. J. Physiol. 591, 443–459. ( 10.1113/jphysiol.2012.237909) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wan W, Yanagisawa H, Gleason RL. 2010. Biomechanical and microstructural properties of common carotid arteries from fibulin-5 null mice. Ann. Biomed. Eng. 38, 3605–3617. ( 10.1007/s10439-010-0114-3) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Holzapfel GA, Gasser TC, Ogden RW. 2000. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. Phys. Sci. Solids. 61, 1–48. ( 10.1023/A:1010835316564) [DOI] [Google Scholar]
- 42.Gashev AA, Davis MJ, Delp MD, Zawieja DC. 2004. Regional variations of contractile activity in isolated rat lymphatics. Microcirculation 11, 477–492. ( 10.1080/10739680490476033) [DOI] [PubMed] [Google Scholar]
- 43.Ferruzzi J, Vorp DA, Humphrey JD. 2011. On constitutive descriptors of the biaxial mechanical behaviour of human abdominal aorta and aneurysms. J. R. Soc. Interface 8, 435–450. ( 10.1098/rsif.2010.0299) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Yin FC, Chew PH, Zeger SL. 1986. An approach to quantification stress–strain of biaxial tissue data. J. Biomech. 19, 27–37. ( 10.1016/0021-9290(86)90106-5) [DOI] [PubMed] [Google Scholar]
- 45.Kamenskiy A, Seas A, Deegan P, Poulson W, Anttila E, Sim S, Desyatova A, MacTaggart J. 2017. Constitutive description of human femoropopliteal artery aging. Biomech. Model. Mechanobiol. 16, 681–692. ( 10.1007/s10237-016-0845-7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.DiCiccio TJ, Efron B. 1996. Bootstrap confidence intervals. Stat. Sci. 189–212. [Google Scholar]
- 47.Davison AC, Hinkley DV. 1997. Bootstrap methods and their application, vol. 1 Cambridge, UK: Cambridge University Press. [Google Scholar]
- 48.Ohhashi T, Azuma T, Sakaguchi M. 1980. Active and passive mechanical characteristics of bovine mesenteric lymphatics. Am. J. Physiol. 239, H88–H95. [DOI] [PubMed] [Google Scholar]
- 49.Rahbar E, et al. 2012. Passive pressure–diameter relationship and structural composition of rat mesenteric lymphangions. Lymphat. Res. Biol. 10, 152–163. ( 10.1089/lrb.2011.0015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Athanasiou D, et al. 2017. The passive biomechanics of human pelvic collecting lymphatic vessels. PLoS ONE 12, 1–12. ( 10.1371/journal.pone.0183222) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kornuta JA, Nepiyushchikh Z, Gasheva OY, Mukherjee A, Zawieja DC, Dixon JB. 2015. Effects of dynamic shear and transmural pressure on wall shear stress sensitivity in collecting lymphatic vessels. Am. J. Physiol. Integr. Comp. Physiol. 309, R1122–R1134. ( 10.1152/ajpregu.00342.2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Gashev AA, Davis MJ, Zawieja DC. 2002. Inhibition of the active lymph pump by flow in rat mesenteric lymphatics and thoracic duct. J. Physiol. 540, 1023–1037. ( 10.1113/jphysiol.2002.016642) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.von der Weid PY, Crowe MJ, Van Helden DF. 1996. Endothelium-dependent modulation of pacemaking in lymphatic vessels of the guinea-pig mesentery. J. Physiol. 493, 563–575. ( 10.1113/jphysiol.1996.sp021404) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Elias RM, Johnston MG. 1990. Modulation of lymphatic pumping by lymph-borne factors after endotoxin administration in sheep. J. Appl. Physiol. 68, 199–208. ( 10.1152/jappl.1990.68.1.199) [DOI] [PubMed] [Google Scholar]
- 55.Ferguson MK, Defilippi VJ. 1994. Nitric oxide and endothelium-dependent relaxation in tracheobronchial lymph vessels. Microvasc. Res. 47, 308–317. ( 10.1006/mvre.1994.1024) [DOI] [PubMed] [Google Scholar]
- 56.Shirasawa Y, Ikomi F, Ohhashi T. 2000. Physiological roles of endogenous nitric oxide in lymphatic pump activity of rat mesentery in vivo. Am. J. Physiol. Liver Physiol. 278, G551–G556. [DOI] [PubMed] [Google Scholar]
- 57.Yokoyama S, Ohhashi T. 1993. Effects of acetylcholine on spontaneous contractions in isolated bovine mesenteric lymphatics. Am. J. Physiol. 264, H1460–H1464. [DOI] [PubMed] [Google Scholar]
- 58.Hagendoorn J, Padera TP, Kashiwagi S, Isaka N, Noda F, Lin MI, Huang PL, Sessa WC, Fukumura D, Jain RK. 2004. Endothelial nitric oxide synthase regulates microlymphatic flow via collecting lymphatics. Circ. Res. 95, 204–209. ( 10.1161/01.RES.0000135549.72828.24) [DOI] [PubMed] [Google Scholar]
- 59.Datar SA, et al. 2014. Altered reactivity and nitric oxide signaling in the isolated thoracic duct from an ovine model of congenital heart disease with increased pulmonary blood flow. Am. J. Physiol. Hear Circ. Physiol. 306, H954–H962. ( 10.1152/ajpheart.00841.2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Walter U. 1989. Physiological role of cGMP and cGMP-dependent protein kinase in the cardiovascular system. Rev. Physiol. Biochem. Pharmacol. 113, 41–88. ( 10.1007/BFb0032675) [DOI] [PubMed] [Google Scholar]
- 61.Aratow M, Hargens AR, Meyer JU, Arnaud SB. 1991. Postural responses of head and foot cutaneous microvascular flow and their sensitivity to bed rest. Aviat. Space Environ. Med. 62, 246–251. [PubMed] [Google Scholar]
- 62.Warner TD, Mitchell JA, Sheng H, Murad F. 1994. Effects of cyclic GMP on smooth muscle relaxation. Adv. Pharmacol. 26, 171–194. ( 10.1016/s1054-3589(08)60054-x) [DOI] [PubMed] [Google Scholar]
- 63.Ohhashi T, Yokoyama S. 1994. Nitric oxide and the lymphatic system. Jpn. J. Physiol. 44, 327–342. ( 10.2170/jjphysiol.44.327) [DOI] [PubMed] [Google Scholar]
- 64.Gasheva OY, Gashev AA, Zawieja DC. 2013. Cyclic guanosine monophosphate and the dependent protein kinase regulate lymphatic contractility in rat thoracic duct. J. Physiol. 591, 4549–4565. ( 10.1113/jphysiol.2013.258681) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Bohlen HG, Zhou X, Unthank JL, Miller SJ, Bills R. 2009. Transfer of nitric oxide by blood from upstream to downstream resistance vessels causes microvascular dilation. Am. J. Physiol. Circ. Physiol. 297, H1337–H1346. ( 10.1152/ajpheart.00171.2009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Sunemoto HT, Komi FI, Hhashi TO. 2003. Flow-mediated release of nitric oxide from lymphatic endothelial cells of pressurized canine thoracic duct. Jpn. J. Physiol. 53, 157–163. ( 10.2170/jjphysiol.53.157) [DOI] [PubMed] [Google Scholar]
- 67.Kesler CT, Liao S, Munn LL, Padera TP. 2013. Lymphatic vessels in health and disease. Wiley Interdiscip. Rev. Syst. Biol. Med. 5, 111–124. ( 10.1002/wsbm.1201) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.von der Weid PY. 2001. Review article: lymphatic vessel pumping and inflammation—the role of spontaneous constrictions and underlying electrical pacemaker potentials. Aliment. Pharmacol. Ther. 15, 1115–1129. ( 10.1046/j.1365-2036.2001.01037.x) [DOI] [PubMed] [Google Scholar]
- 69.Kurtz KH, Moor AN, Souza-Smith FM, Breslin JW. 2014. Involvement of H1 and H2 receptors and soluble guanylate cyclase in histamine-induced relaxation of rat mesenteric collecting lymphatics. Microcirculation 21, 593–605. ( 10.1111/micc.12138) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Torrisi JS, et al. 2016. Inhibition of Inflammation and iNOS improves lymphatic function in obesity. Sci. Rep. 6, 1–12. ( 10.1038/srep19817) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Mizuno R, Koller A, Kaley G. 1998. Regulation of the vasomotor activity of lymph microvessels by nitric oxide and prostaglandins. Am. J. Physiol. 274, R790–R796. [DOI] [PubMed] [Google Scholar]
- 72.Weiler M, Kassis T, Dixon JB. 2012. Sensitivity analysis of near-infrared functional lymphatic imaging. J. Biomed. Opt. 17, 066019 ( 10.1117/12.906447) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Weiler M, Dixon JB. 2013. Differential transport function of lymphatic vessels in the rat tail model and the long-term effects of indocyanine green as assessed with near-infrared imaging. Front. Physiol. 4, 215 ( 10.3389/fphys.2013.00215) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
This article has no additional data.