Multi-stability in cellular differentiation enabled by a network of three mutually repressing master regulators

Abstract

Identifying the design principles of complex regulatory networks driving cellular decision-making remains essential to decode embryonic development as well as enhance cellular reprogramming. A well-studied network motif involved in cellular decision-making is a toggle switch—a set of two opposing transcription factors A and B, each of which is a master regulator of a specific cell fate and can inhibit the activity of the other. A toggle switch can lead to two possible states—(high A, low B) and (low A, high B)—and drives the ‘either-or' choice between these two cell fates for a common progenitor cell. However, the principles of coupled toggle switches remain unclear. Here, we investigate the dynamics of three master regulators A, B and C inhibiting each other, thus forming three-coupled toggle switches to form a toggle triad. Our simulations show that this toggle triad can lead to co-existence of cells into three differentiated ‘single positive' phenotypes—(high A, low B, low C), (low A, high B, low C) and (low A, low B, high C). Moreover, the hybrid or ‘double positive' phenotypes—(high A, high B, low C), (low A, high B, high C) and (high A, low B, high C)—can coexist together with ‘single positive' phenotypes. Including self-activation loops on A, B and C can increase the frequency of ‘double positive' states. Finally, we apply our results to understand cellular decision-making in terms of differentiation of naive CD4⁺ T cells into Th1, Th2 and Th17 states, where hybrid Th1/Th2 and hybrid Th1/Th17 cells have been reported in addition to the Th1, Th2 and Th17 ones. Our results offer novel insights into the design principles of a multi-stable network topology and provide a framework for synthetic biology to design tristable systems.

1. Introduction

Elucidating the operating principles of complex regulatory networks driving cellular decision-making is a central question in dynamical systems biology. A central tenet involved in decision-making is the ability of cells to exhibit more than one stable state (phenotype) in response to varying intracellular and/or extracellular conditions, without altering their genetic content. This feature is called as multi-stability (co-existence of more than one stable state/phenotype) and is implicated in cellular differentiation and reprogramming [1]. Thus, decoding the emergent dynamics of multi-stable biological networks hold great promise not only for mapping the cellular differentiation paths, but also for synthetic biology and regenerative medicine applications [2,3].

A commonly observed network motif involved in enabling multi-stability is a toggle switch, i.e. a set of two opposing transcription factors A and B, each of which is a master regulator of a specific cell fate and can inhibit the activity of the other through direct or indirect mechanisms. This mutual repression can allow for two states—(high A, low B) and (low A, high B)—and drives the ‘either-or’ choice between two cell fates for a common progenitor cell [2]. For instance, in haematopoietic stem cells, mutual repression between PU.1 and GATA1 can drive a common myeloid progenitor to a myeloid cell fate (high PU.1, low GATA1) or an erythroid one (low PU.1, high GATA1) [2]. This mutual exclusion of the two master regulators in the two states is critical for establishing stable cellular identities and can shepherd an ‘all-or-none' response instead of a graded one [4–6]. The construction of a toggle switch synthetically in E. coli set the stage for synthetic biology, when cells were shown to exhibit two states (bistability) and the ability to flip between them in response to transient stimuli [7]. Toggle switches and bistability is present in diverse biological contexts [8–10] and have received enough theoretical attention for their dynamics too [11–14].

One or both of the two master regulators in a toggle switch (A and B) can self-activate. Such self-activating toggle switches can allow for the existence of one more stable state (medium A, medium B) in addition to the two driven by a toggle switch. This third state often corresponds to a common progenitor cell state, as seen across many instances of cellular differentiation [2,15]. This ‘intermediate' progenitor state is often ‘metastable' and can differentiate to one of the two relatively more stable terminal states [2]. However, the dynamics of networks giving rise to three distinct states with a common progenitor have not been as well studied [16], despite instances of such decision-making seen in differentiation of CD4 expressing T-cells [17,18].

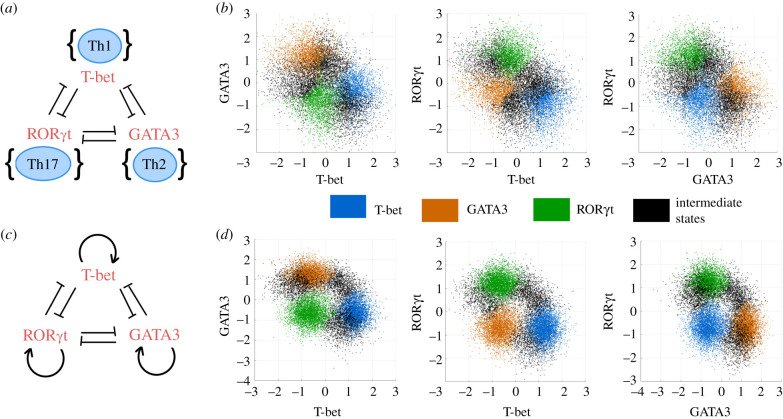
Here, we investigate the emergent dynamics of a set of three mutually repressing master regulators (A, B and C) and show that this ‘toggle triad' can lead to the co-existence of three distinct differentiated or ‘single positive' phenotypes—(high A, low B, low C), (low A, high B, low C) and (low A, low B, high C). In addition, the three ‘double positive' states—(high A, high B, low C), (high A, low B, high C) and (low A, high B, high C)—can also be seen to coexist with ‘single positive' phenotypes, although at a lower frequency. Adding self-activation on these master regulators can enrich for the existence of these ‘double positive' phenotypes that can be thought of as intermediate cell states between the corresponding ‘single positive' or differentiated states. Our results offer a mechanistic explanation of how a ‘toggle triad' formed among RORγT, GATA3 and T-bet can allow for three distinct T-cell states—Th1 (high T-bet, low GATA3, low RORγT), Th2 (low T-bet, high GATA3, low RORγT) Th17 (low T-bet, low GATA3, high RORγT) as well as corresponding hybrid cell fates originating from a common progenitor state (naive CD4⁺ T cell).

2. Results

2.1. Toggle triad can allow for co-existence of three phenotypes (tristability)

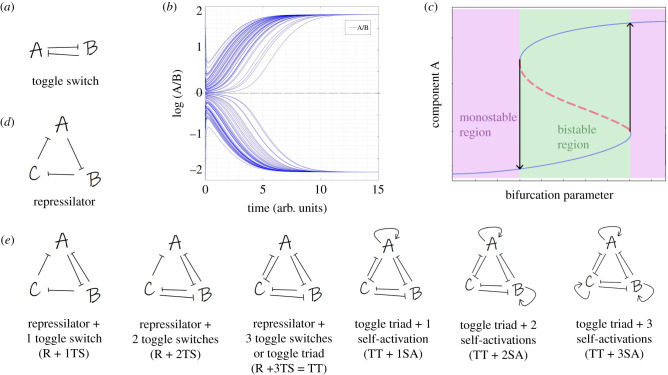
The emergent dynamics of simple two-component and three-component networks such as toggle switch and repressilator has been well investigated [11–14,19–21]. A toggle switch (i.e. a set of two mutually repressing transcription factors) (figure 1a) can lead to two phenotypes—(high A, low B) and (low A, high B)—thus A/B ≪ 1 or A/B ≫ 1 for the two stable states (figure 1b). This stark difference in the relative levels of A and B in the two states can drive cellular differentiation, as seen in multiple scenarios during embryonic development [2]. These two phenotypes may coexist (bistable region) for a certain range of parameters (green shaded region in figure 1c); however, tuning the levels of various cell-intrinsic or cell-extrinsic signals can lead to one of the states being destabilized, thus leading to two different monostable regions (pink shaded regions in figure 1c).

Figure 1.

Network schematics. (a) Toggle switch. (b) Dynamics of a toggle switch—different initial conditions can lead to two states: A/B ≫ 1 or A/B ≪ 1. (c) Schematic of the bifurcation diagram of a toggle switch. Solid blue curves indicate stable states; red dotted curves indicate unstable states. Bidirectional arrows show transition among different states. Green shaded region shows bistable region; pink shaded regions show two possible monostable regions. (d) Schematic of a repressilator. (e) Schematics of network topologies—repressilator with one, two or three toggle switches ((i) R + 1TS, (ii) R + 2TS, (iii) R + 3TS = toggle triad), toggle triad with one, two or three self-activations ((iv) TT + 1SA, (v) TT + 2SA, (vi) TT + 3SA).

A repressilator (figure 1d; a cyclic arrangement of three inhibitory transcription factors), on the other hand, does not lead to multiple stable states, instead it can display sustained or damped oscillations. Here, we investigate the dynamics of various possible couplings between the topology of these two well-characterized network motifs in different three-component systems. In a repressilator topology, either one (R + 1TS), two (R + 2TS) or three (R + 3TS) toggle switches were integrated. The network formed by a set of three mutually repressing regulators is hereafter referred to as a ‘toggle triad' (TT). Further, one, two or three of these regulators have been considered to be self-activatory as well (TT + 1SA; TT + 2SA; TT + 3SA) (figure 1e).

Next, to investigate the robust dynamical features of the abovementioned network topologies, we used a recently developed computational tool, RAndom CIrcuit PErturbation (RACIPE) [22]. RACIPE takes the network topology as an input and converts it into a set of coupled ordinary differential equations (ODEs) to represent the set of interactions in that network topology. RACIPE samples 10 000 sets of parameters within a biologically relevant range, i.e. it generates an ensemble of mathematical models, each with a different parameter set. For every chosen parameter set, RACIPE chooses a random set of initial conditions for each node in the network, simulates the dynamics and reports the different possible steady-state values for each node. Thus, each parameter set or kinetic model simulated via RACIPE corresponds to a different combination of parameters, reflecting cell-to-cell heterogeneity in biochemical reaction rates. An ensemble of models denotes the behaviour of a cell population and statistical tools are then applied to identify the robust dynamic properties of the given network.

Here, each kinetic model is a set of three-coupled ODEs, each of which tracks the dynamics of the levels of three interconnected molecular players A, B and C in various network topologies. Each of them has innate rates of production and degradation; the net production rate is affected by transcriptional regulation from other nodes; for instance, the inhibition of B by A in repressilator (R), repressilator + 1 toggle switch (R + 1TS), repressilator + 2 toggle switches (R + 2TS) and the toggle triad (figure 1d). The set of differential equations is solved numerically to attain steady-state values of each node. For each given parameter set, depending on the initial condition, each of these molecular players can converge to one or more possible steady states enabled by the given parameter set. Thus, a circuit considered can be potentially multi-stable (i.e. two or more phenotypes).

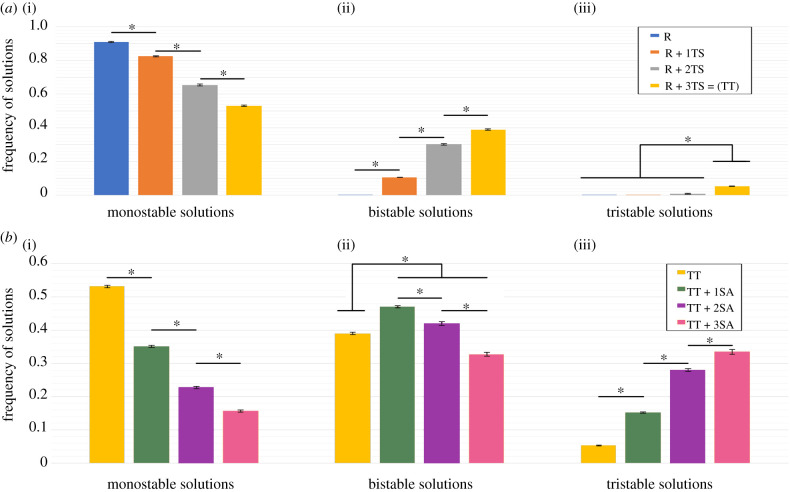
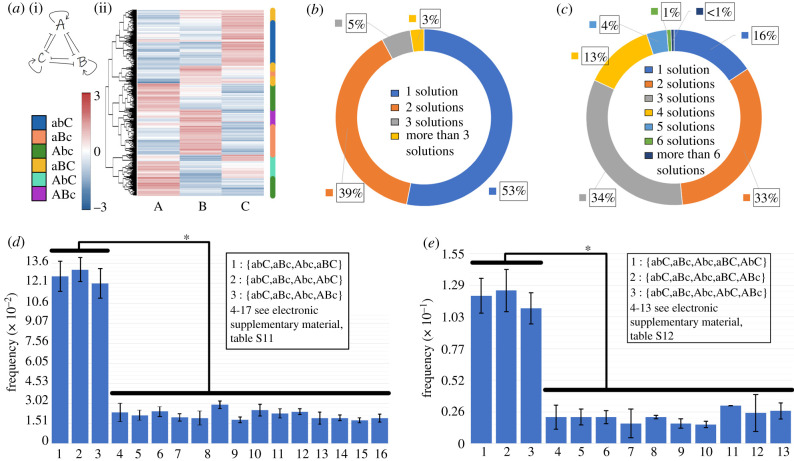
For all seven network topologies, R, R + 1TS, R + 2TS, TT, TT + 1SA, TT + 2SA, TT + 3SA (figure 1d), we use RACIPE to quantify the number of parameter sets that led to only one phenotype (monostable) as well as those that led to two (bistable) and three (tristable) phenotypes. A repressilator has been shown to be capable of generating sustained or damped oscillations but not multi-stability; thus, as expected, the parameter sets generated by RACIPE enabled either monostability (damped oscillations) or sustained oscillations (figure 2a, electronic supplementary material, figure S1). As we include more inhibitory links in the network topology, moving from a repressilator to a toggle triad, the frequency of parameter sets leading to monostability decrease continuously, and those leading to multi-stable solutions—either bistable or tristable—increase (figure 2a). Next, we investigate the dynamics of toggle triad with one or more self-activations included (TT, TT + 1SA, TT + 2SA, TT + 3SA) via RACIPE (figure 2b). A toggle triad has approximately 53% of parameter sets driving monostability; this frequency sharply decreases as one or more self-activations were included in the network topology. Instead, the frequency of parameter sets enabling tristability monotonically increase as we add more self-activations, while that of parametric combinations corresponding to bistability increases initially but decreases again (figure 2b). Put together, a toggle triad—with or without one or more self-activation links (TT, TT + 1SA, TT + 2SA, TT + 3SA)—is capable of exhibiting tristability, i.e. co-existence of three distinct stable states (phenotypes).

Figure 2.

RACIPE outputs for networks shown in figure 1e. (a,b) Frequency of parameter sets used by RACIPE that enable monostable, bistable and tristable solutions for different networks. N = 3 independent RACIPE replicates were done; error bars denote standard deviation. * denotes p < 0.05 for a Student's t-test.

2.2. Toggle triad can enable three predominant states—(high A, low B, low C), (low A, high B, low C) and (low A, low B, high C)

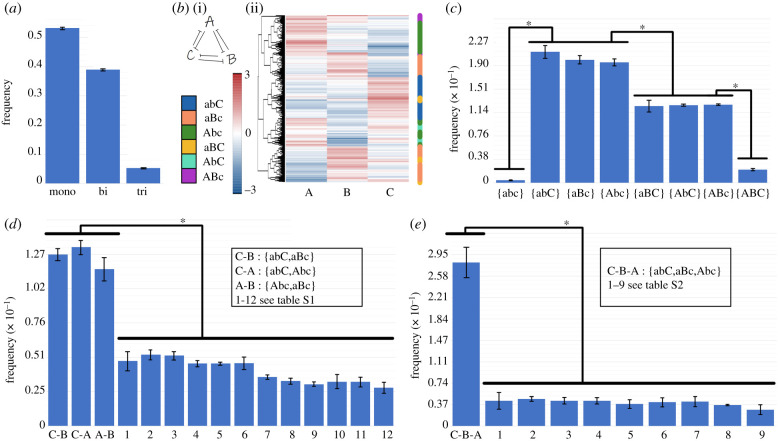
We next characterized the different steady states/phenotypes that a toggle triad can allow for, as identified by RACIPE. A toggle triad allows for approximately 53% monostable cases, approximately 39% bistable cases and approximately 5% tristable cases (figure 3a). We collated the levels of A, B and C obtained from all parameter combinations obtained via RACIPE and plotted them as a heatmap. This heatmap revealed three predominant states—(high A, low B, low C), (low A, high B, low C) and (low A, low B, high C)—represented by {Abc}, {aBc} and {abC}, respectively, hereafter. In addition to these states, a few instances of (high A, high B, low C), (high A, low B, high C) and (low A, high B, high C)—denoted by {ABc}, {AbC} and {aBC} states, respectively, hereafter—were also observed (figure 3b). These results indicate that a toggle triad can enable for states with one of the master regulators being relatively higher than the other two (‘single positive' states), as well as those with two master regulators being relatively higher than the third one (‘double positive' states).

Figure 3.

Characterization of a toggle triad. (a) Frequency of monostable, bistable and tristable solutions for a toggle triad. (b) (i) Heatmap showing the all solutions for a toggle triad; (ii) the nomenclature shown capitalizes the node whose levels are relatively high. Thus, Abc denotes (A-high, B-low, C-low), aBc denotes (A-low, B-high, C-low), abC denotes (A-low, B-low, C-high) (three ‘single positive' states). ABc denotes (A-high, B-high, C-low), AbC denotes (A-high, b-low, C-high), and aBC denotes (A-low, B-high, C-high) (three ‘double positive' states). ABC denotes (A-high, B-high, C-high) (triple positive), abc denotes (A-low, B-low, C-low) (triple negative) states. (c) Frequency of 8 = (2³) possible monostable solutions. (d,e) Frequency of different bistable and tristable cases; with the most frequent ones being combinations of Abc, aBc and abC = {Abc, aBc}, {aBc, abC}, {abC, Abc} (bistable) and {aBc, Abc, abC} (tristable). Error bars represent the standard deviation over n = 3 independent replicates of RACIPE. *: p < 0.05 for Student's t-test.

Reinforcing the trends seen in the heatmap, we observed that the distributions of levels of each of the three players A, B and C obtained via all RACIPE solutions was largely bimodal (electronic supplementary material, figure S2), indicating that each node in the network can exist in either a ‘high' or a ‘low' state. The minima of the distribution was around zero; thus, it was chosen as the cut-off for defining ‘high' versus ‘low' expression (see Methods). Together, a total of eight (= 2³) states can exist for a toggle triad. Further, we quantified the relative frequency of these eight possible steady states among monostable solutions. Among the parameter sets enabling monostable solutions, approximately 60% of cases led to the ‘single positive' {Abc}, {aBc}, {abC} states, approximately 36% of cases led to the ‘double positive' {ABc}, {aBC}, {AbC} states, while only 4% of the cases led to ‘triple positive' (high A, high B, high C—{ABC}) or ‘triple negative’ (low A, low B, low C—{abc}) states (figure 3c). Owing to the symmetric nature of the toggle triad, there was striking symmetry in the number of parameter cases leading to each of the three ‘single positive' or ‘double positive’ states as well; i.e. approximately 60/3 = 20% of parameter sets each converged to {Abc}, {aBc} or {abC} as a steady state, and approximately 36/3 = 12% of parameter sets converged to {ABc}, {aBC} or {AbC} as a steady state (figure 3c). Given the negligible frequency of the ‘triple positive' and the ‘triple negative' solutions, they were excluded from our further analysis.

We next examined the frequency distribution of parameter sets leading to bistable solutions. Here, a total of 15 (=⁶C₂; number of ways to choose two out of six solutions) phases (i.e. combinations of steady states). The three most common phases were the ones with coexisting ‘single positive' states, i.e. {Abc, aBc}, {aBc, abC} and {Abc, abC}, totalling up to approximately 42% of all parameter sets (figure 3d, electronic supplementary material, table S1). The remaining 12 combinations of steady states were obtained from a cumulative approximately 56% of parameter sets enabling bistability. Similarly, among a total of 20 (=⁶C₃; number of ways to choose three out of six solutions) tristable solutions, the most frequent combination was the set of coexisting ‘single positive' states, i.e. {Abc, aBc, abC} (approx. 30% parameter sets) (figure 3e, electronic supplementary material, table S2). Put together, these results suggest that one of the underlying design principles of a toggle triad is to allow the existence (or co-existence) of phenotypes where the levels of one of the three components is much larger than the remaining two, i.e. both A/B ≫ 1 and A/C ≫ 1 (i.e. {Abc}), or both B/A ≫ 1 and B/C ≫ 1 (i.e. {aBc}) or both C/A ≫ 1 and C/B ≫ 1 (i.e. {abC}).

2.3. The dynamical traits of a toggle triad

To further test that the above-mentioned design principles are specific to the toggle triad topology, we investigated the dynamics of multiple three-component networks where one or more of the six inhibitory links in a toggle triad has/have been replaced with an activatory link (circuits C1–C14; electronic supplementary material, figure S3). All of the 14 circuits failed to exhibit at least one of the salient features of a toggle triad, when comparing the state frequency for parameter sets enabling monostable solutions: (i) the frequency of ‘triple positive' and ‘triple negative' states is negligible (8/14 cases have 18% or more parameter sets leading to either of these two states), (ii) the relative frequency of all three ‘single positive' states was the same, (iii) the relative frequency of all three ‘double positive' states was the same and (iv) the ‘single positive' states were more frequent than the ‘double positive' ones (electronic supplementary material, table S3). As expected, the circuit with all inhibitory links in a toggle triad replaced by activation (C2) showed the ‘triple negative' and ‘triple positive' states as the most predominant ones. Similarly, when comparing the results for bistable and tristable scenarios, none of the 14 circuits showed the co-existence of two (in case of bistable) or three (in case of tristable) ‘single positive' cases as the predominant trend as seen in cases of a toggle triad (electronic supplementary material, tables S4, S5). Finally, the percentage distribution of parameter sets that led to monostable, bistable and tristable solutions was quite different for these 14 circuits as compared to a toggle triad (electronic supplementary material, table S6 and figure S4–S9). To gain further confidence in these results via RACIPE, we simulated the dynamics of toggle triad and circuit C2 using an asynchronous Boolean modelling approach [23]—a parameter-independent approach—and observed similar trends as seen in RACIPE, suggesting the key role of network topology instead of specific parametric combinations in enabling these robust design dynamical principles of a toggle triad (electronic supplementary material, table S7). Overall, these results strengthen the association of a toggle triad formed by A, B and C with the existence/co-existence of these states—(high A, low B, low C), (low A, high B, low C) and (low A, low B, high C).

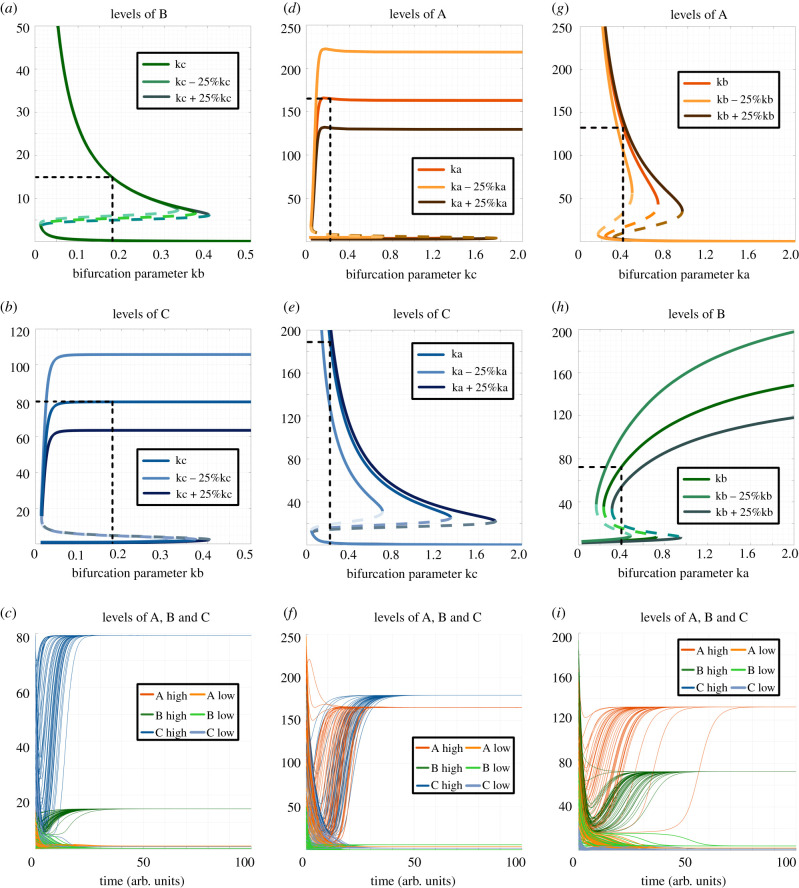
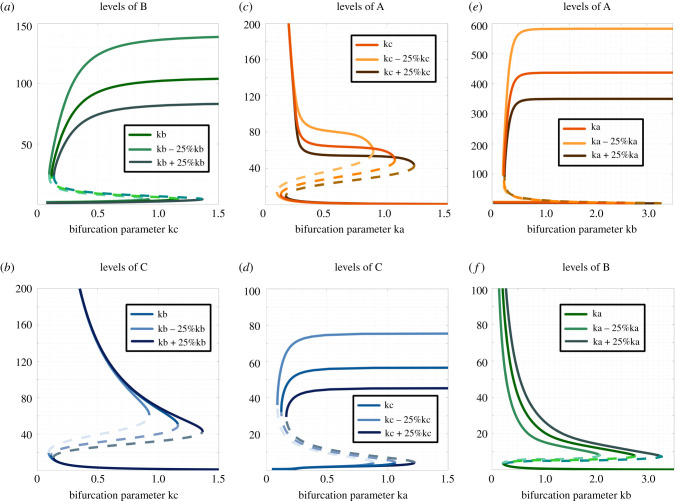
To further characterize the parameter space for the co-existence of states, we drew bifurcation diagrams for multiple parameter sets identified via RACIPE that enabled the three most frequent bistable phases—{Abc, aBc}, {aBc, abC} and {Abc, abC}. For a representative parameter set pertaining to the bistable phase enabling (low A, high B, low C) and (low A, low B, high C) (i.e. {aBc, abC}), the degradation rate of B (kb) was chosen as bifurcation parameters. Over a wide range of parameter values of kb spanning an order of magnitude (0.01–0.4), both the states aBc and abC were observed to coexist. At very high values of kb, the (low A, high B, low C) state, i.e. aBc was no longer seen; instead, the system had only the (low A, low B, high C) state (figure 4a–c). It was encouraging to see that this trend of bistability was qualitatively maintained even when the degradation rate of C (i.e. kC) was varied by ±25% relative to the one identified by RACIPE (figure 4a,b), thus suggesting that the co-existence of more than one such ‘single positive' state can be a robust dynamical feature of a toggle triad.

Figure 4.

Bifurcation diagrams and dynamics plots for representative cases of bistable phases. (a) Bifurcation diagram of expression level of component B with kb as bifurcation parameter for the bistable phase {aBc, abC}. (b) The same as (a) but for component C. (c) Dynamics plots of expression levels of components A, B and C for the bistable phase {aBc, abC}, showing convergence to two different states with varied levels of B and C (levels of A are low in both cases). (d) Bifurcation diagram of the expression level of component A with kc as bifurcation parameter for the bistable phase {Abc, abC}. (e) Same as (d) but for component C. (f) Dynamics plots of expression levels of components A, B and C for bistable phase {Abc, abC}, showing convergence to two different states with varied levels of A and C (levels of B are low in both cases). (g) Bifurcation diagram of expression level of component A with ka as bifurcation parameter for the bistable phase {aBc, Abc}. (h) Same as (g) but for component B. (i) Dynamics plots of expression levels of components A, B and C for the bistable phase {aBc, Abc}, showing convergence to two different states with varied levels of A and B (levels of C are low in both cases). Parameter values for columns A–C, D–F and G–I are given correspondingly in electronic supplementary material, table S13. The bifurcation diagrams for ‘low' components (component A in (a–c), component B in (d–f), component C in (g–i)) are shown in electronic supplementary material, figure S11.

Similarly, for the bistable phase enabling (high A, low B, low C) and (low A, low B, high C) states (i.e. {Abc, abC}), these states coexisted over a wide range of parameter values of kc spanning an order of magnitude (0.05–1.8) (figure 4d–f). This robust behaviour was maintained for scenarios when the degradation rate of A (i.e. kA) was either increased or decreased by 25% of the value identified via RACIPE (figure 4d,e). Consistent results were observed for the {Abc, aBc} state as well (figure 4g–h), as well as additional parameter sets for these three most common bistable phases (electronic supplementary material, figure S10, S11). Put together, these results reveal that the parameter space associated with a toggle triad can allow for co-existence of ‘single positive' states and possible switching among them under the influence of intrinsic noise.

Next, to better decode the co-existence of ‘single positive' and ‘double positive’ states, we performed similar bifurcation analysis for the bistable phases containing one ‘single positive' and one ‘double positive' state. For a representative parameter set pertaining to the bistable phase enabling {aBC, abC}, we performed bifurcation analysis for the degradation rate of C (i.e. kc), and observed bistability over an order of magnitude (kc = 0.1–1.4; figure 5a,b). The bistable nature was conserved for ±25% variations in kb. Similar patterns were seen for {Abc, AbC} (figure 5c,d) and {aBc, ABc} states (figure 5e,f).

Figure 5.

Bifurcation diagrams for bistable phase with combination of a ‘single positive' state and a ‘double positive' state. (a) Bifurcation diagram of expression level of component B with kc as bifurcation parameter for the bistable phase {aBC, abC}. (b) Same as (a) but for component C. (c) Bifurcation diagram of the expression level of component A with ka as bifurcation parameter for the bistable phase {Abc, AbC}. (d) Same as (c) but for component C. (e) Bifurcation diagram of the expression level of component A with kb as bifurcation parameter for the bistable phase {aBc, ABc}. (f) Same as (e) but for component B. Corresponding parameter sets for columns a-b, c-d and e-f are given in electronic supplementary material, table S13.

Further, we chose a representative parameter case corresponding to tristable phase containing ‘single positive' states—{Abc, aBc, abC}. For parameters identified via RACIPE, the system converged to three distinct steady states (electronic supplementary material, figure S12A). Altering the values of kb and/or kc disrupted tristability and led to the three monostable regions—(low A, high B, low C) (low kb; electronic supplementary material, figure S12B), (low A, low B, high C) (low kc; electronic supplementary material, figure S12C) and (high A, low B, low C) (high kb and kc; electronic supplementary material, figure S12D). Similar results were seen for another parameter set obtained via RACIPE for tristability (electronic supplementary material, figure S13).

These results suggest that the tristability of a toggle triad—co-existence of three ‘single positive' states—can be disrupted if one of the three components has a very different stability (i.e. half-life) as compared to the others.

2.4. Toggle triad with self-activations enrich for the existence of ‘double positive' states

Next, we probed the dynamics of a toggle triad with self-activations on all three nodes (A, B, C) (TT + 3SA). We collated the steady-state levels of A, B and C obtained from all parameter combinations obtained via RACIPE for this circuit and plotted them as a heatmap. Similar to the case of a toggle triad, the ‘single positive' (high A, low B, low C), (low A, high B, low C) and (low A, low B, high C) states were predominant. However, as compared to a toggle triad, there was a marked enrichment of the ‘double positive' states—(high A, high B, low C), (high A, low B, high C) and (low A, high B, high C), i.e. {ABc}, {AbC} and {aBC} states, respectively (figure 6a). Furthermore, in the case of a toggle triad with self-activations, the number of parameter sets enabling monostability was 3.3-fold lower as compared to a toggle triad (53% for TT versus 16% for TT + 3SA) and a 6.8-fold increase in those enabling tristability (5% for TT versus 34% for TT + 3SA) (figure 6b,c). The toggle triad with self-activation also exhibited tetrastable, pentastable and hexastable behaviour (13% parameter sets for tetra-stability, 4% for penta-stability) (figure 6c).

Figure 6.

Characterization of toggle triad with three self-activations (TT + 3SA). (a) (i) Heatmap showing the all solutions for a TT + 3SA; (ii) the nomenclature shown capitalizes the node whose levels are relatively high. Thus, Abc denotes (A-high, B-low, C-low}, aBc denotes (A-low, B-high, C-low), abC denotes (A-low, B-low, C-high) (three ‘single positive’ states). ABc denotes (A-high, B-high, C-low), AbC denotes (A-high, b-low, C-high) and aBC denotes (A-low, B-high, C-high) (three ‘double positive' states). (b) Frequency of monostable, bistable and tristable solutions in a toggle triad (TT) shown as a pie chart. (c) Frequency of monostable, bistable, tristable, tetrastable and pentastable solutions for a TT + 3SA case shown as a pie chart. (d,e) Frequency of different tetrastable and pentastable phases are combinations of Abc, aBc, abC, aBC, AbC, ABc = {Abc, aBc, abC, aBC}, {Abc, aBc, abC, AbC}, {Abc, aBc, abC, ABc} (tetrastable) and {aBc, Abc, abC, aBC, AbC}, {aBc, Abc, abC, ABc, AbC}, {aBc, Abc, abC, aBC, ABc} (pentastable). Error bars denote the standard deviation of n = 3 independent RACIPE simulations. * denotes statistical significance (p < 0.05 for Student's t-test).

The predominance of the ‘single positive' states and their combinations prevailed in monostable, bistable and tristable parameter sets for the case of a toggle triad with three self-activations (electronic supplementary material, table S8–10). In the tetrastable cases, the top three most predominant combinations contained all the three ‘single positive' states with one of the three possible ‘double positive' states—{Abc, aBc, abC, ABc}, {Abc, aBc, abC, AbC} and {Abc, aBc, abC, aBC} (figure 6d and electronic supplementary material, table S11). Similarly, in pentastable cases, the top three most predominant combinations contained all three ‘single positive' states with two of the three possible ‘double positive’ states—{Abc, aBc, abC, ABc, aBC}, {Abc, aBc, abC, AbC, aBC} and {Abc, aBc, abC, ABc, AbC} (figure 6e and electronic supplementary material, table S12), unraveling the dynamical traits of a toggle triad where each of the master regulators can self-activate. Put together, these results suggest that a toggle triad with self-activation can enrich for the (co-) existence of such ‘double positive' states.

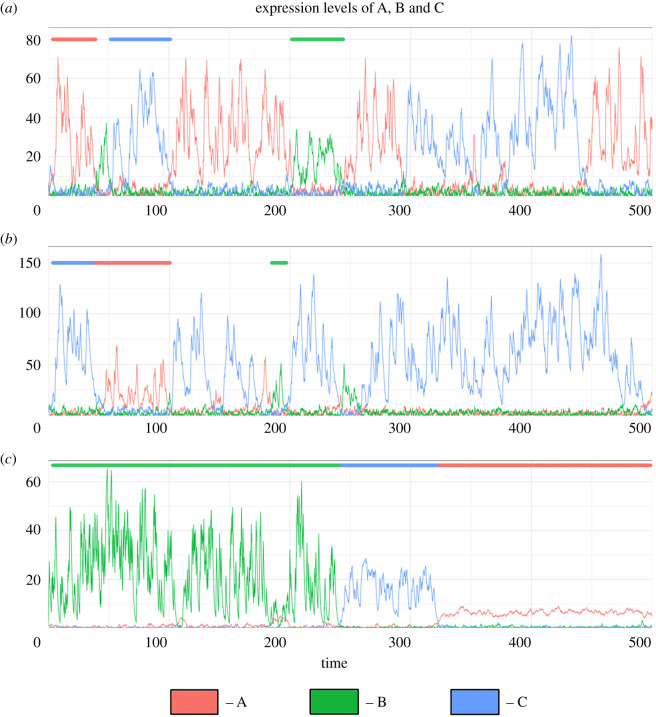
So far, our analysis has focused on deterministic dynamics. Given that molecular fluctuations can have a profound impact on phenotypes chosen by the system [24], including those for a toggle switch [12], we analysed the toggle triad with self-activation using sRACIPE (stochastic version of RACIPE) [25]. Stochastic simulations using sRACIPE shows spontaneous switching among different possible states—at least among all ‘single positive' ones, across multiple parameter sets. ‘Double positive' states are also seen albeit with lower residence times (figure 7a–c; electronic supplementary material figure S14, S15).

Figure 7.

sRACIPE results for one of the replicates of three different parameter sets used. (a) Dynamics plot showing switching between states for parameter set 1. Colour bars on top representatively mark the regions of each of the states—green bar shows (low A, high B, low C), red bar shows (high A, low B, low C) and blue bar shows (low A, low B, high C). (b,c) Same as (a) but for a replicate of parameter set 2 and 3 respectively. The plots for two other replicates for each of the parameter sets are shown in electronic supplementary material, figure S14, S15. Parameter values for sRACIPE for all the three replicates and parameter sets are given in electronic supplementary material, table S13.

2.5. Design principles of multi-stability enabled by toggle triad with/without self-activation

As discussed above, a toggle triad with/without self-activation can be monostable or multi-stable. Thus, we investigated different parameter combinations identified by RACIPE enabling the three most frequent monostable ({Abc}, {aBc}, {abC}), three most frequent bistable ({Abc, aBc}, {Abc, abC}, {aBc, abC}) and the most frequent tristable ({Abc, aBc, abC}) phases. We hypothesized that the relative strengths of different regulatory links in the network led to these different phases.

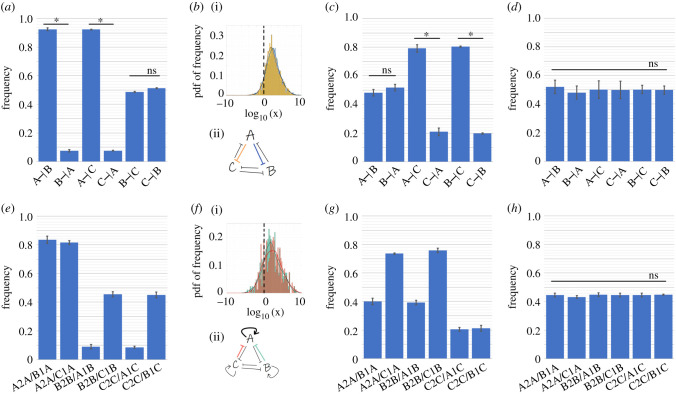
In RACIPE formulation, the effect of inhibition from one node to another is captured by a shifted Hill function described by three independent parameters: n (cooperativity), λ (fold change) and H₀/(g/k) (relative half-maximal concentration or threshold) [22]. The higher the value of n, the stronger the repression and the higher the value of H₀/(g/k), the weaker the repression. For inhibitory links, λ varies between 0 (very strong repression) to 1 (no effect). Thus, the higher the value of x = n/(λ*H₀/(g/k)), the stronger the corresponding inhibition. For parameter sets enabling {Abc}, i.e. (high A, low B, low C), we hypothesized that the inhibition of B and C by A is stronger than the inhibition of A by B and C. To test this hypothesis, we quantified the values of x for A inhibiting B (x(A –|B)) and those of B inhibiting A (x(B –|A)) for all parameter sets enabling {Abc}. We found that for 90% of parameter sets, x(A –|B) > x(B –|A) (figure 8a, columns 1 and 2; figure 8b); a similar trend was seen for toggle switch between A and C, i.e. x(A –|C) > x(C –|A) (figure 8a, columns 3 and 4). However, no such trend was seen for toggle switch between B and C (figure 8a, columns 5 and 6). The large degree of overlap seen in distributions for x(A –|B)/x(B –|A) and for x(A –|C)/x(C –|A) suggest that in most parameter sets enabling (high A, low B, low C) state, B and C are both simultaneously strongly inhibited by A (figure 8b). Consistent corresponding trends were seen for parameter sets enabling {aBc} and {abC} monostable phases (electronic supplementary material, figure S16A,B,D,E).

Figure 8.

Design principles of toggle triad (TT) and that with self-activation (TT + 3SA). (a) Frequency of dominance of six inhibitory links for the case of monostable (A high, B low, C low) (i.e. {Abc}) in TT. X –|Y denotes the frequency of parameter sets when the inhibition of X on Y was stronger than the that of Y on X; thus adjacent two columns total up to 1. (b) (i) Probability distribution functions of histograms of frequency of values of x(A–|B)/x(B–|A) (blue) and values of x(A–|C)/x(C–|A) (yellow) in TT for monostable case {Abc}. The x-axis is log₁₀ transformed and the dotted line represents the numerical value 1. (ii) Schematic showing that A inhibiting B and C are stronger links than B and C inhibiting A overall for parameter sets corresponding to monostable {A} (c) Same as (a) but for bistable (i.e. {Abc, aBc}) in TT. (d) Same as (a) but for tristable case {Abc, aBc, abC} in TT. (e) Frequency of parameter cases for which self-activation dominates upon incoming inhibitory link, for monostable case {Abc} in TT + 3SA. X2X/X1Y denotes the percentage of parameter sets for which X self-activation is stronger than Y inhibiting X. (f) (i) Probability distribution functions of histogram of frequency of x(A2A)/x(B1A) and x(A2A)/x(C1A) in TT + 3SA. The x-axis is log₁₀ transformed and the dotted line represents the numerical value of 1. (ii) Schematic showing that for most of the parameter sets corresponding to {Abc}, self-activation of A dominates inhibition of A by B or C. (g) Same as (e) but for bistable case {Abc, aBc} in TT + 3SA. (h) Same as (e) but for tristable case {Abc, aBc, abC} in TT + 3SA. * denotes statistical significance (p < 0.01 for Student’s t-test). ‘ns' denotes statistically non-significant cases. Parameters corresponding to figure 8, electronic supplementary material figure S16 are given in tables S14, S15.

For the bistable phase {Abc, aBc}, we hypothesized that inhibition of C by A and B is stronger than inhibition of A and B by C. Indeed, we saw that 80% of parameter sets had x(A –|C) > x(C –|A) and x(B –|C) > x(C –|B) (figure 8c, columns 3–6) but the relative strengths of mutual inhibition between A and B were not skewed (figure 8c, columns 1–2). Similar corresponding trends were seen for other bistable phases {Abc, abC}, {aBc, abC} (electronic supplementary material, figure S16C,F). For the tristable phase {Abc, aBc, abC}, the distributions of relative strengths of inhibition in any of the three toggle switches was not imbalanced or skewed (figure 8d) as seen for monostable or bistable cases, suggesting that tristability is enabled only when the strengths of mutual inhibition among all three components are relatively well balanced.

In the case of toggle triad with self-activation, we defined x = n*λ/(H₀/(g/k)) for the self-activatory links because the corresponding values of λ are higher than 1, and the higher the value of λ, the stronger the self-activation. For parameter sets in this case enabling {Abc}, i.e. (high A, low B, low C), we hypothesized that the self-activation of A is stronger than inhibition of A by B and C. Indeed, for over 80% of parameter sets, x(A2A)/x(B1A) > 1 and x(A2A)/x(C1A) > 1, where x(A2A) represent the strength of self-activation, and x(B1A) and x(C1A) denote the strength of inhibition of A by B and C, respectively (figure 8e, columns 1,2). Reminiscent of trends seen for toggle triad, the values x(A2A)/x(B1A) and x(A2A/C1A) span multiple orders of magnitude, and their overlap suggests that the self-activation of A is stronger than both the inhibition by B and that by C incumbent on A (figure 8f). Conversely, the number of parameter sets showing a stronger self-activation of B and C relative to their inhibition by A is less than 10% (figure 8e, columns 3,5). The relative strengths of links in the self-activating toggle switch between B and C show no such imbalance in distribution as expected; 50% of parameters have x(B2B)/x(C1B) > 1 and the remaining 50% have x(B2B)/x(C1B) < 1 (figure 8e, columns 4, 6).

For approximately 75% of parameter sets enabling the bistable phase {Abc, aBc}, self-activations of A and B was found to be stronger than inhibition of A and B by C (figure 8g, columns 2, 4). Conversely, the self-activation of C was weaker than inhibition of C by A and B (figure 8g, columns 5, 6). As expected, the self-activatory toggle switch between A and B was found to be well balanced (figure 8g, columns 1, 3), thus enabling the co-existence of (high A, low B, low C) and (low A, high B, low C) states. Consistent corresponding trends were seen for other parameter sets and phases (electronic supplementary material, figure S16G–L).

For the parameter sets enabling a tristable phase {Abc, aBc, abC}, all three nodes displayed a delicate balance in relative strengths of inhibition by other two nodes and self-activation (figure 8h). Interestingly, the frequency of parameter sets for which self-activation was stronger than the inhibition received was slightly smaller than 50% (figure 8h), suggesting that strong self-activation may not enable tristability of these ‘single positive' states. These results are reminiscent of observations for a self-activating toggle switch between A and B, where a very strong self-activation of A and B relative to mutual inhibition led to only the ‘double positive' (or hybrid A/B) state, and the two ‘single positive’ states (high A, low B) and (low A, high B) disappeared [15]. Thus, strong self-activation on all three components may enable the co-existence of three ‘double positive' states.

Put together, this analysis reveals the patterns in multi-dimensional parameter space which enable a toggle triad (with/without self-activation) to display such a wide diversity in dynamical behaviour—the existence of three distinct states and the co-existence of any two or all three states.

2.6. Th1/Th2/Th17 cell differentiation: a case study of toggle triad

Upon activation, naive helper T cells differentiate towards a specific helper T cell subset. In the presence of specific activating signals, a majority of these cells differentiate towards a particular subset expressing a lineage-specific transcription factor (master regulator). However, a small but significant number of cells may also express multiple master regulators [26]. To understand if the presence of cells expressing multiple master regulators may be explained through the toggle triad system described above, we undertook the case study involving three helper T cell subsets, Th1 (T-bet), Th2 (GATA3) and Th17 (RORγT). Assuming that these master regulators may mutually repress each other [18] (figure 9a), we projected the steady-state solutions obtained from the heatmap for a toggle triad (figure 3a) on the two-dimensional scatter plots for (T-bet, GATA3) axes, (T-bet, RORγT) axes and (GATA3, RORγT) axes. The plots showed the emergence of three clusters, each corresponding to a ‘single positive' state—blue (high T-bet, low GATA3, low RORγT state), orange (low T-bet, high GATA3, low RORγT state) and green (low T-bet, low GATA3, high RORγT state) (figure 9b, electronic supplementary material, figure S17, S18), corresponding to Th1, Th2 and Th17 cell fates, respectively. The hybrid ‘double positive' (black dots) states were also observed in addition to the ‘single positive' states—(high T-bet, high GATA3, high RORγT), (high T-bet, low GATA3, low RORγT) and (low T-bet, high GATA3, high RORγT), although at a lower frequency than the ‘single positive' ones. These states can be mapped to hybrid Th1/Th2, Th2/Th17 and Th1/Th17 cell types.

Figure 9.

CD4 T-cell differentiation. (a) Network showing proposed interaction among the master regulators of Th1, Th2 and Th17—T-bet, GATA3 and RORγT—respectively. (b) Two-dimensional scatter plots projecting solutions from the heatmap for a toggle triad network (figure 3). (c) Network of T-bet, GATA3 and RORγT including self-activations. (d) Same as (b) but for solutions from the heatmap for a toggle triad with three self-activations (figure 5). Blue coloured dots denote Th1 (high T-bet, low GATA3, low RORγT), orange coloured dots denote Th2 (low T-bet, high GATA3, low RORγT) and green coloured dots denote Th17 (low T-bet, low GATA3, high RORγT) state. Black dots denote the different hybrid states—Th1/Th2, Th2/Th17 and Th1/Th17: (high T-bet, high GATA3, high RORγT), (high T-bet, low GATA3, low RORγT) and (low T-bet, high GATA3, high RORγT), respectively. Data from respective heatmaps were subjected to k-means clustering to identify these six states (three ‘single positive’ and three ‘double positive' ones).

GATA3, T-bet and RORγT have been found to self-activate directly and/or indirectly [27,28]. Thus, next, we included self-activation loops (figure 9c), and projected the steady-state solutions obtained from the heatmap for a toggle triad with self-activation (figure 5) on the two-dimensional scatter plots for (T-bet, GATA3) axes, (T-bet, RORγT) axes and (GATA3, RORγT) axes. Here, we observed the hybrid ‘double positive’ states at a relatively higher frequency as compared to the toggle triad (figure 9d, electronic supplementary material, figure S17, S18). Hence, using the toggle triad model, we can predict the existence and provide a possible mechanistic explanation for the existence of stable hybrid helper T cell phenotypes, which has been shown experimentally at least for Th1/Th2 and Th1/Th17 cells.

3. Discussion

Dissecting the dynamics of regulatory networks driving cellular differentiation and reprogramming is important to identify the trajectories that cells can take in the high-dimensional gene expression landscape as they commit to a cell fate. The recent deluge in experimental technologies has enabled inferring these networks and identifying ‘master regulators' of different cell fates. Probing these networks from a dynamical systems perspective has helped characterize the ‘landscape' of cell differentiation as proposed by Waddington over seven decades ago in which a cell—represented by a ball—rolls down into one or more possible branching valleys, each of which represents a stable cellular identity [29].

A frequent occurring network motif that has been identified in developmental decision-making and investigated from a dynamical systems perspective is a toggle switch—a double negative (hence, overall positive) feedback loop between two master regulators A and B. It has been shown to exhibit bistability with the two states being (high A, low B) and (low A, high B), representing a competition between A and B in enforcing the identity they drive and simultaneously repressing the one driven by their competitor [17]. Other well-studied motifs are negative feedback loops with two components (A activates B, B reduces the levels of A, such as p53-MDM2 [30]) or three components (A inhibits B, B inhibits C and C inhibits A—a repressilator [20,31]) that can lead to sustained or damped oscillations. Often, such positive and negative feedback loops are intricately interlinked in natural biological networks to allow for a more diverse dynamic repertoire enabling bistability and/or oscillations [32–39]. Moreover, such feedback loops may be synchronized within a cell or across cellular populations to facilitate coordinated dynamics [40–42]. However, most theoretical attempts to investigate the coupled networks have been focused on bistable systems.

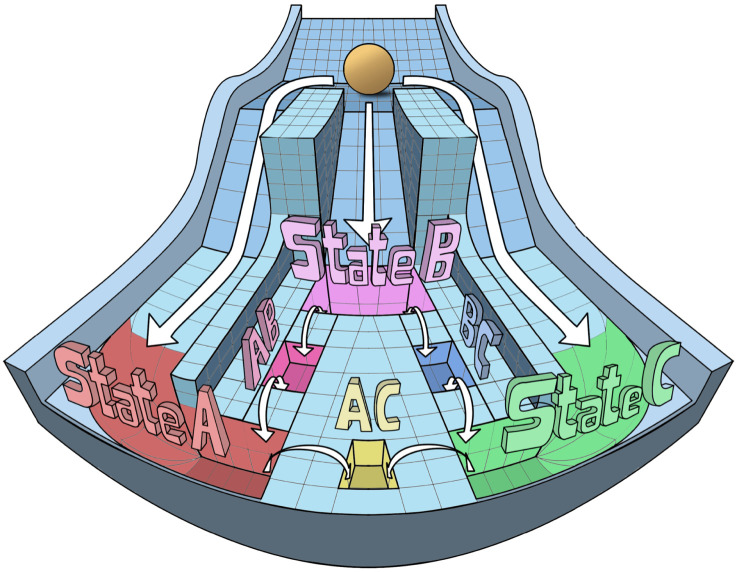
Here, we present a fundamentally different dynamical trait that can be achieved by three-coupled toggle switches, or in other words, three mutually inhibitory ‘master regulators' A, B and C forming a toggle triad. Our simulations show that the toggle triad network topology can enable tristability, with the three stable states being (high A, low B, low C), (low A, high B, low C) and (low A, low B, high C). Further, three more intermediate/hybrid states among these ‘single positive’ states can be enabled by a toggle triad, particularly when A, B and C can self-activate—(high A, high B, low C), (high A, low B, high C) and (low A, high B, high C). In the Waddington landscape perspective, these three ‘double positive' states can lie between two terminal ‘single positive' states and can promote trans-differentiation among them (figure 10). A previous modelling effort also suggested these possible six states for a toggle triad [16]; our approach through RACIPE enables two additional insights: (i) a higher relative frequency of ‘single positive' states as compared to the ‘double positive' ones and (ii) increase in ‘double positive' states in presence of self-activation.

Figure 10.

Waddington landscape for a toggle triad. Modified Waddington's landscape to demonstrate the differentiation of three distinct ‘single positive' states (states A, B and C), and three putative ‘double positive' states (hybrid states A/B, A/C and C/B) from a common progenitor. These six states can be obtained from a toggle triad with/without self-activation.

We applied these results to reproduce the dynamics of naive CD4⁺ helper T cells that differentiate to Th1, Th2 or Th17 [43]. Transcription factors T-bet, GATA3 and RORγT are considered to be the ‘master regulators' of these cell fates, respectively [28]. GATA3 and T-bet can self-activate directly or indirectly and repress the activities or targets of one another [28,44], similar to a ‘toggle switch' between two ‘master regulators' seen in multiple scenarios [2]. In addition to the two mutually exclusive states (high GATA3, low T-bet and low GATA3, high T-bet in this case), self-activation can allow for the stable existence of a hybrid state (high GATA3, high T-bet in this case) [45–47]. Indeed, in vitro and in vivo experimental evidence has identified such ‘double positive' individual cells stably co-expressing GATA3 and T-bet, referred to as a Th1/Th2 hybrid phenotype for the duration of weeks in vitro and months in vivo [46,48–51]. Intriguingly, hybrid Th1/Th2 cells can arise directly from the CD4⁺ naive T cell precursors and/or reprogrammed from the Th2 cells [48,49], thus indicating phenotypic plasticity, a direct consequence of multi-stability in underlying biological networks [52]. Such plasticity can be explained by stochastic switching seen among the multiple states seen in a toggle triad with self-activation. Further, hybrid Th1/Th17 cells that stably persist in vivo have been experimentally identified; they express intermediate levels of both Th1 and Th17 signature transcription factors and exhibit unique transcriptional and metabolic states as compared to Th1 and Th17 cells [53]. The stable in vivo existence of both hybrid Th1/Th2 and Th1/Th17 phenotypes suggests that their relationship may be expressed as ‘toggle switches' with self-activation.

Recent single-cell analysis has strengthened the evidence for these hybrid phenotypes [54,55], revealing that the expression levels of various ‘master regulators' in a population of cells is not limited to extreme high or low values [56], reminiscent of hybrid phenotypes seen in other biological scenarios [57,58]. Our analysis here is restricted to investigating steady-state (long-term) behaviours; however, approaches focusing on short-term dynamics of three-node and four-node networks have revealed important design principles related to noise attenuation [59–61]. The possible role of such functional traits in CD4⁺ T-cell decision-making needs to be investigated.

In addition to self-activation of T-bet and GATA3 discussed above, our model suggests self-activation of RORγT, which has been recently reported [27]. As an extension of this analysis, we propose a toggle triad involving Th1, Th2 and Th17 cells that reproduces all of the aforementioned predictions and suggests that a hybrid Th2/Th17 cell could exist. While the stable existence of such cells and any phenotypic plasticity between Th2 and Th17 cells have not yet been reported, our model predicts their possible existence, especially when GATA3, RORγT and T-bet can self-activate themselves. Finally, the toggle triad model strengthens the hypothesis that the mixed cellular phenotypes are stable cellular identities with specific functional traits, and not just a transient co-expression of these lineage-determining transcription factors, as seen often in common progenitor cells [62].

Besides offering valuable insights into the dynamics of cellular decision-making, our results also pave the way towards designing tristable systems synthetically. Major efforts in synthetic biology have been, so far, targeted towards switches, cascades, pulse generators and oscillators [63–67]. The proposed network topology can be constructed to enable three distinct cell states, whereas including self-activation can facilitate the programming to achieve three hybrid cell states as well.

4. Materials and methods

4.1. Random circuit perturbation analysis

4.1.1. Simulation

RACIPE is a computational tool that investigates the dynamics of a given network topology [22]. A topology file is given as the input to the program. It then simulates, for every parameter set, the network as a system of ODEs developed based on the input file. For every run of the simulation, every kinetic parameter in the mathematical model is sampled from the defined biologically relevant range, thus giving multiple parameter sets. For each parameter set, the ODEs are solved for 100 initial conditions (default choice). The RACIPE simulation reports the steady-state values for each component of the network for every parameter set in the solution file. For all our analyses, we have used the default ranges for sampling the parameters, sampled 10 000 parameter sets and 1000 initial conditions for every parameter set. Depending on the number of steady states the system converges to for a given parameter set, the system is classified as monostable, bistable, tristable all the way to decastable. Even if one initial condition converges to a different steady state, RACIPE considers the system to be multi-stable for that parameter set.

A generic differential equation for component A affected by component B is denoted by RACIPE as follows:

$$\frac{\text{d}\mathrm{A}}{\text{d}\mathrm{t}}={\mathrm{g}}_{\mathrm{A}}^{\ast }{\mathrm{H}}^{\mathrm{S}}(\mathrm{B},\hspace{0.17em}\mathrm{B}0\mathrm{A},\hspace{0.17em}\mathrm{nBA},\hspace{0.17em}\lambda \mathrm{BA})\text{–}{\mathrm{k}}_{\mathrm{A}}^{\ast }\mathrm{A},$$

where g_A and k_A are corresponding production and degradation rates, H^S (B, B0A, nBA, λBA) denotes a shifted Hill function [22] defined as follows:

$$\begin{array}{rl}{\mathrm{H}}^{\mathrm{S}}(\mathrm{B},\hspace{0.17em}\mathrm{B}0\mathrm{A},\hspace{0.17em}\mathrm{nBA},\hspace{0.17em}\lambda \mathrm{BA})& ={\mathrm{H}}^{\text{–}}(\mathrm{B})+\lambda \mathrm{B}{\mathrm{A}}^{\ast }(1\text{–}{\mathrm{H}}^{\text{–}}(\mathrm{B})),\hspace{0.17em}\text{where }{\mathrm{H}}^{\text{–}}(\mathrm{B})\\ & =1/(1+{(\mathrm{B}/\mathrm{B}0\mathrm{A})}^{nBA})\end{array}$$

4.1.2. Normalization of steady states

The steady-state solution provided by RACIPE simulation are in log2 scale. We normalized the obtained steady states in the solution files in two steps. To account for extremes in sampling of the production and degradation rate parameters, we performed g/k normalization. We divided every steady-state value (E_i) in the solution file by the ratio of the production and degradation rate of the respective component (g_i/k_i) of the network of the corresponding parameter set. Following that, we performed z-score normalization. We calculated the mean (E_in) and standard deviation (σ_in) for every component ‘i’ over all parameter sets after the g/k normalization. The final transformation formula for every steady state is as follows:

$${\mathrm{Z}}_{\mathrm{i}}=(({\mathrm{E}}_{\mathrm{i}}/({\mathrm{g}}_{\mathrm{i}}/{\mathrm{k}}_{\mathrm{i}}))-{\mathrm{E}}_{\mathrm{in}})/{\mathrm{\sigma }}_{\mathrm{in}},$$

where Z_i is the final normalized expression. We found the distributions of every component to be largely bimodal in nature (electronic supplementary material, figure S2) with the centre of the two modes to be around 0. Thus, we chose to define the states ‘high' and ‘low' as greater than and smaller than 0 respectively.

4.1.3. Clustering and replicates

For the hierarchical clustering shown in heatmaps (figures 3 and 5) and other supplementary figures (electronic supplementary material, figure S4–S9), the clustergram function in MATLAB was used. For colouring of the scatter plots in figure 6, k-means clustering (k = 6) was used to identify the clusters. Since k-means clustering can provide variant results for every run of the function, we confirmed the clusters by running the clustering function for the same data thrice, the latter two replicates (electronic supplementary material, figure S17, S18) for the networks of TT and TT + 3SA, respectively. For every network shown in the main text and electronic supplementary material, RACIPE simulations were run thrice to obtain three independent replicates. Further analyses were then performed on these replicates, with the data presented as mean ± standard deviation (shown by error bars).

4.2. Boolean analysis

For Boolean analysis as well for TT and C2 circuits, a topological file is given as the input. The file determines the nodes and edges of the network. The edges are of two types, activatory and inhibitory. The analyses carried out were by two methods, synchronous and asynchronous update of the nodes. The constraint of equal weightage to inhibitory and activating links was used [23,68]. The updating of the nodes follows a simple majority rule. The node is updated to 1 if the sum of activations to the node is higher than inhibitions and updated to 0 for the opposite case. The steady state is said to be reached if there is no change in the updates for a few time-steps. We have run the simulations for 10 000 initial conditions randomly sampled over all possible states of the network.

4.3. Bifurcation analysis

Bifurcation diagrams were plotted using the continuation software PyDSTool [69].

4.4. sRandom circuit perturbation simulations

We performed sRACIPE simulations on either the TT or TT + 3SA to generate a set of random parameter sets and simulated the system with a fixed amount of noise in one of the parameters. We used the webserver facility of Gene Circuit Explorer (GeneEx) to simulate stochastic dynamics of gene regulatory circuits—https://shinyapps.jax.org/5c965c4b284ca029b4aa98483f3da3c5/.

Data accessibility

This article has no additional data.

Authors' contributions

M.K.J. designed and supervised research; A.S.D., S.S. and S.H. conducted research; A.S.D., S.S., S.J. and M.K.J. analysed data; all authors participated in writing and revision of the manuscript.

Competing interests

The authors declare no conflict of interests.

Funding

This work was supported by Ramanujan Fellowship (SB/S2/RJN-049/2018) awarded to M.K.J. by Science and Engineering Research Board, Department of Science and Technology, Government of India.