Effect of school closures on mortality from coronavirus disease 2019: old and new predictions

Abstract

Objective

To replicate and analyse the information available to UK policymakers when the lockdown decision was taken in March 2020 in the United Kingdom.

Design

Independent calculations using the CovidSim code, which implements Imperial College London’s individual based model, with data available in March 2020 applied to the coronavirus disease 2019 (covid-19) epidemic.

Setting

Simulations considering the spread of covid-19 in Great Britain and Northern Ireland.

Population

About 70 million simulated people matched as closely as possible to actual UK demographics, geography, and social behaviours.

Main outcome measures

Replication of summary data on the covid-19 epidemic reported to the UK government Scientific Advisory Group for Emergencies (SAGE), and a detailed study of unpublished results, especially the effect of school closures.

Results

The CovidSim model would have produced a good forecast of the subsequent data if initialised with a reproduction number of about 3.5 for covid-19. The model predicted that school closures and isolation of younger people would increase the total number of deaths, albeit postponed to a second and subsequent waves. The findings of this study suggest that prompt interventions were shown to be highly effective at reducing peak demand for intensive care unit (ICU) beds but also prolong the epidemic, in some cases resulting in more deaths long term. This happens because covid-19 related mortality is highly skewed towards older age groups. In the absence of an effective vaccination programme, none of the proposed mitigation strategies in the UK would reduce the predicted total number of deaths below 200 000.

Conclusions

It was predicted in March 2020 that in response to covid-19 a broad lockdown, as opposed to a focus on shielding the most vulnerable members of society, would reduce immediate demand for ICU beds at the cost of more deaths long term. The optimal strategy for saving lives in a covid-19 epidemic is different from that anticipated for an influenza epidemic with a different mortality age profile.

Introduction

The United Kingdom’s national response to the coronavirus disease 2019 (covid-19) pandemic has been widely reported as being primarily led by modelling based on work, using an individual based model (IBMIC) from Imperial College London,1 although other models have been considered. In this paper, we maintain the distinction between epidemiological “model” (IBMIC) and software implementation as “code” (CovidSim). The key paper (Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce covid-19 mortality and healthcare demand) investigated several scenarios using IBMIC with the best parameterisation available at the time.2 Contrary to popular perception, the lockdown, which was then implemented, was not specifically modelled in this work. As the pandemic has progressed, the parameterisation has been continually improved as new data become available. The main conclusions of Report 9 were not especially surprising. Mortality from covid-19 is around 1%,3 so an epidemic in a susceptible population of 70 million people would cause many hundreds of thousands of deaths. In early March 2020, the case doubling time in the UK might have been around three days,4 meaning that within a week cases of covid-19 could go from accounting for a minority of available intensive care unit (ICU) beds to exceeding capacity. Furthermore, with a disease onset delay of more than a week and limited or delayed testing and reporting in place, there would be little measurable warning of the surge in ICU bed demand. One table in Report 9, however, shows that closing schools reduces the reproduction number of covid-19 but with the unexpected effect of increasing the total number of deaths. In this paper, we reproduce the main results from Report 9 and explain why, in the framework of the IBMIC model, these counterintuitive results were obtained. We chose not to re-parameterise the model as we wanted to replicate the information available to policymakers at the time, specifically highlighting policies for which suppressing the outbreak and saving lives were conflicting choices.

Methods

IBMIC was developed from an influenza pandemic model.1 5 6 The original code used for Report 9 has not been released. However, the team at Imperial College London, headed by epidemiologist Neil Ferguson, collaborated with Microsoft, GitHub, and the Royal Society Rapid Assistance in Modelling the Pandemic (RAMP) initiative to recreate the model in the CovidSim code: this version has been stringently externally validated.7 We used GitHub tagged version 0.14.0 plus additional patches dated before 3 June 2020, the full technical details of which are published elsewhere.8 Ferguson et al9 supplied the input files relevant to Report 9 that were included in the GitHub release.

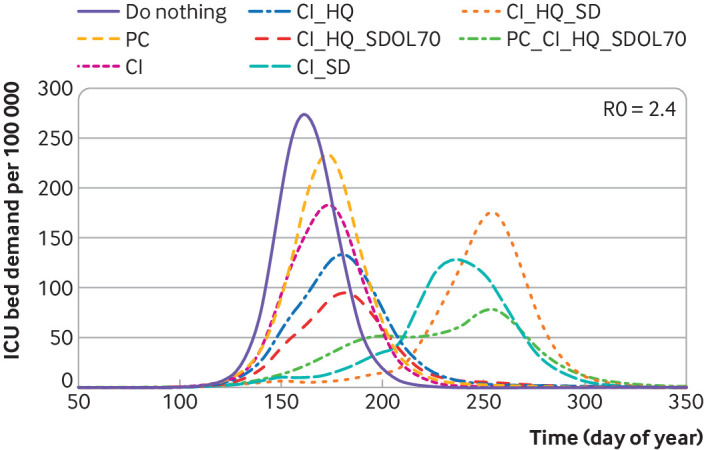
CovidSim performs simulations of the UK at a detailed level without requiring personal data. The model includes millions of individual “people” going about their daily business—for example, within communities and at home, schools, universities, places of work, and hospitals. The geographical representation of the UK is taken from census data, so the distribution of age, health, wealth, and household size for simulated people in each area is appropriate. The model also includes appropriate numbers, age distribution, and commuting distances of people in the simulated schools and workplaces, each in line with national averages. The network of interactions is age dependent: people interact mainly with their own age group and with family, teachers, and carers. The virus (severe acute respiratory syndrome coronavirus 2) initially infects random members of this network of interacting coworkers, strangers, friends, and family. Whenever an infected person interacts with a non-infected person, there is a probability that the virus will spread. This probability depends on the time and proximity of the interaction and the infectiousness of the person according to the stage of the disease. Infected people might be admitted to hospital and might die, with the probability dependent on age, pre-existing conditions, and stage of the disease. This extremely detailed model is then parameterised using the best available expert clinical and behavioural evidence,5 with coronavirus specific features being updated as more coronavirus specific data become available from the worldwide pandemic.8 Therefore, the model has the required complexity to consider non-pharmaceutical interventions, which would reduce the number of interactions between simulated people in the model (table 1). To predict policymaking, it is assumed that these interventions are implemented when demand for ICU beds reaches a particular “trigger” level. As the model contains far more realistic detail than the data available, the results are averages over many runs with different starting conditions, all of which are consistent with known data. The real epidemic is just one of these possibilities, so the code determines the range of scenarios for which plans should be made. This is particularly important when the numbers of localised outbreaks are low: the prediction that local spikes will occur somewhere is reliable, and the most likely places can be identified, but predicting exactly when and where is not possible with the level of data available. All interventions reduce the reproduction number and slow the spread of the disease. However, a counterintuitive result presented in Report 9 (table 3 and table A1 in that report) is the prediction that, once all other considered interventions are in place, the additional closure of schools and universities would increase the total number of deaths. Similarly, adding general social distancing to a scenario involving household isolation of suspected cases (case isolation) and household quarantine of family members, with appropriate estimates for compliance, was also projected to increase the total number of deaths.

Table 1.

Peak demand for UK-wide intensive care unit beds (in 000s) for different intervention scenarios and different intensive care unit (ICU) triggers during the coronavirus disease 2019 epidemic

Trigger*	Time	PC	CI	CI_HQ	CI_HQ_SD	CI_SD	CI_HQ_SDOL70	PC_CI_HQ_SDOL70
0.1	1st wave	152	119	87	8†	20	62	33
0.1	Total	152	119	87	115	84	62	51†
0.3	1st wave	153	119	87	10†	22	62	34
0.3	Total	153	119	87	115	73	62	48†
1	1st wave	154	119	87	11†	22	62	35
1	Total	154	119	87	104	59	62	37†
3	1st wave	159	119	87	13†	22	62	37
3	Total	159	119	87	82	40	62	37†

CI=case isolation (home isolation of suspect cases), HQ=household quarantine of family members; SD=general social distancing; SDOL70=social distancing of over 70s; PC=place closures, specifically schools and universities.

^*For each trigger value of cumulative intensive care unit (ICU) cases (in 000s), the peak demand for ICU beds, and the peak during the first wave when the interventions were in place are shown.

^†Optimal strategy for minimising peak demand.

More details of these non-pharmaceutical interventions are provided in table 2 of Report 9 (also reproduced in table 2).

Table 2.

Definition of interventions from Report 9 considered in CovidSim

Label	Policy	Description
CI	Case isolation in the home	Symptomatic cases stay at home for seven days, reducing non-household contacts by 75% for this period. Household contacts remain unchanged. Assume 70% of households comply with the policy
HQ	Voluntary home quarantine	Following identification of a symptomatic case in the household, all household members remain at home for 14 days. Household contact rates double during this quarantine period, contacts in the community reduce by 75%. Assume 50% of households comply with the policy
SDOL70	Social distancing of those over 70 years of age	Reduce contacts by 50% in workplaces, increase household contacts by 25%, and reduce other contacts by 75%. Assume 75% compliance with policy
SD	Social distancing of entire population	All households reduce contact outside household, school, or workplace by 75%. School contact rates unchanged, workplace contact rates reduced by 25%. Household contact rates assumed to increase by 25%
PC	Closure of schools and universities	Closure of all schools, 25% of universities remain open. Household contact rates for student families increased by 50% during closure. Contacts in the community increase by 25% during closure

Patient and public involvement

Patients or the public were not involved in the design, conduct, reporting, or dissemination plans of our research. All data used were retrieved from existing public sources, as referenced. We plan to share this on social media, Twitter, and blogs.

Results

To reproduce the result tables for the scenarios presented in Report 9, we averaged over 10 simulation runs with the same random number seeds as used in the original report. The simulations are run for 800 days, with day 1 being 1 January 2020. The simulated intervention period lasts for three months (91 days), with some interventions extended for an additional 30 days. In reality, interventions were in place for rather longer, which delayed the second wave but had little effect on deaths. The mitigation scenarios in Report 9 considered reproduction numbers of R0=2.2 and R0=2.4. As highlighted by Ferguson et al,8 the results we obtain here are not precisely identical to those in Report 9 because they are an average of 10 stochastic realisations, the population dataset has changed to an open source one, and the algorithm used to assign individuals from households to other places such as schools, universities, and workplaces has been modified to be deterministic. We also count deaths in all waves, not just the first. The stochasticity gives a variance of around 5% in total number of deaths and ICU bed demand between different realisations using different random numbers. More important is the uncertainty of the timing of the peak of the infections between realisations, which is around five days. We compared these predictions to the death rates from the actual trajectory of covid-19.10 11 NHS England stopped publishing data on critical bed occupancy in March 2020,12 so it was not possible to compare ICU data from the model with real world data.

Table 1 shows the demand for ICU beds and table 3 shows the total number of deaths; in both, the same mitigation scenarios as presented in Report 9 were used. As in Report 9, for each mitigation scenario we considered a range of ICU triggers. In table 1 we report the peak ICU bed demand across the full simulation for each trigger, as was presented in Report 9, but we also include the peak demand for ICU beds during the period of the intervention (first wave). The latter we define as the period during which general social distancing was in place when implemented.

Table 3.

Predicted total number of UK-wide deaths (in 000s) from coronavirus disease 2019 for different intervention scenarios and different triggers for the interventions based on ICU admissions during the coronavirus disease 2019 epidemic

Trigger*	Time	PC	CI	CI_HQ	CI_HQ_SD	CI_SD	CI_HQ_SDOL70	PC_CI_HQ_SDOL70
0.1	1st wave	418	354	252	21†	39	177	75
0.1	Total	496	416	355	440	402	262†	357
0.3	1st wave	456	378	281	32†	58	200	104
0.3	Total	495	416	355	437	390	261†	356
1	1st wave	479	398	310	48†	86	223	139
1	Total	494	416	355	428	370	261†	351
3	1st wave	490	407	325	70†	114	237	172
3	Total	495	416	355	411	347	262†	342

PC=place closures; CI=case isolation; HQ=household quarantine; SD=social distancing; SDOL70=social distancing of over 70s only.

^*For each trigger value of cumulative ICU cases (000s), the total deaths across the full simulation and during the first wave are shown.

^†Optimal strategies for minimising short term and long term deaths.

Table 3 reports the total number of deaths across the entire simulation as well as the number of deaths at the end of the first wave, again defined as the time at which general social distancing was lifted.

Table 1 and table 3 present the full simulation numbers, which are essentially the same as those presented in table A1 in Report 9. Table 3 also illustrates the counterintuitive result that adding school closures to a scenario with case isolation, household quarantine, and social distancing in people older than 70 years would increase the total number of deaths across the full simulation. Moreover, it shows that social distancing in those over 70 would be more effective than general social distancing.

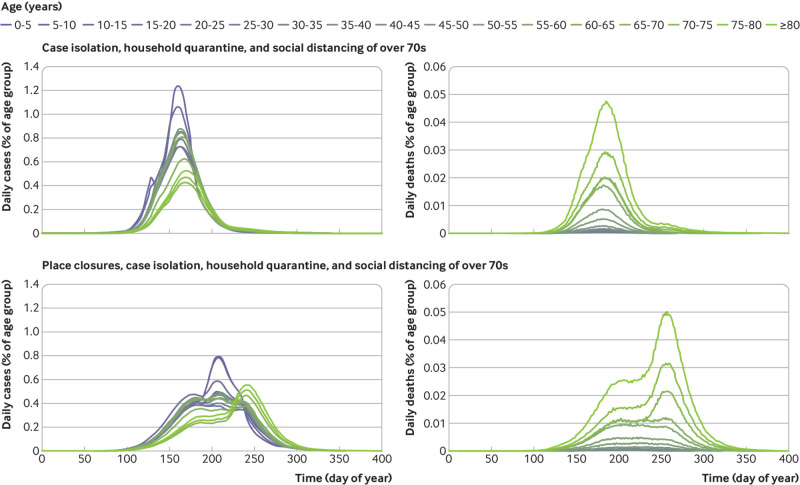
Table 1 and table 3 show that in some mitigation scenarios the peak demand for ICU beds and most deaths occur during the period when the intervention is in place. There are, however, other scenarios when the opposite is true. The reason for this is illustrated in figure 1. The mitigation scenarios of “do nothing,” place closures, case isolation, case isolation with household quarantine, and case isolation, household quarantine, and social distancing of over 70s are as presented in figure 2 of Report 9. We also show some additional scenarios (case isolation and social distancing; case isolation, household quarantine, and general social distancing; and place closures, case isolation, household quarantine, and social distancing of over 70s) that are not shown in figure 2 of Report 9 but are included in table 1 and table 3 and in the tables in Report 9.

Fig 1.

Flattening the curve. The first five curves are the same scenarios as presented in figure 2 of report 9. Three additional scenarios are also shown (summarised in table 1 and table 3). The scenario of place closures, case isolation, household quarantine, and social distancing of over 70s would minimise peak demand for intensive care but prolong the epidemic, resulting in more people needing intensive care and more deaths. These findings illustrate why adding place closures to a scenario with case isolation, household quarantine, and social distancing of over 70s can lead to more deaths than the equivalent scenario without place closures. Doing so suppresses the infection when the interventions are present but leads to a second wave when interventions are lifted. In the model this happened in July 2020, after a 91 day lockdown: in practice the first lockdown was extended into August, so the second wave was postponed to September. The total number of deaths in the scenario of case isolation, household quarantine, and social distancing of over 70s is 260 000, whereas when place closures are included the total number is 350 000. Similarly, comparing general social distancing with equivalent scenarios without social distancing, the second wave peak in the case isolation, household quarantine, and general social distancing scenario is higher than the first wave peak in the case isolation and household quarantine scenario. ICU=intensive care unit; PC=place closures; CI=case isolation; HQ=household quarantine; SDOL70=social distancing of over 70s; SD=general social distancing

In the simulations presented here, the main interventions are in place for three months and end on about day 200 (some interventions are extended for an additional 30 days). Figure 1 shows that weaker intervention scenarios lead to a single wave that occurs during the period in which the interventions are in place. Hence the peak demand for ICU beds occurs during this period, as do most deaths.

Stronger interventions, however, are associated with suppression of the infection such that a second wave is observed once the interventions are lifted. For example, adding place closures to case isolation, household quarantine, and social distancing of over 70s substantially suppresses the infection during the intervention period compared with the same scenario without place closures. However, this suppression then leads to a second wave with a higher peak demand for ICU beds than during the intervention period, and total numbers of deaths that exceed those of the same scenario without place closures.

We therefore conclude that the somewhat counterintuitive results that school closures lead to more deaths are a consequence of the addition of some interventions that suppress the first wave and failure to prioritise protection of the most vulnerable people.

When the interventions are lifted, there is still a large population who are susceptible and a substantial number of people who are infected. This then leads to a second wave of infections that can result in more deaths, but later. Further lockdowns would lead to a repeating series of waves of infection unless herd immunity is achieved by vaccination, which is not considered in the model.

A similar result is obtained in some of the scenarios involving general social distancing. For example, adding general social distancing to case isolation and household quarantine was also strongly associated with suppression of the infection during the intervention period, but then a second wave occurs that actually concerns a higher peak demand for ICU beds than for the equivalent scenario without general social distancing.

Figure 2 provides an explanation for how place closure interventions affect the second wave and why an extra intervention might result in more deaths than the equivalent scenario without this intervention. In the scenario of case isolation, household quarantine, and social distancing of over 70s but without place closures, a single peak of cases is seen. The data are broken down into age groups, showing that younger people contribute most to the total number of cases, but that deaths are primarily in older age groups. Adding the place closure intervention (and keeping all other things constant) gives the behaviour shown in the second row of plots. The initial peak is greatly suppressed, but the end of place closures while other social distancing is in place prompts a second peak of cases among younger people. This then leads to a third, more deadly, peak of cases affecting elderly people when social distancing of over 70s is removed. Postponing the spread of covid-19 means that more people are still infectious and are available to infect older age groups, of whom a much larger fraction then die.

Fig 2.

Simulated values for daily numbers of people with coronavirus disease 2019 and deaths related to two scenarios. Interventions are triggered by reaching 100 cumulative intensive care unit cases. After the trigger, all the interventions are in place for 91 days: the general social distancing runs to day 194 and the enhanced social distancing for over 70s runs for an extra 30 days. Results are broken down into age categories, with social distancing of over 70s interventions affecting the three oldest groups. In the case isolation, household quarantine, and social distancing of over 70s scenario, a single peak of cases is seen, with greatest infection in the younger age groups but most deaths in the older age groups. In the place closures, case isolation, household quarantine, and social distancing of over 70s scenario, three peaks occur in the plot of daily cases, with the first peak appearing at a similar time to the other scenario, but with reduced severity. The second peak seems to be a response to the ending of place closure and mostly affects the younger age groups; therefore has little impact on the total number of deaths. The third peak triggered by relaxing social distancing of over 70s affects the older age groups, leading to a substantial increase in the total number of deaths

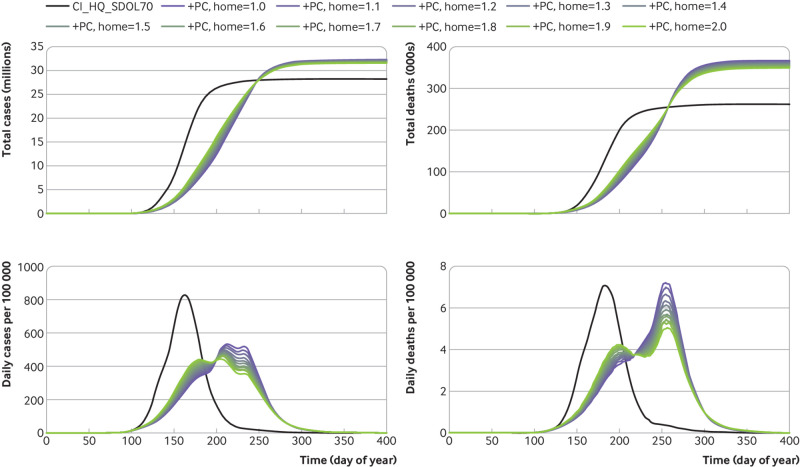
One criticism of school closure is that reduced contact at school leads to increased contact at home, meaning that children infect high risk adults rather than low risk children. We investigated this by increasing the infection rate at home to an extremely high level. Figure 3 shows that this makes an insignificant difference compared with the overall effect of adding school closures (despite the description of place closure interventions in table 2 of Report 9, university closures are not included in the scenario parameter file representing place closure, case isolation, household quarantine, and social distancing of over 70s9) to the other interventions.

Fig 3.

Effect of place closures. Comparison of the case isolation, household quarantine, and social distancing of over 70s scenario with the same scenario but place closure included. After the trigger at 100 cumulative intensive care unit cases, all the interventions are in place for 91 days: general social distancing runs to day 194 and social distancing for over 70s runs for an extra 30 days. With place closure the effect of increasing the amount of in-household interactions by a factor (home) of up to 2 is shown, which results in cases being shifted from first to later waves, but the additional place closure intervention always results in an increase in total number of cases and deaths. PC=place closures; CI=case isolation; HQ=household quarantine; SDOL70=social distancing of over 70s

Description of a second wave in CovidSim

Although Report 9 discusses the possibility that relaxing the interventions could lead to a second peak later in the year, we wanted to explore this in more detail using the newer CovidSim code and latest set of parameter files.8

The interventions we consider are place closures, case isolation, household quarantine, and general social distancing, which are implemented using the PC_CI_HQ_SD parameter file. Specifically, we use the parameter file available in the data/param_files subdirectory of the GitHub repository. The only modification was to change the duration of the interventions to 91 days.

These interventions start in late March (day 83) and last for three months (91 days). These simulations are also initialised so that about 15 600 deaths occur by day 100 (9 April) in all scenarios, mostly in people infected before the interventions were implemented. Initialisation is done by modifying the “number of deaths accumulated before alert” parameter in the preUK_2.0.txt parameter file. This compares with how the Report 9 simulations were initialised, which used the reported deaths to 14 March. The results are presented in figure 4. The top panel shows the cumulative number of deaths, using data from National Records of Scotland11 and Connors and Fordham,13 whereas the bottom panel shows ICU bed demand per 100 000 people. Although our simulations include Northern Ireland, the available reported data do not. Therefore, the simulation results and data presented in figure 4 are only for England, Wales, and Scotland. We also consider a range of reproduction numbers and find that values higher than those considered in Report 9 best reproduce the data, with a value between 3.0 and 3.5 probably providing the best fit. This is consistent with the analysis presented in Flaxman et al,14 but we acknowledge that the data could also be fitted by changes to the other scenario parameters. In both panels we also show the “do nothing” scenario for a reproduction number of 3.0.

Fig 4.

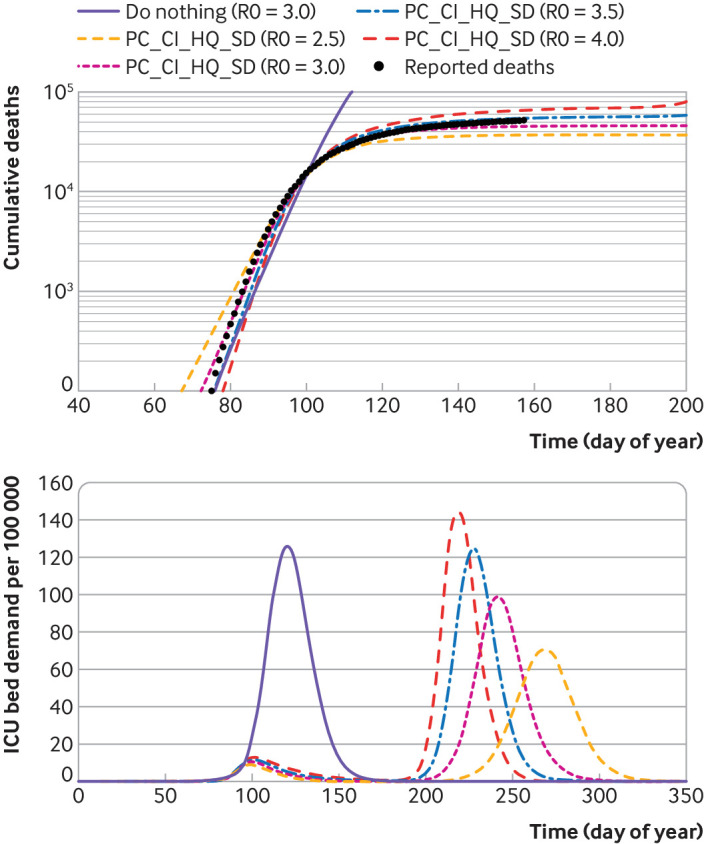
Refit of the IBMIC March parameterisation based on death data through to June. Top panel shows cumulative deaths in the first wave, using data from National Records of Scotland11 and Connors and Fordham.13 Bottom panel shows demand for intensive care unit (ICU) beds per 100 000 people, including an unmitigated second wave. A range of reproduction numbers were considered and values higher than that considered in Report 9 were found to best reproduce the data. A good fit also requires an assumption that the epidemic started in January 2020, earlier than was previously assumed in Report 9. CovidSim is seen to provide a good fit to the data with a reproduction number between 3.0 and 3.5 and predicts that the demand for ICU beds would probably be limited to around 10 per 100 000 people

The scenarios presented in figure 4 are predicted to substantially reduce the demand for ICU beds.

The best fit to the code suggests about 10% infection rate in the first wave. Random antibody testing at the time of writing (June 2020) suggests that about 5% of the population test positive for antibodies to coronavirus,13 15 although the large number of deaths in care homes suggest the post-lockdown first wave was concentrated in the over 70s age group. (An editorial published in The BMJ on 19 September 2020 suggests this 5% could be an underestimate because IgA antibodies and T cell immunity were overlooked.16) With only 5-10% immunity after the lockdown, the epidemiological situation at the outset of the second wave is similar to that of March. Consequently, the number of second wave infections is predicted to be similar to that of the first wave, with a somewhat lower death rate.

In practice, it seems that mandatory and voluntary interventions short of a full lockdown will continue and maintain the reproduction number closer to 1 This will mean slower exponential growth of the second wave and keep the peak demand for ICU beds manageable, although since the epidemic is prolonged, the effect on total deaths is smaller. It is worth noting that a reproduction number of 1 is also the value that prolongs the need for interventions for the longest. At this level, the inhomogeneity of transmissions, particularly the unpredictability of superspreading events, becomes critical. Despite the level of detail in the model, the data are insufficient to model real people: we observed that for a major national epidemic, insufficient data introduce an uncertainty of about five days in the predictions. At a local level, and with a lower reproduction number, this uncertainty in the timing of the epidemic is greatly increased: it is impossible to predict when a particular town will experience an outbreak (specifically, different towns experience outbreaks in different runs of the code).

Discussion

In this paper we used the recently released CovidSim code8 to reinvestigate the mitigation scenarios for covid-19 from IBMIC presented in mid-March 2020 in Report 9.2 The motivation behind this was that some of the results presented in the report suggested that the addition of interventions restricting younger people might actually increase the total number of deaths from covid-19.

We find that the CovidSim code reliably reproduces the results from Report 9 and that the IBMIC can accurately track the data on death rates in the UK. Reproducing the real data does require an adjustment to the parameters and a slightly higher reproduction number than considered in Report 9 and implies an earlier start to the epidemic than suggested by the report. We emphasise that the unavailability of these parameters in early March 2020 is not a failure of the IBMIC model.

We confirm that adding school and university closures to case isolation, household quarantine, and social distancing of over 70s would lead to more deaths compared with the equivalent scenario without the closures of schools and universities. Similarly, general social distancing was also projected to reduce the number of cases but increase the total number of deaths compared with social distancing of over 70s only. We note that in assessing the impact of school closures, UK policy advice has concentrated on reducing total number of cases and not the number of deaths.17

The qualitative explanation is that, within all mitigation scenarios in the model, the epidemic ends with widespread immunity, with a large fraction of the population infected. Strategies that minimise deaths involve the infected fraction primarily being in the low risk younger age groups—for example, focusing stricter social distancing measures on care homes where people are likely to die rather than schools where they are not. Optimal death reduction strategies are different from those aimed at reducing the burden on ICUs, and different again from those that lower the overall case rate. It is therefore impossible to optimise a strategy for dealing with covid-19 unless these three desirable outcomes are prioritised.

We find that scenarios that are very effective when the interventions are in place, can then lead to subsequent waves during which most of the infections, and deaths, occur. Our comparison of updated model results with the published death data suggests that a similar second wave will occur later this year if interventions are fully lifted. More realistically, if the case isolation, household quarantine, and social distancing of over 70s strategy is followed, alongside other non-pharmaceutical intervention measures such as non-mandatory social distancing and improved medical outcomes, the second wave will grow more slowly than the first, with more cases but lower mortality.

Since this paper was first written (June 2020), UK policy has moved to more local interventions. CovidSim models the geography of all towns, but only the simulated people are representative of the true population. This uncertainty means that the model cannot reliably predict which town will experience an outbreak. Specifically, whereas the timing of the national outbreak is uncertain by days, the timing of an outbreak in a town is uncertain by months. IBMIC is the most precise model available, but substantially more personal data would be needed to obtain reliable local predictions.

Finally, we re-emphasise that the results in this work are not intended to be detailed predictions for the second wave of covid-19. Rather, we re-examined the evidence available at the start of the epidemic. More accurate information is now available about the compliance with lockdown rules and age dependent mortality. The difficulty in shielding care home residents is a particularly important set of health data that was not available to modellers at the outset.

Nevertheless, in all mitigation scenarios, epidemics modelled using CovidSim eventually finish with widespread infection and immunity, and the final death toll depends primarily on the age distribution of those infected and not the total number.

What is already known on this topic

• Detailed models of individual interactions, which can take many hours of supercomputer time to run, are a reliable way to predict the course of an epidemic and investigate counterfactual scenarios

• The IBMIC model is the most detailed individual based model of the United Kingdom appropriate for simulation of the spread of an epidemic

• The UK-wide lockdown as a result of coronavirus disease 2019 (covid-19) was implemented as a highly effective way of reducing the spread of the epidemic

What this study adds

• The model used for Report 9 was independently validated and verified, and predicts that, in the absence of an effective vaccine for covid-19, school closures would result in more overall deaths than no school closures

• Mitigating a covid-19 epidemic requires a different strategy from an influenza epidemic, with more focus on shielding elderly and vulnerable people

• While total infections are at a low level, covid-19 manifests as localised spikes; currently available data are insufficient to reliably predict where these will occur