The impact of implementing HIV prevention policies therapy and control strategy among HIV and AIDS incidence cases in Malaysia

Abstract

Malaysia is faced with a high HIV/AIDS burden that poses a public health threat. We constructed and applied a compartmental model to understand the spread and control of HIV/AIDS in Malaysia. A simple model for HIV and AIDS disease that incorporates condom and uncontaminated needle-syringes interventions and addresses the relative impact of given treatment therapy for infected HIV newborns on reducing HIV and AIDS incidence is presented. We demonstrated how treatment therapy for new-born babies and the use of condoms or uncontaminated needle-syringes impact the dynamics of HIV in Malaysia. The model was calibrated to HIV and AIDS incidence data from Malaysia from 1986 to 2011. The epidemiological parameters are estimated using Bayesian inference via Markov chain Monte Carlo simulation method. The reproduction number optimal for control of the HIV/AIDS disease obtained suggests that the disease-free equilibrium was unstable during the 25 years. However, the results indicated that the use of condoms and uncontaminated needle-syringes are pivotal intervention control strategies; a comprehensive adoption of the intervention may help stop the spread of HIV disease. Treatment therapy for newborn babies is also of high value; it reduces the epidemic peak. The combined effect of condom use or uncontaminated needle-syringe is more pronounced in controlling the spread of HIV/AIDS.

1. Introduction

Since the first case of human immunodeficiency virus (HIV) in Malaysia was reported in 1986, HIV, which leads to acquired immunodeficiency syndrome (AIDS), has spread to all parts of Malaysia (MOH, 2015). According to HIV Estimations and Projections under the Ministry of Health, at the end of 2013, Malaysia was estimated to have 86,324 people living with HIV (PLHIV) (MOH, 2012, 2015). However, there is still a need for data collection from the country, indicating that the magnitude and trend of HIV/AIDS are very high (MOH, 2015). The National Strategic Plan, established in 2002 under the auspices of the Ministry of Health, has made significant progress in controlling the spread of HIV/AIDS nation-wide (MOH, 2012). For instance, a significant reduction in numbers was reported from 6978 HIV cases in 2002 to 3393 HIV cases reported in 2013 (MOH, 2012). Some of the problems and challenges identified include how to assess the effectiveness of various preventive measures and control strategies accurately from the public health policy point of view (Apenteng & Ismail, 2015). These objectives are clearly stated in the Malaysia National Strategic Plan on HIV/AIDS prevention, control, and treatment programmes (MOH, 2012, 2015). Malaysia is a country with a concentrated HIV epidemic, with infection rates as high as 5 percent among most-at-risk populations (MARPS). This most at-risk population includes people who inject drugs (PWID), sex workers, transgender, and men who have sex with men (MSM) subpopulation (Huang & Hussein, 2004; Reid et al., 2007; Singh et al., 2013).

Mathematical models are powerful tools for investigating human infectious diseases, such as HIV and AIDS, contributing to the understanding of the dynamics of infections which can provide valuable information for public health policymakers (Bramson et al., 2015; Luboga et al., 2010; Padilla, Reyes, & Connolly, 2012). Many models have been developed to analyze the effectiveness of the control strategies in the past (Abdullah et al., 2002; Levine et al., 2015; Negredo et al., 2015; Nyabadza & Mukandavire, 2011; Sripan et al., 2015). Epidemic models date back to the early twentieth century, to a set of three articles from 1927, 1932, and 1933 by Kermack and McKendrick (Kermack & McKendrick, 1927; 1991a; 1991b). Today, there is a growing need to model the effects of environmental factors, including treatment therapy on newborn babies, condom use, and the supply of uncontaminated needle-syringe on the spread of HIV and AIDS. Such models will provide an understanding of how the spread of HIV/AIDS could be minimized. Cai, Guo, & Wang, 2014 investigated an HIV/AIDS epidemic model with treatment to find out the impact of remedy on HIV (Cai, Guo, & Wang, 2014). Huo and Feng presented global stability for HIV and AIDS epidemic models at different latent levels and treatment in 2013 (Huo & Feng, 2013). Mathematical analyses of a different strain of HIV/AIDS and at population-based levels with antiretroviral therapy have been modeled (Bhunu et al., 2009; Eaton & Hallett, 2014; Falconer et al., 2009; Tamizhmani et al., 2004; Wilson & Zhang, 2011). Greenhalgh, Doyle, & Lewis, 2001 formulated a mathematical treatment of AIDS and the use of condoms in San Francisco, USA. They suggested that the use of condoms has important implications for control of the disease to reduce the spread of HIV (Greenhalgh, Doyle, & Lewis, 2001). In the past, the use of Markov chain Monte Carlo (MCMC) techniques in fitting statistical epidemiological models was conventional (Berzuini et al., 1997; Calderhead, 2008). Recently, MCMC has been put to advantageous use in estimating existing and formulated models (Neal and Terry Huang 2015; Solonen et al., 2013; Sun, Xiao, Peng, & Wang, 2013; Xun et al., 2013). The computational intractability of the model developed in this paper will be addressed using MCMC methods.

To the best of our knowledge, existing mathematical models of HIV dynamics models failed to incorporate the following: firstly, the infected individuals are capable of having children that are either infected or do not have the disease; secondly, by putting the new-born babies who may be exposed to HIV on treatment therapy, and thirdly, incorporating the use of condom as well as a supply of uncontaminated needle-syringes. We used compartmental models to understand the effects of persistent spread and the control of HIV in Malaysia. We assumed homogeneous mixing among the entire high-risk population for simplicity. We then formulated a nonlinear mathematical model to describe the impact of preventive measures on the spread of HIV. We used this formulated model to understand the HIV epidemic in Malaysia comprehensively and to explore policy-related questions, including an investigation of the impact of treatment therapy for new-born babies and the use of condoms or uncontaminated needle syringes on the dynamics of HIV in Malaysia. It is assumed that susceptible become infected via sexual contacts as well as people who inject drugs and that all of the infectives eventually developed AIDS. This approach is different from the ones in most of the papers referenced or cited. It is hoped that the empirical results will improve our understanding of the HIV and AIDS epidemic. Our ultimate goal is to help in formulating a useful model for public-health control strategies. We expect our intermediate results may apply to other countries to control the spread of HIV/AIDS.

2. Materials and methods

2.1. Data

We constructed a deterministic population-based compartmental model of HIV/AIDS transmission with intervention measures. Data for the model were obtained from Malaysia epidemiological data on HIV and AIDS yearly reported cases (MOH, 2012). We chose the year 1986 as a starting point since 1986 was when the first HIV case made its debut, HIV has become one of the country’s most severe health and development challenges. In 1986, the total population in Malaysia was 16,329,400. In 1986, three individuals clinically confirmed HIV patients, and these cases represented the initial infected $I_1\left(0\right)$ (compartment), and one individual developed AIDS (the $A_1\left(0\right)$ compartment).

2.2. Formulation of the model

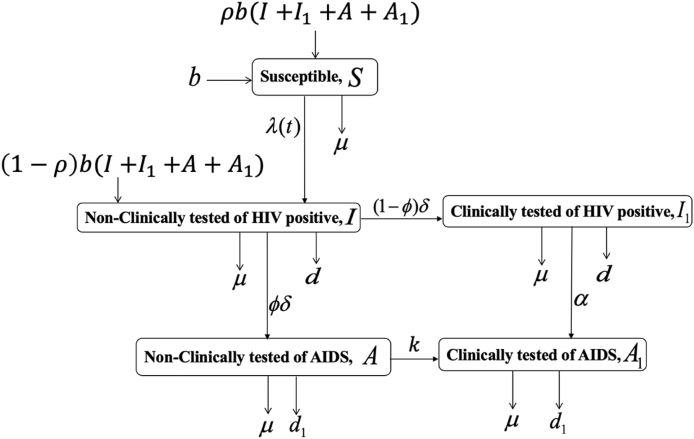
The five compartments $SI{I}_{1}A{A}_1$ model adopted here is specified by adding disease preventive measures: treatment therapy for new cases and condom use or supply of uncontaminated needle-syringes. Let $S\left(t\right)$ be the number of susceptible individuals in the population, $I\left(t\right)$ be the number of non-clinically confirmed (early-stage infection) HIV carriers, $I_1\left(t\right)$ be the number of clinically confirmed HIV positive individuals, $A(t$) be the number of non-clinically tested AIDS cases, and $A_1\left(t\right)$ be the number of clinically confirmed AIDS patients at a time $\left(t\right)$. The size of the total population is given by $N\left(t\right)=S\left(t\right)+I\left(t\right)+I_1\left(t\right)+A\left(t\right)+A_1\left(t\right)$. We assume the disease occurs with equal probability across all sexually active age groups. Susceptible individuals become infected at rates $\lambda \left(t\right)=(1-\eta )\beta \frac{I+\sigma I_1+{\sigma }_{1}A+{\sigma }_2{A}_1}{N}S$, where $\eta$ is the product of preventive measure (condom use or supply of uncontaminated syringe-needle) and the efficacy of the intervention to prevent the acquisition of infection by susceptible individuals. The parameter $\beta$ is the probabilities of transmission per either sexual action or contaminated syringe-needle use. The assumption here is that the protection (preventability) $\eta$ reduces the risk of infection and transmission, $0<\eta <1$. The endpoint $\eta =0$ would depicts that preventive measure is useless or meaningless, and $\eta =1$ implies that preventive measure is comprehensively effective. The parameters $\sigma$,${\sigma }_1$ and${\sigma }_2$ are modification factors accounting for varying levels of spreading of clinically tested HIV-positive, non-clinically tested AIDS and clinically tested AIDS individuals. Moreover, we incorporate infants whose mothers are HIV/AIDS patients. Krist & Crawford-Faucher, 20022 showed that aggressive maternal antiretroviral treatment therapy and management during pregnancy and labor, followed by after birth treatment of neonatal zidovudine decreases the risk of mother to baby transmission of HIV (Krist & Crawford-Faucher, 2002). Antiretroviral therapy can suppress HIV and stop the progression of the disease (WHO, 2014). Prevention of vertical transmission of HIV has been at the forefront of global prevention efforts. Let $b$ represent birth rate; we assume that out of $b(I+I_1+A+A_1)$ newborns who are exposed to maternal HIV infection, a fraction $\rho$ (where $\rho$ is the product of the treatment rate and diagnosis rate) are identified and successfully undergo treatment therapy. That is, $\rho b\left(I+I_1+A+A_1\right)$babies move to the susceptible class. The remaining babies $(1-\rho )b(I+I_1+A+A_1)$ are not identified during pregnancy or at birth and enter the non-clinically tested compartment $I$. Let $\delta$ be the rate at which individuals exit the non-clinically tested HIV class, a fraction $\phi$of $\delta ,$ where $0<\phi <1$, progress to the non-clinically tested AIDS class $A$; whereas the remaining $(1-\phi )\delta$ of non-clinically tested HIV patients move to the class of individuals who are clinically tested HIV positive. The progression rate of clinically tested HIV individuals to clinically tested AIDS class is represented by $\alpha$. We also assume that natural death is constant across all compartments of the model at rate $\mu .$The parameters $d$and$d_1$denote additional death rates due to HIV and AIDS positive, respectively. Finally, $k$ represents the progression of non-clinically AIDS to clinically tested AIDS class. See Fig. 1 for the flow diagram of the model.

Fig. 1.

Flow diagram of the model.

With these assumptions, the model is described by the following set of nonlinear differential equations:

$$\frac{dS}{dt}=bS+\rho b\left(I+I_1+A+A_1\right)-\left(1-\eta \right)\beta \frac{I+\sigma I_1+{\sigma }_{1}A+{\sigma }_2{A}_1}{N}S-\mu S$$ (1)

$$\frac{dI}{dt}=\left(1-\rho \right)b\left(I+I_1+A+A_1\right)+\left(1-\eta \right)\beta \frac{I+\sigma I_1+{\sigma }_{1}A+{\sigma }_2{A}_1}{N}S-\left(\mu +\delta +d\right)I$$ (2)

$$\frac{d{I}_1}{dt}=\left(1-\phi \right)\delta I-\left(\alpha +\mu +d\right)I_1$$ (3)

$$\frac{dA}{dt}=\phi \delta I-\left(\mu +k+d_1\right)A$$ (4)

$$\frac{d{A}_1}{dt}=kA+\alpha I_1-\left(\mu +d_1\right)A_1$$ (5)

The total population is

$$\frac{dN}{dt}=bN-\mu N-d\left(I+I_1\right)-d_1(A+A_1)$$ (6)

To determine whether the disease continues to spread, we must find the stability of the disease-free equilibrium point. The basic reproduction number ($R_0$) is the expected number of secondary cases produced by a single infection in a completely susceptible population(Van Den Driessche & James, 2002; Hethcote, 2000; Huo & Feng, 2013; Jones, 2013). Thus, the disease will not continue to spread if $R_0<1$. To determine whether the disease will continue to spread, we must study the dynamics when$R_0>1$. If the infection persists ($R_0>1$), then either the system will be stable around the interior equilibrium, or there may exist a periodic attractor. Using the notations by Van Den Driessche and James (2002), $F_i\left(x\right)$ is the rate of appearance of new infections in compartment $i$, and $V_i\left(x\right)$ represents the rate of infections from one compartment to another. Here, $F_i$ and $V_i$ are given by

$$F_i=\left(\begin{array}{c}\left(1-\rho \right)b\left(I+I_1+A+A_1\right)+(1-\eta )\beta \frac{I+\sigma I_1+{\sigma }_{1}A+{\sigma }_2{A}_1}{N}S\\ 0\\ 0\\ 0\end{array}\right)$$ (7)

$$V_i=\left(\begin{array}{c}(\mu +\delta +d)I\\ -(1-\phi )\delta I+(\alpha +\mu +d)I_1\\ -\phi \delta I+\left(\mu +k+d_1\right)A\\ -\alpha I_1-kA+(\mu +d_1)A_1\end{array}\right)$$ (8)

The corresponding Jacobian matrices at the disease-free equilibrium ($S\left(0\right)=N\left(0\right),\mathrm{0,0,0,0}$) are as follows:

$$F=\left(\begin{array}{cccc}C+D& C\sigma +D& C{\sigma }_1+D& C{\sigma }_2+D\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right),$$

where $C=\left(1-\eta \right)\beta$ and $D=\left(1-\rho \right)b$.

$$V=\left(\begin{array}{cccc}\mu +\delta +d& 0& 0& 0\\ -(1-\phi )\delta & \alpha +\mu +d& 0& 0\\ -\phi \delta & 0& \mu +k+d_1& 0\\ 0& -\alpha & -k& \mu +d_1\end{array}\right)$$

The basic reproduction number ($R_0$) is the spectral radius of$F{V}^{-1}$. That is,

$$R_0=\frac{\left(1-\eta \right)\beta f+\left(1-\rho \right)b(\mu +k+d_1)g}{\left(\mu +\delta +d\right)\left(\alpha +\mu +d\right)\left(\mu +k+d_1\right)\left(\mu +d_1\right)}$$

where

$$f=\left(k+d_1+\mu \right)[d_1\alpha +\left(1-\phi \right)\sigma d_1\delta +\left(1-\phi \right){\sigma }_2\alpha \delta +d_1\mu +\alpha \mu +\left(1-\phi \right)\sigma \delta \mu +{\mu }^2+d\left(d_1+\mu \right)]+(d+\alpha +\mu )({\sigma }_{2}k+{\sigma }_1(d_1+\mu ))\phi \mathrm{\delta }$$

and

$$g=d_1(\alpha +\mu +(1-\phi )\delta )+d(d_1+\mu +\phi \mathrm{\delta })+(\alpha +\mu )(\delta +\mu )$$

3. Model validation

We explore the use of Markov chain Monte Carlo (MCMC) simulation method to estimate uncertainty in all the unknown parameters incorporated in our proposed model. MCMC methods are useful to obtain samples from the posterior distributions(Putter et al., 2002). In choosing an optimal parameterization to fit this model, several considerations play a role. For example, it is essential to note that it is advantageous to transform the unknown parameters to attempt to minimize correlation and to make sure that constraints on parameters are naturally fulfilled. Let $D$ denote the epidemiological data, and $\theta =(\beta ,\alpha ,\eta ,\mu ,\phi ,\rho ,\delta ,k,b,\sigma ,{\sigma }_1,{\sigma }_2,d,d_1)$ denote a set of the model parameters, as well as the missing data. Let the joint probability distribution to be$P(D,\theta )$ overall random quantities. The joint distribution consists of two main parts, that is the prior distribution $P\left(\theta \right)$and likelihood$P\left(D|\theta \right)$. These two will give a full probability model as$P(D,\theta )=P\left(D|\theta \right)P\left(\theta \right)$. We use the Bayes theorem $P\left(\theta |D\right)=\frac{P\left(\theta \right)P\left(D|\theta \right)}{\int P\left(D|\theta \right)P\left(\theta \right)d\theta }$ to determine the distribution of $\theta$ conditional on $D$(for more information see (Eaton & Hallett, 2014)). For a good introduction to MCMC methods, we refer to (Apenteng & Ismail, 2015; Laine, 2008; Soetaert & Petzoldt, 2010). The posterior for the parameters are estimated as:

$$p\left(\theta |y,{\sigma }^2\right)\propto exp\left(-0.5\left(\frac{SS\left(\theta \right)}{{\sigma }^2}\right)\right).p\left(\theta \right)$$ (9)

where $SS$ is the sum of squares function $SS\left(\theta \right)={\sum (y_i-f(t_i,{\theta }_i))}^2$and $p\left(\theta \right)$is a non-informative prior for $\theta$ indexing the model, where we assume that $p\left(\theta \right)\equiv 1$. To obtain proper results from the MCMC method, a constrained least squares approach is necessary to provide initial estimates of $\theta$. In addition, the model is not identifiable, and thus constraints on the parameters are warranted. Local sensitivity analysis (Soetaert & Petzoldt, 2010) was used to obtain suitable initial parameter estimates of $\theta$. For the reciprocal of the error variance$\left({\sigma }^{-2}\right)$, a gamma distribution is used:

$$p\left({\sigma }^2\right)~\text{Γ}\left(\frac{n_0}{2},\frac{n_0}{2}{S}_0^2\right).$$ (10)

The reciprocal of the error variance at each MCMC step is sampled from a gamma distribution (Gelman et al., 2013) as follows:

$$p({\sigma }^2\left|(y,\theta )\right)~\text{Γ}\left(\frac{n_0+n}{2},\frac{n_0{S}_0^2+SS\left(\theta \right)}{2}\right),$$ (11)

where $n_0$ and $n$ are input arguments to the function and the number of observations, respectively. Observe that the function $f(t_i,{\theta }_i)$ in $SS\left(\theta \right)$ solves the system of equations (1), (2), (3), (4), (5), (6). The unknown parameters were estimated using the FME package in R software (Soetaert & Petzoldt, 2010). The estimated parameters obtained were used as an initial guess to ensure good convergence of the MCMC chain (Apenteng & Ismail, 2015). The Metropolis Hasting algorithm (Christen et al., 2005; Haario et al., 2006; Solonen et al., 2013) was applied to our epidemiological dataset. The method samples from the posterior distribution by constructing Markov chains that converge to the target posterior distribution.

4. Results

The estimated epidemiological parameters, together with their 95% credible intervals (CI), are shown in Table 1, and these were used to calculate the basic reproduction number$R_0$. We observe that estimated parameters have shorter CI widths. Interestingly, the lower limits of parameters $\phi ,{\sigma }_2$ and $d$ are less than zero. This, of course, is not surprising since the system is underdetermined.

Table 1.

Summary of the estimated parameters.

Parameter	Estimated Value	95% CI	Source
$\beta$	9.9100e-01	(9.8885e-01, 9.9314e-01)	Estimated
$\alpha$	8.2160e-02	(8.1993e-02, 8.2327e-02)	Estimated
$\delta$	8.9020e-01	(8.8691e-01, 8.9348e-01)	Estimated
$\varphi$	6.3300e-04	(-6.5920e-05, 1.3319e-03)	Estimated
$\sigma$	2.4950e-01	(2.4801e-01, 2.5098e-01)	Estimated
${\sigma }_1$	9.9990e-01	(9.9818e-01, 1.0016e+00)	Estimated
${\sigma }_2$	1.0861e-12	(-6.2360e-03, 6.236e-03)	Estimated
$\eta$	4.8050e-02	(4.4412e-02, 5.1687e-02)	Estimated
$b$	1.0400e-02	(7.1726e-03, 1.3627e-02)	Estimated
$\mu$	3.3690e-01	(3.3443e-01, 3.3937e-01)	Estimated
$d$	2.9560e-09	(-2.2106e-03, 2.2107e-03)	Estimated
$d_1$	4.3740e-02	(4.1194e-02, 4.6286e-02)	Estimated
$k$	4.8390e-03	(2.8273e-03, 6.8507e-03)	Estimated
$\rho$	9.0990e-01	(9.0712e-01, 9.1267e-01)	Estimated

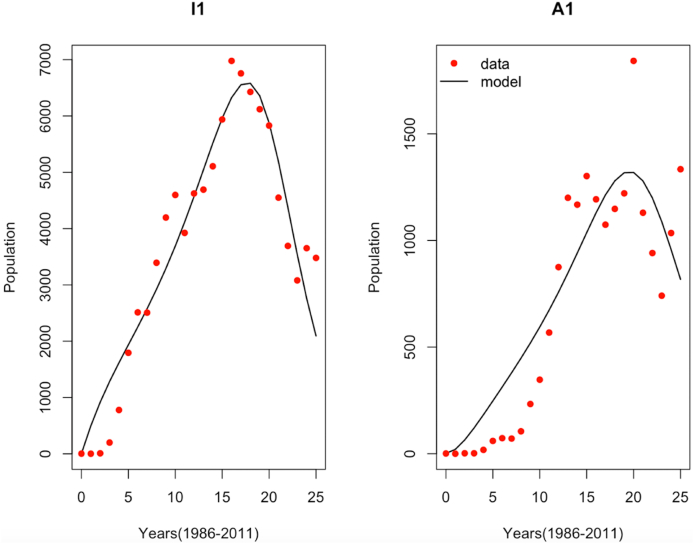
The plot of the data and the best-fit model for yearly reported cases of clinically tested HIV positive and AIDS are shown in Fig. 2. We observe that generally, the reported HIV and AIDS incidence data are calibrated and validated well during the 25 years. However, the calibration and validation during the first five and ten years for the HIV and AIDS incidence cases respectively perform poorly.

Fig. 2.

Fitted model for HIV and AIDS cases.

Table 2 presents a summary of the sensitivity analysis of the estimated epidemiological parameters. We observe that the parameter $\beta$ has both the highest while ${\sigma }_2$ has the lowest $L_1$ and $L_2$ norms. This suggest that the parameter ${\sigma }_2$ has the least effect on the output variables and less sensitive, while $\beta$ is the highly sensitivity parameter.

Table 2.

Summary of sensitivity parameters.

Parameter	Estimated Values	$L1$	$L2$	Mean	Min	Max
$\beta$	9.9100e-01	5.6000e+00	8.8000e-01	5.6000e+00	0.0000e+00	9.7000e+00
$\alpha$	8.2160e-02	4.9000e-01	7.6000e-02	1.5000e-01	−5.2000e-01	9.2000e-01
$\delta$	8.9020e-01	1.6000e+00	2.7000e-01	−1.5000e+00	−3.1000e+00	6.5000e-01
$\varphi$	6.3300e-04	2.3000e-03	3.8000e-04	2.2000e-03	−5.7000e-04	4.6000e-03
$\sigma$	2.4950e-01	1.4000e+00	2.2000e-01	1.4000e+00	0.0000e+00	2.5000e+00
${\sigma }_1$	9.9990e-01	3.8000e-01	5.6000e-02	3.8000e-01	0.0000e+00	5.2000e-01
${\sigma }_2$	1.0861e-12	8.1000e-13	1.4000e-13	8.1000e-13	0.0000e+00	1.6000e-12
$\eta$	4.8050e-02	2.8000e-01	4.4000e-02	−2.8000e-01	−4.9000e-01	0.0000e+00
$b$	1.0400e-02	4.3000e-02	9.6000e-03	4.3000e-02	0.0000e+00	2.1000e-01
$\mu$	3.3690e-01	4.2000e+00	6.8000e-01	−4.2000e+00	−8.4000e+00	0.0000e+00
$d$	2.9560e-09	2.4000e-08	3.7000e-09	−2.4000e-08	−3.9000e-08	0.0000e+00
$d_1$	4.3740e-02	6.7000e-02	1.2000e-02	−6.7000e-02	−1.6000e-01	4.3000e-03
$k$	4.8390e-03	4.7000e-03	1.3000e-03	−8.2000e-04	−4.8000e-03	5.6000e-02
$\rho$	9.0990e-01	1.1000e-01	1.7000e-02	−1.1000e-01	−1.9000e-01	0.0000e+00

The pairwise relationships among the parameters are shown in Fig. 3. We observe that most of the relationships are linear. For example, there is a strong positive linear relationship between parameters $\beta$ and $\phi$. In addition, there is a strong negative linear relationship between $\alpha$ and $d$.

Fig. 3.

Pairs plot of the MCMC samples for the fourteen parameters.

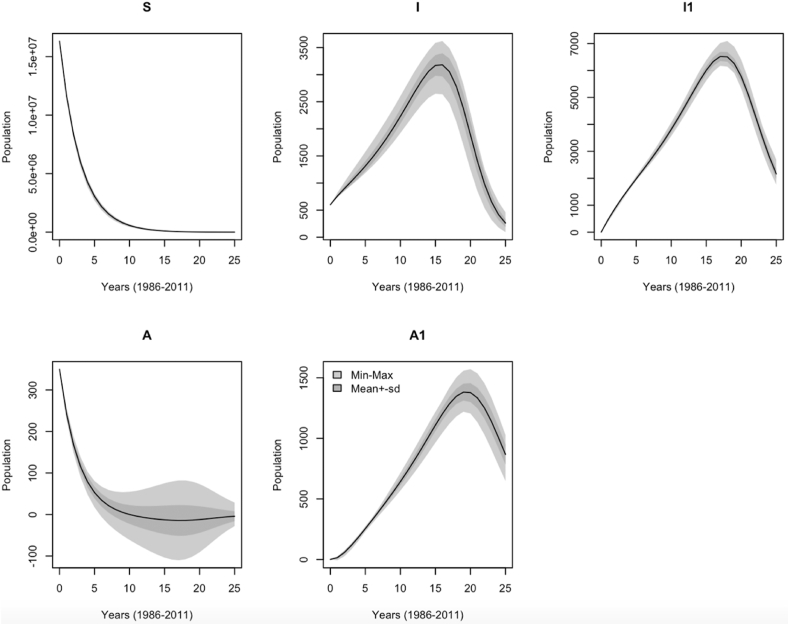
Fig. 4 shows yearly reported HIV positive and AIDS cases based on parameter distribution as generated with the MCMC simulation of the calibration period from 1986 to 2011. The high variances were observed in the following compartment order: ($A>I>A_1>I_1>S$). This shows that there was predictive accuracy of the model, reflected by the variance of the predictive distribution. The large number for the variance is due to either the uncertainties in the model or noise in data collection, and the model fits the noisy data reasonably well.

Fig. 4.

Predictive envelopes of the model showing the sensitivity range of yearly reported HIV and AIDS cases. The light grey shade by Min-Max represents the minimum and maximum model response at each time step, whereas the dark grey shade by Mean$\pm$sd refers to the mean model response plus/minus one standard deviation.

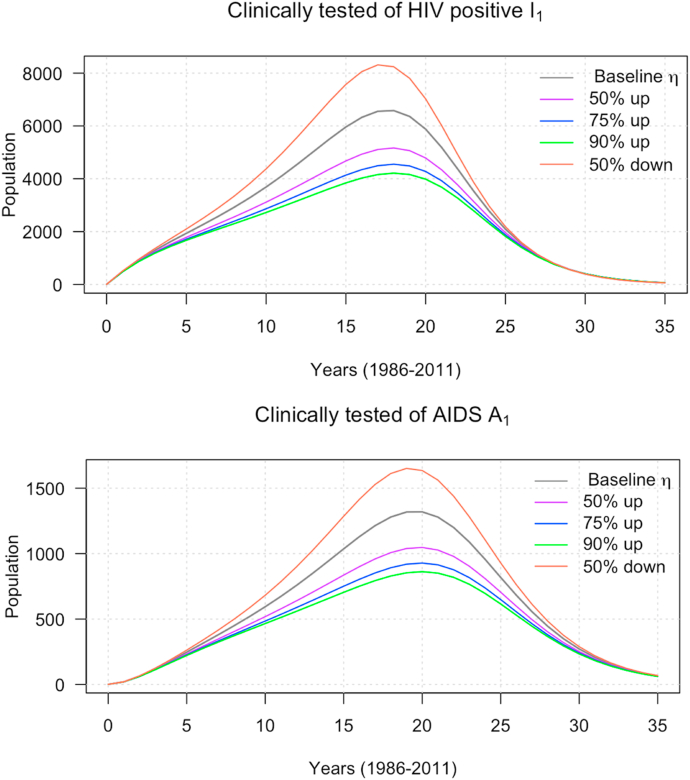
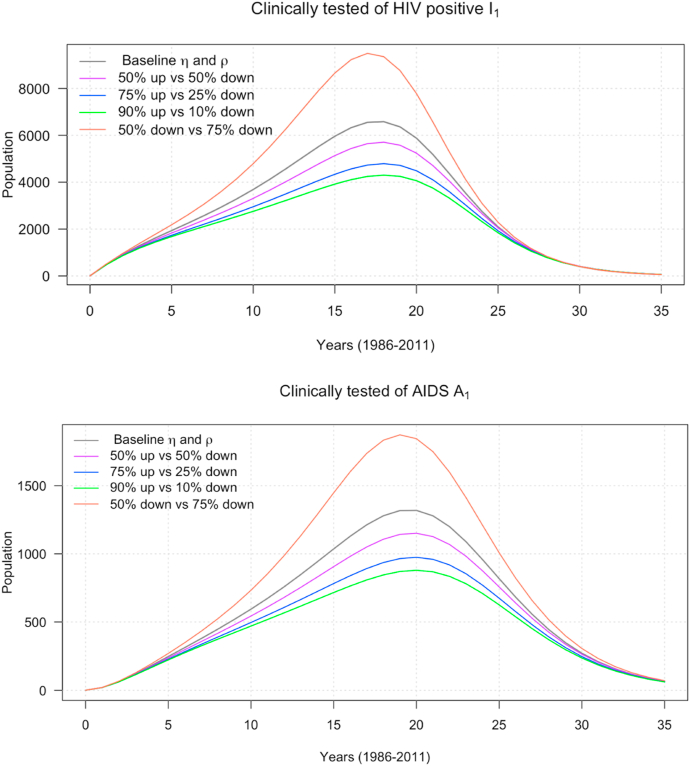
Next, we investigate the impact of the treatment therapy for new-born babies’ control parameter $\rho$, and the use of condoms or uncontaminated needle syringes $\eta$ on HIV and AIDS incidence. We begin by considering the effect of increasing baseline parameter $\eta$ while $\rho$ is fixed. Fig. 5 depicts the impact as we increase baseline $\eta$ from 50% to 90% and decrease by 50%. We notice that both HIV and AIDS incidence cases have the same effect as we increase or decrease $\eta$ from the baseline. Furthermore, the spread of the HIV and AIDS peak between years 15 and 20. This suggests that increasing the baseline will help to reduce the spread of the disease.

Fig. 5.

The impact of control strategy $\eta$ on HIV and AIDS incidence cases.

Finally, we consider the combined effect of increasing or decreasing $\eta$ and decreasing $\rho$ from their baseline values. The results of the impact on HIV and AIDS incidence cases are shown in Fig. 6. From the figure, we observe that the peaks, both HIV and AIDS incidence drop as we increase $\eta$ and decrease $\rho$. It is worth noting that the newborn who went through treatment therapy was comprehensively successful with $\rho$ almost equals to one. Thus, $\rho$ can only be decreasing in one direction compare with $\eta$.

Fig. 6.

The impact of control strategy $\eta$ and $\rho$ on HIV and AIDS incidence cases.

Summary and conclusion

HIV disease is caused by the human immunodeficiency virus that infects humans. Over time, they cause AIDS. Once affected, the immune system is destroyed within a few months. In this paper, we modeled the practical impact of given treatment therapy for new-born babies exposed to HIV, and the use of condoms, or the supply of uncontaminated needle-syringes on reducing HIV and AIDS incidence in Malaysia. We assumed that there were sexual interactions between the susceptible and all the infectious sub-populations, and known exposed new-born babies undergo successful treatment therapy during pregnancy or after birth. The model parameters were estimated using the FME package in R software. We also explored the use of MCMC simulation method to determine the uncertainty in all the unknown parameters incorporated in our proposed model.

It is well known that if (basic reproduction number)$R_0<1$, then, the spread of disease will die out, and if$R_0>1$, then, the infection will persist and continue to spread. Based on the estimated parameters, we computed the reproduction number to be 1.1799, implying that the disease-free equilibrium is unstable. This is not a good indicator from the public health point of view since the aim is to stabilize the infection at the disease-free equilibrium.

Sensitivity analysis was performed to identify the parameters that influence the spread of the disease; this is important to make forecasts and predictions. Sensitivity analysis can also help in public health policy decisions. The results show that the probability transmission per either unprotected sexual action or contaminated needle-syringe use had the highest sensitivity value, and impacts the dynamics of HIV transmission in Malaysia. As stated in the model formulation, the parameter, $\eta$, decreases the transmission probability. More aggressive adoption of condoms and uncontaminated needle-syringe use is very crucial to control the spread of HIV. We varied and further examined the effects of the parameters $\eta$ and $\rho$. As exhibited in Fig. 5, a larger $\eta$ reduces the peak of the epidemic curve significantly, and the number of infected individuals (the area under the epidemic curve). For example, in Fig. 5, with a baseline value $\eta =4.8050\text{e}-02$, the epidemic peak happens at about 6500 clinically tested HIV, and about 1300 clinically confirmed AIDS patients. A 50% increment in the baseline produces less confirmed HIV/AIDS cases (purple curves). The reduction in HIV/AIDS patients is more pronounced with a higher increase in the $\eta$; see Fig. 5. We considered the combined effects of the $\eta$ and $\rho$ to demonstrate further, their impact on the dynamics of the proposed model. As shown in Fig. 6, the right combination implementation of these preventive measures is the key to curb the disease in the absence of a vaccine for a cure. We strongly recommend a comprehensive adoption of condoms or uncontaminated needle syringe use and treatment therapy for newborn babies preventive measures to the general public and public health policymakers to contain the disease.

Our results have some limitations, which should be acknowledged. Estimates for the model were obtained based on the yearly reported national cases of HIV/AIDS data. The lack of complete datasets from the onset of the HIV and AIDS disease to date may affect results. Nevertheless, our estimate of the epidemiological parameters, as well as the basic reproduction number of our study, is the first important step in quantifying the magnitude and trend of the HIV/AIDS epidemic in Malaysia. The study provides vital information to both researchers and public health policymakers.

Declaration of competing interest

The authors have no conflict of interest to declare.

Handling editor: Hulin Wu