Stress increases the permeability of the mitochondrial inner membrane by activating permeability transition pores (PTPs), likely composed of ATP synthase or the adenine nucleotide translocator. By measuring water flux during calcium-activated mitochondrial swelling, Neginskaya et al. estimate that if these proteins are involved in PTP, only a small fraction becomes transformed into the pore on a single mitochondrion.
Abstract
Mitochondrial permeability transition (PT) is a phenomenon of stress-induced increase in nonspecific permeability of the mitochondrial inner membrane that leads to disruption of oxidative phosphorylation and cell death. Quantitative measurement of the membrane permeability increase during PT is critically important for understanding the PT’s impact on mitochondrial function. The elementary unit of PT is a PT pore (PTP), a single channel presumably formed by either ATP synthase or adenine nucleotide translocator (ANT). It is not known how many channels are open in a single mitochondrion during PT, which makes it difficult to quantitatively estimate the overall degree of membrane permeability. Here, we used wide-field microscopy to record mitochondrial swelling and quantitatively measure rates of single-mitochondrion volume increase during PT-induced high-amplitude swelling. PT was quantified by calculating the rates of water flux responsible for measured volume changes. The total water flux through the mitochondrial membrane of a single mitochondrion during PT was in the range of (2.5 ± 0.4) × 10−17 kg/s for swelling in 2 mM Ca2+ and (1.1 ± 0.2) × 10−17 kg/s for swelling in 200 µM Ca2+. Under these experimental conditions, a single PTP channel with ionic conductance of 1.5 nS could allow passage of water at the rate of 0.65 × 10−17 kg/s. Thus, we estimate the integral ionic conductance of the whole mitochondrion during PT to be 5.9 ± 0.9 nS for 2 mM concentration of Ca2+ and 2.6 ± 0.4 nS for 200 µM of Ca2+. The number of PTPs per mitochondrion ranged from one to nine. Due to the uncertainties in PTP structure and model parameters, PTP count results may be slightly underestimated. However, taking into account that each mitochondrion has ∼15,000 copies of ATP synthases and ANTs, our data imply that PTP activation is a rare event that occurs only in a small subpopulation of these proteins.
Introduction
Permeability transition (PT) is a phenomenon of the sudden increase in permeability of the mitochondrial inner membrane during stress conditions (Bernardi et al., 2015; Zoratti and Szabò, 1995). PT leads to the disruption of mitochondrial energy metabolism and eventually cell death. It is believed that PT is a critical event responsible for cell and tissue damage in a wide range of acute conditions, including strokes and heart attacks. The principal causes of PT are reactive oxygen species (ROS) and excessive accumulation of intramitochondrial calcium (Halestrap and Richardson, 2015). Experimentally, PT can be studied by several methods, such as following the gradual leak of the fluorescent probe out of the mitochondrial matrix (Hüser et al., 1998) or changes in light scattering caused by osmotic swelling of the mitochondria (Baev et al., 2018). These methods enable the study of PT regulation and kinetics but do not quantify membrane permeability changes. The central goal of this study was to use the swelling assay to quantitatively measure inner membrane permeability at the level of the single mitochondrion during calcium-induced PT.
The swelling assay is based on the principle that an increase of membrane permeability due to PT activation initially results in the equilibration of small molecules across the mitochondrial inner membrane. This equilibration is followed by high-amplitude swelling of the mitochondria due to the water influx driven by oncotic pressure created by membrane-impermeable matrix proteins (Baev et al., 2018; Lorimer and Miller, 1969). High-amplitude swelling eventually leads to rupture of the mitochondrial outer membrane and formation of mitoplasts (mitochondria lacking outer membrane). The swelling of the mitoplast proceeds further until the oncotic pressure inside the mitoplast is compensated by the elastic forces of the inner membrane. Kinetics of swelling is usually measured in a large population of suspended mitochondria (Carraro and Bernardi, 2020). These experiments allow the determination of the average rate of PT activation but do not allow quantification of the rates of solute fluxes through an individual mitochondrion (mitoplast). Using light microscopy, we measured the rate of single-mitoplast volume increase due to water influx through the membrane. These measurements allowed us to quantify the values of the membrane permeability to water during PT. Using this value, we translated membrane permeability values into units of ionic current and calculated the total number of permeability transition pores (PTPs; elementary units of PT) in a single mitochondrion.
Materials and methods
Mitoplast preparation
Mouse liver mitochondria were isolated by homogenization and differential centrifugation in isolation buffer (225 mM mannitol, 75 mM sucrose, 1 mM EGTA, and 5 mM HEPES, pH 7.2) completed by fatty acid–free BSA in 1 mg/ml of buffer (Sigma Aldrich; Elustondo et al., 2015). The dissected liver was rinsed three times with isolation buffer and minced into small pieces with scissors. Tissue was collected and homogenized with a Teflon pestle four or five times on ice. The liver homogenate was transferred into a 1.5-ml microcentrifuge tube and centrifuged at 600 g for 10 min at 4°C. The supernatant was collected and centrifuged at 4°C for 10 min at 9,000 g. Then, the supernatant was discarded, and the pellet was resuspended in 50 µl sucrose buffer (250 mM sucrose, 100 µM EGTA, and 5 mM HEPES, pH 7.2) and kept on ice.
Isolated mitochondria were incubated in isotonic KCl solution (150 mM KCl and 5 mM HEPES, pH 7.4) containing 5 mM succinate (in the presence of 2 µM rotenone) as mitochondrial substrate, 1 mM Na2HPO4, and 250 µM EDTA. Mitochondria in the same solution were placed at the glass bottom of the 1-ml imaging/recording chamber and incubated for 5–10 min to allow mitochondria to settle on the bottom of the chamber. Following incubation, mitochondria were gently washed two times with the same solution to remove detached organelles and debris. To induce PT and swelling, mitochondria were microperfused using a syringe pump with the same KCl solution in the presence of substrate supplemented either with 2 mM Ca2+ or 200 µM Ca2+ (final concentrations of free Ca2+ in the perfused area of the chamber are 2 mM and 100 µM, respectively). The rate of perfusion flow was maintained at 200 µl/h. Due to continuous perfusion during the experiment, the concentration of the free calcium was kept constant, so the overall calcium load did not depend on the amount of mitochondria in the recording chamber. The perfusion with Ca2+-containing solution led to mitochondrial PT activation, mitochondrial swelling, and rupture of the outer mitochondrial membrane. Formation of mitoplasts and changes in their diameter were monitored and recorded in real time with a light microscope (Nikon Eclipse TE300) with a PlanApo Nikon objective (40×, Ph2; NA = 0.95) and a digital camera (Accu-Scope).
Mitochondrial membrane potential measurement
The membrane potential of isolated mitochondria was measured with the fluorescent dye tetramethylrhodamine–methyl ester (TMRM; Hüser et al., 1998). Isolated mitochondria were incubated for 30 min in sucrose buffer containing 200 nM of TMRM. Then, mitochondria were placed on the bottom of the recording chamber and perfused with Ca2+ as described previously. All the solutions in the experiment for membrane potential measurement contained 200 nM of TMRM.
Patch-clamp experiments
Patch-clamp procedures and analysis were performed as described previously (Kinnally et al., 1991; Pavlov et al., 2001). Briefly, membrane patches were excised from mitoplasts right after the formation of a gigaseal using micropipettes with resistances of 20–40 MΩ at room temperature. The solution for patch-clamp recordings was symmetrical 150 mM KCl and 5 mM HEPES, pH 7.4. The voltage clamp was performed with the excised configuration of the patch-clamp technique using an Axon Axopatch 200B Microelectrode Amplifier (Molecular Devices) in the inside-out mode. Voltages are reported as pipette electrode potentials.
Water flux rate estimation
The volumes of the mitoplasts in each moment of observation were calculated with the aid of ImageJ software and an in-house MATLAB computer program. The rate of the water flux through the inner mitochondrial membrane was calculated from the rates of mitoplast volume change.
Quantification and statistical analysis
Clampfit 10.7 (Molecular Devices) and Origin 2019 (OriginLab Corporation) were used for the analysis of channel activity and for statistical analysis. Experimental errors of volume measurements were proportional to the objective resolution error 0.29 µm according to the following formula: Student’s t test (P < 0.05) was used to determine the significant difference in water fluxes and total ion conductance of the mitochondrial membrane.
Results
Under basal conditions, energized isolated mitochondria maintain a condensed shape due to low permeability of the inner membrane and the ability to regulate ionic and osmotic homeostasis. This shape is characterized by multiple cristae enclosed within the outer membrane (Haworth and Hunter, 1979). However, excessive accumulation of calcium leads to a dramatic increase in inner membrane permeability and mitochondrial swelling. Mitochondrial swelling is caused by the oncotic pressure of the membrane-impermeable molecules located inside the mitochondrial matrix. The overall strategy of our study was to quantify the permeability of the inner mitochondrial membrane by measuring the rates of the water influx (changes in mitoplast volume).
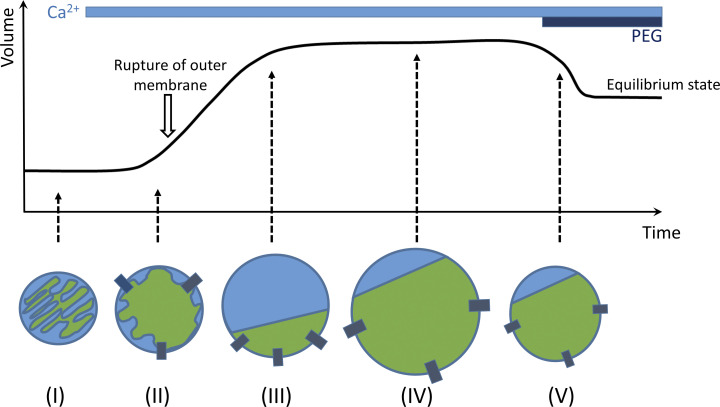
Schematics of mitochondrial/mitoplast swelling stages during the experiment are shown in Fig. 1. Initially, intact mitochondria have multiple cristae (Fig. 1, I). At the early stages of swelling, cristae disappear, but the outer membrane is still intact (Fig. 1, II). Further swelling leads to the rupture of the outer membrane and formation of mitoplasts (Fig. 1, III). Mitoplast swelling continues until the oncotic pressure is equilibrated with the elastic forces of the inner membrane (Fig. 1, IV). At the latest stages of the experiment, swelling can be reversed by increasing the oncotic pressure of the external solution through the addition of the polyethylene glycol (PEG) molecules (>1.5 kD) that are too large to traverse the PTP (Fig. 1, V).
Figure 1.
Schematics of the experimental approach. Calcium addition to the intact energized mitochondria (I) causes activation of PT and induces mitochondrial swelling (II), which eventually results in outer membrane rupture and formation of mitoplasts (III). The increase in mitoplast volume during PT is caused by water influx into the matrix due to the oncotic pressure and stops when this pressure is compensated by inner membrane elastic forces (IV). The addition of the membrane-impermeable PEG (>1.5 kD) at the end of the experiment leads to an increase in external oncotic pressure, causing mitoplast shrinkage to the steady state (V). At the steady state, the value of oncotic pressure inside the mitoplast is at equilibrium with internal oncotic pressure (see also Fig. 5 A).
Measurements of the rate of water flux through the whole mitochondrion during PTP opening
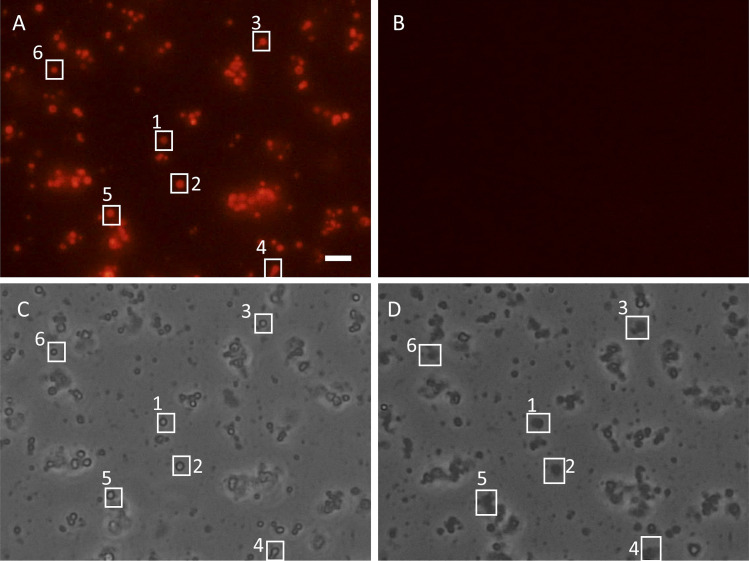
Experiments were performed with freshly isolated, energized mitochondria that were placed on the glass bottom of the recording chamber. To test the functional state of the isolated mitochondria and integrity of the inner membrane, we first measured their membrane potential using fluorescent probe TMRM. TMRM is a cationic membrane-permeable probe that accumulates only in mitochondria with membrane potential (Berezhnaya et al., 2018). As shown in Fig. 2, energized mitochondria can be identified by the red (TMRM) staining (Fig. 2 A). To induce PT and swelling, we perfused mitochondria with the same bath solution supplemented with either 2 mM or 100 µM of free Ca2+. Treatment of isolated mitochondria with Ca2+ led to the PT, causing loss of the mitochondrial membrane potential detected as the disappearance of TMRM fluorescence (Fig. 2 B). As can be seen in the bright-field image of the same region, mitochondrial depolarization was accompanied by the mitochondrial swelling, further confirming the activation of the PT (compare corresponding white boxes in Fig. 2, C and D; and Fig. 3).
Figure 2.
Detection of PT activation by measurement of mitochondrial membrane potential. (A and B) Isolated energized mitochondria (5 mM succinate/2 µM rotenone) stained with TMRM (200 nM) before (A) and after (B) activation of PT with 2 mM Ca2+. Note the loss of mitochondrial membrane potential caused by PT detected with TMRM fluorescence disappearance (B). (C and D) Bright-field images of the same mitochondrion before (C) and after (D) PT activation. Loss of mitochondrial membrane potential went along with mitochondrial swelling (D). Boxes 1-6 correspond to the representative individual mitochondria that responded to the calcium addition by depolarization and swelling. Scale bar = 5 µm.
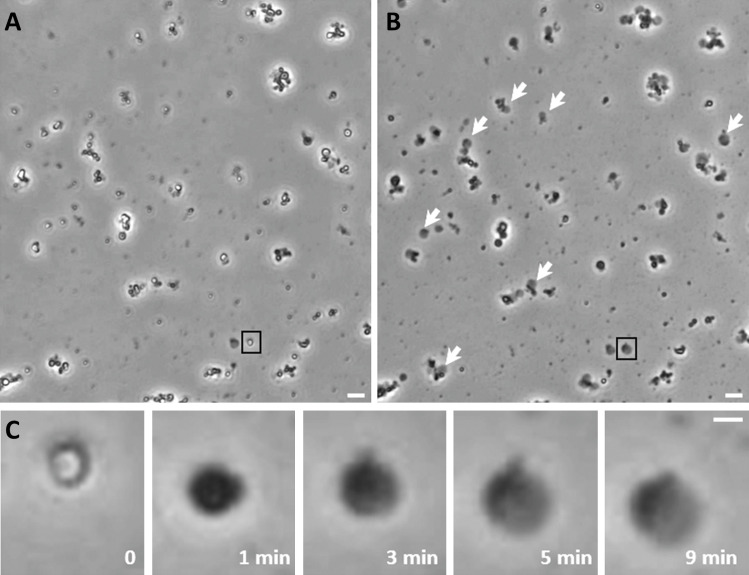
Figure 3.
Mitochondrial swelling detection with a bright-field microscope. Mitochondrial swelling was induced by microperfusion of freshly isolated, energized (5 mM succinate/2 µM rotenone) mouse liver mitochondria with calcium (200 µM or 2 mM) in the presence of phosphate. (A) Isolated mitochondria before perfusion with calcium. (B) The same field as in A after perfusion for 10 min with the calcium-containing solution (2 mM). White arrows indicate mitoplasts formed after calcium-induced PT activation. (C) Magnified images of the mitochondrion shown in black boxes in A and B. Note the transition of normal (0) into swollen (1 min) mitochondrion and into mitoplast (3 min). Also note the initial outer membrane rupture (first evident at 3 min), eventually resulting in a swollen mitoplast with the pieces of the outer membrane appearing as a dark spot (5 and 9 min). Rates of volume change were calculated for the mitoplast stage of swelling. Scale bars = 4 µm for A and B, 1 µm for C.
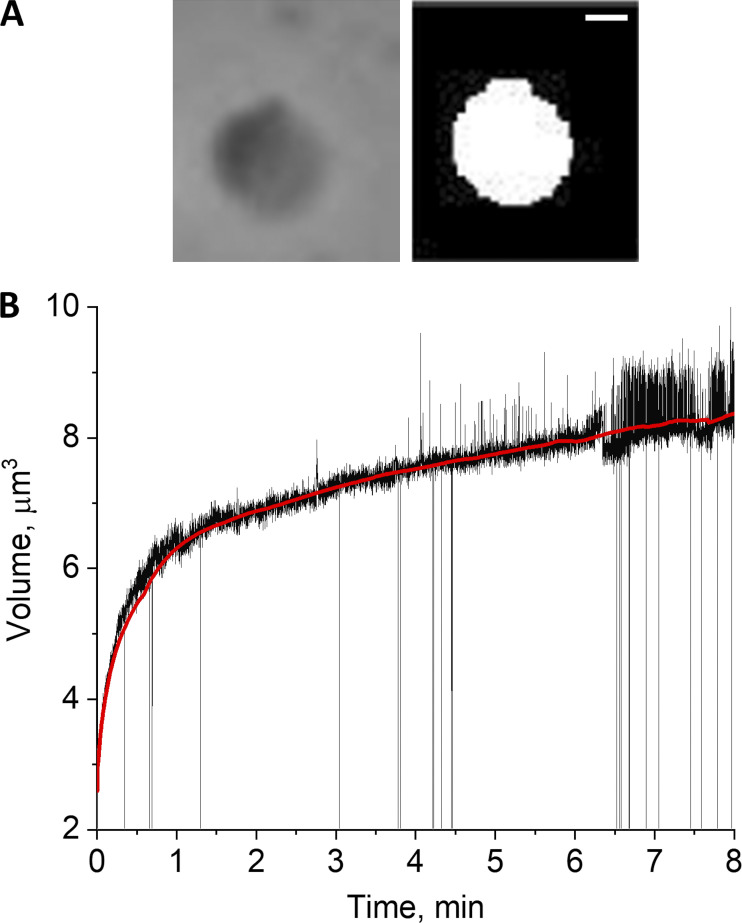
The swelling was observed continuously with a light microscope and video was recorded (Fig. 3). The use of a 40×/0.95 NA objective allowed us to determine the edge of the mitoplast with a resolution of 0.29 µm and to remain in focus over the course of swelling due to the depth of field of 1 µm. Notably, using this approach, we quantified only the size change of the mitoplasts but not mitochondria. As illustrated in Fig. 3, before outer membrane rupture, swelling causes a change in light scattering but not in the size of the mitochondrion. Because we cannot determine the exact moment of the outer membrane rupture, we used the latest periods of mitoplast swelling when calculating water fluxes. To measure the changes in the size of the mitoplast, video recordings were processed with ImageJ and an in-house MATLAB algorithm (Fig. 4). This program allowed us to track the rate of change in mitoplast radii throughout the experiment. Mitoplast volume was calculated with the formula for sphere volume
where r is measured mitoplast radius in each moment of observation (Fig. 4). Integrated water flux through a single mitoplast membrane was calculated as
where V is the volume of mitoplast and t is time. To determine Jint, we used linear fit where the slope of the fitting line reflects the value (Fig. 5 B, black arrow).
Figure 4.
Data acquisition and processing and detection of the rates of mitoplast volume change. (A) Original (left) and software-processed (right) images of the mitoplast that was used for swelling rate analysis. Scale bar = 1 µm. (B) Plot generated by calculation of mitoplast volume from the measured radius of software-processed image, assuming spherical geometry of the mitoplast. Data are presented as mitoplast volume as a function of swelling time. Red line represents trend of volume changes.
Figure 5.
Estimation of the oncotic pressure inside the mitoplast and normalized water flux through a single mitochondrion inner membrane. (A) Swelling is caused by water influx after PT induction. The addition of PEG following maximal swelling causes shrinkage of the mitoplast until the oncotic pressures inside and outside the mitoplast are equilibrated (plateau region at the end of the experiment in B). (B) The value of pressure created by PEG was considered equal to the value of oncotic pressure inside the mitoplast of the equilibrium volume during the swelling phase (black arrow). The calculation of water flux driven by this pressure during swelling was done for this specific volume. Slope of linear fitting reflects the rate of water flux inside the matrix (dashed blue line under the arrow). Red arrow points to the initial moment of PEG addition when the rate of shrinkage was calculated. (C) Water flux was recalculated for swelling in 2 mM Ca2+ (n = 14) and 200 µM Ca2+ (n = 15) per 1 mOsm of driving pressure and presented as normalized water flux. Mean ± SEM. *, P < 0.05.
Using this approach, we calculated that the average rate of the water flux across the mitochondrial membrane of a single mitochondrion was = (2.5 ± 0.4) × 10−17 kg/s for swelling in 2 mM Ca2+ (n = 14) and = (1.1 ± 0.2) × 10−17 kg/s for swelling in 200 µM Ca2+ (n = 15). Notably, water flux through the membrane is directly proportional not only to the membrane permeability but also to the driving force of the oncotic pressure. Thus, to obtain the absolute values of the flux, we measured the value of the oncotic pressure. To do this, we used PEG 8000. PT allows free passage of molecules of <1.5 kD. PEG 8000, with an average molecular weight of 8 kD, cannot enter the matrix, creating an external oncotic pressure, which results in shrinkage of swollen mitoplasts (Fig. 5 A). As a consequence of the shrinkage, the oncotic pressure inside the mitoplast increases. At the point when the external and internal pressures are equal, mitoplast shrinkage stops and allows us to estimate the oncotic pressure inside the mitoplast (Fig. 5 B). We found that a 1% concentration of PEG 8000 in the solution produces shrinkage of mitoplasts to ∼70% of the maximal swollen volume. At this point, the oncotic pressure created by PEG 8000 is equilibrated by the oncotic pressure inside the mitoplast. This concentration of PEG 8000 corresponds to the oncotic pressure of 10 mOsm. The rates of water flux through the mitoplast were calculated at this specific 70% point from the rates of volume change (Fig. 5 B, black arrow) at which estimated oncotic pressure inside the mitoplast during the swelling stage was considered to be 10 mOsm.
Jint values, when normalized to the driving force created by oncotic pressure (recalculation for 1 mOsm oncotic pressure), translated to = (2.5 ± 0.4) × 10−18 kg/s for swelling in 2 mM Ca2+ (n = 14) and = (1.1 ± 0.2) × 10−18 kg/s for swelling in 200 µM Ca2+ (n = 15; Fig. 5 C). The significant difference between water influx during PT activated by different calcium concentrations (P < 0.05) is likely due to the sensitivity of the PT toward increased calcium concentrations.
Calculation of water flux rates based on shrinkage and estimation of the contribution of non-PT water permeability
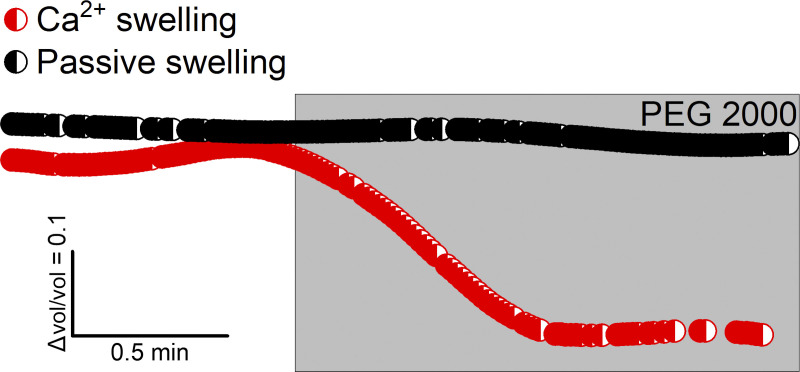
The approach of calculation of water flux from the rates of mitoplast swelling does not allow us to evaluate contribution of the water flux across the mitochondrial membrane that is not associated with the PT. Indeed, it has been demonstrated before that the inner membrane of the intact mitochondria is water permeable (Tedeschi and Harris, 1955; for details, see review by Bernardi [1999]), presumably due to the presence of the aquaporin channels (Calamita et al., 2005), although this view has been challenged (Yang et al., 2006). To evaluate the contribution of the water fluxes through an intact inner membrane, we measured water flux in the individual mitoplasts under conditions of the classic light-scattering assay of mitochondrial shrinkage performed by Haworth and Hunter (1979). In these experiments, PT is measured from the rates of mitochondrial shrinkage induced when oncotic pressure is created outside the mitoplast by the addition of the impermeable molecules. Specifically, we subjected isolated mitochondria to the external pressure of PEG 2000 after passive swelling in isotonic KCl solution without substrates and after swelling in the presence of 2 mM Ca2+. Passive swelling does not induce PT and thus allows us to estimate water efflux through the intact inner membrane when the mitochondrion shrinks. Perfusion of passively swollen mitochondria with the recording solution containing 1% of PEG 2000 led to a very small decrease in mitoplast volume (10 min of perfusion caused only a slight decrease in volume), whereas mitochondria with calcium-induced PT shrank much faster and to a larger degree. As can be seen in Fig. 6, the decrease in the volume of passively swollen mitoplasts after 2 min was negligibly small when compared with the volume loss in mitoplasts after PT-associated swelling. This result indicates that calcium-induced PT dramatically increases the passage of water molecules through the inner mitochondrial membrane. Importantly, our data are in good agreement with the work of Haworth and Hunter, who reported that significant shrinkage of the mitochondria occurs only when PT is activated and is not detected when the mitochondrial membrane is intact (Haworth and Hunter, 1979). This suggests that, although under normal conditions permeability of the inner membrane to water can significantly contribute to the changes in mitochondrial volume, this permeability is much lower than the permeability of the membrane during PT. Because our experimental measurements were made at the latest stages of mitoplast swelling, the contribution of this “non-PT” water influx is negligible (Fig. 6).
Figure 6.
Estimation of water flux through inner mitochondrial membrane in normal conditions. Relative changes of volume of passively swollen mitoplasts (that reflects permeability of intact inner membrane) and mitoplasts after calcium-induced PT activation under the external oncotic pressure of 1% PEG 2000. Slow mitoplast shrinkage after passive swelling when compared with PT swollen mitoplasts indicate that PT dramatically increases permeability of inner membrane to water. Thus, at the latest stage of mitoplast swelling after PT activation, the contribution of water influx through the intact part of the inner membrane is negligible.
Next, we verified our estimation of the inner mitochondrial membrane permeability by calculation of water efflux during mitoplast shrinkage. The advantage of this approach is that, at the initial moment following PEG addition to the swollen mitoplasts, the oncotic pressure that drives water flux is equal to the external oncotic pressure of PEG. We perfused mitoplasts with 1% of PEG 2000, which created external pressure of 40 mOsm.
The value of water efflux through the membrane of a single whole mitoplast during shrinkage calculated from the slope of linear fit (Fig. 5 B, red arrow) was = (5.2 ± 0.7) × 10−17 kg/s. The value when normalized to the driving force created by oncotic pressure (recalculation for 1 mOsm oncotic pressure) translated to = (1.3 ± 0.2) × 10−18 kg/s for swelling in 2 mM Ca2+ (n = 12).
Calculation of the ionic flux across PT membrane and of the number of PTPs
Calculation of water fluxes gave us a quantitative measure of the membrane permeability during PT. However, in most biological applications, the most relevant parameter that characterizes membrane transport is expressed in units of electric current generated by the ion flux across the membrane. To calculate PT in units of ionic current, we took advantage of the fact that PT occurs through the opening of the nonselective channel PTP with conductance of up to 1.5 nS. Here, we first estimated the size of the single PTP channel and the water flux that it could produce. Knowing these parameters, we have been able to calculate two important values: the ionic conductance of the membrane during PT and the density of the PTP channels per mitochondrion.
First, we measured the conductance of the single PTP in the mitoplasts under our experimental conditions (Fig. 7). Specifically, we tested the electrophysiological properties of the inner mitochondrial membrane. An excised configuration of patch clamp was performed immediately after calcium-induced swelling (Fig. 7, A–C). A total of 28 membranes were tested for both conditions; 10 of them demonstrated channel activity after calcium treatment in which conductance was decreased upon addition of the cyclosporine A–PTP inhibitor (Fig. 7 D). The partial block by cyclosporine A is consistent with previous reports of the effects of these compounds on the PTP channel activity in both native and reconstituted systems (Brustovetsky et al., 2002; Kinnally et al., 1992; Neginskaya et al., 2019; Szabó and Zoratti, 1991). We detected channels with transition sizes of 530 ± 20 pS (n = 5 of 10 detected channels) and 910 ± 70 pS (n = 2 of 10), which presumably represent the substates of a multiconductance PTP channel. The maximal transition size detected was 1,500 ± 100 pS (n = 3 of 10), which corresponds to a fully open PTP channel in high-conductance mode.
Figure 7.
Electrophysiological characterization of the PT. (A and B) Perfusion tube (right) used for microperfusion and patch pipette (left) used for current measurements. B is the zoomed-in version of A. Scale bars = 20 µm for A, 8 µm for B. (C) Schematics of the patch-clamp experiment in excised mode. (D) Patch-clamp recording of the PTP. Note the substates of the detected multiconductance PTP channel. Addition of cyclosporine A (CsA) caused partial closure of the channel. The detection frequency of channel activity is 36% (n = 28). Mitoplasts were formed by the calcium-induced swelling of the energized mitochondria.
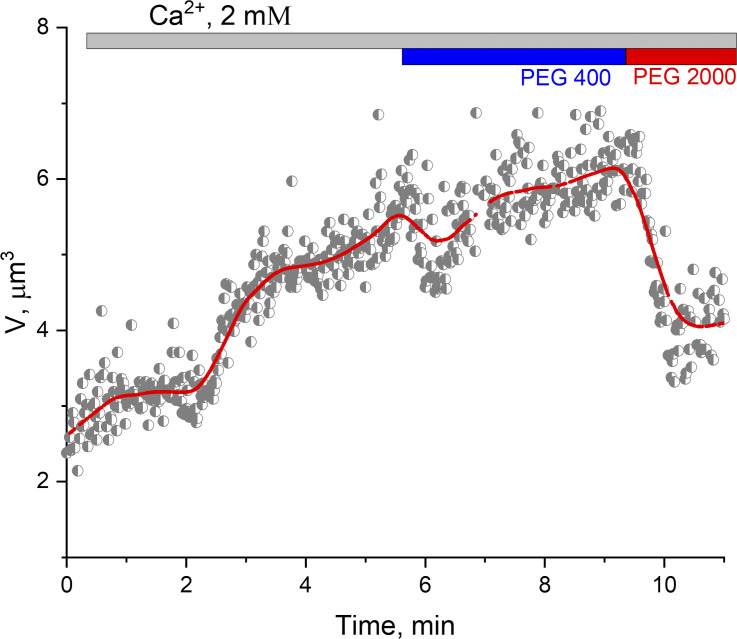
Taking into account that PTP can also function in the low-conductance mode (Ichas et al., 1997; Ichas and Mazat, 1998), we performed sizing experiments to test the likely PTP mode (low-conductance PTP or high-conductance PTP). We estimated pore size by performing shrinkage experiments with 400 D and 2,000 D PEG molecules. Specifically, we perfused isolated mitochondria swollen in the presence of calcium with PEGs with molecular weights of 400 and 2,000 D (Fig. 8). PEG 400 did not cause shrinkage of the mitoplasts, whereas perfusion with PEG 2000 led to the shrinkage, indicating that PTP was permeable for PEG 400 but not for PEG 2000. Overall, PEG experiments suggest that in our estimates of the PTP size, we can assume that it was primarily present in its high-conductance conformation.
Figure 8.
The effect of PEGs with different molecular weights on the shrinkage of PT-induced mitoplasts. Mitochondrial swelling was induced by microperfusion with 2 mM Ca2+. Shrinkage was performed as described in Fig. 5. PEG 400 did not lead to mitoplast shrinkage, indicating permeability of the inner mitochondrial membrane to the molecules of 400 D molecular weight after PT activation with calcium. PEG 2000 (2,000 D) led to mitoplast shrinkage. The experiment confirmed the presence of the classical PTP channel with molecular cutoff ∼1.5 kD. V, volume.
These results confirmed that Ca2+-induced PT in our experimental design could be explained by the opening of the classic PTP that was in its high-conductance mode (∼1.5 nS) in all mitoplasts and presumably had a size that allows transport of molecules up to 1.5 kD. The weakly selective pore with the conductance of 1.5 nS in 150 mM KCl solution is expected to have the diameter of ∼2 nm (Massari and Azzone, 1972; Pavlov et al., 2001). Taking this into account, we performed further calculations assuming that PTP can be modeled as a cylinder with 2-nm diameter and 4-nm length.
The number of pores per single mitochondrion was calculated as the ratio of the rates of water flux through the whole mitoplast and water flux through a single PTP with a diameter of 2 nm:
where Jint is calculated empirically from as was described above, while and k is the parameter defined by the geometry of the pore (Borg et al., 2018). is proportional to ΔP that is equal to the oncotic pressure.
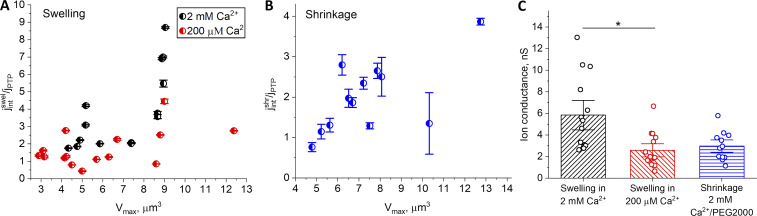
Simulation of water flux through the nanoscale tube with parameters of the modeled pore (Borg et al., 2018) demonstrated that predicted water flux through the single pore is J = 5 × 10−14 kg/s at 200 mPa pressure. Taking into account a linear relationship between pressure and water flux through the pore and the results of single-channel simulations (Borg et al., 2018), we can calculate that under our experimental conditions, per 1 mOsm of driving pressure, the rate of water flux through a single PTP equals 0.65 × 10−18 kg/s. By dividing the normalized water flux rate through the mitoplast by the value of the flux through a single pore, we obtained the total number of PTPs per mitoplast (Fig. 9, A and B). The results of these calculations are presented in Fig. 9, which summarizes the results of measurements from six independent experiments: three for each calcium concentration for the swelling assay and two independent experiments for the shrinking assay. Each data point represents an individual mitoplast. According to these measurements and calculations, the number of PTP channels per single mitochondrion range from one to a maximum of nine for the 2 mM Ca2+ swelling calculations (Fig. 9 A).
Figure 9.
The number of PTP channels and ionic conductance per single mitochondrion. (A and B) Each data point in A and B represents the ratio of the water flux through the whole mitoplast and water flux through the single pore with a diameter of 2 nm. This ratio reflects the estimation of the number of pores in the individual mitochondrion after PT activation with calcium. (A) Calculations based on the rate of mitochondrial swelling. Data points were collected from six individual experiments. (B) Calculations based on the rate of mitochondrial shrinkage. Data points were collected from two individual experiments. (C) Overall ionic conductance of the single mitochondrion during calcium-induced PT. Mean ± SEM. *, P < 0.05; n = 14 for swelling in 2 mM Ca2+; n = 15 for swelling in 200 µM Ca2+; n = 12 for shrinkage in 2 mM Ca2+/PEG 2000. Vmax, maximum volume.
In summary, we can conclude that the average ionic conductance of the mitochondrial membrane ranges from 2.6 to 13.1 nS (with an average of 5.9 ± 0.9 nS; n = 14) for 2 mM Ca2+ and from 0.7 to 6.7 nS (with an average of 2.6 ± 0.4 nS; n = 15) for 200 µM Ca2+ when based on swelling rate calculations (Fig. 9 C).
Ionic conductance calculated from the shrinking assay ranges from 1.1 to 5.9 nS (average is 3.0 ± 0.4 nS; n = 12; Fig. 9 C). The estimated number of PTP channels that activated during PT was in a range from one to four.
Relationship between PTP count and geometry and surface charge of the model pore
In our calculations, we used the model that was based on two approximations: we considered that the pore size has a 2-nm diameter and that the surface area of the pore is not charged. However, taking into account that the exact structure of the PTP channel is not known, we have to consider how uncertainty in these parameters might affect our estimates.
Due to the lack of knowledge about the structure of PTP, there is no precise estimation of its diameter. The predicted diameter of the pore available in the literature varies from 2 to 4 nm in different reports (Bernardi, 1999; Carroll et al., 2019; Massari and Azzone, 1972; Szabó and Zoratti, 1992). The lowest estimation of pore diameter based on adenine nucleotide translocator (ANT) structure is 2.1 nm (Bround et al., 2020). We based our calculations on the lowest reported pore diameter, which gives us the maximal number of pores per mitochondrion, but it should be acknowledged that, based on the pore size, the actual count could be lower.
The second critical assumption of our approach is that the rates of the water flux through the pore are estimated for the flow with no interactions with the pore wall (e.g., in a pristine carbon nanotube). The structure of PTP is not defined, but according to its weak ion selectivity, we can assume that the walls of the PTP would be polar (Hilder et al., 2010, 2011a, 2011b). Thus, in our estimates, we should take into account that water flux might be considerably slower than in an uncharged pore. Based on the literature data, the surface charge of the walls (“polar carbon nanotubes”) of the 7-nm-diameter pore would decrease the flow through the pore (Majumder and Corry, 2011) by up to 30%. Considering the pore size of 2 nm and the distribution of velocity along the tube cross-section (Majumder and Corry, 2011), we can roughly estimate that the surface charge of the polar pore will give us a 50% decrease in water flow, and thus increase the calculated upper limit of pores to 14.
Overall, we can conclude that variety in pore parameters might affect the estimate of the number of pores and needs to be taken into account. The variability of the pore size might give some overestimate of the number of PTPs, whereas variability of the pore surface charge might underestimate the number of PTPs. In either case, these considerations still support the key conclusion that the number of PTPs in a single mitochondrion is very low.
The relative accuracy of our pore parameters is also evident by comparison with the experimental data of water flux through the bacterial channel α-hemolysin. The bacterial channel α-hemolysin has the single-channel conductance of 1.0–1.3 nS, matching that measured in the high-conductance mode of PTP. This bacterial channel’s pore is cylindrical, and its water permeability has been measured (Paula et al., 1999). The normalized water flux through the bacterial channel α-hemolysin is ∼1.5 × 10−18 kg/s, which is of the same order of magnitude as used in our calculations.
Discussion
In this study, for the first time, we quantitatively measured the PT at the level of a single mitochondrion. To do this, we calculated the water fluxes through the inner mitochondrial membrane during calcium-induced swelling after PT induction. We found that overall conductance of a single mitochondrion during calcium-induced PT varies as a function of the external calcium concentration. It is 5.9 ± 0.9 nS for 2 mM of Ca2+ and 2.6 ± 0.4 nS for 200 µM of Ca2+. Similar values were obtained by calculations based on the flux of water out of the mitochondrial matrix during shrinkage after the external oncotic pressure was increased. The slight discrepancy between two methods was perhaps caused by differences in the estimation of the oncotic pressure. Taking into account that the size of a single PTP is ∼2 nm (corresponding to a ∼1.5-nS ion-conducting pore), we calculated that the number of pores during PT did not exceed nine.
Although direct calculations presented in this study have never been done, our data are consistent with previous observations at the level of the single organelle. Indeed, previous studies using patch clamping of the mitoplasts that involve excised patch configuration demonstrated that, in most cases, only a single-channel PTP (or no PTP) is detected (Kinnally et al., 1989, 1991, 1992; Szabó et al., 1992; Szabó and Zoratti, 1991). Taking into account that the excised patch contains a relatively large fragment of the mitochondrial inner membrane, this suggests that the density of PTP channels should be relatively low. This was consistent with patch-clamp experiments presented in the present study when only ∼36% of patches had channel activity. Interestingly, the original recordings of the whole-mitoplast currents by Sorgato and colleagues in 1987 were performed in the presence of 200 µM Ca2+ in the recording solution (Sorgato et al., 1987). Although highly speculative at this point, it is tantalizing to propose that they might have recorded the integral current reflecting PTP activity. The current values seen in these experiments are consistent with very few pores, but further experiments will be needed to confirm this interpretation. Further, very recent imaging data measuring single mitochondrial swelling under conditions similar to those presented in this work demonstrated that swelling occurs in a steplike manner, suggesting that it is induced by the activation of a relatively small number of pores (Morikawa et al., 2014; Shibata et al., 2019). Interestingly, this study reported that despite the fact that all mitochondria undergo depolarization indicating PT activation, not all of them swell, suggesting an intriguing possibility that the high-conductance mode of PTP is not activated in every mitochondrion. This means that the number of high-conductance PTPs can actually be zero in some specific organelles.
An unusually low probability of the PTP activation can have important implications in our understating of the possible molecular mechanisms of this channel’s activation. Current models of PTP suggest that it is formed by the calcium-induced transition of either ANT or ATP synthase into the large ion-conducting pore. It is estimated that the amount of ANT and ATPase in mitochondria is 100 to 200 pmol/mg of ANT and ATPase proteins, which translates to ∼15,000 copies of each protein per mitochondrion (Lauquin and Vignais, 1976; Roux et al., 1996; Schwerzmann et al., 1986; Zoratti et al., 2005). Current models assume that PTP is activated by calcium binding to the (unknown) binding site that causes channel opening. If this were the case, one would expect a much higher number of PTP channels than detected in the experiment. Indeed, we did not find a dramatic increase in membrane conductance with the rise of calcium concentration, which suggests that PT activation unlikely involves simple calcium biding to the putative calcium-binding site. These results are consistent with previous reports which indicate that PT activation depends not on the mitochondrial free calcium but rather on total calcium load (Chalmers and Nicholls, 2003). In our experiments, both concentrations of free calcium would provide sufficient total calcium load to induce PT, but the overall outcome will not strongly depend on the free calcium. Furthermore, it was reported that the PTP channel can be detected in the mitochondrial membranes isolated in the absence of EGTA (conditions favoring PT) without the requirement of having calcium in the recording solution (Kinnally et al., 1991).
This suggests that the mechanism of PTP activation and/or its molecular organization is very different from the currently envisioned simple calcium-binding mechanism. Within currently existing models, we can see several possibilities, which we describe next.
One of the current models of the PTP posits that its activation involves two conformational changes within ATP synthase: dissociation of the F1 subunit from FO subunit and activation of the “c-ring” channel (PTP; Alavian et al., 2014; Mnatsakanyan et al., 2019). We hypothesize that under this scenario, most of the c-rings of the subunit FO are expected to be in nonconducting states, probably due to the presence of lipids inside the c-ring, whereas the small subpopulation of these c-rings can be transformed into large pores.
Another model suggests that PTP is formed with the direct participation of the dimers of ATP synthase (Carraro et al., 2014; Giorgio et al., 2013; Urbani et al., 2019). This work demonstrated that highly purified dimers form channels with properties resembling PTP. However, it shows that only a small fraction of purified dimers are actual calcium-activated channels when reconstituted into the planar lipid bilayers. This suggests that not every native enzyme can be converted into the PTP. It is tantalizing to hypothesize that in order to form PTP, ATP synthase dimer needs to be in the specific conformational state. One of the possibilities involves the participation of dimers containing misfolded proteins (He and Lemasters, 2002). Similar mechanisms might take place in PT found in cells lacking components of the ATP synthase, which would likely involve not all but only a subpopulation of misfolded species of the ANT (He et al., 2017a, 2017b; Karch et al., 2019; Neginskaya et al., 2019). According to this model, we can anticipate that high levels of ROS increase the number of misfolded proteins, including ATP synthases and ANT, which would increase the probability of forming PTPs. In this scenario, even low calcium loads could lead to the activation of PTP. It will be interesting to probe the rates of swelling in the presence of increased ROS in order to investigate potential differences between calcium- and ROS-induced PT.
Notably, it has been reported recently that the c-subunit of the ATP synthase is an amyloidogenic peptide, which, similarly to other amyloids, is capable of forming fibrils and oligomers (Amodeo et al., 2020). When reconstituted into the lipid bilayer, c-subunit β-sheet oligomers can form large ion pores. It is intriguing to propose that these toxic forms of the c-subunit might play a critical role in PTP formation.
In summary, we report that during calcium-activated PT, the membrane conductance in the whole mitoplast varies with calcium concentration and can be estimated at the levels of 5.9 ± 0.9 nS for 2 mM Ca2+ and 2.6 ± 0.4 nS for 200 µM Ca2+, with the total number of pores estimated to be in the range from 1 to 10 per single mitochondrion. This number is unusually low, taking into account the large number of copies of putative PTP-forming proteins present in each organelle.
Acknowledgments
Eduardo Ríos served as editor.
We thank Prof. Sergey Noskov (University of Calgary, Calgary, Alberta, Canada) for fruitful discussion regarding model parameters and Prof. Paolo Bernardi (University of Padua, Padua, Italy) for critical comments regarding control experiments.
This work was supported by grants from the National Institutes of Health (GM115570) and the American Heart Association (18TPA34230060) to E.V. Pavlov.
The authors declare no competing financial interests.
Author contributions: M.A. Neginskaya and E.V. Pavlov designed and performed experiments with isolated mitochondria; M.A. Neginskaya, E.V. Pavlov, and J.N. Bazil analyzed and interpreted data; M.A. Neginskaya and E.V. Pavlov wrote the initial draft of the manuscript; J.O. Strubbe, B.A. West, J.N. Bazil, and G.F. Amodeo wrote the software; S. Yakar prepared animals for mitochondria isolation; and J.N. Bazil and E.V. Pavlov supervised the research. All authors wrote and edited the manuscript.
References
- Alavian K.N., Beutner G., Lazrove E., Sacchetti S., Park H.A., Licznerski P., Li H., Nabili P., Hockensmith K., Graham M., et al. . 2014. An uncoupling channel within the c-subunit ring of the F1FO ATP synthase is the mitochondrial permeability transition pore. Proc. Natl. Acad. Sci. USA. 111:10580–10585. 10.1073/pnas.1401591111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amodeo G.F., Lee B.Y., Krilyuk N., Filice C.T., Valyuk D., Otzen D., Noskov S., Leonenko Z., and Pavlov E.V.. 2020. C subunit of the ATP synthase is an amyloidogenic channel-forming peptide: possible implications in mitochondrial pathogenesis. bioRxiv. 2020.01.16.908335 10.1101/2020.01.16.908335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baev A.Y., Elustondo P.A., Negoda A., and Pavlov E.V.. 2018. Osmotic regulation of the mitochondrial permeability transition pore investigated by light scattering, fluorescence and electron microscopy techniques. Anal. Biochem. 552:38–44. 10.1016/j.ab.2017.07.006 [DOI] [PubMed] [Google Scholar]
- Berezhnaya E., Neginskaya M., Uzdensky A.B., and Abramov A.Y.. 2018. Photo-induced oxidative stress impairs mitochondrial metabolism in neurons and astrocytes. Mol. Neurobiol. 55:90–95. 10.1007/s12035-017-0720-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernardi P. 1999. Mitochondrial transport of cations: channels, exchangers, and permeability transition. Physiol. Rev. 79:1127–1155. 10.1152/physrev.1999.79.4.1127 [DOI] [PubMed] [Google Scholar]
- Bernardi P., Rasola A., Forte M., and Lippe G.. 2015. The mitochondrial permeability transition pore: channel formation by F-ATP synthase, integration in signal transduction, and role in pathophysiology. Physiol. Rev. 95:1111–1155. 10.1152/physrev.00001.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borg M.K., Lockerby D.A., Ritos K., and Reese J.M.. 2018. Multiscale simulation of water flow through laboratory-scale nanotube membranes. J. Membr. Sci. 567:115–126. 10.1016/j.memsci.2018.08.049 [DOI] [Google Scholar]
- Bround M.J., Bers D.M., and Molkentin J.D.. 2020. A 20/20 view of ANT function in mitochondrial biology and necrotic cell death. J. Mol. Cell. Cardiol. S0022-2828(20)30194-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brustovetsky N., Tropschug M., Heimpel S., Heidkämper D., and Klingenberg M.. 2002. A large Ca2+-dependent channel formed by recombinant ADP/ATP carrier from Neurospora crassa resembles the mitochondrial permeability transition pore. Biochemistry. 41:11804–11811. 10.1021/bi0200110 [DOI] [PubMed] [Google Scholar]
- Calamita G., Ferri D., Gena P., Liquori G.E., Cavalier A., Thomas D., and Svelto M.. 2005. The inner mitochondrial membrane has aquaporin-8 water channels and is highly permeable to water. J. Biol. Chem. 280:17149–17153. 10.1074/jbc.C400595200 [DOI] [PubMed] [Google Scholar]
- Carraro M., and Bernardi P.. 2020. Measurement of membrane permeability and the mitochondrial permeability transition. Methods Cell Biol. 155:369–379. 10.1016/bs.mcb.2019.10.004 [DOI] [PubMed] [Google Scholar]
- Carraro M., Giorgio V., Šileikytė J., Sartori G., Forte M., Lippe G., Zoratti M., Szabò I., and Bernardi P.. 2014. Channel formation by yeast F-ATP synthase and the role of dimerization in the mitochondrial permeability transition. J. Biol. Chem. 289:15980–15985. 10.1074/jbc.C114.559633 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll J., He J., Ding S., Fearnley I.M., and Walker J.E.. 2019. Persistence of the permeability transition pore in human mitochondria devoid of an assembled ATP synthase. Proc. Natl. Acad. Sci. USA. 116:12816–12821. 10.1073/pnas.1904005116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chalmers S., and Nicholls D.G.. 2003. The relationship between free and total calcium concentrations in the matrix of liver and brain mitochondria. J. Biol. Chem. 278:19062–19070. 10.1074/jbc.M212661200 [DOI] [PubMed] [Google Scholar]
- Elustondo P.A., Negoda A., Kane C.L., Kane D.A., and Pavlov E.V.. 2015. Spermine selectively inhibits high-conductance, but not low-conductance calcium-induced permeability transition pore. Biochim. Biophys. Acta. 1847:231–240. 10.1016/j.bbabio.2014.10.007 [DOI] [PubMed] [Google Scholar]
- Giorgio V., von Stockum S., Antoniel M., Fabbro A., Fogolari F., Forte M., Glick G.D., Petronilli V., Zoratti M., Szabó I., et al. . 2013. Dimers of mitochondrial ATP synthase form the permeability transition pore. Proc. Natl. Acad. Sci. USA. 110:5887–5892. 10.1073/pnas.1217823110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halestrap A.P., and Richardson A.P.. 2015. The mitochondrial permeability transition: a current perspective on its identity and role in ischaemia/reperfusion injury. J. Mol. Cell. Cardiol. 78:129–141. 10.1016/j.yjmcc.2014.08.018 [DOI] [PubMed] [Google Scholar]
- Haworth R.A., and Hunter D.R.. 1979. The Ca2+-induced membrane transition in mitochondria. II. Nature of the Ca2+ trigger site. Arch. Biochem. Biophys. 195:460–467. 10.1016/0003-9861(79)90372-2 [DOI] [PubMed] [Google Scholar]
- He L., and Lemasters J.J.. 2002. Regulated and unregulated mitochondrial permeability transition pores: a new paradigm of pore structure and function? FEBS Lett. 512:1–7. 10.1016/S0014-5793(01)03314-2 [DOI] [PubMed] [Google Scholar]
- He J., Carroll J., Ding S., Fearnley I.M., and Walker J.E.. 2017a Permeability transition in human mitochondria persists in the absence of peripheral stalk subunits of ATP synthase. Proc. Natl. Acad. Sci. USA. 114:9086–9091. 10.1073/pnas.1711201114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- He J., Ford H.C., Carroll J., Ding S., Fearnley I.M., and Walker J.E.. 2017b Persistence of the mitochondrial permeability transition in the absence of subunit c of human ATP synthase. Proc. Natl. Acad. Sci. USA. 114:3409–3414. 10.1073/pnas.1702357114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hilder T.A., Gordon D., and Chung S.H.. 2010. Synthetic chloride-selective carbon nanotubes examined by using molecular and stochastic dynamics. Biophys. J. 99:1734–1742. 10.1016/j.bpj.2010.06.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hilder T.A., Gordon D., and Chung S.H.. 2011a Computational modeling of transport in synthetic nanotubes. Nanomedicine (Lond.). 7:702–709. 10.1016/j.nano.2011.02.011 [DOI] [PubMed] [Google Scholar]
- Hilder T.A., Gordon D., and Chung S.H.. 2011b Synthetic cation-selective nanotube: permeant cations chaperoned by anions. J. Chem. Phys. 134:045103 10.1063/1.3524310 [DOI] [PubMed] [Google Scholar]
- Hüser J., Rechenmacher C.E., and Blatter L.A.. 1998. Imaging the permeability pore transition in single mitochondria. Biophys. J. 74:2129–2137. 10.1016/S0006-3495(98)77920-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ichas F., and Mazat J.P.. 1998. From calcium signaling to cell death: two conformations for the mitochondrial permeability transition pore. Switching from low- to high-conductance state. Biochim. Biophys. Acta. 1366:33–50. 10.1016/S0005-2728(98)00119-4 [DOI] [PubMed] [Google Scholar]
- Ichas F., Jouaville L.S., and Mazat J.P.. 1997. Mitochondria are excitable organelles capable of generating and conveying electrical and calcium signals. Cell. 89:1145–1153. 10.1016/S0092-8674(00)80301-3 [DOI] [PubMed] [Google Scholar]
- Karch J., Bround M.J., Khalil H., Sargent M.A., Latchman N., Terada N., Peixoto P.M., and Molkentin J.D.. 2019. Inhibition of mitochondrial permeability transition by deletion of the ANT family and CypD. Sci. Adv. 5 eaaw4597 10.1126/sciadv.aaw4597 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinnally K.W., Campo M.L., and Tedeschi H.. 1989. Mitochondrial channel activity studied by patch-clamping mitoplasts. J. Bioenerg. Biomembr. 21:497–506. 10.1007/BF00762521 [DOI] [PubMed] [Google Scholar]
- Kinnally K.W., Zorov D., Antonenko Y., and Perini S.. 1991. Calcium modulation of mitochondrial inner membrane channel activity. Biochem. Biophys. Res. Commun. 176:1183–1188. 10.1016/0006-291X(91)90410-9 [DOI] [PubMed] [Google Scholar]
- Kinnally K.W., Antonenko Y.N., and Zorov D.B.. 1992. Modulation of inner mitochondrial membrane channel activity. J. Bioenerg. Biomembr. 24:99–110. 10.1007/BF00769536 [DOI] [PubMed] [Google Scholar]
- Lauquin G.J., and Vignais P.V.. 1976. Interaction of (3H) bongkrekic acid with the mitochondrial adenine nucleotide translocator. Biochemistry. 15:2316–2322. 10.1021/bi00656a011 [DOI] [PubMed] [Google Scholar]
- Lorimer G.H., and Miller R.J.. 1969. The osmotic behavior of corn mitochondria. Plant Physiol. 44:839–844. 10.1104/pp.44.6.839 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majumder M., and Corry B.. 2011. Anomalous decline of water transport in covalently modified carbon nanotube membranes. Chem. Commun. (Camb.). 47:7683–7685. 10.1039/c1cc11134e [DOI] [PubMed] [Google Scholar]
- Massari S., and Azzone G.F.. 1972. The equivalent pore radius of intact and damaged mitochondria and the mechanism of active shrinkage. Biochim. Biophys. Acta. 283:23–29. 10.1016/0005-2728(72)90094-1 [DOI] [PubMed] [Google Scholar]
- Mnatsakanyan N., Llaguno M.C., Yang Y., Yan Y., Weber J., Sigworth F.J., and Jonas E.A.. 2019. A mitochondrial megachannel resides in monomeric F1FO ATP synthase. Nat. Commun. 10:5823 10.1038/s41467-019-13766-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morikawa D., Kanematsu K., Shibata T., Haseda K., Umeda N., and Ohta Y.. 2014. Detection of swelling of single isolated mitochondrion with optical microscopy. Biomed. Opt. Express. 5:848–857. 10.1364/BOE.5.000848 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neginskaya M.A., Solesio M.E., Berezhnaya E.V., Amodeo G.F., Mnatsakanyan N., Jonas E.A., and Pavlov E.V.. 2019. ATP synthase c-subunit-deficient mitochondria have a small cyclosporine A-sensitive channel, but lack the permeability transition pore. Cell Rep. 26:11–17.e2. 10.1016/j.celrep.2018.12.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paula S., Akeson M., and Deamer D.. 1999. Water transport by the bacterial channel alpha-hemolysin. Biochim. Biophys. Acta. 1418:117–126. 10.1016/S0005-2736(99)00031-0 [DOI] [PubMed] [Google Scholar]
- Pavlov E.V., Priault M., Pietkiewicz D., Cheng E.H., Antonsson B., Manon S., Korsmeyer S.J., Mannella C.A., and Kinnally K.W.. 2001. A novel, high conductance channel of mitochondria linked to apoptosis in mammalian cells and Bax expression in yeast. J. Cell Biol. 155:725–731. 10.1083/jcb.200107057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roux P., Le Saux A., Fiore C., Schwimmer C., Dianoux A.C., Trézéguet V., Vignais P.V., Lauquin G.J., and Brandolin G.. 1996. Fluorometric titration of the mitochondrial ADP/ATP carrier protein in muscle homogenate with atractyloside derivatives. Anal. Biochem. 234:31–37. 10.1006/abio.1996.0046 [DOI] [PubMed] [Google Scholar]
- Schwerzmann K., Cruz-Orive L.M., Eggman R., Sänger A., and Weibel E.R.. 1986. Molecular architecture of the inner membrane of mitochondria from rat liver: a combined biochemical and stereological study. J. Cell Biol. 102:97–103. 10.1083/jcb.102.1.97 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shibata T., Yoneda M., Morikawa D., and Ohta Y.. 2019. Time-lapse imaging of Ca2+-induced swelling and permeability transition: Single mitochondrion study. Arch. Biochem. Biophys. 663:288–296. 10.1016/j.abb.2019.01.016 [DOI] [PubMed] [Google Scholar]
- Sorgato M.C., Keller B.U., and Stühmer W.. 1987. Patch-clamping of the inner mitochondrial membrane reveals a voltage-dependent ion channel. Nature. 330:498–500. 10.1038/330498a0 [DOI] [PubMed] [Google Scholar]
- Szabó I., and Zoratti M.. 1991. The giant channel of the inner mitochondrial membrane is inhibited by cyclosporin A. J. Biol. Chem. 266:3376–3379. [PubMed] [Google Scholar]
- Szabó I., and Zoratti M.. 1992. The mitochondrial megachannel is the permeability transition pore. J. Bioenerg. Biomembr. 24:111–117. 10.1007/BF00769537 [DOI] [PubMed] [Google Scholar]
- Szabó I., Bernardi P., and Zoratti M.. 1992. Modulation of the mitochondrial megachannel by divalent cations and protons. J. Biol. Chem. 267:2940–2946. [PubMed] [Google Scholar]
- Tedeschi H., and Harris D.L.. 1955. The osmotic behavior and permeability to non-electrolytes of mitochondria. Arch. Biochem. Biophys. 58:52–67. 10.1016/0003-9861(55)90092-8 [DOI] [PubMed] [Google Scholar]
- Urbani A., Giorgio V., Carrer A., Franchin C., Arrigoni G., Jiko C., Abe K., Maeda S., Shinzawa-Itoh K., Bogers J.F.M., et al. . 2019. Purified F-ATP synthase forms a Ca2+-dependent high-conductance channel matching the mitochondrial permeability transition pore. Nat. Commun. 10:4341 10.1038/s41467-019-12331-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang B., Zhao D., and Verkman A.S.. 2006. Evidence against functionally significant aquaporin expression in mitochondria. J. Biol. Chem. 281:16202–16206. 10.1074/jbc.M601864200 [DOI] [PubMed] [Google Scholar]
- Zoratti M., and Szabò I.. 1995. The mitochondrial permeability transition. Biochim. Biophys. Acta. 1241:139–176. 10.1016/0304-4157(95)00003-A [DOI] [PubMed] [Google Scholar]
- Zoratti M., Szabò I., and De Marchi U.. 2005. Mitochondrial permeability transitions: how many doors to the house? Biochim. Biophys. Acta. 1706:40–52. 10.1016/j.bbabio.2004.10.006 [DOI] [PubMed] [Google Scholar]