Abstract
Feedback on chest compressions and ventilations during cardiopulmonary resuscitation (CPR) is important to improve survival from out-of-hospital cardiac arrest (OHCA). The thoracic impedance signal acquired by monitor-defibrillators during treatment can be used to provide feedback on ventilations, but chest compression components prevent accurate detection of ventilations. This study introduces the first method for accurate ventilation detection using the impedance while chest compressions are concurrently delivered by a mechanical CPR device. A total of 423 OHCA patients treated with mechanical CPR were included, 761 analysis intervals were selected which in total comprised 5 884 minutes and contained 34 864 ventilations. Ground truth ventilations were determined using the expired CO2 channel. The method uses adaptive signal processing to obtain the impedance ventilation waveform. Then, 14 features were calculated from the ventilation waveform and fed to a random forest (RF) classifier to discriminate false positive detections from actual ventilations. The RF feature importance was used to determine the best feature subset for the classifier. The method was trained and tested using stratified 10-fold cross validation (CV) partitions. The training/test process was repeated 20 times to statistically characterize the results. The best ventilation detector had a median (interdecile range, IDR) F1-score of 96.32 (96.26 – 96.37). When used to provide feedback in 1-min intervals, the median (IDR) error and relative error in ventilation rate were 0.002 (−0.334 – 0.572) min−1 and 0.05 (−3.71 – 9.08)%, respectively. An accurate ventilation detector during mechanical CPR was demonstrated. The algorithm could be introduced in current equipment for feedback on ventilation rate and quality, and it could contribute to improve OHCA survival rates.
Keywords: Cardiopulmonary resucitation (CPR), ventilation, mechanical CPR, thoracic impedance, adaptive filter, random forest
I. Introduction
OUT of hospital cardiac arrest (OHCA) is an important public health problem. The annual incidence of treated OHCA in industrialized countries is between 35 and 60 cases per 100 000 persons, with survival rates below 10 % [1], [2]. High-quality cardiopulmonary resuscitation (CPR) maintains an artificial flow of oxygenated blood by means of chest compressions and ventilations, and is essential to improve OHCA survival [3]. Advanced life support resuscitation guidelines recommend both uninterrupted and high quality chest compressions, and concurrent ventilations with rates of approximately 10 breaths per minute (min−1) after patient intubation [4]. Hyperventilation should be avoided because it increases intrathoracic pressure and may result in degraded hemodynamics [5]. However, hyperventilation during CPR is frequent with ventilation rates far exceeding the recommended values [6]–[8].
Chest compression detection systems are available on portable cardiac monitors. These technologies use accelerometers or changes in thoracic impedance to detect chest compressions [9]. During treatment, CPR feedback devices may help to improve rescuer compliance with treatment guidelines [10], [11]. After treatment, episode debriefing based on these recorded data may allow for retrospective performance assessment and quality improvement programs [12]. However, similar technologies for feedback on ventilation based on the impedance are not currently commercially available. The capnogram is the continuous measure of the partial pressure of expired CO2 in respiratory gases. Capnography is the standard method for detecting ventilations during CPR [13], [14], but this signal is not available until the placement of an advanced airway. Thoracic impedance, which is recorded by most defibrillators to check pad placement and to adjust defibrillation energy, also provides detailed information on CPR activity [15]. Thoracic impedance varies with air volume changes in the lungs, and can therefore be used to identify ventilations. Even when capnography is available, impedance-based detection of ventilations is important, either to improve the accuracy of capnography-based ventilation detection algorithms [13], or to provide indirect evidence of tidal volume and peak positive ventilation pressures that cannot be inferred from the capnogram [16], [17].
Impedance ventilation waveforms are varied in shape, and the impedance signal is very sensitive to motion artifacts [18], [19]. Furthermore, during CPR the impedance presents a chest compression component with a spectrum that may overlap that of the ventilation waveforms [20]. Before intubation, if CPR is delivered in sequences of 30 compressions followed by 2 ventilations (standard 30:2 CPR), ventilations can be reliably identified during compression pauses [16]. After intubation, chest compressions and ventilations are given concurrently. Several ventilation detection algorithms have been proposed for this scenario [13], [20], [21], frequently using the adaptive filtering techniques originally conceived to remove chest compression artifacts from the electrocardiogram [22], [23]. Since manual chest compressions are variable in rate and depth, these adaptive filters often need accelerometer data to model the chest compression artifact [20].
Mechanical chest compression devices ensure high-quality chest compressions and have become popular in OHCA treatment. To date, there is no conclusive evidence of improved survival with mechanical CPR [24], [25], but the use of these devices has become widespread in scenarios like patient transport, invasive procedures, or prolonged resuscitation [26]. Mechanical chest compressions are stable in rate and depth, so there is no need for accelerometer data to model compressions [27], [28]. However, removing the mechanical chest compression component from the impedance is challenging because it has larger amplitudes and more spectral components than those observed during manual CPR [29].
The goal of this study was to determine whether an impedance-based algorithm can accurately detect ventilations during concurrent mechanical chest compressions. For this purpose, we implemented an adaptive filter to obtain the ventilation waveform from the raw impedance signal, designed features to characterize the impedance ventilation waveform, constructed an optimal model to identify true ventilations using a Random Forest (RF) with the best feature subset, and evaluated the performance of the model to detect ventilations and measure ventilation rate. A preliminary version of this work has been reported [30].
II. Materials
The study dataset was part of a large OHCA data repository collected by the Dallas-Fort Worth Center for Resuscitation Research, as part of the Resuscitation Outcomes Consortium [31]. A cohort of 567 patients treated between October 2012 and March 2016 were initially considered, those that contained concurrent impedance and capnography recordings as well as confirmed mechanical CPR according to the OHCA epistry data. Signals were acquired with the MRx monitor-defibrillator (Philips Medical Systems, Andover, MA, USA). The MRx measures impedance by applying a 32 kHz alternating current through the defibrillation pads and measuring the resulting voltage. The impedance signal was digitized with a sampling rate of 200 Hz and an amplitude resolution of 0.74 mΩ per least significant bit. The capnogram was acquired using Microstream (sidestream) technology, and the signal was sampled at 40 Hz with 0.004 mmHg resolution. Finally, mechanical chest compresions were given using the LUCAS-2 chest compression device (Physio-Control Inc / Jolife AB, Lund, Sweden), that delivers piston-driven compressions at a fixed rate of 100 min−1 and predefined depth between 1.5 – 2 inches. All signals from the MRx device were converted to an open format using custom Matlab (MathWorks Inc., Natick, MA) tools.
Signal intervals with confirmed LUCAS-2 use were extracted from the initial 567 patients. Chest compressions were automatically detected in the impedance signal using the algorithm proposed by Ayala et al [32], and LUCAS-2 use was identified when the chest compression rate was fixed at 100 min−1 with small variability (see Fig 1b). The inclusion criteria for the intervals was: minimum duration of 100 s with mechanical CPR, interpretable impedance and capnography signals, and no pauses in chest compressions longer than 20 s. In the dataset there were 8 917 min of confirmed mechanical CPR use with concurrent chest compressions, from which 5 884 min were used. Two were the main reasons to exclude 3 033 min. First, the lack of a proper gold standard to annotate ventilations because capnography was either unavailable (2 642 min) or strongly artefacted and thus uninterpretable (177 min). Second, low quality impedance or disconnections of the impedance channel (391 min). The latter give an estimate of how often impedance was unusable for ventilation detection during mechanical CPR (4.4% of the available minutes). So finally, 761 analysis intervals from 423 patients were included in the study, with a median (interquartile range, IQR) time of mechanical CPR per patient of 13 (8 – 19) minutes, and a median (IQR) duration of the analysis intervals of 5.4 (3.2 – 10.6) minutes. The median (IQR) proportion of time with concurrent compressions per patient was 98.6 (96.9 – 100)% in our data, so most of the time ventilations were provided concurrently with mechanical CPR.
Fig. 1:
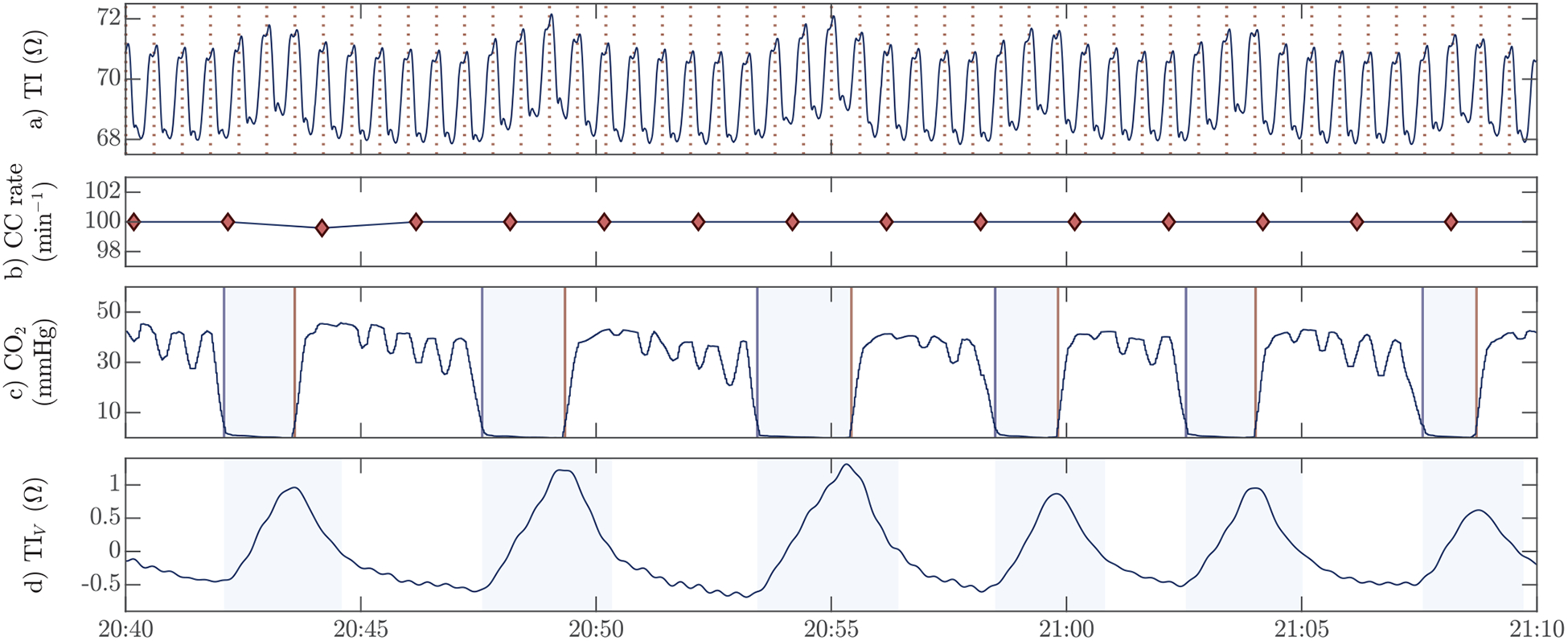
An example of the signals in the study dataset with: (a) the raw thoracic impedance with chest compressions indicated by vertical dashed lines, (b) the compression rate computed every 2 s, (c) the capnogram to annotate the ground truth ventilations, and (d) the ventilation induced changes in the impedance obtained through signal processing from the raw impedance in (a) and used to detect ventilations. The compression rate in (b) was used to confirm the use of the LUCAS-2 device, and the shaded intervals in the capnogram (c) correspond to the true insufflation intervals. The shaded intervals in (d) are those in which a detected ventilation was considered a true positive detection, and correspond to the insufflation intervals extended by one second.
The capnogram was used to annotate ground truth ventilations. First, the delay between the impedance and the capnogram caused by gas transport in the sampling tube (sidestream) was visually assessed and corrected. The delay in the capnogram line was different for each patient, with a median (IQR) value of 3.3 (3.1–3.5) s. Then, for each ventilation the insufflation (downfall) and expiration (uprise) onsets were automatically detected in the capnogram using the algorithm introduced by Aramendi et al [14] (see Fig 1c), and then manually inspected and revised. The revised annotations were considered the ground truth ventilations. The time interval between the onsets of inspiration and expiration marked the window for which ventilation detections in the impedance were considered correct (see Fig 1d). As shown in the figure, the window for correct detections was prolonged by 1-sec after expiration onset to properly count those cases in which the impedance peak occurred shortly after expiration had started. In total, 34 864 true ventilations were annotated in the capnogram, with a median (IQR) of 72 (43 – 108) ventilations per patient.
III. Methods
The ventilation detection method is composed of the three stages shown in Fig 2. First, the raw impedance signal is filtered to obtain the ventilation waveform component. Then, impedance fluctuations are detected and their peak times () identified using a greedy peak detector. The start and end of the fluctuation are calculated and its waveform is characterized by a vector of features xi. The greedy detector is designed to detect all candidate ventilations, with the tradeoff of producing many false positive detections. So the final stage is a machine learning classifier based on the waveform features to discriminate true ventilations (green) from false positives (red).
Fig. 2:
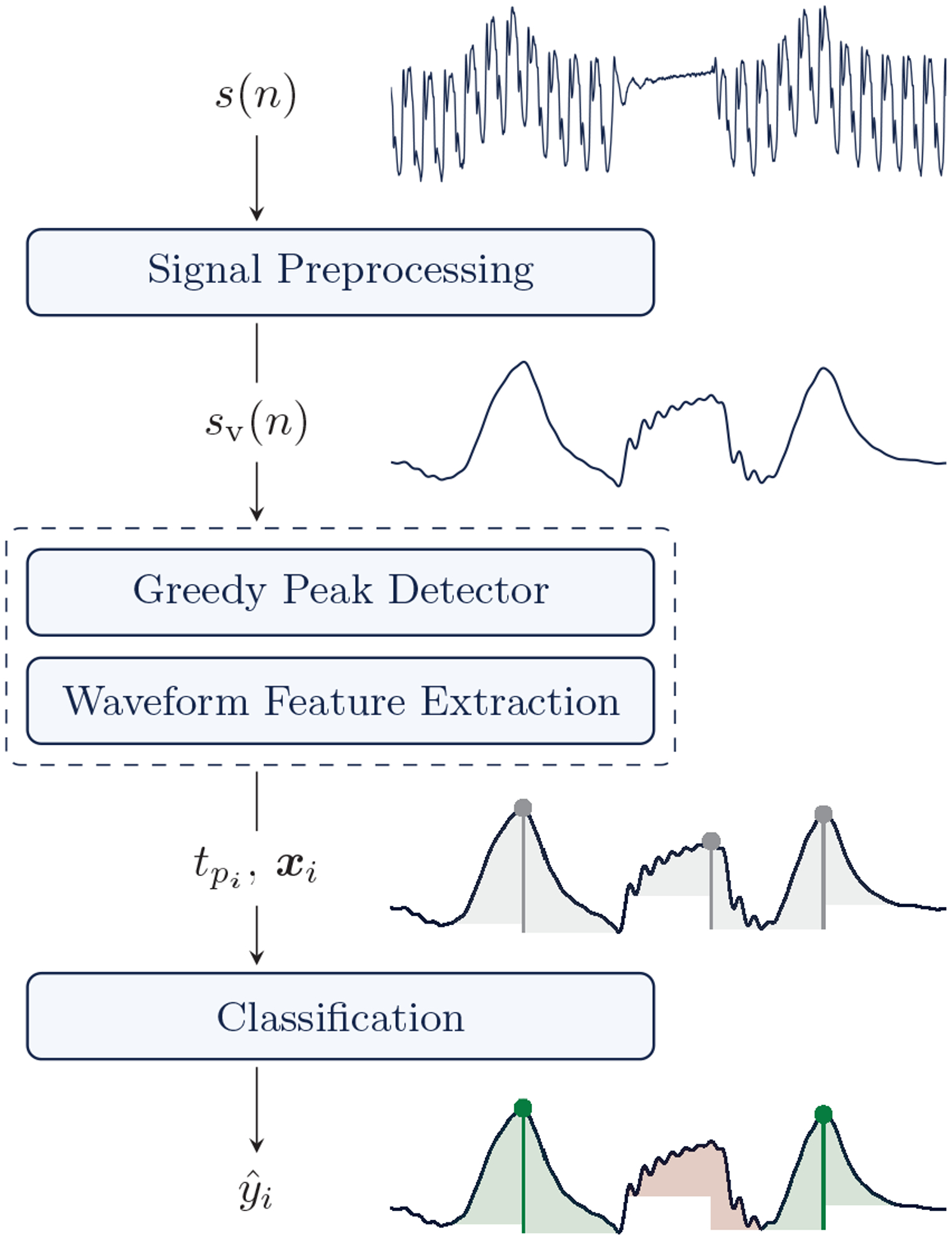
Block diagram of the ventilation detection algorithm. The impedance signal s(n) is filtered to obtain its ventilation component sv(n). Then a greedy peak detector detects the instants of the potential ventilations (), and a waveform feature vector xi is computed. The final classifier discriminates true ventilations (green) from false positive peak detections (red) using the waveform features.
A. Signal preprocessing
The raw impedance signal was first downsampled to fs = 50 Hz to ease the design of the filters and reduce the computational load. In what follows n is the sample index so time is t = n · Ts, where Ts = 20 ms is the sampling period. A high-pass filter with 0.05 Hz cut-off frequency was used to remove the DC component, and a low pass filter with a 2.5 Hz cut-off was used to remove high frequency residuals, including the high frequency components caused by chest compressions. Both filters were designed as 4-tap Butterworth filters, and zero-phase filtering was deployed. Finally, the most critical element was a Least Mean Squares (LMS) filter used to remove chest compression components.
The LMS algorithm was used in the classical configuration to cancel harmonic interferences [33], but adapted to mechanical chest compression components following the model introduced by Isasi et al [28]. The block diagram of the filter is shown in Fig 3, which follows the notation used in this subsection. The assumption is that after high pass and low pass filtering, the impedance signal contains two additive components:
| (1) |
where sv(n) and sc(n) are the ventilation and compression components, respectively. These components are uncorrelated since they represent two independent treatments, compressions by the mechanical device and ventilations by the rescuer. The compression component is modeled as a quasi-periodic signal using a truncated Fourier-series representation with fundamental frequency fc = 1.667 Hz (100 min−1), and time-varying amplitudes ak(n) and bk(n) to adapt to changes in the impedance signal:
| (2) |
where ωc = 2πfc/fs = 0.209 is the discrete angular frequency of the LUCAS-2 chest compressions, and N is the number of harmonics in the model. In matrix notation the chest compression component is sc(n) = x⊤(n)w(n), where:
| (3) |
| (4) |
are the reference signal (harmonics) and coefficient vectors, respectively. The LMS algorithm computes the w(n) coefficients to minimize the mean squared error E{|e(n)|2} between the desired signal d(n) = s(n) and the estimated chest compression component ŝc(n):
| (5) |
so the error signal is then the estimated ventilation component, e(n) = sv(n). The error is minimized using the steepest descent algorithm, and the gradient at time n of the squared error is:
| (6) |
The filter coefficients are updated in the opposite direction, following:
| (7) |
where the step-size parameter μ determines the adaptation speed and tracking capabilities of the filter. The values for the LMS filter were set to μ = 0.15 and N = 3 after some preliminary tests.
Fig. 3:
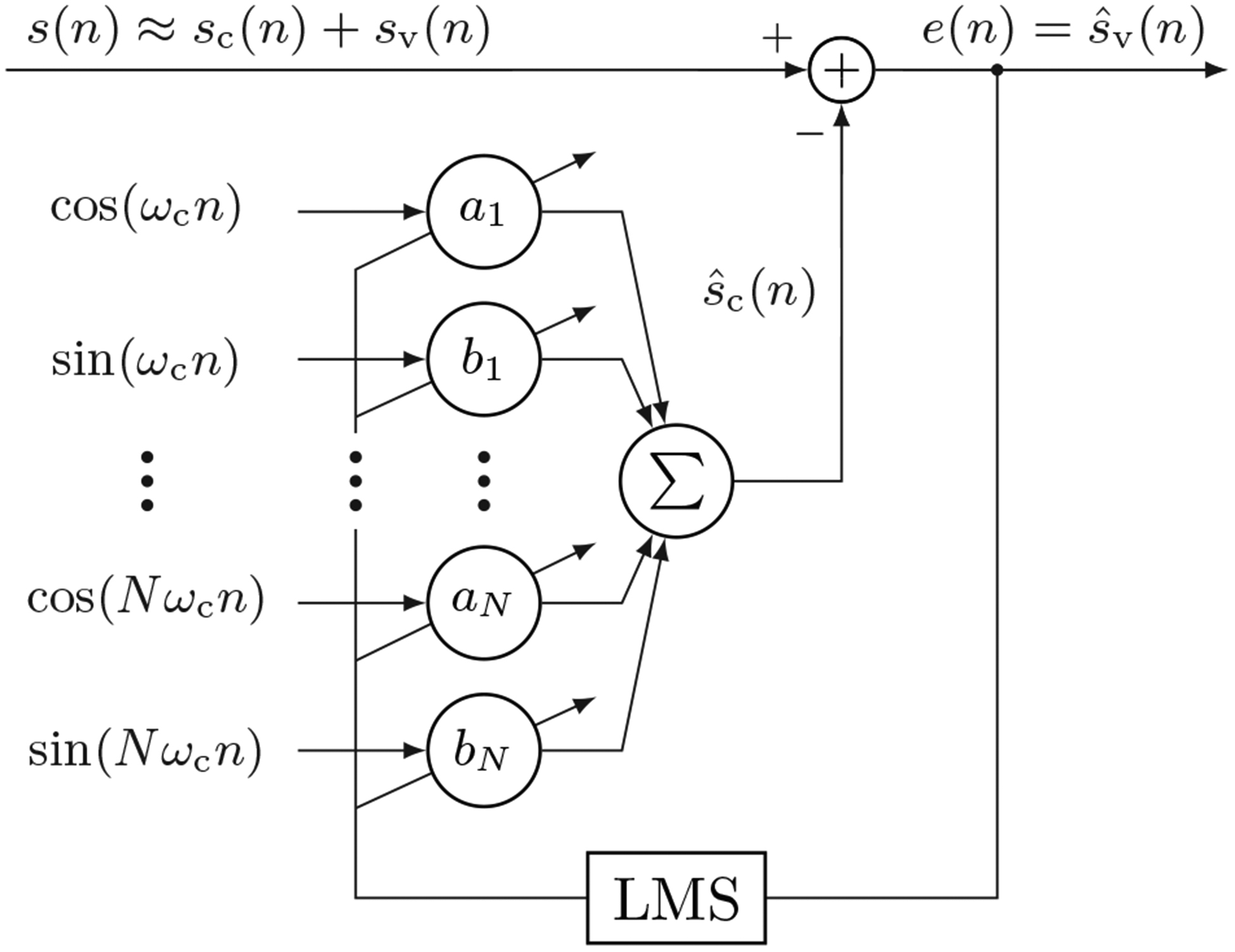
Block diagram of the LMS filter used to remove the mechanical chest compression component from the impedance.
B. Greedy peak detector
A greedy peak detector was designed to detect local maxima in the impedance ventilation component, sv(n). For each detected local maximum i three fiducial time points were calculated: the start of the ventilation (, insufflation onset), the peak time (, end of insufflation), and the end of the ventilation (, end of expiration). As shown in Fig. 4 (shaded intervals) an interval of approximately 5 s was defined before and after each local maximum to search for and :
| (8) |
| (9) |
These thresholds were obtained after some preliminary tests, but are sensible values considering how ventilations should be provided. During CPR, ventilation breaths should be delivered over 1 s (insufflation) [4], so a minimum of 0.45 s is a conservative threshold to capture even quick ventilation events. Recommended ventilation rates are 10 min−1 [4], or about 6 s per ventilation, so the 5.5 s threshold for insufflation/exhalation includes even very slow ventilations. Finally, the minimum separation between detections was fixed at ΔTm = 1.5 s, which is sufficient for hyperventilation rates of up to 40 min−1.
Fig. 4:
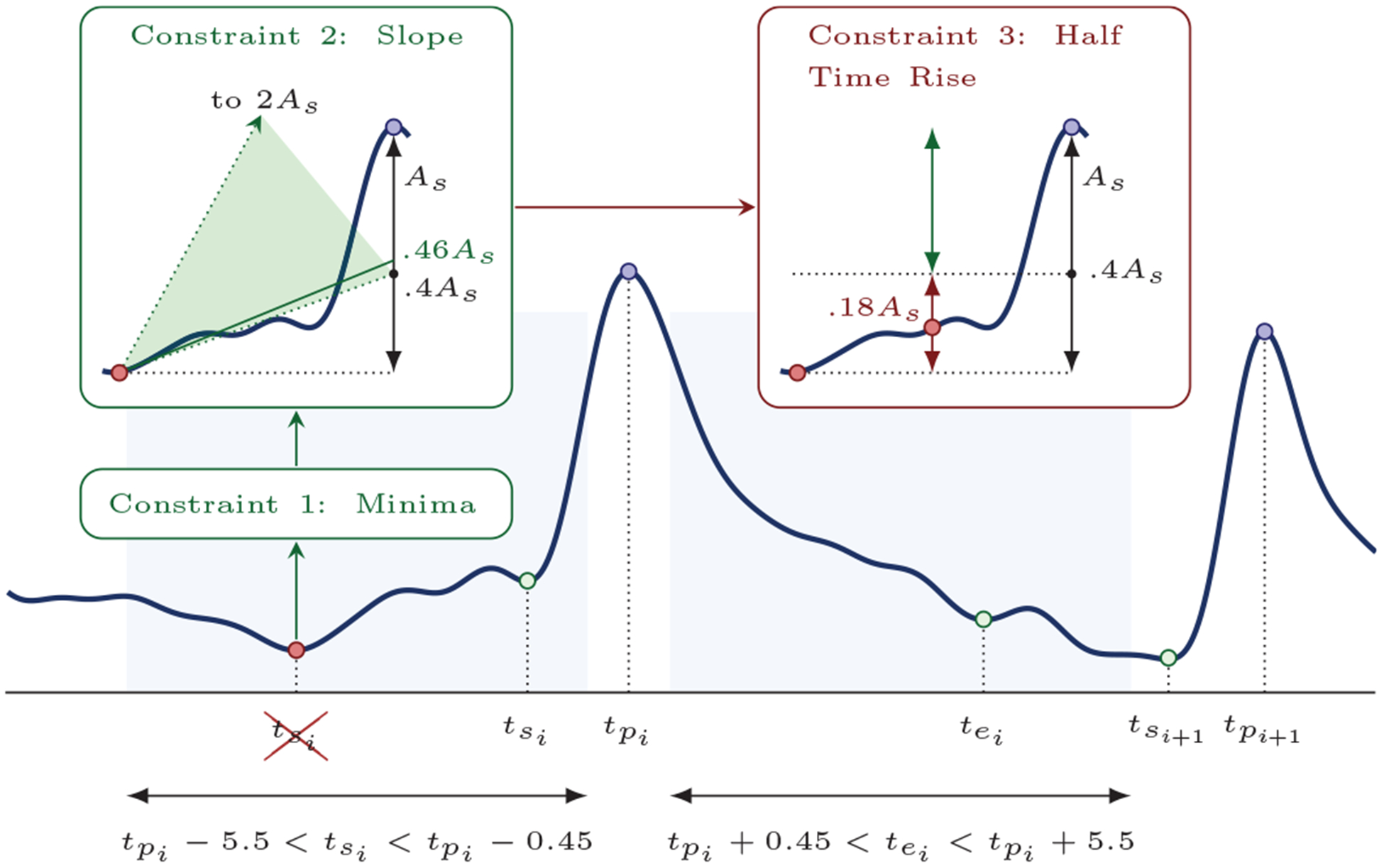
Peak detection algorithm. The shaded intervals indicate the search intervals for the start/end of ventilations, and the constraints on how to determine these points. In the example for ventilation i the first global minimum in the search interval was discarded because it did not meet constraint 3.
Three constraints were imposed to find and in the intervals defined in eqs (8) and (9). The constraints are graphically illustrated in the example in Fig. 4, and were applied in order to all potential timepoints in the search interval for the fiducial points. For the start of ventilation the constraints were:
must correspond to the smallest impedance value in the interval (, ).
- The mean slope of the impedance in the interval (, ), ms, and the total rise in impedance amplitude from to , As, were computed. The projection of that slope to the peak position had to be in the following range:
This is a starting slope constraint relative to ventilation amplitude. Low projection values are usually the result of a slow baseline recovery towards zero, while high ones are caused by compression component residuals and signal distortions.(10) The rise in amplitude between and the mid point to (half-time rise) should be at least 0.4 · As, to prevent selecting at some point far from the actual ventilation.
A similar procedure was followed for , but with these conditions on constraint 2:
| (11) |
and a half-time fall of 0.2 · As for constraint 3. The values are smaller for expiration because ventilation waveforms in the impedance tend to be concave for insufflation and convex for expiration. Finally, all peaks for which or could not be found were discarded, and for all the detected peaks the condition that two consecutive ventilations did not overlap was imposed ().
C. Waveform Feature extraction
Fourteen features were extracted for each detected peak to characterize the ventilation fluctuation waveform. The first four features were the duration of insufflation and expiration, and , respectively; and the amplitude change in impedance for the insufflation and expiration intervals, and , respectively. Ten waveform moments were also computed, five for each ventilation phase. Let us denote by and the vectors with the samples of either the insufflation or expiration phase of ventilation i, but normalized so that the total sum of the samples is unity. So for the insufflation phase we have of length and for the expiration phase of length . Let us also denote by zi = [0, 1, 2, … , L − 1]/L a vector of length or depending on the case, with equispaced values between 0 and 1. Then or can be regarded as a probability density functions in the [0, 1] support interval, and we could compute their moments of order as:
| (12) |
| (13) |
The features and , form the 10 waveform features used to parametrize the waveform during the insufflation and expiration phases, respectively.
D. Peak classification
Potential ventilations from the greedy detector were compared to ground truth annotations, and labeled as true positives (yi = 1, actual ventilation) or false positives (yi = 0, no ventilation). When more than one peak detection fell in the interval for true positive detections (Fig 1d), the one with closest to the expiration onset in the capnogram was regarded as true positive, and the rest as false positives. After peak detection and feature extraction data was formatted as a set of instance-label pairs , where yi are the true/false ventilation labels for the detected peaks, contains the M features for peak , and Np is the number of detected peaks. The last step was to develop a Random Forest classifier to discriminate true from false ventilation detections.
A RF is an ensemble of nearly uncorrelated decision trees. Decision trees present some desirable characteristics like independence from the underlying data distribution, robustness to outliers, and protection from correlated and/or bad predictors. However, individual trees are poor classifiers, deep trees are prone to overfitting and shallow trees to underfitting. Aggregating the decisions of B uncorrelated decision trees boosts classifier performance [34]. To uncorrelate the Tb(x) (b = 1, ⋯ B) trees, these are trained with Nb bootstrap samples of the training data of size Nb < Np, formed by randomly sampling the data with replacement. In addition, the RF algorithm randomizes the feature space by randomly selecting a subset of Mb features at each tree split (Mb < M). The final decision of the B trees for the sample xi is obtained as the majority vote of the ŷi,b = Tb(xi) for b = 1, ⋯ B. We chose an in-bag fraction Nb/Np of 0.5, the number of trees was fixed to B = 100, and the number of predictors per split to the default value of . Preliminary tests indicated that the choice of these RF parameters was not critical.
Data were partitioned using a 10-fold CV strategy to train and validate the classifier. At each iteration 9 folds were used as training data and the remaining fold as test data. The folds were partitioned patient wise and in a balanced way, so that each fold contained approximately 10% of the ground truth ventilation annotations [35]. All the calculations were weighted patient-wise to avoid biasing the results towards the patients with more ventilations in the dataset. Since the results may depend on the 10-fold CV partition used to train and validate the classifier, using a single 10-fold CV partition may overestimate or underestimate the accuracy of our method. To avoid biasing the results, the process was repeated 20 times with different random 10-fold CV partitions. And the accuracy metrics were statistically characterized using the 20 values obtained for each partition.
One of the salient characteristics of RF classifiers is a built-in feature ranking called feature importance. Importance was measured using the permuted out-of-bag (OOB) error. For a given tree, the subset of the training data left out in the bootstrap sample (out-of-bag samples) is used to evaluate the model’s predictions. Then the values for that feature in the OOB sample instances are randomly shuffled, and the decrease in prediction accuracy is measured. The decrease is larger for more important features. The process is repeated for all trees and features, resulting in a ranking of the features from the most important to the least. Recursive feature elimination (RFE) based on feature importance was used to reduce the number of features [36], [37]. Starting from a full feature model (M = 14), at each step the classifier was trained and the individual importance of each feature was computed. Then, the least important feature was removed and the process repeated until a model with a single feature was obtained. In this way we had 14 different models, from M = 14 to M = 1. The feature elimination process was carried out 200 times, once per test fold.
E. Evaluation of the detector
The performance of the ventilation detector was evaluated in terms of sensitivity (Se), positive predictive value (PPV) and F1-score (F1), computed as:
| (14) |
where TP, FP and FN are the true positive, false positive and false negative detections, respectively. There is a large imbalance in the number of ventilations that each patient contributed to the dataset, which is associated to how much time the mechanical compressor was used on each patient. In order make the method applicable to as many patients as possible, we weighted the contribution of each patient equally. This was done by calculating the metrics in equations (14) individually for each patient, and then averaging those values for the final Se, PPV and F1 for the complete set.
IV. Results
A. Classification performance
Ventilation detection was evaluated in two stages, first for the greedy detector and then after adding the classifier. The greedy detector outputted 55 908 detections, from which 34 615 were actual ventilations and 21 223 were false positives. The greedy peak detector missed 249 ventilations (0.71% of the total amount), which were regarded as false negative detections for the complete algorithm in the subsequent performance evaluations. The patient-weighted Se, PPV and F1 for the greedy detector were 99.36%, 62.04% and 76.27%, respectively.
The classifier corrected the false positive detections. The best compromise for simplicity and performance was obtained for a classifier with M = 6 features. After adding the classification block, the median (interdecile range, IDR) value of Se, PPV and F1 for the complete algorithm were 96.26 (96.15 – 96.31)%, 96.37 (96.32 – 96.43)% and 96.32 (96.25 – 96.36)%, respectively. The effect of the number of features, M, in the performance of the algorithm is presented in Fig 5. The figure shows that performance was very stable for M ≥ 6.
Fig. 5:
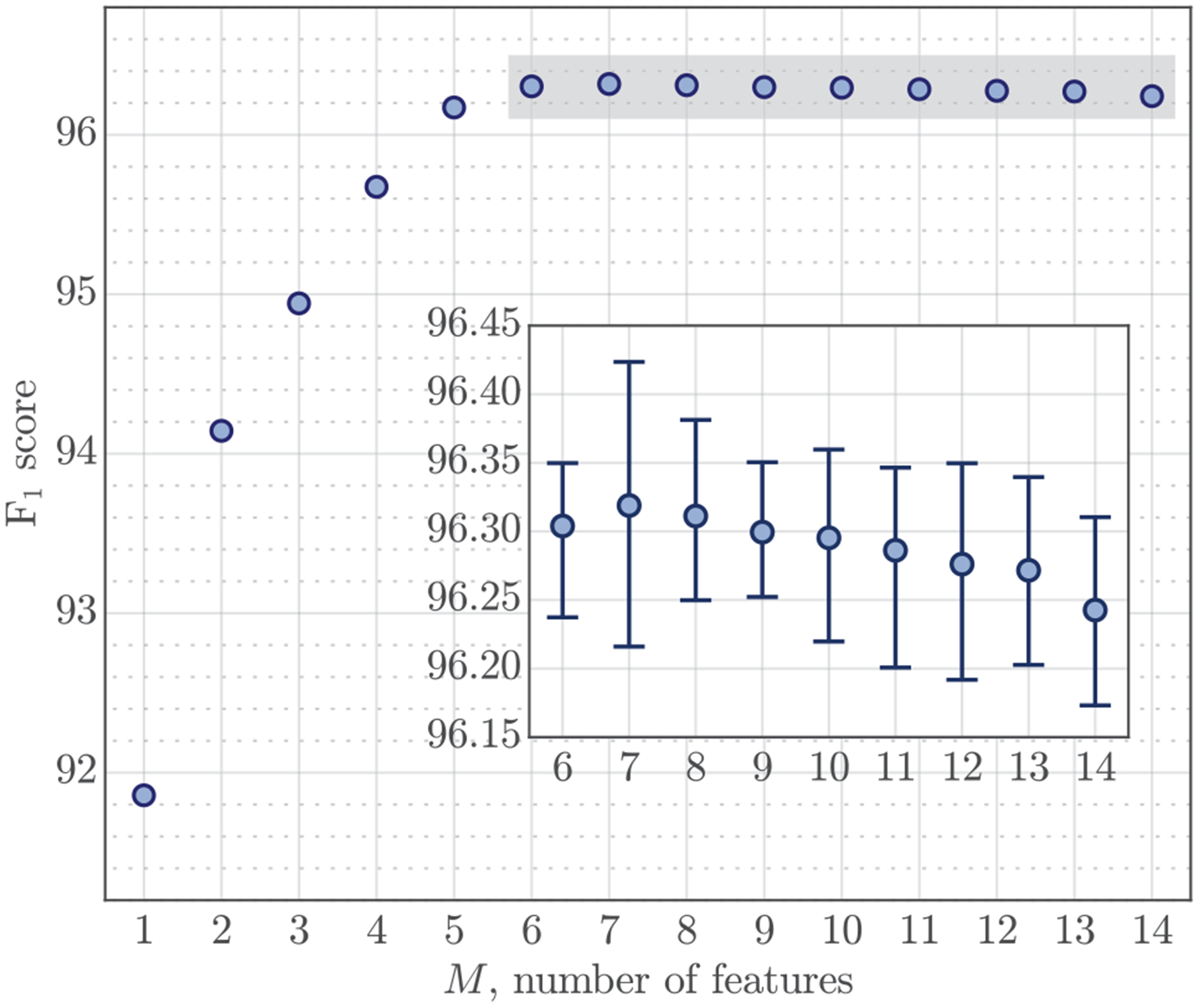
Performance of the detector as a function of the number of features used in the detector. For M ≥ 6 performance stabilizes, and the median (IDR) values are zoomed out (F1 ≥ 96.15 %) in the box.
The selection probability for each feature was estimated as the proportion of times they were selected, these probabilities are shown in Fig 6. For models with more than six features all four amplitude-duration features were included, and the amplitude of the insufflation phase (AI) was the best predictor. A model that used only AI produced an F1 score of 91.85 (91.78 – 91.94)%. No amplitude constraints were imposed on the greedy detector, so most false positives were caused by small impedance fluctuations, thus the importance of AI. The model tends to select AI over AE because of the difficulty to accurately determine the end of exhalation, although both predictors are very correlated (pearson correlation coefficient of ρ = 0.894). Waveform moments were also very correlated within the insufflation and exhalation phases. The smallest correlation coefficients were found between moments 1 and 5, with values of 0.931 and 0.915 for insufflation and exhalation, respectively. Consequently, features μE2 and μE3 could be used interchangeably (see Fig 6), and when only one was used it became the second most selected feature. The selection probabilities for the moments of the insufflation phase were more evenly distributed.
Fig. 6:
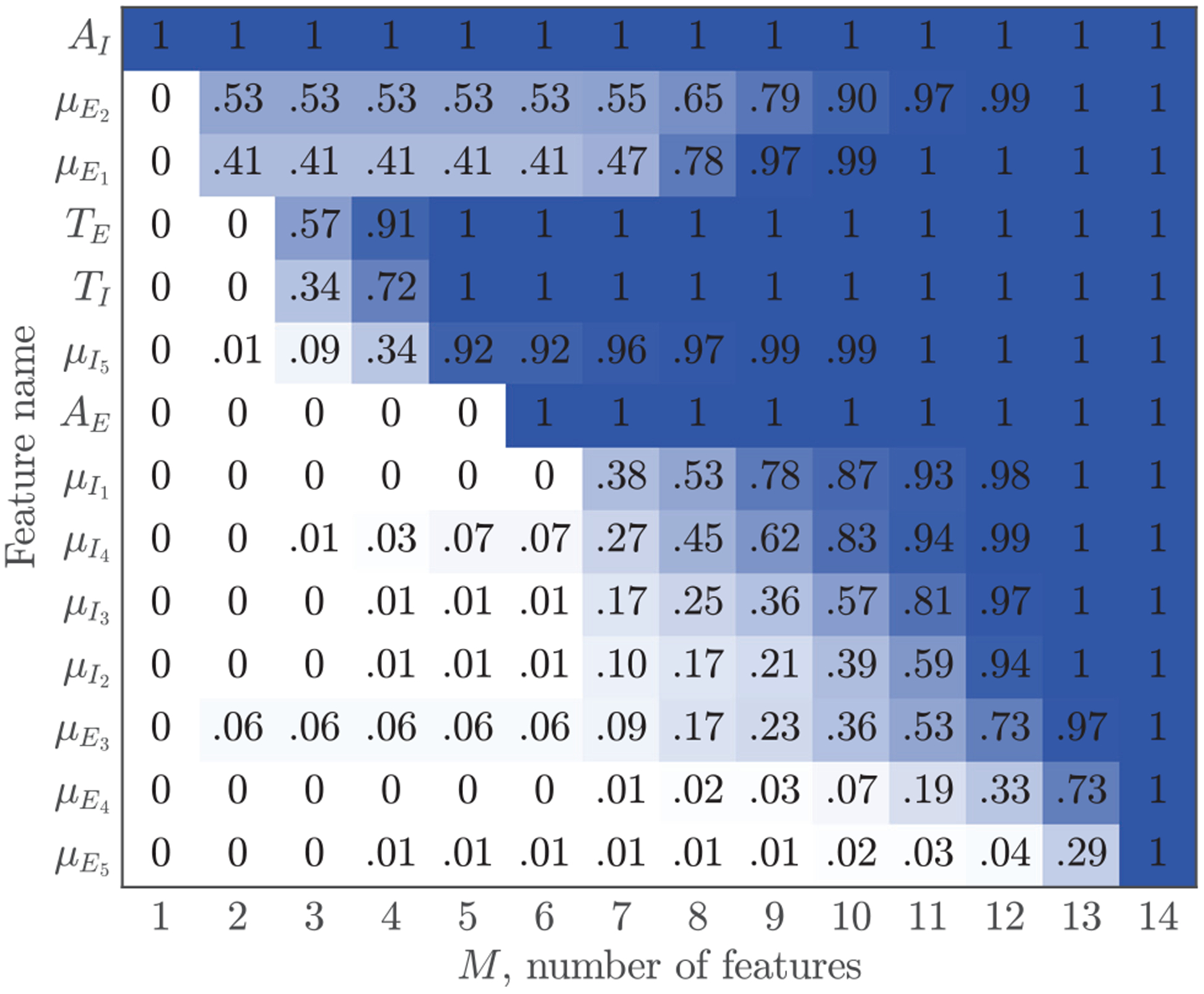
Probability of selecting a feature ordered by the number of times features were selected.
Finally, Fig 7 shows some typical examples of the errors made by the ventilation detection algorithm. Most missed detections were caused by abrupt changes in impedance, mostly caused by pauses in chest compressions, that produce transient effects when using the LMS filter, or by very shallow ventilations with short durations and possibly low insufflated volumes. Most false positives were caused by low frequency components in the impedance, such as motion artifacts caused by rescuers during treatment.
Fig. 7:
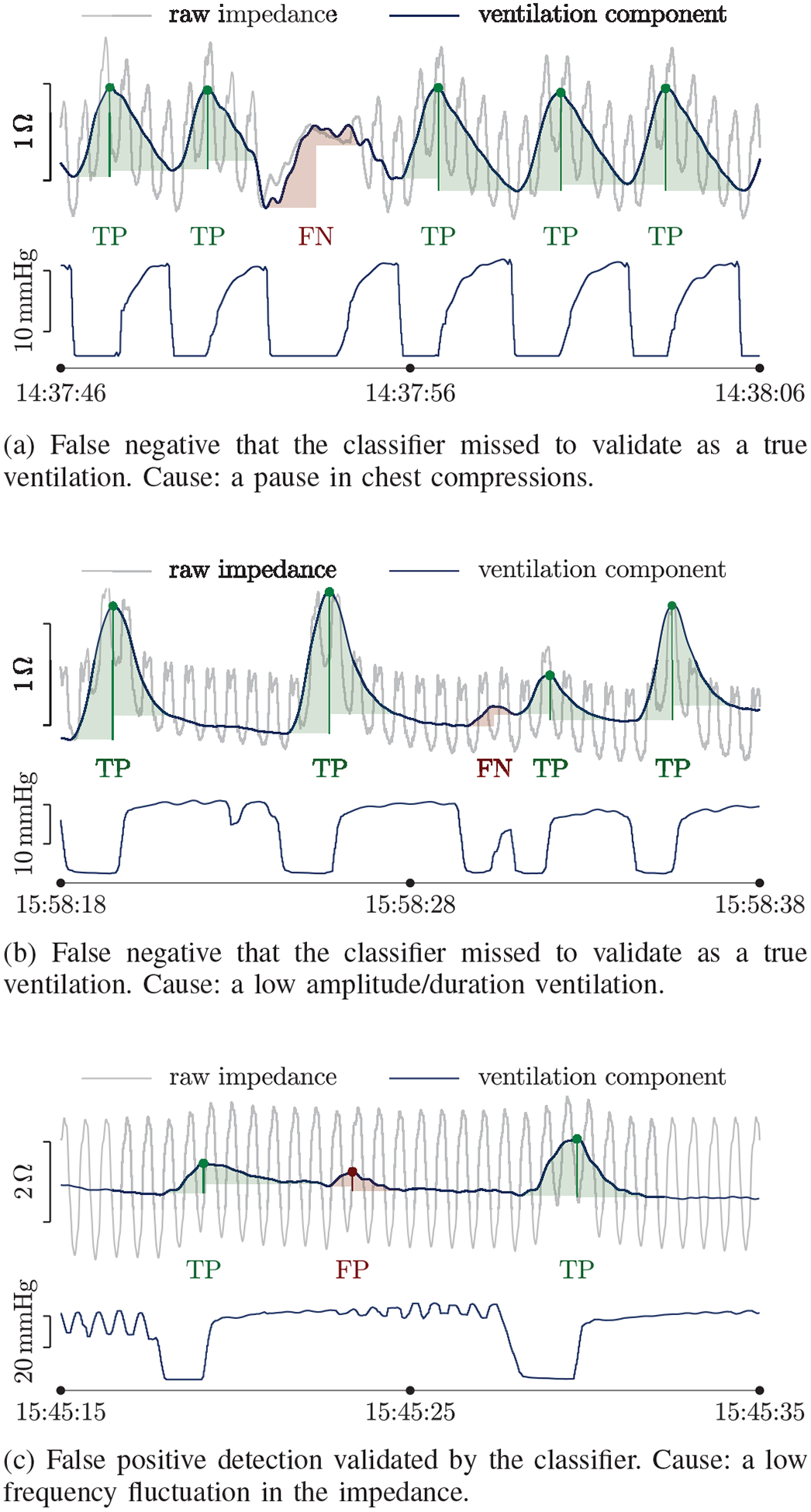
Examples of incorrect ventilation detections. Each example shows the impedance in grey with the ventilation component superposed in blue, and the capnogram with the ground truth ventilations below. The ventilations output by the detector are indicated by dots and are shaded in green (true positive, TP) or red (false positive, FP). The missed ventilations (false negative, FN) are shaded in red.
B. Analysis per patient
A relevant sub-analysis is to evaluate how the method performs for each patient, and to evaluate in what proportion of patients feedback on ventilations could be accurately provided. Fig 8 shows the distributions for the performance metrics per patient. In the boxplot each sample represents a patient, and for each patient the median value for the metric over the 20-CV partitions is represented. The proportion of patients with very low performance metrics (under 90%) is depicted in the right panel. As shown in the figure, accurate ventilation detection was possible in a large proportion of patients. The F1-score was above 95% for 77.1% of patients, and above 98 % for 49.4% of patients. For a few patients accurate ventilation detection was not possible with F1 scores under 75% (n = 8). For these patients the amplitude of the impedance ventilation component was small (< 0.2 Ω), probably because the insufflated volume was low [16].
Fig. 8:
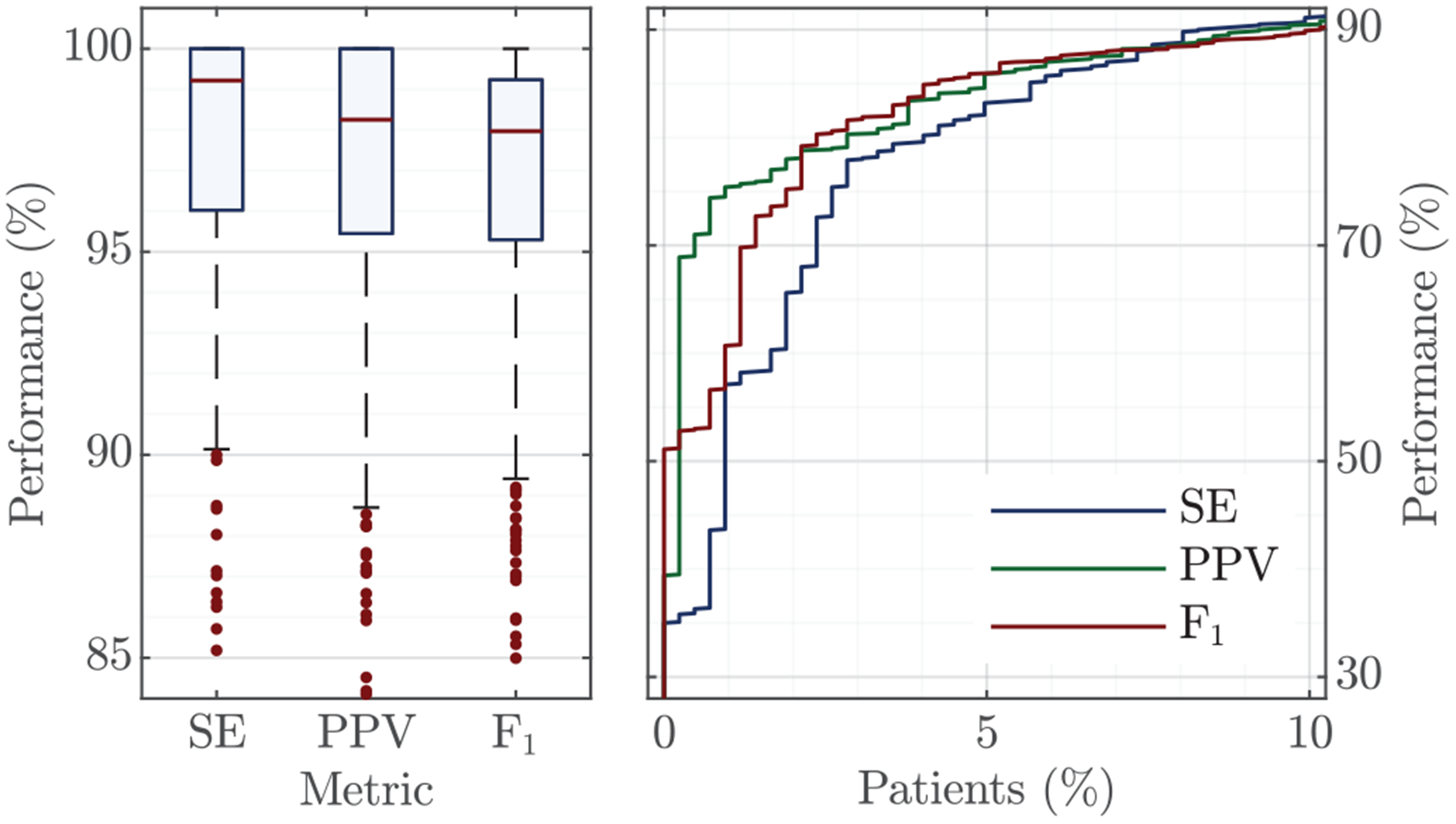
Per patient performance metrics for all n=423 patients as boxplots (left), and for the 10% (n=43) of patients with lowest detection accuracy (right). The rightmost graph only shows the proportion of patients in the low accuracy range (< 90%).
C. Feedback on ventilation rate
The most important application of a ventilation detector during OHCA treatment is to provide feedback on ventilation rates. For this purpose the algorithm was implemented in the way it would be incorporated to a monitor-defibrillator. The detector was programmed to analyze 1-min signal intervals, and to give feedback on that minute with no information on future impedance values. The ventilation rate was calculated every 15-s, that is, with a 75% overlap between the 1-min windows. For each window, ventilation time instants () were calculated using the process outlined in Fig 2. The ventilation rate for the interval was calculated as:
| (15) |
These values were compared to those obtained from the capnogram’s ground truth annotations, in which ventilation instants were annotated in the exhalation onset (rise in CO2). The analysis included all patients, but a separate analysis was done excluding the patients (n = 43) with low accuracy (F1 < 90%). For those patients, the impedance had either long intervals of lower quality signal, and/or very low amplitude ventilation components which could be associated to low insufflated volumes [16]. A separate sub-analysis was done excluding those patients, because in those cases the actual problem is not with ventilation rate but with the quality of ventilations (volumes) or with the quality of the signal used to give feedback. The Bland-Altman plot for feedback on ventilation rate is shown in Fig 9. The global 90% levels of agreement (LoA) were (−0.82, 1.40) min−1 for all patients, and (−0.51, 1.10) min−1 when the low F1 patients were excluded. The moving average LoAs for different VR intervals are shown in the figure, in red when all patients were included and in green after excluding low F1 patients. Rate was overestimated at rates under 6 min−1 and underestimated at rates above 10 min−1, although errors were small in all cases. The median (IDR) error and relative error in ventilation rate for all patients were 0.002 (−0.334 – 0.572) min−1 and 0.05 (−3.71 – 9.08)%, respectively. Excluding the low F1 patients the error and relative error were 0.002 (−0.204 – 0.351) min−1 and 0.06 (−2.45 – 5.11)%, respectively. So ventilation feedback could be provided with errors under 9% for all patients, and under 5% for the patients with better quality impedance, which in our dataset amounted for over 90% of patients.
Fig. 9:
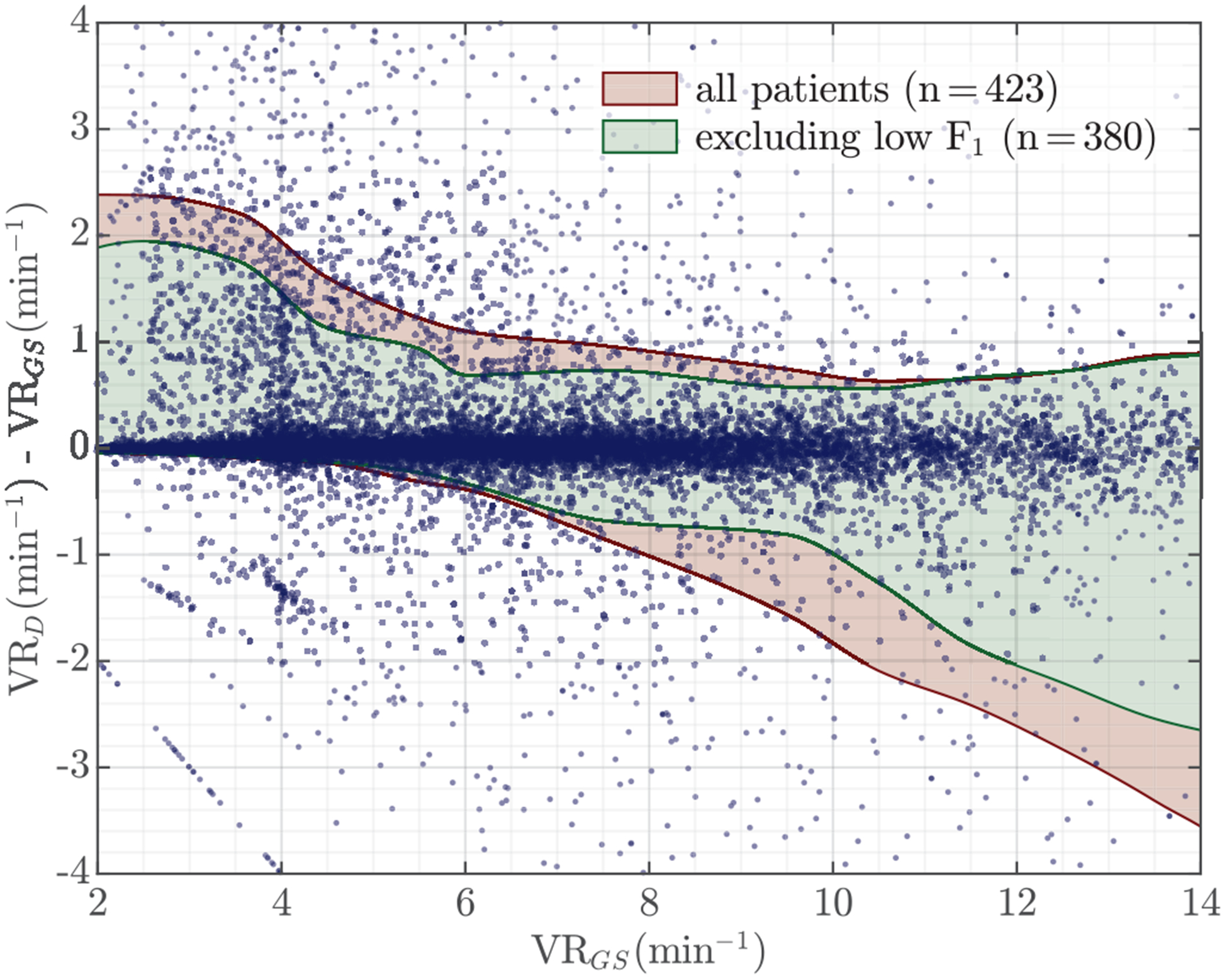
Bland-Altman plot for feedback on ventilation rate (VR). Ventilation rates were computed using 1-min impedance signal intervals and compared to the ground truth VR obtained from the capnogram. Moving average levels of agreement (LoA) are shown in red for all patients, and in green when the patients for which the ventilation detector’s F1-score was under 90% were excluded (n = 43).
V. DISCUSSION AND LIMITATIONS
This paper presents a new approach to impedance-based ventilation detection during mechanical CPR that combines adaptive signal processing and machine learning techniques. As shown by our results, accurate ventilation detection is possible with median (IQR) Se and PPV per patient of 99.2 (96.0 – 100)% and 98.3 (95.4 – 100)%, respectively (see Fig 8, left). Previous studies have addressed the detection of ventilations during manual CPR using the impedance and capnogram signals, a comparative assessment of our method to those methods is shown in table I. Our results are comparable to those obtained using state-of-the art algorithms based on the capnogram [14], and were better than those obtained for impedance based methods during manual CPR [13], [20], [21]. Two reasons could explain why results were better for mechanical than for manual CPR in impedance ventilation detection. First, chest compression components in the impedance are much more stable during mechanical CPR because the piston is at a fixed position in the patient’s chest, and compressions are always delivered in the same way by the machine [29]. Moreover, since the patient is fixed to the mechanical compressors, other movement artifacts and low quality signal intervals are less frequent. Second, our approach combined adaptive signal processing and machine learning, while the methods presented for manual CPR either relied on overly complex adaptive filters [20], or were based on rule-based detection of ventilations [13], [21]. In the future, new approaches similar to the one presented in this study could be demonstrated during manual CPR to exploit the potential of machine learning algorithms [27], and thus provide a better estimate of how accurate impedance based ventilation detection could be during manual CPR.
TABLE I:
Comparison of the median (IQR) Se and PPV per patient of our algorithm (from Fig 8, left) during mechanical CPR with methods to detect ventilations during manual CPR.
| Per-patient performance | ||
|---|---|---|
| Studies | Se (%) | PPV (%) |
| Impedance (manual CPR) | ||
| Risdal et al [20] | 90.6 (12.5) | 97.4 (8.0) |
| Alonso et al [21] | 92.2 (87.4–95.8) | 81.0 (67.2–90.5) |
| Edelson et al [13] | 78 (67–89) | 87 (77–96) |
| Capnogram (manual CPR) | ||
| Edelson et al [13] | 82 (75–93) | 91 (85–95) |
| Aramendi et al [16] | 99.0 (95.7–100) | 97.6 (94.8–100) |
| Our study (mechanical CPR) | 99.2 (96.0–100) | 98.3 (95.4–100) |
A key application of the ventilation detector is ventilation rate feedback during CPR to ensure compliance with the recommended rate of 10 min−1. In our data, ventilation rates were abnormally low, the median (IQR) ventilation rate per patient was 6.0 (4.5 – 8.0) min−1, and rates only exceeded the recommended values in 12.5% of our patients (for a detailed account see supplementary materials. These low ventilation rates were associated with some distinct ventilation patterns (see figures in supplementary materials). In many cases the patients were not ventilated for intervals of up to one minute, ventilation rates were very low, or the ventilation pattern followed the one observed during 30:2 CPR. Interestingly, the ventilation rates in our data are similar to the 7 min−1 ventilation rate observed during 30:2 CPR in a recent study [38], or to the 8 min−1 reported for the early stages of treatment during ALS [39]. Our data demonstrates the need for tools like the one presented in this study, both for feedback during treatment but also as a tool for retrospective analysis of large OHCA datasets that could shed light into how patients are being ventilated in the different phases of a resuscitation episode.
Finally, this study has some limitations. First, the algorithm was trained and tested using a 10-fold CV architecture and should be further validated in an independent dataset. Second, the algorithm was tailored to a piston driven mechanical CPR device (LUCAS-2), but there are other mechanical CPR technologies based on load distribution bands (the Autopulse system by Zoll) in which chest compression components may be different. Third, the algorithm can only be used during mechanical CPR and given the cost of mechanical CPR devices many EMS agencies still rely on manual chest compressions, although there is an increased trend towards the use of mechanical devices. And fourth, data was obtained from the Philips MRx device, so the algorithm may need to be readjusted to be used in other monitor-defibrillators with different impedance acquisition circuitry.
VI. CONCLUSIONS
This study demonstrates the feasibility of an accurate impedance-based ventilation detection during concurrent mechanical CPR. The method efficiently combines adaptive signal processing techniques to obtain and detect ventilation waveforms, with a machine learning algorithm to identify true ventilations. This ventilation detection algorithm could be used before advanced airway placement and capnography are available during resuscitation, but also to obtain additional information on ventilation such as insufflated volumes that are not available from the capnogram. Its use would broaden both the time feedback on ventilation is available, but also the available information on the quality of ventilations. Moreover, the method could also be used to retrospectively assess the effects of ventilations during CPR in OHCA outcomes, by applying the detector to large datasets of resuscitation episodes.
Supplementary Material
Acknowledgments
This work was supported by the Spanish Ministerio de Ciencia, Innovación y Universidades through grant RTI2018-101475-B100, jointly with the Fondo Europeo de Desarrollo Regional (FEDER), by the Basque Government through grant IT-1229-19, and by NIH grant HL 077887.
References
- [1].Berdowski J, Berg RA, Tijssen JGP, and Koster RW, “Global incidences of out-of-hospital cardiac arrest and survival rates: Systematic review of 67 prospective studies.” Resuscitation, vol. 81, pp. 1479–1487, Nov. 2010. [DOI] [PubMed] [Google Scholar]
- [2].Myat A, Song K-J, and Rea T, “Out-of-hospital cardiac arrest: current concepts.” Lancet, vol. 391, pp. 970–979, Mar. 2018. [DOI] [PubMed] [Google Scholar]
- [3].Kleinman ME et al. , “Part 5: Adult basic life support and cardiopulmonary resuscitation quality: 2015 american heart association guidelines update for cardiopulmonary resuscitation and emergency cardiovascular care.” Circulation, vol. 132, pp. S414–S435, Nov. 2015. [DOI] [PubMed] [Google Scholar]
- [4].Link MS et al. , “Part 7: Adult advanced cardiovascular life support: 2015 american heart association guidelines update for cardiopulmonary resuscitation and emergency cardiovascular care.” Circulation, vol. 132, pp. S444–S464, Nov. 2015. [DOI] [PubMed] [Google Scholar]
- [5].Henlin T, Michalek P, Tyll T, Hinds JD, and Dobias M, “Oxygenation, ventilation, and airway management in out-of-hospital cardiac arrest: a review.” BioMed research international, vol. 2014, p. 376871, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Aufderheide TP and Lurie KG, “Death by hyperventilation: a common and life-threatening problem during cardiopulmonary resuscitation.” Critical care medicine, vol. 32, pp. S345–S351, Sep. 2004. [DOI] [PubMed] [Google Scholar]
- [7].O’Neill JF and Deakin CD, “Do we hyperventilate cardiac arrest patients?” Resuscitation, vol. 73, pp. 82–85, Apr. 2007. [DOI] [PubMed] [Google Scholar]
- [8].Vissers G et al. , “The effect of ventilation rate on outcome in adults receiving cardiopulmonary resuscitation.” Resuscitation, vol. 138, pp. 243–249, May 2019. [DOI] [PubMed] [Google Scholar]
- [9].Coult J, Blackwood J, Rea TD, Kudenchuk PJ, and Kwok H, “A method to detect presence of chest compressions during resuscitation using transthoracic impedance.” IEEE J. Biomed. Health Inform, May 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Kramer-Johansen J, Edelson DP, Losert H, Köhler K, and Abella BS, “Uniform reporting of measured quality of cardiopulmonary resuscitation (CPR).” Resuscitation, vol. 74, pp. 406–417, Sep. 2007. [DOI] [PubMed] [Google Scholar]
- [11].Hostler D et al. , “Effect of real-time feedback during cardiopulmonary resuscitation outside hospital: prospective, cluster-randomised trial.” BMJ, vol. 342, p. d512, Feb. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Edelson DP et al. , “Improving in-hospital cardiac arrest process and outcomes with performance debriefing.” Archives of internal medicine, vol. 168, pp. 1063–1069, May 2008. [DOI] [PubMed] [Google Scholar]
- [13].Edelson DP et al. , “Capnography and chest-wall impedance algorithms for ventilation detection during cardiopulmonary resuscitation.” Resuscitation, vol. 81, pp. 317–322, Mar. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Aramendi E et al. , “Feasibility of the capnogram to monitor ventilation rate during cardiopulmonary resuscitation,” Resuscitation, vol. 110, pp. 162–168, 2017. [DOI] [PubMed] [Google Scholar]
- [15].Stecher FS, Olsen J-A, Stickney RE, and Wik L, “Transthoracic impedance used to evaluate performance of cardiopulmonary resuscitation during out of hospital cardiac arrest.” Resuscitation, vol. 79, pp. 432–437, Dec. 2008. [DOI] [PubMed] [Google Scholar]
- [16].Aramendi E et al. , “A novel technique to assess the quality of ventilation during pre-hospital cardiopulmonary resuscitation.” Resuscitation, vol. 132, pp. 41–46, Nov. 2018. [DOI] [PubMed] [Google Scholar]
- [17].Berve PO et al. , “Transthoracic impedance measured with defibrillator pads-new interpretations of signal change induced by ventilations.” Journal of clinical medicine, vol. 8, May 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Ansari S, Ward K, and Najarian K, “Epsilon-tube filtering: reduction of high-amplitude motion artifacts from impedance plethysmography signal.” IEEE J. Biomed. Health Inform, vol. 19, pp. 406–417, Mar. 2015. [DOI] [PubMed] [Google Scholar]
- [19].Ansari S, Ward KR, and Najarian K, “Motion artifact suppression in impedance pneumography signal for portable monitoring of respiration: An adaptive approach.” IEEE J. Biomed. Health Inform, vol. 21, pp. 387–398, Mar. 2017. [DOI] [PubMed] [Google Scholar]
- [20].Risdal M, Aase SO, Stavland M, and Eftestøl T, “Impedance-based ventilation detection during cardiopulmonary resuscitation.” IEEE Trans. Biomed. Eng, vol. 54, pp. 2237–2245, Dec. 2007. [DOI] [PubMed] [Google Scholar]
- [21].Alonso E et al. , “Reliability and accuracy of the thoracic impedance signal for measuring cardiopulmonary resuscitation quality metrics.” Resuscitation, vol. 88, pp. 28–34, Mar. 2015. [DOI] [PubMed] [Google Scholar]
- [22].Husøy JH et al. , “Removal of cardiopulmonary resuscitation artifacts from human ECG using an efficient matching pursuit-like algorithm.” IEEE Trans. Biomed. Eng, vol. 49, pp. 1287–1298, Nov. 2002. [DOI] [PubMed] [Google Scholar]
- [23].Irusta U, Ruiz J, de Gauna SR, Eftestøl T, and Kramer-Johansen J, “A least mean-square filter for the estimation of the cardiopulmonary resuscitation artifact based on the frequency of the compressions.” IEEE Trans. Biomed. Eng, vol. 56, pp. 1052–1062, Apr. 2009. [DOI] [PubMed] [Google Scholar]
- [24].Rubertsson S et al. , “Mechanical chest compressions and simultaneous defibrillation vs conventional cardiopulmonary resuscitation in out-of-hospital cardiac arrest: the LINC randomized trial.” JAMA, vol. 311, pp. 53–61, Jan. 2014. [DOI] [PubMed] [Google Scholar]
- [25].Wik L et al. , “Manual vs. integrated automatic load-distributing band CPR with equal survival after out of hospital cardiac arrest. the randomized CIRC trial.” Resuscitation, vol. 85, pp. 741–748, Jun. 2014. [DOI] [PubMed] [Google Scholar]
- [26].Perkins GD et al. , “Mechanical versus manual chest compression for out-of-hospital cardiac arrest (PARAMEDIC): a pragmatic, cluster randomised controlled trial.” Lancet, vol. 385, pp. 947–955, Mar. 2015. [DOI] [PubMed] [Google Scholar]
- [27].Isasi I et al. , “A multistage algorithm for ECG rhythm analysis during piston-driven mechanical chest compressions.” IEEE Trans. Biomed. Eng, vol. 66, pp. 263–272, Jan. 2019. [DOI] [PubMed] [Google Scholar]
- [28].Isasi I et al. , “A machine learning shock decision algorithm for use during piston-driven chest compressions.” IEEE Trans. Biomed. Eng, vol. 66, pp. 1752–1760, Jun. 2019. [DOI] [PubMed] [Google Scholar]
- [29].Aramendi E et al. , “Filtering mechanical chest compression artefacts from out-of-hospital cardiac arrest data.” Resuscitation, vol. 98, pp. 41–47, Jan. 2016. [DOI] [PubMed] [Google Scholar]
- [30].Jaureguibeitia X et al. , “Impedance based automatic detection of ventilations during mechanical cardiopulmonary resuscitation,” in Proc. 41st Annual Int. Conf. of the IEEE Engineering in Medicine and Biology Society (EMBC), Jul. 2019, pp. 19–23. [DOI] [PubMed] [Google Scholar]
- [31].Nichol G et al. , “Regional variation in out-of-hospital cardiac arrest incidence and outcome.” JAMA, vol. 300, pp. 1423–1431, Sep. 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Ayala U et al. , “Automatic detection of chest compressions for the assessment of CPR-quality parameters.” Resuscitation, vol. 85, pp. 957–963, Jul. 2014. [DOI] [PubMed] [Google Scholar]
- [33].Xiao Y and Tadokoro Y, “LMS-based notch filter for the estimation of sinusoidal signals in noise,” Signal Processing, vol. 46, no. 2, pp. 223–231, 1995. [Google Scholar]
- [34].Breiman L, “Random forests,” Machine learning, vol. 45, no. 1, pp. 5–32, 2001. [Google Scholar]
- [35].Krstajic D, Buturovic LJ, Leahy DE, and Thomas S, “Cross-validation pitfalls when selecting and assessing regression and classification models,” Journal of cheminformatics, vol. 6, no. 1, p. 10, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Gregorutti B, Michel B, and Saint-Pierre P, “Correlation and variable importance in random forests,” Statistics and Computing, vol. 27, no. 3, pp. 659–678, 2017. [Google Scholar]
- [37].Isasi I et al. , “Automatic Cardiac Rhythm Classification With Concurrent Manual Chest Compressions,” IEEE Access, vol. 7, pp. 115 147–115 159, 2019. [Google Scholar]
- [38].Sanson G et al. , “Impact of ‘synchronous’ and ‘asynchronous’ cpr modality on quality bundles and outcome in out-of-hospital cardiac arrest patients.” Internal and emergency medicine, vol. 14, pp. 1129–1137, Oct. 2019. [DOI] [PubMed] [Google Scholar]
- [39].Wik L et al. , “Quality of cardiopulmonary resuscitation during out-of-hospital cardiac arrest.” JAMA, vol. 293, pp. 299–304, Jan. 2005. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


