Characterization of SARS-CoV-2 dynamics in the host

Abstract

While many epidemiological models were proposed to understand and handle COVID-19 pandemic, too little has been invested to understand human viral replication and the potential use of novel antivirals to tackle the infection. In this work, using a control theoretical approach, validated mathematical models of SARS-CoV-2 in humans are characterized. A complete analysis of the main dynamic characteristic is developed based on the reproduction number. The equilibrium regions of the system are fully characterized, and the stability of such regions is formally established. Mathematical analysis highlights critical conditions to decrease monotonically SARS-CoV-2 in the host, as such conditions are relevant to tailor future antiviral treatments. Simulation results show the aforementioned system characterization.

1. Introduction

By December 2019, an outbreak of cases with pneumonia of unknown etiology was reported in Wuhan, Hubei province, China (Lu, Stratton, & Tang, 2020). On January 7, a novel betacoronavirus was identified as the etiological agent by the Chinese Center of Disease Control and Prevention (CCDC), and subsequently named as Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) (Gorbalenya, 2020). On February 11, the World Health Organization (WHO) named the disease as Coronavirus disease 2019 (COVID-19) (Who, 2020). Although prevention and control measures were implemented rapidly, from the early stages in Wuhan and other key areas of Hubei Who, 2020, the first reported cases outside of China showed that the virus was starting to spread around the world (whotimeline, 2020).

On March 11, with more that 111.800 cases in 114 countries, and 4921 fatalities cases, COVID-19 was declared a pandemic by the WHO (whotimeline, 2020). So far, with more than 7.000.000 total cases confirmed in 213 countries and territories (Coronavirus disease 2019, COVID-19), and an estimated case-fatality rate (CFR) of 5.7% (H1N1 pandemic, CFR < 1%) (Who, 2020), the potential health risks are evident.

The virus spreads mainly from person-to-person through respiratory droplets produced when an infected person coughs, sneezes or talks (How covid-19 spreads). The nonexistence of vaccines or specific therapeutic treatments, preventive measures such as social and physical distancing, hand washing, cleaning and disinfection of surfaces and the use of face masks, among others, have been implemented in order to decrease the transmission of the virus.

Epidemiological mathematical models (Acuna-Zegarra, Comas-Garcia, Hernandez-Vargas, Santana-Cibrian, Velasco-Hernandez, 2020, Alanis, Member, Hernandez-vargas, Nancy, Ríos-rivera, 2020, Giordano et al., 2020, Read, Bridgen, Cummings, Ho, Jewell, 2020) have been proposed to predict the spread of the disease and evaluate the potential impact of infection prevention and control measures in outbreak management (Anderson, Heesterbeek, Klinkenberg, & Hollingsworth, 2020). However, mathematical models at in-host level that could be useful to understand the SARS-CoV-2 replication cycle and interaction with immune system as well as the pharmacological effect of potential drug therapies (Liu, Zhou, Li, Garner, Watkins, Carter, Smoot, Gregg, Daniels, Jervey, et al., Mitjà, Clotet, 2020) are needed. So far, there are approximately 109 trials (including those not yet recruiting, active, or completed) to asses pharmacological therapy for the treatment of COVID-19 in adult patients (Sanders, Monogue, Jodlowski, & Cutrell, 2020), including antiviral drugs (i.e. Hydroxychloroquine, Remdesivir, Lopinavir/Ritonavir, Ribavirin), immunomodulatory agents (i.e. Tocilizumab) and immunoglobulin therapy, among others. Recently, Hernandez-Vargas & Velasco-Hernandez, 2020 proposed different intra-host mathematical models (2 based on target cell-limited model, with and without latent phase, and another considering immune response) for 9 patients with COVID-19. Numerical results in Hernandez-Vargas & Velasco-Hernandez, 2020 showed intra-host reproductive number values consistent to influenza infection (1.7-5.35).

Although models in Hernandez-Vargas & Velasco-Hernandez, 2020 have been fitted to COVID-19 patients data, a control theoretical approach is needed to characterize the model dynamics. Even when the equilibrium states are known, a formal stability analysis is needed to understand the model behavior and, mainly, to design efficient control strategies. Note that the target cell model has been employed previously taking into account pharmacodynamic (PD) and pharmacokinetic (PK) models of antiviral therapies (Boianelli, Sharma-Chawla, Bruder, Hernandez-Vargas, 2016, Hernandez-Mejia, Alanis, Hernandez-Gonzalez, Findeisen, Hernandez-Vargas, 2019), and this can be potentially done also for COVID-19.

In this context, the main contribution of this article is twofold. First, a full characterization of equilibrium and stability proprieties is performed for the COVID-19 target cell-limited model (Hernandez-Vargas & Velasco-Hernandez, 2020). Then, formal properties concerning the state variables behavior before convergence - including an analysis of the virus peak times - are given. A key aspect in the target cell model for acute infections shows some particularities such as it has a minimal nontrivial stable equilibrium set, whose stability does not depend on the reproduction number. On the other side, assuming a basic reproduction number greater than 1, the virus would not be cleared before the target cells decreases below under a given critical value, which is independent of the initial conditions.

The article is organized as follows. Section 2 presents the general in-host target cell-limited model used to represent SARS-CoV-2 infection dynamic. Section 3 characterizes the equilibrium sets of the system, and establishes their formal asymptotic stability, by proving both, the attractivity of the equilibrium set in a given domain, and its $ϵ-\delta$ (Lyapunov) local stability. Then, in Section 4, some dynamical properties of the system are stated, concerning the values of the states at the infection time $t=0$. In Section 5 the general model for the SARS-CoV-2 infection is described and the general characteristics of the infection are analyzed. Finally, Section 6 gives the conclusion of the work, while several mathematical formalisms - necessary to support the results of Sections 3 and 4 - are presented in the Appendices.

1.1. Notation

$\mathbb{R}$ and $\mathbb{I}$ denote the real and integer numbers, respectively. The real vector space of dimension n is denoted as ${\mathbb{R}}^n$. ${\mathbb{R}}_{\ge 0}^n$ represents the vectors of dimension n whose components are equal or greater than zero. The distance from a point $x\in {\mathbb{R}}^n$ to a set $\mathcal{X}\subset {\mathbb{R}}^n$ is defined by $\parallel x{\parallel }_{\mathcal{X}}:={\inf }_{z\in \mathcal{X}}\parallel x-z{\parallel }_2$ where ‖ · ‖₂ denotes the norm-2. The open ball of radius ϵ around a point $x\in {\mathbb{R}}^n,$ with respect to set $\mathcal{X},$ is defined as ${\mathbb{B}}_{ϵ}\left(x\right):={\{z\in \mathcal{X}:\parallel x-z\parallel }_2<ϵ\}$. For the real function $f\left(z\right)=z{e}^z,$ the so-called Lambert function is defined as the inverse of f( · ), i.e., $W\left(z\right):=f^{-1}\left(z\right)$ in such a way that $W\left(f\right(z\left)\right)=z$.

2. SARS-CoV-2 in-host mathematical model

Although incomplete by definition, mathematical models of in-host virus dynamic improve the understanding of the interactions that govern infections and, more importantly, permit the human intervention to moderate their effects (Hernandez-Vargas, 2019). Basic in-host infection dynamic models usually include the susceptible cells, infected cells, and the pathogen particles (Ciupe & Heffernan, 2017). Among the most used mathematical models, the target cell-limited model has been employed to represent and control HIV infection (Legrand, Comets, Aymard, Tubiana, Katlama, Diquet, 2003, Perelson, Kirschner, De Boer, 1993, Perelson, Ribeiro, 2013), influenza (Baccam, Beauchemin, Macken, Hayden, Perelson, 2006, Hernandez-Mejia, Alanis, Hernandez-Gonzalez, Findeisen, Hernandez-Vargas, 2019, Larson, Dominik, Rowberg, Higbee, 1976, Smith, Perelson, 2011), Ebola (Nguyen, Binder, Boianelli, Meyer-Hermann, & Hernandez-Vargas, 2015), dengue (Nikin-Beers, Ciupe, 2015, Nikin-Beers, Ciupe, 2018) among others.

In this work, we consider the mathematical model proposed by Hernandez-Vargas & Velasco-Hernandez, 2020 given by the following set of ordinary differential equations (ODEs) :

$$\dot{U}\left(t\right)=-\beta U\left(t\right)V\left(t\right),U\left(0\right)=U_0,$$ (2.1a)

$$\dot{I}\left(t\right)=\beta U\left(t\right)V\left(t\right)-\delta I\left(t\right),I\left(0\right)=I_0=0,$$ (2.1b)

$$\dot{V}\left(t\right)=pI\left(t\right)-cV\left(t\right),V\left(0\right)=V_0,$$ (2.1c)

where U [cells], I [cells] and V [copies/mL] represent the susceptible cells, the infected cells, and the virus load, respectively. The parameter β $\left[{(copies/mL)}^{-1}da{y}^{-1}\right]$ is the infection rate of susceptible cells by the virus. δ $\left[da{y}^{-1}\right]$ is the death rate of infected cells. p $\left[(copies/mL)da{y}^{-1}cell{s}^{-1}\right]$ is the replication rate of free virus from the infected cells. c $\left[da{y}^{-1}\right]$ is the degradation (or clearance) rate of virus V. The effects of immune responses are not explicitly described in this model, but they are implicitly included in the death rate of infected cells (δ) and the clearance rate of virus (c) (Baccam et al., 2006).

The parameter values of the target cell model were fitted by Hernandez-Vargas & Velasco-Hernandez, 2020 using viral kinetics reported by Wölfel et al. (2020) in patients with COVID-19. The Differential Evolution (DE) algorithm was shown to be more robust to initial guesses of parameters than other mentioned methods (Torres-Cerna, Alanis, Poblete-Castro, Bermejo-Jambrina, & Hernandez-vargas, 2016). Akaike information criterion (AIC) was used to compare the goodness-of-fit for models that evaluate different hypotheses in Hernandez-Vargas & Velasco-Hernandez, 2020. The target cell model showed better fitting than exponential growth and logarithmic decay models as well as the target cell model with eclipse phase (Hernandez-Vargas & Velasco-Hernandez, 2020).

The model (2.1) is non-negative, which means that U(t) ≥ 0, I(t) ≥ 0 and V(t) ≥ 0, for all t ≥ 0. If we denote x(t) ≔ (U(t), I(t), V(t)), then the states are constrained to belong to the invariant set:

$$\mathbb{X}:=\{x\in {\mathbb{R}}_{\ge 0}^3\}.$$ (2.2)

Another meaningful set is the one consisting in all the states in $\mathbb{X}$ with strictly positive amount of virus and susceptible cells, i.e.,

$$\mathcal{X}:=\{x\in \mathbb{X}:U>0,V>0\}.$$ (2.3)

Note that the set $\mathcal{X}$ is an open set.

The initial conditions of (2.1) are assumed such at a healthy steady state before the infection time $t=0,$ i.e., $V\left(t\right)=0,$ $I\left(t\right)=0,$ and $U\left(t\right)=U_0,$ for t < 0. At time $t=0,$ a small quantity of virions enters to the host body and, so, a discontinuity occurs in V(t). Indeed, V(t) jumps from 0 to a small positive value V ₀ at $t_0=0$ (formally, V(t) has a discontinuity of the first kind at t ₀, i.e., ${\lim }_{t\to 0^{-}}V\left(t\right)=0$ while ${\lim }_{t\to 0^{+}}V\left(t\right)=V_0>0$). The same scenario arises, for instance, when an antiviral treatment affects either parameter p or β. The jump of p or β can be considered as a discontinuity of the first kind. In any case, for the time after the discontinuity, the virus may spread or be cleared in the body, depending on its infection effectiveness. The following (mathematical) definition is given

Definition 1 Spreadability of the virus in the host —

Consider the system (2.1), constrained by the positive set $\mathbb{X},$ at some time t ₀, with U(t ₀) > 0, I(t ₀) ≥ 0 and V(t ₀) > 0 (i.e., $x\left(t_0\right)=(U\left(t_0\right),I\left(t_0\right),V\left(t_0\right))\in \mathcal{X}$). Then, it is said that the virus spreads in the host for t > t ₀ if there exists at least one t* > t ₀ such that $\dot{V}\left(t^{*}\right)>0$.

The latter definition states that the virus spreads in the body host if V(t) has at least one local maximum. On the other hand, the virus does not spread if V(t) is strictly decreasing for all t > t ₀. As it will be stated later on (Property 1), ${\lim }_{t\to \infty }V\left(t\right)=0$ for system (2.1), independently of the fact that the virus reaches or not a maximum (this is a key difference between acute and chronic infection models (Ciupe, Heffernan, 2017, Hernandez-Vargas, 2019)).

The infection severity can be related with the virus spreadability established in Definition 1. Liu et al. (2020b) have shown that patients with severe COVID-19 tend to have a high viral load and a long virus shedding period. The mean viral load of severe cases was around 60 times higher than that of mild cases, suggesting that higher viral loads might be associated with severe clinical outcomes. Furthermore, they found that the viral load of severe cases remained significantly higher for the first 12 days after the appearance of the symptoms than those of corresponding mild cases. Mild cases were also found to have an early viral clearance, with 90% of these patients repeatedly testing negative on reverse transcription polymerase chain reaction (RT-PCR) by day 10 post symptoms onset (pso). By contrast, all severe cases still tested positive at or beyond day 10 pso. In addition, Zheng et al. (2020) reported (from a study with 96 SARS-CoV-2 patients, 22 with mild and 74 with severe disease) a longer duration of SARS-CoV-2 in lower respiratory samples of severe patients. For patients with severe disease the virus permanence was significantly longer (21 days, 14-30 days) than in patients with mild disease (14 days, 10-21 days; p=0.04). Moreover, higher viral loads were detected in respiratory samples, although no differences were found in stool and serum samples. While these findings suggest that reducing the viral load through clinical means and strengthening management should help to prevent the spread of the virus, they are preliminary and it remains controversial whether virus persistence is necessary to drive the dysfunctional immune response characteristic of COVID-19 patients (Tay, Poh, Rénia, MacAry, & Ng, 2020).

Remark 1

Note that the virus spreadability may or may not cause a severe infection (a disease that eventually causes host death) which depends on how much time the virus is above a given value.

To properly establish conditions under which the virus does not spread for t > 0 (i.e., after the infection time $t=0$) the so-called in-host basic reproduction number is defined next.

Definition 2

The intra-host basic reproduction number $\mathcal{R}$ is defined as the number of infected cells (or virus particles) that are produced by one infected cell (or virus particle), at a given time. Its mathematical expression is given by:

$$\mathcal{R}\left(t\right):=U\left(t\right)\frac{\beta p}{c\delta }.$$ (2.4)

Particularly, for $t=0,$ this number describes the number of infected cells produced by one infected cell, when a small amount of virus, V ₀, is introduced into a healthy stationary population of uninfected target cells, U ₀,

$${\mathcal{R}}_0:=U_0\frac{\beta p}{c\delta }.$$ (2.5)

A discussion about the way this value is obtained is given in Appendix 2. The relation between the basic reproduction number at the infection time (${\mathcal{R}}_0$) and the virus spreadiblity is stated in the next theorem.

Theorem 2.1

Consider the system (2.1) , constrained by the positive set $\mathbb{X},$ at the beginning of the infection, i.e., $U\left(0\right)=U_0>0,$ $I\left(0\right)=0$ and $V\left(0\right)=V_0>0$ (i.e., $x\left(0\right)=\left(U\right(0),I(0),V(0\left)\right)\in \mathcal{X}$ ). Then, a sufficient condition (not necessary) for the virus not to spread is given by ${\mathcal{R}}_0<1$ .

Proof

In Theorem 4.1, 4, it is shown that if the virus spreads, then ${\mathcal{R}}_0>1$. This means that (contrapositive of the statement) if ${\mathcal{R}}_0\le 1$ (particularly, ${\mathcal{R}}_0<1$), then the virus does not spread in the host body. □

Before proceeding with a full dynamic analysis of system (2.1), let us define first the so-called critical value of the susceptible cells, which is a threshold to properly understand the spread of the virus.

Definition 3

The critical value for U, ${\mathcal{U}}_c,$ is defined as

$${\mathcal{U}}_c:=\frac{c\delta }{p\beta }=\frac{U_0}{{\mathcal{R}}_0},$$ (2.6)

which, for fixed system parameters β, p, δ and c, is a constant.

Note that $U\left(t\right)<{\mathcal{U}}_c$ if and only if $\mathcal{R}\left(t\right)<1,$ for every t ≥ 0.

2.1. Equilibrium set characterization

By equating $\dot{U},$ $\dot{I}$ and $\dot{V}$ to zero in (2.1), it can be shown that the system only has healthy equilibria of the form $x_s=(U_s,0,0),$ with U_s being an arbitrary positive value, i.e., U_s ∈ [0, ∞). Thus, there is only one equilibrium set, which is the disease-free one, and it is defined by

$${\mathcal{X}}_s:=\{(U,I,V)\in {\mathbb{R}}^3:U\in [0,\infty ),I=0,V=0\}.$$ (2.7)

To examine the stability of the equilibrium points in ${\mathcal{X}}_s,$ system (2.1) can be linearized at a general state $x_s\in {\mathcal{X}}_s$. From (2.1) we have $\dot{U}=f(U,I,V),$ $\dot{I}=g(U,I,V),$ $\dot{V}=h(U,I,V)$. Then, the Jacobian matrix is given by

$$\begin{array}{c}\hfill J=\left(\begin{array}{ccc}{\displaystyle \frac{\partial f}{\partial U}}& {\displaystyle \frac{\partial f}{\partial I}}& {\displaystyle \frac{\partial f}{\partial V}}\\ {\displaystyle \frac{\partial g}{\partial U}}& {\displaystyle \frac{\partial g}{\partial I}}& {\displaystyle \frac{\partial g}{\partial V}}\\ {\displaystyle \frac{\partial h}{\partial U}}& {\displaystyle \frac{\partial h}{\partial I}}& {\displaystyle \frac{\partial h}{\partial V}}\end{array}\right)=\left(\begin{array}{ccc}-\beta V& 0& -\beta U\\ \beta V& -\delta & \beta U\\ 0& p& -c\end{array}\right),\end{array}$$

which evaluated at any point $x_s\in {\mathcal{X}}_s$ reads

$$\begin{array}{c}{A}_s=\left(\begin{array}{ccc}0& 0& -\beta U_s\\ 0& -\delta & \beta U_s\\ 0& p& -c\end{array}\right),\end{array}$$

with U_s ∈ [0, ∞). Then, the eigenvalues (λ ₁, λ ₂, λ ₃) are given by the solution to $Det(A_s-\lambda I)=0,$ i.e.,

$$\lambda [-{\lambda }^2-(c+\delta )\lambda +(\beta U_{s}p-c\delta )]=0.$$

The first eigenvalue is trivially given by ${\lambda }_1=0$. The other two, are given by:

$${\lambda }_{2,3}=-\frac{(c+\delta )\pm \sqrt{{(c+\delta )}^2+4c\delta (\frac{U_s}{{\mathcal{U}}_c}-1)}}{2}.$$

To analyze the eigenvalues qualitatively, note that for $U_s={\mathcal{U}}_c$

$${\lambda }_{2,3}=-\frac{(c+\delta )\pm (c+\delta )}{2},$$

which means that ${\lambda }_2=0$ and ${\lambda }_3=-(c+\delta )<0$ (given that c, δ > 0). Furthermore, λ ₂ < 0 and λ ₃ < 0 for $U_s<{\mathcal{U}}_c$; and λ ₂ > 0 and λ ₃ < 0 for $U_s>{\mathcal{U}}_c$. Since the maximum eigenvalue is the one dominating the stability behavior of the equilibrium under consideration, it is possible to infer how the system behaves near some segments of ${\mathcal{X}}_s$. The first intuition is that the equilibrium set

$${\mathcal{X}}_s^1:=\{(U,I,V)\in {\mathbb{R}}^3:U\in [0,{\mathcal{U}}_c),I=0,V=0\},$$ (2.8)

is stable, and that the equilibrium set

$${\mathcal{X}}_s^2:=\{(U,I,V)\in {\mathbb{R}}^3:U\in [{\mathcal{U}}_c,\infty ),I=0,V=0\},$$ (2.9)

is unstable. These are just intuitions, given that one of the eigenvalues of the linearized system is null and so the linear approximation cannot be used to fully determine the stability of the nonlinear system (Theorem of Hartman (1982); Perko (2013)). To formally prove the asymptotic stability of ${\mathcal{X}}_s^1$ in a given domain, it is necessary to show its global attractivity (in such domain) and local $ϵ-\delta$ stability.

3. Asymptotic stability of the equilibrium sets

A key point to analyze the general asymptotic stability (AS) of system (2.1) is to consider stability of the complete equilibrium sets ${\mathcal{X}}_s^1$ and ${\mathcal{X}}_s^2,$ and not of the single points inside them (as defined in Definition 5, Definition 6 and 7, in Appendix 1). As it is shown in the next subsections, there is no single AS equilibrium points in this system, although there is an AS equilibrium set (i.e., ${\mathcal{X}}_s^1$).

As stated in Definition 7, in 1, the AS of ${\mathcal{X}}_s^1$ requires both, attractivity and $ϵ-\delta$ stability, which are stated in the next two subsections, respectively. Then, in Section 3.3 the AS theorem is formally stated.

3.1. Attractivity of set ${\mathcal{X}}_s^1$ in $\mathcal{X}$

Before proceeding with the formal theorems of the attractivity of ${\mathcal{X}}_s^1,$ let us consider the following key property of system (2.1) concerning the attractivity of ${\mathcal{X}}_s$.

Property 1 (Attractivity of

${\mathcal{X}}_s$ ) Consider system (2.1) constrained by the positive set $\mathbb{X},$ at some arbitrary time t ₀, with U(t ₀) > 0, I(t ₀) ≥ 0 and V(t ₀) > 0 (i.e., $x\left(t_0\right)=(U\left(t_0\right),I\left(t_0\right),V\left(t_0\right))\in \mathcal{X}$ ). Then, U _∞ ≔ lim_t → ∞ U(t) is a constant value smaller than U(t ₀), $I_{\infty }:={\lim }_{t\to \infty }I\left(t\right)=0$ and $V_{\infty }:={\lim }_{t\to \infty }V\left(t\right)=0,$ which means that $x\left(t\right)=\left(U\right(t),I(t),V(t\left)\right)$ tends to some state in ${\mathcal{X}}_s$ .

Proof

Since $\dot{U}\left(t\right)\le 0$ for all t ≥ 0 and all $(U\left(t_0\right),I\left(t_0\right),V\left(t_0\right))\in \mathcal{X},$ by (2.1a) U(t) is a decreasing function (no oscillation can occur). Since U(t ₀) > 0 and V(t ₀) > 0, then $U_{\infty }={\lim }_{t\to \infty }U\left(t\right)$ is a constant value in [0, U(t ₀)). Given that U(t) converges to a finite fixed value, then $\dot{U}\left(t\right)=0$ as t → ∞ by (2.1a). This implies - by the same Eq. (2.1a) - that $U\left(t\right)V\left(t\right)=0$ as t → ∞ and, so, from Eq. (2.1b), that $\dot{I}\left(t\right)=-\delta I\left(t\right)$ as t → ∞. Then $I_{\infty }={\lim }_{t\to \infty }I\left(t\right)=0$. Finally, by Eq. (2.1c)), $\dot{V}\left(t\right)=-\delta V\left(t\right)$ as t → ∞. Then $V_{\infty }={\lim }_{t\to \infty }V\left(t\right)=0,$ which completes the proof. □

Property 1 states that ${\mathcal{X}}_s$ is an attractive set for system (2.1), in $\mathcal{X},$ but not the smallest attractive set. Next, conditions are given to show that the smallest attractive set is given by ${\mathcal{X}}_s^1$.

Theorem 3.1 (Attractivity of

${\mathcal{X}}_s^1$ ) Consider system (2.1) constrained by the positive set $\mathbb{X}$ . Then, the set ${\mathcal{X}}_s^1$ defined in (2.8) is the smallest attractive set in $\mathcal{X}$ . Furthermore, ${\mathcal{X}}_s^2,$ defined in (2.9) , is not attractive.

Proof

The proof is divided into two parts. First it is proved that ${\mathcal{X}}_s^1$ is an attractive set, and then, that it is the smallest one.

Attractivity of ${\mathcal{X}}_s^1$ :

The attractivity of ${\mathcal{X}}_s$ in $\mathcal{X}$ was already proved in Property 1. So, to prove the attractivity of ${\mathcal{X}}_s^1$ in $\mathcal{X}$ (and to show that ${\mathcal{X}}_s^2$ is not attractive) it remains to demonstrate that $U_{\infty }\in [0,{\mathcal{U}}_c)$. From system (2.1), by replacing (2.1a) in (2.1b), it follows that

$$\dot{I}\left(t\right)=\beta U\left(t\right)V\left(t\right)-\delta I\left(t\right)=-\dot{U}\left(t\right)-\delta I\left(t\right),$$ (3.1)

which implies that

$$I\left(t\right)=(-\frac{1}{\delta })(\dot{I}\left(t\right)+\dot{U}\left(t\right)).$$ (3.2)

Rearranging (2.1c) yields

$$V\left(t\right)=\frac{1}{c}(pI\left(t\right)-\dot{V}\left(t\right)).$$ (3.3)

Then, replacing (3.2) in (3.3), we have

$$V\left(t\right)=[p(-\frac{1}{\delta })(\dot{I}\left(t\right)+\dot{U}\left(t\right))-\dot{V}\left(t\right)]\frac{1}{c}.$$ (3.4)

Finally, by substituting (3.4) in (2.1a), and multiplying by 1/U(t) both sides of the equation (without loss of generality we can assume that $U\left(t\right)\ne 0$), it follows that

$$\frac{1}{U\left(t\right)}\dot{U}\left(t\right)=\frac{\beta p}{c\delta }\dot{U}\left(t\right)+\frac{\beta p}{c\delta }\dot{I}\left(t\right)+\frac{\beta }{c}\dot{V}\left(t\right).$$ (3.5)

This latter equation can be integrated, for general initial conditions U ₀, I ₀ and V ₀, as follows:

$$\ln \left(\frac{U\left(t\right)}{U_0}\right)=\frac{\beta p}{c\delta }(U\left(t\right)-U_0)+\frac{\beta p}{c\delta }(I\left(t\right)-I_0)+\frac{\beta }{c}(V\left(t\right)-V_0).$$ (3.6)

Now, by defining U _∞ ≔ lim_t → ∞ U(t), I _∞ ≔ lim_t → ∞ I(t), V _∞ ≔ lim_t → ∞ V(t), and recalling from Property 1 that $I_{\infty }=V_{\infty }=0,$ the latter equation for t → ∞, reads

$$\ln \left(\frac{U_{\infty }}{U_0}\right)=\frac{\beta p}{c\delta }(U_{\infty }-U_0)+\frac{\beta p}{c\delta }(I_{\infty }-I_0)+\frac{\beta }{c}(V_{\infty }-V_0)=\frac{\beta p}{c\delta }{U}_{\infty }-{\mathcal{R}}_0-\frac{\beta p}{c\delta }{I}_0-\frac{\beta }{c}{V}_0=\frac{\beta p}{c\delta }{U}_{\infty }-{\mathcal{R}}_0+{\mathcal{K}}_0,$$ (3.7)

where ${\mathcal{R}}_0:=\frac{\beta p}{c\delta }{U}_0$ (as it was defined in (2.5)) and

$${\mathcal{K}}_0:=-\frac{\beta }{c}(\frac{p}{\delta }{I}_0+V_0).$$ (3.8)

Note that ${\mathcal{R}}_0$ is a function of U ₀ while ${\mathcal{K}}_0$ is a function of I ₀ and V ₀ and, furthermore, ${\mathcal{R}}_0>0$ and ${\mathcal{K}}_0<0$ for every $x_0=(U_0,I_0,V_0)\in \mathcal{X}$. Then, after some manipulation, (3.7) reads

$$-\frac{\beta p}{c\delta }{U}_{\infty }{e}^{-\frac{\beta p}{c\delta }{U}_{\infty }}=-\frac{\beta p}{c\delta }{U}_0{e}^{-{\mathcal{R}}_0}{e}^{{\mathcal{K}}_0}=-{\mathcal{R}}_0{e}^{-{\mathcal{R}}_0}{e}^{{\mathcal{K}}_0}.$$ (3.9)

Now, by denoting

$$z=z({\mathcal{R}}_0,{\mathcal{K}}_0):=-{\mathcal{R}}_0{e}^{-{\mathcal{R}}_0}{e}^{{\mathcal{K}}_0},$$ (3.10)

and

$$y:=-\frac{\beta p}{c\delta }{U}_{\infty },$$ (3.11)

the latter equation can be written as

$$W\left(z\right)=y,$$ (3.12)

or

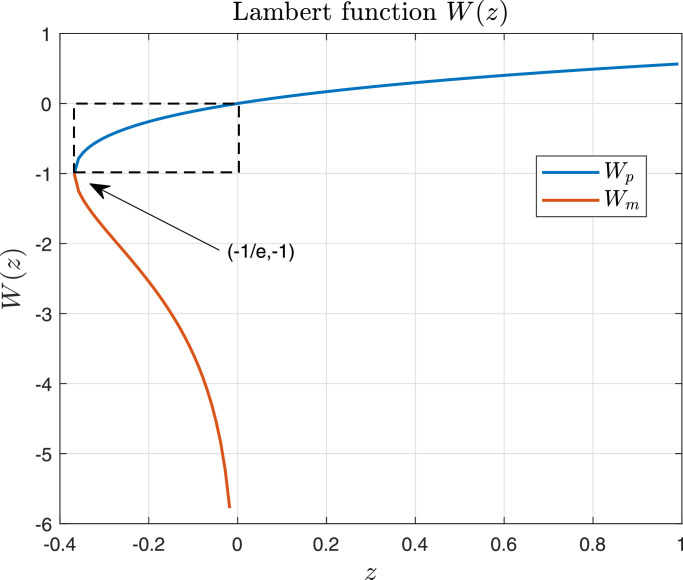
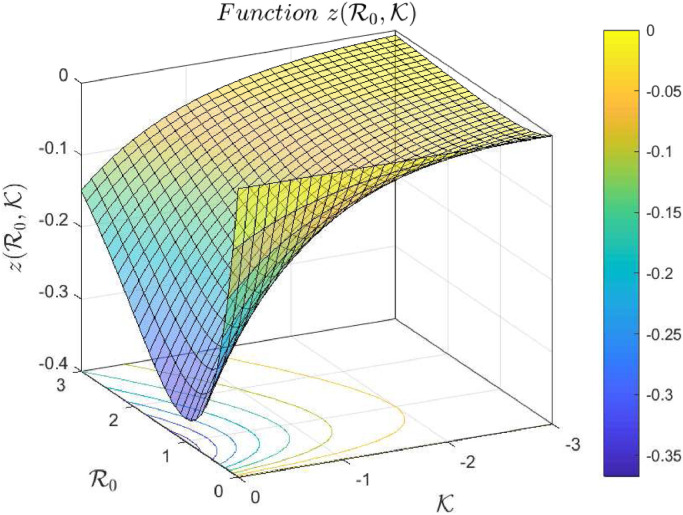
$$W(-{\mathcal{R}}_0{e}^{-{\mathcal{R}}_0}{e}^{{\mathcal{K}}_0})=-\frac{\beta p}{c\delta }{U}_{\infty },$$ (3.13)

where W( · ) is a Lambert function. Fig. 1 shows the graph of such a function, where it can be seen that it has two branches, denoted as W_p and W_m. However, $W(·)=W_p(·)$ in this case, since $W_m\to -\infty$ for $z\to 0^{-},$ which has not biological sense. Note that U _∞ is a finite value in [0, U ₀). Also $-1/e<z({\mathcal{R}}_0,{\mathcal{K}}_0)\le 0$ for ${\mathcal{R}}_0>0$ and ${\mathcal{K}}_0<0$ (Fig. 2 shows a plot of function $z({\mathcal{R}}_0,{\mathcal{K}}_0)$ for negative values of ${\mathcal{K}}_0$ and positive values of ${\mathcal{R}}_0$), and W_p maps $(-1/e,0]$ into $(-1,0],$ which implies that

$$1>-W\left(z({\mathcal{R}}_0,{\mathcal{K}}_0)\right)\ge 0,$$ (3.14)

for ${\mathcal{R}}_0>0$ and ${\mathcal{K}}_0<0$. Thus, by (3.13), it follows that

$$\begin{array}{ccc}\hfill U_{\infty }& =& -\frac{c\delta }{\beta p}W(-{\mathcal{R}}_0{e}^{-{\mathcal{R}}_0}{e}^{{\mathcal{K}}_0})\hfill \\ & =& -{\mathcal{U}}_{c}W(-{\mathcal{R}}_0{e}^{-{\mathcal{R}}_0}{e}^{{\mathcal{K}}_0})\hfill \\ & \in & [0,{\mathcal{U}}_c),\hfill \end{array}$$ (3.15)

which completes the proof.

${\mathcal{X}}_s^1$ is the smallest attractive set:

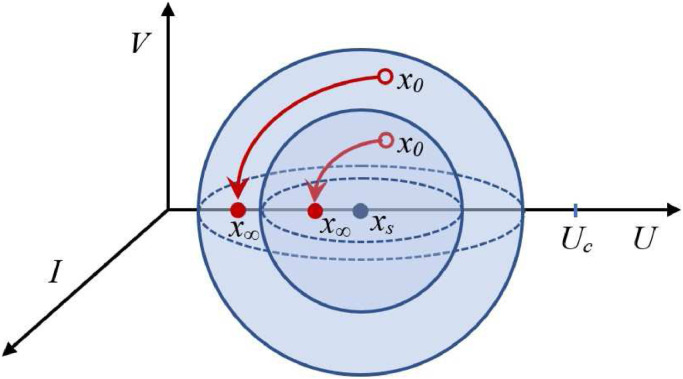
It is clear from the previous analysis, that any initial state $x_0=(U_0,I_0,V_0)$ in $\mathcal{X}$ converges to a state $x_{\infty }=(U_{\infty },0,0)$ with $U_{\infty }\in [0,{\mathcal{U}}_c)$. This means that ${\mathcal{X}}_s^2$ is not attractive in $\mathcal{X}$. Let us consider now a state $x_s\in {\mathcal{X}}_s^1$ and an arbitrary small ball of radius ϵ > 0, w.r.t. $\mathcal{X},$ around it, ${\mathbb{B}}_{ϵ}\left(x_s\right)\in \mathcal{X}$. Take two arbitrary initial states $x_{0,1}=(U_{0,1},I_{0,1},V_{0,1})$ and $x_{0,2}=(U_{0,2},I_{0,2},V_{0,2})$ in ${\mathbb{B}}_{ϵ}\left(x_s\right),$ such that U _0,1 ≠ U _0,2 and V _0,1 ≠ V _0,2. These two states converge, according to Eq. (3.15), to $x_{\infty ,1}=(U_{\infty ,1},0,0)$ and $x_{\infty ,2}=(U_{\infty ,2},0,0),$ respectively, with $U_{\infty ,1},U_{\infty ,2}\in [0,{\mathcal{U}}_c)$. Given that function z(R, K) is monotone (injective) in ${\mathcal{R}}_0$ (and so in U ₀) and W(z) is monotone (injective) in z, then U _∞,1 ≠ U _∞,2. This means that, although both initial states converge to some state in ${\mathcal{X}}_s^1,$ they necessarily converge to different points. Therefore neither single states $x_s\in {\mathcal{X}}_s^1$ nor subsets of ${\mathcal{X}}_s^1$ are attractive in $\mathcal{X}$. So, ${\mathcal{X}}_s^1$ is the smallest attractive set and the proof is concluded. □

Remark 2

Note that ${\mathcal{X}}_s^1$ and ${\mathcal{X}}_s^2$ are in the closure of the open set $\mathcal{X},$ which is not in $\mathcal{X}$. In other words, Theorem 3.1 shows that any initial state in $\mathcal{X}$ converges to a point onto the boundary of $\mathcal{X}$ that does not belong to $\mathcal{X}$. Furthermore note that, an initial state of the form (U ₀, 0, 0), $U_0>{\mathcal{U}}_c,$ (i.e., a state in ${\mathcal{X}}_s^2$) cannot be attracted by any set since it is an equilibrium state (every state in ${\mathcal{X}}_s^2$ will remain unmodified). This is the reason why it is not possible to consider the attractivity of ${\mathcal{X}}_s^2$ in $\mathcal{X}$.

Fig. 1.

Lambert function. W(z) has two branches, denoted as W_p (in blue) and W_m (in red). Both branches are defined for $z\in [-1/e,0]$; however ${\lim }_{z\to 0^{-}}{W}_p=0$ while ${\lim }_{z\to 0^{-}}{W}_m=-\infty ,$ which means that only the branch W_p will be used in our analysis, as it is shown in the proof of Theorem 3.1.

Fig. 2.

Function $z({\mathcal{R}}_0,{\mathcal{K}}_0),$ for ${\mathcal{R}}_0\ge 0$ and ${\mathcal{K}}_0\le 0$. Note that $z({\mathcal{R}}_0,{\mathcal{K}}_0)>-1/e=-0.3679$ for all values of ${\mathcal{R}}_0\ge 0$ and ${\mathcal{K}}_0\le 0$.

3.2. Local $ϵ-\delta$ stability of ${\mathcal{X}}_s^1$

The next theorem shows the formal Lyapunov (or $ϵ-\delta$) stability of the equilibrium set ${\mathcal{X}}_s^1$.

Theorem 3.2

Consider system (2.1) constrained by the positive set $\mathbb{X}$ . Then, the equilibrium set ${\mathcal{X}}_s^1$ defined in (2.8) is locally $ϵ-\delta$ stable.

Proof

Let us consider a particular equilbrium point x_s ≔ (U_s, 0, 0), with $U_s\in [0,{\mathcal{U}}_c)$ (i.e., $x_s\in {\mathcal{X}}_s^1$). Then a Lyapunov function candidate is given by (similar to one used in Nangue (2019) for chronic infections)

$$J\left(x\right):=U-U_s-U_s\ln \left(\frac{U}{U_s}\right)+I+\frac{\delta }{p}V.$$ (3.16)

This function is continuous in $\mathbb{X},$ is positive for all nonegative x ≠ x_s and, furthermore, $J\left(x_s\right)=0$. Function J evaluated at the solutions of system (2.1) reads:

$$\begin{array}{ccc}\hfill \frac{\partial J\left(x\left(t\right)\right)}{\partial t}& =& \frac{\partial J}{\partial x}\dot{x}\left(t\right)=\left[\frac{\mathit{dJ}}{\mathit{dU}}\frac{\mathit{dJ}}{\mathit{dI}}\frac{\mathit{dJ}}{\mathit{dV}}\right]\left[\begin{array}{c}-\beta U\left(t\right)V\left(t\right)\\ \beta U\left(t\right)V\left(t\right)-\delta I\left(t\right)\\ \mathit{pI}\left(t\right)-\mathit{cV}\left(t\right)\end{array}\right]\hfill \\ & =& \left[(1-\frac{U_s}{U\left(t\right)})1\frac{\delta }{p}\right]\left[\begin{array}{c}-\beta U\left(t\right)V\left(t\right)\\ \beta U\left(t\right)V\left(t\right)-\delta I\left(t\right)\\ \mathit{pI}\left(t\right)-\mathit{cV}\left(t\right)\end{array}\right]\hfill \\ & =& (-\beta U\left(t\right)V\left(t\right)+U_s\beta V\left(t\right))+(\beta U\left(t\right)V\left(t\right)-\delta I\left(t\right))+(\delta I\left(t\right)-\frac{\delta c}{p}V\left(t\right))\hfill \\ & =& U_s\beta V\left(t\right)-\frac{\delta c}{p}V\left(t\right)=V\left(t\right)(U_s\beta -\frac{\delta c}{p}).\hfill \end{array}$$ (3.17)

Now, given $U_s\in [0,{\mathcal{U}}_c),$ with ${\mathcal{U}}_c=\frac{\delta c}{\beta p},$ it follows that $\dot{J}\left(x\left(t\right)\right)\le 0$ for every $x\in \mathbb{X}$ (note that it is not true that $\dot{J}\left(x\left(t\right)\right)<0$ for x ≠ x_s, as shown next, in Remark 3). Then, J is a Lyapunov function for system (2.1), which means that each $x_s\in {\mathcal{X}}_s^1$ is $ϵ-\delta$ stable (see Theorem A.1 in 1). Therefore, it is easy to see that the equilibrium set ${\mathcal{X}}_s^1$ is also $ϵ-\delta$ stable, which completes the proof. □

Remark 3

Note that, in the latter proof, it is not true that $\dot{J}\left(x\left(t\right)\right)<0$ for every nonegative x ≠ x_s. If for instance, the function $\dot{J}\left(x\left(t\right)\right)$ is evaluated at ${\widehat{x}}_s=(\widehat{U},0,0),$ with $\widehat{U}\ne U_s,$ we have that $\dot{J}\left({\widehat{x}}_s\left(t\right)\right)=0$. In fact, $\dot{J}\left(x\left(t\right)\right)$ is null along the whole U axis, given that this axis is an equilibrium set. This means that the (individual) states in ${\mathcal{X}}_s^1$ are $ϵ-\delta$ stable, but not attractive.

A schematic plot of such a behavior can be seen in Fig. 3 .

Remark 4

A similar behavior can be seen in system $\dot{x}=Ax,$ when $A=[0-1;0-1],$ or the 2-state Kermack–McKendrick epidemic model (Brauer, 2005, Brauer, Castillo-Chavez, Castillo-Chavez, 2012): $\dot{S}=\beta SI,$ $\dot{I}=\beta SI-\delta I,$ being S the susceptible and I the infected individuals. In this latter model, ${\mathcal{R}}_0:=(\delta /\beta )S_0$ and the critical value for S is $S_c=\delta /\beta$. The AS set is given by all the states of the form x_s ≔ (S_s, 0), with S_s ∈ [0, S_c). Furthermore, for this system, the maximum of I occurs when $S=S_c$.

Fig. 3.

Every point in ${\mathcal{X}}_s^1$ is $ϵ-\delta$ stable but not attractive. Initial states x₀ starting arbitrarily close to x_s remain (for all t ≥ 0) arbitrarily close to x_s, but do not converge to x_s. As a consequence, set ${\mathcal{X}}_s^1$ is AS but the points inside it are not.

3.3. Asymptotic stability of ${\mathcal{X}}_s^1$

In the next Theorem, based on the previous results concerning the attractivity and $ϵ-\delta$ stability of ${\mathcal{X}}_s^1,$ the asymptotic stability is formally stated.

Theorem 3.3

Consider system (2.1) constrained by the positive set $\mathbb{X}$ . Then, the set ${\mathcal{X}}_s^1$ defined in (2.8) is smallest asymptotically stable (AS) equilibrium set, with a domain of attraction given by $\mathcal{X}$ .

Proof

The proof follows from Theorems 3.1, which states that ${\mathcal{X}}_s^1$ is the smallest attractive in $\mathcal{X},$ and 3.2, which states the local $ϵ-\delta$ stability of ${\mathcal{X}}_s^1$. □

A critical consequence of the latter Theorem is that no equilibrium point in ${\mathcal{X}}_s$ (neither in ${\mathcal{X}}_s^1,$ nor in ${\mathcal{X}}_s^2$) can be used as setpoint in a control strategy design. The effect of antivirals (pharmocodynamic), for instance, is just to reduce the virus infectivity (by reducing the infection rate β) or the production of infectious virions (by reducing the replication rate p) (Hernandez-Vargas, 2019). So, the previous stability analysis is still valid for such controlled systems, since only a modification of some of the parameters defining ${\mathcal{U}}_c$ is done. In such a context, only a controller able to consider the whole set ${\mathcal{X}}_s^1$ as a target (a set-based control strategy, as zone MPC (Ferramosca, Limon, González, Odloak, Camacho, 2010, González, Rivadeneira, Ferramosca, Magdelaine, Moog, 2020)) will be fully successful in controlling system (2.1). Further details concerning antiviral treatments are given next, in Section 4.1.

4. Characterization for different initial conditions

In this section some further properties of system (2.1) concerning its dynamic are stated, based on the initial conditions at the infection time $t=0$. The objective is to fully characterize the states behavior in a qualitative way, including the times at which the virus and the infected cells reach their peaks. First, Property 2 states some characteristics of U _∞ for different initial conditions. Then, Theorem 4.1 states a general relationship between the peak times of V and I and the time at which U reaches its critical value ${\mathcal{U}}_c$.

Property 2

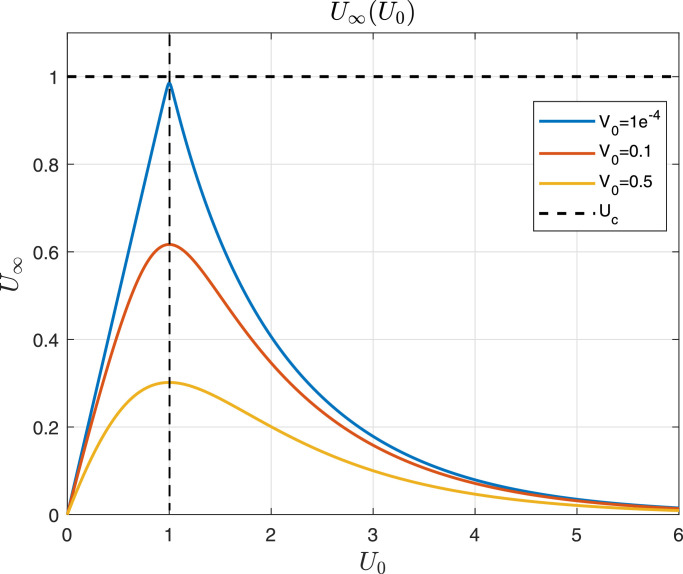
Consider system (2.1) , constrained by the positive set $\mathbb{X},$ at the beginning of the infection, i.e., $U\left(0\right)=U_0>0,$ $I\left(0\right)=0$ and $V\left(0\right)=V_0>0$ (i.e., $x\left(0\right)=\left(U\right(0),I(0),V(0\left)\right)\in \mathcal{X}$ ). Consider also that V ₀ is small enough to describe the beginning of the infection. Then,

• 1. U _∞ → 0 when U ₀ → ∞ or U ₀ → 0.
• 2. $U_{\infty }\to {\mathcal{U}}_c$ when $U_0\to {\mathcal{U}}_c$ .
• 3. $0<U_{\infty }(U_{0,1},I_0,V_0)<U_{\infty }(U_{0,2},I_0,V_0)<{\mathcal{U}}_c,$ for initial conditions $U_{0,1}<U_{0,2}<{\mathcal{U}}_c$ .
• 4. $0<U_{\infty }(U_{0,2},I_0,V_0)<U_{\infty }(U_{0,1},I_0,V_0)<{\mathcal{U}}_c,$ for initial conditions ${\mathcal{U}}_c<U_{0,1}<U_{0,2}$ .

Proof

If $I_0=0$ and V ₀ ≈ 0 then ${\mathcal{K}}_0\approx 0$. Therefore $W(-{\mathcal{R}}_0{e}^{{\mathcal{K}}_0-{\mathcal{R}}_0})\approx W(-{\mathcal{R}}_0{e}^{-{\mathcal{R}}_0}),$ and $U_{\infty }\approx -{\mathcal{U}}_{c}W(-{\mathcal{R}}_0{e}^{-{\mathcal{R}}_0})$ by (3.13).

• 1. $W(-{\mathcal{R}}_0{e}^{-{\mathcal{R}}_0})\to 0$ when $-{\mathcal{R}}_0{e}^{-{\mathcal{R}}_0}\to 0,$ which means that either ${\mathcal{R}}_0\to 0$ or ${\mathcal{R}}_0\to \infty$. This implies that U ₀ → 0 or U ₀ → ∞, respectively.
• 2. $W(-{\mathcal{R}}_0{e}^{-{\mathcal{R}}_0})\to -1$ when $-{\mathcal{R}}_0{e}^{-{\mathcal{R}}_0}\to -1/e,$ which is true if ${\mathcal{R}}_0\to 1$ or, the same, when $U_0\to {\mathcal{U}}_c$.
• 3. $z\left({\mathcal{R}}_0\right)=-{\mathcal{R}}_0{e}^{-{\mathcal{R}}_0}$ is strictly decreasing for ${\mathcal{R}}_0\in (0,1)$ (note that ${{\mathcal{R}}_0}_1:=\frac{c\delta U_{0,1}}{\beta p}$ and ${{\mathcal{R}}_0}_2:=\frac{c\delta U_{0,2}}{\beta p}$ are in (0,1), since they are smaller than ${\mathcal{U}}_c$), while $-W_p(·)$ is strictly decreasing in $(-1/e,0)$. So, $0<-W_p(-{{\mathcal{R}}_0}_1{e}^{-{{\mathcal{R}}_0}_1})<-W_p(-{{\mathcal{R}}_0}_2{e}^{-{{\mathcal{R}}_0}_2})<1,$ which implies that $0<U_{\infty }(U_{0,1},I_0,V_0)<U_{\infty }(U_{0,2},I_0,V_0)<{\mathcal{U}}_c$.
• 4. $z\left({\mathcal{R}}_0\right)=-{\mathcal{R}}_0{e}^{-{\mathcal{R}}_0}$ is strictly increasing for ${\mathcal{R}}_0\in (1,\infty ),$ while $-W_p(·)$ is strictly decreasing in $(-1/e,0)$. So, $0<-W_p(-{{\mathcal{R}}_0}_2{e}^{-{{\mathcal{R}}_0}_2})<-W_p(-{{\mathcal{R}}_0}_1{e}^{-{{\mathcal{R}}_0}_1})<1,$ which implies that $0<U_{\infty }(U_{0,2},I_0,V_0)<U_{\infty }(U_{0,1},I_0,V_0)<{\mathcal{U}}_c$. Fig. 4 shows U _∞ as a function of U ₀, taking V ₀ as a parameter. □

Theorem 4.1 Virus behavior from the infection time —

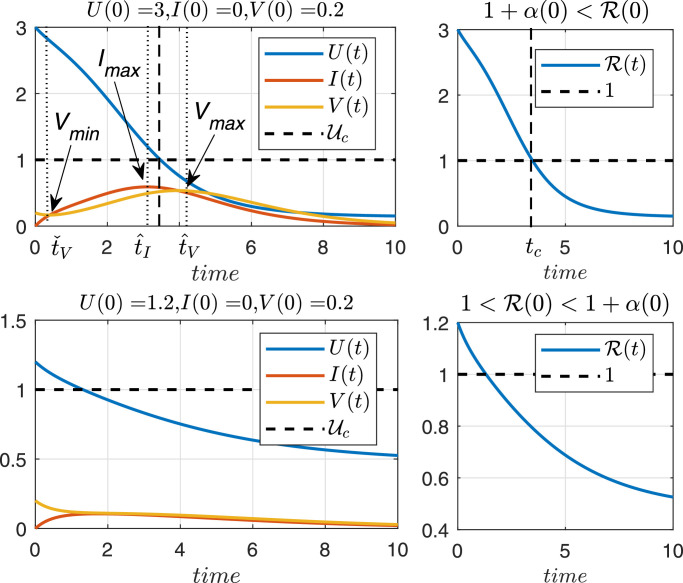
Consider system (2.1) , constrained by the positive set $\mathbb{X},$ at the beginning of the infection, i.e., $U\left(0\right)=U_0>0,$ $I\left(0\right)=0$ and $V\left(0\right)=V_0>0$ . If the virus spreads (according to Definition 1 ), then ${\mathcal{R}}_0>1+\alpha \left(0\right),$ for some α(0) > 0 (or, the same, $U_0>{\mathcal{U}}_c$ ) and there exist positive times ${\check{t}}_V,$ ${\widehat{t}}_I,$ t_c and ${\widehat{t}}_V,$ such that ${\check{t}}_V<{\widehat{t}}_I<t_c<{\widehat{t}}_V,$ where ${\check{t}}_V$ and ${\widehat{t}}_V$ are the times at which V(t) reaches a local minimum and a local maximum, respectively, ${\widehat{t}}_I$ is the time at which I(t) reaches a local maximum, and t_c is the time at which U(t) reaches ${\mathcal{U}}_c$ . Furthermore, $\dot{V}\left(t\right)<0$ for all $t>{\widehat{t}}_V$ .

Proof

First, note that $\dot{V}\left(0\right)=pI\left(0\right)-cV\left(0\right)<0$ since the initial conditions are $I\left(0\right)=0$ and V(0) > 0. Even more, assuming the virus spreads, which means that V(t) reaches a local maximum at some time ${\widehat{t}}_V>0$. Therefore, V(t) must reach a local minimum at some $0<{\check{t}}_V<{\widehat{t}}_V$.

Now, by Lemma 1 in Appendix 3, it is $\mathcal{R}\left({\check{t}}_V\right)>1$ and $\mathcal{R}\left({\widehat{t}}_V\right)<1,$ respectively, and it is easy to see that $\mathcal{R}\left(t\right)$ is a decreasing function, so it follows that ${\mathcal{R}}_0>\mathcal{R}\left({\check{t}}_V\right)>1$. Then there exists α(0) > 0 such that ${\mathcal{R}}_0>1+\alpha \left(0\right)$ and, besides, $0<{\check{t}}_V<t_c<{\widehat{t}}_V$.

From the minimum and maximum conditions of V, at times ${\check{t}}_V$ and ${\widehat{t}}_V,$ we have $\dot{V}\left({\check{t}}_V\right)=0,$ $\ddot{V}\left({\check{t}}_V\right)>0$ and $\dot{V}\left({\widehat{t}}_V\right)=0,$ $\ddot{V}\left({\widehat{t}}_V\right)<0,$ respectively. After some algebraic computation, it is easy to see that $\dot{I}\left({\check{t}}_V\right)>0$ and $\dot{I}\left({\widehat{t}}_V\right)<0,$ which means that I(t) must reach a maximum at some time ${\widehat{t}}_I,$ fulfilling ${\check{t}}_V<{\widehat{t}}_I<{\widehat{t}}_V$. Moreover, it must be

$$\dot{I}\left({\widehat{t}}_I\right)=\beta U\left({\widehat{t}}_I\right)V\left({\widehat{t}}_I\right)-\delta I\left({\widehat{t}}_I\right)=0.$$ (4.1)

Given that $\dot{V}\left(t\right)>0$ for ${\check{t}}_V<t<{\widehat{t}}_V$ (it goes from its minimum to its maximum), then by (2.1.a), $I\left({\widehat{t}}_I\right)>\frac{c}{p}V\left({\widehat{t}}_I\right)$. Replacing this latter condition in (4.1), it follows that

$$(\beta U\left({\widehat{t}}_I\right)-\frac{\delta c}{p})V\left({\widehat{t}}_I\right)>\beta U\left({\widehat{t}}_I\right)V\left({\widehat{t}}_I\right)-\delta I\left({\widehat{t}}_I\right)=0,$$ (4.2)

which implies that $\mathcal{R}\left({\widehat{t}}_I\right)=\frac{\beta pU\left({\widehat{t}}_I\right)}{\delta c}>1$ and, then, ${\widehat{t}}_I<t_c$. Therefore, $t_0<{\check{t}}_V<{\widehat{t}}_I<t_c<{\widehat{t}}_V,$ which concludes the proof. □

Remark 5

The value of α(0) is necessary to properly understand and characterize the system behavior according to the initial conditions and parameters. In epidemiological models (SIR, etc.), where ${\mathcal{R}}_0>1$ is a necessary and sufficient condition for the disease to spread in a population, in our case ${\mathcal{R}}_0>1$ is not a sufficient condition for the virus to spread in the host body. The only thing Theorem 4.1 ensures (by its contrapositive) is that a sufficient condition for the virus to not spread in the host body at time t > 0 is given by ${\mathcal{R}}_0<1$ (or $U\left(0\right)<{\mathcal{U}}_c$). See Fig. 6, lower plot, for an example. The value of α(0) can be computed numerically and it is usually small in comparison with ${\mathcal{R}}_0$ (for all the patients simulated in Section 5, $\alpha \left(0\right)<1\times {10}^{-4}$).

Fig. 4.

According to Eq. (3.13), U_∞(U₀) is plotted for different values of V₀. All parameters are equal to 1 for simplicity, which means that ${\mathcal{U}}_c=1$.

Fig. 6.

Time evolution of U, I and V, with unitary parameters β, δ, p, c, for initial conditions $U_0=3,I_0=0,V_0=0.2$ (upper plot) and $U_0=1.2,I_0=0,V_0=0.12$ (lower plot).

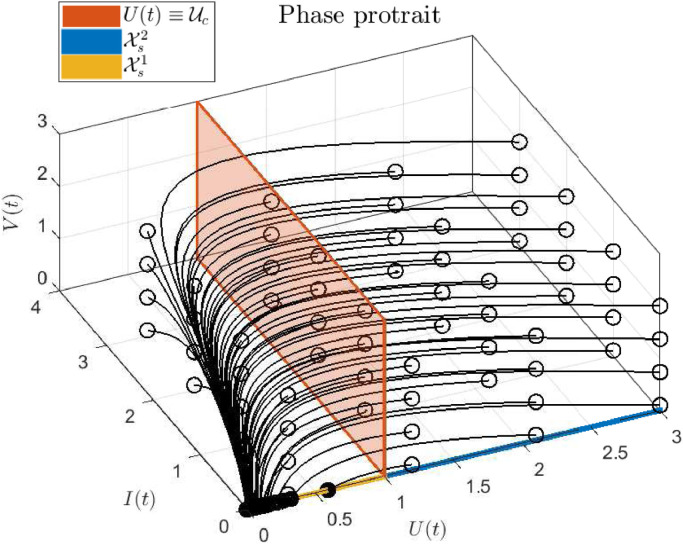
To clarify the results of this section, Figs. 5 and 6 show a phase portrait and a state time evolution corresponding to system (2.1), when all parameters are equal to 1 (for simplicity), which means that ${\mathcal{U}}_c=1$. The first plot (Fig. 5) depicts how every state trajectory - even those starting close to ${\mathcal{X}}_s^2$ - converges to ${\mathcal{X}}_s^1$. As stated in Property 2, U _∞ approaches ${\mathcal{U}}_c$ from below, as U(0) approaches ${\mathcal{U}}_c$ from above. Also it can be seen how the virus load starts to decrease only once U(t) is smaller than ${\mathcal{U}}_c,$ as stated in Theorem 4.1. On the other hand, the second plot (Fig. 6) shows the time evolution of U, I and V, for two different initial conditions. In the upper plot, initial conditions are selected such that $1+\alpha \left(0\right)<{\mathcal{R}}_0,$ while in the lower plot, the initial conditions produce $1<{\mathcal{R}}_0<1+\alpha \left(0\right)$. As it can be seen, only in the first case the virus spread in the host body (i.e., $\dot{V}\left(t\right)>0,$ for some t > 0), as stated in Theorem 4.1.

Fig. 5.

Phase portrait of system (2.1), with unitary parameters. Empty circles represent the initial states, while solid circles represent final states. Note that only the initial states with $U_0>{\mathcal{U}}_c=1$ corresponds to scenarios with ${\mathcal{R}}_0>1$.

4.1. Remarks concerning antivirals treatments

Even though the analysis of potential antiviral treatments is out of the scope of this work, in this section some comments concerning the implications of Theorem 4.1 (and the system characterization) will be made. The antiviral effect can be modeled as a reduction of the virus infectivity in the presence of reverse transcriptase inhibitors (by reducing the infection rate β) and/or as a reduction in the production of infectious virions in the presence of protease inhibitors (by reducing the replication rate p). Let us assume that the antiviral pharmacodynamics (PD) corresponding to an antiviral is modeled as $p(1-\eta \left(t_r\right))$ (the analysis for β is almost the same), being η(t_r) ∈ (0, 1) the effectiveness of the antiviral and t_r the time of treatment initiation. The antiviral pharmacokynetics (PK) is not considered for simplicity, which means that the antivirals instantaneously modify η at time t_r. Then, as the virus monotonically goes to zero only once U(t) is below U_c, the antiviral will be effective (in the sense that the virus load starts decreasing as the treatment begins, and it does not increase again) only if the value of η(t_r) is such that $U\left(t_r\right)<{\mathcal{U}}_c\left(t_r\right):=\frac{c\delta }{p(1-\eta \left(t_r\right))\beta }$ (i.e., such that $\mathcal{R}\left(t_r\right)<1+\alpha \left(t_r\right)\approx 1$). This condition defines a threshold for the antiviral effectiveness (say, a minimal critical value η^c(t_r)) that may explain, from a pure mathematical point of view, why some antiviral may not work for some patients.

From a control theory point of view, the assertions made in Theorem 4.1 means that a control strategy devoted to steers V(t) to zero at any time by administering a time-variant dose of antivirals (for instance by using η(t) < η^c(t), for t > t_r), may be counterproductive. Indeed, to slow down V(t) by decreasing p or β, implies that ${\mathcal{U}}_c=\frac{c\delta }{p\beta }$ increases, but also soften the decreasing behavior of U(t). As a result, the time t_c (and so, the virus peak time ${\widehat{t}}_V$) may be delayed, which means that V(t) is maintained in a high level for a longer time. According to preliminary simulations, the delay of the virus peak may be significantly long for antiviral with maximal effectiveness smaller than the critical value.

5. Characterization of the SARS-CoV-2 target cell model

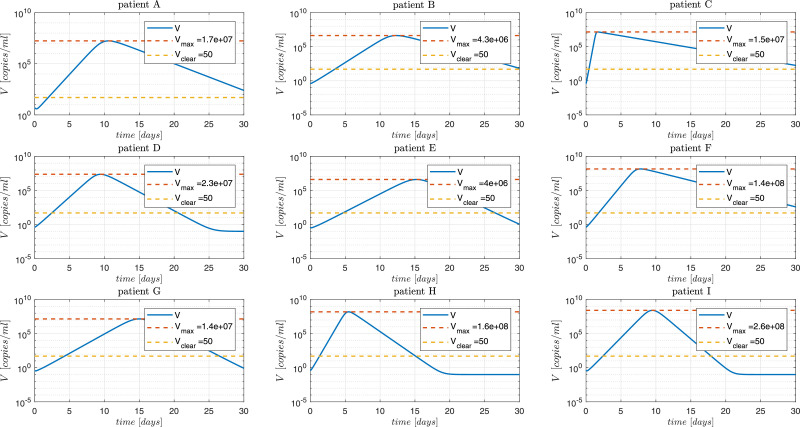
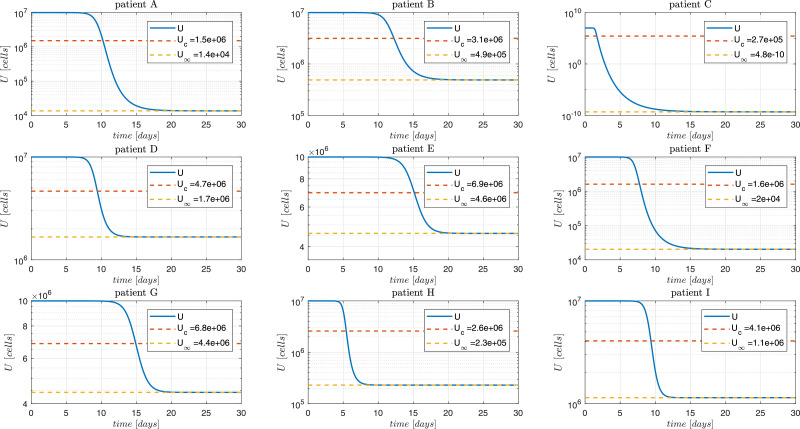
In this section, the model parameters in (2.1) will be associated to the patients labeled as A, B, C, D, E, F, G, H and I - reported in Wölfel et al. (2020). The initial number of target cells U ₀ is estimated as approximately 10⁷ cells (Hernandez-Vargas & Velasco-Hernandez, 2020). I ₀ is assumed to be 0 while V ₀ is determined by interpolation considering an incubation period of 7 days (note, that V ₀ ranges from 0.02 to 5.01 copies/mL which is below the detectable level of about 100 copies/mL). Moreover, the onset of the symptoms is assumed to occurs 4 to 7 days after the infection time (day 0, Figs. 7 and 8 ). The parameters and the initial conditions (U ₀, I ₀ and V ₀, with $t_0=0$ the infection time) of each patient are collected in Table 1 .

Fig. 7.

SARS-CoV-2 Dynamics. The continuous blue line is the simulation with parameter values presented in Hernandez-Vargas & Velasco-Hernandez, 2020. The patient labeling is as presented in Wölfel et al. (2020). V_clear denotes a value of 50 [copies/ml] under which the virus is not detectable.

Fig. 8.

Susceptible cells dynamics. The continuous blue line is the simulation with parameter values presented in Hernandez-Vargas & Velasco-Hernandez, 2020. The patient labeling is as presented in Wölfel et al. (2020). Simulation for the patient C shows a very low value of U_∞ (practically zero), which suggests that the selected value of $U_0=1.0e^7$ may be large.

Table 1.

Target limited cell model parameter values for different patients with COVID-19 (Hernandez-Vargas & Velasco-Hernandez, 2020).

Patient	β	δ	p	c
A	$9.98\times {10}^{-8}$	0.61	9.3	2.3
B	$1.77\times {10}^{-7}$	14.11	20.2	0.8
C	$8.89\times {10}^{-7}$	79.51	134.4	0.4
D	$3.15\times {10}^{-8}$	45.51	620.2	2.0
E	$5.61\times {10}^{-8}$	7.51	96.4	5.0
F	$1.41\times {10}^{-8}$	37.61	995.0	0.6
G	$1.77\times {10}^{-8}$	8.21	338.4	5.0
H	$1.58\times {10}^{-8}$	21.11	927.8	1.8
I	$4.46\times {10}^{-9}$	4.21	994.6	4.3

According to the system analysis of the previous sections, some relevant dynamical values are shown in Table 2 . Constant α(0) (defined in Theorem 4.1) is smaller than $10\times {10}^{-4}$ for all the patients, so it is not taken into account for the study.

Table 2.

Characterization Parameters of patients with COVID-19.

Patient	${\mathcal{U}}_c$	U∞	${\mathcal{R}}_0$	${\mathcal{K}}_0$	${\widehat{t}}_I$	tc	${\widehat{t}}_V$	Vmax
A	1.51 × 106	1.36 × 104	6.61	$-2.17\times {10}^{-7}$	10.16	10.24	10.58	1.73 × 107
B	3.15 × 106	4.88 × 105	3.18	$-6.87\times {10}^{-8}$	11.54	12.26	12.32	4.35 × 106
C	2.66 × 105	$4.81\times {10}^{-10}$	37.57	$-6.89\times {10}^{-7}$	1.43	1.67	1.69	1.47 × 107
D	4.65 × 106	1.67 × 106	2.15	$-4.89\times {10}^{-9}$	9.04	9.42	9.44	2.33 × 107
E	6.94 × 106	4.58 × 106	1.44	$-3.48\times {10}^{-9}$	15.02	15.16	15.24	4.03 × 106
F	1.61 × 106	2.03 × 104	6.21	$-7.28\times {10}^{-9}$	7.12	7.76	7.78	1.42 × 108
G	6.84 × 106	4.43 × 106	1.46	$-1.1\times {10}^{-9}$	14.80	14.92	15.00	1.44 × 107
H	2.59 × 106	2.3 × 105	3.86	$-2.72\times {10}^{-9}$	5.16	5.44	5.48	1.577 × 108
I	4.08 × 106	1.14 × 106	2.45	$-3.21\times {10}^{-10}$	9.28	9.38	9.50	2.60 × 108

Figs. 7 and 8 show the dynamics of V and U. As expected, the states converge to ${\mathcal{X}}_s^1,$ although significantly different behaviors can be observed for the different patients. From Fig. 8 it can be seen that the healthy cells final value U _∞ is reduced in cases of patients with large values of ${\mathcal{R}}_0,$ in spite all simulations have the same initial U ₀. This can be explained from the fact that $W\left({\mathcal{R}}_0{e}^{-{\mathcal{R}}_0}{e}^{{\mathcal{K}}_0}\right)$ is monotonically decreasing for ${\mathcal{R}}_0>1$ (see Figs. 1 and 2), and therefore, $0<U_{\infty }\left({\mathcal{R}}_{01}\right)<U_{\infty }\left({\mathcal{R}}_{02}\right)$ for R ₀₁ > R ₀₂ > 1 (see Property 2, above). Note that the susceptible cells of patient C converges to U _∞ equals to $4.810\times {10}^{-10}\left[cell\right],$ which can be explained by the fact that this patient has a reproduction number (${\mathcal{R}}_0$) of 37.57, which is 5.2 times above the cohort mean value of 7.21. Fig. 7 and Table 2 show that the viral load of patient C reaches the peak at 1.69 days post infection (dpi) (40.56 hours post infection, hpi).

Furthermore, from Fig. 7, it can be seen that for all the cases the viral load spreads (i.e.: the virus presents a peak) although ${\mathcal{R}}_V\left(0\right)<0$ for all patients (i.e., $I_0=0$). This can be justified since $U_0\gg {\mathcal{U}}_c$ and, therefore, ${\mathcal{R}}_0$ will be greater than $1+\alpha \left(0\right)$ for all patients (note that, $\alpha \left(0\right)<10\times {10}^{-4}$). Moreover, from Table 2, we can corroborate that ${\widehat{t}}_I>t_c>{\widehat{t}}_V$ which is in accordance to what is stated in Theorem 4.1.

Concerning the immune response, this model makes the assumption that it is constant and independent on viral load as well as infected cells. Furthermore, neither innate or adaptive response are modeled, being the viral load dynamic mainly limited by target cells availability. Since recent studies have shown a dysfunctional immune response (i.e.: lymphogenia, desregulated secretion of pro-inflammatory cytokines, excessive infiltration of monocytes, macrophages and T cells, among others) (Diao, Wang, Tan, Chen, Liu, Ning, Chen, Li, Liu, Wang, et al., 2020, Tay, Poh, Rénia, MacAry, Ng, 2020), this effect should be added in the proposed model, in order to have a more reliable representation (and, eventually, a more realistic control objective). In addition, a more reliable standard to measure the severity of disease could be related with the viral spreadability as well as the deregulated inflammatory response.

6. Conclusions

In this work a full dynamical characterization of a COVID-19 in-host target-cell model is performed. It is shown that there exists a minimal stable equilibrium set depending only on the system parameters. Furthermore, it is shown that there exists a parameter-depending threshold for the susceptible cells that fully characterizes the virus and infected cells qualitative behavior. Simulations demonstrate the potential utility of such system dynamic characterization to tailor the most valuable pipeline drugs against SARS-CoV-2.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Stability theory

In this section some basic definitions and results are given concerning the asymptotic stability of sets and Lyapunov theory, in the context of non-linear continuous-time systems. All the following definitions are referred to system

$$\dot{x}\left(t\right)=f\left(x\left(t\right)\right),x\left(0\right)=x_0,$$ (A.1)

where x is the system state constrained to be in $\mathbb{X}\subseteq {\mathbb{R}}^n,$ f is a Lipschitz continuous nonlinear function, and ϕ(t; x) is the solution for time t and initial condition x.

Definition 4 Equilibrium set —

Consider system A.1 constrained by $\mathbb{X}$. The set ${\mathcal{X}}_s\subset \mathbb{X}$ is an equilibrium set if each point $x\in {\mathcal{X}}_s$ is such that $f\left(x\right)=0$ (this implying that $\varphi (t;x)=x$ for all t ≥ 0).

Definition 5 Attractivity of an equilibrium set —

Consider system A.1 constrained by $\mathbb{X}$. A closed equilibrium set ${\mathcal{X}}_s\subset \mathbb{X}$ is attractive in $\mathcal{X}\subset \mathbb{X}$ if ${\lim }_{t\to \infty }{\parallel \varphi (t;x)\parallel }_{{\mathcal{X}}_s}=0$ for all $x\in \mathcal{X}$.

Any set containing an attractive set is attractive, so the significant attractivity concept in a constrained system is given by the smallest one.

Definition 6 $ϵ-\delta$ local stability of an equilibrium set —

Consider system A.1 constrained by $\mathbb{X}$. A closed equilibrium set ${\mathcal{X}}_s\subset \mathbb{X}$ is $ϵ-\delta$ locally stable if for all ϵ > 0 it there exists δ > 0 such that in a given boundary of ${\mathcal{X}}_s,$ ${\parallel x\parallel }_{{\mathcal{X}}_s}<\delta ,$ it follows that ${\parallel \varphi (t;x)\parallel }_{{\mathcal{X}}_s}<ϵ,$ for all t ≥ 0.

Definition 7 Asymptotic stability (AS) of an equilibrium set —

Consider system A.1 constrained by $\mathbb{X}$. A closed equilibrium set ${\mathcal{X}}_s\in \mathbb{X}$ is asymptotically stable (AS) in $\mathcal{X}\subset \mathbb{X}$ if it is $ϵ-\delta$ locally stable and attractive in $\mathcal{X}$.

Theorem A.1 Lyapunov theorem (Khalil & Grizzle, 2002) —

Consider system A.1 constrained by $\mathbb{X}$ and an equilibrium state $x_s\in {\mathcal{X}}_s\subset \mathbb{X}$ . Let consider a function $V\left(x\right):{\mathbb{R}}^n\to \mathbb{R}$ such that V(x) > 0 for x ≠ x_s, $V\left(x_s\right)=0$ and $\dot{V}\left(x\left(t\right)\right)\le 0,$ denoted as Lyapunov function. Then, the existence of such a function implies that $x_s\in {\mathcal{X}}_s$ is $ϵ-\delta$ locally stable. If in addition $\dot{V}\left(x\left(t\right)\right)<0$ for all x ≠ x_s and $\dot{V}\left(x_s\right)=0,$ then $x_s\in {\mathcal{X}}_s$ is asymptotically stable.

Appendix B. Derivation of the basic reproduction number ${\mathcal{R}}_0$

The derivation of the basic reproduction number ${\mathcal{R}}_0$ will be given by means of the concept of next-generation matrix (van den Driessche, 2017). Consider system (2.1) and the healthy equilibrium $x_0=(U_0,0,0),$ which is stable in the absence of virus. Of the complete state of system (2.1), $x=(U,I,V),$ only two states depend on infected cells, that is I and V. Let us rewrite the ODEs for this two states in the form

$$\begin{array}{ccc}\hfill \dot{I}\left(t\right)& =& {\mathcal{F}}_I\left(x\right)-{\mathcal{G}}_I\left(x\right)\hfill \\ \hfill \dot{V}\left(t\right)& =& {\mathcal{F}}_V\left(x\right)-{\mathcal{G}}_V\left(x\right)\hfill \end{array}$$

where ${\mathcal{F}}_i\left(x\right),$ $i=\{I,V\},$ is the rate of appearance of new infections in compartment i, while ${\mathcal{G}}_i\left(x\right),$ $i=\{I,V\},$ is the rate of other transitions between compartment i and the other infected compartments, that is

$$\begin{array}{ccc}{\mathcal{F}}_I\left(x\right)=\beta U\left(t\right)V\left(t\right)\hfill & \text{and}\hfill & {\mathcal{G}}_I\left(x\right)=\delta I\left(t\right)\hfill \\ {\mathcal{F}}_V\left(x\right)=0\hfill & \text{and}\hfill & {\mathcal{G}}_V\left(x\right)=-pI\left(t\right)+cV\left(t\right)\hfill \end{array}$$

If we now define

$$F={\left[\begin{array}{cc}{\displaystyle \frac{\partial {\mathcal{F}}_I\left(x\right)}{\partial I}}& {\displaystyle \frac{\partial {\mathcal{F}}_I\left(x\right)}{\partial V}}\\ \\ {\displaystyle \frac{\partial {\mathcal{F}}_V\left(x\right)}{\partial I}}& {\displaystyle \frac{\partial {\mathcal{F}}_V\left(x\right)}{\partial V}}\end{array}\right]}_{x=x_0}=\left[\begin{array}{cc}0& \beta U_0\\ 0& 0\end{array}\right]$$

and

$$G={\left[\begin{array}{cc}{\displaystyle \frac{\partial {\mathcal{G}}_I\left(x\right)}{\partial I}}& {\displaystyle \frac{\partial {\mathcal{G}}_I\left(x\right)}{\partial V}}\\ \\ \frac{{\displaystyle \partial {\mathcal{G}}_V\left(x\right)}}{\partial I}& {\displaystyle \frac{\partial {\mathcal{G}}_V\left(x\right)}{\partial V}}\end{array}\right]}_{x=x_0}=\left[\begin{array}{cc}\delta & 0\\ -p& c\end{array}\right]$$

then matrix $F{G}^{-1},$ represents the so-called next-generation matrix. Each (i, j) entry of such a matrix represents the expected number of secondary infections in compartment i produced by an infected cell introduced in compartment j. The spectral radius of this matrix, that is, the maximum absolute value of its eigenvalues, defines the basic reproduction number ${\mathcal{R}}_0$.

For the specific case of system (2.1), the next-generation matrix is given by

$$F{G}^{-1}=\left[\begin{array}{cc}{\displaystyle \frac{\beta p{U}_0}{c\delta }}& {\displaystyle \frac{\beta U_0}{c}}\\ \\ 0& 0\end{array}\right]$$

Therefore, the basic reproduction number ${\mathcal{R}}_0$ is given by

$${\mathcal{R}}_0=:\frac{\beta p{U}_0}{c\delta }$$

Notice that ${\mathcal{R}}_0$ coincides with the entry (1,1) of matrix $F{G}^{-1},$ thus meaning that ${\mathcal{R}}_0$ represents the expected number of secondary infections produced in compartment I by an infected cell originally in I.

Appendix C. Technical lemma

The next Lemma characterizes the virus minimum and maximum times, for system (2.1), in terms of the value of the reproduction number $\mathcal{R}\left(t\right)$.

Lemma 1

Consider system (2.1) , constrained by the positive set $\mathbb{X},$ at the beginning of the infection $t=0,$ with U(0) > 0, I(0) ≥ 0 and V(0) > 0 (i.e., $x\left(0\right)=\left(U\right(0),I(0),V(0\left)\right)\in \mathcal{X}$ ).

Then,

• 1. if V(t) reaches a local minimum at time $t_V^{*}>t_0,$ then $\mathcal{R}\left(t_V^{*}\right)>1,$
• 2. if V(t) reaches a local maximum at time $t_V^{*}>t_0,$ then $\mathcal{R}\left(t_V^{*}\right)<1,$ and
• 3. if V(t) reaches an inflection point at time $t_V^{*}>t_0$ (a point in which $\dot{V}=0$ and $\ddot{V}=0$ ), then $t_V^{*}=t_c,$ where t_c is the (unique) time at which $\mathcal{R}$ reaches 1 (i.e., $\mathcal{R}\left(t_c\right)=1$ or, the same, $U\left(t_c\right)={\mathcal{U}}_c$ ).

Proof

Any of the three hypothesis (V(t) reaches a local minimum, a local maximum or a inflection point) implies that

$$\dot{V}\left(t_V^{*}\right)=pI\left(t_V^{*}\right)-cV\left(t_V^{*}\right)=0,$$ (C.1)

which means that

$$V\left(t_V^{*}\right)=p/cI\left(t_V^{*}\right).$$ (C.2)

Consider the critical case of an inflection point, i.e.,

$$\ddot{V}\left(t_V^{*}\right)=p\dot{I}\left(t_V^{*}\right)-c\dot{V}\left(t_V^{*}\right)=p\dot{I}\left(t_V^{*}\right)=0.$$ (C.3)

Thus $\dot{I}\left(t_V^{*}\right)=0$ which, by (2.1.b) at $t_V^{*},$ is equivalent to

$$\dot{I}\left(t_V^{*}\right)=\beta U\left(t_V^{*}\right)V\left(t_V^{*}\right)-\delta I\left(t_V^{*}\right)=0.$$ (C.4)

Now, by (C.2), we have

$$(\frac{\beta p}{c}U\left(t_V^{*}\right)-\delta )I\left(t_V^{*}\right)=0.$$ (C.5)

Given that $I\left(t_V^{*}\right)>0$ (note that I(t) is positive for all t > 0), then $\frac{\beta p}{c}U\left(t_V^{*}\right)-\delta =0,$ or

$$\mathcal{R}\left(t_V^{*}\right)=\frac{\beta p}{c\delta }U\left(t_V^{*}\right)=1.$$ (C.6)

This way if an inflection point does occurs at $t_V^{*},$ then $t_V^{*}=t_c,$ where t_c is the time at which $\mathcal{R}=1$. This proves item (iii).

Furthermore, if V reaches a local minimum at $t_V^{*},$ then $\ddot{V}\left(t_V^{*}\right)>0$ (instead of $\ddot{V}\left(t_V^{*}\right)=0,$ as it is in (C.3), which by (C.2) implies that

$$\mathcal{R}\left(t_V^{*}\right)=\frac{\beta p}{c\delta }U\left(t_V^{*}\right)>1.$$ (C.7)

This proves item (i).

On the other hand, if V reaches a local maximum at $t_V^{*},$ then $\ddot{V}\left(t_V^{*}\right)<0$ (instead of $\ddot{V}\left(t_V^{*}\right)=0,$ as it is in (C.3)), which by (C.2) implies that

$$\mathcal{R}\left(t_V^{*}\right)=\frac{\beta p}{c\delta }U\left(t_V^{*}\right)<1.$$ (C.8)

This proves item (ii). □