Exploring whole-genome duplicate gene retention with complex genetic interaction analysis

Abstract

Whole-genome duplication has played a central role in genome evolution of many organisms, including the human genome. Most duplicated genes are eliminated and factors that influence the retention of persisting duplicates remain poorly understood. Here, we describe a systematic complex genetic interaction analysis with yeast paralogs derived from the whole-genome duplication event. Mapping digenic interactions for a deletion mutant of each paralog and trigenic interactions for the double mutant provides insight into their roles and a quantitative measure of their functional redundancy. Trigenic interaction analysis distinguishes two classes of paralogs, a more functionally divergent subset and another that retained more functional overlap. Gene feature analysis and modeling suggest that evolutionary trajectories of duplicated genes are dictated by combined functional and structural entanglement factors.

Introduction:

Whole genome duplication (WGD) events are pervasive in eukaryotes, shaping genomes of simple single-celled organisms, such as yeast, and more complex metazoans, including humans. Most duplicated genes are eliminated after WGD because one copy accumulates deleterious mutations, leading to its loss. However, a significant proportion of duplicates persists, and factors that result in duplicate gene retention are poorly understood but critical for understanding the evolutionary forces that shape genomes.

Rationale:

Quantifying the functional divergence of paralog pairs is of particular interest because of the strong selection against functional redundancy. Negative genetic interactions identify functional relationships between genes and provide a means to directly capture the functional relationship between duplicated genes. Genetic interactions occur when the phenotype associated with a combination of mutations in two or more different genes deviates from the expected combined effect of the individual mutations. A negative genetic interaction refers to a combination of mutations that generates a stronger fitness defect than expected, such as synthetic lethality. Here, we use systematic analysis of digenic and trigenic interaction profiles to assess the functional relationship of retained duplicated genes.

Results:

To map both digenic and trigenic interactions of duplicated genes, we profiled query strains carrying single deletion mutations and the corresponding double deletion mutations for 240 different dispensable paralog pairs originating from the yeast WGD event. In total, we tested ~550,000 double and ~260,000 triple mutants for genetic interactions and identified ~4,700 negative digenic interactions, and ~2,500 negative trigenic interactions. We quantified the trigenic interaction fraction, defined as the ratio of negative trigenic interactions to the total number of interactions associated with the paralog pair. The distribution of the resulting trigenic interaction fractions was distinctly bimodal, with two-thirds of paralogs exhibiting a low trigenic interaction fraction (diverged paralogs) and one-third showing a high trigenic interaction fraction (functionally redundant paralogs). High trigenic interaction fraction paralogs showed a relatively low asymmetry in their number of digenic interactions, low rates of protein sequence divergence, and a negative digenic interaction within the gene pair.

We correlated position-specific evolutionary rate patterns between paralogs to assess constraints acting on their evolutionary trajectories. Paralogs with a high trigenic interaction fraction showed more correlated evolutionary rate patterns and thus were more evolutionary constrained than paralogs with a low trigenic interaction fraction. Computational simulations that modeled duplicate gene evolution revealed that as the extent of the initial entanglement (overlap of functions) of paralogs increased, so did the range of functional redundancy at steady-state. Thus, the bimodal distribution of the trigenic interaction fraction may reflect that some paralogs diverged, primarily evolving distinct functions without redundancy, while others converged to an evolutionary steady-state with substantial redundancy due to their structural and functional entanglement.

Conclusion:

We propose that the evolutionary fate of a duplicated gene is dictated by an interplay of structural and functional entanglement. Paralog pairs with high levels of entanglement are more likely to revert to a singleton state. In contrast, unconstrained paralogs will tend to partition their functions and adopt divergent roles. Intermediately entangled paralog pairs may partition or expand non-overlapping functions while also retaining some common, overlapping functions, such that they can both adopt paralog-specific roles and maintain functional redundancy at an evolutionarily steady-state.

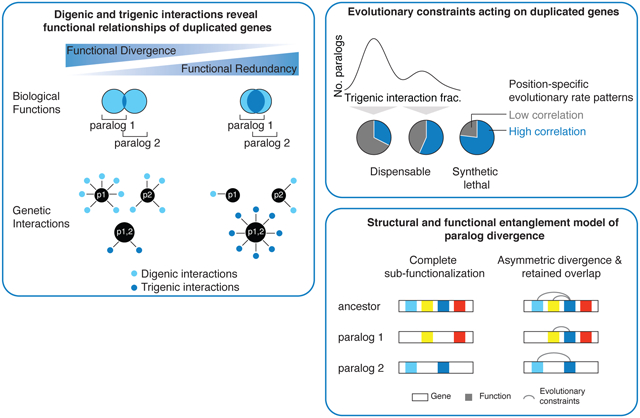
Fig. 0. Complex genetic interaction analysis of duplicated genes.

Trigenic interaction fraction, which incorporates digenic and trigenic interactions, captures the functional relationship of duplicated genes and follows a bimodal distribution. High trigenic interaction fraction paralogs are under evolutionary constraints reflecting their structural and functional entanglement.

One sentence summary:

Exploring evolutionary trajectories of duplicated genes with complex genetic interaction analysis

Most eukaryotic genomes, including the human genome, contain a substantial fraction of duplicated genes (1-7). Gene duplication is generated by two main mechanisms: segmental duplication (small-scale duplication), due to error prone DNA replication, and simultaneous duplication of all genomic segments (whole-genome duplication), due to a variety of polyploidy events (3, 8). Gene duplication provides a source of new genes (9) and duplicate retention may lead to development of specialized functional modules involving paralogous proteins through ‘subfunctionalization’, which promotes biological complexity (10). Nevertheless, following duplication most paralogs are eliminated from the genome because the functional redundancy of duplicated genes is evolutionarily unstable, as one gene copy may accumulate intrinsically deleterious mutations and be removed from the genome by selection (11). However, a significant fraction of duplicates has been retained over evolution. Thus, understanding the molecular mechanisms that underlie duplicate gene retention may provide insights into the evolutionary forces that shape genomes.

Approximately 100 million years ago, the budding yeast, Saccharomyces cerevisiae, arose from a whole-genome duplication (WGD) event, and, after a massive gene loss, retained 551 duplicate gene pairs (6, 7, 12). Quantifying functional divergence of each paralog pair is of particular interest because of the strong selection against functional redundancy. Paralog functional divergence has been estimated by the rates of evolutionary divergence of coding and regulatory regions (6, 12-14), gene ontology (GO) semantic distance (15-17), metabolic flux analysis (18, 19), similarity of gene expression profiles (3, 10, 20-23), changes in the encoded protein abundance of one sister upon perturbation of another (24) and analysis of similarity of partners within the protein-protein interaction network (25).

Genetic interaction analysis provides a powerful means to directly capture the functional relationship between duplicated genes. Genetic interactions occur when a combination of mutations in different genes results in an unexpected phenotype, deviating from a model based on the integration of the individual mutant phenotypes. A negative genetic interaction occurs when a combination of mutations leads to a more severe fitness defect than expected (26). An extreme example of a negative digenic interaction is synthetic lethality, which occurs when two mutations, neither of which is lethal on its own, combine to generate an inviable double mutant phenotype (27, 28). Negative genetic interactions often occur between genes that impinge on a common essential function. A positive genetic interaction occurs when a combination of mutations results in a phenotype that is less severe than expected from the phenotypes associated with the single mutants. For example, digenic suppression is observed when a double mutant exhibits a greater fitness than the sickest single mutant (29). A previous global digenic interaction network in yeast identified ~550,000 negative and ~350,000 positive genetic interactions (30). The profile of genetic interactions for a specific query gene provides a quantitative measure of function (31, 32), and a network based on genetic interaction profile similarity reveals a hierarchy of functional modules, including pathways and complexes, bioprocesses and cellular compartments (30).

A systematic analysis of the digenic interactions between duplicated gene pairs in yeast revealed functional redundancy, whereby ~30% of pairs interacted (relative to ~3.6% for random gene pairs) (33-37). Nevertheless, this observation may indicate that the overall contribution of duplicate retention to the ability of an organism to tolerate mutations, mutational robustness, is relatively low, since total functional compensation is only observed for a minor fraction of duplicates (38). Mechanisms that drive duplicate retention may be influenced by gene dosage effects, or functional divergence through asymmetric evolution (33). Retention of duplicates may result from sub-functionalization, such that duplicates degenerate in some of their function differentially and result in a pair of genes that function fully as the single ancestral copy, which is an outcome postulated by the duplication-degeneration-complementation model (39). Evidence of functional partitioning of ancestral functions, include but are not limited to biochemical function (40), gene expression regulatory elements (22) and subcellular localization patterns (41). Here, we expanded upon the use of genetic interaction profiles to capture the functional relationship of duplicated genes. We compared trigenic interactions for double mutant query strains deleted for both members of nonessential paralog pairs to the corresponding digenic interaction profiles for each single mutant sister gene, and we quantified a spectrum of functional redundancy among paralogs. A correlative analysis of the gene features suggests that the evolutionary trajectories of retained duplicated genes can be driven by genes encoding functionally and structurally constrained proteins, to which we refer as ‘entangled’.

Mapping trigenic interactions for duplicated genes

We constructed 240 double mutant query yeast strains, each deleted for a pair of nonessential WGD paralog genes (Table S1-S4). These are dispensable paralog pairs and represent 44% (240/551) of unique WGD paralog pairs (12), a number of which were not included, either because the pair was essential or refractory to double mutant query strain construction (42). Using colony size as a proxy for cell fitness, we measured the growth phenotypes of the set of 240 double mutant query strains and the corresponding 480 single mutants (Table S5) (42), which correlated well with previous large-scale measurements of single (Pearson correlation coefficient, r = 0.51, p = 3×10⁻³⁰) and double (Pearson correlation coefficient, r = 0.72, p = 2×10⁻²³) mutant fitness (30) (Fig. S1A-D).

The set of single and double mutant query strains were used to score digenic and trigenic interactions, respectively (Fig. 1). We crossed the queries to a diagnostic array of nonessential gene deletion mutants and essential gene mutants, carrying temperature-sensitive alleles, which span all major cellular processes and cover ~1,200 genes representing ~20% of the yeast genome (37). In total, we examined 537,911 double and 256,861 triple mutants for genetic interactions. Query strains deleted for an individual paralog gene were screened for digenic interactions and double-mutant query strains, deleted for both paralogs, were screened for trigenic interactions in two replicate screens with four colonies per screen (Fig. S2A-C) (37). Negative and positive interactions were quantified for digenic and trigenic interactions (30, 32) , which were determined from validation of trigenic interactions of the CLN1-CLN2 double-mutant query, as previously described (37). This resulted in an estimated recall (sensitivity) of ~60%, and a precision of ~75% (37). Additionally, we used replicate screens to independently estimate the false discovery rate as a function of recall, which resulted in a consistent estimate of > 75% precision (<25% FDR) (Fig. S2D).

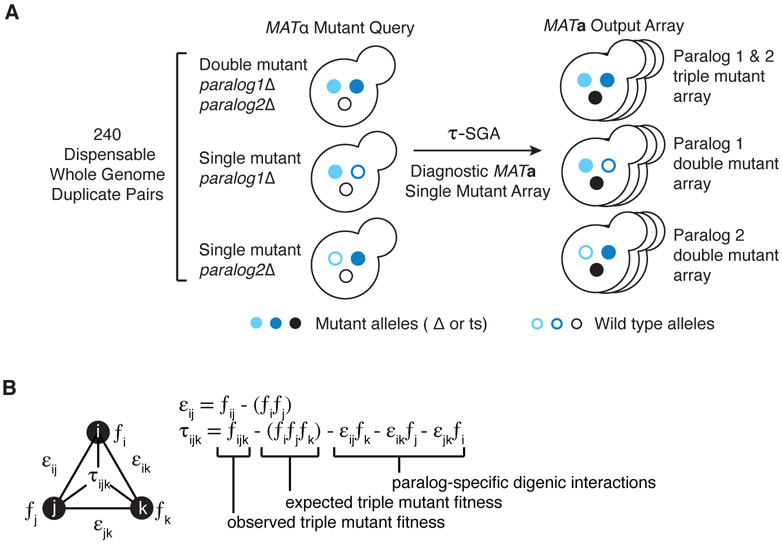
Fig. 1. Triple-mutant synthetic genetic array (SGA) analysis for paralogs.

(A) An illustration of triple-mutant SGA experimental approach in which a query set of 240 dispensable paralog pairs originating from the whole-genome duplication in yeast was screened for trigenic interactions. Three types of screens were carried out in parallel, whereby triple mutant fitness was estimated by crossing a double mutant query strain deleted for both paralogs (light and dark blue filled circles) is crossed into a diagnostic array of single mutants (black filled circles) (37). After induction of meiosis in heterozygous triple mutants, sequential replica pinning steps are used to select haploid triple-mutant progeny. Single-mutant control query strains are screened in parallel to estimate paralog-specific double mutant fitness. (B) We used the τ-SGA scoring method, to identify trigenic interactions quantitatively by combining double and triple mutant fitness estimates derived from colony size measurements (37).

This analysis identified 4,650 negative and 2,547 positive digenic interactions, as well as 2,466 negative and 2,091 positive trigenic interactions (Table S1, S2, S4). Importantly, about one-third of negative and one-quarter of positive trigenic interactions were of the ‘novel’ class, identifying connections that were not observed in their corresponding digenic interaction network (Fig. 2). Indeed, for 129 paralog pairs, the corresponding single genes displayed only sparse digenic interaction profiles on the global genetic interaction network (30) (Table S6). However, they exhibited more novel trigenic interactions (~40% negative and ~31% positive trigenic interactions) than average, indicating that paralog pair trigenic interactions expanded the known global genetic interaction network. The remaining two-thirds of negative and three-quarters of positive trigenic interactions overlapped a previously identified digenic interaction and thus represent ‘modified’ class of trigenic interactions (Fig. 2). Paralogs with more negative trigenic interactions than digenic interactions showed predominantly novel and modified negative trigenic interactions, which overlapped exclusively with negative digenic interactions indicating functional redundancy (Fig. S3A).

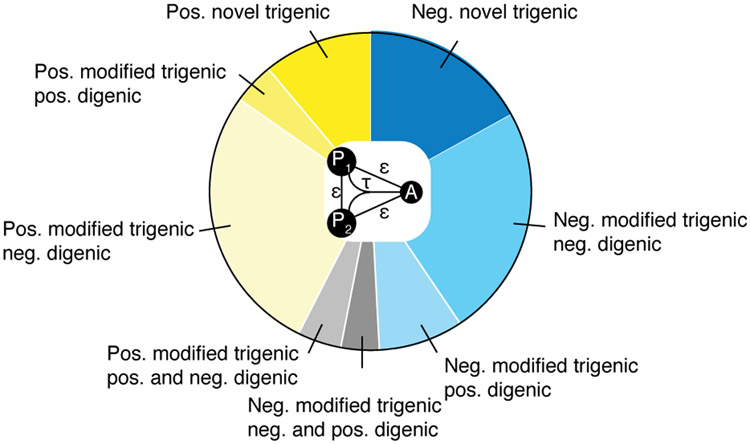
Fig. 2. Distribution of different types of trigenic interactions for paralogs.

Pie chart comparing the different types of trigenic interactions for all paralogs depicts negative ((τ or ε ) < −0.08, p < 0.05) and positive ((τ or ε) > 0.08, p < 0.05) genetic interactions in blue and yellow, respectively. A trigenic interaction between a double mutant query and the array strain is called ‘novel’ (dark blue/dark yellow), if there is no significant digenic interaction between either single mutant control query and the array strain or between the query gene pair. Trigenic interactions that overlap with one or more negative or positive digenic interactions are called ‘modified’ and are further classified by the type of the digenic interaction. All trigenic interactions of double mutant query strains (P₁-P₂) that show a negative or a positive digenic interaction between query gene pair (P₁-P₂) (∣ε∣ > 0.08, p < 0.05), are considered ‘modified’. Interactions may be further classified by digenic interactions (if any) between a single mutant query control strain and the array strain (P₁ and/or P₂-A negative, P₁ and/or P₂-A positive). Modified trigenic interactions that overlap: 1) digenic interactions of the same sign are in medium blue/yellow, 2) digenic interactions of the opposite sign are in light blue/yellow and 3) a mix of positive and negative digenic interactions are depicted in grey.

Genetic interaction profiles highlight functional divergence of duplicated genes

The functional relationship between paralogs should be captured by their negative genetic interactions. Consistent with previous observations (32, 33), we observed that duplicates showed fewer negative digenic interactions than singletons (Wilcoxon rank sum test, p = 6×10⁻⁸, Fig. S3B), which is suggestive of a general trend in which paralogs retain functional redundancy. We predicted that highly divergent gene pairs should exhibit a relatively high number of paralog-specific negative digenic interactions (Fig. 3). In contrast, functionally overlapping paralogs should be biased towards trigenic interactions and display few paralog-specific interactions (Fig. 3). To assess this possibility, we computed the trigenic interaction fraction, defined as the ratio of negative trigenic interactions to the total number of all negative interactions (digenic and trigenic) associated with the paralog pair (Fig. 3).

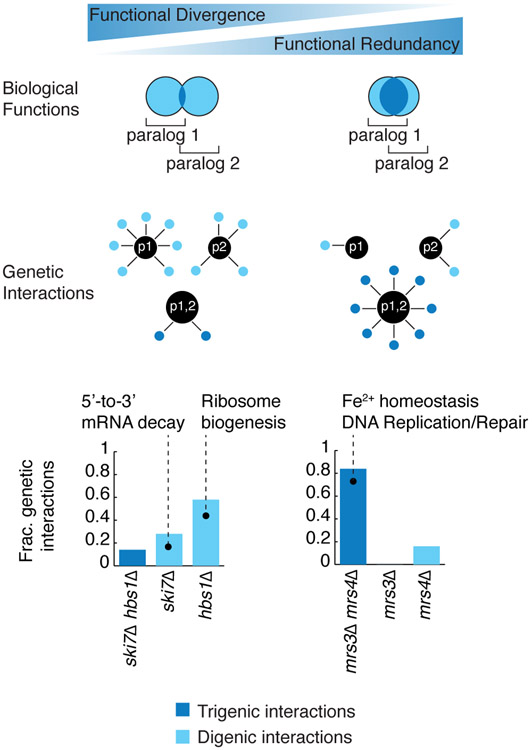
Fig. 3. Mapping functional relationship of paralogs through their digenic and trigenic interactions.

This schematic depicts highly divergent paralogs with little functional overlap and functionally redundant paralogs with an extensive functional overlap, which are represented by the Venn diagrams. Diverged paralogs are predicted to exhibit many digenic interactions, indicative of their paralog-specific functions and few trigenic interactions, whereas functionally redundant paralogs are expected to show sparse digenic interactions and numerous trigenic interactions, indicative of their functional overlap. Divergent paralogs, such as SKI7-HBS1 behave consistent with the expectation and display fewer trigenic than digenic interactions. However, functional redundant paralogs, such as MRS3-MRS4, display a higher fraction of trigenic interactions with a corresponding drop in the fraction of paralog-specific digenic interactions. The fraction of different types of genetic interactions is illustrated using bar graphs. The fraction of total genetic interactions attributed to the trigenic interactions associated with a par1Δ par2Δ double mutant query, deleted for both paralogs, is depicted as a dark blue bar, whereas the fraction of digenic interactions associated with each paralog single deletion mutant, par1Δ or par2Δ, is shown as a light blue bar.

From this analysis we observed that double mutants involving duplicates showed a range of trigenic interaction degree compared to digenic interactions. This indicated that complex genetic interactions may reveal their functional redundancy (Fig. S3B). For example, SKI7-HBS1 is a paralog pair that showed a relatively low trigenic interaction fraction (Fig. 3). While the SKI7 and HBS1 gene products both recognize stalled ribosomes and initiate mRNA degradation, they do so in a different manner (43). Ribosomes that stall upon encountering an in-frame stop codon at the 3’ end of a transcript are recognized by Ski7, which in turn recruits the RNA exosome (44). In contrast, ribosomes stalled within the coding region of a transcript, possibly due to an unusual structural conformation or damage in the mRNA, are recognized by Hbs1, which initiates mRNA cleavage in an RNA exosome-independent manner (45). Our model (Fig. 3) predicts that the digenic interaction profiles of the paralogs should reflect their independent function. Indeed, SKI7 showed digenic interactions with genes involved in mRNA 3' end protection and 5'-3' mRNA decay, such as PAT1 and LSM1, whereas HBS1 interacted with numerous genes involved in ribosome biogenesis and recycling. Thus, the low trigenic interaction fraction of the SKI7-HBS1 gene pair (Fig. 3) appears to reflect the functional divergence of these paralogs (39, 40, 43).

Conversely, the MRS3-MRS4 duplicate pair showed a high trigenic interaction fraction (~0.85) (Fig. 3). These paralogs are members of the eukaryotic-specific mitochondrial carrier family, which transports compounds, including nucleotides, amino acids, carboxylates, small inorganic ions and vitamins, across the inner mitochondrial membrane linking cytosolic and mitochondrial biochemical pathways (46). MRS3-MRS4 encode highly similar mitochondrial carrier proteins with high affinity for Fe²⁺, which they transport across the inner mitochondrial membrane (47). The corresponding vertebrate homolog, mitoferrin, is involved in erythropoiesis by maintaining mitochondrial iron homeostasis (48). The MRS3-MRS4 trigenic interactions involved genes related to cell redox homeostasis, such as GRX3, TSA1, TRX3. The processes that regulate Fe²⁺ homeostasis are important components of the cellular defense mechanism against oxidative damage. Indeed, the MRS3-MRS4 trigenic interactions were also enriched for genes involved in DNA replication and repair, including genes encoding members of the Rad51-Rad57 complex (RAD51, RAD54, RAD55, RAD57), the Rad5-Rad6-Rad18 complex (RAD5), DNA replication factor C complex (CTF8, CTF18), the MRX complex (MRE11, XRS2), the Holliday junction resolvase complex (MUS81, MMS4) and nucleotide-excision repair factor 3 complex (TFB1, SSL1) (49). Together these examples illustrate how the trigenic interaction fraction may reflect the degree of functional overlap of paralogs.

Distribution of trigenic interaction fraction among retained paralog pairs

In total, we measured the trigenic interaction fraction for 161 paralog pairs that showed at least six total trigenic or digenic interactions (Table S7). These paralog pairs displayed a range of trigenic interaction fraction (Fig. 4A). In fact, the distribution of the resulting trigenic interaction fractions was distinctly bimodal, with 114 paralog pairs exhibiting a relatively low trigenic interaction fraction (below 0.4) while a smaller subset of 47 paralogs displayed a higher trigenic interaction fraction (above 0.4), suggesting that comparison of digenic and trigenic interaction profiles is an effective way to differentiate paralog pairs and provide insights into the extent of functional overlap between a given duplicated gene pair (Fig. 4A, Table S7). This distribution of trigenic interaction did not differ for subsets of duplicated genes that originated by distinct mechanisms, such as ohnologs, which originated from whole-genome duplication, or homeologs, which originated from hybridization between species (42, 50). We confirmed that the genetic interaction profiles we generated are robust to array size in that we observed a significant correlation for the trigenic interactions obtained from the diagnostic array and the genome-wide array, which were derived from screening 11 double mutants with their single mutant control query strains in two replicates each (Fig. S4). The strength of correlation between replicates was not affected appreciably with decreasing stringency for either digenic or trigenic interactions (Fig. S2A-C), indicating that our conclusions are not dependent on an interaction score threshold. The remaining 79 paralog pairs, representing about a third of all screened pairs, were characterized by sparse genetic interaction profiles. These paralogs span a diverse set of biological processes and tend to belong to larger gene families (one-sided ttest, p = 0.04, Table S9), which may confer higher order redundancy and reduce second- and third-order genetic interactions.

Fig. 4. Trigenic interaction fraction correlates with fundamental physiological and evolutionary properties.

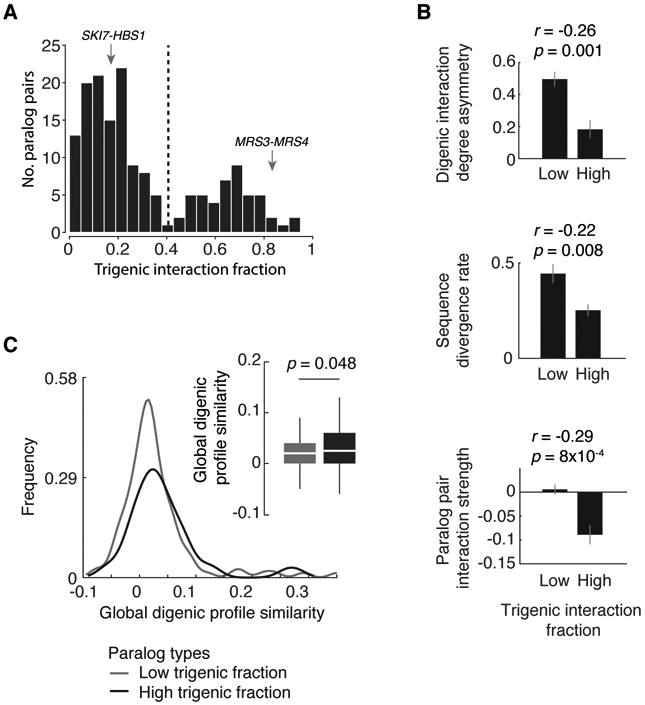
(A) Negative trigenic interaction fraction distribution of screened paralogs, (τ or ε) < −0.08, p < 0.05; paralogs with at least 6 trigenic or digenic interactions in one of the screens are considered. Representative examples of paralogs with a low (SKI7-HBS1) and high (MRS3-MRS4) trigenic interaction fraction are marked with an arrow. (B) Physiological and evolutionary properties for paralogs characterized by varying fraction of trigenic interactions were measured. Spearman correlation coefficient is denoted by ‘r’ with its associated p value and was used to measure the strength of the correlation between the trigenic interaction fraction and the three features being examined: digenic interaction degree asymmetry, sequence divergence rate and paralog pair interaction strength. The correlation was measured on the entire data set and is noted above the bar plots. The bar plots serve to visualize the trend, in which trigenic interaction fraction cut-off of 0.4 was used based on negative interactions (τ or ε) < −0.08, p < 0.05 to identify paralogs with low and high trigenic interaction fraction. Mean of specified features are depicted; error bars reflect SEM. (C) The distribution of global digenic profile correlation similarity (30) was compared for paralogs with high and low trigenic interaction fraction. A trigenic interaction fraction cut-off of 0.4 was used based on negative interactions (τ or ε) < −0.08, p < 0.05. Analyses are restricted to paralogs with at least 6 total trigenic or digenic interactions in one of the screens. Significance was assessed using one-tailed Wilcoxon rank sum test.

Trigenic interaction fraction, digenic interaction profiles, and paralog properties

The trigenic interaction fraction of paralog pairs was also associated with several fundamental physiological and evolutionary properties (Fig. 4B, Table S5, Table S7, Table S10). Paralogs with a high trigenic interaction fraction tend to exhibit low asymmetry with respect to their number of digenic interactions. The asymmetry score measures whether the digenic profile of one paralog is composed of substantially more interactions than its corresponding duplicate and it correlates with divergent evolution of paralog gene sequences (33). Consistent with this observation, a high trigenic interaction fraction also correlated with relatively low rates of protein sequence divergence (Fig. 4B). We also observed a high trigenic interaction fraction in paralogs whose double mutant showed a negative digenic interaction, which is often associated with functionally related genes (Fig. 4B) (30, 37).

Conversely, paralogs with a low trigenic interaction fraction often showed a high asymmetric score for their digenic degrees (Fig. 4B). Consistent with our hypothesis that a low trigenic fraction is indicative of functional divergence (Fig. 3, 4A), a high asymmetry score may reflect that one paralog has evolved a specialized role. For example, a paralog displaying relatively few digenic interactions under standard conditions may only be expressed and functional under a different environmental condition or during a specialized developmental program. Indeed, in the case of 4 asymmetric paralog pairs, expression of the low degree sister was induced during sporulation, a meiotic developmental program that cells enter in response to a low carbon and low nitrogen environment. Specifically, GIS1 in GIS1-RPH1 paralog pair, HES1 in HES1-KES1, ECI1 in ECI1-DCI1 and DON1 in DON1-CUE5 showed higher meiotic gene expression (Table S11) (51). For another 7 asymmetric paralog pairs, the low degree paralog was required for filamentous growth (52) and for another 15 asymmetric pairs, the gene expression of the lowdegree sister was induced under glucose starvation (Table S11) (53). In total, 22 of 63 asymmetric pairs (~35%) have a paralog that may have been retained for function in a different condition or during a specialized program (Table S11).

The retention of gene duplicates may also be related to gene dosage (54). For example, some duplicates appear to be maintained due to selection for high levels of expression, as in the case of metabolic genes that provide high enzymatic flux (18). Whole-genome duplication events also enable maintenance of stoichiometric balance of protein complex members consistent with the high rate of duplication among components of the ribosome (35). Dosage duplicates are associated with a severe fitness defect when either one of the paralogs is deleted, and a greater digenic interaction profile similarity than other duplicates, indicating that they have retained functional redundancy (33, 38). Because dosage duplicates should have substantial functional redundancy, we reasoned that they might also tend to have a higher trigenic interaction fraction. While the paralogs with a greater digenic interaction profile similarity also tend to have a higher trigenic interaction fraction (Fig. 4C), potential dosage duplicates (33) were found within both the high and low trigenic interaction fraction distributions (Table S10). Thus, the functional redundancy associated with the subset of paralogs with a higher trigenic interaction fraction is probably not driven solely by dosage mechanisms.

The evolution of regions important for protein localization may lead to differential sub-cellular localization of some paralogous proteins and play a role in their retention by enabling specific paralog functions in distinct parts of the cell (41, 55). However, because on average duplicated genes do not appear to evolve a relocalization more frequently than singletons, this may not represent a major mechanism driving paralog retention (56). We observed that paralogs with different subcellular localization patterns tended to show a modestly higher trigenic interaction fraction than those with the same subcellular localization patterns (Wilcoxon ranksum test, p < 0.05,), suggesting that differentially localized paralogs may retain some functional overlap.

Defining paralog function using trigenic interactions

To characterize the roles of paralog pairs with overlapping functions, we mapped their trigenic interactions onto the global digenic interaction profile similarity network (30) (Fig. 5A). Using this approach, trigenic interactions associated with paralog pairs that have a relatively high trigenic interaction fraction can be examined for enrichment within defined bioprocesses. For example, the sbe2Δ sbe22Δ double mutant showed few paralog-specific interactions and numerous trigenic interactions, with a trigenic interaction fraction of ~0.69 (Table S7). The proteins encoded by the SBE2-SBE22 pair share ~ 51% amino acid sequence identity and have relatively well characterized functions in the transport of cell wall components from the Golgi to the cell surface (57). The SBE2-SBE22 negative trigenic interactions involved genes enriched for gene ontology (GO) annotations related to vesicle mediated transport and cell wall organization (Fig. 5B), and include interactions with an ARF-like small GTPase secretion pathway (ARL1, ARL3, SYS1, YPT6), the exocyst (SEC4), and the chitin biosynthesis pathway (CHS5, CHS6).

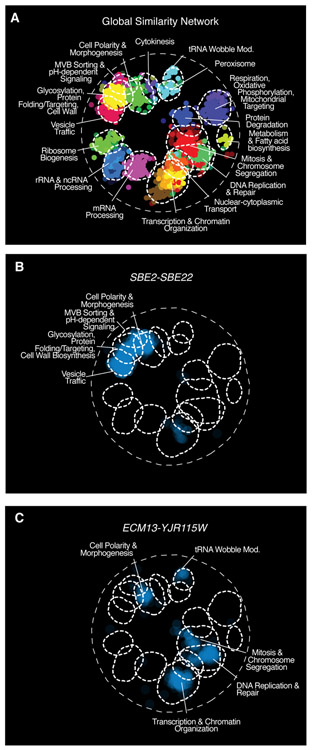
Fig. 5. Trigenic interaction fraction reveals the functional divergence of duplicated genes and illuminates gene function.

(A) SAFE (70) analysis was used to visualize regions of the global digenic interaction profile similarity network (30) that were enriched for genes in the trigenic interaction profiles of the following paralog pairs (B) SBE2-SBE22 and (C) ECM13-YJR115W. Blue indicates the enrichment related to negative trigenic interactions, τ < −0.08, p < 0.05.

Previously, we showed that trigenic interactions, similar to digenic interactions, are functionally informative and are enriched among genes annotated to the same biological process (37). Mapping paralog trigenic interaction profiles onto the global digenic interaction profile similarity network enables the functional annotation of previously uncharacterized paralogs. For example, ECM13-YJR115W showed a trigenic interaction fraction of 0.77 with 12 negative digenic and 40 negative trigenic interactions, suggesting high functional redundancy (Fig. S5A, Table S7). These paralogs are fungal specific and share 39% identity and 70% similarity at the amino acid sequence level. The genes that comprise the ECM13-YJR115W trigenic interaction profile were positioned mainly within the mitosis and DNA replication and repair clusters on the global digenic profile network (Fig. 5C). ECM13-YJR115 trigenic interaction profile is correlated to the digenic interaction profiles of CCT4 and CCT5, which encode members of the cytosolic chaperonin Cct ring complex that participates in the assembly of tubulin, and RBL2, which is involved in microtubule morphogenesis, suggesting a possible microtubule-related role for this paralog pair (30) (Fig. S5B). The ecm13Δ yjr115wΔ double mutant was specifically sensitive to benomyl, a microtubule disrupting agent (Fig. S5C&D), and showed a delay in spindle nucleation and polymerization (Fig. S5E). Moreover, the Ecm13 protein interacts with Dad2 and Dad4, which are components of the Dam1 complex that links kinetochores to microtubules to facilitate chromosome segregation (58). Consistent with a role in spindle function and chromosome segregation, we found that both GFP-Ecm13 and GFP-Yjr115w showed a distinct nuclear localization (Fig. S5F). Another poorly characterized pair is STB6-STB2, which encodes proteins that bind the SIN3 transcriptional repressor and may impinge on the MTC pathway, suggesting a role in aromatic amino acid permease secretion (30) (Fig. S5G-J).

Correlation analysis of position-specific evolutionary rate patterns between paralogs

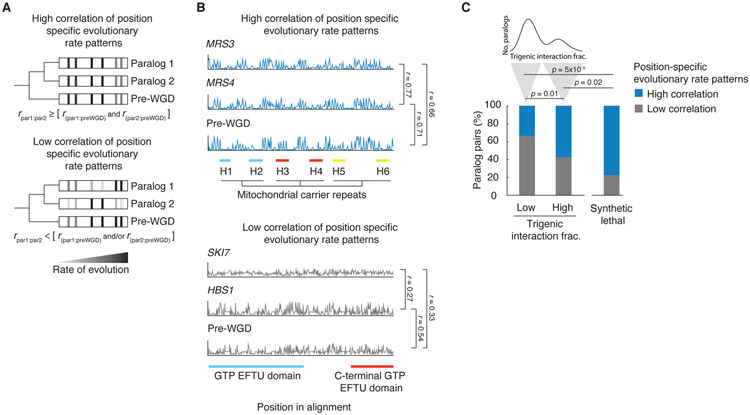
To further explore the factors that drive paralog retention and produce a spectrum of functional redundancy, we considered the relationship between divergent evolution, structure, and function. A negative correlation of trigenic interaction fraction with measures of divergent evolution may be indicative of the constraints that govern this process (Fig. 4B). Amino acid conservation in specific positions indicates evolutionary constraints on amino acid residues that are important for protein function, including those involved in oligomerization, protein-protein interactions, and protein-substrate interactions (59). We therefore used the correlation of position-specific evolutionary rate patterns between paralogs as a measure of evolutionary divergence of the sequence constraints (42). We reasoned that if both paralogs share constraints on specific residues of protein domains during evolution and evolve similarly after the WGD, then they would be expected to be more similar to each other than the pre-WGD species. On the other hand, if paralogs do not share constraints on specific residues of protein domains during evolution and evolve differently after the WGD, then they would be less similar to each other than to the pre-WGD species. We therefore designated a set of pairs with a high correlation of position specific evolutionary rate patterns as evolutionary constrained pairs for which the correlation of rates between extant sisters was greater than or equal to both the correlations between each sister and the pre-WGD homolog. Paralog pairs with little correlation in their position-specific evolutionary rate patterns have different sequence constraints, and therefore are likely to have different structure and function (Fig. 6A, Table S12).

Fig. 6. The evolution of retained overlap due to evolutionary constraints acting on duplicated gene sequences.

(A) Schematic depiction of the analysis of correlated evolutionary sequence changes across paralog sequences reflecting evolutionary constraints on paralogs. Correlated rates of evolution for specific columns in multiple sequence alignments for the pre-WGD homolog and each paralog are denoted with a grey to black gradient, from low to high, respectively. High correlation of position specific evolutionary rate patterns identify residues with similar evolutionary constraints. Paralogs with correlated rates (r _par1:par2) that are greater than or equal to that of each paralog and with the corresponding preWGD (r _par1:preWGD and r _par1:preWGD ) were designated as having a high correlation of position specific evolutionary rate pattern, and paralogs with correlated rates (r _par1:par2) that were less than that of either paralog or both paralogs with the preWGD (r _par1:preWGD and/or r _par1:preWGD ) were designated as having a low correlation of position specific evolutionary rate pattern. r refers to the Pearson correlation coefficient between the respective sequences. (B) Examples of evolutionary rates for positions in the alignments for representative paralogs, which show a high correlation of position-specific evolutionary rate patterns (MRS3-MRS4) and a low correlation of position-specific evolutionary rate patterns (SKI7-HBS1). The position in the alignment is plotted on the x-axis and the rate of evolution at a particular position divided by the average rate of evolution for all residues in the given sister paralog is plotted on the y-axis. The scale of the y-axis has been fixed for each paralog pair. Pfam domains are annotated. The MRS3-MRS4 alignment shows three mitochondrial carrier repeats, each composed of two α-helices (H1&H2 (blue), H3&H4 (red), H5&H6 (yellow)) followed by a characteristic motif PX[D/E]XX[K/R]X[K/R](20-30 residues)[D/E]GXXXX[W/Y/F][K/R]G connecting each pair of membrane-spanning domains by a loop. SKI7-HBS1 alignment shows GTP EFTU (blue) and C-terminal GTP EFTU (red) domains. The Hbs1-like N-terminal motif lies outside of the alignment window. (C) Fraction of nonessential and essential paralogs that show a high or low correlation of position-specific evolutionary rate patterns. The paralogs with low and high trigenic interaction fraction belong to the part of the distribution shown above; trigenic interaction fraction cut-off of 0.4 was used based on negative interactions score (τ or ε) < −0.08, p < 0.05 and contains the set of paralogs that were used for the correlated evolution analysis. Significance was assessed with Fisher’s exact test.

For example, the proteins encoded by the MRS3-MRS4 gene pair show a high correlation in their position-specific evolutionary rate patterns and also have high protein sequence identity (~76%) (Fig. 6B, S6A). While both MRS3 and MRS4 encode high-affinity mitochondrial Fe²⁺ transporters, the MRS3 protein displays an additional Cu²⁺ transport function (60). The general mitochondrial carrier function is structurally constrained because all mitochondrial carrier proteins have a tripartite structure with 3 similar segments, each of which is about 100 amino acids in length and forms two membrane spanning alpha-helices (Fig. S7A) (61). Interestingly, these proteins appear to have properties that are favorable for retention after duplication because multiple mitochondrial carrier protein genes were retained after the yeast WGD. Indeed, of the 35 different mitochondrial carrier protein genes in the yeast genome, 10 are encoded by 5 WGD paralog pairs (62).

Our study interrogated 4 mitochondrial carrier protein WGD pairs, including MRS3-MRS4, YIA6-YEA6, YMC1-YMC2, and ODC1-ODC2. Like the MRS3-MRS4 paralog pair, YIA6 and YEA6 are connected by a negative digenic interaction and show a high trigenic interaction fraction, which is consistent with a retained functional redundancy. In contrast, both the YMC1-YMC2 and ODC1-ODC2 paralog pairs displayed relatively few trigenic interactions. Indeed, the YMC1-YMC2 pair displays a low correlation of position specific evolutionary rate patterns and thus low level of functional redundancy (Table S12). On the other hand, ODC1-ODC2 displays a relatively high correlation of position specific evolutionary rate patterns (Table S12); however, their functional overlap may be masked by the presence of other mitochondrial carrier proteins since they belong to a large gene family with multiple paralog members, expanded also by small-scale duplications (Table S9). Moreover, we combined our genetic analysis with literature curated data to map a genetic network underlying numerous mitochondrial carrier protein genes, and the YMC1-YMC2 and ODC1-ODC2 paralogs appear to form a highly connected subnetwork (Fig. S8), suggesting these two paralog pairs display a more complex functional redundancy.

In contrast to MRS3-MRS4, the SKI7-HBS1 proteins show a relatively low correlation in their position-specific evolutionary rate patterns and thus show a low sequence identity (~26%) with an asymmetric rate of sequence divergence, whereby Ski7 appears to be diverging faster than Hbs1 (Table S10). Detailed inspection of these proteins revealed that the Hbs1 protein resembles the pre-WGD homolog, and Ski7 has adopted a more divergent fate, suggesting its evolved role was not constrained structurally by the pre-WGD (Fig. 6B, S6B). Despite retaining the EF Tu GTP binding domain (PF00009), it is present in a highly divergent form. Ski7 also lost critical sequences encoding an Hbs1-like N-terminal motif (PF8938) and sequences encoding the EF Tu C-terminal domain (PF03143), highlighting the evolutionary divergence of Ski7 from Hsb1 and the pre-WGD homolog (Fig. 6B, S6B).

By calculating the level of correlation of position specific evolutionary rate patterns between members of the duplicate pair in relation to the pre-WGD homolog (Fig. 6A), we assessed the evolutionary constraints acting on paralogs (Fig. 6C). We found that paralogs with a high trigenic interaction fraction were composed of a significantly higher number of paralogs with correlated evolutionary rate patterns and thus were more evolutionary constrained than those characterized by a low trigenic interaction fraction (Fisher’s exact test, p = 0.01) (Fig. 6C). Moreover, paralogs that show a synthetic lethal genetic interaction are considered highly functionally redundant. This subset of essential paralogs shows a higher correlation in their position-specific evolutionary rate patterns, which suggests that these genes are more evolutionary constrained than those within the subset of highly redundant nonessential paralogs displaying a high trigenic interaction fraction (Fisher’s exact test, p = 0.02) (Fig. 6C, Table S13). Hence, it appears that some paralogs are highly structurally constrained or ‘entangled’, which limits their divergence leading to the maintenance of functional overlap, but presumably within a context that also enables the evolution of novel functions.

Modeling simulates the divergent evolution of paralogs with retained functional redundancy

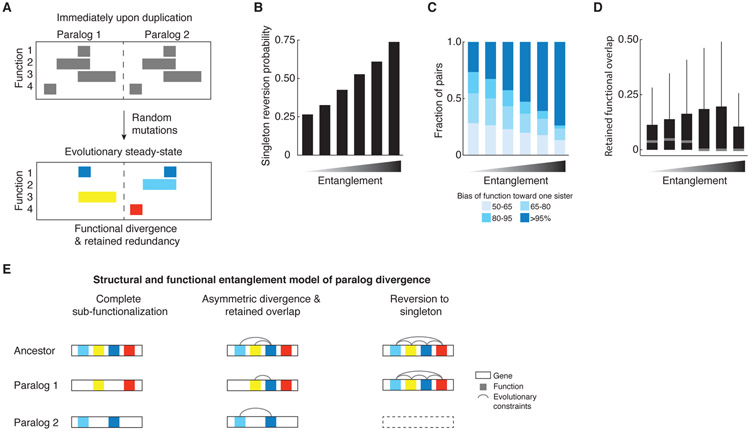
We also explored functional redundancy and paralog retention using in silico modeling in an attempt to test two alternate hypotheses. Under the first hypothesis, the retained nonessential paralog pairs with a high trigenic interaction fraction — and thus a high functional overlap — are inherently unstable over evolutionary time and would eventually diverge completely losing any common functionality. Under the alternate hypothesis, retained paralogs may converge to an evolutionary steady-state, in which paralogs with retained functional overlap cannot segregate certain functional regions without a fitness cost. We computationally generated “genes” of fixed length, in which regions of random length were assigned responsibility for a function, and a random number of such functions was generated for each gene, such that these functional regions were allowed to overlap. Then we duplicated each gene and began introducing random “degenerative” mutations, which would render the affected paralog unable to perform any function associated with the mutated region (Fig. 7A). We discarded any lineage as unfit when any one of the original functions could not be carried out by at least one sister and continued simulating mutations until the pair reached steady-state and could tolerate no additional mutations. The extent of overlap of functions in each randomly generated ancestral gene at the start of paralog evolution provides a measure of their initial structural and functional ‘entanglement’, generating a baseline from which we assessed their evolutionary trajectories (42).

Fig. 7. In silico evolutionary model.

(A) Schematic depiction of the in silico evolutionary model. The pair evolves through random mutations until it reaches an evolutionarily stable-state that can sustain no further mutations without a loss of function. Top panel shows a pair at the start of the evolutionary trajectory and bottom panel shows a pair that achieves a division of labor with a retention of a common function (dark blue blocks), the loss of which is prevented because it would compromise the unique functions of each paralog (yellow, light blue, red). (B-D) Evolutionary fates of paralogs with functional and structural entanglement. Paralogs were generated to represent a range of overlapping functional domains at the onset of their evolutionary trajectory and the propensity to assume specific paralog properties was quantified. In each case, x-axis represents bins of initial functional overlap as a fraction of “gene” length at the start of the simulations (< 10%, 30%, 50%, 70%, 90%, 100%, respectively); y-axis depicts the propensities of paralogs to (B) revert to a singleton state, (C) evolve functional asymmetry, (D) retain functional overlap at the evolutionary steady-state. (E) The structural and functional entanglement model of paralog divergence. A pair will evolve by sub-functionalization, if it is modular and is composed of partitionable functions (left). A paralog pair that is very structurally and functionally entangled will have a high probability of reversion to a singleton state since one of the sisters will quickly degenerate (right). Paralogs with an intermediate level of entanglement at the time of duplication will tend to partition some and retain some overlapping functions, allowing for specialization of a common activity (middle).

These simulations revealed that, for a large fraction of paralog pairs, the mutation process resulted in a singleton state with only one of the sisters being retained. A sizable fraction of simulations, however, ended with paralogs in a stable steady-state in which no more mutations could be tolerated in either paralog, while still maintaining viability. Analysis of the simulation results revealed that the particular trajectory a given paralog pair followed was correlated with the level of functional entanglement. Specifically, paralog pairs that started with the highest levels of entanglement immediately upon duplication were more likely to revert to a singleton state. This suggests that duplicated genes generally cannot tolerate genetic perturbations when they lack functionally independent regions (Fig. 7B, S9A). Among paralog pairs that were retained at steady-state, increased entanglement at the point of duplication also led to a broader bias in the functional asymmetry (ratio of functional responsibilities) at steady-state. Thus, paralogs diverge asymmetrically when they begin their evolutionary trajectory with a protein sequence containing extensive entanglement (Fig. 7C, S9B,C). Consistent with this observation from our simulations, paralog evolution can show asymmetric bias with respect to functional redundancy (Fig. 4B).

Our modeling further revealed that as the extent of the initial entanglement of paralogs increased, so did the range of steady-state functional overlap, which is represented by constrained domains at steady-state (Fig. 7D, S9D). This suggests that the bimodal distribution of the trigenic interaction fraction (Fig. 4A) may reflect one subset of WGD paralogs diverged substantially so that each of the sister paralogs has a distinct function, and another subset of retained WGD paralogs reached an evolutionary steady-state despite retained functional overlap, perhaps as a result of their structural and functional entanglement (Fig. 7E). For example, in case of SKI7-HBS1, Ski7 diverged from Hbs1 by losing the Hbs1-like N-terminal motif and the EF Tu C-terminal domain, while retaining a highly diverged form of the EF Tu GTP binding domain, reflecting a modular, structural and functional organization of the protein (Fig. 6B). On the other hand, MRS3-MRS4 encode mitochondrial carrier proteins dedicated to transport of small inorganic ions, and, thus, their divergence would be predicted to occur in specific residues that modulate ion specificity (Fig. 6B, Fig. S7).

We propose that the evolutionary fate of a duplicated gene can be governed by an interplay of structural and functional entanglement (Fig. 7E). If a duplicated gene contains several easily partitioned functions, then it will most likely sub-functionalize; on the other hand, an entangled pair, which is highly restricted structurally and functionally would have a tendency to revert to a singleton state as one of the genes is predicted to quickly become non-functional. However, given multiple functions and an intermediate level of entanglement, a gene pair has a chance of partitioning or expanding some non-overlapping functions, while retaining others in common, and yet be evolutionarily stable.

Discussion:

We measured digenic and trigenic genetic interaction profiles for 240 double gene deletion mutants of dispensable WGD paralog pairs to address the long-standing question of why paralogs with overlapping functions are retained on an evolutionary time scale. More specifically, by combining both paralog-specific digenic interactions and the paralog pair trigenic interactions in a single metric, the trigenic interaction fraction, we quantified the spectrum of the retained functional redundancy of dispensable paralogs. This approach quantifies the functional overlap of retained paralog pairs and sheds light on cellular roles of poorly characterized pairs by revealing functional redundancy.

Definitions of functionally redundant or divergent paralogs using genetic interactions appear to be consistent with classification from protein-protein interaction studies (25). For example, in the case where a paralog is deleted and the sister responds by gaining specific protein-protein interactions, then the paralogs should compensate for each other’s loss and thus should exhibit a high trigenic interaction fraction. Indeed, four such paralogs were examined in our study and they showed a propensity to exhibit high trigenic interaction fractions. In particular, NUP53-ASM4 and OSH6-OSH7, showed high trigenic interaction fractions of 0.49 and 0.80, respectively. On the other hand, some paralogs share protein-protein interactions that are lost for both paralogs when only one sister is deleted, suggesting that though these paralogs may cooperate, they do not fully compensate for each other (25). We examined two such known paralogs, PEX25-PEX27 and GSY1-GSY2, and they exhibited low trigenic interaction fractions of 0.19 and 0.25, respectively. Beyond these examples, genetic interaction profiling provides a functional readout and allows assessment of pairs of genes that do not have extensive protein-protein interaction profiles, and therefore provides a complementary view of functional redundancy.

Our framework to interrogate how WGD paralog evolution relates to the evolutionary stability of retained common functions and asymmetric functional divergence. By computing the extent of correlated evolution in sister paralogs (Fig. 6), we identified paralogs that show highly correlated position specific evolutionary rate patterns and thus are under strong evolutionary constraints to retain some of their ancestral function, reflecting their structural and functional entanglement. This was further explored by our in silico model (Fig. 7), which predicts that low levels of entanglement are sufficient to drive asymmetric sub-functionalization, while more complex sequence-function relationships with higher structural entanglement can result in fixation of functional redundancy. Indeed, our modeling shows that given some level of moderate structural entanglement and the potential for multifunctionality, a substantial fraction of duplicate pairs converge to a steady-state in which they retain functional overlap. This result offers a possible explanation as to the persistence of the functional overlap in paralogs, which is not simply due to paralogs diverging slowly from one another. We propose that the results of our in silico modeling may explain why the trigenic interaction fraction tends to follow a bimodal distribution (Fig. 4A, 7). The upper mode of the distribution represents the set of duplicate pairs that will likely remain fixed in a partially functionally redundant state, while the lower mode represents duplicates that already have or are diverging in function. Because ohnologs and homeologs (42, 50) show the same distribution of trigenic interaction fraction, this model of paralog divergence and retention of functional redundancy also likely applies to gene duplicates of various ages and origins beyond whole-genome duplication, which may include small-scale duplicates.

In the simulation analysis we modeled functions as being supported by contiguous sequence domains. However, since our model treats every position along a “gene” as statistically independent, positions contributing to a common function would not need to contiguous, and the conclusions would remain the same for functional domains encoded by discontinuous sequences. Therefore, the model has the flexibility to capture a wide variety of different physiological scenarios that might display structural or functional entanglement, such as independent modular domains, linearly distant contact sites within a secondary, tertiary or quaternary structure, or even regulatory regions beyond coding boundaries or elsewhere within the genome. It is important to note that this definition of structural and functional entanglement is distinct from the simple physical entanglement of proteins restricted to the basic organization of polypeptide chains (63).

The question of why subfunctionalization does not proceed to completion leading to fixation of duplicated genes with some specific functions, yet exhibiting a certain level of functional redundancy remains an outstanding problem in evolutionary biology. Constraints that prevent complete divergence may allow paralogs to retain the ability to function in parallel biochemical pathways or macromolecular complexes and result in a retention of redundancy (18, 43, 64). More specifically, despite functional divergence of independent domains, incomplete subfunctionalization of paralogs could be driven by a structurally and functionally overlapping ancestral domain (35). There are few existing models of duplicate evolution that specifically address the existence of redundancy in a steady-state. There are models that address different potential modes of functional divergence, such as neo- or sub-functionalization (39, 65). However, reasons for the persistence of functional redundancy have remained elusive. It is noteworthy that previous simple computer simulations, which incorporated mutation rates of genes and the varying contribution of their functions to the overall fitness, have also identified situations in which redundancy can be maintained indefinitely (66-68). Interestingly, it has been shown that paralogs that are selected to function as distinct homomers also retain the ability to heterodimerize, which may prevent functional divergence between paralogs (69). In general, our findings support fixation of overlapping functional redundancy for a substantial proportion of yeast paralogs.

Methods summary

To study the functional divergence of duplicated genes, 240 double mutants and 480 corresponding single mutant control ‘query’ strains, involving dispensable WGD pairs in the budding yeast Saccharomyces cerevisiae S288C, were constructed using PCR-mediated gene deletion followed by tetrad analysis. Paralog 1 deletion was marked with natMX4, while paralog 2 was deleted and replaced with K. lactis URA3. Single mutant control strains deleted for each one of the paralogs were also marked with the relevant control marker, which was inserted at the benign HO locus. Query strain fitness and query gene pair genetic interactions were measured using high-density synthetic genetic array (SGA) analysis. To obtain trigenic interactions, double mutant query strains along with their respective single mutant control query strains were subjected to trigenic-SGA analysis (τ-SGA), which involves a number of automated replica pinning steps. Each query strain was mated to a diagnostic array of 1200 strains, consisting of deletion mutants of nonessential genes and temperature-sensitive alleles of essential genes, providing a representative view of the global digenic interaction network. Briefly, the query and array strains were mated on rich media, MATa/α diploids were selected on media containing G418 and clonNAT, sporulation was induced by transferring to media with low levels of nitrogen and carbon sources, and MATa meiotic haploid progeny was selected on haploid selection media. Triple mutants were then selected by first pinning onto haploid selection media containing G418, lacking uracil, and then onto haploid selection media containing both G418, clonNAT, lacking uracil. Every query strain was screened in two independent replicates.

Colony size was measured as a proxy for fitness and digenic and trigenic interactions were scored using a quantitative model. Trigenic interactions were classified into novel vs. modified by overlapping with digenic interactions. Functional information embedded within digenic and trigenic interactions was assessed by their enrichment with external functional standards, such as protein-protein interactions, subcellular localization, co-expression and coannotation. Trigenic interaction fraction was calculated as the ratio of the negative trigenic interaction degree relative to the total negative digenic and trigenic interaction degree. Correlation of trigenic interaction fraction with physiological and evolutionary features included quantification of genetic interactions within a paralog pair, asymmetry of digenic interactions of members of each paralog pair and sequence divergence rate, which was calculated as the raw difference between the fold-changes in substitutions per site in post-WGD clades. The potential for paralog induction during developmental programs was assessed in (1) meiosis using published meiotic mRNA-seq and ribosome profiling datasets, (2) filamentous growth using a published measure of invasion, as well as (3) glucose starvation conditions using published gene expression dataset. Dosage selection was estimated using global digenic interaction profile correlation similarity.

SAFE (Functional annotations based on the Spatial Analysis of Functional Enrichment) of the global genetic interaction profile similarity network was used to annotate gene function. Enrichment was calculated using the overlap of trigenic interactions with a neighborhood on the global digenic interaction similarity network. Novel paralog function for ECM13-YJR115W was interrogated using a drug sensitivity spot assay on media containing benomyl, and a liquid growth curve analysis on media containing latrunculin B. Spindle morphology was monitored by expressing Tub1-GFP, as well as sfGFP fusion proteins of Ecm13 and Yjr115w and imaging the resulting strains using a spinning-disc confocal microscope. Novel paralog function for STB2-STB6 was monitored by Bap2-GFP localization in stb2Δ stb6Δ double mutant deletion strains and quantified using CellProfiler.

To measure evolutionary constrains on paralogs, evolutionary rates for specific amino acid columns in multiple sequence alignments were computed using the discrete gamma model of protein evolution, as implemented in PAML for the pre-WGD sequences and for each paralog separately. Pearson correlation coefficients were computed between the rates of the pre-WGD clade to each paralog (pre-WGD & Paralog 1 and pre-WGD and Paralog 2), and between the two paralogs (Paralog 1 and Paralog 2) to classify paralogs into those with low and high correlation of position specific evolutionary rate patterns. BioGRID was used to curate genetic interactions for the mitochondrial carrier protein family. Paralog divergence was simulated using a computational framework in which a gene of fixed length was generated, annotated with hypothetical functions and subjected to random degenerative mutations at a constant rate. Evolution to a steady state was achieved when no more divergence mutations could be tolerated while maintaining viability. The resulting paralogs were binned according to each pair’s initial level of structural entanglement, which is the level of mutable positions within a gene that carry out two or more functions to quantify the number of paralogs that reverted to singleton state, completely diverged or retained functional overlap. For a more detailed description of the experimental and computational analyses refer to the supplementary materials.