Abstract
Transmit efficiency specifies the amplitude of the magnetic resonance excitation field produced over a region of interest with respect to the radiofrequency power deposited in the sample. This metric is highly important at ultra-high field magnetic resonance imaging (≥7T), where excitation inhomogeneities and electric field interference effects could prevent achieving the desired flip angle distribution while satisfying the power safety limits. The aim of this work was to introduce an approach to calculate a theoretical upper bound on the transmit efficiency (OPTXE) for RF shimming, independent from any particular coil design. We computed the OPTXE for head-mimicking uniform spherical samples and a realistic heterogeneous head model by maximizing the square of the net transmit field per unit power deposition. The corresponding radiofrequency shimming weights were used to combine the analytical surface current modes into ideal current patterns. OPTXE grew monotonically as the target excitation voxel approached the surface of the object, and overall decreased at higher field strengths, presenting similar trends both in the uniform sphere and heterogeneous head model. Arrays with increasing number of loops could closely approach OPTXE in the central region of the object, but performance decreased closer to the surface and at higher magnetic field strengths. The performance of 32 loops for a two-dimensional excitation region at 7T increased from 34% to 93% when they were arranged based on the shape of the ideal current patterns. OPTXE provides an absolute reference to evaluate coil designs and RF shimming algorithms, whereas ideal current patterns could serve as guidelines for novel coil designs at ultra-high field. The uniform sphere model enables rapid analytic simulations and provides a good approximation of the OPTXE distribution in a realistic heterogeneous head model with comparable dimensions.
Keywords: Ideal Current Patterns, Maximum Transmit Efficiency, MRI, RF Coil Performance, RF Shimming, Optimal Transmit Efficiency
INTRODUCTION
A common approach to assess the efficiency of a transmit coil is to evaluate the amplitude of the magnetic field () it produces over a region of interest (ROI) with respect to the radiofrequency (RF) power deposited in the body. Transmit efficiency (TXE) becomes highly important at ultra-high field (UHF) magnetic resonance imaging (MRI) (≥ 7 T), where inhomogeneities and electric field interference effects could prevent achieving the desired excitation while satisfying the safety constraints on specific absorption rate (SAR).1 Multiple channel transmission can be used to improve the fidelity of the excitation profile and minimize SAR.1–4 Evaluating TXE for a transmit array requires measuring the power correlation matrix between the channels,5–7 in addition to the amplitude for each of them. Furthermore, TXE depends on the particular weighting configuration chosen to drive the distinct channels for RF shimming8–11 or parallel transmission.12–14
Zhu et al. proposed a TXE metric15 for transmit arrays, which could be used both to measure coil performance of existing configurations and to find the optimal shimming weights that maximize TXE of a given array in a target region.16 However, while the resulting TXE would characterize the maximum performance that the particular transmit array could achieve for a given imaging task, it would not tell how much room for improvement may exist in principle, nor provides any insight into the optimal coil design that truly maximizes TXE.
It has been shown that theoretical performance limits could be used as absolute references against which to evaluate RF coil performance and to derive guidelines for optimal coil design.1,17–25 For example, the ultimate intrinsic signal-to-noise ratio (UISNR) could be used to assess receive arrays,26–29 while the associated ideal current patterns could be employed to guide coil design.30–33 Ultimate performance bounds were also used to investigate transmit array performance, in terms of SAR and excitation homogeneity, as a function of the number of coil elements in RF shimming and parallel transmission.1,34 However, they have not been used yet to obtain physical insight on optimal transmit array design.
The aim of this work is to introduce a formalism to calculate the theoretical upper bound, consistent with electrodynamic constraints, for the TXE metric described above. We named this quantity optimal transmit efficiency (OPTXE). Our goal is to provide an absolute reference to assess coil performance, independent of any particular design, and derive new physical insights into the design of optimal transmit coils.
METHODS
The transmit efficiency metric for RF shimming
RF shimming10,11 was proposed to mitigate inhomogeneities by adequately adjusting the relative amplitudes and phases of multiple transmit elements driven with the same RF waveform. Since there are multiple possible choices for such weighting configurations, it is not straightforward to define a metric to assess the efficiency of a transmit array in RF shimming. In this work, we use the same TXE metric as Deniz et al.,16 which is defined as the square of the magnitude within an excitation ROI per unit dissipated RF power over the entire volume of the sample:15,16
| (1) |
where σ(r) is the conductivity of the sample. The net and E(r) fields at each spatial location r can be expressed as the weighted combination of the unit-current fields (, en(r)) of the coils of a N-channel transmit array:
| (2) |
Here wn are the complex-valued RF shimming coefficients that correspond to the driving amplitude and phase modulation of the nth transmit coil. The net for a target excitation ROI that includes Q spatial locations, or voxels, can be written in matrix form as , where C is a Q × N matrix with . The average transmit field squared in the ROI can be expressed as
| (3) |
where Γ = CHC/Q is an N × N positive-definite complex Hermitian matrix, with the superscript H denoting the conjugate transpose operation. By exploiting field superposition, the total deposited, or absorbed, RF power can be calculated as
| (4) |
where Φ is an N × N positive-definite complex Hermitian RF power covariance matrix whose elements are
| (5) |
with i, j ∈ {1, .. , N} and the superscript * denoting the complex conjugation. By substituting Equations 3 and 4, the TXE metric in Equation 1 can be rewritten as the ratio of two quadratic forms
| (6) |
with units of (μT)2/W. The problem of finding the maximum of η can be treated as a generalized eigenvalue problem (Γw = λΦw), which has a closed-form solution and guarantees finding a global optimum.15,16,35 More specifically, the largest eigenvalue corresponds to the maximum TXE (ηmax) and the associated eigenvector gives the corresponding RF shimming weights (wmax) that yield the maximum TXE. Note that in the case of a single transmit channel, the matrices Γ and Φ reduce to scalars, and the metric captures strength squared per unit power, which is compatible with the conventional approach to evaluate transmit efficiency as the amplitude of divided by the square root of absorbed power.
An upper bound on transmit efficiency
In order to calculate the theoretically largest value for the chosen TXE metric (i.e., the OPTXE), independent of any particular coil design, we employed a basis of orthogonal electromagnetic (EM) current modes flowing on a surface surrounding the sample as the elements of a hypothetical infinite array.1,18–22,25,31 The equations introduced above for the case of finite arrays remain valid, with N indicating the number of modes instead of coils. According to the surface equivalence, or Huygens’s, principle, any EM field distribution inside the source-free volume contained by a closed surface can be generated by a current distribution flowing on the surface.36 Since the operator that maps surface electric currents to incident electromagnetic (EM) fields over the object is compact,37 TXE is guaranteed to converge to its largest value, which is the OPTXE, as the number of basis current modes is increased. This property, which can be exploited both for the case of analytical computations in uniform spherical samples and numerical computations in heterogeneous head models,38 allowed us to use a finite number of modes to compute the OPTXE.
Optimal transmit efficiency in a head-mimicking uniform sphere
We used a simulation framework31 based on dyadic Green’s functions (DGF),39 which enables the rapid analytic calculation of the OPTXE in a homogeneous spherical sample. The method begins by defining a current distribution on a spherical surface with radius b, surrounding a uniform sphere:31,39
| (7) |
where r (radial), θ (polar), and φ (azimuthal) are spherical coordinates and K is the surface current density, which can be expressed as a weighted sum of basis current modes:31,40
| (8) |
Here l and m are mode indices, lmax is the expansion order, is the imaginary unit, is the unit vector in the radial direction, and Xl,m is a vector spherical harmonic (see Appendix). and are the complex-valued series expansion coefficients for the magnetic-type (divergence-free) and electric-type (curl-free) surface current contributions, respectively. The net EM field generated by the current modes inside the sphere can be calculated using the appropriate DGF (see Appendix) as
| (9) |
Here, ω is the angular frequency, μ0 is the free-space permeability, is the free-space wavenumber and ϵ0 is the free-space permittivity. Also, is the complex wavenumber inside the lossy, dielectric sphere with relative permittivity ϵr and electric conductivity σ. Ml,m and Nl,m are spherical vector wave functions used to construct the DGF, whereas and are weighting coefficients derived by multiplying the series expansion coefficients by a transformation matrix T, which accounts for boundary conditions at the surface of both the spherical sample and the current-bearing spherical surface. By treating the current modes as elements of a transmit array, we could use the fields in Equation 9 to construct the matrices Γ and Φ in Equation 3 and 4, respectively. The number of modes was then increased until the largest eigenvalue, which can be computed numerically (e.g., with the Matlab function eigs(Γ, Φ, 1)), converged to its maximum value . The corresponding eigenvector (), which contains the RF shimming coefficients ( and ), was substituted in Equation 8 to calculate the ideal current patterns (ICP) yielding OPTXE as a weighted combination of the surface current modes.23,31
OPTXE calculations were performed for spherical samples with uniform, frequency-dependent electrical properties, mimicking average brain gray and white matter38 for various magnetic field strengths (see Table 1). We simulated spherical objects with different radii a = 7.5, 10, 15 cm. The radius of the current-bearing spherical surface was set as b = a + D, with D = 1.5 cm in all cases (Figure 1a). We calculated OPTXE and ICP for single voxel locations across the diameter of the sample, as well as for 2D circular excitation ROI’s, centered in the axial plane, and 3D spherical excitation ROI’s, concentric with the sample (Figure 1b). For both types of ROI, we considered different radii: 0.3a, 0.6a, 0.9a. Using the same formalism, we also searched for the eigenvector that minimizes inhomogeneity and compared the resulting TXE, uniformity and ICP with those for the optimal case. We used an expansion order lmax = 45, which ensured convergence of all calculations (see Supporting Information Figures S3, S4, and S5).
TABLE 1.
Dielectric Properties of Average Brain Tissue
| Bo [T] | 0.5 | 1.5 | 3 | 7 | 10.5 | 14 | 21 |
| Larmor Frequency [MHz] | 21.3 | 63.9 | 127.7 | 298.0 | 447.0 | 596.1 | 894.1 |
| Dielectric Constant εr | 157.5 | 82.7 | 63.1 | 51.9 | 49.1 | 47.6 | 45.9 |
| Conductivity σ [1/Ωm] | 0.30 | 0.40 | 0.46 | 0.55 | 0.61 | 0.66 | 0.76 |
Figure 1: Sample geometries and relevant simulation settings.
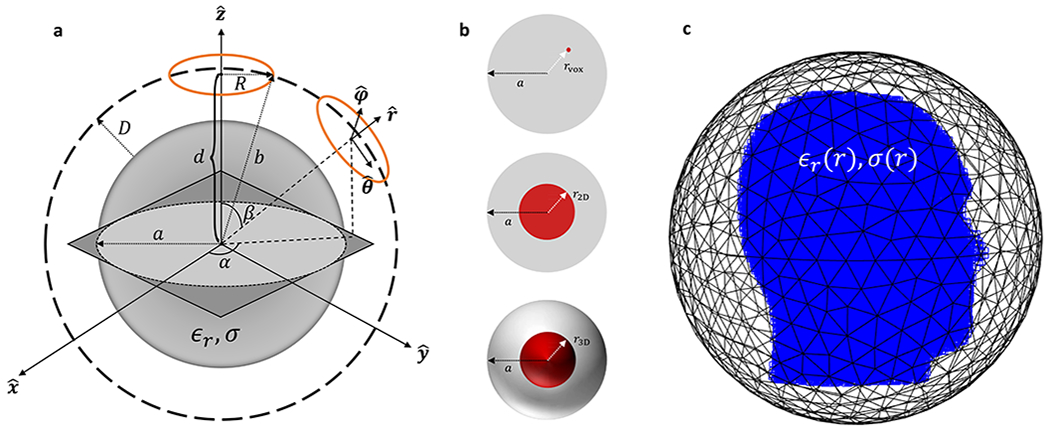
(a) Schematic representation of the homogeneous spherical sample with frequency dependent electrical properties ϵr, σ and radius a surrounded by a current-bearing 2D spherical surface with radius b. Circular loop coils (orange) with radius R are arranged on the spherical surface and can be appropriately rotated by azimuthal (α) and polar (β) angles to compose different finite arrays designs. (b) OPTXE was calculated for single voxels across the diameter of the sample, 2D circular disk excitation ROI’s on a transverse plane through the center of the object, and 3D spherical excitation ROI’s concentric with the spherical sample. (c) Schematic representation of “Duke” inhomogeneous realistic head model surrounded by a triangulated current-bearing spherical shell.
Optimal transmit efficiency in a realistic heterogeneous head model
We cropped the head of the Duke numerical body model38 and discretized it using 5 mm voxel resolution (Figure 1c). We employed electric surface currents distributed on a perfectly electrically conducting spherical shell enclosing the head model. We discretized the current distribution using a triangulated grid with Rao-Wilton-Glisson (RWG)41 basis functions fn(r). For every n RWG basis element of the triangulated shell we computed the incident electric field and magnetic flux density at all q voxels of the head model, using the free-space DGF to form the shell-to-head coupling matrices N and K:
| (10) |
where the DGFs that map electric current sources to observed electric fields and magnetic fields were calculated, respectively, as:
| (11) |
with denoting the free-space scalar wave Green’s function and the identity dyadic. The coupling matrices in Equation 10 are low-rank due to the smoothing property of the Green’s functions for remote elements interactions,37 which allowed us to use a truncated singular value decomposition (SVD) to approximate them with a prescribed approximation error. In particular, we applied SVD to the coupling matrix, K = USV*, and truncated with 10−5 relative tolerance. This step can be considered equivalent to generating an orthonormal numerical basis of incident magnetic flux densities. All possible incident magnetic flux densities can then be expressed as a linear combination of these basis modes with an accuracy up to the above specified tolerance, using binc = Ua, where a denotes the weighting coefficients. The corresponding orthogonal incident electric fields basis is derived as einc = NVS−1a. Finally, we used an in-house volume integral equation solver with piecewise linear basis functions42 to compute the total (incident plus scattered) EM fields in the realistic heterogeneous head model for each incident electric field basis vector. While Γ (Equation 3) can be calculated directly from the total magnetic field, Φ was computed with a numerical integration quadrature scheme that included the contributions of the piecewise linear terms. As for the analytic case, the number of modes was increased until the largest eigenvalue converged to the OPTXE. OPTXE maps were calculated for different field strengths, adjusting the electrical properties of the numerical head model to the corresponding Larmor frequency.
Maximum transmit efficiency for finite arrays
For the case of a uniform dielectric sphere, the maximum TXE of finite coil arrays can be calculated within the same analytic DGF framework used for the OPTXE, by appropriate weighted combinations of the basis modes in Equation 8. In particular, the weights to simulate circular loop coils can be derived analytically:31
| (12) |
where α and β define the angular position of the center of the loop coil on the current-bearing spherical surface, d is the distance from the center of the spherical sample to the center of the loop coil and R is the radius of the loop coil (Figure 1a). The and RF power covariance matrices for the loop array can be calculated in a straightforward manner by applying the weights in Equation 12 to the corresponding matrices for the full set of modes.
For the case of the realistic head model, the incident EM fields of finite coil arrays can be modeled within a simplified wire integral equation framework, where each segment of a coil is assumed to have a constant current, proportional to its length, radiating in free-space. Then, the total EM fields can be computed with the same volume integral equation solver42 as for the basis fields. The maximum TXE for the array is then computed as for the basis functions by solving the generalized eigenvalue problem.
We investigated the TXE of various loop arrays as a percentage of the OPTXE, for different values of the main magnetic field strength. For the case of the uniform sphere, we calculated the maximum TXE for different excitation ROI’s for arrays with an increasing number (8, 16, 24, 32) of fully encircling loops, as well as belt-shaped arrays with an increasing number (8, 16, 24, 32) of loops symmetrically arranged around the central axial plane of the spherical sample. For the case of the head model, we designed an array with 8 loops arranged on a cylindrical surface surrounding the sample and three helmet-shaped arrays with 16, 24, and 32 loops.
RESULTS
The OPTXE for single voxels along the sphere diameter exponentially increased as the target voxel approached the surface of the sphere (Figure 2), displaying a similar trend to that reported for the UISNR.20,21 The OPTXE decreased as the main magnetic field increased, but for target voxels in the central region of the sphere began to gradually increase again for field strengths larger than 7T, especially for small samples. For example, OPTXE at the center was 4.9 (μT)2/W and 2.57 (μT)2/W at 7T for the spheres with a = 7.5 cm and 10 cm, respectively, while it was 9.55 (μT)2/W and 3.39 (μT)2 at 21T, corresponding to 95% and 32% improvements. Figure 3 show a temporal snapshot (ωt = 0) of the density of ICP yielding OPTXE at various voxel locations for different field strengths. Supporting Information Video S1 shows how the same ICP evolve in time. Note that, similar to the case of UISNR,31 the ICP for OPTXE at the central voxel took the form of two large distributed loops precessing at Larmor frequency at every field strength, whereas they alternated between distributed single-loop and figure-eight shapes for intermediate voxels, becoming increasingly complex at higher field strengths.
Figure 2: Optimal transmit efficiency as a function of voxel position, for different spherical sample size and magnetic field strength.
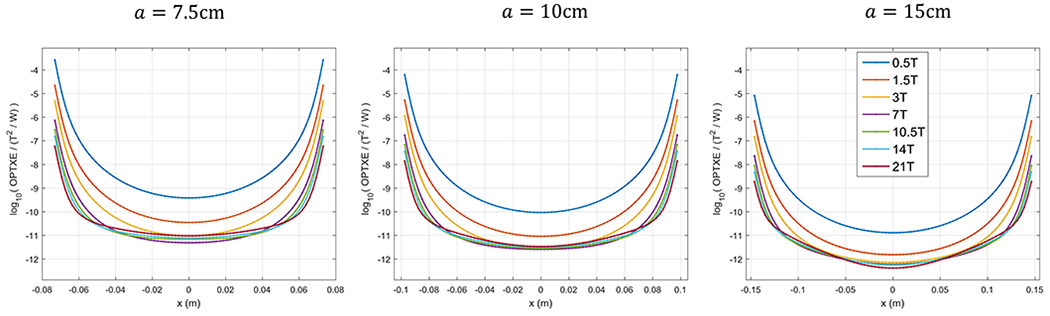
OPTXE is plotted in logarithmic scale across the diameter of spherical samples with radii a = 7.5, 10, 15 and brain-mimicking electrical properties at the corresponding magnetic field strengths B0 = 0.5, 1.5, 3, 7, 10.5, 14, 21T. OPTXE decreases for larger objects and as the magnetic field strength increases up to 7T. At voxels closer to the center, OPTXE increases again for magnetic field strengths > 7T, except for the largest sphere. Near the edge of the spherical sample, OPTXE is order of magnitudes higher than at the center, for all object sizes and field strengths.
Figure 3: Snapshots of ideal current patterns yielding the optimal transmit efficiency at different voxel positions, for various main magnetic field strengths.
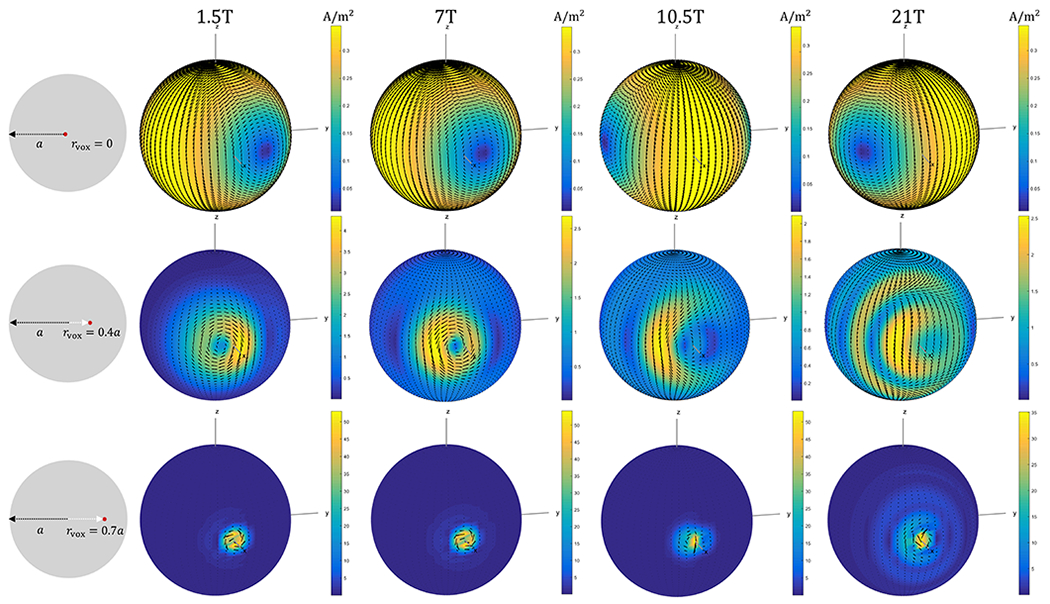
The density of ideal current patterns at ωt = 0 is shown for the spherical sample with radius a = 10 cm, for voxels at the center (rvox = 0), at an intermediate position (rvox = 0.4a), and near the surface (rvox = 0.7a). The voxel positions are shown in the first column. The other columns show the corresponding ideal current patterns for increasing B0 = 1.5, 7, 10.5, 21T. The shape and density of the ideal current patterns vary significantly among different voxel positions. Specifically, at the center, they resemble two large distributed loops on opposite sides of the sphere precessing at the Larmor frequency for all field strengths. At the intermediate and near-the-surface positions, they become increasingly localized around the target voxel. As the magnetic field increases, their shape becomes more complex, especially for intermediate voxel positions.
The OPTXE for increasing size of the 2D excitation ROI is shown in Figure 4. Except for small ROI’s, where behavior aligns with that reported for the central voxel (Figure 2), OPTXE decreased with increasing field strength for all sphere radii. Interestingly, at low field (0.5T, 1.5T and 3T) the OPTXE was constant until the size of the ROI was approximately 0.65a. For larger ROI sizes, OPTXE increased double-exponentially, although leading to impractical results, as shown in Figure 5 and described in the Discussion. At field strengths equal or larger than 7T, the OPTXE had a global minimum that corresponded to smaller ROI sizes as B0 increased. In particular, for the case of a spherical sample with a = 10 cm, the global minima were found for r2D = 0.7a, 0.675a, 0.625a, 0.5a at 7T, 10.5T, 14T, 21T, respectively. For the larger object (a = 15 cm) the global minima at the same field strengths corresponded to r2D = 0.525a, 0.45a, 0.4a, 0.375a.
Figure 4: Optimal transmit efficiency as a function of the size of the two-dimensional excitation region of interest, for different spherical sample size and magnetic field strength.
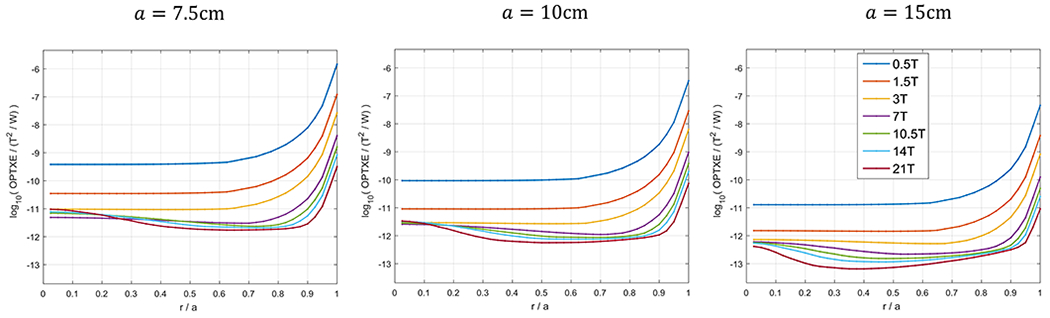
OPTXE is plotted in logarithmic scale for spherical samples with radii a = 7.5, 10, 15 cm and brain-mimicking electrical properties, adjusted for each magnetic field strength. The OPTXE is higher for smaller object sizes. The OPTXE in 2D ROI’s remains approximately constant until the ROI size approaches the diameter of the sphere section, at which point it starts to rapidly increase due to the contributions of the edge voxels where OPTXE is high (see Figure 2).
Figure 5: Comparison of and absorbed RF power distributions associated with the first eigenvalue (i.e., optimal transmit efficiency) and the eigenvalue that minimizes inhomogeneity within a 2D excitation ROI.
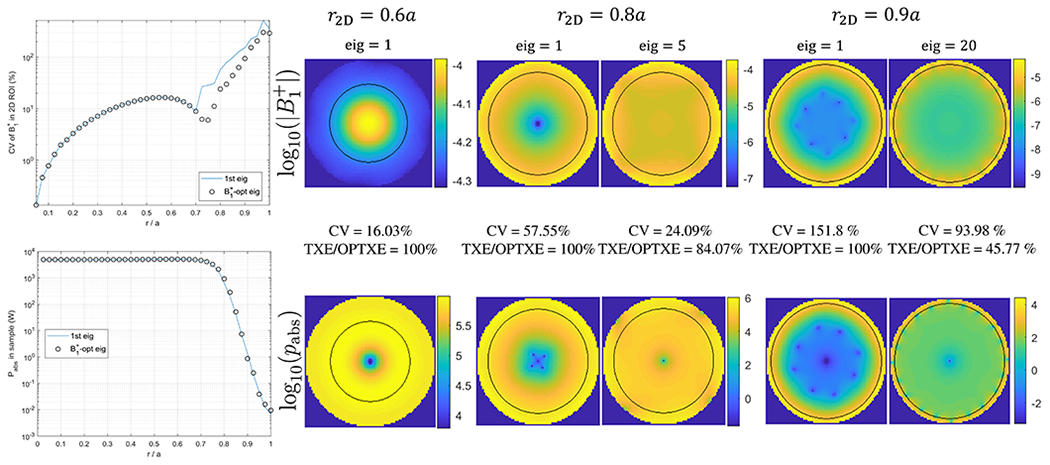
The largest eigenvalue that maximizes TXE also minimizes the coefficient of variation (CV) of within the ROI until r2D = 0.7a. For larger ROI’s, the eigenvalue that maximizes homogeneity results in slightly lower TXE and increased RF power deposition. When the radius of the ROI approaches the radius of the spherical sample it is more difficult to achieve a homogeneous distribution.
Figure 5 compares MR excitations for the largest eigenvector that maximizes TXE vs. the eigenvector that minimizes inhomogeneity. In the case of ROI radius of 0.8a, using the fifth eigenvalue resulted in a coefficient of variation (CV) of 24% for within the ROI, compared with 58% when using the largest (first) eigenvalue, while still achieving 84% of the OPTXE. The tradeoff associated with improving homogeneity is higher for an ROI radius of 0.9a, where decreasing the CV of from 152% to 94% corresponds to giving up approximately 50% of the OPTXE. When the radius of the ROI is equal to the radius of the sphere, it is not possible to reduce variability without losing nearly all TXE. Note that in the case of ROI’s with radius until 0.7a, the largest eigenvalue maximizes TXE while achieving excellent homogeneity within the ROI.
Figure 6 shows temporal snapshots of ICP yielding OPTXE in a small and a large 2D ROI for various field strengths. Supporting Information Video S2 shows the corresponding full-time evolution. For the small ROI, the ICP resembled large distributed loops precessing at the Larmor frequency, whereas for the large ROI the patterns became more localized around the excitation plane, taking the shape of ellipses. As the operating frequency increases, propagation delay and wave phenomena affected the shape of the ICP. The behavior of OPTXE for 3D excitation ROI’s of increasing size resembled that observed for 2D ROI’s and is shown in the Supporting Information Figures S1, S2, and S5.
Figure 6: Snapshots of ideal current patterns yielding the optimal transmit efficiency, for two sizes of the two-dimensional excitation ROI and different main magnetic field strengths.
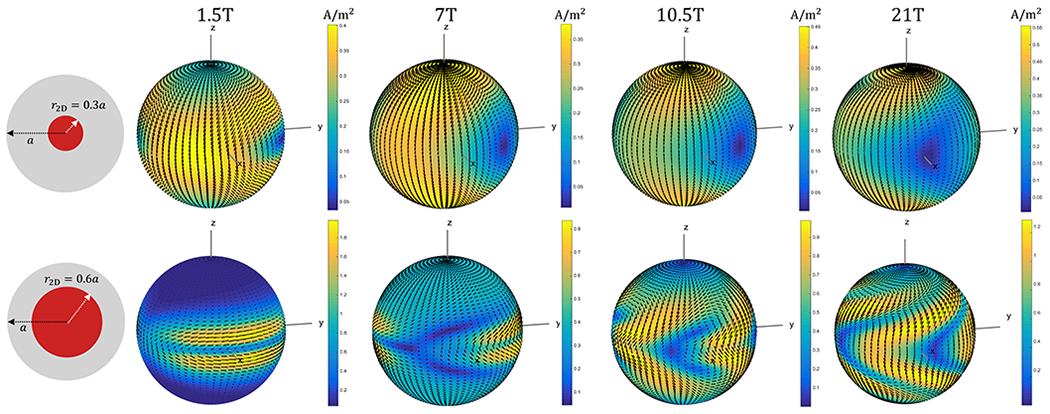
The density of ideal current patterns at ωt = 0 is shown for the spherical sample with radius a = 10 cm, for circular disk ROI’s of size r2D = 0.3a and r2D = 0.6a. The corresponding 2D ROI’s are shown in the schematics of the first column. The shape and density of the ideal current patterns differ significantly as the 2D ROI size changes. Specifically, at r2D = 0.3a, they resemble two compressed distributed loops of elliptical shape on opposite sides of the sphere precessing at the Larmor frequency. For the larger 2D ROI, the eccentricity of the elliptical shape also increases, and the ideal current patterns become more localized around the excitation plane. As the magnetic field strength increases, the ideal current patterns become more complex, with wave and propagation delay affecting their shape.
Figure 7 shows the absolute transmit performance (100*TXE/OPTXE) of encircling arrays of loops at every voxel in the central axial plane, for different magnetic field strengths. In all cases, OPTXE was approached more closely as the number of loops increased. However, overall array performance decreased at higher fields, suggesting that more coils and different type of coils, e.g., electric dipoles,43 may be needed to approach the OPTXE. While at 3T 8 and 32 loops achieved 95% and 99%, respectively, of the OPTXE at the central voxel, the performance of the same arrays was 50% and 96% at 10.5T. The performance at high field dropped considerably for intermediate voxel locations. For example, at rvox = 0.5a, 8 and 32 loops yielded 31% and 80% performance, respectively, at 3T, but reached only 16% and 56% of the optimum at 10.5T. Figure 8 explores the performance of belt-shaped arrays with different number of elements for maximum TXE inside 2D ROI’s of increasing size. As for the individual voxel optimizations (Figure 7), we found an inverse relationship between field strength and performance, and a direct one between number of elements and performance. In particular, at 3T all arrays could achieve close to 100% performance for certain sizes of the excitation ROI, whereas at 10.5T at least 24 loops were needed to achieve more than 80% performance. While OPTXE was approximately constant for increasing size of the 2D ROI’s (Figure 4), the performance of the belt-like arrays varied significantly. At all field strengths, array performance was maximum for an ROI with radius greater than 50% of the sphere radius, with such optimal ROI size increasing with main magnetic field strength.
Figure 7: Absolute transmit performance of finite arrays with an increasing number of elements encircling the spherical sample, at different main magnetic field strengths.
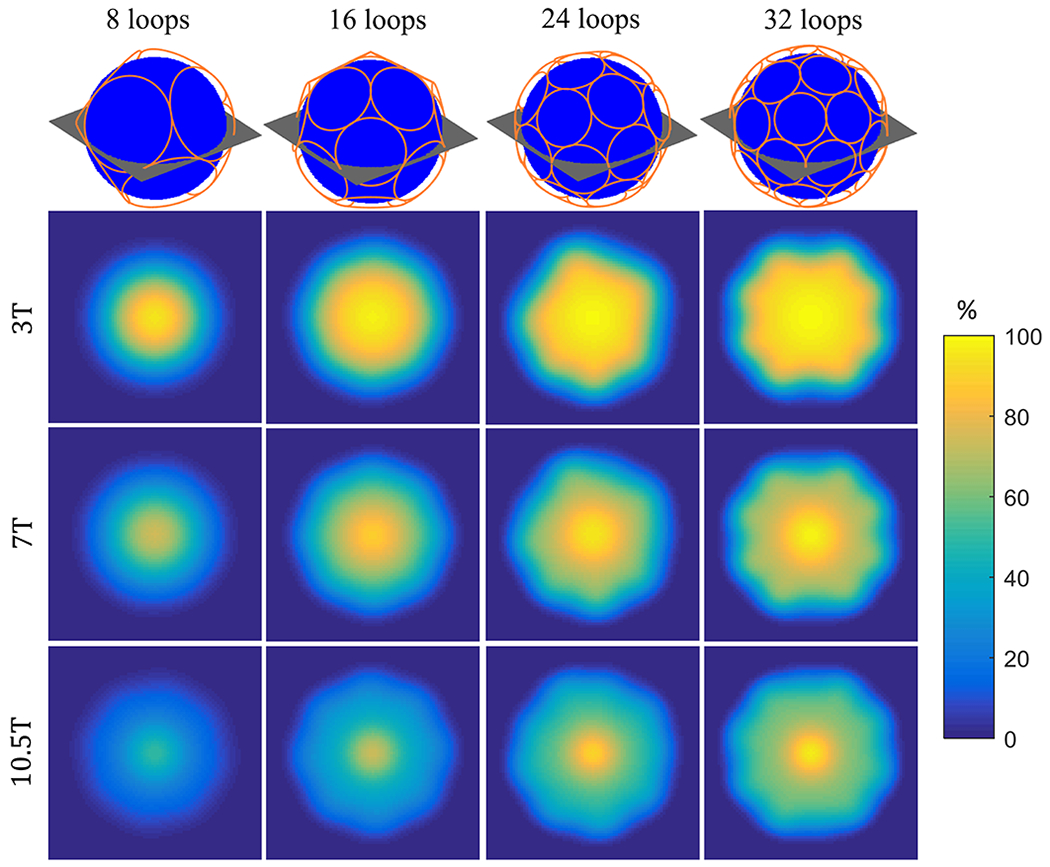
Performance maps displaying maximum TXE as a percentage of the OPTXE at each voxel of the central axial plane of the spherical sample with a = 10cm are shown for various finite arrays and for increasing B0. Absolute transmit performance is higher over a broader region when the number of transmit loops increases, but more than 32 elements seem to be required to approach the optimal performance at higher magnetic field strengths.
Figure 8: Absolute transmit performance of finite arrays with an increasing number of elements arranged like a belt around the central plane of the spherical sample, as a function of the size of the 2D excitation ROI.
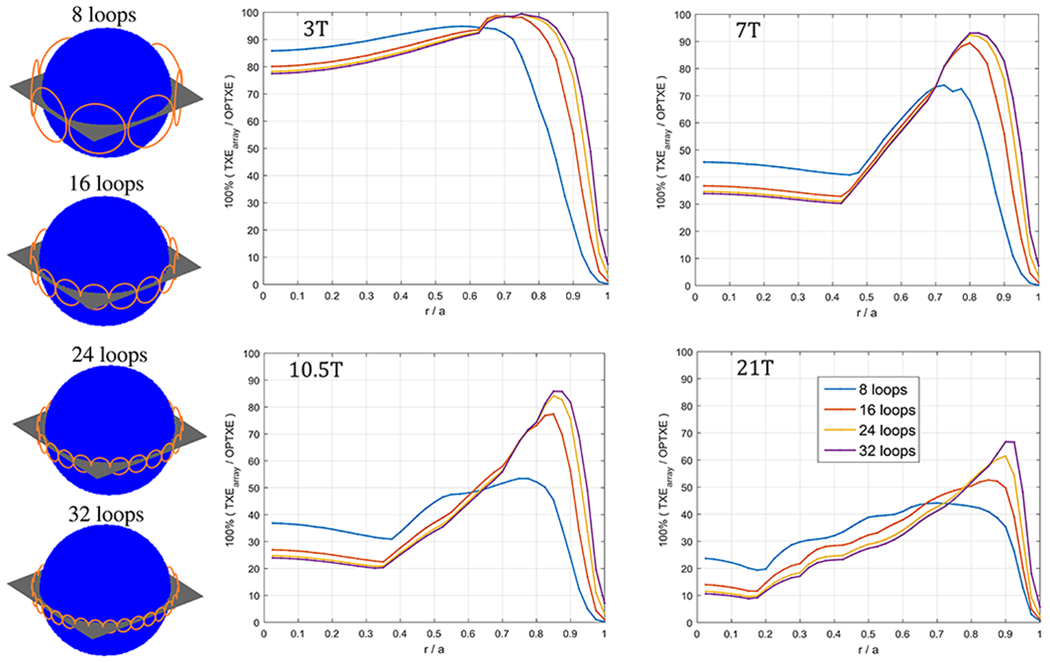
Schematics of the finite arrays are shown in the first column. Array performance is plotted as a percentage of the OPTXE for increasing size of the 2D circular disk excitation ROI for the spherical sample with a = 10 cm. Absolute transmit performance is higher when the array configuration is more consistent with the shape of the ideal current patterns (Figure 6). Array performance increases with the number of elements, but decreases at higher field strength.
Figure 9 compares the spatial distribution of the OPTXE in the heterogeneous head model and the uniform sphere at different field strengths. The uniform sphere had radius 10 cm to match the dimension of the head model along y-axis. At the center of the head, OPTXE decreased from 19.5 (μT)2/W to 2.95 (μT)2/W and 2.69 (μT)2/W when the field strength increased from 1.5T to 7T and 10.5T, respectively, corresponding to an 85% and 86% drop. The corresponding OPTXE values at the center of the sphere at 1.5T, 7T, and 10.5T were 9.12, 2.57, and 2.82(μT)2/W, respectively. The central OPTXE profile for the head-mimicking sphere and the realistic head model almost overlapped along the dimension of the head that matched the diameter of the sphere (i.e., the y-profile).
Figure 9: Comparison of the optimal transmit efficiency in the heterogeneous head model and the head-mimicking uniform sphere, as a function of voxel position and for different magnetic field strengths.
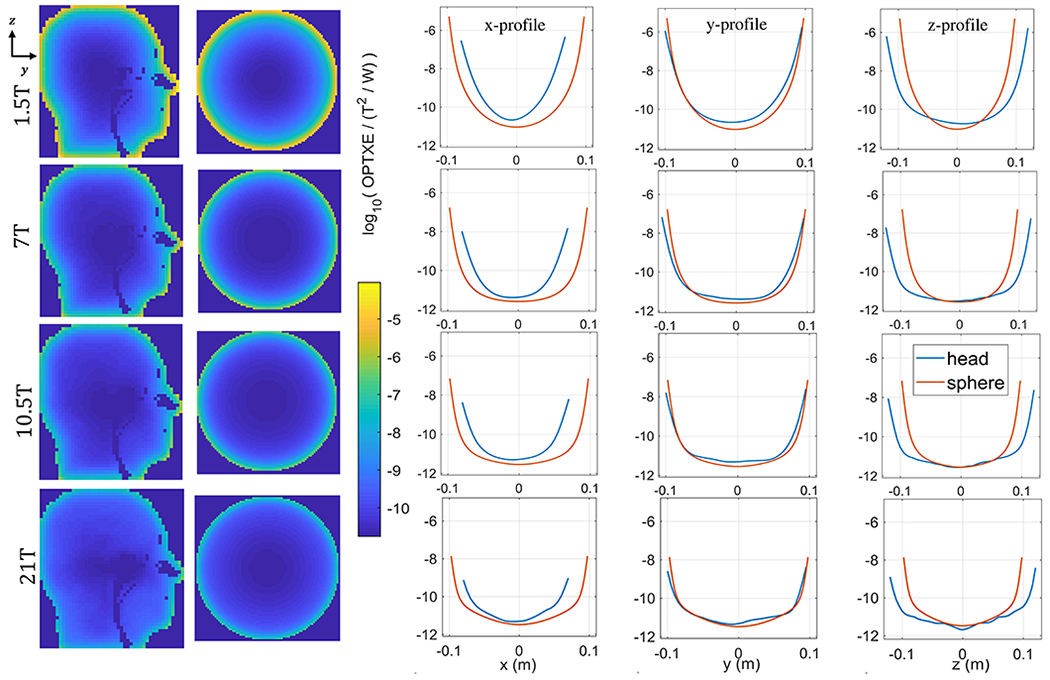
OPTXE is plotted in logarithmic scale for the central sagittal plane of the “Duke” head model and the spherical sample with radius a = 10 cm, for B0 = 1.5T, 7T, 10.5T, 21T. OPTXE profiles along the x, y, and z axes are in agreement between the two objects, especially for the case of the y-profile, for which the dimension of the head matches the radius of the sphere. OPTXE decreased with increasing field strength for both the heterogeneous head model and the uniform sphere.
The performance maps for finite arrays with increasing number of transmit coils were also similar between the uniform sphere (Figure 7) and the heterogeneous head model (Figure 10). Specifically, 8 loops could reach a performance of only 45% for a voxel at the center of the brain at 7T, while 32 loops achieved approximately 70% of the OPTXE. Compared to the case of the homogeneous sphere, performance maps were less uniform in the realistic head, especially at higher field strengths, reflecting the non-uniform geometry and tissue distribution, which affects the propagation of the EM field.
Figure 10: Absolute transmit performance of finite arrays with an increasing number of elements encircling the “Duke” realistic head model, at different main magnetic field strengths.
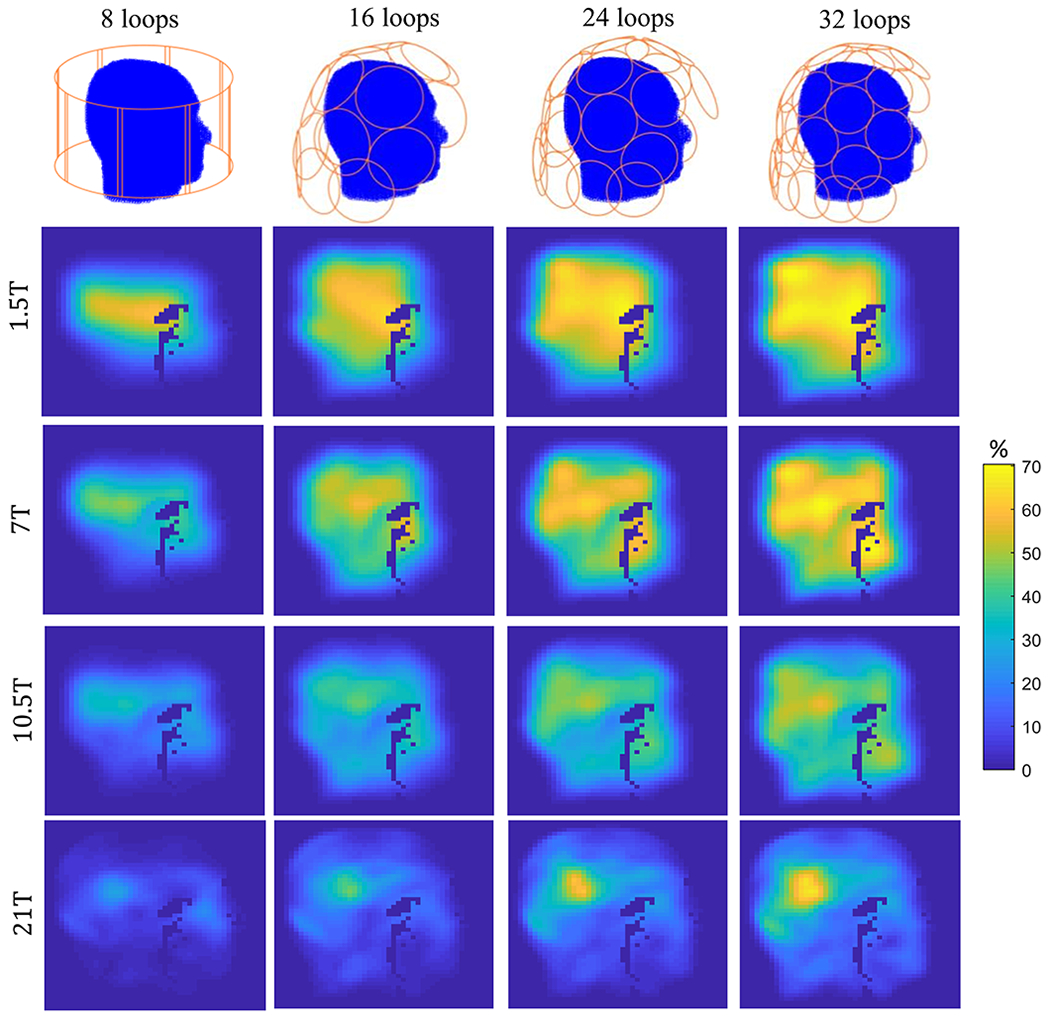
Performance maps displaying maximum TXE as a percentage of the OPTXE at each voxel of the central sagittal plane of “Duke” are shown for various finite arrays and for increasing B0. As for the case of the uniform sphere, absolute transmit performance becomes higher over a broader central region when the number of transmit loops increases.
DISCUSSION
We introduced the OPTXE, a novel theoretical upper bound for the performance of transmit coils, and investigated its behavior using head-mimicking uniform spherical samples and a heterogeneous head model, for different magnetic field strengths and target excitations. The distribution of the OPTXE for single voxels across the diameter of the spherical sample resembled that reported for the UISNR.20,21 The resulting OPTXE presented rotational symmetry, had its minimum at the center and grew exponentially as the target voxel position approached the surface of the sphere. However, note that OPTXE cannot be equal to the UISNR, which by definition is scaled by the square of B0. Furthermore, the UISNR optimization constrains the receive sensitivity to be equal to one at the voxel of interest while minimizing noise everywhere in the sample, whereas the OPTXE optimization we proposed maximizes directly the ratio of transmit sensitivity and RF power deposition. As a result, the optimal RF shimming weights are not equal in the two cases, yielding different distributions of the net magnetic and electric field. The shape and amplitude of the ICP associated with OPTXE and UISNR for the same voxel are also different, except at the center of the object, where they are dominated by one mode24.
OPTXE decreased as B0 increased, for almost all cases considered in this work. Only for the smallest spherical sample size, the OPTXE slightly increased near the center when going from ultra-high to extreme fields (>10.5T). This could be due to the RF wavelength becoming small enough compared to the object to cause field focusing effects near the center of the sphere.44 Another difference with respect to previous work on UISNR is that here we calculated OPTXE not only for single voxels, but also for larger target excitation regions, which provides a more compact (single number vs. map) coil assessment and more widely applicable benchmarks for optimal transmit coil design. We found the behavior of OPTXE to be similar for 2D and 3D excitation ROI’s. In particular, OPTXE remained approximately constant for increasing size of the excitation region, until the radius of the ROI approached the radius of the spherical sample, at which point the high values observed for superficial voxels began to dominate the OPTXE within ROI. However, while maximizing TXE, this scenario would result in a highly inhomogeneous distribution, with nearly zero field in the central region. Using the same theoretical formalism, we showed that it could be possible to tradeoff a percentage of TXE and search for the eigenvector that minimizes inhomogeneity (Figure 5). We also observed that at UHF, especially for large objects, the OPTXE slightly decreased from its central value when the ROI’s were large enough to include intermediate voxels (Figure 4). This behavior suggests that it could be more challenging to optimize TXE over certain ROI’s when their size is comparable to the wavelength, leading to field focusing effects, or when both wavelength and field penetration are small compared to the size of the spherical sample.
The ICP yielding OPTXE at single voxels resembled the ICP associated with UISNR at the same locations.31 In particular, their shape was identical for the central voxel, consisting of distributed current loops precessing at the Larmor frequency around the direction of the main magnetic field (Supporting Information Video S1). This was expected, since only one mode survives at the center of the sphere24 and in both cases its role is to closely track spins precessing at the voxel of interest. The only difference is the opposite direction of the precession of the current loops, which accounts for the fact that for OPTXE is the transmit sensitivity that is maximized, whereas for UISNR is the receive sensitivity. These patterns could, for example, be achieved by quadrature birdcage coils.45 At low fields, for voxels closer to the surface of the object, the ICP took the form of single loops alternating with figure-eight shapes, suggesting that surface quadrature coils46 could be a better fit. At higher field strengths, the ICP for voxels away from the center became increasingly complex, suggesting that asymmetric quadrature coils might perform better than traditional closed loops. In fact, previous work showed that transmit/receive performance could be improved by considering the asymmetry of the EM field at high frequencies in the coil design process.47–49 Asymmetries and other effects due to wave propagation phenomena for increasing B0 were even more evident in the ICP for the case of 2D and 3D excitation ROI’s (Supporting Information Videos S2 and S3). We also observed that the ICP became more localized and had considerably higher density around the excitation plane as the radius of the 2D ROI was increased. Interestingly, at 21T, for the case of 3D ROI’s, the ICP seemed concentrated around the two poles of the sphere. This behavior reflects our optimization approach, which normalizes with respect to total input power, regardless of how the power is distributed over the individual channels. As a result, while maximizing TXE, the highly localized ICP associated with large excitation ROI’s do not represent realistic performance benchmarks for coil design. In fact, the power limits of individual channels in current MR transmit technology make it impractical to have large RF shims amplitudes concentrated on a small number of channels. Furthermore, despite optimal overall TXE, the distribution within the ROI would be highly inhomogeneous, with poor excitation in the central region that would compromise image quality. This issue could be avoided by trading off TXE for reduced inhomogeneity, as suggested above, and by excluding high order modes from the optimization. Supporting Information Figure S6 shows that by using such approach it could be possible also to obtain more uniformly distributed current patterns, while still achieving a large percentage of the OPTXE. However, while the more distributed current patterns result in lower peak current density, the corresponding SAR overall increases (Supporting Information Figure S6). This is expected,1 because in this case the optimization was forced to prioritize homogeneity over TXE. This effect can be seen also in Figure 5, where SAR is clearly higher for the eigenvalues that reduce the CV of compared to the ones that maximize TXE.
Nevertheless, having realistic, distributed current patterns as a benchmark is useful, since we showed that it is possible to approach the optimal performance with finite arrays, especially when the coil configuration resembles the shape of the ICP. Array performance near the center (Figure 7) increased with the number of transmit coils surrounding the spherical sample at all field strengths. In fact, with more and smaller loops the overall array current patterns can better mimic the corresponding ICP, which form large distributed loops (Figure 3). Array performance was lower for voxels near the surface, where ICP consist of small localized loops that cannot be approximated using encircling arrays with a limited number of large loops. At low field, 16 transmit loops or more could achieve a large performance over an extended excitation region, whereas such region shrank for higher B0. This suggests that to approach OPTXE at UHF, either more coils or different type of coils, e.g., electric dipoles,26 may be needed. While our results show general trends that provide physical insight into coil design, note that other factors, for example losses associated with lumped elements, or imperfect matching and decoupling, could affect TXE of actual transmit arrays.
Figure 8 also shows that the performance of an array depends strongly on how closely its elements can reproduce the corresponding ICP yielding OPTXE. More specifically, the belt-like arrays achieved considerably higher performance in those cases for which the ICP were localized around the excitation central plane and resembled a belt of loops (Figure 6). At 7T, for example, the belt-like array with 32 loops could reach only 34% of the OPTXE for ROI’s radii smaller than 0.4a, corresponding to distributed ICP, whereas for ROI’s radii between 0.6a and 0.9a, with ICP focused along the central plane, the performance was as high as 93%. The radius of the 2D ROI associated with the largest performance increased with field strength. This can also be explained from the ICP in Figure 6, which show that the focusing of the ICP around the excitation plane happens for larger ROI’s as the field strength increases.
The uniform dielectric sphere has been extensively used as a model of the human head to enable rapid analytic simulations to investigate ultimate performance limits and explore dependencies on multiple design parameters. However, while useful for deriving general trends and guidelines for coil design, the spherical model is intrinsically limited when investigating the performance of specific head coil designs. In this work, we proposed a novel numerical framework to calculate the EM generated by basis functions defined on a shell enclosing the object, and employed it to calculate the OPTXE inside a realistic heterogeneous head model. Previous work had used random electric and magnetic dipoles distributed inside a thick voxelized layer surrounding the object as basis functions to calculate UISNR21 and ultimate SAR amplification factor22 in realistic head models. Another work used the same numerical approach to investigate ultimate transmit performance in a realistic model of the human pelvis for a specific RF shimming excitation that imposes constructive interference at the central voxel.50 Our implementation is intrinsically more accurate because it relies on SVD rather than randomized SVD to compress the numerical basis and it usually requires less degrees of freedom for discretizing the current sources. We validated our numerical approach against the analytical DGF computations for the case of a uniform sphere (Supporting Information Figure S7). We found that the relative error remained low (around 2.5%) for an extended central region, but increased rapidly for voxels close to the surface, due to the staircase approximation of the curvature of the sphere. Such error at the surface is expected when using voxelized geometries, but we showed that it could be considerably reduced by refining the resolution of the computational domain. While our numerical calculations for the realistic head were limited to 5 mm resolution, due to computational time and memory capacity of the graphics processing unit, we expect higher accuracy than in Supporting Information Figure S7, because the surface curvature of the head model is overall smaller than for the sphere. Note also that obtaining accurate OPTXE values near the surface is not critical for assessing finite arrays, since their absolute performance is anyway nearly 0% at these locations, where the OPTXE grows exponentially.
Previous work on UISNR using realistic head models21 demonstrated that the sphere with average brain electrical properties is a good approximation for the head and this work confirms such observation for the case of the OPTXE (Figure 9). In particular, we showed that when the diameter of the sphere is equal to the dimension of the head, the sphere is expected to be a remarkably accurate approximation, even at the surface voxels (see y-profile in Figure 9). This could be explained by the analytical and numerical (via SVD) eigenfunction expansions being similar for volumes with coinciding boundaries. In fact, as more modes are added while calculating the OPTXE, the resulting maximum eigenvalue distributions would become smoother and more similar for the two models, despite the higher inhomogeneity of the realistic head model. As a result, the calculation of the OPTXE in the realistic head model requires more modes for convergence, since EM fields with higher degrees of freedom, or higher spatial frequency, are required for generating the same smooth OPTXE distribution. The validity of the uniform sphere head approximation is also supported by the general trends of array performance with respect to field strength and number of coil elements, remaining valid in the case of a realistic head model.
An advantage of the analytical framework is that the ICP for a spherical sample can be calculated in a straightforward manner as a weighted sum of the surface current basis modes, using the optimal RF shimming coefficients associated with OPTXE. Instead, in the case of a realistic head model, linear combinations of the discretized RWG basis functions do not necessarily result in continuous current patterns on the shell surrounding the object. Two promising approaches to calculate ICP for arbitrary dielectric objects and current-bearing surfaces have been recently proposed43,51 and will be further explored in future work. Future work will also include exploring OPTXE and the associated ICP for body imaging at ultra-high field MRI, where optimizing transmit efficiency is critical.
In this work, we have introduced a formalism to calculate the OPTXE for RF shimming, but our approach could be generalized to parallel transmission. This would require adding the time dependence to Equation 2, in order for the phase and amplitude of the different transmit channels to be updated at each time point. Note, however, that one advantage of using RF shimming is that, since the weights are fixed, there is a single optimal value and a single set of ICP associated with each excitation task, which facilitates the interpretation of the results. Furthermore, while the case of parallel transmission could be explored in simulation, it is not yet clear how a local power calibration could be noninvasively and robustly conducted in practice in order to evaluate the TXE of actual arrays with respect to the OPTXE. On the other hand, the global RF power covariance matrix for RF shimming can be measured experimentally.5–7 This could enable to use absolute transmit performance – TXE/OPTXE – as a metric to evaluate actual RF coils in phantom experiments, similar to what was proposed for the receive case.28 Furthermore, since the TXE (Equation 1) does not depend on acquisition parameters as the SNR, no scaling factors would be needed for the comparison with the OPTXE. However, the proper hardware to measure the RF power correlation matrix and accurate B1+ calculation would still be required.5–7,16
CONCLUSION
In this work, we introduced a formalism to calculate the OPTXE, which is an upper bound on transmit performance consistent with electrodynamic principles that is achievable for a given imaging sample and target excitation region. The OPTXE is independent of the particular array and coil combination, thus can be used as an absolute reference to evaluate both coil designs and RF shimming algorithms. We calculated OPTXE analytically for a uniform sphere with average brain electrical properties and proposed a novel numerical approach to calculate OPTXE for a realistic heterogeneous head model. We showed that the overall behavior of the OPTXE is similar for the two models. At UHF, finite arrays with as many as 32 transmit loops could approach OPTXE only in the central region of the object, suggesting that more transmit channels or different type of coils may be needed to optimize performance. We showed that ICP associated with OPTXE could provide useful insight into optimal coil design.
Supplementary Material
Supporting Information Figure S1: Optimal transmit efficiency as a function of the size of the three-dimensional excitation region of interest, for different spherical sample size and magnetic field strength. OPTXE is plotted in logarithmic scale for spherical samples with radii a = 7.5, 10, 15 cm and brain-mimicking electrical properties, adjusted for each magnetic field strength. Similarly to the case of 2D ROI’s (Figure 4), the OPTXE in 3D spherical ROI’s remains approximately constant until the ROI approaches the size of the sphere, at which point it rapidly grows to its highest value.
Supporting Information Figure S2: Snapshots of ideal current patterns yielding the optimal transmit efficiency, for two sizes of the three-dimensional excitation ROI and different main magnetic field strengths. The density of ideal current patterns at ωt = 0 is shown for the spherical sample with radius a = 10 cm, for the spherical 3D excitation ROI’s of size r3D = 0.3a and r3D = 0.6a, shown in the first column. Ideal current patterns are largely distributed around the sphere for B0 ≤ 7T, but they become more concentrated near the poles of the sphere at higher magnetic field strengths.
Supporting Information Figure S3: Convergence of the optimal transmit efficiency calculations as a function of voxel location, for different main magnetic field strengths and object sizes. OPTXE convergence is plotted in logarithmic scale for expansion order lmax ranging from 0 to 45, yielding a maximum of N = (lmax + 1)2 = 2116 modes. Note that each mode includes both the curl-free and divergence-free components in Equation 8. Results are shown for sphere radii a = 7.5, 10, 15 cm and uniform brain-mimicking electrical properties adjusted for the corresponding frequency at B0 = 0.5, 1.5, 3,7, 10.5, 14,21 T. The convergence was assessed for three voxel locations at rvox = 0, 0.5a, 0.95a. The closer a voxel is to the surface of the sphere the larger the number of modes required for convergence. The convergence is also slower at higher field strengths, which is more evident for larger object sizes and the intermediate voxel location.
Supporting Information Figure S4: Convergence of the optimal transmit efficiency calculations as a function of the size of the two-dimensional region of interest, for different main magnetic field strengths and object sizes. OPTXE convergence is plotted for the same number of modes, sphere radii and B0 shown in Supporting Information Figure S3, for different sizes (r2D = 0.3a, 0.6a, 0.9a) of a 2D circular disk ROI. More modes are required for convergence with larger excitation regions and at higher field strengths. This can be seen more clearly for larger object sizes and especially for the 2D ROI with r2D = 0.6a.
Supporting Information Figure S5: Convergence of the optimal transmit efficiency calculations as a function of the size of the three-dimensional region of interest, for different main magnetic field strengths and object sizes. OPTXE convergence is plotted for different sizes (r3D = 0.3a, 0.6a, 0.9a) of a spherical 3D ROI concentric with the sample. Results are shown for the same range of expansion order, magnetic field strength and object size used in Supporting Information Figure S3. OPTXE for 3D ROI’s converged faster than for the corresponding 2D ROI’s. For example, for the large sphere (a = 15cm) and intermediate ROI size (r3D = 0.6a), the number of modes needed for convergence was 1, 5, 30 for 0.5T, 7T and 21T, respectively, which corresponds to 3%,11%,18% of the modes required for OPTXE convergence in 2D ROI’s with the same radius (Supporting Information Figure S4).
Supporting Information Figure S6: Comparison between ideal current patterns yielding the optimal transmit efficiency and those more homogeneously distributed over the current-bearing surface to minimize inhomogeneity. While providing a theoretical optimum, ICP for large excitation ROI’s could be difficult to realize in practice with existing multiple channel transmit technology. By limiting the expansion order of the electromagnetic basis used for the optimization (lmax = 15 vs. 45) and selecting the eigenvalue that maximize homogeneity within the particular ROI, it is possible to obtain more realistic current patterns, while trading off only a small percentage of TXE. However, the resulting SAR could increase considerably.
Supporting Information Figure S7: Comparison between the proposed numerical framework and the analytic DGF framework for the calculation of OPTXE in a uniform sphere. OPTXE was calculated inside a 7.5 and a 10 cm radius uniform sphere (ϵr = 49.1 and σ = 0.61 S/m) at 7T. The current-bearing spherical shell was placed at 3 cm distance from the sphere. For the numerical case, the sphere was discretized with 5 mm resolution and the numerical basis was truncated with 10−5 approximation error. The relative error in the OPTXE with respect to the analytic solution remained small (around 2.5%) for voxels in the central region of the sphere, but increased for voxels closer to the edge, due to the staircase approximation of the curved surface of the sphere (a). The overall error was smaller for the case of OPTXE in 2D (b) and 3D (c) excitation ROI’s. The error of the numerical calculation near the surface could drop significantly by refinement of the computational grid, as shown in (d). The resolution of the computational grid in the case of the head model was constrained to 5 mm by the memory size of the graphics processing unit.
Supporting Information Video S1: Animated version of Figure 3, showing ideal current patterns for single voxel excitations, precessing at the Larmor frequency for different values of the main magnetic field strength. Note that a PDF-viewer capable of Java-Script, such as the Adobe Acrobat Reader, is required in order to run the animation.
Supporting Information Video S2: Animated version of Figure 6, showing ideal current patterns for different sizes of the two-dimensional excitation region, precessing at the Larmor frequency for various magnetic field strengths. Note that a PDF-viewer capable of Java-Script, such as the Adobe Acrobat Reader, is required in order to run the animation.
Supporting Information Video S3: Animated version of Supporting Information Figure S2, showing ideal current patterns for different three-dimensional excitation regions, precessing at the Larmor frequency for various magnetic field strengths. Note that a PDF-viewer capable of Java-Script, such as the Adobe Acrobat Reader, is required in order to run the animation.
ACKNOWLEDGMENTS
This work was supported in part by NIH R01 EB024536, NSF 1453675, Skoltech-MIT Next Generation Program and it was performed under the rubric of the Center for Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), a NIBIB Biomedical Technology Resource Center (NIH P41 EB017183).
FUNDING INFORMATION: National Institutes of Health, Grant/Award Numbers: R01EB024536 and P41 EB017183; National Science Foundation, Grant/Award Number: CAREER 1453675. Skoltech-MIT Next Generation Program.
ABBREVIATIONS USED:
- CV
coefficient of variation
- DGF
dyadic Green’s function
- EM
electromagnetic
- ICP
ideal current patterns
- MRI
magnetic resonance imaging
- OPTXE
optimal transmit efficiency
- RF
radiofrequency
- ROI
region of interest
- RWG
Rao-Wilton-Glisson
- SAR
specific absorption rate
- SVD
singular value decomposition
- TXE
transmit efficiency
- UHF
ultra-high field
- UISNR
ultimate intrinsic signal-to-noise ratio
APPENDIX
Mode expansion of the EM field inside a dielectric sphere
We constructed the DGF for a dielectric sphere using the method of superposition:39
| (A.1) |
where r′ is the position of the current sources, r is the position at which the EM field is observed and a is the radius of the sphere. Since we are interested in calculating the EM field inside the sphere, we select the second branch:
| (A.2) |
k0 and kin are the wavenumbers in free-space and inside the sphere, respectively, Cl and Dl are calculated by applying the Dirichlet boundary conditions,31 and the spherical vector wave functions are defined as:
| (A.3) |
With k being the appropriate wave number at the position of interest. ψl,m = jl(kr)Yl,m(θ, φ) are the eigenfunctions that are solutions to the scalar wave equation with
| (A.4) |
where is the associated Legendre function of order (l, m) and jl is the spherical Bessel function of order l. The superscript + in Equation A.2 indicates that the spherical Hankel function of the first kind and order l is used in place of the spherical Bessel function of the same order.
The electric field inside the sphere can be calculated using Equations 7, 8, A.1, and A.2 as:
| (A.5) |
from which we can define the coefficients in Equation 9:
| (A.6) |
| (A.7) |
where the vector spherical harmonics are defined as39
| (A.8) |
in which, is the unit vector in the radial direction. The integrals in Equations A.6 and A.7 can be solved by applying the orthogonality relations of the vector spherical harmonics,40 yielding v = Tw with , and:31
| (A.9) |
We can then calculate the magnetic field in Equation 9 using Maxwell’s equation B(r) = i/ω∇ × E(r) and the symmetrical relations of the vector wave functions.39 Note that, although we consider only electric current sources, the basis in Equation 8 can represent all possible EM field distributions within the sample because the currents equivalence principle can be formulated with either only electric or only magnetic currents.52 It should be noted that we used the eiωt harmonic time variation for all fields and currents, which is omitted for brevity.
Calculation of the transmit sensitivities and electric fields covariance matrices
For each mode, we can construct the transmit sensitivity matrix as:
| (A.10) |
Cl,m(rq) is a Q × 2 matrix that includes both the divergence-free and curl-free contributions and accounts for the boundary conditions:
| (A.11) |
The RF power covariance matrix for the modes can be calculated as:
| (A.12) |
where Φl,m = THRLT is a 2 × 2 diagonal matrix and RL is given by:31
| (A.13) |
and the global covariance matrix with dimensions 2N × 2N for all the modes is:
| (A.14) |
REFERENCES
- 1.Lattanzi R, Sodickson DK, Grant AK, Zhu Y. Electrodynamic constraints on homogeneity and radiofrequency power deposition in multiple coil excitations. Magn Reson Med 2009;61:315–334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Deniz CM, Alon L, Brown R, Sodickson DK, Zhu Y. Specific absorption rate benefits of including measured electric field interactions in parallel excitation pulse design. Magn Reson Med 2012;67:164–174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.van den Bergen B, van den Berg CAT, Bartels LW, Lagendijk JJW. 7T body MRI: B1 shimming with simultaneous SAR reduction. Phys Med Biol 2007;52:5429–5451. [DOI] [PubMed] [Google Scholar]
- 4.Eryaman et al. , Minimum SAR for RF Shimming by Allowing Spa&al Phase Varia&on, Proc. Intl. Soc. Mag. Reson. Med 17 (2009): 4777. [Google Scholar]
- 5.Zhu Y In vivo RF power and SAR calibration for multi-port RF transmission. In Proceedings of the 17th Annual Meeting of ISMRM, Honolulu, Hawaii, USA, 2009. p. 2585. [Google Scholar]
- 6.Alon L, Deniz CM, Lattanzi R, Wiggins G, Brown R, Sodickson DK, Zhu Y. An automated method for subject specific global SAR prediction in parallel transmission. In Proceedings of the 18th Annual Meeting of ISMRM, Stockholm, Sweden, 2010. p. 780. [Google Scholar]
- 7.Zhu Y, Alon L, Deniz CM, Brown R, Sodickson DK. System and SAR characterization in parallel RF transmission. Magn Reson Med 2012;67:1367–1378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Vaughan JT, Adriany G, Snyder CJ, Tian J, Thiel T, Bolinger L, Liu H, DelaBarre L, Ugurbil K. Efficient high-frequency body coil for high-field MRI. Magn Reson Med 2004;52:851–859. [DOI] [PubMed] [Google Scholar]
- 9.Vaughan JT, Hetherington HP, Otu JO, Pan JW, Pohost GM. High frequency volume coils for clinical NMR imaging and spectroscopy. Magn Reson Med 1994;32:206–218. [DOI] [PubMed] [Google Scholar]
- 10.Hoult DI, Phil D. Sensitivity and power deposition in a high-field imaging experiment. J Magn Reson Imaging 2000;12:46–67. [DOI] [PubMed] [Google Scholar]
- 11.Ibrahim TS, Lee R, Baertlein BA, Abduljalil AM, Zhu H, Robitaille PM. Effect of RF coil excitation on field inhomogeneity at ultra high fields: a field optimized TEM resonator. Magn Reson Imaging 2001;19:1339–1347. [DOI] [PubMed] [Google Scholar]
- 12.Katscher U, Bornert P, Leussler C, van den Brink JS. Transmit SENSE. Magn Reson Med 2003;49:144–150. [DOI] [PubMed] [Google Scholar]
- 13.Zhu Y Parallel excitation with an array of transmit coils. Magn Reson Med 2004;51:775–784. [DOI] [PubMed] [Google Scholar]
- 14.Padormo F, Beqiri A, Hajnal JV, Malik SJ. Parallel transmission for ultrahigh-field imaging. NMR in Biomedicine. 2016. September;29(9):1145–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhu Y, Deniz CM, Alon L, Fautz HP, Sodickson DK. Understanding parallel transmit array efficiency. In Proceedings of the 18th Annual Meeting of ISMRM, Stockholm, Sweden, 2010. p. 1518. [Google Scholar]
- 16.Deniz CM, Brown R, Lattanzi R, Alon L, Sodickson DK, Zhu Y. Maximum efficiency radiofrequency shimming: Theory and initial application for hip imaging at 7 tesla. Magn Reson Med 2013. May;69(5):1379–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ocali O, Atalar E. Ultimate intrinsic signal-to-noise ratio in MRI. Magn Reson Med 1998;39:462–473. [DOI] [PubMed] [Google Scholar]
- 18.Schnell W, Renz W, Vester M, Ermert H. Ultimate signal-to-noise ratio of surface and body antennas for magnetic resonance imaging. IEEE Trans Antennas Propag 2000;48:418–428. [Google Scholar]
- 19.Ohliger MA, Grant AK, Sodickson DK. Ultimate intrinsic signal-to-noise ratio for parallel MRI: electromagnetic field considerations. Magn Reson Med 2003;50:1018–1030. [DOI] [PubMed] [Google Scholar]
- 20.Wiesinger F, Boesiger P, Pruessmann KP. Electrodynamics and ultimate SNR in parallel MR imaging. Magn Reson Med 2004;52:376–390. [DOI] [PubMed] [Google Scholar]
- 21.Guérin B, Villena JF, Polimeridis AG, Adalsteinsson E, Daniel L, White JK, Wald LL. The Ultimate Signal-to-Noise Ratio in Realistic Body Models. Magn Reson Med 2017, 78: 1969–1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Guérin B, Villena JF, Polimeridis AG, Adalsteinsson E, Daniel L, White JK, Rosen BR, Wald LL. Computation of ultimate SAR amplification factors for radiofrequency hyperthermia in non-uniform body models: impact of frequency and tumour location. International Journal of Hyperthermia. 2018. January 2;34(1):87–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Pfrommer A, Henning A. The ultimate intrinsic signal-to-noise ratio of loop-and dipole-like current patterns in a realistic human head model. Magn Reson Med. 2018. November;80(5):2122–2138. [DOI] [PubMed] [Google Scholar]
- 24.Lee HH, Sodickson DK, Lattanzi R. An analytic expression for the ultimate intrinsic SNR in a uniform sphere. Magn Reson Med. 2018. November;80(5):2256–2266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Georgakis IP, Polimeridis AG, Lattanzi R. Ultimate intrinsic transmit efficiency for RF shimming. ISMRM; Paris: 2018:0139. [Google Scholar]
- 26.Lattanzi R, Wiggins GC, Zhang B, Duan Q, Brown R, Sodickson DK. Approaching ultimate intrinsic signal-to-noise ratio with loop and dipole antennas. Magn Reson Med. 2018. March;79(3):1789–1803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Vaidya MV, Sodickson DK, Lattanzi R. Approaching ultimate intrinsic SNR in a uniform spherical sample with finite arrays of loop coils. Concepts Magn Reson 2014;44:53–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lattanzi R, Grant AK, Polimeni JR, Ohliger MA, Wiggins GC, Wald LL, Sodickson DK. Performance evaluation of a 32-element head array with respect to the ultimate intrinsic SNR. NMR Biomed 2009;23:142–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Celik H, Eryaman Y, Altintaş A, Abdel-Hafez IA, Atalar E. Evaluation of internal MRI coils using ultimate intrinsic SNR. Magn Reson Med. 2004. September;52(3):640–9. [DOI] [PubMed] [Google Scholar]
- 30.Gao Y, Chen W, Zhang X. Investigating the Influence of Spatial Constraints on Ultimate Receive Coil Performance for Monkey Brain MRI at 7 T. IEEE Trans Med Imaging. 2018. July;37(7):1723–1732. [DOI] [PubMed] [Google Scholar]
- 31.Lattanzi R, Sodickson DK. Ideal current patterns yielding optimal signal-to-noise ratio and specific absorption rate in magnetic resonance imaging: computational methods and physical insights. Magn Reson Med 2012;68:286–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chen G, Cloos M, Lattanzi R, Sodickson DK and Wiggins G, Bent Electric Dipoles: A Novel Coil Design Inspired by the Ideal Current Pattern for Central SNR at 7 Tesla; 22nd Scientific Meeting of the International Society for Magnetic Resonance in Medicine (ISMRM) Milan (Italy), 11-16 May 2014, p. 402. [Google Scholar]
- 33.Wiggins GC, Zhang B, Lattanzi R, Chen G and Sodickson DK, The electric dipole array: an attempt to match the ideal current pattern for central SNR at 7 Tesla; 20th Scientific Meeting of the International Society for Magnetic Resonance in Medicine (ISMRM) Melbourne (Australia), 5-11 May 2012, p. 541. [Google Scholar]
- 34.Haemer GG, Vaidya M, Collins CM, Sodickson DK, Wiggins GC, Lattanzi R. Approaching ultimate intrinsic specific absorption rate in radiofrequency shimming using high-permittivity materials at 7 Tesla. Magn Reson Med. 2018. July;80(1):391–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Prieto RE. A general solution to the maximization of the multidimensional generalized Rayleigh quotient used in linear discriminant analysis for signal classification. In Acoustics, Speech, and Signal Processing, 2003. Proceedings. (ICASSP’03). 2003 IEEE International Conference on 2003. April 6 (Vol. 6, pp. VI–157). IEEE. [Google Scholar]
- 36.Ishimaru A Wave Propagation and Scattering in Random Media. New York: Academic; 1978. [Google Scholar]
- 37.Hochman A, Villena JF, Polimeridis AG, Silveira LM, White JK, Daniel L. Reduced-order models for electromagnetic scattering problems. IEEE Transactions on Antennas and Propagation. 2014. June;62(6):3150–62.13. [Google Scholar]
- 38.Christ A, Kainz W, Hahn EG, Honegger K, Zefferer M, Neufeld E, Rascher W, Janka R, Bautz W, Chen J, Kiefer B. The Virtual Family—development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys Med Biol 2009;55:N23–N38. [DOI] [PubMed] [Google Scholar]
- 39.Tai CT. Dyadic Green Functions in Electromagnetic Theory: Institute of Electrical and Electronics Engineers. Piscataway, New Jersey; 1994. [Google Scholar]
- 40.Jackson JD. Classical electrodynamics. New York: John Wiley & Sons; 1999. [Google Scholar]
- 41.Rao S, Wilton D, Glisson A. Electromagnetic scattering by surfaces of arbitrary shape. IEEE Transactions on antennas and propagation. 1982. May;30(3):409–18. [Google Scholar]
- 42.Georgakis IP, Giannakopoulos II, Litsarev MS, Polimeridis AG. A Fast Volume Integral Equation Solver with Linear Basis Functions for the Accurate Computation of Electromagnetic Fields in MRI. arXiv preprint arXiv:1902.02196. 2019. February 6. [Google Scholar]
- 43.Sodickson DK, Lattanzi R, Vaidya M, Chen G, Novikov DS, Collins CM, Wiggins GC. The Optimality Principle for MR signal excitation and reception: New physical insights into ideal radiofrequency coil design. arXiv preprint arXiv:1808.02087. 2018. August. [Google Scholar]
- 44.Vaidya MV, Collins CM, Sodickson DK, Brown R, Wiggins GC, Lattanzi R. Dependence of B1+ and B1− Field Patterns of Surface Coils on the Electrical Properties of the Sample and the MR Operating Frequency. Concepts Magn Reson Part B Magn Reson Eng. 2016. February;46(1):25–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hayes CE, Edelestein WA, Schenck JF, Mueller OM, Eash M. An efficient, highly homogeneous radiofrequency coil for whole-body NMR imaging at 1.5 T. J Magn Reson 1985;63:622–628. [Google Scholar]
- 46.Kumar A, Bottomley PA. Optimized quadrature surface coil designs. Magma 2008;21:41–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Reykowski A, Fischer H. V-cage and V-array: novel coil structures for higher field strengths. In: Proceedings of the 13th Annual Meeting of ISMRM, Miami Beach 2005. p 950. [Google Scholar]
- 48.Duan Q, Sodickson DK, Lattanzi R, Zhang B, Wiggins GC. Optimizing 7T spine array design through offsetting of transmit and receive elements and quadrature excitation. In: Proceedings of the 18th Annual Meeting of ISMRM, Stockholm; 2010. p 51. [Google Scholar]
- 49.Wiggins GC, Zhang B, Lattanzi R, Sodickson DK. B1+ and SNR optimization of high field RF coils through offsetting of transmit and receive elements. In: Proceedings of the 17th Annual Meeting of ISMRM, Honolulu; 2009. p 2951. [Google Scholar]
- 50.Steensma BR, Van den Berg CAT, Klomp DWJ, Luijten PR, Raaijmakers AJE. Comparing realistic coil arrays to the ultimate intrinsic coil performance: a simulation study. ISMRM Workshop on Ultrahigh Field Magnetic Resonance, Dubrovnik (Croatia), 31 March – 3 April 2019. [Google Scholar]
- 51.Georgakis IP, Polimeridis AG, Lattanzi R. Ideal current patterns for optimal SNR in realistic heterogeneous head models. ISMRM. Montreal 2019:1036. [Google Scholar]
- 52.Martini E, Carli G, Maci S. An equivalence theorem based on the use of electric currents radiating in free space. IEEE Antennas and Wireless Propagation Letters. 2008;7:421–4. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information Figure S1: Optimal transmit efficiency as a function of the size of the three-dimensional excitation region of interest, for different spherical sample size and magnetic field strength. OPTXE is plotted in logarithmic scale for spherical samples with radii a = 7.5, 10, 15 cm and brain-mimicking electrical properties, adjusted for each magnetic field strength. Similarly to the case of 2D ROI’s (Figure 4), the OPTXE in 3D spherical ROI’s remains approximately constant until the ROI approaches the size of the sphere, at which point it rapidly grows to its highest value.
Supporting Information Figure S2: Snapshots of ideal current patterns yielding the optimal transmit efficiency, for two sizes of the three-dimensional excitation ROI and different main magnetic field strengths. The density of ideal current patterns at ωt = 0 is shown for the spherical sample with radius a = 10 cm, for the spherical 3D excitation ROI’s of size r3D = 0.3a and r3D = 0.6a, shown in the first column. Ideal current patterns are largely distributed around the sphere for B0 ≤ 7T, but they become more concentrated near the poles of the sphere at higher magnetic field strengths.
Supporting Information Figure S3: Convergence of the optimal transmit efficiency calculations as a function of voxel location, for different main magnetic field strengths and object sizes. OPTXE convergence is plotted in logarithmic scale for expansion order lmax ranging from 0 to 45, yielding a maximum of N = (lmax + 1)2 = 2116 modes. Note that each mode includes both the curl-free and divergence-free components in Equation 8. Results are shown for sphere radii a = 7.5, 10, 15 cm and uniform brain-mimicking electrical properties adjusted for the corresponding frequency at B0 = 0.5, 1.5, 3,7, 10.5, 14,21 T. The convergence was assessed for three voxel locations at rvox = 0, 0.5a, 0.95a. The closer a voxel is to the surface of the sphere the larger the number of modes required for convergence. The convergence is also slower at higher field strengths, which is more evident for larger object sizes and the intermediate voxel location.
Supporting Information Figure S4: Convergence of the optimal transmit efficiency calculations as a function of the size of the two-dimensional region of interest, for different main magnetic field strengths and object sizes. OPTXE convergence is plotted for the same number of modes, sphere radii and B0 shown in Supporting Information Figure S3, for different sizes (r2D = 0.3a, 0.6a, 0.9a) of a 2D circular disk ROI. More modes are required for convergence with larger excitation regions and at higher field strengths. This can be seen more clearly for larger object sizes and especially for the 2D ROI with r2D = 0.6a.
Supporting Information Figure S5: Convergence of the optimal transmit efficiency calculations as a function of the size of the three-dimensional region of interest, for different main magnetic field strengths and object sizes. OPTXE convergence is plotted for different sizes (r3D = 0.3a, 0.6a, 0.9a) of a spherical 3D ROI concentric with the sample. Results are shown for the same range of expansion order, magnetic field strength and object size used in Supporting Information Figure S3. OPTXE for 3D ROI’s converged faster than for the corresponding 2D ROI’s. For example, for the large sphere (a = 15cm) and intermediate ROI size (r3D = 0.6a), the number of modes needed for convergence was 1, 5, 30 for 0.5T, 7T and 21T, respectively, which corresponds to 3%,11%,18% of the modes required for OPTXE convergence in 2D ROI’s with the same radius (Supporting Information Figure S4).
Supporting Information Figure S6: Comparison between ideal current patterns yielding the optimal transmit efficiency and those more homogeneously distributed over the current-bearing surface to minimize inhomogeneity. While providing a theoretical optimum, ICP for large excitation ROI’s could be difficult to realize in practice with existing multiple channel transmit technology. By limiting the expansion order of the electromagnetic basis used for the optimization (lmax = 15 vs. 45) and selecting the eigenvalue that maximize homogeneity within the particular ROI, it is possible to obtain more realistic current patterns, while trading off only a small percentage of TXE. However, the resulting SAR could increase considerably.
Supporting Information Figure S7: Comparison between the proposed numerical framework and the analytic DGF framework for the calculation of OPTXE in a uniform sphere. OPTXE was calculated inside a 7.5 and a 10 cm radius uniform sphere (ϵr = 49.1 and σ = 0.61 S/m) at 7T. The current-bearing spherical shell was placed at 3 cm distance from the sphere. For the numerical case, the sphere was discretized with 5 mm resolution and the numerical basis was truncated with 10−5 approximation error. The relative error in the OPTXE with respect to the analytic solution remained small (around 2.5%) for voxels in the central region of the sphere, but increased for voxels closer to the edge, due to the staircase approximation of the curved surface of the sphere (a). The overall error was smaller for the case of OPTXE in 2D (b) and 3D (c) excitation ROI’s. The error of the numerical calculation near the surface could drop significantly by refinement of the computational grid, as shown in (d). The resolution of the computational grid in the case of the head model was constrained to 5 mm by the memory size of the graphics processing unit.
Supporting Information Video S1: Animated version of Figure 3, showing ideal current patterns for single voxel excitations, precessing at the Larmor frequency for different values of the main magnetic field strength. Note that a PDF-viewer capable of Java-Script, such as the Adobe Acrobat Reader, is required in order to run the animation.
Supporting Information Video S2: Animated version of Figure 6, showing ideal current patterns for different sizes of the two-dimensional excitation region, precessing at the Larmor frequency for various magnetic field strengths. Note that a PDF-viewer capable of Java-Script, such as the Adobe Acrobat Reader, is required in order to run the animation.
Supporting Information Video S3: Animated version of Supporting Information Figure S2, showing ideal current patterns for different three-dimensional excitation regions, precessing at the Larmor frequency for various magnetic field strengths. Note that a PDF-viewer capable of Java-Script, such as the Adobe Acrobat Reader, is required in order to run the animation.


