Exploring the neighbourhood-level correlates of Covid-19 deaths in London using a difference across spatial boundaries method

Abstract

This paper explores neighbourhood-level correlates of the Covid-19 deaths in London during the initial rise and peak of the pandemic within the UK – the period March 1 to April 17, 2020. It asks whether the person-level predictors of Covid-19 that are identified in reports by Public Health England and by the Office of National Statistics also hold at a neighbourhood scale, remaining evident in the differences between neighbours. In examining this, the paper focuses on localised differences in the number of deaths, putting forward an innovative method of analysis that looks at the differences between places that share a border. Specifically, a difference across spatial boundaries method is employed to consider whether a higher number of deaths in one neighbourhood, when compared to its neighbours, is related to other differences between those contiguous locations. It is also used to map localised ‘hot spots’ and to look for spatial variation in the regression coefficients. The results are compared to those for a later period, April 18 – May 31. The findings show that despite some spatial diffusion of the disease, a greater number of deaths continues to be associated with Asian and Black ethnic groups, socio-economic disadvantage, very large households (likely indicative of residential overcrowding), and fewer from younger age groups. The analysis adds to the evidence showing that age, wealth/deprivation, and ethnicity are key risk factors associated with higher mortality rates from Covid-19.

Highlights

• •Develops a new method of spatial analysis to look at differences between neighbourhoods in their number of Covid-19 deaths in London during spring 2020.
• •Presents a detailed analysis of the neighbourhood-level correlates of Covid-19 mortality grounded in public health analysis of the individual-level predictors of increased risk.
• •Maps localised ‘hot’ spots of the disease in London and how these shifted in the period before and after its peak.
• •Adds to the evidence base that age, wealth/deprivation and ethnicity are key risk factors associated with higher mortality rates from Covid-19.

1. Introduction

This purpose of this paper is to combine methodological innovation with an exploration of the neighbourhood-level correlates of the Covid-19 deaths that occurred, in London, during the initial rise and peak of the pandemic, within the UK, during the spring of 2020. It does so by introducing and applying a difference across spatial boundaries method to data published by the Office of National Statistics (ONS) on May 1, 2020 (ONS, 2020). These data give the number of deaths involving Covid-19 in England and Wales by the residential neighbourhood of the deceased, for deaths that occurred within the period from March 1 to April 17 (and registered by April 18). The focus of the study is on explaining why neighbourhoods that are located next to each other have different numbers of Covid-19 deaths.

The data are of interest because they cover the period when this (first) wave of Covid-19 was spreading, infecting, and killing fastest within the UK. Separate government statistics, published online at https://coronavirus.data.gov.uk (and revised after their initial publication), record 47 lab-confirmed cases in the UK prior to March 1, with a sharp rise in the number of daily new confirmations from the first week of March to a peak on April 22, 2020 (5487 new cases). The first Covid-19 attributed deaths in the UK were between late February and early March: the first to be announced was on March 5 but is now known to have been preceded by a small number of other fatalities from a few days to a week earlier. At the time of writing (autumn 2020, when the infection rate is again rising), the daily number of deaths peaked on April 8 at 1073 deaths. Presently, there are 20 to 30 deaths per day but the number of infections now exceeds the initial, April peak.

By the beginning of June 2020, the number of deaths had reached 38,423, with the UK having one of the highest per capita Covid-19 death rates in Europe and the world (Burn-Murdoch and Giles, 2020). By then, geographical variation at the regional and sub-regional scales was evident. Early analysis by the ONS reported that “London had the highest age-standardised mortality rate […] statistically significantly higher than any other region and almost double the next highest rate” (ONS, op. cit.). Between March 1 to April 17, the eleven local authorities with the highest age-standardised mortality rates for Covid-19 related deaths were all London Boroughs. A later report, by Public Health England (2020), confirms that London had the highest age-standardised death rate from Covid-19 of any region as of May 13, as well as the highest number of deaths each week until the week ending April 18 when it was exceeded by the North West region. Following the relaxing of the national ‘lockdown’ in England, in June, regional spikes of Covid-19 infection have tended to be outside the capital, including parts of Leicestershire, Great Manchester, West Yorkshire, and East Lancashire where local lockdowns have been enforced. This paper does not consider those infections but focuses on London in the earlier period. A note on the present situation is left to the conclusion.

That the wave impacted London sooner than other regions reflects the capital’s position as a global city with a total population, population density, and geographical connectivity (both to the UK and to the rest of the world) greater than for other UK settlements. Similar claims could be made of New York and some of the geographical contributors to the Covid-19 outbreak there. Nevertheless, it was, at the time, a reversal of the usual mortality pattern for England because London’s population typically is younger and, in parts, much more affluent than in other regions. Public Health England (op. cit., p.30) noted this, observing that “regional inequalities in Covid-19 mortality rates are greater than those seen previously for all cause mortality and the geographic gradient is different. London had the highest Covid-19 mortality rates, but the lowest baseline all cause mortality rates.” However, London is also an unequal city, a situation reflected in the Covid-19 mortality statistics: whereas the ethnically diverse and more deprived Borough of Newham had the highest age-standardised rate, with 144 deaths per 100,000 population (followed by Brent with 141.5 and Hackney with 127.4), in more affluent Kingston-upon-Thames the rate was 43 deaths per 100,000.

The interest of this paper is in whether the person-level predictors of Covid-19 that are discussed in the report by Public Health England and reviewed below translate to a neighbourhood scale, remaining evident in the differences between closely located neighbourhoods. If so, then it testifies to the demographic, socio-economic and ethno-cultural geographies that shape London, their relationships to Covid-19 as risk factors, and to the geographical patterning of the mortality rates from the virus, in the capital, as well as how spatial inequalities can function at localised scales (in the differences between neighbours).

To explore the neighbourhood-level relationships, a difference across spatial boundaries method is advanced. The idea, which is likened to a spatial difference-in-difference approach, is to look at the difference in the numbers of Covid-19 deaths across the boundaries of neighbouring locations and see if those are related to other differences in the compositions of those contiguous neighbours. The presumption is that, all things being equal, places that are close together ought to exhibit similar levels of mortality because the broader geographical context (their spatial setting) is the same and because the disease is transmitted through close contact with other people. Although the principle is straightforward, it induces a grouping effect in the data that is addressed through a multilevel Poisson model inspired by work addressing similar structures in migration data (Zhang et al., 2020).

The paper proceeds with a review of what is known about the individual correlates of Covid-19 fatalities in England, using this as the basis to select potential predictors at the neighbourhood-level. The difference across spatial boundaries method is outlined together with a modelling strategy for handling the highly co-linear nature of the variables. The results are presented with evidence of the spatially varying nature of some of the correlates and then compared with a subsequent data release by the ONS for a period immediately after the first. Spatial ‘hot spots’ in the disease are mapped; areas with a statistically significant higher number of deaths than their neighbours. Whilst many of those hot spots change over the period March 1 – April 17 to April 18 – May 31, reflecting the spatial diffusion of the disease, the demographic and social composition of neighbourhoods continue to be predictive, with a greater number of deaths associated with fewer from younger populations, more from Black and Asian (but not Chinese) ethnic groups, lower average income, and with other indictors of socio-economic disadvantage, including greater percentages who are unemployed or who have never worked, and households containing large numbers of people. The analysis supports other research showing that age, wealth/deprivation, and ethnicity are key risk factors associated with higher mortality rates from Covid-19. The data used for this analysis and a short tutorial on how to fit the models are available at https://rpubs.com/profrichharris/Health-Place-Covid.

2. Literature review

This paper draws especially on the report published by Public Health England (2020) about disparities in the risk and outcomes of Covid-19 in England. That report looks at the risk factors under eight main headings: age and sex, geography (a regional geography, highlighting the higher infections and deaths in London at that time), deprivation, ethnicity, occupation, inclusion in health groups, deaths in care homes, and comorbidities. Its conclusions extend but are consistent with the earlier analysis by the ONS (2020).

The report finds that over half the deaths in confirmed cases of Covid-19 (as of May 13) were among people aged 80 years or older. The probability of death from the virus is about seventy times greater for those aged eighty or over when compared with people aged under 40 (and about three times higher for those aged 40 to 49, nine times higher for those aged 50 to 59, 27 times greater for those aged 60 to 69, and 50 times greater for those aged 70 to 79). For all age groups, the mortality rate is greater for males than for females: overall, the age-standardised rate for males is twice that for females. As well as increasing with age, the mortality rate increases with the level of neighbourhood deprivation, reaching an age standardised rate that is over twice as great in the most deprived locations (for males and for females) when compared to the least.

The relationship of Covid-19 mortality to deprivation continued to be evident in the confirmed infection cases during June. Although this paper is about London, subsequent to the period of this study, other towns and cities overtook it with higher infection rates. One news outlet used the headline ‘England's North-South Covid-19 divide’ to comment that “only eight of the country's fifty worst-hit authorities are in the south”, drawing on Public Health England data for the week June 15–21 (Chalmers, 2020). Whilst the statistic is true, for that particular week, less so is the interpretation of it because it is not really a north-south divide but an urban deprivation verses rural one. Although many of the “worst-hit” authorities are now in or towards the north of England (often locations where traditional manufacturing industries have declined), they are also in the Midlands and in parts of the South East (and there have been localised outbreaks in other parts of the UK, too, not exclusively England – presently the national infection rate is greater in Wales). The absence from the list, by that time, of London, reveals the disease’s spatial diffusion beyond, as well as the earlier impact of the disease in the capital. However, sub-regional inequalities remain, including within London: as of September 27, 2020 the infection rate in the London Borough of Islington was 362.9 cases per 100,000 of the population, just over half that of the more deprived and ethnically diverse Borough of Brent (with a rate of 689.0; the national rate, for England, was 664.0).

A characteristic of the fifty ‘northern’ local authorities is that they are much more ethnically diverse than is typical for England – places such as Leicester (the first part of England to have an enforced ‘local lockdown’, enacted in the beginning of July, at the same time as rules in the rest of the country were greatly relaxed), Bradford, Barnsley, Rochdale, Bedford, and Oldham, amongst others. Leicester and Bradford, together with Kirklees, Blackburn with Darwen, Oadby and Wigston, and Rochdale top another media list of ‘20 areas of England at most risk of coronavirus resurgence’ as of July 2020 (Garside, 2020). Notably, these are also some of the most ethnically segregated local authorities in the country (Harris and Johnston, 2020; although less so than in the past: Catney, 2015). However, their relationship to Covid-19 is less likely a story of segregation as of the geographical correlates of segregation – deprivation, occupation types, dwellings, and so forth. If so, then we should expect to see a similar story for the earlier period in London.

Ethnic diversity is also characteristic of London Boroughs like Newham, Brent, and Hackney, which the ONS’ analysis identified as having the highest mortality rates in the period March 1 to April 17. These are amongst the boroughs with the highest deprivation rates in London. There is a very wide literature showing how deprivation intersects with ethnicity in the UK (for a recent assessment see Byrne et al., 2020). That intersectionality is present in the Covid-19 statistics: in the period from March 20 to May 7, 2020, the deaths amongst Black males were 3.9 times higher than expected, compared with 2.9 and 1.7 times for Asian and White British males, respectively. The higher mortality for minority groups has been observed in other countries too (Full Fact, 2020). In the United States, for example, non-Hispanic American Indian or Alaska Native persons have had a rate approximately five times greater than that for non-Hispanic white persons, as have non-Hispanic black persons. For Hispanic or Latino persons, the increase is approximately four times (CDC, 2020).

Not all differences between the ethnic groups are explained by socio-economic dis-/advantage: even after accounting for deprivation and for the effects of sex, age, and region, the Public Health England report finds that people of Bangladeshi ethnicity have about twice the risk of a Covid-19 related death when compared to the White British. For other ethnic groups it is between 10 and 50 per cent greater. Whether it is desirable to account for deprivation is a moot point: doing so risks a statistical contrivance that dissociates an ethnic group with the reality of their lived experience (an issue of co-linearity that is returned to later in this paper).

Immigrants also face greater risk. The report observes that the increase in deaths, relative to the average for the same period in earlier years, is greater for migrants than for those born in the UK, especially for those born in Central and Western Africa. Only the death rate for those born in the EU is not statistically significantly higher than for those born in the UK (although it remains higher). Occupation makes a difference, with some jobs bringing people closer into contact with others, thereby increasing the risk of infection. Such occupations include frontline medical staff, the emergency services, bus and taxi drivers, teachers, and those working in the hospitality industry – jobs that (in the National Health Service, for example) are reliant on international migration to the UK.

Those in care homes have been most vulnerable, with the number of deaths widely reported by the UK media as a national scandal because of the lack of protective equipment and inadequate testing for the disease within those care homes (and causing further political consternation when the Prime Minister appeared to deflect the blame for those deaths on to the care homes themselves). In 2020, the care sector in England and Wales had approximately 20,000 more deaths during March and April than is usual for an average year, which equates to 2.3 times more than expected. Care homes accounted for 43 per cent of all deaths from Covid-19 in the week ending May 8. Underlying health conditions, including respiratory infections, are a contributory factor and not limited to the most elderly. The report finds that a higher percentage of Covid-19 related death certificates mention diabetes, hypertension, kidney disease, obstructive pulmonary disease, and dementia than do other (all cause) death certificates (Public Health England, 2020).

3. The geography of Covid-19 fatalities in London during the initial period

Because they give the number of Covid-19 deaths per Middle Level Super Output Area (MSOA), the data published by the ONS allow for geographical modelling at a sub-regional scale, within London Boroughs. These data give only a tally of the deaths and are not age standardised. To protect confidentiality, “a small number of deaths have been reallocated between neighbouring areas” (ONS, 2020).

MSOAs are the third tier of the Census geography for England and Wales (third when aggregating upwards from the smallest, which are Output Areas). Although MSOAs represent a formal specification of neighbourhood designed to prevent personal information disclosure within a consistent geographical framework for the reporting and analysis of socio-economic and other data, their boundaries are not arbitrary. They were designed with the criteria of broadly equal population size, socio-economic homogeneity (based on accommodation type and tenure), and spatial compactness of the zones (Cockings et al., 2011). The mean number of Covid-19 deaths per MSOA was 2.81 nationally but 5.03 in London over the March to April reporting period. The higher average is partly because MSOAs in London contain more people (about 9100 residents, on average, in 2018, compared to an average of 8200 for England and Wales) but not entirely so: the estimated death rate from Covid-19 per thousand of the adult population was 0.44 for England and Wales, 0.73 for London (about 65 per cent greater).

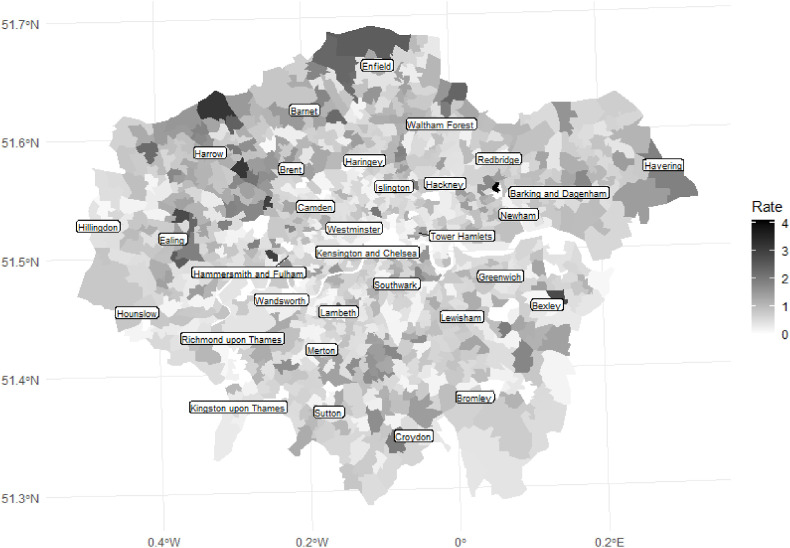
Fig. 1 maps the estimated death rate for the MSOAs across London for the period March 1 to April 17. It reveals both spatial heterogeneity and spatial clustering: the rate varies across the study region but there is a pattern of positive spatial autocorrelation with higher rates surrounded by other higher rates and lower with lower. Traditionally, Moran’s value is used to quantify spatial autocorrelation. Here it is +0.17 when comparing the rate for each MSOA with its contiguous neighbours. However, the value lacks the intuition that many assume of it: it does not vary from -1 to +1 like a traditional correlation coefficient but has a range dependent on the spatial weights matrix (Brunsdon and Comber, 2018; de Jong et al., 1984); here it ranges from -0.70 to +1.02. A more interpretable measure is the usual Pearson correlation, calculated as the correlation between the rate for each MSOA and its spatial lag (the average rate for each MSOA's contiguous neighbours). That gives a value of +0.32, a medium sized effect (Cohen, 1988).

Fig. 1.

Estimated death rate from Covid-19 per 1000 of the population during the period March 1 to April 17, 2020, by MSOAs in London.

It is unsurprising to find geographical patterns in the death rates. Given that the risk of infection is linked to age, occupation, ethnicity, and other attributes that tend broadly to be shared by residents of the same neighbourhood so the ethno-cultural, socio-economic, and demographic geographies that are seen in London’s residential patterns will be reflected, to at least some degree, in the geography of the death rates. The question is, to what degree? This might be answered by fitting a standard regression model – or, potentially, a spatial model (Ward and Gleditsch, 2018) to allow for spatially autocorrelated errors and/or the mutual dependence of the death rates across the MSOAs (because of the spatial transmission of the disease by proximity) – using, for example, the predictors of Covid-19 vulnerability identified by Daras et al. (2020), which are the proportions of the population, (a) living in care homes, (b) admitted to hospital in the past five years for a long-term health condition, (c) from an ethnic minority background, and (d) living in overcrowded housing.

A limitation of doing so is that the variables will be highly colinear, as they will be also with other associated factors such as age and occupation. (This co-linearity is likely why Daras et al. find income deprivation not to be statistically significantly related to Covid-19 mortality despite the known association of deprivation with vulnerability to the disease). None of the variables is strictly causal with, perhaps, the exception of pre-existing health conditions: living in a care home does not cause death by Covid-19; nor does being Black or Asian. They are generally social factors that increase exposure to the disease and therefore the fatality risk. As risks, they are co-constructed by underlying social and economic systems and the inequalities they generate. It is this that has led to Covid-19 being described as a syndemic, characterised by biological and social interactions upon health (Horton, 2020).

However, the key reason for using neither a ‘standard’ nor spatial regression model is an interest in a growing body of research looking at spatial discontinuities – the (sometimes-abrupt) differences between places that are next to each other. Given the expectation that closely located places will display similar attributes because of their shared, broader-scale context then it is geographically interesting to examine when and where that expectation is not met, here in regard to Covid-19 deaths although the general statement is also true: when, for example, the differences between adjacent places are large and coincide with socioeconomic differences or physical features such as housing types, or boundaries formed by roads, railways, or rivers (Mitchell and Lee, 2014). They invite examination of what created the differences and of the on-going impact they have on the populations who live there (Anciaes et al., 2016; Kramer, 2018). They have generated interest in methods of spatial analysis that do not smooth-over spatially significant microscale discontinuities (Dong et al., 2020) that have been described as social frontiers (Dean et al., 2019).

Consider, for example, that there is a neighbourhood in Little Ilford, Newham (about 14 km east from the centre of London) that caught the media’s attention (Goodier, 2020). There were 22 Covid-19 deaths there during March 1 to April 17; a rate, measured as previously, of 4.0 – the highest of any MSOA in England and Wales for the period. In an adjoining neighbourhood, the number was zero. Why the difference? It may relate to the housing stock: the former has more terraced properties and fewer flats/apartments, with greater levels of overcrowding. However, the more plausible explanation is that it also contains a care home whereas its neighbour does not. This, then, is a difference across a boundary that relates to other differences between the attributes of the two neighbourhoods. Modelling those differences requires a departure from traditional regression; the following section outlines why. It is the most technical part of the paper and may, if preferred, be skipped with the knowledge that the analysis looks at the differences between neighbourhoods that share a border, with all of the dependent and independent variables (including the control variables) being measures of difference between pairs of MSOAs. Because most MSOAs have more than one contiguous neighbour, a multilevel model is required.

4. Model design and specification

In general terms, if $y_i$ is the number of Covid-19 deaths in neighbourhood $i$ and $y_j$ is the number of Covid deaths in neighbourhood $j$, then the difference between the two, $∆y_{\left(ij\right)}=y_i-y_j$. Let $n$ be the number of MSOAs in London (982, excluding the City of London, omitted because it is primarily a financial not residential area) and $\mathbf{W}$ a contiguity matrix, of dimension $n$ by $n$, where $w_{ij}=1$ if $i$ and $j$ share a border, else $0$. Calculate $∆y_{\left(ij\right)}$ if $w_{ij}=1$ but retain only those values where $y_i\ge y_j$; or, if $y_i=y_j$, keep the place with the greater death rate. Discarding the other values prevents what would otherwise amount to duplicated information because $\mathbf{W}$ is symmetric and $∆y_{\left(ij\right)}=-∆y_{\left(ji\right)}$ . The outcome is a vector of values, call it $\mathbf{y}$, of length approximately equal to $nm/2$, where $m$ is the average number of contiguous neighbours per neighbourhood. This vector is the response variable in the model, measuring the across border differences in the number of Covid-19 deaths for pairs of contiguous MSOAs.

Predictors of those differences are created in much the same way. For example, the difference in the number of Covid-19 deaths may be related to the difference in the average house price of two contiguous neighbourhoods. For this, there is no constraint that $x_i\ge x_j$ that would parallel $y_i\ge y_j$, where $x$ is the predictor variable (the average house price): $i$ may have more deaths than $j$ but less expensive housing. The only requirement is that it matches up with the $y$ -variable; that is, the same pairs of MSOAs are used. Where there are $k$ such predictor variables, let $\mathbf{X}$ represent the matrix of predictors, of dimension approximately equal to $nm/2$ by $k$.

In principle, a regression model can then be fitted of the form, $f\left(\mathbf{y}\right)=\mathbf{X}\mathbf{\beta }+\mathbf{\epsilon }$. This is either a Poisson or negative binomial model (they produce near identical results) because $\mathbf{y}$ contains only positive integers, with many contiguous MSOAs having no difference in their numbers of Covid-19 deaths (typically because both had zero, or both had one or two), some but fewer having a difference of one, fewer still two, and so forth. In the model, $\mathbf{y}$ is, at minimum, conditional on the differences in the numbers of adults living either side of MSOA boundaries. This is required because MSOAs are of unequal population sizes and the greater the number of people who live in an MSOA, the greater the expected number of deaths. The adult population is used because of the lower likelihood that children will die from Covid-19 (and perhaps also be infected by it; the current medical evidence is not decisive on the matter). Essentially, its inclusion creates a death rate. In the analysis, additional control variables are included. Those are described in the following section.

The model can also be written as,

$$f\left(∆y_{\left(ij\right)}\right)={\beta }_0+{\beta }_1\left(∆x_{1\left(ij\right)}\right)+{\beta }_2\left(∆x_{2\left(ij\right)}\right)+\dots +{\beta }_k∆\left(x_{k\left(ij\right)}\right)+{\epsilon }_{\left(ij\right)}$$ (1)

where, as previously,

$$∆y_{\left(ij\right)}=\left(y_i-y_j\right),∆x_{1\left(ij\right)}=\left(x_{1i}-x_{1j}\right),∆x_{2\left(ij\right)}=\left(x_{2i}-x_{2j}\right),\text{etc}.$$

An advantage of the model is the potential to address omitted variable bias where it arises due to some or more (unmeasured) contextual variables impacting on any two locations that share a border. Assume that the number of Covid-19 deaths at location, $i$ is a function of some known predictor variables ($x_{1i},x_{2i}$, $x_{3i}$, etc.) as well as some local, unmeasured effect, $\gamma$. Suppose the same is true of location, $j$. Because it is the pairwise differences in the attributes of $i$ and $j$ that are modelled so the value for this dyad is $f(∆y_{\left(ij\right)})={\beta }_0+{\beta }_1\left(x_{1i}-x_{1j}\right)+{\beta }_2\left(x_{2i}-x_{2j}\right)+\dots +\left(\gamma -\gamma \right)+\epsilon$, which leads to the omitted, contextual variable being differenced to zero. This is true only if $\gamma$ impacts equally on $i$ and $j$, a very strong assumption. Whilst partly bolstered by appeal to Tobler’s (1970) well-known ‘first law of geography’ – “everything is related to everything else but near things are more related than distant things” – and remembering that $i$ and $j$ are neighbours, with a shared border, if it really were a law rather than a rule-of-thumb then the spatial discontinuities would not exist that this and other research are interested in. In practice, it is hoped that the locations are sufficiently close to share some contextual similarities.

The main disadvantage of the approach is that it induces a group structure in the data. To understand why, observe that the average London MSOA has 5.7 contiguous neighbours. If location $i$ has a number of deaths that is very much higher than, say, each of five neighbours then that unusual number is going to be present in each of the five across-boundary differences because each is subtracted from $y_i$. Since each of these dyads has a dependence upon $i$ they cannot be independent of each other. It also faces the issue that although some neighbours are quite distinct from each other, many are not. This can entail the modelling of small differences that, in some cases, will lead to estimation errors (specifically, identification problems and the model not converging to a solution as matrices approach singularity). Changing the optimisation procedure can assist (the ‘nlminbwrap’ optimiser was found to be most stable when using the R package, lme4 for the model fitting; Bates et al., 2015) as, on occasion, can comparing the results with a negative binomial model to check they are in agreement.

An alternative is to use a standard general linear model with the actual attributes of each location and not the pairwise differences with their neighbours. This is attractive because of its simplicity. However, as alluded to in the preceding section, such a method addresses a different research question: one (the model of differences) seeks to explain why some neighbourhoods have a higher (or lower) number of Covid-19 deaths than their contiguous neighbours; the other looks at why some neighbourhoods have a higher (or lower) number of Covid-19 deaths when compared to the average for all neighbourhoods in the study. In addition, what the standard model cannot easily do is explore if the correlates of increased Covid-19 deaths exhibit spatial variation in their effect sizes across the study region (nor, in their basic form, can spatial regression models such as the spatial error model or the spatially lagged Y model). The difference across boundaries method can. Again, this is considered later in the paper.

But why not use a standard general linear model with the variables still measuring the differences between neighbours? The answer returns to the problem of an induced group structure and the inter-dependence between locations that have one or more neighbour in common. The same problem was recognised in earlier work looking at differences in the ethnic compositions of adjacent neighbourhoods but side-stepped by deliberately focusing on the most extreme cases and their change over time (Harris, 2014) – it intentionally took a biased sample. Such an approach is not suitable here. Instead, parallels are drawn with recent work in migration modelling that reformulates the standard gravity model within a multilevel framework, recognising that neither multiple flows from the same origin (to different destinations) nor to the same destination (from different origins) are independent of each other (Zhang et al., 2020). Flows are nested within origins and within destinations – a cross-classified structure.

By analogy, the difference in the number of Covid-19 deaths, $y_{\left(ij\right)}$, may be likened to a ‘flow’, where $i$ is the ‘origin’ and $j$ the ‘destination’. Following the previous notation, the multilevel model is

$$f(∆y_{\left(ij\right)})={\beta }_0+{\beta }_1\left(∆x_{1\left(ij\right)}\right)+{\beta }_2\left(∆x_{2\left(ij\right)}\right)+\dots +{\beta }_k\left(∆x_{k\left(ij\right)}\right)+{\mu }_{0i}+{\vartheta }_{0j}+{\epsilon }_{\left(ij\right)}$$ (2)

with the effects of the ‘origins’ and the ‘destinations’ accommodated within a (cross-classified) random intercepts, Poisson model (again, a negative binomial model could be used but the results were found to be the same to about the third decimal place of the regression coefficients and, computationally, take much longer to estimate). Under this model, there are three ways that an MSOA can have a number of Covid-19 deaths significantly higher than a neighbour, conditional on the control variable(s) and, where included, other predictor variables. The first is when it has a higher-than-expected number of deaths than its neighbours. This circumstance is represented by positive and significant values of ${\mu }_{0i}$ (for the ‘origins’). The second is when its neighbour has fewer-than-expected deaths. This is represented by positive and significant values of ${\vartheta }_{0j}$ (for the ‘destinations’). Thirdly, a combination of the above.

Closer inspection of the model likens it to a difference-in-difference approach. Assume that the ‘treatment’ (an unfortunate nomenclature given the circumstances) is the causes of Covid-19 and that these are applied differentially to two neighbouring locations that are paired together because of their contiguity and presumed contextual similarity. The number of Covid-19 deaths per MSOA is the excess above the number of non-Covid deaths (also reported by the ONS) at time $t_1$. If that number of non-Covid deaths is representative of a ‘pre-treatment’ state at some notional time, $t_0$, then we have ${\left(y_{t_1}-y_{t_0}\right)}_i-{\left(y_{t_1}-y_{t_0}\right)}_j={\left(y_{\text{ALL DEATHS}}-y_{\text{NON}-\text{COVID}}\right)}_i-{\left(y_{\text{ALL DEATHS}}-y_{\text{NON}-\text{COVID}}\right)}_j$, which is a difference-in-difference measurement, equal to ${\left(y_{\text{COVID}}\right)}_i-{\left(y_{\text{COVID}}\right)}_j$, i.e. $∆y_{\left(ij\right)}$. In practice, neither the numbers nor rates of Covid and non-Covid deaths are independent of each other. Care homes, for example, have higher amounts of both, potentially because the cause of death becomes less distinct.

Spatial difference-in-difference models take various forms – compare, for example, Delgado and Florax (2015), who modify a standard econometric specification to allow for spatial interaction between proximate neighbours, with Heckert (2015), whose modification incorporates geographically weighted regression. In the present case, the spatial element comes from the differencing across contiguous neighbours and the inclusion of the random intercepts, ${\mu }_{0i}$ and ${\vartheta }_{0j}$, which are similar to calculating the (conditional) difference between an MSOA and its spatial lag.

5. Model variables and estimation

Taking into consideration the risk factors reviewed in the Public Health England (2020) report, Table 1 identifies seven empirical domains for consideration in the neighbourhood-level model: age composition of the neighbourhoods; ethnic composition; indicators of in-migration from other countries; socio-economic classification (social class); indicators of neighbourhood wealth or deprivation, including health deprivation; housing stock; and, household size and residential overcrowding. Although UK Census data generally provide a rich source of neighbourhood information for a wide range of socio-economic and demographic variables, the last census was in March 2011, nine years before the start of the Covid-19 pandemic in the UK. Unless there is regular like-for-like replacement of populations within neighbourhoods then the Census is measuring the composition and characteristics of neighbourhoods from almost a decade past – how they were, not necessarily how they are. For this reason, Census data have been supplemented with other information.

Table 1.

The data sources used in the analysis.

DEPENDENT VARIABLE:
Source: ONS Number of registered Covid-19 deaths, March 1 – April 17, 2020
PREDICTOR VARIABLES:
Age
Source: ONS Mid-2018 population estimates:
TWENTIES: Percentage of the residential population aged in their twenties
THIRTIES: Percentage aged in their thirties
FORTIES: Percentage aged in their forties
FIFTIES: Percentage aged in their fifties
SIXTIES: Percentage aged in their sixties
SEVENTIES: Percentage aged in their seventies
EIGHTY+: Percentage aged in their eighties or above
Ethnicity
Source: 2011 Census:
WBRI: Percentage of the residential population that identified as White British
WOTH: Percentage White Other (but neither Irish nor Travellers)
INDIAN: Percentage Indian
PAKISTANI: Percentage Pakistani
BANG: Percentage Bangladeshi
CHINESE: Percentage Chinese
AOTH: Percentage Other Asian
BAFR: Percentage Black African
BCRB: Percentage Black Caribbean
BOTH: Percentage Other Black
MIXED: Percentage of Mixed (joint) ethnicity
In-migration from overseas
Source: National Insurance Number Registrations of Overseas Nationals (London Datastore, from Department for Work and Pensions), 2014–17 data:
EU: Estimated percentage of residential mid-2018 population from EU countries
EUROTH: Estimated percentage from other European countries
AFRICAN: Estimated percentage from African countries
ASIAN: Estimated percentage from Asian countries
RoW: Estimated percentage from the rest of the world
National Statistics Socio-Economic Classification (NS-Sec)
Source: 2011 Census:
GROUP1: Percentage of the population aged 16 or over in higher managerial or administrative and professional occupations
GROUP2: Percentage in lower managerial or administrative and professional occupations
GROUP3: Percentage in intermediate occupations
GROUP4: Percentage who are small employers and own account workers
GROUP5: Percentage in lower supervisory and technical occupations
GROUP6: Percentage in semi-routine occupations
GROUP7: Percentage in routine occupations
GROUP8: Percentage who have never worked or are long-term unemployed
Neighbourhood wealth or deprivation
Source: HM Land Registry:
HPRICE: Average (trimmed mean) price of property sold, 2017–Feb 2020
Source: ONS (available from London Datastore):
INCOME: Estimated mean household annual income, 2015–16
Source: English Indices of Deprivation (2019) (Ministry of Housing, Communities & Local Government)
EDU: Mean education, skills and training score (averaged from Lower Level Super Output Area)
HEALTH: Mean health deprivation and disability score
HOUSING: Mean barriers to housing and services deprivation score
Housing Stock
Source: HM Land Registry:
DETACHED: Percentage of properties sold 2017–Feb 2020, detached
SEMI: Percentage of properties sold, semi-detached
TERRACED: Percentage of properties sold, terraced
FLATS: Percentage of properties sold, flats or apartments
Household size and over-crowding
Source: 2011 Census:
HHLD1: Percentage of households one person households
HHLD2: Percentage of two person households
HHLD3: Percentage of three person households
HHLD4: Percentage of four person households
HHLD5: Percentage of five person households
HHLD6: Percentage of six person households
HHLD7: Percentage of seven person households
HHLD8+: Percentage of households with eight persons or more
HIGHOCC: High occupancy. Percentage of households with 3 or 4 persons and one room
SHARED3+: Percentage of dwellings shared by 3 or more households
CONTROL VARIABLES:
Source: ONS Mid-2018 population estimates:
Number of adult residents in the area (fitted as a first and second order polynomial)
Population density (Number of persons in the MSOA divided by its area)
Source: ONS:
Number of deaths per 1000 of the adult population not attributed to Covid-19 over the study Period
Source: Care Quality Commission
Number of residential care home beds in the MSOA

Table 1 provides the complete list of data sources. Note that it describes the ‘raw’ variables: recall that, in the models, it is the difference in their value for two contiguous neighbourhoods that is used. This is true for all the variables, the dependent variable, the predictor variables, and the controls. To assist in those models’ interpretation, each of the raw variables, except the dependent variable, is scaled prior to calculating the differences (converted to a z-score, with a mean of zero for London).

The variables are highly co-linear both across and within the domains. This creates two modelling problems. First, in the estimation of the effect sizes and their statistical significance. Second, in the artificiality of trying to separate-out the specific effects of the various variables when the reality and the lived experience is that they are so closely entwined.

To address these issues, a four-fold modelling strategy is employed. First, each of the variables is used ‘by itself’ to predict the difference in the number of Covid-19 deaths but always with the inclusion of the control variables. Those are the differences in the number of adult residents (as a first and second order polynomial), the population density, the non-Covid death rate, and in the number of residential care home beds in the contiguous neighbours.

The results are shown in Table 2 , wherein those shaded in a lighter grey are positive and statistically significant at a 95 per cent confidence or above, and those shaded in a darker grey are negative and statistically significant at the same. They accord with prior expectations: areas containing more younger adults than their neighbours, more of the White British, having greater affluence, and/or more managerial or professional occupations had lower numbers of Covid-19 deaths, as did those places with more of the White Other group, Chinese populations, two person households, and/or more immigration from places other than the EU, Africa, and Asia (which suggests the Americas and Australasia and perhaps a younger population working in the hospitality industry). Areas with more elderly populations than their neighbours, higher percentages of Black and Asian (except Chinese) ethnic groups, greater deprivation, more people in lower-paid jobs, who are long-term unemployed or who have never worked, and/or larger household sizes had higher numbers of deaths.

Table 2.

The results from a series of separate regressions, using the named variable in each domain to predict the difference in the number of Covid-19 deaths between contiguous MSOAs. See text for further details.

It is instructive to compare the effect sizes shown in Table 2 with those obtained from using corresponding variables, also ‘one at a time’ but still with control variables, in the simpler, general linear model (mentioned earlier) that has the actual attributes of each location instead of their differences with contiguous neighbours. There are limits to this comparison because, as previously explained, they are modelling different outcomes. Nevertheless, it is reassuring to find that they broadly accord. The Spearman’s rank correlation between the two sets of estimated effect sizes is $r_s=0.852$. Of the fifty coefficients, 45 have the same sign (either positive or negative) in both sets of models. Of the remaining five, none is statistically significant at a 95 per cent confidence in the models of differences; two are in the more traditional model (DETACHED and HHLD3). On average, the effect sizes estimated by the difference across boundaries method are about 60 per cent the size of those estimated by the conventional model.

Because these are neighbourhood data, there is a risk of committing the ecological fallacy and assuming, perhaps wrongly, that relationships at a neighbourhood level are indicative of individual risks. It is possible, for example, that those aged in their eighties or above are living in the same places as other people and it is those other people, not those in their eighties, who are more likely to die from Covid-19. The same may be true of those from ethnic minorities, with low incomes or living in large households. However, it is unlikely given what is already known about Covid-19. Instead, what is interesting is how the risk factors of age, being from one of most ethnic minority groups, and of deprivation stand-up at the neighbourhood scale.

This was not pre-ordained: in much the same way that neighbourhood relationships need not apply at an individual scale, individual risk factors need not be evident at the neighbourhood scale. That they are testifies to the socio-economic, demographic, and ethnic geographies – and inequalities – that characterise London’s growth and development both in the past and today (Cheshire and Uberti, 2014; Whitfield, 2017) and to the argument that the disease is socially as well as biologically determined. That they are evident even between neighbours suggests that it is not only broad scale regional and sub-regional factors that contribute to health outcomes but also the ‘smaller scale’ differences between closely located places. Only the effects of pre-existing medical conditions (primarily due to a lack of available data) and of being an immigrant (from Africa especially) do not reveal themselves as a greater risk factor as they did in the Public Health England report.

Within Table 2, some variables are additionally highlighted with a box drawn around them. These relate to the second stage of the modelling strategy. Within each domain, a top-down modelling process has been used, beginning with a model that includes every individually significant variable from that domain and then eliminating one variable at a time based on three criteria: analyses of variance that compare the ‘full model’ with models that omit each individual variable in turn; removing the variables with least statistical confidence; and, addressing high levels of co-linearity (co-variance). The highlighted variables are the ones that remain at the end of the process – what might loosely be termed the key variables in each domain. Remaining evident are the negative effects of an elderly population, of having greater percentages of various ethnic minority populations, of lower average income, of higher numbers who have never worked or who are long term unemployed, and who live in very large households (which is likely indicative of residential overcrowding).

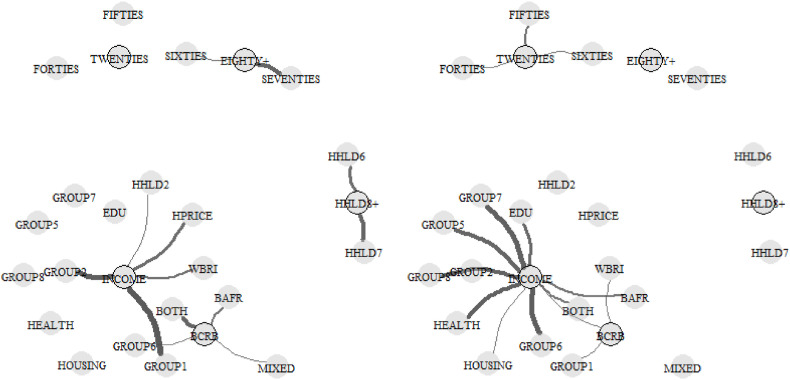
The third stage is to combine those key variables across the domains and undertake a further process of variable elimination using the same criteria as before (again, with the control variables in place). The final five variables, with their coefficients and standard errors are: TWENTIES, -0.091 (0.024); EIGHTY+, +0.132 (0.027); BCRB, +0.099 (0.029); INCOME, -0.100 (0.026), and HHLD8+, +0.079 (0.021). It is important to keep in mind that each of these is predictive not only of higher numbers of Covid-19 deaths but also of other variables that are themselves associated with higher deaths. This leads to the fourth stage of the modelling strategy, which is to use connected graphs to visualise the correlations between the five variables and the rest (Harris, 2020). The connections are shown in Fig. 2 , with positive correlations to the left and negative correlations to the right. Correlations of magnitude less than 0.5 are omitted, as are intra-correlations between ‘the rest' and not the key variables. This leaves only large effects between the five and other variables displayed. For example, higher average income in an MSOA when compared to neighbouring MSOAs is positively correlated with the percentages of managerial and professional occupations, as well as with the percentage of White British residents. It is negatively associated with the percentages of Black residents.

Fig. 2.

Showing the connections between the five variables in the final model (shown with a black border) and the other associated variables. Positive correlations are to the left. Negative correlations are to the right. The thicker the connecting line the greater the correlation. Correlations of magnitude less than 0.5 are omitted.

A further stage of analysis reveals geographical variation in the relationships between the five variables and the numbers of Covid-19 deaths. So far the analysis has employed a random intercepts model (see Equation (2)), in which positive and significant values of one set of residuals (${\mu }_{0i}$) represent places with significantly more deaths than their neighbours, having now accounted for the five predictor variables and for the additional control variables. This model may be extended so that,

$$\begin{array}{c}f\left(y_{\left(ij\right)}\right)={\beta }_0+{\beta }_{1i}\left(x_{1\left(ij\right)}\right)+{\beta }_2\left(x_{2\left(ij\right)}\right)+\dots +{\beta }_k\left(x_{k\left(ij\right)}\right)+{\mu }_{0i}+{\vartheta }_{0j}+{\epsilon }_{\left(ij\right)}\\ {\beta }_{1i}={\beta }_1+{\mu }_{1i}\end{array}$$ (3)

which, in Equation (3), allows the effect size for a variable, $∆x_{1\left(ij\right)}$, to vary in a random slope model, across all the pairs of MSOAs where MSOA, $i$ has more Covid-19 deaths than its neighbour, $j$. From this, places that add significantly to the average effect (where values of ${\mu }_{1i}$ are significantly greater than ${\beta }_1$) can be identified, indicating spatial non-stationarity in the modelled effect. Presently this would be reliant on very localised estimates because an MSOA is considered in relation only to its contiguous neighbours. However, the model can be refitted to assess the differences between second-order neighbours (the neighbours of neighbours); or, third-order neighbours, fourth-order, and so forth, here to the tenth-order – a limit chosen largely for pragmatic reasons: by the tenth-order the number of neighbours is becoming very large (think of it as a circular wave, the circumference of which rises with the square of the distance from its origin as it spreads out).

Together those refitted models provide ten sets of estimates of the spatial variation in the effect size (of${\mu }_{1i})$. Taking those estimates that are not positive and significant at a 95% confidence interval to be zero, the values are combined into a weighted average, giving most weight to the first-order neighbours estimation, next most to the second-order neighbours, and declining to zero under a Gaussian decay at a hypothetical eleventh-order estimation (which does not need to be calculated because its weight is zero). Setting the cut-off at eleven means that the tenth-order estimation still contributes to the sum, albeit not greatly and that, in broad terms, differences in the attributes of MSOAs are considered over a distance of about 7–8 km. The net result has similarities to Geographically Weighted Regression (Fotheringham et al., 2002) when one variable in the model has as effect size that is permitted to be spatially varying whilst all the other regression coefficients are held constant.

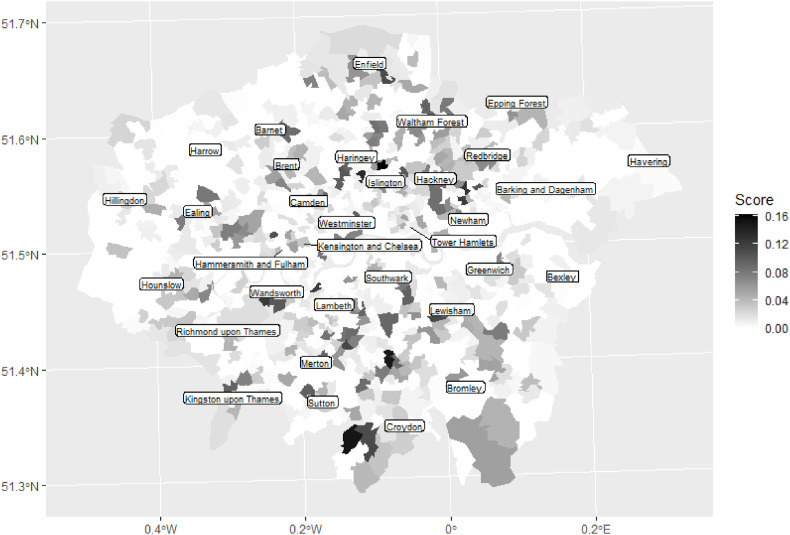
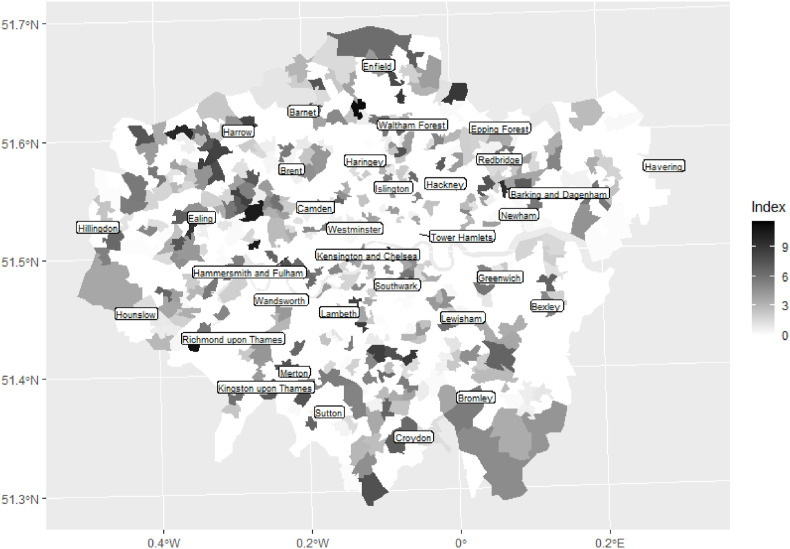
Of the five variables, the ones that appear to exhibit most spatial variation are BCRB, INCOME, and HHLD8. For consistency, the negatives of TWENTIES, INCOME and HHLD8 are used so that all variables then have a positive relationship with the number of Covid-19 deaths. This, and the earlier scaling of the variables, allow the five weighted sums to be added together per MSOA, giving an overall composite score for which a higher value indicates that greater differences for an MSOA vis-à-vis its neighbours in especially the income, large households, and Black Caribbean variables, are associated with higher numbers of Covid-19 deaths locally. That composite score is mapped in Fig. 3 . It is highest, on average, in the London Boroughs of Croydon, Waltham Forest and Newham.

Fig. 3.

Composite score indicating where localised differences in especially the low income, large households, and Black Caribbean variables tend to be associated with higher numbers of Covid-19 deaths.

6. Do the predictors change in the ‘post-peak’ period?

To this point, the analysis has focused on the period corresponding to the rise and peak of the spring 2020 wave of the Covid-19 pandemic in London. However, the ONS has released further data, for the period March 1 to May 31, 2020. From these and the initial data (for March 1 to April 17), the number of Covid-19 deaths in the period April 18 to May 31 can be calculated and used to see if the neighbourhood-level predictors have changed over the period, doing so by re-running the modelling process for the later data.

Before doing so, it is informative to map any changing geography in the ‘hot spots’ of the disease for the two periods. This is achieved by modelling the differences in the number of Covid-19 deaths for each period conditional on no predictor variables other than the control variables and looking at how the MSOA-level residuals vary geographically (specifically, with reference to Equation (2), by extracting positive and significant values of ${\mu }_{0i}$). As with the random slopes models, this is repeated for first-order neighbours up to the tenth, with the values combined in a weighted sum at each MSOA, giving most weight to the nearest (contiguous) neighbours and then declining, in a Gaussian decay, with distance.

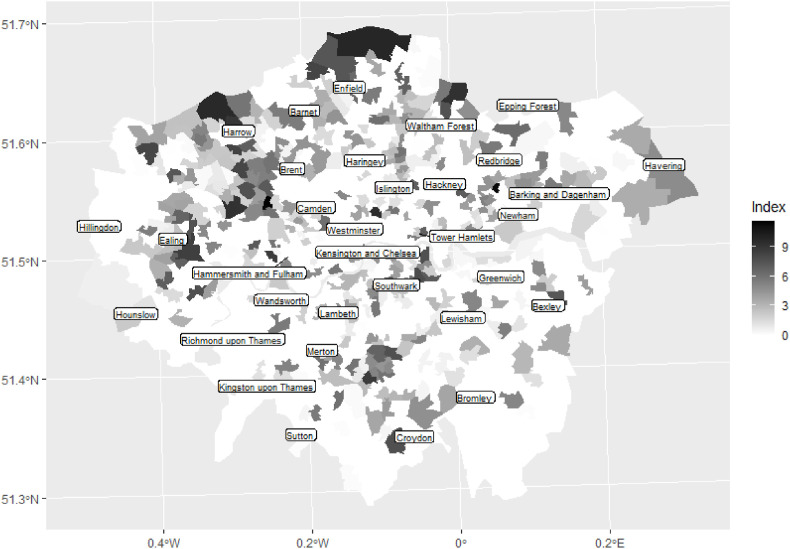
The maps are shown in Fig. 4, Fig. 5 . Of the 394 MSOAS that had a non-zero score in the period March 1 to April 17, 54 per cent had a non-zero score in the second. This might imply continuity in which places, within their local vicinity, had more deaths than their neighbours but, in fact, the Spearman’s correlation in their rankings is only $r_S=0.28$. Highest amongst the places with a non-zero score in the first period are MSOAs in each of Harlesden (Brent), Little Ilford (Newham), and Chase, (Enfield) but where those MSOAs are ranked 1, 2 and 3 for the first period, in the second they drop to 99, 249, and 58, respectively. Of the places with an above median, non-zero score in the first period, 81 per cent had a lower index score in the second period, and 49 per cent of the places with a non-zero score in the second period did not appear in the first. These statistics, as well as the maps, suggest a process of spatial diffusion in the disease. However, there are some MSOAs that remain as high amongst the ‘hot spots’ throughout, including one in Chingford Green (Waltham Forest), in Upper Norwood (Croydon), and in Greenford Broadway (Ealing).

Fig. 4.

‘Hot spots’ of Covid-19 deaths in the period March 1 to April 17, 2020. See text for details.

Fig. 5.

‘Hot spots’ of Covid-19 deaths in the period April 18 to May 31, 2020. See text for details.

The question is whether the process of diffusion changes the relationships between the neighbourhood-level predictors of Covid-19 and the numbers of deaths, here focusing back on the differences between the attributes of each MSOA and its first-order neighbours. The results of the models are shown in Table 3 and mirror those for Table 2 (still separately regressing each variable against the differences in the numbers of Covid-19 deaths between contiguous neighbours but including the control variables in each instance).

Table 3.

As for Table 2 but using the Covid-19 data for the period April 18 to May 31 instead of March 1 to April 17, 2020.

Comparing Table 2 with Table 1, the general trend is for the magnitude of the effect sizes to decrease, which is consistent with the spatial diffusion of a contagious disease. The main exceptions are the THIRTIES, BANG, HPRICE, and SHARED3+ variables, of which the last is surprising because it is associated with fewer deaths yet is a potential measure of overcrowding. However, it is also positively correlated with younger populations and negatively correlated with older ones. Variables that are statistically significant (at a 95 per cent confidence or greater) are broadly the same as for the earlier period, except the effects of older age groups appear to have waned (perhaps because they were better isolated during lockdown). Across the domains, the key variables are sometimes a subset of those previously highlighted but immigration from Asian countries emerges as new (and associated with more deaths), as does health deprivation and the aforementioned SHARED3+ variable.

Following the top down-process of variable elimination across all the domains, only three variables remain, where previously it was five, the coefficients of which (and their standard errors) are: THIRTIES, -0.049 (0.023); GROUP1, -0.094 (0.022); and HHLD8, +0.055 (0.021). Continuing to be important are the age of residents, wealth, and large household sizes within neighbourhoods. Ethnicity appears to drop out but that is because of the co-linearity – as before, it is important to keep in mind that the three remaining variables are predictive not only of Covid-19 deaths but also of other associated variables. In particular, higher income neighbourhoods are associated with the White British; lower income neighbourhoods with residents who are Black.

The overall impression is one of the disease’s spatial diffusion yet those from minority ethnic groups, deprived areas and/or large households remain associated with higher numbers of deaths throughout both periods. Younger populations are associated with fewer deaths.

7. Conclusion

This paper has presented the results of a difference across spatial boundaries method of analysis, looking at which variables are associated with neighbourhoods in London that had higher numbers of Covid-19 deaths than their nearest, contiguous neighbours during the spring of 2020. It finds that individual risk factors identified in work by the Office of National Statistics (ONS, 2020) and by Public Health England (2020) remain evident in the differences between neighbours. Whilst undoubtedly a function of the broader-scale demographic, social economic, and ethno-cultural geographies that characterise London’s neighbourhoods, it also evidences that localised differences in the attributes of neighbourhoods can have statistically significant differences in health outcomes.

‘Hot spots’ of the disease shift over the period from March to May 2020 and the effect sizes of the neighbourhood-level correlates diminish slightly in the period after the peak of the pandemic in the spring 2020 wave. Both observations are consistent with the transmission and spatial diffusion of a contagious disease from which no one is (initially) immune. Nevertheless, a greater number of deaths continues to be associated with Asian and Black ethnic groups, socio-economic disadvantage, very large households, and fewer from younger age groups. The analysis therefore adds to the evidence showing that age, wealth/deprivation, and ethnicity are key risk factors associated with higher mortality rates from Covid-19. It also strengthens the argument to regard Covid-19 as a syndemic, not just a pandemic.

Writing, now, in the autumn of 2020, the broad regional trends in Covid-19 infections have changed. The attention is still on London, but recently upon asking why the capital appears to be coping relatively well in keeping the infection rate down when compared to all other regions except the South East and South West. As Harris and Cheshire (2020) observe, the percentage of jobs, in London, in financial and insurance activities is almost double that of England as a whole, as is the percentage working in information and communication. These jobs are well suited to home working, which lowers the risk of infection. It is possible that London is doing better because many of its population have the ability to better self-isolate through home-working or even to sell-up and move to less densely populated locations. However, London's apparently lower infection rate has been disputed, said to have arisen from a shortage of testing facilities. In fact, as of today (September 28, 2020), talk in the media is of a potential lockdown in London soon. In any case, whilst home-working or moving to the country might be options for some, they are not viable for all. Consequently, spatial differences in the jobs available and inequalities in the labour market are manifest, both at regional and sub-regional scales, in rates of Covid-19 infections and fatalities. Tragically, the evidence of the human cost of Covid-19 is that whilst it places everyone at risk, places are not equally risky. Instead, those risks are magnified by geographies of social-economic inequality, some at localised scales, in the capital as elsewhere in the country.