Interim Monitoring for Futility in Clinical Trials with Two Co-primary Endpoints Using Prediction

Abstract

We discuss using prediction as a flexible and practical approach for monitoring futility in clinical trials with two co-primary endpoints. This approach is appealing in that it provides quantitative evaluation of potential effect sizes and associated precision, and can be combined with flexible error-spending strategies. We extend prediction of effect size estimates and the construction of predicted intervals to the two co-primary endpoints case, and illustrate interim futility monitoring of treatment effects using prediction with an example. We also discuss alternative approaches based on the conditional and predictive powers, compare these methods and provide some guidance on the use of prediction for better decision in clinical trials with co-primary endpoints.

1. Introduction

The use of more than one primary endpoint has become a common design feature in clinical trials evaluating preventative or therapeutic interventions in many disease areas such as cardiovascular disease, infectious disease and oncology. In complex diseases, co-primary endpoints (CPE) may be preferable to multiple primary endpoints (MPE) since the cause of disease may be multi-factorial with contributions from genetic, environmental, lifestyle and other factors. Furthermore the disease may have different and interdependent outcomes. Examples include Alzheimer’s disease, migraine, Parkinson’s disease, irritable bowel syndrome, and Duchenne and Becker muscular dystrophy. According to the two recently released regulatory guidance documents, i.e., Food and Drug Administration (FDA) draft guidance on “Multiple Endpoints in Clinical Trials” (FDA, 2017), and the European Medical Agency (EMA) draft guideline on “Multiplicity Issues in Clinical Trials” (CHMP, 2016), CPE are defined when evaluating if the test intervention is superior (or non-inferior) to the control on all primary endpoints. Failure to demonstrate superiority (or non-inferiority) on any single endpoint implies that the effect of the test intervention to the control intervention cannot be concluded. In contrast, designing the trial to evaluate an effect on at least one of the primary endpoints is MPE. Although CPE are a special case of MPE, it is important to recognize their differences in the Type I and II error controls in the design and analysis of clinical trials. For CPE, no adjustment is needed to control the Type I error rate. However, an adjustment to control Type II error rate is necessary as the Type II error rate increases as the number of endpoints being evaluated increases. On the other hand, for MPE, an adjustment is required for the Type I error, but not for the Type II error. Hamasaki et al. (2018) summarize the concepts and related issues of CPE and MPE in clinical trials.

CPE could offer an attractive design feature as they capture a more complete characterization of the effect of an intervention. However, they create challenges. Generally it is more difficult to achieve statistical significance on all of the endpoints, compared with a single endpoint case. Such trials often require large sample sizes to maintain the desired power due to the conservative Type I error and the inflated Type II error. Many CPE trials have failed to demonstrate a joint effect on all of the primary endpoints. For example, Green et al. (2009) reported the results of a multicenter, randomized, double-blind placebo-controlled trial in patients with mild Alzheimer disease (Tarenflurbil study), where CPE were cognition as assessed by the Alzheimer Disease Assessment Scale Cognitive Subscale (ADAS-Cog) and functional ability as assessed by the Alzheimer Disease Cooperative Study Activities of Daily Living (ADCS-ADL). The study was sized for 1,600 participants in total (equally sized groups) based on a power of 96% to detect the between-group joint difference in the two primary endpoints (using a one-sided test at 2.5% significance level, with the standardized mean differences between the two groups of 0.2 for both endpoints, assuming zero correlation between the two endpoints). As a result, the Tarenflurbil trial failed to demonstrate a beneficial effect of tarenflurbil as the observed ADCS-ADL scores in the tarenflurbil group were smaller (smaller scores being worse) than for the placebo group. If the design had included an interim futility assessment, then the trial may have been stopped earlier, preventing patients from being exposed to an ineffective intervention unnecessarily and thus saving valuable resources and time.

In practice, one well-accepted approach for interim monitoring is to use group-sequential designs. Group-sequential designs offer the possibility of stopping a trial early for efficacy and/or futility and such designs in clinical trials with CPE have been discussed by several authors (Asakura et al., 2014, 2015, 2017; Cheng et al., 2014; Hamasaki et al., 2015, 2018; Hung and Wang, 2009; Jennison and Turnbull, 1993; Schüler et al., 2017; Sugimoto et al., 2019). However group-sequential designs and other related methods such as conditional and predictive power-based methods do not provide formal evaluation regarding potential effect size estimates and associated precision with continuation of the trial to aid in go/no-go decision-making.

In this paper, we discuss an extension of the prediction method by Evans et al. (2007) and Li et al. (2009) to interim futility monitoring in clinical trials with CPE, especially two endpoints being evaluated as co-primary since the two co-primary case is fundamental and provides the basis for extending more than two endpoint case. Using the prediction could be a flexible and practical approach for monitoring interim data of clinical trials with CPE. This extension is appealing in that it provides quantitative evaluation of potential effect sizes and associated precision, with endpoint measurement continuation, thus providing statisticians and investigators with a better understanding of the pros and cons associated with continuation of endpoint measurement. We describe the statistical visualization for plotting the prediction as such visualizations could help to make complex scenarios more accessible, understandable and usable. In contrast to the prediction, we also discuss alternative approaches based on the conditional and predictive powers.

The paper is structured as follows: in Section 2, we describe the construction of predicted regions for CPE when two endpoints are continuous. In addition, we briefly outline the conditional and predictive power approaches for CPE. In Section 3, we illustrate interim monitoring of treatment effects using prediction and other approaches using an example. In Section 4, we discuss strengths and limitations of the predicted regions and provide guidance for use of the prediction method. In Section 5, we summarize the findings and discuss extensions such as applications to binary and time-to-event endpoints and more than two endpoints.

2. Tools for futility monitoring clinical trials with two CPE

2.1. Statistical settings

Consider a randomized clinical trial comparing the test intervention (T) with the control intervention (C) based on two continuous outcomes to be evaluated as CPE. Let n and rn be the total number of participants on the T and the C groups, respectively, where r is the sample size ratio and r = 1 means equally-sized group. Suppose that one interim monitoring is planned when n₁ and rn₁ participants are accumulated on the T and the C groups, respectively. Let responses to the T be denoted by Y_Tki and responses to the C by Y_Ckj (k = 1,2; i = 1, … n; j = 1, …, rn). Assume that (Y_T1i, Y_T2i) and (Y_C1j, Y_C2j) are independently bivariate normally distributed as (Y_T1i, Y_T2i) ~ N₂(μ_T, Σ) and (Y_C1j, Y_C2j) ~ N₂(μ_C, Σ), where μ_T and μ_C are mean vectors given by μ_T = (μ_T1, μ_T2)^T and μ_C = (μ_C1, μ_C2)^T respectively. The common covariance matrix Σ is given by Σ = {ρ_kk′σ_kσ_k′} with $\text{var}\left[Y_{\text{T}ki}\right]=\text{var}\left[Y_{\text{C}kj}\right]={\sigma }_k^2$ and corr[Y_Tki, Y_Tk′i] = corr[Y_Ckj, Y_Ck′j] = σ_kk′ (k ≠ k′)

Let δ_k and Δ_k denote the mean difference and the standardized mean difference between the T and the C respectively, where δ_k = μ_Tk − μ_Ck and Δ_k = δ_k/σ_k (k = 1,2). Suppose that positive value of δ_k indicate favorability of the T over the C, and there is an interest in evaluating the T is superior to the C on two endpoints. The hypotheses for each endpoint are H_0k: δ_k ≤ 0 versus H_1k: δ_k > 0, and each hypothesis is tested at significance level α_k. The hypotheses for CPE are ${\text{H}}_0^{\text{CPE}}:{\cup }_{k=1}^K{\text{H}}_{0k}$ versus ${\text{H}}_1^{\text{CPE}}:{\cap }_{k=1}^K{\text{H}}_{1k}$. The size of test for CPE is α if each hypothesis is tested at significance level α_k = α as the size is at most α with α = max(α₁, …, α_K) (Berger, 1982).

2.2. Predicted regions

In this section, we discuss predicting mean difference estimates and constructing predicted regions for CPE. A predicted mean difference estimate ${\tilde{\delta }}_k$ is a predicted value of the mean difference estimate for Endpoint k at a future timepoint and can be calculated as a weighted average of the observed mean difference at the monitoring and predicted mean difference regarding the data yet to be observed, for example:

$${\tilde{\delta }}_k=(n_1{\widehat{\delta }}_{k1+}{n}_2{\tilde{\delta }}_{k2})/n,$$

where ${\widehat{\delta }}_{k1}$ is the observed mean difference at the monitoring, ${\tilde{\delta }}_{k2}$ is the predicted mean difference regarding the data yet to be observed and n₂ is the number of participants yet to be observed.

Predicted regions are predicted confidence regions which could be constructed individually for the mean difference for each endpoint or simultaneously for the mean difference for both endpoints. A predicted interval (PI) composes the predicted region and a 100(1 − α)% PI for the mean difference between two means on Endpoint k:

$${\tilde{\delta }}_k\pm t_{(1+r)n-2}(\alpha /2)\sqrt{\frac{(1+r)}{rn}}{\tilde{s}}_k,$$

where ${\tilde{s}}_k$ is the predicted standard deviation, t_(1+r)n−2(α/2) is the upper 100(α/2)th percentile of the t-distribution with (1 + r)n − 2 degrees of freedom. The predicted standard deviation ${\tilde{s}}_k$ is the predicted value of the pooled estimate of the standard deviation, where

$${\tilde{s}}_k^2=\frac{(n-1){\tilde{s}}_{\text{T}k}^2+(rn-1){\tilde{s}}_{\text{C}k}^2}{(1+r)n-2},$$

and ${\tilde{s}}_{\text{T}k}^2$ and ${\tilde{s}}_{\text{C}k}^2$ are the predicted values of the variance estimates of the T and C groups. The joint predicted region for the mean difference vector for both endpoints is described as the region of δ = (δ₁, δ₂) which satisfy the following equation:

$${(\tilde{\mathit{\delta }}-\mathit{\delta })}^{\text{T}}{\tilde{\mathit{V}}}^{-1}(\tilde{\mathit{\delta }}-\mathit{\delta })\le \frac{2(1+r)n}{r{n}^2}\frac{(1+r)n-2}{(1+r)n-3}{F}_{2,(1+r)n-3}(\alpha ),$$

where $\tilde{\delta }=({\tilde{\delta }}_1,{\tilde{\delta }}_2)$, $\tilde{\mathit{V}}=({\tilde{s}}_1^2,{\tilde{s}}_2^2)$ and F_2,(1+r)n−3(α) is the upper 100αth percentile of the F-distribution with (2, (1 + r)n − 3) degrees of freedom.

In addition, we here consider constructing predicted regions using the PIs for each endpoint. Such regions can be more simply constructed and interpreted compared to the joint region as the limits of a PI for each endpoint would correspond to decision-making regarding the hypothesis for each endpoint in “co-primary” situation. There is another advantage for making decisions based on the predicted regions using the PIs that the decisions do not depend on the correlation among the endpoints, which is a nuisance parameter. The joint predicted regions for the mean difference vector for both endpoints need some assumption regarding the correlation and it may affect the decision-making. On the other hand, the predicted regions using the PIs cannot assess a joint probability that both endpoints cover the true effect sizes or other various alternatives simultaneously. Therefore, quantitative evaluation of the joint region for both mean difference vectors, together with the predicted regions using the PIs for each endpoint could lead to better decision-making in stopping a trial early for futility.

In addition, the coverage probability that the PIs for both endpoints cover the true effect sizes, which will be referred to as conjunctive coverage probability, could be lower than the coverage probability on each endpoint (which will be referred to as marginal coverage probability) or the coverage probability of predicted region for the mean difference vector, as is the case with confidence intervals (CIs). Basically, predicted regions do not always cover true mean differences with the confidence levels (e.g., 95%), as long as mean differences are predicted based on the observed data. Conversely, coverage probability could be larger than the confidence level when the assumed effect sizes are close to the true effect sizes. For the details, please refer to Appendix A1.

A predicted mean difference ${\tilde{\delta }}_{k2}$, regarding the data yet to be observed, can be calculated by simulated future data, assuming that current trend continues, H₁ is true, H₀ is true, or other values under various scenarios. The predicted standard deviations ${\tilde{s}}_{\text{T}k}$ and ${\tilde{s}}_{\text{C}k}$ can also be estimated based on the simulated future data assuming that the pooled variance observed at the monitoring is true. Generating the future data many times by using simulation could incorporate sampling variation. When all of the primary endpoints are continuous, the multivariate normal distribution could be used for simulating the data yet to be observed. That generates a large number of predicted mean difference estimates and PIs, and an appropriate summary of them can aid in go/no-go decision-making. While they could be summarized as the final predicted region by taking means or medians of the limits of those PIs, it does not account for the sampling variation as discussed in Li et al. (2009). Graphical methods analogous to predicted interval plots (PIPs) in Li et al. (2009) could be extended to the multiple endpoints scenario and would be intuitive and helpful for comprehensive evaluation of the treatment effects at interim monitoring. The steps for constructing the joint predicted regions for both endpoints and the predicted regions using the PIs for each endpoint are given in Appendix A2.

The predicted mean difference estimates and PIs provide quantitative evaluation of potential size of mean differences and associated precision. PIs allow us flexible decision-making, especially for futility evaluation as it does not basically cause an inflation of Type I error rate and a loss of power as no formal test is performed. Early stopping for futility would be considered when the predicted mean difference estimates are not clinically meaningful. “Clinical meaningfulness” would depend on the disease area, the primary objective of the trial and other information such as the safety profile. In one situation, for example, where the upper bound of a PI for the mean difference is smaller than the lowest “acceptable” mean difference, it might be reasonable to discontinue the trial for futility.

Here we consider that the trial is monitored when 258 participants per intervention group are observed, while the planned sample size is 516 per group to detect the joint effect of (Δ₁, Δ₂) =(0.2, 0.2) for two CPE, with the significance level of 2.5% and the power of 80%, for one-sided test in the fixed-sample size design. We suppose that the standardized difference in means of (0.2, 0.2) is observed at interim and evaluate the predicted mean difference estimates and PIs.

Figure 1 plots the mean difference estimates and PIs. We adopt two-dimensional plots regarding the mean differences for two endpoints. The average PIs are shown in dashed lines, and the 95% CIs based on the observed data at monitoring are shown in solid lines. In this example the average PIs are based on the means of 95% PIs from 100,000 generated datasets of the future data. The gray circles represent the proportions (0.05, 0.2, 0.5, 0.8, 0.95 and 0.99) of predicted mean difference estimates inside them. Each point corresponds to each set of predicted mean difference estimates and closely-spaced points represent high probability density of the predicted mean difference estimates. The lines on a bar represent values of δ₁ or δ₂ where the empirical cumulative distribution function of the predicted mean difference estimates is 0.05m (m = 1, …, 20). We assume that the current trend continues (i.e., the assumed mean difference is 0.2 for both endpoints) for Figure 1(a), and the effect size of (0.0, 0.0) is true for Figure 1(b), where the observed mean difference at monitoring is (0.2, 0.2), standard deviation is 1.0 and the correlation between endpoints is 0.5. One could simulate the future data under various assumptions regarding the effect sizes and correlations, and evaluate whether the trial should stop for futility or not. In this case, the trial seems to be promising because almost all of the predicted mean difference estimates would be larger than zero and the average PI of (0.08, 0.32) for each endpoint would be sufficiently large, under the assumption where the current trend continues, and many of the predicted mean difference estimates would be larger than zero even when the effect size of zero for both endpoints is assumed to be true. Figure 1(c) illustrates that very few predicted mean difference estimates are larger than the planned effect size and the lower limits of average predicted region is smaller than zero, when the observed mean difference at monitoring is 0.0 for both endpoints and assuming the current trend continues. In this case, the lower limits of average PIs would be almost zero even when the effect size of 0.2 for both endpoints is assumed to be true, for Figure 1(d), and one would consider discontinuation of the trial with evaluating the trial seems to be unpromising.

Figure 1.

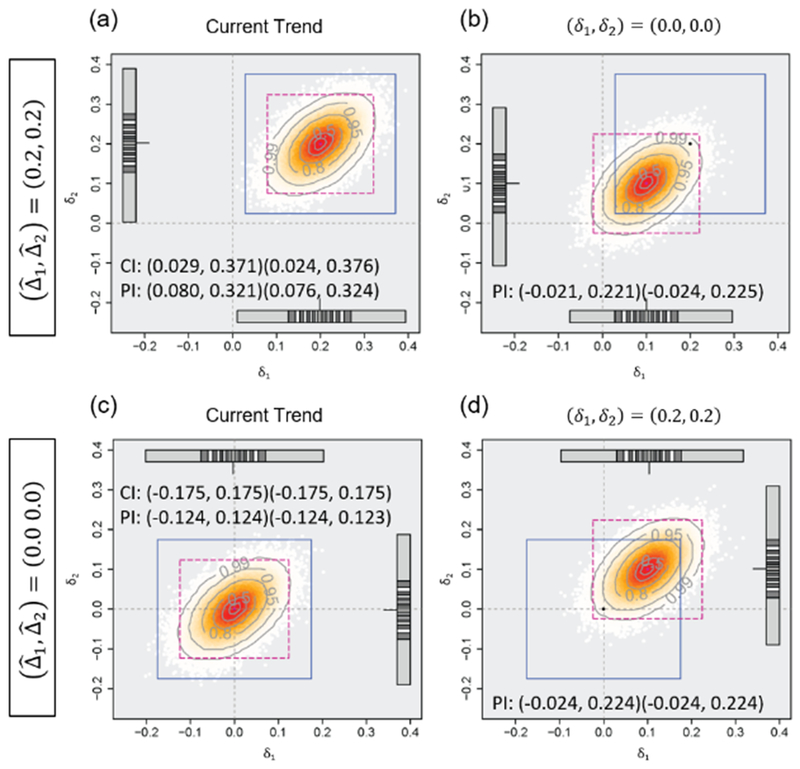
Predicted mean difference estimates and average 95% predicted intervals based on the observed mean difference of (0.2, 0.2) or (0.0, 0.0), the standard deviation of 1.0 and the correlation between the endpoints of 0.5, assuming the current trend continues or the null/alternative hypothesis is true, when 258 participants are observed (the planned sample size is 516). The number of generated datasets is 100,000.

2.3. Conditional power

Stochastic curtailment is another practical approach for monitoring of clinical trials. Conditional power (CP) provides conditional probability of rejecting H₀ at the final analysis under the observed treatment effect at interim and the assumed treatment effect and variance, as a frequentist paradigm, and given by

$$\mathrm{CP}=\mathrm{Pr}\left[{\bigcap }_{k=1}^2{Z}_k>z(\alpha )|\widehat{\Delta }\right]=1-{\varphi }_2\left[\frac{z(\alpha )\sqrt{2n}-\mathit{z}\sqrt{2n_1}-n_2\Delta }{\sqrt{2n_2}}|\mathit{\rho }\right],$$ (1)

where ϕ₂(·|ρ) is the cumulative distribution function of the standardized bivariate normal distribution with the known correlation matrix ρ with its the off-diagonal element ρ₁₂, Δ is the vector of the standardized mean differences, $\widehat{\Delta }$ is the vector of the observed values of Δ, z is the vector of the observed values of $Z_k=({\stackrel{‒}{Y}}_{\text{T}k}-{\stackrel{‒}{Y}}_{\text{C}k})∕({\sigma }_k\sqrt{(1+r)∕(nr)})$, k = 1,2, and z(α) is the upper 100αth percentile of the standardized normal distribution. Because Δ is unknown, it is customary to substitute $\widehat{\Delta }$, which is the estimated standardized mean difference at interim, or the assumed standardized mean difference during trial planning.

The advantage of evaluating the CP is providing quantitative information regarding statistical significance based on the observed treatment effects. Considering early stopping based on the CP would be helpful for futility evaluation, as is the case with a single endpoint where a criterion of 20% is often used (Ware et al., 1985; Dmitrienko et al., 2006). One could also recalculate sample size so that the CP reaches the targeted power when the interim data implies the low possibility of rejecting the null hypothesis (Asakura et al., 2014, 2015; Mehta and Pocock, 2011).

On the other hand, an issue for CP is that the probability depends on an assumption regarding effect sizes and correlation between the endpoints and the decision may change with it. Similarly to a single endpoint case which is discussed in Posch et al. (2003), the decision-making based on CP with the estimated effect sizes from interim observed data as if the current observed trend continues could lead to misleading conclusions. One could evaluate Conditional Power Contour Plot (CPCP) in order to see how the CP varies with potential effect sizes, while it still depends on the assumed correlations. Figure 2 illustrates CPCP with the same situation as that in Section 2.2, where the observed mean difference at monitoring is (0.2, 0.2) and (0.0, 0.0), standard deviation is 1.0 and correlation between the endpoints is 0.5. When the observed effect size of (0.2, 0.2) is observed, for example, the CP would be 93.2% or 16.3%, depending on the assumed effect size of (0.2, 0.2) or (0.0, 0.0), on the left-hand plot. On the other hand, when the effect size of zero is observed for both endpoints, CP would be 16.3% or 0.0%, on the right-hand plot.

Figure 2.

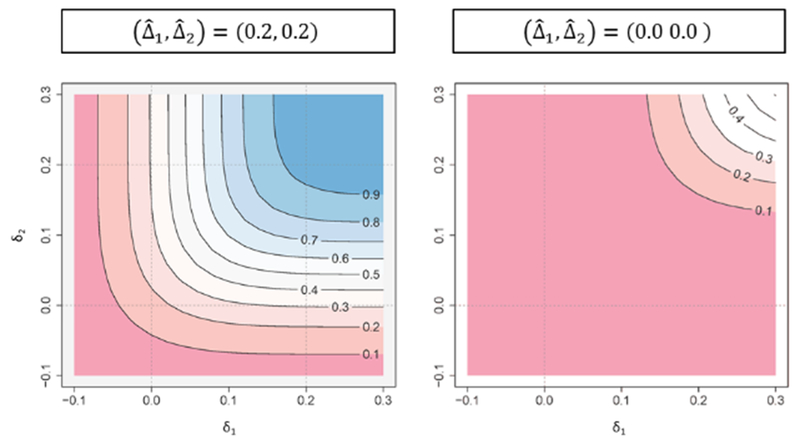
Conditional power contour plot based on the observed effect size ((0.2, 0.2) or (0.0, 0.0)) when 258 participants are observed (the planned sample size is 516). The horizontal axis (δ₁) and the vertical axis (δ₂) represent the assumed effect sizes.

2.4. Predictive power

While CP provides the conditional probability of rejecting H₀, it could not provide appropriate information regarding whether the trial would be promising or not, when the treatment effects are wrongly assumed. Predictive power (PP), which is a weighted average of the CP over a range of δ_k, has been discussed as a hybrid of frequentist and Bayesian paradigms by Herson (1979), Choi et al. (1985) and Spiegelhalter et al. (1986). Interim evaluation of efficacy or futility based on PP is similar to that based on the CP. On the other hand, selection of prior distribution of δ_k is an issue because there is no “correct” prior when evaluating PP (Spiegelhalter, 2004). One option is use of noninformative prior, while some authors have pointed that it tends to easily stop the trial for futility (e.g., please see Herson (1979), Spiegelhalter et al. (1986), and Jennison and Turnbull (1990)).

In this paper, we discuss PP based on noninformative prior with CPE:

$$\mathrm{PP}=\int \int \mathrm{Pr}\left[{\bigcap }_{k=1}^2{Z}_k>z(\alpha )|\mathit{\delta }\right]\pi (\mathit{\delta }|\widehat{\Delta })d{\delta }_{2}d{\delta }_1=1-{\varphi }_2\left[\frac{z_{\alpha }\sqrt{\raisebox{1ex}{$n_1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}-\mathit{z}}{\sqrt{\raisebox{1ex}{$n_2$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}}|\mathit{\rho }\right],$$ (2)

where ρ is the correlation matrix. We find that the magnitude relation between CP (where the observed effect sizes are assumed to be true) and PP depends on the information time and z, because the argument of ϕ₂ in (2) differs from that in (1) by a factor $\sqrt{n_1∕n}$ after Δ is replaced by $\widehat{\Delta }$ (Jennison and Turnbull, 2000). If one makes a decision only based on a cut-off value regarding “the conditional probability of trial success” (e.g., 20%), the decision may differ depending on which scale would be used. The futility criteria are identical whichever scales would be evaluated, and should treat the scales as methods to express the futility criteria, similarly as in a single endpoint situation by discussed Gallo et al. (2014).

Analogously to the single endpoint case (for example, please see Emerson et al. (2005), the futility evaluation based on PP could address some of the issues with CP such as the assumptions regarding effect sizes if there is a reliable prior distribution of δ. Although PP can be used to predict whether statistical significance would be attained at some future timepoint, accounting for the observed data at an interim, the foundational issues for CP approach still exists in PP approach, that is, PP does not provide quantitative evaluation of potential size of mean differences and associated precision.

In the same example in Section 2.2 and 2.3, where the observed mean difference at monitoring is (0.2, 0.2) and (0.0, 0.0), standard deviation is 1.0 and correlation between the endpoints is 0.5, the PPs based on noninformative prior would be 82.4% ($({\widehat{\Delta }}_1,{\widehat{\Delta }}_2)=(0.2,0.2)$) and 0.5% ($({\widehat{\Delta }}_1,{\widehat{\Delta }}_2)=(0.0,0.0)$).

3. An illustration

We illustrate the concepts with an example from the Tarenflurbil study (Green et al., 2009) described in the Introduction. Recall that the study was designed to evaluate if tarenflurbil was superior to placebo on two CPE: (i) change score from baseline on the ADAS-cog, and (ii) change score on the ADCS–ADL. The original design called for 800 participants per intervention group to provide a power of 96% to detect the joint between-group difference in the two primary endpoints using a one-sided test at the 2.5% significance level, with an alternative hypothesis of a standardized mean difference of 0.2 for both endpoints. The correlation between the two endpoints was assumed to be zero. Although a negative change score from baseline on the ADAS-Cog indicates improvement, suppose that a positive value of a decrease in the score is preferable, consistently throughout this paper. We consider one interim monitoring for futility evaluation when 200, 400 or 600 participants per group are observed (i.e., at 25%, 50% or 75% information time), with three situations where (i) observed effect sizes for both endpoints are the same as those at the planning ($({\widehat{\Delta }}_1,{\widehat{\Delta }}_2)=(0.2,0.2)$), (ii) observed effect sizes are positive but smaller than those at the planning ($({\widehat{\Delta }}_1,{\widehat{\Delta }}_2)=(0.1,0.1)$) and (iii) observed effect sizes are negative ($({\widehat{\Delta }}_1,{\widehat{\Delta }}_2)=(-0.01,-0.04)$), with the observed correlation of 0.3 between the endpoints. In each situation we compare the decisions based on the PIs, CP and PP calculated at the interim monitoring.

Figures 3, 4, and 5 and Table 1 display the mean difference estimates and the PIs, the CPs and the PPs in the three situations. When the planned effect size of 0.2 are observed for both endpoints as in situation (i), at any of the timings for the monitoring, almost all of the predicted mean difference estimates would be larger than zero and the average PI of (0.10, 0.30) for both endpoints would cover sufficiently large effect sizes assuming the current trend continues. In this situation, predicted effect size estimates would support the decision based on CP or PP, which are 98.2%, 99.6% and nearly 100% for CP (where the observed effect sizes are assumed to be true), and 79.0%, 96.0% and nearly 100% for PP, at 25%, 50% and 75% information time, to continue the trial (or consider early stopping for efficacy). When the observed effect sizes are smaller than those at the planning as in situation (ii), some of the predicted mean difference estimates would have negative values and lower limits of the PIs, assuming the current trend, are almost zero. However, if optimistic effect sizes of (0.2, 0.2) are assumed, the PIs would cover modestly large values, and it would not provide strong evidence of early stopping. If a futility criterion of 20% based on the CP or PP is considered, all the approaches would support trial continuation because the CP would be 31.7%, 32.1% and 33.1% (where the observed effect sizes are assumed to be true) and the PP would be 30.8%, 31.5% and 32.7%, at 25%, 50% and 75% information time. In the last situation, the observed effect sizes at interim are the same as those actually observed in this trial (at the final analysis). Even if the optimistic effect sizes of (0.2, 0.2) are assumed, the predicted mean difference estimates would not be large enough and a part of them have negative values at 50% and 75% information time. The average PIs would also cover zero and upper limits of them would be smaller than the planned effect sizes. Early stopping for futility is implied by prediction method and it would support the decision of futility based on CP (where the observed effect sizes are assumed to be true) or PP, which would be nearly 0%. When the negative effect sizes are observed at 25% information time, on the other hand, the average PIs may not imply early stopping with modestly large values under an optimistic assumption.

Figure 3.

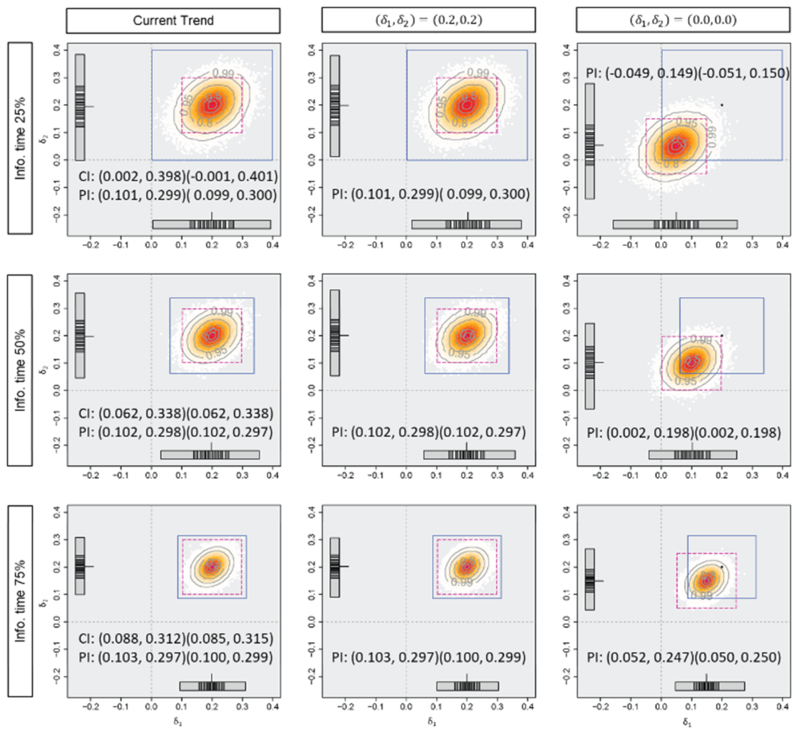
Predicted mean difference estimates and average 95% predicted intervals with the observed mean difference of (i) (0.2, 0.2), the standard deviation of 1.0 and the correlation of 0.3 at 0.25, 0.50 and 0.75 information time in Tarenflurbil trial. The horizontal axis (δ₂) and the vertical axis (δ₂) represent the effect sizes. The number of generated datasets is 100000.

Figure 4.

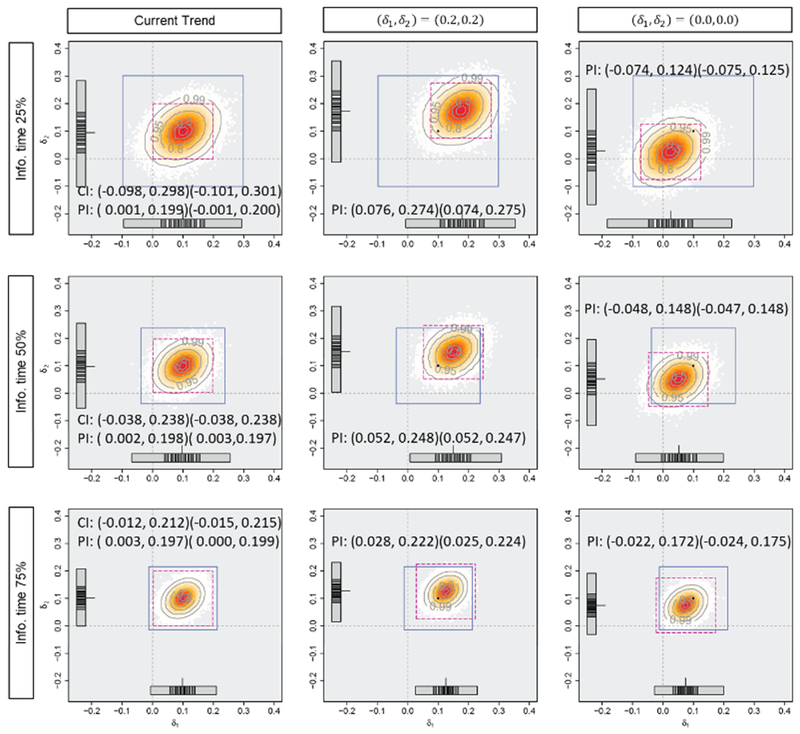
Predicted mean difference estimates and average 95% predicted intervals with the mean difference of (ii) (0.1, 0.1), the standard deviation of 1.0 and the correlation of 0.3 at 0.25, 0.50 and 0.75 information time in Tarenflurbil trial. The horizontal axis (δ₁) and the vertical axis (δ₂) represent the effect sizes. The number of generated datasets is 100000.

Figure 5.

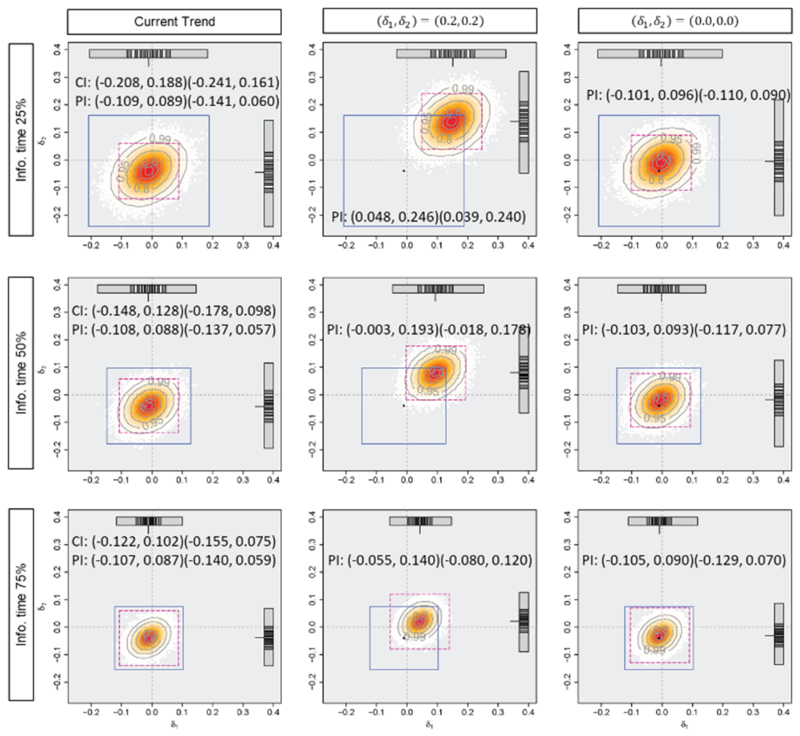
Predicted mean difference estimates and average 95% predicted intervals with the observed mean difference of (iii) (−0.01, −0.04), the standard deviation of 1.0 and the correlation of 0.3 at 0.25, 0.50 and 0.75 information time in Tarenflurbil trial. The horizontal axis (δ₁) and the vertical axis (δ₂) represent the effect sizes. The number of generated datasets is 100000.

Table 1.

Conditional power and predictive power with the observed effect size of (i) (0.2, 0.2), (ii) (0.1, 0.1) or (iii) (−0.01, −0.04) at 25%, 50% and 75% information time in the tarenflurbil trial.

Observed effect size	Information time	Type of power	Assumed effect size or prior	Power (%)
(i) (0.2, 0.2)	25%	CP	Observed	98.2
			Alternative	98.2
			Null	3.5
		PP	Noninformative	79.0
	50%	CP	Observed	99.6
			Alternative	99.6
			Null	32.1
		PP	Noninformative	96.0
	75%	CP	Observed	>99.9
			Alternative	>99.9
			Null	96.4
		PP	Noninformative	>99.9
(ii) (0.1, 0.1)	25%	CP	Observed	31.7
			Alternative	92.9
			Null	0.6
		PP	Noninformative	30.8
	50%	CP	Observed	32.1
			Alternative	87.1
			Null	1.7
		PP	Noninformative	31.5
	75%	CP	Observed	33.1
			Alternative	75.7
			Null	5.5
		PP	Noninformative	32.7
(iii) (−0.01, −0.04)	25%	CP	Observed	<0.01
			Alternative	74.7
			Null	<0.001
		PP	Noninformative	1.4
	50%	CP	Observed	<0.01
			Alternative	18.5
			Null	<0.01
		PP	Noninformative	<0.01
	75%	CP	Observed	<0.01
			Alternative	<0.01
			Null	<0.01
		PP	Noninformative	<0.01

Figures 3, 4 and 5 show that the timing of monitoring has an impact on the variation of the predicted treatment effects. The variation of predicted mean difference estimates are smaller with later monitoring. The range of (δ₁, δ₂) which PIs cover with high proportions is wider and that with low proportions is narrower with the monitoring at 75% information time than that at 25% or 50% information time. The timing also has an impact on the magnitude of the average PIs when the assumptions regarding effect sizes are different from those observed at the monitoring. Predicted mean difference estimates and PIs with earlier monitoring would be more sensitive to the assumption regarding the effect sizes, while the average PIs would not depend on the timing when assuming the current trend continues. Prediction would provide the information regarding an impact of the uncertainty of the interim results on the estimated treatment effects at the final analysis.

The table shows that neither CP nor PP provides the information regarding the variation of the future results. The CP varies depending on the timing of the monitoring, especially when the assumed effect sizes are different from the observed effect sizes, while neither the CP, where the observed effect sizes are assumed to be true, nor the PP, based on the noninformative prior, would not depend very much on the timing.

4. Guidance for practical use

Group-sequential designs, CP and PP are fundamental approaches for interim evaluation of efficacy and/or futility. When group-sequential designs are used in CPE clinical trials, the decisions at interim analyses are affected by the choice of boundary, and could be very conservative (i.e., early stopping is rarely allowed) with conservative boundaries such as O’Brien-Fleming type boundary (Asakura et al., 2014, 2015, 2017; Hamasaki et al., 2015).

CP and PP can provide clear information regarding statistical significance. However, CP and PP depend on the assumption regarding the effect sizes and decision-making with a futility criterion which is usually prespecified might be complex. In addition, they fail to convey information regarding clinical relevance. The prediction method can convey information regarding effect sizes and associated precision, and allow flexible decision-making for futility evaluation. They could incorporate sampling variation by predicting the future data by simulation. Assumptions regarding the treatment effects are required in order to predict the data yet to be observed, including unknown parameters or nuisance parameters such as correlations among the endpoints. Predicted effect size estimates under various assumptions should be comprehensively evaluated. This enables visualization of the sensitivity of the predicted estimates to those assumptions. Constructing predicted regions do not cause an inflation of Type I error rate and loss of power as no formal test is performed.

In contrast to traditional use of CP and PP, a decision would be made based on the predicted estimates evaluated under various assumptions. Therefore, since both of the information regarding clinical significance and statistical significance are essential for interim monitoring of clinical trials, use of prediction method in conjunction with other approaches such as group-sequential approach, CP or PP approach is recommended for better decision-making. We summarized the strengths and limitations of prediction method, CP and PP in Table 2.

Table 2.

Strengths and limitations of prediction, and conditional and predictive powers

Methods	Strengths	Limitations
Prediction	• Provides information regarding potential effect size estimates and associated precision under several scenarios • Does not cause an inflation of Type I error rate and loss of power as no formal test is performed • Can be combined with other error-spending strategies • Provides visualizations which could help to make complex scenarios more accessible, understandable and usable	• Does not provide a clear threshold for stopping a trial (e.g., stopping boundary) • Does not provide a clear value directly used for study modification (e.g., sample size recalculation)
Conditional power	• Provides clear information regarding statistical significance • Can be used for recalculating sample size	• Fails to convey information regarding clinical relevance • Incorporates only within study information • Depends on an assumption regarding effect sizes and correlation between the endpoints and thus the decision may change with them • Needs to prespecified thresholds for the decision-making
Predictive power	• Provides clear information regarding statistical significance • Can be used for recalculating sample size • Incorporates study data and prior information to make predictions	• Fails to convey information regarding clinical relevance • Depends on an assumption regarding effect sizes and correlation between the endpoints and thus the decision may change with them • Provides a incorrect prediction when prior information is misspecified • Needs to prespecified thresholds for the decision-making

When the prediction method is used for futility monitoring in clinical trials, there are the two major questions. The first one is how much data should be generated by simulation. The number of replications for simulations should be carefully chosen to control simulation error in summarizing predicted regions and related statistics, and to make the predicted region stable. Note that increasing the numbers will not change the estimates. Based on our experience, we usually construct the regions with at least 10,000 replications. However, we recommend that plots are created with a couple numbers of replications, e.g., 1,000, 10,000 and 100,000 and observe the results plotted. This could help to decide the appreciate numbers for specific situation.

The other question is what kind of scenario for mean differences could be considered. As suggested in Evans et al. (2007), the scenarios include (a) H₁ is true, (b) H₀ is true, (c) the current trend continues, or (d) best- or worst-case scenarios are true. In addition to mean differences, one may consider various assumptions regarding the predicted values of standard deviation of the difference and correlation between the endpoints. Standard deviation and correlation are not of interest as they are the nuisance parameters, but should be accounted for both hypothesis testing and confidence intervals for the parameters of interest at the final analysis. Incorporating assumptions regarding the standard deviations and correlation into the constructions of joint predicted regions (and conditional and predictive powers) could make the decision-making more complicated, especially when using observed values of standard deviations and correlation.

To avoid complicated decision-making, we may evaluate the standardized mean differences rather than non-standardized ones. As shown in Sections 2 and 3, the predicted regions using the PIs for each endpoint do not depend on the correlation. Comparing this with the other plots or related statistics could help improve decision-making. Also, as shown in Asakura et al. (2014), CP does not change appreciably with the correlation and thus there is no major advantage in recalculating the sample size with the potential correlation values when the standardized mean difference for one endpoint is 1.5 times larger than that of other. Even when the standardized mean differences are approximately equal, the effect of correlation is modest in improving CP if the two endpoints are not highly correlated (e.g., 0.8 to 1.0).

The timing of interim monitoring is an important consideration. Its impact on the operating characteristics of group-sequential methods with a single endpoint (Togo and Iwasaki, 2013; Xi et al., 2017) or co-primary endpoints (Asakura et al., 2014, 2017; Hamasaki et al., 2015) have been discussed. When the prediction method is used, the timing of interim evaluation should be carefully considered given its impact on the size and variation of the predicted mean difference estimates. Earlier monitoring would be more sensitive to the assumption regarding the effect sizes.

5. Summary

Clinical trials with CPE enable us to comprehensively evaluate an intervention’s multidimensional effect. On the other hand, such trials require larger sample sizes compared to trials with a single endpoint and require careful planning to ensure efficiency. Information during trial planning could be substantially uncertain, and some trials would fail unless the accuracy of the design assumptions is evaluated at the interim. Interim monitoring in clinical trials with CPE provides an important opportunity to evaluate whether the trial is proceeding well, examine the necessity of a change of the study plan including early stopping for efficacy or futility, recalculation of the sample size and the extension or shortening of trial duration, as is the case of trials with a single endpoint.

In this paper, as an extension of work in Evans et al. (2007) and Li et al. (2009), which serve as the basis for the software EAST PREDICT and have been used to monitor trials (e.g., Evans et al., 2007; Asakura et al., 2017), we have discussed prediction methodology to monitor CPE clinical trials, especially two endpoints being evaluated as co-primary, in contrast to CP and PP. This extension is appealing in that it provides quantitative evaluation of potential effect sizes and associated precision, with trial continuation, thus providing statisticians and investigators with a better understanding of the pros and cons associated with trial continuation. The graphical methods may also provide data monitoring committees (DMCs) with useful visual displays that could enhance their ability to make informed recommendations.

In this paper, we have discussed the most fundamental situation where continuous outcomes are as parameters of interest and the number of endpoints is two. In some disease areas, however, binary endpoints or time-to-event endpoints are employed as CPE. In trials with irritable bowel syndrome, for example, proportions of patients with adequate improvement in abdominal pain intensity and stool frequency or stool consistency are evaluated. Time-to-event endpoints are common in oncology trials with overall survival and time to progression or progression free survival, for example. Our approach using prediction is applicable to other endpoint scales including binary and time-to-event endpoints in a straightforward way, by predicting the future data. In the single endpoint setting, Evans et al. (2007) and Li et al. (2009) discussed constructing PIs on binary or time-to-event endpoint scales, and it could be extended to the CPE case. On the other hand, how to define the association among binary or time-to-event endpoints is more complicated than that with continuous endpoints. As discussed in Hamasaki et al. (2013) and Sugimoto et al. (2013, 2017, 2019), characteristics of the dependence and censoring scheme among the endpoints should be carefully considered for time-to-event endpoints. When incorporating censoring scheme such as competing risks into prediction, even PIs for each endpoint could depend on the correlations among endpoints unlike the case of continuous endpoints. Evans et al. (2007) discussed two more aspects of constructing PIs for time-to-event endpoints. One is that censoring due to loss-to-follow-up or the timing of the interim monitoring should be considered distinctively for simulating the future data. The latter kind of censored values need to be predicted, while the former censored values would never be observed. The other is that one has an option to evaluate the additional precision with extension of the duration of follow-up or the decrease in precision with a shortening of follow-up by comparing PIs based on the extended or shortened trial duration and planned trial duration.

In some disease areas such as migraine pain, co-primary endpoints are required to evaluate the treatment effects. While we have considered the situation with two CPE, the prediction methods discussed in this paper can be extended to any number of endpoints. The application of the graphics introduced in this paper, on the other hand, would require creativity.

While we have mainly focused on futility evaluation in this paper, prediction could be utilized to evaluate efficacy with appropriate consideration regarding Type I error rate control. For example, use of repeated confidence intervals, discussed in Jennison and Turnbull (1989) in conjunction with PIs would be an option to control Type I error rate.

Appendix A1: Coverage probability of average predicted intervals

Coverage probability of predicted intervals could be higher or lower than their confidence level. Table A1 displays the conjunctive coverage probabilities and the marginal coverage probabilities of average PIs for two endpoints. The number of replications for evaluation by Monte-Carlo simulation is 100,000. Coverage probability is higher as the correlation among the endpoints increases. Coverage probabilities are lower than the confidence level of 95% when the observed effect sizes are assumed to be correct. Coverage probabilities are close to 1 when the assumed effect sizes are correct, and much lower, when the true effect size is zero for both endpoints even though PIs are calculated under the planned effect size.

Table A1.

Conjunctive and marginal coverage probabilities of average 95% predicted intervals calculated under the assumption where the planned effect size of 0.2 for both of the two endpoints or the observed effect size is true at the interim monitoring at 50% information time. The planned sample size of 516 is calculated based on a one-sided test with targeted power of 80% at the significance level of 2.5%, assuming no correlation between the endpoints.

True effect size	ρ	Conjunctive coverage probability (marginal)
		Planned effect size	Observed effect size
(0.2, 0.2)	0.0	0.989 (0.995)	0.697 (0.834)
	0.3	0.990 (0.995)	0.705 (0.835)
	0.5	0.989 (0.994)	0.720 (0.835)
	0.8	0.991 (0.995)	0.757 (0.833)
	0.99	0.994 (0.995)	0.818 (0.835)
(0.1, 0.1)	0.0	0.900 (0.949)	0.694 (0.833)
	0.3	0.905 (0.949)	0.704 (0.834)
	0.5	0.911 (0.950)	0.720 (0.835)
	0.8	0.923 (0.949)	0.757 (0.834)
	0.99	0.944 (0.950)	0.817 (0.835)
(0.0, 0.0)	0.0	0.479 (0.692)	0.696 (0.834)
	0.3	0.517 (0.691)	0.704 (0.834)
	0.5	0.547 (0.691)	0.719 (0.834)
	0.8	0.601 (0.691)	0.760 (0.836)
	0.99	0.674 (0.693)	0.819 (0.836)

Appendix A2: Steps to construct a joint predicted region for both endpoints and predicted regions using PI for each endpoint by generating the future data

Step 1: Generate the data yet to be observed based on the bivariate normal distributions (N₂(μ_T, Σ)) and (N₂(μ_C, Σ)) based on assumptions regarding the mean differences, the common variance and the correlation between the endpoints.

Step 2: Calculate (i) the predicted mean difference estimate ${\tilde{\delta }}_k$, as the weighted average of the observed mean difference ${\widehat{\delta }}_{k1}$ at interim and the predicted mean difference ${\tilde{\delta }}_{k2}$ based on the generated data, and (ii) the joint predicted region for both endpoints and/or predicted regions using PI for each endpoint, satisfying

$${(\tilde{\mathit{\delta }}-\mathit{\delta })}^{\text{T}}{\tilde{\mathit{V}}}^{-1}(\tilde{\mathit{\delta }}-\mathit{\delta })\le \frac{2(1+r)n}{r{n}^2}\frac{(1+r)n-2}{(1+r)n-3}{F}_{2,(1+r)n-3}(\alpha )$$

and

$${\tilde{\delta }}_k-{\delta }_k\le t_{(1+r)n-2}(\alpha /2)\sqrt{\frac{(1+r)}{rn}}{\tilde{s}}_k,$$

respectively, where k = 1,2, $\tilde{\delta }=({\tilde{\delta }}_1,{\tilde{\delta }}_2)$, $\tilde{\mathit{V}}=({\tilde{s}}_1^2,{\tilde{s}}_2^2)$, ${\tilde{s}}_k$ is the predicted standard deviation, F_2,(1+r)n−3(α) is the upper 100αth percentile of the F-distribution with (2, (1 + r)n − 3) degrees of freedom and t_(1+r)n−2(α/2) is the upper 100(α/2)th percentile of the t-distribution with (1 + r)n − 2 degrees of freedom.

Step 3: Repeat Steps 1 and 2 many times and visualize the calculated predicted mean difference estimates and predicted regions, and summarize them by taking means or medians of them.