Machine learning–based prediction of transfusion

Abstract

Background

The ability to predict transfusions arising during hospital admission might enable economized blood supply management and might furthermore increase patient safety by ensuring a sufficient stock of red blood cells (RBCs) for a specific patient. We therefore investigated the precision of four different machine learning–based prediction algorithms to predict transfusion, massive transfusion, and the number of transfusions in patients admitted to a hospital.

Study Design and Methods

This was a retrospective, observational study in three adult tertiary care hospitals in Western Australia between January 2008 and June 2017. Primary outcome measures for the classification tasks were the area under the curve for the receiver operating characteristics curve, the F₁ score, and the average precision of the four machine learning algorithms used: neural networks (NNs), logistic regression (LR), random forests (RFs), and gradient boosting (GB) trees.

Results

Using our four predictive models, transfusion of at least 1 unit of RBCs could be predicted rather accurately (sensitivity for NN, LR, RF, and GB: 0.898, 0.894, 0.584, and 0.872, respectively; specificity: 0.958, 0.966, 0.964, 0.965). Using the four methods for prediction of massive transfusion was less successful (sensitivity for NN, LR, RF, and GB: 0.780, 0.721, 0.002, and 0.797, respectively; specificity: 0.994, 0.995, 0.993, 0.995). As a consequence, prediction of the total number of packed RBCs transfused was also rather inaccurate.

Conclusion

This study demonstrates that the necessity for intrahospital transfusion can be forecasted reliably, however the amount of RBC units transfused during a hospital stay is more difficult to predict.

Abbreviations

AP

average precision

AUC

area under the receiver operating characteristic curve

CCI

Charlson Comorbidity Index

DRG

diagnosis‐related group

FFP

fresh frozen plasma

GB

gradient boosting

Hb

hemoglobin

LR

logistic regression

NNs

neural networks

PBM

patient blood management

RBC

red blood cell

RFs

random forests

RMSE

root mean squared error

ROC

receiver operating characteristic

1. INTRODUCTION

Due to the implementation of patient blood management (PBM) ¹ in the past few years, the number of transfusions is decreasing in most developed countries. ² Although most, if not all, patients benefit from the implementation of PBM, ³ it can be speculated that there are certain patient populations in whom applying the principles of PBM has a more pronounced influence on outcome. Presumably, the patients who benefit most from a PBM program are those who are most likely to undergo transfusion in the course of the hospital stay. ⁴ These are typically those patients who either suffer bleeding or encounter anemia around their hospitalization. Many of them might have better outcomes if the triad of anemia, bleeding, and transfusion could be avoided or treated properly. ³ In this context, transfusion can therefore be seen as a consequence of the combination of anemia and blood loss in many cases, and thus can be used retrospectively as an indicator to identify those patients, who have the highest necessity to focus on bleeding, anemia, and transfusion, to avoid each of these. ⁵ Purposeful application of PBM is possible, and special efforts can be delivered to this patient group with the aim to avoid the triad of anemia, bleeding, and transfusion.

Furthermore, the proper identification of patients who need a transfusion of RBCs could help blood suppliers to improve the supply of blood products ⁶ for the hospital. Both the provision of too much blood and the provision of too little blood are either expensive and unnecessary or dangerous for the safety of the patient. Therefore, prediction of transfusion needs might also help to economize the supply chain of blood providers. ⁷

There are several publications that describe the influencing factors on perioperative transfusion, ⁸ , ⁹ , ¹⁰ but to date only small studies exist ¹¹ , ¹² , ¹³ that evaluate a multimodal, machine learning–based prediction model in a large jurisdictional cohort. Therefore, it is the aim of this study to evaluate a machine learning–based prediction model, based on a large cohort, and to test this model by cross validation. We hypothesize that modern machine learning tools can predict the necessity for transfusion reliably and thus help to identify the patient group that might benefit from a PBM program the most.

2. MATERIAL AND METHODS

This is a multicentric, retrospective study with one cohort. The data included in this study were sourced from the Western Australia PBM data system. This system consolidates data from five core hospital information systems: patient administration, laboratory, transfusion medicine, theater management, and emergency department. Details of the linking are published elsewhere. ³ The study included all emergency and elective multiday‐stay inpatients aged 18 years and older who were admitted to the three adult tertiary care hospitals in Western Australia between January 2008 and June 2017. The data are not restricted to a few specific specialties but contain 74 different ones, from which the top 10 were hematology, tracheostomy, general surgery, gastroenterology, orthopedics, cardiothoracic surgery, trauma, vascular surgery, urology, and cardiology.

The study was reviewed by the Royal Perth Hospital Human Research Ethics Committee and received institutional approval from the three sites involved. An overview of the most important demographic and preoperative data included are presented in Table 1. In this table, mean values are provided for numerical features along with standard deviations shown in parentheses. In total, the data consisted of 233 577 hospital stays from 144 420 unique patients.

TABLE 1.

Demographic data

Variable	All patients N = 206 271 (100%)	Had no RBC transfusion n = 180 615 (87.6%)	Had RBC transfusion n = 25 656 (12.4%)	Had transfusion but no massive transfusion n = 24 688 (12.0%)	Had massive transfusion n = 968 (0.4%)
Patients, n (%)
Hospital 1	60 246 (29.2)	53 085 (29.4)	7161 (2.8)	6943 (28.1)	218 (22.5)
Hospital 2	29 832 (14.5)	25 986 (14.4)	3846 (1.5)	3752 (15.2)	94 (9.7)
Hospital 3	116 193 (56.3)	101 544 (56.2)	14 649 (5.7)	13 993 (56.7)	656 (67.8)
Specialty, n (%)
General surgery	47 471 (23.0)	43 411 (24.0)	4060 (15.8)	3737 (15.1)	323 (33.4)
General medicine	37 510 (18.2)	32 286 (17.9)	5224 (20.4)	5109 (20.7)	115 (11.9)
Orthopedics	29 449 (14.3)	25 348 (14.0)	4101 (16.0)	4054 (16.4)	47 (4.9)
Cardiology	27 699 (13.4)	26 159 (14.5)	1540 (6.0)	1445 (5.9)	95 (9.8)
Other	64 142 (31.1)	53 411 (29.6)	10 731 (41.8)	10 343 (41.9)	388 (40.1)
Age, y, median (range)	65 (48‐78)	65 (47‐78)	70 (56‐81)	71 (56‐81)	60 (76‐43)
Sex, n (%)
Female	90 213 (43.7)	78 625 (43.5)	11 588 (45.2)	11 317 (45.8)	271 (28.0)
Male	116 058 (56.3)	101 990 (56.5)	14 068 (54.8)	13 371 (54.2)	697 (72.0)
Charlson comorbidity index	0 (0/1)	0 (0/1)	1 (0/3)	1 (0/3)	1 (0/3)
Length of stay, d, median (range)	4 (3‐8)	4 (2‐7)	9 (2‐19)	9 (5‐19)	19 (9‐35)
Length of stay ICU, h, median (range)	0 (0‐0)	0 (0‐0)	0 (0‐0)	0 (0‐0)	90 (24‐216)
Anemia at admission
None	120 425	116 193	4232	3963	269
Mild	39 871	36 066	3805	3598	339
Severe	7354	862	6492	6339	153
Hemoglobin concentration admission, g/dL, median (range)	12.9 (11.2‐14.3)	13.2 (11.7‐14.5)	9.5 (7.9‐11.5)	9.4 (7.9‐11.5)	10.9 (8.9‐12.9)
RBC transfusion, median (range)	0 (0‐0)	0 (0‐0)	2 (2‐4)	2 (2‐4)	11 (5‐17)
Cryo transfusion, median (range)	0 (0‐0)	0 (0‐0)	0 (0‐0)	0 (0‐0)	4 (0‐9)
FFP transfusion, median (range)	0 (0‐0)	0 (0‐0)	0 (0‐0)	0 (0‐0)	6 (2‐10)
Platelet transfusion, median (range)	0 (0‐0)	0 (0‐0)	0 (0‐0)	0 (0‐0)	1 (0‐3)
Complications
Postprocedural	14 353	9220	5133	4655	478
Infections	2704	1278	1426	1318	108
Cardiovascular	14 401	9529	4872	4507	365
Respiratory	7358	4564	4564	2556	238
Gastrointestinal	7815	7815	2794	2484	174
Genitourinary	7237	5157	2658	2374	191
Hematological	4350	866	3484	3253	231
Mortality (%)	2.2	1.6	6.4	5.9	18.1

Note: Demographic parameters of patients included.

The data preprocessing and cleaning was done as following:

1. We removed patients for whom the hemoglobin (Hb) at admission time was missing. Additionally, patients with unknown sex and patients with unusual admission dates were removed. This left us with 206 271 stays from 131 041 unique patients.

2. We removed variables that contain information collected after admission, as we wanted to develop a predictive model at admission time at the hospital. Further, all variables containing free text were removed, since we could not use them easily for our prediction. This led to the following 21 features remaining: age at admission, sex, elective/nonelective, primary diagnosis code, secondary diagnosis codes, diagnosis‐related group (DRG) code, Charlson Comorbidity Index (CCI), admission Hb level (g/L), had any transfusion (red blood cells [RBCs], fresh frozen plasma [FFP], platelets, cryoprecipitate), had RBC transfusion, had massive transfusion, total number of cryoprecipitate units transfused, total number of plasma units transfused, total number of platelet units transfused, total number of RBC units transfused, in‐hospital mortality.

3. We encoded the year of the admission as an additional numerical feature, as the transfusion consumption became less over time.

4. We standard normalized all numerical variables (eg, age at admission, admission Hb, etc.).

5. The primary diagnosis code, given as an International Classification of Diseases, Revision 10 code, was split, and only the first part of the code was used as an additional feature.

6. If the primary or secondary diagnosis code occurred in <0.1% of the records (fewer than 206 occurrences in the data set), they were set to category “minor.”

7. Afterwards, all categorical features were one‐hot encoded. One‐hot encoding is a widely used encoding scheme. It works by creating a column for each category present in the feature and assigning a 1 or 0 to indicate the presence of a category in the data. The final data set had 1357 columns.

We chose the occurrence of RBC transfusion (binary outcome, classification) and the occurrence of massive transfusion (binary outcome, classification) as classification targets. Massive transfusion was defined as transfusion of at least 10 RBCs within 24 hours during hospital stay. For the two classification scenarios, we employed the model selection procedure for four state‐of‐the‐art machine learning methods: logistic regression (LR), random forests (RFs), ¹⁴ artificial neural networks (NNs), ¹⁵ and gradient boosting (GB). ¹⁶ Additionally we predicted the number of RBC transfusions (integer outcome).

To investigate the ability of machine learning to learn these outcomes, the following model selection procedure was performed: from the cohort we set aside 10% of the data for parameter tuning (20 461 rows; 13 104 unique patients). The remaining 90% of the data was used for training and test set using fivefold cross validation to assess each methodʼs ability to generalize to previously unseen cases. If a patient had several hospital admissions, then all of the admissions of this person were either solely attributed to the training or the test set. This is necessary to avoid overestimation of the model’s ability to generalize to previously unseen data. The procedure was performed for all five folds. The best hyperparameters for our methods were chosen by an extensive random search (see Appendix S1 A and B, available as supporting information in the online version of this paper).

For the classification task, the models were evaluated on the following criteria: balanced accuracy, area under the receiver operating characteristics [ROC] curve (AUC), precision (also known as positive predictive value, recall, F₁ score, and average precision (AP; the area under the precision recall curve). We fixed the decision threshold to the value that maximized the F₁ score, which is the harmonic mean between precision and recall. The F₁ score was chosen here due to its robustness to class imbalance (assigning all patients to the larger class would result in a very high accuracy but a very low sensitivity).

Additionally, we predicted the number of RBC transfusions using four different regression models: RFs, artificial NNs, Huber regression,¹⁷ and GB. We predicted the number of transfusions for each patient individually for those patients who received at least one RBC transfusion. To estimate the quality of methods, a linear regression between the number of RBC transfusions predicted and the number of RBC transfusions actually administered has been performed. We calculated the root mean squared error (RMSE) and the R ² score.

3. RESULTS

Overall, 206 271 inpatient admissions were included in the final data set of our 10‐year study. An overview of the demographic data is given in Table 1. The median patient age was 65 years (interquartile range, 30 y), and 43.7% of patients were women. Of these admissions, 12.4% of patients received at least 1 unit of RBCs. In total, 93 375 units of RBCs, 24 662 units of cryoprecipitate, 26 016 units of FFP, and 19 384 units of platelets were transfused. In the group of patients who received at least 1 unit of RBCs, the median number of RBCs transfused was 2. The median of all other components (cryoprecipitate, FFP, platelets) in this group was 0, indicating that typically 2 RBCs were administered with the aim to increase Hb concentration, rather than to treat acute bleeding with concomitant coagulopathy in most of the cases. Only 0.5% of all patients underwent massive transfusion. In these, a median of 11 RBC units, 4 cryoprecipitate units, 6 FFP units, and 1 unit of platelets were transfused.

Using our four predictive models, transfusion of at least 1 unit of RBCs could be predicted rather accurately. Using NNs, LR, RFs, and GB the AUCs were 0.966, 0.965, 0.963, and 0.966, respectively. The F₁ scores were 0.749, 0.748, 0.743, and 0.755, respectively, and the corresponding average precision values were 0.828, 0.820, 0.821, 0.835, respectively (for details see Table 2 and Figure 1). The features overall that were most important (details of how the importance of features were calculated can be found in Appendix S1 C, available as supporting information in the online version of this paper) for prediction of transfusion of at least 1 unit of RBCs were the Hb at admission, the age of the patient and the CCI (see Table 3). The CCI predicts the 1‐year mortality for a patient who may have a range of comorbid conditions.

TABLE 2.

Prediction of transfusion

Method	AUC	AP	BA	Sens	Spec	Prec	NPV	F1
Neural network	0.966 (± 0.004)	0.828 (± 0.012)	0.870 (± 0.008)	0.898 (± 0.007)	0.958 (± 0.009)	0.719 (± 0.022)	0.970 (± 0.006)	0.749 (± 0.006)
Logistic regression	0.965 (± 0.005)	0.820 (± 0.011)	0.856 (± 0.006)	0.894 (± 0.012)	0.966 (± 0.009)	0.749 (± 0.008)	0.966 (± 0.004)	0.748 (± 0.010)
Random forest	0.963 (± 0.004)	0.821 (± 0.011)	0.858 (± 0.004)	0.584 (± 0.006)	0.964 (± 0.006)	0.737 (± 0.011)	0.966 (± 0.006)	0.743 (± 0.006)
Gradient boosting	0.966 (± 0.003)	0.835 (± 0.013)	0.864 (± 0.008)	0.872 (± 0.006)	0.965 (± 0.005)	0.747 (± 0.025)	0.968 (± 0.007)	0.755 (± 0.007)

Note: Statistical parameters of the prediction of transfusion vs no transfusion by different models.

Abbreviations: AP, average precision; AUC, area under the receiver operating characteristic curve; BA, balanced accuracy; F₁, harmonic mean of precision and recall; NPV, negative predictive value; Prec, precision or positive predictive value; Sens, sensitivity; Spec, specificity.

The bold values is the highest (best) for each method respectively.

FIGURE 1.

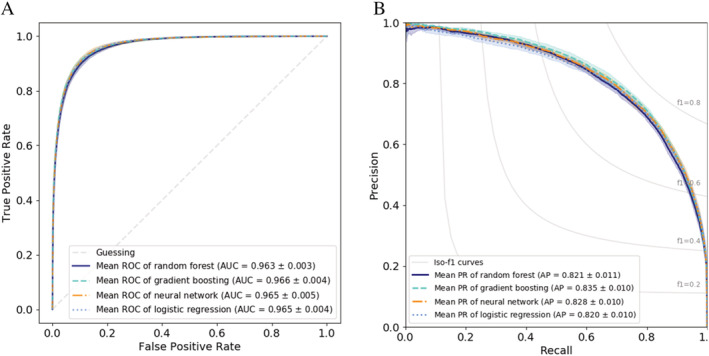
Transfusion of at least 1 RBC unit. Transfusion of at least 1 RBC unit. A, ROC curves for the different methods. B, Precision‐recall curve for the different methods [Color figure can be viewed at wileyonlinelibrary.com]

TABLE 3.

Feature importance for transfusion

Rank	Random forest		Gradient boosting		Logistic regression
	Feature	Importance	Feature	Importance	Feature	Importance
1	Hb at admission	137.95	Hb at admission	157.49	Hb at admission	32.43
2	Secondary diagnosis code D64.9: Anemia, unspecified	49.09	Age	101.28	Secondary diagnosis code D64.9: Anemia, unspecified	14.50
3	Age	36.53	CCI	33.03	DRG F10B: Interventional coronary procedures	10.34
4	Secondary diagnosis code D50.0: Iron deficiency	26.04	Secondary diagnosis code D64.9: Anemia, unspecified	15.54	Secondary diagnosis code D50.0: Iron deficiency	9.32
5	CCI	18.31	Hb at admission grouped	12.82	Secondary diagnosis code D62: Acute posthemorrhagic anaemia	6.90
6	Secondary diagnosis code D62: Acute posthemorrhagic anaemia	16.62	Sex	11.53	DRG minor class	6.52
7	Sex	10.16	Secondary diagnosis code Y92.22: Health service area	10.88	DRG F41B: Circulatory disorders, Adm	5.69
8	Secondary diagnosis code D63.0: Anemia neuroplastic disease	7.36	Admission year 8	8.03	DRG I68B: Nonsurgical spinal disorders, minor complexity	5.67

Note: Feature importance for transfusion of at least 1 RBC unit for random forest, gradient boosting, and logistic regression. Details of how the importance of features was calculated can be found inAppendix S1 C, available as supporting information in the online version of this paper.

Abbreviations: CCI, Charlson Comorbidity Index; DRG, diagnosis‐related group; Hb, hemoglobin.

Use of the four methods of predicting massive transfusion was less successful. Although the AUC values of the ROC analysis were quite high (0.945, 0.949, 0.932, 0.947, respectively), the AP values were rather low (0.162, 0.176, 0.174, 0.184, respectively) due to the asymmetric nature of this prediction task (Table 4 and Figure 2). The features overall that were most important for prediction of transfusion were also not that clear anymore (Table 5).

TABLE 4.

Prediction of massive transfusion

Method	AUC	AP	BA	Sens	Spec	Prec	NPV	F1
Neural network	0.945 (± 0.014)	0.162 (± 0.028)	0.656 (± 0.034)	0.780 (± 0.049)	0.994 (± 0.002)	0.206 (± 0.060)	0.997 (± 0.001)	0.245 (± 0.046)
Logistic regression	0.949 (± 0.012)	0.176 (± 0.021)	0.645 (± 0.042)	0.721 (± 0.055)	0.995 (± 0.002)	0.211 (± 0.032)	0.997 (± 0.000)	0.241 (± 0.031)
Random forest	0.932 (± 0.018)	0.174 (± 0.031)	0.671 (± 0.030)	0.002 (± 0.003)	0.993 (± 0.002)	0.191 (± 0.025)	0.997 (± 0.000)	0.244 (± 0.026)
Gradient boosting	0.947 (± 0.013)	0.184 (± 0.037)	0.661 (± 0.038)	0.797 (± 0.055)	0.995 (± 0.002)	0.238 (± 0.038)	0.997 (± 0.000)	0.269 (± 0.039)

Note: Statistical parameters of the prediction of massive transfusion vs no massive transfusion by different models.

Abbreviations: AP, average precision; AUC, area under the receiver operating characteristic curve; BA, balanced accuracy; F₁, harmonic mean of precision and recall; NPV, negative predictive value; Prec, precision or positive predictive value; Sens, sensitivity; Spec, specificity.

The bold values is the highest (best) for each method respectively.

FIGURE 2.

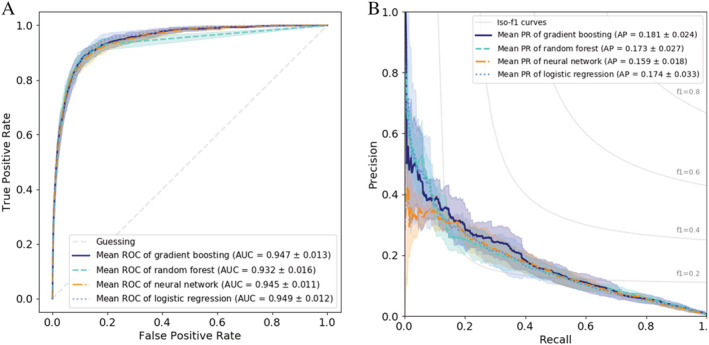
Massive transfusion. Prediction of massive transfusion. A, ROC curves for the different methods. B, Precision‐recall curve for the different methods [Color figure can be viewed at wileyonlinelibrary.com]

TABLE 5.

Feature importance for massive transfusion

Rank	Random forest		Gradient boosting		Logistic regression
	Feature	Importance	Feature	Importance	Feature	Importance
1	Hb at admission	73.38	Hb at admission	111.55	DRG: Uncommon group	7.79
2	Age	37.01	Age	77.77	Primary diagnosis code: Uncommon diagnosis	5.94
3	Secondary diagnosis code D62: Acute posthemorrhagic anemia	26.09	CCI	30.64	Secondary diagnosis Z72.0: Tobacco use	5.79
4	CCI	23.62	DRG minor class	22.00	Secondary diagnosis code U73.9: Unspecified activity	5.28
5	Secondary diagnosis code T81.0: Hemorrhage	22.22	Secondary diagnosis T81.0: Hemorrhage	18.07	Hb at admission	5.27
6	DRG: Uncommon group	20.68	Secondary diagnosis D62: Acute posthemorrhagic anemia	17.28	DRG F62B: Heart failure and shock …	5.19
7	DRG A06B: Tracheostomy …	18.25	Primary diagnosis code: Uncommon diagnosis	15.71	Age	4.99
8	DRG: Uncommon group	17.47	Sex	14.93	DRG F62A: Heart failure and shock …	4.67

Note: Feature importance for massive transfusion for random forest, gradient boosting, and logistic regression. Details of how the importance of features was calculated can be found in Appendix S1 C, available as supporting information in the online version of this paper.

Abbreviations: CCI, Charlson Comorbidity Index; DRG, diagnosis‐related group; Hb, hemoglobin.

Since prediction of massive transfusion is not reliable with the features available, it is also not surprising that the prediction of the number of RBCs transfused was unsatisfactory. Depending on the model used, the R ² score was 0.152 for NNs, 0.122 for Huber regression, 0.137 for ordinal regression, 0.135 for RFs, and 0.176 for GB, with RMSE of 16.549, 17.140, 16.890, and 16.094, respectively, for each of these models (Table 6), indicating that the actual number of transfusions cannot be predicted accurately with the features used.

TABLE 6.

Prediction of number of RBCs transfused

Method	RMSE	R 2
Baseline: Mean	19.533 (± 1.488)	0.000 (± 0.000)
Baseline: Median	22.236 (± 1.273)	−0.140 (± 0.022)
Neural network	16.549 (± 1.200)	0.152 (± 0.008)
Huber regression	17.140 (± 1.379)	0.122 (± 0.009)
Random forest	16.890 (± 1.295)	0.135 (± 0.004)
Gradient boosting	16.094 (± 1.344)	0.176 (± 0.014)

Note: Statistical parameters of the prediction of the number of RBCs transfused by different models.

Abbreviations: MAE, mean absolute error; RMSE, root mean square error; R ², coefficient of determination.

4. DISCUSSION

Predicting the number of patients transfused during their hospital stay will likely be useful for two different reasons. First of all, it enables reliable management of the supply chain for allogeneic blood, ⁶ , ⁷ but more importantly, it also could help to classify the risk profile of an individual patient to undergo transfusion, ¹¹ pointing out the necessity in this specific patient to implement the measures of PBM as thoroughly as possible. However, at the time point of hospital admission, only a very low number of features is known that could help to predict the necessity for transfusion in the following time course. Using modern machine learning tools, we could reliably predict which patients will be in need for transfusion of RBCs with a manageable number of features provided at hospital admission. In contrast to other studies, we did not restrict prediction to one patient group, like others have done ¹⁸ , ¹⁹ but provided a model that can be used over a broad range of indications. However, although this prediction has proven to be very reliable for classification of “transfusion” vs “no transfusion,” we found out for our database that the total number of RBC transfusions per patient and the occurrence of massive transfusion in a specific patient cannot be predicted reliably, a phenomenon that has been described in liver transplantations by other groups. ²⁰ This is (a) mainly due to the strong asymmetry of this classification task, and (b) likely due to the fact that the features containing the necessary information are probably not part of our data set. It can be speculated that the reasons for massive transfusion mainly do not occur before the treatment process has started, and therefore it will be impossible to predict massive transfusion in advance. Furthermore, the influencing factors for the number of RBCs necessary might not be known at the time point of prediction.

Modern methods of machine learning have the potential to revolutionize prediction tasks in many areas of daily life, especially in the medical field. ²¹ Whereas a few years ago it was possible to perform linear categorization tasks only with the help of LR models, nowadays many nonlinear relationships can also be described reliably with the help of modern methods of machine learning, for example, decision trees or NNs. However, the accuracy of these modern methods outperforms the classical approach significantly only if the underlying data cannot be described linearly. ²² In our data set, the application of a LR model already led to surprisingly good results for the classification task of transfusion vs no transfusion.

Depending on the outcome parameters, the best prediction performance was achieved by GB, which is reflected by the high AUC, the high precision recall values, and the best F₁ score. This makes GB a valuable tool for our clinical setting, although it must be stated that the other methods were just slightly worse and that there is no clear winner regarding the different machine learning methods.

In addition to the very high negative predictive value, which was delivered by all methods, the acceptable positive predictive value of all methods plays an important role for our clinical scenario. In >70% of the cases where the model predicts that transfusion will be administered, the patient will actually be transfused. In >99.5% of cases where the model indicates that a transfusion would not be administered, the patient will actually not be transfused.

This mathematical selectivity can be used for different clinical situations. First of all, using our GB model transfusion probability could be calculated for every hospital admission after first blood sampling. Currently, patients are mainly allocated to a PBM program in the lead‐up to a surgical procedure, whereas medical patients are often ignored. ²³ However, this approach neglects the potential to identify all patients (including those not in the lead‐up to a surgical procedure) that could benefit from initiation of PBM. Surprisingly, admission type (elective or nonelective) and DRG code do not play the most dominant role in our model, indicating that surgery is only one contributing factor for transfusion needs. Although PBM should not be seen as a measure initiated only in a specific group of (surgical) patients but more as a general paradigm to treat all patients, it seems advisable that the patients with the highest risk for transfusion are identified in advance of the hospital stay to take necessary measures.

The three features found to be most important in our model are the Hb at admission, the patientʼs age, and the CCI score. It is well known that these three features can play an important role for the prediction of transfusion in the clinical setting, ²⁴ but we achieved the best classification results using modern machine learning tools. Of note, all publications describing prediction of transfusion so far deal with specific clinical situations, mainly total hip or total knee replacement. Classification quality of these models is generally below our model, despite the fact that in these publications more specific features could be used due to the uniform preparation of these specific patient groups.

We also trained LR models with features we identified as the most important (Hb at admission, age, and CCI) to check if additional features significantly help or not. The additional features are indeed very helpful and the results of this ablation study can be found in Appendix S1 D, available as supporting information in the online version of this paper.

The strength of our prediction model is the high number of patients that could be used for the training process. To our knowledge, this is one of the biggest data sets that has been used for such a task in a general hospital population. Furthermore, we used data from three different centers. Most of the other publications use typically smaller data sets from one center in specific clinical situations. Therefore, our predictive model can be used in a huge number of clinical scenarios without the necessity to be adapted to a new training set. Our training set is from Western Australian hospitals that implemented PBM during the data collection time period. ³ As a consequence, PBM measures might play a minor role at the beginning of data collection and might play a bigger role at the end. Therefore, we cannot exclude some time series effects that might occur during the collection phase from 2008 to 2017. We used the year of admission as a feature, since for later usage of our model every newly included patient will have a higher year of inclusion than all the patients of the training set. However, this fact most likely reflects daily clinical practice nowadays, since nearly all hospitals are in the process of implementation of PBM at the moment, and therefore transfusion habits might change over time generally. As a consequence, we cannot exclude that our model will have worse results for prediction of transfusion needs in the three Australian centers beginning in a few years, when PBM is implemented thoroughly throughout all of the hospitals.

We used only a very narrow feature set that is available at hospital admission. This approach enables transferability of our model to other hospitals. The drawback of this approach is restricted precision of our model due to some missing features that might help to identify patients at risk for transfusion. However, we cannot deduce from our results that any of the predicted transfusions could be avoided by alternative treatment. Therefore, at this stage clinical applicability is somewhat reduced, since the help of any additional efforts to reduce the risk of bleeding, anemia, and transfusion is unclear.

We used four different prediction models for our investigation. LR was used as the “gold standard” of classification tasks. RFs, GB, and NNs were used as the more modern competitors that also enable out‐of‐the‐box nonlinear modeling. These tools have been demonstrated to be very successful for prediction purposes in the medical field. However, there are also other methods that have not been used in our study and could outperform our results.

5. CONCLUSION

With use of modern machine learning algorithms, transfusion can be predicted reliably at the time point of hospital admission. Prediction of the amount of RBCs transfused or prediction of massive transfusion was less successful. Having the knowledge of which patients are at risk for anemia, bleeding, and transfusion after admission might help in the future to improve their treatment and outcome.

Supporting information

Appendix S1. Supporting Information.

Mitterecker A, Hofmann A, Trentino KM, et al. Machine learning–based prediction of transfusion. Transfusion. 2020;60:1977–1986. 10.1111/trf.15935