Abstract
The OSIRIS‐REx mission has observed multiple instances of particles being ejected from the surface of near‐Earth asteroid (101955) Bennu. The ability to quickly identify the particle trajectories and origins is necessary following a particle ejection event. Using proven initial orbit determination techniques, we can rapidly estimate particle trajectories and ejection locations. We present current results pertaining to the identification of particle tracks, an evaluation of the estimated orbits and the excess velocity necessary to induce the particle ejection from the surface, and the uncertainty quantification of the ejection location. We estimate energies per particle ranging from 0.03 to 11.03 mJ for the largest analyzed events and velocities ranging from 5 to 90 cm/s, though we exclude the highest‐velocity particles in this technique. We estimate ejection times for eight events and constrain six of the analyzed ejection events to have occurred between about 16:30 and 19:00 local solar time, with the largest events occurring between 16:30 and 18:05.
Keywords: active asteroids, particle ejection events, Bennu ejection activity, particle trajectory reconstruction
Key Points
We present orbit determination techniques used to reconstruct particle ejections from near‐Earth asteroid Bennu
We estimate energies per particle ranging from 0.03 to 11.03 mJ and velocities ranging from 5 to 90 cm/s for the largest analyzed events
We find ejection times between about 16:30 and 19:00 local solar time for most events analyzed
1. Introduction
Orbital A, the first orbital campaign around Bennu by the OSIRIS‐REx (Origins, Spectral Interpretation, Resource Identification, and Security‐Regolith Explorer) mission, began on 31 December 2018. After a week of orbital operations, optical navigation (OpNav) images revealed particles emanating from the surface of Bennu (Hergenrother et al., 2019; Lauretta et al., 2019). Initial assessments were made of the risk to the spacecraft in an active environment, and the orbital campaign continued. The observation cadence was modified to better detect potential future events and study the phenomena. Detailed Survey, a set of 14 hyperbolic science flybys spanning close approaches ranging between 3 and 5 km at multiple solar longitudes, provided the detection of the next major particle event, which occurred in April 2019. Multiple ejection events have since been observed over the course of multiple mission phases and heliocentric distances, showing particles being ejected from the surface of Bennu with a range of velocities, inducing hyperbolic or ballistic trajectories, with some particles entering short‐lived orbits lasting several days (Lauretta et al., 2019).
Ejection events originating from Bennu's surface can be tracked over the course of several images in many cases thanks to dedicated particle imaging at high frequency. Highly energetic events eject particles that are captured in only a minimal set of images due to the high velocity of the particles relative to the image frequency. At least two successive images are required to obtain initial estimates of the origin of the event (Pelgrift et al., 2020). These short‐arc data sets are enhanced when particles are “streaked” in a single exposure. Streaked particles can be used in cases where two images of an individual particle are not available. However, more accurate estimates of the particle's distances and velocities are acquired when particles can be tracked across three or more images, using angles‐only initial orbit determination (IOD) techniques, as we show here.
The use of optical images for angles‐only IOD is widely applied in the determination of celestial orbits as well as in the space situation awareness (SSA) community (Gauss, 1963; Gibbs, 1889; Schaeperkoetter & Mortari, 2011; Taff, 1984). Short‐arc IOD techniques have successfully been utilized in the determination of asteroid ephemerides (Bowell et al., 2002; Chesley, 2004; Gronchi, 2004). These techniques have been expanded from traditional angles‐only IOD to include admissible region constraints on the orbit solution due to limited amounts of information from short‐arc data sets (Gronchi, 2004; Milani et al., 2004, 2005; Spoto et al., 2018). Short‐arc angles‐only asteroid orbit determination utilizes ground‐based measurements. The SSA community has expanded IOD techniques to the use of space‐based imaging platforms (DeMars et al., 2009; Hussein et al., 2014; Kaya & Snow, 1991; Snow & Kaya, 1992). Charlier (1910, 1911) postulated four potential solutions to the IOD problem using angles‐only observations regardless of the location of the observer. Wie and Ahn (2017) expanded upon Charlier's postulations to provide guidelines concerning the multiple solutions of angles‐only orbit solutions. General angles‐only orbit solutions disregard the uncertainties associated with the orbital solution. This limitation has been investigated through Gauss's solution via Binz and Healy (2017) utilizing sigma points to ascertain more representative uncertainties when compared to traditional least squares‐based solutions.
We present IOD‐based methods and estimates of particle trajectories and velocities for multiple ejection events, based on detections of particles by the navigation camera NavCam 1—part of the Touch and Go Camera System (TAGCAMS) (Bos et al., 2018)—during the Orbital A and Detailed Survey phases of the OSIRIS‐REx mission, between January and April 2019. We describe the techniques that we used to determine particle tracks (positive associations of particles across subsequent images). An explanation of how the initial trajectories are estimated and the assumptions pertaining to that analysis is provided. Additionally, we describe an uncertainty quantification of the particle ejection locations and time and the respective excess body‐fixed velocities that were induced on the particles to release them from the surface.
2. Particle Detection
OpNav images taken during the Orbital A phase from an eccentric, 1.6 by 2.1 km terminator frozen orbit fully covered the near‐asteroid environment by slewing to two nadir‐offset pointing orientations, allowing for the asteroid to be encompassed completely in each single image. Pairs of images were taken every 2 hr with 7 min between each off‐nadir image target. During a single imaging sequence, NavCam 1 took a long‐exposure image (5 s) to obtain an overexposed image of Bennu with stars in the background for spacecraft attitude estimation and a short‐exposure image (1.38 ms) for feature detection used for landmark‐based navigation. The first detected particle ejection event was observed in imaging data collected on 6 January 2019 at 20:56:21 UTC. The occurrence of an ejection event preceding the long‐exposure image epoch (moment in time) was determined from a simple visual inspection; subsequent detailed analysis resulted in the identification of 200 individual particles originating near the surface of Bennu (Lauretta et al., 2019).
The two other largest events (>70 observed particles) observed during Orbital A occurred on 19 January and 11 February. These events were identified using an increased observation cadence (Lauretta et al., 2019), allowing for particle associations over three or more images, whereas the 6 January event was limited to two‐image associations. An event occurring on 19 April ejected 18 particles that were tracked over several images. Smaller events (generally three to nine observed particles) have continuously been observed throughout the Orbital A and Detailed Survey phases, as well as instances of particles in closed orbits lasting several days before impacting the surface (Lauretta et al., 2019).
2.1. Initial Track Association
Once a particle event is detected, the OpNav team determines the two nearest NavCam 1 images that were taken immediately after the event occurred. The long‐exposure images are primarily used for particle detection, with the short‐exposure images, when possible, being used as context for Bennu's orientation at the time of the event. These images are distorted due to the camera's inherent optical design and must be undistorted using in‐flight calibrations (Pelgrift et al., 2018). Once the image is undistorted, camera‐to‐object vectors in the inertial frame from the spacecraft can be determined.
Each long‐exposure image contains numerous stars due to the relatively large field of view (FOV) of the NavCam 1 imager. We distinguish stars from particles by using a star catalog (UCAC4 supplemented with Tycho2) and by taking advantage of the fact that all the stars in an image pair have the same apparent motion with respect to Bennu. The remaining nonstellar point sources are inspected to determine tracks.
A set of nonstellar point sources are tracked from the first image to the second. This process, described in more detail by Pelgrift et al. (2020), is performed by obtaining a pattern of objects and determining the relative distance between each object in a pattern from one image to the next. Associations of particles are determined by eye, and the process is repeated until all associations are exhausted. Within each image, particles appear as streaks or point sources. Those objects that are determined to be streaking over the image exposure provide a direct measure of the velocity in the camera plane, while the velocity of point sources must be inferred over the associated track.
2.2. Filtering Particle Detection
After the detection of the 19 January event, an automated method of filtering and detecting particles was deemed necessary to keep the mission apprised of recent changes in the near‐Bennu environment. First, image processing steps are applied to locate groupings of bright pixels and fit a point spread function to these groups to locate the subpixel center of the possible detection. These image processing steps include applying a median filter that flattens the image to remove most of the stray light, threshold flattening of the image, followed by label threshold. Next, a “quality” value is assigned to each possible detection based on the observed photometric and astrometric properties that attempts to capture the probability that detection is real. These quality values are then filtered to extract detections that are likely real objects before passing the results to human analysts and other analysis software. These steps are implemented in the Goddard Image Analysis and Navigation Tool and described in detail in Liounis et al. (2020).
3. Methods for Initial Determination of Particle Ejection Event Trajectories
3.1. Traditional Angles‐Only Orbit Determination
The particle optical data lend to be approached as an angles‐only IOD problem. There are several methods that can be used to determine a trajectory that fits angular data alone. The most common techniques are Laplace's, Gauss's, double‐r iteration, and Gooding's methods (Gibbs, 1889; Gooding, 1997; Taff, 1984). These techniques have been used to solve a variety of problems involving angular data observed from Earth. Each method uses numerical techniques to associate three images (six angular measurements) with the six‐state parameters defining a unique orbit. Gauss's method is traditionally used for interplanetary orbits where the observer is distant from the object and not necessarily the bounding body. We use Gauss's method, which fits all three data points, whereas other methods only fit a subset of the data. Although Gauss's method breaks down for angular separations greater than 60°, for the data set obtained from the particle ejection events, the variation in the angular measurements is less than 60° from epoch to epoch.
Image data are converted from pixel‐line coordinates to right ascension (RA) and declination (DEC) from the spacecraft in the inertial International Celestial Reference Frame. Background stars in an overexposed image taken during the imaging sequence allow the inertial orientation of the image to be estimated. The RA and DEC define a unit direction vector from the spacecraft to the ejected particle. Some inferences can be made of potential distances from the spacecraft to the particle; however, no direct measurement can be obtained. The unit direction vector for each particle, , can be obtained as
where δi is the DEC and αi is the RA of observation i. The position vector of the debris particle relative to the spacecraft, rs/c, is thus
The slant range, ρi, must be solved to determine a unique orbit for a given particle. Gauss's method solves this problem iteratively by making some assumptions about the distance to the particle by determining the correct roots of a polynomial expressing the slant range of the middle observation. At this stage, an eighth‐order polynomial must be solved, which may contain a variety of real and complex roots. The solution will always reside in the real root; however, for the case where an observer is in an orbit around the central body and not on its surface, as in most Earth‐based cases, four roots can be expected. The determination of the true positive real root to solve the problem is necessary, and here we follow the guidelines determined by Charlier (1910, 1911) and Wie and Ahn (2017). It is assumed that the true positive real root that solves the angles‐only orbit determination problem is the one that has the smallest angular separation from the boresight of the camera or the root defining the smallest angle between the radial vector and the observation. These two assumptions eliminate all the other spurious roots when more than one positive real root exists. The results of this method provide the initial conditions necessary to begin a higher‐fidelity modeling of the ejection event.
Admissible regions can be used to help constrain the state space when angles‐only IOD techniques are performed. The SSA community successfully utilizes admissible regions for space‐based imaging platforms to constrain Earth orbiters. These admissible regions place constraints on the potential state space of the slant range, ρi, and its rate, , to obtain a representation of solutions of the full state space of position and velocity. One admissible region commonly applied to asteroid ephemeris estimation and employed by the SSA community relies on the fact that the energies of the orbits are such that they are not hyperbolic.
For this work, we expand upon these approaches to the admissible region by applying them to the state space of angular measurements and initial slant range instead of just the slant range and its rate. A constraint bound applied in this work assumes that the radius of periapsis of the orbital solution immediately after the event must be less than the radius of the event location on the surface. The state space is further limited through the constraint that the particle must be in front of the camera toward the asteroid and within the FOV of the imager. This helps to eliminate spurious solutions in the IOD process that produce initial state estimates that have the particle in leading or trailing orbits relative to the spacecraft in the same orbital plane. The initial energies of the event are further constrained to be greater than the velocity necessary to be released from the surface (Scheeres et al., 2019).
We also used a least squares IOD technique as a check on the solutions obtained by Gauss's method and to obtain initial estimates on the ephemeris uncertainty for particles imaged over more than three epochs. This method assumes that the first image of the event was detected near the surface so that the particle is roughly the same distance from the camera as the spacecraft is from Bennu, putting the particle in the vicinity of Bennu's surface. The second image is used to constrain the direction of the velocity and obtain an initial estimate of the speed based on the time elapsed between the two images. From this, an initial approximation of the position and velocity of the particle is obtained, confining it to a region near the surface of Bennu. A least squares solver is then used to minimize the RA and DEC residuals for particles containing at least three observation times to obtain an exact solution (if three observations are given) or an overdetermined solution (more than three observations) of the initial state of the particle. We compare this solution to that from the Gauss's method as a consistency check before invoking any surface and event time‐constrained trajectory estimation. Trajectory solutions obtained through these methods provide uncorrelated trajectories between the particles.
3.2. Constrained Angles‐Only Particle Model
Due to the quantity of particles detected and initial event reconstruction of their origin, a few assumptions can be made about the location of the origin of the particles. If one assumes that each individual particle leaves the surface independently of the others, then the traditional angles‐only orbit determination should be used. However, another possibility is that an ejection event occurs when particles leave the same region simultaneously. In the supplementary materials of Lauretta et al. (2019), the assumption of simultaneous particle release is evaluated for the 19 January and 11 February events. That analysis removes the assumption of simultaneous ejection but assumes that the particles ejected from the same location. The resulting distributions of possible event times largely fall within the time frames estimated by assuming simultaneous ejection. Thus, the assumption of simultaneously release is reasonable within the expected ejection time uncertainties.
When a single energetic event occurs, the problem of determining the location of the event can be constrained to have a pseudoangular observation occur at the event epoch and location. As is the case for the ejection events discovered and data association techniques used, it is likely that at least two epochs of images containing the same debris particle are obtained. When only two epochs are available for a single particle, that gives four observations (two sets of RA and DEC) and six unknowns necessary to estimate the full state of the particle's trajectory (three components each of position and velocity), producing an indeterminate system in our approach (Pelgrift et al., 2020, describe an alternative approach for analysis of such cases). However, when at least three particles are seen in two sets of images each, that produces 12 observations with 12 unknowns (the three components of velocity for each particle and the three components of position common to all the particles). If at least three particles are determined from a single event spanning at least two epochs, it is possible to estimate the location of that ejecta origin with conic trajectories. Any number of particles or observations more than this allows for an overdetermined system to be solved.
Another constraint that we applied when estimating an ejection event was assuming that the event originated on the surface of the asteroid. We used the Bennu shape model (Barnouin et al., 2019) to create a constraint between the event location in latitude and longitude and the position at that location, reducing the number of unknowns by one. A benefit is that the estimation of the ejection location will naturally follow the topography, producing a more consistent solution and realization of the uncertainty in the location of the event. The disadvantage of this approach is that it produces a correlated solution between all of the particle trajectories and the time at which the event occurs.
4. Particle Event Reconstruction
Due to the relatively infrequent cadence of imaging during the 6 January event, particle associations were only detected in two sets of images, so this event cannot be directly reconstructed using our approach. The increase in the imaging cadence after the 6 January event allowed for more successive images of particles during the subsequent events on 19 January and 11 February. Another relatively large (>15 observed particles) event occurred on 19 April with particle associations detected in more than two sets of images. In addition, six ejection events with three to nine particles occurred between January and June 2019. Of these smaller events, five are analyzed in this work, spanning January to April. One of the events is excluded because it only had two particles with two‐image epochs for each particle. Our reconstruction analysis therefore focuses on the three largest events that meet our criteria (19 January, 11 February, and 19 April), as well as five smaller events (29 January, 4 February, 5 February, and two events on 8 February), to give insight into the location, trajectories, and amount of energy necessary for the particles to be released from the surface and enter either hyperbolic or ballistic trajectories.
We determine initial state estimates of position and velocity from the IOD process for individual particles. We assume that, after being accelerated by the ejection mechanism, the particles continue on conic orbits influenced only by point‐mass gravity, the event was instantaneous, and all the particles left the asteroid from the same location. Two approaches are then taken for reconstruction of the event time and location. One approach assumes that the event occurred on the surface of the asteroid based on the shape model. Another approach does not make this assumption but rather estimates a coincident inertial point from which all the particles left and is used as a check on the previous assumptions. Once we verified that first solution demonstrated that the particles left the surface of Bennu, we confidently apply this additional constraint utilizing the shape model, requiring that the event location solution exists on the asteroid surface.
4.1. Particle Event Data Set
The 19 January event data set analyzed in this work contains 35 nonstreaked particles detected and tracked over multiple images, out of 88 particles detected during the event. Streaked particles are not used in this analysis since they generally are not observed over enough images to infer complete trajectory information. As a result, we specifically exclude the highest‐velocity particles from our analysis. The number of observations per particle ranges from two to six. Particles were observed for up to 1.5 hr after the event occurred. Similarly, the 11 February data set contains 30 nonstreaked particles tracked over multiple images (of 72 total observed particles), with two to four images per particle track. The 19 April data set contains 18 total particles being tracked over two images. This is the only event analyzed in this work with fewer than three images for a single particle. Estimation of this event is possible due to the ejection location surface constraint and the total number of particles. The five smaller events analyzed each contains at least one particle that was tracked over three images with the remaining only being tracked over two images.
The relative geometry as viewed from the spacecraft does not allow for direct visualization of the events. Each event was imaged with the potential radiant point of the particle ejection on the opposite side of Bennu and the spacecraft below the horizon of the event location.
We may not have observed all of the ejected particles. Each particle ejection event occurred prior to the first image being taken. The highest‐velocity particles may have left the NavCam 1 FOV before imaging that detected the event began. Further, it is possible that a fraction of the particles moving at slow velocities were never visible above the asteroid's limb (or the “saturation limb” for the long‐exposure images that can extend about 20–40 m above the surface depending on the exposure length and viewing geometry). For any phase angle and range, there is a limit to the faintness at which objects are detectable. In addition, the ejection angle can produce trajectories that are in front of or behind the asteroid or in shadow for some time and thus are not observed by the camera.
4.2. Particle Event Trajectories
The three largest analyzed events produced particle trajectories that ranged from suborbital to hyperbolic. From the 19 January event, 16 of the tracked particles entered into suborbital trajectories, with eight becoming hyperbolic. The 11 February event produced 20 suborbital and 5 hyperbolic particles. Figure 1 shows the estimated suborbital and hyperbolic trajectories for the 11 February event as viewed from above Bennu's north (+Z) pole, aligned with the terminator. The 19 April event produced 6 suborbital trajectories and 12 hyperbolic trajectories. The longest‐lived suborbital particle remained in the Bennu environment for 2 days (never completing a full orbit), and the shortest remained for only 40 min before impacting. No direct measurements have indicated that these specific events created short‐lived orbiting particles that exist over multiple revolutions; however, there is a candidate particle that originates a few hours after the 19 January event epoch (Lauretta et al., 2019). We suggest that this orbiting particle may be associated with the 19 January event and either was not visually captured in the imaging or was launched by reimpact of the 19 January particles.
Figure 1.
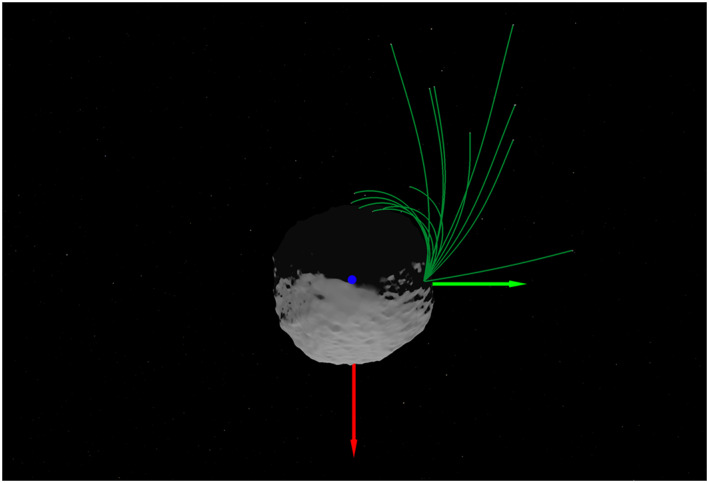
Reconstructed particle trajectories from the 11 February event. The trajectories (in green) range from ballistic or suborbital, which reimpact within a few hours, to hyperbolic, leaving the Bennu environment completely within a few hours. Particle events occur in the late afternoon (local solar time), gaining velocity from Bennu's rotation as they move toward the nightside of the asteroid. The red, green, and blue axes correspond to the x, y, and z axes (respectively) of the Bennu Sun Anti‐Angular Momentum (SAM) frame (Williams et al., 2018).
Table 1 gives the estimated times, locations, and energies for our 19 January, 11 February, and 19 April trajectory reconstructions. We determine the local solar time (LST) to be 16:38:01 for the 19 January event, 18:05:31 for the 11 February event, and 16:34:54 for the 19 April event. Although these events occurred within a relatively narrow time range, they span multiple latitudes and longitudes.
Table 1.
Particle Event Data Set, Parameter Estimates, and Event Energies for Three Major Events
| 19 January 2019 | 11 February 2019 | 19 April 2019 | |||||
|---|---|---|---|---|---|---|---|
| Number of particles analyzed | Fit | 24 | 25 | 18 | |||
| Rejected | 11 | 5 | 0 | ||||
| Total | 35 | 30 | 18 | ||||
| Estimated value | Uncertainty (1‐sigma) | Estimated value | Uncertainty (1‐sigma) | Estimated value | Uncertainty (1‐sigma) | ||
|---|---|---|---|---|---|---|---|
| Event time (UTC) | 00:53:41 | 4 s | 23:27:28 | 6 s | 01:58:08 | 32 s | |
| Longitude (°) | −24.60 | 0.09 | 60.17 | 0.08 | −134.85 | 2.52 | |
| Latitude (°) | 20.63 | 0.30 | 20.68 | 0.37 | 18.60 | 1.03 | |
| Local solar time | 16:38:01 | 23 s | 18:05:31 | 22 s | 16:34:54 | 685 s | |
| Event energy (mJ) | Min a | 0.04 | 0.03 | 0.17 | |||
| Mean a | 0.80 | 0.26 | 1.24 | ||||
| Max a | 6.53 | 2.70 | 11.03 | ||||
| Cumulative | 19.17 | 6.48 | 22.28 | ||||
Note. Event reconstruction assumes that all the particles left the surface at the same time during the ejection event. Energy estimates per particle are based on the estimated body‐fixed velocity assuming a 3‐cm‐diameter sphere (Lauretta et al., 2019) with a density of 2 g/cm3 (based on Bennu meteorite analog; Hamilton et al., 2019).
Energies are computed on a per particle basis.
Of the five smaller events investigated, three occurred in the late afternoon (between 18:00 and 19:00), in accord with the 19 January, 11 February, and 19 April events. The other two smaller events, which both occurred on 8 February, have estimated LSTs of 01:00 LST and 12:44 LST. The variation in the estimated LST of all analyzed events is shown in Figure 2. Table 2 provides the ejection times, locations, and local solar times for the smaller events. Similar to the three larger events, the five smaller events analyzed also span multiple latitudes and longitudes.
Figure 2.

Local solar time variation and uncertainties for the estimated events examined in this work. A majority of the events had reconstructed LST estimates between 16:00 and 19:00. Error bars are 1 sigma (too small to see behind the points; see Tables 1 and 2 for values).
Table 2.
Particle Event Times and Locations for the Five Smaller Events
| Event date | Event time (UTC) | Longitude (°) | Latitude (°) | Local solar time | ||||
|---|---|---|---|---|---|---|---|---|
| Estimated value | Uncertainty (1‐sigma) | Estimated value | Uncertainty (1‐sigma) | Estimated value | Uncertainty (1‐sigma) | Estimated value | Uncertainty (1‐sigma) | |
| 29 Jan 2019 | 00:12:12.33 ± 31 s | 102.29 ± 0.62 | 17.94 ± 0.93 | 18:51:06 ± 69 s | ||||
| 4 Feb 2019 | 06:22:14.70 ± 101 s | 110.73 ± 2.97 | 33.40 ± 22.25 | 18:50:55 ± 234 s | ||||
| 5 Feb 2019 | 04:17:08 ± 121 s | 65.23 ± 6.28 | −41.15 ± 0.64 | 18:20:11 ± 1,653 s | ||||
| 8 Feb 2019 | 06:29:39.57 ± 1 s | −120.70 ± 0.08 | 41.55 ± 0.05 | 12:44:39 ± 20 s | ||||
| 8 Feb 2019 | 20:50:12.54 ± 1.6 s | −59.46 ± 0.10 | 31.38 ± 0.04 | 01:00:06 ± 36 s | ||||
Note. Assumptions are the same as in Table 1.
4.3. Surface Location Uncertainty Quantification
We use two methods to obtain estimates of the uncertainty of the particle ejection event location and time. A least squares estimation is performed with each measurement weighting appropriately scaled to the expected errors in the OpNav astrometric processing and potential errors in the conic trajectory fit compared to a high‐fidelity dynamical model. The a posteriori covariance is directly obtained from the estimation process. The least squares estimation has the potential to latch onto a local minima and overoptimistic uncertainties associated with the a posteriori state estimate. An alternate uncertainty quantification method is used to determine if the least squares estimation solution and associated uncertainty is appropriate. Namely, a Markov chain Monte Carlo analysis is performed for each of the data sets to provide insight into the a posteriori distribution of the system.
Figure 3a gives the estimated surface locations uncertainties for all of the events analyzed in this work, showing a wide range of latitudes and longitudes for the reconstructed event locations. Figures 3b through 3d show the expected probability variation in the particle ejection location by estimating the distribution using a Gaussian kernel density (contours). Also shown are the initial state estimates from the IOD process (red dots) without constraining the location and time of the event to be the same for the particles. Three observation epochs immediately after the event allow for a general understanding of the event's location and time. Figure 4 shows the probability distribution of the LST of the event from the a posteriori distribution estimate. For each particle ejection event, the LST is believed to be known to less than 5 min in time of day on the surface (see also Table 1).
Figure 3.

Estimated ejection locations and 3‐sigma uncertainties for (a) all analyzed events with zoomed in locations of the largest analyzed particle ejection events, with uncertainties, for (a) 19 January, (b) 11 February, and (c) 19 April. Reconstructed particle ejection locations occur over a variety of surface locations. The red dots in (b) through (d) represent the IOD conic fit trajectories and how closely the initial trajectory locations from three or more observations agree with the estimated location of the ejection site. The contours represent the kernel density estimate probability from the Markov chain Monte Carlo simulation of the a posteriori distribution. The red ellipse represents the 3‐sigma estimated uncertainties in the event location.
Figure 4.

Probability distribution of variation from the estimated LST for particle ejection events on (a) 19 January, (b) 11 February, and (c) 19 April. The distribution is derived from the Markov chain Monte Carlo simulation of the a posteriori distribution of the particle event location and assumes that all particles left the asteroid surface simultaneously.
4.4. Particle Event Directions and Energy
The energy necessary to create an event can be derived from the body‐fixed relative velocities of the individual particles. Each particle leaves the surface in a different direction, inducing a different inertial orbital trajectory. The observation data set is likely biased toward particles in a certain direction based on the spacecraft relative orientation and the illumination conditions. In addition, the data set analyzed in this work does not utilize the highest speed particles detected from streaked images and does not include velocities of particles that were not obtained in multiple images. The result is a biased event energy toward the lower‐velocity particles. The estimated body‐fixed velocities induced by the three largest particle events analyzed range from 5 to 90 cm/s and from 4 to 45 cm/s for the smaller events (Figure 5). Assuming that each individual particle is 3 cm in diameter (Lauretta et al., 2019) with an average density of 2 g/cm3 (based on Bennu meteorite analog; Hamilton et al., 2019), the specific event energy per particle would range from 0.03 to 11.03 mJ (Table 1). The total induced event kinetic energy of the observed particles in this data set, which does not include the high‐speed streaking particles, is 19.17 mJ for 19 January, 6.48 mJ for 11 February, and 22.28 mJ for 19 April (the data arcs are too short to provide an accurate estimate of the mass of the particles based on the dynamics alone). Lauretta et al. (2019) estimated higher‐fidelity event energies of 15 to 100 mJ for 19 January and 1 to 6 mJ for 11 February based on photometry of individual particles over a range of possible albedos (particle diameters ranging from <1 to 6 cm), utilizing trajectory and velocity estimates from analytical techniques described in detail in this work and in Pelgrift et al. (2020).
Figure 5.
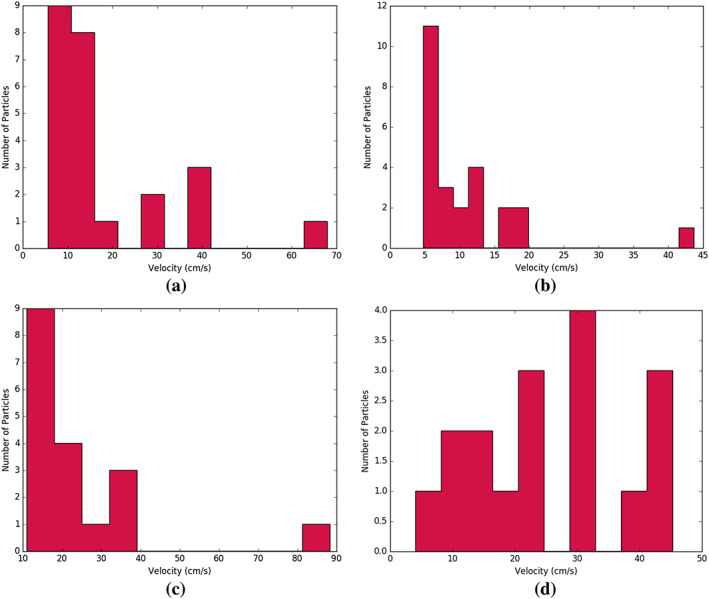
Estimated body‐fixed velocity variation for particle ejection events on (a) 19 January, (b) 11 February, and (c) 19 April, as well as (d) five smaller events. The majority of the observed particles had velocities less than 15 cm/s, resulting in suborbital ejection trajectories.
Most of the observed particle trajectories relative to the local frame of reference tend to proceed in the eastward direction, the direction of maximum angular velocity from Bennu's spin. Particles have also been observed to launch westward from the ejection location. To counteract the rotational velocity on the surface at 20° latitude (10 cm/s) and achieve a hyperbolic trajectory that would have been detected in an image, a particle would have to eject with a velocity >30 cm/s. This value changes over the surface at different latitudes and azimuth/elevation angles. Figure 6 shows the local site azimuth and elevation of each of the ejected particles associated with the three largest events (panels a–c) and the five small events (panel d), with the estimated body‐fixed excess velocities that the event induced on the particle to release it from the surface. To understand the direction of the launch, we look at the average launch vector at the site and the associated half cone angles of each particle's estimated ejection direction relative to that average launch vector: 19 January had an average launch vector RA and DEC of 114.9° and 67.1° with an average and maximum half cone angle of 27.7° and 76.2°; 11 February had an average launch vector RA and DEC of 27.8° and 80.0° with an average and maximum half cone angle of 24.4° and 82.2°; and 19 April had an average launch vector RA and DEC of −145.9° and 62.7° with an average and maximum half cone angle of 31.5° and 68.9°.
Figure 6.

Azimuth, elevation, and estimated body‐fixed ejection velocity of particles observed for the (a) 19 January, (b) 11 February, and (c) 19 April events and (d) five smaller events. Azimuth starts north at 0° with positive angle sweeping clockwise toward east at 90°. The radial component of the figure is the local site elevation.
5. Limitation of Trajectory Estimation Approach
The approach to trajectory reconstruction presented in this work is to rapidly estimate initial state conditions of the particle immediately after ejection from the surface of Bennu. The approach taken by Pelgrift et al. (2020) allows for an immediate evaluation of potential ejection sites, particle velocities, and LSTs following a particle event using the least amount of image data possible. We expand on the approach in Pelgrift et al. (2020) by using a variety of IOD techniques and constraints to define the situation presented by the particle ejections. The benefit of this approach over that taken by Pelgrift et al. (2020) is in the use of orbital motion of the particles rather than the linear assumption that they present. The main limitations of the analysis presented here are that it requires at least detections across three or more images, unless there are three particles detected in two images each, and that it does not use high‐fidelity force propagation of the particle trajectories. High‐fidelity force propagation is an involved and lengthy process, and the techniques developed here are a precursor to any more in‐depth ephemeris estimation. The short‐arc ephemeris estimation assumption using Gauss's technique with admissible regions and a least squares solver produce accurate velocity direction and magnitude estimates of the ejection location when supplied to a higher‐fidelity force model propagation of the particles. After several hours of particle propagation, the conic model can be up to 10 pixels off depending on the size or shape of the particle, how close to the surface its apoapse is, and the influence of solar radiation pressure. To alleviate this, we adjust the weighting of the optical image data for the least squares and Markov chain Monte Carlo analysis to account for a potential trajectory error on the order of a dynamical propagation in a high‐fidelity force model of each particle.
6. Conclusions
To characterize the particle ejection events from asteroid Bennu observed by OSIRIS‐REx, we developed an IOD technique utilizing angles‐only measurements for particle event reconstruction by constraining the particles for a given event to have the same epoch. Multiple short‐arc IOD techniques were used to determine the particle trajectories and their origins. Advances in short‐arc asteroid ephemeris estimation and admissible regions were used with success to constrain the initial state of the particles at the moment of their release from Bennu's surface. Of importance for ongoing analyses to determine a mechanism for these particle ejection events is their source locations on the asteroid surface and the LSTs at which they occurred. We find a range of surface locations but a relatively narrow span of LSTs (between about 16:30 and 19:00 LST) for the three of the largest events and three of the smaller events analyzed in this work. Two of the smaller events lie outside of this range. All of the analyzed events produced particle trajectories that ranged from suborbital to hyperbolic with no particles being tracked entering into multiple revolution orbits. We estimate ejection velocities in the Bennu body‐fixed frame ranging from about 5 to 90 cm/s. The resulting total energy released during the particle event ranged from 6.48 to 22.28 mJ for the three largest analyzed events, assuming that each particle is a sphere with density of 2 g/cm3 and diameter of 3 cm. The techniques developed in this work leverage proven IOD algorithms and expand upon some of the limitations presented by Pelgrift et al. (2020). We are able to quickly and accurately reconstruct event locations and event velocities to instantiate more detailed trajectory analysis using high‐fidelity force propagation.
Acknowledgments
We are grateful to the entire OSIRIS‐REx Team for making the Bennu encounter possible. This material is based upon the work supported by the National Aeronautics and Space Administration (NASA) under Contracts NNM10AA11C and NNG13FC02C issued through the New Frontiers Program. A portion of this work was conducted at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the NASA.
Leonard, J. M. , Adam, C. D. , Pelgrift, J. Y. , Lessac‐Chenen, E. J. , Nelson, D. S. , Antreasian, P. G. , et al. (2020). Initial orbit determination and event reconstruction from estimation of particle trajectories about (101955) Bennu. Earth and Space Science, 7, e2019EA000937 10.1029/2019EA000937
This article is a companion to Liounis et al. (2020), https://doi.org/10.1029/2019EA000843 and Pelgrift et al. (2020), https://doi.org/10.1029/2019EA000938.
Data Availability Statement
NavCam 1 images are available as part of the TAGCAMS bundle in the Planetary Data System (PDS) (Bos et al., 2019). Data are delivered to the PDS according to the OSIRIS‐REx Data Management Plan available in the OSIRIS‐REx PDS archive (Crombie & Selznick, 2019). The data used to generate the figures in this paper are available via Figshare data repository (Leonard, 2020). The software used in this analysis is proprietary to KinetX, Inc.; however, the generation of the observables and estimation procedure is given in section 3. For our orbit analysis, we used the NAIF SPICE toolkit (C. H. Acton, 1996; C. Acton et al., 2017) and spacecraft trajectories with associate mission‐related kernels made available in the OSIRIS‐REx PDS NAIF archive (https://naif.jpl.nasa.gov/pub/naif/pds/pds4/orex/orex_spice/).
References
- Acton, C. , Bachman, N. , Semenov, B. , & Wright, E. (2017). A look towards the future in the handling of space science mission geometry. Planetary and Space Science, 150, 9–12. 10.1016/j.pss.2017.02.013 [DOI] [Google Scholar]
- Acton, C. H. (1996). Ancillary data services of NASA's Navigation and Ancillary Information Facility. Planetary and Space Science, 44(1), 65–70. 10.1016/0032-0633(95)00107-7 [DOI] [Google Scholar]
- Barnouin, O. S. , Daly, M. G. , Palmer, E. E. , Gaskell, R. W. , Weirich, J. R. , Johnson, C. L. , Al Asad, M. M. , Roberts, J. H. , Perry, M. E. , Susorney, H. C. M. , Daly, R. T. , Bierhaus, E. B. , Seabrook, J. A. , Espiritu, R. C. , Nair, A. H. , Nguyen, L. , Neumann, G. A. , Ernst, C. M. , Boynton, W. V. , Nolan, M. C. , Adam, C. D. , Moreau, M. C. , Rizk, B. , D'Aubigny, C. Y. D. , Jawin, E. R. , Walsh, K. J. , Michel, P. , Schwartz, S. R. , Ballouz, R.‐L. , Mazarico, E. M. , Scheeres, D. J. , McMahon, J. W. , Bottke, W. F. , Sugita, S. , Hirata, N. , Hirata, N. , Watanabe, S.‐I. , Burke, K. N. , DellaGiustina, D. N. , Bennett, C. A. , Lauretta, D. S. , & The OSIRIS‐REx Team (2019). Shape of (101955) Bennu indicative of a rubble pile with internal stiffness. Nature Geoscience, 12(4), 247–252. 10.1038/s41561-019-0330-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Binz, C. R. , & Healy, L. M. (2017). Direct uncertainty estimates from angles‐only initial orbit determination. Journal of Guidance, Control, and Dynamics, 41(1), 34–46. [Google Scholar]
- Bos, B. , Jackman, C. , & Lauretta, D. S. (2019). Origins, Spectral Interpretation, Resource Identification, Security, Regolith Explorer (OSIRIS‐REx): Touch‐and‐Go Camera Suite (TAGCAMS) Bundle. NASA Planetary Data System, urn:nasa:pds:orex.tagcams (https://sbn.psi.edu/pds/resource/orex/tagcams.html).
- Bos, B. J. , Ravine, M. A. , Caplinger, M. , Schaffner, J. A. , Ladewig, J. V. , Olds, R. D. , Norman, C. D. , Huish, D. , Hughes, M. , Anderson, S. K. , Lorenz, D. A. , May, A. , Jackman, C. D. , Nelson, D. , Moreau, M. , Kubitschek, D. , Getzandanner, K. , Gordon, K. E. , Eberhardt, A. , & Lauretta, D. S. (2018). Touch and Go Camera System (TAGCAMS) for the OSIRIS‐REx asteroid sample return mission. Space Science Reviews, 214(1), 37 10.1007/s11214-017-0465-2 [DOI] [Google Scholar]
- Bowell, E. , Virtanen, J. , Muinonen, K. , & Boattini, A. (2002). Asteroid orbit computation. Asteroids III, 1, 27–43. [Google Scholar]
- Charlier, C. V. L. (Dec. 1910). On multiple solutions in the determination of orbits from three observations. MNRAS, 71(2), 120–124. 10.1093/mnras/71.2.120 [DOI] [Google Scholar]
- Charlier, C. V. L. (1911). Second note on multiple solutions in the determination of orbits from three observation. MNRAS, 71(5), 454–460. 10.1093/mnras/71.5.454 [DOI] [Google Scholar]
- Chesley, S. R. (2004). Very short arc orbit determination: The case of asteroid 2004 FU162 . Proceedings of the International Astronomical Union, 2004(IAUC197), 255–258. [Google Scholar]
- Crombie M. K., & Selznick S. (Eds.). (2019). Origins, Spectral Interpretation, Resource Identification, Security, Regolith Explorer (OSIRIS‐REx): Mission Bundle. NASA Planetary Data System, urn:nasa:pds:orex.mission. (https://sbn.psi.edu/pds/resource/orex/orexmission.html)
- DeMars, K. J. , Jah, M. K. , & Schumacher Jr, P. W. (2009). The use of short‐arc angle and angle rate data for deep‐space initial orbit determination and track association. In Proc. of the Eighth US/Russian Space Surveillance Workshop, (Wailea, HI).
- Gauss, K. F. (1963). Theory of the motion of the heavenly bodies moving about the sun in conic section. New York: Dover. [Google Scholar]
- Gibbs, J. W. (1889). On the determination of elliptical orbits from three complete observations. Memoires National Academy of Science, 4(2), 79–104. [Google Scholar]
- Gooding, R. H. (1997). A new procedure for the solution of the classical problem of minimal orbit determination from three lines of sight. Celestial Mechanics and Dynamical Astronomy, 66(4), 387–423. 10.1007/BF00049379 [DOI] [Google Scholar]
- Gronchi, G. F. (2004). Classical and modern orbit determination for asteroids. Proceedings of the International Astronomical Union, 2004(IAUC196), 293–303. [Google Scholar]
- Hamilton, V. E. , Simon, A. A. , Christensen, P. R. , Reuter, D. C. , Clark, B. E. , Barucci, M. A. , Bowles, N. E. , Boynton, W. V. , Brucato, J. R. , Cloutis, E. A. , Connolly, H. C. Jr. , Hanna, K. L. D. , Emery, J. P. , Enos, H. L. , Fornasier, S. , Haberle, C. W. , Hanna, R. D. , Howell, E. S. , Kaplan, H. H. , Keller, L. P. , Lantz, C. , Li, J.‐Y. , Lim, L. F. , McCoy, T. J. , Merlin, F. , Nolan, M. C. , Praet, A. , Rozitis, B. , Sandford, S. A. , Schrader, D. L. , Thomas, C. A. , Zou, X.‐D. , Lauretta, D. S. , & OSIRIS‐REx Team (2019). Evidence for widespread hydrated minerals on asteroid (101955) Bennu. Nature Astronomy, 3(4), 332–340. 10.1038/s41550-019-0722-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hergenrother, C. W. , Maleszewski, C. K. , Nolan, M. C. , Li, J.‐Y. , d'Aubigny, C. Y. D. , Shelly, F. C. , Howell, E. S. , Kareta, T. R. , Izawa, M. R. M. , Barucci, M. A. , Bierhaus, E. B. , Campins, H. , Chesley, S. R. , Clark, B. E. , Christensen, E. J. , DellaGiustina, D. N. , Fornasier, S. , Golish, D. R. , Hartzell, C. M. , Rizk, B. , Scheeres, D. J. , Smith, P. H. , Zou, X.‐D. , Lauretta, D. S. , & The OSIRIS‐REx Team (2019). The operational environment and rotational acceleration of asteroid (101955) Bennu from OSIRIS‐REx observations. Nature Communications, 10(1), 1291 10.1038/s41467-019-09213-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hussein, I. , Roscoe, C. , Wilkins, M. , & Schumacher, P. (2014). Probabilistic admissible region for short‐arc angles‐only observations. In Advanced Maui Optical and Space Surveillance Technologies Conference.
- Kaya, D. A. , & Snow, D. E. (1991). Short arc initial orbit determination using angles‐only space based observations. In AAS and AIAA, Astrodynamics Specialist Conference, Durango, CO, Aug. 19–22, 1991. 29 p.
- Lauretta, D. S. , Hergenrother, C. W. , Chesley, S. R. , Leonard, J. M. , Pelgrift, J. Y. , Adam, C. D. , al Asad, M. , Antreasian, P. G. , Ballouz, R. L. , Becker, K. J. , Bennett, C. A. , Bos, B. J. , Bottke, W. F. , Brozović, M. , Campins, H. , Connolly, H. C. Jr. , Daly, M. G. , Davis, A. B. , de León, J. , DellaGiustina, D. N. , Drouet d'Aubigny, C. Y. , Dworkin, J. P. , Emery, J. P. , Farnocchia, D. , Glavin, D. P. , Golish, D. R. , Hartzell, C. M. , Jacobson, R. A. , Jawin, E. R. , Jenniskens, P. , Kidd, J. N. Jr. , Lessac‐Chenen, E. J. , Li, J. Y. , Libourel, G. , Licandro, J. , Liounis, A. J. , Maleszewski, C. K. , Manzoni, C. , May, B. , McCarthy, L. K. , McMahon, J. W. , Michel, P. , Molaro, J. L. , Moreau, M. C. , Nelson, D. S. , Owen, W. M. Jr. , Rizk, B. , Roper, H. L. , Rozitis, B. , Sahr, E. M. , Scheeres, D. J. , Seabrook, J. A. , Selznick, S. H. , Takahashi, Y. , Thuillet, F. , Tricarico, P. , Vokrouhlický, D. , & Wolner, C. W. V. (2019). Episodes of particle ejection from the active asteroid (101955) Bennu. Science, 366(6470), eaay3544 10.1126/science.aay3544 [DOI] [PubMed] [Google Scholar]
- Leonard, J. (2020). Figure Data for Initial Orbit Determination and Event Reconstruction From Estimation of Particle Trajectories About (101955) Bennu. figshare. Collection. 10.6084/m9.figshare.c.5115782 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liounis, A. , Small, J. L. , Swenson, J. C. , Lyzhoft, J. R. , Ashman, B. W. , Getzandanner, K. M. , Moreau, M. C. , Adam, C. D. , Leonard, J. M. , Nelson, D. S. , Pelgrift, J. Y. , Bos, B. J. , Chesley, S. R. , Hergenrother, C. W. , & Lauretta, D. S. (2020). Autonomous detection of particles and tracks in optical images. Earth and Space Science. (Special collection companion paper), e2019EA000843 10.1029/2019EA000843 [DOI] [Google Scholar]
- Milani, A. , Gronchi, G. F. , Knežević, Z. , Sansaturio, M. E. , & Arratia, O. (2005). Orbit determination with very short arcs: II. Identifications. Icarus, 179(2), 350–374. 10.1016/j.icarus.2005.07.004 [DOI] [Google Scholar]
- Milani, A. , Gronchi, G. F. , Vitturi, M. D. M. , & Knežević, Z. (2004). Orbit determination with very short arcs. I admissible regions. Celestial Mechanics and Dynamical Astronomy, 90(1–2), 57–85. 10.1007/s10569-004-6593-5 [DOI] [Google Scholar]
- Pelgrift, J. Y. , Lessac‐Chenen, E. J. , Adam, C. D. , Leonard, J. M. , Nelson, D. S. , McCarthy, L. , Sahr, E. M. , Liounis, A. , Moreau, M. , Bos, B. J. , Hergenrother, C. W. , & Lauretta, D. S. (2020). Reconstruction of active Bennu particle events from sparse data. Earth and Space Science. (Special collection companion paper), e2019EA000938 10.1029/2019EA000938 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pelgrift, J. Y. , Sahr, E. M. , Nelson, D. S. , Jackman, C. D. , Benhacine, L. , Bos, B. J. , Rizk, B. , d'Aubigny, C. , Golish, D. , Dellagiustina, D. , & Lauretta, D. S. (2018). In‐flight calibration of the OSIRIS‐REx optical navigation imagers. Paper presented at 1st Annual RPI Workshop on Image‐Based Modeling and Navigation for Space Applications, Rensselaer Polytechnic Institute, Troy, NY, June 4‐5.
- Schaeperkoetter, A. V. , & Mortari, D. (2011). “A comprehensive comparison between angles‐only initial orbit determination techniques,” AAS 11‐116, AAS/AIAA Space Flight Mechanics Meeting, New Orleans, LA, February 13–17.
- Scheeres, D. J. , McMahon, J. W. , French, A. S. , Brack, D. N. , Chesley, S. R. , Farnocchia, D. , Takahashi, Y. , Leonard, J. M. , Geeraert, J. , Page, B. , Antreasian, P. , Getzandanner, K. , Rowlands, D. , Mazarico, E. M. , Small, J. , Highsmith, D. E. , Moreau, M. , Emery, J. P. , Rozitis, B. , Hirabayashi, M. , Sánchez, P. , Van Wal, S. , Tricarico, P. , Ballouz, R.‐L. , Johnson, C. L. , Al Asad, M. M. , Susorney, H. C. M. , Barnouin, O. S. , Daly, M. G. , Seabrook, J. A. , Gaskell, R. W. , Palmer, E. E. , Weirich, J. R. , Walsh, K. J. , Jawin, E. R. , Bierhaus, E. B. , Michel, P. , Bottke, W. F. , Nolan, M. C. , Connolly, H. C. Jr. , Lauretta, D. S. , & The OSIRIS‐REx Team (2019). The dynamic geophysical environment of (101955) Bennu based on OSIRIS‐REx measurements. Nature Astronomy, 3(4), 352–361. 10.1038/s41550-019-0721-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snow, D. E. , & Kaya, D. A. (1992). Short arc orbit determination using angles‐only space based observations In AAS/AIAA Space Flight Mechanics Conference, AAS 92‐112, 24‐26 February 1992 (pp. 57‐74). Colorado Springs, CO. [Google Scholar]
- Spoto, F. , Del Vigna, A. , Milani, A. , Tommei, G. , Tanga, P. , Mignard, F. , Carry, B. , Thuillot, W. , & David, P. (2018). Short arc orbit determination and imminent impactors in the Gaia era. Astronomy & Astrophysics, 614, A27 10.1051/0004-6361/201732104 [DOI] [Google Scholar]
- Taff, L. G. (1984). On initial orbit determination. The Astronomical Journal, 89, 1426–1428. 10.1086/113644 [DOI] [Google Scholar]
- Wie, B. , & Ahn, J. (2017). On selecting the correct root of angles‐only initial orbit determination equations of Lagrange, Laplace, and Gauss. The Journal of the Astronautical Sciences, 64(1), 50–71. 10.1007/s40295-016-0097-x [DOI] [Google Scholar]
- Williams, B. , Antreasian, P. , Carranza, E. , Jackman, C. , Leonard, J. , Nelson, D. , Page, B. , Stanbridge, D. , Wibben, D. , Williams, K. , Moreau, M. , Berry, K. , Getzandanner, K. , Liounis, A. , Mashiku, A. , Highsmith, D. , Sutter, B. , & Lauretta, D. S. (2018). OSIRIS‐REx flight dynamics and navigation design. Space Science Reviews, 214(4), 69 10.1007/s11214-018-0501-x [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
NavCam 1 images are available as part of the TAGCAMS bundle in the Planetary Data System (PDS) (Bos et al., 2019). Data are delivered to the PDS according to the OSIRIS‐REx Data Management Plan available in the OSIRIS‐REx PDS archive (Crombie & Selznick, 2019). The data used to generate the figures in this paper are available via Figshare data repository (Leonard, 2020). The software used in this analysis is proprietary to KinetX, Inc.; however, the generation of the observables and estimation procedure is given in section 3. For our orbit analysis, we used the NAIF SPICE toolkit (C. H. Acton, 1996; C. Acton et al., 2017) and spacecraft trajectories with associate mission‐related kernels made available in the OSIRIS‐REx PDS NAIF archive (https://naif.jpl.nasa.gov/pub/naif/pds/pds4/orex/orex_spice/).


