How has the relationship between oil and the US stock market changed after the Covid-19 crisis?

Highlights

• •We study the relationship between oil and the US stock market.
• •We compare the relationship before and after the onset of the Covid-19 crisis.
• •To do so, we compute upside and downside correlations between the two markets.
• •We find that both upside and downside correlations increased after the crisis.

Abstract

In this paper, we investigate how the relationship between oil and the US stock market has changed after the onset of Covid-19 crisis. To do so, we compute upside and downside correlations between the two markets. Our findings are as follows. First, we document the correlation asymmetry: the downside correlation is higher than the upside correlation. Second, we find that both upside and downside correlations increased after the crisis. This indicates that after the start of the Covid-19 crisis, a positive (negative) oil shock is even better (worse) news for the stock market than an equivalent shock before the crisis.

1. Introduction

The Covid-19 pandemic severely impacted the dynamics of global financial markets over the last months. One of the notable impacts is a large decline and rebound of oil market and US stock market. Investors seem to be paying more attentions to oil markets because the oil demand might signal whether and how the global economy recovers from the damage caused by the Covid-19 pandemic.

In this paper, we investigate how the relationship between oil markets and the US stock market has changed after the Covid-19 pandemic crisis. For this purpose, we compute the correlation asymmetry between the oil market and the US stock market, using the concept of exceedance correlations used by Longin and Solnik (2001) and Ang and Chen (2002). The correlation asymmetry is defined as the difference between upside and downside correlations. The upside correlation is computed as a correlation under the condition when both the oil and stock market show positive returns. The downside correlation is computed as a correlation under the condition when both the oil and stock market shows negative returns.

Our main finding is that the correlation asymmetry has changed after the global financial markets entered the Covid-19 crisis. Before the crisis, the correlation asymmetry arose only from the downside correlation. Specifically, the empirical downside correlation was higher than the theoretical value computed from the bivariate normal distribution with historical unconditional correlation, while the upside correlation was close to the theoretical value. This indicates that before the crisis, the correlation between the oil market and the US stock market became higher only when both markets declined.

After the onset of the Covid-19 crisis, the correlation asymmetry has become more pronounced. Both upside and downside correlations increased over the last four months. This indicates that after the start of the Covid-19 crisis, a positive (negative) oil shock is even better (worse) news for the stock market than an equivalent shock before the start of the crisis.

We formally test whether the empirical conditional correlations can be explained with the bivariate normal distribution by employing H statistic proposed by Ang and Chen (2002). We document statistical evidence of non-normality. As a robustness check, we also apply a nonparametric test proposed by Hong et al. (2007). We confirm that there exists correlation asymmetry.

We then examine which model can explain the correlation asymmetry. We estimate a bivariate normal mixture, a bivariate t-distribution mixture, and a threshold dynamic conditional correlation model. We document that the t-distribution mixture model outperforms the other models.

Finally, we discuss the economic impact of failing to capture the asymmetry for portfolio optimization. We consider an investor with a power utility function. We document that the benefit of capturing the correlation asymmetry increased after the start of the Covid-19 crisis.

The rest of the paper is organized as follows. Section 2 reviews the literature. Section 3 explains our econometric approach. Section 4 describes the data used in this study. Section 5 discusses our empirical results. Section 6 concludes.

2. Literature

There have been several empirical studies focusing on the relationship between the oil and stock markets.

The most closely related paper is González-Pedraz et al. (2015). They compute exceedance correlation to study the relationship between the oil and stock markets during the 1990–2010 period. Consistent with our finding, they find that the downside correlation is higher than the upside correlation between the oil and stock markets.

Filis et al. (2011) employ a dynamic conditional correlation model to investigate how the correlations between stock and oil prices evolve. They document that the oil market is not a safe haven for protection against stock market decline.

Barragán et al. (2015) apply wavelet analysis for studying the correlation between oil and stock markets. They find evidence of contagion when stock market declined in 2008 and 2011.

Baruník et al. (2016) also use wavelet analysis for studying the correlations between gold, oil and stocks. They show that correlations among these assets increased and became homogenous after the 2008 crisis.

Different from these studies, we focus on the change in the relationship between the oil market and the US stock market after Covid-19 pandemic hits the global economy.

3. Econometric approach

3.1. Definition of exceedance correlation

To study the correlation asymmetry, we employ the exceedance correlations used by Longin and Solnik (2001) and Ang and Chen (2002). The exceedance correlation consists of the upside correlation ${\rho }^{+}\left(\theta \right)$ and the downside correlation ${\rho }^{-}\left(\theta \right)$. These two correlations are defined as

$${\rho }^{+}\left(\theta \right)=\text{corr}({\widetilde{ϵ}}_x,{\widetilde{ϵ}}_y|{\widetilde{ϵ}}_x>\theta ,{\widetilde{ϵ}}_y>\theta ),\text{where}\theta \ge 0.$$ (3.1)

$${\rho }^{-}\left(\theta \right)=\text{corr}({\widetilde{ϵ}}_x,{\widetilde{ϵ}}_y|{\widetilde{ϵ}}_x<\theta ,{\widetilde{ϵ}}_y<\theta ),\text{where}\theta \le 0,$$ (3.2)

where θ is called threshold. ${\widetilde{ϵ}}_x$ and ${\widetilde{ϵ}}_y$ are stochastic variables and standardized: $\text{E}\left[{\widetilde{ϵ}}_x\right]=\text{E}\left[{\widetilde{ϵ}}_y\right]=0$ and $\text{Var}\left[{\widetilde{ϵ}}_x\right]=\text{Var}\left[{\widetilde{ϵ}}_y\right]=1$. The standardization allows us to set the threshold level θ independent of the volatility level of variables, x and y. In our empirical analysis, the stochastic variable $\tilde{x}$ is a log return of an oil price and the stochastic variable $\tilde{y}$ is a log return of a stock market index.

We define the exceedance correlation ρ^e(θ) as

$$\begin{array}{c}\hfill {\rho }^e\left(\theta \right)=\{\begin{array}{c}{\rho }^{+}\left(\theta \right),\text{where}\theta \ge 0.\hfill \\ {\rho }^{-}\left(\theta \right),\text{where}\theta \le 0.\hfill \end{array}\end{array}$$

Notice that the exceedance correlation has two values at $\theta =0$. If data is generated by a symmetric distribution, ${\rho }^{+}\left(0\right)={\rho }^{-}\left(0\right)$. Otherwise, ${\rho }^{+}\left(0\right)\ne {\rho }^{-}\left(0\right)$.

In what follows, we compare empirical exceedance correlations ${\tilde{\rho }}^e\left(\theta \right)$ with theoretical values ρ^e(θ, ρ^normal) under a bivariate normal distribution with historical unconditional correlation ρ^normal. If the empirical exceedance correlations are different from the theoretical values, it indicates non-normality of the relationship between two assets. We discuss a formal test of non-normality based on H statistic proposed by Ang and Chen (2002). The details are discussed in the Appendix A.

If ${\rho }^{+}\left(\theta \right)\ne {\rho }^{-}(-\theta ),$ we consider that there exists correlation asymmetry. To show the existence of correlation asymmetry, we conduct a nonparametric test developed by Hong et al. (2007). Their test is model-free because it does not rely on a specific symmetric distribution. In our empirical analysis, we conduct this nonparametric test, although we do not discuss the detailed procedure here because of the space limitation.

3.2. Normal mixture model

We estimate a normal mixture model and test whether the estimated normal mixture model can describe the (asymmetric) empirical exceedance correlations. We denote ${\widetilde{ϵ}}_t={({\widetilde{ϵ}}_x,{\widetilde{ϵ}}_y)}^{\prime }$. The normal mixture model is specified as

$$\begin{array}{c}\hfill {\widetilde{ϵ}}_t\sim \{\begin{array}{c}N({\mu }_u,{\Sigma }_u),\text{with}\text{probability}p.\hfill \\ N({\mu }_d,{\Sigma }_d),\text{with}\text{probability}1-p.\hfill \end{array}\end{array}$$ (3.3)

where N is a bivariate normal distribution. μ_u and μ_d are the vector of the means under each state ($s_t=u,d$). Σ_u and Σ_d are the covariance matrix under each state ($s_t=u,d$). In what follows, we denote the vector of the variances at each state with ${\sigma }_u^2=({\sigma }_{x,u}^2,{\sigma }_{y,u}^2)$ and ${\sigma }_d^2=({\sigma }_{x,d}^2,{\sigma }_{x,d}^2),$ respectively. Similarly, the correlation at each state is denoted with ρ_u and ρ_d, respectively. p is the mixing probability of two states ($\text{Prob}(s_t=u)=p$).

Note that we ensure that the unconditional average $\text{E}\left[{\widetilde{ϵ}}_x\right]=\text{E}\left[{\widetilde{ϵ}}_y\right]=0$ and the unconditional variance $\text{Var}\left[{\widetilde{ϵ}}_x\right]=\text{Var}\left[{\widetilde{ϵ}}_y\right]=1$. Therefore, given μ_u and p, μ_d is solved. Given σ_u and p, ${\sigma }_d^2$ is also solved.

3.3. t-distribution mixture model

We also estimate a t-distribution mixture model. The t-distribution mixture model is specified as

$$\begin{array}{c}\hfill {\widetilde{ϵ}}_t\sim \{\begin{array}{c}T({\mu }_u,{\Sigma }_u,{\nu }_u),\text{with}\text{probability}p.\hfill \\ T({\mu }_d,{\Sigma }_d,{\nu }_d),\text{with}\text{probability}1-p.\hfill \end{array}\end{array}$$ (3.4)

where T is a bivariate t-distribution. ν_u and ν_d are the degree of freedom for the t-distribution under each state ($s_t=u,d$). The other parameters are defined as the same way as in the normal mixture model.

Similar to the normal mixture model above, we ensure that the unconditional average $\text{E}\left[{\widetilde{ϵ}}_x\right]=\text{E}\left[{\widetilde{ϵ}}_y\right]=0$ and the unconditional variance $\text{Var}\left[{\widetilde{ϵ}}_x\right]=\text{Var}\left[{\widetilde{ϵ}}_y\right]=1$. Therefore, given μ_u and p, μ_d is solved. Given σ_u, ν_u, ν_d, and p, ${\sigma }_d^2$ is also solved.

3.4. Threshold DCC model

As an alternative approach, we employ a threshold dynamic conditional correlation (DCC) model which is an extension of DCC model developed by Engle (2002).1 Let us consider

$$\widetilde{ϵ}\sim N(\mathbf{0},{\Sigma }_t),$$ (3.5)

where 0 is a zero vector. Following Cappiello et al. (2010), we define ${\Sigma }_t=Q_t^{*-1}{Q}_t{Q}_t^{*-1}$ where $Q_t^{*}$ is a diagonal matrix with $Q_{ii,t}^{*}=\sqrt{q_{ii,t}}$. It guarantees the positive semi-definiteness of Σ_t.

The core of the threshold DCC model is the dynamics of Q_t specified as

$$\begin{array}{ccc}\hfill Q_t& =& (\overline{R}-{\alpha }_{\rho }\overline{R}-{\beta }_{\rho }\overline{R}-{\sigma }_{\rho }^{+}{\overline{N}}^{+}-{\sigma }_{\rho }^{-}{\overline{N}}^{-})+{\alpha }_{\rho }{Q}_{t-1}+{\beta }_{\rho }{ϵ}_t{ϵ}_t^{\prime }\hfill \\ & & +{\sigma }_{\rho }^{-}{n}_t^{-}{n_t^{\prime }}^{-}+{\sigma }_{\rho }^{+}{n}_t^{+}{n_t^{\prime }}^{+},\hfill \end{array}$$ (3.6)

where $n_t^{-}=I_{\{{ϵ}_x<0,{ϵ}_y<0\}}·{ϵ}_t$ and $n_t^{+}=I_{\{{ϵ}_x>0,{ϵ}_y>0\}}·{ϵ}_t$. An indicator function $I_{\{·\}}=1$ if the condition is satisfied. Otherwise, $I=0$. For $\overline{R}=\text{E}\left[{ϵ}_t{ϵ}_t^{\prime }\right],$ the mean-reverting level of correlation $\overline{\rho }={\overline{R}}_{12}={\overline{R}}_{21}$. The expectations ${\overline{N}}^{+}=\text{E}\left[n_t^{+}{n}_t^{{+}^{\prime }}\right],$ and ${\overline{N}}^{-}=\text{E}\left[n_t^{-}{n}_t^{{-}^{\prime }}\right]$ are replaced with sample average. ρ ₀ is a correlation value at $t=0$. In summary, $\overline{\rho },$ α_ρ, β_ρ, ${\sigma }_{\rho }^{+},$ ${\sigma }_{\rho }^{-},$ ρ ₀ are constant parameters to be estimated.

4. Data

We download the historical data of the prices of WTI oil price and S&P 500 index from FRED, the website of the Federal Reserve Bank of St. Louis. We have two sample periods: The pre-Covid crisis period starts from May 18, of 2010 to January 31, of 2020. The Covid-crisis period starts from February 3, of 2020 to May 31, of 2020. Our main results below are qualitatively similar if we select January 1, of 2020 as start date of the Covid-19 crisis. We use daily log return. We exclude April 20, of 2020 because of negative price of WTI. As a robustness check, we also conduct the same analysis for the historical data of Brent oil prices obtained from FRED.

5. Results

5.1. Testing correlation asymmetry

Table 1 shows estimated parameters of a GARCH model for each variable. For both WTI and S&P 500, the mean-reverting level of volatility $\overline{\sigma }$ and volatility of volatility β increased after the onset of the Covid-19 crisis. We use a GARCH-filtered return in our analysis below to disentangle the impact of time-varying volatility from correlations.

Table 1.

Estimates of GARCH model parameters. The standard deviations of each parameter are calculated based on QML(=Quasi Maximum Likelihood) estimator. The GARCH model is specified as ${\sigma }_t^2=\omega +\alpha {\sigma }_{t-1}^2+\beta {ϵ}_{t-1}^2$ where $\omega =(1-\alpha -\beta ){\overline{\sigma }}^2$. *** shows that the estimate is statistically significant at the 1% level.

Pre-crisis	$\overline{\sigma }$	α	β
WTI	1.39%⁎⁎⁎	0.92⁎⁎⁎	0.07⁎⁎⁎
S&P 500	0.49%	0.79⁎⁎⁎	0.17
During-crisis	$\overline{\sigma }$	α	β
WTI	2.77%⁎⁎⁎	0.76⁎⁎⁎	0.22⁎⁎⁎
S&P 500	0.97%	0.65⁎⁎⁎	0.28

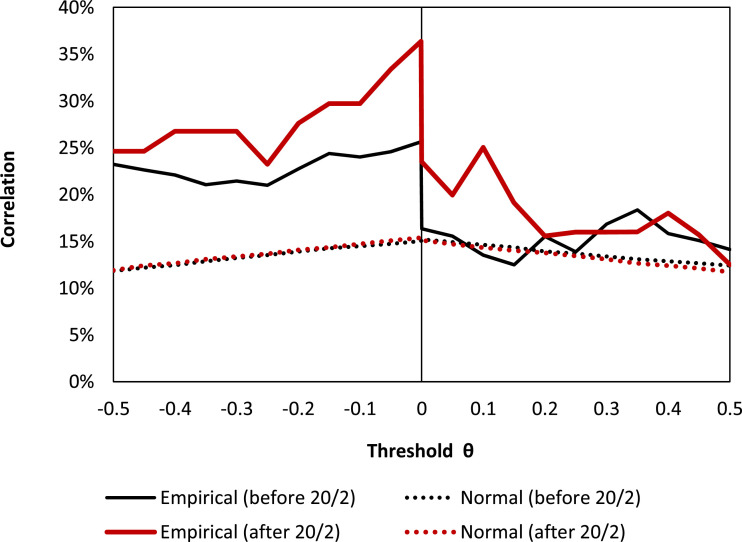
Fig. 1 shows the exceedance correlations between WTI and S&P 500 index. The x-axis is threshold θ. The y-axis is the correlation ρ^e(θ). The black-colored solid line shows empirical exceedance correlations during the pre-Covid-19 crisis. The black-colored dotted line is the exceedance correlations based on the estimated bivariate normal distribution. We can observe the correlation asymmetry: the downside correlation is higher than the upside correlation. It is also higher than its theoretical value based on the bivariate normal distribution. By contrast, the upside correlation is close to its theoretical value. This empirical pattern is qualitatively the same as the exceedance correlations between international stock markets documented by Longin and Solnik (2001).2

Fig. 1.

Exceedance correlations between WTI oil and the S&P 500 index. The black-colored solid line is the empirical exceedance correlation before the Covid-19 crisis period (2010/5-2020/1). The red-colored solid line is the empirical exceedance correlation during the Covid-19 crisis period (2020/2-2020/5). The black-colored dotted line is theoretical exceedance correlations under bivariate normal distributions with historical unconditional correlations ${\overline{\rho }}_{normal}=32.8\%$ before the crisis. The red-colored dotted line is theoretical exceedance correlations under bivariate normal distributions with historical unconditional correlations ${\overline{\rho }}_{normal}=32.9\%$ during the crisis. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Now let us look at the red-colored solid line that shows empirical exceedance correlations during the Covid-19 crisis. The red-colored dotted line is the exceedance correlations based on the estimated bivariate normal distribution. Interestingly, the red-colored solid line indicates that both the upside and downside correlations become higher after the onset of the Covid-19 crisis. Although we cannot identify causality from correlation, this result suggests that after the start of the Covid-19 crisis, a positive (negative) oil shock is even better (worse) news for the stock market than an equivalent shock before the crisis.

Table 2 shows the empirical estimates of upside and downside correlations ($\widehat{{\rho }^{+}}\left(0\right)$ and $\widehat{{\rho }^{-}}\left(0\right)$), as well as the H statistic with two different specifications of the weight (H_E and H_T) under bivariate normal distributions. Note that all of these exceedance correlations are computed using standardized log returns after we filter out volatility by the GARCH model.

Table 2.

Exceedance correlations and H statistics under normal distribution. ${\widehat{\rho }}^{+}\left(0\right)$ is the empirical estimate of the upside correlation with zero threshold. ${\widehat{\rho }}^{-}\left(0\right)$ is the empirical estimate of the downside correlation with zero threshold. ${\rho }_{normal}^{+}\left(0\right)$ and ${\rho }_{normal}^{-}\left(0\right)$ are the theoretical value of upside and downside correlations under a bivariate normal distribution, respectively. H stastistics are computed using bivariate normal distribution as a benchmark. H_E is the H statistic with the equal weight. H_T is the H statistic with threshold-dependent weight. ** and *** indicate statistical significance at the 5% and the 1% level, respectively.

Pre-crisis	${\widehat{\rho }}^{+}\left(0\right)$	${\rho }^{+}(0,{\rho }_{normal})$	${\widehat{\rho }}^{-}\left(0\right)$	${\rho }^{-}(0,{\rho }_{normal})$	HE	HT
	16.4%	15.1%	25.6%	15.1%	0.074⁎⁎⁎	0.068⁎⁎⁎
During-crisis	${\widehat{\rho }}^{+}\left(0\right)$	${\rho }^{+}(0,{\rho }_{normal})$	${\widehat{\rho }}^{-}\left(0\right)$	${\rho }^{-}(0,{\rho }_{normal})$	HE	HT
	23.5%	15.2%	36.4%	15.2%	0.330⁎⁎⁎	0.203⁎⁎

We make two observations: First, H statistic is statistically significant in all cases. It provides an empirical evidence of non-normality. Second, H statistic increased after the start of the Covid-19 crisis. It indicates that non-normality is more pronounced over the last four months.

Note that we obtain similar results for the exceedance correlations between Brent oil and Euro stoxx 50.

As a robustness check, we conduct a nonparametric test by Hong et al. (2007). We find that the statistical significance of correlation asymmetry is weak (10%) before the Covid-19 crisis. However, it becomes stronger (1%) after the crisis.

5.2. Performance comparison of mixture models and threshold DCC model

Tables 3 , 4 , 5 show estimated parameters of the normal mixture, t-distribution mixture, and the threshold DCC models, respectively, to fit the bivariate dynamics of WTI and S&P 500. The estimation methodology is based on maximum likelihood estimation. We generate exceedance correlations based on these estimated parameters for each model and then compute H statistic under each model. By looking at H statistic, we can see whether and to what extent these three models with estimated parameters can explain the correlation asymmetry.

Table 3.

Estimates of the normal mixture model parameters. The t value of each parameter is calculated based on QML(=Quasi Maximum Likelihood) estimator. ** and *** show the estimate is statistically significant at the 5% level and 1% level, respectively. Note that ${\mu }_x^d,$${\mu }_y^d,$${\sigma }_x^d$ and ${\sigma }_y^d$ are computed from the conditions of $\text{E}\left[{ϵ}_t\right]=0$ and $\text{Var}\left[{ϵ}_t\right]=1$.

	Pre-crisis	During-crisis
${\mu }_x^u$	0.17⁎⁎⁎	0.08⁎⁎⁎
${\mu }_y^u$	0.11⁎⁎⁎	0.04⁎⁎⁎
${\sigma }_x^u$	0.71	0.96⁎⁎⁎
${\sigma }_y^u$	0.76⁎⁎⁎	0.72⁎⁎⁎
ρu	0.17	0.22
ρd	0.27	0.37
p	0.72	0.89
${\mu }_x^d$	$-0.44$	$-0.64$
${\mu }_y^d$	$-0.29$	$-0.35$
${\sigma }_x^d$	1.42	1.10
${\sigma }_y^d$	1.41	2.19

Table 4.

Estimates of the t-distribution mixture model parameters. The t value of each parameter is calculated based on QML(=Quasi Maximum Likelihood) estimator. ** and *** show the estimate is statistically significant at the 5% level and 1% level, respectively. Note that ${\mu }_x^d,$${\mu }_y^d,$${\sigma }_x^d$ and ${\sigma }_y^d$ are computed from the conditions of $\text{E}\left[{ϵ}_t\right]=0$ and $\text{Var}\left[{ϵ}_t\right]=1$.

	Pre-crisis	During-crisis
${\mu }_x^u$	0.16⁎⁎⁎	0.08⁎⁎
${\mu }_y^u$	0.11⁎⁎⁎	0.04⁎⁎⁎
${\sigma }_x^u$	0.71	0.96
${\sigma }_y^u$	0.76	0.72
ρu	0.18	0.24⁎⁎⁎
ρd	0.28⁎⁎	0.39⁎⁎⁎
p	0.69	0.85⁎⁎⁎
νu	10718	8.53
νd	6.78	3.37
${\mu }_x^d$	$-0.35$	$-0.45$
${\mu }_y^d$	$-0.23$	$-0.23$
${\sigma }_x^d$	1.16	0.00
${\sigma }_y^d$	1.14	1.05

Table 5.

Estimates of threshold DCC model parameters. The t value of each parameter is calculated based on QML(=Quasi Maximum Likelihood) estimator. ** and *** show the estimate is statistically significant at the 5% level and 1% level, respectively.

	Pre-crisis	During-crisis
$\overline{\rho }$	0.33	0.33
αρ	0.96⁎⁎⁎	0.45⁎⁎⁎
βρ	0.01	0.21
${\sigma }_{\rho }^{+}$	0.02⁎⁎⁎	$-0.{17}^{***}$
${\sigma }_{\rho }^{-}$	0.01	0.21
ρ0	0.31	0.99

Table 6 shows the upside and downside correlations as well as H statistic under the three estimated models. The H statistic under any of these three models is smaller than H statistic under the bivariate normal distribution in Table 2. For example, H_T is 0.203 under the bivariate normal model during the crisis while H_T is 0.163, 0.139, and 0.193 for the normal mixture, t-distribution mixture, and the threshold DCC models, respectively. Also, we can see that the t-distribution mixture mode is the best performer in both two periods in terms of H_T.

Table 6.

H statistics under three different bivariate models. H statistics are computed using three different modes as a benchmark. The normal mixture, t-distribution mixture, and threshold DCC models are denoted with nm, tm, and DCC, respectively. H_E,i is the H statistic with the equal weight under the i model. H_T,i is the H statistic with threshold-dependent weight under the i model.

Pre-crisis	HE,nm	HT,nm	HE,tm	HT,tm	HE,DCC	HT,DCC
	0.071	0.061	0.067	0.056	0.066	0.061
During-crisis	HE,nm	HT,nm	HE,tm	HT,tm	HE,DCC	HT,DCC
	0.266	0.163	0.239	0.139	0.315	0.193

5.3. Estimated economic impact

We evaluate the economic impact of failing to capture the correlation asymmetry, following the procedure described in the Appendix B. Because we are interested in the pure impact of the correlation asymmetry, we turn off GARCH volatility dynamics and use the constant volatility equal to the sample standard deviation during 2019/6-2020/5. The mean of the return for each asset is also set equal to the average return during the same period. For the portfolio optimization problem, we use a bivariate normal mixture model as a true model describing dynamics of two assets. We use Monte Carlo simulation to compute the expected utility. We set simulation paths equal to 1,000,000.

We find that the impact of not capturing the correlation asymmetry is $-0.34\%$ before the Covid-19 crisis and $-0.54\%$ after the start of the crisis. The portfolio return is reduced by these values in relative terms. The result suggests that the economic benefit of capturing the correlation asymmetry increased after the start of the Covid-19 crisis.

6. Conclusion

In this paper, we investigate how the relationship between the oil market and the US stock market has changed after the onset of Covid-19 crisis. Our focus is correlation asymmetry between the two markets. In doing so, we compute upside and downside correlations, following Longin and Solnik (2001) and Ang and Chen (2002). We conduct statistical tests and discuss the economic impact of failing to capture the asymmetry for portfolio optimization.

The main message of this paper is that the correlation asymmetry becomes more pronounced after the start of the crisis. Specifically, both upside and downside correlations increased. This indicates that after the start of the Covid-19 crisis, a positive (negative) oil shock is even better (worse) news for the stock market than an equivalent shock before the crisis.

CRediT authorship contribution statement

Yuji Sakurai: Conceptualization, Methodology, Writing - original draft. Tetsuo Kurosaki: Data curation, Formal analysis, Writing - review & editing.

Appendix A. Description of the H statistic

To make our paper self-explanatory, we explain the definition of the H statistic developed by Ang and Chen (2002) in this subsection.

The H statistic is defined as

$$H={\left[\sum _{i=1}^{N_{\theta }}w\left({\theta }_i\right){({\tilde{\rho }}^e\left({\theta }_i\right)-{\rho }^e({\theta }_i,\varphi ))}^2\right]}^{1/2},$$ (A.1)

where ϕ is a vector of model parameters. N_θ is the total number of thresholds θ_i. $\tilde{\rho }\left({\theta }_i\right)$ is the empirical exceedance correlation computed based on actual data.

ρ(θ_i, ϕ) is the theoretical value of the exceedance correlation calculated under the benchmark model. For a bivariate normal distribution, ϕ is reduced to the correlation parameter ρ_normal. In our empirical analysis, we use the historical unconditional correlation as ${\widehat{\rho }}_{normal}$. If the empirical exceedance correlation is described by the normal distribution, the H statistic should be close to zero.

There are two specifications for the weight w(θ_i). The first specification is the equal weight defined as

$$w\left({\theta }_i\right)=1/N_{\theta }.$$ (A.2)

The second specification is the threshold-dependent weight defined as

$$w\left({\theta }_i\right)=\frac{T\left({\theta }_i\right)}{{\sum }_{i=1}^{N_{\theta }}T\left({\theta }_i\right)},$$ (A.3)

where the number of samples T(θ) is defined as

$$\begin{array}{c}\hfill T\left(\theta \right)=\{\begin{array}{c}\sum _{t=1}^{N_T}{1}_{\{{\widetilde{ϵ}}_x<\theta ,{\widetilde{ϵ}}_y<\theta \}},\text{if}\theta \le 0.\hfill \\ \sum _{t=1}^{N_T}{1}_{\{{\widetilde{ϵ}}_x>\theta ,{\widetilde{ϵ}}_y<-\theta \}},\text{if}\theta \ge 0.\hfill \end{array},\end{array}$$ (A.4)

where N_T is the total number of sample. Notice that ${\sum }_{i=1}^{N_{\theta }}w\left({\theta }_i\right)=1$ for both specifications.

Following Ang and Chen (2002), our preference is the second approach H_T to the first approach H_E because H_T takes into account that the number of samples satisfying the condition decreases as the absolute level of the threshold θ increases. Hence, the weight is designed to be smaller for the larger threshold θ in the second specification.

To test non-normality of the H statistic, we need to compute its standard deviation. To do so, we generate two stochastic variables sampled from the bivariate normal distribution with ρ_normal and compute the H statistic for the generated time series. The time length is the same as the empirical data. For each path, one estimate of the H statistic is obtained. We iterate the procedure 1000 times and calculate the standard deviation of the H statistic.

Appendix B. Economic impact of correlation asymmetry

We assume that an investor has a power utility function.

$$U=\text{E}\left[\frac{W_T^{1-\gamma }}{1-\gamma }\right],$$ (B.1)

where the final wealth W_T is calculated as

$$W_T=W_0(w_{oil}\exp \left(r_{oil}\right)+w_{stock}\exp \left(r_{stock}\right)+(1-w_{oil}-w_{stock})\exp \left(r_f\right)),$$ (B.2)

where r_oil and r_stock are log returns of the oil and the US stock index, respectively. W ₀ is the initial wealth. w_oil and w_stock are the allocation for the oil and the stock index, respectively. We consider that the estimated bivariate normal mixture model is a true model for r_oil and r_stock. γ is the risk aversion parameter. We set $\gamma =4$ following Ang and Chen (2002). We also assume that the risk-free rate $r_f=0$ in our empirical analysis because the time frequency of our data is daily and it is natural to assume that the daily risk-free return is close to zero during the Covid-19 crisis.

First, we solve the portfolio optimization problem under the estimated bivariate normal mixture model.

$$U^{*}={\text{max}}_{w_{oil},w_{stock}}{\text{E}}_{nm}\left[\frac{W_T^{1-\gamma }}{1-\gamma }\right].$$ (B.3)

Second, we solve the portfolio optimization problem under the bivariate normal distribution in which the correlation is set to the empirical unconditional correlation.

$$(w_{oil}^{**},w_{stock}^{**})={\text{argmax}}_{w_{oil},w_{stock}}{\text{E}}_{normal}\left[\frac{W_T^{1-\gamma }}{1-\gamma }\right],$$ (B.4)

where $w_{oil}^{**}$ and $w_{stock}^{**}$ are the optimal allocation under the normal distribution.

Third, we calculate the expected utility under the normal mixture model but with the quasi-optimal allocation ($w_{oil}^{**},$ $w_{stock}^{**}$).

$$U^{**}={\text{E}}_{nm}\left[\frac{W_T^{1-\gamma }}{1-\gamma }\right]\text{with}{w}_{oil}^{**}\text{and}{w}_{stock}^{**}.$$ (B.5)

Fourth, we compute the certainty equivalent wealth for both cases as follows:

$$W_T^k={\left((1-\gamma )U^k\right)}^{1/(1-\gamma )},$$ (B.6)

where $(W_T^k,U^k)=(W_T^{*},U^{*})$ or $(W_T^{**},U^{**})$.

Finally, we define the economic impact of not capturing the correlation asymmetry as

$$\text{Economic}\text{Impact}=\frac{{(W_T^{**}/W_0)}^d-1}{{(W_T^{*}/W_0)}^d-1}-1,$$ (B.7)

where d is set equal to 252 in order to annualize the value of the economic impact. Equation (B.7) shows that how much an investor could lose the return on their wealth if they do not capture the correlation structure correctly, compared to the case when they correctly capture it. The impact is measured in relative term.

Note that the economic impact is always negative because $W_T^{**}$ is smaller than $W_T^{*}$ given the fact that the sub-optimal expected utility U ^⁎⁎ is lower than the optimized expected utility U*.