Modelling unitary fields and the single‐neuron contribution to local field potentials in the hippocampus

Abstract

Key points

• We simulate the unitary local field potential (uLFP) generated in the hippocampus CA3, using morphologically detailed models.

• The model suggests that cancelling effects between apical and basal dendritic synapses explain the low amplitude of excitatory uLFPs.

• Inhibitory synapses around the soma do not cancel and could explain the high‐amplitude inhibitory uLFPs.

• These results suggest that somatic inhibition constitutes a strong component of LFPs, which may explain a number of experimental observations.

Abstract

Synaptic currents represent a major contribution to the local field potential (LFP) in brain tissue, but the respective contribution of excitatory and inhibitory synapses is not known. Here, we provide estimates of this contribution by using computational models of hippocampal pyramidal neurons, constrained by in vitro recordings. We focus on the unitary LFP (uLFP) generated by single neurons in the CA3 region of the hippocampus. We first reproduce experimental results for hippocampal basket cells, and in particular how inhibitory uLFP are distributed within hippocampal layers. Next, we calculate the uLFP generated by pyramidal neurons, using morphologically reconstructed CA3 pyramidal cells. The model shows that the excitatory uLFP is of small amplitude, smaller than inhibitory uLFPs. Indeed, when the two are simulated together, inhibitory uLFPs mask excitatory uLFPs, which might create the illusion that the inhibitory field is generated by pyramidal cells. These results provide an explanation for the observation that excitatory and inhibitory uLFPs are of the same polarity, in vivo and in vitro. These results suggest that somatic inhibitory currents are large contributors to the LFP, which is important information for interpreting this signal. Finally, the results of our model might form the basis of a simple method to compute the LFP, which could be applied to point neurons for each cell type, thus providing a simple biologically grounded method for calculating LFPs from neural networks.

In conclusion, computational models constrained by in vitro recordings suggest that: (1) Excitatory uLFPs are of smaller amplitude than inhibitory uLFPs. (2) Inhibitory uLFPs form the major contribution to LFPs. (3) uLFPs can be used as a simple model to generate LFPs from spiking networks.

Key points

• We simulate the unitary local field potential (uLFP) generated in the hippocampus CA3, using morphologically detailed models.

• The model suggests that cancelling effects between apical and basal dendritic synapses explain the low amplitude of excitatory uLFPs.

• Inhibitory synapses around the soma do not cancel and could explain the high‐amplitude inhibitory uLFPs.

• These results suggest that somatic inhibition constitutes a strong component of LFPs, which may explain a number of experimental observations.

Introduction

The local field potential (LFP) recorded from the hippocampus is rich in variety of signal during different network states. Sharp waves (Buzsaki, 1986), ripples (Buzsaki et al. 1992; Ylinen et al. 1995), theta (Bullock & McClune, 1990; Buzsaki, 2002) and gamma (Colgin & Moser, 2010) are different types of waveform found in the LFP. These patterns of activity are population phenomena, which require synchronized contributions of a large number of neurons. However, it was not until 2009 (Glickfeld et al. 2009) and 2010 (Bazelot et al. 2010) that researchers showed that the LFP not only reflects synchronized network behaviour, but also the field produced by just a single basket cell activity in the rat hippocampus in vitro. Previously, the field triggered by a single neuron (called unitary field potential or uLFP) was thought to be of too small an amplitude to be recordable above the noise level (Rall & Shepherd, 1968). Why is the hippocampal basket cell so special then? The axon of a basket cell does not extend very far from the cell body (soma) and it mostly targets the bodies and proximal dendrites of nearby pyramidal cells. In the hippocampus, pyramidal cell somata are packed in a single layer called the stratum pyramidale, leading to the axon of a basket cell to form what appears to be the shape of a basket (hence the name). The synaptic currents induced in the postsynaptic population are therefore clustered in space.

However, in 2017 Teleńczuk et al. (2017 a) showed that not only in the hippocampus but also in in the neocortex in vivo in humans and in monkeys, it is possible to extract unitary fields generated by not only single inhibitory but also by single excitatory neurons. Surprisingly, however, the two signals were of the same polarity despite being generated by currents of opposite sign. Moreover, there was a systematic time lag between them, with excitatory fields peaking later than inhibitory fields. It was hypothesised that excitatory uLFPs may in fact be disynaptic inhibitory uLFPs: when a single pyramidal neuron fires, it induces the firing of inhibitory neurons which in turn generate the uLFPs. It is very likely that the same happens in the hippocampus where the pyramidal neuron‐basket neuron connections are known to be very reliable (Miles, 1990).

In the present paper, we seek for plausible mechanisms to explain these observations, considering the hippocampus. We first reproduced the basket cell in vitro experiments in the model. We show that, indeed, the extent of the axon of a basket cell creates a high likelihood of triggering relatively large extracellular fields. We show how this signal spreads within different hippocampal layers. Next, we repeat the same simulations for two pyramidal cells with very different axon reach. Here, we show that the excitatory uLFP in vitro is of a much smaller amplitude than the inhibitory uLFP, although the exact location and size will depend on the axon extent and where it is cut during the slicing procedure. Finally, we check if the hypothesis of Teleńczuk et al. (2017 a) is also correct for the hippocampal data. By superimposing the excitatory uLFP with inhibitory uLFP after a short delay we show that, indeed, the excitatory uLFP is being masked, leading to a pyramidal cell‐triggered inhibitory field. Finally, we propose that uLFPs calculated by our model might form the basis of phenomenological models of the LFP, by convolving the generated spiking activity of point neuron models with calculated unitary fields for specific cell types in space and time. This in turn will enable better and faster understanding of recorded LFPs.

Materials and methods

Passive cellular models

Computational models were based on morphologically reconstructed pyramidal neurons from the rat hippocampal CA3 area. The morphologies were obtained from the NeuroMorpo.org online database and were integrated into the NEURON simulator (Hines & Carnevale, 1997) (Neuron 7.3) for simulations of the postsynaptic neurons. The NeuronEAP python library (Telenczuk & Telenczuk, 2016) (under Python 2.7) was used to calculate the LFP. The time step of all the simulations was 0.025 ms. Passive membrane parameters were membrane resistance of Rm = 10,000 Ohm‐cm², axial resistivity of ra = 35.4 Ohm‐cm and specific membrane capacitance of cm = 1 μF cm^‐2. Other details about morphological arrangements are given in the Results section.

Size of the slice

The soma of the presynaptic cell was assumed to be at coordinate (0,0,0). This assumption was used to calculate the time for the synapse onset (a synapse placed further from the presynaptic cell soma would activate slightly later). The propagation velocity in the axon for inhibitory and excitatory neurons which we used for those calculations are indicated in the 1. We did not model the activity of the presynaptic cell. The slice size extended from ‐500 to 500 μm in length, ‐500 to 800 μm in height, and ‐200 to 200 μm (400 μm) in thickness which is the commonly used slice width in experimental studies interested in measuring LFP (Bazelot et al. 2010; Maier et al. 2011). The somata of postsynaptic cells were placed throughout the length and the width of the slice and within ‐40 to 40 μm in height direction (i.e. pyramidal cell layer).

Postsynaptic population

To model the postsynaptic population, we inspected multiple CA3 pyramidal cell morphologies which were reconstructed from the rat hippocampus and which we downloaded from the NeurMorpho.org online database. This inspection was done in two ways: (i) visually, where we checked if the neurons did not look flatter and if the overall dendritic tree appeared uninjured (Fig. 1A ), and (ii) quantitatively, where we monitored the change of size in diameter of the dendrites making sure that it decreased with the distance from the soma (Fig. 1B ) as the diameter of the dendrites is of crucial importance for calculating the correct extracellular field. We decided to take all the selected reconstructions from the database of a single lab, and we chose Amaral (Ishizuka et al. 1995). This selection process led us to 20 distinct CA3 pyramidal cell morphologies which we then translated vertically, with apical dendrites facing up (Fig. 1A ). We randomly drew the morphologies from the pool of those 20 preselected cells to form the postsynaptic population. The number of segments varied between the cells but it was on a scale of around 2000 segments per cell. The morphologies remained passive throughout the simulations. We decided to use only morphologies of pyramidal neurons, as they form the largest postsynaptic population, while other connections are mostly made to CA1 neurons (Li et al. 1994; Wittner et al. 2006; Bezaire and Soltesz, 2013; Donoso et al. 2018).

Figure 1. Model characteristics.

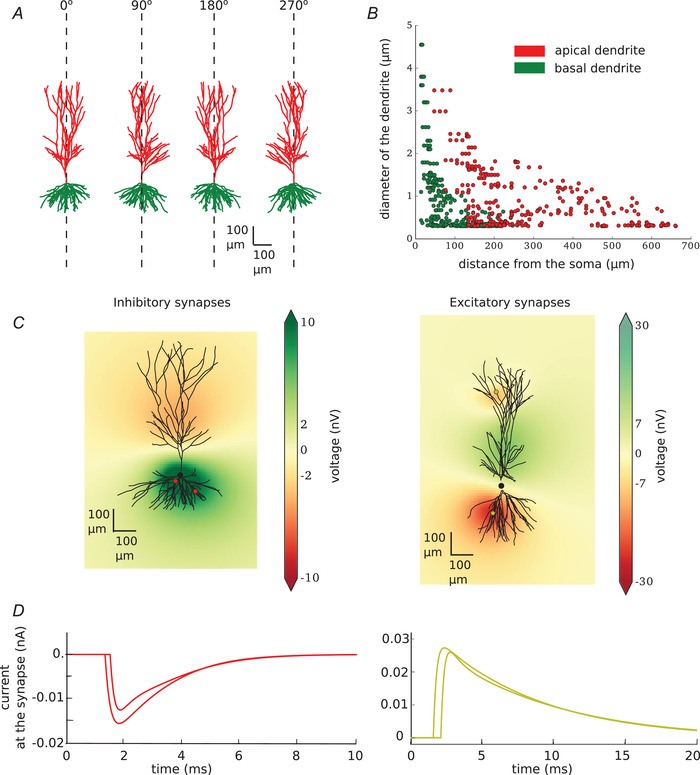
A, example of morphology used in the modelled population (20 different morphologies are used). All of the neurons are reconstructed uploaded by Amaral and can be downloaded from neuromor‐pho.org (ID of the neuron shown in this figure: c81463). They are recorded in the rat CA3 area of the hippocampus. All of the neurons were translated to be vertically oriented with apical dendrites on the top and basal dendrites on the bottom. B, width of the apical (red) and basal (green) dendrites as the function of their distance from the soma. C, single neuron with two inhibitory (left) or two excitatory (right) synapses. Synapses are visualised as red (inhibitory) or yellow (excitatory) dots on the dendritic tree. Local field potential is shown at 2.5 ms after the beginning of the simulation (synapses were activated at 1 ms). D, current at the inhibitory (left, red) and excitatory (right, yellow) synapses. [Color figure can be viewed at wileyonlinelibrary.com]

Synaptic input

Next, we placed synapses on each of the postsynaptic neurons. Each synapse was placed directly on the dendrite. The parameters and number of the synapses (Table 1) differed for the two presynaptic cell types and were in agreement with the literature. All postsynaptic neurons received at least one synapse; further synapses were added with probabilities indicated in Table 1. The amplitudes and time constants of simulated synaptic currents are also given in Table 1. Synaptic current is usually measured from the soma, which is not a problem in the case of the basket cells, which place their synapses in the soma. However, it may cause discrepancies in case of input from pyramidal neurons which place their synapses far from the soma. To account for this we used the values calculated for the current at the dendrite as given in the paper by Guzman and colleagues (Guzman et al. 2016 a).

Table 1.

Cell parameters. Parameters used for modelling of basket cell (inhibitory) and pyramidal neurons (excitatory) together with the references to the original measurements. If in the ‘excitatory’ column there are two different numbers given, the first number relates to Cell A and the second to Cell B

Name	Inhibitory	Excitatory
# of postsynaptic cells	1000 (Miles et al. 1996; Klausberger et al. 2003)	1600, 2210
total # of synapses placed	3435	2282, 2953
# of synapses on each target	1–6 (Gulyas et al. 1993; Klausberger et al. 2003)	1–2 (Guzman et al. 2016 a)
probability of creating each next synapse	0.5	0.42 (Guzman et al. 2016 a)
membrane potential	‐70 mV	‐57 mV (Kowalski et al. 2016)
propagation velocity in the axon	0.5 m/s	0.45 m/s (Meeks & Mennerick, 2007)
synapse reversal potential	‐75 mV (Buhl et al. 1995; Wang and Buzsaki, 1996; Bartos et al. 2002)	0 Mv
synapse rising tau	0.45 ms (Miles et al. 1996; Bartos et al. 2002; Bazelot et al. 2010)	0.26 ms (Guzman et al. 2016 b)
synapse decaying tau	1.2 ms (Miles et al. 1996; Bartos et al. 2002; Bazelot et al. 2010)	6.71 ms (Guzman et al. 2016 b)
maximum synapse conductance	5 nS (Bartos et al. 2002)	0.54 nS (Guzman et al. 2016 a)
external resistivity	3.5 Ωm	3.5 Ωm

Calculation of the local field potential

To calculate the LFP generated by activation of the synapses on each neuron in space, we used the NeuronEAP python library (Telenczuk & Telenczuk, 2016) which is based on the linear source approximation which calculates the summed potential generated by currents originating from line sources with known sizes and positions (Wilson & Bower, 1992; Holt, 1997). In all calculations, we used an extracellular conductivity of 0.3 Sm (Nunez et al. 2006). Figure 1C shows an example of LFP for two randomly placed inhibitory (left) and excitatory (right) synapses. The current at each of the synapses is plotted in Fig. 1D . Note the difference in latency caused by the axonal propagation delays.

Active cellular models

In some control simulations, we used voltage‐dependent channels, which were taken from models of hippocampal pyramidal cells developed previously (Traub & Miles, 1991; Migliore & Shepherd, 2002). The active cell models had voltage‐dependent Na+, K+ and h‐type channels distributed through the cell, with densities of 5 mS/cm² for Na+, 5 mS/cm² for K+ and from 5 to 10 mS/cm² for Ih. These values were not validated in detail against physiological measurements, but represent the typical range of channel densities found in soma and dendrites.

In this configuration, the LFP generated by excitatory synaptic inputs was affected by the presence of voltage‐dependent currents (Fig. 2, top panels), diminishing the LFP amplitude, with a peak effect close to 1 µV, and generally smaller. In contrast, the LFP from inhibitory inputs was little affected by the presence of voltage‐dependent currents (Fig. 2, bottom panels). Because of these limited effects, and the fact that the simulation time is considerably larger with voltage‐dependent currents, we considered only passive neurons in simulations involving large populations of morphologically reconstructed neurons.

Figure 2. Impact of voltage‐dependent conductance on single‐cell local field potentials.

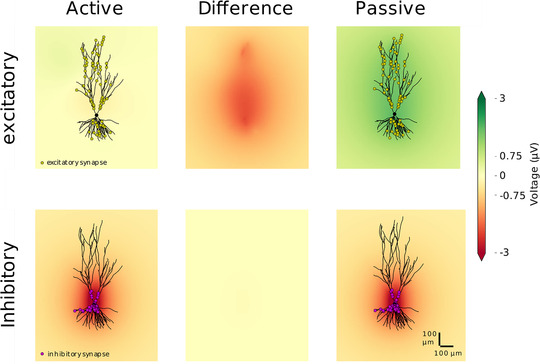
The local field potential was calculated from the activation of synapses in single‐cell simulations, comparing passive and active neurons. The active cell had additional Na+, K+ and h‐type channels distributed through the cell (see Methods). 100 synapses, excitatory (top) or inhibitory (bottom), were placed on a single postsynaptic pyramidal cell (NeuroMorpho.org ID: NMO 00199 (Ishizuka et al. 1995)) according to their biological localisation (excitatory synapses distanced from the soma and inhibitory synapses at the soma and nearby dendrites). The coloured field is the field generated by the activation of the synapses on the neuron with active channels (left) and on the passive neuron (right). The field is displayed at the time point with the largest absolute difference between the field produced by the active and passive neuron. The difference at this time point is shown in the middle panels. [Color figure can be viewed at wileyonlinelibrary.com]

The program codes are openly available in a public repository (Telenczuk et al. 2020) (see details in the Additional Information Section).

Results

Inhibitory unitary field potential

First, we reproduced the published experimental results of Bazelot and colleagues (Bazelot et al. 2010) in the model. We placed 1000 pyramidal cells in space to mimic the slice configuration (Miles et al. 1996) (as indicated in Materials and Methods; location of the somata of the postsynaptic cells: Fig. 3A ). Next we created at least one, and a maximum of six, inhibitory synapses on each of the cells. The highest probability of creating a synapse was within the pyramidal cell layer or, within stratum lucidum (Miles et al. 1996). Throughout the length of the slice the probability decreased with the distance from the body of the presynaptic cell with a Gaussian profile. The exact location of the synapses is indicated by red dots in Fig. 3B . Red histograms show the distribution of the synapses throughout the length of the slice (Fig. 3B top histogram) and throughout the hippocampal layers (Fig. 3B histogram on the right). Four randomly chosen morphologies of postsynaptic neurons with somata represented by black dots were also drawn to give an idea of the spread of dendritic trees through the layers (Fig. 3B ).

Figure 3. Inhibitory unitary field potential.

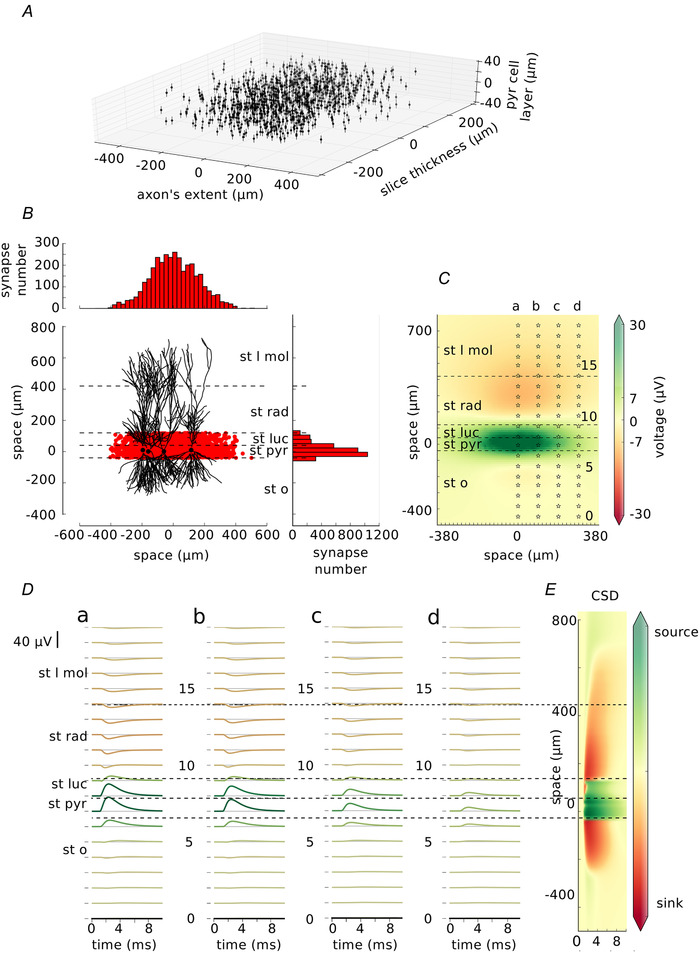
A, distribution of the postsynaptic neurons within a slice. Each dot represents a soma of one pyramidal cell. B, distribution of the synapses. Each red dot shows the location of the inhibitory synapse within the length of the slice and within the hippocampal layers. 3435 inhibitory synapses were placed on the postsynaptic targets. Their distribution in both axes is shown on the top and on the right. Four, randomly selected, exemplary postsynaptic neurons with their somata indicated by black dots are drawn for better understanding of spatial relations. C, local field potential at 2.5 ms from the start of the simulation (synapses were activated at 1 ms). Stars show the locations of the electrodes (0–19) with each fifth electrode marked by a number. Electrodes form 20‐electrode arrays marked a–d. D, traces recorded by the electrode array a–d corresponding to the locations from C. Traces are coloured by their maximum absolute peak corresponding to the colour map in (C). E, current source density analysis done on the field average across the length of the axon (x direction). Layers: st l mol – stratum lacunosum moleculare, st rad – stratum radiatum, st luc – stratum lucidum, st pyr – stratum pyramidale, st o – stratum oriens. [Color figure can be viewed at wileyonlinelibrary.com]

Next, we simulated the activation of the synapses and we calculated how the generated current spreads through the cells and in the extracellular space. From those currents we calculated the LFP within 10 ms of the simulation time. An example of LFP (1.5 ms after the activation of the closest synapses) is shown in Fig. 3C . The LFP is shown across different layers of the hippocampus: stratum lacunosum moleculare (St l mol), stratum radiatum (st rad), stratum lucidum (st luc), stratum pyramidale (st pyr) and stratum oriens (st o). Not surprisingly, the potential of the highest amplitude is recorded around the location of the synapses. Columns of stars marked a–d represent the location of the array of electrodes placed along the hippocampal layers. Each electrode in an array is numbered 0–19. Such recordings of LFP in the CA3 area of the hippocampus in vitro have been previously performed experimentally using eight electrodes (Bazelot et al. 2010, 2016). The traces obtained from each electrode are shown in Fig. 3D . Their amplitude decreases with the distance of the presynaptic neuron with agreement to Bazelot et al. (2010). The location of the electrode has an influence on the amplitude and deflection of the recorded signal. Finally, we calculated current source density analysis which clearly shows the source of the current in the pyramidal cell layer and nearby.

Next, to compare our findings with the published experimental results we selected one of the largest signals (array a, electrode 7) and we measured its amplitude, and the time from the beginning of the rise to the peak of the signal (Fig. 4A ). In the paper by Bazelot and colleagues (Bazelot et al. 2010) the mean amplitude of the recorded signal was 28.1 μV whereas recording from our largest waves was 36.7 μV. Although Bazelot and colleagues did not specify rise‐to‐peak time, the timings read from their figures are similar (1.53 ms in Fig. 4A ). After that, we checked how the location of the maximum and minimum peaks of the signal vary depending on the location of the electrode in different layers.

Figure 4. Characteristics of inhibitory unitary local field potentials.

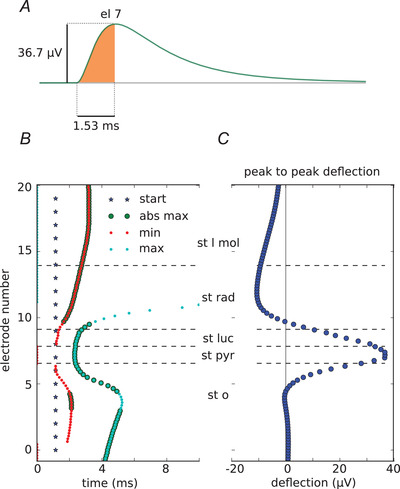
A, recording from electrode 7, array a (location shown in Fig 3 C). The area shaded in orange indicates the measurements: the amplitude of 36.7 μV and time to peak of 1.15 ms. B, stars show the beginning of the synapse activation. Times to minimum and maximum peak of each trace recorded by array a are indicated by red and blue dots, respectively. Enlarged dots indicate that the peak was the absolute maximum in the trace. Time to peak varies between layers. The peak arrives the earliest (start of the rise to peak: 1.53 ms) in stratum pyramidale while it is as late as 3.05 ms in stratum moleculare (time from blue line to bold red and blue dots). C, peak‐to‐peak deflection within different hippocampal layers. The highest positive peak is in stratum pyramidale but it points downwards in stratum radiatum and stratum lacunosum moleculare. [Color figure can be viewed at wileyonlinelibrary.com]

To this end we took measurements from all the electrodes in the electrode array and we checked for the maximum and minimum in time. The time of the peaks varied, largely depending on where the electrode was placed (Fig. 4B ). Finally, we measured the peak‐to‐peak deflection throughout different layers, the distribution of which we show in Fig. 4C . It shows how the amplitude and the deflection of the measured signal might change with just a very slight shift of the electrode within the hippocampal layers.

Excitatory unitary field potential

Axonal trees of pyramidal neurons are very different from those of basket cells. They tend to be very long (200 mm for CA3b to 500 mm for CA3c pyramidal neurons (Ropireddy et al. 2011), as compared with 900–1300 μm in basket cells (Klausberger et al. 2003)) and longitudinal projections of single axons can extend very far (even to 70% of the dorsoventral extent of the hippocampus) (Lorente de No, 1934; Sik et al. 1993; Li et al. 1994) (but see Norenberg et al. (2010) in Dentate Gyrus).

To model uLFPs produced by single pyramidal neurons, we used morphologically reconstructed pyramidal neurons from rat CA3 (see Methods). We searched the NeuroMorpo.org online database for the best preserved pyramidal cell axons from the rat CA3. We selected two cells: one with NeuroMorpho.org ID: NMO 00187 (Turner et al. 1995) which we will call Cell A (Fig. 5A left) and a second cell with NeuroMorpho.org ID: NMO 00931 (Scorcioni & Ascoli, 2005), which we will call Cell B (Fig. 5A right). Next, we rotated them so that the dendritic tree was oriented vertically and we calculated the length of the axon in each 50 μm × 50 μm bin. Blue histograms in Fig. 5A left and right show the total length of the axon within 50 μm bin in each axis (and summed across other axes) for Cell A and Cell B, respectively (the length of the axon in the z‐direction is not shown). The axon is drawn in blue and the location of the soma is indicated by the red star. Next, we cut the axon to the slice of size: ‐500 μm to 500 μm from the soma of the presynaptic pyramidal cell in the x‐direction, by ‐500 μm to 800 μm in the y‐direction and by ‐200 μm to 200 μm in the z‐direction. The extent of the slice in two directions is shown by the green rectangle and the remaining length of the axon by green histograms in Fig. 5A . We calculated the total length of the axons by adding all the measurements from all the bins. Total length of the axon of Cell A was 468.57 mm; after the cutting, only 11.16 mm remained (being around 2% of the original axon). The total length of the axon of Cell B was 205.17 mm; after cutting, 14.12 mm remained (around 7% of the original axon). By giving these numbers we want to emphasize how small a fraction of the pyramidal cell axon remains in the experimental slice. This has also been pointed out previously (Ishizuka et al. 1990).

Figure 5. Excitatory unitary field.

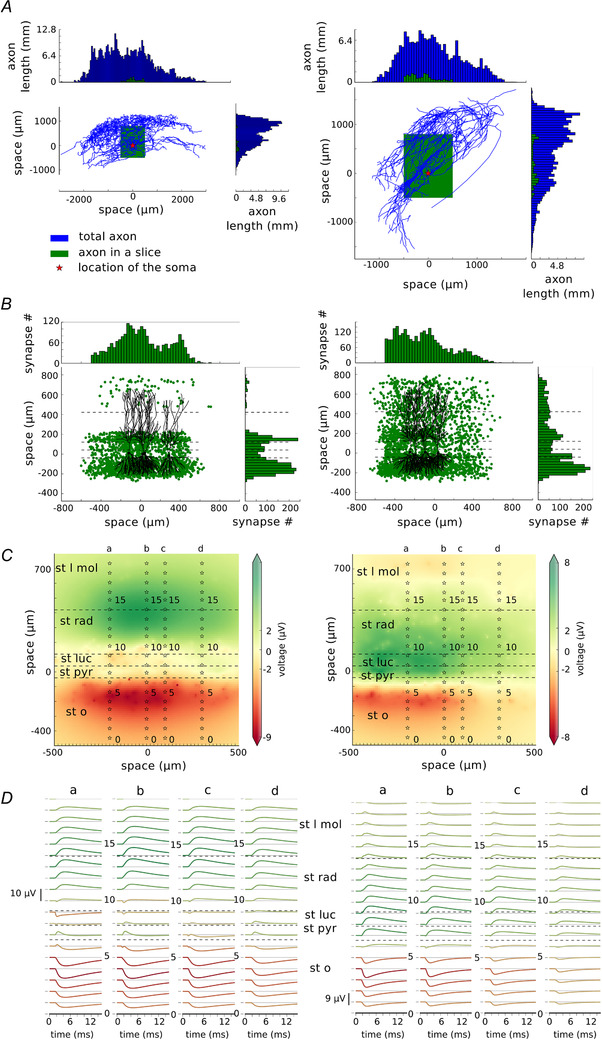
A, axon morphologies of two CA3 pyramidal cells, Cell A (left, ID: NMO 00187) and Cell B (ID: NMO 00931) downloaded from NeuroMorpho.org. These cells were rotated so that their dendrites are placed vertically. Blue histograms show the length of the axon in each 50 μm bin in two axes. Axon morphologies are indicated by blue lines with the red star showing the location of the soma. Green rectangles show where the axon was cut consistently with the size of a typical slice (‐500 μm to 500 μm from the soma in the length of the slice, ‐500 μm to 800 μm in the height and ‐200 μm to 200 μm in the width of the slice). Green histograms show the length of the axon remaining after the cutting. B, the distribution of the excitatory synapses in the model for Cell A (left) and Cell B (right). The distribution follows the distributions calculated by the length of the axon in A, but with constraints given by the morphologies of the postsynaptic cell population. Four randomly chosen morphologies of postsynaptic cells were drawn for easier visualisation of the spatial relations. C, local field potential plotted at 5.5 ms after the beginning of the simulation with four electrode arrays (a–d) placed at ‐200, 0, 100 and 300 μm from the presynaptic cell soma. D, traces recorded by each of the electrode arrays marked as a–d. st l mol – stratum lacunosum moleculare, st rad – stratum radiatum, st luc – stratum lucidum, st pyr – stratum pyramidale, st o – stratum oriens. [Color figure can be viewed at wileyonlinelibrary.com]

It is known that inter‐varicosity distance on the CA3 pyramidal axon is on average 4.7 µm (Sik et al. 1993; Li et al. 1994; Wittner et al. 2007). We combined this information with the calculated length of the axon to estimate the probability of placing a synapse within each 50 μm bin. The total number of synapses placed by Cell A should be around 2400 and placed by Cell B should be around 3000. A CA3 pyramidal neuron in 58% of cases places one synapse on its postsynaptic target and in the remaining 42% of cases it places two synapses (Guzman et al. 2016b ). Therefore, we created the postsynaptic cell population of Cell A to be 1600 and of Cell B to be 2210 cells. We gave the probability of placing a synapse matching the distribution of the cut axon, by doing so we ended up with the synapse distribution as indicated by the green dots and green histograms in Fig. 5B (left and right for Cells A and B, respectively). Cell A placed 2282 synapses and Cell B placed 2953 synapses on its postsynaptic targets.

Next, we calculated the LFP generated by the two neurons. The snapshot of those calculations at time 5.5 ms from the beginning of the simulation is depicted in Fig. 5C (Cell A, left; and Cell B, right). Here, we placed four electrode arrays at ‐200 μm, 0 μm, 100 μm and 300 μm from the presynaptic cell body (stars in Fig. 5C indicated by a–d) because due to the non‐symmetrical axon, the synapse distribution is also non‐symmetrical. Unitary field potentials recorded by each of the electrodes (Fig. 5D ) differ largely from those recorded by the activation of basket cell synapses. As expected, the distribution of uLFPs depends on the shape and the extent of the axon. The uLFP for Cell A reaches an amplitude no larger than 10 V. However, at st pyramidale where recordings are most frequently performed, the uLFPs are of an amplitude near 0 μV (peak‐to‐peak in electrode 7 array b is 2.2 μV), with the highest amplitude (up to 8 μV in peak‐to‐peak measurements in array b, and 8.53 μV in electrode 4, array a) in the distant layers such as stratum radiatum and stratum oriens (Fig. 5D ). The uLFP generated by Cell B is of a different distribution. Here, the signal is comparably large in the pyramidal cell layer, even though the strongest signal can be found in st oriens and towards the left part of the slice (Fig. 5D a right, 200 μm away from the soma of the presynaptic cell). However, even the highest uLFP is still of an amplitude not larger than 9 μV.

Finally, we checked the timing of the highest and lowest uLFP peaks within different layers of the hippocampus at location 0 μm from the presynaptic cell body (Fig. 6A ). The time of the absolute maximum peaks differed by as much as 6 ms depending on the location of the measurement. The profile of the peak‐to‐peak deflection differed between the two cells (Fig. 6B left, Cell A; right, Cell B) and it changed across the different layers.

Figure 6. Characteristics of excitatory unitary local field potentials (uLFP). Results for Cell A are on the left and for Cell B are on the right.

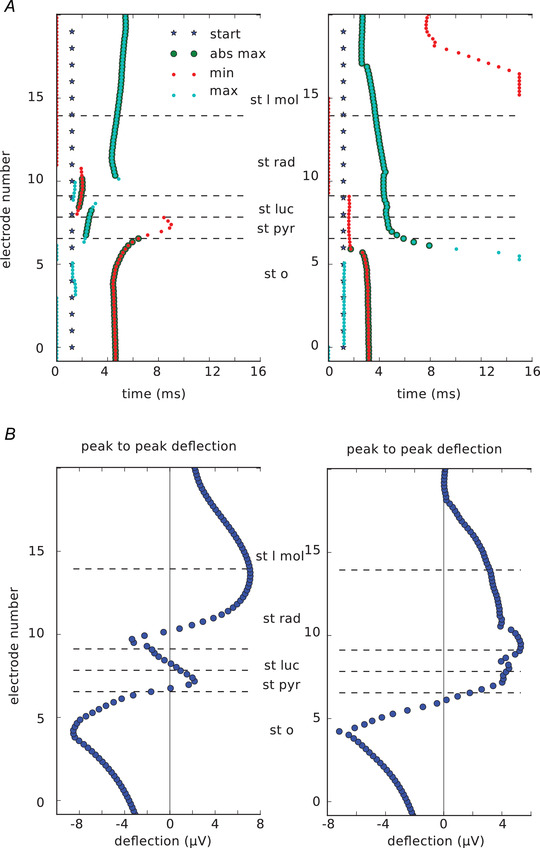
A, stars show the beginning of the synapse activation. Time to minimum and maximum peak of each trace recorded by array b in Fig 5 C (0 μm from the presynaptic soma) is indicated by red and blue dots, respectively. Enlarged dots indicate that the peak was the absolute maximum in the trace. Time to peak varies between layers. B, peak‐to‐peak deflection within different hippocampal layers. It varies between the two cells (left and right). st l mol – stratum lacunosum moleculare, st rad – stratum radiatum, st luc – stratum lucidum, st pyr – stratum pyramidale, st o – stratum oriens. [Color figure can be viewed at wileyonlinelibrary.com]

We conclude that for the two pyramidal neurons the excitatory uLFP might prove difficult to measure experimentally in vitro. One would need to place an extracellular electrode in the correct location, which differs from cell to cell.

Masking of excitatory uLFP with inhibitory uLFP

Pyramidal cells form only a few synapses on their basket cell targets. However, those connections are known to be very reliable (Miles, 1990). Recently, Teleńczuk and colleagues proposed that the unitary fields triggered by the activation of the excitatory neurons which we recorded from the human and monkey neocortex were in fact bisynaptic inhibitory unitary fields (Telenczuk et al. 2017 a). We believe that this might also be true in the hippocampus. To check if this is indeed plausible, we superimposed the excitatory uLFPs generated by Cell A and Cell B with the inhibitory uLFP after a 3 ms time delay (Fig. 7) (Miles & Wong, 1984; Miles, 1990). The LFP at 5.5 ms after the beginning of the simulations shows a much stronger contribution of the inhibitory uLFP with very strong positive field around the stratum pyramidale (Fig. 7A ). The recordings from the a–d electrode arrays reveal very minor excitatory uLFP contributions compared with the strong inhibitory uLFP contributions (Fig. 7). Our results show that, indeed, it might be difficult to separate excitatory uLFP from the inhibitory one without the use of manipulations that would block specific cell types. Please also note that in our model both inhibitory and excitatory neurons are located at coordinate (0,0,0), therefore the signal is strong for both. However, in the real recordings it is more likely that the somata will be shifted.

Figure 7. Masking of excitatory unitary local field potentials (uLFP) with inhibitory uLFP. Results for Cell A are on the left and for Cell B are on the right.

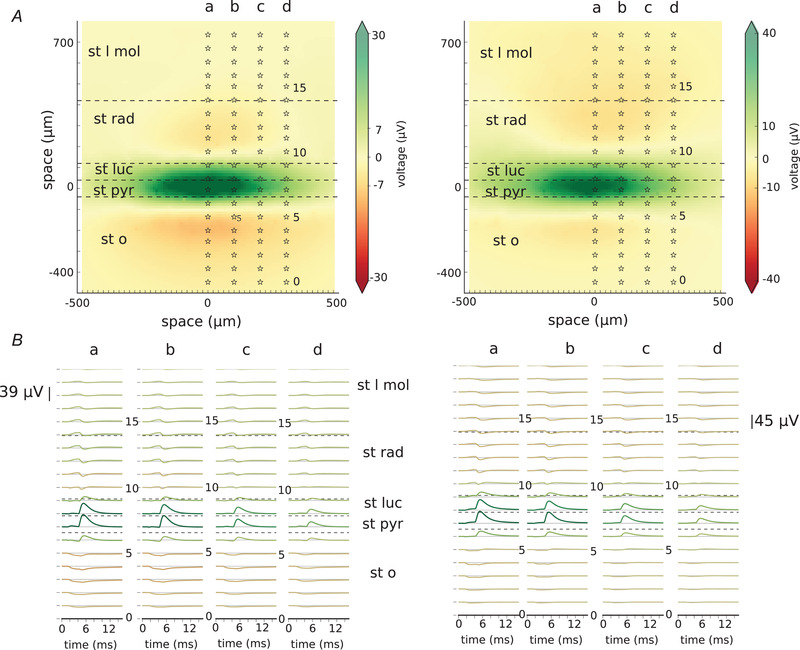
A, local field potential at time 5.5 ms from the beginning of the simulation. At time 1 ms, excitatory synapses were activated (of Cell A on the left, of Cell B on the right) followed by the activation of inhibitory synapses at time 3 ms. Stars show the location of the electrodes belonging to the arrays marked a–d. B, traces showing recordings from the electrode arrays marked a–d in A. st l mol – stratum lacunosum moleculare, st rad – stratum radiatum, st luc – stratum lucidum, st pyr – stratum pyramidale, st o – stratum oriens. [Color figure can be viewed at wileyonlinelibrary.com]

Discussion

In this paper, we have used numerical simulations of morphologically reconstructed neurons to investigate the single‐neuron contribution to LFPs, the so‐called unitary LFPs or uLFPs. In agreement with previous studies in the hippocampus (Glickfeld et al. 2009; Bazelot et al. 2010) and the neocortex (Telenczuk et al. 2017 a), we found that inhibitory uLFPs are of a larger amplitude than excitatory uLFPs. Consequently, the LFP signal is expected to be dominated by inhibitory currents. We discuss these findings below, their significance and what perspectives they offer for further work.

Our biophysical model was based on reproducing published experimental results (Bazelot et al. 2010) of inhibitory unitary field in the hippocampal CA3 slice from the rat. Next, we used the same model to find out what is the excitatory unitary field produced by pyramidal neurons in the same area. We show that pyramidal neurons also produce unitary field potentials, although of much smaller amplitude and with a very different spatial profile which depends on their exact axonal architecture. Due to limited computational resources we were unable to calculate the field generated by the full pyramidal cell axon (in vivo condition). However, if such resources are available, it would be of interest to check if the excitatory uLFP remains of the same amplitude if the whole axon morphology is considered.

By comparing the two types of uLFP, we found that it is likely that the excitatory uLFP is further masked by the inhibitory uLFP triggered by pyramidal–basket cell interaction.

The explanation for the dominance of inhibitory uLFPs is based on the particularities of the pyramidal cell morphology, as illustrated in Fig. 8. Excitatory synapses, which are located exclusively in apical, oblique and basal dendrites, produce single‐synapse LFPs which are of various polarities, according to their positions (DeFelipe & Fariñas, 1992; Gulyas et al. 1993; Megas et al. 2001). For example, basal dendrite synapses and apical synapses will produce dipoles of opposite polarity, so will partially cancel (Fig. 8A ). This cancellation explains why the uLFP of excitatory synapses is of relatively small amplitude. Inhibitory synapses on pyramidal cells also contact the various parts of the dendrites and will suffer from the same cancelling effect (Fig. 8B ). This cancellation will thus also occur even if inhibitory synapses are depolarizing. However, inhibitory synapses have, in addition, a very high density in the perisomatic region, which not only causes strong inhibition, but it also always forms the same dipole. These dipoles on each pyramidal cell sum up, and yield a uLFP of larger amplitude (Fig. 8C ). This explanation suggests that the spatial distribution of synapses in the cell, and its asymmetry, determine the respective excitatory and inhibitory contributions to LFPs. This explanation is supported by our computational models and should be valid for a large range of parameters, since it is essentially dependent on cell morphology and the distribution of synapses in different regions of the cell.

Figure 8. Proposed biophysical origin of the dominant contribution of somatic inhibition in the local field potential (LFP).

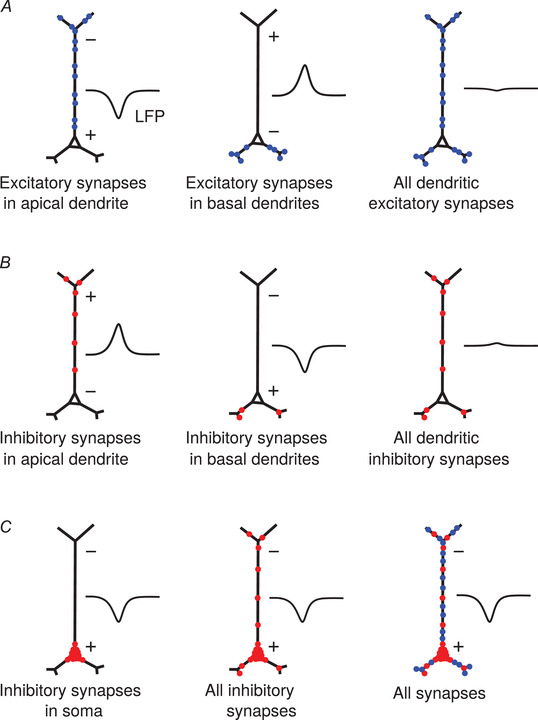
A, excitatory synapses occurring in the apical dendrite (left) or in basal dendrites (middle) produce dipoles of opposite sign. All dendritic synapses therefore produce an LFP of moderate amplitude (right). B, the same cancellation applies to inhibitory synapses in apical and basal dendrites. C, inhibitory synapses in the soma always form the same dipole (left), which will dominate when all inhibitory synapses are present (middle) or with all synapses (right). [Color figure can be viewed at wileyonlinelibrary.com]

In addition, we showed that the axon morphology of pyramidal neurons has a critical influence on the uLFP recorded along the radial and lateral axes (Fig. 5). The morphologies of the axon can vary drastically across neurons, which in turn determine the final distribution of the synapses on their target cells. Importantly, most slice preparations cut a significant part of the axonal arbour leading to a pronounced decrease in the number of synaptic terminals, which could additionally weaken the effect of pyramidal neurons on the LFP compared with the inhibitory neurons.

Inhibitory neurons are generally thought not to contribute to the LFP due to their spherical symmetry which generates a closed‐field geometry that produces little electric field (Lorente de No, 1934). This argument holds mainly for the far‐field potentials directly resulting from interneurons. Here, we show that inhibitory neurons contribute significantly to the LFP, through their postsynaptic effect on pyramidal cells. Thus, we consider here the postsynaptic contribution of the neurons, which does not depend on the dendritic shape of the presynaptic inhibitory neurons, but rather on the reach of their axonal arbour and the morphology of the postsynaptic neuron. This change of paradigm from presynaptic to postsynaptic view has very important consequences for the interpretation of the LFP in terms of activities of specific neuron types and the modelling of these signals. According to this paradigm, excitatory synapses on pyramidal neurons contribute little to the LFP, due to cancelling effects (Fig. 8A ). However, their contribution can still be visible through disynaptic mechanisms. In fact, the synapses of pyramidal neurons on basket cells are strong (Miles, 1990), so single action potentials of pyramidal neurons can reliably activate some basket cells. These, in turn, can produce IPSPs on pyramidal cells, which resulting LFP will thus be associated with the action potentials of the pyramidal neurons. Our model shows that this disynaptic mechanism can lead to a measurable contribution of pyramidal neurons to the LFP, as observed experimentally. This also explains why in the presumed unitary field deduced from human recordings, inhibitory uLFP always have the same polarity and peak earlier than excitatory uLFP (Telenczuk et al. 2017a ), consistent with the disynaptic nature of the latter.

Thus, these findings help with the correct interpretation of the LFP signal. Not only does the present modelling study provide a mechanistic explanation for previous experimental results, but it also suggests a new interpretation of the LFP signal. Because the LFP signal in the tissue is a sum of each neuron's contribution (uLFPs), our paradigm predicts that the LFP mostly reflects the somatic inhibitory currents in pyramidal cells. Note that this paradigm also predicts that soma‐targeting interneurons should be much more visible in the LFP compared with dendrite‐targeting inhibitory cells.

Can these considerations apply to more global signals recorded at the surface of the brain (electrocorticography, ECoG) or from the scalp (EEG)? Assuming that ECoG and EEG signals result from the electric dipoles made by pyramidal cells, the same considerations as above should apply. Our paradigm predicts that these signals should also be dominated by inhibitory activity, and primarily reflect somatic IPSPs on pyramidal cells in the cortex. The testing of such a prediction should be investigated in future models.

Note that this interpretation assumes that the single‐neuron contributions to LFP sum linearly, but in practice this summation may suffer from various non‐linear effects. Deviations from a simple linear summation may result from different factors, such as the dense packing of dendritic processes in extracellular space, and the fact that there may be complicated spatial interactions between membrane and return currents. Extracellular conductivity may also be different in various regions of the neuropil, and extracellular space may also have diffusive and capacitive effects that may make the summation frequency dependent (Bedard et al. 2004, 2006). These effects should be evaluated by more precise models taking these interactions into account.

Other limitations of the present study are that, first, it did not include the LFP contribution of synaptic currents in inhibitory cells. However, these neurons are mostly spherically symmetrical, so that their dipolar contribution is limited. Second, it did not include the possible contribution of intrinsic currents, which were shown to influence LFPs, such as Ih (Reimann et al. 2013; Sinha and Narayanan, 2015; Ness et al. 2016) or K+ conductances (Destexhe, 1998). Including these currents in single‐cell simulations showed moderate effects for excitatory LFPs and nearly no effect for inhibitory uLFPs (Fig. 2), and the difference between the two was actually larger in the presence of intrinsic currents. Third, we did not consider the possible influence of glia which may also influence LFPs on a slow time‐course through ionic buffering. Fourth, we did not consider the non‐local interactions. For instance, the activity of so‐called detonator synapses in the stratum lucidum (arriving from single excitatory Dentate Gyrus (DG) neurons) is large enough to initiate spikes (Andersen et al. 2006; Vyleta et al. 2016; Lee et al. 2019). It could be of interest to study how the activation of a single DG neuron connected to several inhibitory and excitatory neurons in the hippocampus affects the uLFP. However, this would require modelling both the primary effects on the uLFP and the contributions of the postsynaptic targets. These interactions may be a topic for a further study.

Finally, our approach suggests a new way to calculate the LFP from networks of point neurons. Previously, Hagen and colleagues (Hagen et al. 2016) proposed calculating the LFP generated from point neuron models by using their hybridLFPy set of Python classes. Their approach gives a good estimation of the field potential; however, it requires a biophysical calculation of the field from a large number of neurons. Here, we propose an alternative approach which for the same type of models should give less precise but faster estimation of the field. In our model we calculate the LFP by convolving the unitary fields with the spiking activity of each point neuron type locating them in space. Those fields can then be summed linearly. The estimation of the field should be sufficient to estimate the LFP from networks of point neurons, which should be useful for a better understanding of network activity; for example, to model different oscillation types. Note that we would expect this not to work in cases where there is a direct contribution of synchronized spikes, such as hippocampal sharp waves (Canakci et al. 2017) or high‐frequency (600 Hz) oscillations in the somatosensory cortex (Telenczuk et al. 2017 b). Applications to model LFP will be developed in further work.

Competing interests

None declared.

Author contributions

MT, BT and AD conceived the study, MT programmed the model and performed numerical simulations, all authors analyzed the results, and wrote the manuscript. AD supervised the study.

Funding

This work was supported by Centre National de la Recherche Scientifique (CNRS, France), the European Community Future and Emerging Technologies program (The Human Brain Project, H2020‐720270 and H2020‐785907), the ANR PARADOX, and the ICODE excellence network.

Biography

Maria Teleńczuk received her Bachelor in Software Development from CIT in Cork, Ireland, followed by a Masters in Computational Neuroscience awarded jointly by Humboldt University of Berlin and Technische University of Berlin, Germany. She pursued her training in neuroscience at Sorbonne University in Paris where she received a PhD degree for her work on the mechanisms of action potential initiation. After completing a modelling study on unitary field potentials at the National Centre of Scientific Research (CNRS) in Gif‐sur‐Yvette, France, she now works at the Institute for Research in Computer Science and Automation (INRIA), Saclay, France, where she applies machine learning methods to solving neuroscientific problems. Her interests include open‐source software development, machine learning, computational modelling and neuroscience.

Data availability statement

The code for the figures of the full morphology model has been deposited and is openly available in the Zenodo repository (Telenczuk et al. 2020). The NeuronEAP Python library used to calculate the local field potential is also open source (Telenczuk & Telenczuk, 2016).