The Bouguer‐Beer‐Lambert Law: Shining Light on the Obscure

Abstract

The Beer‐Lambert law is unquestionably the most important law in optical spectroscopy and indispensable for the qualitative and quantitative interpretation of spectroscopic data. As such, every spectroscopist should know its limits and potential pitfalls, arising from its application, by heart. It is the goal of this work to review these limits and pitfalls, as well as to provide solutions and explanations to guide the reader. This guidance will allow a deeper understanding of spectral features, which cannot be explained by the Beer‐Lambert law, because they arise from electromagnetic effects/the wave nature of light. Those features include band shifts and intensity changes based exclusively upon optical conditions, i. e. the method chosen to record the spectra, the substrate and the form of the sample. As such, the review will be an essential tool towards a full understanding of optical spectra and their quantitative interpretation based not only on oscillator positions, but also on their strengths and damping constants.

If August Beer would have had a chance to combine Pierre Bouguer's findings and Johann Heinrich Lambert's law with his own results under consideration of James Clerk Maxwell's relations, he would have ensured the Bouguer‐Beer‐Lambert law to be well‐funded on electromagnetic theory. At least, he would have made users well aware of its limitations. Since he died too early, it is the goal of this review to complete his work in this regard.

1. Introduction

The Bouguer‐Beer‐Lambert (BBL) law, as it is presented in many spectroscopy textbooks,1, 2, 3, 4, 5 raises high expectations in its users. The most serious, and quite understandable, expectation certainly is that it is exact – meaning that it provides an accurate description of the effects arising from interaction between light and matter. Therefore, any deviation from it is usually interpreted as variation of the chemical interactions in the sample or a change in molecular structure on the level of a unit cell. All these effects would typically result in a changed energy difference between the electronic/vibrational states, which undoubtedly can serve as a valid explanation for the observations. Unfortunately, a correct interpretation of absorption spectra is not as simple. Basically, all factors that influence band position, height and shape can be divided into three different groups. One group indeed can be very well summarized as chemical interactions. However, there is a second group of wave optics based effects, which comprises all phenomena resulting from the wave nature of light. As we will demonstrate within this review, these have tremendous influence on the spectra as well. Therefore, to be able to make any deductions about the chemical nature of the sample or use the data for quantification, it is vital to correct the spectra for these effects beforehand.

In this review, all these so‐called chemical interactions will not play any role and will be excluded from discussion. The same holds true for any deviations from the BBL law, which are caused by instrumental errors, e. g. insufficient resolution, detector nonlinearity etc. We explicitly focus on deviations, which are caused by the fact that the BBL law is often only remotely compatible with electromagnetic theory. The notion that the BBL law is not consistent with electromagnetic theory might seem strange to most readers, in particular, because often derivations suggest exactly this compatibility, like, e. g. the linear connection between the differential change of intensity and intensity itself as well as the distance travelled by the light. That this connection is not generally correct is not obvious.

Since originally, we were also firm believers that this compatibility is a given, a short historical overview starting with Beer's work and concerning the development of the BBL law and electromagnetic theory might allow to understand the sources of confusion and from where the incompatibilities arose.

1.1. Historical Overview

The work of Pierre Bouguer and Johann Heinrich Lambert dealing with spectrophotometry of the atmosphere was well known to August Beer as can be seen from his book Grundriss des photometrischen Calcüles which was published in 1854.6 Accordingly, Beer described this part of the Beer‐Lambert law as following from the simplest assumption that the loss of the intensity of light transmitted through an infinitesimally thin layer of a homogeneous medium is proportional to this intensity and to the layer thickness. This leads to a differential equation provided by Bouguer, and, in its final mathematical form, by Lambert, the solution of which, reads:

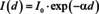
Here, I ₀ is the initial intensity of the light, I(d) is the intensity after travelling the distance d in the medium and α is its Napierian absorption coefficient. In fact, Beer used the words transmitted through, but it is important to emphasize that he considered this as an approximation. Since Bouguer and Lambert dealt with the absorption of the atmosphere, reflection losses did not need to be considered, because the index of refraction of air is very close to unity and transmitting through the atmosphere becomes in good approximation equivalent to propagating within. As we will see later on, this makes a very important difference. Accordingly, two years earlier, in his seminal paper about the determination of absorption of red light in colored liquids, Beer corrected for reflection losses, before concluding that transmittance stays constant, within experimental errors, as long as the product of the volume fraction of the solute and the thickness of the cuvette, ϕ ⋅ d, stays constant.7

Beer did not introduce the molar concentration c (which is the product of the volume fraction and the inverse partial molar volume), neither did he combine eqn. (1) with the law found by him, nor did he introduce the quantity absorbance. In fact, Beer also wrote a comprehensive book about optics published in 1853, in which he excluded absorption from the discussion right from the start, since space, air, water and glass are completely transparent and colorless. In addition, it is easy to assess the modifications which are necessary for absorption.8 It is pure speculation at this point, but if he had not died so young, he might have formulated the Bouguer‐Beer‐Lambert law by himself. Instead, it took much longer before the law that we know as BBL law was formulated (for an overview of the developments, cf. Figure 1).

Figure 1.

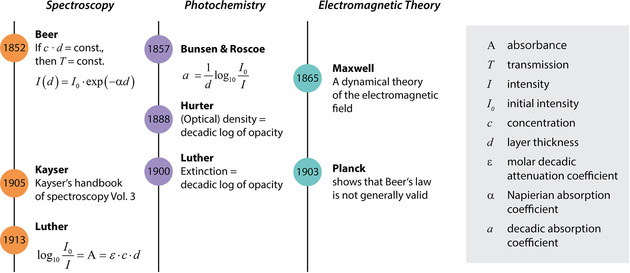
Timelines of important historical developments for the development of the (Bouguer‐)Beer‐Lambert law in its current form.

Five years after Beer's seminal paper, in 1857, Bunsen and Roscoe made a big step towards the modern formulation of the BBL law.9 The topic of Bunsen's and Roscoe's paper was the photochemical absorption of light. Despite the different pathway of the absorbed energy, the law concerning the absorption of light is the same. The way in which they expressed the absorptivity a is given by:

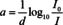
It seems that the next 50 years, important steps to further develop eqn. (2) were exclusively made in photochemistry. In 1888, Hurter defined the (optical) density as the natural logarithm of the opacity, which is defined as 1−I/I ₀ and equal to the absorbed fraction of light, if reflectance is neglected.10 Twelve years later, in 1900, Luther defined the German term Extinktion,11 which is equivalent to the quantity absorbance, as the natural logarithm of opacity.

In spectroscopy, it seems it took some time until this definition was used. The reference for spectroscopy at that time was Kayser's handbook which consisted of four volumes with about 2400 pages altogether. In the third volume, Kayser introduced several different formulations of the absorption law, but the modern formulation was not among them.12 It seems that the first time the modern formulation was used in which the Bouguer‐Lambert law and Beer's law were merged, was again a paper from Luther published in 1913.13 Accordingly, the absorbance A is given by

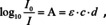
in which ϵ is the molar decadic absorption coefficient, so that ϵ ⋅ c=a.

In parallel to the developments in spectroscopy and photochemistry, also the field of optics made important progress. The most important step was unquestionably Maxwell's theory, which led to interpreting light as electromagnetic wave.14 The consequences of this finding were, however, not as drastic as one might think. Snell's law, e. g., was derived under the assumption that light is an elastic wave and so were the early attempts to explain the change of the index of refraction with the color or the frequency/wavelength of light. While first derivations did not include the phenomenon of absorption, it was Helmholtz who understood, as early as 1875, its importance to describe anomalous dispersion (which usually means the range of the index of refraction, where it decreases with increasing frequency around and due to absorption bands. Most of the time the index of refraction decreases with decreasing frequency; in addition, points can be found in a spectrum where dispersion is zero).15 While Helmholtz did not take into account Maxwell's findings, Max Planck's flavor of dispersion theory was well grounded on electromagnetic theory.16 At this time, the physicists were already well aware of the fact that absorption and dispersion are two sides of the same coin. Therefore it is not surprising that Max Planck also investigated the consequences of dispersion theory on Beer's law in detail in his original formulation (which is that transmittance is constant when ϕ ⋅ d stays constant).17 Certainly, Planck could not derive the concentration dependence of absorbance, since this was a widely unknown quantity at that time, but he could already show that for strong absorption Beer's law cannot hold. It is remarkable that such an important finding of a Nobel laureate could have been forgotten, but in light of the golden twenties in physics, which culminated in the discovery and formulation of quantum mechanics this might be understandable.

While Beer's part of the BBL law remained therefore merely an empiric law, it was known to the infrared spectroscopists of this time that the Bouguer‐Lambert part is a, sometimes very, rough approximation. Explicitly, this was emphasized in the work of Marianus Czerny, a former PhD student of Heinrich Rubens (known for the “reststrahlen” method) who investigated the infrared spectrum of thin cuts of NaCl in order to compare the experimental results with those obtained from dispersion theory.18 In addition, this is also detailed in one of the first books about infrared spectroscopy authored by Clemens Schaefer and Frank Matossi.19 After 1945 the infrared community split and the knowledge of the former researchers prevailed in the community where inorganic crystals or layered materials are of primary interest. In contrast, Coblentz's school became prevalent for the interpretation of spectra of organic and biological samples, while infrared spectrometers were translated from the lab to a marketable product.20

2. Deviations between the Bouguer‐Lambert Law and Electromagnetic Theory: Non‐linear Thickness Dependence

It may be obvious from the historical overview, but we want to emphasize explicitly that the BBL law and spectroscopy on the one hand and electromagnetic theory founded on Maxwell's equations and dispersion theory on the other hand were developed at the same time. Being chemists by training, we know from our experience that it seems that in depth knowledge of Maxwell's equations or dispersion theory is not necessary for evaluating spectra using the BBL law. The BBL law appears to be a condensed form of all that is important to know for understanding absorption and one can solidly rely on it. Often this may be indeed the case. But sometimes subtle or less subtle deviations from the BBL law occur, which cannot be explained either by chemical interactions or as hardware‐related. A theoretical comparison between the BBL law and electromagnetic theory indeed suggests that the BBL law is approximately correct under certain circumstances, while it can be completely inappropriate under other conditions. One of these conditions under which the BBL generally fails is related to the absorbance derived from reflection spectra of layers on highly reflecting materials (transflection spectra). Such spectra seem on first view to resemble transmission spectra. For biomedical applications of infrared spectroscopy, e. g., substrates like CaF₂ are too expensive and not mechanically stable enough to fit into the standard protocol of the pathologist. Therefore, it seems that transflection is not only the appropriate technique to choose, but the ideal solution for the particular demands. For transflection, a highly reflecting substrate is used, e. g. gold, silver or aluminum coated glass slides. However, when transflection spectra of layers with different thicknesses are compared, it becomes obvious that absorbance (defined in this case as log₁₀ (R ₀/R), where R is the reflectance with and R ₀ the reflectance without the layer) has a completely unexpected dependence from the layer thickness which is not at all linear as one might have expected. Not only that absorbance does not increase linearly with the thickness, it can even decrease! Consequently, the relative intensity ratio of two bands does not stay constant with changing thickness (as it would be the case, if the BBL law were valid), which strongly hinders spectral interpretation. A second unexpected behavior relates to the peak positions, which can be both, blue‐ or redshift, with increasing thickness. Both effects can interact and generate asymmetric peak shapes. For larger thicknesses, these effects are so substantial that the reflectance approaches that of an indefinitely thick layer where the incident light does not reach the highly reflecting substrate. Even satellite peaks can appear which are not directly linked to a vibrational mode. In the context of the BBL law, none of these effects can be explained. The reason is that for the BBL law to hold, the intensity in the absence of absorption must not change. In particular, it must not depend on the distance from the interface between layer and incidence medium or between layer and substrate. This is obvious, because what should decrease the intensity if nothing is absorbed? To make matters worse, the intensity can not only decrease but increase up to a value twice as high as the originally incident intensity.21, 22 To understand this seemingly strange behavior of light, one has to go one step back and consider that light intensity is nothing else but the electric field strength squared, i. e. the electric field intensity. Based on Maxwell's wave equation, we know that parts of the properties of light are explained by defining it as an electromagnetic wave which can be described by electric and magnetic field changes perpendicular to its propagation direction. A phenomenon that can be understood only in the wave picture, is the occurrence of interference, cf. Figure 2. The related effects are due to the fact that waves can superimpose each other and their amplitudes add vectorially so that the resultant amplitude can take on any value from the mere addition (constructive interference) to the difference (destructive interference; in particular, if the amplitudes are equal, the resulting amplitude ranges from twice the amplitude to zero). Accordingly, if the sample consists of a slab of finite thickness (e. g. a free‐standing film), a part of the propagating wave within the slab is transmitted after it hits the second boundary (the surface or interface between layer and exit medium), but another part is reflected. It is this reflected part that interferes with the forward travelling part, even for non‐coherent light as it is emitted from a light bulb or a black body. The resulting interference leads to electric field intensities that differ depending on the location within the slab, the wavelength and the thickness of the slab. For particular relations between wavelength and thickness standing wave patterns occur. The electric field intensity can therefore become everything between zero and twice of the original value at certain points within the slab. Now, since absorption is proportional to the electric field intensity, it is reduced or increased depending on whether at the particular wavelength/frequency the interference is overall destructive or constructive. Changing the thickness means that the interference patterns change within the layer/slab. Thereby, a linear dependence of absorbance from thickness cannot occur. In addition, the position of maximum absorbance is determined not only by the wavelength or frequency where the absorption constant is at maximum but is also influenced by the electric field intensity. It is the product of absorption coefficient and electric field intensity that determines the position of the maximum absorption and this product does not necessarily have its maximum at the same wavelength or frequency as the absorption coefficient. This effect is responsible for the shift of the maxima and, in the extreme case, for the appearance of satellite peaks. Note that this effect is not limited to thin layers. As we will see later, it also plays a role for particles and leads to so‐called sphere modes and shape effects in general.

Figure 2.

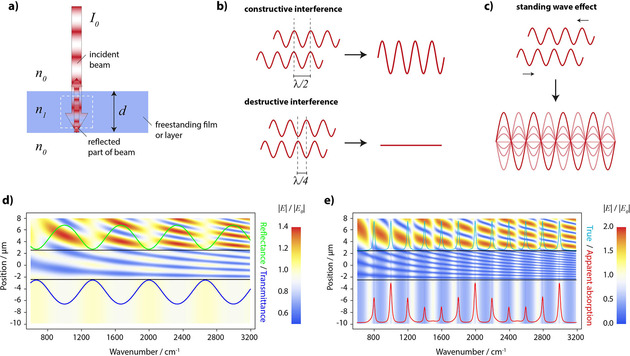
The phenomenon of wave interference. a) scheme of the sample geometry. b) the two extreme cases of interference. c) formation of a standing wave. d) electric field map of a freestanding non‐absorbing layer and the spectral positions of corresponding fringes in the reflectance and transmittance spectrum. e) electric field map of a freestanding absorbing layer having an absorption peak every 200 cm⁻¹. All absorptions have the same peak value of the absorption coefficient (true absorption). The resulting spectrum shows strongly altered peak intensities, peak shapes and positions (apparent absorption).

We want to emphasize again that the position of the maximum absorption can shift without any structural changes on the level of molecular structure or unit cell. A multitude of different optical effects can cause such shifts. A direct consequence is that the position of the absorbance maximum does in general not agree with the energy difference between two quantum mechanical states of the oscillators of a material of interest. Deriving this energy difference often requires comparably complex spectral evaluation procedures based on electromagnetic theory (chemometrics will therefore be unable to provide these!). Overall, it is astonishing that we allow matter to behave like waves in order to understand the absorption process, but by using the BBL law we deny the same to light and, thereby, negate its wave properties! In the following, we will investigate the errors that we commit if we use the BBL law instead of electromagnetic theory for some common techniques in some more detail and discuss how we can correct them.

2.1. Layers on a Highly Reflecting Substrate – Transflection

In principle, it is known since a comparably long time that absorbance derived from transflection measurements shows strong deviations from the BBL law.23 Over the decades, the effect was observed and described several times.22, 24, 25, 26, 27, 28, 29 To illustrate it, it is of advantage to think of a hypothetic material which has absorptions every 200 wavenumbers with the same peak absorption coefficient, which means that the oscillators are of equal strength. We then place a layer of this hypothetic material with a thickness of, say, 5 microns on a gold substrate and calculate the electric field strengths and intensities as well as the reflectance, the absorbance and so‐called absorptance, which is defined as 1‐R‐T. Since the transmittance is zero for gold layers thicker than about 50 nm, the absorptance is given in this case simply by 1‐R. The result is displayed in Figure 3 a). As can be seen, the absorptance peaks do not display equal intensity, albeit they are caused by equally strong oscillators. In contrast they show a modulation. This modulation is a consequence of the varying electric field intensities. For not too strong peaks the modulation is depending on the average electric field intensity of the layer at a certain wavenumber since absorption (in the sense of a process) is proportional to it.22 For absorbance we find that its dependence on the electric field intensity is non‐linear (except for small absorbances, since it can be shown that in the limit of very small absorption coefficients and thicknesses the values of absorbance and absorptance become increasingly similar). These non‐linear changes of the absorbance with thickness have also been illustrated on the example of the C=O vibration of Poly(methyl methacrylate) (PMMA). In this example the changes of the band position and the shape changes are clearly visible. For thicker layers, the dependence of the absorbance of the thickness becomes nearly chaotic and the bands begin to even split.30 While for thinner layers the absorbance can be corrected comparably easy,31 the correction for thicker layers is more complicated.30 So far, the only method to properly correct the absorbance is based on electromagnetic theory.

Figure 3.

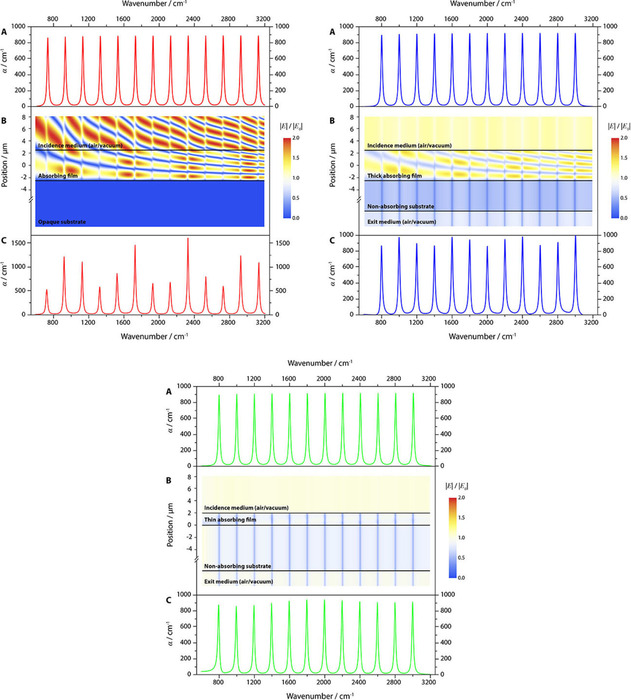
Interference effects in layers on different substrates. The panels A show the true absorptivity spectra which were used as input. The panels B show the corresponding field maps as function of position and wavenumber. The panels C show the resulting apparent absorptivity spectra. The panels on the left illustrate the interference effects for a 5 μm thick film on gold, into which the electric field can nearly not penetrate. The center panel shows the same for an identical film on silicon. For the film on CaF₂ (right panel), we assumed a thickness of 2 μm.

2.2. Layers on a Substrate with High Index of Refraction – Transmission

Common substrates with refractive indices higher than many potential layers, including organic or biologic layers, are, e. g., in the infrared spectral range Si, ZnSe or ZnS. Those materials are transparent, so that transmission spectra can be recorded. Due to their comparably high index of refraction they also still have a high reflectance. Since absorbance in case of transmittance measurements is defined as

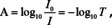
the problem arises that intensity losses through reflectance are erroneously increasing the absorbance. Because the index of refraction is a function of the wavenumber/wavelength/frequency, it is usually not possible to correct this problem by subtracting a constant from the absorbance calculated from eqn. (4). It seems that an easy solution to this problem would be to measure the transmittance of the substrate T with the layer and the transmittance of the substrate without layer T ₀ and then calculate the absorbance by

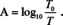
This is unfortunately not possible. The reason is that the transmittance spectrum of the substrate with the layer shows an undulating, wave‐like baseline, with so‐called interference fringes, in contrast to that of the substrate. Sometimes it is argued that this undulating baseline is caused by the fact that light is actually reflected and transmitted multiple times. Recurrently, these multiple reflections were made also responsible for deviations from the BBL law.24, 32, 33, 34, 35 Indeed, if the surface/interface of a layer is transmitted by light, part of the light is reflected from this first surface that is hit by the light. The part of the light that is transmitted through the surface then hits, after passing through the layer, the backside surface of the layer. Again, the difference between the indices of refraction of the layer and the air causes a part of the light to be reflected. This part travels back to the first surface, where again a part is reflected and travels in the original direction until it hits the backside and so on and so forth. The same, however, also happens in case of the substrate, the spectra of which (usually) do not show any undulating baseline. There are two differences between layer and substrate, which are responsible for the disappearance of interference fringes in the substrate spectra. Firstly, usually the substrate is much thicker than the layer. The larger thickness leads to a much shorter wavelength of the undulations, usually so short that the fringes are spectrally not resolved (for thin Si substrates, however, a resolution of 1 cm⁻¹ may be enough to render the undulations visible). Secondly, often thickness variations are present. These shift the undulations so that on average they are cancelled. For layers with their usually smaller thickness, however, this is usually not the case. The undulations are caused by interference, which is why they are also called interference fringes. In case of highly reflecting metals as substrates (or thin layers of them on glass) they are suppressed, which is why measuring in transflection originally seemed to be advantageous, because one could get rid of the baseline undulations. Many different methods have been devised to remove the fringes, like roughening of the surfaces which is not recommended because of the increase of scattering leading to diffuse reflection, a further reason for deviations from the Beer‐Lambert law, which cannot be removed analytically (which is why it is beyond the scope of this review). Another method is the removal of the fringes in the Fourier‐transformed spectrum,36 which seems to be very elegant, because in the ideal case in this spectrum only one point needs to be removed. Also, the wave‐like baseline could be fitted with functions based on sine and cosine and this fit can then be subtracted from the absorbance spectrum.37, 38 These methods certainly remove the baseline, but as we already know from transflection, interference also changes band intensities, shifts peaks and changes band shapes and the same also happens in the transmittance spectra of layers on highly reflective substrates (cf. Figure 3),39 and, by the way, also in case of freestanding films.21, 40 Accordingly, applying these methods would just take care of a small part of the problem. Fortunately, there are different methods to remove not only the fringes, but also the other effects caused by interference.39, 41, 42, 43, 44 These are so far all based on electromagnetic theory.

2.3. Layers on Index‐matched Substrates – Transmission

A convenient way to get rid of the unwanted influences of wave interference seems to be the employment of index‐matched substrates like CaF₂ for organic or biological films. Indeed, if transmission spectra of such films on CaF₂ are recorded, it seems that no fringes are present. Only closer inspection reveals that they are in fact still there, but, as in case of transflection, of very minor intensity. It therefore appears that the problem is indeed solved. Recently it has been shown that this is not the case.28, 45 The reason is that absorption is inseparably connected to a change of the index of refraction (anomalous dispersion), which is the stronger the stronger absorption is.45 Therefore, an index‐matched substrate may have exactly the same index of refraction in the region where the layer is transparent, but this match is lost in spectral regions where the layer shows absorption. The deviations from the Beer‐Lambert law for layers with a thickness of about 1 μm amount to about 30 %, but they decrease with layer thickness (see Figure 3), e. g. for layers of more than 4 μm below 5 %, which might be tolerable. Peak shifts are comparably small and usually below 2 cm⁻¹. Below about 1000 cm⁻¹, CaF₂ begins to strongly absorb. It is possible to use it as a substrate down to about 800 cm⁻¹, but in this spectral region the deviations are much stronger than in the regions above. A way to correct spectra, again on the basis of optical theory, has been introduced by us.45

2.4. Thin Cuvettes – Transmission

If cuvettes are thick, i. e. if the distance between the sides of the cuvette wall is millimetre‐thick like in UV‐Vis spectroscopy, it is possible to use eqn. (5) where T ₀ is the transmission of the cuvette with solvent. While it seems an intuitive way to correct experimental spectra, this is not possible for thin cuvettes as they are often used in infrared spectroscopy. Their thicknesses are in the range of some ten μm and often it is the spectrum of the liquid material that is of interest and not a solution. In this case one might think that the spectrum of the empty cuvette would be the reference spectrum or blank, but then the difference in refractive index between the cuvette walls and the air leads again to interference fringes which change when the cuvette is filled with a liquid. The fringes in the spectrum of the empty cuvette can be used to determine the actual thickness of the cuvette, but they are unwanted in the spectra of the liquid. Also, as for thin films, they are an indication that deviations from the BBL can be expected.46, 47 The reference spectrum that must be used is that of the cuvette material, which when ideally transparent, can be of arbitrary thickness. An algorithm for the removal of fringes was suggested already in 1975 by Hawranek et al.48 This algorithm determines the function of the complex index of refraction, the real part of which is the refractive index and the imaginary part is constituted by the absorption index which is given by $k\left(\tilde{v}\right)=a\left(\tilde{v}\right)/\left(4\pi \tilde{v}{log}_{10}e\right)$ and builds the basis from which many of the in other sections introduced correction methods are derived. In principle, every correction of the absorbance requires a determination of the optical constants n and k, i. e. either the complex index of refraction function or the dielectric function. Note that, even if no apparent fringes are present for the filled cuvette, this does not mean that interference is not at play. In this case the same applies as for films on an index‐matched substrate (previous section) – the interference fringes are suppressed in non‐absorbing regions, but around bands errors may be substantial and might need correction. It may as well be that the usual thickness of such cuvettes is large enough to marginalize errors, but this is speculation as long as a corresponding investigation has not been carried out.

2.5. Attenuated Total Reflection

The attenuated total reflection (ATR) technique distinguishes itself from other techniques by the fact that textbooks indeed mostly honour the fact that measurements by ATR inherently produce deviations from the BBL law. Maybe this is the case because the early literature about ATR already clearly pointed out these deviations. Here we want to emphasize the seminal work of Hansen.49 Accordingly, the equation

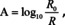
where R ₀ is the reflectance of the unloaded ATR accessory and R the reflectance when the sample is in contact with the ATR crystal, is to a good degree usable only for weak absorptions, i. e. for absorptions with an index of absorption smaller than about 0.1. This is a severe limitation, because even organic and biological materials with their comparably weak absorptions do have many bands that are much stronger. In particular if they feature C−O, C=O or O−H functional groups, but also C−H bands can be over the limit, e. g. the stretching vibrations in Polyethylene. For biological samples in particular the amide I band must be mentioned, the peak value of which is about 2.5 times higher than the limit.50 This limitation seems to be counterintuitive. Usually ATR spectroscopy is used in particular to investigate strong bands, as those lead to the problem that only very thin layers can be investigated in transmission, otherwise transmittance becomes too low. But this is not the only challenge when ATR spectra shall be investigated quantitatively. While ATR spectra displayed in −log₁₀ R following eqn. (6) look on the first view very similar to those gained from transmittance absorbance, they are not. It is not only that the intensities especially for lower wavenumbers need to be corrected, since the so‐called effective thickness (this is the thickness which leads to absorbance values equal to those from transmission experiments) increases with decreasing wavenumber.51 It can also be shown by electromagnetic theory that ATR absorbance is a function of the index of refraction and the penetration depth (the thickness at which the evanescent wave is reduced to 1/e of its original intensity), which is itself a function of the index of refraction. This means that the absorbance band maxima are redshifted towards the maxima of the index of refraction and that the band shapes can strongly change.52, 53, 54, 55 A simple way to reduce this problem is to use high index ATR crystal materials like Si and Ge and to apply high angles of incidence. Unfortunately, this means that the penetration depths and, thereby, the overall intensities are reduced and by that the sensitivity of the method. On the other hand, this helps to avoid the use of the ATR method out of its specifications, which means that ATR spectra become ordinary (external) reflectance spectra. What are these specifications? First and foremost, the angle of incidence must be larger than the critical angle θ_c which is given by

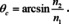
n ₂ is the index of refraction of the sample and n ₁ that of the ATR crystal. If e. g. the crystal consists of diamond or ZnSe (both have about the same index of refraction of 2.4) and the angle of incidence is 45°, then the index of refraction of the sample must be smaller than 1.7. This means that this very popular combination of crystal and angle of incidence cannot be used e. g. for charcoal, because it is then external reflection which is measured and there is no longer a zero baseline, since such spectra resemble more the index of refraction than the index of absorption function. Even when the index of refraction of a sample in the transparency region between MIR and Vis is lower than the limit, there is a persisting problem introduced by dispersion. As we have already discussed, every absorption is accompanied by a change of the refractive index. Therefore, several overlapping weak bands or a medium strong band like a C=O vibration leads to a spectral range for which the critical angle is larger than 45° for said ATR crystals.54 This means that a part of the radiation in this spectral range is actually transmitted into the sample, but not absorbed. It is, however, only possible to measure the percentage of absorption of the (total) reflection and not if this is solely due to absorption. In other words, it is not possible to determine if the spectrum switches in some region from an ATR spectrum to an external reflection spectrum. Consequently, the measured absorbance values in ranges with a higher critical angle than the actual angle of incidence (cf. eqn. (7)) can be much higher than they actually are. Again, this is not a problem if electromagnetic theory is used to evaluate the spectra. Corresponding procedures automatically take into account reflection losses that are due to transmission. The only problem is that for the correction the polarization state of the incident light must be known. Unfortunately, most of the modern accessories do not allow a polarizer to be used and the optics of the instruments lead to the fact that light cannot be assumed to be naturally polarized, so that the polarization state remains unknown. This is also a knockout‐criterion for the use of ATR with inorganic materials. Their absorptions and corresponding changes of the index of refraction are usually so strong that ATR spectra must be corrected by procedures based on electromagnetic theory to render them interpretable.

Overall, it is important to realize that absorbance calculated from reflectance (reflectance absorbance, −log₁₀(R/R ₀)) is different from that computed from transmittance (transmittance absorbance, −log₁₀(T/T ₀)). Furthermore, −log₁₀(R/R ₀) based on transflection might be different from that obtained from ATR measurements. Transmittance absorbance depends on the nature of the substrate, if it is not freestanding. An overview of these differences is provided in Figure 4 for PMMA and Spinel based on calculated spectra (for Spinel the substrates and the ATR‐crystal were assumed to be transparent).

Figure 4.

Comparison of the influence of sample geometry, technique and substrate on absorbance spectra (film thickness 1 μm and 500 nm for Au).

3. Deviations between Beer's Law and Dispersion Theory: Non‐linear Concentration Dependence

In the last section, we discussed the dependence of the absorbance from the electric field intensity. While a strong dependence was obvious, absorbance was not linearly depending on it. If we keep this dependence in mind and focus on the right part of eqn. 3,

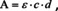
then the question arises, which of the quantities on the right side of the relation can be linked to the electric field intensity. It certainly cannot be the thickness nor can it be the concentration. The only quantity that remains is the molar absorption coefficient, which, however, is known to be a substance specific quantity, and, as such cannot depend on the electric field intensity. So apparently, the left side depends on the electric field intensity, while the right does not. What is our mistake? To find it, it must be emphasized that this part of the BBL law is empiric. Sometimes it is suggested that the linear concentration dependence simply follows from the fact that the molar absorption coefficient can be calculated by56, 57

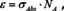
where σ_Abs is the absorption cross section of an absorbing moiety like a molecule and N_A is Avogadro's constant. This does not solve the problem, but merely shifts it, as it implies that absorption cross sections are specific quantities and that they are additive. So it seems that we are caught in a circular argument. Absorbance is additive on the molar level and linearly depending on the concentration because when the absorption cross sections of one mole of molecules are added then the molar absorption coefficient results. This reasoning cannot directly be checked for a single molecule, but what we can do is e. g. to check the additivity of the absorption cross sections of small spherical particles by numerically solving Maxwell's equations with methods like the Finite Difference Time Domain (FDTD) method,58 as the theoretical results agree very well with experiments.59

3.1. Non‐additivity of the Absorption Cross‐sections of Small Spheres

While the absorption and scattering cross‐sections of a single sphere can be calculated from analytical formulas provided by Gustav Mie,60 numerical methods are needed once the spheres are no longer isolated from each other. This already is an indication that there is some kind of interaction between neighboring spheres and scattering is one reason for strong deviations from Beer's law.61 We can reduce this interaction by choosing spheres that are very small compared to the wavelength. In this limit, scattering is very low. E.g., for two spheres of amorphous SiO₂ with a radius of 125 nm, the scattering cross section is about 1 % of the absorption cross section in the range around the Si−O stretching vibrations (7.7–10 μm wavelength).58 In the extreme case, the minimal distance between two spheres is zero, so that they touch each other. In this case, three different principal arrangements have to be considered, cf. Figure 5. For the first two arrangements, a light wave is impinging perpendicularly to a connecting line between the centres of the spheres. The two arrangements differ concerning the polarization of the wave, which is either parallel to the connecting line or perpendicular to it. The third arrangement assumes that the light wave is impinging along the connecting line, so that the second sphere is directly behind the first – it can be said that the first shadows the second.58

Figure 5.

Calculated field maps for a) one sphere b–d) two touching spheres with a radius of 125 nm of amorphous SiO₂ at 1142 cm⁻¹. For a–c) light is incident perpendicular, along the line of view and the arrows indicate the polarization direction. In case of d) light is incident from the right. The lower panel shows the corresponding absorption cross section spectra (in case of a) twice that of the single sphere).

The numerical calculations show that for any of three principal arrangements the absorption cross section is less than twice that of a single sphere, the value we would assume if absorption cross sections were additive. Accordingly, the presence of a second sphere changes the absorption cross section of the first and vice versa. The effect becomes smaller with increasing distance between the (centres of the) spheres, and can be said to vanish for a distance of about 8 times the radius.58 This distance is a function of the strength of the absorption band; therefore, it can vary from band to band. In other words, for weaker bands the distance will be smaller, for stronger bands larger. This result corresponds to observations of deviations from Beer's law (i. e. the linear dependence of absorbance from concentration) for solutions where the adherence to Beer's law can change from band to band.62 As a rule of thumb, this kind of interaction should vanish for densities lower than about 1 ‰ of that of a condensed phase, which is essentially the density of gas at standard conditions which can be considered as ideal. Quite interesting is that the absorption cross section of the arrangement where one sphere shadows the other is practically the same as the configuration where the incident light as well as the polarization direction are both perpendicularly to the connecting line between the centres of the spheres. Obviously the concept of shadowing, which seems to be behind the so‐called absorption flattening,56, 63, 64 and is often invoked to explain deviations from Beer's law, is a misconception in this context. Indeed, shadows belong to the realm of ray optics where the wavelengths are small compared to the dimensions of the objects. Once it is the other way around, i. e. the objects are small compared to the wavelength, the wave bends around the first object and interacts with the object behind, nearly as if the first object were transparent. The situation is very comparable to that in acoustics, where for bass sounds the source cannot be easily located as the waves bend around obstacles, while high frequency sounds can be shadowed by objects in the line of sight and, thereby, weakened in intensity, which allows localizing their origin.

With regard to Beer's law, it is also instructive to study how the spectral features change if we investigate the spectrum of a single sphere in dependence of its radius/volume. For very small sphere radiuses and weak absorption, the absorption cross sections scale in good approximation linearly with the volume of the sphere, cf. Figure 6. For larger spheres, absorption increases less strong, since part of the light is reflected and travels larger distances inside the sphere (for stronger absorption light may no longer be able to be transmitted). Even larger deviations are generated when the sphere size is no longer small compared to the wavelength, because then scattering becomes the dominating effect over absorption in removing part of the light from the primary light wave. Again, the sphere modes play a strong role and strong variations of the baseline can appear as well as changes of the absorption band shapes away from the symmetric shape towards a more dispersion‐like shape.65 Such inhomogeneities can strongly alter absorbance spectra, in particular for biological samples consisting of tissue or bacterial cells.66, 67 Shape effects may then also play a role.68 Unfortunately, there is no analytical way to correct such features. It seems, however, that their influence on the spectra is diminished the higher the densities of the scattering centres are.69

Figure 6.

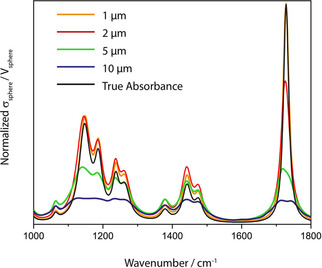
Calculated normalized absorption cross sections of PMMA spheres of different radius in comparison with the true absorbance spectrum of PMMA.

3.2. Derivation of Beer's Law from Electromagnetic Theory and Dispersion Theory

As we have already discussed, there must be a connection between the concentration dependence of absorbance and dispersion theory, and it was just because absorbance was not yet a popular quantity that Max Planck did not derive this dependence. In fact, Max Planck would have found that concentration is not linearly depending on concentration in general for two reasons; one reason is linked to Maxwell's theory and a second reason is that the applied electric field (of the incident light wave) is generally not the same as that which is actually effective. For the moment, we neglect this second reason and just focus on the first. To understand this first reason, we need to introduce some basic concepts from electromagnetic theory. On a macroscopic level we will view matter as a continuum while on the microscopic level we know that matter consists of moieties, i. e. molecules or unit cells, which constitute dipole moments $\overrightarrow{p}$ that are linked linearly for not too high electric field strengths to these fields:

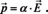
In eqn. (10) and in the following, α is the mean polarizability of the moiety (and not the Napierian absorption coefficient!). In the ideal case, the different moieties do not show interaction. The macroscopic property, the polarization $\overrightarrow{P}$ , is then simply the microscopic dipole moment multiplied by the number of dipole moments per unit volume N:

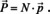
On the other hand, the macroscopic equivalent to eqn. (10) is given by,

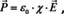
where χ is the electric susceptibility and ϵ ₀ the vacuum permittivity. If we put (10) into (11) and equate the result with eqn. (12), we obtain:

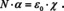
If we solve for χ and use that χ=ϵ_r−1, where ϵ_r is the relative dielectric constant, we get:

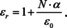
This seems to be nowhere close to Beer's law (eqn. (8)), but the molar concentration is readily introduced, since N is already a concentration, and it is linked to the molar concentration by N=N_A ⋅ c. Therefore,

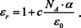
At this point we make use of the result of Maxwell's wave equation according to which the relative dielectric constant is related to the index of refraction n by ϵ_r=n ²:

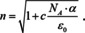
For small $\chi ,\sqrt{1+\chi }\approx 1+\chi /2$ . Accordingly,

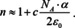
If we include absorption, the index of refraction becomes complex $\widehat{n}=n+ik$ and the same is true for the polarizability. If we focus only on the imaginary part, eqn. (17) transforms into,

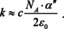
Finally, we use the connection between absorbance and the index of absorption,

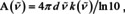
To arrive at Beer's law:70, 71

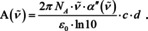
Thus, according to electromagnetic theory, it is not the index of absorption, which is proportional to the concentration, but the imaginary part of the mean polarizability. Indeed, if we would not use the approximation that simplifies (16) to eqn. (17), we would find that the molar absorption coefficient is a function of the inverse index of refraction, and, therefore, itself a function of concentration. For small concentrations, we see from eqn. (16) that the refractive index stays close to unity and Beer's empiric law will hold good, cf. Figure 7.

Figure 7.

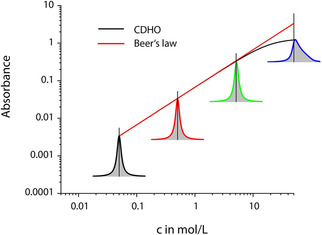
Comparison between the concentration dependence of absorbance predicted by Beer's law and by the classical damped harmonic oscillator (CDHO) model (often also termed Lorentz‐ or Drude‐Lorentz model). The deviation from linearity disappears, if instead the peak values the dependence of the area of the band is plotted over concentration (for c ⋅ d=const., the band area is also constant).

To understand the limits in a more quantitative way, it is possible to model the wavenumber dependence of the polarizability, or, in other words, to determine the dispersion of the polarizability. To do this, a representation of a transition from one quantum state to a higher level by a harmonic oscillator can be assumed. This model works well for vibrational modes, but can also be employed for electronic states as long as those are localized (the model usually does not work well for solids like semiconductors, but may represent an electronic excitation of a molecular entity satisfactorily). The harmonic oscillator is characterized by a resonance position ${\tilde{v}}_0$ , which is the same as for unforced vibrations. Under the effect of an electric field, this oscillation is driven with a strength proportional to the square of the charge q and to the inverse of the reduced mass μ. Accordingly, the dispersion of the dielectric function can be modeled as,71

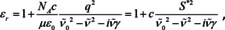
with $S{{}^{*}}^2=q^2{N}_A/\left(\mu {ϵ}_0\right)$ , wherein S* is the molar oscillator strength. Eqn. (21) may look familiar to many readers and alien at the same time. The familiarity is based on the relationship of this so‐called Lorentz oscillator to the Lorentz profile that is omnipresent in optical spectroscopy to model absorbance spectra, e. g. to achieve peak separation in case of overlapped bands. The Lorentz profile has been derived by Hendrik Lorentz from the Lorentz oscillator under the same constraint that was applied to get from eqn. (16) to (17).72, 73 In other words, employing a Lorentz profile instead of a Lorentz oscillator is nothing else but to assume strict linearity between absorbance and concentration. Under this assumption, the damping constant becomes the half width of the absorbance band and the oscillator strength the absorbance amplitude. The Lorentz profile inherits the symmetric shape from the band of the imaginary part of the relative dielectric function.

If the approximation that converts a Lorentz oscillator to a Lorentz profile is not valid, i. e. if the molar oscillator strength squared times the concentration becomes too large, the Lorentz oscillator leads to asymmetric absorbance bands the maxima of which are blue shifted compared to the oscillator position, cf. Figure 7. The intuitively accessible reason is that the molar absorption constant, and, by that, the absorbance, is a function of the inverse index of refraction. The inverse index of refraction has a maximum that is blue shifted relative to the oscillator position and is asymmetric, which is why absorption bands become correspondingly modulated when the oscillator strengths becomes too high. For symmetry forbidden transitions in the UV, as well as for many oscillators of organic and biological materials the Lorentz profile is a good approximation even for neat materials, whereas infrared bands of inorganic materials are usually so strong that the use of a Lorentz profile is justified rarely. This is also the reason why absorbance as a quantity is usually not used to display the infrared spectra of inorganic materials.

At this point it may be justified to adopt another view and discuss the role of the molar absorption coefficient. We have already seen in the preceding section that the absorption cross section in the special case of small spheres is depending on the polarization and the distance of the spheres as well as from their volumes. Correspondingly, the molar absorption coefficient cannot be a specific quantity, because it depends on the concentration and the optical properties of the sample. In this section we have made some implicit assumptions which include the absence of anisotropy (our medium is isotropic in the sense that a scalar dielectric function is sufficient to describe it). We also have assumed that our medium is continuous and homogeneous. Nevertheless, we found that even under these conditions the molar absorption coefficient is not a specific quantity, since it is inversely proportional to the index of refraction. This dependency alone causes it actually to be not a material but a wave property. On the first view, this may seem as a meaningless distinction, but for good reason it is the complex index of refraction that enters Maxwell's wave equation and not the dielectric constant/function. In more complex settings, like in case of anisotropic materials, the simple correlation ϵ_r=n ² is no longer valid and for the same material parameters (the same dielectric function tensor) optical properties like the size of certain domains relative to the wavelength of light may factor in. Under these conditions, ϵ_r=n ² may not even be valid for isotropic, i. e. randomly oriented systems.74

3.3. Integrated Absorbance

In former times one of the most often discussed reason for deviations from Beer's law was (insufficient) spectral resolution. If the molar absorption coefficient is known only for the peak value, a spectral resolution not small enough relative to the peak width may seem to be the major cause of deviations. From the last section it is, however, obvious that Beer's law is generally not valid pointwise. Therefore, it seems that a convenient solution, which is to determine the band area instead of the peak values,75, 76, 77 is also not correct. Indeed, if Beer's law were valid for every spectral point, it is easy to show that the integrated absorbance, i. e. the area under the peak, would be proportional to the concentration.78 Since this is only approximately the case of what use would be the extra effort to determine the peak area? If a band is indeed symmetric, something which a band fit with a Lorentz profile could prove, then taking the band area instead of the peak value may be able to decrease the error. On the other hand, if a band fit has been carried out, the integration of a band is actually no longer needed, because this fit determines the oscillator parameters, and, among them, the oscillator strength, the square of which is proportional to concentration. The same is certainly correct for asymmetric bands when for the band fit a Lorentz oscillator is employed instead the Lorentz profile.78 Since band fits are usually not used in this respect, the concept may seem strange. There is a way to independently prove that it is correct. In spectroscopy often the so‐called Kramers‐Kronig relations are used.79 These relations connect the real part of a complex function with the imaginary part and vice versa. They hold at the same time for the complex dielectric function, the complex index of refraction function and the complex function of the polarizability. Based on the Kramers‐Kronig relations and the dispersion relations from which the former have been obtained originally, so‐called sum rules can be derived.80 One of these sum rules deals with the index of absorption, and it states that the integral over the product of wavenumber and index of absorption is proportional to the squared oscillator strength. This product is nothing else, apart from a constant, but the absorbance, which establishes the equality between integrated absorbance and oscillator strength squared. The latter, however, is proportional to the concentration, which proves that Beer's law still holds with regard to the squared oscillator strength(s) and the absorbance band area.78 To come back to the problem of resolution, the former conclusion points out that there is actually no problem, since even when the measured intensity is not spectrally resolved, it is still proportional to the concentration, and even more so, if a band is asymmetric, as long as its spectral range is fully covered (cf. Figure 7). Unfortunately, this conclusion is only correct as long as local fields do not play a role, something which will be discussed in the next section.

3.4. Beyond Beer's Law – The Clausius‐Mosotti and the Lorentz‐Lorenz Relations

It might not be obvious, but from eqn. (17) one can conclude that for small variations the index of refraction is predicted to be also linearly depending on concentration.81 This is in principle known for nearly as long as Beer's law. In contrast to the latter, the corresponding law was not formulated for the concentration, but for the density instead. The constant of the corresponding law is called the Gladstone‐Dale constant, referring to John Hall Gladstone and Thomas Dale who suggested this law.82 We recently showed that a related law formulated for the concentration still works at resonance.81

Interestingly, there is a law corresponding to eqn. (16), also dealing with the dependence from density instead of concentration, which is called the Newton‐Laplace rule.

Finally, there is a third law in this regard, which is called the Lorentz‐Lorenz relation and it also deals with the dependence of the index of refraction from the density, but it can be derived in the same way as eqns. (16) and (17).83 The result then reads:

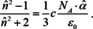
Since absorption and refraction are closely connected, it is instructive to examine how the Lorentz‐Lorenz relation evolves from the Gladstone‐Dale and the Newton‐Laplace rule, to see what the corresponding levels of theory for absorption are. First, the assumption behind Lorentz‐Lorenz is that matter is no continuum. Instead, microscopic entities like molecules constitute it. The new aspect, which was so far not considered, is that the applied electric field induces a dipole moment locally which interacts with the dipole moments around it, so that those are changed. This variation again induces changes in the first dipole moment and so on and so forth. As a result, the local electric field is higher than the one applied on the macroscopic level. There are different theories to calculate the local field, but if we assume the local field of Lorentz, then eqn. (13) is changed into,

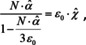
the result of which is the Clausius‐Mosotti relation for the dielectric constant and the Lorentz‐Lorenz relation for the squared refractive index. While both relations are usually used in transparent regions, they certainly hold in absorbing regions as well. Therefore, the complex index of refraction is employed in eqn. (22). Before we discuss the consequences, let us first derive approximate formulae for small concentrations. In this case, the index of refraction is not very different from unity. We can therefore assume that under this condition ${\widehat{n}}^2+2\approx 3$ and relation (22) simplifies to

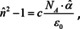
which is the complex equivalent to eqn. (16). Accordingly, the solution gained under the assumption that the local field is the same as the macroscopically applied field and corresponds to the Newton‐Laplace rule. The equivalent to the Gladstone‐Dale rule is then obtained by the assumption that $\sqrt{1+\chi }\approx 1+\chi /2$ ,

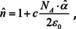
which is nothing else but Beer's law if we focus on its imaginary part. From the preceding section we know that it is, depending on the molar oscillator strength, valid up to densities of about 1/10 of the density of the neat substance. For higher densities, the next level of the theory (eqn. (24)) predicts the bands to become asymmetric and the peaks to shift to the blue. What are the consequences of a local electric field different from the applied? Following Max Planck's and Hendrik Lorentz's work on dispersion theory,16, 17, 72 there is only one consequence which is a redshift instead of a blueshift (cf. Figure 8c). This redshift is depending on the molar oscillator strength and the concentration of the single oscillator both Planck and Lorentz assumed.83 Accordingly, except from a few (less than a handful) of textbooks, the opinion is that the same is also true for systems of more than one oscillator. Only Max Born pointed out in his famous textbooks, that this is in general not correct.84, 85 Instead, macroscopically a system of coupled oscillators results, in which both, the resonance position as well as the strength of an oscillator depends on those of all oscillators located elsewhere in a spectrum and their concentrations. Those of you familiar with the dispersion relations and dispersion analysis (the sophisticated form of band fitting), may ask the question, how is it possible then to fit those coupled systems with the same relations that are based on uncoupled oscillators? It has been shown already in 1925, that it is always possible to mathematically recast the dispersion relations amended by the Lorentz‐Lorenz theory to the original forms.86 However, the correspondingly altered squared oscillator strength is then no longer proportional to the concentration. This challenge cannot be met by integration of the band area in general. Usually however, the oscillator strengths of the bands in the UV‐Vis spectral region are much stronger than those in the infrared region. Accordingly, while the latter are strongly influenced by the former, the area of all bands in the UV‐Vis might still be proportional to the concentration, while the resonance positions are strongly redshifted,83, cf. Figure 8 d). For the infrared bands, the local field effect leads to a strong increase of the intensity by a factor on the order of 100 %. In other words, if the same amount of oscillators would not be in condensed form (i. e. like in a gas, with d much larger, but c ⋅ d kept constant), the absorbance would be about less than half.83 From another point of view, the increased local field strength, leads to an even stronger increased electric field intensity to which absorption is proportional. This means that absorbance for neat materials in a condensed state can be a meaningless quantity. Instead one might have to analyze the data by dispersion analysis employing eqn. (22).

Figure 8.

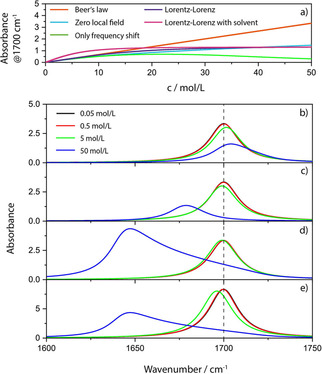
Upper panel: Concentration dependence of the absorbance according to the different levels of theory. Lower panel: Absorbance band position, intensity and shape changes for different concentrations for c ⋅ d=const. and levels of theory. b) CDHO, c) CDHO with redshift proportional to the squared oscillator strength, d) full Lorentz‐Lorenz model and e) full Lorentz‐Lorenz model assuming a solution in a solvent with the same dielectric background (please note the different scale of e)).

The good news is that as long as the oscillators are suspended in vacuum, and the effects discussed in section 3.1 concerning the non‐additivity of the absorption cross sections are negligible, local field effects are still predicted to not set in strongly earlier than at a density of 10 % of the neat condensed phase,83 cf. Figure 8 a). The situation is somewhat different if the oscillators are located in a solvent (Figure 8 e)). At this point, we still do not take any chemical interactions into account, i. e. we assume that the process of dissolving only means the dissolved molecules are placed in the holes between the molecules of the solvent without changing the polarizability of solvent or solute (no chemical reactions with the solvent, no association of molecules of the solute etc.). This is a situation that can be modelled with eqn. (22). The usual assumption then is that the polarizabilities of the solvent and the solute weighted by their mole fraction are simply additive. Even if we assume that we focus on a band of the solute with no overlap with the band of the solvent, the absorptions are strongly coupled and the increase of the local field will considerably alter oscillator strength and redshift bands of the solute, whereas the bands of the solvent will be blue shifted relative to the neat solvent. The former effect was noted as early as 1878 and is called Kundt's rule (Kundtsche Regel).87 When Kundt noticed that different solvents cause different redshifts, he empirically investigated the probable cause of the effect and found that the stronger the index of refraction is and the stronger its dispersion, the stronger is the redshift of the band of a solute. In other words, since absorption and change of the index of refraction are two sides of the same coin, the stronger the absorption of the solvent is (in other spectral regions), the more the band of the solute is redshifted (Kundt had no possibility to quantify peak values). Aside from the bandshift, the change of the absorption with increasing concentration is much stronger than without the solvent, which means that the molar absorption coefficient function measured in a solvent can be much greater than that without solvent. Additionally, deviations from linearity can start earlier,83 but most probably not earlier than the effect that causes the non‐additivity of the absorption cross sections. All in all, it is not generally necessary to force a straight line through experimental values of the absorbance in dependence of concentration. As long as the change of concentration does not become too small, e. g. a Gaussian regression can be employed for quantitative analysis.88

3.5. Thick Cuvettes and Pellets – Transmission

It is nevertheless well known that in spectrophotometry eqn. (5) quite often leads to a straight line, which means that Beer's law is applicable. To make this work, merely from the perspective of optical deviations from the Beer‐Lambert law, concentrations should be less than about 1 ‰ of the neat substance (higher for weaker absorptions – lower for stronger ones) based on the issues discussed in the preceding sections. Furthermore, cuvettes need to be thick so that any coherence related effects, as they were discussed for thin cuvettes, do not occur. This alone, however, does not suffice. If one would use the BBL law as it is presented in textbooks, i. e. according to eqn. (3), it would not work. Instead, eqn. (5) has to be employed.40 The reason for this is that the transmittance of the solution requires to be normalized by ratioing it to the transmittance of the pure solvent. If optical theory is applied to this case, it can be shown that only the ratio decays exponentially with concentration as required, but only if some further prerequisites are met.40 One of these is that the index of refraction of the solvent (or of the pellet material – for pellets in principle the same applies as for thick cuvettes) should be as close to unity as possible. The second requirement is that the index of refraction of the solution must not be too different from that of the solvent. As it is obvious from the preceding section, this also limits the concentration of the solute.

3.6. Sample Heterogeneity and Mixing Rules

Sample heterogeneity and resulting consequences were already discussed in several sections. It must be emphasized that the simple relations provided in sections 3.2–3.4 are based not only on the precondition that the medium is macroscopically and microscopically isotropic, but also that it is perfectly homogeneous. For real samples this is never the case and, therefore absorption cross sections are not additive, even though the heterogeneities are small compared to the resolution limit (i. e. they would not be visible under a microscope). In section 3.1 we also touched upon what happens when the heterogeneities are no longer small compared to wavelength, but the onset of scattering is only one effect that leads to deviations from the Beer‐Lambert law. If we assume samples that consist of two different constituents, the simplest mixing rule according to the Lorentz‐Lorenz model would be that89, 90

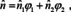
where ϕ ₁ and ϕ ₂ are the volume fractions of the constituents 1 and 2. This corresponds to the simplified form of eqn. (25) and is consistent with Beer's law if there is no volume excess due to mixing40 (note, however, that for many techniques, a simple mixture of the absorption indices or, equivalently, the absorbances, without considering the refractive index is not sufficient!90). The corresponding form to eqn. (24) would be89

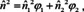
and the form related to the Lorentz‐Lorenz relation (22) is89, 91

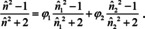
It is obvious that these mixing rules are no longer compatible with Beer's law, and not only because we use the volume fraction (which is connected to the molar concentration in ideal systems via c_i=ϕ_i ⋅ d_i/M_i with density d_i of the neat compound and its molar mass M_i), cf. Figure 9. A serious consequence is e. g. that absorbance spectra do no longer show an isosbestic point, even if they are genuine two component systems.92

Figure 9.

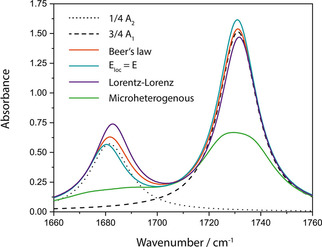
Absorbance spectra for a 5 μm thick two‐component layer on CaF₂ with ϕ₁=0.75 according to Beer's law (eqn. (26), orange curve), the assumption of a zero local field of Lorentz (eqn. (27), turquoise curve), according to Lorentz‐Lorenz (eqn. (28), violet curve) and for micro‐heterogeneous mixing (eqn. (29), green curve).

The latter mixing rule is not the only one, which has been developed over the centuries, because simulated spectra based on the mixing rules quite often do not resemble the actual spectrum well. Further mixing rules are the Onsager‐Böttcher theory,93 the Maxwell Garnett model and the Bruggeman formula,94 to name just the most important. For all these mixing rules, it is required that the regions or domains where one constituent is the only or the dominating one, are small compared to the wavelength ($\le$ 1/10 λ) and/or the resolution limit of light, i. e. the sample is micro‐homogeneous. In other words, if spectra taken with a microscope from different locations of the sample differ significantly from each other, then these mixing rules are not sufficient (micro‐heterogeneous sample). The reason is that the transmittance T and reflectance R of a larger area or volume of the sample are always area or volume averaged quantities:89, 95

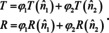
Here ϕ_i represents either the volume fraction (transmittance) or the fraction of the surface area (reflectance) of microscopically large domains completely consisting of either component 1 or 2. If components 1 and 2 are not completely immiscible or if the domains are not or not all larger than the resolution limit, then the mixing rules become even more complicated, whereas if the conditions are fulfilled, eqn. (29) is readily extendable to more than 2 components, as are eqs. (26)–(28).

The immediate consequence of (29) is that Beer's law cannot hold for microscopically heterogeneous samples, since

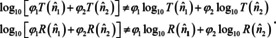
The deviations can be considerable even for weak oscillators, in particular if the volume fractions of the different materials are of the same order (cf. Figure 9).89 In this case, the bands strongly flatten for micro‐heterogeneous samples compared to micro‐homogeneous samples with the same composition (this might explain the band flattening which is often erroneously explained with shadowing, cf. section 3.1). For larger layer thicknesses or oscillator strengths, the spectra can be altered to the point where the original components are no longer recognizable. The special case where the second material is transparent had already been treated in 1952.96 Probably because it was shown later that the errors in case of pressed pellets were small,97 (which is no argument, because for pressed pellets, the sample powder should consist only of particles small compared to wavelength, so that above theory does not apply!) this problem did not get the attention it deserves. It might seem that it can be relieved by using imaging methods, but this requires to perform imaging at the resolution limit, otherwise the spectra of the pixels are averaged according to eqn. (29) and corresponding errors will result at the borders between substances.

4. Some Further Challenges Regarding the Bouguer‐Beer‐Lambert Law

4.1. Introducing Anisotropy – Linear Dichroism Theory

In addition to heterogeneity, a further complication is the fact that most molecules or unit cells are anisotropic. Based on a simple model it can be shown that in this case absorbance is not related linearly to concentration.98 Usually linear dichroism theory is applied to systems where anisotropy plays a role,99, 100 which not only inherits all shortcomings detailed so far, but is strictly applicable only to molecules of a gas. According to this theory, it is only the angle between transition moment and light polarization that determines absorption. Gases, however, are not anisotropic. Liquids and solids, on the other hand, have interfaces. Since only the electric field components tangential to the interface are continuous, a second angle becomes important and influences absorption, which is the angle of the transition moment relative to the interface.101 As a consequence, linear dichroism theory is a limiting theory the performance of which improves with vanishing anisotropy and band strength. For C=O vibrations deviations of up to 50 % are possible.102 In case of inorganic materials with their usually much stronger absorptions linear dichroism theory is generally inadequate. In fact, it was already obsolete long before it was founded.101, 103 A wave‐optics based treatment of anisotropy is nowadays usually based on 4×4 matrix formalisms,104, 105, 106 and used, e. g., in generalized spectroscopic ellipsometry. These formalisms automatically also take into account the interference effects described in the previous sections.

4.2. Circular Dichroism and 2D Correlation Absorption Spectroscopy

Neither in literature related to circular dichroism spectroscopy nor to 2D correlation spectroscopy any consequences of the absorbance being non‐linearly related to sample thickness or to concentration have ever been investigated. The, to our best knowledge, only paper which discusses such deviations from the BBL law for circular dichroism completely focuses on chemical interactions as sources for errors.107 Similar to biological samples, however, (chiral) Mie scattering as a source of error, e. g. resulting from large biopolymers, has been discussed.108 For most measurements performed with liquids in cuvettes with cm thickness deviations, if noticed, can be assumed to be small for the reasons detailed in section 3.6, but as soon as thin cuvettes need to be used as in the IR spectral region, interference effects will come into play (cf. section 2.4). For solid samples, and in particular if plasmonic enhanced chiral detection schemes are employed,109 converting transmittance into absorbance loses meaningfulness, but instruments often only use this quantity.

One of the predominant features of 2D correlation spectroscopy is that it is extremely sensitive to non‐linearity.110 In particular in the asynchronous spectra, thickness and concentration related non‐linearity can be detected much more easily. In this context, it is required to investigate the spectral signatures of non‐linearity that is inherent to absorbance to avoid misinterpretation. So far, this challenge has seemingly not been realized, but investigations to quantify the influences are dearly needed and in progress.

5. Conclusion and Outlook

The Bouguer‐Beer‐Lambert law shares an important property with the ideal gas law, which is that it is a limiting law that is accurate only under some very restrictive preconditions. For gases, it is correct only for comparably large distances between the molecules, another commonality with the ideal gas law. Even when chemical interactions are excluded, there is a cornucopia of different sources of error spectroscopists should be well aware of. Compared to the Bouguer‐Beer‐Lambert law, the ideal gas law has one big advantage – thanks to its name – it is never mistaken as being correct in reality. Given the multitude of potential pitfalls and sources of error, our suggestion would be to rename the BBL law to ideal absorption law to make it clear that in many situations a more sophisticated data treatment and careful interpretation is necessary.

If on the other hand, such a sophisticated data treatment is ensured, i. e. electromagnetic theory is applied, it becomes possible to understand band shifts and the intensities of spectra. The latter would finally render the next big step in spectroscopy possible, which was anticipated more than six decades ago, but never took place in a widespread manner, namely a fully quantitative evaluation of optical spectra.

Conflict of interest

The authors declare no conflict of interest.

Biographical Information

Thomas Mayerhöfer obtained his diploma in chemistry in 1996 at the University of Regensburg and his PhD at the Friedrich Schiller University in Jena in 1999, followed by a habilitation in 2006 about using Maxwell's equations‐based approaches to describe anisotropy and orientation effects in optics and IR‐spectroscopy. Since then he was further contributing to the field of spectroscopic optics on such topics as quantitative analysis of the spectra of monoclinic and triclinic crystals, surface enhanced infrared and VCD spectroscopy and, last but not least, how to connect the Bouguer‐Beer‐Lambert law with electromagnetic theory and wave optics.

Biographical Information

Jürgen Popp studied chemistry at the universities of Erlangen and Würzburg. Since 2002, he has been a chair for Physical Chemistry at the Friedrich Schiller University Jena, and in 2006, became the Director of the Leibniz Institute of Photonic Technology, Jena. His core research focus is biophotonics, in particular the development and application of frequency‐, time‐ and spatially resolved innovative laser microspectroscopical methods and techniques for biomedical diagnostics as well as environmental and food analysis. He has published more than 900 journal papers and is editor/author/contributor of more than 20 books on Biophotonics.

Biographical Information

Susanne Pahlow obtained her diploma in chemistry in 2010 at the Friedrich Schiller University in Jena. Afterwards she joined the biophotonics group of Prof. Dr. Jürgen Popp at the Leibniz Institute of Photonic Technologies (IPHT) and worked in the field of Raman microspectroscopy, specializing in the identification of bacteria. In 2016 she defended her PhD thesis with the topic “Innovative Sample Preparation Strategies and Detection Methods for Microorganisms” and currently works as a postdoctoral researcher at the IPHT. Her main research interests are establishing Raman compatible sample preparation strategies, investigating new capture probes for microorganisms and chemical surface modification techniques.

T. G. Mayerhöfer, S. Pahlow, J. Popp, ChemPhysChem 2020, 21, 2029.