Abstract
Understanding the origin of new species is a central goal in evolutionary biology. Diverging lineages often evolve highly heterogeneous patterns of genetic differentiation; however, the underlying mechanisms are not well understood. We investigated evolutionary processes governing genetic differentiation between the hybridizing campions Silene dioica (L.) Clairv. and S. latifolia Poiret. Demographic modelling indicated that the two species diverged with gene flow. The best‐supported scenario with heterogeneity in both migration rate and effective population size suggested that a small proportion of the loci evolved without gene flow. Differentiation (F ST) and sequence divergence (d XY) were correlated and both tended to peak in the middle of most linkage groups, consistent with reduced gene flow at highly differentiated loci. Highly differentiated loci further exhibited signatures of selection. In between‐species population pairs, isolation by distance was stronger for genomic regions with low between‐species differentiation than for highly differentiated regions that may contain barrier loci. Moreover, differentiation landscapes within and between species were only weakly correlated, suggesting that linked selection due to shared recombination and gene density landscapes is not the dominant determinant of genetic differentiation in these lineages. Instead, our results suggest that divergent selection shaped the genomic landscape of differentiation between the two Silene species, consistent with predictions for speciation in the face of gene flow.
Keywords: barrier loci, demographic modelling, ecological speciation, genomic landscape, Silene
1. INTRODUCTION
Understanding the origin of new species is a central goal in evolutionary biology. Speciation is a gradual process in most cases (Coyne & Orr, 2004; Seehausen et al., 2014). At early stages of divergence, genetic differentiation between lineages is restricted to small parts of the genome, whereas, at the end of the speciation process, the cessation of gene flow results in genome‐wide differentiation (Burri, 2017; Wolf & Ellegren, 2017). Evolutionary processes driving such heterogeneous genetic differentiation are poorly understood, with comparatively few empirical reports on intermediate stages of speciation (Ravinet et al., 2017; Wolf & Ellegren, 2017). One important determinant of the evolutionary processes at work is the demographic history of lineage divergence (Ravinet et al., 2017). When geographical barriers prevent gene flow, genetic drift and adaptation can proceed independently in each lineage. Under this scenario, high differentiation may commonly arise in regions of low recombination and reduced effective population size (N e) because linked selection is more pronounced and genetic drift is stronger in these regions (Burri, 2017; Burri et al., 2015; Nachman & Payseur, 2012). Under a contrasting scenario, speciation occurs with ongoing gene flow. Here, regions of high differentiation may arise because of selection against migrant alleles and/or hybrid genotypes at some loci (barrier loci) and neighbouring genomic regions whereas the remainder of the genome is homogenized by gene flow. Theoretical studies indicate that divergence with gene flow is most likely when loci controlling reproductive barriers are clustered in the genome or situated in regions of low recombination (Butlin & Smadja, 2018; Yeaman, Aeschbacher, & Bürger, 2016). A third common scenario combines divergence in allopatry with gene flow upon secondary contact. In this case, gene flow erodes differentiation at loci unlinked to adaptive differentiation or reproductive isolation. This situation may also prompt the evolution of further reproductive barriers (reinforcement) when intermediate hybrids are selected against (Butlin & Smadja, 2018). More complex scenarios that allow for changes in population size and recurrent bouts of gene flow are also supported by empirical data (Christe et al., 2017). Divergent selection, background selection and gene flow leave distinct population genomic signatures (see below); however, it is clear that realistic demographic scenarios are a prerequisite to interpret the genomic landscape of differentiation.
Genetic differentiation and gene flow vary strongly throughout the genome due to the pervasive effects of background selection and conserved genomic features, such as recombination rate variation, mutation rate and gene density (Ravinet et al., 2017; Wolf & Ellegren, 2017). However, demographic models have only just begun to incorporate these heterogeneities (Christe et al., 2017; Rougemont & Bernatchez, 2018; Roux et al., 2014, 2016; Tine et al., 2014). Models based on diffusion approximation (Gutenkunst, Hernandez, Williamson, & Bustamante, 2009) or on approximate Bayesian computation (Roux et al., 2016) of the joint site frequency spectrum can explicitly include heterogeneous migration rates. Heterogeneities in conserved genomic features and thus background selection, on the other hand, can be modelled by allowing effective population size, Ne, to vary among loci (Charlesworth, 2009; Roux et al., 2016). Including heterogeneity in both migration rate and in Ne in demographic models often improves model fit and can affect demographic inference (Rougemont & Bernatchez, 2018; Roux et al., 2016). In addition, including heterogeneity in Ne is needed to prevent spurious detection of heterogeneity in migration rate. Interestingly, Roux et al. (2016) found strongest support for heterogeneous migration rates in taxon pairs at intermediate stages along the speciation continuum, in the so‐called “grey zone” of speciation. This finding aligns with empirical results on the genomic landscape of differentiation, reviewed in Ravinet et al. (2017) and Wolf and Ellegren (2017). At later stages of speciation, gene flow may rapidly cease leading to a genome‐wide rise of differentiation (Flaxman, Wacholder, Feder, & Nosil, 2014).
Genetic differentiation is commonly measured using Wright's fixation index, F ST, which is sensitive not only to changes in gene flow, but also to alterations of genetic diversity within lineages (Burri, 2017; Cruickshank & Hahn, 2014; Wolf & Ellegren, 2017). Sequence divergence, often measured as d XY, in contrast, is expected to increase primarily due to reductions in gene flow (barrier loci) or as a result of lineage sorting in ancestral populations (Nachman & Payseur, 2012; Richards, Servedio, & Martin, 2019). Joint increases in d XY and F ST are therefore expected at barrier loci but not at loci with high differentiation due to background selection, particularly at intermediate stages of speciation (Cruickshank & Hahn, 2014; Nachman & Payseur, 2012; Ravinet et al., 2017). Several studies have further inferred an important role of divergent selection in the generation of highly differentiated loci by testing for reductions in sequence diversity and for an excess of rare variants (Nielsen, 2005), for example, in three‐spined sticklebacks (Feulner et al., 2015; Marques et al., 2017; Samuk et al., 2017), cichlids (Malinsky et al., 2015; Meier, Marques, Wagner, Excoffier, & Seehausen, 2018) and poplars (Wang, Street, Scofield, & Ingvarsson, 2016). Moreover, admixture analyses and analyses of multiple population pairs in different geographical contexts have identified genomic regions with reduced gene flow, as in sea bass (Duranton et al., 2018) and Darwin's finches (Han et al., 2017). Thus, even though many of these approaches remain challenging, the combined use of different population genomic estimates and analyses helps to elucidate processes affecting genetic differentiation.
Ideally, speciation genomic studies relate to well‐investigated reproductive barriers and the genes controlling them. The nature, strength and genetic architecture of reproductive barriers determine the course and completion of the speciation process (Flaxman et al., 2014). Speciation may be driven by geographical separation and/or by ecological divergence (Coyne & Orr, 2004; Rundell & Price, 2009; Seehausen et al., 2014). In many systems, however, speciation proceeds through the accumulation of multiple extrinsic and intrinsic reproductive barriers, which may be associated with a large number of traits and/or complex genetic architectures (reviewed in Wolf & Ellegren, 2017). Importantly, highly polygenic genetic architectures may be transient in time and effects of individual loci may be too small to be detected (Rockman, 2012; Yeaman, 2015). Nonetheless, integrating the genetic control of reproductive barriers with population genomic analyses is necessary to understand the speciation process.
We investigated the closely related campions, Silene dioica (L.) Clairv. and S. latifolia Poiret (Caryophyllaceae), a plant system with ongoing hybridization but near‐complete reproductive isolation (reproductive isolation index, RItotal > 0.98) (Karrenberg & Favre, 2008; Karrenberg et al., 2019; Minder, Rothenbuehler, & Widmer, 2007). The two species have separate sexes (dioecy) with XY sex determination and largely overlapping European distributions (Friedrich, 1979). Reproductive isolation mainly results from adaptation to different habitats and from pollinator‐mediated assortative mating (Favre, Widmer, & Karrenberg, 2017; Goulson & Jerrim, 1997; Karrenberg et al., 2019). Pink‐flowered S. dioica occurs in colder habitats, whereas white‐flowered S. latifolia is found in warmer and more disturbed habitats (Friedrich, 1979; Karrenberg & Favre, 2008). Intrinsic pre‐ and postzygotic barriers, such as pollen competition and environmentally independent hybrid breakdown, are comparatively weak, suggesting that ecological divergence drives speciation (Favre et al., 2017; Karrenberg et al., 2019). The genetic architecture of traits associated with various reproductive barriers involves a large number of loci that are distributed over most of the genome but often concentrated in chromosome centres (Liu & Karrenberg, 2018). Hu and Filatov (2015) estimated net nonsynonymous sequence divergence (D a) between the species to be 0.0027 for autosomal loci, similar to animal systems at intermediate stages of speciation (Roux et al., 2016). Demographic models further suggest that divergence with gene flow is more likely than strict isolation (Guirao‐Rico, Sánchez‐Gracia, & Charlesworth, 2017; Hu & Filatov, 2015; Muir, Dixon, Harper, & Filatov, 2012); however, secondary contact scenarios have not been tested and heterogeneity in migration rates or effective population size was not modelled thus far.
In this study, we investigate evolutionary processes driving genetic differentiation between S. dioica and S. latifolia and using range‐wide population sampling and a reduced representation sequencing technique (double‐digest RAD sequencing; Peterson, Weber, Kay, Fisher, & Hoekstra, 2012), together with previous results on QTL mapping for traits associated with reproductive barriers (Liu & Karrenberg, 2018). We first explore population differentiation and the demographic history of the two species taking into account heterogeneity in migration rate and effective population size. As a second step, we describe the genomic landscape of differentiation using linkage maps (Liu & Karrenberg, 2018) and test for signatures of selection in highly differentiated regions. Moreover, we investigate whether regions with elevated differentiation are associated with QTLs for reproductive barrier traits (Liu & Karrenberg, 2018) or with reduced gene flow. This approach allows us to evaluate evidence for putative barrier loci/regions and to infer the evolutionary forces generating them.
2. MATERIALS AND METHODS
2.1. Sampling of species and populations
We sampled 11 populations of S. dioica and 9 populations of S. latifolia throughout their distribution ranges (Figure 1a). For each population, maternal seed families (known mother, unknown father(s)) were collected from individuals at least 5m apart to avoid sampling closely related individuals. Seeds of 8–12 maternal families per population, except for the S. latifolia population from Russia (RUS1), which was sampled as a pooled seed lot without family structure, were grown in the greenhouse at the Evolutionary Biology Centre, Uppsala University, Sweden (Table S1, Supporting Information). 189 individuals of S. dioica (17.0 per population on average, range: 10–23) and 162 individuals of S. latifolia (18.1 per population on average, range: 9–22) were sampled for DNA extraction and ddRAD sequencing (Table S1).
Figure 1.
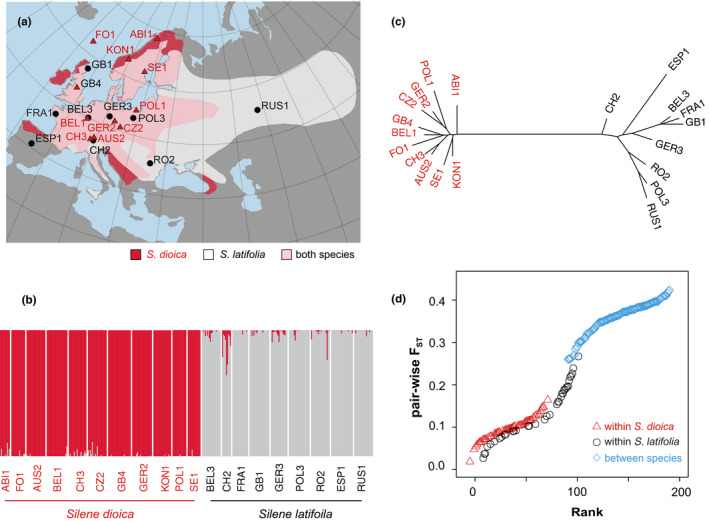
(a) Geographical distribution of Silene dioica (triangles, 11 populations) and S. latifolia (circles, 9 populations, map from Karrenberg et al. (2019), used with permission); (b) bar plot of a structure analysis with K = 2, the number of species included in the study; (c) unrooted phylogenetic tree using a neighbour‐joining method based on Nei's genetic distance; (d) ranked F ST values between population pairs within S. dioica, within S. latifolia and between the two species [Colour figure can be viewed at wileyonlinelibrary.com]
2.2. ddRAD sequencing and genotyping
Genomic DNA from silica‐dried leaf tissue was extracted using Qiagen's DNeasy Plant Mini Kit (Qiagen, Germany) and quantified using a Qubit dsDNA HS Fluorometer (Life Technologies, Sweden). We prepared libraries for double‐digest RAD sequencing (ddRAD‐seq) with the restriction enzymes EcoRI and TaqαI as described in Liu and Karrenberg (2018). Briefly, enzymatically digested DNA was ligated with barcoded adaptors and size‐selected to ~550 bp (Peterson et al., 2012). In total, nine 48‐plex libraries were sequenced on Illumina HiSeq 2500 systems at the SNP&SEQ Technology Platform of SciLifeLab, Uppsala, Sweden, using 125‐bp paired‐end chemistry and two libraries per lane.
ddRAD‐seq data were processed following the dDocent pipeline v2.2 (Puritz, Hollenbeck, & Gold, 2014). First, we demultiplexed raw reads using the process_radtag function of Stacks (Catchen, Hohenlohe, Bassham, Amores, & Cresko, 2013). We then pruned bases of low quality and adapter sequences with trimmomatic (Bolger, Lohse, & Usadel, 2014). We implemented bwa‐mem v0.7.16 (Li, 2013) to align cleaned reads to reference contigs that were previously assembled from eight individuals from Switzerland with deeply sequenced ddRAD‐seq libraries (Liu & Karrenberg, 2018). There is currently only a partial genome sequence of S. latifolia (one third of the 2.8 Gbp genome) with short scaffolds (N 50 = 10,785 bp) available (Krasovec, Chester, Ridout, & Filatov, 2018). We extended the ddRAD‐seq generated reference from Liu and Karrenberg (2018) with contigs from the present study built from unmapped pairs of reads with occurrences of at least 4X within an individual and present in at least 4 individuals using the de novo RAD assembler Rainbow (Chong, Ruan, & Wu, 2012). The extended ddRAD‐seq reference was 95,040,562 bp long in total, corresponding to 3.4% of the S. latifolia genome. We aligned reads to our extended ddRAD‐seq reference with bwa‐mem with a mismatch penalty of 3 and excluded highly clipped sequences containing more than 10 soft‐clipped bases (Li, 2013). We employed Freebayes (Garrison & Marth, 2012) for variant calling on the basis of populations with a minimum mapping quality score of 5 and a minimum base quality of 5 (see below for more stringent filtering after this initial step).
Raw variants were filtered using vcftools (Danecek et al., 2011) with the following criteria: a minimum quality score of 30, a minimum individual read depth of 6X and a minimum genotype call rate of 70% across all samples excluding those that were genotyped at <6% of all sites. We decomposed multinucleotide variants called by Freebayes (Garrison & Marth, 2012), such as linked SNPs within several bp, into separate single SNPs using the vcfallelicprimatives command from vcflib (Garrison, 2012). To filter spurious SNPs potentially due to paralogs, we excluded SNPs at which allele balance (AB) for heterozygous genotypes was below 0.25 or above 0.75, SNPs covered by both forward and reverse reads and SNPs with excessive read depth (>100×) (O'Leary, Puritz, Willis, Hollenbeck, & Portnoy, 2018). We included rare variants, which potentially evolved recently, to avoid biased estimation of site frequency spectra (no filter for minor allele frequency).
2.3. Population structure
We analysed population structure using admixture (Alexander, Novembre, & Lange, 2009). To avoid inclusion of linked loci, we randomly selected one SNP per contig. The input file was prepared using plink (Purcell et al., 2007). We examined the clustering of individuals in admixture with the number of groups (K) set to two (the number of species) and to 20 (the number of populations). In addition to the admixture analysis, we also assessed the relationships between populations using a neighbour‐joining tree based on genetic distance in the r package hierfstat (Goudet, 2004) and a principal component analysis (PCA) using the glPca command in the r package adegenet (Jombart, 2008).
2.4. Demographic modelling
To investigate the evolutionary history of the lineage split between S. dioica and S. latifolia, we performed demographical modelling based on the folded joint site frequency spectrum (SFS) using the software ∂a∂i, which implements a diffusion approximation‐based approach (Gutenkunst et al., 2009). We randomly selected one SNP per reference contig (average length 251 bp), a total of 10,415 SNP, for subsequent analysis in order to increase independence among SNPs for composite likelihood ratio tests. ∂a∂i analyses have been shown to produce robust results despite their simplifying assumptions (McCoy, Garud, Kelley, Boggs, & Petrov, 2014), such as neutrality and absence of linked selection, which usually cannot be assessed with the data at hand (Christe et al., 2017; Rougemont & Bernatchez, 2018) as is the case here as well. To avoid close relatedness among individuals, we only included two randomly selected individuals of different families per population. The derived SFS was projected onto 20 haploid samples, corresponding to 10 diploid individuals in each group to maximize the number of segregating sites.
We first considered a standard set of demographic scenarios: strict isolation without gene flow (SI), isolation with gene flow (IM), secondary contact (SC) and ancient migration (AM) (Figure S1). As a second step, we added population expansion to each of these models (“exp” models). Further models allowed for heterogeneity in migration rate, m (“hm” models), effective population size, N e, (“hn” models) or both m and Ne (“hmhn” models). For these latter models, loci were first partitioned into different sets with freely estimated proportions and separate SFSs were calculated for each set. Models including heterogeneity in m considered two sets of loci (2 SFSs): barrier loci without migration (m = 0) and loci for which m was estimated (m> 0). Heterogeneity in N e ("hn" models) was also modelled using two sets of loci (2 SFSs), each with freely estimated N e values (Ne 1 and Ne 2). Our most complex models ("hmhn" models) used four sets of loci (4 SFSs): m = 0 and Ne 1, m = 0 and Ne 2, m > 0 and Ne 1, and m > 0 and Ne 2. In total, we assessed 18 demographic models and optimized each with the observed joint SFS using 20 replicate runs with perturbed parameters as starting points. We excluded SC models that did not converge and had very short periods of unrealistically high gene flow (2Nem > 30) (personal communication, Ryan Gutenkunst). Nested model comparisons were performed using likelihood ratio tests; comparisons of non‐nested models were based on the Akaike information criterion (AIC).
In addition, we used simulations to assess goodness of fit of the best‐supported model as suggested by R. Gutekunst (https://github.com/dportik/dadi_pipeline/tree/master/Goodness_of_Fit). This approach is similar to parametric bootstrap for a chi‐square goodness‐of‐fit test between the observed SFS and model SFS for the best‐fitting model. We simulated 100 SFSs using model parameter estimates of the best‐fitting model and re‐optimized the model for each simulated SFS. Chi‐square and likelihood ratio statistics for goodness‐of‐fit tests between observed and model SFS were then compared to distributions of these statistics for tests between simulated and model SFS.
We estimated the demographic parameters from the best‐supported model, including divergence time, effective population sizes (Ne), migration rates (m) and proportions of the different types of loci (where included), with 95% confidence intervals constructed using 500 rounds of resampling SNPs from contigs. In ∂a∂i, divergence time is inferred in units of 2Nref generations. Nref constitutes the ancestral effective population size and can be estimated based on θ = 4 Nref μ L, where θ denotes the population mutation rate, μ the mutation rate per site per generation, and L the effective sequence length involved. We estimated L as the total base number of the reference contigs meeting SNP filtering criteria (read depth > 5 per individual; genotype call rate: >70% of the individuals, excluding individuals genotyped at < 6% of the sites). We used a generation time of one year and a mutation rate μ of 7.92 × 10–9 for estimating population size and divergence time (Krasovec et al., 2018).
2.5. Calculation of differentiation, sequence divergence and diversity statistics
We calculated differentiation between the two species as hierarchical F‐statistics ("hierarchical F ST") to account for population structure within species using AMOVA models in the R package hierfstat (Goudet, 2004) for both SNPs and contigs. We also calculated Nei's estimate of F ST (Nei, 1987) between all population pairs (between species and within species). We calculated sequence divergence, d XY, between the two species using a custom Perl script . Within each species, we computed genetic diversity (π) using vcftools (Danecek et al., 2011) and estimated Tajima's D (Takahata & Nei, 1985) using a custom Perl script. For contig‐based calculations dependent on sequence length (d XY, π and Tajima's D), we determined sequence length as number of bases meeting SNP filtering criteria in each contig as described above.
2.6. Genome scans using linkage maps
We examined genome‐wide patterns in differentiation, sequence divergence and diversity statistics by anchoring contigs onto the two linkage maps constructed in a previous study from two F2 crosses between S. dioica and S. latifolia: F2DL (1,470 markers) and F2LD (1,265 markers) (Liu & Karrenberg, 2018). Average marker spacing on these maps was of 0.51 cM and 0.54 cM for the 11 autosomes and 0.33 and 0.32 cM on sex chromosomes for F2DL and F2LD, respectively (Liu & Karrenberg, 2018). We used linkage maps because only a partial physical genome sequence for S. latifolia (one third of the genome) is available to date (Krasovec et al., 2018). However, patterns along linkage maps, which are based on recombination rates, are useful in themselves (Wolf & Ellegren, 2017). We treated the two linkage maps separately here because only 20% of the contigs with mapped markers occurred on both maps, whereas the remaining contigs were unique to each map in these highly variable species (Liu & Karrenberg, 2018). Uncertainty in marker order on a consensus map, particularly in marker‐dense regions, may lead to spurious patterns. We used local polynomial regression (LOESS) curves along each linkage group to represent patterns for each statistic (Cleveland, 1979).
2.7. Genomic landscapes and signatures of selection
As a first step, we analysed correlations between contig‐based F ST and d XY using a permutation test in the R package coin (Hothorn, Hornik, Wiel, & Zeileis, 2006). We further identified genomic islands of elevated differentiation as contig sequences with hierarchical F ST exceeding the 95% quantile of the F ST value distribution for all contigs. To assess signatures of selection in these highly differentiated regions, we compared d XY, π and Tajima's D between the differentiation islands and background regions using Mood's median test in the R package coin (Hothorn et al., 2006). The above analyses were performed both for mapped contigs (data from both linkage maps combined, N = 1,327) and for all contigs in our data set (N = 10,415).
2.8. Within‐ versus between‐species differentiation
Genetic differentiation landscapes within and between species are expected to correlate if they are mainly governed by variation in conserved genomic features, such as recombination rate variation and gene density (Berner & Roesti, 2017; Burri, 2017; Haenel, Laurentino, Roesti, & Berner, 2018; Stankowski et al., 2019). We compared the between‐species differentiation landscape (hierarchical F ST) to within‐species differentiation landscapes using the population pairs with the highest overall F ST within each species. We further evaluated correlations of hierarchical F ST and within‐species F ST for both mapped and all contigs using a permutation test in the r package coin (Hothorn et al., 2006).
2.9. Differentiation and divergence near QTLs for reproductive barrier traits
We first compared the location of highly differentiated regions to the previously identified QTLs for traits associated with reproductive barriers between S. dioica and S. latifolia (Liu & Karrenberg, 2018). We further used nonparametric Wilcoxon tests to examine whether contigs mapping closest to QTLs for traits associated with assortative pollination or ecological differentiation (Liu & Karrenberg, 2018) have significantly elevated hierarchical F ST or dXY (one‐tailed tests) or differ in within‐species differentiation (two‐tailed tests) as compared to contigs closest to random positions. For this analysis, we combined data across the two independently constructed linkage maps (Liu & Karrenberg, 2018) with 1,470 (F2DL cross) and 1,265 markers (F2LD cross) and started with 110 randomly selected positions per map. Random positions were discarded if there was no mapped contig within 5cM. Assortative pollination QTLs comprised QTLs for flower colour, flower size, flower number and stem height, and ecological differentiation QTLs included QTLs for first‐year flowering, specific leaf area, leaf succulence and survival (Liu & Karrenberg, 2018).
2.10. Patterns of isolation by distance within and between species
Increases in genetic differentiation with geographical distance (isolation by distance, IBD) arise in populations connected by gene flow. At barrier loci, however, gene flow is restricted, and thus, a weakening of IBD is expected as compared to loci with low differentiation between species. To test whether barrier loci indeed experience reduced gene flow between species, we analysed associations of genetic differentiation in between‐species population pairs (between‐species F ST) and geographical distance in differentiation islands (hierarchical F ST above 5% quantile of the overall distribution) and in regions with low differentiation (hierarchical F ST below the 25% quantile of the overall distribution). To control for phylogeographical patterns in each species and for shared heterogeneity in gene flow, we also applied these analyses to population pairs within each species using the same groups of loci. A lack of IBD in between‐species population pairs can be attributed to a reduction in between‐species gene flow if the same regions exhibit IBD within species. We tested for associations of F ST and geographical distance using Mantel permutation tests implemented in the R package vegan (Oksanen et al., 2019).
3. RESULTS
3.1. Sequencing output
We obtained on average 4,303,869 reads per individual from ddRAD sequencing, which in total yielded 1,799,882,123 reads. After filtering, we retained 87,006 SNPs for the downstream analysis with an average read depth of 21.2 per individual. These SNPs were located on 10,415 contigs with an average length of 251 bp. 1,327 contigs were present on linkage maps (817 contigs on the F2DL map, 632 contigs on the F2LD map and 122 contigs on both maps).
3.2. Population structure and overall FST
We used a set of 10,415 SNPs (random selection of one SNP per contig) to analyse population structure. With K = 2, two groups are clearly separated, corresponding to S. dioica and S. latifolia, with limited admixture in a few populations (Figure 1b), particularly the Swiss population of S. latifolia (CH2). With K = 20, the number of natural populations included in the study, all populations could be recognized, although there was evidence for considerable introgression or allele sharing within species (Figure S2). A phylogenetic tree based on genetic distance as well as a principal component analysis also showed two clusters, consisting of populations from each species and with greater variation among S. latifolia populations than among the S. dioica populations (Figure 1c; Figure S3).
The overall hierarchical F ST between S. dioica and S. latifolia was 0.28, as estimated from AMOVA (Table 1). Average pairwise weighted F ST was 0.357 (range: 0.261–0.424) for between‐species population pairs, 0.099 (range: 0.019–0.165) for population pairs within S. dioica and 0.136 (range: 0.027–0.267) for population pairs within S. latifolia (Figure 1d). This is in agreement with the phylogenetic tree, where branch lengths of S. latifolia populations were longer than those of S. dioica populations (Figure 1c). Note that hierarchical FST was calculated using a two‐level hierarchical structure (species and populations), whereas pairwise weighted F ST was calculated for each population pair separately.
Table 1.
Summary of population genetic statistics for the campions Silene dioica (11 populations) and S. latifolia (9 populations) based on reduced representation sequencing (ddRAD‐seq)
| Statistic | Value | |
|---|---|---|
| Mean | Median | |
| Number of SNPs | 87,006 | |
| Number of contigs | 10,415 | |
| Hierarchical F ST between species | 0.278 | |
| d XY between species | 5.28 × 10–3 | 3.36 × 10–3 |
| Pairwise F ST within S. dioica | 0.098 | 0.096 |
| Pairwise F ST within S. latifolia | 0.136 | 0.128 |
| π within S. dioica | 2.18 × 10–3 | 1.40 × 10–3 |
| π within S. latifolia | 2.48 × 10–3 | 1.70 × 10–3 |
| Tajima's D within S. dioica | −0.156 | −0.475 |
| Tajima's D within S. latifolia | −0.156 | −0.435 |
3.3. Demographic history of lineage divergence
Models involving migration generally outperformed the strict isolation (SI) models significantly based on AIC (Figure 2; Figure S1, Table S2, Supporting Information). These models, isolation with migration (IM), secondary contact (SC) and ancient migration (AM), were significantly improved by adding population expansion ("exp" models) or heterogeneity in migration rate (“hm” models), effective population size (“hn” models) or both migration rate and population size (“hmhn” models, Figure 2; Table S2). Under each scenario (IM, SC and AM), “hmhn” models had the best fit, as indicated by likelihood ratio tests (Table S2). The overall best‐supported model in terms of AIC was the IMhmhn model (Figures 2 and 3a; Table S2). SChmhn and AMhmhn models fit the data nearly as well; however, in both scenarios, the estimated duration of the phase without gene flow was close to zero, such that they converged to the IMhmhn model (Tables S2 and S3).
Figure 2.
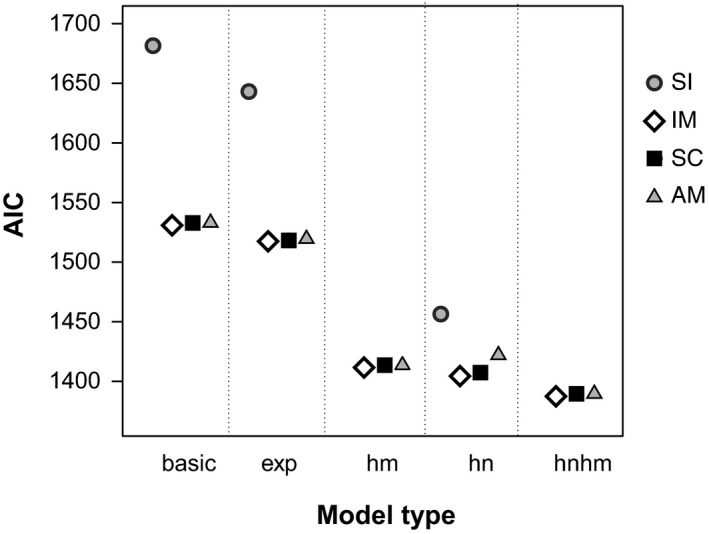
Akaike's information criterion (AIC) for demographic models of the lineage split between the campions Silene dioica and S. latifolia in four scenarios: strict isolation (SI), isolation with migration (IM), secondary contact (SC) and ancient migration (AM). Models contained no further parameters (“basic”), allowed for population expansion (“exp”) or included heterogeneity in migration rate (“hm”), effective population size (“hn”) or both parameters (“hmhn”). “hm” and “hmhn” models were not calculated for the SI scenario which does not include any migration
Figure 3.
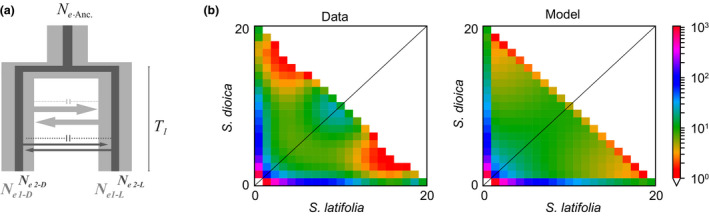
(a) Illustration of the best‐supported demographic model, isolation with migration with heterogeneous migration rate and population size (“IMhmhn”). Light grey represents loci evolving with large population size (NeD1, NeL1), and dark grey represents the loci with reduced population size (NeD2, NeL2); arrows indicate migration and barrier loci (dotted lines, not drawn to scale). (b) Joint site frequency spectra of the data and under the IMhmhn model [Colour figure can be viewed at wileyonlinelibrary.com]
The observed joint site frequency spectrum (SFS) of the data was similar to the one generated by the best‐supported IMhmhn model, except for a more pronounced pattern along the diagonal in the observed SFS: loci with high frequencies in one species but low frequencies in the other were underrepresented in the model as compared to the data (Figure 3b). Normalized model residuals were mainly in the range of −2 to 2, with a bias towards positive residuals (Figure S4a,b). Goodness‐of‐fit tests between observed SFS and model SFS for the IMhmhn model yielded chi‐square and likelihood ratio values close to modes of the distributions of these statistics for tests between simulated SFS and model SFS, indicating that this model fits the data well (Figure S4c,d, https://github.com/dportik/dadi_pipeline/tree/master/Goodness_of_Fit).
Under the best‐supported IMhmhn model, the proportion of loci with reduced effective population size [P(Ne2 and m> 0) + P(Ne2 and m = 0)] was estimated to be 61.2% (CI: 24.5%–90.3%) and 4.7% (CI: 0.3%–68.9%) of the loci conformed to a scenario of divergence without gene flow with m = 0 [P(Ne1 and m = 0) + P(Ne2 and m = 0)]. The distribution of resampling estimates for the percentage of loci with m = 0 was strongly right‐skewed and had an interquartile range of 1.8%–7.9%. Most of these potential barrier loci with m = 0 had reduced Ne (4.4% of all loci with m = 0 and low Ne2; 0.4% of all loci with m = 0 and high Ne1, Table 2).
Table 2.
Demographic parameters in the best‐supported demographic model (IMhmhn) of the lineage divergence between the campions Silene dioica and S. latifolia: isolation with migration with heterogeneous migration rate (m = 0 and m> 0) and heterogeneous effective population size (Ne1 and Ne2); subscripts stand fsor S. dioica (D) and S. latifolia (L) and for the direction of gene flow, from S. dioica into S. latifolia (D > L) and vice versa (L > D)
| Parameter | Median | Mean | 2.5% quantile | 97.5% quantile |
|---|---|---|---|---|
| Ne‐ Anc a | 493,717 | 493,816 | 442,387 | 554,670 |
| T (myrs) a | 0.1200 | 0.1230 | 0.0867 | 0.2328 |
| P (Ne1 and m > 0) a | 38.47% | 34.79% | 7.61% | 73.29% |
| P (Ne1 and m = 0) | 0.36% | 1.12% | 0.02% | 7.70% |
| P (Ne2 and m > 0) | 55.91% | 54.04% | 13.60% | 80.78% |
| P (Ne2 and m = 0) | 4.37% | 9.98% | 0.08% | 63.27% |
| Ne1/Ne2 | 4.05 | 5.54 | 3.15 | 19.55 |
| Average Ne‐D | 188,526 | 203,114 | 157,506 | 342,749 |
| Average Ne‐L | 278,607 | 305,737 | 217,667 | 594,703 |
| Ne1‐D | 349,269 | 520,893 | 194,732 | 2,194,182 |
| Ne2‐D | 86,348 | 89,987 | 41,776 | 152,002 |
| Ne1‐L | 516,534 | 795,367 | 282,767 | 4,209,389 |
| Ne2‐L | 127,756 | 134,887 | 61,423 | 233,284 |
| Average M L>D | 0.22 | 0.36 | 0.14 | 1.43 |
| Average M D>L | 0.33 | 0.53 | 0.23 | 2.40 |
| M1‐L>D (Ne1‐D loci) | 0.43 | 1.58 | 0.27 | 13.17 |
| M2‐L>D (Ne2‐D loci) | 0.10 | 0.21 | 0.06 | 1.72 |
| M1‐D>L (Ne1‐L loci) | 0.63 | 2.36 | 0.45 | 17.11 |
| M2‐D>L (Ne2‐D loci) | 0.15 | 0.31 | 0.09 | 2.24 |
Parameters were estimated with 500 rounds of resampling of SNPs from contigs (see Section 2).
Ne ‐Anc, ancestral population size; T, divergence time in million years (myrs); P, percentage of loci.
The estimated median population migration rates across the genome from the IMhmhn model were 0.22 (95% CI: [0.14–1.43]) migrants per generation from S. latifolia to S. dioica and 0.33 (95% CI: [0.23–2.4]) from S. dioica to S. latifolia (Table 2). We obtained an effective population size of 188,526 (95% CI: [157,506–342,278]) for S. dioica and 278,607 (95% CI: [217,667–594,702]) for S. latifolia. The divergence time between S. dioica and S. latifolia was estimated to be 0.120 million years (95% CI: [0.087–0.233] myrs) assuming a generation time of one year (Table 2).
3.4. Genomic landscape of differentiation, sequence divergence and diversity
Hierarchical F ST on both SNP‐ and contig‐based levels fluctuated widely across the genome (cross F2DL: Figure 4; cross F2LD: Figure S5, Supporting Information). Both hierarchical F ST and sequence divergence, d XY, reached peaks around the middle of most linkage groups on both linkage maps (Figure 4; Figure S5, Supporting Information), in spite of largely different SNP markers on the two maps (Liu & Karrenberg, 2018). F ST and d XY were significantly, but moderately, correlated (mapped contigs: r = 0.347, p < .001; all contigs: r = 0.464, p < .001, based on 9,999 permutations, Figures S6a,b, Supporting Information). Highly divergent regions in the middle of linkage groups often contained loci with reduced nucleotide diversity (π) and more negative Tajima's D in one or both species (Figure 4, Figures S7, S8).
Figure 4.
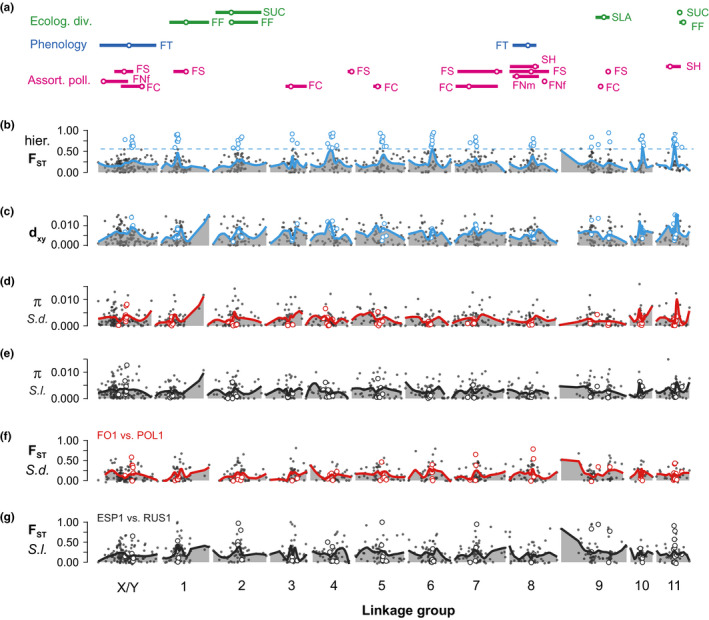
Genomic landscapes and QTLs for traits associated with reproductive barriers between the campions Silene dioica and S. latifolia based on a linkage map of the F2DL cross (for the F2LD cross, see Figure S3); (a) locations (circles) and 1.5 LOD drop intervals (lines) of QTLs related ecological divergence (FF: first‐year flowering; SUC: leaf succulence; SLA: specific leaf area), phenology (FT: flowering time) and assortative pollination (FC: flower colour; FS: flower size; FNf and FNm: flower number for females and for males; SH: stem height); (b) hierarchical F ST between the two species with the 95% quantile of overall F ST distribution (dashed line); (c) sequence divergence (d XY); (d) and (e) nucleotide diversity (π) within S. dioica (S.d.) and within S. latifolia (S.l.); (f) and (g) F ST of the most differentiated population pair within S. dioica and within S. latifolia. Lines in panels (b)–(g) are drawn using LOESS functions; in all panels, empty circles represent contigs with between‐species F ST exceeding the 95% quantile (genomic islands of differentiation) [Colour figure can be viewed at wileyonlinelibrary.com]
For mapped contigs, d XY was significantly elevated in genomic islands of differentiation as compared to the genomic background, and both π and Tajima's D were significantly reduced in both species (Figure 5; Table S4). Results were very similar when using all contigs, except that π was not significantly reduced in differentiation islands within S. latifolia (Figure S9, Table S4).
Figure 5.
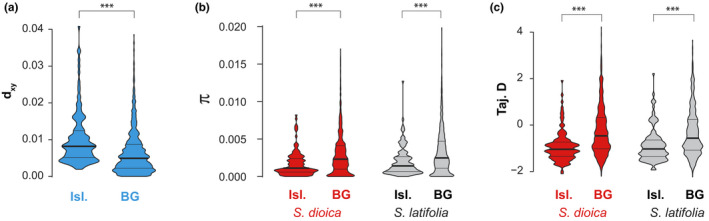
Violin plots for population genetic statistics in the campions Silene dioica and S. latifolia in genomic islands of differentiation (Isl.) and the genomic background (BG) for contigs mapped onto linkage maps: (a) sequence divergence (d XY); (b) genetic diversity (π); and (c) Tajima's D. Within each violin, the horizontal lines represent the 25%, 50% (median, thick lines) and 75% quantiles. Results from Mood's median tests are given on the top (***, p‐Value < .001) [Colour figure can be viewed at wileyonlinelibrary.com]
3.5. Within‐ versus between‐species differentiation
The genomic landscapes of differentiation between species generally did not coincide with those of highly differentiated population pairs within S. latifolia (ESP1 versus RUS1, overall F ST = 0.27) or within S. dioica (FO1 versus POL1, overall F ST = 0.16, Figure 1d, Figure 4; Figure S5). Within‐species comparisons had less pronounced F ST peaks in the middle of several linkage groups as compared to between‐species hierarchical F ST, whereas the remaining linkage groups showed no obvious differentiation peaks in within‐species comparisons (Figure 4; Figure S5). Correlations of within‐species F ST and between‐species hierarchical F ST were weak (mapped contigs: r = 0.028, p = .319 for S. dioica and r = 0.11, p < .001 for S. latifolia; all contigs: r = 0.071, p < .001 for S. dioica and r = 0.147, p < .001 for S. latifolia, Figure S6c–f).
3.6. Differentiation and divergence near QTLs for reproductive barrier traits
Many QTLs for traits associated with reproductive barriers mapped to genomic regions with high F ST and d XY (Figure 4; Figure S5). However, we did not find significant evidence (p < .05) for elevations of F ST or dXY in contigs at or near QTLs for traits associated with assortative pollination or ecological differentiation as compared to contigs closest to randomly drawn map positions (Figure S10).
3.7. Patterns of isolation by distance
Within S. dioica, pairwise F ST was only weakly associated with geographical distance (Figure 6a; Figure S11a, Table S5). Within S. latifolia, in contrast, we detected a pronounced isolation‐by‐distance pattern with significant associations of pairwise F ST with geographical distance (Figure 6b; Figure S11b, Table S5). In both species, differentiation islands exhibited slightly elevated pairwise F ST and a tendency for a weaker correlation between pairwise F ST and geographical distance as compared to loci with low between‐species differentiation (Figure 6; Figure S11, Table S5). In between‐species population pairs, pairwise F ST correlated strongly and significantly with geographical distance at loci with low between‐species differentiation. At differentiation islands, in contrast, no significant increase in pairwise F ST with geographical distance was detected, suggesting that many of these loci resist gene flow and constitute putative barrier loci (Figure 6c; Figure S11c, Table S5). For these latter analyses, we excluded pairwise comparisons to one S. latifolia population (CH2) that showed strongly reduced pairwise F ST for highly differentiated regions, and moderately reduced pairwise F ST for regions with low differentiation (grey symbols, Figure 6c; Figure S11c). This population also exhibited signs of admixture (Figure 1b).
Figure 6.
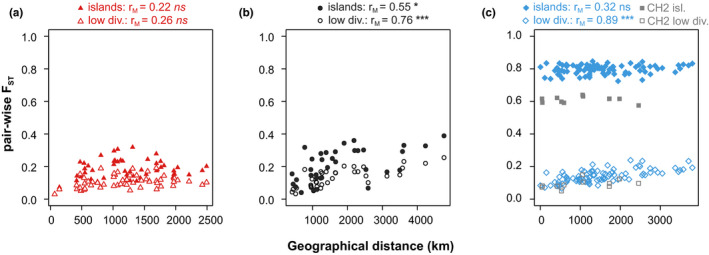
Scatterplots of pairwise differentiation (FST) against geographic distance (km) for population pairs within Silene dioica (a), within S. latifolia (b) and between the two species (c) based on contigs mapped to linkage maps. For between‐species population pairs, comparisons to the Swiss population of S. latifolia (CH2) are displayed separately (see text). Pairwise FST is given for between‐species differentiation islands (above 95% quantile of FST filled symbols) and for regions of low between‐species differentiation (below 25% quantile of FST, empty symbols). Results of Mantel tests are indicated at the top; ns , p > .05; *, p < .05; ***, p < .001 [Colour figure can be viewed at wileyonlinelibrary.com]
4. DISCUSSION
In this study, we used demographic modelling combined with population genomic analyses to infer evolutionary processes leading to divergence between two closely related and hybridizing campion species, Silene dioica and S. latifolia. Together, our results support a model where the two species diverged with gene flow but have evolved putative barrier loci at which gene flow is reduced. Our analyses further indicate that background selection alone cannot explain the genomic pattern of differentiation, suggesting that divergent selection also contributed.
4.1. Demographic history supports divergence with gene flow and barrier loci
Demographic analyses suggest that S. dioica and S. latifolia diverged with gene flow, in line with evidence for ongoing hybridization in natural populations of the two species (Karrenberg & Favre, 2008; Minder et al., 2007). Similar scenarios of comparatively advanced divergence (hierarchical F ST = 0.28 in our study) combined with persistent gene flow are only rarely reported, for example in Japanese sticklebacks (Ravinet et al., 2018) and Heliconius butterflies (Martin et al., 2013). Demographic analyses in many other systems, in contrast, point to divergence in para/allopatry with gene flow only during secondary or intermittent contact (Christe et al., 2017; Duranton et al., 2018; Tine et al., 2014). In our analysis, secondary contact (SC) and ancient migration (AM) models had only slightly less support than the best‐supported isolation with migration (IM) models (but with an AIC difference exceeding 2). However, periods without gene flow in AM and SC models were extremely short, such that they effectively converged to the best‐supported IM model. Nonetheless, we cannot exclude more complex demographic scenarios such as multiple short periods of allopatry combined with population expansion (Christe et al., 2017). Large effects of population expansion are unlikely though, based on simple IM models with population expansion in this study, as well as in Muir et al. (2012) and in Guirao‐Rico et al. (2017). We are therefore confident that our isolation with migration model captures the main aspects of the two species' demographic history.
Our demographic models included and supported heterogeneity in both migration rate and effective population size. This is in line with results from various animal systems where heterogeneous migration rates were most common at intermediate stages of speciation, whereas support for heterogeneity in effective population size varied across systems irrespective of the speciation stage (Roux et al., 2016). Note that ABC modelling used in Roux et al. (2016) incorporated heterogeneity in N e and m using hyperprior distributions whereas our best‐supported ∂a∂i model partitioned loci into four subsets: loci with and without migration each combined with high and low Ne, which was more tractable in this framework. We estimated that a small part of the loci evolved without gene flow (median 4.7%, 95% confidence interval: 0.1%–70.9%, interquartile range: 1.8%–7.9%) and can thus be considered as potential barrier loci. The great majority of loci without gene flow also had reduced Ne (Ne2, Table 2), and this is consistent with models of speciation with gene flow (Ravinet et al., 2017; Seehausen et al., 2014; Yeaman et al., 2016). However, effects of heterogeneity in population size and migration on the joint site frequency spectrum can be difficult to distinguish from each other (Christe et al., 2017; Rougemont & Bernatchez, 2018; Roux et al., 2016).
Our results generally agree with previous demographic analyses in the two species that used more limited data sets and simpler models but also rejected strict isolation scenarios in favour of divergence with gene flow (Guirao‐Rico et al., 2017; Hu & Filatov, 2015; Muir et al., 2012). We estimated divergence time to be 0.12 million years before present, considerably more recent than estimates of Muir et al. (2012), Hu and Filatov (2015) and Guirao‐Rico et al. (2017). This is likely a consequence of including heterogeneity in population size and migration rate in demographic models in this study, as indicated by comparisons of estimates under the best‐supported model and under a model similar to those employed in previous studies (Guirao‐Rico et al., 2017; Hu & Filatov, 2015; Muir et al., 2012). Our divergence time estimate places the lineage split close to the onset of the most recent glaciation in Europe with rapid environmental changes (Hewitt, 2000). However, this estimate is contingent on a generation time of one year observed for these species (Favre et al., 2017; Hu & Filatov, 2015; Muir et al., 2012), but generation time can also be two or three years in colder environments (Favre et al., 2017). Average migration rate estimates (M = 2Nem) from our best‐supported model (0.22 [CI: 0.14–1.43] and 0.33 [0.23–2.4] from S. latifolia into S. dioica and vice versa) were similar to those reported by Muir et al. (2012) but lower than those reported by Hu and Filatov (2015). Estimates of migration rate were further consistent with near‐complete reproductive isolation, mostly through adaptation to the habitat and to pollinators (Karrenberg et al., 2019). The proportion of the gene pool replaced by the other species per generation m was estimated to be ca. 6 × 10–7 here; this value can be roughly compared to the probability of F1 hybrid production, Phyb (Sambatti, Strasburg, Ortiz‐Barrientos, Baack, & Rieseberg, 2012). Phyb, estimated from the strength of total reproductive isolation, was several orders of magnitude larger than m (Phyb = 1 − RItotal: 0.010–0.036, depending on the direction) (Karrenberg et al., 2019), suggesting that additional ecological or genetic reproductive barriers may exist. Note, however, that Phyb corresponds to recent or ongoing gene flow whereas m is an average estimate over the time since divergence between the two species.
4.2. Accentuated differentiation (F ST) and sequence divergence (d XY) in linkage group centres suggest the evolution of barrier loci
Genetic differentiation, in terms of hierarchical F ST between species, and sequence divergence (d XY) were both accentuated in the middle of most linkage groups on the linkage maps. Elevated differentiation in chromosome centres has been described for diverse taxa and attributed to reduced crossover rates in the middle of chromosomes (Berner & Roesti, 2017; Haenel et al., 2018; Nachman & Payseur, 2012). Unfortunately, we do not have estimates of recombination rate (recombination frequency (cM) per physical genome distance (Mbp)), because scaffolds in the available partial genome sequence of S. latifolia (one third of the genome) are short (N50 = 10,785 bp) (Krasovec et al., 2018). In our study, F ST and d XY were positively correlated and highly differentiated regions (genomic islands of differentiation) had an approximately twofold higher median d XY as compared to remaining genomic regions. In a divergence‐with‐gene flow scenario, as in the species studied here, these results are suggestive of reductions in gene flow and thus barrier loci colocalizing in low‐recombination regions (Cruickshank & Hahn, 2014; Nachman & Payseur, 2012; Rafajlović, Emanuelsson, Johannesson, Butlin, & Mehlig, 2016; Ravinet et al., 2017; Seehausen et al., 2014; Yeaman et al., 2016); however, we cannot exclude that lineage sorting in the ancestor, rather than new mutations, also contributed to the pattern (Pease, Haak, Hahn, & Moyle, 2016; Richards et al., 2019). Evidence for genomic islands with elevated F ST and d XY is comparatively rare and has been reported for Darwin's finches (Han et al., 2017), European sea bass (Duranton et al., 2018) and poplars (Wang et al., 2016). Our findings are in contrast to other systems where differentiation landscapes are mainly shaped by background selection acting on a heterogeneous recombination landscapes: under this scenario, d XY is not elevated or even reduced in regions of high differentiation and differentiation landscapes across replicate species pairs are strongly correlated (Burri, 2017; Nachman & Payseur, 2012), as reported in sunflowers (Renaut et al., 2013), monkeyflowers (Stankowski et al., 2019) and different bird lineages (Burri et al., 2015; Delmore et al., 2018; Vijay et al., 2017). As another form of linked selection, parallel local selection may also arise in low‐recombination regions and thereby contribute to correlated differentiation landscapes (Berner & Roesti, 2017; Samuk et al., 2017; Yeaman et al., 2016). In our study, we found only weak correlations of F ST between species with F ST between highly divergent populations within species. Overall, our results are thus consistent with an important role of barrier loci in generating the differentiation landscape.
4.3. Signature of selection at highly differentiated regions
Genomic islands of high differentiation show significant signatures of selection within both species: reduced sequence diversity and an overrepresentation of rare variants (reduced and negative Tajima's D). These regions also exhibited elevated sequence divergence, d XY, suggesting that they experienced reduced gene flow and may contain putative barrier loci (Irwin et al., 2018). Reproductive isolation between the two species is mainly associated with adaptation to the habitat and, presumably, to pollinators (Favre et al., 2017; Goulson & Jerrim, 1997; Karrenberg et al., 2019). In our study, many QTLs for traits associated with reproductive barriers, including ecological divergence or assortative pollination, appeared to colocalize with highly differentiated regions on linkage maps. Average F ST and dXY near QTLs for reproductive barrier traits, however, were not significantly elevated as compared to the genomic background. These results could, on the one hand, be a consequence of limited genome coverage with our reduced representation data. On the other hand, the genetic architecture of RI traits is complex in our system (Liu & Karrenberg, 2018) and selection footprints may be too weak to detect them in the current study. Additional reproductive barriers may be involved as well as intrinsic incompatibilities that locally reduce gene flow. Signatures of selection in highly divergent regions have also been detected in ecotypes or early‐stage ecological speciation in three‐spined sticklebacks (Feulner et al., 2015; Marques et al., 2017; Samuk et al., 2017) and in cichlids (Malinsky et al., 2015; Meier et al., 2018), as well as in more advanced stages of speciation in poplars (Wang et al., 2016). Our results thus provide additional evidence for an important role of divergent selection in generating the genomic landscape of differentiation.
4.4. Gene flow between species is limited at highly differentiated loci
Within S. latifolia, we detected significant isolation‐by‐distance patterns consistent with postglacial range expansion, whereas an isolation‐by‐distance pattern was very weak in S. dioica, possibly because geographical distance does not reflect dispersal routes very well in mountainous regions (Hathaway, Malm, & Prentice, 2009; Prentice, Malm, & Hathaway, 2008; Rautenberg, Hathaway, Oxelman, & Prentice, 2010). In between‐species population pairs, F ST significantly increased with geographical distance at loci with low differentiation between species, indicating that the two species are connected by gene flow. At highly differentiated loci, in contrast, no significant F ST increase with geographical distance was detected, suggesting that many of these loci constitute barrier loci. This is in line with results of heterogeneous gene flow from our demographic analysis. Between‐species comparisons involving one S. latifolia population from Switzerland, with comparatively high admixture, had generally reduced between‐species F ST, particularly for highly differentiated loci. This is likely due to recent hybridization and introgression in this population. Ongoing hybridization has previously been documented for this area (Karrenberg & Favre, 2008; Minder et al., 2007). Overall, these results suggest that highly differentiated regions contain loci that raise barriers to gene flow between species.
5. CONCLUSION
Multiple lines of evidence support the evolution of barrier loci during speciation with gene flow in the campions Silene dioica and S. latifolia: (1) demographic analyses indicate divergence with heterogeneous gene flow, (2) differentiation (F ST) and sequence divergence (d XY) were positively correlated and elevated in the middle of most linkage groups, (3) highly differentiated regions exhibited signatures of selection, and (4) isolation‐by‐distance patterns suggest that S. dioica and S. latifolia are connected by gene flow at regions with low differentiation but not at islands of high differentiation. Previous studies showed that strong cumulative reproductive isolation in this system results mainly from adaptation to the habitat and to pollinators (Karrenberg et al., 2019) and is based on traits with polygenic genetic architectures (Liu & Karrenberg, 2018). The results of this study thus align well with theoretical predictions for lineage divergence in the face of homogenizing gene flow with barrier loci evolving more readily in central parts of chromosomes which often have reduced recombination (Berner & Roesti, 2017; Haenel et al., 2018; Ravinet et al., 2017; Seehausen et al., 2014; Yeaman et al., 2016). Empirical evidences for these predictions are, thus far, scarce and dominated by systems at early stages of speciation (Feulner et al., 2015; Malinsky et al., 2015; Marques et al., 2017; Meier et al., 2018; Samuk et al., 2017). Later‐stage cases appear to be rare, presumably because gene flow is expected to cease rapidly at later stages of speciation leading to rapid genome‐wide differentiation (Flaxman et al., 2014; Ravinet et al., 2018; Riesch et al., 2017). The Silene system represents a comparatively advanced stage of speciation with still highly heterogeneous differentiation. The data presented here suggest that this heterogeneity in differentiation is generated by divergent selection driving the evolution of barrier loci.
Author contributions
The study was designed by S.K., X.L. and S.G. The laboratory work was performed by X.L. with the help of laboratory assistants. The analyses were conducted by X.L. with input from S.K. and S.G. The manuscript was written by S.K. and X.L. with contributions from S.G.
Supporting information
Fig S1‐S11
Table S1‐S5
ACKNOWLEDGEMENTS
We are thankful to Emelie Hallander, Karin Steffen and Rasmus Jansson for assistance with plant cultivation and molecular laboratory work, and to Alex Buerkle, Pär Ingvarsson and Martin Lascoux for insightful comments on this work. We are most grateful to our colleagues T. Finderup Nilsen, M. van Kleunen, F. van Rossum, C. Rixen, M. Sochor, L. Giminez, A‐M Fosaa, D. Charlesworth, A. Favre, M. Uscka‐Perzanowska, A. Spinu, V. Semerikov, N. Kutlunina and A. Pop for kindly collecting and sending seeds for this project. This study was supported by the Science for Life Laboratory and the National Genomics Infrastructure (NGI), Sweden. Computations were performed on resources provided by SNIC through the Uppsala Multidisciplinary Center for Advanced Computational Science (UPPMAX) under projects SNIC 2017/7‐406 and uppstore2017241. This research was funded by project grant no. 2012‐03622 of the Swedish Research Council (Vetenskapsrådet) to SK.
Liu X, Glémin S, Karrenberg S. Evolution of putative barrier loci at an intermediate stage of speciation with gene flow in campions (Silene). Mol Ecol. 2020;29:3511–3525. 10.1111/mec.15571
Data Accessibility
Double‐digest RAD (ddRAD) sequencing data will be available on NCBI's Short Read Archive (SRA, SUB7812013 https://www.ncbi.nlm.nih.gov/sra/PRJNA649094). The data in variant call format (VCF) file, Perl codes for genetic analysis, R codes for plotting and Python codes for demographical modelling are available on Dryad (https://doi.org/10.5061/dryad.6djh9w0zd).
REFERENCES
- Alexander, D. H. , Novembre, J. , & Lange, K. (2009). Fast model‐based estimation of ancestry in unrelated individuals. Genome Research, 19, 1655–1664. 10.1101/gr.094052.109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berner, D. , & Roesti, M. (2017). Genomics of adaptive divergence with chromosome‐scale heterogeneity in crossover rate. Molecular Ecology, 26, 6351–6369. 10.1111/mec.14373 [DOI] [PubMed] [Google Scholar]
- Bolger, A. M. , Lohse, M. , & Usadel, B. (2014). Trimmomatic: A flexible trimmer for Illumina sequence data. Bioinformatics, 30, 2114–2120. 10.1093/bioinformatics/btu170 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burri, R. (2017). Interpreting differentiation landscapes in the light of long‐term linked selection. Evolution Letters, 1, 118–131. 10.1002/evl3.14 [DOI] [Google Scholar]
- Burri, R. , Nater, A. , Kawakami, T. , Mugal, C. F. , Olason, P. I. , Smeds, L. , … Ellegren, H. (2015). Linked selection and recombination rate variation drive the evolution of the genomic landscape of differentiation across the speciation continuum of Ficedula flycatchers. Genome Research, 25, 1656–1665. 10.1101/gr.196485.115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butlin, R. K. , & Smadja, C. M. (2018). Coupling, reinforcement, and speciation. The American Naturalist, 191, 155–172. 10.1086/695136 [DOI] [PubMed] [Google Scholar]
- Catchen, J. , Hohenlohe, P. A. , Bassham, S. , Amores, A. , & Cresko, W. A. (2013). stacks: An analysis tool set for population genomics. Molecular Ecology, 22, 3124–3140. 10.1111/mec.12354 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth, B. (2009). Fundamental concepts in genetics: Effective population size and patterns of molecular evolution and variation. Nature Reviews Genetics, 10, 195–205. 10.1038/nrg2526 [DOI] [PubMed] [Google Scholar]
- Chong, Z. , Ruan, J. , & Wu, C.‐I. (2012). Rainbow: An integrated tool for efficient clustering and assembling RAD‐seq reads. Bioinformatics, 28, 2732–2737. 10.1093/bioinformatics/bts482 [DOI] [PubMed] [Google Scholar]
- Christe, C. , Stölting, K. N. , Paris, M. , Fraїsse, C. , Bierne, N. , & Lexer, C. (2017). Adaptive evolution and segregating load contribute to the genomic landscape of divergence in two tree species connected by episodic gene flow. Molecular Ecology, 26, 59–76. 10.1111/mec.13765. [DOI] [PubMed] [Google Scholar]
- Cleveland, W. S. (1979). Robust locally weighted regression and smoothing scatterplots. Journal of the American Statistical Association, 74, 829–836. 10.1080/01621459.1979.10481038 [DOI] [Google Scholar]
- Coyne, J. A. , & Orr, H. A. (2004). Speciation (545 pp.). Sunderland, MA: Sinauer. [Google Scholar]
- Cruickshank, T. E. , & Hahn, M. W. (2014). Reanalysis suggests that genomic islands of speciation are due to reduced diversity, not reduced gene flow. Molecular Ecology, 23, 3133–3157. 10.1111/mec.12796 [DOI] [PubMed] [Google Scholar]
- Danecek, P. , Auton, A. , Abecasis, G. , Albers, C. A. , Banks, E. , DePristo, M. A. , … Genomes Project Analysis, G. (2011). The variant call format and VCFtools. Bioinformatics, 27, 2156–2158. 10.1093/bioinformatics/btr330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delmore, K. E. , Lugo Ramos, J. S. , Van Doren, B. M. , Lundberg, M. , Bensch, S. , Irwin, D. E. , & Liedvogel, M. (2018). Comparative analysis examining patterns of genomic differentiation across multiple episodes of population divergence in birds. Evolution Letters, 2, 76–87. 10.1002/evl3.46 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duranton, M. , Allal, F. , Fraïsse, C. , Bierne, N. , Bonhomme, F. , & Gagnaire, P.‐A. (2018). The origin and remolding of genomic islands of differentiation in the European sea bass. Nature Communications, 9, 2518 10.1038/s41467-018-04963-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Favre, A. , Widmer, A. , & Karrenberg, S. (2017). Differential adaptation drives ecological speciation in campions (Silene): Evidence from a multi‐site transplant experiment. New Phytologist, 213, 1487–1499.https://doi:10.1111/nph.14202 [DOI] [PubMed] [Google Scholar]
- Feulner, P. G. D. , Chain, F. J. J. , Panchal, M. , Huang, Y. , Eizaguirre, C. , Kalbe, M. , … Milinski, M. (2015). Genomics of divergence along a continuum of parapatric population differentiation. PLoS Genetics, 11, e1004966 10.1371/journal.pgen.1004966 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flaxman, S. M. , Wacholder, A. C. , Feder, J. L. , & Nosil, P. (2014). Theoretical models of the influence of genomic architecture on the dynamics of speciation. Molecular Ecology, 23, 4074–4088. 10.1111/mec.12750 [DOI] [PubMed] [Google Scholar]
- Friedrich, H. C. (1979). Caryophyllaceae In Rechinger K. H. (Ed.), Illustrierte Flora von Mitteleuropa, 2nd ed Hamburg: Parey. [Google Scholar]
- Garrison, E. (2012). Vcflib: A C++ library for parsing and manipulating VCF files. Retrieved from https://github.com/ekg/vcflib [Google Scholar]
- Garrison, E. , & Marth, G. (2012). Haplotype‐based variant detection from short‐read sequencing. arXiv:1207.3907
- Goudet, J. (2004). hierfstat, a package for R to compute and test hierarchical F–statistics. Molecular Ecology Notes, 5, 184–186. 10.1111/j.1471-8286.2004.00828.x [DOI] [Google Scholar]
- Goulson, D. , & Jerrim, K. (1997). Maintenance of the species boundary between Silene dioica and S. latifolia (red and white campion). Oikos, 79, 115–126. 10.2307/3546096 [DOI] [Google Scholar]
- Guirao‐Rico, S. , Sánchez‐Gracia, A. , & Charlesworth, D. (2017). Sequence diversity patterns suggesting balancing selection in partially sex‐linked genes of the plant Silene latifolia are not generated by demographic history or gene flow. Molecular Ecology, 26, 1357–1370. 10.1111/mec.13969 [DOI] [PubMed] [Google Scholar]
- Gutenkunst, R. N. , Hernandez, R. D. , Williamson, S. H. , & Bustamante, C. D. (2009). Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genetics, 5, e1000695 10.1371/journal.pgen.1000695 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haenel, Q. , Laurentino, T. G. , Roesti, M. , & Berner, D. (2018). Meta‐analysis of chromosome‐scale crossover rate variation in eukaryotes and its significance to evolutionary genomics. Molecular Ecology, 27, 2477–2497. 10.1111/mec.14699 [DOI] [PubMed] [Google Scholar]
- Han, F. , Lamichhaney, S. , Grant, B. R. , Grant, P. R. , Andersson, L. , & Webster, M. T. (2017). Gene flow, ancient polymorphism, and ecological adaptation shape the genomic landscape of divergence among Darwin's finches. Genome Research, 27, 1004–1015. 10.1101/gr.212522.116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hathaway, L. , Malm, J. U. , & Prentice, H. C. (2009). Geographically congruent large‐scale patterns of plastid haplotype variation in the European herbs Silene dioica and S. latifolia (Caryophyllaceae). Botanical Journal of the Linnean Society, 161, 153–170. 10.1111/j.1095-8339.2009.01003.x [DOI] [Google Scholar]
- Hewitt, G. (2000). The genetic legacy of the Quaternary ice ages. Nature, 405, 907–913. 10.1038/35016000 [DOI] [PubMed] [Google Scholar]
- Hothorn, T. , Hornik, K. , Wiel, M. A. , & Zeileis, A. (2006). A Lego system for conditional inference. The American Statistician, 60, 257–263. 10.1198/000313006X118430 [DOI] [Google Scholar]
- Hu, X. S. , & Filatov, D. A. (2015). The large‐X effect in plants: Increased species divergence and reduced gene flow on the Silene X‐chromosome. Molecular Ecology, 25, 2609–2619. 10.1111/mec.13427 [DOI] [PubMed] [Google Scholar]
- Irwin, D. E. , Milá, B. , Toews, D. P. L. , Brelsford, A. , Kenyon, H. L. , Porter, A. N. , … Irwin, J. H. (2018). A comparison of genomic islands of differentiation across three young avian species pairs. Molecular Ecology, 27, 4839–4855. 10.1111/mec.14858 [DOI] [PubMed] [Google Scholar]
- Jombart, T. (2008). adegenet: A R package for the multivariate analysis of genetic markers. Bioinformatics, 11, 1403–1405. 10.1093/bioinformatics/btn129 [DOI] [PubMed] [Google Scholar]
- Karrenberg, S. , & Favre, A. (2008). Genetic and ecological differentiation in the hybridizing campions Silene dioica and S. latifolia . Evolution, 62, 763–773. 10.1111/j.1558-5646.2008.00330.x [DOI] [PubMed] [Google Scholar]
- Karrenberg, S. , Liu, X. , Hallander, E. , Favre, A. , Herforth‐Rahmé, J. , & Widmer, A. (2019). Ecological divergence plays an important role in strong but complex reproductive isolation in campions (Silene). Evolution, 73, 245–261. 10.1111/evo.13652. [DOI] [PubMed] [Google Scholar]
- Krasovec, M. , Chester, M. , Ridout, K. , & Filatov, D. A. (2018). The mutation rate and the age of the sex chromosomes in Silene latifolia . Current Biology, 28, 1832–1838. 10.1016/j.cub.2018.04.069 [DOI] [PubMed] [Google Scholar]
- Li, H. (2013). Aligning sequence reads, clone sequences and assembly contigs with BWA‐MEM. arXiv:1303.3997
- Liu, X. , & Karrenberg, S. (2018). Genetic architecture of traits associated with reproductive barriers in Silene: Coupling, sex chromosomes and variation. Molecular Ecology, 27, 3889–3904. 10.1111/mec.14562 [DOI] [PubMed] [Google Scholar]
- Malinsky, M. , Challis, R. J. , Tyers, A. M. , Schiffels, S. , Terai, Y. , Ngatunga, B. P. , … Turner, G. F. (2015). Genomic islands of speciation separate cichlid ecomorphs in an East African crater lake. Science, 350, 1493–1498. 10.1126/science.aac9927 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marques, D. A. , Lucek, K. , Haesler, M. P. , Feller, A. F. , Meier, J. I. , Wagner, C. E. , … Seehausen, O. (2017). Genomic landscape of early ecological speciation initiated by selection on nuptial colour. Molecular Ecology, 26, 7–24. 10.1111/mec.13774 [DOI] [PubMed] [Google Scholar]
- Martin, S. H. , Dasmahapatra, K. K. , Nadeau, N. J. , Salazar, C. , Walters, J. R. , Simpson, F. , … Jiggins, C. D. (2013). Genome‐wide evidence for speciation with gene flow in Heliconius butterflies. Genome Research, 23, 1817–1828. 10.1101/gr.159426.113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCoy, R. C. , Garud, N. R. , Kelley, J. L. , Boggs, C. L. , & Petrov, D. A. (2014). Genomic inference accurately predicts the timing and severity of a recent bottleneck in a nonmodel insect population. Molecular Ecology, 23, 136–150. 10.1111/mec.12591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meier, J. I. , Marques, D. A. , Wagner, C. E. , Excoffier, L. , & Seehausen, O. (2018). Genomics of parallel ecological speciation in Lake Victoria cichlids. Molecular Biology and Evolution, 35, 1489–1506. 10.1093/molbev/msy051 [DOI] [PubMed] [Google Scholar]
- Minder, A. M. , Rothenbuehler, C. , & Widmer, A. (2007). Genetic structure of hybrid zones between Silene latifolia and Silene dioica (Caryophyllaceae): Evidence for introgressive hybridization. Molecular Ecology, 16, 2504–2516. 10.1111/j.1365-294X.2007.03292.x [DOI] [PubMed] [Google Scholar]
- Muir, G. , Dixon, C. J. , Harper, A. L. , & Filatov, D. A. (2012). Dynamics of drift, gene flow, and selection during speciation in Silene . Evolution, 66, 1447–1458. 10.1111/j.1558-5646.2011.01529.x [DOI] [PubMed] [Google Scholar]
- Nachman, M. W. , & Payseur, B. A. (2012). Recombination rate variation and speciation: Theoretical predictions and empirical results from rabbits and mice. Philosophical Transactions of the Royal Society B: Biological Sciences, 367, 409–421. 10.1098/rstb.2011.0249 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei, M. (1987). Molecular evolutionary genetics. New York, NY: Columbia University Press. [Google Scholar]
- Nielsen, R. (2005). Molecular signatures of natural selection. Annual Review of Genetics, 39, 197–218. 10.1146/annurev.genet.39.073003.112420 [DOI] [PubMed] [Google Scholar]
- Oksanen, J. , Blanchet, F. G. , Friendly, M. , Kindt, R. , Legendre, P. , McGlinn, D. , Wagner, H. (2019). vegan: Community Ecology Package. R package version 2.5‐5. Retrieved from: https://CRAN.R‐project.org/package=vegan
- O'Leary, S. J. , Puritz, J. B. , Willis, S. C. , Hollenbeck, C. M. , & Portnoy, D. S. (2018). These aren’t the loci you’e looking for: Principles of effective SNP filtering for molecular ecologists. Molecular Ecology, 27, 3193–3206. 10.1111/mec.14792 [DOI] [PubMed] [Google Scholar]
- Pease, J. B. , Haak, D. C. , Hahn, M. W. , & Moyle, L. C. (2016). Phylogenomics reveals three sources of adaptive variation during a rapid radiation. PLoS Biology, 14, e1002379 10.1371/journal.pbio.1002379 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterson, B. K. , Weber, J. N. , Kay, E. H. , Fisher, H. S. , & Hoekstra, H. E. (2012). Double digest RADseq: An inexpensive method for de novo SNP discovery and genotyping in model and non‐model species. PLoS One, 7, e37135 10.1371/journal.pone.0037135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prentice, H. C. , Malm, J. U. , & Hathaway, L. (2008). Chloroplast DNA variation in the European herb Silene dioica (red campion): Postglacial migration and interspecific introgression. Plant Systematics and Evolution, 272, 23–37. 10.1007/s00606-007-0629-8 [DOI] [Google Scholar]
- Purcell, S. , Neale, B. , Todd‐Brown, K. , Thomas, L. , Ferreira, M. A. R. , Bender, D. , … Sham, P. C. (2007). PLINK: A tool set for whole‐genome association and population‐based linkage analyses. American Journal of Human Genetics, 81, 559–575. 10.1086/519795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puritz, J. B. , Hollenbeck, C. M. , & Gold, J. R. (2014). dDocent: A RADseq, variant‐calling pipeline designed for population genomics of non‐model organisms. PeerJ, 2, e431 10.7717/peerj.431 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rafajlović, M. , Emanuelsson, A. , Johannesson, K. , Butlin, R. K. , & Mehlig, B. (2016). A universal mechanism generating clusters of differentiated loci during divergence‐with‐migration. Evolution, 70, 1609–1621. 10.1111/evo.12957 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rautenberg, A. , Hathaway, L. , Oxelman, B. , & Prentice, H. C. (2010). Geographic and phylogenetic patterns in Silene section Melandrium (Caryophyllaceae) as inferred from chloroplast and nuclear DNA sequences. Molecular Phylogenetics and Evolution, 57, 978–991. 10.1016/j.ympev.2010.08.003 [DOI] [PubMed] [Google Scholar]
- Ravinet, M. , Faria, R. , Butlin, R. K. , Galindo, J. , Bierne, N. , Rafajlović, M. , … Westram, A. M. (2017). Interpreting the genomic landscape of speciation: A road map for finding barriers to gene flow. Journal of Evolutionary Biology, 30, 1450–1477. 10.1111/jeb.13047 [DOI] [PubMed] [Google Scholar]
- Ravinet, M. , Yoshida, K. , Shigenobu, S. , Toyoda, A. , Fujiyama, A. , & Kitano, J. (2018). The genomic landscape at a late stage of stickleback speciation: High genomic divergence interspersed by small localized regions of introgression. PLOS Genetics, 14, e1007358 10.1371/journal.pgen.1007358 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renaut, S. , Grassa, C. J. , Yeaman, S. , Moyers, B. T. , Lai, Z. , Kane, N. C. , … Rieseberg, L. H. (2013). Genomic islands of divergence are not affected by geography of speciation in sunflowers. Nature Communications, 4, 1827 10.1038/ncomms2833 [DOI] [PubMed] [Google Scholar]
- Richards, E. J. , Servedio, M. R. , & Martin, C. H. (2019). Searching for sympatric speciation in the genomic era. BioEssays, 41, e1900047 10.1002/bies.201900047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riesch, R. , Muschick, M. , Lindtke, D. , Villoutreix, R. , Comeault, A. A. , Farkas, T. E. , … Nosil, P. (2017). Transitions between phases of genomic differentiation during stick‐insect speciation. Nature Ecology & Evolution, 1, 82 10.1038/s41559-017-0082 [DOI] [PubMed] [Google Scholar]
- Rockman, M. V. (2012). The QTN program and the alleles that matter for evolution: All that’s gold does not glitter. Evolution, 66, 1–17. 10.1111/j.1558-5646.2011.01486.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rougemont, Q. , & Bernatchez, L. (2018). The demographic history of Atlantic salmon (Salmo salar) across its distribution range reconstructed from approximate Bayesian computations*. Evolution, 72, 1261–1277. 10.1111/evo.13486 [DOI] [PubMed] [Google Scholar]
- Roux, C. , Fraïsse, C. , Castric, V. , Vekemans, X. , Pogson, G. H. , & Bierne, N. (2014). Can we continue to neglect genomic variation in introgression rates when inferring the history of speciation? A case study in a Mytilus hybrid zone. Journal of Evolutionary Biology, 27, 1662–1675. 10.1111/jeb.12425 [DOI] [PubMed] [Google Scholar]
- Roux, C. , Fraisse, C. , Romiguier, J. , Anciaux, Y. , Galtier, N. , & Bierne, N. (2016). Shedding light on the grey zone of speciation along a continuum of genomic divergence. PLoS Biology, 14, e2000234 10.1371/journal.pbio.2000234 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rundell, R. J. , & Price, T. D. (2009). Adaptive radiation, nonadaptive radiation, ecological speciation and nonecological speciation. Trends in Ecology & Evolution, 24, 394–399. 10.1016/j.tree.2009.02.007 [DOI] [PubMed] [Google Scholar]
- Sambatti, J. B. , Strasburg, J. L. , Ortiz‐Barrientos, D. , Baack, E. J. , & Rieseberg, L. H. (2012). Reconciling extremely strong barriers with high levels of gene exchange in annual sunflowers. Evolution, 66, 1459–1473. 10.1111/j.1558-5646.2011.01537.x [DOI] [PubMed] [Google Scholar]
- Samuk, K. , Owens, G. L. , Delmore, K. E. , Miller, S. E. , Rennison, D. J. , & Schluter, D. (2017). Gene flow and selection interact to promote adaptive divergence in regions of low recombination. Molecular Ecology, 26, 4378–4390. 10.1111/mec.14226 [DOI] [PubMed] [Google Scholar]
- Seehausen, O. , Butlin, R. K. , Keller, I. , Wagner, C. E. , Boughman, J. W. , Hohenlohe, P. A. , … Widmer, A. (2014). Genomics and the origin of species. Nature Reviews: Genetics, 15, 176–192. 10.1038/nrg3644 [DOI] [PubMed] [Google Scholar]
- Stankowski, S. , Chase, M. A. , Fuiten, A. M. , Rodrigues, M. F. , Ralph, P. L. , & Streisfeld, M. A. (2019). Widespread selection and gene flow shape the genomic landscape during a radiation of monkeyflowers. PLoS Biology, 17, e3000391 10.1371/journal.pbio.3000391 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahata, N. , & Nei, M. (1985). Gene genealogy and variance of interpopulational nucleotide differences. Genetics, 110, 325–344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tine, M. , Kuhl, H. , Gagnaire, P.‐A. , Louro, B. , Desmarais, E. , Martins, R. S. T. , … Reinhardt, R. (2014). European sea bass genome and its variation provide insights into adaptation to euryhalinity and speciation. Nature Communications, 5, 5770 10.1038/ncomms6770 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vijay, N. , Weissensteiner, M. , Burri, R. , Kawakami, T. , Ellegren, H. , & Wolf, J. B. W. (2017). Genomewide patterns of variation in genetic diversity are shared among populations, species and higher‐order taxa. Molecular Ecology, 26, 4284–4295. 10.1111/mec.14195 [DOI] [PubMed] [Google Scholar]
- Wang, J. , Street, N. R. , Scofield, D. G. , & Ingvarsson, P. K. (2016). Variation in linked selection and recombination drive genomic divergence during allopatric speciation of european and american aspens. Molecular Biology and Evolution, 33, 1754–1767. 10.1093/molbev/msw051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf, J. B. W. , & Ellegren, H. (2017). Making sense of genomic islands of differentiation in light of speciation. Nature Reviews: Genetics, 18, 87–100. 10.1038/nrg.2016.133 [DOI] [PubMed] [Google Scholar]
- Yeaman, S. (2015). Local adaptation by alleles of small effect. The American Naturalist, 186, S74–S89. 10.1086/682405 [DOI] [PubMed] [Google Scholar]
- Yeaman, S. , Aeschbacher, S. , & Bürger, R. (2016). The evolution of genomic islands by increased establishment probability of linked alleles. Molecular Ecology, 25, 2542–2558. 10.1111/mec.13611 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig S1‐S11
Table S1‐S5
Data Availability Statement
Double‐digest RAD (ddRAD) sequencing data will be available on NCBI's Short Read Archive (SRA, SUB7812013 https://www.ncbi.nlm.nih.gov/sra/PRJNA649094). The data in variant call format (VCF) file, Perl codes for genetic analysis, R codes for plotting and Python codes for demographical modelling are available on Dryad (https://doi.org/10.5061/dryad.6djh9w0zd).


