Revisiting the Limiting Factors for Overall Water‐Splitting on Organic Photocatalysts

Abstract

In pursuit of inexpensive and earth abundant photocatalysts for solar hydrogen production from water, conjugated polymers have shown potential to be a viable alternative to widely used inorganic counterparts. The photocatalytic performance of polymeric photocatalysts, however, is very poor in comparison to that of inorganic photocatalysts. Most of the organic photocatalysts are active in hydrogen production only when a sacrificial electron donor (SED) is added into the solution, and their high performances often rely on presence of noble metal co‐catalyst (e.g. Pt). For pursuing a carbon neutral and cost‐effective green hydrogen production, unassisted hydrogen production solely from water is one of the critical requirements to translate a mere bench‐top research interest into the real world applications. Although this is a generic problem for both inorganic and organic types of photocatalysts, organic photocatalysts are mostly investigated in the half‐reaction, and have so far shown limited success in hydrogen production from overall water‐splitting. To make progress, this article exclusively discusses critical factors that are limiting the overall water‐splitting in organic photocatalysts. Additionally, we also have extended the discussion to issues related to stability, accurate reporting of the hydrogen production as well as challenges to be resolved to reach 10 % STH (solar‐to‐hydrogen) conversion efficiency.

While half‐reactions using organic photocatalysts for hydrogen production are encouraging, systems with high efficiency without using sacrificing electron donors (SED) and showing full overall water‐splitting are still largely absent. Critical factors that are limiting the overall water‐splitting using organic photocatalysts are summarized, with a supplementary discussion on remaining challenges.

1. Introduction: Rise of Polymeric Photocatalysts for Hydrogen Production

The realm of photocatalytic hydrogen production is dominated by inorganic photocatalysts, particularly by those that are made from transition metal oxides and sulphides.1 Recently, however, C−C/C−H/C−N bonded and π‐conjugated polymeric materials have evolved as promising alternative to widely investigated inorganic semiconductor photocatalysts.2 The high Interest in the conjugated polymers photocatalysts are mainly fuelled by their accessibility, low cost, and versatile tunability of their chemical and optical properties. One notable point is that inorganic photocatalysts are mostly inactive for the hydrogen evolution for the photons of upper wavelengths in visible light (550 nm to 700 nm). In contrast, polymeric photocatalysts have a potential to overcome this limitation. Distinct from their inorganic counterparts, organic photocatalysts are potential “600 nm‐class photocatalyst” for solar fuel production.3 There are practical reasons for stressing on the 600 nm‐class photocatalysts. Except for solar driven PV‐electrolysis, attaining a targeted 10 % STH (solar‐to‐hydrogen) efficiency is challenging with current set of inorganic photocatalysts that work below 600 nm. Contrarily, it was theoretically demonstrated that a tandem structure of light‐absorbing materials with band gaps in the range of 1.6–1.8 eV would have practical implication in achieving a STH efficiency at >25 % when optimum device design related requirements are full‐filled.4

From the materials perspective, conjugated polymers form a new class of highly porous organic polymers with 2D or 3D network topologies composed solely of light elements.5 A custom‐made highly porous but robust 2D or 3D networks can be formed by linking suitably chosen functionalized molecular building units using thermodynamically controlled covalent chemistry (see, Figure 1 for example).6 Additionally, with reversible network‐forming reaction, disordered porous structure can be reorganized into long‐range crystallinity by self‐healing of the structural defects.6 This synthetic flexibly is indeed seductive, while the emerging possibilities are tantalizing to fall in high research interest with this genre of material. Indeed, a growing interest is evident by the increased volume of research articles published on porous organic frameworks.

Figure 1.

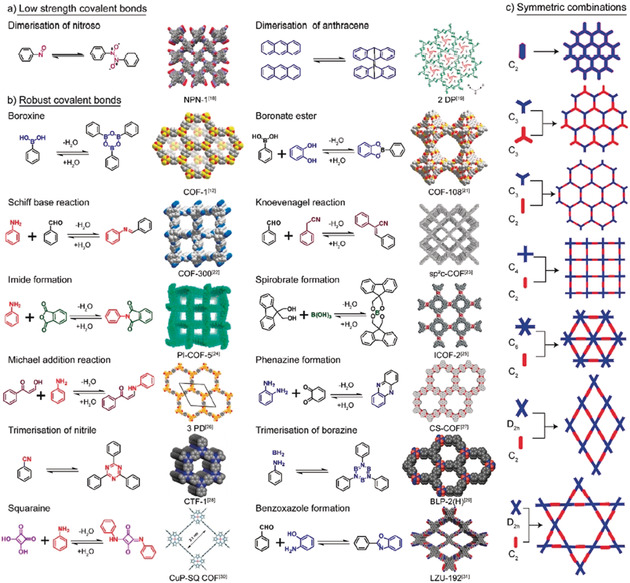
Synthesis pathways of porous organic frameworks with covalent bonds of a) low strength, b) robust bonds, and c) symmetric combinations. Reproduced with permission from ref. 7. Copyright 2019, American Chemical Society.

Historically, the first attempt of using an organic photocatalysts for solar hydrogen evolution can be dated back to 1985, when Yanagida et al. reported [linear poly(p‐phenylene)s] for H₂ evolution under UV‐light irradiation (λ>366 nm).8 This discovery incepted a new generation of photocatalysts for solar‐energy conversion beyond well‐known inorganic photocatalysts. However, the interest on organic photocatalysts for H₂ evolution waned over the time due to their structural instabilities under photocatalytic conditions. Additionally, their extremely poor quantum yield of hydrogen (<0.05 %) also negatively drove the continuing research enthusiasm. As a result, research in this direction made slow progress with very few achievements until the report of graphitic carbon nitride (g‐C₃N₄) in 2009.9 The g‐C₃N₄ is highly robust in any pH of the solution. It confluences the interest on polymeric photocatalyst to a new height evident by hundreds of publications in the following years.10 Consequently, the past few years have witnessed the development of many different kinds of organic photocatalyst materials. Carbon sub‐nitrides (such as C₂N, C₃N), graphene oxide (GO), microporous polymers networks (MPN), conjugated organic frameworks (COF), conjugated triazine framework (CTF), conjugated microporous polymers (CMPs), silicate conjugate frameworks (SiCOF), conjugated phosphinine frameworks (CPF) etc., for example, are few notable polymeric photocatalysts.11 A historical development of polymeric photocatalysts is shown in Figure 2 where the field also contains alternative classifications such as compactified polymers (e.g.Pdots) or collapsed MOFs. Interested readers are suggested to read the recently published articles cited in ref. 3 for a comprehensive overview of the synthesis, physicochemical attributes and applications of organic photocatalysts.

Figure 2.

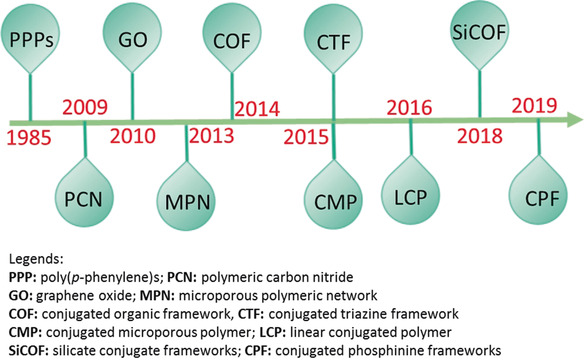
Historical development of selected organic photocatalysts for hydrogen evolution reaction.

Among the polymeric photocatalysts, carbon nitrides are extensively studied and reviewed comprehensively elsewhere.10, 12 Therefore, we have excluded carbon nitride for our ongoing discussion. The renewed interest in conjugated polymeric photocatalysts beyond carbon nitride for hydrogen evolution via water‐splitting is pioneered by Cooper et al.11n Over the last five years, research has been progressed to refine the physicochemical properties and development of new derivatives of conjugated polymer for photocatalytic hydrogen evolution. The current progress in synthesis, characterization and applications of polymeric photocatalysts have recently been reviewed elsewhere.2, 3, 5

It is evident that the conjugated polymeric photocatalysts are well active in hydrogen production via half‐reaction of water‐splitting (i.e. reduction reaction, 2H⁺+2 e⁻→H₂) in presence of a sacrificial electron donor (SED). For hydrogen production from SED‐Water solution, it can be disputable to use the generic term “water‐splitting”.13 To be economically viable and to conform to the notion of “green fuel”, hydrogen must be produced purely through water‐splitting without sacrificial agents. To date, the success in overall water‐splitting using polymeric photocatalysts is very limited. To make progress, exclusive analysis of the limiting factors and ways to alleviate these limitations are highly important. This minireview article aims to serve this purpose.

Following the introduction, the present status of overall water‐splitting in organic photocatalysts is discussed. After this, a discussion has been made on four fundamental rate limiting factors and possible routes to manage each critical factors for successful overall water‐splitting. We have also briefly discussed the contemporary disputes in reporting the hydrogen production rate with recommendation for accurate photocatalytic measurements for faithful assignments of performance and durability. Additionally, we have highlighted a few steps to achieve targeted 10 % STH conversion efficiency in large scale.

2. Status of Overall Water‐Splitting in Organic Photocatalysts

Releasing hydrogen from water involves two simultaneous reactions, namely oxidation and reduction reactions, also known as redox reactions. In photocatalytic hydrogen production, a photocatalyst is central to accommodate these redox reactions. Ideally, a photocatalyst should be a semiconductor with a band gap energy, (i.e. energy difference between conduction band minimum, CBM and valence band maximum, VBM) at least equivalent to electrochemical potential (≈1.23 eV) required to drive water‐splitting reactions.14 However, every practical photocatalyst should have additional band gap energy to accommodate the losses from the resulting photovoltage at the surface and the overpotentials of the reactions. In fact, most of the semiconductors loses 0.3–0.5 eV from the band gap to the obtained photovoltage, while the total overpotential for the hydrogen evolution reaction (HER) and oxygen evolution reaction (OER) is at least 0.3 eV for an appreciable rate of the reaction. Therefore, a practical photocatalyst should have a band gap of 1.8 to 2.0.15 This is a necessary condition but not sufficient for overall water‐splitting reactions. Because the 1.8–2.0 eV can be obtained through many different combinations of CBM and VBM. Strictly, CBM must be at a more negative potential than that of proton reduction reaction (H⁺/H₂=0.0 V vs. standard hydrogen electrode, SHE at pH 0 plus the HER overpotential) while VBM must be at more positive potential than that of oxidation reaction (O₂/H₂O=1.23 V vs. SHE at pH 0 plus the OER overpotential) for a given pH of the solution. These stringent requirements therefore limit the selection of appropriate photocatalyst materials that could accommodate overall water‐splitting reactions. In an organic photocatalyst, the HOMO and LUMO levels plays the roles of the CBM and VBM. The critical problem with organic photocatalysts is that the reorganization energy upon relaxation of the excited state is often significantly higher than the energy required for electrochemical charge transfer. Moreover, aggregated organic photocatalyst endowed with denser orbitals transforms to a situation similar to the inorganic nanosystems.3

In such a limiting case of finding a single photocatalyst for overall water‐splitting, we are fortunately left with “something is better than nothing” options. For example, if a crystalline/molecular photocatalyst could have only CBM/LUMO (or VBM/HOMO) that meets the proton reduction potential (or oxidation potential), it can be used for hydrogen evolution reaction (HER) or oxygen evolution reaction (OER), respectively. It implies that a combination of HER and OER photocatalysts in appropriate fashions could also render overall water‐splitting reactions. This scheme is commonly known as Z‐Scheme. Nowadays, it is one of the most preferred way when overall water‐splitting is a matter of interest in a particulate photocatalytic system.16 In comparison with a one‐step system, however, where a single photocatalyst could drive the overall water‐splitting reactions, Z‐Scheme has to endure complex device design and higher cost. More importantly, charge transfer needs to overcome additional processes associated with interface in‐between the two materials. In addition, Z‐Scheme is a two‐photon absorbing system for production of one electron‐hole pair. Therefore, spectral matching of the two absorptions is required to optimize the performance in a solar spectrum. These difficulties in performing homogeneous and well‐behaved interfaces in the Z‐Scheme often drives many of the researchers to stay in comfort with only one of the half reactions, either HER or OER. As a result, in a plethora of hundreds of HER or OER photocatalysts, we have limited number of archival publications on overall water‐splitting despite a continuous efforts of over four decades.

In case of organic HER or OER photocatalysts, most of the research has also been invested to the development of HER photocatalysts, while an insignificant progress has been made in developing OER photocatalyst.3a, 11t Consequently, progress in overall water‐splitting on organic photocatalysts lags far behind when compared to inorganic counterparts.

To the best of our knowledge, there is only one archival report on overall water‐splitting using organic photocatalyst. As is shown in Figure 3, CMPs nanosheets prepared by oxidative coupling of 1,3,5‐tris‐(4‐ethynylphenyl)‐benzene (TEPB) and 1,3,5‐triethynylbenzene (TEB) are demonstrated for splitting of pure water (pH≈7) into stoichiometric amounts of H₂ and O₂ with an apparent quantum efficiency (AQE) of 10.3 % for TEPB and 7.6 % for TEB at 420 nm.17 The reported STH conversion efficiency of PTEPB and PTEB, however, are more modest with 0.60 % and 0.31 %, respectively under the full solar spectrum. When aza‐fused CMP was coupled with C₂N in a Z‐Scheme fashion, it exhibited a STH of 0.23 %. With incorporation of reduced graphene oxide as the solid electron mediator, the STH of this Z‐Scheme system was increased to 0.40 %.18

Figure 3.

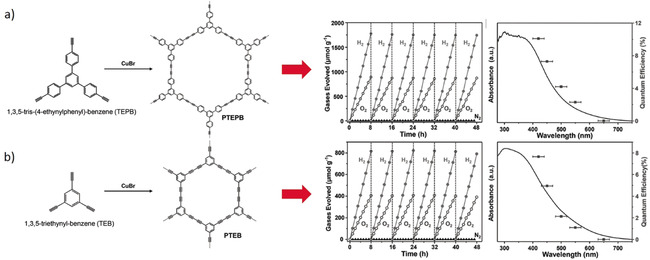
Synthesis and overall water‐splitting on a) PTEPB and b) PTEB. Adopted with permission from ref. 17. Copyright 2017, Wiley‐VCH.

Clearly, the STH values are way below the targeted STH of 10 %. It manifests the fact that it is challenging to construct an overall water‐splitting system with solely organic photocatalysts. Although future research can be endured to combine inorganic photocatalyst in organic backbones for enhanced STH, this is not within the scopes of this article. We rather focus on diagnosis of what limits the overall water‐splitting on organic photocatalysts and how these limiting factors can potentially be overcome.

Success of the aforementioned exemplary overall water‐splitting was assigned to efficient charge separation and transportation of photogenerated excitons by virtue of band alignment in Z‐Scheme heterostructures. This result infers part of the possible pathways to overcome the problems related to overall water‐splitting. However, overpotentials and energy alignments in each accumulated step are large enough to sacrifice the overall efficiency.

3. Revisiting the Limiting Factors for Design of an Overall Water‐Splitting System

We identify four essential factors that are rate determinant for design of an efficient overall water‐splitting system based on organic photocatalysts. We believe that simultaneous optimization of these limiting factors is crucial. Below we provide exemplified discussion on why each of the four factors are rate determinant, the challenges for each step, and what are next possible steps to be taken care of to abate unwanted processes.

3.1. Mediating Charge Separation in Organic Photocatalysts

Efficient solar energy conversion to chemical energy requires efficient charge photogeneration to be coupled with multielectron redox reactions. Efficiency and the associated sequences of charge photogeneration is material specific. For example, photoexcitation directly generates free charge carriers in inorganic semiconductors (e.g. Si) due to the strong interatomic electronic interactions and environment with a high dielectric constant. Unlike inorganic materials, photoexcitation of organic materials creates electrostatically bound exciton (excited electron and hole) due to low dielectric constants and weaker noncovalent electronic interactions.14a Because of spatially separated and localized electron and holes wave functions, the excitons are Coulombically bound.19 The magnitude of Coulomb interaction between the excitons determines the strength of the electrostatic binding energy of the electron–hole pair, the exciton binding energy (E _b), which is usually greater than the thermal energy at room temperature (∼25 meV). Additionally, electron‐lattice and electron‐electron interactions may also contribute to the appreciable binding energy.

Exciton must be dissociated within its lifetime into free charge carriers to be extracted as electric current or to initiate redox reactions. This additional event of dissociation process in case of organic semiconductor is one of the critical reason for their lower solar energy conversion efficiency compared to inorganic semiconductors.20 The dissociation of the exciton requires that the binding energy (E _b), that mainly depend on the dielectric constant and the Bohr radius of relevant charge carriers, is overcome by an energy alignment difference between the charge transfer states of the donor and acceptor part in the system.

Dissociation of initial exciton (also known as singlet) immediately follows various energy transfer steps such as charge separated state (CS), charge transfer state (CT), and possible singlet‐to‐triplet conversion before finally separated into free charge carriers.21 An initial separation of the electron and hole after a short‐lived (nanoseconds) singlet dissociation is achieved by energetically downhill electron transfer from the donor excited‐state to the acceptor state. Subsequent secondary electron (and hole) transfers results in a long‐lived (milliseconds to seconds) CS state which can be coupled to multielectron redox chemistry for solar energy conversion and storage. The free energy of resulted long‐lived charge carriers are significantly lower than that of the initial charge separated state. This loss of free energy is inevitable, and is associated with both driving electron transfer steps to bypass unwanted charge recombination pathways back to the ground state and preventing thermally driven electron transfer back to the initial short‐lived excited state.22 Charge photogeneration therefore comes at a significant energy cost that has an impact upon the overall energy conversion efficiency. Clearly, efficient photogeneration of charge carriers is the foremost critical step to endow overall water‐splitting in organic photocatalysts.

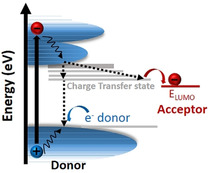
Research efforts have been invested to overcome the challenges with efficient charge photogeneration in organic photocatalyst. For example, inspired by the rapid charge transfer in donor–acceptor (D–A) heterojunction based solar cells,24 a D–A construction has been exercised to overcome the poor charge separation in polymeric photocatalysts.25 A D–A based system facilitates the spontaneous migration of charges from donor to the acceptor.26 It is because the light induced excitons (E _exc) have greater energy than that of both the charge transfer state (E _CT) and E _LUMO of the acceptor (see, Figure 4 a). Therefore, E _CT and E _LUMO are the crucial determinants for the efficient electron transfer to the acceptor. One desirable criterion for continuous charge transfer from donor to acceptor is that E _CT should be at higher energy level than E _LUMO of the acceptor. Otherwise, excitons will fall back to ground state and subsequently recombine.11w, 12, 24 Therefore, a high energy difference between the donor and acceptor and a low energy loss in E _CT is highly desirable. However, meeting these requirements simultaneously in conjugated polymers remains a grand challenge.

Figure 4.

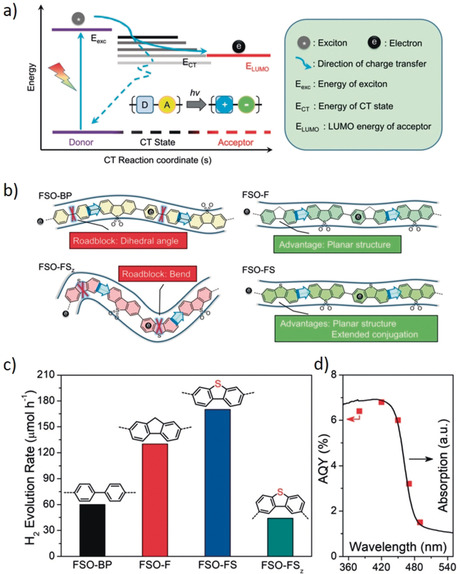
D–A based photocatalyst systems for hydrogen evolution. a) Illustration of the energy levels summarizing the main processes involved in charge transfer in D–A based system. b) Molecular structures and characteristics of the four D–A conjugated polymers used in the current study of interest. c) H₂ evolution rates of these D–A conjugated polymers under visible‐light irradiation (λ>420 nm). d) Wavelength dependence of apparent quantum yield (AQY) on H₂ evolution using FSO‐FS. Copyright 2019, Wiley‐VCH. Adopted with permission from ref. 23.

A way to minimize the energy loss is to overcome the large E _b.27 Recently, it has demonstrated that a delocalized environment for charge migration in the CT state would decrease the E _b, and enhance the charge transfer process.19 It indicates that tailoring the local donor–acceptor structure is necessary to reduce E _b. Recently, a proof‐of‐concept to modulate the E _b and E _CT in the linear CPs by tailoring the local conjugation and the charge transfer pathway has been reported, where four different linear CPs containing different electron donors were investigated.23 Dibenzothiophene‐S,S‐dioxide (FSO) was used as a typical electron acceptor whereas biphenyl (BP), fluorene (F), and dibenzothiophene (FS), with different E _exc values were chosen as the electron donors to construct the local D–A heterojunction (Figure 4 b). The relationship between E _b, E _CT, and the photocatalytic performance of these linear D–A conjugated polymers were investigated using combined experimental and theoretical studies.

All of these polymers exhibit an intrinsic absorption edge at around 480 nm that corresponds to the optical gap of 2.55–2.66 eV. The experimentally determined E _b was 104 meV for FSO‐BP, 91 meV for FSO‐F, and 88 meV for FSO‐FS. However, E _b values increase when the linear structure is transformed into a zigzag structure, most likely because of the much lower charge delocalization in the zigzag conformation. It was therefore reported that a planar structure with extended conjugation are beneficial for minimizing E _b through the construction of a more delocalized pathway for charge transfer. The hydrogen evolution rate (HER) of FSO‐BP, FSO‐F, FSO‐FS, and FSO‐FS_z were 60, 130 170, and 44 μmol h⁻¹ at λ>420 nm (Figure 4 c), respectively. The enhancement in hydrogen evolution is in good agreement with the respective E _b. In best case, an AQE of 6.8 % at 420 nm was achieved, Figure 4 d.

The aforementioned examples strongly suggest that a high quantum yield of long‐lived dissociated electron–hole pair with minimal loss of free energy is the rate determinant. Excitons are electrically neutral and therefore their translational motions remain unaffected by electric fields. Exciton rather moves through intramolecular or intermolecular diffusion typically with a Förster‐type incoherent energy transfer process. In case of porous organic materials which are attributed with defects and aggregates, dissociated exciton in CS states may undergo trapping in the tail of the inhomogeneously broadened density of states associated with defects due to downhill energy transfer from initial free energy state to subsequent CS states. As such, exciton migration will rely on thermal fluctuations, and if excitons are vibrationally excited, excitons might also undergo intramolecular vibrational relaxation.28 Consequently, exciton dissociation may take place from either the vibrationally excited “hot” exciton29 or the thermally equilibrated and geometrically relaxed “cold” exciton.28, 30 In understanding and ultimately controlling the dissociation of polymer excitons, the diffusion length, defined by the distance an exciton migrate before relaxing back to the ground state, has to be taken into account. Excitons must essentially be dissociated within the diffusion length.31 During internal conversion from light harvesting to charge separation, energy loss is inevitable. Consequently, the energy and electron transfer processes to accommodate a sufficient excited‐state energy in photocatalytic system must be extremely fast to compete with the energy loss.32 Ultrafast techniques (e.g. ultrafast transient absorption spectroscopy), time‐resolved spectroscopic techniques (e.g. time‐resolved electronic spectroscopy (TRES), time‐resolved infrared spectroscopy (TRIR), and time‐resolved photoelectron spectroscopy (TRPES) etc.) are widely being used to probe the electronic excited‐state as well as the formation of new chemical species such as charge‐separated states can be tracked in real time.14a, 32

Another important consideration is to design organic photocatalysts with a high effective conjugation length to allow a broader light harvesting window in the solar spectrum, but in the same time keep them quite rigid to minimize the losses from reorganization energy after initial excitation, and additionally, an asymmetric coupling to the acceptor/donor part that minimize the electron/hole back transfer without a large loss of free energy in the process. As many of the electrostatic interaction in the organic material system are quite long ranged due to the low dielectric constant in the system, strategies of incorporation of elements with higher polarizability of the electrons such as halogens or embedding of higher dielectric materials in the blend are advisable.

3.2. Engineering Band Positions for Enabling Oxygen Evolution in Polymeric Photocatalysts

Water oxidation half‐reaction involves four electron transfer processes with O−H bond cleavage and O−O bond formation. The required overpotential for this reaction is usually very large (>700 mV) with sluggish O−O bond formation kinetics.33 Conjugated polymers rarely exhibit any high activities for photocatalytic oxygen evolution from water, because of either mismatched band position or the lack of a driving force to satisfy sufficient overpotential.3a Therefore, optimization of the molecular structure to obtain suitable band positions and control over the band structure are necessary for water oxidation reactions.

One possible way to adjust the band positions would be the systematic variation of the co‐monomer components to adapt the electron donor‐acceptor functionalities in molecular structure. It was shown that if the conjugated polymers would have the electron acceptor as the building block in the molecular structure, incorporating electron donors with different strengths could lead to a controlled modulation in the band structure. In those polymeric materials, oxidation potential decreases inversely with an increase in the amount of electron donors, and vice versa.34

Recently, this concept has been employed to tune the band positions of conjugated triazine‐based polymers (CTP) for photocatalytic oxygen evolution (see Figure 5).35 Deliberate incorporation of phenyl units of different lengths as electron donors into the meta‐positions on the triazine rings would tune the band position and the band gap. DFT calculations showed that the band gap of the triazine‐based polymers could be decreased from 2.98 to 2.36 eV by increasing the number of phenyl units per linkage from 1 to 3. Correspondingly, a red shift in optical absorption was confirmed from UV/Vis diffuse reflectance spectra. The intrinsic absorption band edge originates from a π→π* electron transition of sp²‐hybridized C and N in the polymeric framework. Significantly, the VB position moves to a higher energy from CTP‐1 to CTP‐3, meaning that the oxidation ability of the VB/HOMO holes decreases. This is also evident from rate of photocatalytic oxygen evolution. For example, CTP‐2 exhibited the best water oxidation activity when modified with cobalt (ca. 3.0 μmol h⁻¹), while CTP‐3 was moderately active in water oxidation. It indicates that the incorporation of increased number of phenyl groups in the polymeric chain could lead to a decrease in the oxidation capacity of the valence holes. Additionally, it was also shown that the increased number of phenyl groups also led to the reduction of the degree of polymerization due to steric hindrance and sluggish mass transfer. Another important aspect is how successfully generated O₂ molecules could act as local electron scavengers and effect the photo‐induced reduction reaction. Here, it is vital to perform the full reaction to see how these effects are influencing each other and incorporate strategies to avoid reactions competing with the desired HER reaction.

Figure 5.

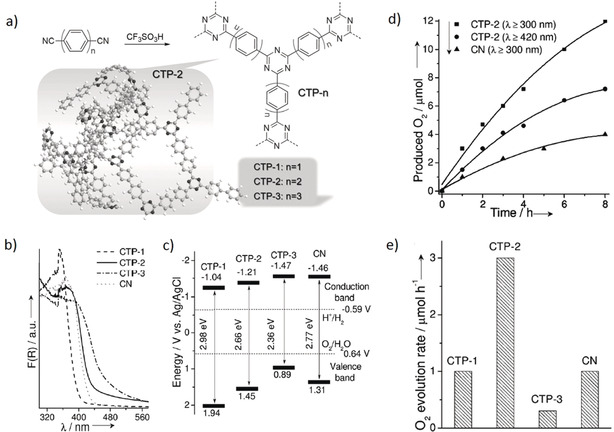
Photophysical and oxygen evolution activity of CTPs. a) en‐route to synthesis of the CTPs, b) UV/Vis DRS spectra demonstrating optical absorption range, c) relative positions of the conduction and valence bands (CB and VB, respectively) estimated from electrochemical Mott–Schottky plots, d) Time course of O₂ production, and e) O₂ evolution rates under UV/Vis light irradiation (λ>300 nm). Copyright 2017, Wiley‐VCH. Adopted with permission from ref. 35.

3.3. Understanding the Role of the Solvent Environment on Redox Reactions

Rational design of molecular structure, an extended overlap into the spectrum of the light source, and reducing the thermodynamic driving force are common approaches for elevating the rate of hydrogen production in polymeric photocatalysts.12, 14a However, rational engineering of the materials properties will remain elusive without an in‐depth understanding of the physical processes occurring around a solvated catalyst. Exact characterization using low intensity light and increased understanding on the underlying photo‐physics of solvated organic photocatalysts are important. Here, the transient protonation/hydroxylation states as well as possible occurrence of surface restructuring and dangling bonds pose the same uncertainty and challenge as for the surfaces in nanostructured inorganic photocatalysts.

The challenges and limited success in overall water‐splitting allure the researcher to employ sacrificial agents to decouple hydrogen evolution from water oxidation for an independent study of both half‐reactions involved in overall water‐splitting.36 In the presence of sacrificial agents, the complete sequence of photoredox reactions for water‐splitting starts with absorption and generation of electron–hole pairs (also known as exciton) followed by separation (by Columbic dissociation or diffusion) at the surface, and transfer of hole to sacrificial electron donor for hydrogen evolution or electron to sacrificial electron acceptor for oxygen evolution. The excitons in the organic materials have a significantly higher binding energy than photogenerated excitons in inorganic materials, which in turn hinders the spontaneous Columbic dissociation of excitons into free electrons and holes at room temperature in organic photocatalysts. Therefore, prolonged exciton lifetime that allow exciton dissociation via diffusion to the polymer–water interface is a preferred pathway in organic materials.22 A longer life‐time, on the other hand, is a result of a more strongly bonded exciton and in turn results in a higher energy alignment offset that is needed for a successful breaking of the exciton. The use of higher dielectric media or charge selective materials/contacts alleviate part of this problem. In the case of a material immersed in water solution, the aqueous medium with higher relative permittivity facilitates the dissociation of the diffused excitons at the polymer‐water interface for subsequent charge transfer to an electron or hole acceptor in the reaction medium depending on the electron affinity or ionization potential.37 Making hydrophobic polymers into hydrophilic polymer nano‐dots (Pdots) is a promising strategy to increase polymer–water interfacial contact, thus improving the photocatalytic performance.38 Proton channels have been also been proved to exist in such Pdots system.39 However, we are still lacking of understanding the mechanism of charge transfer and the limit of the least necessary energy offset to drive the reaction at an appreciable rate. In addition, compelling evidence of the properties and functional survival of the transient species created in presence of sacrificial agents and its relevance for the unassisted reaction are still lacking.

Recent investigation on solvated polymers’ surface hinged the microscopic interactions between selected polymers (such as, polyphenylene, dibenzo[b,d]thiophene sulfone‐co‐phenylene, and dibenzo[b,d]thiophene sulfone as models of P1, P7, and P10 polymers, respectively) and reaction mixture, Figure 6.40 It was concluded that the microstructure of the polymer, degree of its solvation, and the polarity of the solvent could influence both the charge transfer and thermodynamic driving forces for hydrogen evolution activity. Interestingly, in TEA‐water mixtures, fluorene oligomer (P1) buried itself in the TEA domain while the sulfonated oligomer (P7 and P10) resided in a fine mixture of aqueous and non‐aqueous domains with its SO₂ groups directed at the water (Figure 6 a,b). This preferential orientation of the SO₂ group developed a shell of water molecules around it that tends to distort the oligomer away from its ground‐state geometry. Correspondingly, the dipoles in neighboring units become anti‐aligned that increase the contact between SO₂ groups and water. As a result, it enhanced the yields of electron polaron intermediates in suspension that was found to be correlated with increased hydrogen evolution in P7 and P10 in compare with P1. Below these cases are explained in more details.

Figure 6.

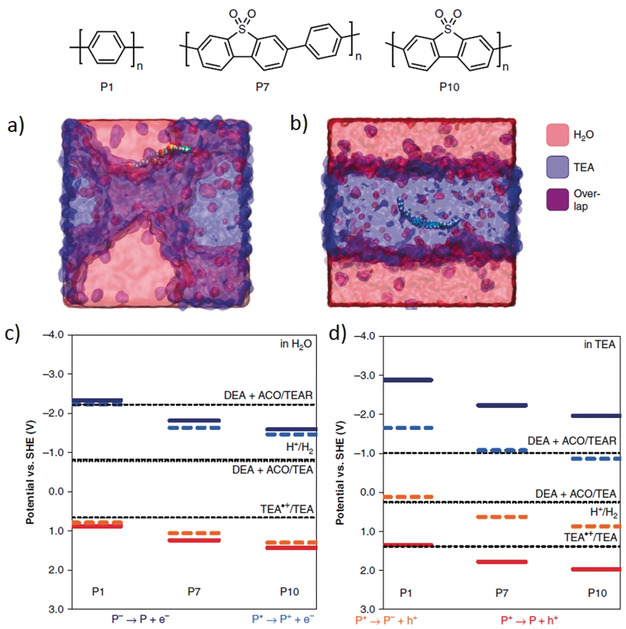
Atomistic molecular dynamics simulations of a) the polar polymer P10 and b) the non‐polar polymer P1 in a mixture of TEA (blue) and water (purple). Calculated ionization potential (IP, red solid line) and electron affinity (EA, blue solid line) for ground‐state oligomers of P1, P7, and P10 together with the exciton electron affinity (EA*, orange dashed line) and ionization potential (IP*, blue dashed line), in comparison with the potentials for proton reduction (H₂/H⁺), overall TEA oxidation (DEA+ACO/TEA), the first TEA oxidation step (TEA^.+/TEA) and the second oxidation step of the TEA oxidation product (DEA+ACO/TEAR), using a c) water or d) TEA solvent environment. Copyright 2018, Nature Publishing Groups. Adopted with permission from ref. 40.

Solvent environment with different values for the dielectric permittivity (ϵ _r = 80.1 for water, ϵ _r = 2.38 for triethanolamine, TEA) controls the population of electrons moving through the bonding network, with hopping mechanism, band conduction as well as possible effects from polaron formation etc, depending on the material system and the shielding environment from the solvent. In presence of TEA, ionization potential of polymer and excited state electron affinity (EA*) become steadily more positive from P1 to P7 to P10, while it becomes less negative down the series in terms of EA of the polymer and the excited state IP (IP*), see Figure 6 c. Regardless of the type of solvents, solvated P1 showed a thermodynamically uphill charge transfer whereas it was downhill for P7 and P10. Because the ionization potential (or excited state ionization potential) and electron affinity (or excited state electron affinity) become changed when interfaced with water or/and TEA. Because of lower dielectric permittivity of TEA, a larger splitting between the IP and EA* potentials of the polymers was shown in TEA than in water that shift the solution potentials to more positive values in TEA, Figure 6 d. The differences in IP and EA resulted in a considerable change (>0.5 eV) in driving force for each polymer for the reduction of protons to hydrogen and for the oxidation of TEA to DEA and acetaldehyde. For further details, we refer the readers to ref. 37c detailing the IP and EA issues related to solid‐state photocatalysts.

Clearly, understanding the effect of local environment and the driving forces for individual charge transfer steps, and the thermodynamic potentials for reduction or oxidation reactions are crucial in design of highly efficient polymeric photocatalysts for overall water splitting in the absence of a SED or as a component in a Z‐Scheme with a second semiconductor. Another important aspect is the determination of the rate laws for solvated photocatalysts, which are largely unexplored for many organic photocatalyst. The emergence of a limiting rate law arises due to competing slow water oxidation/reduction kinetics with rapid recombination (nano‐ to micro‐second) of photogenerated excitons.37e, 41 The rate law quantify the rate of constant proton reduction within the lifetime of photogenerated electrons and can also be valuably used to distinguish different contributions. For example, if the lifetime of an electron liberated from an exciton in a photocatalyst is 1 s, rate constant of one‐electron reduction reactions must be slower than 1 s⁻¹.42 Establishing the rate laws therefore provides important information to distinguish between the most common reaction paths and propose a mechanism for hydrogen evolution.

Commonly practiced strategies to accelerate the kinetics of proton reduction to molecular hydrogen are the inclusion of (i) sacrificial electron donor (i.e. TEA) to increase the lifetime of electron, and (ii) co‐catalyst to aid the spatial separation of electrons and holes. However, there is an increasing concern to use these strategies for cost effective pure water‐splitting.

3.4. Improving Electrocatalytic Performance of Organic Photocatalysts

In contrast to purely electrocatalytic water‐splitting in which the charges and driving force for relevant redox reactions are provided with an external electrical potential, driving force in photocatalytic water‐splitting is provided with photogenerated free electron‐hole pairs. Regardless of how the charges are generated and transported to the active sites in an electrocatalytic or photocatalytic system, the fundamental mechanisms of reactant to product formation is exclusively a local electrochemical process. Similar to electrocatalyst, the electrocatalytic performance of photocatalyst for specific reactions can therefore be evaluated in terms of current density (j ₀), overpotential (η), Tafel slope and so on, as long as the photocatalysts are designed to allow longer charge transport compared to the more locally generated charges in direct photocatalysis. The j ₀ with respect to the oxidation of water is a measure to the intrinsic charge transfer rate between OER electrocatalyst and the reactant intermediates. The Tafel slope evaluates the reaction rate constant (i.e. a faster increase in j with a smaller change in η),43 and can also be utilized to pinpoint the rate determining reaction mechanism.44 It can thus be very informative for the surface reaction properties of the process while disregarding the photo‐generation process. A comprehensive understanding of the origin of reactivity can be pursued with experimentally measured values of these descriptors. Additionally, turnover frequency and volcano plot may define the activity trend. With experimental results in hand, DFT can be employed to define the adsorption energies, reaction thermodynamics, activation barriers, and the active sites on surfaces of solid catalysts under ideal conditions.43 As quantum mechanical theory cannot reliably predict the surface reconstruction or phase transition of the surface at applied bias in a solvent environment, combined theoretical and experimental studies are therefore valuable to guide modification of the materials for the desired catalytic activities.43, 45

Published literature on carbon‐based catalysts provide a good starting point for tuning electrocatalytic activities of organic photocatalysts containing also other elements, particularly for π‐conjugated covalent organic frameworks. For example, heteroatom doped (e.g., N and S) graphene nanostructures were shown to adjust efficiently the electron‐donor property and electrocatalytic activity with enhanced H* adsorption‐desorption ability of graphene. Because of doping induced synergistic coupling effect (i.e. both charge redistribution and enhances charge transfer process), doped graphene exhibited enhanced HER activity with low onset potential and high exchange currents, Figure 7.46

Figure 7.

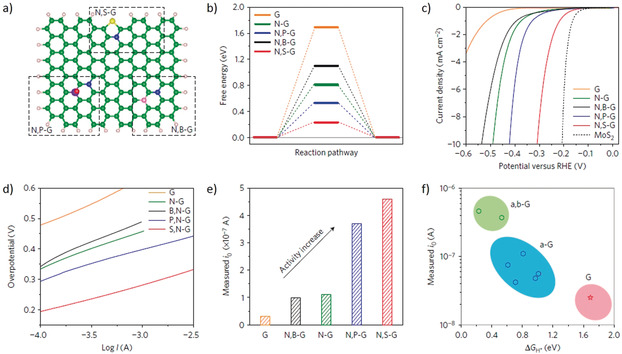
a) Atomic configurations of three dual‐doped graphene. b) The three‐state free energy diagram for the pure, single‐ and dual‐doped graphene models. c) Polarization curves. d) Tafel slopes. e) Exchange current. f) Volcano plots. Adopted with permission from ref. 46. Copyright 2016, Nature Publishing group.

Given that the protons are readily available, proton and electron transfer can be independent or correlated, known as concerted mechanism, before reacting together to form a final product (e.g. molecular hydrogen). However, if generation of protons from a substrate (e.g. at a catalyst/water interface) involves intermediate reactions, the formation of the final product should follow a coupled electron and proton transfer in which the sequential reaction can proceed along two parallel channels either electron transfer then proton transfer (ET/PT) or vice versa (i.e. PT/ET).47 In the context of water splitting, it may therefore be of prime interest to explore the different mechanism whether a liberated electron (or proton) is the first step to subsequently pull out a proton (or electron) acting as fixed donor state; or if an electron jump back and forth between donor and acceptor states for a gradually extracted proton. This in‐depth understanding will provide a clearer picture on the rate control of reaction cycles from intermediates to final products. The photoinduced PCET reactions depend on not only on the change in bond angles of the catalyst but also on the reorganization of the solvent environment, and often inherently represent nonequilibrium processes. Here electron or proton transfer can also be completed before the thermal equilibrium or a steady‐state situation. Therefore, Marcus theory of electron transfer48 may not be applicable in describing the PCET. Instead, the ultrafast dynamics of such systems can be captured by nonadiabatic molecular dynamics simulations on electron‐proton vibronic surfaces.49

4. Meeting 10 % STH Efficiency

The average cost of hydrogen production via particulate photocatalytic devices is estimated to reside in the range of 1.6–3.5 USD kg⁻¹ for STH values of 5–10 % assuming a 5 year lifetime of the catalysts.50 Given the latest progress in photocatalytic STH efficiencies that is ≈1 % now,51 with uncertain lifetime, is this a far distant target? If we are able to absorb UV light up to 400 nm with an AQE of 100 %, it is possible to achieve a STH value of ≈2 %, while it is 25 % for 700 nm with AQE of 100 %, and 10 % for 520 nm with AQE of 100 % and with AQE of 60 % for 650 nm, see Figure 8.52 These statistics are full of hope. It is indicative that a narrow band gap photocatalyst (<2.0 eV) would be the ideal to achieve the 10 % target. Organic photocatalyst, because of their tuneable band structures, could therefore still be a promising approach. The challenges instead lie in achieving the near unity quantum efficiency and prolonging the lifetime of the catalysts. What does an AQE of 100 % mean at a given wavelength of photon? It simply means that every single absorbed photon at that particular wavelength generates one electron, and all the photogenerated electrons are transported to the reaction sites with zero recombination and utilized for hydrogen production. The reported AQE for organic photocatalysts is currently below 13 % at their optimal wavelength. An AQE of 13 % means, out of 100 generated electrons, 87 electrons are lost due to recombination and trapping. Therefore, optical (light absorption, reflection, and scattering) and electronic (generation, recombination, trapping, and transport of electrons and holes) properties of the photocatalyst must be optimized to improve the AQE, and therefore, the STH.

Figure 8.

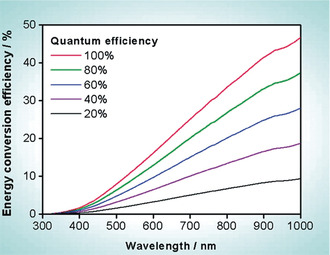
Calculated solar energy conversion efficiency as a function of wavelength for overall water splitting using photocatalysts with various quantum efficiencies. Solar irradiance used for the calculation is taken from AM 1.5G data. Copyright 2010, ACS. Adopted with permission from ref. 52.

Given that the STH efficiency is far below the targeted minimum, discussion on the scalability for large‐scale deployment at this point seems less important as more work is needed to develop and improve the fundamental operation. One can also note that STH efficiency is one of the many prime parameters for mass scale implementation. A detailed discussion on other relevant parameters is beyond the scope of this article. However, we will here articulate a few limiting factors which if are not addressed timely may impediment the prospects of large‐scale deployment later. For example, particulate photocatalysts suspended in aqueous solution are commonly used for water splitting. However, translating laboratory‐scale particle suspension systems into commercially competitive industrial settings is a grand challenge. Designing photocatalysts with high STH value will solve part of the problem in pursuit of large‐scale implementation. In a cost‐of‐system analysis, larger areas or containers required would add more to the system cost, and could in many cases dominate the overall cost. To date, PV‐electrolysis approaches is more appealing for hydrogen production in terms of efficiency and cost.

In addition, dispersing a large amount of particulate photocatalysts in a large amount of water and keeping it near homogenously suspended to avoid precipitation is seemingly not feasible, and would incur added energy and maintenance cost. This problem becomes more intricate if we account for the separation and collection of the photocatalyst powder from the suspension for further use, or additional cost for positioning the large containers with optimal light absorption or tracking the movement of the sun for maximum efficiency. A modular photocatalyst would be a potential way out of this problem. Strategies need to be found for depositing photocatalyst powders onto a specific substrate to prepare a module of specific size and dimension with stability and selectivity. Research efforts are evolving in this regard.53 Module may then be interconnected to form a panel. Like an integrated PEC/PV system that uses solar cells and photoelectrodes, a reactor for large‐scale photocatalytic water splitting may be constructed with shallow horizontal pools or beds consisting of water and a panel‐type photocatalysts. It would then also naturally be compared to the merits of inorganic panel type approaches in either PEC or PEC/PV approaches.

5. Accurate Reporting of Hydrogen Evolution

Appropriate reporting of hydrogen production is essential for reproducibility and benchmarking. The reporting of hydrogen production per gram catalyst (i.e. mol h⁻¹ g⁻¹) is not optimal and could in some cases be misleading. Instead, it is recommended to report the optimal rate of hydrogen evolution (i.e. mol h⁻¹) independent of the amount of photocatalyst used (i.e. mol h⁻¹ g⁻¹).12, 54 Because, light absorption become saturated after an optimal amount of photocatalyst spent, Figure 9,54b and would then instead reflect how much care the researchers have spent on adding sufficient amount of catalysts for the exposed reaction sites in their specific system and light intensity used. As the measured gas evolution rate vary with the experimental conditions and light source used, current practice of comparing the photocatalysts based on hydrogen production rate, however, is not sufficient enough. Here, it is advisable that one also report AQE and/or STH values at specific wavelengths to provide a measure that can be critically compared to other studies. An assessment of the performance using a wide spectrum light source naturally also requires information of the intensity and spectrum of the light source used.

Figure 9.

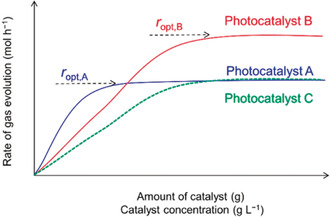
Influence of amount of photocatalyst on the rate of gas evolution. Adopted with permission from ref. 54b. Copyright 2017, ACS.

The detailed information on the type of reactor used (internal or external irradiation photocatalytic reactors), intensity of light source, wavelength of the light, mass of the photocatalyst, and absence/presence of sacrificial agents and cocatalyst(s) need to be provided for the reproducibility. To avoid effects from ambient air, the reactor is required to be either perfectly sealed or the reaction should be performed under vacuum or under a flow of inert gas for correct estimation of the evolved gases under controlled conditions. It may typically be done by degassing the reaction solution completely through inert gas flow. The gas chromatograph must also be carefully calibrated using standard gases to quantify the amount of evolved gas. If N₂ is detected in the gas chromatograph, it is an indication that the reaction solution was intruded by ambient air or inadequate removal of dissolved air. N₂ detection in the case of (oxy)nitride photocatalysts represent the self‐oxidation of the photocatalyst.55 For either cases, N₂ evolution is not expected in water‐splitting reactions. A very important aspect is also to ensure that commonly used catalysts metals (Pt, Pd) utilized in the production of the organic photocatalyst, or by the vendor of the starting products, are quantified. This is of crucial importance, as any traces of these metals would artificially improve the rate of the investigated reactions. For the same reason, Pt counter electrodes should be avoided.

To confirm that the hydrogen/oxygen are evolved solely through photocatalytic reactions, it is recommended to check if the (i) catalytic reactions proceed in dark, (ii) evolved amounts gases increase linearly with the irradiation time, and (iii) turnover number is greater than hydrogen presents within the catalyst. If the condition (iii) is not met, the system could still be catalytic but measurements that are more precise, such as isotope marking, need to be performed to distinguish the catalytic part from the any photo degradation process. In overall water splitting, H₂ and O₂ should preferably be evolved at a stoichiometric ratio of 2:1 during the whole course of catalytic reaction or passing the induction period of some of the photocatalysts under light irradiation. Deviations from this ratio can then be ascribed to recombination reactions for either of the gas evolution reactions, or if measured at a low amount, also come from photo degradation of carbohydrate groups. In sacrificial hydrogen production, evolved hydrogen must be greater in quantity than the molar quantity of hydrogen (if any) present in the chemical structure of the photocatalyst and the SED. Otherwise, it can represent self‐decomposition of the photocatalyst and SED with or without proton reduction. Here, medium to long term‐stability measurements (10–100 h) are advised and should of course show unchanged performance during measurements if no degradation or catalyst surface inhibiting reaction occurs. If the performance instead is decreasing monotonically, longer measurements are required where the final period of constant performance should be taken as the resulting catalytic efficiency. It is also recommended that final state characterization is performed to assure that the starting material is intact and not changed into another organic chemical or a metal oxide if metals are present in the setup.

To be compatible with universally standard practice, STH value should obtain under one sun using a certified and calibrated solar simulator. An intensity of 100 mW cm⁻² with the AM1.5G solar spectrum is the standard when reporting results from PEC water splitting and for solar cells efficiencies, and the same standard is recommended for determination of the STH efficiency for photocatalysis.

6. Conclusion and Outlook

Organic photocatalyst has potential to be materials of choice for sustainable and cost‐effective hydrogen production. Like their inorganic counterpart, organic photocatalysts can be competitively implemented in large‐scale hydrogen production for a reaction system with an STH of 10 %, a lifetime of 10 years, an annual depreciation rate of 4 %, and an allowable cost of 102 USD m⁻².50, 56

Despite the history of organic photocatalysts dates back to at least 1985, with early work on oligo‐ and poly(p‐phenylene)s for hydrogen evolution in the presence of a sacrificial electron donor (SED), this area has only gained serious attraction since 2009, after the demonstration of catalytic carbon nitride materials. This resulted in many follow‐up studies on carbon nitride and enriched the polymeric photocatalyst family with the introduction of conjugated microporous polymers, linear conjugated polymers, triazine‐type materials, covalent organic frameworks (COFs), and their heterostructures.

The activity of polymeric photocatalysts for hydrogen and/or oxygen evolution is a complex interplay of the absorption of photons, charge carrier dissociation and transport at the band positions, and the wettability of their surfaces, etc. Optimizing all these properties in a single photocatalyst material is a daunting challenge, because these properties are mutually interdependent or may have contrasting or antagonistic dependencies. Therefore, improving one property may adversely affect another. For example, incorporating polar building blocks into the polymer skeleton might increase the wettability of the polymer, but at the same time, it blue‐shifts the absorption spectrum at a cost of limiting the absorption of longer wavelength photons in the solar spectrum. Copolymerization is one the most exercised techniques to incorporate foreign linkers as local building blocks of the pristine polymer. Another aspect, particularly for 3D CMPs, is that drop in activity can occur with changes in the polymerization method, raises the question of whether the change might be associated with a difference in the efficiency of the polymerization method.

Light absorption creates strongly bound excitons in organic semiconductors because of their low‐dielectric constant and lack of extended orbital overlaps. Improving the exciton dissociation in organic photocatalysts is one of the key steps for the realization of highly efficient photocatalytic systems. A well‐founded and detailed understanding of the mechanism of exciton dissociation and its dependence on material parameters are still missing for many polymeric photocatalysts used in aggregated and condensed form. The same difficulty arises for the materials and material blends used in organic solar cells. One of the most effective ways to promote exciton dissociation in low dielectric materials is incorporating a donor–acceptor (D–A) system in which an electron from the excited donor transfers to the ground state acceptor molecule, and thus forms a charge transfer state.57 This initial charge transfer step usually takes place on an ultrafast timescale. The excess energy that is liberated during the transfer of the excited donor electron to the acceptor aids in complete dissociation of the excitons. Therefore, the energy difference between the lowest unoccupied molecular orbital (LUMO) level of the donor and the acceptor needs to be optimized for a high dissociation rate.58 Utilization of interfacial dipoles charge collecting electrodes may also be conducive to improve exciton dissociation.26, 59 Here other strategies, such as asymmetric charge transfer from either change in symmetry of the orbitals after charge transfer or from sterically tuned overlaps are options for future avenues for exciton delocalization without a high free energy penalty.

To improve the HER and OER in organic photocatalyst, a rational design of the emerging organic catalysts should be followed by in‐depth understanding of the electrocatalytic reaction mechanisms at the molecular level through fundamental and theoretical studies of model catalysts using in situ, ex‐situ and operando techniques. A routinely used strategy to improve the photocatalytic performance of a semiconductor photocatalyst is to integrate co‐catalysts with the photocatalyst for enhanced rate of hydrogen‐ or oxygen‐evolution reaction (HER or OER), respectively. This separates the function of the photo generation of charges in one material with subsequent charge transfer and more effective catalytic properties in an adjacent material. There is still under‐developed understanding of presently used organic semiconductor‐electrocatalyst interfacial phenomena (i.e. optical effects, surface recombination, band bending, interface‐charge trapping, and precise reaction mechanisms). The current understanding of these interfacial phenomena has evolved around well‐defined metallic or semiconductor electrocatalysts. However, such phenomena cannot always be directly transferred to porous, hydrated, and redox‐active solid organic materials because of their non‐ideal electronic interfaces.

The challenges remain in the structural design of organic photocatalysts to accommodate beneficial physicochemical attributes for photocatalytic redox reactions. Because it is seemingly impossible to change one parameter within these polymers without changing several others. Changing the linker length impacts the chemical structure and electronic properties, degree of polymerization and number of terminal groups, the surface area and porosity, and the polarity and hydrophobicity etc. Therefore, how can a rational design of organic photocatalysts be possible and general to all material types is an open question. Exploitation of recently emerged integrated computational and experimental high‐throughput approach may be useful to sort out highly efficient organic photocatalyst out of large pool of monomers, reaction pathways, and reaction conditions.11t

Conflict of interest

The authors declare no conflict of interest.

Biographical Information

Mohammad Ziaur Rahman received PhD in Chemical Engineering from the University of Adelaide, Australia in 2018. He was a Researcher at the Department of Materials Sciences and Engineering, Angstrom Laboratory, Uppsala University, Sweden. He is currently a Postdoctoral Research Fellow at the School of Chemical Engineering, The University of New South Wales, Sydney, Australia. His primary research interest includes photovoltaics, and photo(electro)chemical energy conversion and storage.

Biographical Information

Haining Tian is Associate Professor at Uppsala University, Sweden, leading a research group of Molecular Devices for Artificial Photosynthesis. He obtained his PhD in Applied Chemistry at Dalian University of Technology (DUT) in 2009 and then moved to Royal Institute of Technology (KTH) as Postdoc and senior researcher until 2014. He was awarded the Göran Gustafsson Prize for young researchers (2016 and 2020), Young Investigator from European Photochemistry Association (2019) and Wallenberg Academy Fellow (2019). His research interests focus on the development and investigation of sustainable materials for solar energy conversion and storage.

Biographical Information

Tomas Edvinsson is professor of solid state physics at Uppsala University, Sweden. He received his Ph.D. at Uppsala University in 2002, and performed a postdoctorate at Uppsala University, Royal Institute of Technology (KTH) and BASF AG until 2007. In September 2007 he established his research group at Uppsala University working on low‐dimensional materials for solar cells and photocatalysis. He is the project leader in several national projects from the Swedish Research Council, the Swedish Energy Agency, a European H2020 project within solar fuels, and acts as reviewer and panel member for national and larger grant organizations (ERC, DFG priority program, among others).

M. Rahman, H. Tian, T. Edvinsson, Angew. Chem. Int. Ed. 2020, 59, 16278.