A stochastic second-order generalized estimating equations approach for estimating association parameters

Abstract

Design and analysis of cluster randomized trials must take into account the intraclass correlation coefficient (ICC), which quantifies the correlation among outcomes from the same cluster. Second-order generalized estimating equations (GEE2) provides a statistically robust way in estimating this quantity and other association parameters. However, GEE2 becomes computationally infeasible as cluster sizes grow. This paper proposes a stochastic variant to fitting GEE2 which alleviates reliance on parameter starting values and provides substantially faster speeds and higher convergence rates than the widely used deterministic Newton-Raphson method. We also propose new estimators for the ICC which account for informative missing outcome data through the use of GEE2, for which we incorporate a “second-order” inverse probability weighting scheme and “second-order” doubly robust (DR) estimating equations that guard against partial model misspecification. Our proposed methods are evaluated through simulations and applied to data from a cluster randomized trial in Bangladesh evaluating the effect of different marketing interventions on the use of hygienic latrines.

1. Introduction

Cluster randomized trials (CRTs), in which individuals are randomly assigned to intervention in groups, have been increasingly implemented to evaluate efficacy and effectiveness of various intervention programs. The intraclass correlation coefficient (ICC) characterizes the degree of similarity of individuals within a community and is crucial in accurately computing sample sizes needed to achieve a certain power level in a CRT. For example, in a matched-pair CRT with 15 pairs and a sample size of 300 within each cluster as seen in the Botswana Combination Prevention Project (Gaolathe et al., 2016; Wang et al., 2014), the power to detect a 40% reduction in the 3-year cumulative incidence (from 2.5% to 1.5%) decreases from 80% to 52% as the ICC increases from 0.001 to 0.005. To achieve 80% power with an ICC of 0.005, assuming all else being fixed, the number of clusters required almost doubles (15 pairs to 27 pairs). When analyzing data from CRTs, a commonly used and robust approach is based on comparisons of a community-level outcome measure of interest. Tests constructed by giving equal weight to each cluster may not be fully efficient, especially when the sizes of clusters vary substantially. The optimal weights depend crucially on the ICC for both parametric tests (e.g., t-test) (Hayes and Moulton, 2009) and nonparametric permutation tests (Braun and Feng, 2001; Wang and De Gruttola, 2017). Despite its importance, obtaining reliable estimates of the ICC remains a major problem in designing CRTs (Donner and Klar, 2000; Hayes and Bennett, 1999; Klar and Donner, 2001). Furthermore, ICC can vary considerably by intervention group and community characteristics (e.g. community size) (Crespi et al., 2009; Wu et al., 2012).

In CRTs, interest often lies in estimating the intervention effect on the cluster – the difference between outcomes in the treated cluster versus the untreated cluster (Carnegie et al., 2016). Mixed models and their extensions (Anderson and Aitkin, 1988; Laird and Ware, 1982; Stiratelli et al., 1984) are a popular choice in estimating the intervention effect while accounting for the clustering effect. Variance modeling for continuous outcomes (Leckie et al., 2014; Paik, 1992; West et al., 2018) have also been proposed. These methods require parametric assumptions and provide a conditional interpretation of intervention effects. Here, we focus on the generalized estimating equations (GEEs) (Liang and Zeger, 1986) approach. This estimation procedure is semiparametric in that it assumes the correct specification of a marginal mean model, instead of a full likelihood, in order to yield a consistent and asymptotically normal estimator of the treatment effect. The GEE approach with correct specification of the working correlation structure is theoretically optimal and has been demonstrated in simulations to have efficiency gains (Fitzmaurice, 1995), while others noted that using independence correlation structure is often adequate (McDonald, 1993; Zeger, 1988). In either case, its misspecification does not affect valid inference (Zeger et al., 1988). As a result of this flexible feature, one typically uses a rough approximation of the ICC through a method of moments approach. When ICC itself is of primary interest, the method of moments approach can be inaccurate. This has motivated the development of second-order generalized estimating equations (GEE2) (Liang and Zeger, 1992; Zhao and Prentice, 1990), which includes an extra stack of estimating equations specifically directed at estimating the ICC. Lipsitz and Fitzmaurice (1996) proposed a conditional estimating equations approach which was demonstrated to have additional efficiency gains.

Several authors (Carey et al., 1993; Ziegler et al., 1998) have noted of convergence problems regarding GEE2. Solving GEE2 is difficult due to the far larger stack of estimating equations for the association parameters, leading to excessive computing time in obtaining solutions to these equations. Carey et al. (1993) championed the use of odds ratios in measuring association, for which they proposed fitting with alternating logistic regression. Their algorithm is computationally efficient because it exploits a clever relationship in the conditional residuals, but is specific to the odds ratio setting. In our context, as the ICC is our parameter of interest, we focus on approaches that model ICCs directly. We develop stochastic methods to alleviate the computational challenges associated with solving GEE2. These stochastic algorithms involve running Fisher scoring / Newton-Raphson on a different subset (minibatch) of the data at each iteration in the spirit of minibatch stochastic gradient descent and the more general class of Robbins-Monro algorithms (Robbins and Monro, 1951). Under mild regularity conditions (Blum, 1954), the algorithm almost surely converges to the same solution as if we performed standard Fisher scoring on GEE2.

It is common to encounter missing outcomes in practice. A second purpose of this paper is to investigate methods that account for missing outcome data. When outcomes are assumed missing completely at random (Rubin, 1976) (outcomes are missing independently of both observed and unobserved data), the GEE2 analysis performed on complete-case CRT data provides consistent and asymptotically normal estimators for the treatment effect and ICC parameters. In the case of missing at random (MAR; outcome missingness is independent of the unobserved variables conditional on the observed variables), GEE2 produces inconsistent estimators unless all factors contributing to the propensity of being missing are included in a correctly-specified outcome model. Extensions (Hall and Severini, 1998) have been proposed where estimating equations are derived assuming multivariate normality and have been shown to retain high efficiency and have minimal bias even under MAR (Lipsitz et al., 2000). Furthermore, Le Cessie and Van Houwelingen (1994) and Parzen et al. (2007) have proposed pseudo-likelihood methods which model both missingness and outcome processes. Our work is based on inverse probability weighting (IPW) and outcome model (OM) augmentation made popular by the semiparametric methods field (Robins et al., 1994; Tsiatis, 2007; Van der Laan and Robins, 2003). In the context of CRTs, there is no natural ordering of the outcomes within a community and the missingness pattern is non-monotone. Currently, methods are available to account for a restricted missing at random mechanism (rMAR; outcome missingness depends only on observed covariates but not on observed outcomes) in the GEE1 case for the estimation of marginal treatment effects (Prague et al., 2016). The resulting estimators are doubly-robust (DR) in the sense that they require either the IPW or outcome model to be correctly specified in order to produce consistent treatment effect estimates. However, properly incorporating this framework for association parameters requires modeling the correlation among missingness indicators for correlated units within a cluster, a potential complication which to the best of our knowledge has previously not been addressed in the literature on semiparametric methods for missing clustered data.

Section 2 gives background on the standard GEE2 (non-stochastic and no missing data). In Section 3, we introduce the Robbins-Monro algorithm and expand on the stochastic paradigm to fitting GEE2, which we coin as stochastic GEE2. Issues such as computational complexity, efficient implementation, and parallelization as a further mechanism in reducing computing time and numerical errors are explored here. In Section 4, we draw from the semiparametric methods to construct IPW and DR variants of GEE2, which we call IPW-GEE2 and DR-GEE2, and explain how to further adapt stochastic GEE2 to these procedures. We evaluate the performance of the proposed estimators and the proposed computational algorithms with simulations in Section 5 and apply the new estimators and algorithms to analyze Bangladeshi sanitation data (Guiteras et al., 2015) in Section 6. We end with a discussion in Section 7. Proofs are relegated to Supplemental Materials.

2. Notation and standard GEE2

Henceforth, we work with binary outcomes Y_ij ∈ {0,1} for subject j = 1,⋯, n_i in cluster i = 1,⋯, I; the framework is readily generalizable to continuous outcomes. Let A_i ∈ {0,1} denote the treatment randomized at the cluster level with $\mathbb{P}\left(A_i=1\right)=p_A$, $Z_i\in {ℝ}^q$ as baseline cluster-level covariates, $X_{ij}\in {ℝ}^m$ as baseline subject-level covariates, and $X_i={\left\{X_{ij}\right\}}_{j=1}^{n_i}$. We denote P(·) as the probability measure associated with its argument i.e. P(a), P(z, x). Let ${\pi }_{ij}=\mathbb{E}\left[Y_{ij}|A_i,Z_i,X_i\right]$ denote the conditional mean outcome and

$${\rho }_{ij{j}^{\prime }}=\text{Cov}\left(Y_{ij},Y_{i{j}^{\prime }}|A_i,Z_i,X_i\right)/\sqrt{\text{Var}\left(Y_{ij}|A_i,Z_i,X_i\right)\text{Var}\left(Y_{i{j}^{\prime }}|A_i,Z_i,X_i\right)}$$

denote the conditional ICC. The quantities of interest are ${\pi }_i^{*}=\mathbb{E}\left[Y_{ij}|A_i\right]$ and ${\rho }_i^{*}=\text{Corr}\left(Y_{ij},Y_{i{j}^{\prime }}|A_i\right)$, which are the treatment-specific mean outcome and ICC. It is clear that ${\pi }_i^{*}$ is a marginalization of π_ij in the sense that ${\pi }_i^{*}=\mathbb{E}\left[{\pi }_{ij}|A_i\right]=\int {\pi }_{ij}dP\left(z_i,x_i\right)$. But, ${\rho }_i^{*}\ne \mathbb{E}\left[{\rho }_{ij{j}^{\prime }}|A_i\right]$ in general. Indeed, it is easy to verify that ${\rho }_i^{*}=\mathbb{E}\left[{\rho }_{ij{j}^{\prime }}^{†}|A_i\right]$, where

$${\rho }_{ij{l}^{\prime }}^{†}\stackrel{\text{def}}{=}\mathbb{E}\left[\frac{\left(Y_{ij}-{\pi }_i^{*}\right)\left(Y_{i{j}^{\prime }}-{\pi }_i^{*}\right)}{{\pi }_i^{*}\left(1-{\pi }_i^{*}\right)}|A_i,Z_i,X_i\right]=\frac{\left({\pi }_{ij}-{\pi }_i^{*}\right)\left({\pi }_{i{j}^{\prime }}-{\pi }_i^{*}\right)+{\rho }_{ij{j}^{\prime }}\sqrt{{\mathcal{V}}_{ij{j}^{\prime }}}}{{\pi }_i^{*}\left(1-{\pi }_i^{*}\right)}$$ (1)

and ${\mathcal{V}}_{ij{j}^{\prime }}={\pi }_{ij}\left(1-{\pi }_{ij}\right){\pi }_{i{j}^{\prime }}\left(1-{\pi }_{i{j}^{\prime }}\right)$.

Let ${\widehat{\pi }}_{ij}$ be an estimator of π_ij, converging to the limit ${\overline{\pi }}_{ij}$, which may or may not equal the true π_ij. Likewise, let ${\widehat{\rho }}_{ij{j}^{\prime }}$ be an estimator of ${\rho }_{ij{j}^{\prime }}$ with limit ${\overline{\rho }}_{ij{j}^{\prime }}$. Standard models for ${\widehat{\pi }}_{ij}$ include logistic or probit regression, while a model for ${\widehat{\rho }}_{ij{j}^{\prime }}$ could be a generalized linear model with link function g(x) = atanh(x), the Fisher z-transform. The Fisher z-transform is commonly used as a variance-stabilizing transformation for the sample correlation coefficient, we apply it here to map the [−1, 1] support of ${\rho }_i^{*}$ onto $ℝ$.

Similarly, let ${\widehat{\pi }}_i^{*}$ and ${\widehat{\rho }}_i^{*}$ be estimators for ${\pi }_i^{*}$ and ${\rho }_i^{*}$ with limits ${\overline{\pi }}_i^{*}$ and ${\overline{\rho }}_i^{*}$, respectively. For example, inference for the causal effect of A_i can be estimated under the model

$$\text{logit}\left({\pi }_i^{*}\left({\beta }_Y^{*};A_i\right)\right)={\beta }_{0Y}^{*}+{\beta }_{AY}^{*}{A}_i,\text{\hspace{1em}atanh}\left({\rho }_i^{*}\left({\alpha }_Y^{*};A_i\right)\right)={\alpha }_{0Y}^{*}+{\alpha }_{AY}^{*}{A}_i$$ (2)

to produce estimators $\left({\beta }_Y^{*},{\alpha }_Y^{*}\right)$. Eq 2 will be referred to as the canonical treatment model (TM). In the absence of missing data, and since A_i is binary, the canonical TM is guaranteed to yield consistent ${\overline{\pi }}_i^{*}={\pi }_i^{*}$ and ${\overline{\rho }}_i^{*}={\rho }_i^{*}$. In the standard GEE2 framework, we would estimate $\left({\beta }_Y^{*},{\alpha }_Y^{*}\right)$ as the solution to the equations

$$0=\sum _{i=1}^I{D}_i^{\top }{V}_i^{-1}{E}_i\stackrel{\text{def}}{=}\sum _{i=1}^I{S}_i^Y\left(A_i,{\beta }_Y^{*},{\alpha }_Y^{*}\right)$$ (3)

where

$$\begin{gathered} D_i=\frac{\partial \left({\pi }_i^{*}\left({\beta }_Y^{*};A_i\right),{\rho }_i^{*}\left({\alpha }_Y^{*};A_i\right)\right)}{\partial {\left({\beta }_Y^{*},{\alpha }_Y^{*}\right)}^{\top }},V_i=\text{Cov}\left(\begin{array}{c}{Y}_i\\ \mathcal{E}\left(Y_i\right)\end{array}\right),E_i=\left(\begin{array}{c}{Y}_i-{\pi }_i^{*}\left({\beta }_Y^{*}\right)\\ \mathcal{E}\left(Y_i\right)-{\rho }_i^{*}\left({\alpha }_Y^{*}\right)\end{array}\right) \\ \mathcal{E}\left(Y_i\right)={\left[\frac{\left(Y_{ij}-{\pi }_i^{*}\right)\left(Y_{i{j}^{\prime }}-{\pi }_i^{*}\right)}{{\pi }_i^{*}\left(1-{\pi }_i^{*}\right)}\right]}_{j<j^{\prime }} \end{gathered}$$

Note that the working covariance matrix V_i need not be correctly specified to produce consistent estimates, but doing so may lead to improved efficiency. The expression $\mathcal{E}\left(Y_i\right)$ involves standardized residuals and is one particular parametrization of GEE2 (Ziegler et al., 2000), but there are others (Liang and Zeger, 1992; Zhao and Prentice, 1990). We choose the above parametrization because it specifically targets the treatment-specific ICC ${\rho }_i^{*}$ instead of, say, the cross moments or covariance, but the proposed framework is applicable to these other parametrizations.

In what follows, Section 3 and 4 will delineate two adaptations of GEE2. The first proposal provides a scheme in reducing the computation time and numerical errors which arise when fitting GEE2. The second proposal devises adjustments to GEE2 which account for missing data through the use of inverse-probability weighting and outcome model augmentation.

3. Proposal I: Stochastic GEE2

3.1. Background: Robbins-Monro Algorithm

GEE2 is ordinarily solved using Newton-Raphson, which has iterations θ₍₀₎, θ₍₁₎,⋯ of the form

$${\theta }_{(\omega +1)}={\theta }_{(\omega )}+H_{(\omega )}^{-1}{G}_{(\omega )}$$ (4)

where

$$H_{(\omega )}=\sum _{i=1}^I{D}_{i(\omega )}^{\top }{V}_{i(\omega )}^{-1}{D}_{i(\omega )},G_{(\omega )}=\sum _{i=1}^I{D}_{i(\omega )}^{\top }{V}_{i(\omega )}^{-1}{E}_{i(\omega )}$$ (5)

Here, a subscript (ω) indicates evaluation at parameter values θ_(ω) = (β_(ω), α_(ω)), and we are using letters H and G to invoke the “Hessian” and “gradient” terminologies prevalent in the stochastic approximation literature. In GEE1, computation is dominated by the inversion of $V_{i(\omega )}^{-1}$, which has computational order $\mathcal{O}\left(\text{max}{n}_i^3\right)$. With GEE2, this increases to $\mathcal{O}\left(\text{max}{n}_i^6\right)$. To reduce this computational burden, we propose a Robbins-Monro (Robbins and Monro, 1951) variant to fitting GEE2.

In general, the Robbins-Monro algorithm states that, when solving for θ in the equation G(θ) = 0, if we instead possess a random variable G(θ) such that $\mathbb{E}[G(\theta )]=G(\theta )$ and iterate θ_(ω+1) = θ_(ω) –γ_(ω)G_(ω), where learning rates γ_(ω) > 0 satisfy $\sum _{(\omega )}{\gamma }_{(\omega )}=\infty$ and $\sum _{(\omega )}{\gamma }_{(\omega )}^2<\infty$, then θ_(ω) → θ₀ in L²-mean (Robbins and Monro, 1951) and almost surely (Blum, 1954), subject to a few additional regularity conditions. The standard choice for learning rates is γ_(ω) = (1 + ω)⁻¹. The Robbins-Monro algorithm is useful whenever we can find a G which is significantly faster to compute than G. For example, consider the general M-estimation problem (for which GEE is a special case) and suppose our estimating equation takes the form $G(\theta )=\sum _{i=1}^I{G}_i(\theta )$. It is easy to confirm that $G(\theta )=\sum _{i\in s}{G}_i(\theta )/p_i$ satisfies $\mathbb{E}[G(\theta )]=G(\theta )$, where s is a randomly chosen subset of U = {1,⋯, I} according to any sampling design with inclusion probabilities $p_i=\mathbb{P}(i\in s)$. Here, instead of performing I function evaluations, we only need to perform | s | evaluations at each iteration. If we take our sampling scheme to be a simple random sample without replacement (SRSWOR) of size υ, this reduces to minibatch stochastic gradient descent (Clémençon et al., 2015). Our focus is different here, because what plagues computation is not many summands corresponding to many clusters, but rather the computation of each summand corresponding to large clusters, which is commonplace in large-scale CRTs (see for example, Gaolathe et al. (2016)). The design of the proposed class of stochastic GEE2 algorithms differs from minibatch stochastic gradient descent in that we are improving iteration speed not through evaluating fewer of the functional summands ${\left\{G_i\right\}}_{i=1}^I$ (i.e. evaluating fewer clusters), but rather evaluating an unbiased and computationally-easier estimate of each summand G_i (done through sampling a subset of individuals per cluster). Also, we shall incorporate stochastic Hessians to form stochastic Fisher scoring / Newton-Raphson iterations ${\theta }_{(\omega +1)}={\theta }_{(\omega )}+{\gamma }_{(\omega )}{H}_{(\omega )}^{-1}{G}_{(\omega )}$, which Byrd et al. (2016) proves to convergence almost surely as well. Unlike the stochastic gradient G, the accuracy for a stochastic Hessian H is more forgiving, hence cruder approximations are often used to improve speed and memory allocation. In the context of GEE2, the Hessians have a palatable closed-form, so we need not resort to this tactic.

3.2. Subsampling

For what we define as the standard stochastic GEE2 algorithm, let U = (U₁,⋯, U_I), where each U_i corresponds to the indices of the outcomes in cluster i, with |U_i| = n_i. At each iteration ω, sample s_i ~ SRSWOR(U_i, υ_i), and concatenate s = (s₁,⋯, s_I). That is, each cluster sample s_i is a simple random sample without replacement of υ_i indices of the ith cluster. Then, perform the Newton-Raphson iteration with just the subsampled units. Notationally, this just replaces H_(ω), G_(ω) in Eq 4 with

$$H_{(\omega )}=\sum _{i=1}^I{D}_{i(\omega )}^{\top }{V}_{i(\omega )}^{-1}{D}_{i(\omega )},G_{(\omega )}=\sum _{i=1}^I{D}_{i(\omega )}^{\top }{V}_{i(\omega )}^{-1}{W}_{i(\omega )}^S{E}_{i(\omega )}$$ (6)

where $W_{i(\omega )}^S$ is a 0–1 weighted diagonal matrix indicating whether an observation is included in s_i, including pairwise indicators for the GEE2 portion. It is easy to verify that H_(ω), G_(ω) are unbiased estimators for H_(ω), G_(ω), respectively. Hence, by the Robbins-Monro conditions, the stochastic iterations (β_(ω), α_(ω)) → (β, α) almost surely as the number of iterations ω → ∞, where (β, α) are the solutions to estimating equations specified in GEE2. Because Hessians are embedded within our procedure, we should select a sizeable subsample to ensure a reliable estimate of the Hessian; we recommend υ_i ≥ 5. We present full details in pseudo code for stochastic GEE2 in Algorithm 1 of Supplemental Materials 2.

3.3. Exploiting sparsity

Stochastic GEE2 addresses two issues: instability and memory demands. Even for simple functions, Newton-Raphson is known for divergence issues due to evaluations near stationary points, where the Hessian is nearly non-invertible. Our proposal naturally alleviates this issue because stochasticity makes it very likely to “jump” off the path of divergence. Secondly, programming the expressions in Eq 6 only require storing a subset of the rows in D_i(ω) or E_i(ω) and columns of $V_{i(\omega )}^{-1}$, hence greatly freeing up RAM on a computer.

One aspect that can be improved, depending on the structure of the working covariance matrix V_i, is computational speed. For example, if we were to assume the off-diagonals $\text{Cov}\left(Y_i,\mathcal{E}\left(Y_i\right)\right)=0$, then iterations for β and α can be separated, with the GEE2 portion Newton-Raphson iterations taking the form ${\alpha }_{(\omega +1)}={\alpha }_{(\omega )}+H_{\alpha (\omega )}^{-1}{G}_{\alpha (\omega )}$. Then, if we take the GEE2 portion working covariance $V_{\alpha i}=\text{Var}\left(\mathcal{E}\left(Y_i\right)\right)$ to be diagonal, we can show (see Supplemental Materials 3) that each iteration has complexity $\mathcal{O}(1)$ (constant time!), given that subset sizes υ_i are not growing with respect to n_i.

We summarize the scenarios and resulting computational complexities in the theorem below:

Theorem:

Let $\text{Cov}\left(Y_i,\mathcal{E}\left(Y_i\right)\right)=0$ and ${\upsilon }_i=\mathcal{O}(1)$ (with respect to cluster sizes n_i). In the presence of standard Newton-Raphson, an iteration of the GEE1 portion with (i) arbitrary covariance, (ii) compound symmetry covariance (equicorrelation), and (iii) independence matrices are of complexities (i) $\mathcal{O}\left({\text{max}}_i{n}_i^3\right)$, (ii) $\mathcal{O}\left({\text{max}}_i{n}_i\right)$, and (iii) $\mathcal{O}\left({\text{max}}_i{n}_i\right)$. Similarly, standard Newton-Raphson on the GEE2 portion yields (i) $\mathcal{O}\left({\text{max}}_i{n}_i^6\right)$, (ii) $\mathcal{O}\left({\text{max}}_i{n}_i^2\right)$, and (iii) $\mathcal{O}\left({\text{max}}_i{n}_i^2\right)$; stochastic Newton-Raphson on the GEE1 portion yields (i) $\mathcal{O}\left({\text{max}}_i{n}_i^3\right)$, (ii) $\mathcal{O}\left({\text{max}}_i{n}_i\right)$, and (iii) $\mathcal{O}(1)$; stochastic Newton-Raphson on the GEE2 portion yields (i) $\mathcal{O}\left({\text{max}}_i{n}_i^6\right)$, (ii) $\mathcal{O}\left({\text{max}}_i{n}_i^2\right)$, and (iii) $\mathcal{O}(1)$.

See proofs in Supplemental Materials 3. Table 1 expresses a clearer schematic of the theorem.

Table 1.

Time complexities for stochastic GEE2 under various working covariance structures.

	Standard		Stochastic
	GEE1 portion	GEE2 portion	GEE1 portion	GEE2 portion
Arbitrary covariance	$\mathcal{O}\left({\text{max}}_i{n}_i^3\right)$	$\mathcal{O}\left({\text{max}}_i{n}_i^6\right)$	$\mathcal{O}\left({\text{max}}_i{n}_i^3\right)$	$\mathcal{O}\left({\text{max}}_i{n}_i^6\right)$
Equicorrelation	$\mathcal{O}\left({\text{max}}_i{n}_i\right)$	$\mathcal{O}\left({\text{max}}_i{n}_i^2\right)$	$\mathcal{O}\left({\text{max}}_i{n}_i\right)$	$\mathcal{O}\left({\text{max}}_i{n}_i^2\right)$
Independence	$\mathcal{O}\left({\text{max}}_i{n}_i\right)$	$\mathcal{O}\left({\text{max}}_i{n}_i^2\right)$	$\mathcal{O}(1)$	$\mathcal{O}(1)$

If we choose to model with equicorrelated ${\rho }_{ij{j}^{\prime }}={\rho }_i$, as commonly done in CRT’s (Crespi et al., 2009; Hayes and Moulton, 2009) and assume independence working covariance for the GEE2 portion, then standard Newton-Raphson on GEE2 would have $\mathcal{O}\left({\text{max}}_i{n}_i\right)$ for the GEE1 portion and $\mathcal{O}\left({\text{max}}_i{n}_i^2\right)$ for the GEE2 portion, hence the overall complexity is $\mathcal{O}\left({\text{max}}_i{n}_i^2\right)$. With stochastic GEE2, while the GEE1 portion remains at $\mathcal{O}\left({\text{max}}_i{n}_i\right)$, the GEE2 portion now becomes $\mathcal{O}(1)$, and hence the overall complexity is $\mathcal{O}\left({\text{max}}_i{n}_i\right)$. Therefore, stochastic GEE2 cuts down the computation per iteration from roughly a quadratic rate to roughly a linear rate. If we allow the GEE1 portion to also have an independence covariance structure, then the effects are even more pronounced, cutting the complexity from $\mathcal{O}\left({\text{max}}_i{n}_i^2\right)$ to $\mathcal{O}(1)$.

3.4. Parallel Stochastic GEE2

While stochastic GEE2 allows faster computations in its iterative fitting procedure, each iteration is not as informative due to additional variation from subsampling. Hence, more iterations are needed to solve the estimating equations, although the additional time in running more iterations is far less significant than the computational savings per iteration. Nevertheless, in pursuit of a variant requiring fewer iterations, we propose the parallel stochastic GEE2 class of algorithms. The general technique of parallelization is expanded upon in Zinkevich et al. (2010). The basic idea is, after sufficiently enough iterations, the stochastic estimates will become unbiased and further iterations are meant to reduce variation from the stochastic nature of the algorithm. Instead, one can run K independent chains of stochastic GEE2 and average the resulting convergent estimates. Both running more iterations on a single chain or averaging over multiple chains has the same effect in reducing the variation in estimates, but with the former, the iterations must be done sequentially and hence the user must wait, while with the latter, the chains can be run in parallel. Pseudocode is provided in Algorithm 2 in Supplemental Materials 2.

Stochastic GEE2 reduces the frequency of divergence, but generally not all of it; there remains a non-negligible probability that the algorithm may diverge. Parallelization inherently solves the convergence issue because at least some of the chains would have converged. The average of these convergent solutions is one estimator, or better yet, one can then feed this estimator as an initial value on another run of parallel stochastic GEE2, since the provided estimate would act as a better initialization. In a sense, parallelization is similar to multistart search (Ugray et al., 2007) because each chain initially fluctuates around the search space, effectively acting as a scattering of starting values. At the same time, this scattering is informative because each chain is still trying to fit on a subset of data. Hence, parallel stochastic GEE2 offers an advantage in intrinsically incorporating information in its multistart search rather than truly random scattering.

4. Proposal II: IPW- & DR-GEE2

Our main objective is a robust and efficient method for estimating association parameters, from which we proceed with the GEE2 framework. The previous section addresses the computational difficulties with GEE2; in this section we propose estimators for settings with missing outcomes. Our proposed solutions to both computational challenges and informative missingness share a similar structure: the stochastic algorithms and missingness-adjusted schemes for GEE2 both utilize weighting, the former to form unbiased stochastic Hessians and gradients, and the latter to form unbiased estimating equations.

4.1. IPW-GEE2

Accounting for missing outcome data in CRTs is challenging under the missing at random (MAR) assumption because there is no natural ordering of the outcomes within a cluster and the missingness cannot be considered as monotone. We consider a submodel of MAR, restricted MAR (rMAR). Let R_ij ∈ {0,1} with R_ij = 0 indicating Y_ij is missing. Then, rMAR is defined as $\mathbb{P}\left(R_{ij}=1|Y_i,A_i,Z_i,X_i\right)=\mathbb{P}\left(R_{ij}=1|A_i,Z_i,X_i\right)$; that is, $R_{ij}╨Y_{ij}|A_i,Z_i,X_i$. To continue with valid inference, we assume that

$${\pi }_{ij}^R\stackrel{\text{def}}{=}\mathbb{P}\left(R_{ij}=1|A_i,Z_i,X_i\right)>0\text{\hspace{1em}and\hspace{1em}}{\eta }_{ij{j}^{\prime }}^R\stackrel{\text{def}}{=}\mathbb{P}\left(R_{ij}{R}_{i{j}^{\prime }}=1|A_i,Z_i,X_i\right)>0,$$

where ${\pi }_{ij}^R$ and ${\eta }_{ij{j}^{\prime }}^R$ are the first- and second-order propensity scores (PS) that characterize the individual and joint missingness processes; inverting these PS gives the inverse-probability weights (IPW). Define the IPW matrix as

$$W_i^R=\text{diag}\left(\underset{\text{IPW}1}{\underbrace{\frac{R_{i1}}{{\overline{\pi }}_{i1}^R\left({\beta }_R\right)},\cdots ,\frac{R_{i{n}_i}}{{\overline{\pi }}_{i{n}_i}^R\left({\beta }_R\right)}}},\underset{\text{IPW2}}{\underbrace{\frac{R_{i1}{R}_{i2}}{{\overline{\eta }}_{i12}^R\left({\beta }_R,{\alpha }_R\right)},\cdots ,\frac{R_{i\left(n_i-1\right)}{R}_{i{n}_i}}{{\overline{\eta }}_{i\left(i_i-1\right)n_i}^R\left({\beta }_R,{\alpha }_R\right)}}}\right)$$

Within the IPW matrix, ${\overline{\pi }}_{ij}^R\left({\beta }_R\right)$ is a model (parametrized by β_R) for ${\pi }_{ij}^R$ and ${\overline{\eta }}_{ij{j}^{\prime }}\left({\beta }_R,{\alpha }_R\right)$ is a model (parametrized by β_R, α_R) for ${\eta }_{ij{j}^{\prime }}^R$; we will henceforth refer to these as the propensity score models (PSM). Since ${\eta }_{ij{j}^{\prime }}^R$ is a function of ${\pi }_{ij}^R$, ${\pi }_{i{j}^{\prime }}^R$, ${\rho }_{ij{j}^{\prime }}^R$, it suffices to fit a model for ${\rho }_{ij{j}^{\prime }}^R$. Note that (β_R, α_R) are nuisance parameters: they are not parameters of interest, but are needed in estimating our target parameters $\left({\beta }_Y^{*},{\alpha }_Y^{*}\right)$. To this end, we propose the inverse probability weighting second-order generalized estimating equations (IPW-GEE2) as

$$\begin{gathered} 0=\sum _{i=1}^I{D}_i^{\top }{V}_i^{-1}{W}_i^R{E}_i \\ 0=\sum _{i=1}^I{S}_i^R\left(A_i,Z_i,X_i,{\beta }_R,{\alpha }_R\right) \end{gathered}$$ (7)

The second line in Eq 7 is used to estimate (β_R, α_R), while the first line is used to estimate $\left({\beta }_Y^{*},{\alpha }_Y^{*}\right)$.

The IPW2 portion in $W_i^R$ is derived by considering that the (j, j′)th element of $\mathcal{E}\left(Y_i\right)$ is missing when either Y_ij or Y_ij′ is missing, which is exactly represented by the product of their missingness indicators R_ijR_ij′. We note that the propensity score model for R_ijR_ij′ must properly account for the correlation among missingness indicators. To the best of our knowledge, these estimating equations are the first instance in which a model is required for the joint missingness indicator R_ijR_ij′ in the context of clustered data. Not properly accounting for the correlation among missingness indicators will in general lead to biased estimates for the association parameters.

4.2. AUG-GEE2

In the absence of missing data, Stephens et al. (2012) proposed the augmented (AUG) estimator to improve efficiency relative to the standard GEE1 by incorporating baseline covariates. The AUG-GEE is constructed by subtracting from GEE its orthogonal projection onto the linear space spanned by score functions corresponding to all smooth parametric models for the treatment assignment mechanism given covariates. Applying this projection to GEE2 in Eq 3, the AUG-GEE2 is given by

$$\begin{gathered} 0=\sum _{i=1}^I\left[D_i^{\top }{V}_i^{-1}{E}_{i^{\prime }}+{\zeta }_i\right] \\ 0=\sum _{i=1}^I{S}_i^Y\left(Z_i^{*},X_i,{\beta }_Y,{\alpha }_Y\right) \end{gathered}$$ (8)

where

$$\begin{gathered} E_i^{\prime }=\left(\begin{array}{c}{Y}_i-{\overline{\pi }}_i\left({\beta }_Y\right)\\ \mathcal{E}\left(Y_i\right)-{\overline{\rho }}_i^{†}\left({\alpha }_Y\right)\end{array}\right),E_i^{″}=\left(\begin{array}{l}{\overline{\pi }}_i\left({\beta }_Y\right)-{\pi }_i^{*}\left({\beta }_Y^{*}\right)\hfill \\ {\overline{\rho }}_i^{†}\left({\alpha }_Y\right)-{\rho }_i^{*}\left({\alpha }_Y^{*}\right)\hfill \end{array}\right), \\ {\zeta }_i=\sum _{a=0}^1{p}_A^a{\left(1-p_A\right)}^{1-a}{D}_i^{\top }(A=a)V_i^{-1}(A=a)E_i″(A=a) \end{gathered}$$

where D_i(A = a), $V_i^{-1}(A=a)$, E′′_i(A = a) are values of D_i, $V_i^{-1}$, E′′_i, respectively, evaluated at A = a; ${\overline{\pi }}_{ij}$ is a model for π_ij; and the components of ${\overline{\mathit{\rho }}}_i^{†}$ are

$${\overline{\rho }}_{ij{j}^{\prime }}^{†}=\frac{\left({\overline{\pi }}_{ij}-{\overline{\pi }}_i^{*}\right)\left({\overline{\pi }}_{i{j}^{\prime }}-{\overline{\pi }}_i^{*}\right)+{\overline{\rho }}_{ij{j}^{\prime }}\sqrt{{\overline{\mathcal{V}}}_{ij{j}^{\prime }}}}{{\overline{\pi }}_i^{*}\left(1-{\overline{\pi }}_i^{*}\right)}$$

akin to Eq 1, with models replacing each population quantity. The last set of equations in Eq 8 containing $S_i^Y$ yields ${\widehat{\pi }}_{ij}$ (converging to ${\overline{\pi }}_{ij}$) and ${\widehat{\rho }}_{ij{j}^{\prime }}$ (converging to ${\overline{\rho }}_{ij{j}^{\prime }}$), collectively known as the outcome models (OM). In the absence of missing data, AUG-GEE2 estimators achieve semiparametric efficiency bound when the OM is correctly specified and remain consistent even when the OM is not correctly specified (Tsiatis, 2007). However, in the presence of rMAR, AUG-GEE2 based on complete-case only does not ensure consistent estimation, even when the OMs are correctly specified (more details are included in Supplemental Materials 4). We note that this AUG-GEE2 based on complete-case only is different from a special case of the DR-GEE2 (as described below in Section 4.3) by setting the weights to 1 for observed outcomes and to 0 for missing outcomes. The latter would enjoy the doubly-robust property and produce consistent estimates when outcome models are correctly specified.

4.3. DR-GEE2

Instead of subtracting the projection using the estimating equations given in Eq 3, we apply this projection on IPW-GEE2 in Eq 7 to also account for the missing data process. The resulting form is thereby called the doubly-robust second-order generalized estimating equations (DR-GEE2):

$$\begin{gathered} 0=\sum _{i=1}^I\left[D_i^{\top }{V}_i^{-1}{W}_i^R{E}_{i^{\prime }}+{\zeta }_i\right] \\ \stackrel{\text{def}}{=}\sum _{i=1}^I{\Phi }_i^Y\left(Z_i^{*},X_i,R_i,{\beta }_Y^{*},{\alpha }_Y^{*},{\beta }_R,{\alpha }_R,{\beta }_Y,{\alpha }_Y\right) \\ 0=\sum _{i=1}^I{S}_i^R\left(Z_i^{*},X_i,{\beta }_R,{\alpha }_R\right),0=\sum _{i=1}^I{S}_i^Y\left(Z_i^{*},X_i,{\beta }_Y,{\alpha }_Y\right) \end{gathered}$$ (9)

If the OMs are correctly specified, then under the rMAR assumption, (β_Y, α_Y) can be consistently estimated based on the complete-case data. DR-GEE2 is doubly robust in the sense that it is consistent and asymptotically normal for $\left({\beta }_Y^{*},{\alpha }_Y^{*}\right)$ under correct specification of either the OM [i.e. ${\overline{\pi }}_{ij}={\pi }_{ij}$ and ${\overline{\rho }}_{ij{j}^{\prime }}={\rho }_{ij{j}^{\prime }}$] or PS [i.e. ${\overline{\pi }}_{ij}^R={\pi }_{ij}^R$ and ${\overline{\rho }}_{ij{j}^{\prime }}^R={\rho }_{ij{j}^{\prime }}^R$] (see proof in Supplemental Materials 4).

As a special case of DR-GEE2, consider the estimator obtained by setting the weights to 1 for observed outcomes and to 0 for missing outcomes. This estimator is consistent when the OM is correctly specified due to its doubly-robust property, but may lead to biased estimation when the OM is not correctly specified. As mentioned before, this estimator is different from the AUG-GEE2 described in Section 4.2.

4.4. Inference for IPW-, AUG-, and DR-GEE2

Let κ be a concatenation of all required parameters for any of the previously described estimation schemes in Sections 4.1 – 4.3. For example, $\kappa =\left({\beta }_Y^{*},{\alpha }_Y^{*},{\beta }_R,{\alpha }_R,{\beta }_Y,{\alpha }_Y\right)$ for DR-GEE2 in Eq 9. Also, let Ψ(·) be a single, stacked summand from one of these estimating equations; for example, Ψ = (Φ^Y, S^R, S^Y)^⊺ for DR-GEE2. A direct application of the theory of M-estimators (Van der Vaart, 2000) yields that $\sqrt{I}\left(\widehat{\mathit{\kappa }}-{\kappa }_0\right)\stackrel{\mathcal{D}}{\to }N(0,\Sigma )$, where Σ = Γ⁻¹Δ(Γ⁻¹)^⊺ is the sandwich estimator with “meat” $\Delta =\mathbb{E}\left[\Psi \left({\kappa }_0\right)\Psi {\left({\kappa }_0\right)}^{\top }\right]$ and “breads” $\Gamma =\mathbb{E}\left[\partial \Psi \left({\kappa }_0\right)/\partial {\kappa }^{\top }\right]$ evaluated at the true parameter values κ₀, from which we can extract components corresponding to $\left({\beta }_Y^{*},{\alpha }_Y^{*}\right)$, the parameters of interest. An estimator Σ can be obtained by replacing Δ with $\widehat{\Delta }=\frac{1}{I}\sum _{i=1}^I{\Psi }_i(\widehat{\mathit{\kappa }}){\Psi }_i{(\widehat{\mathit{\kappa }})}^{\top }$ and Γ with $\widehat{\Gamma }=\frac{1}{I}\sum _{i=1}^I\partial {\Psi }_i(\widehat{\mathit{\kappa }})/\partial \kappa$.

4.5. Embedding IPW-, AUG-, and DR-GEE2 with Stochastic GEE2

Fitting the PSM and OM requires just the standard GEE2, so the stochastic analog is the same as defined in Section 3.2. We do, however, need to adjust the TM for IPW-, AUG-, and DR-GEE2.

Structurally speaking, the inclusion of subsampling matrix W^S in stochastic GEE2 is similar to the IPW matrix W^R in IPW-GEE2. Indeed, in fitting IPW-GEE2 with a stochastic variant, we simply adjust gradient and Hessian iterations in Eq 6 with W^S ↦ W^RW^S. There are two possible candidates for the new W^S. We could use the exact W^S scheme in the original stochastic GEE2 defined in Section 3.2. But, this is likely to sample missing outcomes, and if there is significant missingness, the iterations would fail due to singular Hessians. A more stable procedure would be to sample $s_i~\text{SRSWOR}\left(U_i^{\text{obs}},{\upsilon }_i\right)$, where $U^{\text{obs}}=\left\{U_1^{\text{obs}},\cdots ,U_I^{\text{obs}}\right\}$ and each $U_i^{\text{obs}}$ correspond to the indices of the non-missing outcomes in cluster i. Let $m_i=\left|U_i^{\text{obs}}\right|$ be the number of non-missing observations per cluster. Then, iterations are performed with $W_{\beta i(\omega )}^{S\text{obs}}=\frac{m_i}{{\upsilon }_i}\left[s_i\right]$ and $W_{\alpha i(\omega )}^{S\text{obs}}=\frac{m_i\left(m_i-1\right)}{{\upsilon }_i\left({\upsilon }_i-1\right)}\left[{\left(s_i\right)}_2\right]$, a weighted indicator matrix for a subsample of the non-missing outcomes. Details are presented in Algorithm 3 of Supplemental Materials 2.

For TM estimating equation portion of AUG-GEE2 in Eq 8, we have components $D_i^{\top }{V}_i^{-1}{\mathbf{E}}_i{}^{\prime }$ and ζ_i. Since AUG-GEE2 deals with the situation without missing data, the subsampling here is straightforward; we embed the same full data subsampling matrix W^S within both $D_i^{\top }{V}_i^{-1}{E}_i{}^{\prime }$ and ζ_i and perform the stochastic iterations. However, forming stochastic DR-GEE2 is not so clear-cut. In Eq 9, the TM estimating equations consist of $D_i^{\top }{V}_i{W}_i^R{E}_i{}^{\prime }$ and ζ_i. For the $D_i^{\top }{V}_i{W}_i^R{E}_i{}^{\prime }$ component, we have missing outcomes, and therefore might seem prudent to use W^Sobs for the reasons above. But, an analogous version for ζ_i will not yield unbiased estimators $\left({\beta }_Y^{*},{\alpha }_Y^{*}\right)$, since W^Sobs contain conditional weights given R (i.e. being observed), yet there are no missing elements in ζ_i. Therefore, we propose simultaneous, independent subsampling schemes for $D_i^{\top }{V}_i{W}_i^R{E}_i{}^{\prime }$ and ζ_i, with the former using observed data subsampling weights W^Sobs and the latter using full data subsampling weights W^S. Details are presented in Algorithm 4 in Supplemental Materials 2.

The stochastic subsampling procedure is flexible and can be applied to different models involved in IPW-, AUG-, or DR-GEE2. For example, if one encounters computational problems when fitting OM or PSM, but not TM, the stochastic variants need only be applied to the estimating equations in line 2 of Eq 9, but not line 1.

5. Simulation

We performed two sets of experiments. The first set explored the statistical properties of IPW-, AUG-, and DR-GEE2 under combinations of correctly specified / misspecified PSMs and correctly specified / misspecified OMs, all of which include the ICC estimates embedded in the working covariance structure in the GEE1 portion, and assuming $\text{Cov}\left(Y_i,\mathcal{E}\left(Y_i\right)\right)=0$ and $\text{Var}\left(\mathcal{E}\left(Y_i\right)\right)=I$. We included analogous estimates from a parametric mixed effects model, GEE1 with independence working covariance structure, the conditional-GEE method of Lipsitz and Fitzmaurice (1996), the Gaussian-GEE method of Lipsitz et al. (2000), and the pseudo-likelihood method of Parzen (2009) for comparison. In the second set of simulations, we compared the algorithmic properties (convergence & run-time) of stochastic DR-GEE2 and standard DR-GEE2 under various cluster size / number of cluster combinations. For stochastic DR-GEE2, the estimating equations for the PSM, OM, and TM were all solved stochastically.

The following two data generation processes for binary data Y_ij (or R_ij) were used:

$$\text{Parzen}\prime \text{s}\text{method}\{\begin{array}{ll}\mathrm{logit}\left({\pi }_{\text{ij}}\right)\hfill & =\left({\beta }_{0\text{Y}}+{\beta }_{0\text{AY}}{\mathrm{A}}_{\text{i}}\right)+{\left({\beta }_{\text{ZY}}+{\beta }_{\text{ZAY}}{\mathrm{A}}_{\text{i}}\right)}^{\top }{Z}_{\text{i}}+{\left({\beta }_{\text{XY}}+{\beta }_{\text{XAY}}{A}_{\text{i}}\right)}^{\text{T}}{X}_{\text{ij}}\hfill \\ \mathrm{atanh}\left({\rho }_{\text{i}}\right)\hfill & =\left({\alpha }_{0\text{Y}}+{\alpha }_{0\text{AY}}{\mathrm{A}}_{\text{i}}\right)+{\left({\alpha }_{\text{ZY}}+{\alpha }_{\text{ZAY}}{\mathrm{A}}_{\text{i}}\right)}^{\top }{Z}_{\text{i}}\hfill \\ \left({\mathfrak{L}}_{\text{i}},{\mathfrak{U}}_{\text{i}}\right)\hfill & =\left(-\sqrt{\frac{\text{min}\left({\pi }_{\text{i}}\right)}{1-\text{min}\left({\pi }_{\text{i}}\right)}},\sqrt{\frac{1-\text{max}\left({\pi }_{\text{i}}\right)}{\text{max}\left({\pi }_{\text{i}}\right)}}\right)\hfill \\ \left({\delta }_{\text{i}},{ϵ}_{\text{i}}\right)\hfill & =\left(\frac{{\mathfrak{U}}_{\text{i}}\left(-{\mathfrak{U}}_{\text{i}}{\mathfrak{L}}_{\text{i}}-{\rho }_{\text{i}}\right)}{\left({\mathfrak{U}}_{\text{i}}-{\mathfrak{L}}_{\text{i}}\right){\rho }_{\text{i}}},\frac{-{\mathfrak{L}}_{\text{i}}\left(-{\mathfrak{U}}_{\text{i}}{\mathfrak{L}}_{\text{i}}-{\rho }_{\text{i}}\right)}{\left({\mathfrak{U}}_{\text{i}}-{\mathfrak{L}}_{\text{i}}\right){\rho }_{\text{i}}}\right)\hfill \\ {\xi }_{\text{i}}|{\mathrm{A}}_{\text{i}},Z_{\text{i}}\hfill & ~\left({\mathfrak{U}}_{\text{i}}-{\mathfrak{L}}_{\text{i}}\right)\text{Beta}\left({\delta }_{\text{i}},{ϵ}_{\text{i}}\right)+{\mathfrak{L}}_{\text{i}}\hfill \\ {\text{Y}}_{\text{ij}}|{\mathrm{A}}_{\text{i}},Z_{\text{i}},X_{\text{i}},{\xi }_{\text{i}}\hfill & ~\text{Bernoulli}\left({\pi }_{\text{ij}}+{\xi }_{\text{i}}\sqrt{{\pi }_{\text{ij}}\left(1-{\pi }_{\text{ij}}\right)}\right)\hfill \end{array}$$

$$\text{Random intercept}\{\begin{array}{ll}\text{logit}\left({\pi }_{\text{ij}}\right)\hfill & =\left({\beta }_{0\text{Y}}+{\beta }_{0\text{AY}}{\mathrm{A}}_{\text{i}}\right)+{\left({\beta }_{\text{ZY}}+{\beta }_{\text{ZAY}}{\mathrm{A}}_{\text{i}}\right)}^{\top }{Z}_{\text{i}}+{\left({\beta }_{\text{XY}}+{\beta }_{\text{XAY}}{\mathrm{A}}_{\text{i}}\right)}^{\top }{X}_{\text{ij}}\hfill \\ {\xi }_{\text{i}}|{\mathrm{A}}_{\text{i}}\hfill & ~\text{N}\left(0,{\left(\frac{1}{3}+\frac{1}{2}{\mathrm{A}}_{\text{i}}\right)}^2\right)\hfill \\ \text{logit}\left({\text{p}}_{\text{ij}}\right)\hfill & ={\xi }_{\text{i}}+\text{logit}\left({\pi }_{\text{ij}}\right)\hfill \\ Y_{\text{ij}}|{\mathrm{A}}_{\text{i}},Z_{\text{i}},X_{\text{i}},{\xi }_{\text{i}}\hfill & ~\text{Bernoulli}\left({\text{p}}_{\text{ij}}\right)\hfill \end{array}$$

Parzen’s method (Parzen, 2009) offers a random-effects form that attains nominal levels of π_ij and ρ_i (i.e. $\mathbb{P}\left(Y_{ij}|A_i,Z_i,X_i\right)={\pi }_{ij}$ and Corr(Y_ij, Y_ij′ | A_i, Z_i) = ρ_i) and specifically generates equicorrelated data. To ensure $0\le {\pi }_{ij}+{\xi }_i\sqrt{{\pi }_{ij}\left(1-{\pi }_{ij}\right)}\le 1$, one must ensure that $-{\mathfrak{U}}_i{\mathfrak{L}}_i-{\rho }_i\ge 0$ for all i. The random-intercept method is the traditional approach to induce correlation among observations in a cluster. With a normal random intercept, the marginal probability of success

$$\mathbb{P}\left(Y_{ij}=1|A_i,Z_i,X_i\right)=\int \mathbb{P}\left(Y_{ij}=1|{\xi }_i,A_i,Z_i,X_i\right)dP\left({\xi }_i\right)=\int \frac{e^{{\xi }_i+L\left(\beta ;A_i,Z_i,X_i\right)}}{1+e^{{\xi }_i+L\left(\beta ;A_i,Z_i,X_i\right)}}dP\left({\xi }_i\right)$$ (10)

where L(β; A_i, Z_i, X_i) is the linear function, is not of the logistic form and does not have a closed-form. Furthermore, the ICC is induced linearly on the logit scale, yet the manifested ICC after performing the expit function and appropriate marginalization varies within-cluster. Hence, it is ill-suited for simulation of equicorrelated binary data. We used Parzen’s method to generate the ideal case of equicorrelated outcomes, while we used the random-intercept method to generate correlated outcomes with a non-exchangeable correlation structure.

5.1. Statistical Properties of IPW-, AUG-, & DR-GEE2 schemes

Let $\mathcal{U}(a,b)$ denote the continuous uniform distribution on (a, b), and let $\mathcal{U}\{a,b\}$ denote the discrete uniform distribution on {a, a + 1,⋯, b − 1, b}. To evaluate the asymptotic properties of GEE2, we set the number of clusters to I = 2000 with cluster sizes $n_i~\mathcal{U}\left\{80,140\right\}$ so that we have average cluster size $\mathbb{E}\left[n_i\right]=110$. We choose settings with a large number of clusters to evaluate the asymptotic properties and to avoid computational issues that will be explored in Section 5.2. We generated A_i ~ Bernoulli(1/ 2) and chose $X_{ij}\in {ℝ}^3$ and $Z_i\in ℝ$. Details regarding generation of X_ij, Z_i and choice of coefficients for Y_ij are presented in Table 2. We also generated R_ij with these same covariates and coefficients for simplicity.

Table 2.

Parameter values in the data generation process

Covariate	Intercept		Xij		Zi
Distribution	–	$\mathcal{U}(20,60)$	$\mathcal{U}(1,10)$	$\mathcal{U}(4,25)$	$\mathcal{U}\left\{80,140\right\}$
Main-effects β·Y	0.11	−0.007	−0.020	−0.040	0.009
Interaction β·AY	0.67	0.012	0.030	0.060	−0.018
Main-effects α·Y	−0.32	–	–	–	0.004
Interaction α·Y	0.96	–	–	–	−0.008

The values in Table 2 were carefully chosen to guarantee $-{\mathfrak{U}}_i{\mathfrak{L}}_i-{\rho }_i\ge 0$ in Parzen’s method. The resulting values for $\mathbb{P}\left(Y_{ij}=1|A_i,Z_i,X_i\right)$ and Corr(Y_ij, Y_ij′ | A_i, Z_i, X_i), after marginalizing out ξ_i, were in the range [0.324, 0.733] and [0.004, 0.306], respectively. For the random-intercept method, the values of $\mathbb{P}\left(Y_{ij}=1|A_i,Z_i,X_i\right)$ and Corr(Y_ij, Y_ij′ | A_i, Z_i, X_i) were in the range [0.333, 0.738] and [0.022, 0.134], respectively. Since R_ij’s were generated from models with the same coefficients, the probabilities of being observed from these two methods are also in the range [0.324, 0.733] and [0.333, 0.738], respectively. The true treatment coefficients $\left({\beta }_Y^{*},{\alpha }_Y^{*}\right)$ in the canonical TM were calculated by numerically integrating out all other covariates except for A_i in π_ij and ${\rho }_{ij{j}^{\prime }}^{†}$:

$$\begin{gathered} \text{expit}\left({\beta }_{0Y}^{*}+{\beta }_{AY}^{*}{A}_i\right)=\underset{{ℝ}^4}{\int }{\pi }_{ij}dP\left(x_{ij}\right)dP\left(z_i\right) \\ \text{tanh}\left({\alpha }_{0Y}^{*}+{\alpha }_{AY}^{*}{A}_i\right)=\underset{{ℝ}^7}{\int }{\rho }_{ij{j}^{\prime }}^{†}dP\left(x_{ij}\right)dP\left(x_{i{j}^{\prime }}\right)dP\left(z_i\right) \end{gathered}$$ (11)

Using Parzen’s method, we obtained the values $\left({\beta }_Y^{*},{\alpha }_Y^{*}\right)=(0.1413,0.1808,0.1238,0.0755)$, and using the random-intercept method, we obtained $\left({\beta }_Y^{*},{\alpha }_Y^{*}\right)=(0.1378,0.1429,0.0307,0.1032)$.

Figure 1 displays the average of parameter estimates and their respective 95% Monte Carlo confidence intervals $\overline{\widehat{\mathit{\theta }}}\pm 1.96\cdot \widehat{\text{SE}}(\overline{\widehat{\mathit{\theta }}})$ over $\mathcal{R}=1000$ simulation experiments. To assess the accuracy of our derived sandwich standard errors, we present two types of Monte Carlo confidence intervals based on $\widehat{\text{SE}}(\overline{\widehat{\mathit{\theta }}})$ calculated using (i) the average of the calculated sandwich standard errors divided by $\sqrt{\mathcal{R}}$ and (ii) the empirical standard error over the $\mathcal{R}$ simulations (i.e. empirical standard deviation divided by $\sqrt{\mathcal{R}}$). Conditional-GEE (Lipsitz and Fitzmaurice, 1996), Gaussian-GEE (Lipsitz et al., 2000), and the pseudo-likelihood methods (Parzen et al., 2007) were fitted directly to the complete-case data with the canonical TM (Eq 2), while the mixed effects model was fitted to the complete-case data using

$$\text{logit}\left\{\mathbb{P}\left(Y_{ij}=1|A_i,{\xi }_i\right)\right\}={\tilde{\beta }}_0+{\tilde{\beta }}_A{A}_i+{\xi }_i\text{\hspace{1em}with\hspace{1em}}{\xi }_i|A_i~N\left(0,{\tilde{\sigma }}_{A_i}^2\right).$$ (12)

Fig. 1.

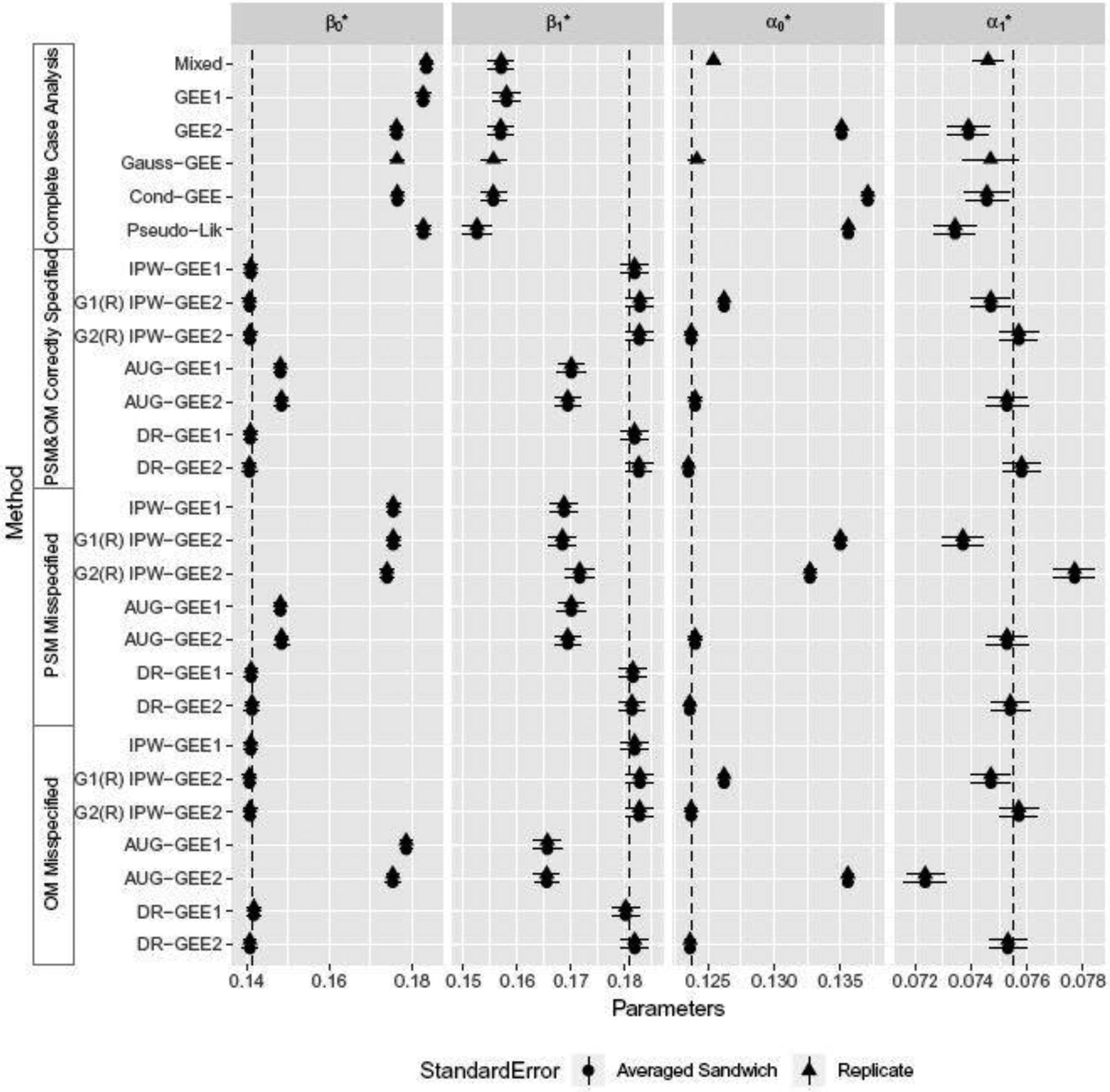
Forest plots for intervals $\overline{\widehat{\mathit{\theta }}}\pm 1.96\cdot \widehat{\text{SE}}(\overline{\widehat{\mathit{\theta }}})$, where $\overline{\theta }$ is the sample average of the $\mathcal{R}=1000$ replicate simulations. Both R_ij’s and Y_ij’s are simulated using Parzen’s method. Dotted vertical lines represent true parameter values.

Estimates of $\left({\beta }_{0Y}^{*},{\beta }_{AY}^{*},{\alpha }_{0Y}^{*},{\alpha }_{AY}^{*}\right)$ were obtained from $\left({\tilde{\beta }}_0,{\tilde{\beta }}_A,{\tilde{\sigma }}_0^2,{\tilde{\sigma }}_1^2\right)$ through marginalizing out the random effects (see Eqs 10). We display Monte Carlo intervals based on the average of estimated analytical standard errors for all except the Gaussian-GEE and mixed effects scenarios. Analytical standard error estimators for ${\widehat{\alpha }}_{0Y}^{*}$ and ${\widehat{\alpha }}_{AY}^{*}$ from Gaussian-GEE were not provided in Lipsitz et al. (2000) nor are they immediately derivable. In mixed effects model settings, estimation of standard errors of ${\widehat{\alpha }}_{0Y}^{*}$, ${\widehat{\alpha }}_{AY}^{*}$ requires standard error estimates of ${\widehat{\tilde{\sigma }}}_0^2$, ${\widehat{\tilde{\sigma }}}_1^2$, for which methods are less developed (Bates, 2010; McCulloch and Searle, 2001; Wu et al., 2012). Mixed effects models naturally handle MAR if the true generation process follows the form in Eq 12. However, both Parzen’s and the random-intercept data generation processes do not: data generated using Parzen’s method do not follow a traditional mixed effects model, and data generated using the random-intercept method include additional covariates.

For the IPW-GEE2 estimates, we used ${\mathcal{G}}_1(R)$ IPW and ${\mathcal{G}}_2(R)$ IPW to distinguish IPW-GEE2 under the settings where the PSMs do not and do account for the correlation among the missingness indicators, respectively, as discussed in Section 4.1. For GEE1 methods, there is no model for correlated missingness, and therefore intervals were omitted. The correctly-specified OM and PSM were

$$\begin{gathered} \text{logit}\left({\pi }_{ij}\right)=\left({\beta }_{0Y}+{\beta }_{0AY}{A}_i\right)+{\left({\beta }_{ZY}+{\beta }_{ZAY}{A}_i\right)}^{\top }{Z}_i+{\left({\beta }_{XY}+{\beta }_{XAY}{A}_i\right)}^{\top }{X}_{ij} \\ \text{atanh}\left({\rho }_{ij{j}^{\prime }}\right)=\left({\alpha }_{0Y}+{\alpha }_{0AY}{A}_i\right)+{\left({\alpha }_{ZY}+{\alpha }_{ZAY}{A}_i\right)}^{\top }{Z}_i \end{gathered}$$ (13)

i.e. the exact model used to generate R_ij’s, Y_ij’s from Parzen’s method. The misspecified OM and PSM were

$$\begin{gathered} \text{logit}\left({\pi }_{ij}\right)={\beta }_{0Y}+{\beta }_{AY}{A}_i+{\beta }_{ZY}^{\top }{Z}_i+{\beta }_{XY}^{\top }{X}_{ij} \\ \text{atanh}\left({\rho }_{ij{j}^{\prime }}\right)={\alpha }_{0Y}+{\alpha }_{AY}{A}_i+{\alpha }_{ZY}^{\top }{Z}_i \end{gathered}$$ (14)

i.e. the model with interaction terms of A_i with Z_i, X_i omitted.

As seen from Figure 1, complete-case analysis (from GEE1, GEE2, conditional-GEE, pseudolikelihood, and mixed effects) led to severe bias in estimating all parameters, with the exception of Gaussian-GEE, where the intervals for association parameters captured the truth. We note that these methods are expected to account for missingness when confounding covariates are included in the model, but the focus here is on marginal intervention effects and hence inclusion of additional covariates would in general target different treatment effect parameters for models with non-identity link functions (marginal vs. conditional). When PSM & OM were correctly specified, ${\mathcal{G}}_1(R)$ IPW-, ${\mathcal{G}}_2(R)$ IPW-, and DR-GEE2 all provided consistent estimates for the mean parameters ${\beta }_{0Y}^{*}$ and ${\beta }_{AY}^{*}$, but ${\mathcal{G}}_1(R)$ IPW-GEE2 failed to estimate association parameters ${\alpha }_{0Y}^{*}$ and ${\alpha }_{AY}^{*}$ consistently. When the PSM was misspecified but the OM was correctly specified, only DR-GEE2 and DR-GEE1 produced consistent estimates of all parameters. AUG-GEE1 and AUG-GEE2 based on complete data only led to biased estimates. On the other hand, when the OM was misspecified, ${\mathcal{G}}_2(R)$ IPW- and DR-GEE2 produced consistent estimates of all parameters, and the bias from AUG-GEE1 and AUG-GEE2 for the mean parameters appeared to be more pronounced. In all scenarios, sandwich variance estimates were close to the true sampling variance. We also observed that the standard error estimates for ${\widehat{\beta }}_{0Y}^{*}$ and ${\widehat{\beta }}_{AY}^{*}$ obtained from DR-GEE1 with independence covariance structure were approximately equal to those obtained from DR-GEE2.

Figure 2 presents analogous results for settings where outcomes were generated using the random-intercept method and missingness indicators were generated using Parzen’s method. As before, the correctly specified and misspecified PSMs were Eqs 13 and 14, respectively. Since data generated under a random intercept logistic model do not follow a marginal logistic model, the OM was misspecified. Nevertheless, we reached similar conclusions regarding the performance of estimators as before. It is interesting to note that DR-GEE2 performed well even when both PSM and OM were misspecified. This may due to the fact that the misspecification of the OM reflected a deviation from the true model only through an omission of the random intercept; this deviation could be modest, especially if the variance of random effects was small.

Fig. 2.

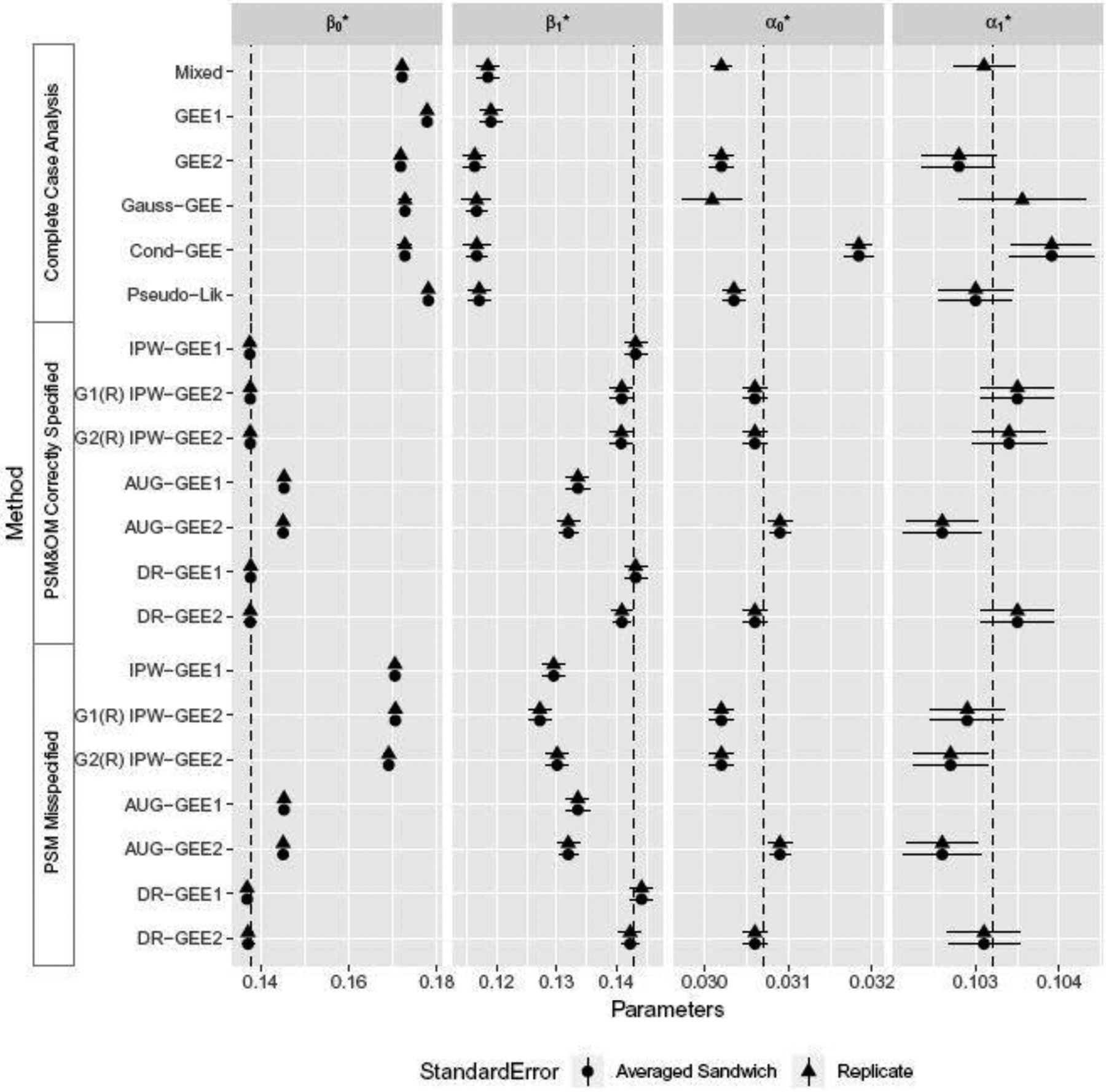
Forest plots for intervals $\overline{\widehat{\mathit{\theta }}}\pm 1.96\cdot \widehat{\text{SE}}(\overline{\widehat{\mathit{\theta }}})$, where $\overline{\theta }$ was the sample average of the $\mathcal{R}=1000$ simulation experiments. R_ij was simulated using the Parzen’s method and Y_ij was simulated using the random-intercept method.

5.2. Algorithmic Characteristic of Standard vs Stochastic DR-GEE2

Having established the consistency of the standard DR-GEE2, in our second set of experiments we compared stochastic and parallel stochastic DR-GEE2. Data were generated in the same way as before, where both outcomes and missingness indicators were generated using Parzen’s method. When fitting DR-GEE2, both PSM and OM were correctly specified. We varied the number of clusters I and cluster sizes n_i, and considered the following three scenarios: $\left(I,\mathbb{E}\left[n_i\right]\right)=(30,30),(300,30),(30,300)$. Figures 3 and 4 present the statistical and algorithmic results respectively. For $\mathbb{E}\left[n_i\right]=30$, we set the subsample sizes $\mathbb{E}\left[{\upsilon }_i\right]=9$ and for $\mathbb{E}\left[n_i\right]=300$, we set $\mathbb{E}\left[{\upsilon }_i\right]=45$; all stochastic scenarios used learning rates γ_(ω) = (ω + 1)⁻¹, where ω indexes the iteration step. For the comparison of running longer iteration chains versus averaging shorter chains, parallel stochastic DR-GEE2 averaged 20 chains, each with one-third of the number of iterations per chain used in stochastic DR-GEE2.

Fig. 3.

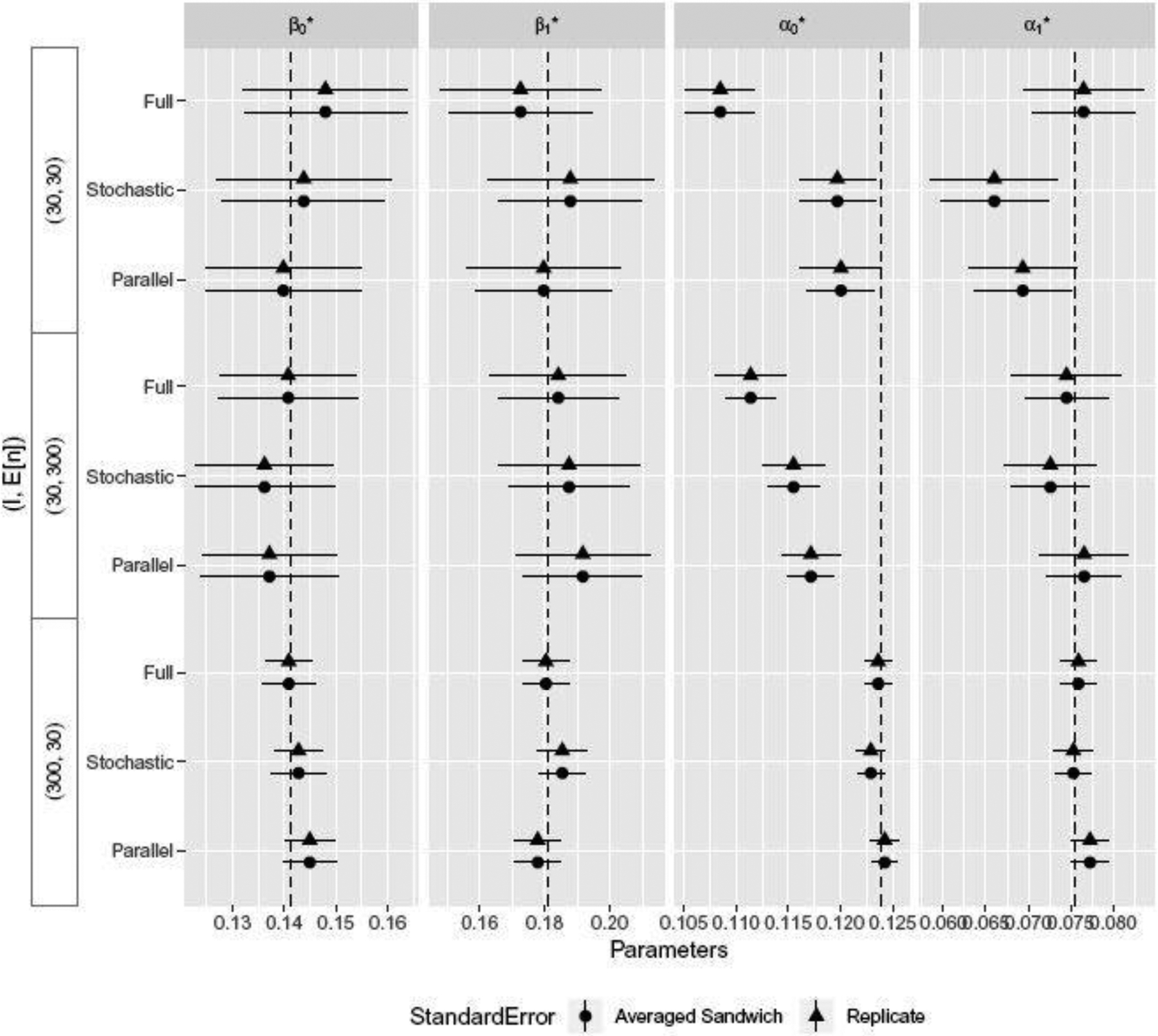
Forest plots for standard, stochastic, and parallel stochastic DR-GEE2 with intervals $\overline{\widehat{\mathit{\theta }}}\pm 1.96\cdot \widehat{\text{SE}}(\overline{\widehat{\mathit{\theta }}})$, where $\overline{\theta }$ is the sample average of θ across the $\mathcal{R}=1000$ replicate simulations.

Fig. 4.

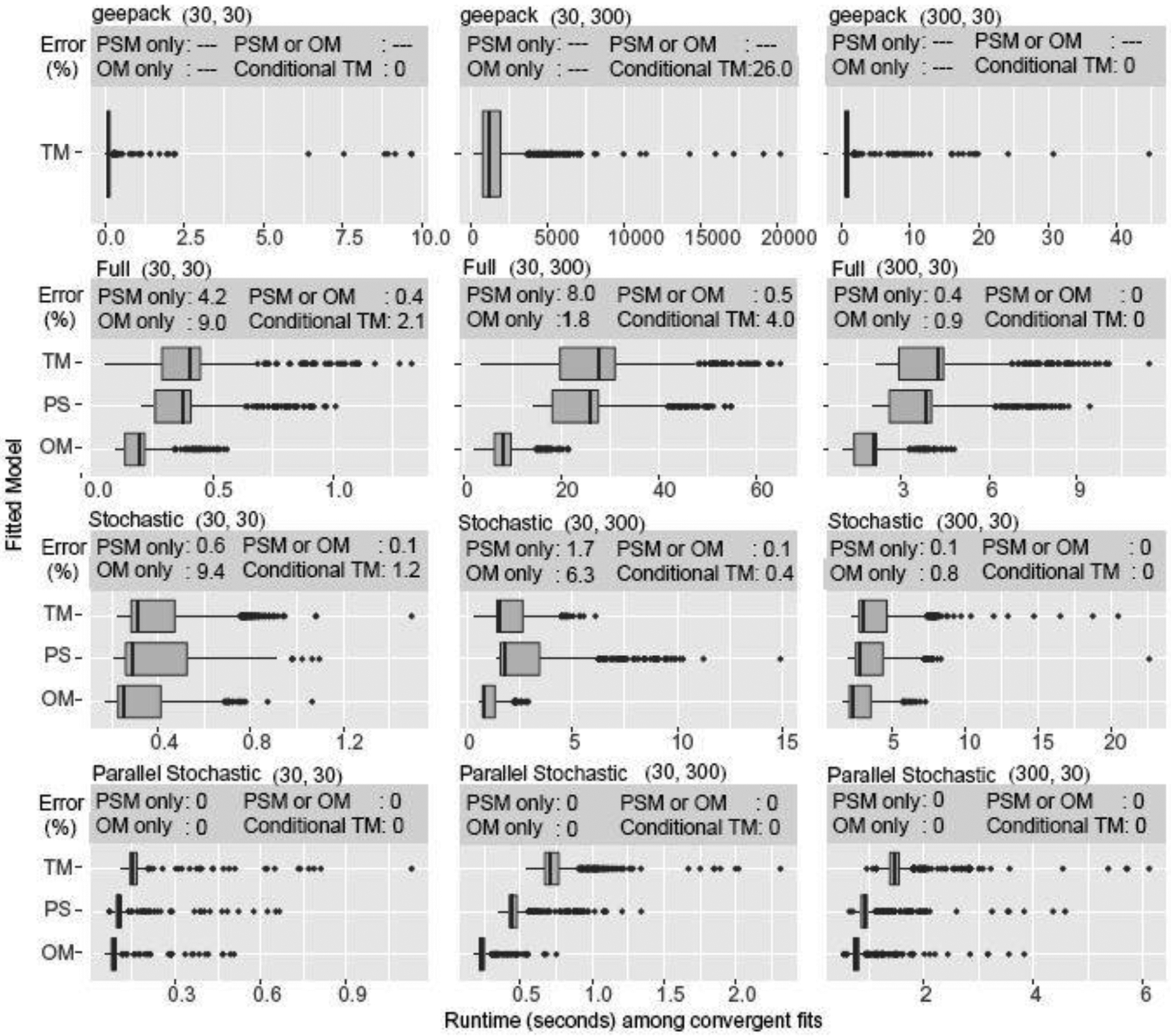
25^th-50^th-75^th percentile boxplots of runtimes for standard, stochastic, and parallel stochastic DR-GEE2. $\mathcal{R}=1000$ replicate simulations. Boxplots are computed on runs which converged. The conditional TM error is the error rate among simulations whence PSM and OM converged. Each replicate simulation was executed in R on a dual-core node on the Orchestra cluster supported by the Harvard Medical School Research Information Technology Group.

As seen in Figure 3, all algorithms yield consistent estimates for the mean parameters (${\beta }_0^{*}$ and ${\beta }_1^{*}$). Overall, the parameter and standard error estimates were similar across standard, stochastic, and parallel stochastic DR-GEE2. When the number of clusters I = 30, estimates for the association parameters (${\alpha }_0^{*}$ and ${\alpha }_1^{*}$) can be biased. Poor performance of GEEs when the number of clusters is small has been noted previously (Mancl and DeRouen, 2001; Morel et al., 2003). For estimating association parameters, the number of clusters needs to be sufficiently large.

Figure 4 presents the run times and error rates associated with standard, stochastic, and parallel stochastic algorithms when fitting DR-GEE2. There were substantial reductions in error rates and run times when stochastic algorithms were used. For the OM, PSM, and TM, stochastic DR-GEE2 provided up to 80% reduction in returned errors (i.e. divergence, large condition numbers of Hessians) and approximately 90% reduction in run times. Parallel stochastic DR-GEE2, as expected, cut computation times by nearly one-third compared to stochastic DR-GEE2 and eliminated all convergence errors. For the purpose of a direct comparison, we did not include the time it took the server to set up the parallel cores for computation. With large datasets, this set-up time would be negligible compared to the overall computing time of days or weeks. In the current settings, this set up time would offset the advantage of parallel stochastic algorithms in terms of run times; nonetheless, the advantage of reducing convergence error rates remains.

We also fitted a complete-case TM using the geese command from R’s geepack package. While geese performed well in the (30, 30) and (300, 30) cases, our stochastic algorithms were associated with faster run times and few errors in the (30,300) cases. Granted, the comparisons were not the most commensurate: geese performed all calculations in the C programming language and wrapped the results into R, while our implementation was entirely in R. Our implementation also included additional time for incorporating the IPW or AUG portions.

6. Application to Sanitation Data

Guiteras et al. (2015) investigated the efficacy of alternative policies to encourage the use of hygienic latrines in developing countries. Communities in rural Bangladesh were assigned to different marketing interventions. Here we focused on comparisons between a supply-side market intervention and a control group. The dataset (accessible at https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/GJDUTV) contains 4837 individuals across 100 clusters with ten individual-level covariates (report diarrhea indicator X₁, male indicator X₂, age X₃, education indicator X₄, Muslim indicator X₅, Bengali indicator X₆, agricultor indicator X₇, stove indicator X₈, water pipes indicator X₉, phone indicator X₁₀) and five cluster-level covariates (village population Z₁, # of doctors Z₂, % landless Z₃, % almost landless Z₄, % access electricity Z₅). Analyses were performed using data from 4768 subjects with complete covariate information.

The overall missingness of the outcome, whether or not hygienic laterines was used, was 3.4%. Results based on a mixed effects model suggested that the supply-side market intervention alone did not increase hygienic latrine ownership (+0.3 percentage points, p-value = 0.90) (Guiteras et al., 2015). We reanalyzed this dataset with GEE2 approaches assuming outcomes were rMAR; covariates for the PS and outcome models were chosen using a backwards stepwise procedure based on the AIC. The resulting models are

$$\begin{gathered} \text{logit}\left({\pi }_{ij}^R\right)={\beta }_{0R}+{\beta }_{AR}{A}_i+\sum _{k\in \{2,3,5,6,7,8,10\}}{\beta }_{XR}^{(k)}{X}_{ijk}+\sum _{k\in \left\{1,2,3,4\right\}}{\beta }_{ZR}^{(k)}{Z}_{ik}+A_i\sum _{k\in \{5,6,8\}}{\beta }_{AXR}^{(k)}{X}_k+A_i\sum _{k\in (2,3,4)}{\beta }_{AZR}^{(k)}{Z}_{ik} \\ \text{atanh}\left({\rho }_i^R\right)={\alpha }_{0R}+{\alpha }_{AR}{A}_i+\sum _{k\in (1,2,3,4\}}{\alpha }_{ZR}^{(k)}{Z}_{ik}+A_i\sum _{k\in \left\{2,3,4\right\}}{\alpha }_{AZR}^{(k)}{Z}_{ik} \end{gathered}$$

$$\begin{gathered} \text{logit}\left({\pi }_{ij}\right)={\beta }_{0Y}+{\beta }_{AY}{A}_i+\sum _{k\in \left\{1,2,3,4,5,8,9,10\right\}}{\beta }_{XY}^{(k)}{X}_{ijk}+\sum _{k\in \left\{1,2,3,4,5\right\}}{\beta }_{zy}^{(k)}{Z}_{ik}+A_i\sum _{k\in \left\{1,3,8\right\}}{\beta }_{AXY}^{(k)}{X}_k+A_i{\beta }_{AZY}^{(5)}{Z}_{i5} \\ \text{atanh}\left({\rho }_i\right)={\alpha }_{0Y}+{\alpha }_{AY}{A}_i+\sum _{k\in \left\{1,2,3,4,5\right\}}{\alpha }_{ZY}^{(k)}{Z}_{ik}+A_i{\alpha }_{AZY}^{(5)}{Z}_{i5} \end{gathered}$$

To better illustrate the use of our methods for settings where missingness is high, we conducted two analyses: one based on the original data, and another after inducing additional missingness. The missingness indicators were generated under Parzen’s method with the following coefficients:

β0R	= 0.7,	${\beta }_{XR}^{\top }$	= (0, 0.3, 0.003, 0, 0.3, 0.3, 0.3, 0.3, 0, 0.3),
${\beta }_{ZR}^{\top }$	= (−0.00048, −0.0014, −0.407, −0.555),	βAR	= −0.7,
${\beta }_{AXR}^{\top }$	= (0, 0, 0, 0, −0.6, −0.6, 0, −0.6, 0, 0),	${\beta }_{AZR}^{\top }$	= (0, 0.022, 0.904, 1.11),
α0R	= 0.35,	${\alpha }_{ZR}^{\top }$	= (0.0000645, 0.000190, 0.0543, 0.074),
αAR	= −0.10,	${\alpha }_{AZR}^{\top }$	= (0, −0.00291, −0.120, −0.148).

Covariates not selected in the stepwise procedure were assigned coefficients 0. The values of nonzero entries of β_R were chosen so that | β_R,pC_ijp | ≤ 0.7, where β_R,p is the pth element of β_R, and C_ijp is the pth element of (1, A_i, X_ij, Z_i). This bound ensures that the missingness probabilities do not wildly fluctuate to 0 or 1. Finally, the values of α_R were chosen to ensure a sizable correlation among the missingness indicators (~ 0.30) and to satisfy the constraints of Parzen’s method. Under this scheme, the overall missingness was 26%.

For both analyses based on the original data and the data with induced missingness, we had difficulty obtaining convergent fits for the OM and PSM, and therefore applied stochastic GEE2 for these models. The estimates of these nuisance parameters were then used in DR-GEE2 to estimate the TM parameters in Eq 2. We had no difficulty fitting the TM, and therefore performed the fitting deterministically. The corresponding GEE2 analyses are included in Figure 5. We also ran the TM stochastically and the results were similar.

Fig. 5.

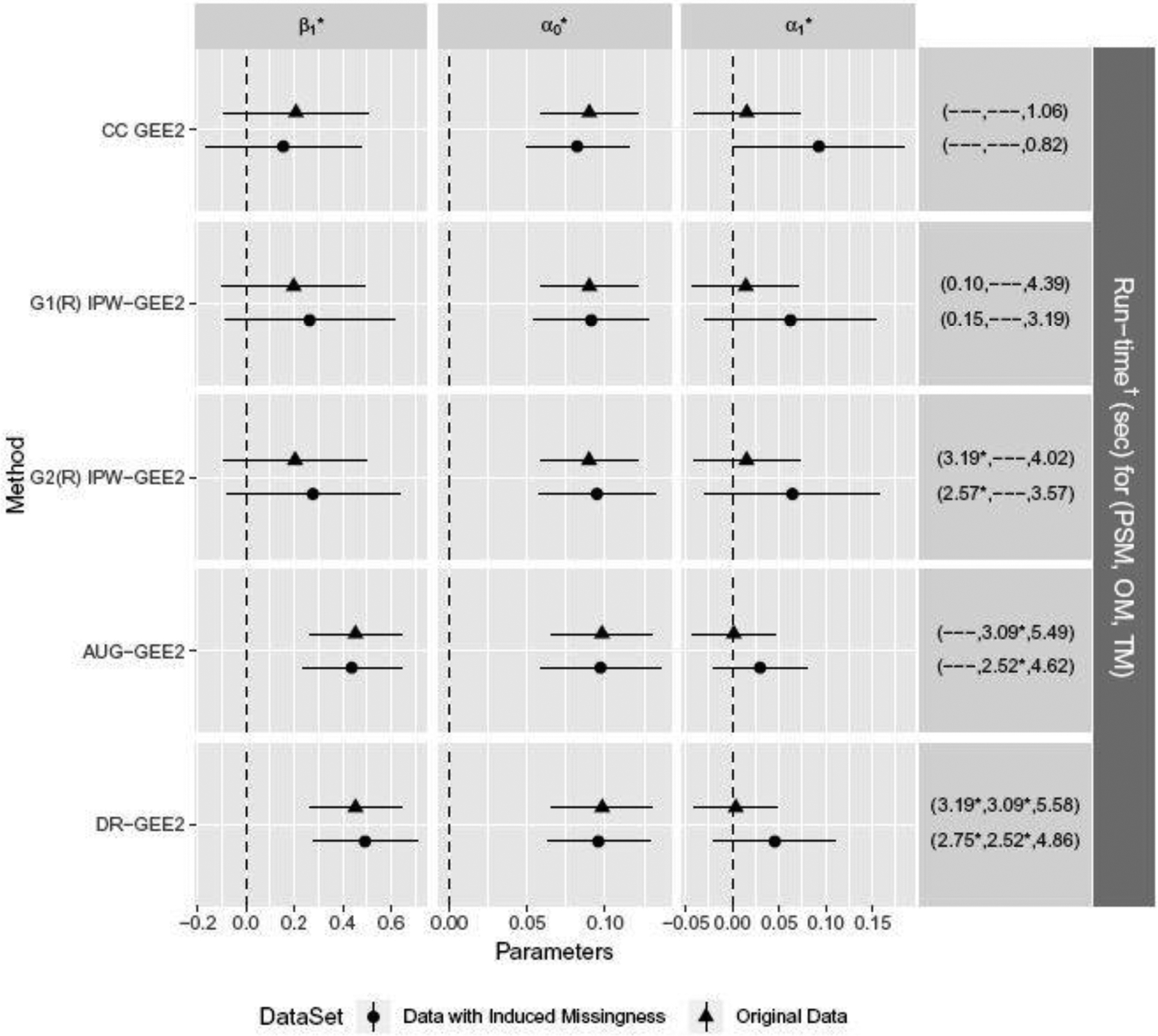
Effects of the supply side-market (A=1) vs. control (A=0) on the probability of hygienic latrine ownership in the sanitation data analysis (Guiteras et al., 2015) using the complete-case GEE2, IPW-GEE2 adjustment (non-adjusting and adjusting for correlation among missingness indicators), and DR-GEE2, assuming outcomes are rMAR.

* Fitted with 50 parallel stochastic GEE2, and averaging convergent estimates.

Reported are median times among convergent estimates.

^† Executed in R on a desktop with Intel(R) Core(TM) i5–4460 CPU @3.20GHz

Based on the original data, DR-GEE2 yielded a significant intervention effect (OR = 1.58, p-value < 0.01), while results from complete-case GEE2 and IPW-GEE2’s suggested no significant intervention effect (p-value > 0.15). This drastic change in the significance of the intervention effect is peculiar, especially given the low proportion of missingness. AUG-GEE2 yielded similar estimates as DR-GEE2 did, which suggests that the augmentation portion heavily influenced the resulting estimates. This implies that, while the sanitation data were obtained from a randomized study, there existed substantial residual imbalance in covariates that were associated with outcome. In such settings, inverse-probability of missingness weighting would not adjust this residual confounding. Methods commonly used for observational studies such as inverse-probability of receiving treatment weighting (Rosenbaum and Rubin, 1983) provide one way to adjust for this; alternatively, augmenting the estimating equations with the outcome model serves the same purpose. The combination of both yields doubly robust estimators for observational studies (Bang and Robins, 2005). For the association parameters, inferences were the same using all methods; the ICC within the control arm was statistically significantly different from 0 (p-value < 0.01 for $H_0:{\alpha }_0^{*}=0$ vs $H_1:{\alpha }_0^{*}\ne 0$), while the intervention-specific ICC was not (p-value > 0.60 for $H_0:{\alpha }_1^{*}=0$ vs $H_1:{\alpha }_1^{*}\ne 0$).

Using the induced-missingness dataset, inference for the intervention effect was similar to that for the original dataset: complete-case GEE2 suggested no significant intervention effect (p-value = 0.34). But there was a significant difference in intervention-specific ICCs (p-value = 0.046). Using the IPW-GEE2 methods, the magnitude of intervention effect estimates increased but remained non-significant (p-value > 0.1 for both), and the differences in ICCs between the two arms decreased and became non-significant (p-value > 0.15 for both). Compared to the IPW methods, both AUG-GEE2 and DR-GEE2 led to a further increased intervention effect (p-value < 0.01) and a further decreased difference in intervention-specific ICCs (p-value > 0.15).

7. Discussion

In this paper, we propose a stochastic algorithm to obtain the solutions to GEE2. This new algorithm substantially increases convergence rate and reduces run-times. It is in particular useful in settings whence either the number of clusters or the size of clusters is large. Accurate estimation of ICCs in general requires adequate number of clusters relative to the cluster size. When the cluster size is large relative to the number of clusters, the standard algorithm suffers from convergence issues. The stochastic algorithm alleviates this problem by performing the estimation on a subsample from each cluster for each iteration.

Another feature of stochastic GEE2 is the inclusion of the Hessian. Much of the literature derived from the Robbins-Monro framework does not incorporate the Hessian matrix into the iterations, instead relying on adaptive gradients and adaptive learning rates (Duchi et al., 2011; Nesterov, 1983; Zeiler, 2012). Traditionally, Hessians are omitted because they are computationally intractable (Bottou, 2012). But in the GEE2 framework, the Hessians are readily computable, and so are their stochastic variants. Each of these frameworks can be built upon each other to form hybrid methods, and indeed, comparisons of these different combinations would be interesting for future work.

We also proposed DR-GEE2 for estimating the marginal treatment effect and treatment-specific ICCs in cluster randomized trials in the presence of informative missing outcome data. We note that, in general, GEE2 is less robust than GEE1 due to the need to correctly specify the second moments. In some settings, for example, a binary outcome with a focus on estimating treatment-specific ICCs, the GEE2 portion represents a saturated model and is correctly specified.

Our estimators are most useful in the settings where estimation of ICCs is the focus. If the interest is solely on marginal treatment effect, using working independence covariance matrix is an attractive approach due to its high efficiency in many settings and its simplicity in avoiding the need to estimate high-order association parameters. In the absence of missing data, standard GEE2 is highly efficient with a correctly specified working covariance structure. More concretely, the class of estimating functions which satisfy the canonical TM in Eq 2 and are regular asymptotically linear (RAL) must be of the form $0=\sum _{i=1}^{I}h\left(A_i\right)E_i$. The choice of index function $h\left(A_i\right)=D_i^{\top }{V}_i^{-1}$, which reduces back to GEE2, results in the efficient score for the canonical TM, hence leading to the minimum asymptotic variance RAL estimator for $\left({\beta }_Y^{*},{\alpha }_Y^{*}\right)$ (Chamberlain, 1986). However, in the case of IPW-GEE2 or DR-GEE2, this choice is no longer optimal and the actual h_opt (A_i) to achieve the efficient score is far more complicated (Stephens et al., 2014). Stephens et al. (2014) showed in simulation studies the efficiency gains from using h_opt (A_i) are modest and very sensitive to the correct specification of all components that comprise h_opt (A_i), which in practice is nearly impossible to achieve. Our simulation studies in Section 5 also provide corroborative evidence supporting the use of an independence covariance structure when estimating the first-order effects.

Although our work was motivated by the need for better estimation of ICCs in cluster randomized trials, the DR-GEE2 estimator can be used in other settings when estimation of ICCs is of interest such as in reliability and agreement studies. We focused our discussion on binary outcomes, but the approach can be adapted to other types of exponential family outcomes in a straightforward manner by modifying the link and variance functions for the corresponding likelihood. When outcomes within clusters are not equicorrelated, our ICC estimators marginalize out factors which contribute to the non-exchangeable structure and return an estimate which can be construed as an “average” correlation.

In the presence of informative missing outcome data, the correlation among missingness indicators needs to be properly accounted for in order to arrive at consistent estimators for the association parameters. We assumed rMAR in the current work. Future research on further relaxing this assumption would be useful.