Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 May 22;141(42):16624–16634. doi: 10.1021/jacs.9b03908

Rapid Structure Determination of Molecular Solids Using Chemical Shifts Directed by Unambiguous Prior Constraints

Albert Hofstetter †, Martins Balodis †, Federico M Paruzzo †, Cory M Widdifield §, Gabriele Stevanato †, Arthur C Pinon †, Peter J Bygrave ‡, Graeme M Day ‡, Lyndon Emsley †,*
PMCID: PMC7540916  PMID: 31117663

Abstract

graphic file with name ja9b03908_0008.jpg

NMR-based crystallography approaches involving the combination of crystal structure prediction methods, ab initio calculated chemical shifts and solid-state NMR experiments are powerful methods for crystal structure determination of microcrystalline powders. However, currently structural information obtained from solid-state NMR is usually included only after a set of candidate crystal structures has already been independently generated, starting from a set of single-molecule conformations. Here, we show with the case of ampicillin that this can lead to failure of structure determination. We propose a crystal structure determination method that includes experimental constraints during conformer selection. In order to overcome the problem that experimental measurements on the crystalline samples are not obviously translatable to restrict the single-molecule conformational space, we propose constraints based on the analysis of absent cross-peaks in solid-state NMR correlation experiments. We show that these absences provide unambiguous structural constraints on both the crystal structure and the gas-phase conformations, and therefore can be used for unambiguous selection. The approach is parametrized on the crystal structure determination of flutamide, flufenamic acid, and cocaine, where we reduce the computational cost by around 50%. Most importantly, the method is then shown to correctly determine the crystal structure of ampicillin, which would have failed using current methods because it adopts a high-energy conformer in its crystal structure. The average positional RMSE on the NMR powder structure is ⟨rav⟩ = 0.176 Å, which corresponds to an average equivalent displacement parameter Ueq = 0.0103 Å2.

1. Introduction

The 40 000–60 000 crystal structures published every year1−4 perfectly illustrate the importance of the knowledge of atomic-level structures of solids, which is key to understanding and predicting their properties. For example, in pharmaceutical compounds, crystal structures guide the understanding of physicochemical and pharmacokinetic properties such as bioavailability and/or solubility.5 However, many active pharmaceutical ingredients (APIs) are only available as powders, and therefore are not amenable to resolution with typical X-ray diffraction (XRD) methods. Structure elucidation can be complicated further if, for example, the crystallites are sub-micrometer in size or the structure contains elements of disorder.

Recently, solid-state nuclear magnetic resonance (NMR)-based crystallography has emerged as a powerful tool to overcome the current limitations in powder structure determination. In contrast to other methods, such as powder XRD6 or electron diffraction,7−10 NMR directly probes the local atomic environment, allowing for structural characterization without the need for long-range order. Advances in solid-state NMR together with the development of accurate methods to calculate chemical shifts,11−13 in particular using plane wave density functional theory (DFT) methods based on the Gauge Including Projector augmented Wave (PAW/GIPAW) approach,14−16 have enabled development of chemical-shift-based NMR crystallography methods. Recently, machine-learning methods have been introduced to facilitate the calculation of accurate chemical shifts.17,18

The NMR crystallography (NMRX) approach, which often involves crystal structure prediction (CSP) protocols, has been used to determine full de novo crystal structures from powders19−24 with an accuracy at least comparable to that of single-crystal XRD,25 as well as to determine elements of structure such as hydrogen bonding, proton positions, and stereochemistry,26−30 or to validate and refine crystal structures of molecular solids and to identify known polymorphs.27,28,31−55

Because CSP can require considerable computational resources, increasing rapidly with the structural degrees of freedom, CSP-based NMRX methods (CSP-NMRX) for de novo structure determination are currently limited to systems with up to about 10 degrees of torsional freedom within the molecule,56 and going beyond this requires some prior knowledge or intuition.23,24 Indeed, in order to circumvent these limitations, CSP methods often make assumptions (for example, based on space groups or predicted conformational energies) to limit the search space of possible structures. However, this can lead to failure of the CSP-NMRX method to determine the correct crystal structure(s) when the correct structure is excluded from the search space.

A common feature of most of the CSP-NMRX methods developed to date is that they exploit geometric constraints from solid-state NMR only in the final step, in order to select the correct crystal structure from an ensemble of predicted structures. Introducing experimental constraints earlier in the CSP process would be an obvious way to guide and accelerate structure determination. The bottleneck for CSP of flexible molecules usually relates to the size of the molecular conformational space, so guidance to constrain the size of the search space would be most valuable if it relates to single-molecule conformations. However, it is not immediately clear how experimental measurements on the crystalline samples would be relevant to restrict the single-molecule conformational space.

Note that an example has been given in which structural information was included at earlier stages of the CSP by biasing the search using semi-empirical molecule-specific pseudo-forces derived from chemical shifts.44

Here, we introduce a CSP-NMRX method to determine crystal structures in which we use unambiguous constraints from solid-state NMR on microcrystalline samples to restrict the CSP search space to relevant regions of conformational space. The approach directs the determination procedure from the first steps toward the correct crystal structure, without the need for assumptions. We parametrize the approach on the crystal structures of cocaine, flutamide, and flufenamic acid and demonstrate a significant acceleration in computational times for these compounds. Most significantly, using chemical shifts calculated with both DFT and machine learning,18 we correctly determine the crystal structure of powdered ampicillin, for which the usual approach via CSP-NMRX would have failed.

2. Methods

Figure 1a schematically illustrates the workflow in a successful case for the current CSP-NMRX approaches.19,42,57 In the first step, the torsional degrees of freedom are explored to generate a comprehensive ensemble of energetically stable single-molecule conformers. The ensemble is then sorted according to the calculated conformational energies, and the lowest energy conformers are selected to proceed to the next step, based on an empirical cutoff energy. Although flexible molecules often do not assume their lowest energy molecular conformation in their observed crystal structures,58 the assumption here is that low-energy crystal structures, including the correct (observed) polymorph, will generally result from low-energy molecular conformers. However, this is not always the case, as will be demonstrated below.

Figure 1.

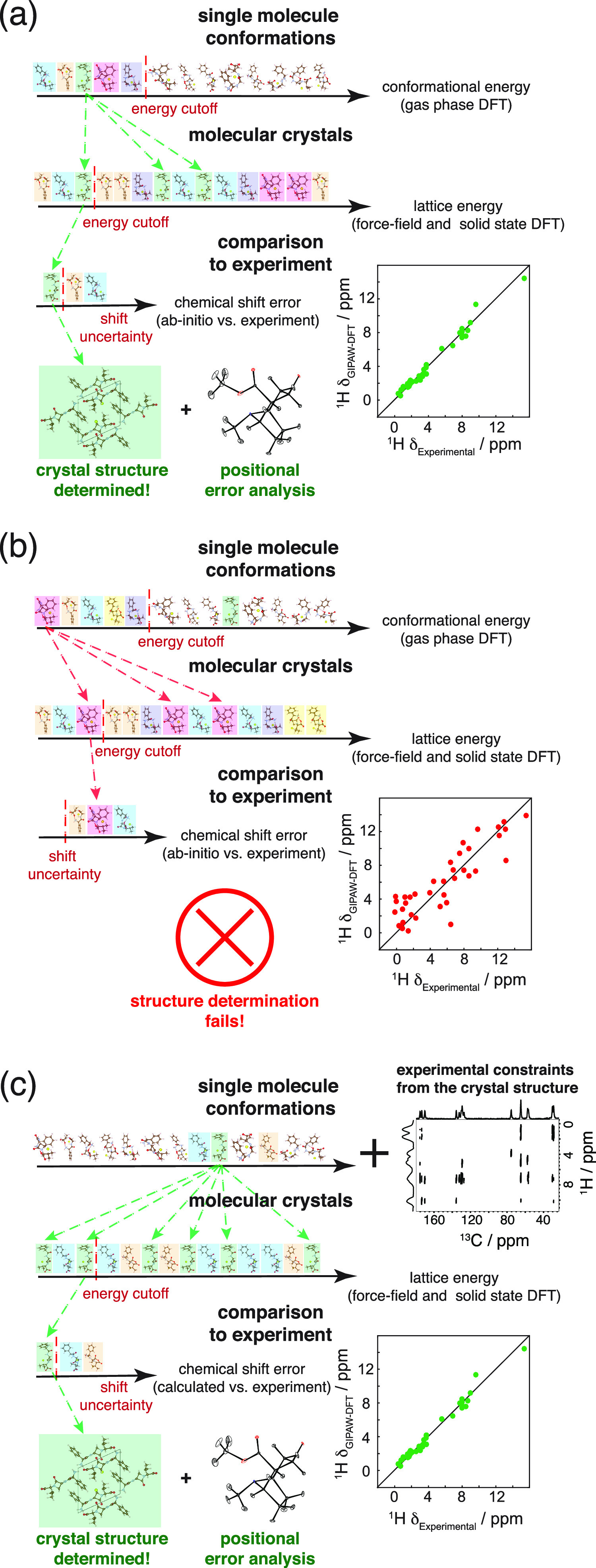
Figure 1

Open in a new tab

Schematic of current and proposed CSP-NMRX methods. (a) An example of a successful structure prediction using the current CSP-NMRX method. (b) An example of a failed structure prediction using the current CSP-NMRX method. (c) An example of the proposed experimentally constrained CSP-NMRX method, which successfully overcomes the failure of the current CSP-NMRX method shown in panel (b). In each panel the structures in the first line depict single-molecule gas-phase conformations sorted by their conformational energy. After application of a given selection criterion, a reduced conformer set is used to generate an ensemble of possible crystal structures (represented by the second line in each panel). The colored boxes are intended as a guide to the eye as to which conformer results in which crystal structures. The third line in each panel represents crystal structures picked from the second line after a further selection criterion is applied. This final set of structures is then compared to the experimental chemical shifts to determine the correct crystal structure. In each panel, the scatter plot shows the experimental 1H chemical shift plotted against the DFT-calculated 1H chemical shift for the trial structure with the lowest error between DFT and experimental chemical shifts.

The selected conformations are then each subjected to a crystal structure search, during which trial structures are generated by varying the unit cell dimensions, center of mass in the cell, packing symmetry, and number of molecules per asymmetric unit. This process can lead to hundreds or thousands of possible crystal structures from each single-molecule conformer. The energy of each structure is then minimized, typically using atom–atom force fields and DFT.59

Next, this ensemble is ranked by calculated lattice energy, and again only the structures below a given cutoff energy are retained. In the final step, these structures are further optimized, typically using periodic boundary DFT calculations, and then the chemical shifts (or other experimental data such as dipolar couplings or chemical shift anisotropies)23,27,49,60−62 for this sub-ensemble of crystal structures are calculated and compared to experimental chemical shifts measured on a powder sample. The differences between the calculated and experimental chemical shift data are then used to determine the crystal structure that is in best agreement with the experimental NMR data acquired using the powder sample. For this structure, positional errors are then calculated using a molecular dynamics approach.25 Note that the computational cost rises sharply when moving from the energy calculations of a single molecule to lattice energy calculations to GIPAW DFT chemical shift calculations, thus requiring the use of successive selection steps to reduce the number of candidate structures at each stage.

From the description of the CSP-NMRX procedure above, it is evident that a gas-phase conformer similar to the one present in the correct crystal structure must be among those initially selected.

Figure 1b illustrates a case where the current CSP-NMRX method fails. Analogously to the previous case, a large ensemble of single-molecule conformers is generated and sorted by conformational energy. However, here, the molecular conformer present in the crystal structure is of very high relative energy in the gas phase, and thus does not pass the selection criteria based on energy. An illustrative example of this case could be when intramolecular hydrogen bonds stabilize the most stable conformations in the gas phase, while the crystal structure conformation is stabilized through intermolecular hydrogen bonds or other interactions only present in the solid phase. Thus, following the normal selection steps based on the conformational energy, the correct conformer is not included in the crystal packing and lattice energy calculation steps, and as a consequence is not present in the trial crystal structures that are compared to the experimental data.

Taking this into account, one could extend the crystal structure determination procedure, and we consider two ways below. One option is to loosen the initial selection criteria, thus allowing more conformers to proceed to the following steps. This approach will increase the computational cost, often prohibitively. Even moderately flexible molecules can have hundreds of conformations, each requiring significant computing; for example, for ampicillin, one of the molecules studied here, the CSP procedure required, on average, just over 3 days of computing on 200 dedicated CPUs per conformer (yielding a total of 54 days for all the conformers). Thus, this approach either involves very long time scales or requires access to very large-scale computing. The second option is to use a different initial selection criterion including information from experiment.

Figure 1c illustrates this second approach, which we introduce here. Contrary to the standard CSP methods, no assumptions based on calculated energy are made in the initial conformer selection process. Instead, a sub-ensemble of conformers is selected using experimental constraints from solid-state NMR experiments on the powdered microcrystalline sample. This approach guides the conformational sub-ensemble selection toward the correct crystal conformer, and thus reduces the chance that the structure determination is limited by possibly erroneous assumptions.

However, experimentally we only have access to the full crystal structures and cannot probe the underlying “virtual” gas-phase conformations independently. Thus, we need to measure experimentally accessible constraints that would be unambiguously fulfilled both in the crystal structure and in the gas-phase conformations. Note that commonly used solid-state NMR constraints, such as the presence of (dipolar-coupling-mediated) cross-peaks in NMR correlation experiments21,63−73 due to internuclear proximity, do not contain unambiguous information about the gas-phase conformations. This is because a cross-peak could arise from either intra- or intermolecular proximity.

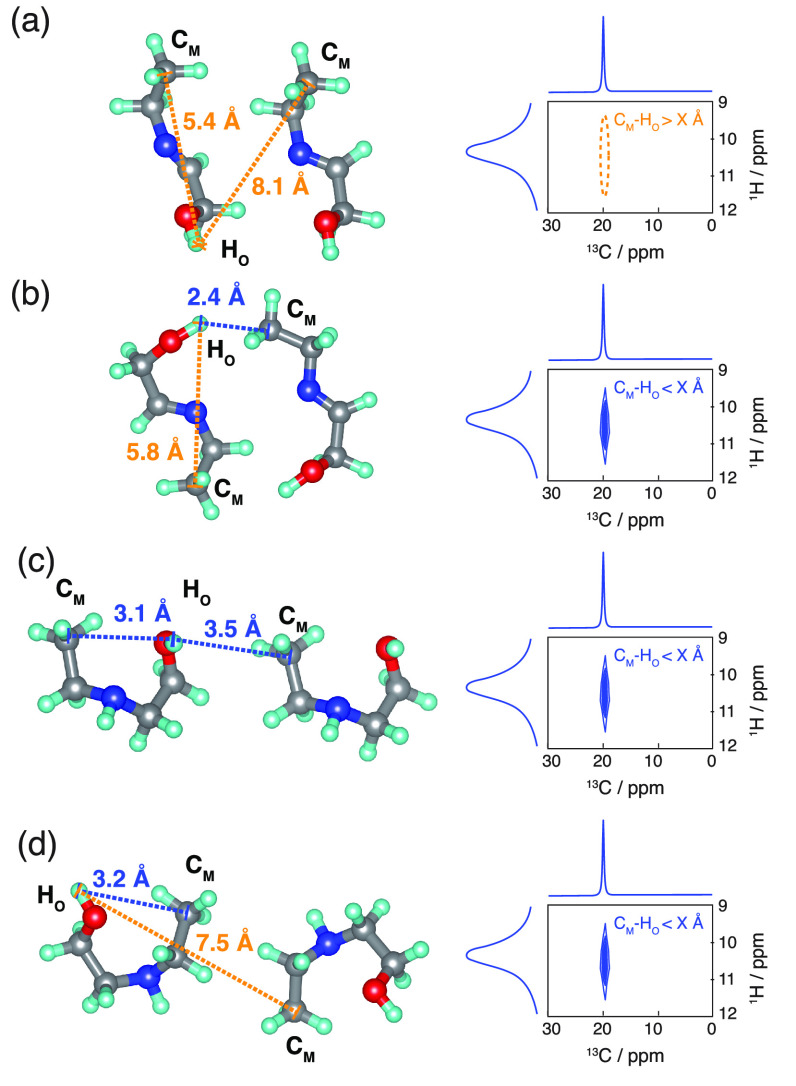
Here we introduce a novel approach that extracts unambiguous conformational constraints on the single-molecule conformations present in crystalline samples. The approach is schematically illustrated in Figure 2, where we differentiate between two conformers (“open” and “closed”) by analyzing a 1H–13C HETCOR spectrum.

Figure 2.

Figure 2

Open in a new tab

Schematic illustrations of 1H–13C HETCOR spectra (right) for four different structural fragments (left) and the derived constraints. Structures (a) and (b) contain an “open” conformer. Structures (c) and (d) contain a “closed” conformer. Blue dotted lines are sufficiently short C–H distances between CM and HO to generate peaks in the spectra. Orange dotted lines are too long to generate peaks. After applying the constraints with a threshold distance of X = 3.5 Å, we see that the absence of a peak in fragment (a) is the only unambiguous constraint.

The 1H–13C HETCOR spectrum contains two different types of information. First, cross-peaks that are present indicate atoms that are close in space. Second, absent cross-peaks contain information about atoms that are more than a certain distance X apart, where X possibly depends on the CP contact time, the experimental setup, and the investigated system. Figure 2 shows that only the information from the absent cross-peaks in the solid-state spectra can be directly transferred to constraints on the single-molecule conformations. This is demonstrated with a thought experiment. If the heteroatoms CM and HO are close in space, then the cross-peak at CM–HO will be present in the HETCOR spectra. However, the cross-peak can result either from a short intramolecular CM–HO distance (i.e., the “closed” conformer) (Figure 2c,d) or from a short intermolecular interatomic distance (which can be from the “closed” or the “open” conformer) (Figure 2b,c). Thus, the presence of a cross-peak does not contain unambiguous information about the single-molecule conformer, as the fragments in Figure 2b–d contain both possible conformations.

An absent cross-peak for CM–HO, however, indicates that CM and HO are at least X Å apart, for both intra- and intermolecular CM–HO distances (Figure 2a). This can only happen for the “open” conformer. Thus, information from the absent cross-peaks is unambiguous regarding the single-molecule conformation and can be used as a constraint on trial structure generation.

Note that the fragment in Figure 2b also contains the “open” conformation but would be expected to contain a cross-peak for CM–HO, and thus will not result in a constraint on the distance between CM and HO. However, such cases only result in fewer constraints on the single-molecule conformer but do not induce any incorrect constraints.

Note also that it is not a priori clear what the threshold distance X is. In general, we expect to reliably see all 1H–13C HETCOR cross-peaks at least up to 3.0 Å.74 To establish a reliable value for the threshold distance X, accessible in the 1H–13C HETCOR experiments used here, we investigate the correlation between interatomic 1H–13C distances and signal intensities of the cross-peaks in the HETCOR experiments recorded for cocaine, flutamide, and flufenamic acid.

For these three compounds, the experiments were performed at different contact times, at different magic-angle spinning rates, and on different spectrometers. Figure S3a shows that for cocaine we have signal-to-noise ratios (SNRs) of up to 80, while flufenamic acid has a maximum SNR of around 10. Additionally, for a 1H–13C HETCOR experiment, where the signal is transferred from the 1H to the 13C, the SNR also depends on the number of protons involved in the transfer, as well as the number of protons overlapping at a given frequency.

To make different spectra comparable, we first estimate that the number of active protons for a given cross-peak in a spectrum is proportional to the maximum signal intensity at a given frequency in ω1. The signal intensity of each cross-peak is then re-normalized by this number of protons. We then consider the difference in overall SNR between spectra by re-normalizing each cross-peak with respect to the maximum proton-normalized SNR per spectrum. This leads to a normalized SNR per 1H, which is comparable across all experiments and which is shown in Figure S3b.

Once we have selected a reliable threshold distance X Å for a given SNR cutoff (this process is described below), the selected threshold distance in combination with each absent HETCOR cross-peak is transformed into a constraint on the conformer space as follows: if the HETCOR cross-peak between Cxand Hyis below the SNR cutoff, it is classified as absent, and so the distance between the atoms Cxand Hymust exceed X Å.

For each single-molecule conformer, all of the generated constraints were checked, and the conformers were sorted according to the number of constraints violated. This procedure allows us to select conformers for the subsequent CSP procedure. If we are confident in the extracted constraints, it is sufficient to select only the sub-ensemble with the lowest number of constraint violations. However, if this sub-ensemble is very small or if additional computational resources are available, the selected sub-ensemble can easily be extended to include structures with a progressively higher number of constraint violations. Accepting conformations with a small number of constraint violations can allow for moderate changes in molecular geometry between the gas phase and crystal structure.

3. Results and Discussion

We first establish the range of reliable threshold distances (X) for a given normalized SNR cutoff (Snorm). For this we investigate the correlation between the normalized SNR and the corresponding interatomic distances for the three trial compounds: cocaine, flufenamic acid, and flutamide.

Then we investigate the application of the parametrized constraints (Snorm and X) to the CSP-NMRX structure determination of these three compounds.

Finally, we perform the full CSP-NMRX crystal structure determination including the unambiguous constraints on microcrystalline ampicillin, where the parametrization of X and Snorm was done without using any prior knowledge regarding the crystal structure.

Parametrization Using Known Structures

For cocaine, flufenamic acid, and flutamide, 1H–13C HETCOR experiments were performed with 1H–13C contact times of 0.5, 0.75, 1.0, and 1.5 ms; 0.1, 0.5, 1.5, 2.0, 3.0, and 3.5 ms; and 0.1, 0.3, 0.5, 0.75, 1.0, 1.25, 1.5, 1.75, and 2.0 ms, respectively. We re-normalized the spectra as described above (see SI for details). The resulting normalized SNR per 1H is then comparable between compounds; see Figure S3b.

However, Figure S3b shows that although there is a correlation between the normalized SNR and the corresponding interatomic distance, there are significant fluctuations. This is expected since the HETCOR experiment is quite simple but is subject to spin diffusion relayed transfer, among others. We find that the effect of these fluctuations can be minimized by only considering correlations/distances from protons that are situated toward the extremities of the molecules. (We note here that this currently results in a reduced number of extracted constraints. If the constraints could be extracted in a more quantitative manner, e.g., by accounting for changes in peak intensities due to 1H–1H spin diffusion, then the selection criteria could be made stronger.) However, these distances are the most information-rich in terms of the overall molecular conformations. We thus only consider cross-peaks resulting from the “terminal” protons shown in Table S5, and marked with a green dotted line in Figure S4a. This results in a clearer correlation between normalized SNR and the corresponding interatomic distances, as shown in Figure S4b.

From Figure S4b it is clear that only a very limited number of interatomic distances below 3 Å result in a normalized SNR above 0.2. We then test a range of Snorm values from 0.08 to 0.22 with threshold distances X ranging from 2.0 to 5.0 Å. For this we used the single-molecule conformer ensembles previously generated for the successful CSP-NMRX structure determination protocol described by Baias et al.42 Our goal was to verify that the proposed parametrization can select the gas-phase conformer that leads to the correct crystal structure while at the same time significantly reducing the total amount of conformers that have to be considered.

Figure 3a shows the set of parameters for which the selection procedure was successful for all three molecules simultaneously. Figure S9 shows the set of successful parameters for each molecule individually. The dashed orange line in Figure 3a shows the limit at which the selection process starts to fail. To obtain maximal selection power, the parameters should be chosen as close as possible to this limit. For cocaine, flufenamic acid, and flutamide, the highest selectivity within the investigated conformer ensembles explored here was obtained using Snorm = 0.14 and X = 3.5 Å.

Figure 3.

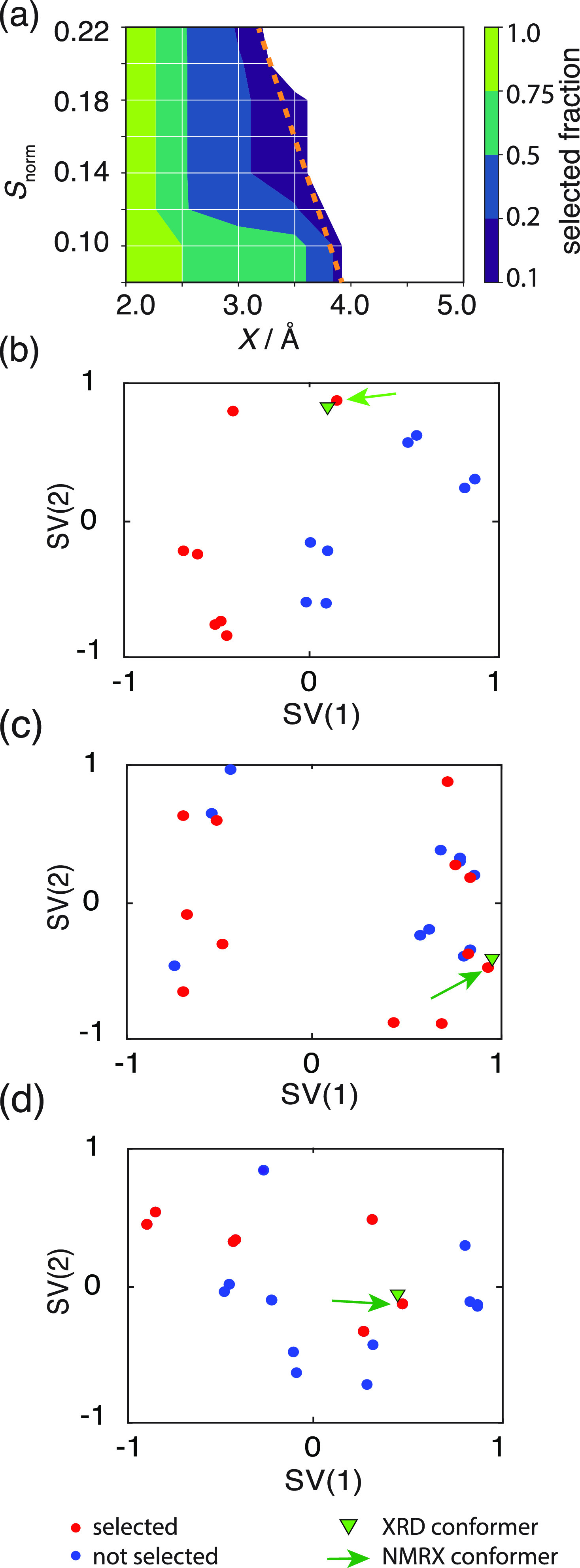
Figure 3

Open in a new tab

(a) Grid search results of the threshold distance X and Snorm cutoff values for flutamide, cocaine, and flufenamic acid. The color-map shows the percentage of selected structures from within the conformer ensemble. The white area indicates the region where the correct conformer is not selected. Optimal selection parameters should select the smallest conformer ensemble that still contains the correct structure. This corresponds to the dark blue regions within the different panels. The dashed orange line denotes the boundary at which the selection process starts to fail. (b–d) Conformer selection for flutamide (b), flufenamic acid (c), and cocaine (d). The panels show the sketch-map projections of the gas-phase ensembles. Red dots represent the structures that are selected where a threshold distance X of 3.5 Å and an Snorm cutoff value of 0.14 were used. The green triangle shows the conformer found in the XRD-generated crystal structure. The green arrow points to the gas-phase conformer which results in the correct crystal structure after the CSP procedure.

To aid our interpretation of the selection procedure, we apply a sketch-map75−78 analysis to the gas-phase conformer ensembles. The details of the sketch-map analysis, including an interpretation of the underlying conformational changes for cocaine, flutamide, and flufenamic acid, are given in Figures S6–S8.

Flutamide

The initial gas-phase ensemble of flutamide conformers generated in the first step of CSP contains 15 conformers,42 of which 7 are in the trans and 8 are in the cis conformation with respect to the amide group (Figure S7). All the absent cross-peaks in a series of 1H–13C HETCOR spectra (Figure 4) were used to generate the conformational constraints shown in Figure 4a. Figure 3b shows the selected sub-ensemble of gas-phase conformers in the sketch map that fulfill the most constraints. The sub-ensembles with the lowest number of violations (2 of 10 total constraints) are selected for the subsequent CSP procedure.

Figure 4.

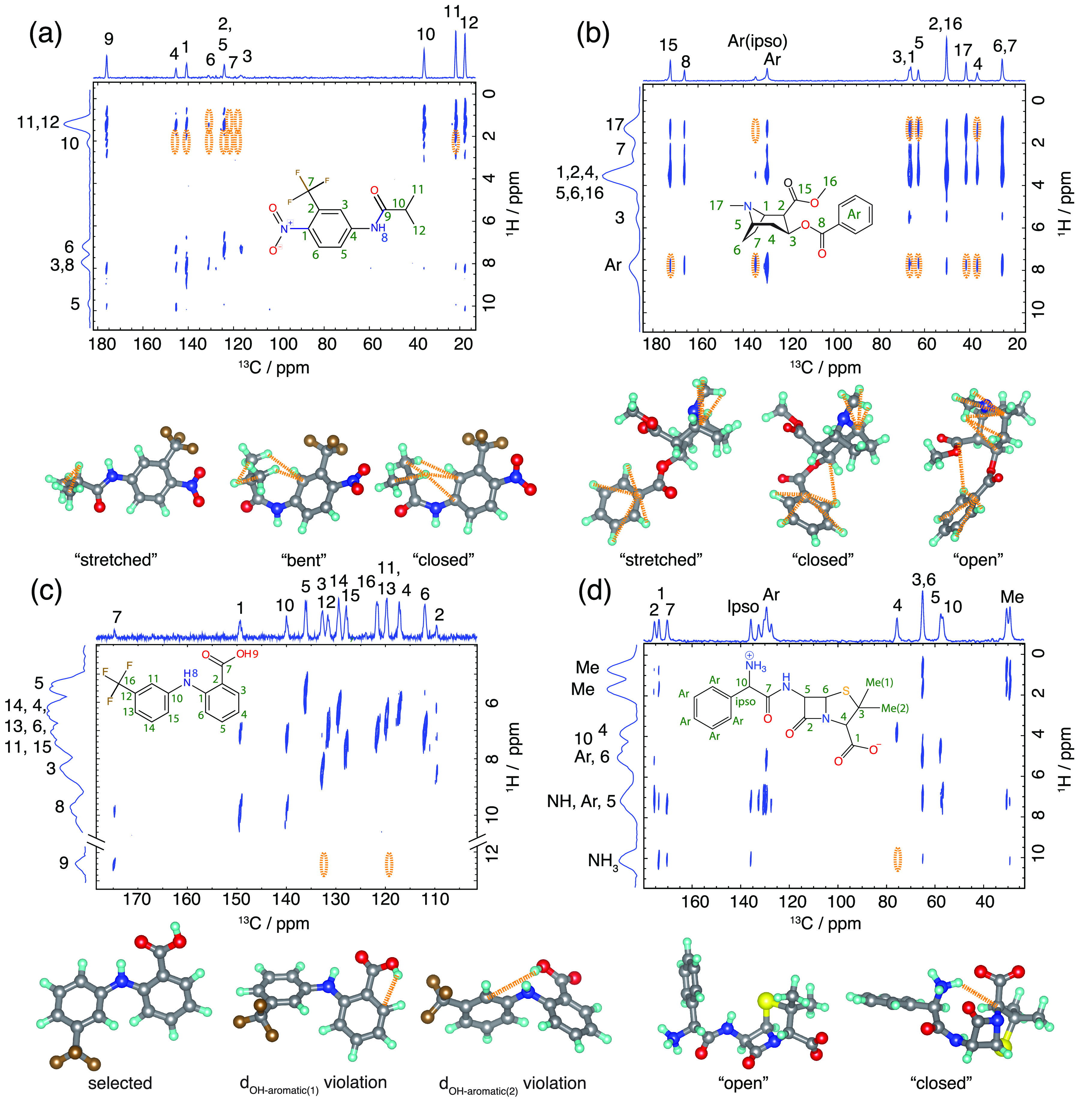
Figure 4

Open in a new tab

The top part in each panel shows the 1H–13C HETCOR spectrum of flutamide with a 1.25 ms 1H–13C cross-polarization contact time (a), cocaine with a 1.0 ms contact time (b), flufenamic acid with a 1.5 ms contact time (c), and ampicillin with a 1.5 ms contact time (d) (further details and raw data in the SI). 13C peaks are assigned based on the literature,79 and 1H peaks are assigned from HETCOR spectra and DFT chemical shift calculations (see SI). The cross-peaks from the terminal protons (Figure S4a) below Snorm = 0.14 were used as constraints on the conformer ensembles and are indicated as orange ellipsoids. The lower part of each panel shows the violated constraints extracted from all of the 1H–13C HETCOR cross-peaks for different example conformers within the ensembles.

Note that these two constraints are violated for all conformers and do not correspond to significant changes in the conformation, as the involved atoms are not separated by more than two bonds. The reduced ensemble contains the gas-phase conformer that led to the correct crystal structure during the subsequent CSP procedure,42 while being able to reduce the gas-phase conformer ensemble from 15 to 7 conformations. This significantly reduces the computational cost of the following CSP steps by approximately 54% (assuming that all conformers lead to similar numbers of putative crystal structures), while still including the correct gas-phase conformer that leads to the observed crystal structure. Additionally, the constraints from the absent cross-peaks uniformly selected the trans form in all 7 conformers (see Figure S10).

Flufenamic Acid

The gas-phase conformer ensemble for flufenamic acid contains 26 molecular conformations.42Figure 3c shows the selection of the sub-ensembles with the lowest number of violations (0 of 2 total constraints) using 1H–13C HETCOR. The extracted constraints are shown in Figure 4c. Note that, for flufenamic acid, there are only two non-aromatic protons and the cross-peaks from the aromatic protons are not distinguishable due to overlap in the 1H dimension. However, the distance constraints extracted solely from the carboxyl proton (see Figures 4c and S12) were sufficient to reduce the number of relevant conformers by 46% (from 26 to 14 conformers), while still selecting the correct conformer, leading to the observed crystal structure.

Cocaine

The initial CSP conformer ensemble for cocaine contains 27 conformers.42Figure 3d shows the selection of the sub-ensembles with the lowest number of constraint violations (2 out of 10 total constraints) extracted from the 1H–13C HETCOR NMR spectrum (Figure 4b). As with flutamide, these two constraints were violated for all conformers and do not correspond to significant changes in the conformation, as the involved atoms are separated by only three bonds. Figure S11 shows that the 1H–13C HETCOR constraints were able to distinguish between the folding (closed and bent forms) and stretching of the cocaine molecule with respect to the aromatic group as well as a flip in the methylamine group. Here, the relevant conformer ensemble is reduced by around 55% (from 27 to 12 conformations) while retaining the conformer that leads to the correct crystal structure.

Crystal Structure Determination of Ampicillin

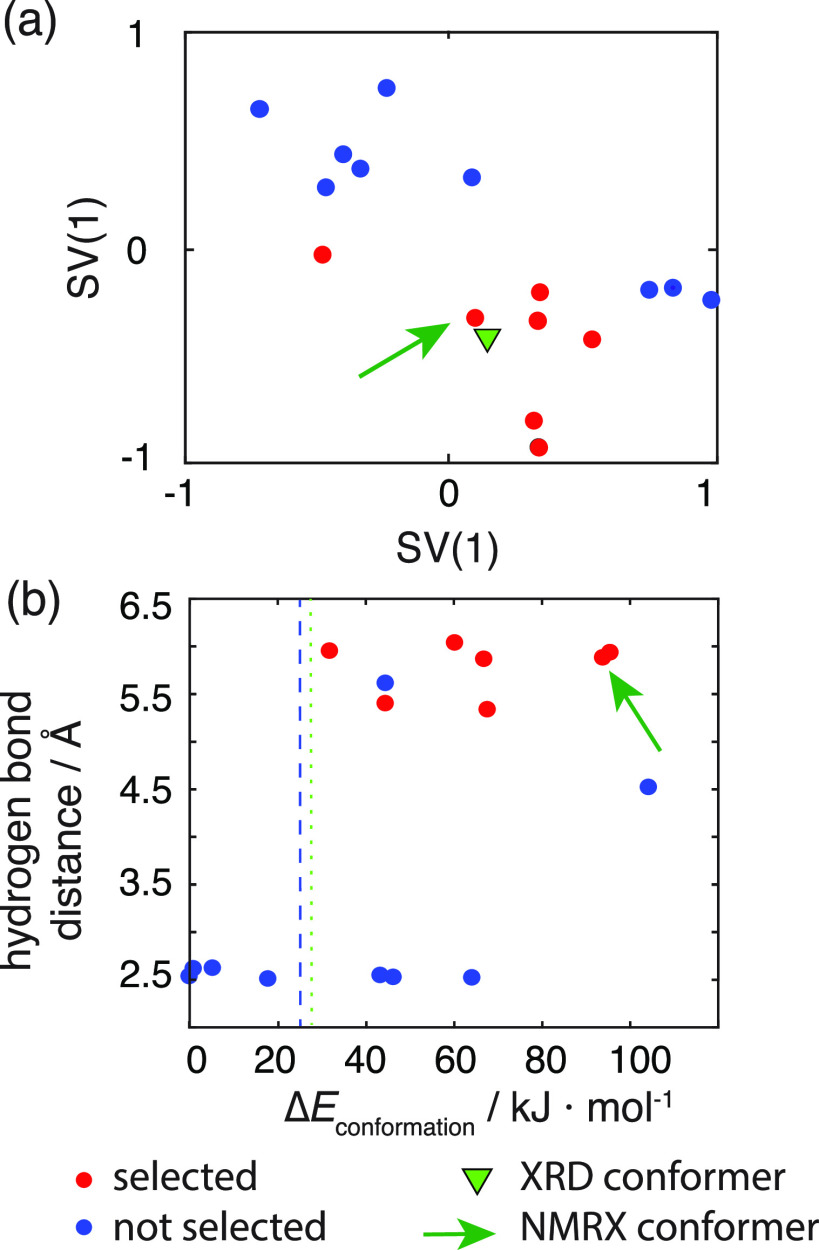
In contrast to the three cases above, the crystal structure determination of ampicillin would have failed using the usual CSP-NMRX protocol. In the first step, an ensemble of 16 locally stable gas-phase conformers was generated (for details, see SI), and the ensemble was then sorted according to the isolated molecule’s conformational energy. Figures 5b and S5 show that all the conformers within 25 kJ·mol–1 of the lowest energy structure are stabilized through an intramolecular hydrogen bond between the amino nitrogen and oxygen atoms of the carboxyl group, the strength of which is enhanced by the zwitterionic nature of the molecule. However, in the known single-crystal XRD structure, these intramolecular hydrogen bonds between charged ends of the molecule are sacrificed to allow the formation of strong, charge-assisted intermolecular hydrogen bonds, with the molecule adopting a more extended, open conformation.

Figure 5.

Figure 5

Open in a new tab

Conformer selection for ampicillin. (a) The panel shows the sketch-map projections of the gas-phase conformer ensemble. Red dots represent the structures which are selected using a threshold distance X = 3.5 Å and Snorm = 0.14. The green triangle denotes the conformer found in the XRD-determined crystal structure. The green arrow points to the gas-phase conformer which results in the correct crystal structure after the CSP procedure. (b) Scatter plot showing the relative difference in the energy (ΔE) for the single-molecule conformers of ampicillin against the shortest intramolecular hydrogen-bond distance (N–O distance). The blue dashed line is the typical cutoff energy (25 kJ/mol) used for conformer selection in CSP. The green dotted line is a guide to the eye to show at which ΔE the conformers with intermolecular hydrogen bonds become accessible. The green arrow shows the conformer which results in the correct crystal structure.

Figure 5b also shows that the single-molecule conformation closest to the crystal conformer is one of the highest energy gas-phase conformers, nearly 100 kJ·mol–1 higher in energy than the lowest energy single-molecule conformer. In the normal CSP method, a cutoff of around 20–25 kJ·mol–1 would typically be applied to the conformational ensemble42,58 to limit the number of conformers that must be considered during the time-consuming crystal packing search. The correct conformer falls well outside this energy range and, thus, would be eliminated at this stage, preventing the successful generation of the observed crystal structure. To successfully determine the correct crystal structure, the subsequent CSP steps would have had to proceed without applying any energetic cutoff on the single-molecule conformers. This would be possible for the 16 conformers of ampicillin using large-scale computing to perform the searches in parallel, but it is problematic as a general method, as the conformational space of even moderately flexible molecules can often include hundreds of individual conformers.58

To address this problem, we apply experimental constraints extracted from 1H–13C HETCOR NMR spectra at different contact times (i.e., 0.1, 0.3, 0.5, 0.75, 1.0, 1.25, 1.5, 1.75, 2.0, and 2.25 ms, detailed in the SI). Figure 4d shows the assigned HETCOR NMR spectrum of ampicillin at a 1.5 ms contact time together with the labeled 2D structure. Following the protocol established for cocaine, flutamide, and flufenamic acid, the SNR was then normalized over all experimental setups as described above. As we did for the other three molecules, we only consider cross-peaks resulting from terminal protons; see Figure S4a. Using Snorm = 0.14 and X = 3.5 Å, that were parametrized on the reference compounds above, the extracted constraints are circled in orange and are shown on three example conformers below the spectra. Figure 5a shows the sub-ensembles with no violations (0 out of 1 total constraint). Figures 4d and S13 show that only conformers without an intramolecular hydrogen bond are selected. Also, from Figure 5b it is clear that the energetically high conformers are preferentially selected. Note that in a classical CSP-NMRX approach these conformers would have not been selected.

For the next step in the CSP procedure, only 7 out of the original 16 structures were considered. This reduces the computational cost by approximately 55%.

For each conformer remaining within this reduced gas-phase ensemble, we generated a crystal structure ensemble using a quasi-random sampling80 of lattice parameters, molecular positions, and orientations within the commonly observed space groups. All 154 000 generated crystal structures were first optimized using an atomic-multipole-based force field,81 followed by dispersion-corrected DFT-D re-optimization of the lowest energy crystal structures, producing a final set of 75 candidate crystal structures. The full procedure is detailed in the SI (section X).

1H chemical shift values were then calculated with GIPAW DFT and a machine-learned method (ShiftML)18 for each candidate structure and compared to the experimental chemical shifts (details are given in the SI). Figure 6 shows the RMSE between DFT-calculated and measured 1H chemical shifts together with the calculated relative lattice energies for the candidate set. Based on currently accepted metrics, we expect a valid structure to have a 1H RMSE of 0.33 ppm (±0.16 ppm) or lower.39 This is indicated as the gray zone in Figure 6. Predicted structures with 1H chemical shift difference within this zone are thus considered to be indistinguishable from experiment with a confidence of 1σ.

Figure 6.

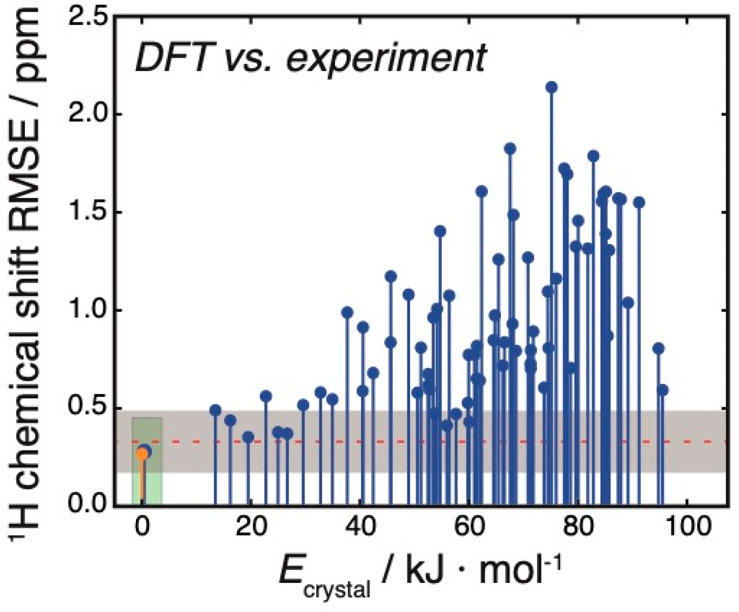
Figure 6

Open in a new tab

Comparison of crystal structure candidates. The structures are sorted according to their relative lattice energy, as specified on the horizontal axis. The vertical axis shows 1H chemical shift RMSE between DFT-calculated and experimental chemical shifts. The orange marker shows the 1H chemical shift RMSE for the single-crystal XRD structure. The red line shows the mean of the expected difference between experimental and DFT-calculated 1H chemical shifts, with the distinguishability limits (at the 1σ level) indicated as the gray shaded zone, as described in the main text.

Figure S15 shows the RMSE between ShiftML-calculated and measured 1H chemical shifts together with the DFT-calculated relative lattice energies for the candidate set. Using a benchmark set of 11 molecular crystal structures with around 150 experimental 1H chemical shifts (as described in the SI, Table S8), we expect a correct structure to have a 1H RMSE of 0.346 ppm (±0.195 ppm) or lower. Note that the RMSE between the experiment and the ShiftML-predicted chemical shifts are broadly similar to the RMSE from DFT-calculated shifts (Figure 6).

Based on the agreement between experimental and calculated 1H chemical shifts, both for ShiftML and DFT, we find that the crystal structure lowest in lattice energy, with a large gap in energy to the next predicted structure, also best produces the experimental NMR chemical shifts from the powdered microcrystalline sample used in the present study (Figures 6 and S15). Thus, we identify this structure as the correct candidate structure. Using chemical shifts calculated either directly from DFT or using ShiftML, several higher energy putative crystal structures produce 1H chemical shifts within the acceptable error bounds. However, none of these alternative structures falls within the usual energy range of observed polymorphism (typically up to 7–8 kJ/mol)82 above the best candidate structure. Thus, our final structure selection relies on both the chemical shifts and the calculated lattice energies.

The structure determined here agrees very well with the known reference structure determined by single-crystal XRD,83 as illustrated in Figure 7a. The deviation in atomic positions in the NMR structure from the powder is 0.278 Å, measured as the RMSD of all heavy atoms (excluding protons) in a 20-molecule cluster taken from the two structures. The single-molecule heavy-atom RMSD is 0.068 Å. The largest deviations in the lattice parameters are a contraction of 6.8% in the b lattice parameter and a unit cell volume of the CSP-NMRX structure 7.4% smaller than the single-crystal structure (see Table S9). This difference in volume is not unexpected, as the NMRX structure is a temperature-free structure resulting from lattice energy minimization, while the single-crystal structure was determined at room temperature. The slightly shorter lattice parameters in the NMRX structure are in line with the expected thermal expansion of an organic molecular crystal.

Figure 7.

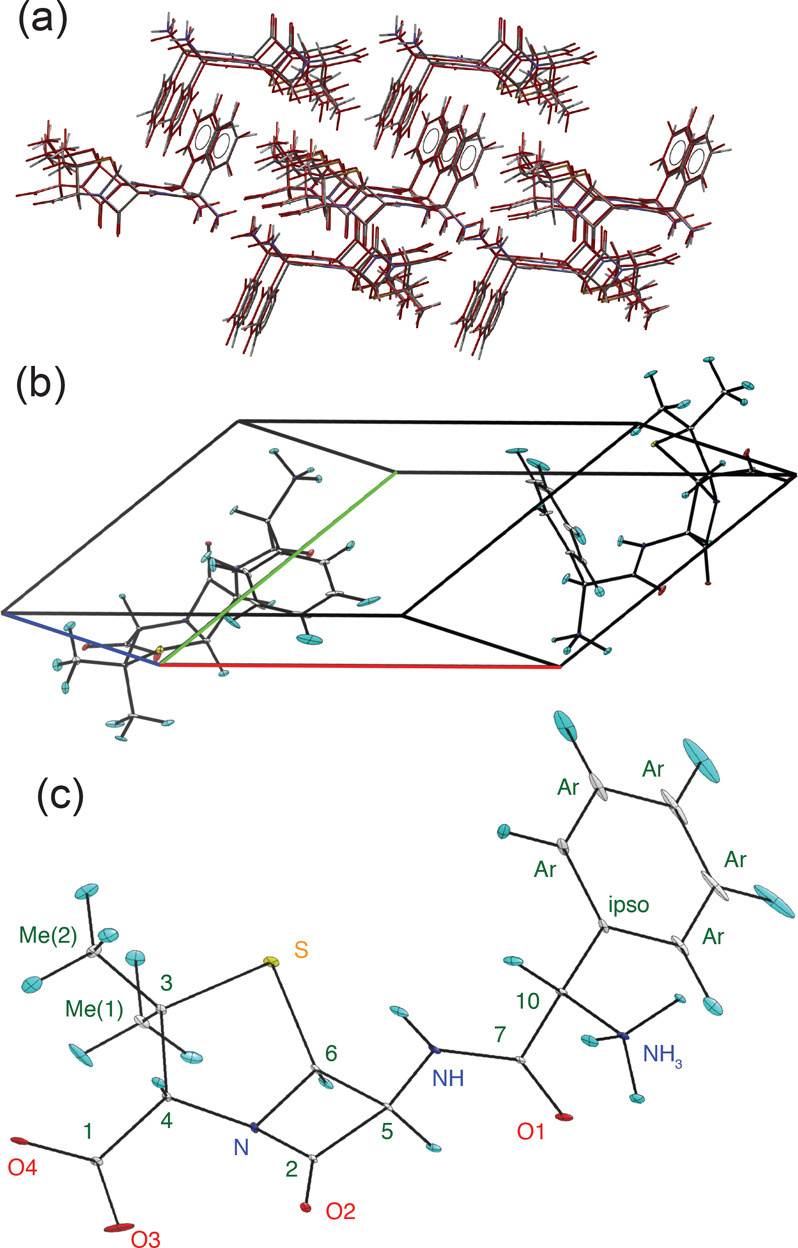
Figure 7

Open in a new tab

(a) Comparison between the structure of ampicillin as determined by the constrained powder 1H CSP-NMRX and the single-crystal XRD determined structure.83 (b,c) ORTEP plots of the ampicillin crystal (b) and single-molecule (c) structure drawn at the 90% probability level. The anisotropic ellipsoids correspond to a 1H chemical shift RMSE of 0.49 ppm and to an average positional RMSE of ⟨rav⟩ = 0.144 Å.

Finally, we proceed with a positional error analysis (see Figure S17) that leads to the fully determined structure shown in Figures 7b,c. The positional error analysis is performed using the DFT-calculated 1H chemical shifts following the procedure outlined by Hofstetter and Emsley25 and is detailed in the SI (using DFT-MD here). The average positional RMSE on the NMR powder structure is ⟨rav⟩ = 0.176 Å, which corresponds to an average equivalent displacement parameter Ueq = 0.0103 Å2. This compares with ⟨rav⟩ = 0.149 Å and Ueq = 0.0074 Å2 for the single-crystal XRD structure.83 Note that the positional RMSE on the single-crystal XRD structure only considers the heavy atoms, while the positional RMSE on the NMR powder structure also includes the 1H atoms.

4. Conclusions

The most severe limitations of CSP-based NMR crystallography are encountered when a molecule has many possible conformers and the molecular conformation adopted in the crystal could be significantly higher in energy than the most stable gas-phase conformation. In such cases, the usual energetic thresholds applied to the conformational ensemble used to generate candidate crystal structures create a risk of missing the true conformer as well as the crystal packing. Here we have demonstrated how the usual CSP-NMRX approach would have failed for a powdered sample of ampicillin due to excluding the required conformer in the first step of CSP.

However, removing any conformer selection and including all possible conformers during crystal structure generation can lead to prohibitively high computational costs. To overcome this, we have proposed a modified CSP-NMRX method which includes unambiguous prior NMR constraints, in this case 1H–13C correlations, at the conformer search stage within CSP. The key development is a novel approach that extracts unambiguous conformational constraints on the single-molecule conformations present in crystalline samples. We parametrized the proposed method on the crystal structure determinations of three flexible molecules that were previously studied using CSP-NMRX: cocaine, flutamide, and flufenamic acid. For all of these compounds we found that the method reproduces CSP-NMRX results and determines the correct crystal structure, while reducing the computational cost by between 46 and 55%. Note that these three molecules are relatively small, and the savings in computational expense will be greater for larger molecules with more conformational degrees of freedom.

We also demonstrated the capability of the novel constrained CSP-NMRX method by successfully determining the crystal structure of powdered ampicillin, which would have been very challenging for previous methods, and either requiring that no energetic limit was applied to conformational energy or likely missing the correct crystal structure. Here, a rough estimation shows that to run the CSP-NMRX calculations, including CSP search, DFT optimization, and chemical shift calculations, for all 16 conformers would take approximately 54 days on 200 dedicated CPUs. By constraining the structural search space, we were able to more than halve this for the full crystal structure determination, while ensuring that the correct conformer is not excluded. We also emphasize that the large reduction in computational resources, demonstrated here, paves the way for the CSP-NMRX-based determination of larger and more flexible molecules, which would previously have been out of the scope of the CSP-NMRX approach.

The compounds studied here were not subjected to any modification prior to the experiments, and they were investigated using powder samples at natural isotopic abundance. The resulting structures have a positional accuracy that is comparable to that of structures from, for example, single-crystal XRD, while including the positions of the light atoms.

We note that the experimentally guided CSP method demonstrated here is not limited to pure NMRX applications but that the derived constraints can be used in any crystal structure determination methodology which needs to limit the number of investigated conformations in order to reduce its computational cost.

We believe that the method is robust, and we have chosen the experimental constraints, based on 1H–13C NMR correlation experiments, for their relative simplicity and ease of access. However, we note that 1H–13C correlation-based experiments are not the only ones that can give conformational constraints. Future work could incorporate other types of experiments, such as 13C–13C correlations or more accurate 1H–13C correlation experiments, which could be simpler to parametrize. Here the extraction of the constraints was performed in a fairly basic and straightforward manner. We believe that if the constraints could be extracted in a more quantitative manner, e.g., by accounting for changes in peak intensities due to 1H–1H spin diffusion, the selection criteria can be made stronger, further reducing the conformational space and improving the computational efficiency and reliability of the methodology.

Acknowledgments

We thank Edgar A. Engel, Andrea Anelli, Felix Musil, and Prof. Michele Ceriotti (EPFL, Lausanne) for developing and parametrizing the version of ShiftML used here, details of which will be reported in another publication. We are grateful for financial support from Swiss National Science Foundation Grant No. 200021_160112. P.J.B. and G.M.D. thank the European Research Council for funding under grant ERC-StG-2012-ANGLE-307358, as well as the EPSRC via grant EP/J01110X/1. GS acknowledges Marie-Sklodowska-Curie Grant 796904. We acknowledge the use of the IRIDIS High Performance Computing Facility and associated support services at the University of Southampton. We also acknowledge the ARCHER UK National Supercomputing Service which was accessed via the UK’s HPC Materials Chemistry Consortium membership, which is funded by the EPSRC (grants EP/L000202, EP/R029431).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.9b03908.

  • Experimental details, NMR spectra and experimental chemical shitfs, calculation details, sketch-map analysis and ShiftML  details, with Figures S1–S17 and Tables S1–S9 (PDF)

  • DFT output files and structure files for all conformers and crystal structures, including the displacement parameters corresponding to the 1H chemical shift RMSD. (ZIP)

  • NMR raw data for HETCOR spectra of ampicillin (ZIP)

  • NMR raw data for HETCOR spectra of cocaine (ZIP)

  • NMR raw data for HETCOR spectra of flufenamic acid (ZIP)

  • NMR raw data for HETCOR spectra of flutamide (ZIP)

The authors declare no competing financial interest.

Supplementary Material

ja9b03908_si_001.pdf (2.1MB, pdf)
ja9b03908_si_002.zip (100.8MB, zip)
ja9b03908_si_003.zip (195.2MB, zip)
ja9b03908_si_014.zip (55.6MB, zip)
ja9b03908_si_019.zip (257.1MB, zip)
ja9b03908_si_027.zip (155MB, zip)

References

  1. Groom C. R.; Bruno I. J.; Lightfoot M. P.; Ward S. C. The Cambridge Structural Database. Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 2016, 72 (2), 171–179. 10.1107/S2052520616003954. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Grazulis S.; Chateigner D.; Downs R. T.; Yokochi A. F.; Quiros M.; Lutterotti L.; Manakova E.; Butkus J.; Moeck P.; Le Bail A. Crystallography Open Database - an open-access collection of crystal structures. J. Appl. Crystallogr. 2009, 42 (4), 726–729. 10.1107/S0021889809016690. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Grazulis S.; Daskevic A.; Merkys A.; Chateigner D.; Lutterotti L.; Quiros M.; Serebryanaya N. R.; Moeck P.; Downs R. T.; Le Bail A. Crystallography Open Database (COD): an open-access collection of crystal structures and platform for world-wide collaboration. Nucleic Acids Res. 2012, 40 (D1), D420–D427. 10.1093/nar/gkr900. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Brown I. D.; Bergerhoff G. Databases of Inorganic Crystal-Structures. Abstr. Pap. Am. Chem. Soc. 1979, (Sep), 36–36. [Google Scholar]
  5. Batisai E.; Ayamine A.; Kilinkissa O. E. Y.; Báthori N. B. Melting point–solubility–structure correlations in multicomponent crystals containing fumaric or adipic acid. CrystEngComm 2014, 16 (43), 9992–9998. 10.1039/C4CE01298D. [DOI] [Google Scholar]
  6. Rietveld H. M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969, 2 (2), 65–71. 10.1107/S0021889869006558. [DOI] [Google Scholar]
  7. Gorelik T. E.; Czech C.; Hammer S. M.; Schmidt M. U. Crystal structure of disordered nanocrystalline αII-quinacridone determined by electron diffraction. CrystEngComm 2016, 18 (4), 529–535. 10.1039/C5CE01855B. [DOI] [Google Scholar]
  8. Das P. P.; Mugnaioli E.; Nicolopoulos S.; Tossi C.; Gemmi M.; Galanis A.; Borodi G.; Pop M. M. Crystal Structures of Two Important Pharmaceuticals Solved by 3D Precession Electron Diffraction Tomography. Org. Process Res. Dev. 2018, 22 (10), 1365–1372. 10.1021/acs.oprd.8b00149. [DOI] [Google Scholar]
  9. Gruene T.; Wennmacher J. T. C.; Zaubitzer C.; Holstein J. J.; Heidler J.; Fecteau-Lefebvre A.; De Carlo S.; Muller E.; Goldie K. N.; Regeni I.; Li T.; Santiso-Quinones G.; Steinfeld G.; Handschin S.; van Genderen E.; van Bokhoven J. A.; Clever G. H.; Pantelic R. Rapid Structure Determination of Microcrystalline Molecular Compounds Using Electron Diffraction. Angew. Chem., Int. Ed. 2018, 57 (50), 16313–16317. 10.1002/anie.201811318. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Jones C. G.; Martynowycz M. W.; Hattne J.; Fulton T. J.; Stoltz B. M.; Rodriguez J. A.; Nelson H. M.; Gonen T. The CryoEM Method MicroED as a Powerful Tool for Small Molecule Structure Determination. ACS Cent. Sci. 2018, 4 (11), 1587–1592. 10.1021/acscentsci.8b00760. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. de Dios A.; Pearson J.; Oldfield E. Secondary and tertiary structural effects on protein NMR chemical shifts: an ab initio approach. Science 1993, 260 (5113), 1491–1496. 10.1126/science.8502992. [DOI] [PubMed] [Google Scholar]
  12. Facelli J. C.; Grant D. M. Determination of molecular symmetry in crystalline naphthalene using solid-state NMR. Nature 1993, 365 (6444), 325–7. 10.1038/365325a0. [DOI] [PubMed] [Google Scholar]
  13. Sebastiani D.; Parrinello M. A New ab-Initio Approach for NMR Chemical Shifts in Periodic Systems. J. Phys. Chem. A 2001, 105 (10), 1951–1958. 10.1021/jp002807j. [DOI] [Google Scholar]
  14. Blochl P. E. Projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50 (24), 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  15. Pickard C. J.; Mauri F. All-electron magnetic response with pseudopotentials: NMR chemical shifts. Phys. Rev. B: Condens. Matter Mater. Phys. 2001, 63 (24), 245101. 10.1103/PhysRevB.63.245101. [DOI] [Google Scholar]
  16. Yates J. R.; Pickard C. J.; Mauri F. Calculation of NMR chemical shifts for extended systems using ultrasoft pseudopotentials. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 76 (2), 024401. 10.1103/PhysRevB.76.024401. [DOI] [Google Scholar]
  17. Cuny J.; Xie Y.; Pickard C. J.; Hassanali A. A. Ab Initio Quality NMR Parameters in Solid-State Materials Using a High-Dimensional Neural-Network Representation. J. Chem. Theory Comput. 2016, 12 (2), 765–73. 10.1021/acs.jctc.5b01006. [DOI] [PubMed] [Google Scholar]
  18. Paruzzo F. M.; Hofstetter A.; Musil F.; De S.; Ceriotti M.; Emsley L. Chemical shifts in molecular solids by machine learning. Nat. Commun. 2018, 9 (1), 4501. 10.1038/s41467-018-06972-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Baias M.; Dumez J. N.; Svensson P. H.; Schantz S.; Day G. M.; Emsley L. De novo determination of the crystal structure of a large drug molecule by crystal structure prediction-based powder NMR crystallography. J. Am. Chem. Soc. 2013, 135 (46), 17501–7. 10.1021/ja4088874. [DOI] [PubMed] [Google Scholar]
  20. Fernandes J. A.; Sardo M.; Mafra L.; Choquesillo-Lazarte D.; Masciocchi N. X-ray and NMR Crystallography Studies of Novel Theophylline Cocrystals Prepared by Liquid Assisted Grinding. Cryst. Growth Des. 2015, 15 (8), 3674–3683. 10.1021/acs.cgd.5b00279. [DOI] [Google Scholar]
  21. Leclaire J.; Poisson G.; Ziarelli F.; Pepe G.; Fotiadu F.; Paruzzo F. M.; Rossini A. J.; Dumez J. N.; Elena-Herrmann B.; Emsley L. Structure elucidation of a complex CO2-based organic framework material by NMR crystallography. Chem. Sci. 2016, 7 (7), 4379–4390. 10.1039/C5SC03810C. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Selent M.; Nyman J.; Roukala J.; Ilczyszyn M.; Oilunkaniemi R.; Bygrave P. J.; Laitinen R.; Jokisaari J.; Day G. M.; Lantto P. Clathrate Structure Determination by Combining Crystal Structure Prediction with Computational and Experimental (129) Xe NMR Spectroscopy. Chem. - Eur. J. 2017, 23 (22), 5258–5269. 10.1002/chem.201604797. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Widdifield C. M.; Nilsson Lill S. O.; Broo A.; Lindkvist M.; Pettersen A.; Svensk Ankarberg A.; Aldred P.; Schantz S.; Emsley L. Does Z’ equal 1 or 2? Enhanced powder NMR crystallography verification of a disordered room temperature crystal structure of a p38 inhibitor for chronic obstructive pulmonary disease. Phys. Chem. Chem. Phys. 2017, 19 (25), 16650–16661. 10.1039/C7CP02349A. [DOI] [PubMed] [Google Scholar]
  24. Nilsson Lill S. O.; Widdifield C. M.; Pettersen A.; Svensk Ankarberg A.; Lindkvist M.; Aldred P.; Gracin S.; Shankland N.; Shankland K.; Schantz S.; Emsley L. Elucidating an Amorphous Form Stabilization Mechanism for Tenapanor Hydrochloride: Crystal Structure Analysis Using X-ray Diffraction, NMR Crystallography, and Molecular Modeling. Mol. Pharmaceutics 2018, 15 (4), 1476–1487. 10.1021/acs.molpharmaceut.7b01047. [DOI] [PubMed] [Google Scholar]
  25. Hofstetter A.; Emsley L. Positional Variance in NMR Crystallography. J. Am. Chem. Soc. 2017, 139 (7), 2573–2576. 10.1021/jacs.6b12705. [DOI] [PubMed] [Google Scholar]
  26. Harper J. K.; Mulgrew A. E.; Li J. Y.; Barich D. H.; Strobel G. A.; Grant D. M. Characterization of stereochemistry and molecular conformation using solid-state NMR tensors. J. Am. Chem. Soc. 2001, 123 (40), 9837–9842. 10.1021/ja010997l. [DOI] [PubMed] [Google Scholar]
  27. Harper J. K.; Grant D. M. Enhancing Crystal-Structure Prediction with NMR Tensor Data. Cryst. Growth Des. 2006, 6 (10), 2315–2321. 10.1021/cg060244g. [DOI] [Google Scholar]
  28. Heider E. M.; Harper J. K.; Grant D. M. Structural characterization of an anhydrous polymorph of paclitaxel by solid-state NMR. Phys. Chem. Chem. Phys. 2007, 9 (46), 6083–97. 10.1039/b711027h. [DOI] [PubMed] [Google Scholar]
  29. Witter R.; Priess W.; Sternberg U. Chemical shift driven geometry optimization. J. Comput. Chem. 2002, 23 (2), 298–305. 10.1002/jcc.10012. [DOI] [PubMed] [Google Scholar]
  30. Sternberg U.; Koch F.-T.; Prieß W.; Witter R. Crystal structure refinements of cellulose polymorphs using solid state 13C chemical shifts. Cellulose 2003, 10 (3), 189–199. 10.1023/A:1025185416154. [DOI] [Google Scholar]
  31. Ochsenfeld C.; Brown S. P.; Schnell I.; Gauss J.; Spiess H. W. Structure assignment in the solid state by the coupling of quantum chemical calculations with NMR experiments: a columnar hexabenzocoronene derivative. J. Am. Chem. Soc. 2001, 123 (11), 2597–606. 10.1021/ja0021823. [DOI] [PubMed] [Google Scholar]
  32. Goward G. R.; Sebastiani D.; Schnell I.; Spiess H. W.; Kim H. D.; Ishida H. Benzoxazine oligomers: evidence for a helical structure from solid-state NMR spectroscopy and DFT-based dynamics and chemical shift calculations. J. Am. Chem. Soc. 2003, 125 (19), 5792–800. 10.1021/ja029059r. [DOI] [PubMed] [Google Scholar]
  33. Harris R. K. NMR crystallography: the use of chemical shifts. Solid State Sci. 2004, 6 (10), 1025–1037. 10.1016/j.solidstatesciences.2004.03.040. [DOI] [Google Scholar]
  34. Harris R. K. NMR studies of organic polymorphs and solvates. Analyst 2006, 131 (3), 351–73. 10.1039/b516057j. [DOI] [PubMed] [Google Scholar]
  35. Mifsud N.; Elena B.; Pickard C. J.; Lesage A.; Emsley L. Assigning powders to crystal structures by high-resolution (1)H-(1)H double quantum and (1)H-(13)C J-INEPT solid-state NMR spectroscopy and first principles computation. A case study of penicillin G. Phys. Chem. Chem. Phys. 2006, 8 (29), 3418–22. 10.1039/B605227D. [DOI] [PubMed] [Google Scholar]
  36. Harris R. K. Applications of solid-state NMR to pharmaceutical polymorphism and related matters. J. Pharm. Pharmacol. 2007, 59 (2), 225–39. 10.1211/jpp.59.2.0009. [DOI] [PubMed] [Google Scholar]
  37. Othman A.; Evans J. S.; Evans I. R.; Harris R. K.; Hodgkinson P. Structural study of polymorphs and solvates of finasteride. J. Pharm. Sci. 2007, 96 (5), 1380–97. 10.1002/jps.20940. [DOI] [PubMed] [Google Scholar]
  38. Salager E.; Stein R. S.; Pickard C. J.; Elena B.; Emsley L. Powder NMR crystallography of thymol. Phys. Chem. Chem. Phys. 2009, 11 (15), 2610–21. 10.1039/b821018g. [DOI] [PubMed] [Google Scholar]
  39. Salager E.; Day G. M.; Stein R. S.; Pickard C. J.; Elena B.; Emsley L. Powder crystallography by combined crystal structure prediction and high-resolution 1H solid-state NMR spectroscopy. J. Am. Chem. Soc. 2010, 132 (8), 2564–6. 10.1021/ja909449k. [DOI] [PubMed] [Google Scholar]
  40. Webber A. L.; Emsley L.; Claramunt R. M.; Brown S. P. NMR crystallography of campho[2,3-c]pyrazole (Z’ = 6): combining high-resolution 1H-13C solid-state MAS NMR spectroscopy and GIPAW chemical-shift calculations. J. Phys. Chem. A 2010, 114 (38), 10435–42. 10.1021/jp104901j. [DOI] [PubMed] [Google Scholar]
  41. Dudenko D.; Kiersnowski A.; Shu J.; Pisula W.; Sebastiani D.; Spiess H. W.; Hansen M. R. A strategy for revealing the packing in semicrystalline pi-conjugated polymers: crystal structure of bulk poly-3-hexyl-thiophene (P3HT). Angew. Chem., Int. Ed. 2012, 51 (44), 11068–72. 10.1002/anie.201205075. [DOI] [PubMed] [Google Scholar]
  42. Baias M.; Widdifield C. M.; Dumez J. N.; Thompson H. P.; Cooper T. G.; Salager E.; Bassil S.; Stein R. S.; Lesage A.; Day G. M.; Emsley L. Powder crystallography of pharmaceutical materials by combined crystal structure prediction and solid-state 1H NMR spectroscopy. Phys. Chem. Chem. Phys. 2013, 15 (21), 8069–80. 10.1039/c3cp41095a. [DOI] [PubMed] [Google Scholar]
  43. Pawlak T.; Jaworska M.; Potrzebowski M. J. NMR crystallography of alpha-poly(L-lactide). Phys. Chem. Chem. Phys. 2013, 15 (9), 3137–45. 10.1039/c2cp43174b. [DOI] [PubMed] [Google Scholar]
  44. Santos S. M.; Rocha J.; Mafra L. NMR Crystallography: Toward Chemical Shift-Driven Crystal Structure Determination of the β-Lactam Antibiotic Amoxicillin Trihydrate. Cryst. Growth Des. 2013, 13 (6), 2390–2395. 10.1021/cg4002785. [DOI] [Google Scholar]
  45. Koike R.; Higashi K.; Liu N.; Limwikrant W.; Yamamoto K.; Moribe K. Structural Determination of a Novel Polymorph of Sulfathiazole–Oxalic Acid Complex in Powder Form by Solid-State NMR Spectroscopy on the Basis of Crystallographic Structure of Another Polymorph. Cryst. Growth Des. 2014, 14 (9), 4510–4518. 10.1021/cg5005903. [DOI] [Google Scholar]
  46. Ludeker D.; Brunklaus G. NMR crystallography of ezetimibe co-crystals. Solid State Nucl. Magn. Reson. 2015, 65, 29–40. 10.1016/j.ssnmr.2014.11.002. [DOI] [PubMed] [Google Scholar]
  47. Paluch P.; Pawlak T.; Oszajca M.; Lasocha W.; Potrzebowski M. J. Fine refinement of solid state structure of racemic form of phospho-tyrosine employing NMR Crystallography approach. Solid State Nucl. Magn. Reson. 2015, 65, 2–11. 10.1016/j.ssnmr.2014.08.002. [DOI] [PubMed] [Google Scholar]
  48. Pinon A. C.; Rossini A. J.; Widdifield C. M.; Gajan D.; Emsley L. Polymorphs of Theophylline Characterized by DNP Enhanced Solid-State NMR. Mol. Pharmaceutics 2015, 12 (11), 4146–53. 10.1021/acs.molpharmaceut.5b00610. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Kalakewich K.; Iuliucci R.; Mueller K. T.; Eloranta H.; Harper J. K. Monitoring the refinement of crystal structures with (15)N solid-state NMR shift tensor data. J. Chem. Phys. 2015, 143 (19), 194702. 10.1063/1.4935367. [DOI] [PubMed] [Google Scholar]
  50. Watts A. E.; Maruyoshi K.; Hughes C. E.; Brown S. P.; Harris K. D. M. Combining the Advantages of Powder X-ray Diffraction and NMR Crystallography in Structure Determination of the Pharmaceutical Material Cimetidine Hydrochloride. Cryst. Growth Des. 2016, 16 (4), 1798–1804. 10.1021/acs.cgd.6b00016. [DOI] [Google Scholar]
  51. Widdifield C. M.; Robson H.; Hodgkinson P. Furosemide’s one little hydrogen atom: NMR crystallography structure verification of powdered molecular organics. Chem. Commun. 2016, 52 (40), 6685–8. 10.1039/C6CC02171A. [DOI] [PubMed] [Google Scholar]
  52. Mali G. Ab initio crystal structure prediction of magnesium (poly)sulfides and calculation of their NMR parameters. Acta Crystallogr., Sect. C: Struct. Chem. 2017, 73 (3), 229–233. 10.1107/S2053229617000687. [DOI] [PubMed] [Google Scholar]
  53. Hartman J. D.; Day G. M.; Beran G. J. Enhanced NMR Discrimination of Pharmaceutically Relevant Molecular Crystal Forms through Fragment-Based Ab Initio Chemical Shift Predictions. Cryst. Growth Des. 2016, 16 (11), 6479–6493. 10.1021/acs.cgd.6b01157. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Hartman J. D.; Kudla R. A.; Day G. M.; Mueller L. J.; Beran G. J. Benchmark fragment-based (1)H, (13)C, (15)N and (17)O chemical shift predictions in molecular crystals. Phys. Chem. Chem. Phys. 2016, 18 (31), 21686–709. 10.1039/C6CP01831A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Hartman J. D.; Beran G. J. O. Accurate 13-C and 15-N molecular crystal chemical shielding tensors from fragment-based electronic structure theory. Solid State Nucl. Magn. Reson. 2018, 96, 10–18. 10.1016/j.ssnmr.2018.09.003. [DOI] [PubMed] [Google Scholar]
  56. Neumann M. A.; van de Streek J.; Fabbiani F. P.; Hidber P.; Grassmann O. Combined crystal structure prediction and high-pressure crystallization in rational pharmaceutical polymorph screening. Nat. Commun. 2015, 6, 7793. 10.1038/ncomms8793. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Baias M.; Lesage A.; Aguado S.; Canivet J.; Moizan-Basle V.; Audebrand N.; Farrusseng D.; Emsley L. Superstructure of a substituted zeolitic imidazolate metal-organic framework determined by combining proton solid-state NMR spectroscopy and DFT calculations. Angew. Chem., Int. Ed. 2015, 54 (20), 5971–6. 10.1002/anie.201500518. [DOI] [PubMed] [Google Scholar]
  58. Thompson H. P. G.; Day G. M. Which conformations make stable crystal structures? Mapping crystalline molecular geometries to the conformational energy landscape. Chem. Sci. 2014, 5 (8), 3173–3182. 10.1039/C4SC01132E. [DOI] [Google Scholar]
  59. Reilly A. M.; Cooper R. I.; Adjiman C. S.; Bhattacharya S.; Boese A. D.; Brandenburg J. G.; Bygrave P. J.; Bylsma R.; Campbell J. E.; Car R.; Case D. H.; Chadha R.; Cole J. C.; Cosburn K.; Cuppen H. M.; Curtis F.; Day G. M.; DiStasio R. A. Jr.; Dzyabchenko A.; van Eijck B. P.; Elking D. M.; van den Ende J. A.; Facelli J. C.; Ferraro M. B.; Fusti-Molnar L.; Gatsiou C. A.; Gee T. S.; de Gelder R.; Ghiringhelli L. M.; Goto H.; Grimme S.; Guo R.; Hofmann D. W.; Hoja J.; Hylton R. K.; Iuzzolino L.; Jankiewicz W.; de Jong D. T.; Kendrick J.; de Klerk N. J.; Ko H. Y.; Kuleshova L. N.; Li X.; Lohani S.; Leusen F. J.; Lund A. M.; Lv J.; Ma Y.; Marom N.; Masunov A. E.; McCabe P.; McMahon D. P.; Meekes H.; Metz M. P.; Misquitta A. J.; Mohamed S.; Monserrat B.; Needs R. J.; Neumann M. A.; Nyman J.; Obata S.; Oberhofer H.; Oganov A. R.; Orendt A. M.; Pagola G. I.; Pantelides C. C.; Pickard C. J.; Podeszwa R.; Price L. S.; Price S. L.; Pulido A.; Read M. G.; Reuter K.; Schneider E.; Schober C.; Shields G. P.; Singh P.; Sugden I. J.; Szalewicz K.; Taylor C. R.; Tkatchenko A.; Tuckerman M. E.; Vacarro F.; Vasileiadis M.; Vazquez-Mayagoitia A.; Vogt L.; Wang Y.; Watson R. E.; de Wijs G. A.; Yang J.; Zhu Q.; Groom C. R. Report on the sixth blind test of organic crystal structure prediction methods. Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 2016, 72 (4), 439–459. 10.1107/S2052520616007447. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Chierotti M. R.; Gobetto R. NMR crystallography: the use of dipolar interactions in polymorph and co-crystal investigation. CrystEngComm 2013, 15 (43), 8599. 10.1039/c3ce41026a. [DOI] [Google Scholar]
  61. Harper J. K.; Barich D. H.; Hu J. Z.; Strobel G. A.; Grant D. M. Stereochemical analysis by solid-state NMR: structural predictions in ambuic acid. J. Org. Chem. 2003, 68 (12), 4609–14. 10.1021/jo020377i. [DOI] [PubMed] [Google Scholar]
  62. Powell J.; Kalakewich K.; Uribe-Romo F. J.; Harper J. K. Solid-state NMR and DFT predictions of differences in COOH hydrogen bonding in odd and even numbered n-alkyl fatty acids. Phys. Chem. Chem. Phys. 2016, 18 (18), 12541–9. 10.1039/C6CP00416D. [DOI] [PubMed] [Google Scholar]
  63. Roberts J. E.; Harbison G. S.; Munowitz M. G.; Herzfeld J.; Griffin R. G. Measurement of heteronuclear bond distances in polycrystalline solids by solid-state NMR techniques. J. Am. Chem. Soc. 1987, 109 (14), 4163–4169. 10.1021/ja00248a006. [DOI] [Google Scholar]
  64. Colombo M.; Meier B.; Ernst R. Rotor-driven spin diffusion in natural-abundance 13C spin systems. Chem. Phys. Lett. 1988, 146 (3–4), 189–196. 10.1016/0009-2614(88)87429-3. [DOI] [Google Scholar]
  65. Raleigh D.; Levitt M.; Griffin R. Rotational resonance in solid state NMR. Chem. Phys. Lett. 1988, 146 (1–2), 71–76. 10.1016/0009-2614(88)85051-6. [DOI] [Google Scholar]
  66. Van Rossum B.-J.; De Groot C. P.; Ladizhansky V.; Vega S.; De Groot H. J. M. A method for measuring heteronuclear (1H-13C) distances in high speed MAS NMR. J. Am. Chem. Soc. 2000, 122 (14), 3465–3472. 10.1021/ja992714j. [DOI] [Google Scholar]
  67. Castellani F.; van Rossum B.; Diehl A.; Schubert M.; Rehbein K.; Oschkinat H. Structure of a protein determined by solid-state magic-angle-spinning NMR spectroscopy. Nature 2002, 420 (6911), 99–102. 10.1038/nature01070. [DOI] [PubMed] [Google Scholar]
  68. Seidel K.; Etzkorn M.; Sonnenberg L.; Griesinger C.; Sebald A.; Baldus M. Studying molecular 3D structure and dynamics by high-resolution solid-state NMR: Application to L-tyrosine-ethylester. J. Phys. Chem. A 2005, 109 (11), 2436–42. 10.1021/jp045605m. [DOI] [PubMed] [Google Scholar]
  69. Elena B.; Pintacuda G.; Mifsud N.; Emsley L. Molecular structure determination in powders by NMR crystallography from proton spin diffusion. J. Am. Chem. Soc. 2006, 128 (29), 9555–60. 10.1021/ja062353p. [DOI] [PubMed] [Google Scholar]
  70. Mollica G.; Dekhil M.; Ziarelli F.; Thureau P.; Viel S. Quantitative structural constraints for organic powders at natural isotopic abundance using dynamic nuclear polarization solid-state NMR spectroscopy. Angew. Chem., Int. Ed. 2015, 54 (20), 6028–31. 10.1002/anie.201501172. [DOI] [PubMed] [Google Scholar]
  71. Dekhil M.; Mollica G.; Bonniot T. T.; Ziarelli F.; Thureau P.; Viel S. Determining carbon-carbon connectivities in natural abundance organic powders using dipolar couplings. Chem. Commun. 2016, 52 (55), 8565–8. 10.1039/C6CC04202C. [DOI] [PubMed] [Google Scholar]
  72. Märker K.; Paul S.; Fernández-De-Alba C.; Lee D.; Mouesca J.-M.; Hediger S.; De Paëpe G. Welcoming natural isotopic abundance in solid-state NMR: probing π-stacking and supramolecular structure of organic nanoassemblies using DNP. Chem. Sci. 2017, 8 (2), 974–987. 10.1039/C6SC02709A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Thureau P.; Sturniolo S.; Zilka M.; Ziarelli F.; Viel S.; Yates J. R.; Mollica G. Reducing the computational cost of NMR crystallography of organic powders at natural isotopic abundance with the help of (13) C-(13) C dipolar couplings. Magn. Reson. Chem. 2019, 57 (5), 256–264. 10.1002/mrc.4848. [DOI] [PubMed] [Google Scholar]
  74. Gu Z.; Ridenour C. F.; Bronnimann C. E.; Iwashita T.; McDermott A. Hydrogen Bonding and Distance Studies of Amino Acids and Peptides Using Solid State 2D1–13C Heteronuclear Correlation Spectra. J. Am. Chem. Soc. 1996, 118 (4), 822–829. 10.1021/ja952130r. [DOI] [Google Scholar]
  75. Cerrioti M.; De S.; Meissner R. H.; Tribello G. A.. Sketch map package, https://github.com/cosmo-epfl/sketchmap/.
  76. Ceriotti M.; Tribello G. A.; Parrinello M. From the Cover: Simplifying the representation of complex free-energy landscapes using sketch-map. Proc. Natl. Acad. Sci. U. S. A. 2011, 108 (32), 13023–8. 10.1073/pnas.1108486108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  77. De S.; Bartok A. P.; Csanyi G.; Ceriotti M. Comparing molecules and solids across structural and alchemical space. Phys. Chem. Chem. Phys. 2016, 18 (20), 13754–69. 10.1039/C6CP00415F. [DOI] [PubMed] [Google Scholar]
  78. De S.; Musil F.; Ingram T.; Baldauf C.; Ceriotti M. Mapping and classifying molecules from a high-throughput structural database. J. Cheminf. 2017, 9, 6. 10.1186/s13321-017-0192-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  79. Antzutkin O. N.; Lee Y. K.; Levitt M. H. 13C and 15N-chemical shift anisotropy of ampicillin and penicillin-V studied by 2D-PASS and CP/MAS NMR. J. Magn. Reson. 1998, 135 (1), 144–55. 10.1006/jmre.1998.1576. [DOI] [PubMed] [Google Scholar]
  80. Case D. H.; Campbell J. E.; Bygrave P. J.; Day G. M. Convergence Properties of Crystal Structure Prediction by Quasi-Random Sampling. J. Chem. Theory Comput. 2016, 12 (2), 910–24. 10.1021/acs.jctc.5b01112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  81. Price S. L.; Leslie M.; Welch G. W. A.; Habgood M.; Price L. S.; Karamertzanis P. G.; Day G. M. Modelling organic crystal structures using distributed multipole and polarizability-based model intermolecular potentials. Phys. Chem. Chem. Phys. 2010, 12 (30), 8478–8490. 10.1039/c004164e. [DOI] [PubMed] [Google Scholar]
  82. Nyman J.; Day G. M. Static and lattice vibrational energy differences between polymorphs. CrystEngComm 2015, 17 (28), 5154–5165. 10.1039/C5CE00045A. [DOI] [Google Scholar]
  83. Boles M. O.; Girven R. J. The structures of ampicillin: a comparison of the anhydrate and trihydrate forms. Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem. 1976, 32 (8), 2279–2284. 10.1107/S0567740876007590. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja9b03908_si_001.pdf (2.1MB, pdf)
ja9b03908_si_002.zip (100.8MB, zip)
ja9b03908_si_003.zip (195.2MB, zip)
ja9b03908_si_014.zip (55.6MB, zip)
ja9b03908_si_019.zip (257.1MB, zip)
ja9b03908_si_027.zip (155MB, zip)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES