A Matrix-free Likelihood Method for Exploratory Factor Analysis of High-dimensional Gaussian Data

Abstract

This paper proposes a novel profile likelihood method for estimating the covariance parameters in exploratory factor analysis of high-dimensional Gaussian datasets with fewer observations than number of variables. An implicitly restarted Lanczos algorithm and a limited-memory quasi-Newton method are implemented to develop a matrix-free framework for likelihood maximization. Simulation results show that our method is substantially faster than the expectation-maximization solution without sacrificing accuracy. Our method is applied to fit factor models on data from suicide attempters, suicide ideators and a control group.

1. Introduction

Factor analysis (Anderson, 2003) is a multivariate statistical technique that characterizes dependence among variables using a small number of latent factors. Suppose that we have a sample ${\mathbf{Y}}_1,{\mathbf{Y}}_2,\dots ,{\mathbf{Y}}_n$ from the p-variate Gaussian distribution ${\mathcal{N}}_p(\mathit{\mu },\mathbf{\Sigma })$ with mean vector μ and a covariance matrix Σ. We assume that $\mathbf{\Sigma }=\mathbf{\Lambda }{\mathbf{\Lambda }}^{\top }+\mathbf{\Psi },$ where $\mathbf{\Lambda }$ is a p × q matrix of rank q that describes the amount of variance shared among the p coordinates and $\mathbf{\Psi }$ is a diagonal matrix with positive diagonal entries representing the unique variance specific to each coordinate. Factor analysis of Gaussian data for p < n was first formalized by Lawley (1940) with efficient maximum likelihood (ML) estimation methods proposed by Jöreskog (1967); Lawley and Maxwell (1962); Mardia et al. (2006); Anderson (2003) and others. These methods however do not apply to datasets with p > n that occur in applications such as the processing of microarray data (Sundberg and Feldmann, 2016), sequencing data (Leek and Storey, 2007; Leek, 2014; Buettner et al., 2017), analyzing the transcription factor activity profiles of gene regulatory networks using massive gene expression datasets (Pournara and Wernisch, 2007), portfolio analysis in stock returns (Ng et al., 2014) and others (Trendafilov and Unkel, 2011). Necessary and sufficient conditions for the existence of MLE when p > n have been obtained by Robertson and Symons (2007). In such cases, the available computer memory may be inadequate to store the sample covariance matrix S or to make multiple copies of the dataset needed during the computation.

The expectation-maximization (EM) approach of Rubin and Thayer (1982) can be applied to datasets with p > n but is computationally slow. So, here we develop a profile likelihood method for high-dimensional Gaussian data. Our method allows us to compute the gradient of the profile likelihood function at negligible additional computational cost and to check first-order optimality, guaranteeing high accuracy. We develop a fast sophisticated computational framework called FAD (Factor Analysis of Data) to compute ML estimates of $\mathrm{\Lambda }\text{and}\mathrm{\Psi }.$ Our framework is implemented in an R (R Core Team, 2019) package called fad.

The remainder of this paper is organized as follows. Section 2 describes the factor model for Gaussian data and an ML solution using the EM algorithm, and then proposes the profile likelihood and FAD. The performance of FAD relative to EM is evaluated in Section 3. Section 4 applies our methodology on a functional magnetic resonance imaging (fMRI) dataset related to suicidal behavior (Just et al., 2017). Section 5 concludes with some discussion. An online supplement, with sections, tables and figures referenced here with the prefix “S”, is available.

2. Methodology

2.1. Background and Preliminaries

Let Y be the n × p data matrix with Y_i as its ith row. Then, in the setup of Section 1, the ML method profiles out μ using the sample mean vector and then maximizes the log-likelihood,

$$\mathcal{l}(\mathrm{\Lambda },\mathrm{\Psi })=-\frac{n}{2}\left\{p\log (2\pi )+\log \det \mathrm{\Sigma }+\mathrm{Tr}{\mathrm{\Sigma }}^{-1}\mathbf{S}\right\}$$ (1)

where $\overline{\mathbf{Y}}={\mathbf{Y}}^{\top }\mathbf{1}/n,\mathbf{S}={(\mathbf{Y}-\mathbf{1}{\overline{\mathbf{Y}}}^{\top })}^{\top }(\mathbf{Y}-\mathbf{1}{\overline{\mathbf{Y}}}^{\top })/n,$ where 1 is the vector of 1s. The matrix S is almost surely singular and has rank n when p > n The factor model (1) is not identifiable because the matrices $\mathrm{\Lambda }\text{and}\mathrm{\Lambda }\mathbf{Q}$ give rise to the same likelihood for any orthogonal matrix Q So, additional constraints (see Anderson, 2003; Mardia et al., 2006, for more details) are imposed.

2.1.1. EM Algorithms for parameter estimation

The EM algorithm (Rubin and Thayer, 1982; McLachlan and Krishnan, 1996) exploits the structure of the factor covariance matrix by assuming q-variate standard normal latent factors and writing the factor model as ${\mathbf{Y}}_i=\mathit{\mu }+\mathbf{\Lambda }{\mathbf{Z}}_i+{\mathit{ϵ}}_i$ where ${\mathit{ϵ}}_i\text{’s}$ are i.i.d ${\mathcal{N}}_p(\mathbf{0},\mathbf{\Psi })\text{and}{\mathbf{Z}}_i’\text{s}$ are independent of ${\mathit{ϵ}}_i\text{’s}$. The EM algorithm is easily developed, with analytical expressions for both the expectation (E-step) and maximization (M-step) steps that can be speedily computed (see Section S1.1).

Although EM algorithms are guaranteed to increase the likelihood at each iteration and converge to a local maximum, they are well-known for their slow convergence. Further, these iterations run in a $(pq+p)$-dimensional space that can be slow for very large p. Accelerated variants (Liu and Rubin, 2002; Varadhan and Roland, 2008) show superior performance in lowdimensional problems but come with additional computational overhead that dominates the gain in rate of convergence in high dimensions. EM algorithms also compromise on numerical accuracy by not checking for first-order optimality to enhance speed. So, we next develop a fast and accurate method for exploratory factor analysis (EFA) that is applicable in high dimensions.

2.2. Profile likelihood for parameter estimation

We start with the common and computationally useful identifiability restriction on $\mathrm{\Lambda }$ that constrains $\mathbf{\Gamma }={\mathrm{\Lambda }}^{\top }{\mathrm{\Psi }}^{-1}\mathrm{\Lambda }$ to be diagonal with decreasing diagonal entries. This scale-invariant constraint is completely determined except for changes in sign in the columns of $\mathrm{\Lambda }.$ Under this constraint, $\mathrm{\Lambda }$ can be profiled out for a given $\mathrm{\Psi }$ as described in the following

Lemma 1. Suppose that $\mathrm{\Psi }$ is a given p.d. diagonal matrix. Suppose that the q largest singular values of $\mathbf{W}=n^{-1/2}\left(\mathbf{Y}-\mathbf{1}{\overline{\mathbf{Y}}}^{\top }\right){\mathrm{\Psi }}^{-1/2}\mathit{\text{are}}\sqrt{{\theta }_1}\ge \sqrt{{\theta }_2}\ge \cdots \ge \sqrt{{\theta }_q}$ and the corresponding p-dimensional right-singular vectors are the columns of V_q Then the function $\mathrm{\Lambda }\mapsto \mathcal{l}(\mathrm{\Lambda },\mathrm{\Psi })$ is maximized at $\widehat{\mathrm{\Lambda }}={\mathrm{\Psi }}^{1/2}{\mathbf{V}}_q\mathbf{\Delta },$ where Δ is a q × q diagonal matrix with ith diagonal entry as ${\left[\max \left({\theta }_i-1,0\right)\right]}^{1/2}.$ The profile log-likelihood equals,

$${\mathcal{l}}_p(\mathrm{\Psi })=c-\frac{n}{2}\left\{\log \det \mathrm{\Psi }+\mathrm{Tr}{\mathrm{\Psi }}^{-1}\mathbf{S}+\sum _{i=1}^q\left(\log {\theta }_i-{\theta }_i+1\right)\right\}$$ (2)

where c is a constant that depends only on Y, n, p and q but not on $\mathrm{\Psi }.$

Furthermore, the gradient of ${\mathcal{l}}_p(\mathrm{\Psi })$ is given by:

$$\nabla {\mathcal{l}}_p(\mathrm{\Psi })=-\frac{n}{2}\mathrm{diag}(\widehat{\mathrm{\Lambda }}{\widehat{\mathrm{\Lambda }}}^{\top }+\mathrm{\Psi }-\mathbf{S}).$$

Proof. See Section S1.2. □

The profile log-likelihood ${\mathcal{l}}_p(\mathrm{\Psi })$ in (2) depends on Y only through the q largest singular values of W So, in order to compute ${\mathcal{l}}_p(\mathrm{\Psi })\text{and}\nabla {\mathcal{l}}_p(\mathrm{\Psi })$ we need to only compute the q largest singular values of W and the right singular vectors. For q << min(n, P), as is usually the case, these largest singular values and singular vectors can be computed very fast using Lanczos algorithm.

Further constraints on $\mathbf{\Psi }(\text{e.g.}\mathbf{\Psi }={\sigma }^2{\mathbf{I}}_p,{\sigma }^2>0)$ can be easily incorporated. Also, $\nabla {\mathcal{l}}_p(\mathrm{\Psi })$ is available in closed form that enables us to check first-order optimality and ensure high accuracy.

Finally, ${\mathcal{l}}_p(\mathrm{\Psi })$ is expressed in terms of S However, ML estimators are scale-equivariant, so we can estimate $\mathrm{\Lambda }\text{and}\mathrm{\Psi }$ using the correlation matrix and scale back to S. A particular advantage of using the sample correlation matrix is that ${\mathcal{l}}_p(\mathrm{\Psi })$ needs to be optimized over a fixed bounded rectangle (0,1)^p that does not depend on the data and is conceivably numerically robust.

2.3. Matrix-free computations

2.3.1. A Lanczos algorithm for calculating partial singular values and vectors

In order to compute the profile likelihood and its gradient, we need the q largest singular values and right singular vectors of W We use the Lanczos algorithm (Baglama and Reichel, 2005; Dutta and Mondal, 2014) with reorthogonalization and implicit restart. Suppose that $m=\max \{2q+1,20\}$ and that ${\mathbf{f}}_1\in {ℝ}^n$ is any random vector with $\Vert {\mathbf{f}}_1\Vert =1.$ Let ${\mathbf{g}}_1={\mathbf{W}}^{\top }{\mathbf{f}}_1,{\alpha }_1=\Vert {\mathbf{g}}_1\Vert ,{\mathbf{F}}_1={\mathbf{f}}_1$ and ${\mathbf{G}}_1={\mathbf{g}}_1.$ For $j=1,\dots ,m$ let ${\mathbf{r}}_j=\mathbf{W}{\mathbf{g}}_j-{\alpha }_j{\mathbf{f}}_j,$ reorthogonalize ${\mathbf{r}}_j={\mathbf{r}}_j-{\mathbf{F}}_j{\mathbf{F}}_j^{\top }{\mathbf{r}}_j$ and set ${\beta }_j=\Vert {\mathbf{r}}_j\Vert ,$ and if $j<m,$ update ${\mathbf{f}}_{j+1}={\mathbf{r}}_j/{\beta }_j,{\mathbf{F}}_{j+1}=\left[{\mathbf{F}}_j,{\mathbf{f}}_{j+1}\right],$ ${\mathbf{g}}_{j+1}={\mathbf{W}}^{\top }{\mathbf{f}}_{j+1}-{\beta }_j{\mathbf{g}}_j,$ reorthogonalize ${\mathbf{g}}_{j+1}={\mathbf{g}}_{j+1}-{\mathbf{G}}_j{\mathbf{G}}_j^{\top }{\mathbf{g}}_{j+1},{\alpha }_{j+1}=\Vert {\mathbf{g}}_{j+1}\Vert ,{\mathbf{g}}_{j+1}={\mathbf{g}}_{j+1}/{\alpha }_{j+1},$ and set ${\mathbf{G}}_{j+1}=\left[{\mathbf{G}}_j,{\mathbf{g}}_{j+1}\right].$

Next, consider the m × m bidiagonal matrix ${\mathbf{B}}_m$ with diagonal entries α₁,α₂,...,α_m with (j, j + 1) entry β_j for $j=1,2,\mathrm{..},m-1$ and all other entries as 0. Now suppose that $h_1\ge h_2\ge \cdots \ge h_m$ are the singular values of B_m and that u_j’s are the v_j’s corresponding right and left singular vectors, which can be computed via a Sturm sequencing algorithm (Wilkinson, 1958). Also, let ${\mathbf{u}}_j={\mathbf{F}}_m{\mathbf{u}}_j\text{and}{\mathbf{v}}_j={\mathbf{G}}_m\mathbf{v}(1\le j\le m).$ Then it can shown that for all $j,{\mathbf{W}}^{\top }{\mathbf{u}}_j=h_j{\mathbf{v}}_j\text{and}\mathbf{W}{\mathbf{v}}_j=h_j{\mathbf{u}}_j+{\tilde{v}}_{j,m}{\mathbf{r}}_m,\text{where}{\tilde{v}}_{j,m}$ is the last entry of v_j. Because $\Vert {\mathbf{r}}_m\Vert ={\beta }_m$ and h₁ is approximately the largest singular value of W, the algorithm stops if ${\beta }_m|{\tilde{v}}_{j,m}|\le h_1\delta$ holds for $j=1,2,\dots ,q,$ where δ is some prespecified tolerance level, and $h_1,h_2,\dots ,h_q\text{and}{\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_q$ are accurate approximations of the q largest singular values and corresponding right singular vectors of W.

Convergence of the reorthogonalized Lanczos algorithm often suffers from numerical instability that slows down convergence. To resolve this instability, Baglama and Reichel (2005) proposed restarting the Lanczos algorithm, but instead of starting from scratch, they initialized with the first q singular vectors To that end, let ${\mathbf{f}}_{m+1}={\mathbf{r}}_m/{\beta }_m\text{and reset}{\mathbf{F}}_{q+1}=\left[{\mathbf{u}}_1,\dots ,{\mathbf{u}}_{\mathbf{q}},{\mathbf{f}}_{m+1}\right].$ Then for $j=1,2,\dots ,q,$ let ${\rho }_j={\beta }_m{\tilde{v}}_{j,m},$ and reset ${\mathbf{r}}_q={\mathbf{W}}^{\top }{\mathbf{f}}_{m+1}-\sum _{j=1}^q{\rho }_j{\mathbf{v}}_j,{\alpha }_{q+1}=\Vert {\mathbf{r}}_q\Vert ,{\mathbf{g}}_{q+1}={\mathbf{r}}_q/{\alpha }_{q+1},$ and ${\mathbf{G}}_{q+1}=\left[{\mathbf{v}}_1,\dots ,{\mathbf{v}}_q,{\mathbf{g}}_{q+1}\right].$ Define $\gamma ={\mathbf{f}}_{m+1}^{\top }\mathbf{W}{\mathbf{g}}_{q+1}$ and ${\mathbf{r}}_{q+1}=\mathbf{W}{\mathbf{g}}_{q+1}-\gamma {\mathbf{f}}_{m+1}.$ For $j=1,2,\dots ,m-q-1,$ compute ${\beta }_{q+j}=\Vert {\mathbf{r}}_{q+j}\Vert ,$ ${\mathbf{f}}_{q+j+1}={\mathbf{r}}_{q+j}/{\beta }_{q+j},{\mathbf{F}}_{q+j+1}=\left[{\mathbf{F}}_{q+j},{\mathbf{f}}_{q+j+1}\right],{\mathbf{g}}_{q+j+1}=(\mathbf{I}-{\mathbf{G}}_{q+j}{\mathbf{G}}_{q+j}^{\top }){\mathbf{W}}^{\top }{\mathbf{f}}_{q+j+1},{\alpha }_{q+j+1}=\Vert {\mathbf{g}}_{q+j+1}\Vert ,{\mathbf{g}}_{q+j+1}={\mathbf{g}}_{q+j+1}/{\alpha }_{q+j+1}$ and ${\mathbf{r}}_{q+j+1}=(\mathbf{I}-{\mathbf{F}}_{q+j+1}{\mathbf{F}}_{q+j+1}^{\top })\mathbf{W}{\mathbf{g}}_{q+j+1}.$ This yields a matrix B_m with entries b_j,j = h_j and b_j,q = ρ_j for j = 1,2,...,q, and b_i,i = ρ_i for q + 1 ≤ i ≤ m and b_{i,i + 1} = α_i for q + 1 ≤ i ≤ m − 1, and all other entries 0. The matrix ${\mathbf{B}}_m$ is not bidiagonal but is still small-dimensioned matrix whose singular value decomposition can be calculated very fast. Convergence of the Lanczos algorithm can be checked as before.

The only way that W enters this algorithm is through matrix-vector products of the forms Wg and ${\mathbf{W}}^{\top }\mathbf{f},$ both of which can be computed without explicitly storing W Overall, this algorithm yields the q largest singular values and vectors in O(qnp) computational cost using only O(qp) additional memory, resulting in substantial gains over the traditional methods (Jöreskog, 1967; Lawley and Maxwell, 1962). These traditional methods require a full eigenvalue decomposition of ${\mathbf{W}}^{\top }\mathbf{W}$ that is of O(p³) computational complexity and requires) O(p²) memory storage space. Having described a scalable algorithm for computing ${\mathcal{l}}_p(\mathrm{\Psi })\text{and}\nabla {\mathcal{l}}_p(\mathrm{\Psi }),$ we detail a numerical algorithm for computing the ML estimators.

2.3.2. Numerical optimization of the profile log-likelihood

On the correlation scale, ${\psi }_{ii}\text{'}\text{s}$ lie between 0 and 1. Under this box constraint, the factanal function in R and factoran function in MATLAB^® employ the limited-memory Broyden-Fletcher-Goldfarb-Shanno quasi-Newton algorithm (Byrd et al., 1995) with box-constraints (L-BFGS-B) to obtain the ML estimator of $\mathrm{\Psi }.$ However, in high dimensions, the advantages of the L-BFGS-B algorithm are particularly prominent. Because Newton methods require the search direction $-\mathbf{H}{(\mathrm{\Psi })}^{-1}\nabla {\mathcal{l}}_p(\mathrm{\Psi }),\text{where}\mathbf{H}(\mathrm{\Psi })$ is the p × p Hessian matrix of ${\mathcal{l}}_p(\mathrm{\Psi }),$ they are computationally prohibitive in high dimensions in terms of storage and numerical complexity. The quasi-Newton BFGS replaces the computation of the exact search direction by an iterative approximation using the already computed values of ${\mathcal{l}}_p(\mathrm{\Psi })\text{and}\nabla {\mathcal{l}}_p(\mathrm{\Psi }).$ The limited-memory implementation, moreover, uses only the last few (typically less than 10) values of ${\mathcal{l}}_p(\mathrm{\Psi })\text{and}\nabla {\mathcal{l}}_p(\mathrm{\Psi })$ instead of using all the past values. Overall, L-BFGS-B reduces the storage cost from O(p²) to O(np) and the computational complexity from O(p³) to O(np). Interested readers are referred to Byrd et al. (1995); Zhu et al. (1994) for more details on the L-BFGS-B algorithm. The L-BFGS-B algorithm requires both ${\mathcal{l}}_p\text{and}\nabla {\mathcal{l}}_p$ to be computed at each iteration. Because $\nabla {\mathcal{l}}_p$ is available as a byproduct while computing ${\mathcal{l}}_p$ (see Section Sections 2.2 and 2.3.1), we modify the implementation to jointly compute both quantities with a single call to the Lanczos algorithm at each L-BFGS-B iteration. In comparison to R’s default implementation (factanal) that separately calls ${\mathcal{l}}_p\text{and}\nabla {\mathcal{l}}_p$ in its optimization routines, this tweak halves the computation time.

3. Performance evaluations

3.1. Experimental setup

The performance of FAD was compared to EM using 100 simulated datasets with true q = 3 or 5 and $(n,p)\in \{(100,1000),(225,3375),(400,8000)\}.$ For each setting, we simulated ${\psi }_{ii}~\text{i.i.d}\mathcal{U}(0.2,0.8)\text{and}{\lambda }_{ij}~\text{i.i.d.}\mathcal{N}(0,1)$ and set μ = 0. We also evaluated performance with (n, p, q) ∈{(160,24547,2),(180,24547,2),(340,24547,4)} to match the settings of our application in Section 4: the true $\mathrm{\Psi },\mathrm{\Lambda },\mathit{\mu }$ were set to be the ML estimates from that dataset.

For the EM algorithm, $\mathbf{\Lambda }$ was initialized as the first q principal components (PCs) of the scaled data matrix computed via the the Lanczos algorithm while $\mathbf{\Psi }$ was started at ${\mathbf{I}}_p-\mathrm{diag}(\mathbf{\Lambda }{\mathbf{\Lambda }}^{\top }).$ PAD requires only $\mathbf{\Psi }$ to be initialized, which was done in the same way as the EM. We stopped FAD when the relative increase in ${\mathcal{l}}_p(\mathrm{\Psi })$ was below ${100}^{{ϵ}_0}\text{and}{\Vert \nabla {\mathcal{l}}_p\Vert }_{\infty }<\sqrt{{ϵ}_0}$ where ϵ₀ is the machine tolerance, which in our case was approximately 2.2 × 10⁻¹⁶. The EM algorithm was terminated if the relative change in $\mathcal{l}(\mathrm{\Lambda },\mathrm{\Psi })$ was less than 10⁻¹⁶ and ${\Vert \nabla {\mathcal{l}}_p\Vert }_{\infty }<{\sqrt{ϵ}}_0,$ or if the number of iterations reached 5000. Therefore, FAD and EM had comparable stopping criteria. For each simulated dataset, we fit models with K = l,2,···,2q factors and chose the number of factors by the Bayesian Information Criterion (BIC): $-2{\widehat{\mathcal{l}}}_k+pk\log n$. (Schwarz, 1978), where ${\widehat{\mathcal{l}}}_k$ is the maximum log-likelihood value with k factors. All experiments were done using R (R Core Team, 2019) on a workstation with Intel E5–2640 v3 CPU clocked @2.60 GHz and 64GB RAM.

3.2. Results

Because BIC always correctly picked q, we evaluated model fit for each method in terms of $\mathcal{l}(\widehat{\mathrm{\Lambda }},\widehat{\mathrm{\Psi }}),d_{\text{R}}=\Vert \mathbf{R}-\mathbf{R}{\Vert }_F/\Vert \mathbf{R}{\Vert }_F\text{and}{d}_{\mathbf{\Gamma }}=\Vert \mathbf{\Gamma }-\mathbf{\Gamma }{\Vert }_F/\Vert \mathbf{\Gamma }{\Vert }_F$ where $\mathbf{\Gamma }={\mathbf{\Lambda }}^{\top }{\mathbf{\Psi }}^{-1}\mathbf{\Lambda }\text{and}\mathbf{R}\text{and}\mathbf{R}$ are the correlation matrices corresponding to $\mathrm{\Sigma }\text{and}\widehat{\mathrm{\Sigma }}=\mathbf{\Lambda }{\mathbf{\Lambda }}^{\top }+\mathbf{\Psi }.$

3.2.1. CPU time

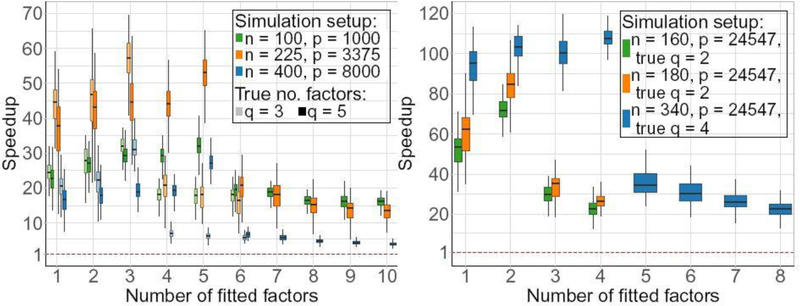
Figure 1 presents the relative speed of FAD to EM. Our compute times include the common initialization times. Specifically, for datasets of size (n, p) ∈{(100,1000),(225,3375),(400,8000)}, FADs was 10 to 70 times faster than EM, with maximum speedup at true q. However, EM did not converge within 5000 iterations in any of the overfitted models. In contrast, FAD always converged but it took longer than in other cases so the speedup is underestimated because of the censoring with EM. Also, the speedup is more pronounced (see Section S2.1) in the data-driven simulations where p is much larger.

Fig. 1.

Relative speed of FAD to EM on (left) randomly simulated and (right) data-driven cases. Lighter ones correspond to true q = 3 and the darker ones correspond to true q = 5.

3.2.2. Parameter estimation and model fit.

Under the best fitted models, FAD and EM yield identical values of ${\mathcal{l}}_p(\widehat{\mathrm{\Lambda }},\widehat{\mathrm{\Psi }}),\widehat{\mathrm{\Psi }},\widehat{\mathrm{\Gamma }},\text{and}\widehat{\mathrm{\Lambda }}{\widehat{\mathrm{\Lambda }}}^{\top }.$ Thus the relative errors (see Figure S2) in estimating these parameters are also identical.

3.3. Additional experiments in high-noise scenarios

We conclude this section by evaluating performance in situations where ostensibly, weak factors are hardly distinguished from high noise by SVD methods and where EM may be preferable (Owen and Wang, 2015). We applied FAD and EM to the simulation setup of Owen and Wang (2015): Here, the uniquenesses were sampled from three inverse Gamma distributions with unit means and variances of 0, 1 and 10, and (n, p) ∈{(200,1000),(100,5000)}. Figure S3 shows that our algorithm was substantially faster while having similar accuracy as EM.

4. Suicide ideation study

We applied EFA to data from Just et al. (2017) on an fMRI study conducted while 20 words connoting negative affects were shown to 9 suicide attempters, 8 suicide non-attempter ideators and 17 non-ideator control subjects. For each subject-word combination, Just et al. (2017) provided voxel-wise per cent changes in activation relative to the baseline in 50×61×23 image volumes. Restricting attention to the 24547 in-brain voxels yields datasets for the attempters, ideators and controls of sizes (n, p) ∈{(180,24547),(160,24547),(340,24547)}. We assumed each dataset to be a random sample from the multinormal distribution. Our interest was in determining if the variation in the per cent relative change in activation for each subject type can be explained by a few latent factors and whether there are differences in these factors between the three groups of subjects.

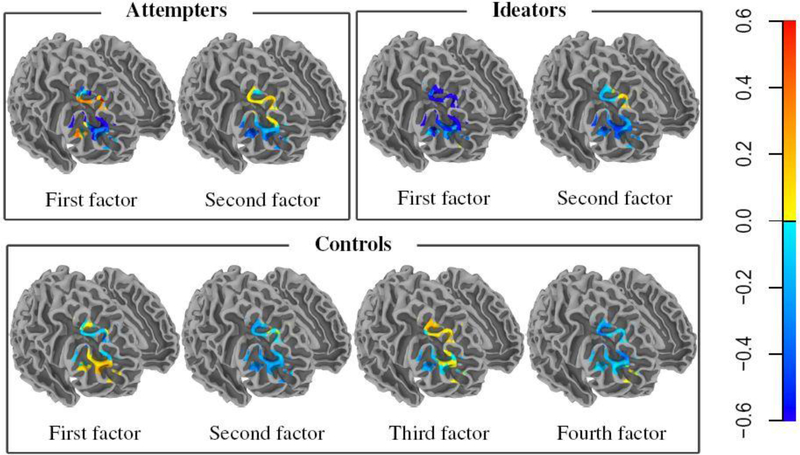
For each dataset, we performed EFA with q = 0,1,2,…,10 factors and using both FAD and EM. Table 1 demonstrates the computational benefits of using FAD over EM. We also used BIC to decide on the optimal q(q_o) and obtained 2-factor models for both suicide attempters and ideators, and a 4-factor model for the control subjects. Figure 2 provides voxel-wise displays of the q₀ factor loadings, obtained using the quartimax criterion (Costello and Osborne, 2005), for each type of subject. All the factor loadings are non-negligible only in voxels around the ventral attention network (VAN) which represents one of two sensory orienting systems that reorient attention towards notable stimuli and is closely related to involuntary actions (Vossel et al., 2014). However, there are differences between the factor loadings in each group and also among them.

Table 1:

CPU times (rounded to the nearest seconds) for FAD and EM applied to the suicide ideation study dataset.

	q	1	2	3	4	5	6	7	8	9	10
Attempters	FAD	3	3	4	5	5	6	6	7	9	9
	EM	146	173	207	198	229	236	228	250	239	254
Ideators	FAD	4	4	5	6	6	6	6	9	9	10
	EM	118	197	207	200	222	244	241	226	258	258
Controls	FAD	5	5	8	7	8	8	9	10	12	13
	EM	300	451	456	407	426	461	483	438	566	519

Fig. 2.

Loading values of fitted factors for suicide attempters, ideators and controls.

For instance, for the suicide attempters, each factor is a contrast between different areas of the VAN, but the contrasts themselves differ between the two factors. The first factor for the ideators is a weighted mean of the voxels while the second factor is a contrast of the values at the VAN voxels. For the controls, the first three factors are different contrasts of the values at different voxels while the fourth factor is more or less a mean of the values at these voxels. Further, the factor loadings in the control group are more attenuated than for either the suicide attempters or ideators. While a detailed analysis of our results is outside the purview of this paper, we note that EFA has provided us with distinct factor loadings that potentially explains the variation in suicide attempters, non-attempter ideators and controls. However, our analysis assumed that the image volumes are independent and Gaussian: further approaches relaxing these assumptions may be appropriate.

5. Discussion

In this paper, we propose a new ML-based EFA method called FAD using a sophisticated computational framework that achieves both high accuracy in parameter estimation and fast convergence via matrix-free algorithms. We implement a Lanczos method for computing partial singular values and vectors and a limited-memory quasi-Newton method for ML estimation. This implementation alleviates the computational limitations of current state-of-the-art algorithms and is capable of EFA for datasets with p >> n. In our experiments, FAD always converged but EM struggled with overfitted models. Although not demonstrated in this paper, FAD is also well-suited for distributed computing systems because it only uses the data matrix for computing matrix-vector products. FAD paves the way to develop fast methods for mixtures of factor analyzers and factor models for non-Gaussian data in high-dimensional clustering and classification problems.