Higher dominance rank is associated with lower glucocorticoids in wild female baboons: A rank metric comparison

Abstract

In vertebrates, glucocorticoid secretion occurs in response to energetic and psychosocial stressors that trigger the hypothalamic-pituitary-adrenal (HPA) axis. Measuring glucocorticoid concentrations can therefore shed light on the stressors associated with different social and environmental variables, including dominance rank. Using 14,172 fecal samples from 237 wild female baboons, we test the hypothesis that high-ranking females experience fewer psychosocial and/or energetic stressors than lower-ranking females. We predicted that high-ranking females would have lower fecal glucocorticoid (fGC) concentrations than low-ranking females. Because dominance rank can be measured in multiple ways, we employ an information theoretic approach to compare 5 different measures of rank as predictors of fGC concentrations: ordinal rank; proportional rank; Elo rating; and two approaches to categorical ranking (alpha vs non-alpha and high-middle-low). Our hypothesis was supported, but it was also too simplistic. We found that alpha females exhibited substantially lower fGCs than other females (typical reduction = 8.2%). If we used proportional rank instead of alpha- versus non-alpha status in the model, we observed a weak effect of rank such that fGCs rose 4.2% from the highest- to lowest-ranking female in the hierarchy. Models using ordinal rank, Elo rating, or high-middle-low categories alone failed to explain variation in female fGCs. Our findings shed new light on the association between dominance rank and the stress response, the competitive landscape of female baboons as compared to males, and the assumptions inherent in a researcher’s choice of rank metric.

Graphical abstract

INTRODUCTION

Glucocorticoids (GCs) perform many physiological roles, including acting as one of the primary hormones of the vertebrate stress response. The stress response is characterized by activation of the sympathetic nervous system and hypothalamic-pituitary-adrenal (HPA) axis (Reeder and Kramer, 2005) and helps restore the organism to homeostasis after a physical or social challenge (Creel et al., 2013; Sapolsky, 2002; Selye, 1936). A responsive HPA axis is essential, and facilitates survival and reproduction. On the other hand, studies of laboratory animals and humans provide some evidence that long-term or chronic stressors can be associated with poor health outcomes or increased mortality (Adler and Rehkopf, 2008; Bartolomucci, 2007; Baum et al., 1999; Campos et al., In review; but see Dowd et al., 2009; Feinstein, 1993; Kristenson et al., 2004; O’leary, 1990; Peuler et al., 2012; Pitman et al., 1988). Further, in wild female baboons (Papio cynocephalus, the subject of this study), higher lifetime fecal GC concentrations were associated with shorter lifespan (Campos et al., In review).

Dominance rank (i.e., social status) is often linked either directly or indirectly to GC levels because social status can affect the type and intensity of stressors an individual experiences (Sapolsky, 2004; Sapolsky, 2005). The relationship between dominance rank and GC concentrations has been examined in fish, birds, and mammals (Beehner and Bergman, 2017; Creel et al., 2013). Several factors have been shown to affect the relationship between rank and GC levels, including sex, breeding structure, coping mechanisms in subordinates, and the acquisition and maintenance of dominance rank (Abbott et al., 2003; Creel, 2001; Creel et al., 2013; Goymann and Wingfield, 2004; Sapolsky, 2004; Sapolsky, 2005). For example, in several cooperatively breeding species such as male and female African wild dogs (Lycaon pictus) and female dwarf mongoose (Helogale parvula), in which the dominant individuals perform the vast majority of breeding, GC concentrations are higher in dominant than in subordinate group members, likely due to the high social and reproductive costs of breeding and maintaining dominance (Creel, 2001; Creel et al., 2013; Creel et al., 1996). In addition, in several species and sexes with linear dominance hierarchies that acquire and maintain dominance via aggressive interactions, such as female ring-tailed lemurs (Lemur catta), male chimpanzees (Pan troglodytes), and male savannah baboons, the energetic demands of maintaining high social status may contribute to elevated fecal or urinary GC levels in the alpha (i.e. top-ranked) individuals or several of the highest-ranking individuals (Cavigelli, 1999; Gesquiere et al., 2011a; Muller and Wrangham, 2004).

In addition to variation across taxa, differences are common among studies of the same species, both within and between each sex. For example, one study of a captive pack of wolves (Canis lupus) in Nova Scotia reported that the lowest-ranking female in a group showed the highest urinary GC concentrations (McLeod et al., 1996), while another study of three wild wolf packs in Yellowstone reported higher fecal GC concentrations in alpha than in subordinate females (Sands and Creel, 2004). Among wild baboons (genus Papio, the subject of this study), results vary both across studies and by sex. Whereas male baboons generally exhibit a robust positive association between rank and GC levels in feces or serum (lower-ranking males have higher GCs), this relationship is context-dependent in some studies and absent in others (reviewed in Beehner and Bergman, 2017). Studies of female baboons have also produced inconsistent results: two studies have found that lower-ranking females have higher fecal GCs, while four studies have found no statistically significant relationship between rank and fecal or serum GCs (reviewed in Beehner and Bergman, 2017).

Some differences among studies of the same species may be explained by differences in how dominance rank is measured. For instance, individuals may be grouped into categories of rank (e.g., high-middle-low) which can mask heterogeneities associated with different rank positions (Figure 1). If dominance rank is enumerated rather than categorized, it may be measured in a variety of ways. The simplest enumeration is ordinal dominance rank, which orders individuals from 1 to n based on their ability to win dyadic interactions (n = number of individuals in the hierarchy; Figure 1). Another common measure is proportional dominance rank (usually referred to as ‘standardized’ or ‘relative’ ranks; e.g., Carter et al., 2014; Fedigan et al., 2008; Roberts and Cords, 2013), which is calculated as the proportion of individuals in the group that the focal dominates (Figure 1). Cardinal rank measures, such as Elo rating or David’s score, are also common (Figure 1; Albers and Vries, 2001; David, 1987). Cardinal measures do not assume equal distance in dominance between adjacently-ranked individuals. Instead, scores are calculated based on the number of wins and losses between each dyad, with the result that some adjacently-ranked individuals may have very close scores, and some may have disparate scores.

Figure 1.

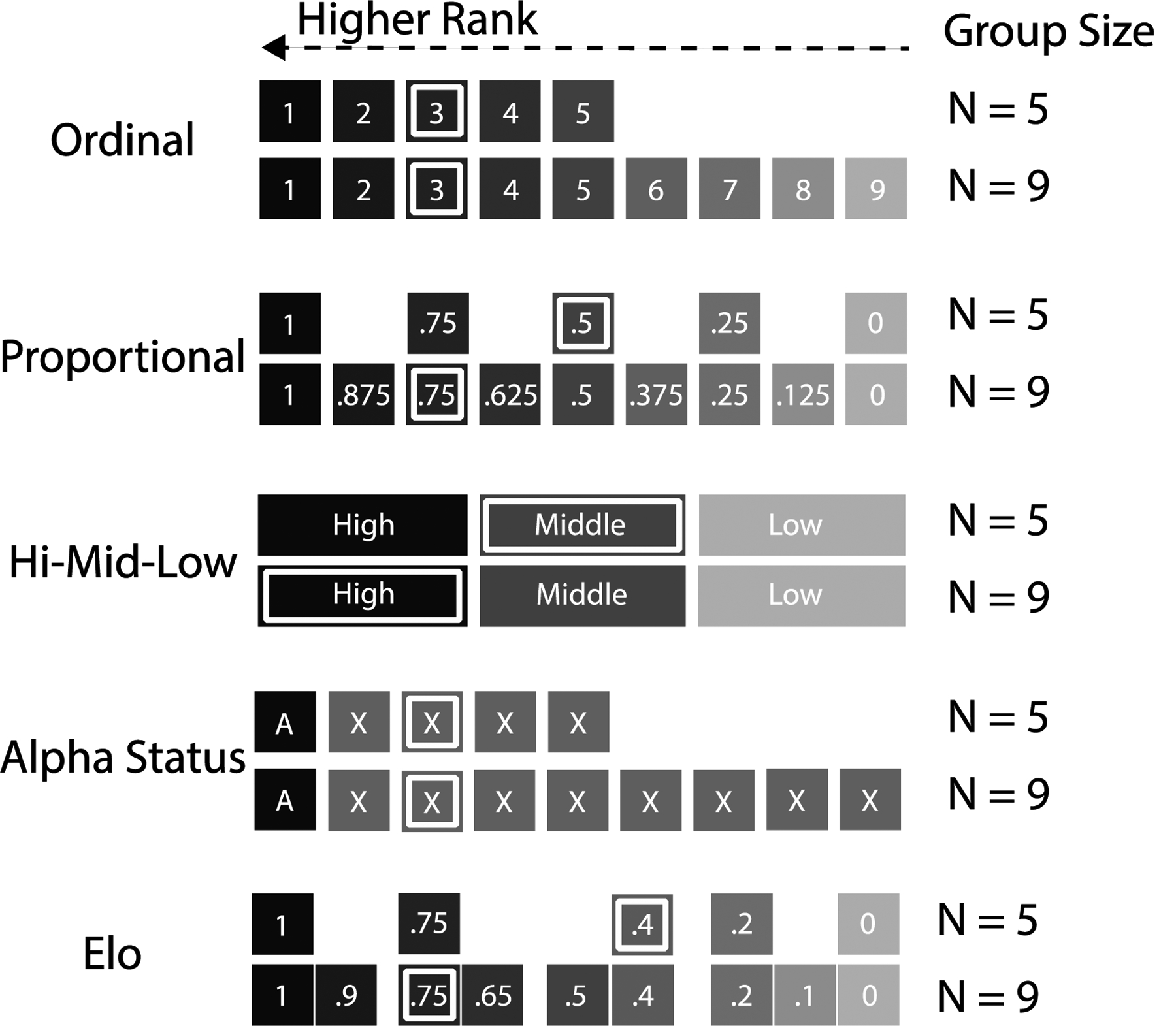
Visualization of the differences between five different rank metrics as a function of group size. Darker shading represents higher rank and thus greater competitive advantage. Boxes with an inner white rectangle identify the position of individuals ranked 3^rd in every group. Using ordinal rank posits that being ranked 3^rd confers the same competitive advantage regardless of group size. Using proportional rank posits that being ranked 3^rd in a group of 9 (proportional rank = 0.75) represents a functionally higher rank than being ranked 3 in a group of 5 (proportional rank = 0.5). Categorical ranks (high-middle-low and alpha status) posit that individuals within rank categories have the same competitive advantage. High-middle-low places individuals of rank 3 with middle-ranked individuals in a group of 5, and with high-ranked individuals in a group of 9; alpha status places individuals of rank 3 in the same non-alpha category regardless of group size. Elo rating assumes that the differences in competitive advantage between adjacently-ordered individuals are not necessarily equal. Here, we give two examples (out of infinite possibilities) of Elo ratings in groups of 5 and 9.

Behavioral studies almost never provide a strong conceptual justification for their choice of rank metric (but see Archie et al., 2014; Schino and Lasio, 2019). However, we propose that each rank metric makes different assumptions about rank-related levels of dyadic resource competition across different group sizes (Figure 1). Ordinal rank assumes a queuing system for monopolizable resources, such that being ranked 3^rd confers the same resource access regardless of group size. The underlying assumption is that the group’s resource base stays (relatively) constant as group size increases. In other words, average per capita resource competition is greater in larger groups, with the burden of this competition disproportionately borne by lower ranking individuals. In contrast, proportional rank assumes that average per capita resource competition stays (relatively) constant across group sizes, even though the burden of competition is still disproportionately borne by lower-ranking individuals. In other words, proportional rank assumes a system in which resource access scales with group size, such that being ranked 3^rd in a group of 5 confers the same resource access as being ranked 5^th in a group of 9; in both cases the focal individual is in the 50^th rank percentile for their group. Importantly, ordinal and proportional rank metrics will produce identical results in statistical analysis if only one social group is studied and no change in group size occurs during the study. However, these two metrics may produce different results if group size fluctuates or the study includes multiple, different-sized groups. Cardinal rank metrics, such as Elo rating, assume that resource competition depends on the power differentials within the group, such that the outcome of resource competition between any pair of individuals will depend on their power differential, not just their rank ordering. Finally, a categorical rank system (e.g., alpha status or not, high-middle-low) assumes that competition or resource access within rank categories will be the same.

Here, we examine the relationship between dominance rank and fecal glucocorticoid concentrations (fGC) in adult female savannah baboons. We do so by testing the ability of five rank metrics – ordinal dominance rank, proportional dominance rank, Elo rating, and two categorical dominance rankings: alpha vs non-alpha and high-middle-low – to predict fGC (an integrated measure of GC secretion; see Methods). To our knowledge, this is the first study to systematically examine which dominance rank metric best predicts fGC concentrations (but see Archie et al., 2014; Schino and Lasio, 2019 for similar techniques to model other outcomes in baboons and mandrills, respectively). This study also represents the largest dataset ever used to analyze predictors of GC concentrations in any wild animal population, using 14,172 fecal samples from 237 females in 15 social groups and spanning 18 years.

Female savannah baboons exhibit linear dominance hierarchies, and high dominance rank carries several fitness-related benefits. High-ranking female baboons have consistent advantages over low-ranking females in one or more of the following traits in different study populations: increased offspring survival, offspring with earlier age at sexual maturity, shorter inter-birth intervals, fewer interruptions while feeding, and/or longer lifespans (Altmann and Alberts, 2003; Altmann et al., 1988; Cheney et al., 2006; Post et al., 1980; Silk et al., 2003; Silk et al., 2010). We hypothesize that high-ranking females have less exposure to energetic and/or psychosocial stressors, and hence less frequent HPA axis activation, than low-ranking females, leading to the prediction that higher-ranking females will have lower fGC concentrations than lower-ranking females. In line with Emlen and Oring’s (1977) socioecological model, we suspect that females primarily compete with other females for food, and that as the size of a baboon group increases, the resource base (food) available to that group also increases (Isbell, 1991). If this increase in resource base is roughly proportional to the increase in group size, we predict that proportional rank will be a better predictor of fGC in our models than ordinal rank, Elo rating, or categorical ranks. The results will increase our understanding of how rank-related competition can predict HPA axis activation in female primates.

METHODS

Study subjects

Subjects were 237 wild adult (i.e., post-menarche) female savannah baboons living in the Amboseli basin of southern Kenya between January 2001 and July 2018. Data on individual baboon life histories and behavior have been collected by members of the Amboseli Baboon Research Project since 1971; fecal sample collection to measure steroid hormones began in 2000. All subjects were identified visually based on individual characteristics and habituated to the presence of observers. Each social group was observed approximately three times per week during five-hour observation periods. Behavioral and demographic data and fecal samples were collected primarily by three of the co-authors (RSM, SNS, JKW), who have been collecting data on this population for between 22 and 36 years. For every fecal sample collected, we were able to assign the subject’s age, group size, reproductive status, and social group on the day of collection and her dominance rank during the month of collection; these variables are described in more detail below.

The Amboseli baboon population is composed primarily of yellow baboons (P. cynocephalus) with some admixture from nearby anubis baboon populations (P. anubis) (Alberts and Altmann, 2001; Charpentier et al., 2012; Tung et al., 2008). Studies of yellow-anubis baboon hybrids in captivity and in the wild have revealed no evidence of hybrid inviability, reduced fertility among hybrids, or ecological barriers to gene flow, and only limited evidence of hybrid dysgenesis (Ackermann et al., 2006; Tung et al., 2008; Wango et al., 2017). To confirm that hybrid status was not associated with our phenotype of interest, we examined admixture levels as part of our analysis (see Modeling and analysis: Additional models).

Over the course of the 18-year study period, the subjects lived in 15 distinct social groups of different sizes. These 15 groups represent the products of permanent group fission and fusion events from 2 original study groups, on which observations began in 1971 and 1980. We excluded samples collected during fission and fusion periods because foraging and sleeping group size changed over the course of hours or days, making it difficult to accurately assess the experienced group size and dominance rank.

All data collection procedures adhered to the regulations of the Institutional Animal Care and Use Committee of Duke, Princeton, and Notre Dame Universities, and to the laws of Kenya.

Measuring fecal glucocorticoid metabolites

Fresh fecal samples (N = 14,172) were collected opportunistically from the 237 subjects. The mean number of fecal samples per subject ± SD was 60 ± 56, with a range of 1 to 279. Fecal samples were processed and stored using methods described by Khan et al. (2002) and Lynch et al. (2003). Fecal glucocorticoid metabolite concentrations represent an integrated measure of glucocorticoid release over several hours or days (Goymann, 2005; Harper and Austad, 2000; Palme et al., 1996). Freeze-dried samples were assayed for fecal glucocorticoid metabolite (fGC) concentrations using a radioimmunoassay technique validated for use with baboon feces (Gesquiere et al., 2011b; Khan et al., 2002; Lynch et al., 2003; see amboselibaboons.nd.edu for full protocol). Hormone values are expressed as ng/g of dried feces. For analysis, fGC data were log-transformed (base 10) to obtain a normal distribution. Each fecal sample was used as a single data point in statistical models. Mean ± SD of fGC concentrations was 77.16 ± 39.40 ng/g dried feces; values ranged from 7.51–758.17 ng/g dried feces.

Measuring dominance rank

Ordinal dominance rank.

Ordinal ranks were assigned monthly for each adult female using observations of wins and losses in dyadic agonistic interactions between adult female study subjects (i.e., post-menarche). A female dominance matrix was created for each month based on these win/loss outcomes, and female rank orderings were then assigned by minimizing entries below the diagonal (Hausfater, 1974). Female ordinal ranks were updated for each month of the study in each social group following this procedure. Females were added to the female matrix the month during which they matured and were removed from the matrix the month after they died. Ordinal ranks represent the ordered list of this matrix; top-ranked females are assigned an ordinal rank of 1, the second-ranked female is rank 2, and so on (Figure 1). Ordinal rank assignment has been extensively described in previous papers (e.g., Hausfater et al., 1982; Onyango et al., 2008). The mean ± SD for ordinal dominance rank in this study was 9.01 ± 6.12 with a range of 1–31.

Proportional dominance rank.

Proportional ranks were calculated as $\left[1-\frac{\mathit{\text{ordinal\hspace{0.17em}rank}}-1}{\mathit{\text{adult female group size}}-1}\right]$ at the first day of each month. This produces a range from 0 (lowest-ranking) to 1 (highest-ranking) for each group-month and represents the proportion of adult females that the focal female dominates. An adult female with an ordinal rank of 3 in a group of 5 adult females and an adult female with an ordinal rank of 5 in a group of 9 adult females will both have a proportional rank of 0.5 (Figure 1). The mean ± SD for proportional rank was 0.52 ± 0.31 with a range of 0–1. As noted above, ordinal and proportional rank metrics will produce identical results in statistical analysis if only one social group is studied and no change in group size occurs during the study.

Elo rating.

Elo ratings were calculated from dyadic interactions among adult females using the EloRating package in R version 3.3.3 (Neumann and Kulik, 2019). Females who matured into the hierarchy (upon reaching menarche) were entered just below their mother or, if the mother was dead, just above older sisters, following nepotistic rank inheritance and youngest ascendency observed in female baboons (Lea et al., 2014). Each month’s Elo rating is then calculated using the prior month’s score as a starting point. To select K, we first produced Elo rating rank orders from a range of K values (10 to 1000, increasing by 5), and calculated the correlation between these orders and the corresponding group-month’s ordinal ranks (see Ordinal dominance rank above). We chose K = 35 because it produced the highest correlation between the Elo rating rank order and ordinal ranks (r = 0.98, p = <2.2×10⁻¹⁶).

After assembling each female’s Elo rating for each month, we then standardized each group-month’s scores to a range from 0 (lowest-ranking in the group) to 1 (highest-ranking in the group). As a result, proportional rank and Elo rating both had the same range, but proportional rank indicates the proportion of individuals dominated with equal distance between individuals, whereas Elo ratings do not assume equal distance between individuals. Instead, the difference in Elo rating between two individuals reflects the probability of the higher-ranked individual winning an interaction. The mean ± SD for Elo rating was 0.48 ± 0.29 with a range of 0–1.

Categorical dominance ranks.

We created two categorical rank metrics: alpha vs non-alpha and high-middle-low. The alpha metric was created by binning individuals as alpha (ordinal rank = 1; n = 19 females, 1201 fecal samples) or not (ordinal rank > 1). Similar binning methods have been used to analyze the relationship between dominance rank and glucocorticoid concentrations in many species and both sexes, including male baboons, female ring-tailed lemurs, and male and female wolves (Cavigelli et al., 2003; Gesquiere et al., 2011a; Sands and Creel, 2004). For the high-middle-low metric, we created three rank categories that were equally sized within each group by partitioning proportional ranks that were greater than 0.66 (high), between 0.66 and 0.34 (middle), and less than 0.34 (low). This approach is similar to methods used previously in analysis of dominance rank and GC concentrations in female primates (e.g., Charpentier et al., 2018; Maestripieri et al., 2008; Setchell et al., 2008; Weingrill et al., 2004). Both categorical dominance ranks were coded as categorical variables in analysis instead of as continuous variables.

Covariates: Measuring group size, age, reproductive status, season, and storage time

Several other factors are known to associate with fGC concentrations in Amboseli baboons: group size (Markham et al., 2015), age (Altmann et al., 2010), reproductive status (Gesquiere et al., 2008), and season (Gesquiere et al., 2008; Gesquiere et al., 2011b). These factors, as well as fecal sample storage time, were included in our models as covariates (see Modeling and data analysis).

Group size.

We used the number of adult females as our measure of group size. The number of adult females in study groups ranged from 4–31 individuals over the course of the study (mean ± SD = 17.54 ± 6.02, Figure S1). Group size was coded as a continuous variable and z-transformed in analysis (see Assessing correlations among variables & model assumptions).

Age.

Date of birth was known to within a few days for 226 (95.4%) of the adult female subjects of this study. For the remaining 11 females (4.6%), age was known to within 6 months. The mean age ± SD of the study subject at the time of fecal sample collection was 10.69 ± 4.52 years with a range of 3.80 – 26.34 years. Age was coded as a continuous variable.

Reproductive status.

Ovarian cycles occur over the course of approximately 32 days in baboons, and include highly visible sexual swellings during the follicular phase (Dixson, 1983; Gesquiere et al., 2007; Gillman, 1942; Wildt et al., 1977). The visible indicators of reproductive status, in addition to behavioral observations of live-born infants, allowed us to designate each female’s reproductive status (cycling, pregnant, or postpartum amenorrhea [PPA]) at the time that each fecal sample was collected. Samples collected within the first week of PPA were excluded from analysis because they reflect the shift in fGC concentrations from pregnancy to PPA (Altmann et al., 2004; Nguyen et al., 2008). Reproductive status was coded as a categorical variable (cycling, pregnant, or PPA).

Season.

The Amboseli basin experiences two seasons: a “dry” season from June through October with virtually no rain, and a “wet” season characterized by unpredictable and variable rainfall from November to May (Gesquiere et al., 2008; Gesquiere et al., 2011b). Season was coded as a categorical variable (dry, wet).

Storage time.

We included two storage variables to account for variation in storage time of fecal samples. Within 1–3 weeks after collection, fecal samples were freeze-dried and then stored as fecal powder at −20°C. We refer to this time period as storage time as fecal powder. Samples were then extracted into methanol, and stored again at −20°C until they there assayed. We refer to this time period as storage time in methanol. Due to variance in shipping and laboratory schedules, fecal samples experienced variance in these two storage time variables. The mean time ± SD that samples were stored as fecal powder was 0.55 ± 0.26 years, with a range from 0.14 – 1.81 years. The mean time ± SD that samples were stored in methanol was 0.49 ± 0.46 years, with a range from 0.01 – 3.51 years. Storage times as fecal powder and in methanol were coded as continuous variables.

Modeling and data analysis

Main models.

We built eight general linear mixed models to test the association between rank and fGC concentrations (glmmTMB package in R version 3.3.3; Brooks et al., 2017; Table 1). All models were fitted using maximum likelihood estimation. We treated the fGC concentrations from each of the 14,172 fecal samples as the response variable in all models (fGCs were log transformed with base 10). The eight models differed in the rank metrics we used, which were coded as fixed effect predictors (Table 1). For ease of reference, we refer to these eight models as the Null model (no rank metric), the ordinal rank (Ord) model, the proportional rank (Prop) model, the Elo rating (Elo) model, the alpha (Alpha) model, the high-middle-low (Hi-Mid-Low) model, the alpha + ordinal (Alpha+Ord) model, and the alpha + proportional (Alpha+Prop) model. All models except the Null model test versions of the general prediction that low-ranking females have higher fGC concentrations than high-ranking females. Table 1 describes the formulas and hypothesized competitive regimes underlying each model.

Table 1.

Descriptions of the eight models used in analyses.

Model designation	Relationships tested	Hypothesis tested by model
Null (Null)	fGC ~ other fixed effects*	Used to assess which rank models performed
	+ random effects**	better than a model without rank.
Ordinal rank	fGC ~ ordinal + other	Average per capita resource competition
(Ord)	fixed effects + random	increases as group size increases and
	effects	increases linearly with each step down in the
		ordinal rank hierarchy.
Proportional rank	fGC ~ proportional + other	Average per capita resource competition is
(Prop)	fixed effects + random	relatively constant across group sizes and
	effects	increases linearly with each step down in the
		proportional rank hierarchy.
Elo rating (Elo)	fGC ~ elo + other fixed	Average per capita resource competition is
	effects + random effects	not necessarily a function of group size and is higher in lower-ranking individuals. The relationship between competition and rank is not necessarily linear because it depends upon power differentials between adjacently-ranked dyads.
Alpha (Alpha)	fGC ~ alpha/not + other	Average per capita resource competition is
	fixed effects + random	discontinuously lower for the highest-ranking
	effects	female in each group.
High middle low	fGC ~ high/mid/low +	Average per capita resource competition is
(Hi-Mid-Low)	other fixed effects +	relatively constant across group size, but is
	random effects	highest in low-ranking females and lowest in high-ranking females.
Alpha + ordinal	fGC ~ alpha/not + ordinal	Average per capita resource competition is
rank (Alpha+Ord)	+ other fixed effects +	discontinuously low for the highest-ranking
	random effects	female in each group, but non-alpha females still compete with each other as in the ordinal rank model.
Alpha +	fGC ~ alpha/not +	Average per capita resource competition is
proportional rank	proportional + other fixed	discontinuously low for the highest-ranking
(Alpha+Prop)	effects + random effects	female in each group, but non-alpha females still compete with each other as in the proportional rank model.

^*other fixed effects = age (continuous), reproductive status (cycling, pregnant, PPA), season (wet, dry), group size (number of adult females, z-transformed), group size², storage time as fecal powder (continuous), storage time in methanol (continuous)

^**random effects = individual ID (categorical) with random slope of age, social group with random intercept (categorical), hydrological year with random intercept (categorical)

To compare the ability of different rank metrics and modeling methods to predict fGC concentrations, we calculated the AIC value for each model. Though these models are not nested (prohibiting model averaging), the datasets used in each model were identical, enabling this information theoretic approach (Anderson and Burnham, 2002; Harrison et al., 2018; Johnson and Omland, 2004). Following standard practice, we used ΔAIC = 2 as a threshold for assigning preference for one model versus another, with a preference for lower AIC scores. We report model output as the predicted percent change in fGCs associated with a one-unit change in the predictor variable. We report 95% confidence intervals, calculated as estimate ± 1.96*SE. These intervals were then converted to percent change using the formula (10^interval−1)*100.

Based on prior studies of predictors of fGC concentrations in females in this population, all models included four additional fixed effects, all assessed on the day of fecal sample collection, that are known to explain variation in female Amboseli baboon fGCs: age (continuous; Altmann et al., 2010), reproductive status (cycling, pregnant, PPA; Gesquiere et al., 2008), season (wet, dry; Gesquiere et al., 2008; Gesquiere et al., 2011b), and group size (number of adult females; Markham et al., 2015). Group size (z-transformed; see Assessing correlations among variables & model assumptions) was included as both a linear and quadratic term following Markham et al (2015), who showed a quadratic relationship between group size and fGC concentrations in adult female savannah baboons. The two storage time variables, in years, were also included as fixed effects. Individual identity was included as a random effect in all models, with random intercept and random slope of age to account for the possibility of different rates of biological aging across the study subjects, as seen in humans and non-human animals, including Amboseli baboons (e.g., Ahadi et al., 2020; Altmann et al., 2010; Anderson et al., In Review). To account for year-to-year variability in the environment, a categorical random effect of year (specifically, the ‘hydrological year’ in which the sample was collected) was included in the models with a random intercept. The hydrological year in Amboseli begins 1 November each year (with the start of the rainy season) and ends the following 31 October). Finally, group identity was included as categorical random effect with random intercept (Table 1). None of the random effects were nested.

Additional models.

We also re-ran all models using a dataset that included each individual’s genetic hybrid score as a continuous fixed effect (hybrid scores exist for only 192 of the 237 study subjects). Across all models, the fixed effect of hybrid score showed a 95% confidence interval that was highly overlapping with zero (Table S2). In addition, Alpha models with and without hybrid score were within 2 AIC units of each other (AIC with hybrid score = −9167.07, AIC without hybrid score = −9167.96, ΔAIC = −0.89). All other predictors showed comparable estimates and confidence intervals to the main models. Therefore, to retain a larger sample size, we excluded hybrid score in our main analysis.

Assessing correlations among variables & model assumptions

Because the lowest ordinal ranks (those with the highest numerical values) only occur in the largest groups, ordinal dominance rank was correlated with the number of adult females in the group. Variance inflation factors (VIFs) were calculated using the faraway package in R version 3.3.3 to assess collinearity between rank and group size (Faraway, 2016). VIFs for group size and group size² in all 8 main models were greater than 27. Because of this inflated variance, group size was z-transformed. VIF scores for group size and group size² were <1.31 and <1.29, respectively, after transformation for all models. No other fixed effects showed inflated VIFs in the models used for this analysis; VIFs of all other predictors in all models were < 1.43.

To check assumptions of normality and homogeneity, we visually inspected quantile-quantile plots and plots of residuals against fitted values. No violations of model assumptions were detected in any case.

Conditional and marginal R² were calculated for the Alpha model using the performance package in R version 3.3.3 (Lüdecke et al., 2020).

RESULTS

Comparison of rank metrics: Alpha status was best predictor of fGCs

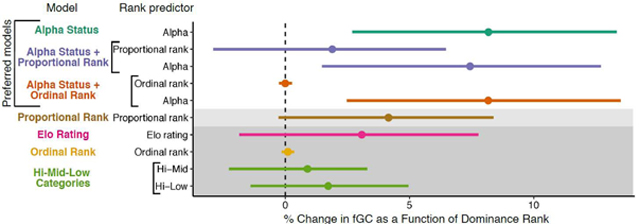
To test which rank metric provided the best prediction of fGC concentrations, we compared AIC scores for models that used different rank metrics. The Alpha model had the lowest AIC value and thus was the most preferred model (Table 2). The Alpha+Prop and Alpha+Ord models were the only other models within 2 AIC units of the Alpha model, indicating that they performed similarly to the Alpha model, though the Alpha+Ord model was at the 2-unit threshold (Table 2). These three models were also the only ones with AIC scores > 2 units smaller than the Null model, indicating that they substantially improved model fit relative to a model without dominance rank (Table 2). The Alpha model explained 25.9% of the variation in fGC concentrations (conditional R² = 25.9%, marginal R² = 9.9%). See Table S3 for R² values of all models.

Table 2.

AIC results for the 8 statistical models, ordered by AIC score from most to least preferred model, along with ΔAICs calculated relative to the Alpha and Null models; models < 2 AIC units smaller than the Null model have a light grey background; the Null model and models that performed worse than the Null have a dark gray background; see Table 1 for model information.

Model	AIC	ΔAIC to Alpha	ΔAIC to Null
Alpha	−9736.07	0.00	−8.68
Alpha+Prop	−9734.68	1.39	−7.29
Alpha+Ord	−9734.07	2.00	−6.68
Prop	−9728.76	7.30	−1.38
Null	−9727.39	8.68	0.00
Elo	−9726.90	9.16	0.48
Ord	−9726.09	9.97	1.29
Hi-Mid-Low	−9724.64	11.43	2.75

The Prop model was preferred over the Null model, but it was within 2 AIC units of the Null. The Elo, Ord, and Hi-Mid-Low models performed worse than the Null model, indicating that adding either of these ranking methods worsened the ability of the model to predict fGC concentrations, although the Elo and Ord models performed only slightly worse than the Null model (Table 2). When comparing the three enumerated rank measures, the Prop model outperformed the Ord model (ΔAIC = 2.7) and neared the 2-unit threshold against the Elo model (ΔAIC = 1.9), but the Elo model was comparable in performance to Ord (ΔAIC = 0.8, Table 2).

The relationship between rank and fGC: Higher fGCs in lower-ranking female baboons

In support of our prediction, lower dominance rank predicted higher fGC concentrations in all models that outperformed the null model (ΔAIC > 2 relative to the Null, which included the Alpha, Alpha+Prop, and Alpha+Ord models; Table 3, Figure 2). The rank coefficients from the Alpha model indicated that alpha females were predicted to have fGC concentrations 8.2% lower than all other adult females in their group (95% CI = 3.2 – 13.4%; Table 3, Figure 2). The rank coefficients for the Alpha+Prop model indicated that controlling for the alpha effect, fGC concentrations were predicted to increase by 1.9% from the highest-ranking to the lowest-ranking female in each group, regardless of group size (coefficient = −1.9%, 95% CI = −6.5 – 2.9%, Table 3, Figure 2). Similarly, the rank coefficients for the Alpha+Ord model indicated that, controlling for the alpha effect, each step down in ordinal rank predicted a 0.002% increase in fGC concentration (95% CI = −0.3 – 0.3%, Table 3, Figure 2). Notably, both the proportional rank effect in the Alpha+Prop model and the ordinal rank effect in the Alpha+Ord model have confidence intervals that highly overlap with 0 (Table 3, Figure 2). The Prop model performed marginally better than the Null model, and the limit of the 95% confidence interval was very close to 0. In the Prop model, the lowest-ranking individual in a group was predicted to have fGC concentrations 4.2% higher than the highest-ranking individual in a group (coefficient = −4.2, 95% CI = −8.4 – 0.27%, Table 3, Figure 2). We interpret these results as a weak effect of proportional rank on fGC concentration. See Table S4 for results of the Null, Elo, Ordinal, and Hi-Mid-Low models.

Table 3.

Converted estimates^b, 95% confidence intervals, and interpretations for the 4 models that performed better than the Null model; see S4 for model results of the other 4 models.

Model & Predictora	Estimateb	Lower 95%b	Upper 95%b	Interpretation
Alpha
Intercept	44.85	40.76	49.35	fGC > 0
Rank: Alpha vs Not	8.18	3.20	13.40	non-alpha > alpha
Age	1.17	0.86	1.48	old > young
Repro: C vs PPAc	0.16	−1.49	1.84	-
Repro: C vs Pc	22.15	19.94	24.41	pregnant > cycling
Season: Wet vs Dry	9.81	8.31	11.32	dry > wet
Group Sized	0.88	−1.11	2.91	-
Group Size	0.99	−0.03	2.02	small & large > mid
Storage Time: Powder	23.25	18.02	28.72	more time > less
Storage Time: Methanol	12.86	10.36	15.43	more time > less
Alpha+Prop
Intercept	45.57	41.09	50.54	fGC > 0
Rank: Alpha vs Not	7.44	2.19	12.96	non-alpha > alpha
Proportional rank	−1.89	−6.46	2.90	-
Age	1.17	0.86	1.49	old > young
Repro: C vs PPA	0.16	−1.49	1.84	-
Repro: C vs P	22.16	19.94	24.41	pregnant > cycling
Season: Wet vs Dry	9.80	8.30	11.32	dry > wet
Group Size	0.96	−1.04	2.99	-
Group Size2	0.98	−0.04	2.01	small & large > mid
Storage Time: Powder	23.20	17.97	28.67	more time > less
Storage Time: Methanol	12.86	10.35	15.42	more time > less
Alpha+Ord
Intercept	44.84	40.73	49.37	fGC > 0
Rank: Alpha vs Not	8.17	3.02	13.58	non-alpha > alpha
Ordinal rank	0.002	−0.25	0.25	-
Age	1.17	0.86	1.48	old > young
Repro: C vs PPA	0.16	−1.49	1.84	-
Repro: C vs P	22.15	19.94	24.41	pregnant > cycling
Season: Wet vs Dry	9.81	8.31	11.32	dry > wet
Group Size	0.88	−1.19	2.99	-
Group Size	0.99	−0.03	2.02	small & large > mid
Storage Time: Powder	23.25	18.01	28.72	more time > less
Storage Time: Methanol	12.86	10.36	15.43	more time > less
Prop
Intercept	49.60	45.57	53.99	fGC > 0
Proportional rank	−4.16	−8.38	0.27	low > high
Age	1.13	0.83	1.43	old > young
Repro: C vs PPA	0.19	−1.46	1.87	-
Repro: C vs P	22.18	19.96	24.44	pregnant > cycling
Season: Wet vs Dry	9.77	8.27	11.29	dry > wet
Group Size	1.19	−0.80	3.23	-
Group Size2	0.86	−0.15	1.88	small & large > mid
Storage Time: Powder	23.11	17.88	28.58	more time > less
Storage Time: Methanol	12.78	10.28	15.34	more time > less

^aFor all categorical variables, the first category listed was the base level.

^bThe Estimate and 95% confidence interval columns have been antilogged, subtracted by 1, and then multiplied by 100 to indicate the percent change in fGC associated with an increase of one unit of the predictor variable. For example, 1.17 for age implies a 1.17% increase in fGC for every year a female baboon ages, and −4.16 for proportional rank implies a 4.16% decrease in fGC from proportional rank of 0 to 1. The intercepts were antilogged only.

^cRepro = reproductive status; C = cycling; PPA= post-partum amenorrhea; P = pregnant

^dGroup size is the number of adult females, z-transformed to avoid variance inflation.

Figure 2.

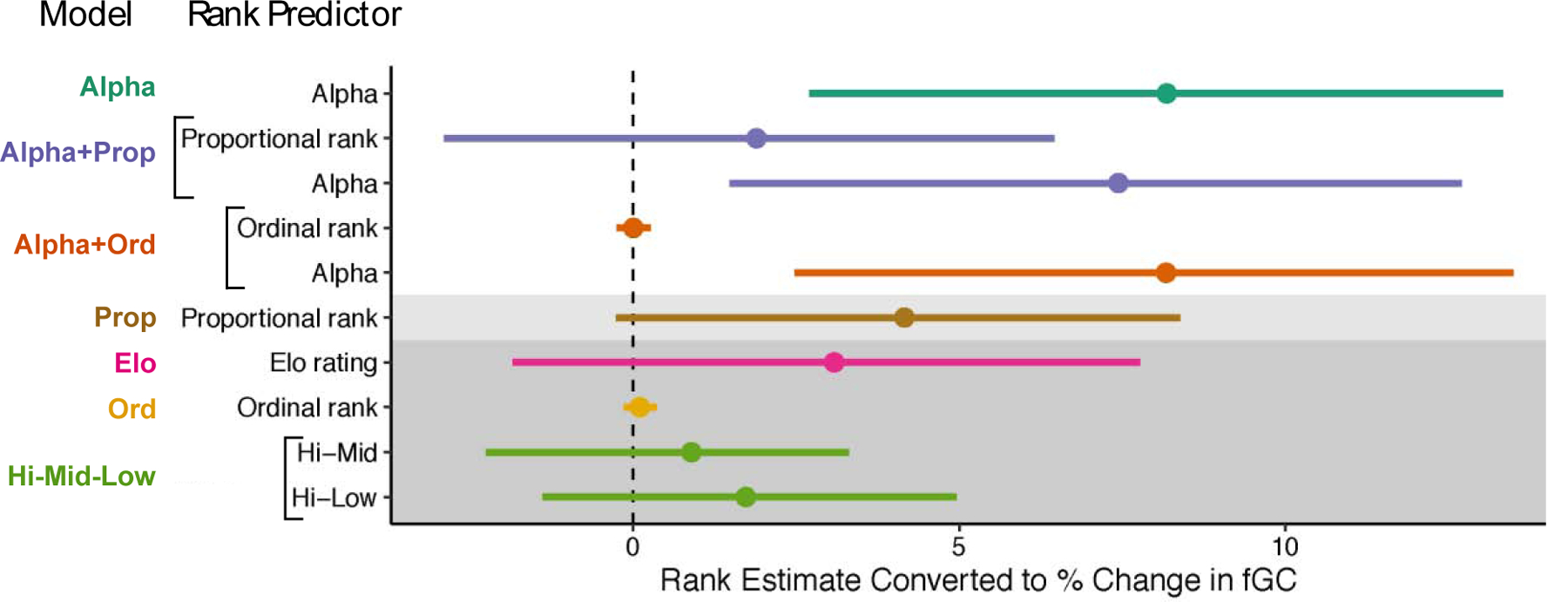
Comparison of rank estimates across the seven models that contained rank. Estimates (points) and 95% confidence intervals (lines) have been converted to percent change in fGC to facilitate comparison by antilogging, subtracting by 1, and then multiplying by 100. All estimates and confidence intervals are also arranged so that positive values indicate higher fGC concentration in lower-ranking individuals (i.e., values for proportional rank and Elo rating were multiplied by −1). Each model is indicated by a unique color. Models are ordered by AIC value, with the most preferred model, Alpha, at the top. Models that were within 2 AIC units smaller than the Null model are shown with a light grey background, and models that had AIC scores larger than the Null model are showed in with a dark grey background. The ordinal rank coefficients appear small because a one-unit change in ordinal rank is much smaller than a one-unit change in all other predictors.

The effects of age, reproductive status, season, group size, and storage time

Consistent with previously published results, fGC concentrations were higher in smaller and larger groups than medium-sized groups (Markham et al., 2015). fGC concentrations were also higher in older individuals, during the dry season than during the wet season, and during pregnancy compared to cycling and PPA (Altmann et al., 2010; Gesquiere et al., 2008; Gesquiere et al., 2011b) (Table 3). Both storage time variables were strong predictors of fGC, with fGC concentration predicted to increase by approximately 23.3% for every year a fecal sample was stored as fecal powder between sample collection and methanol extraction and 12.9% for every year a fecal sample was stored in methanol between extraction and assay (fecal powder: 95% CI = 18.0 – 28.7%; methanol: 95% CI = 10.4 – 15.4 in Alpha model, Table 3). All of these estimates were very similar for all models. Coefficients and standard deviations for random effects are reported in Table S5. Variance in fGC concentrations explained by each fixed effect predictor of the Alpha model are reported in Table S6.

DISCUSSION

Summary of results

In general, higher dominance rank was associated with lower fGC concentrations in female Amboseli baboons. This effect was best predicted by a model in which alpha females were treated as a separate category from all other females; all models that treated alpha females as a separate category, including the Alpha, Alpha+Prop, and Alpha+Ord models, were preferred over the Null model. In the Alpha model, which showed the lowest AIC score, alpha females were predicted to have fGC concentrations 8.2% lower than all other females. These results are broadly consistent with our original hypothesis that low-ranking females have more frequent HPA activation than high-ranking females, but our original hypothesis also failed to fully capture the nuances of the competitive landscape for female baboons in our population. A more accurate model is that alpha females experience substantial reductions in fGC levels compared to non-alpha females – indicating less HPA axis activation – while proportional rank has very modest linear effects on log(fGC) levels for all other females in the hierarchy, with higher fGC levels in lower-ranking individuals.

In addition to our findings about dominance rank, we also found that storage time both as fecal powder and in methanol can have a substantial effect on GC concentrations. Our results are only observational, however, and we encourage future researchers to perform more long-term tests (>1 year) of storage effects on fecal hormone concentrations (e.g., Hunt and Wasser, 2003; Shutt et al., 2012).

Alpha status as a predictor of fGC concentration

We found that alpha females experience substantially lower fGCs than other females in the hierarchy. These findings suggest a discontinuity in the stressors experienced by alpha females compared to non-alpha females. We were surprised to observe this pattern: differences in fGCs between alpha and non-alpha individuals are most commonly observed in cooperatively-breeding species, or in other contexts in which resources are discontinuously distributed so that alpha individuals benefit disproportionately (e.g., alpha males often have priority of access to mating with estrus females).

Why might alpha females have disproportionately lower fGC concentrations than other females? We propose two possible explanations. First, in the Amboseli baboon population, alpha females maintain their rank longer than non-alpha females: alpha females rarely lose rank to their mature daughters as they age, while this type of rank loss with age is typical for lower-ranking females (Combes and Altmann, 2001). Importantly, changes in dominance rank have been associated with increases in fGC concentrations in female chacma baboons, particular for low-ranking females (Engh et al., 2006). Hence, alpha females might have lower fGCs because they experience fewer rank changes than non-alpha females, thus evading the stressors associated with rank shifts. Second, females may receive aggressive acts primarily from females that rank directly above them, similar to Archie et al’s (2014) hypothesis. If so, then alpha females are in a particularly privileged position by having no females ranked above them.

Whereas the alpha vs non-alpha rank metric produced the three most preferred models (Alpha, Alpha+Prop, Alpha+Ord models), the other categorical rank metric, Hi-Mid-Low, produced a model that fared worse than the Null model. This result highlights the importance of thinking carefully before categorizing a continuous variable. The alpha vs non-alpha model tests the specific hypothesis that competition is different for alpha versus non-alpha individuals, but the high-middle-low predictor is essentially a simplified version of testing a linear, quadratic, or piecewise proportional rank effect; creating these categories may simply add noise to a continuous effect. Though studies commonly categorize ranks, our study along with Gesquiere et al. (2011a) support the idea that in group-living species without clear reproductive roles, dominance rank is best treated by enumerating ranks and/or differentiating alphas from non-alphas.

Proportional rank and ordinal rank

The better performance of the proportional rank model (Prop) than the ordinal rank model (Ord) is similar to the pattern documented by Archie et al (2014), who reported that injury risk in female Amboseli baboons was better predicted by proportional rank than by ordinal rank. Further, in spite of the observation – reported here and in previous work (Markham et al., 2015) – that average fGC concentrations are lowest in mid-sized social groups, our findings from the Prop and Alpha+Prop models suggest that, with the exception of the alpha females, the percent change in fGC concentration between high- and low-ranking females in a group may remain somewhat constant across group sizes.

The better performance of proportional than ordinal rank in predicting fGC concentrations is particularly salient because proportional and ordinal rank metrics make different assumptions about the resource-driven competitive regimes acting within a group. As noted above, an ordinal rank metric assumes that the average per capita resource competition increases as group size increases (i.e., the group’s resource base stays constant as group size increases), and that this increase in competition is disproportionately experienced by low-ranking females. In such a scenario, the number of individuals that are ranked above the focal individual is the most relevant factor that determines their access to resources. In contrast, a proportional rank metric – which was preferred over the ordinal metric in our study – assumes that average per-capita resource competition stays relatively constant with group size (i.e., the resource base is larger in larger groups). In this scenario, the lowest-ranking female in a given group is still the most disadvantaged individual with respect to competition, but the lowest-ranking female in a large group does not experience disproportionately more competitive exclusion than the lowest-ranking female in a small group.

Differences among studies of female baboons

Six prior studies investigated the relationship between female rank and GC concentrations (either feces or serum) in baboons, including two studies of the Amboseli population (Amboseli [Papio cynocephalus]: Beehner et al., 2006; Sapolsky et al., 1997) (chacma baboons [Papio ursinus]: Crockford et al., 2008; Seyfarth et al., 2012; Weingrill et al., 2004; Wittig et al., 2008) (Table S7). Of these six, only two, both in chacma baboons, revealed a statistically significant relationship between dominance rank and fGC concentrations. In both cases, high-ranking females had lower fGC concentrations than low-ranking females, as in our study: one study showed a simple linear relationship between rank and fGC concentrations, while the other showed that high-ranking chacma females experienced more rapid decreases in fGC concentrations after a period of male rank instability (Seyfarth et al., 2012; Wittig et al., 2008). One of these studies measured rank proportionally (Seyfarth et al 2012), and the other measured rank ordinally (Wittig et al 2008). The other four studies showed no statistically significant association between female baboon rank and GC concentrations.

Our results shed some light on possible sources of difference between these studies of rank and GC concentrations in female baboons. First, the studies differed in the rank metric they used. Three of these six studies used the ordinal rank metric, one used the proportional rank metric, one used the high-middle-low categorical rank metric, and in one study the rank metric was not stated but was likely ordinal or proportional (Table S7). No studies tested an alpha-or-not rank metric. Most of these studies only included one study group and/or spanned a short time period – conditions under which proportional and ordinal rank will be highly correlated. However, Beehner et al’s (2006) study in Amboseli used ordinal rank measures for females in five social groups over five and a half years, raising the possibility that a main effect of proportional dominance rank was missed in that analysis. In a re-analysis of samples from that publication, we did not find a statistically significant effect of alpha status or proportional rank on fGC concentrations, though this could be due to relatively low statistical power in this dataset (p_alpha = 0.569, p_proportional = 0.205, N=1,209 samples from 67 pregnant females, see Supplementary re-analysis of Beehner et al 2006 in Supplementary materials).

Second, the method of analysis may be important (e.g., computing a correlation vs. running mixed effects models). All previous studies of female baboons included other variables likely to be associated with GCs, either via multivariate regressions, mixed effects regressions, or ANCOVA analyses (Table S7). Two main methodology differences occurred across studies: (1) some studies included random effects such as individual identity and some did not, and (2) some studies calculated mean GC concentrations over standard time periods as the unit of analysis (e.g., a monthly measure of GC) while other studies used each sample as a data point. Whereas differences in the model types used for analysis are unlikely to account for differences between studies (i.e., regression vs. ANCOVA), the use of fixed effects and the data processing techniques may contribute to difference between studies. For example, if we remove the random effect of individual from the Ord model, ordinal rank predicts a 0.20% increase in fGC for every step down in rank, with a confidence interval that no longer overlaps with zero (95%CI = 0.07% – 0.32%).

Third, temporal or spatial variation may occur in demographic or environmental variables that affect GC secretion. Indeed, the six studies spanned two baboon species, three baboon populations, and different habitats, durations, demographic contexts, and time periods. Within-group competition may vary across populations, groups, years, and seasons; when within-group competition is high, we would expect a stronger relationship between dominance rank and fGC levels. Therefore, demographic or environmental factors are likely sources of differences among these studies.

Finally, all of the studies employed sample sizes that were at least an order of magnitude smaller than ours, indicating that effects of dominance rank on GCs in female baboons may be small and noisy enough to require a large dataset for detection (Table S7). To examine the statistical power of previous studies while assuming the same effect size as our study, we performed a power analysis by randomly sub-sampling our dataset 10,000 times, each time selecting the same number of study subjects and fecal samples as two prior studies in Table S7 (532 fecal samples from 22 females: Wittig et al 2008; 260 fecal samples from 10 females: Weingrill et al 2004). We ran each sub-sample in the Prop model and calculated the proportion of replicates that yielded statistically significant p-values of proportional rank (p ≤ 0.05). (We did not replicate this analysis with the Alpha model because these models would have relied on extremely small sample sizes of alpha females.) In these replications based on samples sizes from Wittig et al (2008) and Weingrill et al (2004), 9.6% and 12.7% and of sub-samples produced a statistically significant effect of proportional rank, respectively (see Supplementary power analysis in Supplementary materials,).

Comparison with male baboons

Our results for female baboons contrast with findings from male baboons. In several studies, high-ranking males experienced higher fecal or serum GC concentrations than middle-or low-ranking males, especially during periods of rank instability. (Bergman et al., 2005; Cheney et al., 2015; Gesquiere et al., 2011a; Sapolsky, 1983). Male baboons in Amboseli show two distinct rank-related patterns of fGC concentrations: elevated fGC concentrations for the alpha male, but relatively low concentrations for the second-ranking (beta) male and a progressive increase in fGC concentrations between the beta male and lower-ranking males (Gesquiere et al., 2011a). Gesquiere et al. (2011a) also demonstrated that alpha males spent more time engaged in energetically costly activities – maintaining dominance rank and mate guarding – than beta males, which may explain the higher fGC concentrations for alpha males compared to other high-ranking and mid-ranking males. The authors also hypothesized that lower ranking males are exposed to higher rates of aggression and have more limited access to food than higher ranking males, which would explain higher fGC concentrations in low-ranking males.

Our models indicated that alpha females experienced lower, not higher, fGC concentrations than other females in the hierarchy. The finding of discontinuously lower fGC concentrations in alpha females compared to non-alpha females suggests that high-ranking females do not experience the types of energetic costs that males seem to incur by maintaining high dominance rank; instead, these alpha females may experience reduced energetic or psychosocial stressors than their group-mates by being at the top. Similar to findings in males, we also observed a weak continuous effect in the non-alpha individuals, with low-ranking individuals having higher fGC concentrations (proportional rank in females, ordinal rank in males).

Hierarchies determined by nepotism or queuing are hypothesized to have weaker relationships between rank and GC concentrations than hierarchies determined by physical contests (Creel et al., 2013; Goymann and Wingfield, 2004; Sapolsky, 2005). In line with this hypothesis, our effect size for Amboseli female baboons was smaller than the effect size seen in Amboseli males. Our Alpha model predicted a 8.2% difference between alpha and non-alpha females, whereas findings from males predicted a 10.7% difference between the alpha and non-alpha males. In the continuous rank measures – proportional rank in females, ordinal rank in males – there was also a difference in magnitude. The Prop model predicted a 4.2% increase in fGC concentrations from the highest- to lowest-ranking individual in a group. In males, there was a predicted 0.995% increase in for every 1-unit increase in ordinal rank (Gesquiere et al., 2011a), which is equivalent to a 9.3% increase from rank 2 to rank 11 (mean monthly adult male group size during this study period = 11.1). The difference in effect sizes between males and females suggests that dominance rank is more closely associated with changes in fGC secretion in males, who must fight for high rank, than in females, who inherit rank from their mothers (Lea et al., 2014).

Social factors contributing to rank effects

We hypothesize that both psychosocial stressors and the level of resource equity are influential in mediating the relationship between rank and fGC concentrations in female baboons. In the case of psychosocial stressors, low-ranking females in Amboseli receive higher rates of aggression and lower rates of grooming than high-ranking females (Akinyi et al., 2013). These patterns are typical across many primate species (Schino, 2001; Seyfarth, 1977). Allogrooming is thought to relieve stress or tension (Boccia et al., 1989; Terry, 1970), with evidence in baboons that (1) females who receive grooming from or give grooming to a relatively small number of core associates have both lower fGC concentrations and show a smaller increase in fGC concentrations during male rank instability compared to females who groom with a larger number of associates, and (2) cycling females who receive more grooming than they give show lower fGC concentrations than females who give more than they receive (Crockford et al., 2008; Wittig et al., 2008).

In addition, several lines of evidence indicate that resource acquisition is not evenly distributed across female baboons of different dominance ranks, in Amboseli and elsewhere. In Amboseli, low-ranking females experienced more feeding interruptions than high-ranking females (Post et al., 1980). Further, low-ranking female Amboseli baboons had longer inter-birth intervals, offspring with later sexual maturation, and slower-growing offspring than high-ranking females, suggesting rank-related differences in resource access (Altmann and Alberts, 2003, 2005). Unequal energetic resource access as a function of dominance rank is a ubiquitous finding across group-living animals; evidence of this pattern, such as rank-related differences in reproductive rate, has been observed in other baboon populations, in other primate species, and in other mammal species (e.g., baboons [Papio ursinus, Papio anubis]: Barton et al., 1996; Barton and Whiten, 1993; Cheney et al., 2006); (other primates [Macaca fuscata, Macaca fascicularis, Cercopithecus aethiops]: Iwamoto, 1974; Saito, 1996; van Noordwijk and van Schaik, 1999; Whitten, 1983); (other mammals [Suricata suricatta, Crocuta crocuta]: English et al., 2014; Holekamp et al., 1996); (for review see: Clutton-Brock and Huchard, 2013); (but see Majolo et al., 2012). Thus, we hypothesize that for female baboons, low rank is associated with (1) increased psychosocial stressors due to increased aggression rates and lack of coping mechanisms and (2) increased energetic stressors due to decreased resource access.

Future directions

Advances in the study of hormone metabolites and other compounds in wild animal excreta have allowed tremendous progress in our ability to ‘get under the skin’ of wild animals using noninvasive research techniques (e.g., Higham et al., 2015; Lafferty et al., 2015; Podlesak et al., 2005; Romero, 2002; Thompson et al., 2009; Wasser et al., 2010). These techniques have allowed us to measure components of the stress response, diet, energetic balance, and immune function, all in the context of an organism’s life history and environment. The resulting findings have provided insight into species differences and sex differences in behavior and physiology that would not have been possible through observational research or laboratory-based experimental work alone. As fecal and urine sample collections from wild animals continue to grow, these insights will only expand as we gain not only statistical power, but also the longitudinal data needed to test important ecological, conservation, and evolutionary hypotheses about interactions between organisms and their environments (e.g., Bădescu et al., 2017; Dantzer et al., 2016; Thompson et al., 2016). We also see important opportunities for cross-study comparative work, involving collaborations across multiple laboratories and syntheses across literature from diverse taxa (e.g., Beehner et al., 2009; Coe et al., 1992; Creel, 2001). In addition, we look forward to research that investigates to what degree, under which conditions, and in which taxa we can measure associations between physiology and fitness (Beehner and Bergman, 2017; Bonier et al., 2009; Creel et al., 2013).

With respect to studies of dominance rank, our study highlights the importance of choosing the best rank metric to measure a trait of interest. Only a handful of studies to date have described or examined the assumptions underlying their choice of rank metric. We see value in taking a new approach, in which researchers attempt to match their choice of rank metric to their study system by drawing on behavioral-ecological theory or empirical evidence. This could be achieved by testing more than one rank metric when testing hypotheses about the competitive environments acting in a given population. In addition, we are interested in testing the strength of the association between female baboon dominance rank and GC levels across different environmental, physiological, and social conditions, similar to work done in other study systems (e.g., Foerster et al., 2011; Rubenstein, 2007; Thompson et al., 2010). Doing so will help reveal when individuals experience the most intense within-group competition. We hypothesize that the relationship between dominance rank and fGC levels will be strongest during periods of greater within-group competition. In addition, the nature of the competition may determine which dominance rank metric best models the relationship between rank and fGCs. For example, a period of low food availability may affect all group members relatively equally, and this period of increased within-group competition may be best modeled using proportional rank as opposed to alpha status. We also see a gap in our understanding of the ‘shape’ of rank-associated phenotypes; we tend to model continuous rank metrics linearly or occasionally quadratically, but competitive environments that can become saturated could produce data that are best fit to a piecewise function or log-linear curve. Thus, further investigation into the competitive environment, via model comparison or looking directly at resource availability and competition, is needed.

HIGHLIGHTS.

• Alpha status predicts low fecal glucocorticoid concentrations in female baboons

• Proportional (i.e., ‘relative’ or ‘standardized’) rank was also a weak predictor

• Other rank metrics were poor predictors of fecal glucocorticoid concentrations

• Our results shed light on within-group competitive processes