Finding the Pattern: On-Line Extraction of Spatial Structure During Virtual Navigation

Abstract

While navigating the world, we pick up on patterns of where things tend to appear. According to theories of memory and studies of animal behavior, knowledge of these patterns emerges gradually over days or weeks via consolidation of individual navigation episodes. Here, we discovered that navigation patterns can also be extracted on-line, prior to the opportunity for off-line consolidation, as a result of rapid statistical learning. Thirty human participants navigated a virtual water maze in which platform locations were drawn from a spatial distribution. Within a single session, participants increasingly navigated through the mean of the distribution. This behavior was better simulated by random walks from a model that had only an explicit representation of the current mean, compared with a model that had only memory for the individual platform locations. These results suggest that participants rapidly summarized the underlying spatial distribution and used this statistical knowledge to guide future navigation.

After finding your way to a restaurant for the first time, you are able to find it more easily the next time. This ability to use past episodes of navigation to achieve current goals is ubiquitous across species (Barry, Coogan, & Commins, 2016; Cornwell, Johnson, Holroyd, Carver, & Grillon, 2008; Judd & Collett, 1998). However, recollecting specific episodes is not the only way to draw on past experiences. When we seek a new location, it may be more efficient to rely on general knowledge aggregated across multiple episodes. For example, if you are looking for a new restaurant, an effective strategy might be to head toward the neighborhood with other restaurants you have liked.

Aggregating across episodes is useful because it allows learning of statistical structure, such as the spatial pattern of locations previously visited. Theories of memory (McClelland, McNaughton, & O’Reilly, 1995) describe this process as resulting from gradual consolidation, in which distinct episodes are integrated off-line during sleep over days to weeks. This memory transformation has been demonstrated in rodents, who after 30 days navigated a familiar arena according to the spatial distribution of previously learned locations rather than individual past locations (Richards et al., 2014).

Recent work suggests that such statistical learning can also occur rapidly, within minutes, potentially in parallel with the encoding of episodes (Schapiro, Turk-Browne, Botvinick, & Norman, 2017). However, many of the studies showing rapid statistical learning examined temporal structure in sequences (Saffran, Newport, & Aslin, 1996; Turk-Browne, Jungé, & Scholl, 2005) or spatial structure in brief arrays of simple objects (Chun & Jiang, 1998; Fiser & Aslin, 2001). Spatial structure is inherently different in navigation, as patterns of locations exist in allocentric rather than egocentric space (i.e., in world-centered coordinates, relative to landmarks). How humans deploy statistical learning during spatial navigation remains an open question.

Here, we tested this question using a virtual analog of the delayed match-to-place water-maze task (Morris, 1984). Across repeated attempts to locate hidden “platforms” within a single session, we quantified how human navigation was informed by previous platform locations and the mean of their spatial distribution. We interpreted this behavior by modeling it with artificial agents who took random walks with knowledge of either individual past platform locations or only the mean location. We hypothesized that participants would shift within session from navigating toward individual platforms (episode-based navigation) to navigating toward their mean (pattern-based navigation) after accruing enough experience to extract a pattern.

Method

Participants

Thirty participants (16 female; age range = 18–22 years) completed the study for course credit. The Yale University Human Subjects Committee approved the study protocol. We arrived at this sample size by conducting a power analysis on data from a pilot study using a bootstrapping procedure and Wilcoxon’s signed-rank test. We drew from 14 pilot participants with replacement to generate a range of sample sizes. We analyzed the increase in number of crossings through platform locations from the first to the second half of the experiment. We chose this metric to estimate power because it is analogous to the canonical escape-latency measure of spatial learning (Cornwell et al., 2008). We ran 1,000 iterations per sample size and calculated the proportion of tests in which the effect was below a significance level of .05. Using this proportion as our estimate of power, we found that a sample size of 30 participants was sufficient to detect this effect with greater than 99% power. This sample size also falls in the range used in other studies that have shown a learning effect on escape latency (range = 15–52; Cornwell et al., 2008; Richards et al., 2014).

Stimuli

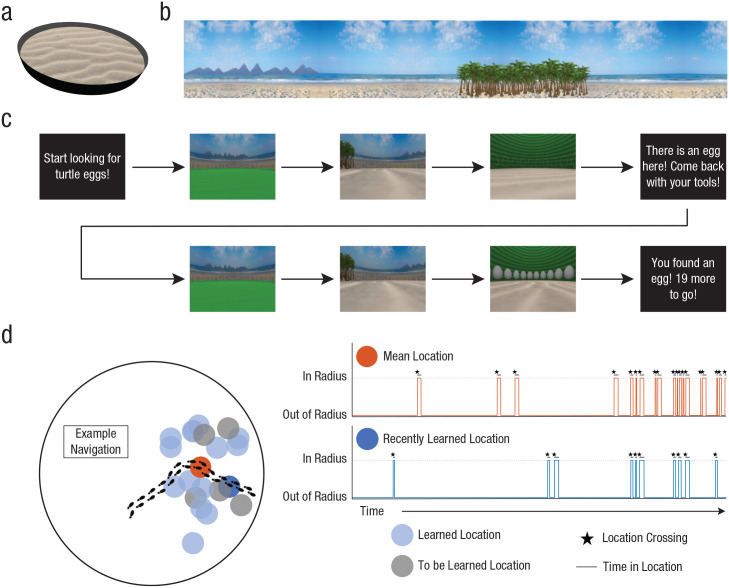
The virtual environment was designed as a circular arena, adapted from Woolley et al. (2015) and constructed in Blender (Version 2.45; https://www.blender.org/). The environment was rendered in MATLAB (MathWorks, Natick, MA), and the Psychophysics Toolbox (Brainard, 1997) was used to display task instructions. The arena was designed graphically with an island theme. The circular floor (radius = 7.85 units) was covered by an image of sand (see Fig. 1a). Mountains on the north end and palm trees on the south end served as landmarks that provided directional headings (see Fig. 1b). The “platforms” were hidden nests of turtle eggs, and following Richards et al. (2014), we drew their locations from a normal distribution of distances d from center (μ = 3.4 units, σ = 0.9067) and a circular normal distribution of angles θ between the platform and the eastern cardinal direction (μ = 0.2618 radians, κ = 8).

Fig. 1.

Task design and performance. The virtual water maze was a circular, beach-themed arena (a). The mountains and palm trees (b) served as north and south directional headings, respectively. Participants were prompted to begin searching at the start of each trial (c). They were initialized in the center of the arena. For the first 5 s, the ground appeared green, and they could only rotate in place. The ground then turned to sand, and participants could freely navigate. When they found an egg, they were instructed to return to the same location on the next trial. On the trial after that, they began searching for a new egg location. We quantified location crossings and time in location during participant navigation (d). The timeline graphs depict results from an example participant who showed increased navigation to both locations over the course of the experiment. The places where the timeline jumps up to the dotted line (indicated by stars) mark the moments when a location was crossed, and the lengths at which the timeline remains along the dotted line (indicated by black lines) correspond to how long the participant was in those locations.

Statement of Relevance.

We spend most of our life in familiar places—homes, neighborhoods, workplaces, and stores. This repetitiveness allows us to learn about the structure of these spaces and to navigate them more efficiently. But how quickly do we learn the spatial structure of our environments? Studies with rodents suggest that this learning happens slowly, over days or even weeks of experience. In this research, we asked whether the same was true for humans. We tested navigation in a novel virtual environment. We found that humans can learn spatial structure very quickly, on the order of minutes. Once learned, they can then use their understanding of the space to guide subsequent navigation. These findings reveal that the human mind is exquisitely sensitive to structure during spatial navigation, which may underlie our ability to rapidly adapt to new environments.

Procedure

Participants were instructed that they were on an island searching for a total of 20 turtle eggs buried below the sand. They had to find one egg at a time by walking around the beach. Participants used the I key to walk forward; the J and L keys to turn left and right, respectively; and the M key to walk backward.

At the beginning of the search for each new egg, the participant’s location was initialized to the center of the arena. For the first 5 s, the ground appeared green, and the I and M keys were locked so participants could only rotate in place left or right. The ground then turned to sand, cuing participants that they could now start moving forward and backward. There was no time limit, so the searches varied in length (40 min total, on average). Participants successfully located an egg when they walked within a one-unit radius of the platform location of that egg. When this occurred, further navigation was locked, and the walls turned green to reveal the outline of an egg. The screen then went black, and participants were instructed to return to the same location (with the cover story of needing to return to the site with the appropriate tools). Their location was then reinitialized at the center of the arena, and they navigated to the latest egg location. The purpose of having them repeat the search was to aid episodic encoding of the egg location in the arena with respect to the landmarks. After finding the egg again, participants were told how many new eggs remained to be found. They then began to search for the next egg (see Fig. 1c).

Data analysis

The main analyses focused on the search paths from trials in which participants first found an egg. We did not include search paths from the first two eggs because it was not yet possible to extract a pattern, and thus episode- and pattern-based navigation could not be distinguished. Raw data consisted of x and y coordinates outputted every 40 ms of navigation.

For each search trial, we quantified pattern- and episode-based navigation as the number of crossings through each representative location. We used the mean of the currently known points (e.g., on Trial 4, the mean of egg locations from Trials 1–3) for pattern-based navigation and the most recently learned egg location (e.g., on Trial 4, crossings through the egg location from Trial 3) for episode-based navigation. We focused on the most recent location because we expected (and observed) this to be more conservative than considering navigation through all previously learned locations (see Fig. S1 in the Supplemental Material available online) or through other individual locations, such as the first learned location or a randomly sampled previous location (see Fig. S2 and Table S1 in the Supplemental Material). That is, among previous locations, participants navigated more to the most recently learned location, so using this as a baseline worked against our hypothesis of greater navigation to the mean location.

To define a mean location crossing (e.g., an instance in which a pair of coordinates was outside the location and the immediately following pair was inside the location), we drew a radius that encapsulated the change in mean representation across trials as more data points (i.e., egg locations) were acquired. For each trial, we quantified the full-width half-maximum of the currently known distribution, and we halved this value to generate a radius around the coordinates of the current mean (see Fig. S3 in the Supplemental Material). To avoid any bias from changes in the size of this mean location radius across the task, we used the same trial-specific radius value for the recently learned location (see Fig. 1d). Other ways of defining the radius threshold yielded similar results (see the Supplemental Text section in the Supplemental Material).

In addition to crossings, we also analyzed the total time spent in the most recent location (for episode-based navigation) and in the current mean location (for pattern-based navigation). We calculated this as the number of raw data points (output every 40 ms) generated within these location radii. To account for differences in trial length, we normalized each measure by the total distance traveled during that trial (see Table S2 in the Supplemental Material for the nonnormalized raw data). We used total distance rather than total time to normalize measures because trial length per se does not increase crossings or time in noncenter locations. Finally, we binned the trials into the first and second halves of the experiment to contrast navigation early in learning with navigation later in learning. The same results were obtained when we treated trial number as a continuous variable (see Supplemental Text).

Although our primary focus was on the search trials, we used the return trials (when participants were instructed to navigate to the location at which they had just found an egg) to examine how general task performance changed across trials. Normalizing the length of the return paths by the distance from starting to ending locations, we found a main effect of trial number on escape latency, β = −1.03, t = −2.91, p = .0037, with search paths getting shorter (i.e., more efficient) across trials (r = −.11, p < .001). We interpreted this improved performance as reflecting learning of the task and environment (Cornwell et al., 2008). We also conducted exploratory analyses of how the mean location influenced navigation on return trials (see Fig. S4 in the Supplemental Material).

Results

Human behavior

We first investigated changes in crossings through, and time spent in, the most recent egg location (episode-based navigation) and the cumulative mean egg location (pattern-based navigation) from the first to second halves of the experiment (see Fig. 2a). Our analyses were based on our a priori prediction that pattern-based navigation would exceed episode-based navigation in the second half. Thus, we ran mixed-effects linear regressions with condition (most recent and cumulative mean), experiment half (first and second), and their interaction as regressors predicting the number of location crossings and the time in each location. To control for effects of distance traveled per trial, we included total distance as a regressor, as well as its interactions with each of our variables of interest. Random intercepts for each participant were also included in the models. We conducted exploratory analyses of different search strategies, including controlling for these strategies in our main analyses (see Fig. S5 in the Supplemental Material).

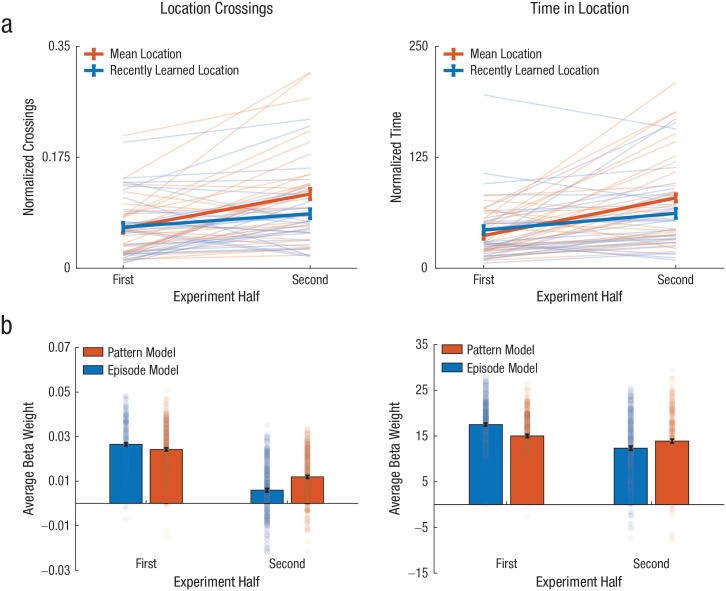
Fig. 2.

Human behavior and model fits for location crossings and time in location. In (a), normalized crossings (left) and normalized time (right) are shown as a function of experiment half (first and second) and condition (mean location and recently learned location). The thin lines represent individual participants’ data for each condition. The bold lines represent the mean across participants for each condition. The error bars represent ±1 within-subject standard errors. In (b), the average beta weights are shown for each model from 1,000 regressions, using simulated agent performance on each experiment half to predict human performance. Results are shown separately for the episode model and the pattern model. A subset of 250 beta weights for each model indicate the distribution of fits. Error bars represent 95% confidence intervals.

The analysis of location crossings revealed a marginal main effect of experiment half, β = 0.02, t = 1.71, p = .085. There were interactions between condition and experiment half, β = 0.03, t = 2.06, p = .043, and between experiment half and distance, β = −0.02, t = −2.52, p = .013; importantly, we did not find an interaction between condition and distance, β = −0.01, t = −1.25, p = .216, indicating that differences in crossings through the cumulative mean and most recent location were not merely a function of overall trial duration and number of steps taken. Comparison with a simple main-effects model revealed that our model better predicted participant behavior, χ²(3) = 13.39, p = .004. We then applied Wilcoxon’s signed-rank test to our predicted Condition × Experiment Half interaction and found more cumulative mean than most recent location crossings during the second half, Z = −2.69, p = .007, r = .49, 95% confidence interval (CI) for the mean difference = [−.04, −.004], but not the first half, Z = −0.45, p = .655, r = .081, 95% CI for the mean difference = [−0.01, 0.02].

The analysis of time in location similarly revealed a main effect of experiment half, β = 16.37, t = 2.21, p = .030. There were again interactions between condition and experiment half, β = 21.73, t = 2.10, p = .039, and between experiment half and distance, β = −20.66, t = −3.10, p = .002, but no interaction between condition and distance, β = 3.18, t = −0.61, p = .541. Compared with a simple main-effects model, our model again provided a better fit to participant data, χ²(3) = 14.58, p = .002. Subsequent tests of the Condition × Experiment Half interaction revealed that participants spent significantly more time in the cumulative mean than in the most recent location during the second half, Z = −3.18, p = .001, r = .58, 95% CI for the mean difference = [−28.78, −7.06], but not the first half, Z = −0.69, p = .490, r = .13, 95% CI = for the mean difference [−5.36, 13.88].

Thus, for both crossings and time in location, participants showed increased pattern-based navigation relative to episode-based navigation over a single session.

Control distribution

To verify that our key results were location specific and not an artifact of averaging or other analysis choices, we repeated the above analyses after rotating the spatial distribution of locations by 90°. If the apparent increase in pattern-based navigation reflected learning of the true distribution, the critical interaction between condition and experiment half should be eliminated. Indeed, using the same regressors as in our main analyses, neither the rotated model of location crossings, β = −0.00090, t = −3.81, p = .705, nor the rotated model of time in location, β = −3.31, t = −1.14, p = .258, revealed a Condition × Experiment Half interaction (see Fig. S6 in the Supplemental Material). We also expected fewer crossings through, and less time spent in, the rotated locations overall. Comparison of the true and rotated distributions revealed robustly more crossings through real locations, Z = −9.12, p < .001, r = .74, 95% CI = [.66, .91], as well as more time spent in real locations, Z = −6.11, p < .001, r = .53, 95% CI = [.39, .65].

Simulated agents

Finally, we wanted to verify that our main findings reflected pattern-based navigation and could not be explained as incidental to episode-based navigation. That is, because the shortest path to certain egg locations was inadvertently through the mean, and the number of such locations increased over time, an agent with knowledge of only previous locations might still show an increase in cumulative mean location navigation from the first to the second half of the experiment.

To address this possibility, we simulated task performance with two biased Gaussian random-walk models—an episode model and a pattern model—and fitted participant behavior with each model’s simulated navigational routes. Random walks have previously been shown to be capable of imitating certain optimal behaviors (Abbott, Austerweil, & Griffiths, 2015). We predicted that if participant behavior were driven by an explicit representation of the distribution mean, it would be better fitted by a randomly navigating agent with access only to the cumulative mean, compared with an agent with access only to the individual past locations (which controls for the amount of incidental mean navigation en route to specific locations).

To approximate participant behavior, we constrained each model’s search duration to recapitulate the group average number of location crossings per trial; for the episode model, this location constraint was the average number of platform crossings, whereas for the pattern model, it was the average number of mean location crossings. We determined which egg locations were crossed by the episode model on each trial, and in what order, by randomly drawing from previously learned locations weighted by recency (Bornstein, Khaw, Shohamy, & Daw, 2017). Thus, the most recently learned egg location was the most likely to be crossed first, though the model would cross through multiple previously learned locations on each simulated trial. For the pattern model, the only location represented was the mean of the currently known locations.

Like human participants, each model was initialized at the origin of a grid. The episode model navigated with Gaussian noise through previously learned locations in the order they were sampled. The pattern model navigated with Gaussian noise through the mean. Steps in two-dimensional space were generated by the equations

$$x_{S+1}=x_S+K\mathrm{and}{y}_{S+1}=y_S+K,$$

where K was drawn from a Gaussian distribution (μ = 0, σ = 1). Distance from the next step to the goal location (a randomly drawn previous egg location for the episode model and the mean for the pattern model) was constrained such that

$$d_{S+1}\le d_S+d_S\mathrm{\varphi },$$

where φ is a temperature parameter initialized at 0.5 that monotonically decreased on each trial. This parameter was used to capture participants’ decreased randomness and increased navigation toward previous locations across trials, as evidenced by the reduction in distance traveled per trial over the course of the experiment.

We simulated 1,000 agents per model and repeated the mixed-effects linear regression on each model’s output. For the episode model (see Fig. S7a in the Supplemental Material), the critical interaction between condition and experiment half was found in analyses of both location crossings, β = −0.02, t = −19.71, p < .001, and time in location, β = −1.89, t = −25.81, p < .001. This was reflected in more crossings through the cumulative mean location in the second half, Z = −16.64, p < .001, r = .53, 95% CI = [.48, .57], relative to the first half, Z = −15.07, p < .001, r = −.46, 95% CI = [−.51, −.41], and more time spent in the cumulative mean location in the second half, Z = −20.48, p < .001, r = .61, 95% CI = [.57, .65], relative to the first half, Z = −21.92, p < .001, r = −.64, 95% CI = [−.68, −.60].

For the pattern model (see Fig. S7b in the Supplemental Material), there was again an interaction between condition and experiment half for both location crossings, β = −0.05, t = −30.13, p < .001, and time in location, β = −2.31, t = −33.07, p < .001. This was again reflected in more crossings through the cumulative mean location in the second half, Z = −26.46, p < .001, r = .84, 95% CI = [.83, .85], relative to the first half, Z = −5.05, p < .001, r = .16, 95% CI = [.10, .22], and more time spent in the cumulative mean location in the second half, Z = −31.10, p < .001, r = .82, 95% CI = [.81, .84], relative to the first half, Z = −8.52, p < .001, r = −.27, 95% CI = [−.32, −.21].

Given that both models demonstrated more pattern-based than episode-based navigation in the second half of the experiment, it is critical for our analyses that this difference be significantly larger in the pattern model than the episode model. If both models displayed analogous increases in mean-based navigation, then we would have failed to generate models that “learn” differently over the course of the task as a function of their different representations. Indeed, in the second half, the ratio of mean navigation to recently learned location navigation was significantly larger in the pattern model than in the episode model, both in crossings, Z = −25.05, p < .001, r = −.71, 95% CI = [−.74, −.68], and time in location, Z = −22.70, p < .001, r = −.66, 95% CI = [−.69, −.62]. This shows that knowledge of episodes alone yielded qualitatively less pattern-based navigation and was not sufficient to explain the full increase in navigation to the mean.

To further support the conclusion that participants extracted the mean, we attempted to fit participant behavior with both models (see Fig. 2b). Specifically, we divided each model’s crossings and time in location per trial into the first and second halves of the experiment (nine trials each after excluding the first two trials). We then ran linear regressions for the 1,000 simulations, separately using each model’s “behavior” to predict participant behavior. Specifically, we z-scored each model’s number of crossings and amount of time in location, and we input the z scores into the regressions. We chose to use z scores instead of raw model performance to ensure a common scale between the two models. The result of this procedure was a distribution of 1,000 beta weights, averaged across participants for each model and experiment half (see Fig. S8 in the Supplemental Material for comparison with an alternative episode model that avoided previous locations). We analyzed the data for crossings and time in location using analyses of variance with two factors (model and experiment half).

In predicting crossings, we found main effects of model, F(1, 999) = 26.66, p < .001, and experiment half, F(1, 999) = 2,031.36, p < .001, as well as an interaction between model and experiment half, F(1, 999) = 128.30, p < .001. This interaction reflected a switch from a greater beta weight for the episode model in the first half of the experiment, t(999) = −4.61, p < .001, d = 0.15, 95% CI = [−0.0033, −0.0013], to a greater beta weight for the pattern model in the second half, t(999) = 11.45, p < .001, d = 0.36, 95% CI = [0.0050, 0.0070].

Likewise, when predicting time in location, we found main effects of model, F(1, 999) = 5.51, p = .019, and experiment half, F(1, 999) = 249.18, p < .001, as well as an interaction, F(1, 999) = 108.83, p < .001. We again observed a switch from dominance of the episode model in the first half, t(999) = −10.21, p < .001, d = 0.32, 95% CI = [−2.96, −2.01], to dominance of the pattern model in the second half, t(999) = 5.09, p < .001, d = 0.16, 95% CI = [0.93, 2.17].

This change over time in the best-fitting model, for both crossings and time in location, provides support for our hypothesis of increased pattern-based navigation as a result of statistical learning within the session.

Discussion

In this study, we compared the role of memories for past locations with generalized knowledge of their spatial patterns. We found evidence of navigation to the mean of the distribution of past locations, and we used computational modeling to show that this pattern extraction was not incidental to having more locations in memory. Consistent with our hypothesis, results showed that navigation shifted from episode based to pattern based.

Theories of memory that posit pattern extraction as occurring gradually over a long timescale (McClelland et al., 1995; Squire & Alvarez, 1995; Winocur & Moscovitch, 2011) have found support in findings from rodents, whose spatial and contextual memories generalize and lose episodic detail over a period of weeks (Richards et al., 2014). However, these frameworks cannot readily explain the rapid transformation we observed in under an hour. To the extent that patterns are extracted on-line, this might suggest an update to conventional theories: Off-line consolidation may operate not only over individual episodes but also over patterns extracted within a day that have already begun the process of memory transformation. Notably, the short timescale we observed is still longer than would be expected on the basis of perceptual averaging (Alvarez, 2011), which involves the immediate extraction of summary statistics from a single, egocentric trial rather than the integration of allocentric information across multiple trials.

A more recent theory—that the hippocampus simultaneously encodes episodes and extracts patterns—fits more naturally with our findings (Schapiro et al., 2017). The existence of both kinds of representation during or after navigation is consistent with the findings of some rodent studies (Leutgeb, Leutgeb, Treves, Moser, & Moser, 2004). The hippocampus is thought to accomplish episodic encoding and statistical learning along different pathways, centering on the CA3 and CA1 subfields, respectively. The reuse of CA1 place cells across environments encountered in the same session (Cai et al., 2016) provides a potential mechanism for rapid pattern extraction during spatial navigation. Although our study was based on the assumption that patterns are extracted across all episodes within a session, future work could explore the dynamics of this process, including primacy biases, recency biases, and incremental learning that forgets and updates representations over time.

Transparency

Action Editor: Philippe G. Schyns

Editor: D. Stephen Lindsay

Author Contributions

K. N. Graves and N. B. Turk-Browne developed the study design with input from J. W. Antony. Testing, data collection, and data analysis were performed by K. N. Graves with input from N. B. Turk-Browne. K. N. Graves drafted the manuscript and incorporated feedback from N. B. Turk-Browne and J. W. Antony. All authors approved the final manuscript for submission.