Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2020 Sep 22;5(39):25087–25094. doi: 10.1021/acsomega.0c02638

Melting Points of OPC and OPC3 Water Models

Yeyue Xiong †, Parviz Seifpanahi Shabane ‡, Alexey V Onufriev ‡,¶,§,*
PMCID: PMC7542584  PMID: 33043187

Abstract

graphic file with name ao0c02638_0008.jpg

A recently introduced family of globally optimal water models, OPC, has shown promise in a variety of biomolecular simulations, but properties of these water models outside of the liquid phase remain mostly unexplored. Here, we contribute to filling the gap by reporting melting temperatures of ice Ih of OPC and OPC3 water models. Through the direct coexistence method, which we make available in the AMBER package, the melting points of OPC and OPC3 are estimated as 242 and 210 K, similar to TIP4P-Ew and SPC/E models, respectively, and appreciably below the experimental value of 273.15 K under 1 bar pressure. Water models of the OPC family were optimized to best reproduce water properties in the liquid phase where these models offer noteworthy accuracy advantages over many models of previous generations. It is not surprising that the accuracy of OPC models in describing the phase transition to the solid state does not appear to offer similar improvements. The new anisotropic barostat option implemented in AMBER may benefit system preparation and simulation outside of the direct coexistence applications, such as modeling of membranes or very long DNA strands.

1. Introduction

Water is one of the most important substances on earth. The water molecule has a deceptively simple structure H2O, yet many anomalies remain unexplained despite decades of efforts.1−5 Computational water models are helpful, but water is known to be difficult to simulate accurately with simplified atomistic water models in a mechanical force field, which tend to be the most computationally efficient. Many water models have been designed dating back at least 50 years ago, yet none is perfect.6 Phase transitions of water are one of the properties of interest, and water has a rather complex phase diagram, considering the existence of its various solid phases such as ice-Ih, ice-II, and ice-III.

Even a single point on the phase diagram, the melting point under 1 bar pressure, is not reproduced accurately by most of the existing simple atomistic water models. For example, among the widely used n-point fixed charge models (Figure 1), the classical TIP3P water model7 (Figure 1a) has a melting point (of ice Ih) as low as 146 K,8 while TIP4P model9 (Figure 1b) is not much better in that respect, 232 K,8 compared with the experimental 273.15 K ice Ih melting point. On the one hand, these discrepancies may not be too critical for the main purpose for which these water models were originally designed, namely, simulations at around 300 K and 1 bar pressure. However, if one wants to model the aqueous environment outside of the “biological range” of ambient conditions, the melting point of a water model can be a very important aspect of its performance. More generally, the fact that a water model cannot reproduce some of the most basic properties of real water should be a concern, as it points to potential problems lurking in the dark, even when the model is used under standard conditions.

Figure 1.

Figure 1

Open in a new tab

Overall geometry of classical n-point fixed charge water models. (a) A three-point model, mimicking an H-O-H structure; (b) a four-point model, offsetting oxygen charge on the 4th point; (c) a five-point model, with two extra charges emulating lone pairs.

Efforts to estimate the melting temperature of a water model have a long history.8,10−23 Among the relatively modern approaches are the Hamiltonian Gibbs–Duhem integration and direct coexistence method. In the Hamiltonian Gibbs–Duhem integration, the energy of liquid–solid coexistence state can be calculated, and thus, the melting point is found.21 The direct coexistence method,24−26 which is applied in this work, is a method where molecular dynamic simulations (NPT ensemble) are carried out for a box of ice and a box of water in direct contact with each other. The upper and lower bounds of the water models melting point can be determined by observing at what temperature the box turns completely solid or completely liquid. This method is straightforward and has become popular in recent years with the increasing computing power available.19,22,23,27 In this work, we apply the direct coexistence method to calculate the melting points of two novel water models developed in our group, OPC (a four-point model, Figure 1b) and OPC3 (a three-point model, Figure 1a). OPC and OPC3 water models were developed differently from the most other common water models. Utilizing the electric multipole moment parameter space, OPC water model was constructed as a global optimum in reproducing six important bulk water properties; similar global optimization was used to develop the OPC3 model, which has three interaction sites instead of four for the OPC model.28,29 With better liquid water properties, better accuracy has been observed in simulations with OPC or OPC3 used as the solvent in several types of biomolecular simulations at ambient temperature.30−35 Still, very little is known about the performance of these models outside of the liquid phase. There is a recent study where OPC and OPC3 were benchmarked in surface tension calculations, and the results show good agreement with the experiment result.36 To add a small, but important piece to the overall picture, here, we examine the performance of OPC family models in simulating the liquid–solid phase change.

2. Results and Discussion

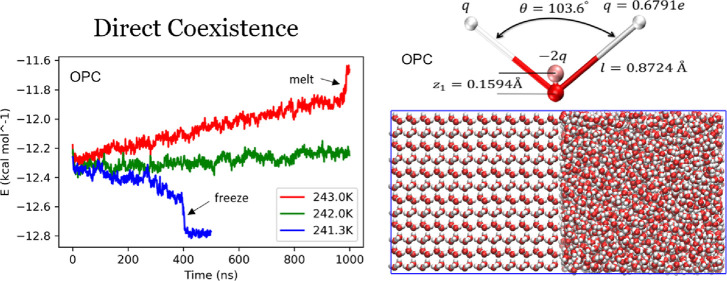
Through the direct coexistence method (Figure 2), the melting point of a water model is calculated within an uncertainty range. In what follows, we consider ice to be an Ih phase, unless otherwise specified. The temperature at which the whole simulation box becomes ice is the lower bound of the melting point, while the temperature where the whole box melts is the upper bound. The temperature difference between the two systems is the uncertainty for the calculated melting point.

Figure 2.

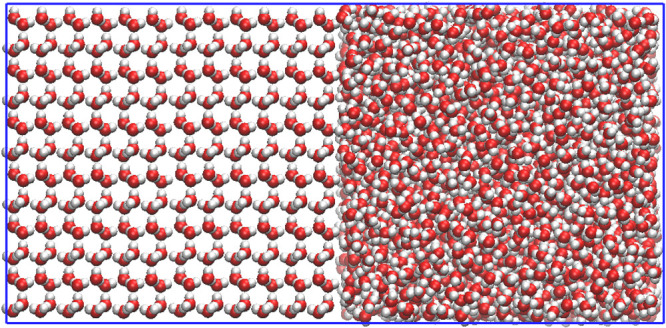
Figure 2

Open in a new tab

Simulation box for the direct coexistence method (93 Å × 56 Å × 45 Å).

The melting or freezing process is monitored through the total energy of the simulation system (Figure 3). During the direct coexistence simulation, if the temperature is higher than the actual melting point of the water model, the total energy of the system will increase until the whole box melts. Similarly, for the simulations with a temperature lower than the water model melting points, the total energy decreases until the whole box becomes ice.

Figure 3.

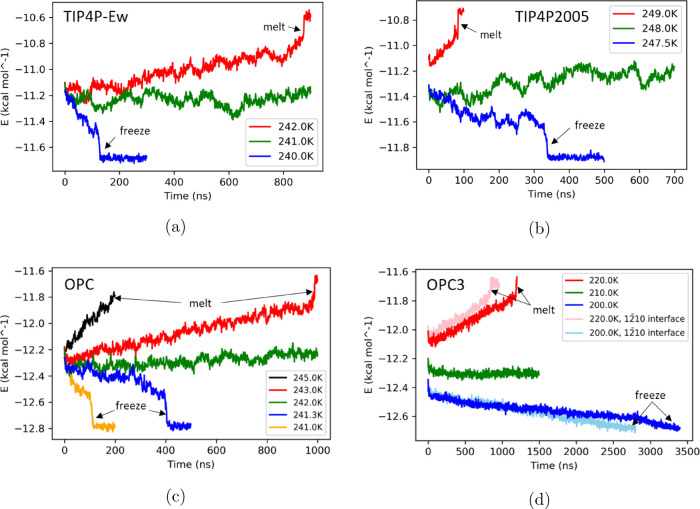
Figure 3

Open in a new tab

Total energy (per mole) of the ice-liquid coexistence system for (a) TIP4P-Ew, (b) TIP4P/2005, (c) OPC, and (d) OPC3 models. The blue, green, and red curves represent total energy recorded for simulations at each model’s low, medium, and high temperatures, respectively. The peak at the end of a red curve shows the point where the whole simulation box becomes liquid. The flat “tail” region at the end of a blue curve corresponds to the state where the whole box is frozen. In (c), additional curves (yellow and black) at different temperatures are shown. With the temperature farther away from the melting point, the phase transition is faster. In (d), the pink and light blue curves are OPC3 simulations with the ice secondary prism (12̅10) plane as the interface. Also note in (d), the blue and light blue curves of OPC3 model do not have the flat “tail”, but we still observed the whole box becoming ice at the last few time steps of the simulation.

We begin by reproducing previously published melting points for TIP4P-Ew and TIP4P/2005 water models (Table 1). From an earlier direct coexistence method studied by Vega et al., the estimated melting points of models TIP4P-Ew and TIP4P/2005 are 242 ± 2 and 249 ± 2 K, respectively.19 These numbers match closely with the melting points of the same two water models as estimated in this work (241.0 ± 1.0 and 248.25 ± 0.75 K, Table 1, Figure 3a,b), even though fine details of the corresponding simulation protocols were not the same, see “Methods”.

Table 1. Calculated Melting Points (Ice Ih) of TIP4P/2005,TIP4P-Ew, OPC, and OPC3 Water Models.

water model melting point (K, this work) melting point (K, previous work19)
TIP4P-Ew 241.0 ± 1.0 242 ± 1
TIP4P/2005 248.25 ± 0.75 249 ± 1
OPC 242.15 ± 0.85  
OPC3 210 ± 10  
Open in a new tab

Here, we demonstrate that (despite being quite accurate in reproducing bulk water properties) OPC and OPC3 models still have melting points far away from the experimental value, 273.15 K. The melting point of the OPC model is estimated as 242.15 K (Table 1, Figure 3c), 31 K lower than the experiment, and close to that of the TIP4P-Ew model, which is 241 K. For the OPC3 model, the estimated melting point is 210 K (Table 1, Figure 3d), 63.15 K lower than the experiment, and it is in the vicinity of the melting points of SPC (190 K) and SPC/E (215 K) models8 but still closer to the experiment than the TIP3P model whose melting point is even lower, 146 K.8 The two comparisons above are within the same types of water models: OPC and TIP4P-Ew are both four-point fixed charge models, while OPC3, SPC, and SPC/E are all three-point fixed charge models. Therefore, we can argue that there may exist intrinsic defects in the three- and four-point fixed charge water models such that even globally optimal models still show relatively large errors in their melting points.

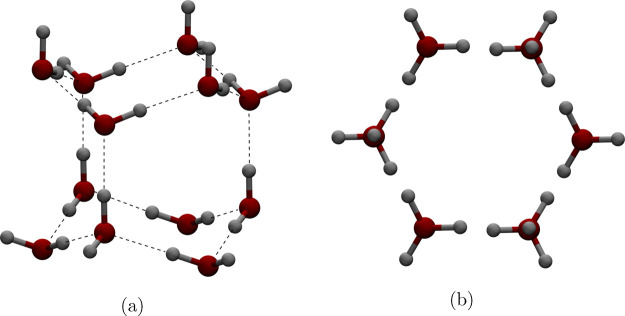
One possible explanation for the lack of accuracy of three- and four-point fixed charge rigid models in reproducing the melting point temperature may have to do with a particular feature of these models’ geometry. In ice Ih, water molecules organize in a well-structured form (Figure 4), and the melting point reflects the amount of energy needed to break the formation. Compared to a real water molecule three-dimensional electron cloud, both three- and four-point fixed charge water models have their point charges confined to the H-O-H plane, facilitating movements of the entire structure along directions out of the H-O-H plane. The relative ease of these movements means that less energy is needed to break the fairly rigid ice structure, thus lowering the melting point. We stress that the above discussion applies to “general purpose” models not specifically fitted to reproduce the water–ice transition. On the other hand, TIP5P, a five-point fixed charge “general purpose” water model (developed without training for the solid phase), has two out-of-plane extra point charges forming a tetrahedron with the two hydrogen atoms.37 This five-point structure makes up for the lack of out-of-plane charge distribution in three- and four-point models, and it was estimated that the TIP5P model melting point is 274 K,8 matching the experiment value of 273.15 K very well.

Figure 4.

Figure 4

Open in a new tab

Hexagonal unit cell formed by 12 water molecules in ice Ih: (a) side view; (b) top view.

It is also worth noting that the time it takes for the whole direct coexistence box to completely freeze or melt is different for each water model studied here especially when comparing the three-point model (OPC3) and the four-point models (OPC, TIP4P-Ew, and TIP4P/2005). For the three four-point water models studied here, the simulation box completely freezes or melts within 1000 ns, with a no larger than a 2 K temperature range around the melting point. The three-point model OPC, however, takes longer for the complete phase transition to occur, especially the freezing process, which takes 3400 ns. To observe the complete range of behaviors, from the freezing to the melting, a much larger temperature range is needed, 20 K instead of 2 K for the four-point models, making the error bar for OPC3 model’s melting point considerably larger than the four-point models estimated in this work. Even with the secondary prism (12̅10) plane (the fastest ice growth plane)23,38 as the solid–liquid interface, the complete melting or freezing process of the OPC3 box is only marginally faster (Figure 3d). This phenomenon, phase changes are much slower with three-point models than with four-point ones, was also observed in a previous study by García Fernández et al. with the SPC/E model.19 A plausible explanation is that OPC3 and SPC/E models both have very low melting points at which simulation systems are of low kinetic energy, leading to a much slower speed of the phase transition. It may be possible that much longer simulation times, tens of microseconds, might reduce the uncertainty of the calculated melting point.

3. Conclusions

In this work, we applied the direct coexistence method to calculate melting points of ice Ih of two novel fixed charge water models, OPC and OPC3. The calculations were performed within AMBER molecular dynamic simulation software suite where we implemented a new option for anisotropic pressure scaling along a specified axis. This added feature may benefit the preparation and simulation of certain molecular systems, such as the direct coexistence simulations, membrane systems, and infinitely long DNA strands. Because implementations of some relevant algorithms (e.g., thermostat options) in AMBER are not exactly the same as those in other packages used in previous melting point studies, we first tested TIP4P-Ew and TIP4P/2005 models and the results match previous findings. This agreement has validated the direct coexistence method in AMBER. With the OPC3 model, we also compared the phase transition speed between two solid–liquid interface choices, the primary prism plane (101̅0) and the secondary prism plane (12̅10) where the latter leads to only marginally faster phase transition than the former.

The calculated melting points of OPC and OPC3 models at 1 bar are 242.15 ± 0.85 and 210 ± 10 K, respectively. These clearly deviate from the experimental value of 273.15 K. Despite having better liquid properties and relatively more accurate simulation outcomes in various contexts, the accuracies in the melting points of OPC and OPC3 are on par with their respective four- and three-point counterparts TIP4P-Ew and SPC/E and inferior to that of a five-point model TIP5P whose estimated melting point (274 K) is very close to the experimental value. Since OPC and OPC3 models are globally optimal, the remaining errors imply the existence of an intrinsic limitation in the ability of three- and four-point fixed charge water models to reproduce the water melting point (unless optimized specifically to reproduce the ice phase). Note that for many properties of super-cooled liquids OPC3 and OPC are quite accurate, including density, heat of vaporization, self-diffusion, and dielectric constant. Thus, it is likely that it is the solid state where these models are in error (which is not surprising, given that they were optimized to best reproduce the liquid state). From the results, we can conclude that OPC and OPC3 may not perform as well in simulating the liquid–solid transition as they do in describing the pure liquid state. Also, considering that the five-point model TIP5P has a rather accurate melting point, one likely intrinsic defect of the three- and four-point fixed charge models with respect to reproducing the liquid-to-solid transition is that these models lack any out-of-HOH-plane charge distribution, which is present in a real water molecule, as well as in the five-point model. Without the out-of-plane charges, it is easier for the ice structure of three- and four-point water models to break due to the weaker out-of-plane interaction between adjacent water molecules, hence the lower melting temperature.

At the same time, the TIP5P model, while being able to simulate the experimental melting point accurately, does not perform well when evaluated on its bulk liquid properties.39 Thus, TIP5P may not be optimal to simulate the liquid–solid phase change either. However, with the out-of-plane charge distribution accounted for, we conjecture that a globally optimal five-point fixed charge water model may be found that performs well in both liquid–solid phase change simulations and liquid bulk simulations.

A polarizable water model40−42 is another promising direction, although the relative computational cost of the corresponding simulations remains a concern, especially in light of the very long equilibration time that may be needed to study phase transitions. The computational expense is arguably the lowest for algorithmically efficient Drude-based polarizable water models.43 Not only that the Drude water models are relatively efficient, our recent study has demonstrated that a globally optimal three-point Drude polarizable water model can, in principle, be as accurate as a five-point nonpolarizable model (over liquid bulk properties) when compared in a carefully controlled optimization procedure.44 However, it is not yet proven whether the added polarizability via the Drude oscillator can make a three- or four-point water model accurately reproduce the liquid–solid phase change. Although the Drude charge can move out of the H-O-H plane, which should be beneficial for reproducing the melting point, the distance it moves out-of-plane is very small and likely not enough to alleviate the intrinsic defect of three- and four-point models. For example, two well-established Drude polarizable water models, COS/G245 and SWM-DP,46 have rather poor melting points, 215 and 186 K, respectively.47 More sophisticated polarizable models such as those of an AMOEBA family48,49 deliver better performance in that respect (e.g., iAMOEBA model: Tm = 261 ± 1  K)50 but at a considerable computational cost.

It is still yet to be seen whether a globally optimal Drude polarizable water model or globally optimal five-point nonpolarizable model can accurately simulate the melting point without compromising on bulk water properties at ambient temperature.

4. Methods

4.1. Direct Coexistence

We apply the direct coexistence method to calculate the melting point of water models. In this method, a fluid–solid interface is created by combining a liquid water box and ice box together. With the fluid–solid interface, the molecular dynamic simulation will not suffer from super-cooling- or super-heating-like simulating pure liquid water or ice.

First, we prepare a box of ice, which satisfies the ice rules.51 The ice rules describe how water molecules are arranged in the “ordinary” ice phase, ice Ih: each oxygen accepts at most two hydrogen atoms from other water molecules through hydrogen bonding, forming a tetrahedron where a water molecule is surrounded by four others. Further, every 12 water molecules form a hexagonal unit cell that can be stacked together periodically, which is the building block to construct an ice box (Figure 4). By construction, the ice box built in this manner has a highly ordered proton arrangement; thus, it is different from ice Ih that exists in nature, which is not “perfect”. Fortunately, it was shown earlier that the initial ice configuration with different proton arrangements does not significantly affect the estimate of the melting point.23 We note that as the ice is being heated in the simulation, a certain amount of disorder is introduced naturally.

A recent study on the direct coexistence method by Conde et al.23 has shown that the accuracy (error bar size) of the calculated melting point is affected by the simulation box size. Here, we chose the box size of 3456 (liquid) + 3456 (solid) water molecules for all the four water models calculated in this work, which according to Conde’s study, results in a reasonable accuracy of ∼1  K error bar for a four-point water model. We consider this box size as an acceptable compromise between accuracy and speed for the purpose of this work.

To create the liquid part of the coexistence box, we heat the ice Ih box to a complete melt; then cool it down to a preselected temperature that is near the estimated water model melting point (temperatures where the ice part does not melt during its equilibration process, see below). For the ice part, we equilibrate the same ice Ih box at the same temperature near melting point. The fluid–solid interface is then created by attaching the liquid water and ice box together where the interface is on the primary prism plane (101̅0) of the ice part (Figures 5,6). Ice grows fast on the primary prism plane (101̅0) but not as fast as the secondary prism plane (12̅10).38 We compared the full phase change time of the OPC3 model between the two prism plane interface choices, the results show only marginal speed difference where using the 12̅10 interface is about 10% faster (Figure 3d).

Figure 5.

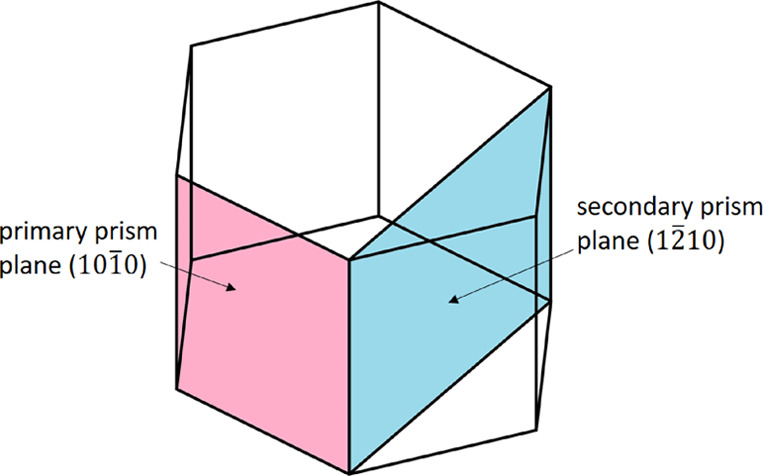
Figure 5

Open in a new tab

Two fluid–solid interface choices with respect to ice hexagonal structure: pink shows the primary prism plane (101̅0); blue shows the secondary prism plane (12̅10).

Figure 6.

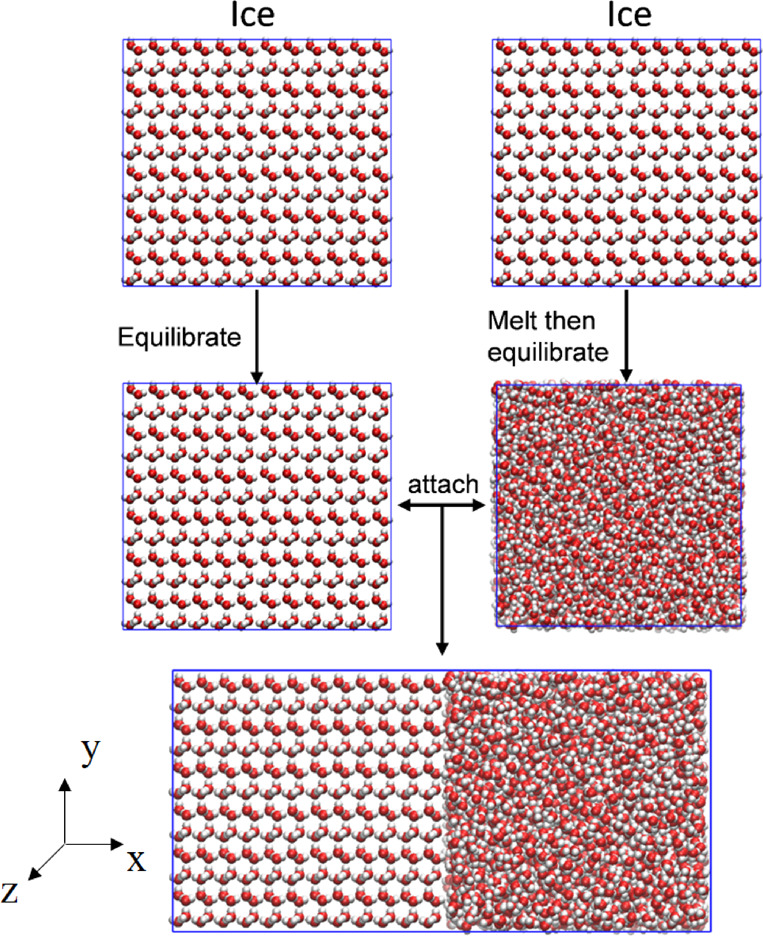
Figure 6

Open in a new tab

Process to prepare the fluid-ice coexistence box.

The simulations were carried out using a modified version of AMBER 2018,52,53 with a new barostat feature for anisotropic box rescaling, see below. A Monte Carlo barostat was used with this new anisotropic pressure scaling setting. The temperature was controlled by a Langevin thermostat with the coupling constant γln = 1.0. For the liquid part of the box, the heating process is a 2 ns NVT simulation at 340 K, the cooling process is a 2 ns NPT simulation at a lower temperature near the estimated melting point (varies for different runs). During the cooling process, we apply the anisotropic pressure scaling to the simulation box where the box size is allowed to adjust to maintain the pressure only along the x direction (normal to the primary prismatic plane (101̅0) of the ice before heating). By applying this anisotropic pressure scaling, the y and z dimensions of the liquid box remain unchanged, and thus, the liquid water and ice boxes can be easily put in contact along the x-axis, Figure 6, so that their y–z faces match exactly. After combining the liquid box and ice box, we perform a short equilibration of the direct coexistence box at the selected temperature (for example, the simulation runs shown in Figure 3c are at temperatures 241.3, 242.0, and 243.0 K, respectively) for a short period (10 ns). Then, we start a longer simulation under the same conditions, in increments of 100 ns, until the whole box melts or freezes. We found that the farther away the temperature is from the melting point, the faster the phase transition completes, (Figure 3c). To find the upper and lower bounds of the melting temperature, we start with testing temperatures with 10 K intervals (e.g., 240 K, 250 K, 260 K, ...) then stop when, at the given temperature, the whole box freezes or melts within 100 ns; we refine that temperature by exploring the transition with 1 K temperature intervals. We stop when the complete phase change takes longer than 1000 ns. If the temperature found in the previous step still has fast phase change, then we further refine the last step by testing 0.1 K intervals. For OPC3 model’s lower bound, temperatures lower than 200 K do not result in faster freezing, and we settled on 200 K where the whole box becomes frozen after 3400 ns of simulation. We ran the simulation three times for each of the boundary temperatures and only accepted the one at which a complete phase change was observed in all of the three runs.

For the direct coexistence box, the simulations are NPT with the default anisotropic pressure scaling option where the three dimensions of the box can freely adjust independently to each other. The independence between the box size changes along three dimensions keeps the system from imposing external force on the liquid–ice interface. The integration time-step was 2 fs. Particle Mesh Ewald (PME, GPU module: pmemd.cuda)54 was used to handle electrostatic interactions, with cut = 8.5Å (AMBER input parameter, nonbonded cutoff distance), and all other settings set to their default values. It is worth noting that in AMBER default settings, the option to account for the van der Waals interactions beyond the cutoff (8.5 Å in this study) via a continuum model is enabled (vdwmeth = 1),52,55 which is critical for OPC and OPC3.28,29,56 The AMBER input files are included in the Supporting Information.

The exact barostat and thermostat algorithms employed in this work are different from some of the previous studies using the same direct coexistence method, such as Vega et al.19 where Parrinello–Rahman barostat and Nosé–Hoover thermostats were used. Despite these methodological differences, our implementation yields essentially the same results as in ref (19) for TIP4P-Ew and TIP4P/2005 water models. Thus, we argue that the modifications we used in AMBER are acceptable for the direct coexistence method. Although the results calculated with AMBER are consistent with previous studies, the simulations take longer for the system to change phase completely. This may be related to the different thermostat and barostat used in this study, or to the different integrator implementations between different programs, and will require further exploration to explain fully.

4.2. New Anisotropic Pressure Scaling Option in AMBER

This anisotropic pressure scaling feature where a user can choose one dimension to allow the simulation box to extend or shrink was not available in AMBER 2018 or any earlier version. The first author of this work implemented the pressure scaling option based on AMBER 2018,52 and it is now available in AMBER 201955 and newer releases (AMBER input parameter “baroscalingdir”). With this new option, the user can choose x, y, or z direction such that the simulation box only adjusts its size along the chosen direction to maintain pressure. For certain molecular systems and simulation types, such as the direct coexistence, infinitely long DNA strands, and membranes, this option should provide the convenience in system preparations, and it is very important for correctly reflecting the natural anisotropy of these simulations.

Acknowledgments

The authors thank Dr. Igor Tolokh for sharing his insights during the results discussions and thank Virginia Tech Advanced Research Computing for providing the computational resources. Funding from NIH R21GM134404 is acknowledged.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c02638.

  • AMBER input files with the simulation control parameters, AMBER topology and coordinate files for the co-existence box for each water model at the reported temperatures (ZIP)

The authors declare no competing financial interest.

Supplementary Material

ao0c02638_si_001.zip (16.9MB, zip)

References

  1. Hasted J. B.The Physics and Physical Chemistry of Water; Franks F., Ed.; Springer New York: Boston, MA, 1972; 255–309. [Google Scholar]
  2. Finney J. L. The water molecule and its interactions: the interaction between theory, modelling, and experiment. J. Mol. Liq. 2001, 90, 303–312. 10.1016/S0167-7322(01)00134-9. [DOI] [Google Scholar]
  3. Brodsky A. Is there predictive value in water computer simulations?. Chem. Phys. Lett. 1996, 261, 563–568. 10.1016/0009-2614(96)00997-9. [DOI] [Google Scholar]
  4. Rahman A.; Stillinger F. H. Molecular Dynamics Study of Liquid Water. J. Chem. Phys. 1971, 55, 3336–3359. 10.1063/1.1676585. [DOI] [Google Scholar]
  5. Brini E.; Fennell C. J.; Fernandez-Serra M.; Hribar-Lee B.; Lukšič M.; Dill K. A. How Water’s Properties Are Encoded in Its Molecular Structure and Energies. Chem. Rev. 2017, 117, 12385–12414. 10.1021/acs.chemrev.7b00259. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Jorgensen W. L.; Tirado-Rives J. Potential energy functions for atomic-level simulations of water and organic and biomolecular systems. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 6665–6670. 10.1073/pnas.0408037102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
  8. Vega C.; Sanz E.; Abascal J. L. F. The melting temperature of the most common models of water. J. Chem. Phys. 2005, 122, 114507. 10.1063/1.1862245. [DOI] [PubMed] [Google Scholar]
  9. Jorgensen W. L.; Madura J. D. Temperature and size dependence for Monte Carlo simulations of TIP4P water. Mol. Phys. 1985, 56, 1381–1392. 10.1080/00268978500103111. [DOI] [Google Scholar]
  10. Karim O. A.; Haymet A. D. J. The ice/water interface: A molecular dynamics simulation study. J. Chem. Phys. 1988, 89, 6889–6896. 10.1063/1.455363. [DOI] [Google Scholar]
  11. Karim O. A.; Kay P. A.; Haymet A. D. J. The ice/water interface: A molecular dynamics simulation using the simple point charge model. J. Chem. Phys. 1990, 92, 4634–4635. 10.1063/1.457730. [DOI] [Google Scholar]
  12. Báez L. A.; Clancy P. Phase equilibria in extended simple point charge ice-water systems. J. Chem. Phys. 1995, 103, 9744–9755. 10.1063/1.469938. [DOI] [Google Scholar]
  13. Vlot M. J.; Huinink J.; van der Eerden J. P. Free energy calculations on systems of rigid molecules: An application to the TIP4P model of H2O. J. Chem. Phys. 1999, 110, 55–61. 10.1063/1.478084. [DOI] [Google Scholar]
  14. Gao G. T.; Zeng X. C.; Tanaka H. The melting temperature of proton-disordered hexagonal ice: A computer simulation of 4-site transferable intermolecular potential model of water. J. Chem. Phys. 2000, 112, 8534–8538. 10.1063/1.481457. [DOI] [Google Scholar]
  15. Gay S. C.; Smith E. J.; Haymet A. D. J. Dynamics of melting and stability of ice 1h: Molecular-dynamics simulations of the SPC/E model of water. J. Chem. Phys. 2002, 116, 8876–8880. 10.1063/1.1471556. [DOI] [Google Scholar]
  16. Arbuckle B. W.; Clancy P. Effects of the Ewald sum on the free energy of the extended simple point charge model for water. J. Chem. Phys. 2002, 116, 5090–5098. 10.1063/1.1451245. [DOI] [Google Scholar]
  17. Nada H.; van der Eerden J. P. J. M. An intermolecular potential model for the simulation of ice and water near the melting point: A six-site model of H2O. J. Chem. Phys. 2003, 118, 7401–7413. 10.1063/1.1562610. [DOI] [Google Scholar]
  18. Koyama Y.; Tanaka H.; Gao G.; Zeng X. C. Melting points and thermal expansivities of proton-disordered hexagonal ice with several model potentials. J. Chem. Phys. 2004, 121, 7926–7931. 10.1063/1.1801272. [DOI] [PubMed] [Google Scholar]
  19. García Fernández R.; Abascal J. L. F.; Vega C. The melting point of ice Ih for common water models calculated from direct coexistence of the solid-liquid interface. J. Chem. Phys. 2006, 124, 144506. 10.1063/1.2183308. [DOI] [PubMed] [Google Scholar]
  20. Vega C.; Abascal J. L. F. Relation between the melting temperature and the temperature of maximum density for the most common models of water. J. Chem. Phys. 2005, 123, 144504. 10.1063/1.2056539. [DOI] [PubMed] [Google Scholar]
  21. Vega C.; Sanz E.; Abascal J. L. F.; Noya E. G. Determination of phase diagrams via computer simulation: methodology and applications to water, electrolytes and proteins. J. Phys.: Condens. Matter 2008, 20, 153101. [Google Scholar]
  22. Conde M. M.; Gonzalez M. A.; Abascal J. L. F.; Vega C. Determining the phase diagram of water from direct coexistence simulations: The phase diagram of the TIP4P/2005 model revisited. J. Chem. Phys. 2013, 139, 154505. 10.1063/1.4824627. [DOI] [PubMed] [Google Scholar]
  23. Conde M. M.; Rovere M.; Gallo P. High precision determination of the melting points of water TIP4P/2005 and water TIP4P/Ice models by the direct coexistence technique. J. Chem. Phys. 2017, 147, 244506. 10.1063/1.5008478. [DOI] [PubMed] [Google Scholar]
  24. Ladd A. J. C.; Woodcock L. V. Triple-point coexistence properties of the lennard-jones system. Chem. Phys. Lett. 1977, 51, 155–159. 10.1016/0009-2614(77)85375-X. [DOI] [Google Scholar]
  25. Ladd A. J. C.; Woodcock L. V. Interfacial and co-existence properties of the Lennard-Jones system at the triple point. Mol. Phys. 1978, 36, 611–619. 10.1080/00268977800101791. [DOI] [Google Scholar]
  26. Cape J. N.; Woodcock L. V. Molecular dynamics calculation of phase coexistence properties: The soft-sphere melting transition. Chem. Phys. Lett. 1978, 59, 271–274. 10.1016/0009-2614(78)89094-0. [DOI] [Google Scholar]
  27. Conde M. M.; Rovere M.; Gallo P. Spontaneous NaCl-doped ice at seawater conditions: focus on the mechanisms of ion inclusion. Phys. Chem. Chem. Phys. 2017, 19, 9566–9574. 10.1039/C7CP00665A. [DOI] [PubMed] [Google Scholar]
  28. Izadi S.; Anandakrishnan R.; Onufriev A. V. Building Water Models: A Different Approach. J. Phys. Chem. Lett. 2014, 5, 3863–3871. 10.1021/jz501780a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Izadi S.; Onufriev A. V. Accuracy limit of rigid 3-point water models. J. Chem. Phys. 2016, 145, 074501 10.1063/1.4960175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Shabane P. S.; Izadi S.; Onufriev A. V. General Purpose Water Model Can Improve Atomistic Simulations of Intrinsically Disordered Proteins. J. Chem. Theory Comput. 2019, 15, 2620–2634. 10.1021/acs.jctc.8b01123. [DOI] [PubMed] [Google Scholar]
  31. Vassetti D.; Pagliai M.; Procacci P. Assessment of GAFF2 and OPLS-AA general force fields in combination with the water models TIP3P, SPCE and OPC3 for the solvation free energy of drug-like organic molecules. J. Chem. Theory Comput. 2019, 1983. 10.1021/acs.jctc.8b01039. [DOI] [PubMed] [Google Scholar]
  32. Tian C.; Kasavajhala K.; Belfon K. A. A.; Raguette L.; Huang H.; Migues A. N.; Bickel J.; Wang Y.; Pincay J.; Wu Q.; et al. ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2020, 16, 528–552. 10.1021/acs.jctc.9b00591. [DOI] [PubMed] [Google Scholar]
  33. Bergonzo C.; Cheatham T. E. Improved Force Field Parameters Lead to a Better Description of RNA Structure. J. Chem. Theory Comput. 2015, 11, 3969–3972. 10.1021/acs.jctc.5b00444. [DOI] [PubMed] [Google Scholar]
  34. Izadi S.; Aguilar B.; Onufriev A. V. Protein–Ligand Electrostatic Binding Free Energies from Explicit and Implicit Solvation. J. Chem. Theory Comput. 2015, 11, 4450–4459. 10.1021/acs.jctc.5b00483. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Gabrieli A.; Sant M.; Izadi S.; Shabane P. S.; Onufriev A. V.; Suffritti G. B. High-temperature dynamic behavior in bulk liquid water: A molecular dynamics simulation study using the OPC and TIP4P-Ew potentials. Front. Phys. 2017, 13, 138203. 10.1007/s11467-017-0693-7. [DOI] [Google Scholar]
  36. Javanainen M.; Lamberg A.; Cwiklik L.; Vattulainen I.; Ollila O. H. S. Atomistic Model for Nearly Quantitative Simulations of Langmuir Monolayers. Langmuir 2018, 34, 2565–2572. 10.1021/acs.langmuir.7b02855. [DOI] [PubMed] [Google Scholar]
  37. Mahoney M. W.; Jorgensen W. L. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. J. Chem. Phys. 2000, 112, 8910–8922. 10.1063/1.481505. [DOI] [Google Scholar]
  38. Olijve L. L. C.; Meister K.; DeVries A. L.; Duman J. G.; Guo S.; Bakker H. J.; Voets I. K. Blocking rapid ice crystal growth through nonbasal plane adsorption of antifreeze proteins. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, 3740–3745. 10.1073/pnas.1524109113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Onufriev A. V.; Izadi S. Water models for biomolecular simulations. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1347 10.1002/wcms.1347. [DOI] [Google Scholar]
  40. Yu H.; van Gunsteren W. F. Accounting for polarization in molecular simulation. Comput. Phys. Commun. 2005, 172, 69–85. 10.1016/j.cpc.2005.01.022. [DOI] [Google Scholar]
  41. Jing Z.; Liu C.; Cheng S. Y.; Qi R.; Walker B. D.; Piquemal J.-P.; Ren P. Polarizable Force Fields for Biomolecular Simulations: Recent Advances and Applications. Annu. Rev. Biophys. 2019, 48, 371–394. 10.1146/annurev-biophys-070317-033349. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Huang J.; Lopes P. E. M.; Roux B.; MacKerell A. D. Jr. Recent Advances in Polarizable Force Fields for Macromolecules: Microsecond Simulations of Proteins Using the Classical Drude Oscillator Model. J. Phys. Chem. Lett. 2014, 5, 3144–3150. 10.1021/jz501315h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Lemkul J. A.; Huang J.; Roux B.; MacKerell A. D. Jr. An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chem. Rev. 2016, 116, 4983–5013. 10.1021/acs.chemrev.5b00505. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Xiong Y.; Onufriev A. V. Exploring optimization strategies for improving explicit water models: Rigid n-point model and polarizable model based on Drude oscillator. PLoS One 2019, 14, 1–22. 10.1371/journal.pone.0224991. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Yu H.; van Gunsteren W. F. Charge-on-spring polarizable water models revisited: From water clusters to liquid water to ice. J. Chem. Phys. 2004, 121, 9549–9564. 10.1063/1.1805516. [DOI] [PubMed] [Google Scholar]
  46. Lamoureux G.; MacKerell A. D. Jr.; Roux B. A simple polarizable model of water based on classical Drude oscillators. J. Chem. Phys. 2003, 119, 5185–5197. 10.1063/1.1598191. [DOI] [Google Scholar]
  47. Kiss P. T.; Bertsyk P.; Baranyai A. Testing recent charge-on-spring type polarizable water models. I. Melting temperature and ice properties. J. Chem. Phys. 2012, 137, 194102. 10.1063/1.4767063. [DOI] [PubMed] [Google Scholar]
  48. Ren P.; Ponder J. W. Polarizable Atomic Multipole Water Model for Molecular Mechanics Simulation. J. Phys. Chem. B 2003, 107, 5933–5947. 10.1021/jp027815+. [DOI] [Google Scholar]
  49. Liu C.; Piquemal J.-P.; Ren P. AMOEBA+ Classical Potential for Modeling Molecular Interactions. J. Chem. Theory Comput. 2019, 15, 4122–4139. 10.1021/acs.jctc.9b00261. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Wang L.-P.; Head-Gordon T.; Ponder J. W.; Ren P.; Chodera J. D.; Eastman P. K.; Martinez T. J.; Pande V. S. Systematic Improvement of a Classical Molecular Model of Water. J. Phys. Chem. B 2013, 117, 9956–9972. 10.1021/jp403802c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Bernal J. D.; Fowler R. H. A Theory of Water and Ionic Solution, with Particular Reference to Hydrogen and Hydroxyl Ions. J. Chem. Phys. 1933, 1, 515–548. 10.1063/1.1749327. [DOI] [Google Scholar]
  52. Case D.; Ben-Shalom I.; Brozell S.; Cerutti D.; Cheatham T.; III V. C.; Darden T.; Duke R.; Ghoreishi D.; Gilson M.. et al. AMBER 2018; University of California: San Francisco, 2018, [Google Scholar]
  53. Case D. A.; Cheatham T. E. III; Darden T.; Gohlke H.; Luo R.; Merz K. M. Jr.; Onufriev A.; Simmerling C.; Wang B.; Woods R. J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Salomon-Ferrer R.; Götz A. W.; Poole D.; Le Grand S.; Walker R. C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. 10.1021/ct400314y. [DOI] [PubMed] [Google Scholar]
  55. Case D.; Ben-Shalom I.; Brozell S.; Cerutti D.; Cheatham T.; III V. C.; Darden T.; Duke R.; Ghoreishi D.; Giambasu G.. et al. AMBER 2019; University of California, San Francisco, 2019, [Google Scholar]
  56. Allen M. P.; Tildesley D. J.. Computer simulation of liquids; Oxford university press: 2017. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c02638_si_001.zip (16.9MB, zip)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES