De Novo Structural Pattern Mining in Cellular Electron Cryotomograms

SUMMARY

Electron cryotomography enables 3D visualization of cells in a near-native state at molecular resolution. The produced cellular tomograms contain detailed information about a plethora of macromolecular complexes, their structures, abundances, and specific spatial locations in the cell. However, extracting this information in a systematic way is very challenging, and current methods usually rely on individual templates of known structures. Here, we propose a framework called “Multi-Pattern Pursuit” for de novo discovery of different complexes from highly heterogeneous sets of particles extracted from entire cellular tomograms without using information of known structures. These initially detected structures can then serve as input for more targeted refinement efforts. Our tests on simulated and experimental tomograms show that our automated method is a promising tool for supporting large-scale template-free visual proteomics analysis.

In Brief

Xu et al. presents a framework called “Multi-Pattern Pursuit” for discovering frequently occurring structural patterns in cellular electron cryotomograms. Test results on simulated and experimental datasets shows that the method is a promising tool for automated, largescale, and template-free visual proteomics analysis inside single cells.

Graphical Abstract

INTRODUCTION

Nearly every major process in a cell is orchestrated by the interplay of macromolecular assemblies and often requires a nonrandom spatial organization in the cell. Therefore, when modeling complex biological functions, it is crucial to know the structure, abundance, and locations of the entire set of macromolecular complexes. Currently, proteomics studies extract protein component lists often from lysed cells, but little is known about how proteins and their complexes are spatially arranged in a crowded cell, limiting the plausibility to model biological functions and 3D architecture of cells (Singla et al., 2018).

Electron cryotomography (ECT) can generate 3D reconstructions of cells in hydrated, close to native states at molecular resolution (Mahamid et al., 2016; Chang et al., 2014). New imaging technologies and automation allows labs to obtain hundreds of electron cryotomograms within several days, potentially containing millions of complexes. It is therefore now possible to detect both structures and spatial positions of large complexes in individual cells. However, the structural discovery of unknown complexes in tomograms still remains very challenging due to a number of factors. First, complexes can vary significantly in shape, size, and cellular abundance. Second, identifying individual complexes is significantly more difficult in cellular tomograms than in tomograms of purified complexes, due to high crowding levels (Lučič et al., 2013) and possibly small copy numbers. Third, experimental structures of most complexes are unknown, which limits the use of template libraries for template-matching methods. Fourth, cell tomograms often have low signal-to-noise ratio (SNR) and low contrast, as the sample is thick (>300 nm). In addition, the tomogram image is modulated by the contrast transfer function effect. Finally, the limited range of tilt angles leads to a partial sampling of images and missing structural components in the Fourier space, resulting in anisotropic resolution and distortions (i.e., the missing wedge effect). Therefore, unlike large organelles, which can be detected by visual inspection, the systematic structural classification and recovery of all accessible complexes in cellular tomograms is difficult and can only be ventured with the aid of highly efficient, automatic, and both template-free and template-based analysis methods.

The pioneering work to quantitatively analyze the spatial organizations of complexes in cellular tomograms used “template matching” (Beck et al., 2009; Bohm et al., 2000; Frangakis et al., 2002; Kuhner et al., 2009; Nickell et al., 2006). This approach uses a given complex’s known high-resolution structure (e.g., X-ray crystallography, NMR, cryoelectron microscopy single-particle reconstruction) to simulate an ECT reconstruction, the template, which is then used to search for matches in the tomogram. Naturally this approach is limited to localizing complexes with known structures, which represent only a small fraction of all the complexes in the cell. Assessing the reliability of detected matches is also challenging (Yu and Frangakis, 2014) because the template structure can misfit its targets, due to either conformational changes or additional bounded components to the structure in vivo, or because the template structure is from a different organism and exhibits a different conformation.

To obtain novel structural information, a few alignment and subtomogram averaging (e.g., Schmid and Booth, 2008) and classification (e.g., Bartesaghi et al., 2008; Xu et al., 2012) approaches have been developed recently. Subtomogram averaging assumes that all subtomograms contain the same structure and iteratively searches for rigid transform parameters for each subtomogram to align all subtomograms. By contrast, classification methods often search iteratively for both rigid transform and categorization parameters to separate subtomograms into structurally homogeneous groups before averaging. Such a classification is much more challenging than averaging. Due to the computationally intensive nature of 3D image processing (especially the subtomogram alignment), current classification methods are often tailored to high-quality hand-picked subtomograms usually containing a relatively small number of structural classes, and are often focused on separating subtle conformational or compositional states of a single complex of interest (e.g., Bartesaghi et al., 2008; Chen et al., 2014; Kuybeda et al., 2013; Scheres et al., 2009). In such cases, the subtomograms are usually obtained by template matching often followed by visual inspection and preselection of high-quality patterns. Although reference-free classification may be applied to such subtomograms, at heart they depend on a template, obtained from a known structure. These approaches have several drawbacks, limiting their use in detecting unknown structures on a proteome-wide scale, i.e., from a highly heterogeneous set of subtomograms obtained through automated template-free particle picking, without the knowledge of structures. In cellular tomograms, automated template-free particle picking produces large numbers of subtomograms containing large numbers of complex classes. For obtaining a high SNR in each class a sufficiently large copy number is needed, and therefore it is necessary to iteratively process a very large number (tens to hundreds of thousands) of subtomograms. However, the computational cost of template-free classification methods is proportional to the number of subtomograms multiplied by the number of structural classes. Therefore, these applications are computationally extremely demanding and not feasible when applied to subtomogram classification on a proteome-wide scale.

Recently, deep learning has been used for classification of heterogeneous sets of simulated subtomograms and has achieved fairly good accuracy (Xu et al., 2017; Yu and Frangakis, 2011). In another paper (Chen et al., 2017), the authors trained convolution neural networks to identify ribosomes, double membrane, microtubules, vesicles, and so forth. These supervised learning methods are important steps in moving toward identification of known patterns in electron cryotomograms; however, they depend on user input of ground truth structures of complexes.

To our knowledge, no subtomogram classification method exists that is specifically optimized for and can be applied to largescale applications in a high structural heterogeneity and unsupervised setting. Therefore, current whole-cell approaches are restricted to a focused analysis of one or a few target complexes of interest, whose low-resolution structures are often known.

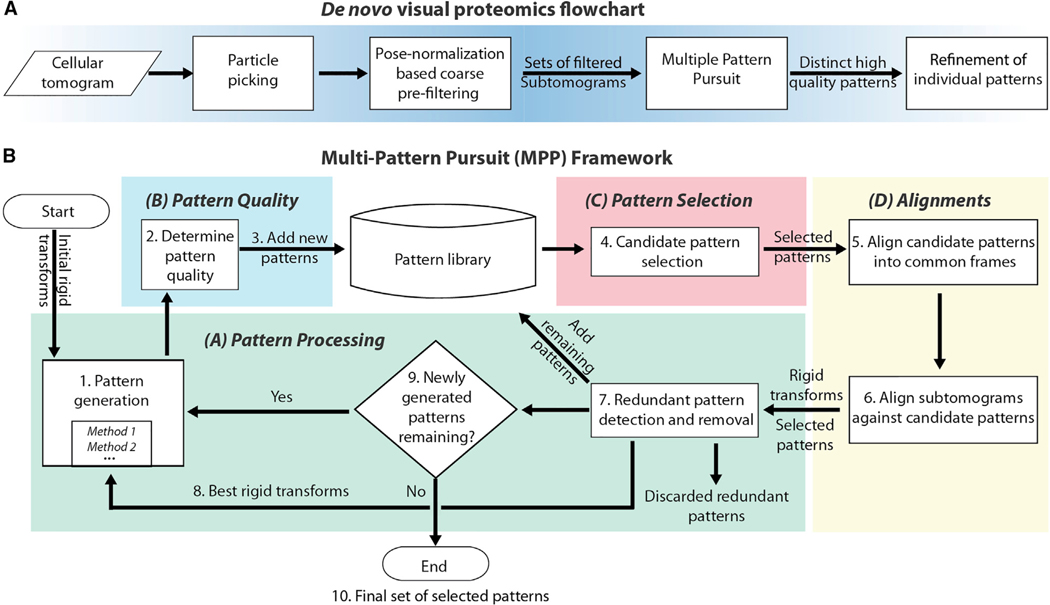
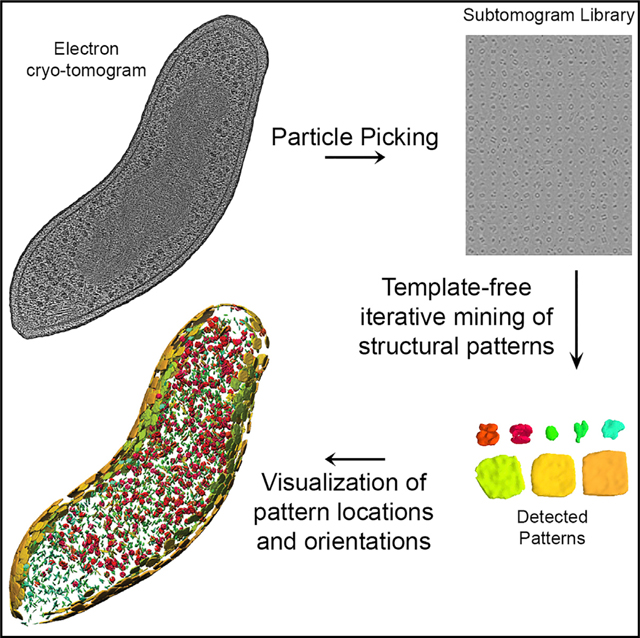
Here, we address this problem through pattern mining, which searches for high-quality structural patterns reoccurring in a cellular tomogram. A structural pattern is defined as a set of aligned subtomograms, which likely contain the same structure and when averaged produce the density map of the complex. To identify patterns, we propose a framework called MultiPattern Pursuit (MPP) (Figure 1), specifically designed for supporting large-scale template-free pattern mining among highly heterogeneous particles to detect structural patterns of variable shapes and sizes from cellular tomograms. MPP takes as input a large set of subtomograms obtained through automated particle picking from entire cell tomograms and produces the shape, abundance, positions, and orientations of the patterns. To our knowledge, our approach and software is one of the first that is specifically optimized to tackle this difficult unsupervised problem at a proteome-wide scale. It consists of a number of methodological innovations, including the MPP framework, imputation-based dimension reduction, reference-guided adaptive subtomogram masking, adaptive smoothing, pose normalization-based prefiltering, and a genetic algorithm for structure refinement.

Figure 1. Overview of the Method.

(A) Overall processing pipeline, including particle picking, preprocessing, and postprocessing steps. The preprocessing step consists of pose normalization-based coarse prefiltering to define sets of subtomograms containing similarly sized particles (STAR Methods: Prefiltering).

(B) MPP framework.

In the flow charts, actions are in boxes, data are on arrows, and diamonds represent decisions. Figure S1 shows details of some of the methods used in overall pipeline.

There are substantial differences between MPP and existing template-free classification methods, in terms of both methodology and scope. Our software is specifically designed to handle (1) large sets of subtomograms extracted from cellular tomograms (tens of thousands); (2) subtomograms of relatively large numbers (tens to hundreds) of different structural classes, with widely varying shapes, sizes, and abundances; and (3) subtomograms extracted from a crowded environment, which may include fragments of neighboring complexes. Also, our aim is not to determine a high-resolution structure of an individual complex, but de novo discovery of many coarse structures and their relative abundance in a heterogeneous sample. These coarse structures can then be further refined to higher resolution by other methods or can serve as templates for a secondary analysis of the tomograms, for instance through machine learning approaches or template matching. The identity of some patterns can be determined by fitting to known structures but in future this will require methods for integrating additional information about the sample, which is not the focus of this study.

RESULTS

Overview of the Method

MPP is an iterative constrained optimization process, which detects frequently occurring structural patterns that maximize a quality score and are distinct from each other with respect to their average density maps and the identity of subtomograms making up the patterns. MPP relies on a very efficient subtomogram alignment (Xu et al., 2012) algorithm based on constrained correlation (Förster et al., 2008; Xu and Alber, 2012) and fast rotational matching (Kovacs and Wriggers, 2002), and an efficient, robust, and flexible parallel architecture that supports high-throughput processing (Frazier et al., 2017).

To run MPP, the tomogram is first segmented into a library of subtomograms by automated particle picking (Figure 1A) (Pei et al., 2016). To increase computational efficiency, a prefiltering step using a pose normalization approach can provide coarse subtomogram alignments (STAR Methods: Prefiltering) and classifications (Figure 1A), which divides subtomograms into different groups that are processed separately by MPP (Figure 1B).

Each MPP run is divided into iterative steps, which are repeated until no new patterns are found (typically ~20–30 iterative cycles). Here, we provide an overview of the method (Figure 1B and STAR Methods: MPP Framework).

Generate patterns (step 1 in Figure 1B) (STAR Methods: Candidate Pattern Generation). Each MPP iteration starts by generating patterns, each containing subtomograms of similar objects in the same orientation. Patterns are generated from all subtomograms with their currently assigned rigid transformations (the first iteration uses random transformations). The transformations were calculated in the previous MPP iteration by aligning each subtomogram to selected candidate patterns and using the best alignment for each subtomogram (step 6 in Figure 1B). The MPP framework is an ensemble method, and multiple methods (clustering, sequential expansion, and genetic algorithm-based single pattern pursuit, STAR Methods: Candidate Pattern Generation) are applied independently to generate patterns from the same dataset. All patterns are then added to a growing pattern library. Clustering of subtomograms is performed in a reduced dimensional space, which accounts for missing wedge effects by an imputation-based strategy. After pattern generation, the subtomograms in each pattern are averaged to generate the pattern density maps.

Determine the quality score of patterns and expand pattern library (steps 2 and 3 in Figure 1B; STAR Methods: Quality Score). We then determine a quality score for each pattern, which measures the variance in the voxel intensities between the constituent subtomograms. We use a spectral SNR-based Fourier shell correlation (SFSC) score, which measures SNR as a result of the variance in the voxel intensities at all spatial frequencies. It is computed efficiently in parallel, can account for missing wedge effects, and is calculated from all subtomograms, which reduces the underestimation of the resolution due to the sample size limit (Liao and Frank, 2010). The quality score and density averages for all newly generated patterns are then added to the pattern library (Figure 1B). MPP also contains procedures to remove redundant patterns from the pattern library.

Select a disjoint set of highest-quality candidate patterns from pattern library (step 4 in Figure 1; STAR Methods: Selection of Disjoint High-Quality Patterns). At each iteration, a new selection of candidate patterns is made from the pattern library. These candidate patterns serve as references for subtomogram alignments in the next iterative step. To make the optimal selection, we search for the combination of patterns that leads to the best combined SFSC quality score and include the highest number of subtomograms from the library without any substantial overlap in terms of subtomogram identities between selected patterns. After pattern selection, all subtomograms are optimally aligned to the density maps of each selected candidate pattern and the transformation for the best alignment score is stored for each subtomogram (align subtomograms against selected patterns, step 6 in Figure 1). Depending on the set of candidate patterns, the transformation for a given subtomogram may vary between iterations, which can lead to new patterns or reassignment of subtomograms to different patterns.

The whole MPP process is repeated until a new iteration does not generate any new, nonredundant candidate patterns and has therefore converged to a final set of patterns. The output is the list of candidate patterns from final iteration, the subtomograms assigned to each pattern, and their rigid transformations, as well as the pattern density averages and locations in the tomogram.

Next, we assessed the performance of our method. We applied MPP to three experimental cellular tomograms from different bacteria species and carried out two types of studies using benchmarks of realistically simulated tomograms.

Individually Simulated Subtomograms

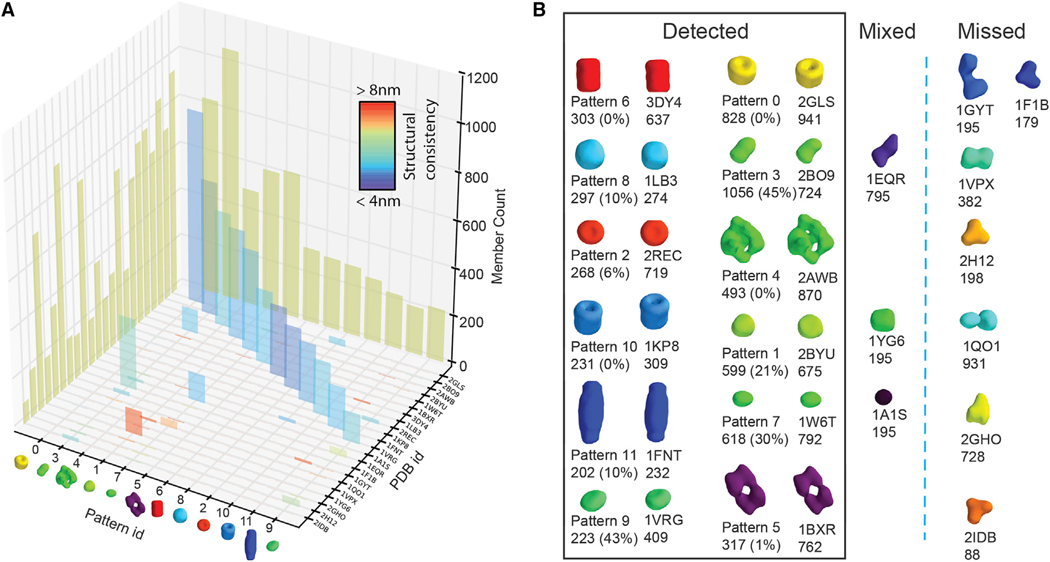
First, we assessed MPP with simulated subtomograms as expected under low crowding conditions. We simulated 11,230 realistic and distorted subtomograms, containing a benchmark mixture of 22 different complexes from the PDB (Berman et al., 2000) with a wide range of size, shape, and abundance (STAR Methods: Simulation of Realistic Tomograms–Individually Simulated Subtomograms) (Figure 2B). To our knowledge, this is a substantially larger number of subtomograms and structural classes than any previously published classification.

Figure 2. Individually Simulated Subtomograms.

MPP results for individually simulated subtomograms of relatively low resolution with a voxel size of 1 nm.

(A) Column plot representation of the contingency table (Table S1C) of the subtomogram membership overlap between true and inferred patterns. The height of each column at each axis corresponds to the total number of subtomograms of the ground truth complex and the total number of subtomograms in the predicted patterns, respectively. The height of each column inside the table corresponds to the number of subtomograms for each ground truth complex in each predicted pattern. The colors of the columns indicate structural consistency between ground truth and corresponding pattern averages, quantified as FSC with cutoff 0.5 (STAR Methods: Validation Procedure).

(B) The isosurfaces of predicted patterns compared with ground truth structures.

The ground truth structures are indicated by their PDB code, and the number of instances and the isosurface representations of the predicted patterns with the number of instances and the false discovery rate (FDR) in parentheses. See also Table S1.

Subtomograms were simulated at voxel spacing of 1.0 nm and resolution of 4 nm. Results converged after 32 iterations and MPP detected 12 patterns from the highly distorted subtomograms, despite the relatively low resolution (Figures 2A and 2B; Table S1). In general, subtomograms of a given complex were highly abundant in no more than one detected pattern (Figure 2A). All 12 patterns were enriched with one dominant complex, and the shapes of all detected pattern averages were very similar to the true complexes (Figures 2A and 2B). Eight patterns uniquely matched complexes with a false discovery rate (FDR) of ≤10%. Among these, four patterns had 0% FDR, meaning that all the subtomograms in each pattern were from the same true class. Also, visually the structures are highly similar to the true complexes (Figure 2B). The structural consistency between the densities of the eight detected complexes and the ground truth structures is high and ranges from 4.7 nm to 5.3 nm (measured by Fourier shell correlation [FSC] with 0.5 cutoff), which is comparable with the applied resolution (Figure 2A and Table S1C). Overall the best performances were achieved with the largest complexes, e.g., glutamine synthetase (PDB: 2GLS, FDR = 0%, 88% particles detected), GroEL (PDB: 1KP8, FDR = 0%, 75% particles detected), and 50S ribosomal subunit (PDB: 2AWB, FDR = 0%, 57% particles detected). Four patterns had larger FDRs (PDB: 2BYU, 21%; 1W6T, 30%; 1VRG, 43%; 2BO9, 45%); however, in each of these patterns essentially only a single complex was falsely co-assigned. This complex had very similar shape to the target complex at the given resolution, which explains why the overall shape of the complex was still well predicted.

Seven complexes were not recovered (PDB: 1F1B, 1GYT, 1VPX, 2H12, 2IDB, 2GHO, and 1QO1). The majority of these had relatively low abundance (<300 instances), relatively small size, and nondiscriminative shape features. Importantly, following MPP’s design strategy, the subtomograms of these complexes were not wrongly assigned to any pattern but were simply left out, emphasizing the importance of the pattern-mining approach in detecting high-quality patterns rather than attempting to classify all the subtomograms.

When repeating our calculations with different initial orientations for all subtomograms, the same complexes were detected with similar FDR ranges (eight complexes with FDR <10%). We also repeated our analysis with different random abundances for the complexes. With larger copy numbers, two additional complexes were detected: Aminopeptidase A (PDB: 1GYT, FDR = 1%, 79% particles detected) and Transaldolase (PDB: 1VPX, FDR = 0%, 48% particles detected). Our analysis suggests that a minimum copy number of 200–300 is necessary to reliably detect complexes at given resolution.

When running MPP on a 300 CPU core cluster with 11,230 subtomograms, one iteration took about 7 h. Pairwise alignment between subtomograms and selected patterns is the most timeconsuming step and took about 6 h.

Complexes under High Crowding Conditions (Subtomograms Extracted from Whole Tomograms Containing Crowded Mixtures)

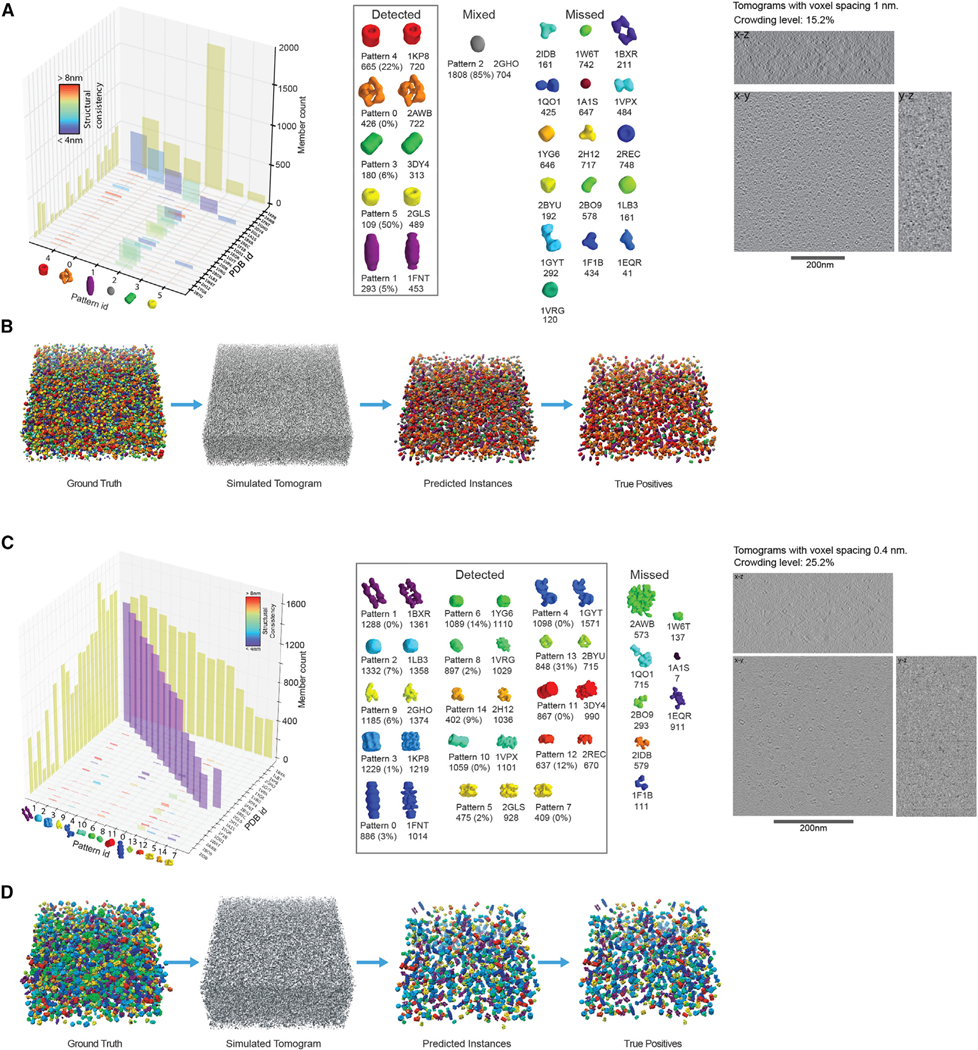
Next, we tested MPP on realistically simulated tomograms of crowded cell cytoplasm, containing mixtures of the same 22 complexes (STAR Methods: Simulation of Realistic Tomograms–Crowded Mixture of Macromolecular Complexes). The crowding level of the simulated tomogram is 15.2%, which falls within the expected range for cell cytoplasm (Guigas et al., 2007) (Figures 3A and 3B). The distortion level of the simulated tomogram is similar to experimental tomograms of whole bacterial cells (STAR Methods: Estimation of Effective-SNR). We used automated “difference-of-Gaussian” particle picking (Voss et al., 2009) to extract subtomograms that likely contain a target complex.

Figure 3. Complexes under High Crowding Conditions.

MPP results for simulated tomogram containing a crowded mixture of complexes.

(A) Left panel: column plot representation of the contingency table for the simulated cellular tomogram of a crowded mixture of complexes (Table S2C) at relatively low resolution with tomogram voxel size = 1 nm. Center panel: isosurface representations of the predicted patterns with the number of instances and FDR in parentheses. Right panel: a slice through a simulated tomogram.

(B) Left panel: isosurface of the ground truth mixture of crowded complexes. Second panel from the left: simulated tomogram. Third panel from the left: isosurface representation of the predicted patterns and their localizations. Fourth panel from the left: true positives among predicted patterns. Dendrogram of hierarchical clustering of templates of macromolecular complexes used for simulation is shown in Figure S2.

(C) Left panel: column plot representation of the contingency table for all ten simulated cellular tomograms of a crowded mixture of complexes (Table S3C) at relatively higher resolution with tomogram voxel size = 0.4 nm. Center panel: isosurface representations of the predicted patterns with the number of instances and FDR in parentheses. Right panel: a slice through one of the simulated tomograms.

(D) Left panel: isosurface of the ground truth mixture of crowded complexes from one of the ten simulated tomograms (~10% of the entire dataset). Second panel from the left: simulated tomogram. Third panel from the left: isosurface representation of the predicted patterns and their localizations. Fourth panel from the left: true positives among predicted patterns.

See also Tables S2 and S3.

The automated particle picking favored extraction of larger complexes. Eleven out of the 22 types of complexes were extracted with at least 200 instances, while 11 mostly smaller complexes had fewer than 140 extracted subtomograms. In total 4,901 particles out of 10,000 instances were detected by particle picking (STAR Methods: Particle Picking and Subtomogram Extraction–Crowded Mixture of Macromolecular Complexes–Low Resolution). Because of crowding, the subtomograms of extracted target complexes may also contain fragments of neighboring structures. Therefore, we applied our method for automatically masking target complexes at each MPP iteration (STAR Methods: Target Complex Region Segmentation). This test case is substantially more challenging than the previous one because errors in automated particle picking and target complex segmentation can influence the MPP performance. Despite these challenges, MPP detected six patterns, four of which with FDRs of ≤23% and very well predicted shapes with structural consistencies between predicted averages and ground truth complexes ranging from 4.3 nm to 4.8 nm (FSC with 0.5 cutoff) (patterns 0, 1, 3, and 4, in Figures 3A and 3B; Table S2). Among these, one (50S ribosome/PDB: 2AWB, discovered as pattern 0) had an FDR of 0%. MPP also predicted two patterns that are a mixture of complexes (patterns 2 and 5) (Figure 3A). These two have structural consistencies ≤6.5 nm and are very similar in shape to the most abundant complex in the pattern. One of these patterns (pattern 5, PDB: 2GLS) contained only two complexes of similar shapes. Detected pattern 2 has the smallest size and is a mixture of more than ten small complexes. Most of these complexes have low abundance after particle picking and are of similar shape, as shown by their tight clustering based on shape similarity (Figure S2). At the given resolution and crowding level, it is not possible to distinguish these small complexes. However, MPP still predicted their similar size and location.

To test the reproducibility of our approach, we simulated another tomogram with different random positions and orientations of the complexes. Now six patterns were successfully recovered at FDR <30%, including the largest complexes (PDB: 1KP8, 2AWB, 3DY4, and 2GLS) and two additional complexes (PDB: 1LB3 and 1FNT) that were detected as a result of increased copy numbers after particle picking.

Next, the MPP analysis was performed on crowded tomograms simulated at higher resolution and lower voxel size (0.4 nm) (Figures 3C and 3D; STAR Methods: Simulation of Realistic Tomograms–Crowded Mixture of Macromolecular Complexes–High Resolution). We simulated ten different tomograms containing a total 35,172 particles (Figure 3C, right panel: center slice of first tomogram). Automated particle picking extracted 18,876 subtomograms. To test the robustness of the approach, we performed three independent MPP runs, starting each individual run with a different initial random orientation for each subtomogram. Despite a high crowding level, MPP showed excellent results and detected 14, 13, and 12 complexes over three runs, respectively (Figures 3C and 3D; Table S3 for run #2). Twelve complexes were detected in all three runs. Two additional complexes were detected in two independent MPP runs, starting each time from different initial subtomogram orientations. For each run, nine complexes were detected with an FDR of <3%, and between four and six complexes were detected at an FDR of 0%. Some complexes could not be detected due to their low copy numbers (e.g., PDB: 1A1S, 7; 1W6T, 137). This observation showcases the importance of performing the analysis with very large sample sizes and the need for highly efficient methods such as MPP that can handle a large number of diverse subtomograms. Finally, we also propose a strategy to combine the results of independent MPP runs: all final patterns from each of the three different MPP runs can be combined into a single pattern library, which then can be used to select the best pattern combinations.

Experimental Cellular Tomograms

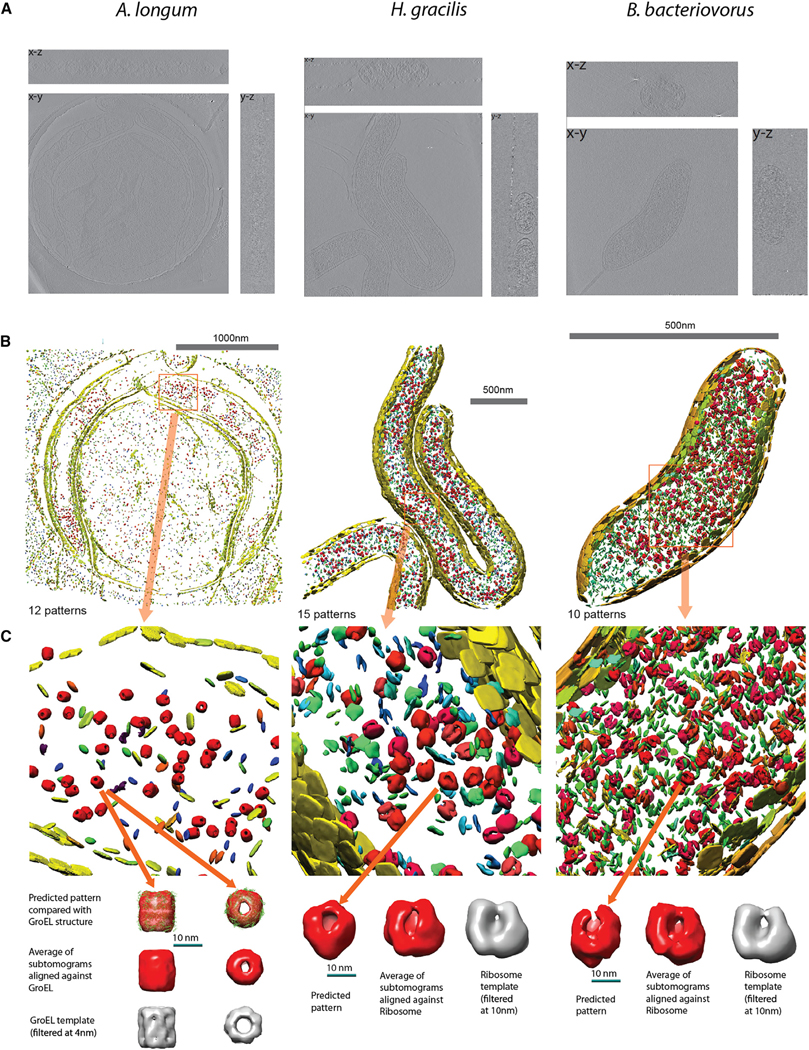
We also tested MPP on three tomograms of whole bacteria, namely single cells of lysed Acetonema longum, intact Hylemonella gracilis, and intact Bdellovibrio bacteriovorus with voxel sizes of 1.2 nm, 0.49 nm, and 0.42 nm, respectively (Figure 4A and STAR Methods: Experimental Tomogram Acquisition). We performed automated, template-free particle picking to extract a total of ~30,000 subtomograms from the three cells. For intact cells (H. gracilis and B. bacteriovorus) only the subtomograms within the cellular region were extracted. However, A. longum appeared lysed and particles were noticeable also at the cell exterior, which was included in the analysis. We then applied preprocessing (STAR Methods: Prefiltering) and applied MPP separately for each cell type.

Figure 4. Discovered Patterns in Three Experimental Cellular Tomograms: A. longum, Intact H. gracilis, and Intact B. bacteriovorus Cells.

(A) Three slices of the electron cryotomogram. A. longum (left), intact H. gracilis (center), and intact B. bacteriovorus (right).

(B) Embedded instances of detected patterns.

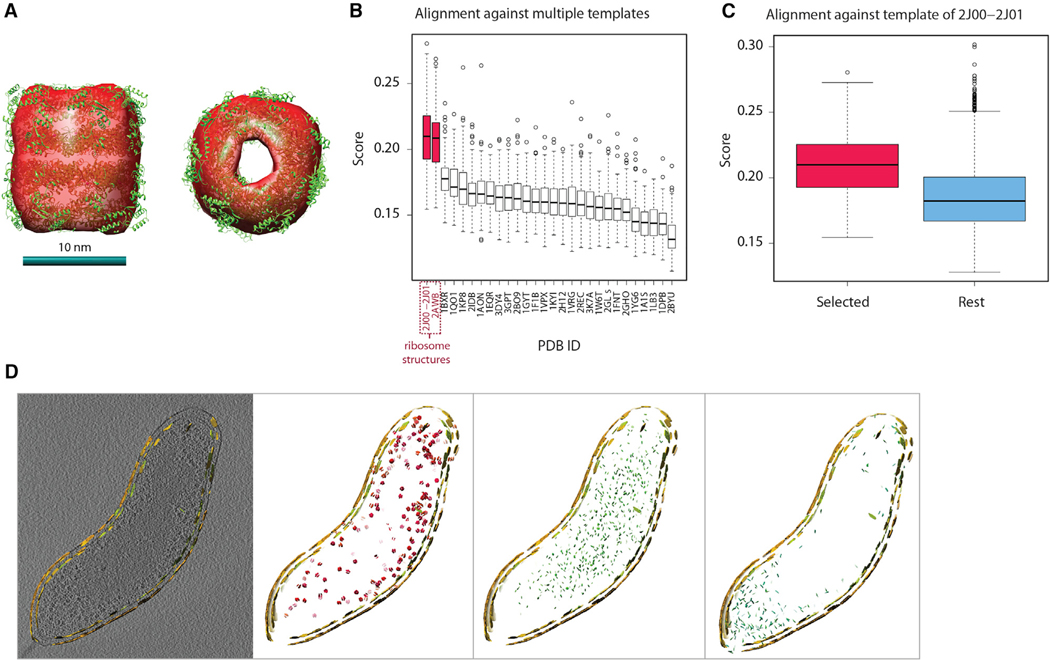
(C) Upper panel: embedded instances, zooming in on a particular region. Lower panel: isosurfaces of one example pattern from each experiment. GroEL-like pattern is also fitted with a known atomic model of GroEL. Isosurface of the average density of the example pattern, aligned with the known structures of the GroEL (PDB: 1KP8) and ribosome complexes (PDB: 2J00–2J01).

See Table S4 and Videos S1, S2, and S3.

MPP discovered 12, 15, and 10 patterns of a relatively high-quality score for A. longum, H. gracilis, and B. bacteriovorus, respectively (Figures 4B and 4C; STAR Methods: Pattern Mining–Experimental Tomograms; Table S4; Videos S1, S2, and S3). The resolution of these patterns (gold standard FSC) ranged from 4.1 to 5.8 nm in A. longum, 3.5 to 10.5 nm in H. gracilis, and 4.8 to 15.0 nm in B. bacteriovorus. The shapes and positions of some patterns already give indications as to the identity of the complexes. For example, several different patterns clearly represented membrane particles lining the cell boundaries (Figures 4B and 4C) (e.g., patterns 2, 3, and 7 for B. bacetriovorus, Table S4F; and patterns 5, 6, and 9 for A. longum, Table S4B). The different membrane patterns varied in their locations, for instance different patterns for the inner and outer membranes. Some larger patterns have a very similar shape and size to GroEL (pattern 4 in A. longum) and ribosome (patterns 0, 1, 2 in H. gracilis; and patterns 0, 1, 9 in B. bacteriovorus), and were also observed at large abundance (e.g., a total of 802 copies of ribosome-like patterns in H. gracilis). We refined these patterns further using the genetic algorithm method (STAR Methods: Candidate Pattern Generation–Genetic Algorithms). Figure 4C shows the high similarity between these structures and the GroEL and 70S ribosome templates simulated from their atomic structures.

Strikingly, we observed a remarkably good fit of the atomic structure of GroEL into the average density of pattern 4 in A. longum (Figure 5A). We also aligned all the subtomograms from each cell type against a collection of the 28 different template structures most abundant in cells. We found that the alignment scores for subtomograms of the GroEL-like pattern 4 were statistically significantly higher to the GroEL template (PDB: 1KP8) than to any other template (one-sided Wilcoxon rank-sum test with p < 3.2⁻¹⁰, without multiple comparison adjustments, Figure S3A), confirming the clear visual similarity of pattern 4 with GroEL. The second closest match was the GroEL/GroES complex (PDB: 1AON), although this template had significantly lower alignment scores. Also, we showed that the subtomograms of pattern 4 had the strongest matches to the GroEL template in terms of alignment scores, compared with all other extracted subtomograms of A. longum (p < 2.2 × 10⁻²²⁰, Figure S3B). These tests indicate that our template-free approach yields similar results to a template-matching approach with GroEL as a template structure. All these observations support the hypothesis that the subtomograms in pattern 4 contain a bacterial analog of the GroEL complex. Interestingly, the high abundance of GroEL complexes (481 instances) is observed only in the A. longum cell and may be related to a stress response. We note that this cell appeared to be dead and lysed before image acquisition (Susin et al., 2006).

Figure 5. Analysis of Tomograms.

(A) The isosurface of the subtomogram average density map of pattern 4 from A. longum, fitted with the known structure of the GroEL (PDB: 1KP8).

(B) Assessment of pattern 1 detected in tomogram of B. bacteriovorus cell. Box plot of the distribution of alignment scores of the subtomograms of pattern 1 against all different template complexes (denoted by PDB code). The complexes are ordered according to median score in descending order. One-sided Wilcoxon rank-sum test with p-value < 1.7 × 10⁻²⁴.

(C) (Red) box plot of the alignment score distribution of subtomograms in pattern 1 (B. bacteriovorus) against the ribosome template complex (PDB: 2J00–2J01). (Blue) box plot of the alignment score distribution of all other extracted subtomograms against the ribosome template. One-sided Wilcoxon rank-sum test with p-value < 6.3 × 10⁻⁶.

(D) A thin section of embedded instances of different patterns, outlined by embedded instances of membrane patterns from tomogram of B. bacteriovorus cell. Left panel: a slice of tomogram. Shown are all membrane patterns in yellow. Second panel from left: patterns 0, 1, 9 containing ribosome structures. Third panel from left): pattern 6. Fourth panel from left: patterns 4 and 5. For analysis of patterns from tomograms of A. longum and H. gracilis, see Figure S3.

Equally convincing are the assessments of ribosome structures in H. gracilis (patterns 0, 1, 2, Figure 4C) and B. bacteriovorus cells. The subtomograms in pattern 0, 1, and 2 had the highest alignment scores with the ribosome template (both the full ribosome PDB: 2J00–2J01 and its 50S subunit with PDB: 2AWB) (Figures S3D and S3F) (p < 4.1 × 10⁻²²) compared with any of the other 26 templates, indicating that all three patterns are most likely ribosome structures. Subtomograms in pattern 1 had significantly higher alignment scores with the ribosome than all remaining extracted subtomograms (p < 2.0 × 10⁻¹²⁵, Figure S3E). All these observations support the hypothesis that these patterns contain a ribosome structure.

Similarly, in B. bacteriovorus, the subtomograms in pattern 1 (resolution 12.0 nm, Figure 4C and Table S4F) were visually similar to the ribosome and had significantly higher alignment scores to ribosome template (PDB: 2J00–2J01 and 50S subunit with PDB: 2AWB) compared with any of the other 26 templates (p < 1.7 × 10⁻²⁴, Figure 5B). Compared with all detected patterns, subtomograms of pattern 1 had the highest alignment scores to the ribosome template (PDB: 2J00–2J01) (Figure 5C) and also had the highest-ranking scores compared with all other extracted subtomograms (p < 6.3 × 10⁻⁶).

Interestingly, we found distinct spatial distributions for different complexes in B. bacteriovorus tomogram. For instance, the ribosomal patterns are excluded from central regions of the cell (Figure 5D, second panel), where the bacterial nucleoid is located. It is likely that ribosomes would be positioned close to, but not directly overlapping with, regions of the nucleoid genome. Ribosome-like structures also are less abundant in the tip region associated with the bacterial flagella motor, although we cannot exclude the possibility of imaging artifacts being partially responsible for the lack of ribosome structures in this region. Interestingly, two smaller patterns (patterns 4 and 5, Figure 5D, fourth panel) were only enriched in the tip of the bacteria where the bacterial flagella motor is located. Another small pattern (pattern 6) in B. bacteriovorus is located exclusively in the area of the nucleoid genome (Figure 5D, third panel). Based on location, size, and abundance we could hypothesize that this pattern may correspond to the RNA polymerase II complex. However, at this stage we can only speculate about the identity of some of the complexes, based on their shape and locations in the cell. In future, one could apply independent refinement methods to increase the resolution of the resulting averages. Higher resolution may provide further evidence to the identity of some complexes.

Currently our method has not detected membrane complexes. Partially this is due to the low resolution of bacterial tomograms (i.e., 0.5–1 nm voxel size approximately). Also, it is possible that the alignment of subtomograms containing membranes is dominated by the membrane portion. In addition, the applied difference-of-Gaussian particle-picking method may not be optimal for detecting membrane particles. We expect that tailored particle picking and increased resolution in combination with refinements optimized for membrane subtomograms may facilitate the detection of membrane complexes in future.

In summary, our aim was not to determine the high-resolution structure for an individual complex, but the large-scale detection of coarse structures and their relative abundance in large heterogeneous samples that can then be the basis for a refined analysis. Further development of methods that integrate other orthogonal datasets would facilitate the identification of the patterns.

DISCUSSION

ECT can produce large quantities of cell tomograms. There is an urgent need for a systematic screening of cell tomograms to detect frequently occurring patterns. Such methods have the potential to discover macromolecular complexes on a large scale. The MPP method is designed for discovering structure models in a systematic and template-free fashion from a large number of subtomograms containing many different structural classes. Because MPP does not rely on any prior structural knowledge, it is complementary to template-based subtomogram classification methods and machine learning approaches for the detection of complexes in tomograms.

In comparison with template-free subtomogram classification, MPP has some important advantages. The computational complexity for template-free classification methods increases with the product of the number of subtomogram classes and the size of the subtomogram library. Therefore, traditional template-free subtomogram classification methods have several drawbacks, which limit their use in detecting unknown structures from highly heterogeneous samples with large numbers of different complexes. MPP is specifically designed to efficiently process such highly heterogeneous datasets extracted at a proteome-wide scale. The resulting pattern library from MPP can then serve as a starting point for additional refinement methods to process and increase the resolution of individual patterns.

Our proof-of-principle MPP applications showed that successful detection of complexes can depend on the copy numbers and also the shape and size of the complexes. For example, larger complexes can generally be more easily detected even at larger voxel sizes. Typically, a minimum number of instances of complexes is necessary to detect structures successfully. As shown in the Results section, at voxel sizes of 1 nm around 300 copies of a complex are necessary for their detection. For example, complex 1GYT could not be detected in a dataset containing only 195 instances, whereas 829 copies of this complex in another dataset led to the successful detection of its structure (see Individually Simulated Subtomograms). For a few complexes (e.g., complex 1F1B), even increased copy numbers were not sufficient to detect the complex structures. The reason for this may be that these complexes are relatively small and/or lack distinct shape features at the given resolution. Crowding levels and resolution can also influence the results of MPP. Increased crowding levels affect the performance of the automatic particle picking, while increased resolution improves the discovery rate in detecting patterns. MPP results can also vary depending on optimization parameters, for example, the number of dimensions used in the dimension reduction step or k value for k-means clustering. However, MPP can be rerun multiple times with different parameter settings and the final sets of candidate patterns can be combined in a common pattern library, which can then be included in a subsequent new MPP run.

Our method represents a substantial step toward visual proteomics analysis inside single cells. Automatic unsupervised pattern mining inside cellular electron cryotomograms is still very challenging, and our approach is only a first step in this direction. Improved methods for particle picking, subtomogram averaging, pattern generation, and quality scores have potential to improve the performance of MPP. On the other hand, together with recent breakthroughs on direct detectors (Jin et al., 2008) and phase plates (Murata et al., 2010), which significantly improve contrast and resolution of cellular ECT data, correlative light and electron microscopy (Chang et al., 2014), and focused ion beam milling (Rigort et al., 2012), which enables ECT to image a substantially larger variety of cell types, we expect that our method can become an integral part of cellular ECT applications. In addition, MPP is also useful for analyzing tomograms of highly heterogenic particle mixtures, such as cell lysates. Moreover, once patterns are detected they can be used by other methods such as template searches, subtomogram classifications, subtomogram averaging methods, and supervised learning methods for further refined structural recovery and separation of protein species. Therefore, our work complements existing template-based and template-free methods and can emerge as an important tool for whole-cell visual proteomics and modeling. In future, we envision the integration of additional information about sample protein compositions and tomogram locations to facilitate the identification of unknown detected complexes.

STAR★METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact FA (alber@usc.edu).

DATA AND SOFTWARE AVAILABILITY

The Source code of the methods, test data and user guide can be found at: http://web.cmb.usc.edu/people/alber/Software/mpp/

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Bdellovibrio bacteriovorus (HD100, wild-type) cells were grown in E. coli S17–1 prey cells at 30°C, Hylemonella gracilis (ATCC 19624, wild-type) cells were grown in ATCC #233 Broth at 26°C and Acetonema longum strain APO-1 (DSM 6540) was grown anaerobically as described (Leadbetter and Breznak, 1996).

METHOD DETAILS

Particle Picking and Subtomogram Extraction

The subtomogram extraction is done through template-free particle picking. The particle picking is based on Difference of Gaussian (DoG) filtering (Voss et al., 2009). First, we filter a tomogram v₁ using a DoG function of σ = 7 nm and k-factor = 1.1, resulting in a filtered tomogram f₁. Then, we search for the collection p₁ of local maxima peaks of f₁. Often, there are false positive peaks, i.e., those peaks that do not correspond to macromolecular complex instances, but rather noisy fluctuations in the non-structural regions. To reduce such false peaks in p₁, we randomly sample voxels to form another volume v₀ of size smaller than original volume (e.g., 400 × 400 × 200 nm³ from low-resolution simulated tomograms). Then we apply the same DoG filtering to obtain a filtered map f₀. Next, we perform local maxima search to obtain a collection p₀ of background peaks. Finally, we selected final peaks from p₁ whose values are larger than 5 times of the standard deviation plus mean of the values of p₀.

Crowded Mixture of Macromolecular Complexes

Low Resolution.

After performing particle picking as mentioned above, in order to evaluate the performance, we identify true class labels of these peaks through the one-to-one correspondence between peak locations and the minimal bounding spheres. Due to the size preference of DoG particle picking, when setting σ = 7 nm, instances of large complexes are more likely to be picked out than instances of small complexes. Centered at each of the 4,901 peaks picked, we cut out a subtomogram of size 30³ voxels. These subtomograms are used as an input of MPP.

High Resolution.

After running particle picking step on each of the tomogram separately, 18,876 subtomograms of size 75³ voxels were extracted in total, among which 18,802 were assigned true class labels.

Experimental Tomograms.

For particle picking, we filtered the tomograms using the DoG function with σ = 7 nm. We then select the top 10,000 peaks and remove those peaks at the boundary of the tomogram. Centered at each peak we extract a subtomogram of size 18³ voxels. The interior cell regions are manually segmented using the Amira software (Mercury Computer Systems), and the peaks outside the cell regions are excluded.

Remarksa.

In this paper, for simplicity, we use DoG with a single fixed s for particle picking. DoG particle picking has size preference of picked particles. In practice, in order to detect patterns of very different sizes, one may systematically perform DoG particle picking using multiple σ (Pei et al., 2016), followed by pattern mining. In addition, other types of template-free particle picking methods may be used instead of using DoG particle picking.

Pre-filtering

MPP is suitable for processing thousands to tens of thousands of subtomograms with affordable computation cost. However, with the advance of automation of ECT imaging techniques, nowadays it is not difficult to acquire a substantially larger amount (for example, more than a million) of subtomograms within a day. Using MPP alone is not computationally feasible for processing such a large amount of subtomograms. Therefore, an efficient coarse filtering of the subtomograms is very useful to reduce the whole collection of subtomograms to substantially smaller subsets containing structures of relatively similar sizes and shapes. Then these subsets can be further independently processed using MPP as described under next section “MPP Framework”. In this paper, we perform such filtering through normalization of translation and rotation of subtomograms followed by clustering.

Intuitively, the normalization of the translation of the particle inside a subtomogram can be done by calculating a key point with respect to the particle, which is invariant to the rotation and translation of the particle. A typical example of such a key point is the center of mass. However, because the suppression of zero frequency signal in the ECT imaging process, the mean intensity value of a subtomogram is often close to the background intensity value (Xu and Alber, 2013). Therefore, it is hard to directly use all image intensities of a subtomogram to accurately estimate a center of mass of the particle. Instead, we use binary segmentation to obtain a coarse shape of the particle and calculate the center of mass of this shape. Level set based segmentation (Chan and Vese, 2001) is a powerful, flexible method that can successfully segment many types of images, including some that would be difficult or impossible to segment with classical thresholding or gradient-based methods. Through such segmentation, a coarse shape of the particle can be represented by the zero-level region of a level set. The normalization of translation can then be calculated on the center of mass of the positive part of the level set instead of on the original image intensities. Given such center of mass, we can further estimate the general orientation (without taking into account missing wedge effect) of the particle by calculating the principal directions by applying PCA to the coarse shape (Figure S1D).

Such a pose normalization procedure can be independently and efficiently applied to individual subtomograms. With the coarse alignment from pose normalization, it is possible to separate particles with very distinct sizes and distinct elongated shapes through simple and efficient clustering techniques like k-means clustering and generate an average representing general shapes. Then averages of subtomograms can be inspected and the corresponding subtomogram sets can be selected further for more focused analysis. Such procedure is highly scalable and can be easily parallelized. It can usually process tens of thousands of subtomograms on a single computer within one day.

Structural Region Segmentation

We formulate the identification of structural regions as a binary region based segmentation problem that minimizes the Chan-Vese model (Chan and Vese, 2001), which is a popular level set based segmentation model. The model can be formulated as follows:

$$\text{arg}mi{n}_{c_1,c_2,\varphi }\mu \int |\nabla H(\varphi )|+\lambda \left[\int {|f-c_1|}^{2}H(\varphi )+\int {|f-c_2|}^2(1-H(\varphi ))\right]$$ (Equation 1)

In Equation 1, $f:{ℝ}^3\to ℝ$ is the intensity of the subtomogram to be segmented. $\phi :{ℝ}^3\to ℝ$ is a level set function that simultaneously defines a boundary contour and segmentation of an image. The boundary contour is taken to be the zero-level set $\{\phi =0\},$ and the segmentation is given by the two regions $\{\phi <0\}\text{and}\{\phi \ge 0\}.$ H is the Heaviside step function $H(x)=\{\begin{array}{c}0,x\le 0\\ 1,x\ge 0\end{array}.$ c₁ and c₂ are the mean intensities inside the two regions.

The first term in Equation 1 measures the total area of the segment boundary. The minimization of the first term encourages the resulting segment boundary to be smooth. The second term measures the difference between image intensity and the mean intensity of the corresponding segments. The minimization of the second term encourages the uniformity of the intensities inside the two regions.

Such an optimization problem can be elegantly solved by evolving the level set function $\phi$ through variational calculus (Chan and Vese, 2001). In practice, we use (Zhang, 2013) as an implementation of the algorithm, where $\phi$ is implemented using a distance transform (Kimmel et al., 1996). For simplification, we choose $\mu =1,\text{and}\lambda =\frac{1}{Var(f)},$ where Var(f) is variance of f. Let ${\phi }^{*}$ be the optimal level set. Suppose the region $R^{\mathit{\text{structure}}}=\{{\phi }^{\star }>0\}$ corresponds to the high electron density in the subtomogram, then R^structure is used to define the structural region inside the subtomogram. Remark: In order to reduce the influence of noise, we usually apply a Gaussian smoothing with σ = 2nm to a subtomogram before segmentation.

Pose Normalization

The pose normalization is performed according to the positive part of ${\phi }^{*}.\text{Let}{\varphi }_1^{*}(\mathit{x})=1_{{\phi }^{*}(x)\ge \mathit{0}}{\phi }^{*}(\mathit{x}),$ where 1 is the indicator function. The pose normalization consists of following steps: First, we calculate a center of mass $c_{{\varphi }_1^{*}}\text{of}{\varphi }_1^{*}.$

$$c_{{\varphi }_1^{*}}=\frac{{\int }_x{\varphi }_1^{*}(x)x}{{\int }_x{\varphi }_1^{*}(x)}$$

Then, we calculate

$$\mathit{W}=\underset{x}{\int }{[{\varphi }_1^{*}(x)]}^2(x-c_{{\varphi }_1^{*}}){(x-c_{{\varphi }_1^{*}})}^T$$ (Equation 2)

Then we calculate the eigen decomposition $\mathbf{W}=\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^{\top }$ of W, where Q is an orthogonal matrix consisting of eigenvectors, and the magnitude of eigenvalues in the diagonal matrix $\text{Λ}$ are ordered in descending order. Finally, the pose normalization is performed by first translating the subtomogram (masked with R^target_ext, STAR Methods: Target complex region segmentation) from $c_{{\varphi }_1^{*}}$ to the center of the subtomogram, then rotating the subtomogram using Q as a rotation matrix.

Remarks.

• The coarse filtering of subtomograms may also be performed through rotation invariant features (Xu et al., 2009, 2011; Chen et al., 2014) combined with clustering. However, to extract structure information from such filtering is not straightforward because rotation invariant features do not provide alignment information. By contrast, for pose normalized subtomograms, coarse representative shapes can be directly obtained from cluster centers or subtomogram averages, which is very useful for manual inspection of these clusters.

• This method may not work when the SNR or contrast is very low. In addition, how to incorporate missing wedge to achieve a better pose estimation is an open problem.

Multi Pattern Pursuit (MPP) Framework

The Multi Pattern Pursuit (MPP) framework takes a collection of subtomograms and searches for structural patterns. A structural pattern is defined as a set of rigidly transformed subtomograms and their density average. These subtomograms are similar to each other and are likely to contain the same structure. MPP aims to maximize the quality (in terms of SFSC score, STAR Methods: Quality Score) of multiple distinct patterns extracted from these subtomograms. MPP is an iterative optimization process that searches for patterns in the pattern space. Such space is the Cartesian product of pattern membership and rigid transform of subtomograms. MPP combines novel components and our previously developed components. Each iteration of MPP consists of following steps (Figure 1B):

1. Based on current rigid transformations T of subtomograms, generate a collection of candidate patterns S^candidate (STAR Methods: Candidate Pattern generation).

2. Determine quality of the patterns in S^candidate in terms of their SFSC scores (STAR Methods: Quality Score).

3. Add S^candidate into the pattern library L: L ← L U S^candidate.

4. Select a set S^sel of highest quality patterns from L under the constraint of minimal subtomogram membership overlap (STAR Methods: Selection of disjoint high-quality patterns).

5. Align the subtomogram averages of patterns in S^sel into common reference frames (STAR Methods: Align averages into common frames).

6. Align all subtomograms against each of the subtomogram averages of all patterns in S^sel.

7. Identify structurally redundant patterns S^redundant in S^sel (STAR Methods: Identification of structurally redundant patterns). Remove patterns in S^redundant from $L:L\leftarrow L\backslash S^{redundant}.$ In other words, patterns in S^redundant will never be selected in future iterations.

8. Update subtomogram transformations T according to the best alignment between the subtomograms and the subtomogram averages of the remaining selected patterns in S^remain = S^sel \ S^redundant.

9. If the patterns in S^remain are all generated from at least n^stop iterations earlier, stop. Otherwise, continue to next iteration.

Remarks

• For high-throughput processing, we use our fast alignment method (Xu et al., 2011). Alternative alignment methods (e.g., Bartesaghi et al., 2008; Chen et al., 2013; Frangakis et al., 2002; Schmid and Booth, 2008; Xu and Alber, 2012, 2013; Yu et al., 2013) may also be used. Alignment methods could fail when the SNR of tomograms is very low.

• By design, our proposed framework can mine multiple patterns simultaneously. This design allows us to save computation cost, also to keep the mined patterns distinct.

• The particles with relatively larger size may contain more signals that may be easier to be discriminated using MPP. In practice, subtomograms of particles with very distinct sizes can be extracted separately with proper sizes, then processed separately using MPP.

• Empirically, we set n^stop = 5, which we found is sufficiently large to minimize the chance of missing new and even higher quality patterns.

• The software implementation of MPP is based on a variant of the TomoMiner platform (Frazier et al., 2017).

Candidate Pattern Generation

The MPP optimization is performed in two stages, which differ in the way candidate patterns are generated. After stage 1 terminates, the MPP starts stage 2 with the rigid transforms T and pattern library L that resulted from stage 1. The main purpose of stage 1 is to obtain updated T so that subtomograms with the same underlying structures are roughly aligned and obtain a first estimate of (the number of) distinct patterns. Stage 1 begins with an initially empty pattern library L and randomly assigned rigid transforms T for all subtomograms, which are updated at the end of every iteration. In stage 1, the pattern generation is performed by a dimension reduction approach (STAR Methods: Pattern Generation - Imputation based dimension reduction) followed by k-means clustering with a fixed cluster number k^k_means_fix, which is usually chosen to over-partition the collection of subtomograms. When the true set of structurally distinct patterns is unknown, an intuitive strategy is to over-partition the number of clusters then identify and remove the clusters leading to redundant patterns (STAR Methods: Identification of structurally redundant patterns).

After stage 1 terminates, the MPP starts stage 2 with the T and L that resulted from stage 1. In stage 2 the subtomogram membership and density averages of the patterns are improved. In stage 2, two independent methods are used to generate candidate patterns (resulting patterns of both methods are added to the pattern library): first, the sequential expansion method (STAR Methods: Candidate pattern generation - Sequential Expansion) and second, dimension reduction followed by k-means clustering in which the cluster number k^{k_means_adaptive} is assigned adaptively according to $|S^{\mathit{\text{remain}}}|$ of the last iteration: $k^{k_{-}means\_adaptive}\approx k^{k_{-}means\_adaptive\_factor}|S^{remain}|,\text{where}{k}^{k\_means\_adaptive\_factor}=1.2$ is a fixed ratio.

Remarks

Each time, the k-means clustering is repeated 10 times and the best clustering result is chosen in order to reduce the chance of being trapped in local minima. We use the k-means++ initialization (Arthur and Vassilvitskii, 2007) to improve convergence. Such a procedure has been implemented in the off the shelf sklearn package (Pedregosa et al., 2011).

Imputation Based Dimension Reduction

Dimension reduction for high dimension data has been extensively studied in different areas. It is very useful for extracting key low dimension features that contain the majority of discriminative signals across images and reducing the influence of non-informative variance. Dimension reduction is also very useful for significantly speeding up clustering. This is because subtomograms are high dimension data, and computation of distances between two subvolumes in a smaller number of dimensions is much more computationally effective than directly calculating distances in their original high dimensional space.

One major obstacle for directly applying existing dimension reduction methods is the missing wedge effect as a result of the limited tilt angle range of captured projection images. As a result, the objects in a subtomogram have anisotropic resolutions across different directions, which introduces bias to the dimension reduction (Bartesaghi et al., 2008; Förster et al., 2008). The missing wedge effect can be described in Fourier space, where the Fourier coefficients in certain regions are missing. The locations of Fourier coefficients $ℱf$ with valid values and missing values can be represented using a missing wedge mask function M.

$$M(\xi )=\{\begin{array}{l}1,iftheFouriercoefficientat\xi isvalid\hfill \\ 0,iftheFouriercoefficientat\xi ismissing\hfill \end{array}$$ (Equation 3)

where $f:{ℝ}^3\to ℝ$ is the function that represents image intensity of a subtomogram; $ℱ$ is the Fourier transform operator; and $\xi \in {ℝ}^3$ is a location in the Fourier space. Two typical types of strategies have been proposed to handle the missing wedge effect for dimension reduction. The first type omits the Fourier coefficients that are not used for dimension reduction (e.g., Heumann et al., 2011). The second type estimates missing values (e.g., Yu et al., 2010). These methods are effective for enhancing the subtle true discriminative signal across aligned subtomograms. However, these methods are generally designed for cases in which the underlying structures of all subtomograms are similar to a single reference density map, which does not apply to a Visual Proteomics setting with the existence of a high degree of structural heterogeneity among subtomograms.

To solve this problem, we propose an imputation strategy. For each subtomogram, we use its current best aligned density map (chosen from the set of pattern density maps in S^remain obtained from the last iteration of MPP as a reference to replace the missing Fourier coefficient values with those from the density map, Figure S1A illustrates the basic idea).

Formally, we want to use Fourier coefficients of a reference density map a as an estimate of the missing Fourier coefficients of a subtomogram f, given that aligning f against a gives the best alignment score compared to aligning f against other maps in the same collection. For simplicity, suppose f has been rigid transformed according to its alignment against a, and M be the corresponding missing wedge mask of f rotated according to the rigid transform. Then we can form a transformed and imputed subtomogram $\widehat{f}$ such that:

$$(ℱ\tilde{f})(\xi )=\{\begin{array}{c}(ℱf)(\xi )\text{if}M(\xi )=1\\ (ℱa)(\xi )\text{if}M(\xi )=0\end{array}$$ (Equation 4)

In principle after imputation, any generic dimension reduction method can be directly applied without any modification to take into account missing wedge effects. Further, in principle, after dimension reduction, in principle the consequent clustering step does not need to take missing wedge effects into account. After imputation, to speed up processing in the dimension reduction, we combine feature selection and feature extraction. We first calculate the average covariance between neighbor voxels in a similar way as our previous work (Xu et al., 2012). We then select a number (usually 10,000) of voxels with highest and positive average covariance (feature selection step) and apply EM-PCA (Roweis, 1998) (feature extraction step) to perform dimension reduction. When the extracted dimension number is relatively small, EM-PCA can be very fast, scalable and memory-efficient compared to other Principal Component Analysis (PCA) methods. It can normally handle tens of thousands of subtomograms using a single CPU core in a couple of hours. Empirically, we found a dimension number of 50 to be able to capture sufficient data variance for clustering the subtomograms.

Remarks.

When using an imputation-based dimension reduction for MPP, all subtomograms are first imputed. The calculation of the principal directions of PCA is done using subtomograms of the non-redundant selected patterns only S^remain obtained from the last iteration. Finally, we project all imputed subtomograms onto the principal directions.

Proof of equivalence between wedge-masked difference and imputed difference: The difference between a and $\widehat{f}$ can be treated as a generalization of the wedge-masked difference proposed in (Heumann et al., 2011), where the wedge-masked difference is equivalent to a special case of our approach where only a single average is used to impute all the aligned subtomograms and calculate differences among these subtomograms. Without band limit, the wedge-masked difference between a reference density map a and an aligned subtomogram f (with corresponding rotated wedge mask M) is calculated as:

$$\begin{array}{c}{ℱ}^{-1}[M(ℱa)]-{ℱ}^{-1}[M(ℱf)]\\ \\ ={ℱ}^{-1}[M(ℱa-ℱf)]\end{array}$$

According to Equation 4,

$$\begin{array}{c}[M(ℱa-ℱf)](\xi )\\ \\ =\{\begin{array}{cc}(ℱa)(\xi )-(ℱf)(\xi )& \mathit{\text{if}}M(\xi )=1\\ 0& \mathit{\text{if}}M(\xi )=0\end{array}\\ \\ =\{\begin{array}{cc}(ℱa)(\xi )-(ℱ\widehat{f})(\xi )& \mathit{\text{if}}M(\xi )=1\\ (ℱa)(\xi )-(ℱ\widehat{f})(\xi )& \mathit{\text{if}}M(\xi )=0\end{array}\\ \\ =(ℱa)(\xi )-(ℱ\widehat{f})(\xi )\end{array}$$

Therefore

$$\begin{array}{c}{ℱ}^{-1}[M(ℱa)]-{ℱ}^{-1}[M(ℱf)]\\ \\ ={ℱ}^{-1}[ℱa-ℱ\widehat{f}]\\ \\ =a-\widehat{f}\end{array}$$

Sequential Expansion

Besides using k-means clustering, we also use sequential expansion as a heuristic for generating candidate patterns. Sequential expansion adds subtomograms from an existing pattern to a new pattern only if their inclusion increases the overall pattern quality. Therefore, sequential expansion allows omission of subtomograms that are likely wrongly assigned to a pattern based on k-means clustering. All subtomograms are ranked according to their alignment score to the pattern average. Then an alignment score cutoff is searched such that the quality of the pattern formed by the set of subtomograms with scores higher than the cutoff which maximizes the quality of the newly formed pattern average. Formally, let S^remain to be the non-redundant patterns selected from the last iteration of MPP. For each subtomogram average a ∈ S^remain, from all subtomograms, we select those that have the highest alignment scores against a compared to all other pattern averages in S^remain. Suppose that in total there are n_a such subtomograms, let $C=\left\{f_1,\dots ,f_{na}\right\}$ be the collection of subtomograms. They are aligned against a and ordered in terms of alignment scores in descending order. Then, for each subcollection $\left\{f_1,\dots ,f_i\right\}\subset C,1<i\le n_a$ of these subtomograms, we can calculate a SFSC score ${\widehat{\rho }}_{i+1}$ (STAR Methods: Quality Score) of these subtomograms. Using the additive property, ${\widehat{\rho }}_{i+1}$ can be calculated efficiently from ${\widehat{\rho }}_i$ without re-scanning over $\left\{f_1,\dots ,f_i\right\}$. Let $i^{*}=\arg {\max }_i{\widehat{\rho }}_i$, a new candidate pattern can be formed using $\left\{f_1,\dots ,f_i\right\}$. In such way, each pattern in ${\mathit{\text{S}}}^{\mathit{\text{remain}}}$ can be used to generate a new candidate pattern.

Genetic Algorithm

In MPP, the candidate patterns are generated by using k-means clustering and sequential expansion. After MPP iterations, converged distinct patterns of highest SFSC scores are produced. After MPP iterations have converged to a distinct set of patterns, we also applied an optional refinement method to individual patterns to achieve even higher quality. We call such type of pattern mining as Single Pattern Pursuit (SPP). SPP assumes that the input collection of subtomograms is dominated by a single structure. Given a collection of subtomograms and their rigid transforms, we want to select a subset of subtomograms that maximizes the SFSC score defined in Equation 6 in (STAR Methods: Quality Score). Such an optimization-based subtomogram selection method does not require a manually specified cutoff to exclude non-homogeneous subtomograms. The optimization of this score is a nontrivial combinatorial optimization problem. We use a Genetic Algorithm (GA) to perform such an optimization. Although such an approach is computationally intensive, it further improves the quality of a pattern with a small set (normally less than 1000) of subtomograms, usually on a single computer within a couple of hours.

A Genetic Algorithm (GA) is a generic optimization technique that mimics the process of natural selection. Initially, the GA starts with a population of randomly generated candidate solutions. GA is an iterative process and the population of candidate solutions in each iteration is called a generation. In each generation, the fitness of every individual candidate solution is evaluated. The individual candidate solutions are randomly selected from the current generation with a probability that is proportional to the fitness of the solutions. The selected solutions are recombined and randomly mutated to form a new generation of candidate solutions.

In order to speed up the convergence, we follow the popular elitism heuristic (Deb et al., 2002) by keeping, besides a population of n candidate solutions, also a population of n top candidate solutions generated so far in previous iterations, and combine these two populations to generate a new generation of candidate solutions so that the top candidate solutions are carried over from one generation to the next unaltered.

In our implementation, given a set of m subtomograms with fixed rigid transforms, we encode a candidate solution as a binary vector $\mathit{o}\in {\{0,1\}}^{\text{m}}$, which corresponds to a candidate pattern. Each element of o is 1 if the corresponding subtomogram is to be included into the corresponding candidate pattern, and 0 otherwise. Given any candidate solution, we can calculate a SFSC score of the average density of the corresponding selected subtomograms according to Equation 6. Such a score then represents the fitness of the corresponding candidate solution.

Our GA procedure is initiated by a population O⁰ of n randomly generated candidate solutions, and an empty pool $B^{\mathit{0}}=\varnothing$ of top solutions. A particular iteration i > 0 consists of the following steps.

1. Given a generation $O^{i-1}$ of the last iteration i − 1, calculate the SFSC score for each candidate solution in $O^{i-1}$.

2. Use the combined population $C^{i-1}=B^{i-1}\cup O^{i-1}$ to form a generation $O^i$ :

   1. Randomly select a pair P of candidate solutions in $C^{i-1}$.
   2. Perform crossover operation (Figure S1B) followed by mutation operation to generate a pair P’ of new candidate solutions.
   3. Add both candidate solutions P’ into the new population $O^i$.
   4. Repeat the above steps until $|O^i|\ge n$.

3. Combine $O^i\text{and}{B}^{i-1}$ to form a new population of top candidate solutions $B^i$.

The iterative process continues until the best candidate solution in B is unchanged for a fixed number of iterations. This selects the best candidate solution as the final solution.

Given currently aligned subtomograms, and a binary vector that indicates which subtomograms are selected, we can calculate a SFSC score defined in Equations 5 and 6 as in Step 1 of the above process. Then the score can be directly used as fitness that determines how likely a candidate solution in $C^{i-1}$ can be selected for reproduction in Step 2a. Suppose $S=\{\widehat{\rho }({\mathit{o}}_1),\dots ,\widehat{\rho }({\mathit{o}}_{2n})\}$ are SFSC scores of the candidate solutions $\{{\mathit{o}}_1,\dots ,{\mathit{o}}_{2n}\}$ in the combined population $C^{i-1}$. Then the probability of selecting an individual candidate solution o_j is calculated as:

$$P(o_j)=\frac{\widehat{\rho }(o_j)-s^{\mathit{min}}}{\sum _k\left[\widehat{\rho }(o_k)-s^{\mathit{min}}\right]},\forall 1\le j\le 2n$$

where $s^{\mathit{min}}:={\min }_1\widehat{\rho }({\mathit{o}}_{\mathbf{l}}).$

Remarks:

In principle, the GA based subtomogram selection method can also be used as an alternative pattern generation method in the MPP framework. However, because the GA approach is significantly more time consuming compared to k-means clustering and sequential expansion approaches, instead of integrating it into the MPP framework, we use it only for refining selected individual patterns predicted using MPP.

Quality Score

In pattern mining, a measure of quality of the subtomogram average is needed for the optimization process. Following the common practice in cryo-electron microscopy (CEM) and cryo-electron tomography (ECT) fields, we measure the quality of a subprogram average by the level of structural details of the pattern that the average can confidently represent, i.e., the resolution of the average, which is widely used for validating subtomogram averages. Such resolution is often calculated through measuring relative uncertainty or reproducibility. There are two main types of such measures (Liao and Frank, 2010): The first type of measure is the Spatial Signal to Noise Ratio (SSNR ) (Penczek, 2002; Unser et al., 1987), which compares homogeneous structural signal against structural and nonstructural variations. The second type of measure, the Fourier Shell Correlation (FSC) (Saxton and Baumeister, 1982), is a measure of reproducibility. FSC is calculated by randomly splitting the set of subtomograms into two halves and by measuring the consistency (at different scales) between the corresponding two averages from the two halves. FSC has different variants (Liao and Frank, 2010).

We use a SSNR based FSC score as a measure of quality. There are several advantages of using such a combination (compared to calculating FSC from splitting the data into two halves). First, SSNR is directly computed from all subtomograms, and therefore it reduces the underestimation of the resolution due to the sample size limit, and there is no uncertainty introduced by the statistical fluctuation from the random choice of splitting (Liao and Frank, 2010). Second, the measure can be efficiently computed in parallel, enabling high-throughput processing due to its additive property (See below under heading Additive property). Third, SSNR can be easily extended to consider missing wedge effects, which is one of the major distortions in the ECT imaging process. On the other hand, our experience shows that the use of SSNR alone as a quality measure may not be sufficient. It has an undesired property: its tends to emphasize low frequency components because the SSNR measure ranges from zero to infinity, and its value decreases dramatically as the frequency increases. Therefore, it would be beneficial to use a normalized measure like FSC that accounts for more high frequency information. To our knowledge, the subtomogram average quality measure has not been used as objective in any existing template-free subtomogram classification methods.

Formally, we denote a set of n aligned subtomograms as $\left\{f_1,\dots ,f_n\right\}$, their Fourier transform as $\left\{F_1,\dots ,F_n\right\}$ and the corresponding wedge masks as $\left\{M_1,\dots ,M_n\right\}$ (as defined in Equation 3). We adapt the standard SSNR measure to take into account the missing wedge effect and derive a SSNR measure ${\eta }_r$ at frequency r:

$${\eta }_r=\frac{{\int }_{\Vert \xi |-r|\le \mathrm{\Delta }r}\widehat{M}(\xi )|\mu (\xi ){|}^2}{{\int }_{\Vert \xi |-r|\le \mathrm{\Delta }r}{\sigma }^2(\xi )}$$ (Equation 5)

where $\mathrm{\Delta }r=1,\xi \in {ℝ}^3$ is a location in the Fourier space, $\widehat{M}$ is the summation of the missing wedge masks:

$$\widehat{M}(\xi )=\sum _i{M}_i(\xi )$$

$$\mu (\xi )=\frac{\sum _i{M}_i(\xi )F_i(\xi )}{\widehat{M}(\xi )}$$

and

$${\sigma }^2(\xi )=\frac{\sum _i{M}_i(\xi ){|M_i(\xi )F_i(\xi )-\mu (\xi )|}^2}{\widehat{M}(\xi )-1}$$

Given the above calculated SSNR, the FSC ${\rho }_r$ at frequency r can be estimated according to (Frank and Al-Ali, 1975; Liao and Frank, 2010):

$${\rho }_r=\frac{{\eta }_r}{2+{\eta }_r}$$ (Equation 6)

We use the sum of FSC over all frequencies (denoted as SFSC) to score the quality of a subtomogram average:

$$\widehat{\rho }=\sum _r{\rho }_r$$

The higher the $\widehat{\rho }$, the higher is the quality of the corresponding subtomogram average of a pattern.

Additive Property of Quality Score

The calculation of FSC can be easily parallelized due to the following property: ${\eta }_r$ can be calculated from $\widehat{M},\sum _i{M}_i{F}_i\text{and}\sum _i{F}_i{\underset{\_}{F}}_i$ where F_i is the complex conjugate of F_i. All these three quantities are additive for disjoint sets of subtomograms.

Selection of Distinct High-Quality Patterns

In contrast to a typical template-free subtomogram classification method, MPP is a constrained optimization method that improves a selection of distinct high-quality patterns (in terms of SFSC scores, defined in Equation 6) from a pattern library, which contains not only the patterns from the current iteration but also patterns generated in any previous iteration. In such case, the overall quality of selected patterns tends to increase with the advance of iterations until reaching convergence at which MPP can hardly improve the pattern quality.

In order to reduce the chance of selecting redundant patterns from the pattern library, we assume that one subtomogram generally can belong to no more than one selected pattern. In other words, we want the selected patterns to be disjoint in terms of their subtomogram set membership.

We propose a greedy pattern selection process (as summarized in Algorithm below). Such process keeps adding patterns into a collection S from the pattern library L based on several search criteria: 1) high quality patterns, 2) minimal overlap in subtomogram membership, and 3) maximal overall subtomogram coverage. This procedure ensures the selection of a disjoint set of patterns with minimal subtomogram overlap between them (i.e., subtomograms are not shared between patterns). First, all patterns in the library are ranked according to their pattern quality measure. Starting with the highest quality pattern, a pattern is added to the collection S if it has the highest ranked quality among all patterns and with subtomogram member overlap smaller than a certain small threshold t^overlap = 0.01 with all the subtomograms of all already selected patterns part of the pattern collection S. To increase coverage, the process selects as many eligible patterns as possible, until no more eligible pattern can be found in the pattern library L.

Algorithm

Require:

A library L of patterns $p_1,p_2,\dots ,p_{|L|}$ with corresponding subtomogram sets $C_{p1},C_{p2},\dots ,C_{p|L|}$, and with corresponding SFSC scores in order: ${\widehat{\rho }}_{p_1}\ge {\widehat{\rho }}_{p_2}\ge \dots \ge {\widehat{\rho }}_{p_{p|L|}}$, a max overlap ratio $t^{\mathit{\text{overlap}}}$

$$\begin{array}{l}1.\text{S}\leftarrow \varnothing \\ 2.\mathbf{\text{for}}i\leftarrow 1\text{to}|L|\mathbf{\text{do}}\\ 3.A\leftarrow {\cup }_{p\in S}{C}_p\\ 4.\mathbf{\text{if}}|C_{pi}\cap A|\le {\text{t}}^{\text{overlap}}|C_{pi}|\mathbf{\text{then}}\\ 5.S\leftarrow S\cup \{p_i\}\\ 6.\mathbf{\text{return}}S\end{array}$$

Remarks.

The design of the heuristics rule of constraining the overlap of subtomogram memberships between selected patterns is mainly for computational feasibility considerations. Other approaches such constraint based optimization and maximum likelihood may help to further improve pattern mining quality and stability. However, how to combine such probabilistic framework with MPP in a computationally feasible way remains a challenging topic.

Align Averages into Common Frames

After selecting a disjoint set S^sel of high-quality patterns according to Methods: Selection of disjoint high-quality patterns, the corresponding pattern averages in S^sel are aligned into common frames. This procedure helps the dimension reduction to focus more on the structural difference among the averages rather than the variance introduced due to orientation and location differences of patterns with similar structures. Such technique has been used in the align-and-classify frameworks (e.g., Bartesaghi et al., 2008). However, the alignment of all averages into a single common frame is not appropriate for a visual proteomics setting, which contains structures of many different complexes of largely different shape and size. The alignment of two averages of largely different structures may be meaningless and can result in large displacements of one structure to outside the boundary of its subtomogram volume. To overcome this limit, we propose an alignment procedure that only aligns pairs of the structurally most similar averages. The procedure is summarized in Algorithm below:

Algorithm

Require:

A set S₀ of patterns, with subtomogram sets ${\mathit{\text{C}}}_1,{\mathit{\text{C}}}_2,\dots ,{\mathit{\text{C}}}_{|S0|}$, with corresponding subtomogram averages $a_1,a_2,\dots ,a_{|S0|}$, and with corresponding SFSC scores in order: ${\widehat{\rho }}_1\ge {\widehat{\rho }}_2\ge \dots \ge {\widehat{\rho }}_{|S_0|}$. Denote the alignment score and translation between a_i and $a_j\text{as}{r}_{i,j}\text{and}{\mathit{t}}_{i,j}$ respectively.

1. Select and order the alignment scores to the subtomogram average pairs $(i_1,j_1),(i_2,j_2),\dots ,(i_{n^{\mathit{\text{pair}}}},j_{n^{\mathit{\text{pair}}}})$, where $i_1,i_2,\dots ,i_{n^{\mathit{\text{pair}}}}\text{and}{j}_1,j_2,\dots ,j_{n^{\mathit{\text{pair}}}}$ are pattern indexes $\in [1,|S_0|]$, such that $r_{i_1,j_1}\ge r_{i_2,j_2}\ge \dots \ge r_{i_{n^{\mathit{\text{pair}}}},j_{n^{\mathit{\text{pair}}}}},{\Vert {\mathit{t}}_{i_p,j_p}\Vert }_2\le t^{\mathit{\text{translation}}},\forall p,\text{and}{i}_p<j_p,\forall p.$

2. $S^{fixed}\leftarrow Ø$

3. $S^{transformed}\leftarrow Ø$

4. $\mathbf{\text{for}}p\leftarrow 1\text{to}|S_0|\mathbf{\text{do}}$

   • 5.
     $\mathbf{\text{if}}{i}_p\notin S^{transformed}\text{and}{j}_p\notin S^{\mathit{\text{fixed}}}\cup S^{\mathit{\text{transformed}}}\mathbf{\text{then}}$

     • 6.
       Apply a rigid transform of ${\mathit{t}}_{ip.jp}\text{on}{a}_{jp}$
     • 7.
       $S^{fixed}\leftarrow S^{fixed}\cup \{i_{\text{p}}\}$
     • 7.
       $S^{\mathit{\text{transformed}}}\leftarrow S^{\mathit{\text{transformed}}}\cup \{j_p\}$

Identification of Structurally Redundant Patterns

When the true set of structurally distinct patterns is unknown, an intuitive strategy is to over-partition the collection of subtomograms then identify and remove the patterns of redundant structures, so that such redundant patterns will never be selected or processed in future iterations.

In principle, one may intuitively select a single similarity cutoff between the averages to identify structurally redundant patterns. However, in a visual proteomics setting, for different pairs of macromolecular complexes, one has to consider different degrees of image and structural differences as a result of varying coverage (i.e., number of subtomograms that contain a complex) and varying sizes for different complexes. Two high resolution subtomogram averages (based on a large number of subtomograms) may show relatively subtle but true differences. On the other hand, two low resolution subtomogram averages with the same underlying structure may show relatively large but false differences due to fluctuations of noise or misalignments of the subtomograms. Therefore, it would be difficult to properly choose a single similarity cutoff to define structural redundancy for all patterns. To overcome this limit, we determine structural redundancy by measuring the statistical discrimination ability of alignment scores through statistical hypothesis testing. This procedure allows more flexibility in detecting systematic differences between two groups of alignment scores generated by aligning a set of subtomograms against two pattern density averages.

We use a statistical test of consistency between set membership and alignment scores to automatically identify structurally redundant patterns. The design of our method is based on the following intuitions: Given a collection of selected candidate patterns, if a pattern has a distinct subtomogram average compared to other patterns and the average reflects the true underlying structure of the subtomograms of the pattern, we expect that the subtomograms of this pattern should specifically well align (in terms of alignment scores) to the average of the pattern, as compared to their alignment against averages of any other pattern. Otherwise, either the subtomogram average of this pattern does not reveal the underlying true structure, or it cannot be discriminated from the subtomogram average of some other patterns because both averages contain structures that are too similar to be discriminated by the alignment scores. We use such a statistical consistency between subtomogram set membership and alignment as a criterion to detect redundant patterns. This is useful for removing candidate patterns whose averages do not reflect the true underlying structure and candidate patterns of redundant structures (that are already considered by another pattern). With the removal of such patterns, the computational cost of MPP can be significantly reduced.

Formally, we define a pattern $p\in S$ as structurally redundant with respect to another pattern $p^{\prime }\in S$, if it has the following properties: 1) p has a lower SFSC score than p’, and 2) through an appropriate hypothesis testing, the alignment scores between the subtomograms of p and the subtomogram average of p is not significantly higher than the alignment scores between the subtomograms of p and subtomogram average of p’. In such a case, the subtomogram average of p’ is likely to provide a better representation of the underlying structure in the subtomograms of p. Consequently, p should be identified as redundant to p’ and be discarded from further processing.

More specifically, we propose a statistical test procedure to detect redundant patterns, which satisfies the above properties. Suppose at the current iteration, a collection of $S=\{p_1,\dots ,p_{|S|}\}$ of disjoint patterns have been selected according to (STAR Methods: Selection of disjoint high quality patterns) and their corresponding subtomogram sets are denoted as $C_1,C_2,\dots ,C_{|S|}$. Their subtomogram averages are denoted as $a_1,a_2,\dots ,a_{|S|}$. Their corresponding SFSC scores are denoted as ${\widehat{\rho }}_1,{\widehat{\rho }}_2,\dots {\widehat{\rho }}_{|S|}$, and the patterns are ordered such that ${\widehat{\rho }}_1\le {\widehat{\rho }}_2\le \dots \le {\widehat{\rho }}_{|S|}$. Furthermore, let $r_{f,a_i}$ be the alignment score between a subtomogram f and the average a_i. For any two patterns p_i and p_j with i < j, we compare the alignment scores $r_{i,j}=(r_{f,a_i},\forall f\in C_i)\text{and}{r}_{i,j}=(r_{f,a_j},\forall f\in C_i)$ using Wilcoxon signed-rank test (Siegal, 1956), which is a paired difference test. If r_i,i is not significantly higher than r_i,j (at a significance level of 0.01), then the subtomograms in C_i do not align specifically well against a_i compared with against a_j. In addition, since ${\widehat{\rho }}_i\le {\widehat{\rho }}_j$, we identify p_i as structurally redundant with respect to p_j.

Remarks

Like any other statistical tests, our statistical test may fail when the number of subtomograms is small or when there is systematic bias in the alignment scores. It also depends on the discrimination ability of alignment scores.

Target Complex Region Segmentation

Molecular crowding within cellular subvolumes has profound effects on macromolecular interactions (Lučič et al., 2013; Rigort et al., 2012) and makes visual proteomics scale analysis significantly more challenging. A subtomogram extracted from a tomogram of the crowded cell cytoplasm may not only contain the target complex of interest, but also some neighboring structures or structural fragments of other complexes. The existence of neighboring structures and noise in the non-structural background regions inside subtomograms biases their alignments (Xu and Alber, 2013) and other processing steps of MPP. To reduce the influence of noise at the background regions and the influence of neighboring structures on the subtomogram analysis, we propose an automatic method that uses a density map as a reference to segment the region occupied by the target complex, mask out regions occupied by neighboring structures, and partially mask out regions occupied by background noise. In the MPP framework, the reference density map is a subtomogram average of a pattern selected based on the information on pairwise alignments of subtomograms against averages of the collection S^remain of patterns (STAR Methods: MPP Framework). When using a reference as a seed, the method automatically identifies a region that includes the target complex with a margin that follows the shape of the target complex, and excludes the regions occupied by potential neighboring structures. This tool is an optional component of the MPP framework.

The basic idea of the procedure is illustrated in Figure S1C. Without loss of generality, we assume high image intensity of subtomograms corresponding to high electron density. Within a given MPP iteration, suppose the subtomogram f is best aligned with pattern’s average a among all other averages of a collection of patterns S^remain. f is smoothed using a Gaussian smoothing with σ = 2nm.

We first apply level set based segmentation on a to identify structural region $R_a^{\mathit{\text{structure}}}$. This is done according to (STAR Methods: Prefiltering - Structural region segmentation). Once a is segmented, we map the mask of the structured region $R_a^{\mathit{\text{structure}}}$ onto f (Figure S1C-ii). We then calculate the mean intensity values of f inside $R_a^{\mathit{\text{structure}}}$ and outside $R_a^{\mathit{\text{structure}}}$, and denote these two values as c₁ and c₂, respectively. We can then minimize the following model to obtain an optimal level set $c_{{\varphi }_1^{*}}$ and structural region $R_a^{\mathit{\text{structure}}}$ in the similar way as done in (STAR Methods: Prefiltering - Structural region segmentation), except with fixed c₁ and c₂:

$${\varphi }_f^{*}={\text{arg}\mathit{min}}_{\varphi }\mu \int |\nabla H(\varphi )|+\lambda \left[\int {|f-c_1|}^{2}H(\varphi )+\int {|f-c_2|}^2(1-H(\varphi ))\right]$$

We then separate the connected components of $R_f^{\mathit{\text{structure}}}$ into two groups: those that overlap with $R_a^{\mathit{\text{structure}}}$ and those that do not. The first group of connected components are defined as the structural regions of the target complex $R_f^{\mathit{\text{structure}}}$. The second group of connected components are defined as the structural regions of neighboring structures $R_f^{\mathit{\text{structure}}}$. Then we perform Watershed segmentation (Volkmann, 2002) on ${\varphi }_f^{*}$ using $R_f^{\mathit{\text{structure}}}$ and $R_f^{\mathit{\text{neighbor}}}$ as initial seeds to partition the subtomogram into two regions, $R_f^{\mathit{\text{target\_ext}}}$ and $R_f^{\mathit{\text{neighbor\_ext}}}$. The final target complex region mask is defined as $R_f^{\mathit{target\_ext}}\cap \{{\varphi }^{\star }>t\max ({\varphi }^{\star })\}$, where t is a negative valued threshold parameter to control the amount of included margin. Such mask follows the shape of the target complex and excludes neighboring structures (Figure S1C-iii).

Remarks

• The existence of neighboring structures besides the target complex in a subtomogram f affects its alignment against a reference a (Xu and Alber, 2013). However, a is only used as an initial seed. Therefore, even if the alignment is not accurate or the density map a does not have the same structure as the underlying structure of f, as long as after alignment $R_a^{\mathit{\text{structure}}}$ overlaps with the true target complex region of f and does not overlap with the neighboring structure region of f, we may still expect a successful segmentation.

• As illustrated in Figure S1C, even if target complex regions of f are apparently disconnected, as long as the target complex regions of f have overlap with $R_a^{\mathit{\text{structure}}}$, the disconnected subunits will still be included in the final segmentation.

• The reason for applying the watershed segmentation on ${\varphi }_f^{*}$ instead of f is because ${\varphi }_f^{*}$ is derived from the distance transform (Kimmel et al., 1996), which represents the signed distances of voxel locations to the structural regions. ${\varphi }_f^{*}$ is usually much smoother than the noisy f. In addition, ${\varphi }_f^{*}$ is a signed distance function that monotonically decreases when the distance to the segment increases. By contrast, due to the suppression of low frequency components in the CTF during the imaging process, f has both above and below background intensity around the surface regions of structures. Therefore, the segmented boundary from the watershed segmentation on ${\varphi }_f^{*}$ would be much more regular than those from watershed segmentation directly on f.

• Due to its complexity, the segmentation of the target complex region is a very challenging problem when applied on a proteome scale. Many factors may lead to the failure of our reference guided segmentation approach. For example, the high degree of distortions in a subtomogram or high degree of misalignments of subtomograms against the reference may lead to under or over segmentation. If a subtomogram is highly crowded, some neighboring structures may appear to be connected with the target complex in the subtomogram, which makes the segmentation unable to exclude the neighboring structure region.

• In order to avoid false segmentation of a subtomogram average when it is very noisy, we assume that $R_a^{\mathit{\text{structure}}}$ has less overlap with the boundary of the subvolume than the non-structural region ${(R_a^{\mathit{\text{structure}}})}^C$ does, and use this assumption to discard bad segmentations.

Noise Reduction of Averages

Sometimes, repeated iterations of alignment and averaging give a structure containing high resolution features resulting from the alignment of noise against itself in a reinforcing manner (Briggs, 2013). Such phenomenon is called over-alignment. In such case, it is beneficial to have an optional step to reduce high frequency noise.

Gaussian smoothing is a commonly used noise reduction technique. Within the class of linear transformations, a Gaussian kernel minimizes the chance of creating new structures in the transformation from a finer to a coarser scale (Sporring et al., 2013). We apply Gaussian smoothing to an average to reduce influence of noise, which is equivalent to applying a Gaussian envelope function in Fourier space. Such an envelope function has the form of:

$$f_{a,c}(x)=a\exp \left(-\frac{x^2}{2C^2}\right)$$

Since our procedure includes estimation of SSNR and FSC, the parameters a and c can be adaptively determined from the estimated FSC through least-squares fitting using the Levenberg-Marquardt algorithm.

Simulation of Realistic Tomograms

For a reliable assessment of the method, simulated tomograms and subtomograms are generated by simulating the actual tomographic image reconstruction process, allowing the inclusion of noise, tomographic distortions due to missing wedge, and electron optical factors such as Contrast Transfer Function (CTF) and Modulation Transfer Function (MTF). We follow a previously applied methodology for realistic simulation of the tomographic image formation processes (Beck et al., 2009; Förster et al., 2008; Nickell et al., 2005; Xu et al., 2011).

The electron optical density of a macromolecule is proportional to its electrostatic potential and the density map can be calculated from the atomic structure by applying a low pass filter at a given resolution. An initial density map is then used as a sample for simulating electron micrograph images at different tilt angles. In ECT the sample is tilted in small increments around a single-axis. At each tilt angle, a simulated micrograph is generated from the sample. In the real imaging process, the tilt angle range is limited. Therefore, our data contain a wedge-shaped region in Fourier space for which no structure factors have been measured (i.e., the missing wedge effect). The missing wedge effect leads to distortions of the density maps. These distortions depend on the structure of the object and its orientation with respect to the direction of the tilt-axis. To generate realistic micrographs, noise is added to the images according to a given SNR level, defined as the ratio between the variances of the signal and noise (Förster et al., 2008). Moreover, the CTF and MTF models distortions from interactions between electrons and the specimen and distortions due to the image detector (Nickell et al., 2005) in a linear approximation. therefore, the resulting image is convoluted with a CTF. Any negative contrast values beyond the first zero of the CTF are eliminated. Typical acquisition parameters that were also used during actual experimental measurements were used: voxel size = 1 nm, the spherical aberration = 2.2 mm, the defocus value = −15 μm, the voltage = 300 kV, the MTF corresponded to a realistic electron detector, defined as $\mathrm{sinc}(\pi \omega /2)$ where ω is the fraction of the Nyquist frequency. Finally, we use a backprojection algorithm (Nickell et al., 2005) to generate a tomogram or a subtomogram from the individual 2D micrographs that were generated at the various tilt angles (Beck et al., 2009; Xu et al., 2011).

Individual Simulated Subtomograms

We randomly selected a collection of PDB structures of 22 macromolecular complexes (Table S1A) of distinct shapes and sizes. The structures were converted into density maps using the pdb2vol program in the situs package (Wriggers et al., 1999) at 1 nm spacing and band pass filtered at 4 nm. The density maps served as input for realistically simulating the cryo electron imaging process with a noise-factor-SNR of 0.005 and tilt angle range ±60°. For each complex, 1000 subtomograms were generated, each containing a randomly rotated and translated complex. We then selected a random copy number (uniformly sampled from 1 to 1000) of simulated subtomograms for each complex. In total, we collected 11,230 subtomograms as an input data set for MPP (Table S1A).

Crowded Mixture of Macromolecular Complexes

Low Resolution.

A density map is generated for each complex (the collection of 22 complexes used in individual simulated subtomograms) at 1 nm voxel spacing and band pass filter the map at 4 nm. We apply level set based segmentation (STAR Methods: Target complex region segmentation) on the density map of each complex. For each segment, we calculate a minimum bounding sphere, which is the smallest sphere that encloses the segment. We randomly place non-overlapping bounding spheres of 9,864 instances of the 22 complexes (with various abundance per type) into a volume V of size 600 × 600 × 200 nm³. Overlap between bounding spheres is prevented by applying molecular dynamics simulations in combination with an excluded volume constraints for all bounding spheres (Pei et al., 2016; Russel et al., 2012). Finally, we embed the density maps of each randomly oriented complex into the 00b0V according to locations of their corresponding bounding spheres. The combined large density map of all complexes had a crowding level (in terms of volume occupancy) of 15.2%, which is within the volume occupancy range (from 5% to 44%) that have been observed in cell cytoplasm (Guigas et al., 2007). The density map of the crowded protein complexes is used to simulate a tomogram with noise-factor-SNR of 50 and tilt angle range ±60° (Figure 3A-Right Panel).

High Resolution.

Nowadays experimental tomograms with much smaller voxel spacing can be captured by current generation of transmission electron microscopes. Similar to low resolution tomograms, 10 different tomograms are simulated, each with approximately 2,500 instances of 22 complexes (with variable abundance) and volume of 400 × 400 × 200 nm³ (Figure 3C right panel). The crowding level of these tomograms is 15% on average. The tomograms are simulated at noise-factor-SNR of 50, tilt angle range ±60°, defocus value = −7 μm, voxel size = 0.4 nm and the spherical aberration = 2.2 mm.

Note

• In description of simulation parameters above we used terms noise-factor-SNR and effective-SNR. Noise-factor-SNR quantifies the level of noise that needs to be added to the projection images to reach a certain effective-SNR for the simulated tomograms. When simulating the tomographic imaging process, noise is added to the voxels of the projection images following a procedure as described in (Beck et al., 2009; Förster et al., 2008; Nickell et al., 2005; Xu et al., 2011), by adding noise values sampled from a Gaussian distribution $\mathrm{\mu }=0\text{and}{\sigma }_{\mathit{\text{noise}}}^2=\frac{{\sigma }_{\mathit{\text{signal}}}^2}{\mathit{\text{noise}}-\mathit{\text{factor}}-SNR}$, where $\mathrm{\mu }\text{and}{\sigma }_{\mathit{\text{noise}}}^2$ are mean and variance of the Gaussian noise distribution and ${\sigma }_{\mathit{\text{signal}}}^2$ is the variance of the signal in the projection image (i.e., the density values of voxels in the projection image from the actual macromolecular complex) (Förster et al., 2008). As mentioned above, the value of the noise-factor-SNR does not represent the final effective signal-to-noise ratio of the tomogram. It is used to calculate how much noise needs to be added to the projection image to simulate tomograms for a given effective-SNR value. To reach effective-SNR levels that are similar to those observed in experimental tomograms, noise-factor-SNR can vary for different tomograms based on the crowding level of the tomogram. The larger the empty space in the projection image, the higher the noise-factor-SNR need to be so that the signal can still be identified in noisy image. The effective-SNR is estimated from aligned subtomograms following a procedure by (Frank and Al-Ali, 1975). Therefore, the effective-SNR value can be estimated from either experimental or simulated tomograms. It is calculated using a method as described by Frank and Al-Ali, 1975: $\mathit{\text{effective}}-SNR=\frac{\sum _{p=1}^N\frac{C_p}{1-C_p}}{N}$ where N is the number of pairs of aligned subtomograms (we chose N = 10,000 for analysis in this paper) and C_p is the pearson-correlation between subtomograms in pair p. For the simulation of individual subtomograms, a noise-factor-SNR of 0.005 and for the simulation of crowded tomograms a noise-factor-SNR of 50 leads to an effective-SNR for the aligned subtomograms that is similar to the effective-SNR calculated from our experimental tomograms (STAR Methods: Estimation of effective-SNR).

• During simulation of tomograms we add CTF to the projection images to add the distortions due to phase flipping and missing frequencies. There are two ways to add CTF, with or without gradient in the defocus. For simulated subtomograms of individual complexes, the tomogram size is approximately 50 nm × 50 nm × 50 nm which is too small to consider gradient defocus. Also, for crowded environments the size of the simulated tomograms is smaller compared to typical experimental tomograms. For smaller tomograms the defocus gradient may have a smaller impact in comparison to larger tomograms, as the range of defocus between farthest points on the simulated tomograms and at the highest tilt angle of 60 degree will be approximately −6.75 μm to −7.25 μm (if we consider −7μm at 0 degree). So, for the purpose of simplifying the simulation process we used an average added CTF at defocus of −7 μm. We agree that the addition of CTF with gradient defocus will have some impact on how the complexes appear in the reconstructed tomogram. As gradient defocus has been used to improve the resolution of subtomogram-averaged structures in experimental tomograms, we anticipate that the effect of using gradient defocus will not significantly affect the detection of coarse-grain patterns via MPP.

Experimental Tomogram Acquisition

A. longum

Cells were frozen and imaged as described previously (Tocheva et al., 2014). Data were collected from −65° to 65°, with an angular step of 1°, a total dose of 200e⁻/Ų, a defocus value of −10μm, and a pixel size of 1.2 nm on a 300 keV FEG G2 Polara transmission electron microscope (TEM) equipped with a lens-coupled 4k-by-4k Ultracam (Gatan, CA) and an energy filter. Data were collected automatically with the UCSF tomography package (Zheng et al., 2007) and reconstructed using the IMOD software package (Kremer et al., 1996) (Figure 4A-Left Panel).

H. gracilis

Cells were grown 48 hr in ATCC #233 Broth (ATCC, Manassas, VA) to OD₆₀₀ = 0.1. 10 nm colloidal gold (Sigma-Aldrich, St. Louis, MO) pretreated with bovine serum albumin was added to the cells to serve as fiducial markers during tomogram reconstruction. 3 μl of the resulting sample was pipetted onto a freshly glow-discharged Quantifoil copper R2/2 200 EM grid (Quantifoil Micro Tools GmbH, Jena, Germany) and plunge-frozen in a liquid ethane propane mixture using an FEI Vitrobot mark-III (FEI Company, Hillsboro, OR). The frozen grid was then imaged in an FEI Tecnai G2 Polara 300 keV field emission transmission electron microscope (FEI Company, Hillsboro, OR) equipped with a Gatan energy filter (Gatan, Pleasanton, CA) and a Gatan K2 Summit direct detector (Gatan, Pleasanton, CA) at the California Institute of Technology. Energy-filtered tilt series of images of the cell were collected automatically from −60° to 60° at 1° intervals using the UCSF Tomography data collection software (Zheng et al., 2007) with total dosage of $75{\text{e}}^{-}/{\text{Å}}^2$, a defocus of −15 μm and a pixel size of 4.9Å. The images were aligned and subsequently reconstructed into a tomogram by weighted back-projection method using the IMOD software package (Kremer et al., 1996) (Figure 4A-Middle Panel).

B. bacteriovorus

HD100 cells were grown as described previously (Lambert and Sockett, 2008) on E. coli S17–1 prey cells in Ca-HEPES buffer at 29°C until most prey cells were cleared from the culture. 10 nm colloidal gold (Sigma-Aldrich, St. Louis, MO) pretreated with bovine serum albumin was added to the cells to serve as fiducial markers during tomogram reconstruction. 3 μl of the resulting sample was pipetted onto a freshly glow-discharged Quantifoil copper R2/2 200 EM grid (Quantifoil Micro Tools GmbH, Jena, Germany) and plunge-frozen in a liquid ethane propane mixture using an FEI Vitrobot mark-III (FEI Company, Hillsboro, OR). The frozen grid was then imaged in an FEI Titan Krios 300 keV field emission transmission electron microscope (FEI Company, Hillsboro, OR) equipped with a Gatan energy filter (Gatan, Pleasanton, CA) and a Gatan K2 Summit direct detector (Gatan, Pleasanton, CA) at the Howard Hughes Medical Institute Janelia Research Campus. Energy- filtered tilt series of images of the cell were collected automatically from −65° to 65° at 1 intervals using the UCSF Tomography data collection software (Zheng et al., 2007) with total dosage of $100{\text{e}}^{-}/{\text{A}}^2$, a defocus of −8μm and a pixel size of 4.2Å. The images were aligned and subsequently reconstructed into a tomogram by weighted back-projection method using the IMOD software package (Kremer et al., 1996).

Pattern Mining

Individual Simulated Subtomograms

The MPP procedure was run on 11,230 simulated subtomograms with initial $k^{\mathit{k\_means\_fix}}=40$. The contingency plot and generated patterns are shown in Figure 1 in the main text.

Crowded Mixture of Macromolecular Complexes

After extracting the 4,901 subtomograms, we apply the MPP procedure to the extracted subtomograms using similar settings as above. During the MPP iterations, we applied our reference guided segmentation (STAR Methods: Target complex region segmentation) to reduce the influence of crowdedness. Table S2 and Figure 2 summarizes the resulting patterns.

Experimental Tomograms

We first perform level set based pose normalization (STAR Methods: Pre-filtering). Then we perform k-means clustering on pose normalized subtomograms to separate the subtomograms into 100 clusters (Tables S4A, S4C, and S4E respectively for each experimental tomogram). Then based on the shape of the cluster centers, we manually select and combine a number of clusters into groups whose averages are similar (of similar sizes). We then applied MPP to subtomograms in each group, with random initial orientations, and an initial $k^{\mathit{k\_means\_fix}}=10$. Pattern 4 among A. longum patterns had a structure similar to the GroEL complex (Figure 4C). For this pattern, we applied our GA based refinement of subtomogram membership (STAR Methods: Candidate pattern generation - Genetic algorithm). The resulting predicted patterns are summarized in Tables S4B, S4D, and S4F respectively for A. longum, H. gracilis and B. bacteriovorus.

Validation Procedure

To measure the performance of MPP, we calculate several quantities for comparing the prediction with ground truth. The first quantity is the membership consistency in terms of the amount of subtomogram membership overlap between a predicted pattern and the true set of a complex. Such membership consistency is represented as a contingency table. We order the columns and rows in the contingency table by identifying best matching using the Hungarian algorithm (Kuhn, 1955). In an ideal case, when properly ordered, such a table would have non-zero entries in the diagonal cells, and zeros elsewhere.

Second, we calculate the False Positives (FP) and False Negatives (FN) to measure the number of instances (i.e., subtomograms) that MPP cannot correctly identify. Suppose, by checking the diagonal entry of a rearranged contingency table, the best matching between complexes and patterns is determined. Suppose a complex c matches a pattern p. The FP of p is the number of instances of pattern p that do not belong to c, although they are predicted as instances of c (because they are in p and p matches c). Given FP, further calculate the False Discovery Rate (FDR) as FP divided by the total number of instances of p. The FDR indicates the level of impurity of p. The FN of c is the number of true instances of c that are not included into p. Given FN, we also calculate the Miss Rate or False Negative Rate (FNR) as FN divided by the total number of instances in c. Note that if p correctly predicted the structure of c, in principle the missed instances (which are counted as false negatives) can be later detected through a template search.

Third, we calculate the structural consistency between the average density map of a pattern and the true density map of the target complex. The consistency is measured in terms of FSC with 0.5 cutoff, which reflects the minimum scale that the predicted and true structures are consistently determined by the cutoff.

Estimation of Effective-SNR

Pattern 4 from Simulated Tomograms

Low Resolution.

We sampled 10,000 pairs of aligned subtomograms of pattern 4, which are dominated by the GroEL complex (PDB: 1KP8). For each pair of subtomograms, we calculate the Pearson correlation of their image intensity, then estimate a corresponding SNR according to (Frank and Al-Ali, 1975): $\mathit{\text{effective-SNR}}=\mathit{\text{effective}}-SNR=\frac{\sum _{p=1}^N\frac{c_p}{1-c_p}}{N}$, where N is the number of pairs of aligned subtomograms and c_p is the pearson-correlation between subtomograms in pair p. Such a procedure gives an SNR estimate of 0.29 ± 0.13 over all subtomograms pairs, which is of similar range to the one estimated from the A. longum cellular tomogram.

High Resolution.

To calculate the effective-SNR in this case, we simulated the tomograms again with same simulation parameters, but instead of orienting complexes randomly, all the complexes were kept in same orientation. This would remove any alignment bias in the SNR estimation. Then we picked the subtomograms for each complex using the ground truth and calculated the effective-SNR using the same method as mentioned in above subsection. Sampling 10,000 pairs of subtomograms (already aligned as in same orientation) and found that the effective-SNR is within the range of 0.002 to 0.031 for different complexes.

Pattern 4 from A. longum

We also estimated the effective-SNR level of subtomograms of pattern 4 using the same procedure as described above. Such procedure gives an SNR estimate of 0.24 ± 0.10 over all subtomograms pairs.

KEY RESOURCE TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and Virus Strains
Acetonema longum strain APO-1	Tocheva et al., 2014	DSM 6540
Bdellovibrio bacteriovorus	Lambert and Sockett, 2008	HD100
Hylemonella gracilis	Canale-Parola et al., 1966	ATCC 19624
Deposited Data
Yeast 20S proteasome in complex with spirolactacystin	Groll et al., 2008	PDB: 3DY4
Recombinant mouse L chain ferritin	Granier et al., 2003	PDB: 1LB3
RECA Hexamer Model	Yu and Egelman, 1997	PDB: 2REC
GroEL-KMgATP	Wang and Boisvert, 2003	PDB: 1KP8
Yeast 20S Proteasome in complex with proteasome activator PA26 from Trypanosome Brucei	Whitby et al, 2000	PDB: 1FNT
Propionyl-CoA carboxylase, beta subunit (TM0716) from Thermotoga Maritima	Joint Center for Structural Genomics (unpublished)	PDB: 1VRG
Glutamine Synthetase	Yamashita et al, 1989	PDB: 2GLS
Human carboxypeptidase A4 in complex with human latexin	Pallares et al, 2005	PDB: 2BO9
Bacterial ribosome from Escherichia coli	Schuwirth et al, 2005	PDB: 2AWB (4V4Q)
M.tuberculosis Acr1(Hsp 16.3) fitted with wheat sHSP dimer	Kennaway et al, 2005	PDB: 2BYU
Octameric Enolase from Streptococcus pneumoniae	Ehinger et al, 2004	PDB: 1W6T
Carbamoyl Phosphate Synthetase complexes with ATP analog AMPPNP	Thoden et al, 1999	PDB: 1BXR
Free aspartyl-tRNA synthetase from Escherichia coli	Rees et al, 2000	PDB: 1EQR
ClpP	Bewley et al, 2006	PDB: 1YG6
Ornithine Carbamoyltransferase from Pyrococcus Furiosus	Villeret et al, 1998	PDB: 1A1S
E. coli Aminopeptidase A (PepA)	Sträter et al, 1999	PDB: 1GYT
Transaldolase (EC 2.2.1.2) (TM0295) from Thermotoga maritima	Joint Center for Structural Genomics (unpublished)	PDB: 1VPX
Acetobacter aceti citrate synthase complexed with oxaloacetate and carboxymethyldethia coenzyme A (CMX)	Francois et al, 2006	PDB: 2H12
Rotary Motor in ATP Synthase from Yeast Mitochondria	Stock et al, 1999	PDB: 1QO1
Recombinant Thermus aquaticus RNA polymerase	Kuznedelov et al, 2006	PDB: 2GHO
3-octaprenyl-4-hydroxybenzoate decarboxylase (UbiD) from Escherichia coli	Northeast Structural Genomics Consortium (unpublished)	PDB: 2IDB
E. Coli Aapartate Transcarbamoylase P268A mutant in the R-state in the presence of N-phosphonacetyl-L-aspartate	Jin et al, 2000	PDB: 1F1B
Software and Algorithms
Multi Pattern Pursuit (MPP)	This work	http://web.cmb.usc.edu/people/alber/Software/mpp/
Integrative Modeling Platform (IMP)	Russel et al., 2012	https://integrativemodeling.org
Octave	Octave version 4.2.0	https://www.gnu.org/software/octave/
IMOD	Kremer et al., 1996	https://bio3d.colorado.edu/imod/
Chimera	Pettersen et al., 2004	https://www.cgl.ucsf.edu/chimera/
Python	Python version 2.7	https://python.org
UCSF Tomography	Zheng et al., 2007	http://www.msg.ucsf.edu/Tomography/tomography_main.html
2D/3D Image segmentation toolbox	Zhang, 2013	http://www.mathworks.com/matlabcentral/fileexchange/24998-2d-3d-image-segmentation-toolbox
TOM software toolbox	Nickell et al., 2005	https://www.biochem.mpg.de/tom
Situs Package	Wriggers et al., 1999	https://situs.biomachina.org/

Highlights.

• New framework for structural pattern mining in electron cryotomograms

• Automated and template-free discovery of complexes

• Complexes such as GroEL and ribosome detected in experimental tomograms