Early prediction of mortality risk among patients with severe COVID-19, using machine learning

Abstract

Background

Coronavirus disease 2019 (COVID-19), caused by severe acute respiratory syndrome coronavirus 2 infection, has been spreading globally. We aimed to develop a clinical model to predict the outcome of patients with severe COVID-19 infection early.

Methods

Demographic, clinical and first laboratory findings after admission of 183 patients with severe COVID-19 infection (115 survivors and 68 non-survivors from the Sino-French New City Branch of Tongji Hospital, Wuhan) were used to develop the predictive models. Machine learning approaches were used to select the features and predict the patients’ outcomes. The area under the receiver operating characteristic curve (AUROC) was applied to compare the models’ performance. A total of 64 with severe COVID-19 infection from the Optical Valley Branch of Tongji Hospital, Wuhan, were used to externally validate the final predictive model.

Results

The baseline characteristics and laboratory tests were significantly different between the survivors and non-survivors. Four variables (age, high-sensitivity C-reactive protein level, lymphocyte count and d-dimer level) were selected by all five models. Given the similar performance among the models, the logistic regression model was selected as the final predictive model because of its simplicity and interpretability. The AUROCs of the external validation sets were 0.881. The sensitivity and specificity were 0.839 and 0.794 for the validation set, when using a probability of death of 50% as the cutoff. Risk score based on the selected variables can be used to assess the mortality risk. The predictive model is available at [https://phenomics.fudan.edu.cn/risk_scores/].

Conclusions

Age, high-sensitivity C-reactive protein level, lymphocyte count and d-dimer level of COVID-19 patients at admission are informative for the patients’ outcomes.

Key Messages

• Age, high-sensitivity C-reactive protein level, lymphocyte count and d-dimer level were informative for the patients’ outcomes.

• Our models are helpful for the clinicians to identify the patients who wae at high risk of death, and interventions can be adopted at an earlier stage to reduce the mortality risk of these patients.

Introduction

The severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) emerged in December 2019, has since spread to nearly 200 countries and territories and had infected nearly 7 million people by the end of May 2020.¹ Approximately 400 000 people had died from coronavirus disease 2019 (COVID-19) worldwide.¹ According to a World Health Organization (WHO) report, the crude fatality rate of COVID-19 varies from country to country. As of 31 March 2020, the highest fatality rate was observed in Italy (nearly 11%), followed by Spain (nearly 8%) and Iran (nearly 6%). The fatality rate is also heterogeneous within a country.² In China, the highest rate was found in Wuhan (nearly 5%).^3–5 In most other provinces, the fatality rate was < 1%.

Demographic, clinical and laboratory features are significantly different between survivors and non-survivors.^4,5 For instance, the non-survivors are older than survivors. Dyspnoea, chest tightness and disorder of consciousness are more common in patients who die than in those who recover. Concentrations of alanine aminotransferase, aspartate aminotransferase, creatinine, creatine kinase, lactate dehydrogenase, cardiac troponin I, N-terminal pro-brain natriuretic peptide and d-dimer are markedly higher in non-survivors than in survivors.^4,6,7 Ascertaining the key factors that contribute to the patients’ outcomes is instrumental for identifying patients at high risk and is critical for patient management, possibly reducing the mortality risk and fatality rate. However, these multilevel data may confuse clinicians with regard to which features indeed impact on COVID-19 patients’ outcomes. In this study, we aimed to develop a clinical model to predict the mortality risk of patients with severe COVID-19 infection, based on demographic, clinical and the first laboratory test data after admission.

Methods

Study participants and covariate collection

Patients who had pneumonia confirmed by chest imaging, and had an ≤94% of oxygen saturation while they were breathing ambient air or a ratio of the partial pressure of oxygen to the fraction of inspired oxygen at or below 300 mm Hg, were defined as patients with severe infection.^8,9 In total, 256 patients with severe laboratory-confirmed COVID-19 infection (126 survivors and 130 non-survivors) admitted to the Sino-French New City Branch of Tongji Hospital, Wuhan, between 28 January 2020 and 11 March 2020, were included. Tongji Hospital was urgently rebuilt and has been assigned by the Chinese government as a designated hospital for severely or critically ill patients with COVID-19.⁴ We collected the demographic (e.g. age and sex), clinical [e.g. fever or not and computed tomography (CT) imaging features] and the first laboratory data after admission (e.g. the high-sensitivity C-reactive protein [hsCRP] level) from the patient’s medical records (Supplementary Figure S1 and Supplementary Table S1, available as Supplementary data at IJE online). The values of biochemistry indexes tested more than 3 days after admission were excluded even if they were part of the first test. For values that were left- or right-truncated (e.g. d-dimer >21 µg/mL), we used the values at the truncated point as the surrogates (e.g. using 21 µg/mL for those with d-dimer level >21 µg/mL). As shown in Supplementary Figure S2, available as Supplementary data at IJE online, patients who had >10% missing values, stayed in the hospital <7 days, were afflicted by a severe disease before admission (e.g. cancer, aplastic anaemia or uraemia), were unconscious at admission or were directly admitted to the intensive care unit (ICU) were excluded. Herein, we supposed that patients who were stayed in hospital <7 days, were unconscious at admission, or were directly admitted to the ICU, were critically ill and were at very high risk of death. Finally, 183 patients were included to construct the predictive models; among them, 115 recovered and were discharged and 68 were died from COVID-19. This study was approved by the National Health Commission of China and Ethics Commission of Tongji Hospital (TJ-IRB20200402). Written informed consent was waived by the Ethics Commission of the designated hospital for emerging infectious diseases.¹⁰

Model development

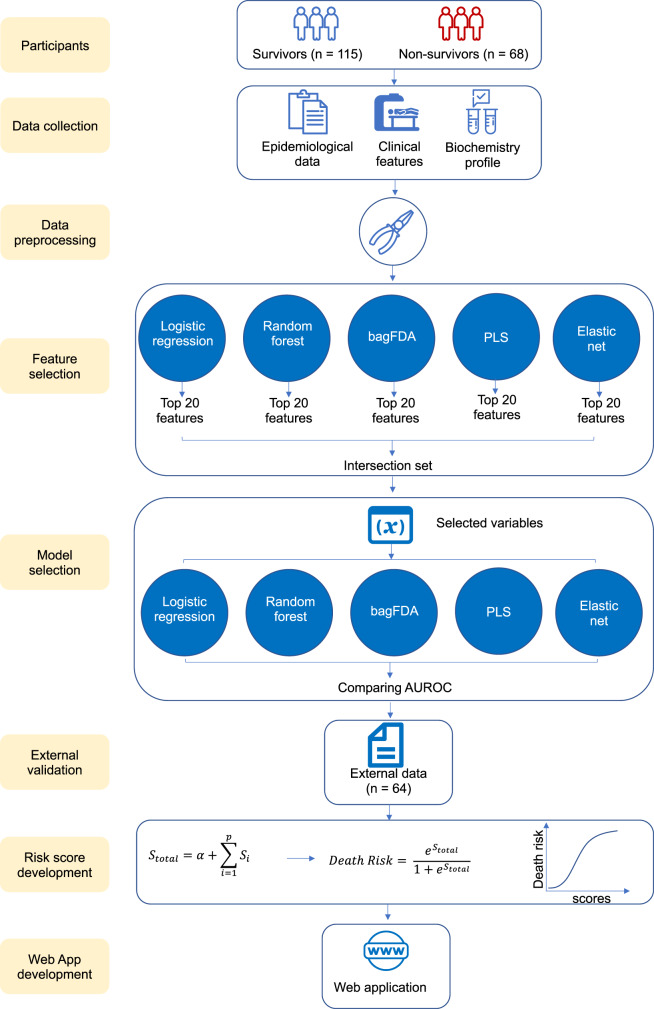
The development of the predictive model consisted of three main stages: (i) data preprocessing; (ii) variable selection and model evaluation; and (iii) external validation (Figure 1).

Figure 1.

The study flow chart. bagFDA, bagged flexible discriminant analysis; PLS, partial least squares; AUROC, area under the receiver operating characteristic curve

Data preprocessing

Covariates with >30% missing data were excluded. For pairs of highly correlated variables (correlation coefficient >0.9), we removed the variable with the higher missing rate. Variables with zero or near-zero variance were also excluded. A rule of thumb for detecting predictors with zero or near-zero variance is as follows: (i) the number of unique values divided by the sample size is small (set to 10% in our study); and (ii) the ratio of the frequency of the most prevalent value to the frequency of the second most prevalent value is large (set to 20 here). Non-normally distributed continuous variables were transformed using a Box Cox transformation. Missing values were imputed using bagging trees. Briefly, bagging, short for bootstrap aggregation, is a general approach that uses bootstrapping in conjunction with any regression or classification model to construct an ensemble. Each model in the ensemble is then used to generate a prediction for a new sample and these predictions are averaged to give the bagged model’s prediction. For each variable requiring imputation, a bagged tree is created where the outcome is the variable of interest and the predictors are any other variables.¹¹ In total, 51 covariates were finally included.

Variable selection and model evaluation

Considering the potential linear and curvilinear relationships between the predictors and the outcome (i.e. survive or die), we initially attempted 10 different machine learning methods to fit the data and selected, in terms of the model performance and property, five of them [logistic regression, partial least squares (PLS) regression, elastic net (EN) model, random forest and bagged flexible discriminant analysis (FDA)] to report (Supplementary Table S2, available as Supplementary data at IJE online). The algorithm of logistic regression has been detailed elsewhere.¹²

PLS is an approach to maximally summarize predictor space variability with the consideration of response. This means that PLS finds components that maximally summarize the variation of the predictors while simultaneously requiring these components to have maximum correlation with the response.¹³ In other words, PLS can be viewed as a supervised procedure of dimension reduction.

The EN is a regularized method that linearly combines the penalties of the LASSO (least absolute shrinkage and selection operator) and Ridge regressions and is widely used to select features.¹⁴ This model combines the two types of penalties:

$${\mathit{SSE}}_{\mathit{Enet}}=\sum _{i=1}^n{(y_i-\widehat{y_i})}^2+{\lambda }_1\sum _{j=1}^P{\beta }_j^2+{\lambda }_2\sum _{j=1}^P|{\beta }_j|$$

where SSE denotes the sum-of-squared error of the EN model, and ${\lambda }_1$and ${\lambda }_2$ denote the penalty of Ridge regression and LASSO regression, respectively. The advantage of this model is that enables effective regularization via the ridge-type penalty with the feature selection quality of the LASSO penalty.¹⁵

Random forest is a supervised learning algorithm. The ‘forest’ suggests an ensemble of decision trees, usually trained with the ‘bagging’ method. The basic algorithm of random forest can be summarized as the follows.

1. Draw a bootstrap sample Z of size N from the training data.

2. Grow a random-forest tree T_b to the bootstrapped data, by recursively repeating the following steps, until the minimum node size n_min is reached:

   1. select m variables at random from the p predictors;
   2. pick the best variable among the m;
   3. split the node into two daughter nodes.

3. Output the ensemble of trees.¹⁶ As with bagging, each tree in the forest casts a vote for the classification of a new sample, and the proportion of votes in each class across the ensemble is the predicted probability vector.¹⁵

Flexible discriminant analysis is a classification model based on a mixture of linear regression models, which uses optimal scoring to transform the response variable so that the data are in a better form for linear separation, and multiple adaptive regression splines to generate the discriminant surface.¹⁷Ten-fold cross validation and the areas under the receiver operating characteristic curves (AUROCs) were used to measure the models’ performance. The performance of the models based on the full data with the optimal tuning parameters are shown in Supplementary Table S2.

For logistic regression, we used stepwise backward to select the variables with the Akaike Information Criterion (AIC) values as the criterion. The variable importance was assessed using the absolute value of the t statistic. For PLS regression, the variable importance measure here was based on the weighted sums of the absolute regression coefficients. The weights were a function of the reduction in the sums of squares across the number of PLS components and were computed separately for each outcome. Therefore, the contribution of a coefficient was weighted proportionally to the reduction in the sums of squares. For the elastic net model, the selected variables were those of coefficients that did not shrink to 0. For the random forest model, the prediction accuracy for the out-of-bag portion of the data was recorded for each tree. Then, the same procedure was performed after permuting each predictor variable. The difference between the two accuracies was then averaged across all the trees and normalized by the standard error.¹⁸ For the bagged FDA model, a series of cutoffs were applied to the predictor data to predict the class. The AUROC, sensitivity and specificity were computed for each cutoff. The trapezoidal rule was used to compute the AUROC, which was used as the measure of variable importance.¹⁵

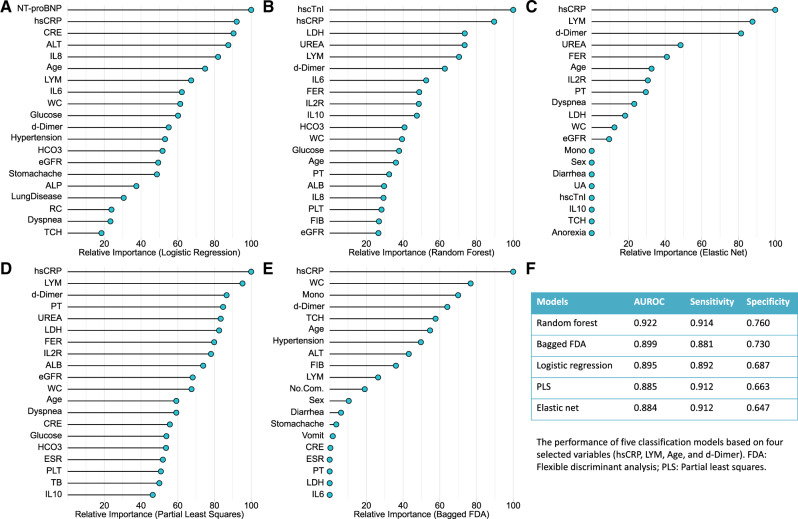
The top 20 most important variables selected by the five models are shown in Figure 2A-E. We chose the intersection set of these variables. Four variables were finally selected (age, hsCRP, lymphocyte count and d-dimer). The five models were refitted using these four variables. The AUROC, sensitivity and specificity, obtained from 10-fold cross validation (CV), were used to evaluate all the alternative models’ performance. Briefly, in the process of 10-fold CV, the samples were randomly partitioned into 10 sets of roughly equal size. The model was fitted using all samples except the first fold, which was defined as the hold-out sample and was used to estimate the model’s performance. This procedure was then repeated nine times and a total of 10 estimates of model’s performance (i.e. AUROC) were obtained. Finally, the 10 re-sampled estimates of performance were summarized (usually with the mean and standard error) and used to understand the relationship between the tuning parameters and model utility.¹⁵

Figure 2.

The top 20 important variables selected by five machine learning models (A-E) and the model performance based on the selected variables (F). NT-proBNP, N-terminal pro-brain natriuretic peptide; hsCRP, high-sensitivity C-reactive protein; CRE, creatinine; ALT, alanine aminotransferase; IL8, interleukin 8; LYM, lymphocyte count; IL6, interleukin 6; WC, white cell count; eGFR, estimated glomerular filtration rate; ALP, alkaline phosphatase; RC, red cell count; TCH, total cholesterol; FIB, fibrinogen; PLT, platelet count; TB, total bilirubin; ALB, albumin; PT, prothrombin time; IL10, interleukin 10; IL2R, interleukin-2 receptor; FER, ferritin; LDH, lactate dehydrogenase; hscTnI, high-sensitivity cardiac troponin I; Mono, monocyte count; UA, uric acid; ESR, erythrocyte sedimentation rate; No.Com., number of basic conditions

External validation

In total, 64 patients with severe laboratory-confirmed COVID-19 infection (33 survivors and 31 non-survivors) admitted to the Optical Valley Branch of Tongji Hospital, Wuhan, were included as the external validation set. We used the selected predictive model to predict the probability of death in these patients. The AUROC, sensitivity and specificity were used to evaluate the model performance.

Cost curves of the predictive model

Cost curve is a graphical technique for visualizing the performance (expected cost) of 2-class classifiers over a range of possible class distributions and cutoffs. Herein, we defined the cost of false-negative was three times more than that of false-positives. The cutoffs predicting the death were ranged from 0.1 to 0.9. The false-negative rates and false-positive rates were calculated by the confusion matrix of the predictive model using different cutoffs. We then visualized the curves between the normalized true positive rates and the normalized expected costs.¹⁹ The normalized true positive rates can be calculated as:

$$P_{+}c\mathit{ost}=\frac{P_{+}{\mathit{Cost}}_{01}}{P_{+}{\mathit{Cost}}_{01}+(1-P_{+}){\mathit{Cost}}_{10}}$$

and the normalized expected costs can be calculated as:

$${\begin{array}{c}\\ C\mathit{ost}\end{array}}_{\mathit{norm}}=\frac{\mathit{FNR}\times { P}_{+}{\mathit{Cost}}_{01}+\mathit{FPR}\times (1-P_{+}){\mathit{Cost}}_{10}}{P_{+}{\mathit{Cost}}_{01}+(1-P_{+}){\mathit{Cost}}_{10}},$$

where the $P_{+}$denotes the true-positive rate, ${\mathit{Cost}}_{01}$denotes the cost of false-negatives, ${\mathit{Cost}}_{10}$denotes the cost of false-positive, FNR denotes the false-negative rate and FPR denotes the false-positive rate.¹⁹

Statistical analysis

Continuous and categorical variables are presented as means (standard deviations) [or medians (interquartile range)] and frequencies (percentages), respectively. We used Student’s t tests, Mann-Whitney U tests, χ² tests and Fisher’s exact tests, where appropriate, to compare the differences between survivors and non-survivors. All analyses were implemented in R 3.6.1 (R Foundation for Statistical Computing, Vienna, Austria). The model development and validation were implemented using the caret package (version 6.0–85).²⁰

Results

Demographics and baseline characteristics of survivors and non-survivors

The covariates included in the predictive models are shown in Table 1. In general, most characteristics were significantly different between the survivors and non-survivors. The non-survivors were more likely to be male and older than the survivors. The proportions of basic conditions (e.g. diabetes and hypertension) were comparable between these two samples. For symptoms at disease onset, the non-survivors reported loss of appetite, dyspnoea and productive cough more often than the survivors. The laboratory test indexes were also significantly different between the deceased patients and those who recovered. For example, the white cell count was higher in the non-survivors than the survivors. Conversely, the lymphocyte count was nearly twice as high in the survivors than in the non-survivors. The non-survivors had more liver and kidney function abnormalities. Specifically, the concentrations of liver enzymes, urea and creatinine were markedly higher in the non-survivors, whereas the albumin level and estimated glomerular filtration rate were lower in this sample. The levels of all the inflammatory factors were higher in the non-survivors than in the survivors. The circulating levels of hsCRP and d-dimer were more than 6-fold and nearly 3-fold higher in non-survivors than in survivors, respectively.

Table 1.

The baseline characteristics and laboratory findings at admission included in the predictive models

	Survivors (n = 115)	Non-survivors (n = 68)	P-value
Baseline characteristics
Sex
Male	57 (49.57)	50 (73.53)	0.002
Female	58 (50.43)	18 (26.47)
Age	60.54 ± 13.19	68.44 ± 9.94	<0.001
Diabetes
Yes	21 (18.26)	14 (20.59)	0.848
No	94 (81.74)	54 (79.41)
Hypertension
Yes	43 (37.39)	30 (44.12)	0.458
No	72 (62.61)	38 (55.88)
Lung disease
Yes	5 (4.35)	10 (14.71)	0.030
No	109 (94.78)	58 (85.29)
No. of underlying conditions
<1	75 (65.22)	41 (60.29)	0.861
≥1	40 (34.78)	27 (39.71)
Signs and symptoms at disease onset
Diarrhoea
Yes	38 (33.04)	29 (42.65)	0.253
No	77 (66.96)	39 (57.35)
Stomach ache
Yes	16 (13.91)	12 (17.65)	0.642
No	99 (86.09)	56 (82.35)
Vomiting
Yes	20 (17.39)	12 (17.65)	1.000
No	95 (82.61)	56 (82.35)
Anorexia
Yes	22 (19.13)	32 (47.06)	0.019
No	82 (71.30)	36 (52.94)
Fever
Yes	101 (87.83)	60 (88.24)	1.000
No	14 (12.17)	8 (11.76)
Dyspnoea
Yes	36 (31.30)	49 (72.06)	<0.001
No	79 (68.70)	19 (27.94)
Bilateral infection (chest CT image)
Yes	78 (67.83)	53 (77.94)	0.142
No	0 (0.00)	1 (1.47)
First SARS-Cov2 nuclei acid test
Positive	72 (62.61)	42 (61.76)	0.659
Negative	20 (17.39)	15 (22.06)
Cough
No cough	23 (20.00)	11 (16.18)	<0.001
Dry cough	68 (59.13)	22 (32.35)
Productive cough	24 (20.87)	35 (51.47)
Vital signs on admission
Count of white cells, ×109/L	5.43 (4.30, 7.00)	8.01 (5.61, 11.36)	<0.001
Count of lymphocytes, ×109/L	1.13 (0.77, 1.45)	0.56 (0.42, 0.75)	<0.001
Count of monocytes, ×109/L	0.42 (0.33, 0.57)	0.35 (0.22, 0.57)	0.025
Count of red cells, ×1012/L	4.10 (3.69, 4.48)	4.26 (3.84, 4.64)	0.084
Count of platelets, ×109/L	206 (160, 267)	165.5 (122.5, 226.0)	0.001
Glucose, mmol/L	5.73 (5.17, 7.00)	7.44 (6.56, 9.43)	<0.001
Erythrocyte sedimentation rate, mm/h	28 (12, 53)	47.0 (25.5, 66.5)	0.003
Alanine aminotransferase, U/L	23 (14, 43)	30.0 (19.5, 41.0)	0.074
Albumin, g/L	35.20 (31.95, 39.35)	31.4 (28.15, 34.10)	<0.001
Total bilirubin, µmol/L	9.30 (7.25, 12.40)	13.05 (9.70, 19.00)	<0.001
Alkaline phosphatase, U/L	66 (53, 84)	81.5 (57.5, 107.5)	0.001
γ-Glutamyl transpeptidase, U/L	27.00 (18.00, 72.50)	45.5 (26.0, 82.0)	0.005
Total cholesterol, mmol/L	3.77 (3.22, 4.51)	3.41 (2.97, 4.00)	0.029
Lactate dehydrogenase, U/L	264.5 (211.0, 340.0)	480.5 (418.0, 600.0)	<0.001
Urea, mmol/L	4.3 (3.5, 5.6)	7.95 (5.75, 10.00)	<0.001
Creatinine, µmol/L	67 (58, 84)	85.5 (69.0, 100.0)	<0.001
Uric acid, µmol/L	251 (196, 333)	239.5 (181.0, 336.5)	0.645
Estimated glomerular filtration rate, ml/min/1.73	93.35 (80.30, 102.80)	77.85 (59.70, 90.85)	<0.001
High sensitivity C-reactive protein, mg/L	14.1 (2.8, 59.5)	87.3 (62.0, 155.6)	<0.001
Potassium, mmol/L	4.17 (3.91, 4.55)	4.42 (4.00, 5.06)	0.011
Sodium, mmol/L	140.30 (137.25, 141.90)	138.55 (136.05, 142.45)	0.255
Chlorine, mmol/L	101.80 (99.15, 103.55)	100.05 (97.70, 102.90)	0.055
Corrected calcium, mmol/L	2.37 (2.28, 2.42)	2.39 (2.36, 2.48)	0.002
Bicarbonate, mmol/L	23.90 (22.35, 25.45)	21.5 (19.2, 24.5)	<0.001
Ferritin, µg/L	578.15 (319.70, 1125.20)	1508.3 (1054.0, 2456.7)	<0.001
Interleukin 2 receptor, U/ml	574.5 (379.5, 928.0)	1137.5 (890.0, 1833.0)	<0.001
Interleukin 6, pg/ml	7.49 (2.14, 27.57)	68.00 (18.66, 137.35)	<0.001
Interleukin 8, pg/ml	11.85 (6.95, 23.55)	26.6 (16.0, 70.7)	<0.001
Interleukin 10, pg/ml	5.00 (5.00, 7.85)	10.5 (6.4, 16.8)	<0.001
Tumour necrosis factor α, pg/ml	8.7 (6.8, 11.4)	11.1 (8.0, 15.9)	0.004
Fibrinogen, g/L	4.50 ± 1.44	5.38 ± 2.04	0.005
Prothrombin time	13.8 (13.2, 14.5)	15.6 (14.0, 17.2)	<0.001
d-dimer, µg/ml FEU	0.94 (0.40, 1.44)	2.70 (1.21, 21.00)	<0.001
High-sensitivity cardiac troponin I, pg/ml	4.5 (2.0, 8.8)	24.40 (9.35, 103.70)	<0.001
N-terminal pro-brain natriuretic peptide	98 (5, 1877)	798 (176, 70000)	<0.001
Interval,a (day)	11 (9, 21)	10.5 (7.0, 15.0)	0.038

Categorical variables are shown in frequency (%). Continuous variables following normal or approximately normal distribution are shown in mean ± standard deviation. Continuous variables not following normal distribution are shown in median (interquartile range).

FEU, fibrinogen equivalent units.

^aThe interval between date of first symptom and date of admission.

Model development and external validation

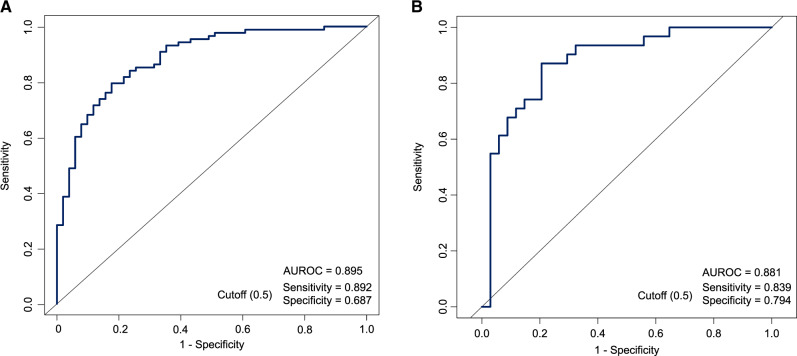
The process of model development is detailed in the Methods section and in Figure 1. The AUROC obtained from 10-fold cross-validation was used to compare the performance of five selected predictive models (Figure 2F). Considering the minor differences between the AUROC of the logistic regression model (0.895) and that of the random forest (0.922) and bagged FDA (0.899), we selected the logistic regression model as the final model because of its simplicity and high interpretability. The AUROCs of all the alternative models based on the full set, reduced set and selected variables are shown in Supplementary Table S3, available as Supplementary data at IJE online. The model performance significantly increased when using the four variables in combination (Figure 3A). The AUROC of the external validation set was 0.881, with a sensitivity of 0.839 and specificity of 0.794 for predicting death when using a probability of death of 50% as the cutoff (Figure 3B).

Figure 3.

The area under the receiver operating characteristic curve (AUROC) of the logistic regression model based on selected variables in the derivation set (A) and the external validation set (B)

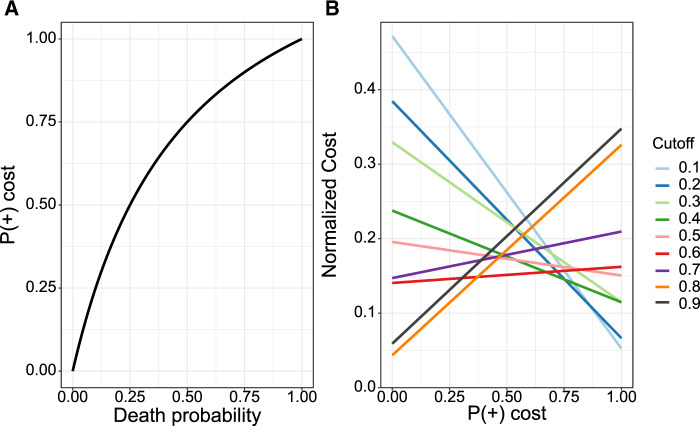
Cost curves of the predictive model

As shown in Figure 4A, the death probability was curvilinearly associated with the normalized $P_{+}$. Figure 4B shows the cost curves with the cutoff ranging from 0.1 to 0.9. When the death probability is <10% (i.e. normalized $P_{+}$ <0.25), the lowest expected cost was observed using cutoff of 0.8. When the death probability increases to 25% (i.e. normalized $P_{+}$ = 0.5), the lowest expected cost was observed with cutoff of 0.6. When the death probability reaches at nearly 50% (i.e. normalized $P_{+}$around at 0.75), the lowest expected cost was observed with cutoff of 0.2.

Figure 4.

The relationship between probability of death and the normalized probability (A) and the cost curves of the predictive models using different cutoffs (B)

Development of risk scores and a web application

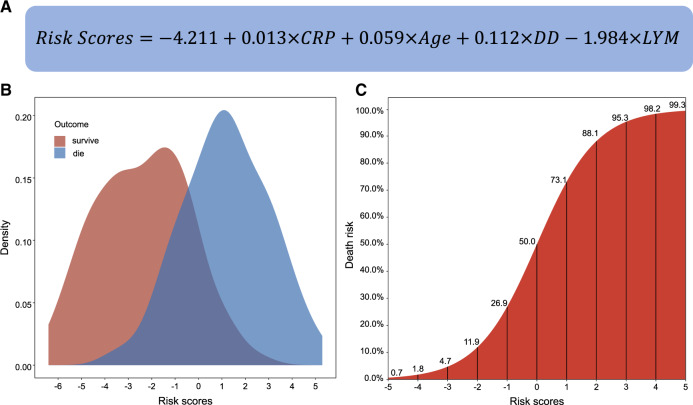
The contributions of the selected variables were assessed using the logistic regression model. The regression coefficients were calculated as the weight of each predictor. The risk score was therefore calculated as:

$$\mathit{Risk} \mathit{score}=\alpha +\sum _{i=1}^4{\beta }_i{x}_i$$

where$\alpha$, $x_i$, and ${\beta }_i$ denote the regression intercept, observed value and coefficients, respectively, of the i^th predictor (Figure 5A). The probability of death can be calculated via:

$$\frac{e^{\mathit{Risk} \mathit{Score}}}{1+e^{\mathit{Risk} \mathit{Score}}}.$$

Figure 5.

The formula to calculate the risk scores (A) and their distributions among survivors and non-survivors (B) and the corresponding probability of death (C)

Figure 5B shows that the risk scores in both the survivors and non-survivors are approximately normally distributed. An S-shaped correlation pattern between the risk scores and probability of death is shown in Figure 5C. The mortality risk exceeds 50% when the risk score is >0. We also calibrated the results of the logistic regression model based on deciles of predicted risk between observations and predictions (Supplementary Figure S3, available as Supplementary data at IJE online). Calibration was acceptable for both derivation and validation sets (Hosmer-Lemeshow statistic χ² = 0.55 and 1.26, respectively; P-values = 0.455 and 0.189, respectively).

To facilitate the application of our predictive model, we also developed an accompanying web tool [https://phenomics.fudan.edu.cn/risk_scores/]. Readers can freely access this website and input the values of hsCRP, age, lymphocyte count and d-dimer to predict the mortality risk and its 95% confidence interval for a COVID-19 patient.

Discussion

COVID-19 is currently a worldwide pandemic.^21–23 The number of laboratory-confirmed patients as well as the number of related deaths are continuously increasing. The fatality rate might further increase along with the increasing number of infected people, because even the most advanced health care systems are likely to be overwhelmed.^24,25 The Chinese Centers for Disease Control and Prevention recently reported that out of more than 70 000 confirmed cases, most of them were classified as mild or moderate, and approximately 20% were classified as severe or critical.²⁶ Even if we assume that the fatality rate is 10% in severe and critically ill cases,⁴ the number of COVID-19 induced deaths is considerable because of the enormous number of infected patients. Identifying the patients at high risk of death is critical for patient management and reducing the fatality rate. In this clinical prediction modelling study, we took full advantage of the multifaceted data of COVID-19 patients at admission, to predict their outcomes. Four variables (i.e. age, hsCRP, d-dimer and lymphocyte count) were selected and used to fit a logistic regression model. The predictive performance of our model was acceptable in both the derivation set and the external validation set. We also developed a web tool to implement our predictive model. Clinicians can use this web tool to predict the mortality risk of COVID-19 patients early. For those patients with a relatively higher probability of death (e.g. >40%), more interventions could be adopted at an earlier stage by clinicians.

In a recent study, older age, d-dimer levels greater than 1 μg/mL and a higher sequential organ failure assessment (SOFA) score at admission were reported to be associated with higher odds of in-hospital death.³ The fatality rate was highly heterogeneous among patients of different ages. For instance, the overall COVID-19 case fatality rate in China was estimated as 0.32% in those aged <60 years and substantially increased to 6.4% in those aged ≥60 years.²⁷ Among those aged 80 years and older, this rate was as high as 13.4%.²⁷ Likewise in Italy, the fatality rate increased from 0.3% among patients aged 30–39 years to 20.2% among those aged ≥80 years.²⁸ In 2019, approximately 23% of the Italian population was aged 65 years or older. This percentage may explain, in part, Italy’s higher case-fatality rate compared with that of other countries.²⁸ In our study, age was selected as a key factor in all the predictive models. The age-dependent deterioration in immunological competence (e.g. B cell and T cell deficiencies), often referred to as ‘immunosenescence’, and the excess production of type 2 cytokines could lead to a deficiency in the control of viral replication and more prolonged pro-inflammatory responses, potentially leading to a poor outcome.^29,30 In this study, the deceased patients had persistent and more severe lymphopenia compared with recovered patients, and the lymphocyte count was selected and incorporated into the predictive model. Defects in function of lymphocytes are age-dependent and are associated with inflammation levels.^31,32

Additionally hsCRP, the most commonly used inflammatory biomarker in the clinic, was selected for our predictive models. Patients with higher levels of hsCRP at admission were deemed to have higher levels of inflammation. In our study, we found that the hsCRP level was more than six times higher in the non-survivors than in the survivors. Although the levels of other inflammatory biomarkers, such as ferritin and the erythrocyte sedimentation rate, were also elevated in the non-survivors, they were not selected and incorporated in the predictive model. This omission might be explained by the higher missing rates of these covariates and their high correlation with hsCRP. Coagulation disorder, characterized by an elevated prothrombin time and d-dimer level, was also frequently observed among COVID-19 patients.^33,34 In our study, the prothrombin time and d-dimer level were significantly higher in the non-survivors than in the survivors. These higher values suggest an increased risk of disseminated intravascular coagulation, which was one of the frequently diagnosed complications among the later stages of COVID-19 illness.^4,33,35

Our study has a number of strengths. First, to ensure the robustness of our predictive model, we enforced strict inclusion and exclusion criteria on the included participants and study data. Second, our results are comparable to others and our predictive model is competitive when compared with previously reported models.^36,37 For example, Liang et al. developed a predicting model based on LASSO and reported that the mean AUROC was 0.88.³⁷ Third, we used advanced modelling strategies to select features and to construct the predictive models. The final model is simple (it included only four variables) and highly interpretable (the model is a linear model, and the effects of the predictors are reflected by the regression coefficients). Moreover, we externally validated the final predictive model. Fourth, we developed an accompanying web tool to facilitate the application of our predictive model by clinicians.

Our study also has limitations. First, the predictive models were constructed based on a relatively small sample size; the interpretation of our findings might be limited. Second, due to the retrospective study design, not all the laboratory tests were performed in all the patients. Some of them might be deleted in the data preprocessing procedure and their roles might be underestimated in predicting patients’ outcomes. Third, patients were sometimes transferred from other hospitals to the two branches of Tongji hospitals, although we excluded patients who did not meet the inclusion criteria. The values of the laboratory tests might be biased by previous antiviral treatment in these patients. Finally, the patients in the derivation set and the validation set were from Tongji Hospital, which is one of the hospitals with a high level of medical care in China. Some critically ill patients who recovered here might die in other hospitals with suboptimal or typical levels of medical care. The cutoff for predicting death should be <50% (e.g. defining patients who have a >30% probability of death as high-risk patients) in these settings. Additionally, there was no rigorous definition for patients with severe COVID-19 infection in our study because of the disease emergency and limited medical resources at the early outbreak of COVID-19 in Wuhan.

In summary, using available clinical data, we developed a robust machine learning model to predict the outcome of COVID-19 patients early. Our model and the accompanying web application are of importance for clinicians to identify patients at high risk of death, and are therefore critical for the prevention and control of COVID-19.

Supplementary Data

Supplementary data are available at IJE online.

Funding

This work was supported by the National Natural Science Foundation of China (grant number: 91846302, 81772170); the National Key Research and Development Program of China (grant numbers: 2017YFC0907000, 2017YFC0907500, 2019YFC1315804); Key Basic Research Grants from the Science and Technology Commission of Shanghai Municipality (grant number: 16JC1400500); Shanghai Municipal Science and Technology Major Project (grant number: 2017SHZDZX01); and the Natural Science Foundation of Hubei (grant no. 2019CFB657).

Author Contributions

Z.L., T.Z., X.C. and C.H. conceptualized the study design. C.H., Q.W., S.L., X.T., X.L. and Y.S. collected the data. Z.L., Y.J., X.Z., K.X. and O.S. performed the statistical analysis. Z.L., C.H., Y.J., X.Z., O.S., K.Y. and X.C. wrote the manuscript. All authors provided critical revisions of the draft and approved the submitted draft.

Conflict of Interest

No author has a competing interest to declare.