HUMAN-MACHINE COLLABORATION FOR MEDICAL IMAGE SEGMENTATION

Abstract

Image segmentation is a ubiquitous step in almost any medical image study. Deep learning-based approaches achieve state-of-the-art in the majority of image segmentation benchmarks. However, end-to-end training of such models requires sufficient annotation. In this paper, we propose a method based on conditional Generative Adversarial Network (cGAN) to address segmentation in semi-supervised setup and in a human-in-the-loop fashion. More specifically, we use the generator in the GAN to synthesize segmentations on unlabeled data and use the discriminator to identify unreliable slices for which expert annotation is required. The quantitative results on a conventional standard benchmark show that our method is comparable with the state-of-the-art fully supervised methods in slice-level evaluation, despite of requiring far less annotated data.

1. INTRODUCTION

Image segmentation, notably semantic segmentation that aims at assigning a class label to each pixel in the image, is one of the main applications in medical image processing. In this regard, deep learning techniques lately have achieved exceptional results in this domain, while constantly pushing the limits of what is possible. The recent advances can be attributed to improvements to algorithms and model architectures along with ever increasing computational power, and availability of big data. However, the big data assumption, which is key for deep learning applications, is at the same time the limiting factor. For many supervised learning approaches, particular in the medical domain, it is often too expensive or even impossible to acquire large amounts of high quality annotations in order to learn a deep learning model at sufficient accuracy. In such cases, semi-supervised learning is a viable solution. In this setting, a large dataset of images is available, however, pixel-level labels only for a fraction of the data. Therefore, semi-supervised and self-supervised learning can be very beneficial in cases where data annotation is immensely difficult and costly, which is often the case in the medical domain [1,2].

Among the semi-supervised learning approaches, one of the most prominent solutions proposed in literature is based on an iterative, Multiple Instance Learning (MIL) framework. In this context, an initial model is trained on the small supervised subset of the data. This model is then used to predict the segmentation for the large unsupervised subset, which is treated as pseudo ground truth in the next training iteration. However, the reliability of the predicted pseudo ground truth is subject to quality fluctuations, depending largely on the labeled subset. Therefore, one of the drawbacks of MIL frameworks is their proneness to process drift, which usually results in many false positives in the training dataset. Furthermore, it has been shown that the performance of simple baselines under semi-supervised setup droops dramatically, when a large amount of unlabeled data contains examples with significant distribution mismatch [3]. To alleviate this problem, we propose a training protocol based on the human-machine collaborative learning paradigm [4,5]. The main idea is to automatically select a subset of more reliable predictions and actively collect annotations for the samples with associated unreliable pseudo ground truth (out-of-distribution samples). This is conducted in a human-in-the-loop fashion, such that the model can be re-trained with more accurate examples, avoiding the risk of drift. The proposed approach involves estimating the uncertainty of the predictions, for which we propose the use of the adversarial discriminator in a GAN. Specifically, we use a cGAN to train G and D using supervised data. On the one hand, G learns how to generate segmentations by conditioning on images. On the other hand, the discriminator D is used for plausibility purposes, assessing the uncertainty of the segmentations with respect to the conditioned image. The intuition behind using GANs is their intrinsic potential to capture the data distribution and uncertainty estimation [6,7]. It has been shown that the discriminator is useful to measure the quality of cross-modal generation tasks [8–10] as well as detecting the outlier samples [11–13]. Since discriminator is tailored to detect out-of-distribution samples and therefore inherently associates uncertainty with the loss.

Related work:

There is a wealth of literature on semantic segmentation, but here we only discuss the most related ones to our work, and refer the reader to the recent surveys by [14]. Pathak et al. [15] propose a weakly supervised semantic segmentation algorithm subject to linear constraints on the output space. Pathak et al. [16] use multiple instance learning (MIL) to generate latent segmentation label maps for supervised training. Wang et al. [17] propose image-specific fine-tuning in order to make a deep neural net adaptive to each specific test image. Gorriz et al. [18] propose an active learning framework with Monte Carlo sampling to model the pixel-wise uncertainty. Ronneberger et al. [19] propose ”U-Net”, a network connecting opposed layers that in particular is used for semantic segmentation. Attracted by their success in the medical image domain, we also used this kind of generator in our GAN framework. Most related to our paper is the work by Luc et al. [20] and Souly et al. [21]. Like us, they propose to use GANs for semantic segmentation. The former propose to use GANs for semantic segmentation through correcting higher-order inconsistencies, and the latter for improved semi-supervised semantic segmentation. Our efforts, however, differ in some substantial ways. First, we propose to directly use an adversarial discriminator for uncertainty modeling in an end-to-end fashion. Second, we augment samples by collecting annotations for low-quality predictions in interaction with a user.

Contributions:

The contributions of the proposed paper are two-fold: (i) We introduce an iterative human-machine collaborative algorithm which uses a GAN framework to apply semi-supervised learning in a human in the loop fashion. (ii) To best of our knowledge, it is the first time that the adversarial discriminators are used to estimate the uncertainty of a prediction. Our study opens up avenues for exploiting new in-expensive interactive solutions to achieve a performance gain in medical image segmentation and other disciplines.

2. PROPOSED FRAMEWORK

Semi-Supervised Conditional GAN:

Recently, GANs were introduced as a method for training generative models [22]. It consists of two adversarial agents that compete with each other during a Minimax game until reaching a Nash equilibrium at convergence of the training phase. Specifically, it decomposes into two main components: a generative model G trying to produce fake data resembling real data and a second agent, a discriminative model D that learns whether a segmentation S_j is consistent with the training dataset.

cGANs [23] constitute an extension of the standard GAN, where the input of the generator as well as discriminator are further tied to a conditional variable. In the following, we assume the conditional variable to be an image $I_j\in \mathcal{I}$ and the target variable a segmentation $S_j\in \mathcal{S}$. Here $\mathcal{I}$ and $\mathcal{S}$ denote the image space and segmentation space, respectively. Thus, G seeks to learn a mapping $\mathcal{I}\to \mathcal{S}$. In contrast, $D:(\mathcal{I},\mathcal{S})\to [0,1]$ tries to distinguish between original samples and those generated by G. In the following we denote the training set consisting of n labeled samples as $\left[I_{lab},S_{lab}\right]={\left\{\left(I_j,S_j\right)\right\}}_{j=1}^n$. With slight abuse of the notation, the cGAN parameters are obtained by optimization of the loss function $\mathcal{L}(.)$,

$$\mathcal{L}\left(D,G\mid \left[I_{\text{lab}},S_{\text{lab}}\right]\right)=\sum _{(I,S)\in \left[I_{\text{lab}},S_{\text{lab}}\right]}[\text{log}D(I,S)]+\sum _{I\in I_{\text{lab}}}{\mathbb{E}}_z[\text{log}(1-D(I,G(z,I)))],$$ (1)

where I_lab and S_lab denote the set of labeled images and segmentation maps, respectively.

In the semi-supervised setting, there exists an additional set of training data consisting of m samples for which no ground truth labels exist, which is denoted by $I_{unl}={\left\{I_j\right\}}_{j=n+1}^{n+m}$. In order to obtain a fully labeled set, G can be employed to produce pseudo ground truth $\tilde{S}=\{{\tilde{S}}_j=G\left(I_j\right):\forall I_j\in I_{unl}\}$, yielding $\left[I_{unl},\tilde{S}\right]={\left\{\left(I_j,{\tilde{S}}_j\right)\right\}}_{j=n+1}^{n+m}$.

Interactive Conditional GAN:

The prediction in the semi-supervised setting is not always reliable and subject to noise. Essentially, pseudo ground truth generated from images that are very different from the annotated data distribution, e.g. out-of-distribution samples, expectedly have high uncertainty. However, estimating to what degree a sample is in-distribution or out-of-distribution is not straightforward.

Our method handles two issues simultaneously: (1) absence of annotation for the unlabeled data, (2) finding the optimal query to annotate. We view segmentation maps of the unlabeled data as latent variable and propose to integrate it out. For the optimal query given a budget K, we propose to solve the following optimization:

$$\underset{G,\alpha }{\text{max}}\underset{D}{\text{min}}\mathcal{L}\left(D,G\mid \left[I_{\text{lab }},S_{\text{lab }}\right]\right)+\sum _{I\in I_{\text{unl }}}{\alpha }_I{\mathbb{E}}_{S~q(S)}[\text{log}D(I,S)],$$ (2)

subject to: 0 ≤ α_I ≤ 1, ${\sum }_{I\in I_{\text{unl }}}{\alpha }_I\le K$, where $\mathcal{L}\left(D,G\mid \left[I_{\text{lab}},S_{\text{lab}}\right]\right)$ is the cGAN over labeled data as in Eq. 1. q(S) is the approximate posterior for the latent segmentation mask, and α_I is a soft selector for the unlabeled image I in the set of unlabeled images (i.e., I ∈ Iunl). Since each α_I is a selector for the unlabeled data to be annotated, K specifies the budget. Note that the second term in Eq. 1 is not a function of S, hence it does not show up in the Eq. 2. Also, we provided the set of selectors to the generator meaning that G can select images to be labeled. Furthermore, if we assume q(S) = δ(S*), where S* is the Maximum A Posterior for S, one can easily find a closed form solution for α_I selectors. Specifically, the generator finds the instances with maximum values of D up to K (top K easy cases), whereas the difficult cases are requested to be annotated by the expert.

Human-Machine Collaborative Learning with GAN:

The proposed approach leverages conditional GAN (cGAN) for facilitating the human-machine collaboration for segmentation. To that end, the generator G is trained to produce accurate label maps corresponding to the conditioned image, while the discriminator D attempts to recognize whether a given segmentation is in accordance with the input image. What is more, D can be used to estimate model uncertainty for unseen images. Specifically, D is used for ranking the predicted segmentations referred to as pseudo ground truth, such that annotations querying is restricted to low-confidence (difficult cases) items. Thus expert annotations are obtained in an active learning fashion for high uncertainty samples only, therefore incurring minimal cost.

3. EXPERIMENTS

Experimental setup and dataset:

For the evaluation, we used the data of the HVSMR 2016 challenge [24]. The dataset consists of 10 3D volumes of cardiovascular magnetic resonance images along with annotations of the ventricular Myocardium and blood pool. To simplify the experiments, the ground truth segmentations are used to simulate the user interaction. In our experiments we employed a GAN implementation as proposed in [25]. The generator network is a “U-Net” with skip connections, and for the discriminator a PatchGAN [26] network is utilized.

Discriminator scores analysis:

As discussed in Sec. 2, the discriminator scores are used to rank the segments predicted by G. In order to study the importance of discriminator scores, we designed a set of experiments. First, an initial model (base) is trained using only a single volume (single patient) of supervised data. Next, this model is used to predict the labels of the semi-supervised set (the excluded volumes from the training). Then the predicted segments are ranked based on the obtained score of D. This is followed by incremental addition of samples from the ranked list to the portion of data, and the calculation of an accumulated average dice score for each portion. The result is presented in Fig. 2, which clearly suggests a correlation between the quality of the predictions (represented by dice score values) and the obtained scores of D. In other words, this observation shows that the high-ranked predicted segmentations contain information that can be used for training a new adversarial net. To ensure consistency between the scores of D and dice scores, we conducted an agreement study, finding that the Pearson correlation is strong and significant (r = 0.98, p-value < 0.001) as shown in figure 2.

Fig. 2:

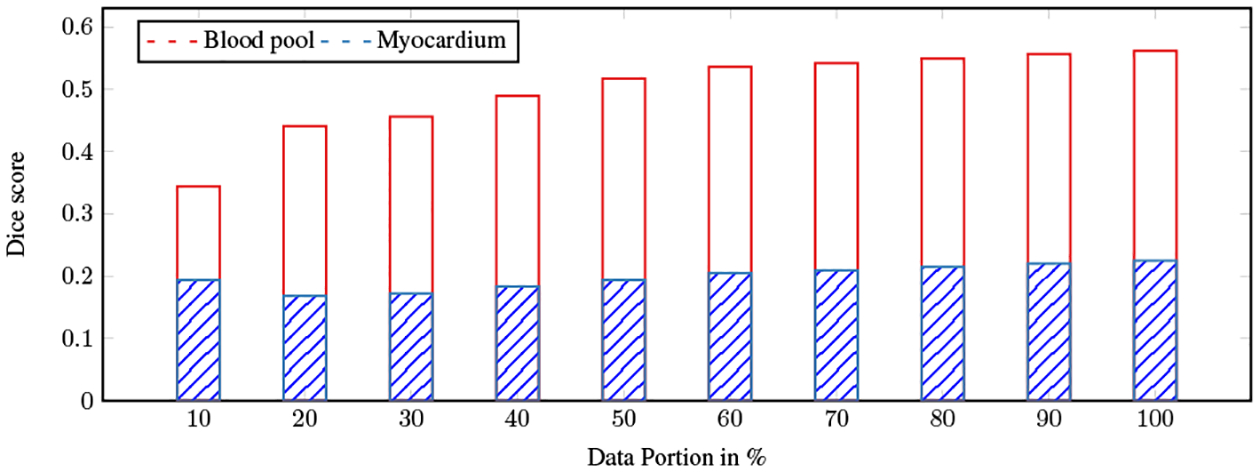
The average dice score of the different partitions: Samples are first sorted by the scores of D in ascending order. The average dice score is then computed for each partition.

Analysis of cGAN performance:

In this experiments we show the effect of varying amounts of supervised data on the behavior of different cGANs, with results presented in Fig. 3. Specifically, we compare the performance of a ranked semi-supervised cGAN, random semi-supervised cGAN and interactive cGAN with respect to increasing the used percentage of data for training. The upper bound, shown by the dashed line, is the maximum accuracy (dice scores) obtained from a supervised cGAN model trained on the entire training set.

Fig. 3:

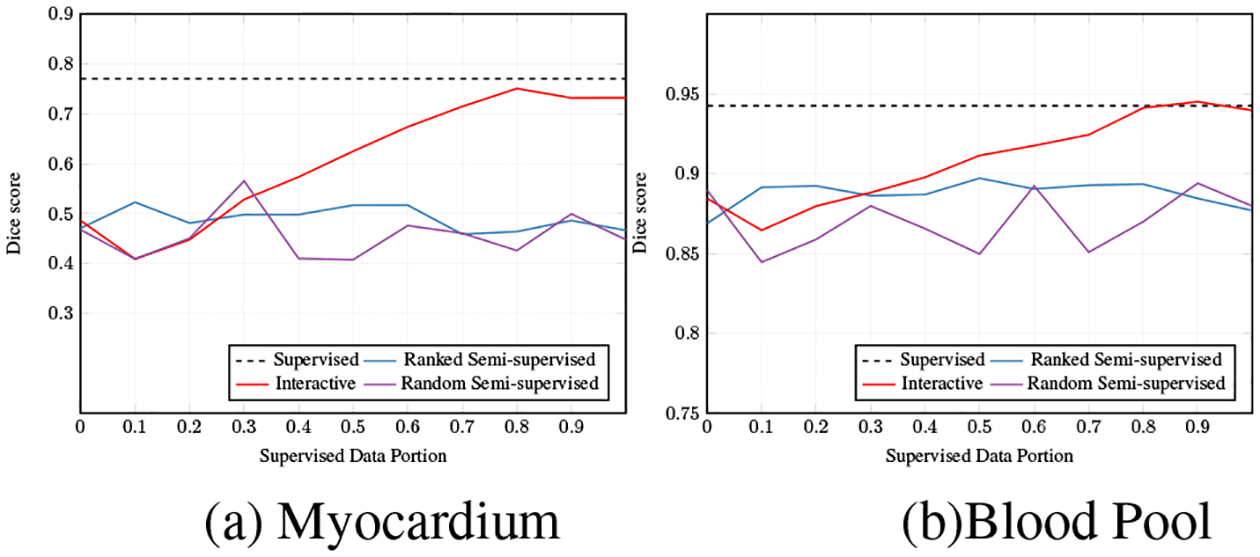
Dice scores for different amounts of supervised data.

The ranked/random semi-supervised cGAN, and interactive cGAN are trained using only a single volume of supervised data for learning the base model. However, in case of two semi-supervised cGAN models, the rest of training data is collected from predictions, and incrementally added to the training set for fine-tuning the base model. The only difference between the ranked semi-supervised cGAN, and random semi-supervised cGAN is that the latter model randomly selects the samples to increase the training data, while the ranked model adds data based on the ranked list obtained from D scores. The predictions are added to the training set in descending order (from the easy cases to the difficult ones), which suggests enhanced stability in comparison with the chaotic behavior of the random model. For fine-tuning the interactive cGAN, not only the predictions for easy samples are used, but also a set of ground truth annotations is collected for difficult cases through user interaction. This model outperforms the preceding variants. As shown in Fig. 3 and Tab. 1, increasing the amount of supervised data (user annotation) leads to a constant improvement, until the model reaches the upper bound. In our studies the interactive cGAN achieved almost the upper bound using only 80% of supervised data.

Table 1:

Dice scores for different amounts of supervised data

	10%	20%	30%	40%	50%	60%	70%	80%	90%
Myocardium	0.41	0.45	0.53	0.57	0.62	0.67	0.71	0.75	0.73
Blood Pool	0.86	0.88	0.89	0.90	0.91	0.92	0.92	0.94	0.95
Average	0.64	0.66	0.71	0.74	0.77	0.80	0.82	0.85	0.84

Quantitative results:

In Tab. 2 a comparative result of dice scores for Myocardium and Blood pool is reported. In case of semi-supervised cGAN models (ranked and random) the average accuracy is reported, while for interactive cGANs different levels of supervisions are reported: low (30%), medium (60%) and high-percentage (80%).

Table 2:

Comparing with state-of-the-art methods. For I-cGAN the percentages of supervised data is indicated

	Dices
Model	Myocardium	Blood pool	Mean
Mukhopadhyay [27]	0.495	0.794	0.645
Tziritas [28]	0.612	0.867	0.740
Shahzad et al. [29]	0.747	0.885	0.816
DenseVoxNet [30]	0.821	0.931	0.876
Fully-Supervised cGAN	0.770	0.943	0.856
Semi-Supervised (Ranked)	0.688	0.887	0.689
Semi-Supervised (Random	) 0.456	0.871	0.663
I-cGAN by ranking (30%)	0.528	0.888	0.708
I-cGAN by ranking (60%)	0.674	0.918	0.796
I-cGAN by ranking (80%)	0.750	0.941	0.846

Qualitative results:

Slices from HVSMR dataset are shown in Fig. 4. The figure shows the pixel-level uncertainty modeling using the D score maps in PatchGAN fashion. The first and second columns show the original input $\mathcal{I}$, and original segments $\mathcal{S}$, respectively. The last two columns illustrate the predicted segments $\tilde{\mathcal{S}}$ and corresponding D score maps $D(\mathcal{I},\tilde{\mathcal{S}})$, respectively. The figure shows the low-quality areas of predicted segments obtaining lower score in the $D(\mathcal{I},\tilde{\mathcal{S}})$ (red). This indicates, in the heat-maps the patch with theIlowest value of D, correspond to the patch with maximum uncertainty or wrong segmentation, while the high-scored patches (blue) represent the high quality segments. The figure further shows that the score of D can successfully detect wrong segments predicted by G.

Fig. 4:

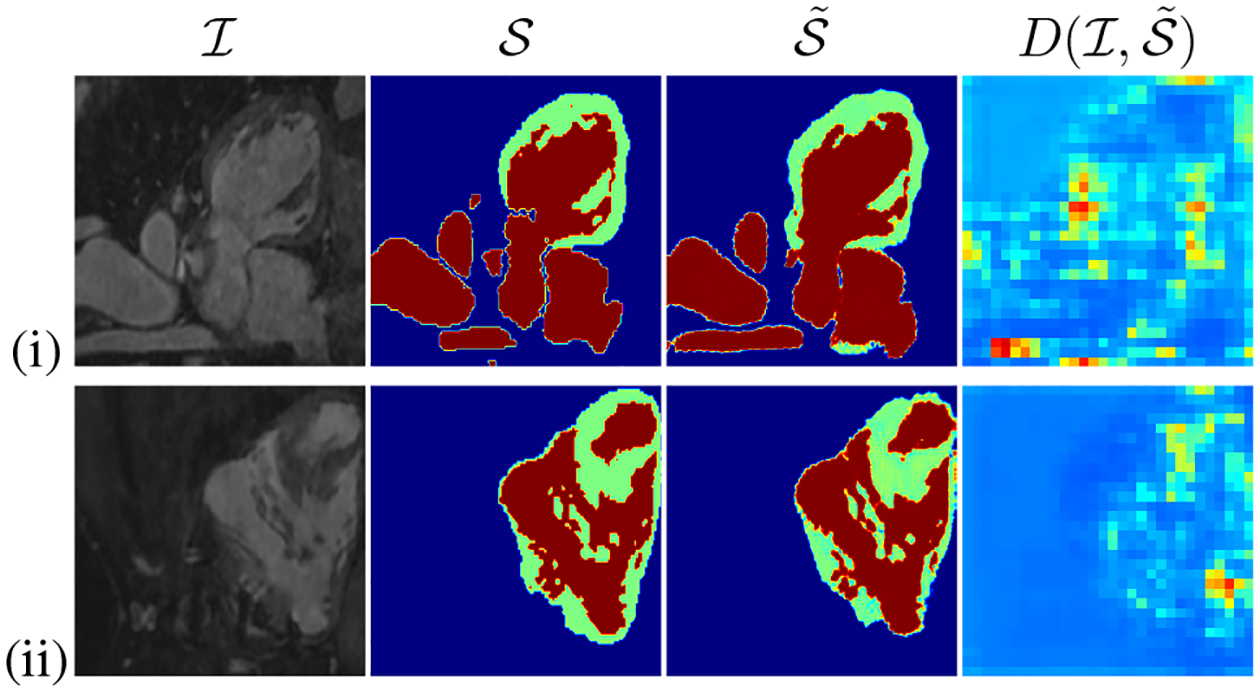
Qualitative results: Original image $\mathcal{I}$, ground truth segmentation $\mathcal{S}$, predicted segmentation $\tilde{\mathcal{S}}$ and discriminator score for predicted segmentation $D(\mathcal{I},\tilde{\mathcal{S}})$.

4. CONCLUSION

The proposed approach shows that combining the notions of human machine collaborative learning with GANs is viable, and D can be used as a measure of uncertainty. Altogether, this allows for obtaining high accuracy segmentations under much more restricted data assumptions. This is achieved by an iterative and selective update of pseudo ground truth data, keeping the human in the loop, where it promises to be most useful, simultaneously keeping interaction at a minimum.

Future work will entail performing the uncertainty computation at finer granularity, e.g. patch-wise, which promises to boost the performance of the approach. Furthermore, future research will also deal with more in-depth study of D as a measure of uncertainty, to consider diversity into ranking. Selection of more diverse samples incorporate in the patch-wise uncertainty measurement comes with potential further boosting in the performance.

Fig. 1:

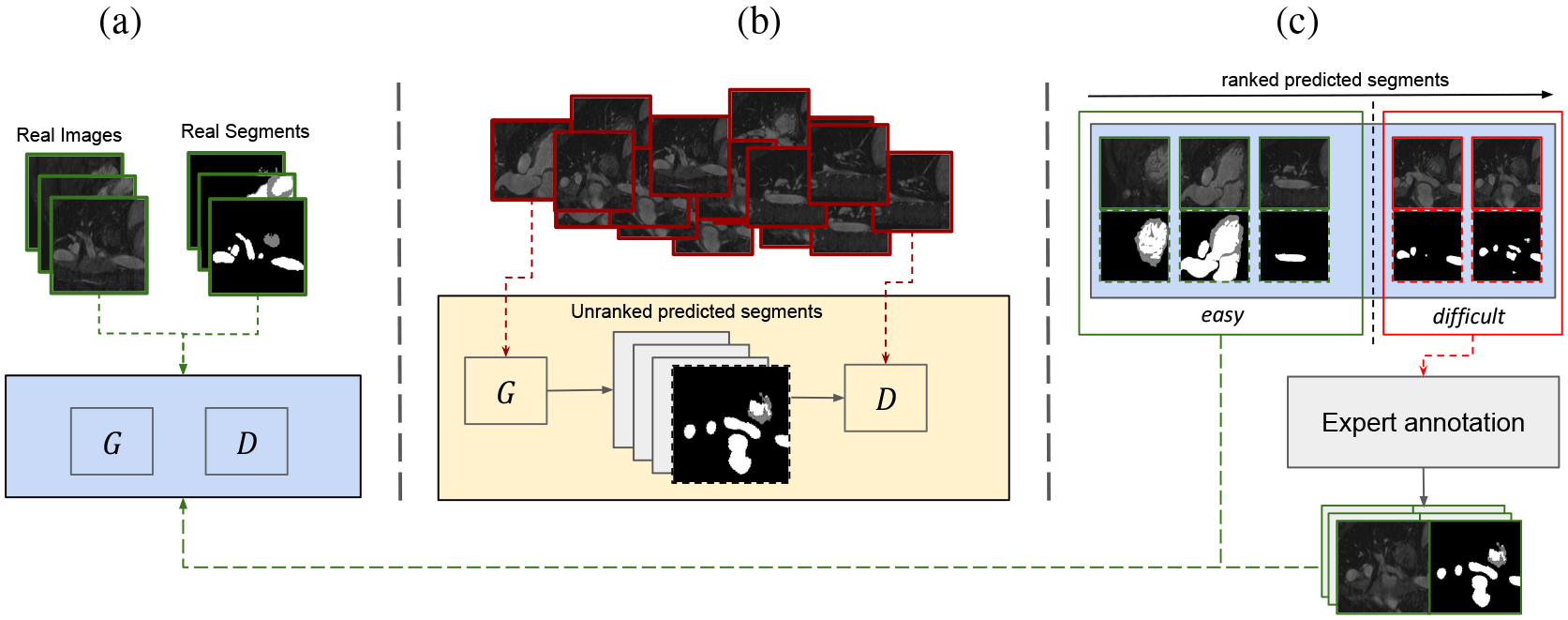
Learning interactive cGAN in a loop: (a) training a base model to generate segments from a small set of annotated data, (b) G generates segment predictions from input images, which are sequentially ranked by D. In (c), stacking the easy predictions with the annotation collected from user on the difficult cases and utilize it to continue the training procedure.