Skip to main content
NCBI home page
Annals of Work Exposures and Health logoLink to Annals of Work Exposures and Health
. 2020 Jul 1;64(8):778–785. doi: 10.1093/annweh/wxaa056

Time-Based Data in Occupational Studies: The Whys, the Hows, and Some Remaining Challenges in Compositional Data Analysis (CoDA)

Nidhi Gupta 1,✉, Charlotte Lund Rasmussen 1,2, Andreas Holtermann 1,3, Svend Erik Mathiassen 4
PMCID: PMC7544002  PMID: 32607544

Abstract

Data on the use of time in different exposures, behaviors, and work tasks are common in occupational research. Such data are most often expressed in hours, minutes, or percentage of work time. Thus, they are constrained or ‘compositional’, in that they add up to a finite sum (e.g. 8 h of work or 100% work time). Due to their properties, compositional data need to be processed and analyzed using specifically adapted methods. Compositional data analysis (CoDA) has become a particularly established framework to handle such data in various scientific fields such as nutritional epidemiology, geology, and chemistry, but has only recently gained attention in public and occupational health sciences. In this paper, we introduce the reader to CoDA by explaining why CoDA should be used when dealing with compositional time-use data, showing how to perform CoDA, including a worked example, and pointing at some remaining challenges in CoDA. The paper concludes by emphasizing that CoDA in occupational research is still in its infancy, and stresses the need for further development and experience in the use of CoDA for time-based occupational exposures. We hope that the paper will encourage researchers to adopt and apply CoDA in studies of work exposures and health.

Keywords: constrained data, ergonomics, isometric log-ratio, work environment

Time use in occupational research

Occupational research and practice has a long-standing interest in the use of time (Bauman et al., 2019). Examples of exposures include time spent in different work tasks (Mathiassen et al., 2005; Svendsen et al., 2005; Lewné et al., 2017; Notø et al., 2017; Pulido et al., 2017), in hazardous environments (Fruin et al., 2004; Stewart et al., 2010), on different physical activities (Thorp et al., 2012; Rasmussen et al., 2018; Gupta et al., 2019), and in specific postures (Mathiassen et al., 2014; Wahlström et al., 2016; Palm et al., 2018).

Such time-based occupational exposures are often expressed in terms of minutes (e.g. per day), hours (e.g. per week), or percentages (e.g. of total working time). Thus, they are compositional: they form parts of a finite total such as a whole day, a whole week, or 100% working time. Therefore, any exposure part, such as time spent in a particular work task, will necessarily range between 0 and 100%, and correlate with time spent in other exposures that are also parts of the total 100%.

Already in 1896, Pearson issued a warning of using standard statistical techniques when handling data adding up to a whole (Pearson, 1896). Since then, different approaches have been suggested on how to manage compositional data. Examples include multivariate pattern analysis (Aadland et al., 2019), fractional multinomial models (Murteira and Ramalho, 2016), isotemporal substitution models (Mekary et al., 2009), modified hierarchical regression (Jansen et al., 2001), and compositional data analysis (CoDA) (Aitchison, 1982). The present paper focuses on the latter, i.e. CoDA, which has received particular attention lately.

The landmark statistical basis of CoDA was developed in the early 1980s (Aitchison, 1982). Since then, CoDA has become an established framework of how to handle compositional data in, e.g. nutritional epidemiology (Leite, 2016), geology (Tolosana-Delgado and von Eynatten, 2009), and chemistry (Buccianti and Pawlowsky-Glahn, 2005). However, in public and occupational health sciences, CoDA has gained attention only recently (Pedišić, 2014; Chastin et al., 2015; Pedisic et al., 2017; Dumuid et al., 2018b; Foley et al., 2018; Bauman et al., 2019), with few papers devoted to exposures at work (Gupta et al., 2018a, 2019; Rasmussen et al., 2018; Hallman et al., 2019; Coenen et al., 2020).

In this paper, we institute CoDA by, (i) explaining why time-based data need to be analyzed using CoDA, (ii) showing how data are processed and analyzed within a CoDA framework, and (iii) pointing at some remaining methodological challenges in CoDA, emphasizing the need for continued development. In giving this introduction to CoDA, we hope that readers will be inspired to adopt and apply CoDA when dealing with time-based occupational exposures.

The whys of CoDA

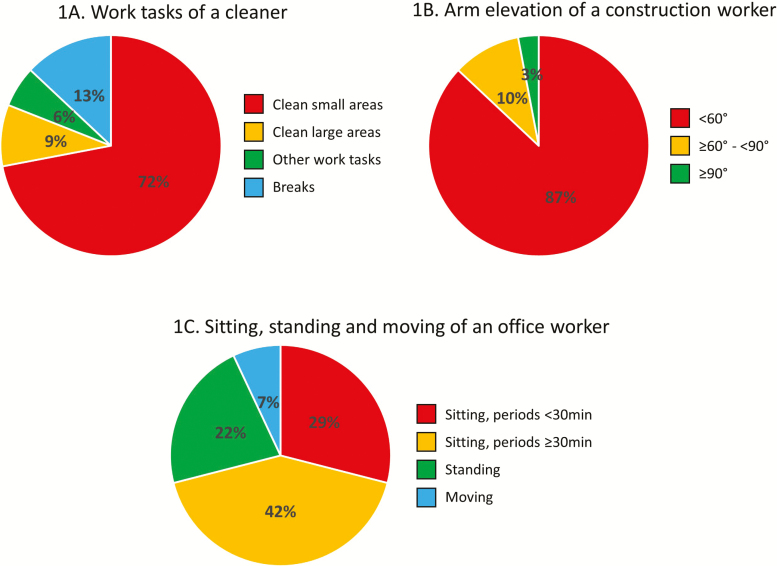
As emphasized above, data on time spent in various exposures, behaviors, or tasks during work are often compositional. Thus, Fig. 1A illustrates a cleaner spending 72, 9, 6, and 13% of the working hours on two different cleaning tasks, other work tasks, and breaks, respectively. These compositional ‘parts’ add up to 100% work time. Similarly, Fig. 1B and C illustrates the distributions of 100% working time in different postures for a construction worker (Fig. 1B) and in different physical behaviors for an office worker (Fig. 1C).

Figure 1.

Figure 1.

Open in a new tab

Examples of compositions of time at work spent: (A) on different tasks for a cleaner; (B) in different categories of arm elevation for a construction worker, and (C) in sitting (in periods of <30 and ≥30 min), standing and moving for an office worker.

Because the composition is a finite total, changing the time spent in one part will inevitably lead to a change in time for at least one of the remaining parts. For example, for the office worker in Fig. 1C, reducing time in long sitting bouts will increase time spent in at least one of the remaining behaviors, i.e. short sitting bouts, standing, or moving. Notably, parts in the composition will still be dependent even if one or more are left out. Thus, even if only time in long sitting bouts (cf. Fig. 1C) is considered of interest in a particular study, it needs to be treated as part of a full composition including the other behaviors. The inevitable presence of those other behaviors also contribute in determining the possible effects of long sitting bouts.

Previous occupational research dealing with compositional data has predominantly made the error of assuming that one part of a composition influences health independent of other parts in that composition. This may result in misleading inferences (e.g. Chastin et al., 2015; Gupta et al., 2018b; Dumuid et al., 2019). As an example, times spent in sedentary behavior and physical activity are very often treated as separate variables in epidemiology, even though they are complimentary parts of a composition (Dumuid et al., 2018b). Negative health effects claimed to result from extensive sitting may, therefore, actually be due to the complimentary behavior, i.e. too little non-sitting (van der Ploeg and Hillsdon, 2017; Stamatakis et al., 2019). Analyzing compositional data using standard methods may even in some cases lead to absurd results, such as confidence intervals (CIs) including values less than 0% or more than 100% time (Coenen et al., 2020).

Similarly, in occupational practice, compositional data are often understood using a standard approach focusing on a single risk factor within the composition of multiple factors. For example, a recent guideline for nurses focused on reducing time spent standing without considering which other compositional parts (e.g. walking or sitting) should then be increased (Waters and Dick, 2015). This approach of addressing only isolated parts of a composition in research and practice needs to be revisited, and CoDA offers a suitable tool for that purpose.

The ‘hows’ of CoDA

Since the first comprehensive proposal of how to deal with compositional data in 1982, several extensive and excellent textbooks have presented CoDA procedures (e.g. Pawlowsky-Glahn et al., 2015). Also, a number of recent papers have, in detail, reviewed and described basic issues in CoDA implementation (Chastin et al., 2015; Dumuid et al., 2018b, 2019, 2020).

CoDA generally comprises a series of steps:

  1. Log-ratio transformation of compositional parts. The point of departure of CoDA is the notion that the information contained in a part of a composition can only be correctly understood if it is expressed relative to information about other part(s). Thus, in a first step of processing data, ratios are formed between compositional parts. Ratios of non-negative numbers can, however, only take non-negative values, and are still constrained. Therefore, in a second step, the ratios are log-transformed in order to arrive at numbers that can vary freely on the entire scale from minus to plus infinity. This two-step log-ratio transformation moves, in mathematical terms, data from a so-called Simplex to the Euclidian space, where standard data operate, and standard statistics can be used (Aitchison, 1986).

Different principles for constructing ratios and performing the log-transformation have been described in the literature (Pawlowsky-Glahn et al., 2015). In current research, the most widely used is the isometric log-ratio (ilr) transformation (Carson et al., 2016; Biddle et al., 2018; Dumuid et al., 2018a,b; Foley et al., 2018; Hallman et al., 2019; Coenen et al., 2020). Using the ilr transformation on a composition with d parts results in d − 1 orthonormal ilr coordinates. This partition can be done in several ways if the composition consists of more than two parts. Which partition to use will depend on the research question. Appendix A, available at Annals of Work Exposures and Health online, exemplifies two possible sets of ilrs pertaining to the four-part composition illustrated in Fig. 1C, including the associated log-transformation formulas.

  • 2. Further analysis using standard statistical methods. After transformation of the composition into a set of log-ratios, standard statistical methods can be applied. Obviously, this must always be preceded by a control of assumptions associated with the intended statistical analyses.

  • 3. Interpretation of results. Since the statistical analyses are performed on log-transformed data, some results, e.g. regression coefficients, are also expressed on a log-scale, making straightforward interpretation of some statistical parameters difficult. Procedures have been proposed, easing the interpretation of results of regression analyses of exposure–outcome associations with compositions as the independent variable(s) (Chastin et al., 2015; Dumuid et al., 2018a, 2019; Gupta et al., 2019); regression analyses with compositions as the dependent variable(s) (Rasmussen et al., 2018; Hallman et al., 2019); and ANOVA or MANOVA addressing differences in compositions between groups (Foley et al., 2018; Gupta et al., 2018b).

Example of a CoDA application: is time sitting at work associated with low-back pain?

In an accelerometer-based study of 209 blue-collar workers (Gupta et al., 2015), workers spent, on average, 478 min at work, distributed between sitting (175 min), standing (205 min), and walking (98 min). The workers reported an average low-back pain (LBP) intensity during the past month of 2.9 (SD 2.6) on a scale from 0 to 9.

The three-part composition was transformed into a set of two ilrs, i.e. ilr1: the log-transformed ratio of sitting to the geometric mean of standing and walking; ilr2: the log-transformed ratio of standing to walking.

We examined the association between the compositions, expressed in terms of the two ilrs, and LBP intensity using multiple linear regression, adjusted for confounders.

The regression coefficient for ilr1 indicated that more sitting time relative to time spent in standing and walking is associated with higher LBP intensity (B = 0.73; 95% CI 0.25, 1.20; P = 0.003). Since the effect size estimate B (and its associated CI) is measured on a logarithmic scale, it needs to be ‘back-transformed’ to the original scale (i.e. minutes) for ease of interpretation. For this purpose, we used the ‘compositional isotemporal substitution’ method (Dumuid et al., 2019). This method interprets regression parameters in terms of the expected difference in LBP intensity (outcome) if time is reallocated to/from sitting from/to standing and walking (Dumuid et al., 2019). The isotemporal substitution procedure is detailed in Appendix B, available at Annals of Work Exposures and Health online.

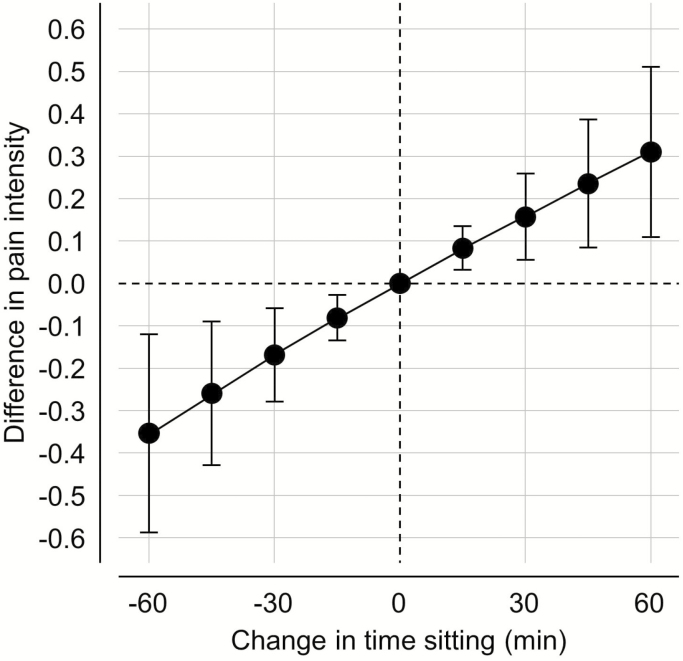
We examined reallocations in the range of −60 to + 60 min of sitting, which was within limits occurring in the source data. Results are illustrated in Fig. 2. For instance, a reallocation of 30 min from sitting to standing and walking is estimated to be associated with a 0.17 (95% CI −0.28, −0.06) lower LBP intensity.

Figure 2.

Figure 2.

Open in a new tab

Isotemporal substitution illustrating the direction and strength of the association between time in sitting, relative to standing and walking, and LBP intensity. Zeroes on the x and y axes correspond to the average composition (175 min sitting, 205 min standing, 98 min walking), and the mean pain intensity (2.9) in the source population, respectively. Numbers on the x-axis show reallocations of time to/from sitting from/to standing and walking (see running text for details). For example, reallocating 60 min from sitting to standing and walking (41 min to standing and 19 min to walking) is estimated to be associated with a LBP 0.36 [95% CI (−0.59, −0.12)] lower than the group average.

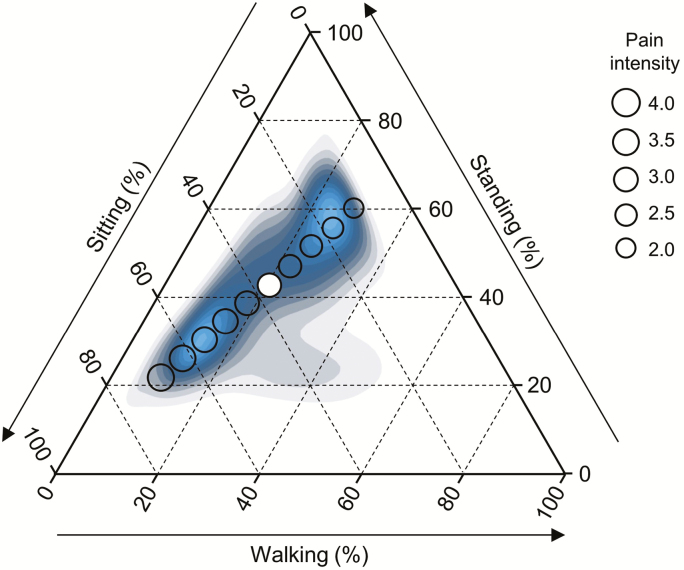
Isotemporal substitutions offer one way to interpret regression estimates based on CoDA. However, they suffer from not being able to answer the obvious question of ‘what is the expected outcome associated with a specified composition?’ Thus, we suggest developing alternative graphical illustrations to answer this question. Fig. 3 shows an example suiting a three-part composition as that in the example study. The figure illustrates the estimated LBP associated with a specific composition within the range represented in the source population. For example, a composition of 24% sitting, 52% standing, and 24% walking is estimated to be associated with a LBP intensity of 2.6 while a composition of 49% sitting, 34% standing, and 17% walking corresponds to an estimated intensity of 3.2. While this ternary plot alternative to isotemporal substitution works well for three-part compositions, it remains a challenge to visualize regression models developed for compositions with four or more parts.

Figure 3.

Figure 3.

Open in a new tab

A ternary plot illustrating the estimated LBP intensity at different compositions of sitting, standing, and walking, according to a CoDA regression analysis among 209 blue-collar workers. The gray-blue contour plot indicates the occurrence of compositions in the source population, with the density of the gray-blue color representing the number of workers; lighter blue color, higher density. For example, many workers had compositions of about 20% sitting, 55% standing, and 25% walking (upper right ‘mountain’), and many had about 60% sitting, 30% standing, and 10% walking (lower left mountain). The circles illustrate the estimated pain intensity for selected compositions, sizes coded as shown in the legend. The white dot shows the average composition and pain intensity in the source population.

Results and interpretations based on a standard analysis approach

We also analyzed the same dataset using a standard (non-compositional) multiple linear regression. We observed—as expected—that it was not possible to include all three behaviors in the regression model at the same time, since their perfect collinearity resulted in a singular covariance matrix. Therefore, two different models were constructed, one including sitting and standing (but not walking); the other including sitting and walking (but not standing).

The estimated association of sitting time with LBP intensity differed considerably between the two models. The model including only sitting and standing resulted in a regression coefficient B for sitting of 0.46 (95% CI −0.06, 0.98; P = 0.08), while the effect of sitting was less pronounced, yet more certain, according to the other model including sitting and walking: B = 0.32 (95% CI 0.01, 0.63; P = 0.04). This illustrates an annoying—and misleading—result of analyzing compositional data using standard procedures, i.e. that the association between a particular behavior and LBP may differ depending on which other behavior is omitted from the statistical model.

The future of CoDA in occupational studies

CoDA is a suitable tool when dealing with data expressing tasks, exposures, and behaviors in terms of time use. Associations between time use and health outcomes, or differences in time use between occupational groups or working conditions need to be examined with consideration to the constrained and correlated nature of compositional data. CoDA takes into account the complete combination of exposures or behaviors, e.g. when determining effects on health, as opposed to the standard approach of addressing one exposure, behavior or risk factor at a time. Thus, CoDA shifts the focus of research and practice from the influence of a single exposure to understanding and intervening on exposures occurring together, as parts of the total time spent at work.

We wish to emphasize, however, that occupational risk prevention strategies also need to consider exposures and behaviors during non-work time. As an example, the effect of high occupational physical activity on workers’ health has been shown to depend on the extent of leisure time physical activity (Holtermann et al., 2012; Hallman et al., 2017). This extension of an occupational health perspective to include non-work exposures that are otherwise most often covered by public health studies is a prerequisite for understanding the contributions of work to health, well-being, and social equality, in a 24/7 approach (Holtermann et al., 2019, 2020). CoDA offers an attractive opportunity for such analyses in allowing information from non-work time to be included in an occupational research context, as part of a full-day composition (Gupta et al., 2019).

In the present paper, we exemplify the use of CoDA in cases where exposure is compositional, such as in regression analysis of effects of physical behaviors on a health outcome such as LBP. We emphasize that CoDA is equally justified if the outcome is compositional; or both the exposure and the outcome, such as illustrated in a recent study on associations between physical behaviors at work and during leisure (Rasmussen et al., 2018).

CoDA procedures and applications have developed considerably since it first appeared in 1982 (Aitchison, 1982), but implementation of CoDA is still in its infancy in the area of work exposures and health. Thus, research is needed to obtain more experience in the pros and cons of CoDA, including addressing a number of issues that still need to be resolved. One important issue is how to deal with zeroes in compositional parts since CoDA builds on log-transformed ratios not allowing such zeroes. Rounded zeroes resulting from very little time being trimmed to a zero, or from the data sampling strategy not detecting a particular exposure that does, in fact, occur at times, can be handled (Martín-Fernández et al., 2011, 2012). Essential, ‘true’ zeroes, however, are still a major challenge in CoDA (Martín-Fernández et al., 2011). Another challenge in CoDA is how to illustrate and interpret CoDA-based results in terms of useful metrics and informative diagrams. We suggested one way of visualizing regression results (cf. Fig. 3), and we encourage further developments addressing this issue. CoDA addresses summary metrics of time use, such as percentages of a time total, but not the real-time sequence of exposure, such as whether periods of walking are followed by standing or by sitting. Some papers have suggested approaches for handling real-time properties of time-use data (e.g. Paraschiv-Ionescu et al., 2013; Chinapaw et al., 2019), and integrating CoDA with such methods would be of high interest.

Conclusion

In this paper, we have presented reasons why tasks, exposures, and behaviors expressed in terms of time need to be processed and analyzed using methods that acknowledge their compositional properties. We have argued that CoDA answers this need, and we have explained how to use CoDA, hoping that the present paper will inspire readers to adopt and apply CoDA. While CoDA may appear unfamiliar and difficult at present, we believe that it will eventually be adopted as a standard approach in studies of work exposures and health.

Funding

Funding for this project was provided by the Danish Working Environment Research Fund (grant no. 01-2015-09 and 01-2015-03) and the Swedish Research Council for Health, Working Life and Welfare (Dnr. 2009-1761).

Conflict of interest

The authors declare no conflict of interest relating to the material presented in this Article. Its contents, including any opinions and/or conclusions expressed, are solely those of the authors.

Supplementary Material

wxaa056_suppl_Supplementary_Appendix_A-1
Click here for additional data file. (21.1KB, docx)
wxaa056_suppl_Supplementary_Appendix_B-1
Click here for additional data file. (16.1KB, docx)

References

  1. Aadland E, Andersen LB, Resaland GK  et al. (2019) Interpretation of multivariate association patterns between multicollinear physical activity accelerometry data and cardiometabolic health in children—a tutorial. Metabolites; 9: 129. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Aitchison J. (1982) The statistical analysis of compositional data. J R Stat Soc Ser B (Methodol); 44: 139–77. [Google Scholar]
  3. Aitchison J. (1986) The statistical analysis of compositional data. London, UK: Chapman & Hall Ltd. [Google Scholar]
  4. Bauman A, Bittman M, Gershuny J (2019) A short history of time use research; implications for public health. BMC Public Health; 19 (Suppl. 2): 607. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Biddle GJH, Edwardson CL, Henson J  et al. (2018) Associations of physical behaviours and behavioural reallocations with markers of metabolic health: a compositional data analysis. Int J Environ Res Public Health; 15: E2280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Buccianti A, Pawlowsky-Glahn V (2005) New perspectives on water chemistry and compositional data analysis. Math Geol; 37: 703–27. [Google Scholar]
  7. Carson V, Tremblay MS, Chaput JP  et al. (2016) Associations between sleep duration, sedentary time, physical activity, and health indicators among Canadian children and youth using compositional analyses. Appl Physiol Nutr Metab; 41 (6 Suppl 3): S294–302. [DOI] [PubMed] [Google Scholar]
  8. Chastin SF, Palarea-Albaladejo J, Dontje ML  et al. (2015) Combined effects of time spent in physical activity, sedentary behaviors and sleep on obesity and cardio-metabolic health markers: a novel compositional data analysis approach. PLoS One; 10: e0139984. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chinapaw MJ, Wang X, Andersen LB  et al. (2019) From total volume to sequence maps: sophisticated accelerometer data analysis. Med Sci Sports Exerc; 51: 814–20. [DOI] [PubMed] [Google Scholar]
  10. Coenen P, Mathiassen S, van der Beek AJ  et al. (2020) Correction of bias in self-reported sitting time among office workers—a study based on compositional data analysis. Scand J Work Environ Health; 46: 32–42. [DOI] [PubMed] [Google Scholar]
  11. Dumuid D, Lewis LK, Olds TS  et al. (2018a) Relationships between older adults’ use of time and cardio-respiratory fitness, obesity and cardio-metabolic risk: a compositional isotemporal substitution analysis. Maturitas; 110: 104–10. [DOI] [PubMed] [Google Scholar]
  12. Dumuid D, Pedisic Z, Palarea-Albaladejo J  et al. (2020) Compositional data analysis in time-use epidemiology: what, why, how. Int J Environ Res Public Health; 17: 2220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Dumuid D, Pedišić Ž, Stanford TE  et al. (2019) The compositional isotemporal substitution model: a method for estimating changes in a health outcome for reallocation of time between sleep, physical activity and sedentary behaviour. Stat Methods Med Res; 28: 846–57. [DOI] [PubMed] [Google Scholar]
  14. Dumuid D, Stanford TE, Martin-Fernández JA  et al. (2018b) Compositional data analysis for physical activity, sedentary time and sleep research. Stat Methods Med Res; 27: 3726–38. [DOI] [PubMed] [Google Scholar]
  15. Foley L, Dumuid D, Atkin AJ  et al. (2018) Patterns of health behaviour associated with active travel: a compositional data analysis. Int J Behav Nutr Phys Act; 15: 26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Fruin SA, Winer AM, Rodes CE (2004) Black carbon concentrations in California vehicles and estimation of in-vehicle diesel exhaust particulate matter exposures. Atmos Environ; 38: 4123–33. [Google Scholar]
  17. Gupta N, Christiansen CS, Hallman DM  et al. (2015) Is objectively measured sitting time associated with low back pain? A cross-sectional investigation in the NOMAD study. PLoS One; 10: e0121159. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gupta N, Dumuid D, Korshøj M  et al. (2018a) Is daily composition of movement behaviors related to blood pressure in working adults?  Med Sci Sports Exerc; 50: 2150–5. [DOI] [PubMed] [Google Scholar]
  19. Gupta N, Korshøj M, Dumuid D  et al. (2019) Daily domain-specific time-use composition of physical behaviors and blood pressure. Int J Behav Nutr Phys Act; 16: 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Gupta N, Mathiassen SE, Mateu-Figueras G  et al. (2018b) A comparison of standard and compositional data analysis in studies addressing group differences in sedentary behavior and physical activity. Int J Behav Nutr Phys Act; 15: 53. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hallman DM, Birk Jørgensen M, Holtermann A (2017) On the health paradox of occupational and leisure-time physical activity using objective measurements: effects on autonomic imbalance. PLoS One; 12: e0177042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Hallman DM, Mathiassen SE, van der Beek AJ  et al. (2019) Calibration of self-reported time spent sitting, standing and walking among office workers: a compositional data analysis. Int J Environ Res Public Health; 16: 3111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Holtermann A, Hansen JV, Burr H  et al. (2012) The health paradox of occupational and leisure-time physical activity. Br J Sports Med; 46: 291–5. [DOI] [PubMed] [Google Scholar]
  24. Holtermann A, Mathiassen SE, Straker L (2019) Promoting health and physical capacity during productive work: the Goldilocks Principle. Scand J Work Environ Health; 45: 90–7. [DOI] [PubMed] [Google Scholar]
  25. Holtermann A, Straker L, Lee IM  et al. (2020) Long overdue remarriage for better physical activity advice for all: bringing together the public health and occupational health agendas. Br J Sports Med; doi:10.1136/bjsports-2019-101719. [DOI] [PubMed] [Google Scholar]
  26. Jansen JP, Burdorf A, Steyerberg E (2001) A novel approach for evaluating level, frequency and duration of lumbar posture simultaneously during work. Scand J Work Environ Health; 27: 373–80. [DOI] [PubMed] [Google Scholar]
  27. Leite ML. (2016) Applying compositional data methodology to nutritional epidemiology. Stat Methods Med Res; 25: 3057–65. [DOI] [PubMed] [Google Scholar]
  28. Lewné M, Johannesson S, Strandberg B  et al. (2017) Exposure to particles, polycyclic aromatic hydrocarbons, and nitrogen dioxide in Swedish restaurant kitchen workers. Ann Work Expo Health; 61: 152–63. [DOI] [PubMed] [Google Scholar]
  29. Martín-Fernández JA, Hron K, Templ M  et al. (2012) Model-based replacement of rounded zeros in compositional data: classical and robust approaches. Comput Stat Data Anal; 56: 2688–704. [Google Scholar]
  30. Martín-Fernández JA, Palarea-Albaladejo J, Olea RA (2011) Dealing with zeros. In Pawlowsky-Glahn V, Buccianti A, editors. Compositional data analysis: theory and applications. Chichester, UK: John Wiley & Sons, Ltd. pp. 47–62. [Google Scholar]
  31. Mathiassen SE, Jackson JA, Punnett L (2014) Statistical performance of observational work sampling for assessment of categorical exposure variables: a simulation approach illustrated using PATH data. Ann Occup Hyg; 58: 294–316. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Mathiassen SE, Nordander C, Svendsen SW  et al. (2005) Task-based estimation of mechanical job exposure in occupational groups. Scand J Work Environ Health; 31: 138–51. [DOI] [PubMed] [Google Scholar]
  33. Mekary RA, Willett WC, Hu FB  et al. (2009) Isotemporal substitution paradigm for physical activity epidemiology and weight change. Am J Epidemiol; 170: 519–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Murteira JMR, Ramalho JJS (2016) Regression analysis of multivariate fractional data. Econom Rev; 35: 515–52. [Google Scholar]
  35. Notø H, Nordby KC, Skare Ø  et al. (2017) Job tasks as determinants of thoracic aerosol exposure in the cement production industry. Ann Work Expo Health; 62: 88–100. [DOI] [PubMed] [Google Scholar]
  36. Palm P, Gupta N, Forsman M  et al. (2018) Exposure to upper arm elevation during work compared to leisure among 12 different occupations measured with triaxial accelerometers. Ann Work Expo Health; 62: 689–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Paraschiv-Ionescu A, Buchser E, Aminian K (2013) Unraveling dynamics of human physical activity patterns in chronic pain conditions. Sci Rep; 3: 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Pawlowsky-Glahn V, Egozcue JJ, Tolosana-Delgado R (2015) Modeling and analysis of compositional data. Chichester, UK: John Wiley & Sons. [Google Scholar]
  39. Pearson K. (1896) Mathematical contributions to the theory of evolution-on a form of spurious correlation which may arise when indices are used in the measurement of organs. Proc R Soc Lond; 60: 489–98. [Google Scholar]
  40. Pedišić Z. (2014) Measurement issues and poor adjustments for physical activity and sleep undermine sedentary behaviour research—the focus should shift to the balance between sleep, sedentary behaviour, standing and activity. Kinesiology; 46: 135–46. [Google Scholar]
  41. Pedisic Z, Dumuid D, Olds TS (2017) Integrating sleep, sedentary behaviour, and physical activity research in the emerging field of time-use epidemiology: definitions, concepts, statistical methods, theoretical framework, and future directions. Kinesiology; 49: 252–69. [Google Scholar]
  42. Pulido JA, Barrero LH, Mathiassen SE  et al. (2017) Correctness of self-reported task durations: a systematic review. Ann Work Expo Health; 62: 1–16. [DOI] [PubMed] [Google Scholar]
  43. Rasmussen CL, Palarea-Albaladejo J, Bauman A  et al. (2018) Does physically demanding work hinder a physically active lifestyle in low socioeconomic workers? A compositional data analysis based on accelerometer data. Int J Environ Res Public Health; 15: 1306. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Stamatakis E, Ekelund U, Ding D et al. (2019) Is the time right for quantitative public health guidelines on sitting? A narrative review of sedentary behaviour research paradigms and findings. Br J Sports Med; 53: 377–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Stewart PA, Coble JB, Vermeulen R  et al. (2010) The diesel exhaust in miners study: I. Overview of the exposure assessment process. Ann Occup Hyg; 54: 728–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Svendsen SW, Mathiassen SE, Bonde JP (2005) Task based exposure assessment in ergonomic epidemiology: a study of upper arm elevation in the jobs of machinists, car mechanics, and house painters. Occup Environ Med; 62: 18–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Thorp AA, Healy GN, Winkler E  et al. (2012) Prolonged sedentary time and physical activity in workplace and non-work contexts: a cross-sectional study of office, customer service and call centre employees. Int J Behav Nutr Phys Act; 9: 128. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Tolosana-Delgado R, von Eynatten H (2009) Grain-size control on petrographic composition of sediments: compositional regression and rounded zeros. Math Geosci; 41: 869. [Google Scholar]
  49. van der Ploeg HP, Hillsdon M. (2017) Is sedentary behaviour just physical inactivity by another name?  Int J Behav Nutr Phys Act; 14: 142. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Wahlström J, Bergsten E, Trask C  et al. (2016) Full-shift trunk and upper arm postures and movements among aircraft baggage handlers. Ann Occup Hyg; 60: 977–90. [DOI] [PubMed] [Google Scholar]
  51. Waters TR, Dick RB (2015) Evidence of health risks associated with prolonged standing at work and intervention effectiveness. Rehabil Nurs; 40: 148–65. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

wxaa056_suppl_Supplementary_Appendix_A-1
Click here for additional data file. (21.1KB, docx)
wxaa056_suppl_Supplementary_Appendix_B-1
Click here for additional data file. (16.1KB, docx)

Articles from Annals of Work Exposures and Health are provided here courtesy of Oxford University Press

RESOURCES