Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2020 Oct 8.
Published in final edited form as: Syst Dyn Rev. 2019 Jan 1;34(4):481–502. doi: 10.1002/sdr.1611

Trajectories of functional ability over the life course: a conceptual model of the interaction of stressor-induced functional loss and resilience

David B Matchar a,b, John P Ansah a,*, Victoria Koh a, Heather E Whitson b,c
PMCID: PMC7544242  NIHMSID: NIHMS1633611  PMID: 33041497

Abstract

Understanding the factors that influence functional ability over the life course is integral to identifying clinical and public health policies to facilitate successful aging. The World Health Organization has advocated a conceptual framework to clarify the policy discussion. We have sought to translate this general framework into an explicit system dynamics model of the interaction of physiological loss, stressors and endogenous responses to produce a familiar variety of trajectories of functional ability over the life courses. Simulation experiments were implemented for both a 30-month duration with only one major stressor; and for the life course with an initial major stressor and subsequent stressors determined by the level of functional ability. For both contexts, variations in the few parameters in the scenarios led to a realistic range of trajectories of function over time.

Introduction

A hallmark of successful aging is a sustained ability to interact physically, socially and psychologically with the world late into the life course. This attribute is determined by functional ability modulated by features of the surrounding environment and, as proposed by the World Health Organization (WHO), can be represented at the individual level as prototypical life course trajectories (Beard et al., 2015). A core objective of aging research is to understand the factors that impact functional ability over one’s lifetime and to inform personal, clinical and public policy decisions that promote successful aging for individuals and populations.

A dominant concept among researchers and clinicians aiming to maximize functional ability in later years is “frailty”, a state of particularly high susceptibility to stressors. Several investigators have developed conceptual models of frailty, especially in older people (Buchner and Wagner, 1992; Bortz, 1993; Fried, 1994; Raphael et al., 1994; Rockwood et al., 1994; Walston and Fried, 1999; Varadhan et al., 2008). Indices of frailty are generally based on the counting of either functional deficits or of health conditions that are associated with functional deficits. Achieving a state of frailty is typically envisioned as the result of loss of physiological reserves reduced through cellular loss and dysfunction (Clegg et al., 2013). The rapid decline later in life is attributed to a decline in physiological reserves to the point that the next stressor is enough to “blow the tree over” (Clegg et al., 2013), manifesting as prolonged hospitalization, nursing home placement and death.

The difficulties with current approaches to conceptualizing frailty have been enumerated in reviews (Whitson et al., 2007; De Alfieri et al., 2011). One difficulty revealed in these reviews is that the many efforts at defining frailty and its determinants describe frailty in different ways that cannot be naturally mapped to one another (e.g. counts of deficits versus counts of conditions noted above). One particular potential shortcoming of existing frailty literature is that, while frailty measures are predictive of who is likely to experience a catastrophic functional loss, it is not clear whether components of frailty measures are also relevant to how one achieves or recovers from the frail state. Most importantly, it is not evident how frailty measures serve to guide what is needed to minimize the occurrence or impact of frailty. In an effort to better target clinical and public health efforts, the concept of frailty has been extended to the idea of “pre-frailty”, where lower counts of deficits or health conditions serve to identify “pre-frail” people who could benefit from aggressive interventions. Unfortunately, measures of pre-frailty suffer from the same difficulties as measures of frailty, namely that the pre-frail designation does not correspond to specific effective actions.

To understand the various patterns of functional ability over the life course, there has been increasing attention to loss due to various life stressors that diminish functional ability and the ability to recover from stressor-induced loss. This ability to recover, termed “resilience” (Cicchetti, 2010), may not merely be the opposite of frailty, although it seems sensible that frailty and resilience are correlated.

From this perspective, the processes underlying the trajectory of function over the life course involves a complex dynamic. Recent work supports this view (Lachman and Agrigoroaei, 2010; Zeng and Shen, 2010; Manning et al., 2014). Beyond the simple result of physiological loss—the process of deterioration with age—the trajectory of functional decline is the manifestation of the interplay between small and large life stressors, and response to those stressors. In addition to physiological responses, this interplay includes psychological and social responses. For example, recent studies indicate that psychological resilience, defined as the tendency to respond in a positive way to life’s challenges, is both a determinant of progression to disability as well as a modulator of the effects of disability on the performance of instrumental activities of daily living (Manning et al., 2014). Complicating the dynamics of the trajectory of functional ability is the presence of feedback loops, in which variables are both the cause and effect (e.g. stressors reduce functional ability and reduced functional ability promotes the occurrence of stressors).

We believe that to understand functional ability over the life course and, particularly, what might we do to enhance that trajectory, it would be valuable to construct a simulation model representing hypotheses about what is driving the diversity of life courses. Simulation modeling provides a valuable complement to empirical studies for understanding dynamically complex phenomena. Based on explicit, testable hypotheses about causal relationships, a model promotes the generation and testing of improved hypotheses about the determinants of functional trajectories both in the short and long term, and the identification of potential interventions to optimize that trajectory based on underlying drivers of functional loss or recovery at the level of the individual.

Here we describe such a conceptual model, implemented as a dynamic and testable simulation. Specifically, we sought to develop a relatively parsimonious dynamic model that can represent a wide variety of trajectories for functional ability described by the WHO (Beard et al., 2015).

Methods

The model representing the dynamic relationship of function, stressors and resilience over the life course was implemented using system dynamics (Forrester, 1961; Sterman, 2000; Homer and Hirsch, 2006). System dynamics modeling captures complexity by focusing on the causal relationships and dynamic feedback mechanisms between different parts of the system (Sterman, 2001). The system dynamics approach has been used to examine health service delivery (Levin and Roberts, 1976; Semwanga et al., 2016); health care quality improvement (Cavana et al., 1999; Hirsch and Immediato, 1999; Wolstenholme et al., 2007); patient flow and waiting time (Wolstenholme, 1999; Lane and Husemann, 2008; Vanderby and Carter, 2010); health human resources (Ishikawa et al., 2013; Ansah et al., 2015); long-term care for the elderly (Ansah et al., 2013); global healthcare management (Homer et al., 2000; Chick et al., 2008; Thompson and Tebbens, 2008); mental health (Huz et al., 1997; Smits, 2010); and chronic disease management (Homer et al., 2004, 2007; Siegel et al., 2011). This model is thematically similar to the health services delivery model by Levin and Roberts.

The model was developed as follows. First, a conceptual model of the dynamic interactions of functional ability, stressors and recovery, supported by evidence from the literature, was developed. Next, the conceptual model was presented to experts on function over the life course, to verify that the structure and assumptions regarding causal relationships are plausible in the context of existing evidence. The model was refined in an iterative process—supported by expert experience—until the model could satisfy requirements concerning its realism, clarity and ability to capture important issues relating to the purpose of the model. The process of establishing model realism and clarity used the Categories of Legitimate Reservation (CLR) rules (Noreen et al., 1995; Dettmer, 1997). We selected CLR compared to other approaches because it is an approach we use often and we have significant experience in using it in a modeling context. The CLR constitute a framework of eight specific tests, or proofs, used to verify cause-and-effect logic. They are clarity, entity existence, causality existence, cause insufficiency, additional cause, cause–effect reversal, predicted effect existence and tautology. The validation process involved a focused group interaction with clinicians and researchers with expertise on function over the life course. First, we presented our initial model and explained briefly the causal links and polarity. After the presentation, the discussion focused on the terminologies/concepts/variables used in the model. The aim was to ensure that the researchers and experts have a common understanding of these terminologies/concepts/variables. We went over each model variable to ensure that all experts accepted the definitions. Most of the variables in the initial model were changed and new variables were suggested. Subsequently, the discussion focused on the suggested causal linkages and polarities. Each proposed causal link was discussed to ensure that they had face validity and were supported by literature. As expected, some causal linkages were refined and new ones were proposed. Following verification, the model was parametrized using synthetic data. Finally, the model was run, and base-case and alternative scenarios were simulated to generate useful insights regarding the trajectory of stressor-induced functional recovery at the individual level.

Model components/parameters

Figure 1 shows the structure of the stressor-induced functional loss and recovery model. Numbers in square brackets in Figure 1 indicate references for relationships between variables represented in the model as shown in Table A1 in the Supporting Information. In the context of a simulation model, these variables take on very specific meaning.

Fig. 1.

Fig. 1.

Open in a new tab

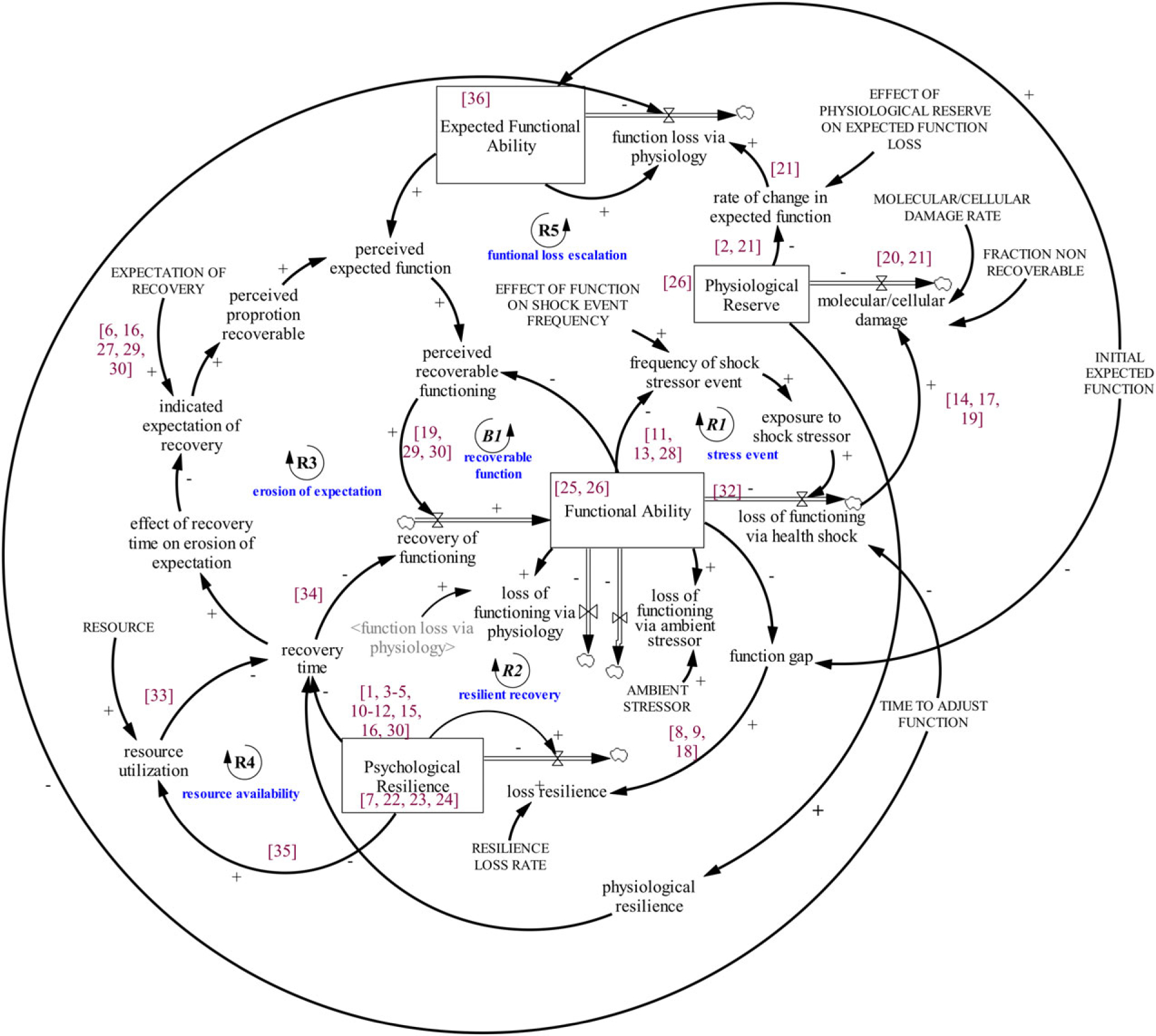
A stressor-induced functional loss and recovery model

Functional ability

Functional ability is the level an individual achieves in day-to-day activities. Since a person’s actual activities reflect the capacity in multiple domains individually and in combination (Pedrosa et al., 2010; Shimada et al., 2010; Bielak et al., 2012), functional ability is defined as an aggregate measure of the constituent domains (physiological, social and psychological). Functional ability, for the purpose of this model, could be assessed by a combined measure of key domains of function, such as the EQ-5D (EuroQol Group, 1990; Brooks, 1996; Herdman et al., 2011; Janssen et al., 2013). Note that the term “functional ability” used here corresponds to the term used by Beard of the WHO as “intrinsic ability”, whereas “functional ability” in the WHO framework includes both intrinsic ability and any environmental enhancements (Beard et al., 2015).

Expected functional ability

Expected function is the optimally achievable function in the absence of stressors. It is the reference function, which declines only via the manifestation of decline in physiological reserves. It provides a benchmark that an individual can compare to functional ability. Note that the adjective “expected” for a modeled quantity refers, in system dynamics parlance, to the value that one might aim for or that might apply in the absence of effects of other factors. The term “benchmark” might be a more intuitive alternative here.

Physiological reserve

Physiological reserve represents the aggregate measure of the performance of body organ systems (neurological, cardiac, hematopoietic, and so on) relative to an optimal level seen in young adulthood. An example of a physiological reserve embedded in the definition is the amount of oxygen consumed for the most intense activity a person typically achieves in daily life relative to that consumed by resting quietly (the metabolic equivalent (MET); Jetté et al., 1990). Other more global measures of physiological reserve have been proposed, such as grip strength (Syddall et al., 2003) or acylcarnitine levels (Lum et al., 2011).

Stressor

A stressor is defined as an event (e.g. surgery, hip fracture or death of a loved one) that reduces functional ability, and its magnitude directly corresponds to the resultant reduction in functional ability. In the context of the life course model, stressors were hypothesized to be of two types: ambient and shock event stressors. Ambient stressors are everyday stressors we are exposed to due to our environment, while shock event stressors are the adverse events that perceptibly affect functional ability as they occur.

Psychological resilience

This reflects a composite of an individual’s psychological features that promote or inhibit recovery. A person with high psychological resilience will, in the wake of a stressor-induced functional loss, respond in a way that promotes the rapid recovery of the loss, whereas an individual with low psychological resilience will respond in a way that leads to slow recovery of loss or deterioration. The Connor–Davidson resilience scale (CD-RISC; Connor and Davidson, 2003) is an example measure of psychological resilience. Note that some authors use the term resilience to refer to a characteristic of a recovery pattern (e.g. a “resilient recovery” is one that is rapid and complete). Here resilience refers to a personal characteristic (i.e. the tendency to respond positively to loss based on traits such as personal mastery, or on past responses to adverse events.)

Physiological resilience (e.g. the ability to heal a wound) is determined by physiological reserve, with the added possibility that low physiological reserve can reduce the rate of recovery both directly (through slowing the rate of recovery from a stressor) and indirectly (through reducing functional ability which can enhance the loss of psychological resilience) (Clegg et al., 2013).

Expectation of recovery

This is the proportion of the lost function (the difference between expected functional ability and current functional ability) that an individual expects will return during recovery. This may reflect optimism (Scheier et al., 1989), an individual’s tendency to weight expected functional ability over functional ability in assessing achievable recovery. A higher expectation implies a faster and more complete recovery, whereas lower expectation suggests otherwise. Note that, while this feature might be considered part of the definition of resilience, here we treat expectation of recovery as a distinct characteristic. Scales such as the life orientation test (LOT; Scheier and Carver, 1985), among many others (Taylor et al., 2004; Glaesmer et al., 2012; Gavrilov-Jerković et al., 2014), may be used to assess a person’s inclination to expect much of themselves relative to their expected function.

Resource availability

Despite the capacity and the will to recover, actual recovery can be inhibited by lack of access to treatment, such as physical therapy or surgical procedures for recovery from hip fracture. Nominally, if typically needed treatments are fully available, affordable and accessible, then recovery is optimal. Above this level, recovery is not further enhanced, but below it is diminished. The term “resource” is used, then, to refer to the degree to which “needed” resources can be brought to bear through availability, affordability or accessibility.

Model structure

The model structure represents the relationships between the parameters described above. Details of the simulation, including all model references, equations and input parameters, are available in Tables A1–A4 in the online Supporting Information.

Recognizing that organ systems (physiological reserves) have excess capacity that allows an individual to accommodate some organ decline without evident loss in actual function (Stern, 2009; Clegg et al., 2013) we introduced the concept of “physiological reserve below which function is measurably affected” (Stern, 2009). We treat this phenomenon as exogenous, though there are suggestions that the underlying mechanism is the result of dynamics where compensatory mechanisms for recovering function become dysfunctional leading to accelerated loss rather than improvement (Clegg et al., 2013). Physiological reserve takes on an initial value determined early in life and decreases via molecular or cellular damage at a constant rate (Baker and Martin, 1997; Sehl and Yates, 2001). Since we track the cumulative value of this parameter, it is referred to as a “stock”. When physiological reserve diminishes beyond the threshold value of “physiological reserves below which function is affected”, physiological reserve decline manifests as functional decline.

Expected functional ability is modeled as a stock and decreases as physiological reserves decline. Functional ability is represented in the model as a stock. It decreases via loss of underlying physiological function as well as exposure to ambient and shock event stressors. It increases by return of recoverable stressor-induced loss. As required for logical consistency, loss of function via physiology is identical for both functional ability and expected functional ability. Hence the difference in the functional ability and expected functional ability is attributable only to exposure to recoverable stressors.

The stress event feedback loop (R1) represents the dynamic relationship between stressors and functional ability. This loop depicts the phenomenon where individuals with low functional ability experience stressors more frequently and of greater intensity than those with high functional ability (e.g. people with low balance and strength are more likely to fall). The consequent stressors further reduce functional ability, which, in turn, leads to greater vulnerability to stressors—a reinforcing loop.

Operationally, stressor events are modeled as instantaneous pulses or “shocks” (Levin and Roberts, 1976), resulting in a fixed magnitude of functional loss at a frequency that increases as functional ability diminishes. A loss of functional ability due to a stressor creates a gap between expected functional ability and functional ability. The gap is referred to as “perceived recoverable function”, which is a weighted average of the difference between the expected functional ability and functional ability. The weight is the value assigned to “expectation of recovery”. A weight of one indicates an expectation that potential for actual function is equivalent to expected function, whereas a weight less than one indicates recovery expectation lower than expected function. Thus recovery of loss of function for the majority of the life course is attributable to two factors: (i) the recognition of a gap between perceived recoverable function and functional ability; and (ii) the marshaling of psychological resilience to respond promptly to a functional loss. The latter factor is modulated by availability, affordability and accessibility of required resources and the physiological reserve required for recovery (physiological resilience).

The recoverable function feedback loop (B1) denotes the reciprocal relationship between the perception of recoverable loss of function and the rate of recovery of stressor-induced functional loss. The higher the expectation of recovery, the greater the perceived recoverable function, and the more an individual engages in activities that promote recovery. Over a similar recovery time, individuals with greater perceived recoverable function tend to recover more function more quickly than those with lower perceived recoverable function. The recoverable function feedback loop relates to the assumption that, as the gap between functional ability and perceived recoverable function closes, recovery rate diminishes (akin to progressively turning off a water tap as a glass becomes full).

Psychological resilience is represented as a stock that can accumulate or deplete over time. The rate at which this stock diminishes can increase as functional ability declines. If so, this sets up a dynamic interaction depicted by the resilient recovery feedback loop (R2). For the resilient recovery feedback loop, a decline in functional ability negatively affects an individual’s ability to interact effectively with their environment, which creates a gap between functional ability and expected functional ability. Over time, as function declines, it gradually erodes the psychological features that promote recovery. Thus individuals with low functional ability lose their rate of response to a lost function more quickly than individuals with high functional ability. A depleted stock of psychological resilience directly increases the time it takes to recover lost function, which consequently inhibits the potential for recovery—a negative reinforcing feedback loop.

The erosion of expectation feedback loop (R3) captures the dynamic relationship between recovery time and expectation of recovery. As recovery time for a lost function increases, the expectation of recovery is postulated to decrease. Consequently, perceived recoverable function is assumed to decrease, leading to suboptimal recovery. However, as indicated in the resource feedback loop (R4), resource levels conditional on high psychological and physiological resilience decrease recovery time (promote faster recovery). Short recovery time, given the model assumptions, will lead to better recovery and increase functional ability and psychological resilience. Lastly, the functional loss escalation feedback loop (R5) shows how an exposure to shock stressor events, could lead to a reduction in expected functional ability via molecular/cellular damages, which in turn causes perceived recoverable functioning and recovery to decrease. As a result, physical function decreases, thereby increasing exposure to more stressors.

Again, note that physiological reserve is indirectly affecting the rate of recovery through an intermediary variable, physiological resilience, and is thus determined by the value of the underlying stock of physiological reserve. In addition, the rate of recovery is directly affected by the current value of physiological reserve, representing, for example, the impact of poor wound healing.

Simulation experiment conditions

Experiment 1

In this experiment an individual experiences constant ambient stress to which he or she is able to respond promptly and effectively. For the purpose of this experiment, we assume that such an individual will not experience any major stressor that significantly decreases functional ability either in the short or long term.

In addition to the experiment, we simulated four scenarios to test the ability of the model to generate a range of realistic trajectories by modifying three inputs: (i) resilience; (ii) expectation of recovery; and (iii) resources. These experiments were implemented under two different contexts: (i) short duration, where the individual experiences both a constant ambient stress and one shock event stressor and functional ability is assessed over 30 months; and (ii) life course, where the individual experiences both a constant ambient stress and initial abrupt stressor, as well as subsequent discrete stressors at a frequency that increases as functional ability declines over the entire life course.

Experiment 2

Here we model the effects of ambient stress on a non-psychologically resilient individual, assuming no major discrete stressors. One example is a person who resides in a high-crime neighborhood and, though they are not a victim of crime, is exposed to ambient stress that progressively erodes their aggregate functional ability.

Experiment 3

This scenario assumes the individual has high psychological resilience and high expectation of recovery as well as resources. An illustration is a 60-year-old person who is highly educated, retired from work and has experienced multiple medical conditions over their life, including successful recovery from a cancer surgery. The initial stressor is a hip fracture but following surgery this person is expected to make full recovery. They have medical insurance that will reimburse for all their medical cost. With the support of their family, they diligently attend rehabilitation sessions in the rehabilitation center near their house.

Experiment 4

Here, we simulate an individual with high initial psychological resilience but relatively low expectation of recovery. An example is a 60 year-old person who has led a full life in their younger days. However, they believe that it is natural to experience functional decline in later years and indeed sees this as a sign to take it easy and let others do for them as a change. As initial stressor, they have a stroke, and while rehabilitation would be recommended, they undergo a few sessions with moderate enthusiasm then drop out. In part, this is due to low expectations from rehabilitation. While they have sufficient resources, they are concerned about diminishing the estate they will leave their children and, given their acceptance of functional loss, they are unwilling to spend resources on medical care.

Experiment 5

This represents an individual with significantly low initial psychological resilience and low expectation of recovery and resources. An illustration is a 60 year-old person who has experienced multiple major disappointments in life (psychological and/or physical), which has led the person to believe that their life is guided by circumstances. They have little family support and receive monthly payouts from the government. They also have diabetes, and eventually develop a severe leg ulcer and their initial stressor is an amputation. They are unwilling to learn to enhance their mobility and is argumentative and defiant towards the nurse who visits them at home to assist with their diabetes care.

Table 1 shows the input values used to implement the scenarios for the short-duration and life course simulation.

Table 1.

Simulation experiments input: short-duration and life course

Parameter Experiment 1 Experiment 2 Experiment 3 Experiment 4 Experiment 5
Baseline expectation of recovery 1 1 1 0.8 0.25
Resources 1 1 1 1 0.25
Initial psychological resilience 100 100 100 100 30
Open in a new tab

Results

The results for functional ability for the five simulation experiment conditions are shown in Figure 2 for the short duration and Figure 3 for the life course. For each simulation duration, we identified five patterns resulting from the five experimental conditions, denoted as (i) optimal trajectory (Experiment 1); (ii) declining trajectory (Experiment 2); (iii) full recovery (Experiment 3); (iv) moderate recovery (Experiment 4); and (v) deteriorating recovery (Experiment 5).

Fig. 2.

Fig. 2.

Open in a new tab

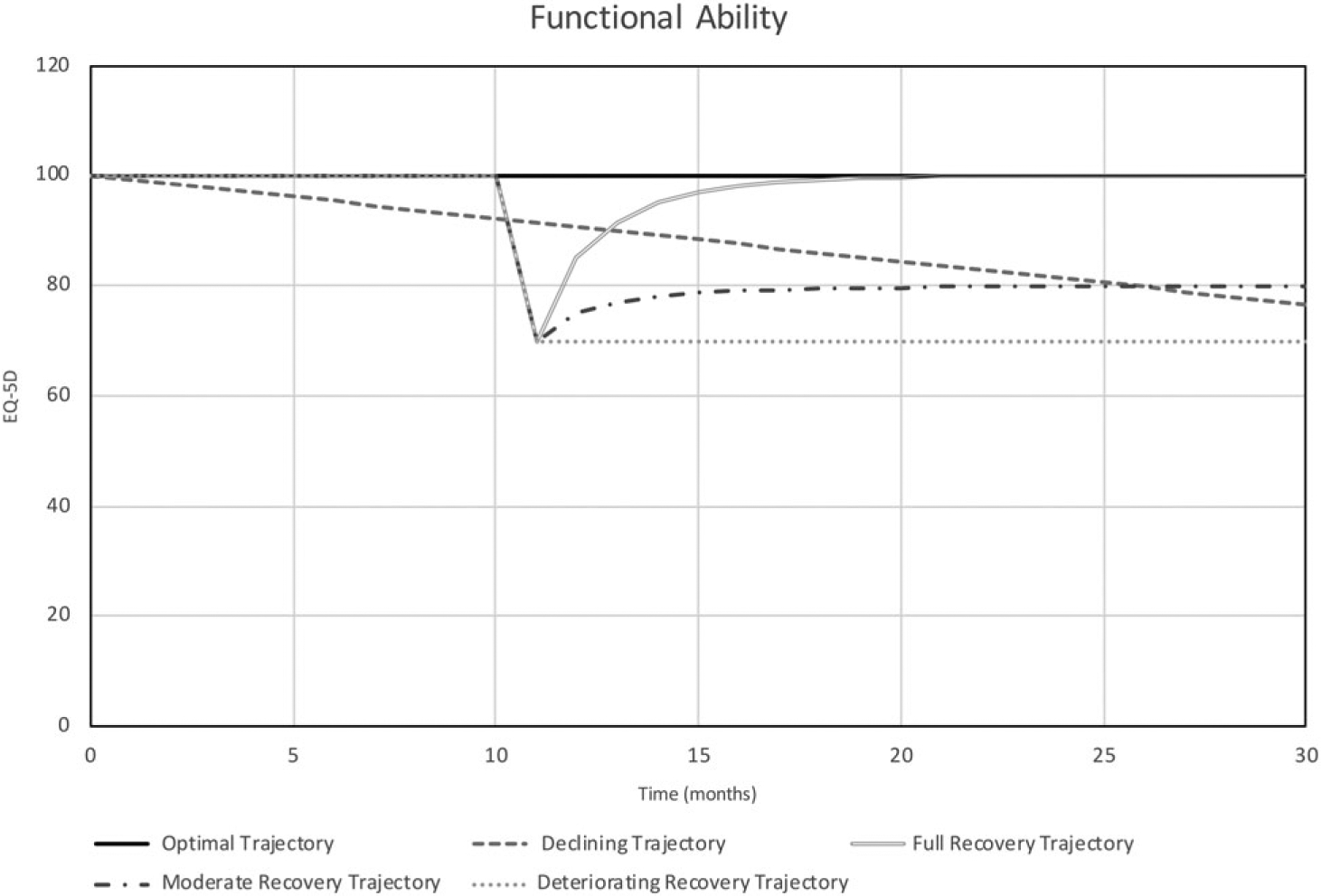
Short-duration patterns of functional ability

Fig. 3.

Fig. 3.

Open in a new tab

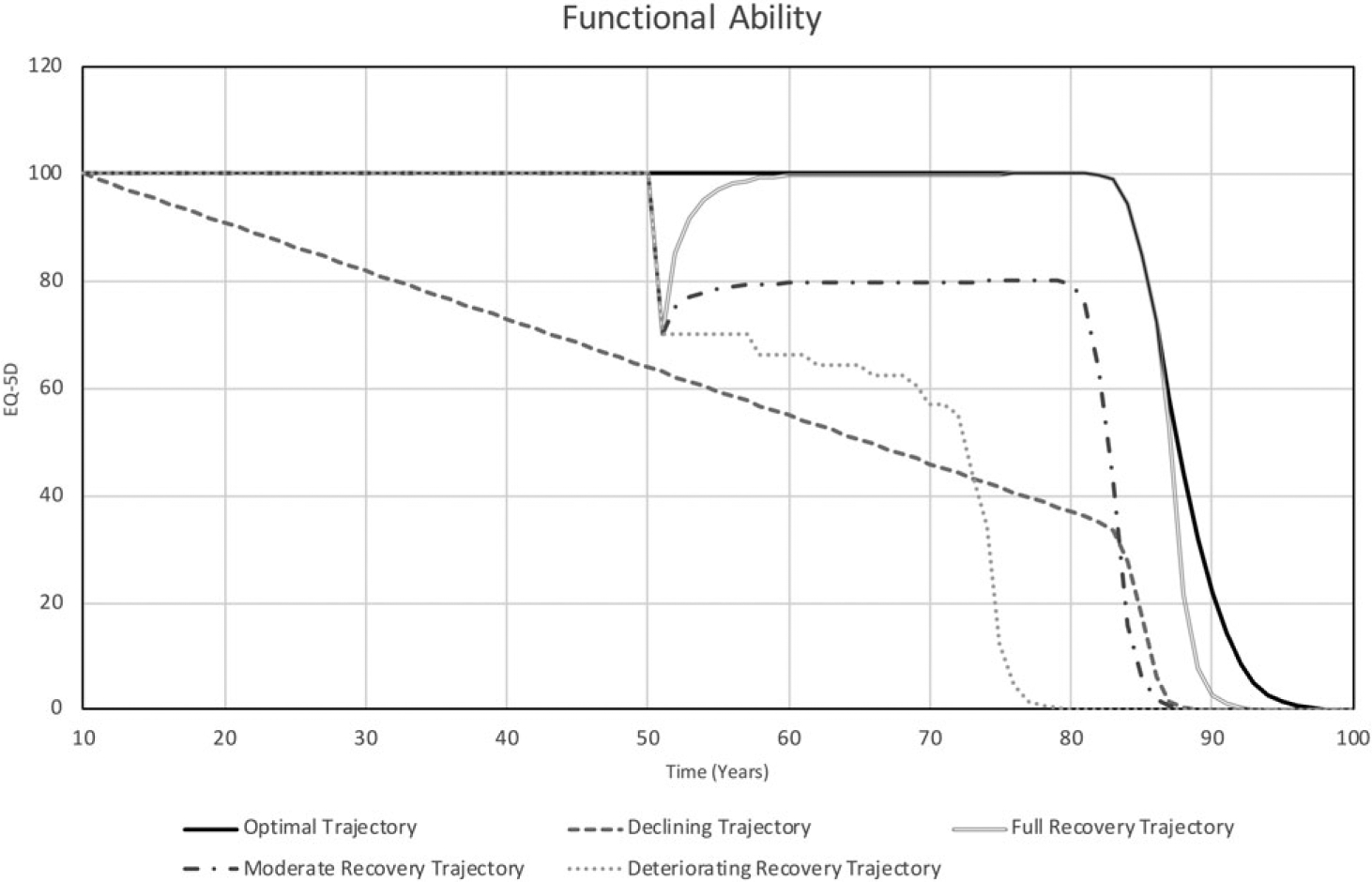
Life course patterns of functional ability

Under the short-duration experiments (Figure 2), for the optimal trajectory pattern, functional ability remains high (100), because we assumed that the individual is able to respond effectively and promptly to ambient stress and that under this scenario they experience no major discrete stressor. In addition, we assume that loss of function due to decline in physiological reserve is imperceptible over 30 months and that ambient stress is dealt with adequately and promptly; thus functional ability is not affected.

In the case of declining trajectory pattern, a constant decline of functional ability is observed over the simulation time. Functional ability decreases from 100 to 76 by the end of the simulation, due to the inadequate response to ambient stress.

For the full recovery trajectory pattern, functional ability bounces back after exposure to a sudden stressor event to the pre-stressor level of function.

In the moderate recovery trajectory pattern, the level of function after exposure to a stressor is projected to improve but settles at a level lower (80) than the pre-stressor function because of lower expectation for recovery.

Lastly, for deteriorating recovery trajectory pattern, the level of function is expected to remain low due to low resilience, low expectation of recovery and low resources. The level of function at the end of the simulation is 70.

Figure 3 shows the trajectories of functional ability over the life course (Peeters et al., 2013). For the optimal trajectory pattern, function remains relatively unchanged from age 10 to about age 80 and thereafter begins to decrease, reflecting the decline in physiological reserves due to molecular/cellular damage—but remain relatively high until end of life. As indicated, optimal trajectory falls to zero by age 96.

For the declining trajectory scenario, a constant decline of functional ability from 100 to 0 is observed at around age 87.

Under the full recovery trajectory pattern, with good psychological resilience, high expectation and available resources, despite the relatively full recovery to the initial stressor, exposure to additional stressors, coupled with decline in physiological reserves further decreases function. Here decline progresses until function reaches zero (death) at age 91.

In the moderate recovery trajectory pattern, because expectation for recovery and access to services are lower than in the optimal trajectory scenario, following the decline in function, life course functional trajectory is further suppressed with a further shortened lifespan. Functional ability in this experiment declines to zero by age 86.

Lastly, under the deteriorating recovery trajectory pattern, the initial stressor-induced decline in function is reinforced by additional exposure to stressors without counterbalancing recovery, which leads to sharp decline in function and a short lifespan. Functional ability is projected to decline to zero by age 77.

Discussion and conclusions

In this paper, we demonstrate a dynamic model of stressor-induced functional loss and recovery that simulates a realistic range of trajectories of functional ability over a short duration and over the life course. The results are consistent with the patterns of functional trajectories described by Beard of the World Health Organization (WHO) (Beard et al., 2015). The results are also consistent with empirical evidence regarding short-term functional recovery after a major stressor—for example, hip fracture (Ming-Yueh et al., 2012), stroke (Kyoung et al., 2014) and postoperative delirium (Saczynski et al., 2012), as well as patterns of functional ability over the life course (Peeters et al., 2013).

Because the proposed model is deterministic, the observed dynamics can be explained by direct causal relationships (Figure 4). The observed patterns expressed in the model result from the ability of individuals to perceive recoverable functioning (lost function that could be recovered) and recovery time, which is the result of marshalling of psychological resilience, conditional on resources to engage in activities that promote recovery and the physiological reserve required for recovery (physiological resilience). Figure 4A shows the perceived recoverable functioning under each scenario, under the short duration. For a given stressor, the higher the expectation of recovery the larger is the perceived recoverable functioning. The ability to close the functioning gap (recover the perceived recoverable functioning) depends on psychological resilience, and is conditional on resource availability and physiological resilience. Nonetheless, since psychological resilience (Figure 4B) is dynamic and changes as functional ability changes, a reduction in function due to exposure to a stressor causes psychological resilience to decrease. Conversely, as function improves so does psychological resilience. Given the level of psychological resilience, conditional on physiological reserve/resilience and resources, recovery time (Figure 4C) is determined. The higher the resilience and resources, the lower is the recovery time (which is equivalent to faster recovery) and vice versa. The recovery time then determines the recovery of the perceived recoverable functioning (Figure 4D).

Fig. 4.

Fig. 4.

Open in a new tab

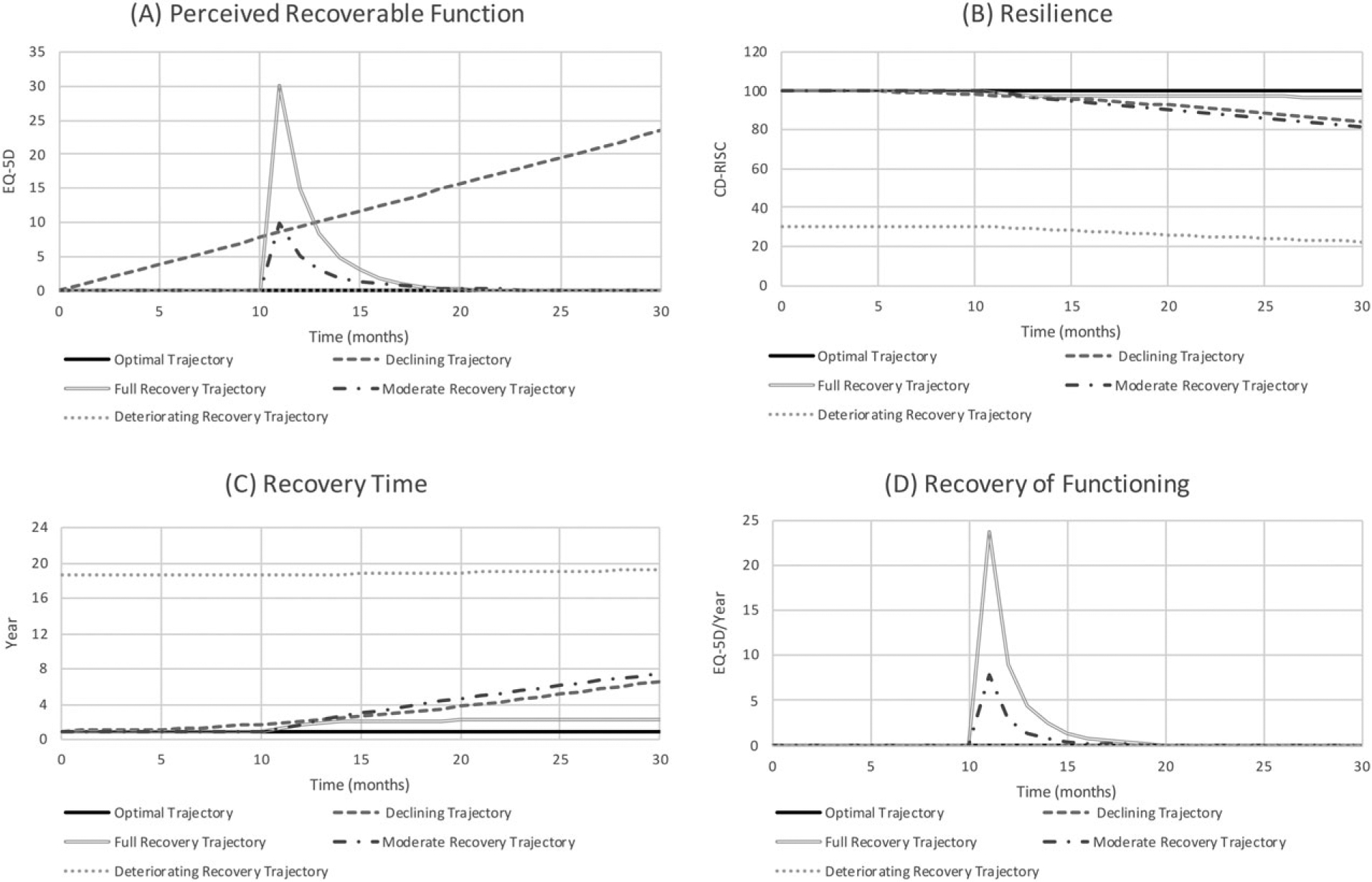
Dynamics of function (short duration)

The dynamics of the life course experiments are similar to the short-duration experiments, except for the assumed decrease in function and exposure to multiple stressors over the course of life. For the life course experiments, a sudden increase in perceived recoverable functioning (Figure 5A) is an indication of a new event (exposure to new stressors). The process of recovering the perceived recoverable functioning requires the marshalling of psychological resilience (Figure 5B), conditional on resources and physiological reserve, and as functional ability decreases due to a decline in physiological reserves and exposure to stressors, psychological resilience decreases. The greater the resilience (psychological and physiological), the shorter is the recovery time (Figure 5C) and recovery of lost function (Figure 5D), and vice versa.

Fig. 5.

Fig. 5.

Open in a new tab

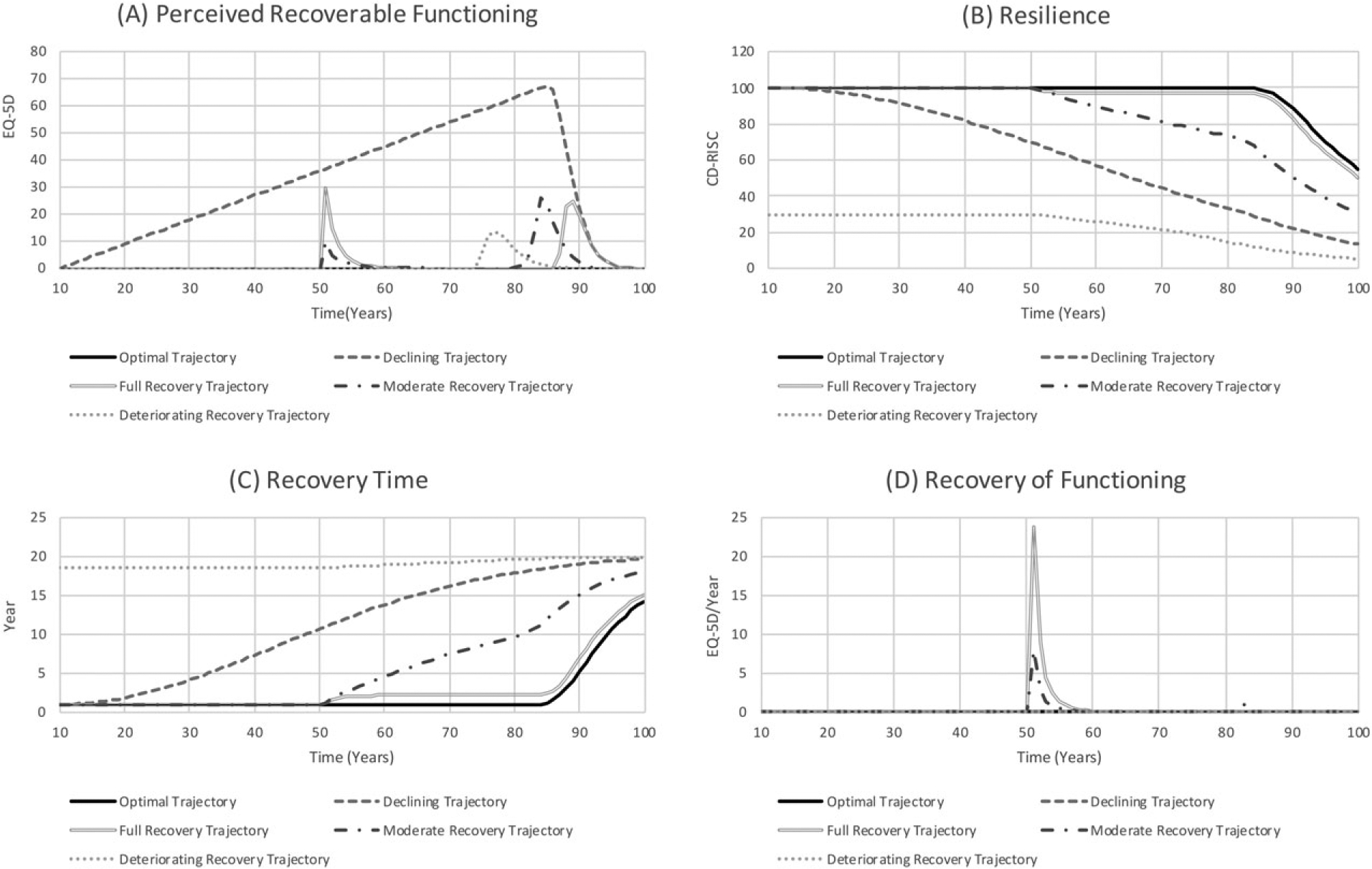
Dynamics of function (life course)

To our knowledge, this is the first macro-level model intended to simulate the diversity of life course trajectories of functional ability. The model is useful in several ways. First, assumptions are explicit; the model provides a set of testable hypotheses. For example, we can study the importance of resilience and the reciprocal nature of its relationship with functional ability. The results of these investigations can then be used to modify structure or input estimates.

A second use of the model is to suggest specific interventions and the mechanisms by which those interventions might improve patterns of decline (Table 2). Some of these interventions may be self-evident, such as exercise to increase functional ability. Others may be less obvious, such as interventions to realistically raise expectations for potential recovery for individuals who otherwise consider reversible losses to be inevitable and permanent; or strategies to make small functional declines evident that would otherwise be disregarded.

Table 2.

Potential interventions to improve patterns of decline

Enhance resources for recovery

  • Make rehabilitation services available, affordable and accessible

  • Implement strategies to improve utilization of available resources for recovery

Build resilience

  • Teach people to anticipate stressors and to respond in a forwarding way when they inevitably occur

  • Work with families and other caregivers to respond to functional decline to promote recovery (e.g. supporting aggressive rehabilitation and not overprotecting)

  • Systematically engage people around the time of stressful events as teachable moments to encourage individuals to respond more resiliently

Improve functional ability

  • Promote exercise

  • Facilitate social engagement

  • Treat conditions (e.g. pulmonary and cardiac rehabilitation, depression)

Reduce the frequency and intensity of stressors

  • Improve chronic disease management to reduce the development of highly stressful complications

  • Reduce environmental hazards (falls risk in built environment, reduce pollution/second hand smoke)

  • Use protective devices/treatments (e.g. hip protectors; flu, pneumococcal and zoster vaccinations)
Open in a new tab

Third, the current model can facilitate systematic evaluation of interventions. The model here suggests intermediate measures that should be affected by an intervention and can serve as primary measures for rapid cycle trials (e.g. uptake of rehabilitation services). Fourth, the model provides a foundation for exploring the impact of potential interventions. For example, based on the causal structure a particular intervention may seem promising, but when its potential impacts are projected quantitatively it becomes apparent that the intervention will require infeasible levels of efficacy or have unacceptable resource requirements.

Lastly, the model could be used to help patients understand the feedback loops that contribute to their health, and also motivate people to take the recommended actions to promote recovery and resilience. In addition, the model could potentially be used for behavioral experiments that can assess group decision making in terms of taking actions to enhance health (as a management flight simulator).

Supplementary Material

Table A1 Model References

Table S1. References for the model.

Table A2 Model equations for short duration model

Table S2. Model equations for short duration model.

Table A3 Model equations for life course model

Table S3. Model equations for life course model.

Table A4 Model inputs for both short duration and life course model

Table S4. Model inputs for both short duration and life course model.

Acknowledgements

This work was supported by the Singapore Ministry of Health’s National Medical Research Council under its STaR Award Grant (grant number NMRC|STaR|0005|2009) as part of the project “Establishing a Practical and Theoretical Foundation for Comprehensive and Integrated Community, Policy and Academic Efforts to Improve Dementia Care in Singapore”.

Biographies

David B. Matchar is Professor of Medicine at Duke University and Director of the Program in Health Services and Systems Research at Duke-NUS Medical School. He holds a MD from University of Maryland. He focuses his research on the evaluation of clinical practice based on “best evidence,” and the implementation and evaluation of innovative strategies to promote practice change.

John P. Ansah is an Assistant Professor in the Program in Health Services and Systems Research at Duke-NUS Medical School. He holds a Ph.D. in the System Science methodology of System Dynamics from University of Bergen. His research interests lie broadly in developing healthcare strategy and planning simulation models that are rigorous, evidence-based and customized to the optimal usefulness of stakeholders to inform policy.

Victoria Koh is a Research Assistant in the Program in Health Services and Systems Research at Duke-NUS Medical School. She holds a BEng from the National University of Singapore. Her main research interest lies in dynamic simulation modeling for health services planning.

Heather E. Whitson is an Associate Professor in Medicine, Ophthalmology and the Deputy Director of the Center for the Study of Aging and Human, at the Department of Medicine, Duke University, Durham. Dr. Whitson’s research is focused on improving care and health outcomes for people with multiple chronic conditions. Within the Duke Aging Center, she leads research efforts aimed at promoting resilience to late-life stressors (e.g., surgery, sensory loss).

Footnotes

Conflict of interest

The authors declare that they have no competing interests.

Supporting information

Additional supporting information may be found in the online version of this article at the publisher’s website.

References

  1. Ansah JP, De Korne D, Bayer S, Pan C, Jayabaskar T, Matchar DB, Lew M, Phua A, Koh V, Lamoureux E, Quek D. 2015. Future requirements for and supply of ophthalmologists for an aging population in Singapore. Human Resources for Health 13: 86. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ansah JP, Matchar DB, Love SR, Malhotra R, Do YK, Chan A, Eberlein R. 2013. Simulating the impact of long-term care policy on family eldercare hours. Health Services Research 48: 773–791. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Baker GT, Martin GR. 1997. Molecular and biologic factors in aging: the origins, causes, and prevention of senescence In Geriatric medicine, Cassel CK, Cohen HJ, Larson EB, Meier DE, Resnick NM, Rubenstein LZ, Sorensen LB (eds). Springer: New York. [Google Scholar]
  4. Beard J, Officer A, de Carvalho IA, Sadana R, Pot AM, Michel JP, Lloyd-Sherlock P, Epping-Jordan JE, Peeters GMEEG, Mahanani WR, Thiyagarajan JA, Chatterji S. 2015. World report on aging and health. World Health Organization: Geneva. [Google Scholar]
  5. Bielak AAM, Anstey KJ, Christensen H, Windor TD. 2012. Activity engagement is related to level, but not change in cognitive ability across adulthood. Psychology and Aging 27: 219–228. [DOI] [PubMed] [Google Scholar]
  6. Bortz WMI. 1993. The physics of frailty. Journal of the American Geriatrics Society 41: 1004–1008. [PubMed] [Google Scholar]
  7. Brooks R 1996. EuroQol: the current state of play. Health Policy 37: 53–72. [DOI] [PubMed] [Google Scholar]
  8. Buchner DM, Wagner EH. 1992. Preventing frail health. Clinics in Geriatric Medicine 8(1): 17. [PubMed] [Google Scholar]
  9. Cavana RY, Davies PK, Robson RM, Wilson KJ. 1999. Drivers of quality in health services: different worldviews of clinicians and policy managers revealed. System Dynamics Review 15(3): 331–340. [Google Scholar]
  10. Chick SE, Mamani H, Simchi-Levi D. 2008. Supply chain coordination and influenza vaccination. Operations Research 56(6): 1493–1506. [Google Scholar]
  11. Cicchetti D 2010. Resilience under conditions of extreme stress: a multilevel perspective. World Psychiatry 9: 145–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Clegg A, Young J, Iliffe S, Rikkert MO, Rockwood K. 2013. Frailty in elderly people. Lancet 381: 752–762. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Connor KM, Davidson JRT. 2003. Development of a new resilience scale: the Connor–Davidson Resilience Scale (CD-RISC). Depression and Anxiety 18: 76–82. [DOI] [PubMed] [Google Scholar]
  14. De Alfieri W, Costanzo S, Borgogni T. 2011. Biological resilience of older adults versus frailty. Medical Hypotheses 76: 304–305. [DOI] [PubMed] [Google Scholar]
  15. Dettmer HW. 1997. Goldratt’s theory of constraints: a systems approach to continuous improvement. ASQC Quality Press: Milwaukee, WI. [Google Scholar]
  16. Euroqol Group. 1990. EuroQol: a new facility for the measurement of health-related quality of life. Health Policy 16: 199–208. [DOI] [PubMed] [Google Scholar]
  17. Forrester JW. 1961. Industrial dynamics MIT Press: Cambridge, MA. [Google Scholar]
  18. Fried LP. 1994. Frailty In Principles of geriatric medicine and gerontology, Hazzard WR, Bierman RL, Blass JP, Ettinger WH, Halter JB (eds). McGraw-Hill Health Professions Division: New York. [Google Scholar]
  19. Gavrilov-Jerković V, Jovanović V, Žuljević D, Brdarić D. 2014. When less is more: a short version of the personal optimism scale and the self-efficacy optimism scale. Journal of Happiness Studies 15: 455–474. [Google Scholar]
  20. Glaesmer H, Rief W, Martin A, Mewes R, Brahler E, Zenger M, Hinz A. 2012. Psychometric properties and population-based norms of the Life Orientation Test Revised (LOT-R). British Journal of Health Psychology 17: 432–445. [DOI] [PubMed] [Google Scholar]
  21. Herdman M, Gudex C, Lloyd A, Janssen MF, Kind P, Parkin D, Bonsel G, Badia X. 2011. Development and preliminary testing of the new five-level version of EQ-5D (EQ-5D-5 L). Quality of Life Research 20: 1727–1736. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Hirsch G, Immediato CS. 1999. Microworlds and generic structures as resources for integrating care and improving health. System Dynamics Review 15(3): 315–330. [Google Scholar]
  23. Homer J, Hirsch G, Milstein B. 2007. Chronic illness in a complex health economy: the perils and promises of downstream and upstream reforms. System Dynamics Review 23(2–3): 313–343. [Google Scholar]
  24. Homer J, Hirsch G, Minniti M, Pierson M. 2004. Models for collaboration: how system dynamics helped a community organise cost-effective care for chronic illness. System Dynamics Review 20(3): 199–222. [Google Scholar]
  25. Homer J, Ritchie-Dunham J, Rabbino H, Puente LM, Jorgensen J, Hendricks K. 2000. Toward a dynamic theory of antibiotic resistance. System Dynamics Review 16(4): 287–319. [Google Scholar]
  26. Homer JB, Hirsch GB. 2006. System dynamics modeling for public health: background and opportunities. American Journal of Public Health 96: 452–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Huz S, Andersen DF, Richardson GP, Boothroyd R. 1997. A framework for evaluating systems thinking interventions: an experimental approach to mental health system change. System Dynamics Review 13(2): 149–169. [Google Scholar]
  28. Ishikawa T, Ohba H, Yokooka Y, Nakamura K, Ogasawara K. 2013. Forecasting the absolute and relative shortage of physicians in Japan using system dynamics model approach. Human Resources for Health 11: 41. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Janssen MF, Pickard AS, Golocki D, Gudex C, Niewada M, Scalone L, Swinburn P, Busschbach J. 2013. Measurement properties of the EQ-5D-5L compared to the EQ-5D-3L across eight patient groups: a multi-country study. Quality of Life Research 22: 1717–1727. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Jetté M, Sidney K, Blumchen G. 1990. Metabolic equivalents (METS) in exercise testing, exercise prescription, and evaluation of functional capacity. Clinical Cardiology 13: 555–565. [DOI] [PubMed] [Google Scholar]
  31. Kyoung BL, Seong HL, Kyung HK, Ki JK, Yang RK, Woo NC, Jun WY, Young DK, Byong YH. 2014. Six-months functional recovery of stroke patients: a multi-time point study. International Journal of Rehabilitation Research 38(2): 173–180. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Lachman ME, Agrigoroaei S. 2010. Promoting functional health in midlife and old age: long-term protective effects of control beliefs, social supports, and physical exercise. PLoS One 5(10): e13297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Lane DC, Husemann E. 2008. System dynamics mapping of acute patient flows. Journal of the Operational Research Society 59(2): 213–224. [Google Scholar]
  34. Levin G, Roberts EB. 1976. The dynamics of human service delivery. Ballinger: Cambridge, MA. [Google Scholar]
  35. Lum H, Sloane R, Huffman KM, Kraus VB, Thompson DK, Kraus WK, Bain JR, Stevens R, Pieper CF, Taylor GA, Newgard CB, Cohen HJ, Morey MC. 2011. Plasma acylcarnitines are associated with physical performance in elderly men. Journal of Gerontology: Medical Sciences 66A(5): 548–553. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Manning LK, Carr DC, Kail BL. 2014. Do higher levels of resilience buffer the deleterious impact of chronic illness on disability in later life? Gerontologist 56(3): 514–524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Ming-Yueh T, Yea-Ing LS, Liang J. 2012. Functional recovery of older hip-fracture patients after interdisciplinary intervention follows three distinct trajectories. Gerontologist 52(6): 833–842. [DOI] [PubMed] [Google Scholar]
  38. Noreen EW, Smith D, Mackey JT, IMA Foundation for Applied Research. 1995. The theory of constraints and its implications for management accounting. North River Press: Great Barrington, MA. [Google Scholar]
  39. Pedrosa H, De Sa A, Guerreiro M, Maroco J, Simoes MR, Galasko D, de Memdonça A. 2010. Functional evaluation distinguishes MCI patients from healthy elderly people: the ADCS/MCI/ADL scale. Journal of Nutrition, Health and Aging 14: 703–709. [DOI] [PubMed] [Google Scholar]
  40. Peeters G, Dobson AJ, Deeg DJH, Brown WJ. 2013. A life-course perspective on physical functioning in women. Bulletin of the World Health Organization 91: 661–670. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Raphael D, Cava M, Brown I, Renwick R, Heathcote K, Weir N, Wright K, Kirwan L. 1994. Frailty: a public health perspective. Canadian Journal of Public Health 86: 224–227. [PubMed] [Google Scholar]
  42. Rockwood K, Fox RA, Stolee P, Robertson D, Beattie BL. 1994. Frailty in elderly people: an evolving concept. Canadian Medical Association Journal 150: 489–495. [PMC free article] [PubMed] [Google Scholar]
  43. Saczynski JS, Marcantonio ER, Quach L, Tamara GF, Gross A, Inouye SK, Jones RN. 2012. Cognitive trajectories after postoperative delirium. New England Journal of Medicine 367: 30–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Scheier MF, Carver CS. 1985. Optimism, coping, and health: assessment and implications of generalized outcome expectancies. Health Psychology 4: 219–247. [DOI] [PubMed] [Google Scholar]
  45. Scheier MF, Matthews KA, Owens JF, Magovern GJ, Lefebvre RC, Abbott RA, Carver CS. 1989. Dispositional optimism and recovery from coronary artery bypass surgery: the beneficial effects on physical and psychological well-being. Journal of Personality and Social Psychology 57: 1024–1040. [DOI] [PubMed] [Google Scholar]
  46. Sehl ME, Yates FE. 2001. Kinetics of human aging. I. Rates of senescence between ages 30 and 70 years in healthy people. Journals of Gerontology, Series A: Biological Sciences and Medical Sciences 56: B198–B208. [DOI] [PubMed] [Google Scholar]
  47. Semwanga AR, Nakubulwa S, Adam T. 2016. Applying a system dynamics modeling approach to explore policy options for improving neonatal health in Uganda. Health Research Policy and Systems 14: 35. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Shimada H, Ishizaki T, Kato M, Morimoto A, Tamate A, Uchiyama Y, Yasumura S. 2010. How often and how far do frail elderly people need to go outdoors to maintain functional capacity? Archives of Gerontology and Geriatrics 50: 140–146. [DOI] [PubMed] [Google Scholar]
  49. Siegel CA, Siegel LS, Hyams JS, Kugathasan S, Markowitz J, Rosh JR, Leleiko N, Mack DR, Crandall W, Evans J, Keljo DJ, Otley AR, Oliva-Hemker M, Farrior S, Langton CR, Wrobel IT, Wahbeh G, Quiros JA, Silber G, Bahar RJ, Sands BE, Dubinsky MC. 2011. Real-time tool to display the predicted disease course and treatment response for children with Crohn’s disease. Inflammatory Bowel Disease 17(1): 30–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Smits M 2010. Impact of policy and process design on the performance of intake and treatment processes in mental health care: a system dynamics case study. Journal of Operational Research Society 61(10): 1437–1445. [Google Scholar]
  51. Sterman J 2000. Business dynamics: systems thinking and modeling for a complex world. Irwin/McGraw-Hill: Boston, MA. [Google Scholar]
  52. Sterman JD. 2001. System dynamics modeling: tools for learning in a complex world. California Management Review 43: 8–25. [Google Scholar]
  53. Stern Y 2009. Cognitive reserve. Neuropsychologia 47(10): 2015–2028. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Syddall H, Cooper C, Martin F, Briggs R, Sayer AA. 2003. Is grip strength a useful single marker of frailty? Age and Aging 3(6): 650–656. [DOI] [PubMed] [Google Scholar]
  55. Taylor WC, Baranowski T, Klesges LM, Ey S, Pratt C, Rochon J, Zhou A. 2004. Psychometric properties of optimism and pessimism: results from the Girls’ Health Enrichment Multisite Studies. Preventive Medicine 38: 69–77. [DOI] [PubMed] [Google Scholar]
  56. Thompson KM, Tebbens RJD. 2008. Using system dynamics to develop policies that matter: global management of poliomyelitis and beyond. System Dynamics Review 24(4): 433–449. [Google Scholar]
  57. Vanderby S, Carter MW. 2010. An evaluation of the applicability of system dynamics to patient flow modeling. Journal of the Operational Research Society 61(11): 1572–1581. [Google Scholar]
  58. Varadhan R, Seplaki CL, Xue QL, Bandeen-Roche K, Fried LP. 2008. Stimulus–response paradigm for characterizing the loss of resilience in homeostatic regulation associated with frailty. Mechanisms of Ageing and Development 129: 666–670. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Walston J, Fried LP. 1999. Frailty and the older man. Medical Clinics of North America 83: 1173–1194. [DOI] [PubMed] [Google Scholar]
  60. Whitson HE, Purser JL, Cohen HJ. 2007. Frailty thy name is … phrailty? Journals of Gerontology, Series A: Biological Sciences and Medical Sciences 62: 728–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Wolstenholme E 1999. A patient flow perspective of UK health services: exploring the case for new intermediate care initiatives. System Dynamics Review 15(3): 253–271. [Google Scholar]
  62. Wolstenholme E, Monk D, McKelvie D, Arnold S. 2007. Coping but not coping in health and social care: masking the reality of running organisations beyond safe design capacity. System Dynamics Review 23(4): 371–389. [Google Scholar]
  63. Zeng Y, Shen K. 2010. Resilience significantly contributes to exceptional longevity. Current Gerontology and Geriatrics Research 2010: Article ID 525693. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Table A1 Model References

Table S1. References for the model.

NIHMS1633611-supplement-Table_A1_Model_References.docx (25.1KB, docx)
Table A2 Model equations for short duration model

Table S2. Model equations for short duration model.

NIHMS1633611-supplement-Table_A2_Model_equations_for_short_duration_model.docx (22.2KB, docx)
Table A3 Model equations for life course model

Table S3. Model equations for life course model.

NIHMS1633611-supplement-Table_A3_Model_equations_for_life_course_model.docx (22.3KB, docx)
Table A4 Model inputs for both short duration and life course model

Table S4. Model inputs for both short duration and life course model.

NIHMS1633611-supplement-Table_A4_Model_inputs_for_both_short_duration_and_life_course_model.docx (19.7KB, docx)

RESOURCES