CycleRank, or there and back again: personalized relevance scores from cyclic paths on directed graphs

Abstract

Surfing the links between Wikipedia articles constitutes a valuable way to acquire new knowledge related to a topic by exploring its connections to other pages. In this sense, Personalized PageRank is a well-known option to make sense of the graph of links between pages and identify the most relevant articles with respect to a given one; its performance, however, is hindered by pages with high indegree that function as hubs and obtain high scores regardless of the starting point. In this work, we present CycleRank, a novel algorithm based on cyclic paths aimed at finding the most relevant nodes related to a topic. To compare the results of CycleRank with those of Personalized PageRank and other algorithms derived from it, we perform three experiments based on different ground truths. We find that CycleRank aligns better with readers’ behaviour as it ranks in higher positions the articles corresponding to links that receive more clicks; it tends to identify in higher position related articles highlighted by editors in ‘See also’ sections; and it is more robust to global hubs of the network having high indegree. Finally, we show that computing CycleRank is two orders of magnitude faster than computing the other baselines.

1. Introduction

Wikipedia is one of the biggest and most used sources of knowledge on the Web. As of this writing, it is the fifth most visited website in the world [1]. Wikipedia is not only a huge repository and collaborative effort; it is also a giant hypertext in which each article has links to the concepts that are deemed relevant to it by the editors [2]. The vast network emerging from the collaborative process provides a rich representation of the connections between concepts, entities and pieces of content, aimed at encompassing ‘the sum of all human knowledge’ [3].

This huge graph has been leveraged for a variety of purposes, including constructing semantic networks [4], natural language processing [5], cross-cultural studies [6,7], complex networks modelling [8] and understanding human navigation of information networks [9]. While one cannot assume that a single article completely encapsulates a concept [10], the link network can be useful in defining the context of an article. Previous research in controversy mapping has shown how this network can be leveraged to analyse the dominating definition of a topic, such as ‘geoengineering’ [11], shedding light on its boundary, context and internal structure. Furthermore, each linguistic community in Wikipedia produces a different network, which allows comparison of the emerging definition of a topic across different language editions [12].

The connections between Wikipedia articles are valuable, but they are also very abundant. The English version has more than 160 million links among its 5.7 million articles [13]. How can one find guidance within this wealth of data? In particular, how can we analyse the network around a specific topic to characterize its definition as emerging from the connections involving and surrounding it?

The contribution of this work is a novel approach to make sense of the Wikipedia link network, which is capable of answering queries such as ‘Which are the concepts that are more relevant concerning a given topic?’

We translate such enquiries into a graph problem. The topic of interest is represented by one article, i.e. a node in the graph called reference node. Given a reference node r, we want to assign a score to every other node in the graph that captures its relevance to r, based on the link structure. The final output is a ranking of nodes, such that the more relevant ones are ranked higher.

One established algorithm to answer this question is Personalized PageRank, a variant of PageRank where the user can specify one or more nodes as queries (seeds) and obtain a score for all the other nodes in the graph that measures relatedness to the seeds. However, we have found that, when applied in the context of Wikipedia, this algorithm does not produce satisfactory results since it usually includes very general articles in top positions.

To overcome these limitations, we have developed a novel algorithm to find the most relevant nodes in the Wikipedia link network related to a topic. The technique, called CycleRank, takes advantage of the cycles that exist between the links and produces a ranking of the different articles related to one chosen by a user. In other words, nodes receive a non-zero score if they can both get to and be reached from the reference node. Instead of walking randomly, the surfer of CycleRank goes out to a node, but it finally comes back.¹

In contrast to PageRank, CycleRank accounts for links in both directions, and it can provide results that are more accurate than those produced by the well-known Personalized PageRank algorithm. While we formulate the problem and validate the results for the Wikipedia link network, we believe the CycleRank algorithm can be applied to any other context where both incoming and outgoing links are important to measure relevance with respect to a given node.

The paper is organized as follows. We first formalize the problem we want to solve in §2. We provide insights on why Personalized PageRank is not a good choice in §3 and we discuss related work in §4. We describe CycleRank in §5, and we evaluate its performance in §6. Conclusions are drawn in §7.

2. Problem statement

Given a graph G = (V, E), where V is a finite set containing n nodes (articles) and E⊆ V × V is a set containing m directed edges (links between articles), we are seeking to build a ranking, i.e. an order relationship between nodes based on their relevance with respect to a reference node r.

In order to achieve this goal, we build a ranking function rf_r that assigns a non-negative score to every node v ∈ V,

$${\mathit{\text{rf}}}_r:V\mapsto [0,+\mathrm{\infty }).$$

The ranking ν_r = [v₁, v₂, …, v_n] is thus given by the total order of scores: if rf_r(v_i) > rf_r(v_j), then node v_i should appear before node v_j (i.e. i < j). Note that we assume there are no ex aequo in any given ranking; this can by achieved by breaking ties randomly.

3. Background

The PageRank algorithm represents an established relevance measure for directed networks [14]; its variant Personalized PageRank may be used to measure relevance within a certain context. PageRank is a measure based on incoming connections, where connections from relevant nodes are given a higher weight. Intuitively, the PageRank of a node represents the probability that, following a random path in the network, one will reach that node. It is computed in an iterative process, as the PageRank of a node depends on the PageRank scores of the nodes that link to it. There are however efficient algorithms to compute it. The idea behind PageRank is that of simulating a stochastic process in which a user follows random paths in a hyperlink graph. At each round, the user either keeps surfing the graph following the link network with probability α or is teleported to a random page in the graph with probability 1 − α. The parameter α is called the damping factor and is generally assumed to be 0.85 [15,16]. During the surfing process, the algorithm assumes equal probability of following any hyperlink included in a page; similarly, when teleported, every other node in the graph can be selected with equal probability.

Personalized PageRank is a variant of the original PageRank algorithm, where the user provides a set of seed nodes. In Personalized PageRank, teleporting is not directed to some random node taken from the entire graph, but to one taken from the seed set. In this way, the algorithm models the relevance of nodes around the selected nodes, as the probability of reaching each of them, when following random walks starting from a node in the seed set.

(a). Limitations of PageRank

At first look, Personalized PageRank seems to be suitable for our use case, as it can be used to represent a measure of relevance of Wikipedia articles strongly linked (directly or indirectly) to the seed.

However, we found unsatisfactory results when applying this algorithm. Very often, pages that are found to be very central in the overall network, such as ‘United States’ or ‘The New York Times’, are included in the top results of completely unrelated queries.

Such central articles act as hubs in the graph; they have such a strong relevance overall that, even starting from a seed article which is not specially related to them, one is very likely to end up reaching them while exploring the graph.

We argue that this is due to different factors. First, paths of any length can be followed; therefore, in a densely connected graph many paths will tend to converge towards the most relevant nodes. This can be limited only partially by lowering the value of the damping factor.

Second, PageRank only accounts for inlinks, and not for outlinks. This is reasonable for Web searches and other contexts where inlinks are a good proxy for relevance, as they represent somehow the value attributed to a node by the other nodes of the graph. In such cases, outlinks have basically no value: it is very easy to add into one’s Web page many outlinks to other pages. In the context of Wikipedia, instead, links from one article to other articles may be subject to being inserted and accepted by the editors’ community as much as incoming links from other articles. So, both outgoing and incoming links can be considered as indicators of relevance. In particular, outlinks to other pages from an article can be a very valuable indicator that these pages are actually related to the topic. For example, if an article contains links to ‘Computer Science,’ then we can assume that its content is related to ‘Computer Science’; on the other hand, we can expect the article ‘United States’ to have only a few links to articles related to ‘Computer Science’, as it is not the main subject of the article.

4. Related work

We discuss here relevant related studies used to establish the foundation of our work.

(a). Identifying related content in Wikipedia

A few previous studies have addressed the problem of recommending relevant Wikipedia articles, starting from a given article, with different approaches including machine learning [17] and Markov chains [18]. Schwarzer et al. [19] used citation-based document similarity measures, and evaluated their effectiveness using as a ground truth links in the ‘See also’ section of an article and readers’ clicks on the links from an article.

With respect to their work, the main difference of our approach is that we focus on the problem of finding relevant related nodes on a graph, and we do not use the text of Wikipedia articles. Our approach not only has the advantage of being completely language independent, but it is applicable to a much broader set of problems.

(b). Link structure in Wikipedia

The foundation of this paper is based on the idea that inlinks and outlinks in Wikipedia have a comparable role to establish relevance. Kamps & Koolen [20] performed a comparative analysis of the link structure of Wikipedia and a selection of the Web—built from ġov websites—and found that traditional information retrieval algorithms such as HITS do not work well on Wikipedia. The root case of this problem, as they observe, is that in Wikipedia inlinks and outlinks are good indicators of relevance, contrasting the general behaviour of the Web where only the former provide this indication.

(c). PageRank and variations

Boldi et al. [16] studied the behaviour of Personalized PageRank as a function of the damping factor α. While they acknowledge that a popular choice of α is 0.85—following the suggestion of the authors of PageRank itself [14]—they discuss both the possibility of choosing smaller values of α as well as values close to 1, finding the latter to be a choice with several theoretical and computational shortcomings. Gleich et al. [15] studied the problem of determining the empirical value for α from the visitor logs of a collection of websites, including Wikipedia. They found that Wikipedia visitors do not tend to teleport, and estimated the distribution of the values of α for Wikipedia to a beta distribution with maximum at α = 0.30. In our experiments, we have considered α = 0.30 and α = 0.85 as values for the damping parameter when executing Personalized PageRank.

We focus on the variations of PageRank that use reverse links or take into account the existence of both inlinks and outlinks. In 2010, Chepelianskii [21] introduced the idea of calculating the pagerank score of nodes on the transposed graph—called CheiRank—as well as on the original graph and performed a study of the correlation between the two scores on a collaboration network. Later that year, Zhirov et al. [22] combined CheiRank and PageRank to produce a single two-dimensional ranking of Wikipedia articles, 2DRank. This method does not assign a score to each node, but just produces a ranking. It was used together with PageRank to rank biographies across different language editions [7].

(d). Cycles in non-directed graphs

Finally, we present related work about loops in undirected graphs. This area of work is interesting because it provides a broader context in which to insert our algorithm and it could be used as a guide to extend our algorithm to undirected graphs. However, we consider this line of work to be very different in scope and purpose from our current work. It has been shown recently that graphs with different structure can be distinguished from one another using a measure defined with non-backtracking cycles, i.e. a closed walk that does not retrace any edge immediately after traversing them [23]. This method is tied to the idea of using the length spectrum of a graph from its Laplacian matrix. Graph spectra are extensively covered in the literature [24].

5. The CycleRank algorithm

We propose a more general approach to the problem, defining a new measure of the relevance with respect to a given node in a directed network, that accounts for both incoming and outgoing links. We call this measure CycleRank, as it is based on the idea of circular random walks.

Starting from the observation that, in PageRank, random walks easily lead to paths that are not related to the topic under consideration, we only consider walks coming back to the starting point within a maximum of K steps. In this way, we guarantee that we only touch pages that are, at least indirectly, both linked from and link to the reference article. Furthermore, no damping factor is needed, as we can assume that all walks just start from the reference node and come back.

Intuitively, a node that is linked from the reference article but does not link to it is likely to be a concept that is not related to that subject, even if it is important to its definition. Specularly, a node that links to the reference article but is not linked from it is likely to be related to it, but not relevant. Nodes that are linked both from and to a reference node are the ones that we expect to be relevant.

Extending this principle, we want then to be able to quantify the relevance of a node with respect to a given reference node, accounting also for the indirect links, i.e. for the number of paths that can be found linking it from and to the reference node. We do this by counting the cycles involving the reference node that pass through a given other node. As short distances represent a stronger relationship, shorter cycles should get higher weights.

We define the CycleRank score CR_r(i) of a node i with respect to a reference node r as follows:

$${\mathit{\text{CR}}}_r(i)=\sum _{k=2}^K{\ell }_r^k(i)\cdot \sigma (k),$$ 5.1

where ${\ell }_r^k(i)$ is the number of cycles of length k that include both node i and r, K is a parameter representing the maximum length considered for cycles and σ( · ) is a scoring function giving different weights to cycles of different length.

In this way, given a reference node r, the CycleRank score of a node i represents the number of cycles including both r and node i, weighted by the scoring function, which depends on the length of the cycle. The reference node is also considered in this computation, and it gets the maximum score as by definition it is included in all the cycles considered.

The threshold K is a parameter whose value can be specified according to the context. It can be set to infinite, but it will never exceed the number of nodes n. It can be typically set to a much lower value for two main reasons: to reduce the computational load and to avoid potential noise deriving from long cycles that include popular nodes far from the reference node. For reference, in our experiments we chose to apply thresholds K = 3 and K = 4, which produce good results with limited computational effort.

The main CycleRank algorithm is shown in algorithm 1. To optimize the score computation, we first filter the graph G through function FilterGraph(G, r, K), removing those nodes that could never appear in cycles including the reference node r with length limited by K. We then compute the score on this network using function ComputeScore().

(a). Preliminary filtering

To reduce the size of the network, algorithm 2 employs a known efficient algorithm to compute the distance from and to the reference node r, and discards all the nodes whose cumulative distance (back and forth) is smaller than K.

• (i)We compute the distance df[v] of each node v from the reference node by performing a breadth-first visit of the graph, early terminating the visit when we reach distance K (algorithm ETBFS—early-terminated breadth-first search, line 6).
• (ii)We discard all nodes for which df[i] > K − 1 (line 7), including those unreachable from r whose distance is +∞. The function removeNodes(G, key=cond) eliminates all nodes in G that do not satisfy the condition expressed by the Boolean expression cond.
• (iii)We compute the distance dt[v] on the transposed network, i.e. the distance from each node v to the reference node (line 9).
• (iv)We compute the length df[v] + dt[v] of the minimum cycle, including v and the reference node, and we discard all nodes for which df[v] + dt[v] > K (line 10).

In this way, we discard all the nodes that are not reached by any cycle of length lower than K. We remap node indexes at each step (lines 8 and 11) so we effectively work with smaller networks. It should be noted that, in the case of K ≥ n, only nodes unreachable from r will be removed, as the length of simple cycles is bounded by the number of nodes n. The removed nodes will all receive a score of zero.

(b). Cycle enumeration

We then proceed to enumerate all simple cycles in the reduced graph. Our algorithm is based on Johnson’s algorithm [25], limited to the query node r and early terminated. Algorithm 3 presents the details. Each node in our algorithm is associated with the following values:

• —score[v], the CycleRank score of node v.
• —blocked[v], a Boolean indicating whether v cannot be further visited when searching for a cycle because we already went through it. The purpose of this vector is to avoid going through the same node more than once, since we are only interested in simple cycles.
• —B[v], a list of nodes that can be unblocked when node v is unblocked.

These variables are then considered global in the rest of the algorithms, to avoid long signatures.

Cycle discovery is performed through a recursive backtrack visit (algorithm 4). In function circuit(G, r, v, K, S), G is the graph, r is the reference node, v is the current visited node, K is the threshold and S is a stack of nodes that have been visited so far.

We use K to early terminate the search for a cycle when we arrive at the maximum length: in line 3, we check whether the current size of the stack is smaller than K, in which case we can proceed in exploring the graph; otherwise, the function returns immediately.

The Circuit() function works by recursively visiting the nodes on the graph; when we visit a node v we add it to the stack S and mark it as blocked, then we visit its neighbours by looping over the adjacent nodes v.adj. If the neighbour w we are visiting is the target node, r in our case, then we have found a cyclic path: the score is updated by calling function UpdateScore() and the unblocking flag flag is set to true. Otherwise, we check whether w is unblocked; if so, it can be visited and we call circuit recursively.

After visiting all the neighbours of v, we check if the current node can be unblocked. Unblocking happens when v is part of a path that formed a cycle. The unblock(G, v) function at line 17 is the same as the one defined by Johnson [25] and we omit here for reasons of space. If we unblock a node v, we unblock all the parent nodes that could lead to v, stored in B[v]. In this way, we are able to explore alternative paths that form a cycle.

(c). Score computation

Function UpdateScore(score, S) updates the score of the nodes recorded in a stack S of length k, by adding σ(k) to the score of every node v ∈ S. Several scoring functions σ can be used; in general, a scoring function should capture the idea that longer cycles contribute less.

We use an exponentially decaying function: σ_exp(k) = e^−k, where the length of a cycle is denoted by k.

We have chosen the denominator to be exponential in the number of nodes; we present some data to support this choice in §6, where we show that the number of cycles increases more than exponentially with cycle length for our dataset. Intuitively, an exponentially decaying scoring function limits the possibility that short cycles become neglectable compared with long cycles in the computation of CycleRank, especially for higher values of k. We empirically validated this intuition by executing the evaluation experiments with linear and quadratic functions; we obtained lower quality results, while with an exponential function we obtained the best results in all experiments for our setting. Different scoring functions can be considered based on the problem at hand and according to structural properties of the network; in networks with lower density and clustering coefficient, having a lower number of cycles and a less skewed σ function may be more suitable (algorithm 5).

6. Experimental evaluation

This section is organized as follows: in §6a we describe the dataset that we have used for our experimental evaluation; §6b describes alternative approaches that we will compare with our proposed approach in addition to Personalized PageRank; §6d provides some example results and their qualitative description for each algorithm; in §6e, we provide a detailed quantitative evaluation with three different evaluation measures based on different ground-truth data. Finally, in §6f, we compare the execution time of our proposed approach against the alternatives.

(a). Dataset description

For our analysis, we used the WikiLinkGraphs dataset, consisting of the network of internal Wikipedia links for the nine largest language editions [13]. The dataset has been developed by us and is publicly available on Zenodo.² The graphs have been built by parsing each revision of each article to track links appearing in the main text, discarding links that were automatically inserted by templates. The dataset contains yearly snapshots of the network and spans 17 years, from the creation of Wikipedia in 2001 to 1 March 2018. For the experiments in this paper, we focused on the WikiLinkGraphs snapshot from English Wikipedia taken on 1 March 2018. This graph has N = 13 685 337 nodes and E = 163 380 007 edges.³

Figure 1 presents the number of cycles by length for a sample of 100 nodes chosen randomly from our dataset. For each page, we plot a triplet of points corresponding to the number of simple cycles of length k = 2, 3 and 4, respectively, that go through that node. We shift this triplet of points by a random offset along the horizontal axis for ease of reading.

Figure 1.

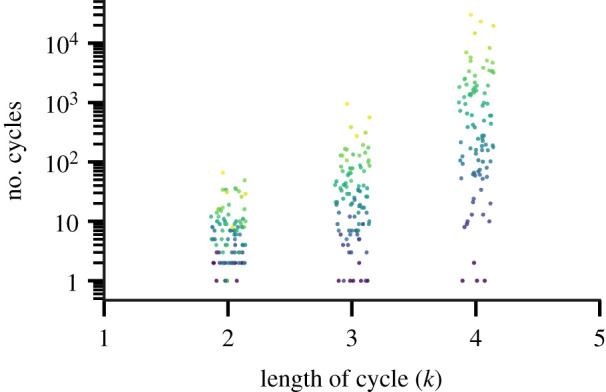
Number of cycles (log scale) by length for a sample of 100 random nodes. For each node in the sample, we have computed the number of cycles of length k = 2, 3, 4. Points representing the values for a single page are shifted on the x-axis by a random offset and coloured with the same colour. The colour gradient depends on the value at k = 4. (Online version in colour.)

Table 1 presents the top 10 pages by indegree and outdegree in the graph. We can see that indegree dominates outdegree by several orders of magnitude. This implies that ranking the top pages by degree (undirected) is de facto equivalent to ranking them by indegree. The difference between the top 1000 pages by indegree and the top 1000 pages by degree is just 34 pages.

Table 1.

Top 10 pages by indegree and outdegree over the most recent snapshot of the WikiLinkGraphs dataset (1 March 2018).

	indegree		outdegree
no.	article	degree	article	degree
1	United States	332 557	list of current US state legislators	8019
2	animal	164 549	list of least concern birds	7907
3	association football	146 836	list of people from Illinois	7827
4	India	126 107	list of birds of the world	6849
5	World War II	124 806	list of stage names	6677
6	arthropod	122 742	list of cities, towns and villages in Kerman Province	5839
7	Germany	121 705	list of film director and actor collaborations	5804
8	insect	118 628	index of Telangana-related articles	5747
9	Canada	115 779	index of Andhra Pradesh-related articles	5684
10	New York City	107 831	list of municipalities of Brazil	5585

Table 2 presents the top 10 results by global PageRank score. Global PageRank and indegree are highly correlated, regardless of the value of the damping parameter. When α = 0.85 the two rankings have a Kendall correlation coefficient of τ = 0.60 (over all pages with indegree greater than zero; n = 8 305 031); if we limit the two rankings to the top 1000 articles, they are still highly correlated with τ = 0.56.

Table 2.

Top 10 pages by (global) PageRank over the most recent snapshot of the WikiLinkGraphs dataset (1 March 2018).

	PageRank, α = 0.30		PageRank, α = 0.85
no.	article	score ( × 10−4)	article	score ( × 10−4)
1	United States	4.64	United States	14.14
2	animal	3.13	World War II	6.54
3	arthropod	2.49	United Kingdom	6.18
4	association football	2.45	Germany	5.57
5	insect	2.42	The New York Times	5.27
6	Germany	2.16	association football	5.25
7	list of sovereign states	2.11	list of sovereign states	5.23
8	India	2.03	race and ethnicity in the United States census	5.00
9	moth	1.85	India	4.91
10	National Register of Historic Places	1.66	Canada	4.68

(b). Alternative approaches

We describe briefly some alternative approaches that we will compare CycleRank with: beyond Personalized PageRank, we will consider the personalized versions of CheiRank and 2DRank, which are all based on Personalized PageRank. From now on, for the sake of brevity, we will omit the specifier ‘personalized’ when mentioning the algorithms; it will be clear from the context if we refer to the regular, global algorithm or the personalized variant.

(i). CheiRank

CheiRank is a ranking algorithm first proposed by Chepelianskii [21] that consists in applying the PageRank algorithm on the transposed graph G^T, i.e. all link directions are inverted. This corresponds to transposing the adjacency matrix when computing PageRank and results in computing the conjugated Google matrix G*.

CheiRank is analogous to PageRank, but it assigns a higher score to nodes with higher outdegree. In the Wikipedia dataset that we are using there are list articles that have several thousands of outgoing links, as shown in table 1. As expected, the articles with the highest global CheiRank score are list articles having high outdegree: out of the top 100 results by global CheiRank with α = 0.30, 87 have the word List, Lists or Index in the title. In the following, we are not showing results for CheiRank since it suffers from analogous limitations to PageRank, and it never resulted on par with the most performing algorithms in our experiments.

(ii). 2DRank

2DRank combines CheiRank and PageRank [22]; it ranks all nodes in a graph, but it does not produce a score as PageRank or CheiRank do. Instead, given the rankings ν^(PR) and ν^(ChR) produced by PageRank and CheiRank, respectively, 2DRank takes the minimum position in which a given node appears in both rankings and builds a new ranking. This process can be visualized in the two-dimensional Cartesian plane: xOy, we build a series of squares with one vertex in the origin, two sides formed by the Cartesian axes and the other two drawn at integer values. Thus, the first square is identified by (0;0), (0;1), (1;1) and (1;0); the second by (0;0), (0;2), (2;2) and (2;0), and so on. By interpreting the position of an item in the PageRank (p) and CheiRank (p*) rankings as the coordinates of a point P(p, p*), this point will fall on one of the edges of the squares drawn before. The position of a node in 2DRank is given by assigning a progressive number to each item, starting from the points that lie on inner squares; if two points lie on the same square the algorithm chooses the one closest to either axis first.

(c). Implementation and reproducibility

We implemented CycleRank in C++. For Personalized PageRank and CheiRank we used the igraph library,⁴ 2DRank was computed directly from PageRank and CheiRank results using a Python script. All code is available under an open source licence at: https://github.com/CycleRank/cyclerank.

(d). Qualitative comparison

Tables 3 and 4 present a comparison between the top 10 results and the highest scores obtained by CycleRank, PageRank and 2DRank, on the WikiLinkGraphs snapshot of the English Wikipedia of 1 March 2018 with reference nodes Computer science and Freddie Mercury, respectively.

Table 3.

Top 10 articles as ranked by CycleRank, PageRank and 2DRank with Computer science as the reference node. The article Computer science, which would appear in the first position by definition, is omitted.

Computer science
	CycleRank, K = 3		CycleRank, K = 4		PageRank, α = 0.30		PageRank, α = 0.85		2DRank, α = 0.30	2DRank, α = 0.85
no.	article	score	article	score	article	score ( × 10−4)	article	score ( × 10−4)	article	article
1	list of computer scientists	13.78	list of computer scientists	175.08	computing	12.48	mathematics	15.57	association for computing machinery	association for computing machinery
1	algorithm	6.36	algorithm	158.78	computational science	12.07	computer	14.42	programming language	programming language
3	artificial intelligence	5.96	artificial intelligence	154.30	Gottfried Wilhelm Leibniz	12.00	computing	12.71	theoretical computer science	Edsger W. Dijkstra
4	theoretical computer science	5.36	mathematics	134.13	mathematics	10.92	association for computing machinery	11.77	artificial intelligence	artificial intelligence
5	mathematics	4.37	programming language	108.42	association for computing machinery	10.91	Gottfried Wilhelm Leibniz	11.71	algorithm	machine learning
6	programming language	4.32	theoretical computer science	100.13	algorithm	10.58	computational science	11.30	programming language theory	algorithm
7	list of pioneers in computer science	4.08	list of pioneers in computer science	88.08	artificial intelligence	9.97	algorithm	11.21	Edsger W. Dijkstra	programming language theory
8	list of important publications in computer science	4.02	Alan Turing	79.11	IBM	9.93	United States	10.23	list of computer scientists	compiler
9	Edsger W. Dijkstra	3.82	logic	75.90	computational complexity theory	9.91	World War II	10.04	data science	theoretical computer science
10	Alan Turing	3.67	outline of software engineering	73.35	logic	9.84	IBM	9.60	machine learning	list of pioneers in computer science

Table 4.

Top 10 articles as ranked by CycleRank, Personalized PageRank and 2DRank with Freddie Mercury as the reference node. The article Freddie Mercury, which would appear in the first position by definition, is omitted.

Freddie Mercury
	CycleRank, K = 3		CycleRank, K = 4		PageRank, α = 0.30		PageRank, α = 0.85		2DRank, α = 0.30	2DRank, α = 0.85
no.	article	score	article	score	article	score ( × 10−4)	article	score ( × 10−4)	article	article
1	Queen (band)	13.78	Queen (band)	484.34	Queen (band)	10.79	Queen (band)	13.40	Queen (band)	Queen (band)
2	Brian May	6.41	Brian May	147.90	The Freddie Mercury Tribute Concert	8.92	London	12.07	Roger Taylor (Queen drummer)	Brian May
3	Roger Taylor (Queen drummer)	4.72	Elton John	97.48	HIV/AIDS	8.78	United States	11.51	Brian May	Roger Taylor (Queen drummer)
4	John Deacon	3.52	Roger Taylor (Queen drummer)	92.80	Queen II	8.65	Rock music	8.99	Made in Heaven	Queen II
5	Made in Heaven	3.37	Michael Jackson	73.33	Mercury Phoenix Trust	8.52	HIV/AIDS	8.99	Queen II	Made in Heaven
6	We Will Rock You (musical)	3.17	John Deacon	64.73	Middlesex	8.48	The Freddie Mercury Tribute Concert	8.73	John Deacon	John Deacon
7	Elton John	3.12	Live Aid	61.51	Parsi	8.45	Roger Taylor (Queen drummer)	8.51	We Will Rock You (musical)	Bohemian Rhapsody
8	The Freddie Mercury Tribute Concert	3.07	Bohemian Rhapsody	60.24	Zoroastrianism	8.39	United Kingdom	8.30	Bohemian Rhapsody	We Will Rock You (musical)
9	Bohemian Rhapsody	3.02	Brit Awards	53.69	Good Old-Fashioned Lover Boy	8.35	BBC	8.24	Greatest Hits (Queen album)	Greatest Hits (Queen album)
10	Greatest Hits (Queen album)	2.97	The Freddie Mercury Tribute Concert	48.50	Millennium stamp	8.33	Queen II	8.07	Panchgani	Charles Messina

These results highlight the limitations of Personalized PageRank described in §3a: in the top positions in the rankings produced with α = 0.85, we see articles such as United States and World War II; these articles act as attractors for the unconstrained random walks of PageRank since they have a very high indegree and have among the highest values of the PageRank score in the overall network, as shown in tables 1 and 2. Indeed, they are, respectively, in first (United States) and second (World War II) position in the overall PageRank ranking for the network. This problem is only partially mitigated by lowering the damping factor to α = 0.30.

However, there are far fewer paths that connect these articles back to the reference nodes. As a result, these articles appear in much lower positions in the ranking produced by the CycleRank algorithm: for example, for Computer science they appear, respectively, in the 400th (United States) and 172nd (World War II) positions. In this way, CycleRank leaves space for articles whose content is more strongly associated with the reference topic to appear at higher positions in the ranking.

Similarly, the Personalized PageRank results for Freddie Mercury suffer from the same problem: United States, London (17th position in the global ranking), United Kingdom (third position in the global ranking) and BBC (53rd position in the global ranking) all appear in the top 10 results for the Personalized PageRank with α = 0.85. This bias is only partially resolved by lowering the damping factor.

2DRank seems to mostly solve this issue, but still includes spurious results such as Charles Messina and Panchgani, which are only partially related to Freddie Mercury.

A more extended qualitative comparison can be found in [26].

(e). Quantitative comparison

To compare our proposed approach against existing algorithms, we need a way to evaluate how good a ranking is with respect to some ground truth. In general, we cannot directly compare the ranking functions, rf_r, because they may vary wildly in absolute values; furthermore, some algorithms we compare with do not define a ranking function but just produce the final ranking.

We provide three different comparison strategies that we encapsulate in three different measures. Each measure is based on a suitable dataset that we use as a ground truth against which we evaluate the performance of each algorithm. At high level, we want to evaluate the following three facets of each ranking algorithm:

• (i)To what extent is it able to maintain the relative ranking of most-clicked links from a given article (ClickStream evaluation)?
• (ii)To what extent is it able to rank the top position articles highlighted by editors in the ‘See also’ section (See-Also evaluation)?
• (iii)To what extent does it tend to give prominence to global ‘superstars’, i.e. nodes that are very popular in the overall network as measured by their high indegree (Indegree evaluation)?

Our evaluation measures are based on those used in the information retrieval literature. In particular, we follow in the footsteps of Schwarzer and collaborators [19], who have also used ClickStream and See-Also for evaluating performance across a large set of topics.

In the following subsections, we describe in detail each measure, the dataset used as a ground truth and the results of the experiments we performed. We also present examples to illustrate qualitatively the results of each experiment.

(i). ClickStream evaluation

The idea of this measure is to test the ability of each algorithm to maintain the relative relevance of a set of topics with respect to the ClickStream dataset [27], which we use as a ground truth. In other words by interpreting clicks on links by Wikipedia readers as a measure of the relative importance of each link in an article, we aim to measure whether the algorithms are able to maintain this relative ranking.

We have chosen the February 2018 release⁵ of the dataset because it is the closest in time to our WikiLinkGraphs snapshot. This dataset contains counts of (source, target) article pairs extracted from the request logs made to Wikipedia’s servers over one month. These data reflect the number of times a Wikipedia visitor has reached the target article from the source article. The fact that a given (source, target) pair appears in the clickstream implies the existence of a link in the source page pointing to the target page; these links may appear as wikilinks in the article source or come from templates. Note that (source, target) pairs with a count of 10 or fewer observations are not present in the dataset. In this way, these data provide an aggregated view on how Wikipedia articles are reached by users and what links they click on, producing a weighted network of articles, where each edge weight corresponds to how often people navigate from one page to another.

The ClickStream dataset also contains special sources to represent, for example, pages in other Wikimedia projects or external search engines;⁶ we filter those out. The dataset in total comprises over 25 million pairs, of which over 15.4 million are links between pages.

From the ClickStream data, we can derive an ordered list of articles, which we can consider as a ranking: our evaluation strategy consists in computing Kendall’s rank correlation coefficient between the ClickStream ranking and the ranking of the same pages produced by the algorithms under consideration. We formalize this evaluation strategy as follows: let $\mathcal{C}$ be the ClickStream dataset, i.e. a set of triplets (v_s, v_t, c) where v_s, v_t ∈ V are, respectively, the source and target articles and $c\in \mathbb{N},c\ge 10$ is the count for the pair (v_s, v_t); we define W_r⊆ V as the set of nodes that appear in the ClickStream dataset with source r, i.e. for some count c

$$W_r=\{w\in V|(r,w,c)\in \mathcal{C}\}.$$

We then use the counts in the ClickStream dataset to define ${\mathit{\text{rf}}}_r^{\mathcal{C}}$ over the set W_r. Given a target w ∈ W_r if the count for the pair (r, w) is c, i.e. if $(r,w,c)\in \mathcal{C}$, then

$${\mathit{\text{rf}}}_r^{\mathcal{C}}(w)=c.$$

The ranking function defined above produces a ranking ${\nu }_r^{\mathcal{C}}=[w_1,w_2,\dots ,w_q]$ of the nodes in W_r. Ties are broken at random. The ranking will be the ground truth for evaluating the performance of each algorithm for node r.

Let ν_r be a ranking of the nodes in V produced by one of the algorithms under consideration when r is the reference node. We restrict this ranking to only those pages that appear in the ClickStream data ${\nu }_r{|}_{W_r}$ and then we build a list of q pairs from the rankings: $[(v_1,w_1),(v_2,w_2),\dots ,(v_q,w_q)]$.

Given two pairs (v_i, w_i) and (v_j, w_j) where i < j, these pairs are said to be concordant if the ranks for both elements agree, i.e. if both v_i > v_j and w_i > w_j, or analogously if v_i < v_j. If v_i = v_j or w_i = w_j two pairs are neither concordant nor discordant. Otherwise they are discordant.

The quality of the ranking, ν_r, is then defined as Kendall’s rank correlation coefficient,

$$\tau ({\nu }_r^{\mathcal{C}},{\nu }_r)=\frac{{\pi }_{+}-{\pi }_{-}}{\left(\genfrac{}{}{0em}{}{q}{2}\right)},$$

where π₊ and π₋ are the number of concordant and discordant pairs, respectively. We say that a ranking ${\nu }_r^1$ is better than a ranking ${\nu }_r^2$ if its rank correlation with the ClickStream ranking is higher: $\tau ({\nu }_r^1)>\tau ({\nu }_r^2)$.

Table 5 presents an example of how this evaluation metric works for the article Computer science: the table shows the ClickStream data and the induced ranking ${\nu }_r^{\mathcal{C}}$, as well as the rankings produced by the CycleRank (${\nu }_r^{\text{(CR)}}$), PageRank (${\nu }_r^{\text{(PR)}}$) and 2DRank (${\nu }_r^{\text{(2D)}}$) algorithms over the same articles. Regardless of the absolute position of these articles, we measure how these rankings agree with the one given by the ClickStream data; a negative value means that the ranking is discordant with the ClickStream ranking.

Table 5.

ClickStream data for the article Computer science (c is the click count, ${\nu }_r^{\mathcal{C}}$ is the ranking induced by the count) and rankings produced by CycleRank with K = 3 (CR) and PageRank with α = 0.30 (PR) after filtering. The Kendall correlation coefficients between ClickStream and the rankings produced by the algorithms presented in the table are computed only over the 10 items displayed.

Computer science
article (Wr)	c	${\nu }_r^{\mathcal{C}}$	${\nu }_r^{\text{(CR)}}$	${\nu }_r^{\text{(PR)}}$	${\nu }_r^{\text{(2D)}}$
computation	1371	1	56	65	77
algorithm	876	2	2	6	5
programming language theory	794	3	17	63	6
computer graphics (computer science)	648	4	43	134	31
computational complexity theory	647	5	33	9	108
human–computer interaction	550	6	47	68	50
computer scientist	480	7	59	20	62
outline of computer science	452	8	204	298	173
computer programming	451	9	62	18	160
programming language	414	10	6	12	2
$\tau ({\nu }_r^{\mathcal{C}},{\nu }_r)$			0.3333	−0.0222	0.2444

Figures 2 and 3 present the results of the ClickStream evaluation over a sample of 1000 random articles. We have built this sample by selecting random Wikipedia articles that have at least five entries in the ClickStream data, i.e. they have at least five links to other Wikipedia articles. In the figures, the (x, y) coordinates of each point are the values of Kendall’s rank correlation coefficient with ClickStream data for PageRank and CycleRank (figure 2) and for 2DRank and CycleRank (figure 3). Thus, if points have their y-coordinate greater than the x-coordinate, i.e. they are above the dashed axis Y = x in the figure, it means that CycleRank is outperforming the other approach for that article. This is the case both for the comparison with PageRank in figure 2, where 68.8% of articles are above the axis, and with a smaller margin for the comparison with 2DRank in figure 3, where 50.2% of articles are above the axis.

Figure 2.

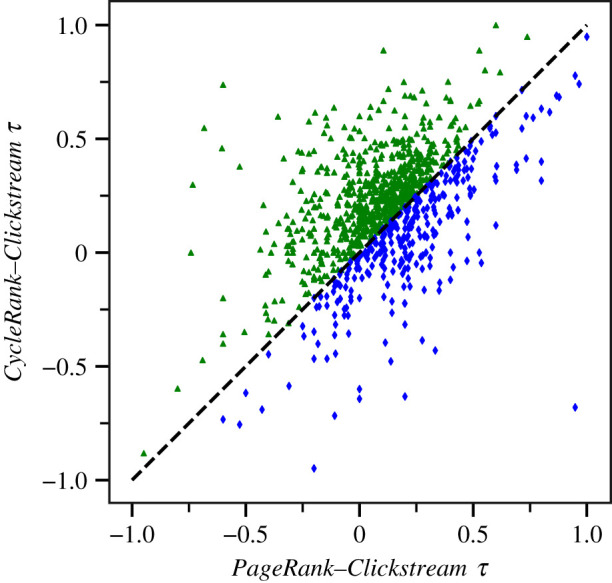
Comparison of the Kendall τ correlation coefficients of the ClickStream ranking with the rankings produced by PageRank (x-coordinate) and CycleRank (y-coordinate) over a sample of 1000 random articles. If for a given article y > x, then the correlation between the CycleRank and ClickStream rankings is higher than the correlation between the PageRank and ClickStream rankings (green triangles), and vice versa for y ≤ x (blue diamonds). (Online version in colour.)

Figure 3.

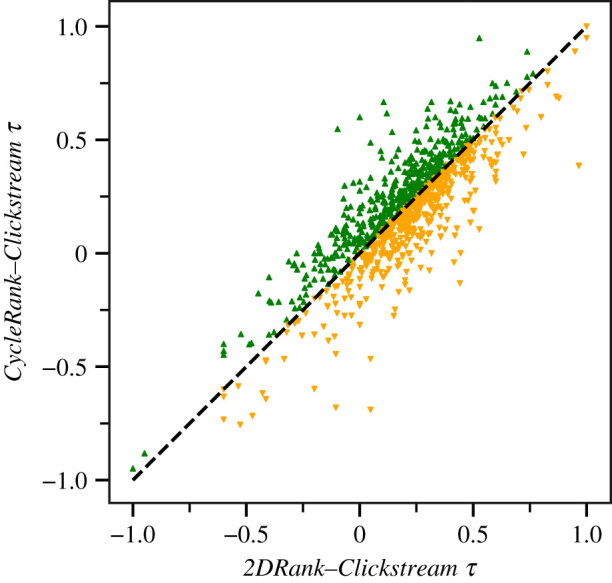
Comparison of the Kendall τ correlation coefficients of the ClickStream ranking with the rankings produced by 2DRank (x-coordinate) and CycleRank (y-coordinate) over a sample of 1000 random articles. If for a given article y > x, then the correlation between the CycleRank and ClickStream rankings is higher than the correlation between the 2DRank and ClickStream rankings (green triangles), and vice versa for y ≤ x (yellow inverted triangles). (Online version in colour.)

Table 6 presents the results of the ClickStream evaluation for different values of the algorithms’ parameters. Each cell reports two percentage values, representing, respectively, the fraction of articles for which the chosen baseline produced a ranking with higher/lower correlation with ClickStream than CycleRank. This corresponds to the proportion of points below and above the Y = x-axis in figures 3 and 3. Asterisks are used to indicate the statistical significance of the difference according to a paired t-test. The best results are obtained by CycleRank with K = 3; in the comparison with 2DRank the difference is not statistically significant.

Table 6.

Results of the ClickStream evaluation over a sample of 1000 random articles. The two percentages reported in each cell represent the proportions of articles for which the correlation is higher for the algorithm indicated by the row and by the column, respectively. The amount missing to sum to 100% corresponds to cases of equal correlation.

		CycleRank
algorithm	parameters	K = 3	K = 4
PageRank	α = 0.30	30.2/68.8***	37.6/59.0***
	α = 0.85	33.4/65.5***	36.2/59.7***
2DRank	α = 0.30	48.2/50.2***	58.4/37.4***
	α = 0.85	48.2/50.4***	56.9/37.7***

Asterisks indicate the significance level according to the p-values obtained from a paired t-test: *p ≤ 0.05; ^**p ≤ 0.001; ^***p ≤ 0.0001.

(ii). See-Also evaluation

We measure the ability of an algorithm to identify relevant articles by using links in the See-Also section of a Wikipedia article as a ground truth. Following Wikipedia policies [28], the section See-Also contains a list of internal links to related Wikipedia articles. These lists may be ordered logically, chronologically or alphabetically, and there is no guarantee that the same criterion is used across multiple pages. For this reason, we treat these lists as non-ordered, that is, we do not treat the pages listed in these sections as being ranked by relevance, but just as a set of related pages.

More formally, let W_r⊆ V be a set of ground-truth nodes that are relevant with respect to a reference node r, and let ν_r be a ranking of the nodes in V. The quality of the ranking ν_r is defined as

$$\xi ({\nu }_r,W_r)=\sum _{w\in W}\xi ({\nu }_r,w),$$

where

$$\xi ({\nu }_r,w)=\frac{1}{i}\text{if}\hspace{0.17em}w=v_i\in {\nu }_r\wedge w\in W.$$

We say that a ranking ${\nu }_r^1$ is better than a ranking ${\nu }_r^2$ if $\xi ({\nu }_r^1)>\xi ({\nu }_r^2)$.

Table 7 presents, as an example, the results of the See-Also evaluation for the article Computer science: the first column lists the name of the articles appearing in the See-Also section of the article Computer science, W_r; the second, third and fifth columns show the position of each article in the ranking produced by CycleRank, PageRank and 2DRank, respectively; the fourth and sixth columns show the difference in evaluation score for each article between CycleRank and Personalized PageRank Δξ(CR − PR) and between CycleRank and 2DRank Δξ(CR − 2D). When CycleRank ranked a page in a higher position than the other approach this difference is positive; otherwise, it is negative.

Table 7.

The first 10 articles appearing in the See-Also section of the Computer science article. We use them to compare CycleRank with K = 3 (CR), PageRank with α = 0.30 (PR) and 2DRank with α = 0.30 (2D). For each article, the table reports the position in which it appears in the ranking produced by each algorithm, and the corresponding difference in scores Δξ. The $\sum \mathrm{\Delta }\xi (W_r)$ is calculated only over the 10 items displayed.

Computer science
article (Wr)	${\nu }_r^{\text{(CR)}}$	${\nu }_r^{\text{(PR)}}$	Δξ CR-PR ( × 10−4)	${\nu }_r^{\text{(2D)}}$	Δξ CR-2D ( × 10−4)
academic genealogy of computer scientists	13	220	723.8	26	384.6
Association for Computing Machinery	16	6	-1041.7	2	-4375.0
Computer Science Teachers Association	207	231	5.0	402	23.4
engineering informatics	447	228	-21.5	399	-2.7
informatics	70	106	48.5	87	27.9
list of academic computer science departments	74	232	92.0	7862	133.9
list of computer scientists	2	110	4909.1	9	3888.9
list of important publications in computer science	9	167	1051.2	18	555.6
list of pioneers in computer science	8	16	625.0	538	1231.4
list of unsolved problems in computer science	92	148	41.1	41	-135.2
outline of software engineering	12	217	787.3	25	433.3
technology transfer in computer science	206	223	3.7	380	22.2
Turing Award	14	49	510.2	17	12.6
$\sum \mathrm{\Delta }\xi (W_r)$			7733.8		2314.4

Figures 4 and 5 show the distribution of the differences in evaluation score over the same sample of 1000 articles used above. Figure 4 compares CycleRank and Personalized PageRank, i.e. the plot is the distribution Δξ(CR − PR), while figure 5 presents analogous results for CycleRank and 2DRank, Δξ(CR − PR).

Figure 4.

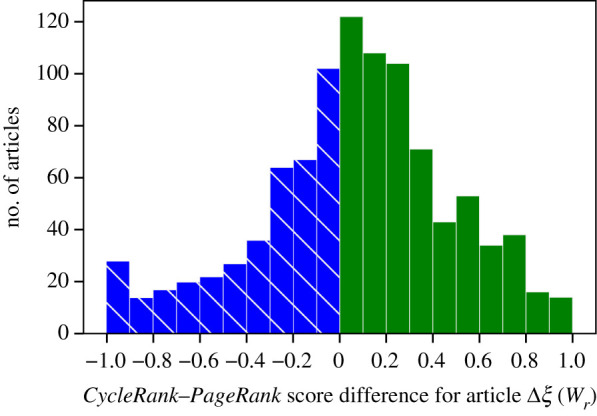
Distribution of Δξ(W_r) between CycleRank and PageRank. When values are positive (solid green bars) CycleRank is able to find See-Also articles in a higher position than Personalized PageRank for a given article, and vice versa when values are negative (blue bars with with white hatch). (Online version in colour.)

Figure 5.

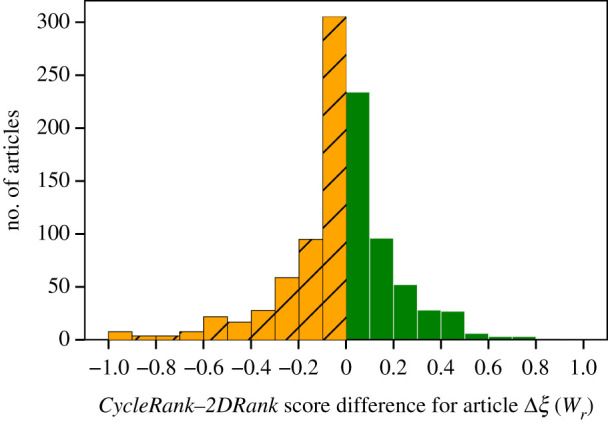
Distribution of Δξ(W_r) between CycleRank and 2DRank. When values are positive (solid green bars), CycleRank is able to find See-Also articles in a higher position than 2DRank for a given article, and vice versa when values are negative (orange bars with with black hatch). (Online version in colour.)

Table 8 presents the results of the See-Also evaluation over a sample of 1000 random articles. We have built this sample with the following characteristics: we selected Wikipedia articles that have at least three links to other existing Wikipedia articles;⁷ in this way, we ensure that the pages used in the sample have enough links.

Table 8.

Results of the See-Also evaluation over a sample of 1000 random articles for CycleRank, PageRank and 2DRank for different values of their parameters. Each cell reports the mean of the difference between the ξ obtained over the sample of 1000 articles. Positive (negative) values indicate higher (lower) performance for CycleRank.

		CycleRank
algorithm	parameters	K = 3	K = 4
PageRank	α = 0.30	0.062***	0.021***
	α = 0.85	0.111***	0.069***
2DRank	α = 0.30	0.017***	−0.065***
	α = 0.85	0.063***	−0.045***

Asterisks indicate the significance level according to the p-values obtained from a paired t-test: *p ≤ 0.05; ^**p ≤ 0.001; ^***p ≤ 0.0001.

As table 8 shows, the best performance is achieved by CycleRank with K = 3, with results that significantly outperform all the other algorithms. The second-best algorithm is 2DRank with α = 0.30. These results confirm that in the context under analysis it is important not only to account for both incoming and outgoing links, as CycleRank and 2DRank do, but also to limit longer paths: indeed, the best results are found for lower values of K and of α, respectively.

(iii). Indegree evaluation

We measure the extent to which an algorithm tends to give prominence to global ‘superstars’, i.e. nodes which are very popular in the overall network as measured by their high indegree. In this section, we use the same measure ξ that we have used in the previous See-Also evaluation, with two modifications. First, we use the top 100 articles by indegree as test set W_r; in this case, lower is better, as it implies a lower presence of global hubs at the top of the ranking produced: we consider a ranking ${\nu }_r^1$ to be better than a ranking ${\nu }_r^2$ if $\xi ({\nu }_r^1)<\xi ({\nu }_r^2)$. Second, as PageRank and 2DRank produce longer rankings, for a fair comparison we cut off all rankings at 1000 results.

Table 9 presents the position in which the top 100 articles by indegree appear in the top 1000 positions of the rankings produced by Personalized PageRank (top), 2DRank (middle) and CycleRank (bottom) with Freddie Mercury as the reference node.

Table 9.

Positions in which the top 100 articles by indegree appear in the rankings produced by CycleRank (top), PageRank (middle) and 2DRank (bottom) with Freddie Mercury as the reference node and their score $\xi ({\nu }_r,w)$. The ranking for PageRank and 2DRank are limited to the top 1000 positions. The $\sum \xi (W_r)$ is calculated only over the 10 items displayed.

Freddie Mercury
	CycleRank, K = 3
νi	article	${\nu }_r^{\text{(CR)}}$	$\xi ({\nu }_r^{\text{(CR)}},w)\hspace{0.17em}(\times \hspace{0.17em}{10}^{-4})$
13	London	88	113.64
63	BBC	364	27.47
87	rock music	55	181.82
$\sum \xi ({\nu }_r^{\text{(CR)}},W_r)$			322.93

	PageRank, α = 0.30
	article	${\nu }_r^{\text{(PR)}}$	$\xi ({\nu }_r^{\text{(PR)}},w)\hspace{0.17em}(\times \hspace{0.17em}{10}^{-4})$
1	United States	363	27.55
4	India	383	26.11
9	Canada	449	22.27
10	New York City	367	27.25
13	London	12	833.33
17	Italy	761	13.14
18	Iran	613	16.31
19	Japan	565	17.70
20	The New York Times	364	27.47
21	California	495	20.20
29	Spain	879	11.38
$\sum \xi ({\nu }_r^{\text{(PR)}},W_r)$			1042.71

	2DRank, α = 0.30
	article	${\nu }_r^{\text{(2D)}}$	$\xi ({\nu }_r^{\text{(CR)}},w)\hspace{0.17em}(\times \hspace{0.17em}{10}^{-4})$
13	London	603	16.58
54	The Guardian	569	17.57
87	rock music	426	23.47
$\sum \xi ({\nu }_r^{\text{(2D)}},W_r)$			57.63

Figure 6 shows the results of the indegree evaluation for PageRank, 2DRank and CycleRank on a sample of 1000 random articles, taking the top N results for each article, with values on N ranging up to 1000. We see that CycleRank is able to obtain a lower score, meaning that it includes fewer pages with high indegree in high position in the rankings it produces.

Figure 6.

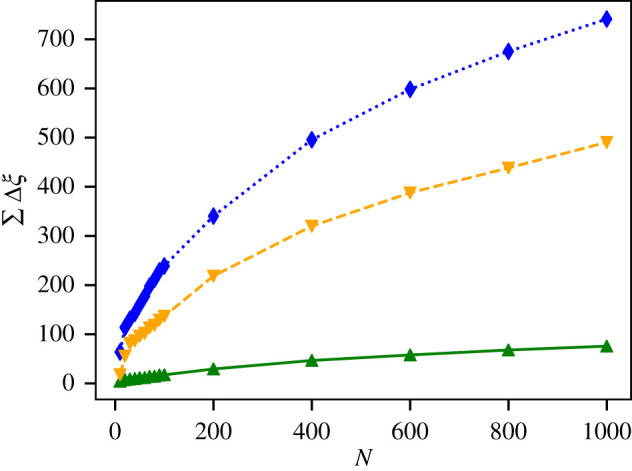
Indegree evaluation scores for PageRank (dotted blue line with diamond markers), 2DRank (dashed orange line with inverted triangle markers) and CycleRank (solid green line with triangle markers), taking the top N articles by indegree. A lower score means that the ranking produced by the algorithm is more robust to global hubs. (Online version in colour.)

(f). Performance analysis

Finally, table 10 evaluates the performance of CycleRank with respect to the alternative approaches. Times are computed by averaging over the sample of 1000 articles used in the See-Also evaluation. Experiments were performed on an HPC cluster, on nodes equipped with Intel Xeon E5-2650V3 (10 core) processors and 256 GB of RAM. Each job computed CycleRank, Personalized PageRank or 2DRank for one given seed node r using only one core and one processor at a time.

Table 10.

Execution time comparison of CycleRank, PageRank, CheiRank and 2DRank for different values of the parameters: maximum cycle length K for CycleRank, and damping parameter α for PageRank, CheiRank and 2DRank. All times are expressed in seconds.

algorithm	parameter	time (s)
CycleRank	K = 3	4 ± 1
	K = 4	10 ± 16
PageRank	α = 0.30	260 ± 13
	α = 0.85	928 ± 80
CheiRank	α = 0.30	258 ± 20
	α = 0.85	374 ± 50
2DRank	α = 0.30	>518
	α = 0.85	>1302

The results presented in table 10 do not take into account the time needed to read the input graph, which required 60 s on average (a value much larger than the time need by CycleRank to execute). Execution times for 2DRank are not obtained directly, but by summing the execution times of Personalized PageRank and CheiRank.

Computing CycleRank is two orders of magnitude faster than computing Personalized PageRank and CheiRank. Since our proposed approach is based on enumerating all cycles going through the reference node, in the worst case—a complete graph—the computational complexity increases exponentially with cycle length, making its computation challenging for higher values of K in very dense graphs. However, we have shown that CycleRank can produce good results for small values of K and has a significant time advantage with respect to Personalized PageRank and 2DRank.

7. Conclusion

This paper introduces CycleRank, a novel algorithm based on cyclic paths that can be used to assign relevance scores to nodes in a directed graph. Given a reference node, the algorithm finds all simple cycles that go through this node and assigns a score to each node that belongs to these cycles. The algorithm is characterized by one parameter, which is the maximum cycle length to be considered.

We have performed an extensive comparison between CycleRank, PageRank and 2DRank, based on three quantitative measures. The first experiment, based on the ClickStream dataset, has shown that the rankings produced by CycleRank align better with readers’ behaviour, with 2DRank obtaining comparable results. The second experiment, based on See-Also links that appear in Wikipedia articles, has shown that CycleRank is able to rank related articles in a higher position. The third experiment, based on pages with high indegree, has shown that CycleRank is more robust to the influence of network hubs. Furthermore, we have shown that our algorithm is faster than the alternatives, offering order-of-magnitude speed-ups with respect to library implementation of Personalized PageRank.

In other words, CycleRank is a viable alternative to Personalized PageRank, especially in the case of graphs where the role of inlinks and outlinks is comparable; our experiments on the Wikipedia link graph have shown that CycleRank achieves better performance in terms of both accuracy and efficiency.

The best results in all the experiments were obtained by CycleRank with K = 3, i.e. limiting the maximum length of cycles to 3. This resonates with what is seen for PageRank and 2DRank in this context, where smaller values of the damping factor α achieve better results, giving lower scores to nodes that are further from the reference node. This could be associated with the high density of the Wikipedia link graph: as soon as a random path gets further away from the reference node, the influence of hubs and of denser areas of the network gets higher. Although CycleRank is better than PageRank and 2DRank at limiting this issue, with higher values of K it is still affected.

The algorithm was developed for the context of the Wikipedia link network, but we believe it has potential to be employed in a variety other contexts. Contexts like knowledge bases or the Web of Data [29] can be seen as analogous to the one considered, with links between entities representing semantic relations to be considered in both directions. In social media, explicit links, such as friendship or followership, and implicit links based on interactions (e.g. retweets or mentions) are often used to model influence between users, and to recommend new contacts [30]. While current models mostly consider influence as uni-directional, CycleRank would allow for the identification of relevance with respect to a specific user accounting not only for their interests and preferences but also for the attention they receive from others.

We believe that the choice of an appropriate scoring function merits further analysis in future research. While we have empirically validated the results on our WikiLinkGraphs dataset for other types of scoring functions, in this work for reasons of space we have presented only a simple exponentially decaying scoring function, for which we obtained the best results. Many variations and extensions could be explored: we expect that linear or quadratic functions would be more apt for sparser networks, while more skewed functions could be used for denser networks; in the latter case, it could be worth exploring the usage of exponential functions with a higher base than Euler’s number, e.g. the average degree of the network, as a proxy for the number of cycles.

We have assumed the starting point for the algorithm to be a single reference node. However, as in the case of Personalized PageRank, it would be possible to take a group of articles as the seed. Then, one could count all paths from any node in the seed to any other node in the seed. Another possible variant would be to specify two different nodes (or groups of nodes) as the source and the target and to consider all paths from the source to the target within K steps. In this way, the measure would not represent the relevance of other nodes with respect to a reference node but to the (directed) relationship between two nodes or groups of nodes. This measure would help to answer questions such as: ‘Which are the most relevant concepts connecting artificial intelligence and human rights, and which are the most relevant concepts the other way round’?

We believe that CycleRank provides a foundation that could be further explored to provide a family of algorithms adapted for different graphs and use cases. The suitability of different solutions could also be studied with respect to the structural properties of the network under analysis, such as its link density or clustering coefficient.

Data accessibility

The datasets and the code used in this article are available. The following datasets have been used: (a) Wikimedia XML dumps are available at: https://dumps.wikimedia.org/; (b) the WikiLinkGraphs dataset is available on Zenodo at: https://zenodo.org/record/2539424; (c) the ClickStream dataset is available at: https://dumps.wikimedia.org/other/clickstream/. The code is available on GitHub at: https://github.com/CycleRank/cyclerank.

Authors' contributions

C.C. conceived the algorithm, designed and performed the experiments and wrote the manuscript. D.L. conceived the study, helped design the experiments and helped draft the manuscript. A.M. supervised the work and helped draft the manuscript. All authors gave final approval for publication and agree to be held accountable for the work performed herein.

Competing interests

We declare we have no competing interest.

Funding

C.C. and D.L. have been supported by the European Union’s Horizon 2020 research and innovation programme under the EU Engineroom project, with grant agreement no. 780643.