Analytical model for electrohydrodynamic thrust

Abstract

Electrohydrodynamic (EHD) thrust is produced when ionized fluid is accelerated in an electric field due to the momentum transfer between the charged species and neutral molecules. We extend the previously reported analytical model that couples space charge, electric field and momentum transfer to derive thrust force in one-dimensional planar coordinates. The electric current density in the model can be expressed in the form of Mott–Gurney law. After the correction for the drag force, the EHD thrust model yields good agreement with the experimental data from several independent studies. The EHD thrust expression derived from the first principles can be used in the design of propulsion systems and can be readily implemented in the numerical simulations.

1. Introduction

Electrohydrodynamic (EHD) flow is the motion of electrically charged fluids under the influence of applied electric fields. EHD thrusters at their heart are simple devices consisting of two electrodes separated by an air gap and connected to a high voltage generator providing electric potential between the electrodes. When a sufficient potential is applied, the electrical breakdown of air occurs in which ions are generated near the high energy anode, known as the ionization region. The ions of the same polarity as anode drift towards the ground cathode, accelerating the bulk flow by collision with the neutral molecules (in the drift region). This EHD flow propulsion phenomenon also referred to in the literature as ionic wind, has been used in many practical applications, such as convective cooling [1–3], electrostatic precipitators (ESP) [4–8], airflow control [9,10] and as a turbulent boundary layer actuators [11]. The success of EHD technology has been limited due to the modest pressure achieved by the EHD thrusters; however, in applications where producing high pressure is not required, the EHD-driven flow can be of interest. Among the advantages of the EHD approach are the ability to operate at a small scale without moving parts, straightforward control of the system and quiet operation. In propulsion applications, EHD converts electrical energy directly to kinetic energy, sidestepping limitation related design and manufacturing of small moving parts, e.g. wings of micro-flyers.

The idea of using corona discharge for EHD thruster was proposed by Brown [12], who thought he has discovered an unknown phenomenon producing force and provided some explanations on the Biefeld–Brown effect. The theoretical aspect of EHD in gas was first investigated by Robinson [13], who demonstrated the ability of electrostatic blowers to generate velocities up to 4 m/s. Recently, a general analytical model was derived for planar, cylindrical and spherical coordinates for one-dimensional electric profiles for charge density, electric potential and electric field strength, which can be used to calculate the one-dimensional velocity profile [14]. The concept of electric wind associated with an EHD thrust was first demonstrated in a one-dimensional model showing that the EHD thrust is dependent on the electric pressure [15]. Christenson & Moller have developed an expression for EHD thrust and found that EHD efficiency can be related to ion mobility [16]. Moreau et al. [17] measured EHD thrust in wire-to-cylinder corona discharge and found that the corona current I is proportional to the square root of the grounded electrode diameter and to $1/d^2$, where d is the spacing between two electrodes. Masuyama et al. [18] investigated both a single and dual-stage EHD thruster and showed that thrust is proportional to the square of voltage beyond the corona inception. Wilson et al. [19] investigated the use of EHD thrust for aircraft propulsion and concluded that corona discharge is not very practical for that application. More recently, Gilmore showed that EHD propulsion could be viable to drive small aircraft [20], which led to the demonstration of flying fixed-wing electro-aerodynamic (EAD) aircraft [21]. Similarly, the EHD thrusters have also been proposed as a propulsion method for small-scale ionocrafts [22–24].

The EHD thrust can be modelled from the first principles as an external force term (Coulomb force) coupled to the Navier–Stokes equations (NSE). A two-part model is required: (i) the description of the ion motion in the electrical field and (ii) the effect of the ion drift on the neutral gas in the flow acceleration region. Several finite-element and finite-volume models have been developed to describe EHD velocity and pressure distributions [25,26]. Pekker et al. first derived an ideal one-dimensional EHD thruster model for calculating maximum thrust and thrust efficiency from the charge conservation equation and the Mott–Gurney law [27]. Mott–Gurney law describes the relation between maximum electric current density and applied voltage in semiconductors [28]. The current density was shown to vary as $J\propto \phi (\phi -{\phi }_o)$, in agreement with the Townsend $(\phi -I)$ relationship [29] in 1914. Since then, the form $I=C\phi (\phi -{\phi }_o)$ has been widely adopted for corona discharge analysis [30–35], where I is the corona current, $\phi$ is the corona voltage, ${\phi }_o$ is the onset corona voltage and C is a fitting parameter. To physically interpret the parameter C, Cooperman showed that $C\propto {\mu }_b/L_c^2$ [36], where ${\mu }_b$ is the ion mobility and $L_c$ is the characteristic length scale. The thrust induced by the ions $(\phi -T)$ relationship can be derived based on Townsend's relationship $(\phi -I)$ [17,18], and the maximum thrust can be defined based on Mott–Gurney law [17]. However, the scientific literature does not report an analytical model to determine the thrust induced from ions from first principles. The closest analytical model [14] couples the electrical properties and EHD driven flow was validated against the EHD velocity measurement, applied for validation of novel numerical algorithms [37] and used in two-dimensional and three-dimensional numerical simulations [25,38,39]; however, this model was not considered for calculations of thrust force.

In this work, we extend the analytical model for EHD flow [14] to formulate the expression for EHD thrust in one-dimensional planar coordinates. The electric current density derived from the model is presented in the form of Mott–Gurney law. The analytical model is validated against the experimental data from three independent experimental studies, including our experiments and the previously published data [17,18].

2. Analytical model

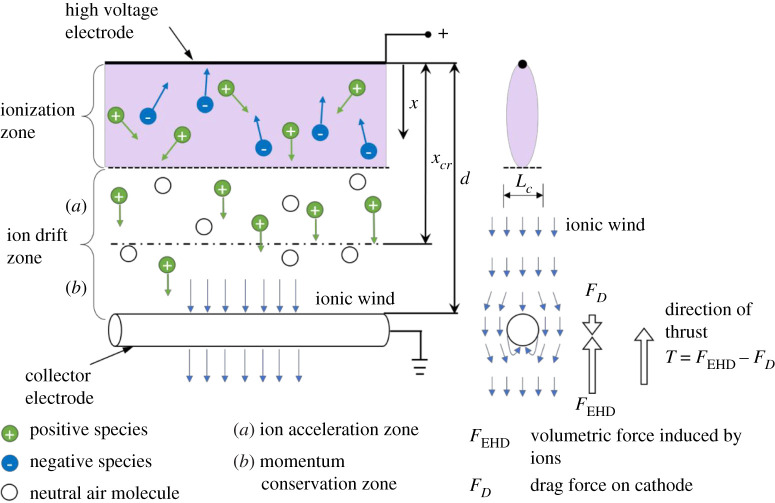
Corona discharge generates a flow of charged species, and the assessment of the charge densities and the electric field is essential for the evaluation of EHD force acting on the fluid. The charged species are generated in the region where the field strength exceeds the threshold for the breakdown of molecules in the fluid. For a wire-to-rod corona discharge, shown in figure 1, ionization occurs near the wire. As the electric field strength decreases away from the emitter electrode, the ionization is hindered, however, the charged species moving in the inner electrode transfer their momentum to neutral molecules via elastic collisions. The charged species concentration in corona discharge can be calculated using the charge continuity equation, considering that three types of charged species are present positive ions, negative ions and electrons. The density $N_k$ of the charged species k is described by the conservation equation [14,40].

$$\frac{\mathrm{\partial }{N}_k}{\mathrm{\partial }t}+\mathrm{\nabla }\cdot [(\mathbf{\text{u}}+{\mu }_k\mathbf{\text{E}})N_k-D_k\mathrm{\nabla }{N}_k]={\omega }_k,$$ 2.1

where $\mathbf{\text{u}}$ is the velocity vector of the bulk flow, $\mathbf{\text{E}}$ is the electric field, ${\mu }_k$ is the ion mobility of charged species k, and D_k is the ion diffusivity of the charged species and ${\omega }_k$ is the production rate of species k (table 1). The ionization can be conceptualized as a combination of two processes (1) ionization process of charged species generation and (2) recombination process where charges recombine. Transport of charged species in the field, their capture by the emitter electrode or ejection from the ionization region can aid or hinder the specific reaction in the plasma volume. One can avoid complex plasma chemistry considerations in the analysis of corona induced EHD in air by making two key assumptions. (i) The ionization occurs only in the region when the electric field strength is greater than a threshold value ∼3 × 10⁶ V m⁻¹ [30]. (ii) The total momentum transferred to the neutral gas molecules in the ionization region is negligible compared to the ion drift region as shown in figure 1. In the ionization region, the momentum transfer is partially offset by the positive and negative species travelling in opposite directions and by a relatively small volume of the ionization region compared to the ion drift region. We assume that the momentum injection takes place in the ion drift region where the net charge density is given by ${\sum }_k{N}_k={\rho }_e$. With these two assumptions, the reduced charge continuity equation can be written as

$$\frac{\mathrm{\partial }{\rho }_e}{\mathrm{\partial }t}+\mathrm{\nabla }\cdot [(\mathbf{\text{u}}+{\mu }_b\mathbf{\text{E}}){\rho }_e-D_e\mathrm{\nabla }{\rho }_e]=0\hspace{0.17em},$$ 2.2

where ${\rho }_e$ is the charge density, ${\mu }_b$ is the ion mobility and is approximated as a constant 2.0 × 10⁻⁴m²/V s [3,25] and $D_e$ is the ion diffusivity. D_e can be determined using the electrical mobility equation.

$$D_e=\frac{{\mu }_b{k}_B{T}_e}{q},$$ 2.3

where $k_B$ is the Boltzmann constant, $T_e$ is the absolute temperature and q is the elementary charge. The analytical expressions for $(\phi -I)\hspace{0.17em}\text{and}\hspace{0.17em}(\phi -T)$ can be derived for steady-state conditions in planar coordinates from the simplified governing for charge density, equation (2.2).

Figure 1.

Diagram of a wire-to-cylinder EHD flow. In positive corona, the negative species produced in the ionization zone recombine with positive species or the emitter (anode). The super-equilibrium positive ions drift to the collector electrode (cathode), accelerating the bulk flow. Thrust force is the resultant of the Coulombic force induced by the ions and drag force on the cathode. The conceptual representation of the EHD system includes (i) ionization region, (ii) flow acceleration region where unipolar ion motion in the gas medium acts as a body force accelerating the flow and (iii) momentum conservation region where the electric force is balanced or overcome by viscous effects. (Online version in colour.)

Table 1.

Nomenclature.

$A$	cross-section area of corona discharge (m2)
$C_D$	drag coefficient of the cathode
$D_e$	ion diffusivity (m2 s−1)
$D_k$	ion diffusivity of charged species k (m2 s−1)
$d$	distance between anode and cathode (mm)
$E$	electric field (V m−1)
$f$	Coulomb force per unit volume (N m−3)
$F_{\mathrm{EHD}}$	volumetric force induced by ions (N)
$F_D$	drag force (N)
$I$	current (A)
$J$	current flux [C/(s•m2)]
$J_L$	current flux at characteristic length scale [C/(s•m2)]
$k_B$	Boltzmann constant
$L_c$	characteristic dimension
$N_k$	density of charged species k
$P$	pressure inside a corona discharge (Pa)
$q$	elementary charge (C)
$S$	cross-sectional area of the cathode (m2)
$T$	thrust force induced by the ions (N)
$T_e$	absolute temperature (K)
$u$	velocity (m s−1)
$v$	mean electric wind velocity (m s−1)
$\beta$	scaling factor for the characteristic length
$\epsilon$	permittivity of air [C/(V•m)]
${\mu }_b$	ion mobility [m2/(V•s)]
${\mu }_k$	ion mobility of charged species k [m2/(V•s)]
${\rho }_e$	charge density (C m−3)
$\rho$	density of fluid (kg m−3)
$\theta$	non-dimensionless quantity for the drag force
$\phi$	electric potential (V)
${\phi }_o$	corona initiation voltage (V)
${\omega }_k$	production rate of charged species

Since the ion drift velocity is considerably higher than the EHD-induced bulk flow, the ion motion is assumed to be quasi-steady, and the equation (2.2) can be rewritten as

$$\mathrm{\nabla }\cdot [(\mathbf{\text{u}}+{\mu }_b\mathbf{\text{E}}){\rho }_e-D_e\mathrm{\nabla }{\rho }_e]=0.$$ 2.4

The forcing on the ions due to the electric field set up by potential between the electrodes is significantly greater, the space charge diffusion has not been typically considered [30]

$$\frac{\mathbf{\text{u}}+{\mu }_b\mathbf{\text{E}}}{D_e}\sim O({10}^4).$$ 2.5

The diffusion term can be neglected, and equation (2.4) can be further reduced

$$\mathrm{\nabla }\cdot [(\mathbf{\text{u}}+{\mu }_b\mathbf{\text{E}}){\rho }_e]=0.$$ 2.6

Guan et al. [25] have shown that space charge density influences the electric field lines (and thus the ion drift direction) in the vicinity of the ionization region for geometries with high angles (greater than 45°) between the bulk flow direction and the line connecting anode and cathode in a point-to-ring geometry. In the geometry where the flow direction is aligned with electrode geometry, the space charge effect is significantly lower, and for the purpose of this derivation, is not considered. The electro-convective velocity due to external flow is negligible compared to the drift velocity $(|\mathbf{\text{u}}|/|{\mu }_b\mathbf{\text{E}}|=O({10}^{-2}))$ in air discharge [30]. The continuity equation can be reduced to

$$\mathrm{\nabla }\cdot [{\mu }_b{\rho }_e\mathbf{\text{E}}]=0,$$ 2.7

where ${\mu }_b{\rho }_e\mathbf{\text{E}}=\mathbf{\text{J}}$ is the current flux. The electric field satisfies Gauss's law

$$\mathrm{\nabla }\cdot \mathbf{\text{E}}=\frac{{\rho }_e}{\epsilon },$$ 2.8

where $\epsilon$ is the permittivity, and for air, it is close to the permittivity of the space. Combining with equation (2.8) the ion transport equation can be written as

$$\frac{{\mu }_b}{\epsilon }{\rho }_e^2-{\mu }_b\mathrm{\nabla }{\rho }_e\mathrm{\nabla }\phi =0.$$ 2.9

Note that equation (2.9) is the same as in Sigmond [30]. Derivations for Cartesian coordinates are similar to Guan et al. [14]. Equation (2.9) can be rearranged as

$$\mathrm{\nabla }\phi =\frac{{\rho }_e^2}{\epsilon \mathrm{\nabla }{\rho }_e}.$$ 2.10

In one dimension (aligned with the flow acceleration), we have

$$\frac{\text{d}\phi }{\text{d}x}=\frac{{\rho }_e^2}{\epsilon (\text{d}{\rho }_e\text{/d}x)}.$$ 2.11

Taking the x-derivative on both sides and substituting into Gauss's law, equation (2.8):

$$\frac{{\text{d}}^2\phi }{\text{d}{x}^2}=-\frac{{\rho }_e}{\epsilon }=\frac{2{\rho }_e(\text{d}{\rho }_e\text{/d}x)(\epsilon (\text{d}{\rho }_e\text{/d}x))-{\rho }_e^2(\epsilon ({\text{d}}^2{\rho }_e\text{/d}{x}^2))}{{(\epsilon (\text{d}{\rho }_e\text{/d}x))}^2}.$$ 2.12

Rearranging

$$3{\left(\frac{\text{d}{\rho }_e}{\text{d}x}\right)}^2={\rho }_e\left(\epsilon \frac{{\text{d}}^2{\rho }_e}{\text{d}{x}^2}\right),$$ 2.13

and seeking the solution in the form

$${\rho }_e=K{x}^n,$$ 2.14

then substituting into equation (2.13), the following expression is yielded

$$3n^2{x}^{2(n-1)}=n(n-1)x^{2n-2}.$$ 2.15

From equation (2.15) $n=-1/2\hspace{0.17em}\text{and}\hspace{0.17em}{\rho }_e=K{x}^{-1/2}$, substitute to $E=-(\text{d/d}x)\phi$

$$-\frac{\text{d}}{\text{d}x}\phi =-\frac{{\rho }_e^2}{(\epsilon (\text{d}{\rho }_e\text{/d}x))}=\frac{2K}{\epsilon }{x}^{1/2}$$ 2.16

and

$$\text{d}\phi =-\frac{2K}{\epsilon }{x}^{1/2}\text{d}x\text{.}$$ 2.17

Integrating on both sides gives

$${\phi }_c-\phi =-\frac{4K}{3\epsilon }{x}^{3/2}\text{.}$$ 2.18

The coefficient K can be written as

$$K=\frac{3\epsilon }{4x^{3/2}}(\phi -{\phi }_c)\text{, }$$ 2.19

where $\phi$ is the applied anode potential and ${\phi }_c$ is the constant potential in a corona discharge, which can be considered as potential at the x-location of the corona onset, or corona initiation voltage ${\phi }_o$. The ion current flux between the anode and cathode is

$$J={\mu }_b{\rho }_{e}E=\frac{9{\mu }_b\epsilon {(\phi -{\phi }_o)}^2}{8x^3}\text{.}$$ 2.20

The relationship in equation (2.20) shows that $J\propto x^{-3}$ and has a similar form to Mott–Gurney law [17,27], i.e. $J=9{\mu }_b\epsilon {\phi }^2\text{/}8d^3$, which describes the space charge saturation limit, where d is the distance between the electrodes and $\phi$ is the applied potential. In corona discharge, the charged species are produced only after the onset potential is reached, so if $\phi$ is replaced by $\phi -{\phi }_o\hspace{0.17em}\text{and}\hspace{0.17em}x=d$, the current flux relation becomes takes the form of Mott–Gurney law.

The EHD flow in planar wire-to-cylinder geometry can be divided into three regions: ionization zone, acceleration zone and momentum conservation region. To define the conditions in the acceleration region, consider $x_{\text{cr}}$, which is the characteristic length scale of the flow acceleration. For wire-to-cylinder geometry, the ionization and drift regions can be approximated as an infinite plane (in the y-direction), where $x_{\text{cr}}$ is the distance from the emitter to an examination position, as shown in figure 1. The current flux at the location $(x_{\text{cr}})$ can be written as

$$J_{\text{cr}}={\mu }_b{\rho }_{e}E=\frac{9{\mu }_b\epsilon {(\phi -{\phi }_o)}^2}{8x_{\text{cr}}{\hspace{0.17em}}^3},$$ 2.21

and

$$I=\int J_{\text{cr}}\mathrm{d}A=J_{\text{cr}}A,$$ 2.22

where A is the cross-sectional area associated with ion interaction with the fluid at the location $x_{\text{cr}}$. For planar geometry (infinite length electrodes), the zone of ion interaction with the fluid can be normalized to a unit length $(L_c\times 1)$. Substituting cross-section area into equation (2.21) gives the current expression

$$I=\frac{9{\mu }_b\epsilon {(\phi -{\phi }_o)}^2}{8L_c{x}_{\text{cr}}}\text{.}$$ 2.23

To simplify, we introduce a characteristic dimension (L_c) that defines the ion-flow interaction region, then equation (2.23) can be reduced to

$$I=\frac{9{\mu }_b\epsilon {(\phi -{\phi }_o)}^2}{8L_c^2}.$$ 2.24

This current–voltage relationship is similar to Townsend's quadratic relationship for the coaxial cylinder electrode configuration $I=C\phi (\phi -{\phi }_o)$, where C is a fitting coefficient, typically obtained from the experiments and it is dependent on the geometry. The physical interpretation of the parameter C is proposed by Cooperman for duct-type electrostatic precipitator as $C\propto {\mu }_b/{L_c}^2$, where ${\mu }_b$ is the ion mobility and $L_c$ is the characteristic length scale [36]. Our derivation also shows a similar physical interpretation of Townsend constant:

$$C=\frac{9{\mu }_b\epsilon }{8L_c^2}\text{.}$$ 2.25

The derived $(\phi -I)$ relationship equation (2.23) is more general than formulations given by Townsend [29], the values of ${\phi }_o\hspace{0.17em}\text{and}\hspace{0.17em}{L}_c$ must be determined for any specific geometry. Once the $(\phi -I)$ relationship is defined, force induced by EHD can be computed as the Coulomb force acting on the volume of fluid by the nonequilibrium concentration of ions between the anode and cathode

$$F_{\text{EHD}}=\int f\text{d}V=\int {\rho }_{e}E\text{d}V={\int }_0^d{\rho }_{e}EA\text{d}x=\frac{Id}{{\mu }_b}\hspace{0.17em}=\frac{9\epsilon {(\phi -{\phi }_o)}^{2}d}{8L_c^2},$$ 2.26

where F_EHD is the volumetric force induced by the ions and f is the force per unit volume.

Previous research [17,18] shows the use of Townsend's current relation in equation (2.26) to determine the EHD force by fitting the constant C. However, the measured thrust does not always agree with the calculated EHD force, because the measured thrust is the result of the Coulombic and drag forces. Predicted thrust force from Townsend's current voltage relationship can be 70% greater than the measured one [17,41], likely due to losses associated with drag and the three-dimensional field effects. The determination of drag on the cathode in a wire-to-cylinder system requires the knowledge of the velocity profile. However, the velocity measurements can be challenging near the high voltage emitter and may not be available. It has been proposed that the mean ionic wind velocity associated with the corona discharge can be determined using the Bernoulli equation, see Moreau et al. [17] The mean velocity v and pressure P in the ionization zone as shown in figure 1 can be approximated

$$P=\frac{1}{2}\rho v^2,$$ 2.27

where $\rho$ is the density of the fluid. The pressure gradient in the one-dimensional coordinate system induced by the corona discharge can be written as

$$f=\frac{\text{d}P}{\text{d}x}.$$ 2.28

Combining equations (2.26) and (2.28), the expression for pressure can be written as

$$P=\int f\text{d}x=\frac{Id}{{\mu }_{b}A}.$$ 2.29

The mean velocity of EHD flow can be determined from the equation (2.27)

$$v=\sqrt{\frac{2Id}{{\mu }_b\rho A}}.$$ 2.30

The mean electric wind velocity can also be calculated using momentum balance over the entire domain by neglecting the pressure and viscous terms

$${\rho }_{e}E=\rho v\frac{\text{d}v}{\text{d}x},$$ 2.31

and

$$\int {\rho }_{e}E\text{d}x=\int \rho v\text{d}v,$$ 2.32

substituting equation (2.26) and integrating over the gap between anode and cathode gives

$$\frac{Id}{{\mu }_{b}A}=\frac{1}{2}\rho v^2.$$ 2.33

After solving for v, the expression is identical to the equation (2.30).

The drag force due to the flow over the cathode can be calculated from the following expression:

$$F_D=\frac{1}{2}\rho v^{2}S{C}_{D,}$$ 2.34

where $F_D$ is the drag force, S is the cross-section area of the cathode and $C_D$ is the drag coefficient of the cathode. Though in the case of corona discharge, the velocity profile is not uniform, equation (2.34) can be used as an approximation. Substituting equation (2.30) into equation (2.34) simplifies it further

$$F_D=\frac{Id}{{\mu }_b}\frac{S{C}_D}{A}=\theta F_{\text{EHD}}.$$ 2.35

Here $\theta$ is a non-dimensionless quantity that is the ratio of the cross-section area of the cathode and corona discharge area multiplied by the drag coefficient of the cathode. The value of $\theta$ has to be less than unity and has to be determined for a specific cathode geometry. Thrust can be written as

$$T=(1-\theta )F_{\text{EHD}}.$$ 2.36

The derived $(\phi -T)$ relationship is more general than particular formulations presented in previous work [17]. This formulation can be used for determining the corona current and thrust forces in planar coordinates. Unlike the thrust force formulations that use Townsend relation with fitting parameter C, our model captures the thrust force generated by ions including aerodynamic losses. Table 2 compares thrust characteristics derived from empirical [28,29] data and our first-principles approach.

Table 2.

Comparison of analytical expressions from state of the art and our work.

	state of the art	current work	comparison
current flux	$J={\displaystyle \frac{9{\mu }_b\epsilon {(\phi )}^{2^{\phantom{\int }}}}{8d^3}}$ Mott–Gurney law [28]	$J={\displaystyle \frac{9{\mu }_b\epsilon {(\phi -{\phi }_o)}^2}{8x^3}}$	current flux at any x; model accounts for ionization onset—φ0
voltage–current characteristics	$I=C\phi (\phi -{\phi }_o)$ Townsend relation [29]	$I={\displaystyle \frac{9{\mu }_b\epsilon {(\phi -{\phi }_o)}^{2^{\phantom{\int }}}}{8L_c^2}}$	length scale Lc provides a physical interpretation to fitting constant—C
voltage–force characteristics	$F_{\mathrm{EHD}}={\displaystyle \frac{C\phi (\phi -{\phi }_o)d}{{\mu }_b}}$	$F_{\mathrm{EHD}}={\displaystyle \frac{9\epsilon {(\phi -{\phi }_o)}^{2^{\phantom{\int }}}d}{8L_c^2}}$	Coulombic force is computed from the first principles
voltage–thrust characteristics	no expression	$T=(1-\theta )F_{\mathrm{EHD}}$	model computes thrust and accounts for aerodynamic losses via parameter $\theta$

3. Model validation—experimental set up

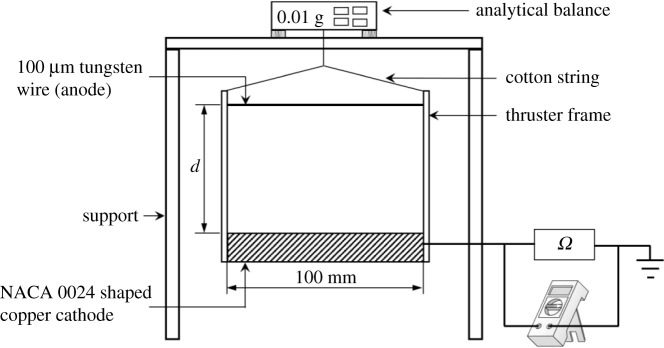
Analytical model validation is performed by comparing to the EHD thrust measurement in a wire-to-aerofoil geometry. In the experiments, we seek two primary correlations (i) voltage–current $(\phi -I)$ based on the cathode current and (ii) voltage–thrust $(\phi -T)$, where the thrust measure directly. Figure 2 shows the schematic of the experimental set-up. The emitter is a 100-μm diameter tungsten wire, the cathode is a symmetrical aerofoil (NACA 0024) fabricated of a 25-μm copper sheet and has a length of 25 mm. A thruster frame of 100 mm wide was built of a polylactic acid polymer. The frame was suspended from an analytical balance Metler Toledo (AE 240) with 40 g capacity and 0.01 g resolution. The distance between the electrodes (d) was varied in the range of 10–30 mm using spacers. The thruster mass is ∼26 g in the 10 mm spacer configuration. A high voltage power supply (Glassman, model EH30P3) was used to set the electric potential between the electrodes. The cathode current was measured based on a voltage drop across a 0.5 MΩ resistor. The electrical connections of both electrodes were established by thin wire (100 µm in diameter) to minimize added weight. The thruster was hung from a hook on the underside of the balance using cotton strings to electrically isolate the balance and to avoid current leakage, and the thrust was measured as a reduction in weight measure by the analytical balance. The experimental procedure is as follows: (i) the high voltage is switched off and the weight of the thruster is measured using the analytical balance (ii) the high voltage is switched on and the difference in the balance measurements is determined, the voltage value is increased in the increments of 1 kV. The experiment was operated in the positive corona mode in a room temperature range of 22–25°C, the relative humidity of 24–26% and ambient pressure. For each distance (d), the voltage was increased from 7 kV (when the thrust force becomes measurable) to ∼29 kV (power supply limit or until a sparkover occurs). To verify the measurements, each experiment was repeated five times.

Figure 2.

Schematic of the experimental set-up. A high voltage is applied between the corona wire and the ion-collecting aerofoil-shaped cathode. The distance and voltage are varied in the experiments.

4. Results and discussion

(a). Voltage current characteristics

The cathode current was obtained as a function of corona voltage and compared with the model in figure 3. The I versus $\phi$ trends are similar to previously reported quadratic trends in the literature for different corona configurations [14,29,42], as shown in equation (2.24). The nonlinearity in the analytical model comes from the ${\phi }_o/\phi$ term in equation (2.24). The trends can be used to evaluate length for the acceleration zone $L_c$. It is convenient to examine the condition $\phi ={\phi }_o$ where the EHD thrust is negligible. At higher corona voltages, the length of the acceleration zone and electric field intensity increases nonlinearly. The previous work [14,30] considers the characteristic dimension L_c as a constant for a given electrode configuration; it was used as a fitting parameter to determine the $(\phi -I)$ curves, which are linearly dependent on d. By the similar logic, the best fit is obtained when $L_c=10+\beta (d-10)\hspace{0.17em}\text{and}\hspace{0.17em}\beta =1$. This relationship is likely to change for a different electrode configuration.

Figure 3.

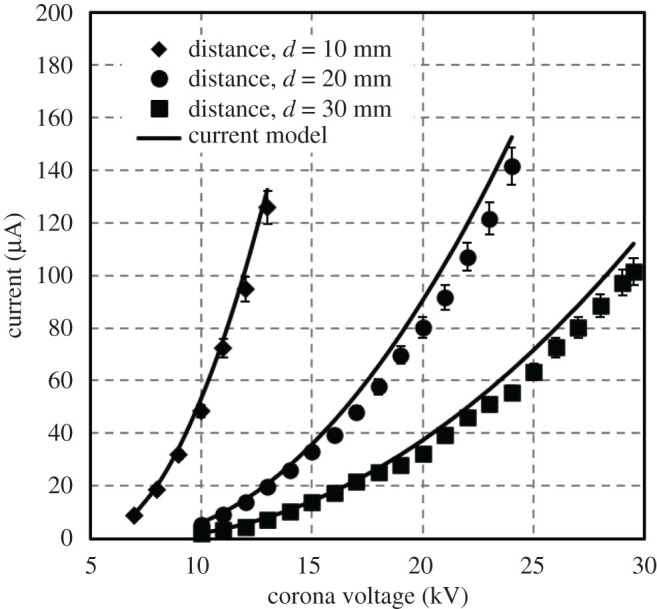
Voltage–current characteristics for the experimental data and the analytical solution.

The analytical model has excellent agreement with the experimental results at lower voltages and within ∼10% at higher voltages. The discrepancy between the model predictions and the experimental results can be due to the current leakage, i.e. ions exiting the control volume and not participating in the momentum exchange. For greater corona voltages, the leakage increases leading to a larger difference between the model and experimental data. The discussion in the thrust data analysis presents several mechanisms that can be contributing to the model underprediction of current and thrust as the voltage and electrode spacing increase.

(b). Electrode spacing effect

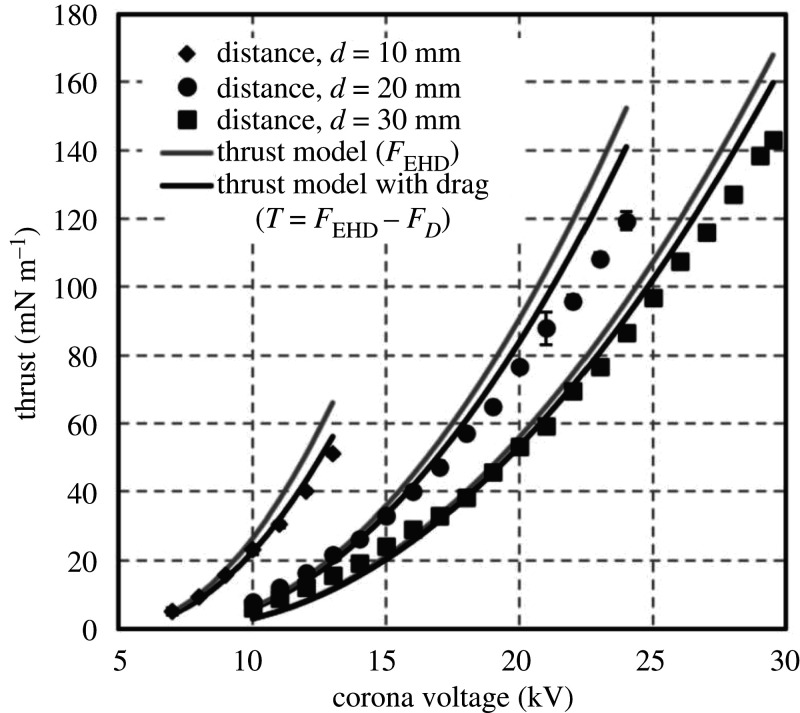
The variation in distance between the electrodes has several effects (i) the strength of the E-field decreases with distance, (ii) the net thrust is proportional to the volume of the ion drift region (iii) greater electrode spacing results in higher viscous losses. Figure 4 compares the voltage–thrust data against and the analytical solution varying d = 10–30 mm and $\phi$ = 7–29.5 kV. The relationship between the thrust and voltage is quadratic, as predicted by equation (2.26), which agrees with the trends reported in the literature for a wire-to-cylinder corona configuration [17,18]. These trends can be used to estimate corona onset voltage ${\phi }_o$; at this condition, the thrust is negligible. The experimental data show that higher thrust is observed at smaller gap lengths for a given voltage as the electrical field strength is greater. However, smaller gap configurations are limited due to earlier electrical breakdown (sparkover leads to a loss of thrust). The experimental thrust data are compared with two different models, (i) model without the aerodynamic drag on the cathode, see equation (2.26) and (ii) model with aerodynamic drag losses equation (2.36). As the voltage increases, the model without drag correction over-predicts the experimental thrust as the aerodynamic drag correction is greater at higher flow velocities. The mean flow velocities generated by the EHD are determined using equation (2.30), and the cathode chord Reynolds number varies from 1000 to 6000. The small dimensions of the cathode and the low velocities amplify the viscous effects and generate high drag [43]. At these low Reynolds number, the drag coefficient of the aerofoil $C_d=0.06$ is used based on previous work on dragonfly aerofoil aerodynamics for Re < 8000 [44]. Here, the drag coefficient is kept constant for all cases. The calculated non-dimensional drag varies $\theta$ = 0.05–0.15 as given in equation (2.35) for different electrode gaps. The analytical model with drag force correction has better agreement with the experimental data at lower voltages. The model agrees within ∼10% at higher voltages.

Figure 4.

Voltage–thrust relationship for varying distances between the anode and cathode for positive corona discharge. The experimental data are compared with the analytical model with and without the aerodynamic drag on the cathode.

(c). EHD thrust model comparison with previous reports

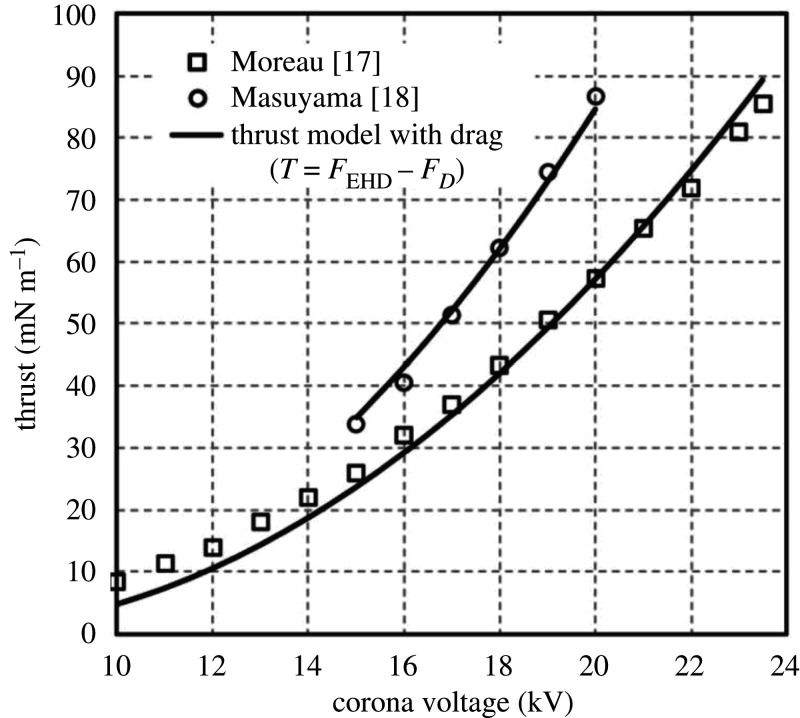
The model with drag correction is compared with the $(\phi -T)$ data in wire-to-cylinder configurations, from the literature [17,18]. Figure 5 plots the comparison for two different electrode gaps: d = 20 mm [18], and d = 30 mm [17]. The fitting parameter L_c = 17 mm gives the best fit for both the studies, the model predicts the data within 10%, overpredicting the thrust at higher voltages. Table 3 summarizes the model parameters used for the comparison of the analytical model and experimental data. The choice of L_c is dependent on the drag force calculations from equation (2.35). In modelling of our experimental data, we have experimentally determined ${\phi }_c$ based on onset current. In the previous data [17,18], the value of ${\phi }_c$ is not known, thus we have chosen ${\phi }_c=6\hspace{0.17em}\text{kV}$ (within the range of our experimental measurements). The agreement can be improved if the values of onset voltage are known. Though it is not apparent in our data or from Moreau et al. [17], Masuyama & Barrett [18] have observed the flattening of the $(\phi -T)$ trend at high voltages and the largest electrode gap conditions. The EHD thrust reaches saturation with the increase of potential. The presented one-dimensional model cannot account for this trend. At this time, we do not have an explanation for the discrepancy between the model and data at the highest voltage; however, we provide several hypotheses that may describe this behaviour. (i) Nonlinear effects in the ionization region, where the increasing E-field does not produce ions at the same rate as in the lower conditions. (ii) The losses in the acceleration region due to the viscous dissipation are greater for the larger electrode gap. (iii) Space charge shielding effect, where a fraction of positive ions does not drift toward the cathode but rather are lost to surroundings (including surfaces around the experimental apparatus). This effect is likely to be enhanced as the distance between the electrodes increases. (iv) One-dimensional assumption cannot be used to describe flow, as the nonlinear E-field leads to the formation of complex flow patterns. Additional investigations are required to test these hypotheses. Three-dimensional numerical modelling could be a good tool to study these effects.

Figure 5.

Comparison of the analytical model and existing thrust data from the literature. The model with drag losses accurately predicts the thrust data for two different cases: 20 mm separation from Masuyama & Barrett [18] and 30 mm separation from Moreau et al. [17].

Table 3.

Model parameters used for state of the art and the current work.

	modelling previous data	modelling our data
${\phi }_c$	d = 20 mm, 6 kV [18]	d = 10 mm, 4.8 kV
	d = 30 mm, 6 kV [17]	d = 20 mm, 6.5 kV
		d = 30 mm, 7 kV
$L_c$	17 mm for both cases	$10+\beta (d-10)\hspace{0.17em}\text{and}\hspace{0.17em}\beta =1$

5. Conclusion

An analytical model describing the EHD thrust is developed in one-dimensioal coordinates and compared with data for wire-to-aerofoil and wire-to-cylinder configurations. The current density expression is analogous to Mott–Gurney law that provides the theoretical maximum of charge density between anode and cathode. The model includes a modified term to account for the corona onset voltage. The derived $(\phi -I)$ relationship has a similar form as Townsend's equation with a modified constant proportional to ${\mu }_b/{L_c}^2$. The EHD thrust force is derived from $(\phi -I)$ relationship accurately predict the thrust at lower voltages. The aerodynamic drag correction improves the agreement at the higher voltages (greater velocities). The model agrees with the experimental data from three independent studies within 10%. The limitations of the model are in predicting the thrust at the increasing voltages; these are likely the results of the simplified assumptions in the viscous losses, ionization region modelling including space charge effects, increased dimensionality of the electric field in large electrode gap geometries.

Data accessibility

All relevant data are within the manuscript.

Authors' contributions

Conceptualization: R.S.V., Y.G. Model development: R.S.V., Y.G. Methodology: R.S.V. Data analysis and interpretation: R.S.V. Project administration: A.M., I.N. Supervision: A.M., I.N. Validation: R.S.V. Writing-original draft: R.S.V., Y.G. Writing-review and editing: R.S.V., A.M., I.N. All authors gave final approval for publication and agree to be held accountable for the work performed therein.

Competing interests

We declare we have no competing interests.

Funding

This work was supported through an academic-industry partnership between Aerojet Rocketdyne and the University of Washington funded by the Joint Center for Aerospace Technology Innovation (JCATI) and is also based upon work supported in part by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), via ODNI Contract 2017-17073100004. The views and conclusions contained herein are those of the author and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of ODNI, IARPA or the U.S. Government.