Theoretical Study of Shallow Distance Dependence of Proton-Coupled Electron Transfer in Oligoproline Peptides

Abstract

Long-range electron transfer is coupled to proton transfer in a wide range of chemically and biologically important processes. Recently the proton-coupled electron transfer (PCET) rate constants for a series of biomimetic oligoproline peptides linking Ru(bpy)₃²⁺ to tyrosine were shown to exhibit a substantially shallower dependence on the number of proline spacers compared to the analogous electron transfer (ET) systems. The experiments implicated a concerted PCET mechanism involving intramolecular electron transfer from tyrosine to Ru(bpy)₃³⁺ and proton transfer from tyrosine to a hydrogen phosphate dianion. Herein these PCET systems, as well as the analogous ET systems, are studied with microsecond molecular dynamics, and the ET and PCET rate constants are calculated with the corresponding nonadiabatic theories. The molecular dynamics simulations illustrate that smaller ET distances are sampled by the PCET systems than by the analogous ET systems. The shallower dependence of the PCET rate constant on the ET donor-acceptor distance is explained in terms of an additional positive, distance-dependent electrostatic term in the PCET driving force, which attenuates the rate constant at smaller distances. This electrostatic term depends on the change in the electrostatic interaction between the charges on each end of the bridge and can be modified by altering these charges. On the basis of these insights, this theory predicted a less shallow distance dependence of the PCET rate constant when imidazole rather than hydrogen phosphate serves as the proton acceptor, even though their pK_a values are similar. This theoretical prediction was subsequently validated experimentally, illustrating that long-range electron transfer processes can be tuned by modifying the nature of the proton acceptor in concerted PCET processes. This level of control has broad implications for the design of more effective charge-transfer systems.

Graphical Abstract

INTRODUCTION

Long-range electron transfer (ET) plays a significant role in a wide range of chemical and biological systems.^1–4 Biomimetic model systems, in which the electron donor and acceptor are connected by molecular bridges, have been designed to investigate the fundamental physical principles underlying such long-range ET reactions. A variety of experimental and theoretical studies have been performed to elucidate the origin of the exponential dependence of ET rate constants on the length of the bridge between the electron donor and acceptor sites.^{1, 5–21} The nature of the bridges and their conformational flexibility can play significant roles in determining the distance dependence of the ET rate constants.^{17, 19, 22–26} Moreover, dependence of the driving force and reorganization energy on the distance may also influence the distance dependence of the ET rate constants.^{21, 27–30}

Many long-range ET reactions in biological systems are also coupled to proton transfer (PT) reactions. These proton-coupled electron transfer (PCET) reactions play critical roles in biological processes such as nitrogen fixation,³¹ photosynthesis,³² respiration,³³ and DNA synthesis.³⁴ A significant amount of attention has been directed toward the dependence of PCET reactions on the proton donor-acceptor distance.^35–43 However, only a relatively small number of studies have focused on the dependence of PCET reactions on the ET donor-acceptor distance.^44–46 Recently, studies of PCET model systems with phenylene or p-xylene bridges^44–46 indicated that PCET rate constants depend on the ET donor-acceptor distances in a similar manner as do the analogous ET systems with the same bridges.^{12, 47–49}

Recently, a series of oligoproline peptides connecting Ru(bpy)₃²⁺ and tyrosine was designed and studied experimentally with a flash-quench transient absorption method.⁵⁰ In these experiments, photogenerated Ru(bpy)₃³⁺ oxidized tyrosine by a concerted PCET process involving intramolecular ET from tyrosine to Ru(bpy)₃³⁺ and proton transfer from tyrosine to the hydrogen phosphate buffer in aqueous solution (Figure 1). The concerted PCET mechanism is supported by the phosphate buffer concentration dependence of the kinetics and the kinetic isotope effects. Moreover, the dependence of the PCET rate constant on the ET donor-acceptor distance was studied by varying the number of oligoproline linkers from n = 1 to 4. The experimentally measured ET distance dependence was found to be much shallower than the corresponding distance dependence measured for analogous bimetallic ET systems with oligoproline bridges ^{13, 51–53} (Figure 1). The shallow distance dependence for the PCET systems relative to the ET systems was proposed to be related to the necessity of employing stronger oxidants for tyrosine, thereby leading to lower tunneling barrier heights within the McConnell superexchange model.^{1, 54}

Figure 1.

(A) ET and (B) PCET systems studied herein, where n = 1 – 4 for each system.

Herein we use a combination of microsecond molecular dynamics (MD) simulations and vibronically nonadiabatic PCET theory^55–57 to further elucidate the ET distance dependence of these oligoproline metallopeptides. This PCET theory has been used to investigate the dependence of the PCET rate constant on the proton donor-acceptor distance for a wide range of systems,^{35–36, 40–41} but the dependence on the electron donor-acceptor distance has not been studied as extensively. We perform microsecond MD simulations of the solvated ET and PCET oligoproline systems with bridges of different lengths, namely one to four proline linkers. We also calculate the ET and PCET rate constants for these systems using nonadiabatic ET and PCET theories, respectively. Analysis of the results provides a physical explanation for the shallower dependence of the PCET rate constant on the ET distance in terms of the net charges on the redox species terminating the bridge, producing an attractive electrostatic interaction that is smaller for the product than for the reactant, thereby decreasing the driving force. This effect becomes more pronounced as the electron donor-acceptor distance decreases. Moreover, our theoretical model predicts that this distance dependence of the PCET rate constant will increase when imidazole rather than hydrogen phosphate is the proton acceptor, even though the relevant pK_a values are similar. This theoretical prediction is subsequently validated experimentally, illustrating how the nature of the proton acceptor can significantly impact the dependence of the PCET rate constant on the ET distance.

METHODS

Molecular dynamics simulations

The ET and PCET systems studied in the present work are shown in Figure 1. The Cambridge Structural Database (CSD) entries TIRTIY⁵⁸ and SOYRIJ⁵⁹ were used to prepare the structures of the metal-containing terminal groups, and the CSD entry SOWJUL⁶⁰ was used to build the proline linkage. For the MD simulations, the AMBER ff14SB force field⁶¹ was employed to model the proline linkage and the terminal Tyr group, the general AMBER force field (GAFF)⁶² was used to model the metal-containing terminal groups, and the TIP3P water force field⁶³ was used to model the solvent. The partial charges of the terminal Tyr group were obtained through a two-stage RESP fitting procedure for two different configurations,^64–65 and the parameters for the metal sites were generated with the MCPB.py program.⁶⁶ Each of the four PCET systems was solvated in 0.1 M [HPO₄]²⁻ buffer solution and neutralized by the addition of K⁺ ions. Each of the four ET systems was solvated in a water box neutralized by the addition of Cl⁻ ions. The long-range electrostatic interactions were treated with the particle mesh Ewald method.⁶⁷ After a careful equilibration procedure, a 1 μs trajectory was propagated using the pmemd.cuda program⁶⁸ for each of the eight systems, with configurations saved every 10 ps. These configurations were used for the analysis of the distributions of the ET donor-acceptor distance. Further details of the force field parameters and MD simulations are provided in the Supporting Informaton (SI).

Theoretical modeling of the ET and PCET reactions

For each ET system, the rate constant was calculated by thermal averaging of the standard nonadiabatic ET rate constant over the ET donor-acceptor distance:⁶⁹

$$k_{\text{ET}}=\int k_{\text{ET}}\left(R_{\text{ET}}\right)P\left(R_{\text{ET}}\right)d{R}_{\text{ET}}$$ (1)

$$k_{\text{ET}}\left(R_{\text{ET}}\right)=\frac{1}{\hslash }{\left|V_{\text{el}}^0\right|}^2\text{exp}\left[-{\beta }_{\text{ET}}\left(R_{\text{ET}}-R_{\text{ET}}^0\right)\right]\sqrt{\frac{\pi }{\lambda k_{\text{B}}T}}\text{exp}\left[-\frac{{\left(\Delta G_{\text{ET}}+\lambda \right)}^2}{4\lambda k_{\text{B}}T}\right]$$ (2)

Here R_ET is the distance between the two Ru ions in the bimetallic ET system and P(R_ET) is the probability distribution obtained from the conformational sampling in the MD simulations. Moreover, k_B is the Boltzmann constant, T is the temperature, and $V_{\text{el}}^0$ is the electronic coupling between the ET donor and acceptor sites with the ET distance $R_{\text{ET}}^0$ corresponding to a single bridge unit (i.e., n = 1). The specific value of $V_{\text{el}}^0$ is not needed for this study because it simply corresponds to an additive constant to ln(k_ET). The coupling attenuation parameter β_ET was set to 1.4 Å⁻¹ according to the ET study of the oligoproline bimetallic systems.¹³ The reorganization energy λ for each of the four ET systems was evaluated using a Marcus two-sphere model⁷⁰ and averaging the resulting values according to the distribution P(R_ET) (see SI). The ET reaction free energy ΔG_ET was determined to be −26.9 kcal/mol on the basis of the relevant reduction potentials (see SI).

In the vibronically nonadiabatic PCET theory,^55–57 the reaction is described in terms of nonadiabatic transitions between reactant and product electron-proton vibronic states. When fluctuations in the environment lead to the degeneracy between a pair of reactant and product vibronic states, the electron and proton tunnel simultaneously with a probability proportional to the square of the vibronic coupling. For each PCET system, the calculation of the rate constants required thermal averaging over both the ET donor-acceptor distance R_ET and the PT donor-acceptor distance R_PT. The thermal averaging over R_ET was analogous to that described for the ET systems, where k_ET is replaced by k_PCET in Eq. (1), and in this case the electron transfer distance is defined as the distance between the Ru³⁺ ion and the geometrical center of the six carbon atoms of the Tyr benzene ring. The probability distribution P(R_ET) was assumed to be the same for the PCET systems with either hydrogen phosphate or imidazole as the proton acceptor.

The nonadiabatic PCET rate constant k_PCET(R_ET) at each fixed ET distance is given by

$$k_{\text{PCET}}\left(R_{\text{ET}}\right)=\frac{1}{\hslash }{\left|V_{\text{el}}^0\right|}^2\text{exp}\left[-{\beta }_{\text{ET}}\left(R_{\text{ET}}-R_{\text{ET}}^0\right)\right]\sqrt{\frac{\pi }{\lambda k_{\text{B}}T}}\times \sum _{\mu }{P}_{\mu }\sum _v\langle {\left|S_{\mu v}\left(R_{\text{PT}}\right)\right|}^2\rangle \text{exp}\left[-\frac{{\left(\Delta G_{\mu v}+\lambda \right)}^2}{4\lambda k_{\text{B}}T}\right]$$ (3)

This PCET rate constant expression accounts for all pairs of reactant and product proton vibrational states μ and ν obtained by solving the one-dimensional Schrödinger equation for a proton moving in the reactant and product electronically diabatic proton potentials, respectively. The rate constant is calculated by averaging over the reactant proton vibrational states μ with Boltzmann populations P_μ and summing over the product proton vibrational states ν. The vibronic coupling is the product of the electronic coupling and the overlap integral S_μν(R_PT) between the reactant and product proton vibrational wavefunctions. The angular brackets denote averaging over the proton donor-acceptor distance R_PT with the Gaussian distribution function:

$$P\left(R_{\text{PT}}\right)=\sqrt{\frac{f_{\text{PT}}}{2\pi k_{\text{B}}T}}\text{exp}\left[-\frac{f_{\text{PT}}{\left(R_{\text{PT}}-R_{\text{PT}}^0\right)}^2}{2k_{\text{B}}T}\right]$$ (4)

Note that this model neglects the dependence of the electronically diabatic proton potentials, as well as the reorganization energy, on R_PT, thereby enabling the thermal averaging over R_PT to be restricted to the overlap integrals.

In the present work, the electronically diabatic proton potentials were represented by Morse potentials corresponding to O-H or N-H bonds (see SI), and the overlap integrals were calculated analytically.⁷¹ Furthermore, $R_{\text{PT}}^0$, which is the equilibrium proton donor-acceptor distance in the reactant state, and the force constant f_PT, which is related to the second derivative of the energy profile along R_PT, were obtained from density functional theory (DFT) calculations (Table S4). As for the ET systems, the reorganization energy for each of the PCET systems was estimated by averaging the R_ET-dependent value obtained from the Marcus two-sphere model according to the distribution P(R_ET) (see SI). For the PCET systems, $V_{\text{el}}^0$ is defined analogously as the corresponding parameter for the ET system but is expected to assume a different value, which is not needed to compute the relevant slopes. For consistency, we used the same electronic coupling attenuation parameter β_ET for both the ET and PCET systems, although β_ET may be different for these two types of systems because of their different thermodynamic properties. To explore this possibility, we also investigated the impact of using different values of β_ET for the ET and PCET systems, but the qualitative conclusions did not change.

The free energy difference ΔG_μν in the PCET rate constant is given by

$$\Delta G_{\mu v}=\Delta G_{\text{PCET}}+{\epsilon }_v-{\epsilon }_{\mu }+\Delta E_{\text{ele}}$$ (5)

where ΔG_PCET is the reaction free energy of the PCET reaction, and ε_μ and ε_ν are the proton vibrational energy levels for the states μ and ν relative to the lowest vibrational states of the corresponding diabatic proton potentials. ΔG_PCET was determined to be −10.0 kcal/mol from the pK_a values and redox potentials of the relevant species (see SI). The additional electrostatic term ΔE_ele, which depends on the distance between the metal center (Ru) and the proton acceptor (PA) group, accounts for the difference in electrostatic interactions between the charges localized on these sites in the reactant and product states in the PCET reaction and is given by

$$\Delta E_{\text{ele }}=\frac{\Delta \left(Q_{\text{Ru}}{Q}_{\text{PA}}\right)}{{\epsilon }_{\text{eff}}{R}_{\text{Ru-PA}}}$$ (6)

Here R_Ru-PA, which is the distance between the metal center and the proton acceptor group, is approximated by R_ET. In this expression, Δ(Q_RuQ_PA) is the difference between the product of the charges on the metal center and the proton acceptor group after and before the PCET reaction. For example, when [HPO₄]²⁻ serves as the proton acceptor, Q_RuQ_PA is (+3e)×(‒2e) before and (+2e)×(‒1e) after the PCET reaction, resulting in Δ(Q_RuQ_PA) = 4e². In this case, because the attractive electrostatic interaction is smaller for the product than for the reactant, this difference is positive and therefore decreases the driving force, particularly at shorter distances. Finally, ε_eff is an empirical factor that accounts for the screening effects of the molecular and solvent environment as well as delocalization of the charges and thus depends on factors such as the solvent, ionic strength, ion pairing, and electronic structure of the donor-bridge-acceptor system. As discussed further below, this factor reflects an average over electrostatic interactions through the solution and/or the molecular bridge. In the present study, this factor was set to 5.1 to reproduce the slope of the experimentally measured ln(k_PCET) versus the computed average ET distances for the system with hydrogen phosphate serving as the proton acceptor. We used the same value of this factor to model the system with imidazole as the proton acceptor and found good agreement with the experimentally measured slope for this system. We emphasize that ΔE_ele adjusts the driving force of the oligoproline peptides by including the electrostatic interactions between the electron donor and acceptor because ΔG_PCET is computed from the thermodynamic properties of the isolated donor and acceptor species.

RESULTS AND DISCUSSION

Probability distributions of ET distances

To characterize the ET donor-acceptor distance fluctuations in the ET and PCET reactions, we analyzed the probability distributions of the ET distances obtained from microsecond MD trajectories. For the ET systems, R_ET was defined as the distance between the two Ru ions, and for the PCET systems, R_ET was defined as the distance between the Ru³⁺ ion and the geometrical center of the six carbon atoms of the Tyr benzene ring. As shown in Figure 2, the probability distribution for each ET system resembles a single Gaussian. In contrast, the probability distribution for each PCET system is broader with a shoulder at smaller distances, indicating that multiple conformations are sampled on the microsecond timescale. The average R_ET values, denoted ${\overline{R}}_{\text{ET}}$, for the PCET systems are slightly smaller than those for the ET systems with the same number of proline residues and exhibit larger fluctuations (Table 1). These differences may be due to the flexibility of the neutral terminal Tyr electron donor group in the PCET systems, which enables sampling of conformations with smaller distances with respect to the positively charged Ru³⁺ center. In contrast, the metal centers in the ET systems are relatively bulky with the bound ligands and are both positively charged, preventing effective sampling of conformations with smaller distances. To understand the role of the counterions in the ET systems, we calculated the radial distribution function (RDF) between the Ru²⁺ and Ru³⁺ metal centers and the Cl⁻ ions for each of the four systems (Figure S4). For all of these systems, the Cl⁻ ions were found closer to the Ru³⁺ than to the Ru²⁺ because of its greater positive charge and smaller ligands.

Figure 2.

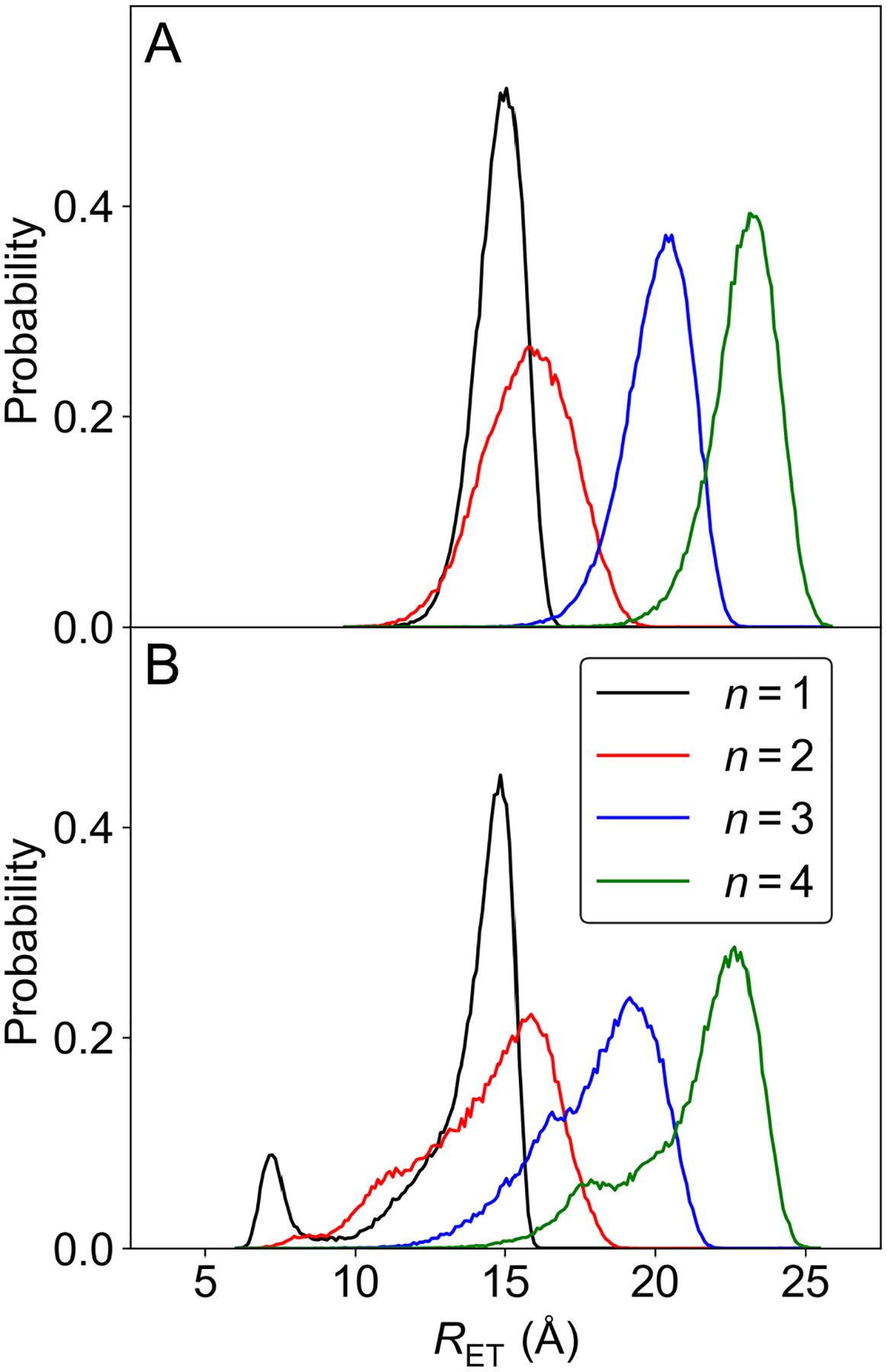
Probability distributions of the ET donor-acceptor distance in (A) the ET systems and (B) the PCET systems, where n is the number of proline residues in the bridge. These results are based on 1 μs MD trajectories for each of the eight systems.

Table 1.

Average ET Distances ${\overline{R}}_{\text{ET}}$ and Standard Deviations for the ET and PCET Systems.^a

n	ET systems	PCET systems
1	14.8±0.8	13.4±2.3
2	15.7±1.5	14.3±2.2
3	20.1±1.1	18.1±1.9
4	22.9±1.1	21.3±2.1

^aThese values were obtained from 1 μs MD trajectories for each system and are in units of Å.

To further analyze the probability distributions for the PCET systems, we fit the distribution for each system to a linear combination of three Gaussians (Table S6 and Figures S5 and S6). We also examined representative conformations corresponding to the distance associated with the maximum of the probability distribution function for the ET systems and the distance associated with each Gaussian component for the PCET systems, as depicted in Figures S7 and S8. The probability distribution function for the PCET system with n = 1 has an additional peak at short distances compared to the probability distribution functions for the longer peptide bridges. The conformation associated with this Gaussian component with R_ET ~7.2 Å (Figure S8) illustrates that the single proline linkage allows the Tyr to curl around in a manner that decreases its distance from the Ru³⁺ center, although it also samples more extended conformations. In contrast, the longer peptide bridges do not have the flexibility to curl in this manner, although they also sample a wide range of extended as well as bent conformations (Figure S8), leading to the shoulders exhibited in Figure 2B.

Experimental and calculated rate constants

The magnitudes of the slopes estimated from the dependence of the experimentally measured ln(k) values on the calculated ${\overline{R}}_{\text{ET}}$ values for the ET and PCET systems studied are provided in the last column of Table 2. The experimentally determined slope for the PCET reactions of the Ru/Tyr system, with hydrogen phosphate as the proton acceptor, is significantly smaller in magnitude than the slope for the ET reactions of the related Ru/Ru system. Note that the ET donor-acceptor distances can also be estimated on the basis of experimental data from related systems or using other strategies (see SI). We found that the slopes obtained with these different options for determining the ET distances do not vary significantly (Table S8 and Figures S9 and S10). For consistency, we present all of the experimental and calculated kinetic data in the main paper in terms of the calculated ${\overline{R}}_{\text{ET}}$ values.

Table 2.

Dependence of the Calculated (Calc.) and Experimentally Measured (Exptl.) ET and PCET Rate Constants on the Calculated ${\overline{R}}_{\text{ET}}$.^a

Proton acceptor	Δ(QRuQPA) (e2)	pKa of proton acceptor	Calc. |slope| (Å−1)	Exptl. |slope| (Å−1)
		ET reaction
N/A	0	N/A	1.37	1.34b
		PCET reaction
[HPO4]2−	4	7.20c	0.59	0.59d
Imidazole	2	6.95e	0.95	0.87f

^aThe calculated (experimental) magnitudes of the slopes are obtained from the calculated (experimental) ln(k) versus the calculated ${\overline{R}}_{\text{ET}}$ values from Table 1.

^bValue for ET in Ru/Ru system (Fig. 1A) determined by plotting the experimental rate constants from Ref. ¹³ as a function of the calculated ${\overline{R}}_{\text{ET}}$ values.

^cValue from Ref. ⁷².

^dValue for Ru/Tyr system (Fig. 1B) with phosphate as proton acceptor determined by plotting the experimental rate constants from Ref. ⁵⁰ as a function of the calculated ${\overline{R}}_{\text{ET}}$ values.

^eValue from Ref. ⁷³.

^fValue for Ru/Tyr system with imidazole as proton acceptor determined by plotting the experimental rate constants measured herein as a function of the calculated ${\overline{R}}_{\text{ET}}$ values.

To elucidate the factors that determine the shallow distance dependence of the PCET reaction rate constant with hydrogen phosphate as the proton acceptor, we calculated k_ET and k_PCET for the eight systems using the nonadiabatic rate constant expressions and parameters given above. The slopes associated with the distance dependence of the rate constants were obtained from linear fits of the calculated values of ln(k) versus the corresponding average distances ${\overline{R}}_{\text{ET}}$ for the ET systems and the PCET systems with hydrogen phosphate as the proton acceptor (Figure 3). The calculated values of ln(k) versus ${\overline{R}}_{\text{ET}}$ were found to behave linearly with slopes that agree well with the corresponding slopes obtained experimentally (Table 2). Note that this agreement was obtained for the PCET systems by fitting the empirical parameter ε_eff to the experimentally determined slope (Figure 3B). As discussed below, however, the same value for ε_eff was used to successfully predict the increased magnitude of the slope for the PCET system with imidazole as the proton acceptor (Figure 3C).

Figure 3.

Comparison of the calculated (calc.) and experimentally measured (exptl.) ET and PCET rate constants as functions of the calculated ${\overline{R}}_{\text{ET}}$ values from Table 1: (A) ET systems, (B) PCET systems with hydrogen phosphate as the proton acceptor, and (C) PCET systems with imidazole as the proton acceptor. The experimentally measured PCET rate constants are second-order with units of M⁻¹s⁻¹, and the calculated rate constants are first-order with units of s⁻¹, assuming the pre-equilibrium formation of a hydrogen-bonded complex. Given that these two rate constants are related by an unknown equilibrium constant, and the electronic coupling $V_{\text{el}}^0$ is unknown, the calculated ln(k) value for n = 1 was shifted to agree with the experimentally determined value for each system. Thus, the red and black data points are identical for n = 1 for each system and appear as red. For the PCET systems in part B, the experiments were performed in 0.05–0.60 M [HPO₄]²⁻ buffer solution at pH = 8.0. For the PCET systems in part C, the experiments were performed in 0.01–0.10 M imidazole at pH 7.6, with details given in the SI. For the ET systems, the experiments were performed in aqueous solutions of 0.13 M tert-butanol and NaClO₄ at pH 6.⁵³ The MD simulations used to compute the probability distributions of ET distances for the PCET systems with hydrogen phosphate as the proton acceptor were performed with 0.1 M [HPO₄]²⁻ buffer concentration, and the probability distributions were assumed to be the same for the PCET systems with imidazole as the proton acceptor. The MD simualtions used to compute the probability distributions of ET distances for the ET systems were performed through neutralization by Cl⁻ counterions.

The parameter ε_eff should be viewed as an empirical factor that accounts for many different effects that are present in the experimental systems but are not included explicitly in our theoretical model. For example, this simple electrostatic model does not include the effects of charge delocalization, ion pairing, or the detailed electronic structure of the molecular system. To examine the fundamental basis for this electrostatic term, we performed constrained DFT calculations on three conformations of the n = 1 PCET system sampled during the MD simulations (Figure S8). The relative energies of the reactant and product states for the PCET reaction were computed by moving the proton from the donor to the acceptor and constraining the charge distribution using constrained DFT. As shown in Table S9, these relative reaction energies exhibit the trend that would be followed using the electrostatic term with ε_eff = 1, as expected for gas phase reactions. The conformations depicted in Figure S8 illustrate that the charges associated with the ends of the bridge interact through the solution or the molecular bridge or a combination thereof. Thus, the value of ~5 should be viewed as the result of averaging over all of these types of interactions, as well as accounting for the other effects mentioned above.

Impact of distance-dependent electrostatic term and validation of theoretical prediction

To understand the physical basis for the significantly different slopes observed for the ET systems and the PCET systems with hydrogen phosphate as the proton acceptor, we investigated the influence of the electrostatic term ΔE_ele on k_PCET. We found that decreasing Δ(Q_RuQ_PA) with all other parameters, including ε_eff, held constant leads to a significant increase in the magnitude of the slope of ln(k_PCET) versus ${\overline{R}}_{\text{ET}}$. Specifically, this slope magnitude is 0.59 Å⁻¹ for Δ(Q_RuQ_PA) = 4e² and is 1.74 Å⁻¹ when Δ(Q_RuQ_PA) = 0, illustrating that the slope becomes similar to that of the ET system when the ΔE_ele term in Eq. (5) is omitted. Moreover, the theoretical model predicts an intermediate slope magnitude of 0.96 Å⁻¹ when Δ(Q_RuQ_PA) = 2e² and all other parameters remain the same. This analysis also assumed that the electronic coupling attenuation parameter β_ET is the same for the ET and PCET systems. This assumption will be removed in additional calculations discussed below but does not change these qualitative trends.

To test this theoretical prediction, the PCET rate constants were experimentally measured for the same oligoproline metallopeptides with imidazole as the proton acceptor. The conjugate acid of imidazole has a pK_a similar to the pK_a of [H₂PO₄]⁻ but is cationic rather than anionic, resulting in Δ(Q_RuQ_PA) = 2e² in the numerator of the electrostatic contribution to the driving force. The magnitude of the slope of the experimental ln(k_PCET) versus ${\overline{R}}_{\text{ET}}$ was found to be 0.87 Å⁻¹, which is in qualitative agreement with our calculated value of 0.95 Å⁻¹ for the system with imidazole as the proton acceptor. Note that using the pK_a value of imidazole instead of phosphate and the Morse potential associated with an N-H rather than an O-H bond impacts the slope by only 0.01 Å⁻¹. The agreement between the experimental measurement and our theoretical prediction provides validation for the theoretical model. It also supports our hypothesis that the electrostatic term ΔE_ele plays an important role in determining the shallow distance dependence of the PCET reaction rate constant with hydrogen phosphate as the proton acceptor.

To separate the effects of the electrostatic term and the probability distribution, we computed the slopes for both ET and PCET with two different electrostatic terms added to the driving force. If we set the electrostatic term ΔE_ele to 0 and 4e²/(ε_effR_ET), we obtain different responses for the ET and PCET distance dependences. Specifically, the magnitude of the slope for the ET rate constant is 1.37 Å⁻¹ and 1.14 Å⁻¹, while the magnitude of the slope for the PCET rate constant with hydrogen phosphate as the proton acceptor is 1.74 Å⁻¹ and 0.59 Å⁻¹, respectively, for these two values of the electrostatic term. Thus, the electrostatic term exerts a much greater impact on the slope for the PCET reaction than for the ET reaction. As discussed below, our analysis suggests that this difference is due to the qualitative differences in the ET donor-acceptor distance probability distributions P(R_ET) for the ET and PCET systems shown in Figure 2.

Impact of probability distributions of ET distances

To further analyze the impact of P(R_ET), we fit the probability distributions obtained from the microsecond MD simulations to a linear combination of three Gaussians for each of the four PCET systems (Table S6 and Figures S5 and S6). To determine the contributions from these Gaussian components to the distance dependence of the PCET rate constants, we calculated the slopes for each of the four systems using only the third (major) Gaussian component, the sum of the second and third Gaussian components, or the sum of all three Gaussian components (Table 3). The magnitude of the slope calculated using only the third Gaussian component is larger than that calculated using the sum of the second and third Gaussian components, which in turn is larger than the magnitude of the slope calculated using the sum of all three Gaussian components. Thus, conformational sampling of the shorter ET distances effectively decreases the magnitude of the slope, leading to a shallower distance dependence. In contrast, the shorter distances are not as accessible for the ET systems, as indicated by the absence of the shoulders in the probability distributions (Figure 2). Note that when ΔE_ele = 0, this effect is not observed.

Table 3.

Influence of Electron Donor-Acceptor Distance Probability Distribution on Distance Dependence of PCET Rate Constant with Hydrogen Phosphate as Proton Acceptor.^a

P(RET)	Calc. |slope| (Å−1)	Calc. |slope| with ΔEele = 0 (Å−1)
Only third Gaussian	0.93	1.65
Only second and third Gaussians	0.81	1.65
All three Gaussians	0.60	1.82

^aThe first, second, and third Gaussian functions used to fit P(R_ET) are centered at increasing values of R_ET (Figures S5 and S6). The calculated magnitudes of the slopes were obtained from the calculated values of ln(k_PCET) versus the calculated ${\overline{R}}_{\text{ET}}$ values using the fitted Gaussian distributions (Table S6).

Interplay between electrostatic term and probability distribution of ET distances

To investigate the interplay between the electrostatic term ΔE_ele and the probability distribution P(R_ET) in determining the distance dependence of the PCET rate constant, we analyzed the dependence of the various terms in the PCET rate constant k_PCET(R_ET) on R_ET (Figure 4). This analysis includes only the term in Eq. (3) corresponding to the lowest reactant and product proton vibrational states, which was found to be the dominant contributor to the overall PCET rate constant (Table S10). This analysis used a constant reorganization energy corresponding to the value computed for the PCET system with n = 1 and hydrogen phosphate as the proton acceptor. The activation term $\Delta G_{00}^{‡}=\text{exp}\left[-\frac{{\left(\Delta G_{00}+\lambda \right)}^2}{4\lambda k_{\text{B}}T}\right]$ increases as R_ET increases (Figure 4A) because ΔE_ele decreases as this distance increases. However, the squared electronic coupling, which is proportional to $\text{exp}\left[-{\beta }_{\text{ET}}\left(R_{\text{ET}}-R_{\text{ET}}^0\right)\right]$, exhibits the opposite trend (Figure 4B). The resulting ln[k_PCET(R_ET)] exhibits a shallower distance dependence at R_ET distances in the range 12 – 16 Å and provides an explanation for the observation that these shorter distances are mainly responsible for the shallow distance dependence of the PCET rate constant (Figure 4C and Table 2). Thus, both the electrostatic term and the R_ET probability distribution play significant roles in determining the shallow distance dependence of the PCET rate constant. Changing ΔE_ele alters the slope in Figure 4A and therefore the curve shape in Figure 4C which, combined with the broadening of P(R_ET) toward shorter distances, leads to the shallow distance dependence of the overall PCET rate constant. This analysis indicates that the dependence of the rate constant on the ET distance can be influenced not only by the electronic coupling prefactor but also by the free energy barrier appearing in the exponential.

Figure 4.

Dependence of (A) negative activation free energy scaled by the thermal energy, −(ΔG₀₀ + λ)²/4λk_BT, (B) natural log of the square of the scaled electronic coupling, where $V_{\text{el}}^2/{\left|V_{\text{el}}^0\right|}^2=\text{exp}\left[-{\beta }_{\text{ET}}\left(R_{\text{ET}}-R_{\text{ET}}^0\right)\right]$, with β_ET taken to be 1.4 Å⁻¹, and (C) ln[k_PCET(R_ET)] on R_ET for the PCET system with hydrogen phosphate as the proton acceptor, including only the lowest reactant and product proton vibrational states.

The relatively flat curve for ln[k_PCET(R_ET)] versus R_ET in Figure 4C at small R_ET predicts similar rate constants for the PCET systems with no proline linkage and with a single proline linkage, assuming the same value for $V_{\text{el}}^0$. This behavior is consistent with experimental data indicating that the PCET system without a proline linkage has a rate constant of 3×10⁶ M⁻¹s⁻¹,⁷⁴ which is similar to the rate constant of 1.4×10⁶ M⁻¹s⁻¹ measured experimentally⁵⁰ for the PCET system with one proline linkage. As mentioned in the Introduction, only a few studies of the dependence of the PCET rate constant on the ET distance have been reported.^{12, 44, 47} In the study of PCET in iron carboxytetraphenylporphyrin complexes, a relatively small slope magnitude of 0.23 Å⁻¹ for the overall distance dependence of the rate constant was measured,⁴⁴ compared to the value of 0.4–0.46 Å⁻¹ measured for ET reactions with the same bridge unit.^{12, 47} In this system, the PCET reaction has an electrostatic term with Δ(Q_RuQ_PA) = e², while the ET reaction has an electrostatic term with Δ(Q_RuQ_PA) = −e² or zero. These different electrostatic terms may account for the lower magnitude of the slope for PCET compared to ET in these systems. In general, these two factors, namely the broad distribution of ET distances and the distance-dependent electrostatic contributions to the driving force, could impact the distance dependence of the rate constants for ET systems as well as PCET systems.

Impact of coupling attenuation parameter

Previous work⁵⁰ has suggested that the coupling attenuation parameter β_ET may be different for the ET and PCET systems, based on the different donor-bridge-acceptor energetics. To investigate this possibility, we repeated these calculations with β_ET = 1.2 Å⁻¹ rather than 1.4 Å⁻¹ for the PCET systems. We found that the experimentally determined slopes for the PCET systems with the two different proton acceptors, phosphate and imidazole, could also be reproduced after readjusting the empirical factor ε_eff in Eq. (6) (Table S11). However, a model in which the value of β_ET was different for the ET and PCET systems, without including the electrostatic term for PCET, cannot reproduce the larger magnitude of the slope with imidazole as the proton acceptor. Thus, the electrostatic term appears to be essential for describing the experimental data, but the different values of β_ET may also be a factor in describing the ET and PCET systems.

CONCLUSIONS

We investigated ET reactions in oligoproline bimetallic systems and PCET reactions in oligoproline metallopeptides using theoretical modeling. We performed microsecond MD simulations for the solvated ET and PCET systems and observed significant differences in the ET donor-acceptor distance probability distributions in these two systems. Specifically, the probability distributions for the ET systems are relatively narrow and symmetric, whereas those for the PCET systems are broader with shoulders at smaller distances, allowing the conformational sampling of these smaller distances on the microsecond timescale of the experiments. Another important distinction between the ET and PCET systems is the contribution to the driving force arising from the change in the electrostatic interaction between the charges at each end of the bridge. Although this electrostatic term is zero for the ET systems, it is positive and increases as the electron donor-acceptor distance decreases for the PCET systems. We emphasize that these effects are not related to fundamental differences between ET and PCET processes but rather are specific to these particular systems.

The ET and PCET rate constants computed with nonadiabatic theories reproduced the experimentally measured dependence of these rate constants on the average ET donor-acceptor distance for varying bridge lengths. The shallower distance dependence of the PCET rate constant with hydrogen phosphate as the proton acceptor was explained in terms of an additional positive, distance-dependent electrostatic term in the driving force, which attenuates the rate constant at smaller distances, in conjunction with the enhanced sampling of smaller distances observed in the MD simulations. The theoretical model predicted an increased magnitude of the slope for the PCET systems when imidazole is the proton acceptor because, although the conjugate acid of imidazole has a similar pK_a value as dihydrogen phosphate, its cationic rather than anionic charge leads to a smaller positive electrostatic contribution to the driving force. This theoretical prediction of an increased magnitude of the slope was subsequently validated by experimental measurements.

This work highlights the impact of the nature of the proton acceptor, particularly its charge, on the ET distance dependence of the PCET rate constant. Because the ET distance dependence of the rate constant can be influenced by not only the conventional β parameter in the electronic coupling prefactor but also by a term in the free energy barrier, the slope associated with the distance dependence assumes a more complex interpretation. These insights into how short-range proton transfer reactions can be used to tune long-range electron transfer reactions have broad implications for designing charge-transfer systems relevant to solar cells, sensors, and other types of devices.