Abstract
Acoustic feedback cancellation is a challenging problem in the design of sound reinforcement systems, hearing aids, etc. Acoustic feedback is inevitable when the acoustic signal path forms a loop between the microphone and loudspeaker. An efficient short duration noise injection algorithm is proposed in this paper to estimate the impulse response of the acoustic feedback path model. The algorithm does not require any prior information about the acoustic feedback path. It is capable of optimally estimate the acoustic feedback path for cancellation, and avoid the occurrence of any howling episode, in varying acoustic environments. Presented algorithm is efficiently implemented on smartphone device having close proximity of loudspeaker and microphone to emulate the feedback condition. The algorithm being platform-independent can also be implemented for any set-up or system. The experimental results of the proposed method shows satisfying results and its ability to track and cancel the acoustic feedback in changing characteristics of the acoustic path.
I. Introduction
Sound reinforcement systems such as classrooms, auditoriums, in-car communications systems, etc. have a microphone and a single or multiple loudspeakers. Signal captured through the microphone is amplified and played back by the loudspeaker. The undesired acoustic coupling between the loudspeaker and input microphone is referred to as the Acoustic Feedback (AF). The AF signal interferes with the desired signal at the input microphone and limits the single and whole purpose of the reinforcement applications. Unstable AF causes annoying sound called “howling” or “whistling” due to an infinite loop.
A large number of literature studies have been published in acoustic feedback cancellation (AFC) for hearing-aid devices (HADs) [1]. Current AFC methods utilize an FIR filter to model the acoustic feedback path [2]. The FIR filter is then placed in the system to cancel the AF effect. Two major challenges are seen while modeling the AF path. Firstly, the AF path keeps changing concerning time and position of loudspeaker and microphone [3]. Secondly, the AF signal is highly correlated with the desired input signal at the microphone. This correlation makes it difficult to correctly estimate the AF path model and leads to a biased estimate of the feedback path model in many AFC techniques, which in turn results in poor cancellation of the AF effect [1]. Adaptive and unbiased estimation of the feedback path will lead to efficient cancellation of the AF. Many adaptive AFC methods use a normalized Least–Mean-Square (NLMS) algorithm to determine an FIR filter and its coefficients. This mostly leads to a biased estimate of the feedback path, due to the aforementioned signals correlation [4], [5]. Furthermore, in almost all NLMS based methods, the order of the FIR filter has to be known, assumed or estimated in advance. Over or underestimation of the filter order can result in excessive computation (i.e. more power consumption) or inaccurate model for the AF path [6]. To obtain a bias-free estimate of the feedback path, decorrelation techniques are combined with adaptive algorithms in literature [1], [7]. Most popular decorrelation techniques are noise injection [8]–[10], prediction error method (PEM) based decorrelation [11], frequency shifting and phase modulation [12].
In this paper, we propose an adaptive short-duration noise injection technique for obtaining an optimum FIR filter for effective AF cancellation. The short duration of white noise is injected into the loud-speaker to compute the feedback path efficiently. The computed feedback path is then placed as shown in Fig. 1 to cancel the feedback. Howling based detection method is used to adapt to the changing nature of the feedback path. Continuous adaption algorithm such as NLMS, PEM-NLMS [11] estimates the biased feedback path which affects the performance of the feedback canceller. Moreover, continuous adaption algorithm takes a very long time (~ 20s) to reach the steady-state value compared to the proposed algorithm which computes the accurate feedback path within few milliseconds (~ 200ms). The proposed AF cancellation algorithm is computationally efficient, requires no advance knowledge of the AF path, can run be implemented on any platform or device in real-time. A smartphone having a microphone and loud-speaker in close proximity can emulate the sound reinforcement system perfectly. Physical configuration, low-latency, and processing ability of the smartphone motivate for the real-time implementation of the AFC system [13].
Fig. 1:
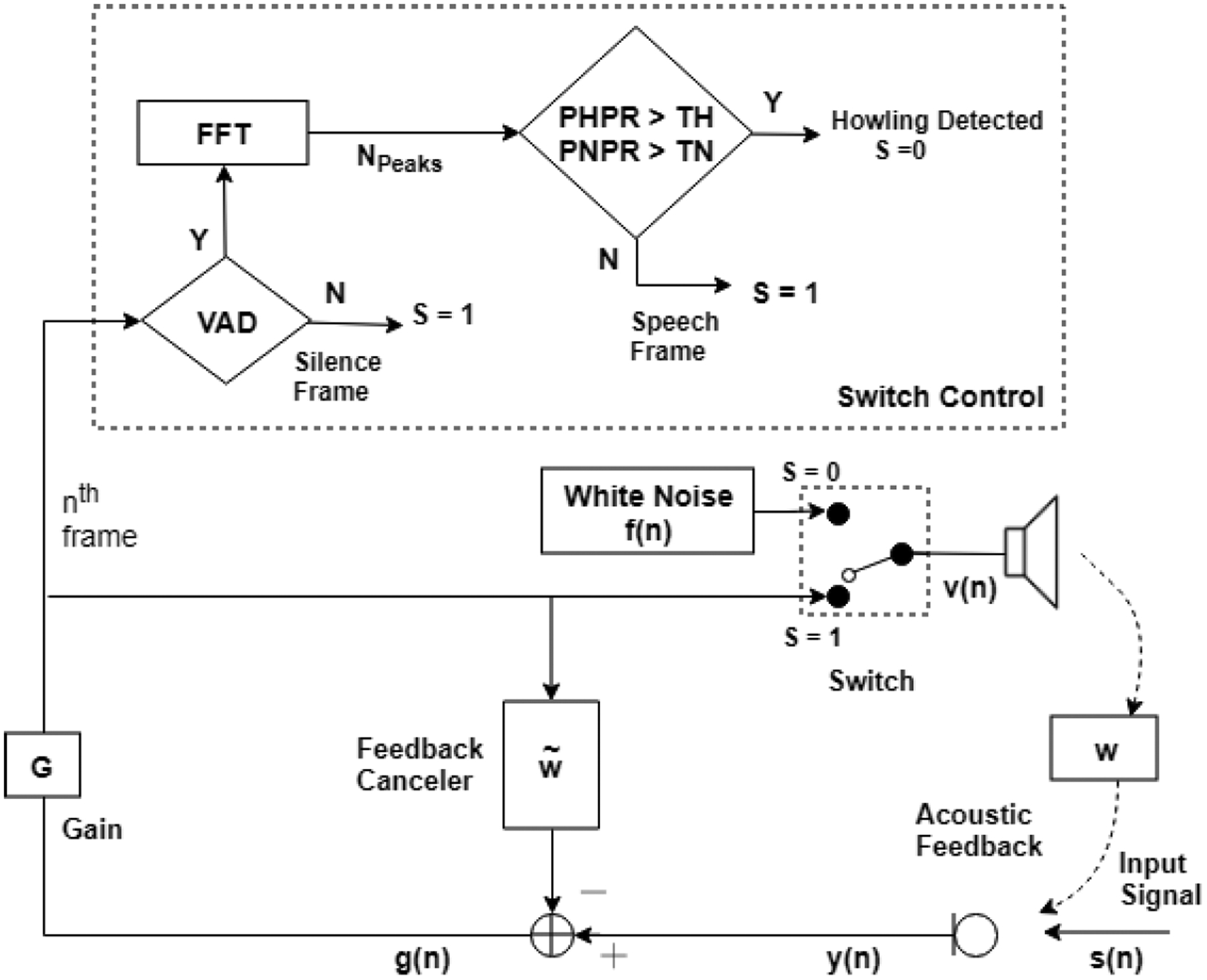
Schematic block diagram of proposed Adaptive Short-duration Noise Injection algorithm based on howling detection switch controlling
The proposed method is explained in section 2. Smartphone implementation and issues are presented in section 3. Performance quantification and evaluation are mentioned in section 4. Finally, section 6 gives a conclusion regarding the paper.
II. Proposed Method
The proposed AFC method, adaptive short-duration noise injection follow into category of non-continuous noise injection type algorithms [1]–[4], [7]. Fig.1 shows the schematic block diagram of the adaptive short-duration noise injection algorithm. The adaptive Noise Injection algorithm for AFC can be achieved in two stages. In stage 1, we adaptively find an optimum model for the acoustic feedback path between the loudspeaker and the microphone. The estimated bias-free feedback path model is then placed as shown figure 1 to cancel the AF. In Stage 2, we keep track of the performance of the AF cancellation method. We monitor the onset of “Howling”, as a criterion, to detect the presence of AF in the system. If the system detects any onset of howling while AFC is running, it automatically injects a short duration of white noise and updates the model of AF path. Then AFC continues using the updated model seamlessly. The two stages of the proposed method are presented next.
A. Acoustic Feedback Path Modeling
We model the AF path with a finite impulse response (FIR) filter whose optimal order and coefficients are derived efficiently. To obtain a bias-free estimate of the feedback path, we set the switch to S = 0 position as shown in figure 1 and inject a previously known zero-mean white Gaussian noise f (n) into the loudspeaker of the smartphone for a short period. We note that the white noise is uncorrelated with the input signal s(n) and the non-linearity introduced by the gain function (if present, e.g. compressor) is now removed for finding the model for AF path. During the noise injection period, the signal y(n) captured by the microphone is
| (1) |
where vector w presents the coefficients of an FIR filter of order P for the actual acoustic feedback path and superscript T denotes the transpose operator. Vector v = [v(n)v(n − 1)… v(n − P + 1)]T denotes P×1 tap delayed output signal of the loudspeaker. During the noise injection, v(n) = f (n). Thus, the cross-correlation between the loudspeaker signal v(n) and the microphone signal y(n) during noise injection mode is
| (2) |
where l represents the correlation lag. ryf (l) denotes the cross-correlation of y(n) and f (n) and rsf (l) denotes the cross-correlation of s(n) and f (n). Auto-correlation vector of f (n) is rff = [rff (l)rff (l − 1)… rff (l − P + 1)]T. The rsf (l) is considered zero for any lag as white noise f (n) is uncorrelated with the input signal s(n). (2) can then be generalized for different lags and written in Matrix/vector form as follows,
| (3) |
where, ryf = [ryf(0)ryf (1)… ryf (l − 1)]T is L × 1 cross correlation vector considering L number of lags. And
| (4) |
Let be the estimate of w which can be found using the least squared estimation. In this work we consider the number of lags L equal to filter order P, then Rff becomes a square matrix and the normal equation will be,
| (5) |
where the superscript “ − 1” represents matrix inversion. Direct inversion of the matrix in (5) requires O(P3) complexity. We will use the Generalized Levinson Durbin (GLD) algorithm which computes (5) in O(P2) operations. Order of the filter is calculated based on the number of the coefficients, after which energy of the filter remains nearly the same even if we increase the order of the filter. [14]
B. Feedback Cancellation and Tracking
An AF path model does not remain constant, it keeps changing depending upon the acoustic environment between the loudspeaker and microphone of the device. The presence of AF effect can be identified and tracked based on the detection of the onset of howling as shown in figure 1. Distinct features of howling in a temporal and spectral domain can be used to differentiate it from the speech signal or music signal. It is important to detect the onset of howling immediately due to the changing nature of the feedback path and for achieving better performance of the AFC system.
1). Voice Activity Detection (VAD):
As the howling starts, there will be no silent frame in the system. This can be used as a temporal feature to detect the start of the howling. VAD algorithm can specify if the current frame is silent. If there is no silent frame in the last N1 frames, the system is either in speech or howling mode and we need to further differentiate between speech and howling. VAD algorithm selected for the proposed method is simple energy-based VAD in which the energy is computed for each frame of input. Assuming that the first few frames of the signal are background noise, the energy of the noise, Enoise is estimated by averaging the energies of these frames. For the nth frame, energy is En and the decision is made as follows:
| (6) |
Where δ is a constant threshold. Enoise can also be updated after certain intervals to keep it updated according to the background level when it detects only noise. If the VAD does not detect any noise/silent frame in previous N1 frames, we further look for a spectral-domain clue to detect the howling. Howling frequency component will have a large magnitude in the spectral domain, so we consider only Npeaks peaks of the spectrum. These selected peaks are called ‘probable howling candidates’ and Npeaks is normally set between 1–10 [15]. These howling candidates will go through the following two criteria explained below to be selected as howling frequency if howling is present.
2). Peak to Harmonic Power Ratio (PHPR):
A spectral feature that determines the ratio of powers of the howling component and its mth harmonic frequency for frame n, i.e.
| (7) |
The harmonic spectral structure is the property of voiced speech and tonal audio signal. Then is then recognized as a howling component if
| (8) |
Where ∩ is the intersection operator and TH is a predefined threshold [16].
3). Peak to Neighboring Power Ratio (PNPR):
Howling components have larger power compared to their mth neighboring frequency components. Therefore, is then recognized as howling component for frame n if it fulfills the following:
| (9) |
| (10) |
Where ∩ is the intersection operator, TN is the predefined threshold [16] and M is the number of FFT points. To summarize, howling is detected if there is no silence in previous N1 frames and criteria 10 and 8 are also satisfied. Short duration noise is injected upon detection of howling rise to update the feedback canceller.
III. Implementation
Proposed adaptive short-duration noise injection algorithm is implemented on Pixel 3 smartphone having Android 9.0 Pie as the operating system. Frame-based structure is used for real-time implementation with a frame size of N = 256 samples (16 ms) and sampling rate of 16 kHz. The processing time of each frame should be less than the frame size for an application to run smoothly without any audio glitches. Android A-Audio C/C++ API is employed for high performance audio processing [17]. Noted input/output latency over several run for the developed framework is between 12.4–16.5 ms. As shown in figure 2, device captures the sound and plays the processed and amplified version of it through the smartphone built-in bottom speaker. When the user turns the AFC algorithm switch ON, the speaker injects a white noise for Nin ject frames and the feedback path model is computed. The derived AF model is then used for the AFC. Length of noise injection signal should be sufficiently longer than the length of impulse response to have accurate correlation values in (5). In case if the howling is detected due to major changes in the feedback path, feedback path model will be updated by injecting the white noise again as per (5).
Fig. 2:
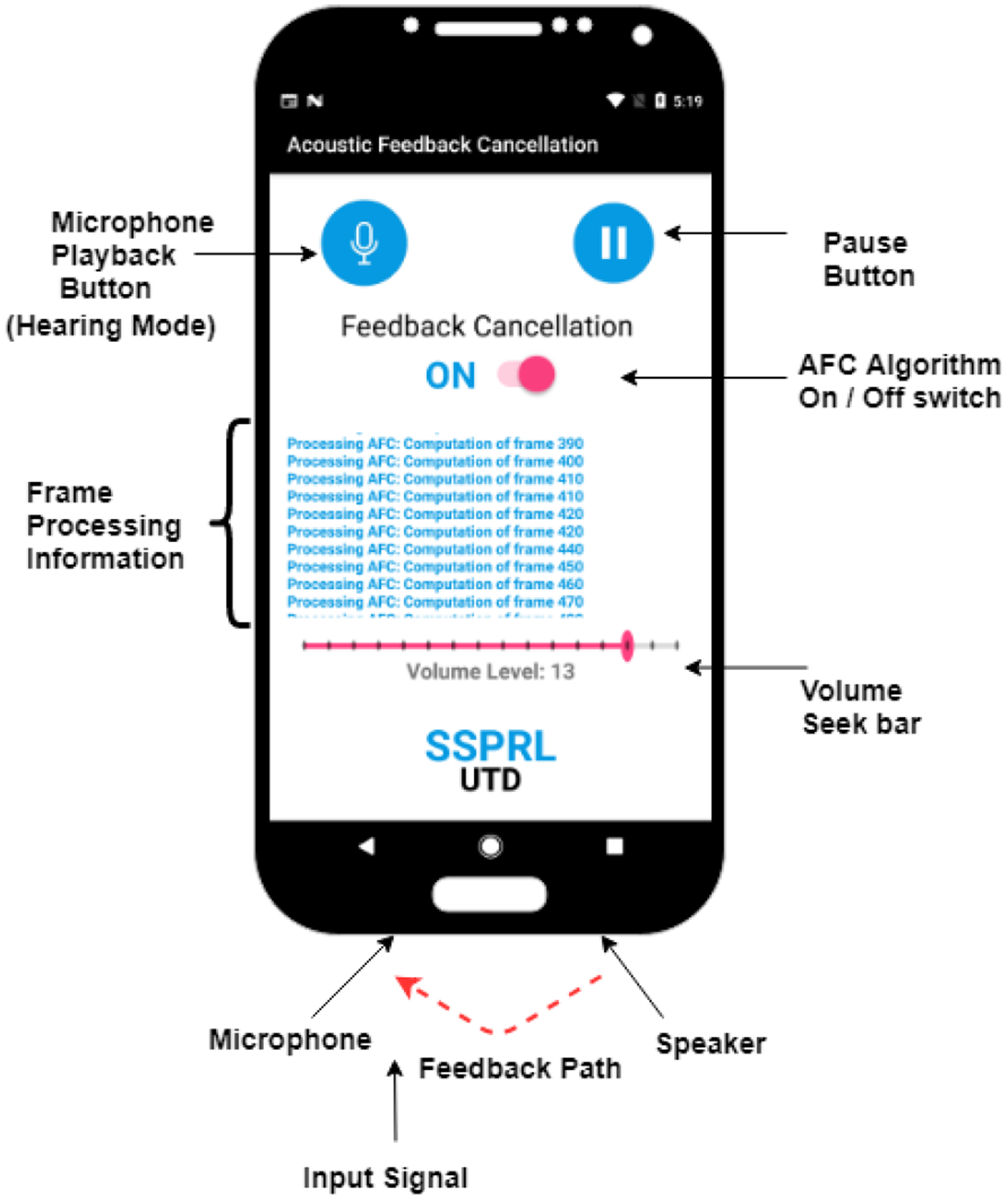
Implementation on smartphone device and graphical user interface
Fig. 3(a) and 3(b) show the AF path model and its magnitude response for the smartphone placed on the table. Fig. 3(c) shows the variations in multiple AF path models derived on each start of the application. These variations in the AF path model can be explained as different microphone initialization delays caused by the operating system of the smartphone even when there is no change in the acoustic environment. The proposed algorithm effectively handles the issue of the initialization of the speaker and microphone object by the operating system. The feedback path model can be seen as impulse response between microphone and loud-speaker of the smartphone. The impulse response is a combination of delay, direct feedback component, early reflections, and reverberant tail. The order of the impulse response was truncated after having the saturation in the energy of the impulse response. In Fig. 3(c), we further observe that most of the energy of the is enclosed within or nearby coefficients of the peak. Thus, in the Fig. 3(a) can be effectively seen as combination of delay and an effective FIR filter .
| (11) |
where D is the number of sample delay as shown in Fig. 3(a). Number of delay samples D and the order of is constant and it is equivalent to the order of . Number of coefficients B in the filter are decided based on the energy content with respect to . As D can increase depending upon the latency of the system used, it can sufficiently reduce the length of FIR filter in need, thus the computational cost. Effect of order of on feedback cancellation performance is carried out in the later section.
Fig. 3:
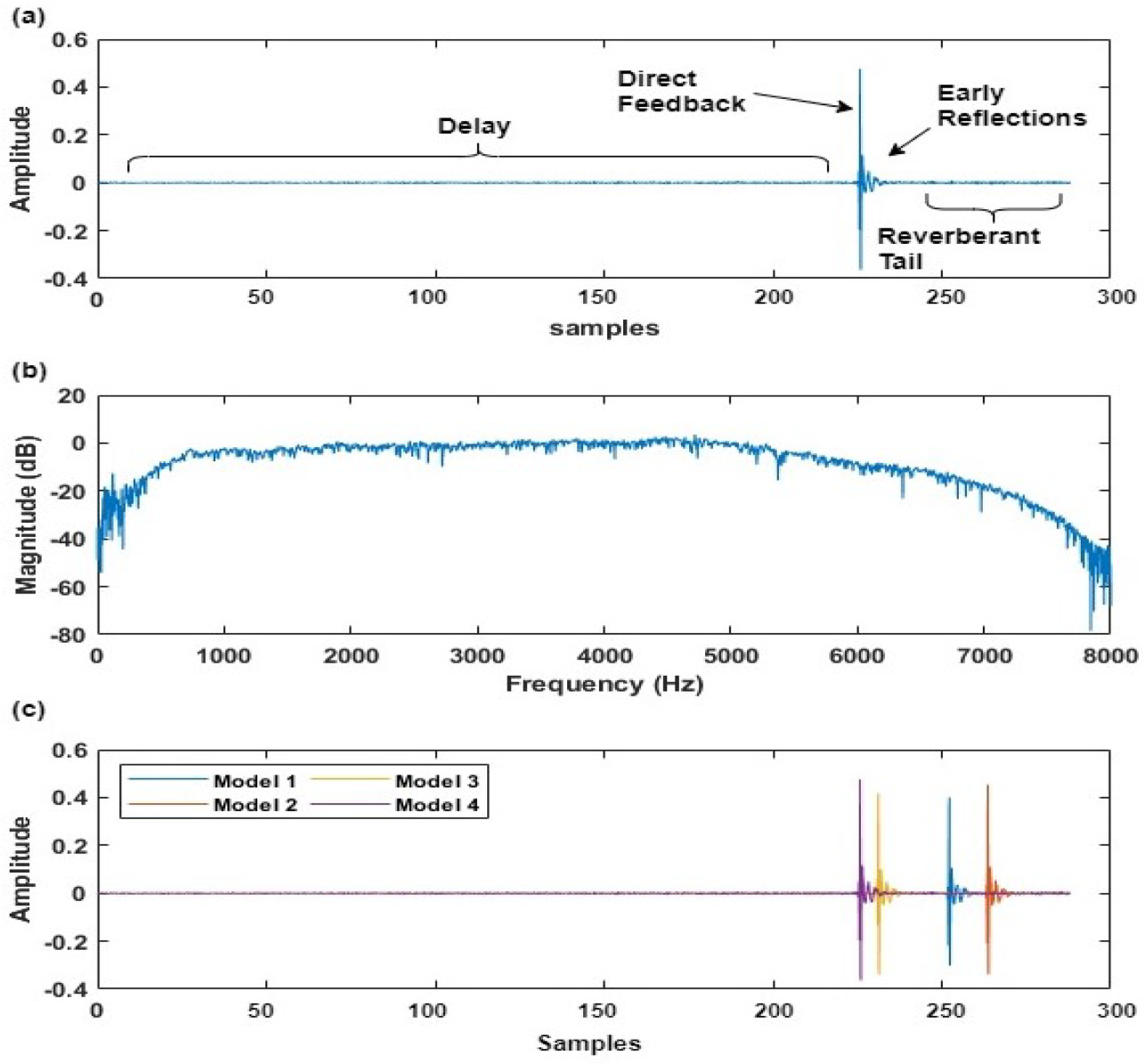
(a) Impulse Response of the AF path model, (b) Magnitude Response of the AF path model and (c) Variations in Impulse Response on starting of the application at different instances.
IV. Experimental Results
A. Howling Detection Accuracy
Let PD and PFA denotes the howling detection and false alarm probabilities respectively for the employed howling detector. A false alarm is counted when there is no howling and howling is said to be detected. A howling is said to be detected correctly when it is detected within first N1 frames of howling. We want the false alarm probability as low as possible to decrease the unnecessary frequent noise injection. We want our probability of howling detection to be as high as possible since the long howling sound in the system can be irritating. Furthermore, howling detection will run continuously in the background for each frame of length N samples. Worst-case complexity when all the components are running is O(N logN) per frame, which is suitable for running it in a real-time application.
For optimum performance of the method, fast and accurate detection of howling is desired. We created a simulation with VAD, PNPR and PHPR components to detect the howling in a given signal. 5 test signals of duration 10 minutes were created by concatenating speech sentences from the HINT database and are contaminated with howling sound at random positions. Howling sounds of feedback were generated from the implemented smartphone application when AFC was off. The average howling sound duration was kept to 100 frames. Detection within the first N1 frames is considered as a true detection. We found the detection method to be working best when parameters are set as N1 = 12 frames, δ = 4, Npeaks = 10, TN = 8dB, M = 2N, TH = 6dB with PD = 0.96 and PFA = 0.15. To take into consideration, low SNR of the signal might affect the performance of employed simple VAD which can degrade PD. Complex VAD can be employed in this case, but it is beyond the scope of this paper.
B. Performance Quantification
Smartphone application is running in playback loop and a test signal s(n) was played from an independent loud-speaker in a regular room. Test signal s(n) was using the HINT database the same as the test signal in subsection IV-A. The output of the smartphone v(n) should preserve the quality and intelligibility of s(n). In effective real-time AFC system, g(n) should be equal to s(n) as shown in Fig.1. For this experiment, an initial 20 seconds the AFC mode was OFF as shown in Fig.4. After 20 seconds, we turned on the AFC mode. White noise was injected for Nin ject = 10 frames. The optimal duration of noise injection was selected based on the previous computation of impulse response. Algorithm calculates the feedback path as per (5). Taking delay into consideration as per (11), now can be seen as a combination of delay and an FIR filter of order B. To quantify the effectiveness of the running AFC, we compared the signal s(n) and g(n). For a perfect AFC system, g(n) should be equal to s(n). In performance evaluation, we considered time-domain root mean square error (RMSE), frequency-domain RMSE, the perceptual evaluation of speech quality (PESQ), and the coherence and speech intelligibility index (CSII) between g(n) and s(n). We further compute the performance of the proposed method as shown in Table I, by considering different effective FIR filter length B based on it’s energy content. 1000 frames of signal s(n) and g(n) were considered in comparison when the system was in AFC “ON” mode after the noise injection.
Fig. 4:
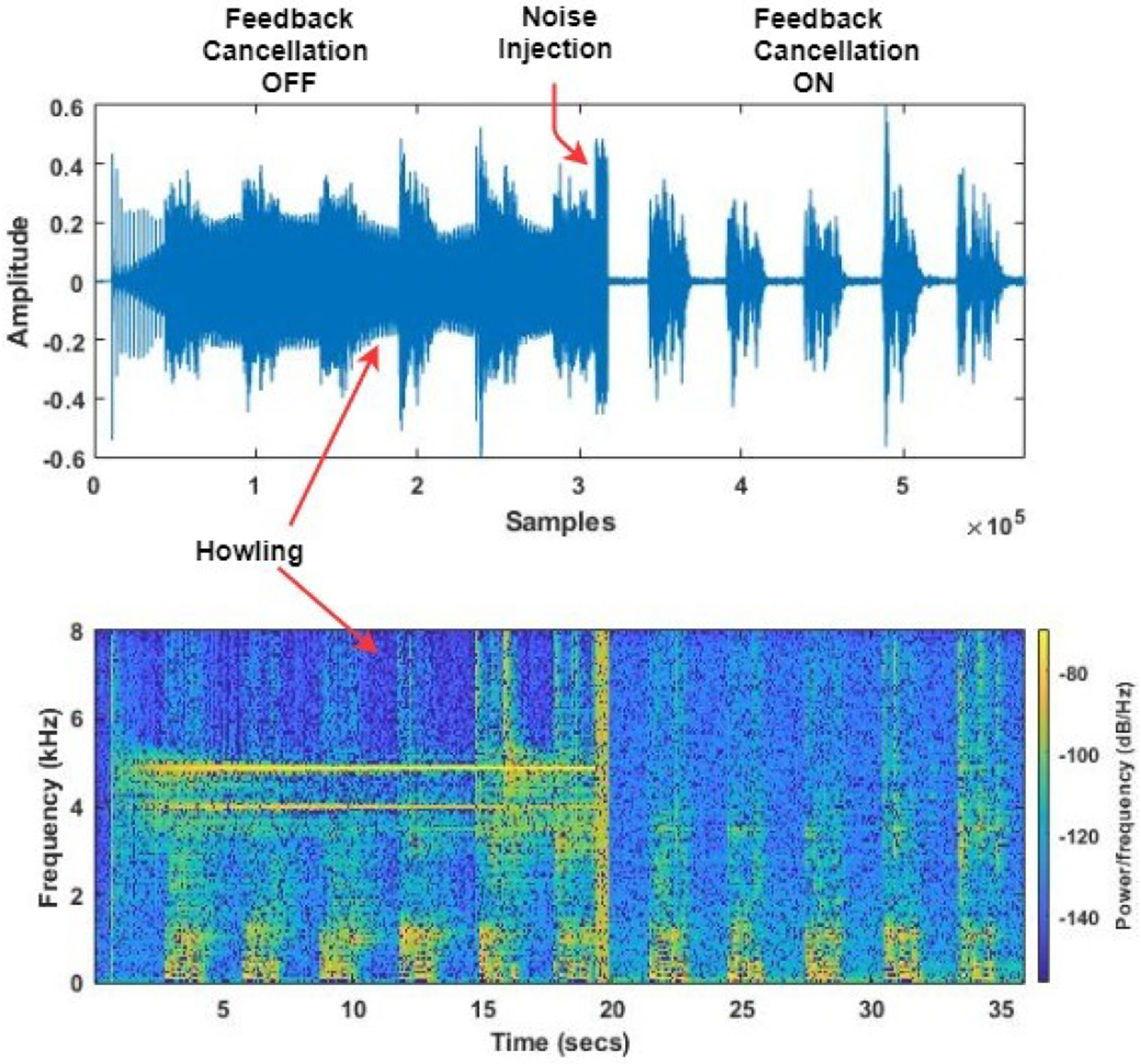
(a)Time domain representation of AFC application when it is “OFF” and “ON” (b) Spectral representation of AFC “OFF” and “ON”
TABLE I:
Performance quantification of feedback cancellation of the proposed method in terms of length of FIR filter
| filter order (B) | Energy(%) | Time Domain Error (RMSE) | Frequency Domain Error (RMSE) | PESQ | CSII |
|---|---|---|---|---|---|
| 60 taps | 92.7 | 5.2 × 10−4 | 8.1 × 10−4 | 4.07 | 0.891 |
| 120 taps | 98.51 | 6.3 × 10−5 | 1.2 × 10−4 | 4.21 | 0.919 |
| 280 taps | 99.8 | 1.6 × 10−5 | 5.5 × 10−5 | 4.28 | 0.922 |
V. Conclusion
Adaptive noise injection algorithm based on howling detection was presented. Bias-free AF path model was calculated using short-duration noise injection irrespective of the position of the microphone and the loudspeaker. Changes in the AF path model were made adaptive based on multi-feature based howling detection. The proposed method was optimized, implemented to run on a smartphone platform in real-time to emulate the feedback scenario. The performance of the proposed AFC method shown in realistic scenarios using standard metrics.
Acknowledgments
This work was supported by the National Institute on Deafness and Other Communication Disorders (NIDCD) of the National Institutes of Health (NIH) under Award 5R01DC015430-04. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.
References
- [1].van Waterschoot Toon and Moonen Marc, “50 years of acoustic feedback control: state of the art and future challenges,” Proc. IEEE, pp. 08–13, 2008. [Google Scholar]
- [2].Greenberg Julie E, Zurek Patrick M, and Brantley Merry, “Evaluation of feedback-reduction algorithms for hearing aids,” The Journal of the Acoustical Society of America, vol. 108, no. 5, pp. 2366–2376, 2000. [DOI] [PubMed] [Google Scholar]
- [3].Spriet Ann, Proudler Ian, Moonen Marc, and Wouters Jan, “Adaptive feedback cancellation in hearing aids with linear prediction of the desired signal,” IEEE Transactions on signal processing, vol. 53, no. 10, pp. 3749–3763, 2005. [Google Scholar]
- [4].Pandey Ashutosh and John Mathews V, “Low-delay signal processing for digital hearing aids,” IEEE Transactions on audio, speech, and language processing, vol. 19, no. 4, pp. 699–710, 2010. [Google Scholar]
- [5].Pradhan Somanath, Patel Vinal, Patel Kashyap, Maheshwari Jyoti, and George Nithin V, “Acoustic feedback cancellation in digital hearing aids: A sparse adaptive filtering approach,” Applied Acoustics, vol. 122, pp. 138–145, 2017. [Google Scholar]
- [6].Siqueira Marcio G and Alwan Abeer, “Steady-state analysis of continuous adaptation in acoustic feedback reduction systems for hearing-aids,” IEEE Transactions on Speech and Audio Processing, vol. 8, no. 4, pp. 443–453, 2000. [Google Scholar]
- [7].Guo Meng, Analysis, design, and evaluation of acoustic feedback cancellation systems for hearing aids, Ph.D. thesis, Citeseer, 2012. [Google Scholar]
- [8].Mishra Parth, Tokgoz Serkan, and Panahi Issa MS, “Robust real-time implementation of adaptive feedback cancellation using noise injection algorithm on smartphone,” in Proceedings of Meetings on Acoustics 175ASA. Acoustical Society of America, 2018, vol. 33, p. 055003. [Google Scholar]
- [9].Khoubrouy Soudeh A and Panahi Issa MS, “Improving misalignment for feedback path estimation in hearing aid by multiple short-time noise injections,” in 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE, 2012, pp. 5230–5233. [DOI] [PubMed] [Google Scholar]
- [10].Renato C Nakagawa C, Nordholm Sven, and Yan Wei-Yong, “Feedback cancellation with probe shaping compensation,” IEEE Signal Processing Letters, vol. 21, no. 3, pp. 365–369, 2014. [Google Scholar]
- [11].Bernardi Giuliano, Toon van Waterschoot Jan Wouters, and Moonen Marc, “An all-frequency-domain adaptive filter with pem-based decorrelation for acoustic feedback control,” in 2015 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA). IEEE, 2015, pp. 1–5. [Google Scholar]
- [12].Guo Meng, Søren Holdt Jensen Jesper Jensen, and Grant Steven L, “On the use of a phase modulation method for decorrelation in acoustic feedback cancellation,” in 2012 Proceedings of the 20th European Signal Processing Conference (EUSIPCO). IEEE, 2012, pp. 2000–2004. [Google Scholar]
- [13].“Android Latency Measurements,” https://source.android.com/devices/audio/latency/measurements, Accessed: 2020-01-28.
- [14].Khoubrouy Soudeh A and Panahi Issa MS, “Order selection of the hearing aid feedback canceller filter based on its impulse response energy,” in 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE, 2012, pp. 5218–5221. [DOI] [PubMed] [Google Scholar]
- [15].Khoubrouy Soudeh A and Panahi Issa, “A method of howling detection in presence of speech signal,” Signal Processing, vol. 119, pp. 153–161, 2016. [Google Scholar]
- [16].van Waterschoot Toon and Moonen Marc, “Comparative evaluation of howling detection criteria in notch-filter-based howling suppression,” Journal of the audio engineering society, vol. 58, no. 11, pp. 923–940, 2010. [Google Scholar]
- [17].“Android Audio Library,” https://developer.android.com/ndk/guides/audio/aaudio/aaudio, Accessed: 2019-11-28.


