Regularized Estimation of Effective Scatterer Size and Acoustic Concentration Quantitative Ultrasound Parameters Using Dynamic Programming

Abstract

The objective of quantitative ultrasound (QUS) is to characterize tissue microstructure by parametrizing backscattered radiofrequency (RF) signals from clinical ultrasound scanners. Herein, we develop a novel technique based on dynamic programming (DP) to simultaneously estimate the acoustic attenuation, the effective scatterer size (ESS), and the acoustic concentration (AC) from ultrasound backscattered power spectra. This is achieved through two different approaches: (1) using a Gaussian form factor (GFF) and (2) using a general form factor (gFF) that is more flexible than the Gaussian form factor but involves estimating more parameters. Both DP methods are compared to an adaptation of a previously proposed least-squares (LSQ) method. Simulation results show that in the GFF approach, the variance of DP is on average 88%, 75% and 32% lower than that of LSQ for the three estimated QUS parameters. The gFF approach also yields similar improvements.

I. Introduction

Despite all the advantages of ultrasound (US) imaging including being real-time and portable, an US image describes tissue mostly qualitatively. Therefore, accurate tissue classification based on ultrasound remains an elusive task. Additionally, ultrasound is highly operator- and system-dependent. Quantitative ultrasound (QUS) deals with the afore-mentioned problems by providing estimates of the acoustic properties of tissue. It commonly investigates radiofrequency (RF) signals to estimate the acoustic attenuation and backscatter coefficient. The effective scatterer size (ESS, the correlation length of subwavelength variations of acoustic impedance) and acoustic concentration (AC, product of the number density of scatterers and the mean square acoustic impedance variation) are two important acoustic features associated with tissue microstructure [1]. These two parameters can be obtained by fitting form factor models to the experimental form factor derived from the backscatter coefficient. The form factor is the Fourier transform of the spatial correlation function of the relative impedance between scatterers and their surrounding [2,3]. It indicates the frequency dependence of backscattered signals and is related to the geometry of the scatterers [2,3]. Estimates of ESS and the AC have been shown to be potentially useful for distinguishing malignant from benign tumors [4], monitoring osteoporotic rheumatic treatment [5], guiding prostate biopsies [6], diagnosing nonalcoholic fatty liver disease [7], and characterizing breast tumors [8], among other applications.

We recently proposed a novel method to estimate attenuation and parameters from a power-law fit to the backscatter coefficient with improved precision. This method is based on a regularized cost function and optimized using Dynamic Programming (DP) [9,10]. Recent work by other groups has also shown that more accurate QUS parameters can be estimated using regularized cost functions [11–14].

Herein, we build on that work to include the use of form factor models to obtain a regularized estimate of ESS, AC, and the effective attenuation. We intend to involve scatterer characterization in backscattering formulas to accurately and precisely estimate AC and ESS in addition to effective attenuation. In the following two sections, we outline two different approaches based on DP for estimating QUS parameters. In both approaches, we exploit the reference phantom method (RPM) to have a system independent algorithm. In the last section, we present our results and compare them to the LSQ method.

II. Methods

The general formula of attenuation is:

$$A(f,z)=exp(-4\alpha fz)$$ (1)

where A is the total attenuation, f is the frequency, z is the depth and α is the effective attenuation coefficient (average attenuation from intervening tissues). A general model for parametrizing the backscatter coefficients is:

$$B(f)=B_{0}G(f)$$ (2)

where B₀ is the magnitude and G(f) is the frequency dependence of backscatter coefficients. Under the condition of weak scattering, the following equation defines G(f) in terms of a form factor model (F(f, a_eff)):

$$G(f)=f^{4}F\left(f,a_{eff}\right)$$ (3)

A. Gaussian form factor

As the microstructure of real tissue is often modeled using scatterers with spherically-symmetrical, Gaussian impedance correlation functions [3], a Gaussian form factor model has been selected as follows:

$$F\left(f,a_{eff}\right)=exp\left(-0.827{\left(k{a}_{eff}\right)}^2\right)$$ (4)

where k is wave number and a_eff is ESS. By substituting (4) in (3), and (3) in (2), we have:

$$B(f)=B_0{f}^{4}exp\left(-0.827{\left(k{a}_{eff}\right)}^2\right).$$ (5)

To estimate ESS and AC, we use the RPM strategy based on normalizing the power spectrum S of the sample (s) by a power spectrum from a reference phantom (r), both of which are estimated from RF signals from a clinical scanner. The spectral ratio can be modeled as:

$$\begin{gathered} \frac{S_S}{S_r}=\frac{B_S(f)A_S(f,z)}{B_r(f)A_r(f,z)} \\ =\frac{B_{0_S}{f}^{4}exp\left(-0.827{\left(k_S{a}_S\right)}^2\right)exp\left(-4{\alpha }_{S}fz\right)}{B_{0_r}{f}^{4}exp\left(-0.827{\left(k_r{a}_r\right)}^2\right)exp\left(-4{\alpha }_{r}fz\right)} \end{gathered}$$ (6)

We assume that the media has a constant sound speed with the frequency dependence of attenuation near f¹. In addition, in order to use RPM, the sample and the reference phantom must have similar sound speed, so k_s = k_r. After taking the natural logarithm from both sides of (6), and substituting ${\mathrm{X}}_1=\text{log}\frac{S_s}{S_r}$, $B=\text{log}\frac{B_{0_s}}{B_{0_r}}$, $a=a_s^2-a_r^2$, and α = α_s − α_r, we have:

$$X_1=B-0.827k^{2}a-4\alpha fz$$ (7)

This equation is summed over the frequency range from f₁ to f₂. The goal is to estimate B, a, and α using DP. Then, using the following equations, $B_{0_s}$, a_s, and α_s can be obtained:

$$B_{0_s}=\text{exp}(B)B_{0_r},a_s=\sqrt{\left(a+a_r^2\right)},{\alpha }_s=\alpha +{\alpha }_r$$ (8)

B. General form factor

According to [15], for Gaussian scatterers and other form factors over a limited range of frequency, F(f, a_eff) and ka ⩽1.2 can be considered as follows:

$$F\left(f,a_{eff}\right)=exp\left(-A{f}^n\right)$$ (9)

where bold A is related to the ESS of tissue by $0.827{\left(\frac{2\pi }{c}a\right)}^n$, c is sound speed within tissue which is assumed to be 1540 m/s , and n~2. After taking the ratio of power spectra of echo signals of sample and reference phantoms in (10), and taking the natural logarithm, we have:

$$\frac{S_s}{S_r}=\frac{B_{0_s}{f}^{4}exp\left(-{\mathit{A}}_s{f}^n\right)exp\left(-4{\alpha }_{s}fz\right)}{B_{0_r}{f}^{4}exp\left(-{\mathit{A}}_r{f}^n\right)exp\left(-4{\alpha }_{r}fz\right)}$$ (10)

$$X_2=B-A{f}^n-4\alpha fz$$ (11)

For the rest of this work, we first assumed n=2, and estimated three parameters B, A, and α. This equation is summed over the frequency range from f₁ to f₂. Then, we considered n as a parameter that should be estimated. In both approaches, once $B_{0_s}$ and a_s (in approach 1) and A_s (in approach 2) are estimated, AC (Nγ²) can be obtained using the following equation:

$$B_{0_s}={\left(\frac{2\pi }{c}\right)}^4{a}_s^6\frac{N{\gamma }^2}{9}$$ (12)

As a first approximation to assess the accuracy and precision of the proposed DP method, we simulated sample and reference power spectra adding white Gaussian noise to B, a, and α and to B, a, n, and α in equations (7) and (11), respectively. Spectra were simulated to come from a layered phantom having a central layer with α=0.7787 dB·cm⁻¹MHz⁻¹, B=0.3222e-5 cm⁻¹-sr⁻¹ MHz⁻ⁿ, α=31 μm, A=13.0269 μmⁿ μsⁿ m⁻ⁿ, n=3.1263 sandwiched between two layers with α=0.5101, B=0.1600e-5, a=35, A=11.3917, n=3.5190 and α=0.5196, B=0.1600e-5, a=35, A=15.7979, n=3.5190. The values for the reference phantom are α=0.5101, B=0.1599e-5, a=35, A=10.3917, n=2. All of these values are used for two simulation approaches. Twenty independent realizations of the power spectra were simulated for each approach through the following equations: Data for approach 1:

$$X_1=\text{log}\frac{B_{0_s}}{B_{0_r}}+{\eta }_{B_i}-0.827k^2\left(\left(a_s^2-a_r^2\right)+{\eta }_{a_i}\right)-4\left(\left({\alpha }_S-{\alpha }_r\right)+{\eta }_{{\alpha }_i}\right)fz,i=1,\dots 20$$ (13)

Data for approach 2:

$$X_2=\text{log}\frac{B_{0_s}}{B_{0_r}}+{\eta }_{B_i}-\left(\left(A_s-A_r\right)+{\eta }_A\right)f^{\left(n_s-n_r\right)+{\eta }_{n_i}}-4\left(\left({\alpha }_s-{\alpha }_r\right)+{\eta }_{{\alpha }_i}\right)fz,i=1,\dots 20$$ (14)

where i refers to an instance of noise and η indicates noise for each variable shown as a subindex. DP and LSQ were applied to the simulated spectra within a frequency range from f₁ = 3.7 MHz to f₂ = 7 MHz similar to the experimental analysis bandwidth in our laboratory and using the following search ranges for both approaches:

$${\left(a_{s_{-}min}-5\right)}^2-a_r^2<a<{\left(a_{s_{-}max}+5\right)}^2-a_r^2$$

$${\alpha }_{s_{-}min}-{\alpha }_r-0.5<\alpha <{\alpha }_{s_{-}max}-{\alpha }_r+0.5$$

$$\text{log}\left(0.1\frac{B_{s\_min}}{B_r}\right)<B<\text{log}\left(10\frac{B_{s\_min}}{B_r}\right)$$

$$n_{s_{-}min}-n_r-2<n<n_{s_{-}max}-n_r+2$$

$$A_{s_{-}min}-A_r-2<A<A_{s_{-}max}-A_r+2$$

The general form of cost function contains two terms, data term, D, and regularization term, R, as follows:

$$C=D+R$$ (15)

where D and R for the first and second approaches are defined as follows:

$$D1=\sum _{f_1}^{f_2}{\left(X_1-B+0.827k^{2}a+4\alpha fz\right)}^2$$ (16)

$$D2=\sum _{f_1}^{f_2}{\left(X_2-B+A{f}^n+4\alpha fz\right)}^2$$ (17)

$$R1=w_{\alpha }\left|{\alpha }_j-a_{j-1}\right|+w_B\left|B_j-B_{j-1}\right|+w_a\left|a_j-a_{j-1}\right|$$ (18)

$$R2=w_{\alpha }\left|{\alpha }_j-a_{j-1}\right|+w_B\left|B_j-B_{j-1}\right|+w_A\left|A_j-A_{j-1}\right|+w_n\left|n_j-n_{j-1}\right|$$ (19)

where j refers to the jth depth.

III. Results

The results of approach 1 are shown in Fig. 1. These results show that the variance of DP is on average 88%, 75% and 32% lower than that of LSQ for α, B, and a, respectively. In approach 2, we first set n to 2. The ground truth value of n in our simulations is also 2. Results are shown in Fig. 2. Then, we set n to be a variable number and estimate it. The results are shown in Fig. 3. These results show that the variance of DP is on average 75%, 100%, and 100% lower than that of LSQ for α, B, and A, respectively. When estimating four parameters, these improvements are 77%, 100% and 100%, 100% respectively for α, B, n and A. Since LSQ does not have the regularization term to limit the estimates of parameters, the parameters get a substantially higher variance compared to DP. In addition, in DP, Eq. (7) and (11) are summed over the frequency range as well as depth in the recursion step. However, considering in LSQ there is no recursion step, the summation is only over the frequency range.

Fig. 1.

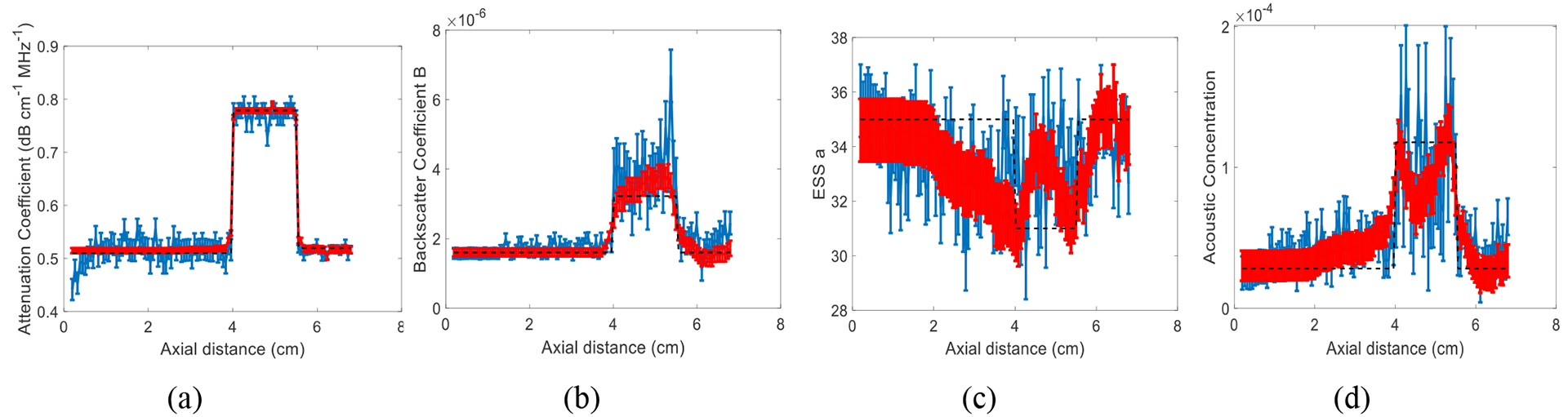
Results of LSQ (blue) and DP (red) methods using approach 1 in a simulated phantom with three layers and 20 instances of added zero-mean Gaussian noise. The error bars show the standard deviation over the 20 instances of noise for attenuation coefficient (a), backscatter coefficient magnitude B (b), ESS a (c), and acoustic concentration (d). The black dashed line is the known values.

Fig. 2.

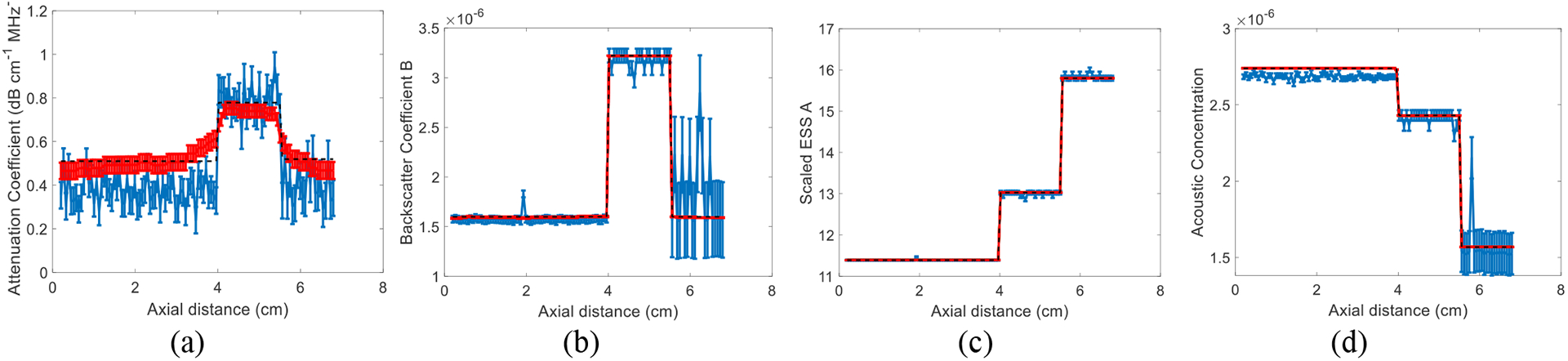
Results of LSQ and DP methods using approach 2 where n is fixed to 2 in a simulated phantom with three layers and 20 instances of added zero-mean Gaussian noise. The error bars in (a-c) show the standard deviation over the 20 instances of noise for attenuation coefficient (a), backscatter coefficient magnitude B (b), scaled ESS A (c), and acoustic concentration (d). The black dashed line is the known values.

Fig. 3.

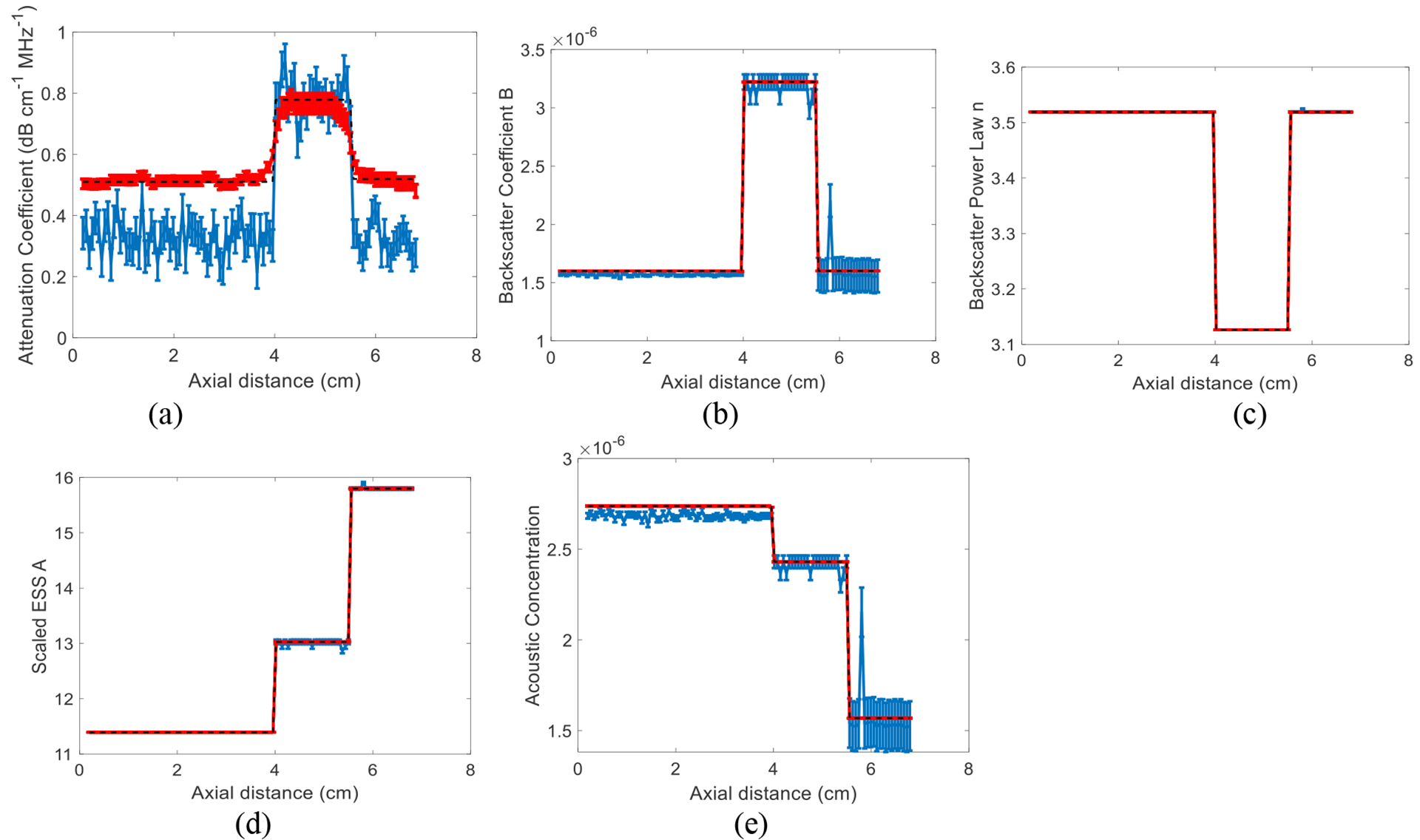
Results of LSQ and DP methods using approach 2 where n is not fixed to 2 and is estimated. The simulated phantom has three layers and 20 instances of added zero-mean Gaussian noise. The error bars show the standard deviation over the 20 instances of noise for attenuation coefficient (a), backscatter coefficient magnitude B (b), backscatter power law n (c), scaled ESS A (d), and acoustic concentration (e). The black dashed line is the known values.

IV. Discussion

The estimation results of Fig. 1 (c) can be substantially improved if the frequency range is chosen such that ka~1. In our simulations, the frequency for which ka=1 for the two scatterer diameters simulated corresponds to 7.662 and 8.651 MHz, whereas the frequency range of this work was set to 3.7 to 7 MHz.

V. Conclusions

In this work, we presented two approaches based on RPM to parameterize backscattering in terms of form factor models. In the first approach, we assumed the Gaussian form factor and proposed DP to estimate ESS and AC. In the second approach, we used a more general form factor formulation which is appropriate for any impedance correlation functions. Here, we estimated more parameters through DP and LSQ. Besides, in both approaches, we simultaneously estimated the attenuation coefficient. We observed DP substantially reduced variance of estimations compared to the LSQ.