How Interpersonal Coordination Affects Individual Behavior (and Vice Versa): Experimental analysis and adaptive HKB model of social memory

Abstract

How one behaves after interacting with a friend may not be the same as before the interaction. The present study investigated which spontaneous coordination patterns formed between two persons and whether a remnant of the interaction remained (“social memory”). Pairs of people sat face–to–face and continuously flexed index fingers while vision between partners was manipulated to allow or prevent information exchange. Trials consisted of three successive twenty–second intervals: without vision, with vision, and again without vision. Steady, transient, or absent phase coupling was observed during vision. In support of social memory, participants tended to remain near each other’s movement frequency after the interaction ended. Furthermore, the greater the stability of interpersonal coordination, the more similar partners’ post-interactional frequencies became. Proposing that social memory resulted from prior frequency adaptation, a model based on Haken–Kelso–Bunz oscillators reproduced the experimental findings, even for patterns observed on individual trials. Parametric manipulations revealed multiple routes to social memory through the interplay of adaptation and other model parameters. The experimental results, model, and interpretation motivate potential future research and therapeutic applications.

Social interactions are pervasive in daily life. People coordinate their body movements with others in order to carry out activities such as conversing, walking with others, eating together, driving motor vehicles, playing sports, dancing, or singing. When an activity ends, the effects of such interactions may persist in the individual as a kind of “social memory.”¹ An example starts with two friends walking together, who may see each other and match step, perhaps speeding up or slowing down from their initial pace (see also Néda, Ravasz, Brechet, Vicsek, & Barabási, 2000; Passos, Davids, & Chow, 2016; Richardson, Dale, & Kirkham, 2007; Rio, Rhea, & Warren, 2014). However, once they go their separate ways, they may find themselves still walking at or near the socially–adopted tempo—a phenomenon investigated here as a kind of persistence or “social memory.” Operationally speaking, after social contact ends and information exchange stops, do quantities that characterize individual behavior return to their initial values? If not, what changes and which factors determine them?

Previous studies have demonstrated that social interactions may take the form of frequency and/or phase coupling (Issartel, Marin, & Cadopi, 2007; Kendon, 1970; Konvalinka, Vuust, Roepstorff, & Frith, 2010; Oullier, de Guzman, Jantzen, Lagarde, & Kelso, 2008; Schmidt, Carello, & Turvey, 1990; Schmidt & O’Brien, 1997; Tognoli, Lagarde, DeGuzman, & Kelso, 2007; Tognoli, 2008), and may be understood in terms of the principles and mechanisms of Coordination Dynamics. Coordination Dynamics describes and explains how the different parts of biological systems, such as human beings, work together to produce spatiotemporal patterns of order and disorder (for review, Kelso, 1995; 2009). For example, when two or more rhythmic elements interact, the pattern that develops is a function of both individual properties and coupling strength (Haken, Kelso, & Bunz, 1985; Kelso, 1984, 1995; Turvey, 1990). Many of the principles of coordination that apply to intrapersonal systems have been found to apply to interpersonal systems as well (Nordham & Kelso, 2016, for review). For instance, a single person’s limb movements are governed by the same coordination dynamics as when two people’s limbs move together (Schmidt, Bienvenu, Fitzpatrick, & Amazeen, 1998). Given this background, it is reasonable to hypothesize that social coordination is affected by both individual properties and the way they are coupled, which accordingly may impact subsequent independent behavior.

What patterns does social coordination take between two individuals and how might those patterns affect people’s ongoing behavior? To be explicit, what is different in people’s solitary behavior before a social interaction begins and after it ends? Previous work used a paradigm in which two people were recorded while producing simple movements before, during, and after social contact in the form of visual information (Oullier et al., 2008; Tognoli et al., 2007). The experiments manipulated whether partners could see one another and thus restricted or permitted the flow of visual information. Pertinent to the current research, Oullier et al. (2008) calculated the power spectrum of each partner’s behavior and then determined their overlap. Partners’ movement frequencies overlapped more after social contact than before. Given that people have idiosyncratic preferences for certain characteristics of their behavior (e.g., preferred, so-called “intrinsic” movement frequencies), it was unexpected that after the coupling stage ended, individual movement frequencies did not fully return to their initially chosen values.

Following Oullier et al.’s (2008) findings, the current focus was to study the dynamics of frequency persistence and change after the end of social coordination and to examine how it is affected by (1) initial individual differences in intrinsic frequency and (2) properties of the coordination patterns formed during social interaction. Regarding (1), we hypothesize that the smaller the initial differences in intrinsic frequency between partners, the greater the likelihood of coupling and forming stable patterns of social coordination. Such a prediction naturally arises from the extended form of the HKB equation (Kelso, DelColle, & Schöner, 1990) in which the patterns of coordination and their stability depend jointly on the difference in intrinsic frequency between the components and on their collective coupling strength. All else being equal, if there is an internalization of the coordination, a so-called social memory, then the closer two individuals are in their choice of initial frequency, the greater the probability that internalized features of the interaction will persist. Regarding (2), we hypothesized that the more stable the coordination pattern formed between two people during an episode of social interaction, the less should be the post-interactional frequency difference. That is, if visual coupling draws the partners closer together, their partner’s frequency should remain closer together after they interact—if in fact each partner has been affected by the interaction. The results support these hypotheses and provide evidence for the existence of social memory. The latter dictates that one or both of the partners had to change during visual coupling and that such change persists in the individual. In order to provide a mathematically accurate description of such frequency adaptation and its persistence, an important extension of the HKB model was required in which dynamics are added to the parameters. As it stands, in the basic HKB model, the parameters of the individual oscillators, such as their eigenfrequencies, are fixed. Here, by introducing dynamics to the eigenfrequencies of the oscillators to capture the fact that during the visual coupling stage of the experiment one or both has to change in order to adopt a common frequency, a quite remarkable match between theory and experiment is obtained. This extended HKB model system exhibits social memory via the mechanism of frequency adaptation (see also Dumas, de Guzman, Tognoli, & Kelso, 2014; Oullier & Kelso, 2009; Righetti, Buchli, & Ijspeert, 2006).

Method

In the experiment, two partners made continuous finger movements while their view of one another was manipulated. This task operationalized a basic form of social interaction in which people perceive the other as they behave simultaneously (see Schmidt & Richardson, 2008; Tognoli, 2008; Tognoli & Kelso, 2015, for reviews). The task setting enabled probing intrinsic behavior, uncovering any coordination patterns that might form during visual contact, as well as the behavior subsequent to an interaction.

Task

Pairs of adult participants (N = 8 pairs) sat facing one another. They were instructed to flex and extend their right index fingers continuously and to maintain a comfortable pace at all times. An electronic liquid–crystal screen enabled or disabled the view that partners had of each other’s moving fingers. Each trial had three stages: moving alone (0–20 sec), moving with mutual sight of the partner (20–40 sec.), and moving alone once again (40–60 sec). Instructions mentioned neither coordinating nor maintaining their own pace, thereby leaving subjects free to adopt any coordination pattern that might spontaneously arise. There were 36 trials per pair, except for two pairs in which the measurement apparatus malfunctioned causing the experimental session to end prematurely (n = 28). Trials in which a partner neglected to move for a prolonged period of time were excluded from the analysis (n = 2). For more details about the experiments, the reader is referred to Tognoli et al. (2007). The latter’s focus was on the electrophysiological correlates of social coordination. The present analysis focuses on the behavioral data obtained in that paradigm, and presents new findings along with a theoretical model.

Data recording

A single axis digital goniometer (F35, Biometrics, Newport, UK) attached to each participant’s right index finger captured their movements, which were recorded and digitized with a bio-amplifier (Compumedic Neuroscan Synamp II, Texas, El Paso). Movement time series were low–pass filtered at 200 Hz, and digitized with a sampling rate of 1000 Hz (in step with EEG recording from both subjects, which is not reported here).

Data analysis

In the experiment, as in many circumstances in real social life, movements were self–paced, such that people chose their own movement parameters, here the frequency of rhythmic movement. The frequency difference (δω) is a well–established quantity in Coordination Dynamics that can be used to measure differences in individual dispositions (Schmidt & Turvey, 1994). When partners see each other’s movements, the possibility of information exchange is created. Therefore, individuals have the opportunity to change, i.e. one or both subjects may change ω due to the influence of their partner. Relative phase (φ), the classic order parameter of coordination dynamics, was used to quantify social coordination during the encounter. The coordination patterns of relative phase during the social contact stage distinguished the forms that interactions could take, e.g., in-phase, anti-phase, intermittent, and so forth.

To remove high–frequency noise while preserving phase, a low–pass bi-directional Butterworth filter (10 Hz, 4th order, 24 dB/octave) was applied to the finger movement time series. Instantaneous relative phase (φ) was calculated using the differences between each of the partners’ phase from the analytic signal given by the Hilbert transform (φ = φ₁ − φ₂). To estimate the instantaneous frequency (ω), an inter-peak interval method was used (Tognoli & Kelso, 2009), supported by the peak identification algorithm of Dijkstra, Schöner, and Gielen (1994). The difference in partners’ frequencies was calculated (δω = ω₁ − ω₂). This quantity may be considered a measure of similarity since the lower the δω, the more similar the partners’ movements are. For comparing the entering and exiting frequency differences, the mean frequency difference was determined for the stages of the trials in which partners moved solo (defined from 0 to 20 s as δω_Enter and from 40 to 60 s as δω_Exit).

Trials were inspected by their trajectories of finger position, instantaneous frequency, and relative phase. An initial visual assessment identified three collective patterns during the social contact stage (from 20 to 40 sec): coordinated, intermittent, and uncoordinated (see, e.g., Figure 1). In-phase trials were those whose relative phase entered into a stable pattern near 0 rad, while anti-phase patterns were those stable around π rad. These in-phase and anti-phase patterns were considered as belonging to a single group, termed “coordinated.” “Intermittent” trials included those that were transiently coupled, observed either as brief periods of phase–locking and phase–wrapping or jumps from one phase relation to another. “Uncoordinated” trials were those in which the relative phase wrapped continuously and exhibited little or no apparent change from independent movement to mutual visibility of the partner.

Figure 1.

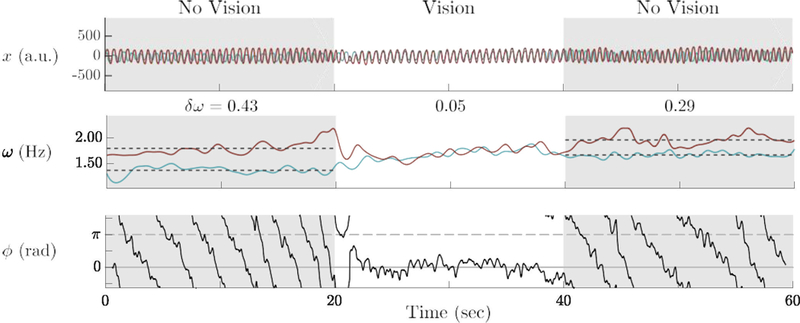
Exemplar trial of a pair’s finger movements: position (x), frequency (ω), and relative phase (φ) over time. Partners had no visual information (and thus no “social contact”) from 0–20 and 40–60 s (shaded background). Partners with different intrinsic frequencies spontaneously phase–locked upon social contact (20–40 s) as seen from the relative phase that was stable near zero. Likewise, thesy matched frequencies as they created a common social pattern (middle plot). Upon cessation of social contact, partners’ frequencies drifted away from the social frequency but did not return to their initial frequencies (40–60 s). Compared to before social contact, partners’ frequencies became more similar afterwards.

Trials were categorized according to the percent of time partners spent coordinating. The duration of episodes of coordination was determined using a quantity called Dwell Percentage (Dwell%), a measure of the time spent dwelling near stability during visual contact. Previously, this measure was validated against the judgment of three expert raters (Kelso, 2009; Tognoli et al., 2007). Dwell% was calculated by first filtering the time series of the relative phase with a low–pass bi-directional 3rd order Butterworth filter (0.25 Hz). Then, the percent of samples was calculated in which the relative phase was changing slowly—i.e. when the derivative of the time series had a value between plus or minus 0.35 rad/sec. When less than 7% of the time was spent dwelling, trials were considered uncoordinated. From 7 to 65%, trials were considered intermittently coordinated. When above 65%, trials were considered coordinated. See Supplemental Figure 14 for details.

Rayleigh z tests of uniformity were performed to determine whether tendencies of coordination occurred for each coordination pattern for each stage. The point–wise relative phase was calculated and samples were grouped according to stage and coordination mode, which were tested for uniformity.

“Social memory” was defined as occurring when post-interactional frequencies were more similar than those pre-interaction. A linear regression coefficient (b) was calculated between δω_Enter and δω_Exit. This process was repeated for each of the coordination groups (coordinated, intermittent, and uncoordinated). The logic behind this analysis was that if the regression coefficient (b) is significantly less than 1, then social memory occurred. If the coefficient were equal to about 1, then no change, no social memory would be considered present. If the coefficients were greater than 1, then the partners drifted apart. Thus, the null hypothesis was tested that b /= 1 (rather than b /= 0) by using $t=\frac{b-1}{SE}$ where t is the t-statistic, b is the coefficient estimate, and SE is the standard error of the estimate. Since δω is symmetric around 0 (that is, the sign of δω is arbitrary), no intercept was used in the regression model. The coefficients of determination (R²) were also calculated. All p-values were Holm–Bonferroni adjusted for multiple comparisons.

Results

First, the spontaneous collective patterns of movement and their relation to the behavior preceding and following social contact were examined. Next, patterns of single trial differences between members of the dyads were investigated. Finally, the relation between the pre- and post-interactional frequencies and the mediating role of coordination mode were established.

Spontaneous collective patterns formed and persisted past visual information exchange

Given that no explicit instructions to coordinate were given to members of the pairs, what (if any) patterns of spontaneous social coordination formed during visual information exchange? An exemplar trial in which spontaneous coordination was observed during the 20 s of visual information exchange is shown in Figure 1. Initially, before social contact began (0–20 s), partners’ movement trajectories showed no phase–locking as expected (Figure 1, top, left). The absence of phase–locking was also clear from the wrapping of relative phase (bottom, left). That is, no particular value became stable over time (bottom plot, left). Following the onset of visual contact (20 s), partners coordinated by phase–locking their movements near 0 rad (bottom plot, center). In parallel, frequencies converged (middle plot, center). Once visual information was removed (40 s), partners were no longer phase–locked, and escaped into a wrapping phase pattern much like the behavior before social contact. When partners’ frequencies deviated from the previous social pattern, they did not return to their original values. Compared to before the social interaction, partners’ frequency difference (δω) decreased.

Trials were categorized according to the collective pattern produced spontaneously during visual contact. Visual inspection indicated three major patterns, objectively categorized by the Dwell% measure: uncoordinated (N = 100), intermittent (N = 105), and coordinated (N = 51). The examples of frequency patterns for each coordination mode shown in Figure 2 reveal that in the coordinated case, frequency matched upon visual contact, while staying more–or–less together in the period post-interaction. The intermittent case showed a characteristic “bouncing” during social contact. Like before, the frequencies in the post-interactional stage were more similar to each other than those pre-interaction. Lastly, in the uncoordinated case, despite not phase–locking during social contact, frequencies attracted subtly; partners’ frequencies were a bit closer post-interaction than pre-interaction.

Figure 2.

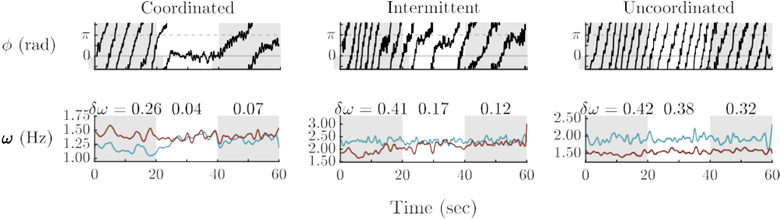
Partners spontaneously coordinated in three patterns: Coordinated, intermittent, and uncoordinated (from left to right). In the coordinated case, there was a long transient into a stable relative phase. Partners’ frequencies met during visual contact and remained so after visual contact ended. The intermittent trial shows alternating episodes of stability (dwelling) and instability (wrapping). Frequency likewise displayed fluctuations: toward the joint frequency when the relative phase was stable and away from the joint frequency when relative phase wrapped. The uncoordinated trial shows typical relative phase (φ) wrapping throughout the trial. Frequency difference (δω) shows that the partners became more similar during, and after visual information exchange.

The relative phase values for each of the spontaneous collective patterns are plotted as histograms in Figure 3. For all types of coordination, relative phase (for all trials) in the stages before and after social contact had relatively flat distributions, suggesting there were no strongly stable relative phase patterns overall. Most notably, in coordinated trials, the histogram before social contact again showed a relatively flat distribution before social contact, but during social contact, a prominent peak occurred near φ = 0 rad with a lesser peak near φ = π rad, the remnants of which persisted after visual contact. However, Rayleigh tests revealed, with the exception of the stages before and after visual contact in the uncoordinated trials (p = .293 and p = 0.643 respectively), that all distributions were significantly different from uniform (p = .003 for intermittent trials after visual contact and p < .001 for the remainder). In sum, the results indicate that whether coordination occurred or not, there was some, even if weak, tendency for coordination during vision.

Figure 3.

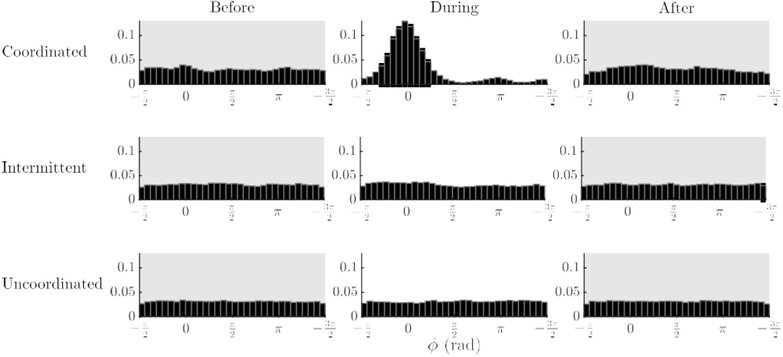
Relative phase histograms varied by coordination pattern and stage: The distribution during social contact for coordinated trials was most noticeable: a large peak near 0 rad and a lesser peak near π rad appeared. Note that all distributions were found to be significantly different from uniform, except for uncoordinated trials in the before and after stages.

The roles of individual participants in entering and exiting social coordination were examined, and revealed rich phenomena (Figure 4). Partners did not always share the burden of adapting to each other’s frequency. To establish social coordination, both matched (Figure 4, A), one matched the other (B), or neither matched (C). After visual information exchange ended, both participants dwelled at the socially–adopted frequency (D), one dwelled and one escaped from the social pattern (E), or both escaped from the social pattern (F). Cases of little change by one participant throughout the trial also occurred (B, blue subject online or light gray in print). During social coordination, subjects tended to increase their frequencies (positive trend in shared frequencies, e.g., Figure 4 B, D, E, F), though in some cases a negative trend was observed (e.g., A). This rich range of phenomena that occurs on individual trials present a challenge to any model, but as we shall show, this challenge can be met.

Figure 4.

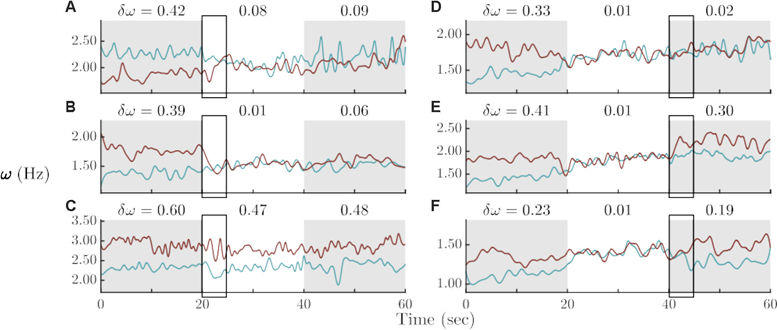
Participants differed in their individual behavior in entering (left column) and exiting (right column) social coordination: During visual contact (after 20 sec), both partners changed their frequency to match the other (A), only one changed to match the other (B), or neither changed (C). After visual contact ended (40 sec), both partners dwelled at the social pattern (D), only one dwelled while the other escaped (E), or both escaped (F).

Frequency difference pre-interaction predicts frequency difference post-interaction

The foregoing examples show single trial evidence that behavior before social contact is different from behavior after social contact. That is, if there were no persistent effect of the social interaction/visual contact on individual behavior, then partners’ frequency difference should be the same preceding and following social contact.

A t-test compared the means of the absolute value of pre-interactional and post-interactional δω and showed a significant difference (t(255) = 4.61, p < .001). Additionally, the degree to which frequency difference pre-interaction predicts that of post-interaction was examined. Overall, the magnitude of δω decreased from before to after social contact (Figure 5). That is, partners’ frequencies indeed tended to be more similar after the interaction than before. A linear regression coefficient less than one was obtained, b = 0.76, 95% confidence interval (CI) [0.71 0.81], t (255) = −9.19, p < .001. Thus, for every 1 Hz of δωEnter, there was 0.76 Hz of δωExit. Seventy–seven percent of the variance in δωExit could be accounted for by δωEnter (R² = 0.77, F(1, 255) = 853.62, p < .001).

Figure 5.

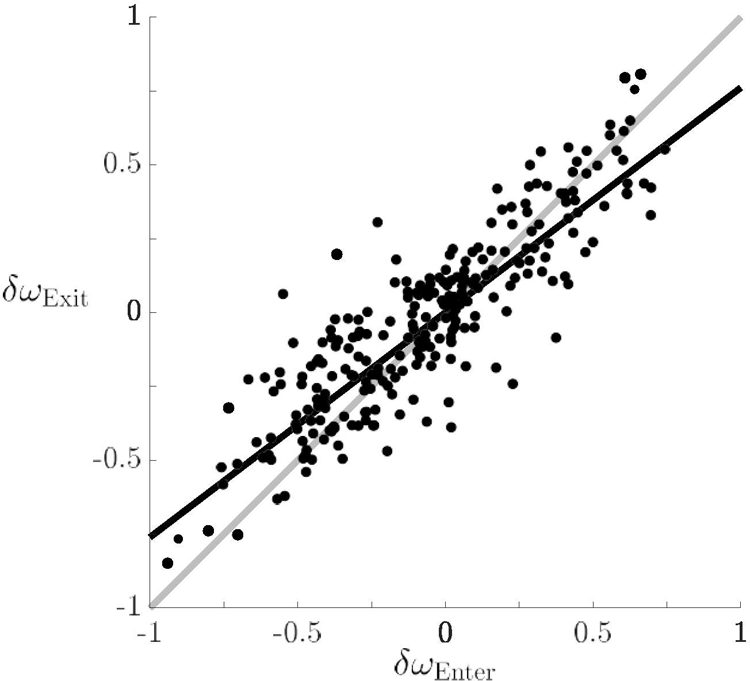
Frequency difference was less after interacting than before: Frequency difference before visual information exchange (δω_Enter) was compared with after (δω_Exit). The regression coefficient is less than 1, indicating that frequencies tended to be more similar after visual contact than before (black line). For reference, the gray line marks identical frequency difference before and after social contact.

To further examine the relation between pre- and post-interactional behavior, the role of coordination pattern during social contact (coordinated, intermittent, uncoordinated) was studied with an additional regression analysis aimed at showing how each coordination pattern affected the relation between δω_Enter and δω_Exit (Figure 6). For uncoordinated trials, the regression coefficient was highest (i.e. least effect of social memory), b = 0.88, 95% CI [0.82 0.94] and not significantly different from the null hypothesis that δω_Enter and δω_Exit are identical, t(99) = −4.17, p = .084. However, intermittent and coordinated trials displayed a rather different pattern, with stability of coordination during social interaction affecting post-interaction movement frequency. For intermittent trials, post-interactional frequencies were more similar, with a lower regression coefficient than the uncoordinated case, which was significantly different from the null hypothesis, b = 0.59, 95% CI [0.50 0.68], t(104) = −8.83, p = .018. For coordinated trials, post-interactional frequencies were the most similar, with an even lower coefficient, which was significantly different from the null hypothesis, b = 0.37, 95% CI [0.20 0.53], t(50) = −7.63, p = .023. The inclusion of coordination groups helped to explain more of the variance, 81% (Multiple R² = 0.81, F (3, 252) = 358.32, p < .001). Taken together, regression analysis suggests more stable interactions during social contact resulted in increasingly similar post-interaction movement frequencies.

Figure 6.

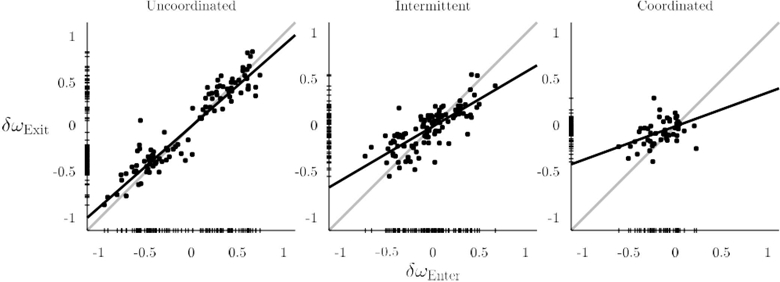
Coordination mode modulated the relation between pre- and post-interactional frequency difference. As stability of coordination during social contact increased (from left to right), a decrease occurred in post-interactional frequency difference relative to that observed before interaction. Partners were especially close in post-interactional frequency on coordinated trials (i.e. slope was closest to zero).

To determine whether the regression coefficients for each coordination pattern were different from one another, the regressions were compared pair–wise. No significant difference was found between the coordinated and intermittent cases, (F(1, 253) = 5.39, p = .084). However, both intermittent and coordinated trials were significantly different from the uncoordinated case (F (1, 253) = 27.82 and 33.81 respectively, ps < .001).

Extending the HKB–Model to Social Memory

In Coordination Dynamics, the Haken–Kelso–Bunz (HKB) model (Haken, Kelso, & Bunz, 1985) provides a quantitative description of movement behavior on both the component level of coupled oscillators and the collective level of relative phase. Originally introduced to capture bistability and the switch from anti-phase to in-phase observed in bimanual coordination when the movement rate exceeds a critical value, the HKB model has been extended to govern the coordination of different limbs (e.g., Jeka & Kelso, 1995; Kelso & Jeka, 1992), visuomotor coordination (Kelso et al., 1990), coordination of movements between two people (e.g., Schmidt et al., 1990, see Nordham & Kelso, 2016 for reviews), and the coordination of human and virtual partners (Dumas et al., 2014; Kelso, de Guzman, Reveley, & Tognoli, 2009; Kostrubiec, Dumas, Zanone, & Kelso, 2015). In the HKB model, limb movements are represented by so-called hybrid oscillators, which contain a van-der-Pol and a Rayleigh term as nonlinearities and are coupled by a nonlinear function that contains differences in the oscillator positions and velocities. Specifically, the HKB model at the component oscillator level reads

$$\begin{array}{c}{\ddot{x}}_1+{\dot{x}}_1\{a{x}_1^2+\beta {\dot{x}}_1^2-\gamma \}+{\mathrm{\Omega }}_1^2{x}_1=\chi \{A_1+B{\left(x_1-x_2\right)}^2\}\left({\dot{x}}_1-{\dot{x}}_2\right)\\ {\ddot{x}}_2+{\dot{x}}_2\{a{x}_2^2+\beta {\dot{x}}_2^2-\gamma \}+{\mathrm{\Omega }}_2^2{x}_2=\chi \{A_2+B{\left(x_2-x_1\right)}^2\}\left({\dot{x}}_2-{\dot{x}}_1\right)\end{array}$$ (1)

where Ω₁ and Ω₂ are the eigenfrequencies (intrinsic frequencies) of the finger movements for the individual subjects, α, β, and γ are linear and nonlinear damping constants, and A₁ and A₂ together with B allow for systematically varying coupling strength. The constant χ is introduced in the present case to allow for the coupling to be switched on or off by setting χ equal to 1 or 0, respectively. The system without coupling represents the condition in which subjects do not see the partner’s finger (first and third stages of the experiment), whereas during the second stage, when the screen was transparent, coupling is made active.

From a modeling perspective, a typical run of the experiment starts out with two different eigenfrequencies Ω₁ and Ω₂ with the coupling switched off (χ = 0) for the first 20 sec, i.e. participants behaving as individual entities. Then, when each partner is able to see the other’s behavior, the coupling is switched on (χ = 1) for 20 s and the two oscillators synchronize. Finally, the screen turns opaque again, the coupling is shut off and the two oscillators are expected to return to their initial frequencies. A numerical simulation of the model in this scenario is shown in Figure 7. Plotted from top to bottom are the time series of the oscillators (x), their observed frequencies (ω_1,2), their eigenfrequencies (Ω_1,2), and their relative phase (φ). When the coupling was switched on, the oscillators synchronized at a common frequency and a constant relative phase. Due to the difference between eigenfrequencies, the relative phase was not 0 rad but at a finite value (Amazeen, Schmidt, & Turvey, 1995; Kelso et al., 1990; Schmidt, Shaw, & Turvey, 1993; Schmidt & Turvey, 1994). Note the behavior during the coupling stage: the observed frequencies (ω_1,2) meet at a common value but the intrinsic frequencies (Ω_1,2) do not change. Despite a finite δω, because phase coupling is strong enough, external frequencies match and the relative phase enters a steady state. When the coupling is switched off, the oscillators’ frequencies return to their original values.

Figure 7.

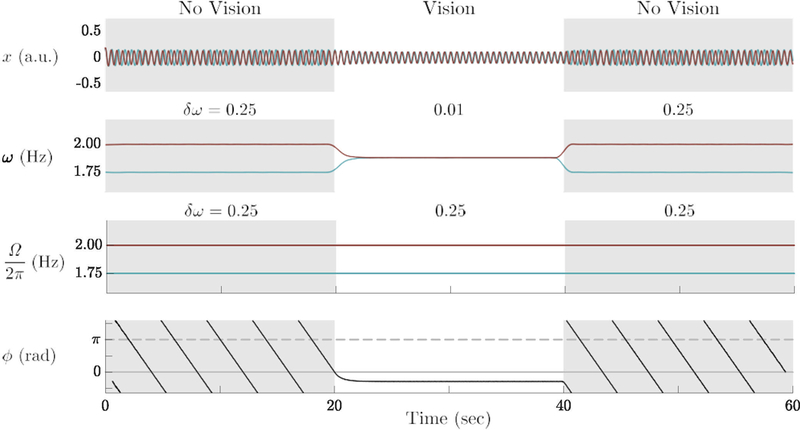
Simulation of the three stage experiment with the HKB model (Eq. 1): Time series for the two oscillators (x_1,2), measured frequencies (ω_1,2), eigenfrequencies (Ω_1,2), and relative phase (φ) (top to bottom). When the coupling is turned on (20–40 sec), the oscillators synchronize at a common frequency and relative phase stabilizes close to 0 rad. When the coupling is turned off (40–60 sec), each partner’s frequency returns to its original value, showing no social memory. Model parameters: α = β = 1, γ = 2, A = −2.00, B = 0.50.

In the form of Eq. 1, the HKB model does not show the phenomenon of social memory found experimentally. In order to capture social memory, the eigenfrequency of one or both of the oscillators has to change during the coupling stage (cf. Lagarde, 2013; Oullier & Kelso, 2009). One possibility to achieve such frequency adaptation is to introduce dynamics to the eigenfrequencies of the oscillators Ω₁ and Ω₂ during the second stage of the trials (see also Dumas et al., 2014; Righetti et al., 2006).

$$\begin{array}{c}{\dot{\mathrm{\Omega }}}_1=\chi {\epsilon }_1{\dot{x}}_1{x}_2\\ {\dot{\mathrm{\Omega }}}_2=\chi {\epsilon }_2{\dot{x}}_2{x}_1\end{array}$$ (2)

The constant χ has a similar purpose as in Eq. 1: to allow adaptation to occur only during the second stage of the trials. ε_1,2 are constant for the adaptation strength of the individual oscillators in which the larger the value of ε, the stronger the oscillator adapts to the frequency of its partner. A simulation of the HKB system with the dynamics for frequency adaptation (Eq. 2) is shown in Figure 8 for a symmetric case, ε₁ = ε₂ (with the same arrangement of the plots as in Figure 7). During the coupling stage, the two eigenfrequencies approach each other and when the coupling is turned off, their difference is smaller than initially and stays that way. Note in Figure 8, the relative phase approaches 0 rad as the eigenfrequency difference decreases, a kind of “symmetry restoration,” which was also noted in numerous experimental trials (see below). This extended HKB model system shows social memory via the mechanism of frequency adaptation.

Figure 8.

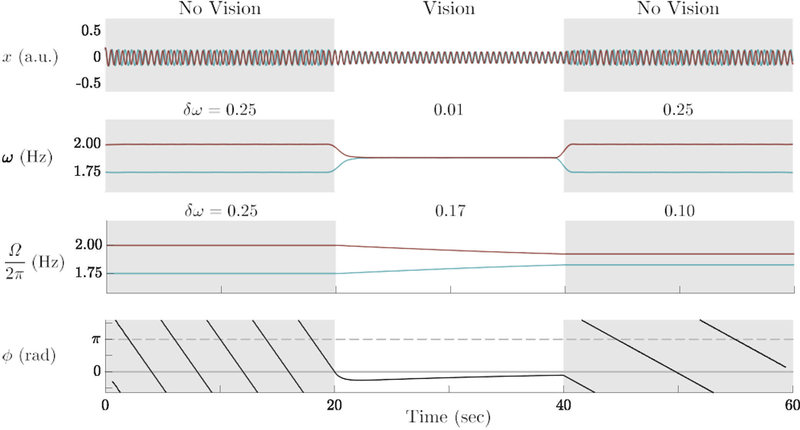
Simulation of the three stage experiment as in Figure 7, but for the extended, frequency adapting HKB system (Eq. 2): When the coupling is turned on (20–40 sec), the eigenfrequency difference shrinks and the locked relative phase approaches 0 rad. When the coupling is switched off (40–60 sec), the frequencies are closer than initially and stay that way, an indication of frequency adaptation qua social memory. Model parameters: same as in Figure 7 with ε_1,2 = 0.50.

Further exploration of the model shows parametric influence on persistence

In the following, we demonstrate that the extended HKB model reflects the variety of experimental findings, such as the effect of observed coordination pattern (uncoordinated, intermittent, and coordinated), the strength and persistence of frequency adaptation, and the way adaptation is achieved, i.e. whether both subjects mutually adapt (symmetric) or just one subject adapts to the other (asymmetric). The parameters from the model that modulate the patterns of social memory (seen as a change in eigenfrequencies, Ω_1,2) are the adaptation strength (ε_1,2), the coupling strength (A_1,2), and the difference in intrinsic frequency (δΩ_1,2) in Eqs. 1 and 2.

The experimental data suggest that how strongly the movement frequencies adapt may vary for different pairs and trials. In the model the adaptation strength is represented by the parameters ε_1,2 in Eq. 2. Three examples show that the parameters ε_1,2 control the reduction of post-interactional frequency difference (Figure 9). With increasing ε (Figure 9, from top to bottom), frequency difference decreases from pre- to post-interaction, ranging from no change after phase–locking (Figure 9, top) to almost complete matching (Figure 9, bottom). Clearly a simple change in the model’s frequency adaptation parameter captures the essential features of the individual trial data.

Figure 9.

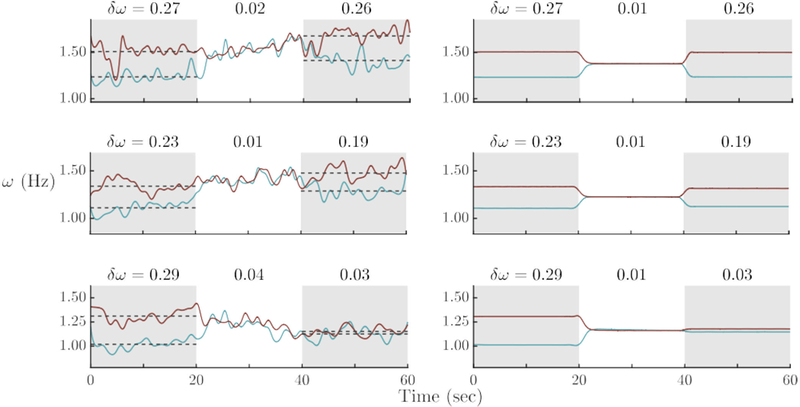
The role of frequency adaptation (ε) in establishing collective behavior during social interaction and post-interactional frequency differences: Experimental trials (left column) and model simulations (right column) in which the stage after social contact is affected by frequency adaptation, increasing from no change (top row) to some mutual change (middle row) to remaining nearly as frequency–coupled as during visual contact. Model parameters: ε_1,2 = 0.02 (top), ε_1,2 = 0.07 (middle), ε_1,2 = 0.70 (bottom), with A_1,2 = −2.00 for all three simulations.

In both the experiment and the model, the initial frequency difference is an important parameter that may determine which of the three coordination patterns is realized in a given trial. In Figure 10, trials from the experiment with three initial frequency differences are compared to simulations from the model in which Ω₁ − Ω₂ is varied leading to uncoordinated, intermittent, and coordinated movements from top to bottom, respectively. As initial frequency difference (δω) decreases, oscillators become increasingly attracted, which appears as increased fluctuations in frequency and increased curvature of the relative phase. When oscillator frequencies become close enough (bottom) they phase–lock consistently. Just like in experimental data (Figure 6 and related text), whether phase–locking occurs or not, post-interactional frequency difference is less after coupling than before. Furthermore, for smaller δΩ_Enter (and therefore more coordinated interactions), the post-interactional frequencies become even closer.

Figure 10.

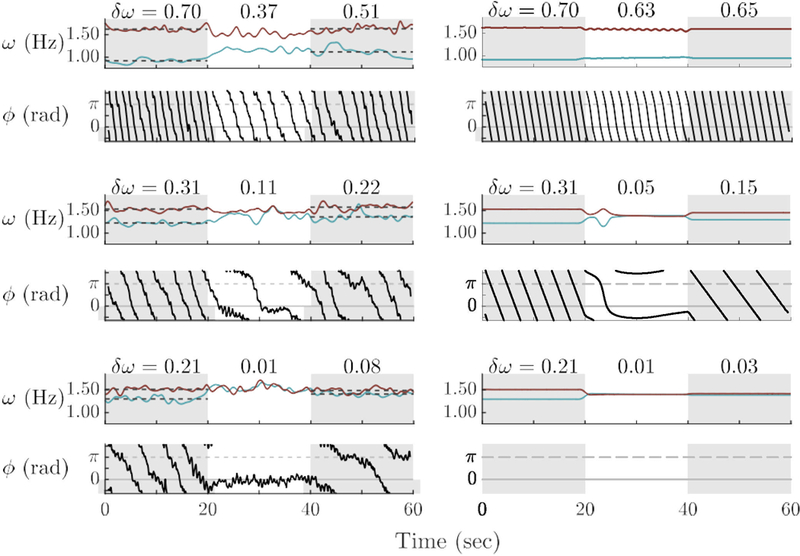
Effect of initial frequency difference (δω) on spontaneous coordination and subsequent individual behavior: Experimental trials (left column) and model simulations (right column) in which varying initial frequency difference (δω) with constant coupling produces three coordination patterns: uncoordinated, intermittent, and coordinated (top to bottom). With high δω (top quartet), participants were initially uncoordinated and remained so when coupling was turned on. Relative phase continued to wrap, though it curved slightly. Frequency difference decreased after coupling ended relative to before. With lower δω (middle quartet) intermittent behavior occurred with partners’ frequencies oscillating toward and away from each other as relative phase switched between wrapping and dwelling. Again, frequency difference decreased after coupling ended. When δω was lowest (bottom quartet), participants coordinated strongly during social contact, their frequencies matching and relative phase stabilizing and shifting to 0 rad. Frequency difference decreased after coupling more in this case than the previous cases. Model parameters: ε_1,2 = 0.50, A_1,2 = −1.50.

Another parameter of the model that affects social memory is the coupling strength term A (even as initial frequency differences are relatively fixed; Figure 11). With increasing coupling terms A_1,2 (Figure 11, top to bottom), the post-interactional frequencies become ever closer. For the participants, such a variation of coupling strength may reflect differences in attention, willingness to cooperate with the partner, underlying strategies, social abilities, and traits (cf. Kelso et al., 2009). Note that the frequency difference post-interaction (δΩ_Exit) decreases in the model with increasing duration or strength of phase–locking as observed experimentally (i.e. proportionally to δΩ_Enter). Accordingly, relative phase wraps with a lesser slope during the post-interactional period, as compared to before (Figure 11, second and third rows).

Figure 11.

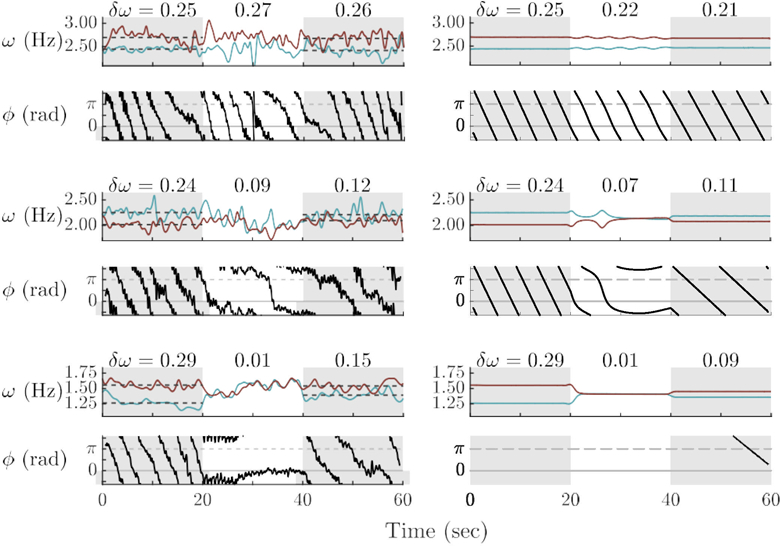
The role of coupling (A) in establishing collective behavior and on subsequent individual behavior: Experimental trials (left column) and model simulations (right column) in which coupling strength (A) was varied given similar initial frequency differences (δω). With low coupling (top quartet), frequencies fluctuated but did not meet, while relative phase became slightly curved. With moderate coupling (middle quartet), frequencies intermittently matched, while relative phase switched between stable and unstable behavior (middle). With higher coupling (bottom quartet) frequencies met and stayed together, while relative phase gradually shifted and stabilized near 0 rad. In all cases, frequency difference decreased from before to after coupling. Model parameters: A_1,2 = −0.25 (top), A_1,2 = −1.00 (middle), A_1,2 = −2.00 (bottom), with ε_1,2 = 0.50.

For the cases discussed so far, the same adaptation and coupling parameters, ε_1,2 and A_1,2, were used for both oscillators, leading to behavior with a certain symmetry. For example, partners enter into a common, constant frequency during the period of interaction, which is quantified by the mean of the two initial frequencies, with a subsequent symmetrical escape after the coupling has ended (see, e.g., Figure 9, right). It can already be seen in the real examples from Figure 9 (left) that the symmetry encountered in the models (right) is a coarse approximation. Participants entered social coordination with varying degrees of frequency difference and exited with varying degrees of frequency persistence. Such cases can be modeled by making the coupling and/or adaptation parameters unequal between the two subjects (A₁ /= A₂ and/or ε₁ /= ε₂). For instance (Figure 12, second row), ε₁ > ε₂ will lead to a faster adaptation of Ω₁ towards Ω₂, which will result in the two frequencies being closer to Ω₂ after the coupling ends. Note that interestingly, during social interaction the shared frequency is not steady, but exhibits an (e.g., upward) trend, a feature that was observed in experimental trials (see Figure 9, left). Finally, it was also possible for a subject’s post-interactional frequency to surpass that of her partner’s. This type of behavior is reproduced with a negative value of ε: higher (or lower) frequency than initially. Similarly, breaking the symmetry in the coupling parameter A leads to cases in which one oscillator changes more strongly than the other in order to establish a common rate, which in the extreme case can mean that only one of them changes and the other stays at the initial frequency.

Figure 12.

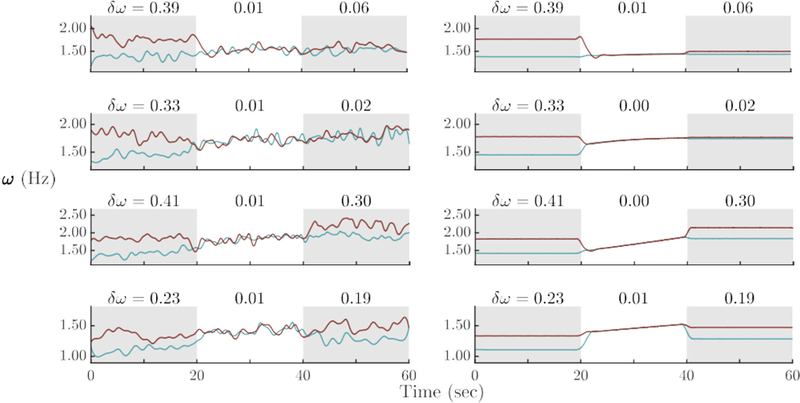
Individual patterns of entering and exiting in human behavior and model: Experimental trials (left column) and model simulations (right column) that account for a variety for different patterns of entering and exiting coordinated states. The symmetry of A’s and ε’s were varied for each partner to create the patterns observed due to individual differences in entering and exiting social coordination. Four examples are shown (blue [light gray] is Partner 1 and red [dark gray] is Parter 2) which represent a variety of different behaviors. The red (or dark gray) partner matched blue (or light gray) and continued to dwell after visual contact ended (first row, A₁ = −0.50, A₂ = −2.50, ε₁ = 0.25, ε₂ = 1.25). Both subjects matched, with the blue (or light gray) subject matching more, while both dwelled at the social frequency (second row, A₁ = −3.25, A₂ = −3.00, ε₁ = 3.50, ε₂ = 0.15). The red (or dark gray) partner matched the blue (or light gray) and escaped to a frequency greater than both the initial and social frequencies, while the blue (or light gray) partner continued at the last social frequency (third row, A₁ = −1.00, A₂ = −3.00, ε₁ = 2.65, ε₂ = −2.00). The blue (or light gray) partner matched the red (or dark gray) and dwelled nearer the social frequency, while the red (or dark gray) partner matched the blue (or light gray) partner by overshooting slightly and dwelling near the social frequency (fourth row, A₁ = −2.00, A₂ = 1.25, ε₁ = 0.45, ε₂ = −0.35). The partner with the higher magnitude of A adapts more to the partner upon coupling (e.g., fourth row). Unequal ε’s lead to a trend in the social frequency. Furthermore, a negative ε allows a person to have a higher (or lower) post-interactional frequency by moving away from the partner (rows three and four).

With the manipulation of just a handful of parameters, ε, A, and δω, it is possible to reproduce the experimental data quite well (Figure 12). Experimental trials (Figure 12, left) and corresponding model simulations (Figure 12, right) are shown for four example trials: not only is the model able to reproduce the target phenomena (δω_Enter and δω_Exit), but also some additional features of experimental data that have previously been overlooked (e.g., drift of the coordination frequencies during interactions, restoration of symmetry in the relative phase) also emerge from the model.

Discussion

In coupled oscillators from the inanimate world of physics, such as pendulum clocks or springs, once coupling is removed, oscillators return to their intrinsic state. That is, such an oscillator returns to its natural frequency if there is one, or to rest. Evidently, those oscillators exhibit no memory—no sustained change—that make the behavior after coupling different than before coupling. What is different, then, about rhythmic movements in human interactions?

The current study investigated how pairs of people enter into spontaneous collective patterns, what their individual roles in establishing those patterns are, as well as how social interaction may alter their consequent independent behavior. Specifically, we inquired, how is post-interactional behavior affected by initial frequency difference and by the patterns formed spontaneously during social interactions?

During visual information exchange and without any instruction to do so, the partners exhibited three main patterns of coordination (cf. Figure 2): uncoordinated, intermittent, and coordinated. Such patterns are well–known in Social Coordination Dynamics (Nordham & Kelso, 2016; Oullier et al., 2008; Oullier & Kelso, 2009; Tognoli et al., 2007; Tognoli, 2008; see Schmidt & Richardson, 2008; Schmidt, Fitzpatrick, Caron, & Mergeche, 2011 for reviews). The spontaneous coordination that was observed during social contact tends to be subtle as partners phase–coupled more often intermittently than consistently. Therefore, simply moving while looking at a partner who is doing the same does not guarantee strong phase–locking. Indeed, personal experience can attest that people tend not to spontaneously and precisely mirror others’ behavior at all times. Rather, intermittent social coordination occurs. Intermittency (or relative coordination; cf. von Holst, 1973) is a signature of underlying metastable dynamics (Kelso et al., 1990; Kelso & Jeka, 1992; Kelso, 1995) in which tendencies for coupling and independence co-exist, thereby permitting systems (from people to neurons, cf. Kelso, 2008; Tognoli & Kelso, 2014) to exhibit both stable and flexible behavior at the same time (Kelso, 1995; Kelso & Engstrøm, 2006; Tognoli, de Guzman, & Kelso, 2011). Such maximally adaptive behavior is ideal for humans who are able to behave separately from others or act jointly according to circumstances.

Examination of individual roles in establishing various patterns of visually–mediated coordination showed that in cases in which people phase–locked, partners did not necessarily behave the same as each other when they entered or exited coordination. Given that partners most often begin with different initial frequencies, for social coordination to occur (via phase–locking), the gap between their frequencies had to be acted upon (or ignored). Therefore, if action was taken, e.g., to match frequencies, one or both of the partners had to change (cf. Figure 4; see also de Poel, 2016; Hart, Noy, Feniger-Schaal, Mayo, & Alon, 2014; Peper, Stins, & de Poel, 2013). In contrast to the onset of social contact, after social contact ended partners could not see each other and thus they could not know what the other was doing. One or both partners independently may have dwelled near the newly adopted social frequency or attempted to return to their original frequency. Indeed, all of these possibilities were observed (cf. Figures 2 and 4).

Were there no effect of visual coupling, individual behavior before social contact should not differ from that of after the interaction. As illustrated in Figures 5 and 6, however, there was a strong tendency for frequencies to become more similar after social contact, which was modulated by the prior mode of coordination. We call this phenomenon a memory (retention of an experience). Whether this memory is subject to consolidation and how long it lasts is a subject of further investigation. We note that the memory effect presents individual differences (differential susceptibility to frequency adaptation as demonstrated by a unique fit of experimental data to diverse degrees of ε, distinct from δω, A, and B, Figures 4 and 12.). This observation is not suggestive of a slow relaxation phenomenon exceeding the temporal window of our trial size—and suggests that an active process is at play. In line with our hypotheses, the strongest, most persistent effect of social interaction occurred following highly coordinated interactions, which had smaller initial frequency differences (Figure 13). Coupling and initial frequency difference had similar effects on the coordination and, subsequently, the degree of social memory (Figures 10 and 11), a reflection of the multiple routes to metastability (Kelso, 2008, 2012; Tognoli & Kelso, 2014). Such collective effects transcended individual differences in entering and exiting social coordination.

Figure 13.

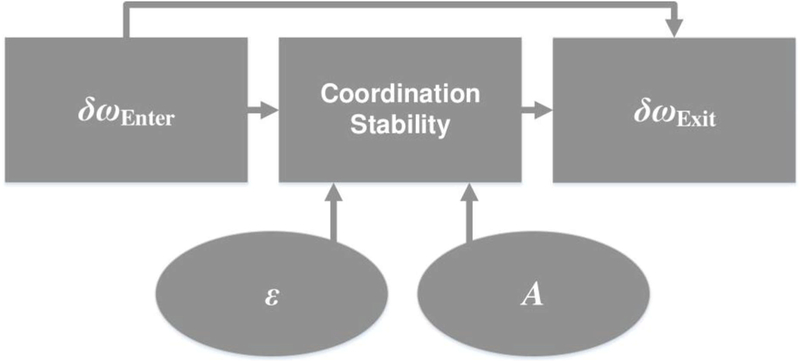
Conceptual model of social coordination and social memory: The exiting frequency difference is affected by its history (i.e. the entering frequency difference). Individual behavior affects interpersonal behavior, that is, initial frequency difference affects the stability of coordination. In turn, the interpersonal affects the individual, i.e. coordination stability affects exiting frequency difference. Adaptation (ε) and coupling (A) affect exiting frequency difference via their effects on phase and frequency coupling during coordination.

In its basic form, the HKB model does not exhibit social memory as we have defined it, nor would we expect it to. That is to say, in HKB, when the coupling is turned off (as in the present experiment) the individual oscillators return to their initial frequency. Remarkably, an extension of the HKB model that includes frequency adaptation is able to reproduce all the experimental findings (for other applications, see also Buchli, Righetti, & Ijspeert, 2008; Dumas et al., 2014; Righetti et al., 2006; Righetti, Buchli, & Ijspeert, 2009). Frequency adaptation explains many aspects of the social memory phenomenon with just a few parameters (see Figure 13). Because the oscillators’ internal frequencies are given the ability to change, adaptation of frequency during social interaction allows the social pattern to persist in individuals well after coupling ends, possibly until meeting another person.² Furthermore, the relative phase during visual contact, which due to symmetry breaking begins with a finite value, gradually approaches 0 rad (or π rad). This happens in contrast to previously reported cases in which relative phase remains stable for the duration of coupled behavior (cf. Kelso, 1995). The newly observed shift toward 0 rad (or π rad) relative phase is the result of the progressive decrease in eigenfrequency difference during adaptation. This shift can thus be considered “symmetry restoration.”

Our extended HKB model of social memory shows that the strength of frequency adaptation (ε) during coupling leads to oscillators with closer eigenfrequencies after coupling ends. In addition, as observed in the present experiment as well as in the model, difference in oscillators’ adaptation rate (ε₁ /= ε₂) validates some experimental insights that different people are more or less susceptible to memory of shared social experience. At the same time, in the model, different adaptation rates lead to a trend in shared frequency during the interaction, which was a feature also observed in the experimental data. When oscillators were set with unequal coupling (A₁ /= A₂), the one with greater magnitude was able to match the other more quickly. Similarly, changing intrinsic frequencies (Ω and δΩ) affected the possible coordination régime and again the degree of social memory. The combination of unequal adaptation and coupling reproduced the individual differences in entering and exiting social coordination in human behavior.

Adaptation has been observed in single neuron responses (Major & Tank, 2004), and of course, lies at the core of an entire research program that deals with “complex adaptive systems” (e.g., Gell-Mann, 1994; Holland, 1975). Future experiments can test specific predictions about the proposed frequency adaptation mechanism of social memory. Given that adaptation has a typical timescale, a greater degree of social memory is expected to occur with longer durations of social contact. Experiments should test the observations of relative phase shift toward the attractor and rate of adopting a shared frequency. To manipulate and test the causal role of frequency difference on subsequent effects on post-interactional frequency difference, metronome pacing could be employed as in many previous experiments. Likewise, studies of spontaneous social interactions could be complemented with experiments in which subjects are instructed to intentionally interact in a specific way, e.g., in-phase, or anti-phase, or indeed to ignore each other’s movements. If the pattern of social interaction is more stable during performance of instructed patterns of social coordination, the present theoretical model predicts enhanced social memory. Tognoli et al. (2007) and Naeem, Prasad, Watson, and Kelso (2012), previously looked at spontaneous and intentional social coordination in both behavior and brain—a comparison of spontaneous and intentional social coordination in the context of the current experimental results thus seems warranted. What remains to be seen is the effect intention has on the patterns of persistence. It is hypothesized that stronger persistence will occur due to intention, via its effect on the coupling strength during the interaction.³

While the current study examined the role of movement frequency in social memory, future work can investigate the role of other coordination variables on social memory. Considering that the degree of social memory was modulated by the stability of rhythmic coordination, variables that alter stability will likely also affect social memory. For instance, coordination stability has been found to be affected by frequency variability, amplitude, and phase portrait nonlinearity (Varlet, Coey, Schmidt, & Richardson, 2012; Varlet et al., 2014; Varlet, Schmidt, & Richardson, 2016). Additionally, coordination stability is modulated by the stability of eye tracking and via visual information (e.g., Bingham, 2004; Roerdink, Ophoff, Peper, & Beek, 2008; Schmidt, Richardson, Arsenault, & Galantucci, 2007; Wilson, Collins, & Bingham, 2005). Stronger coupling, which was shown to enhance frequency adaptation, is predicted to lead to longer, more persistent social memory.

A history of interactions with others shapes one’s own behavioral dispositions. Thus, repeated interactions, such as those that occur within a community, could culminate in the inhabitants converging upon a common preferred movement frequency or range of frequencies. Indeed, unique walking paces in different cities have been identified (Bornstein & Bornstein, 1976). When people act in the world, they exchange information and retain the characteristics of previous interactions in their movements. This suggests a collective shaping of behavior over periods of time that extend beyond the duration of any single interaction and shapes the dynamics of crowd behavior, cultural rituals, and communicative movements. It would seem that frequency adaptation, in which each member of the group adapts to the other, is an essential aspect of such collective behavior.

While many studies have shown that people can coordinate with non-human rhythmic stimuli (e.g., Byblow, Chua, & Goodman, 1995; Kelso et al., 1990; Kilner, Hamilton, & Blakemore, 2007; Romero, Kallen, Riley, & Richardson, 2015; Wimmers, Beek, & van Wieringen, 1992), a question concerns the extent to which the behaviors studied here and in the field of social coordination dynamics in general relate to strictly social behavior? The current research may be considered as part of an effort to discover how sophisticated social behaviors can emerge from very simple mechanisms of coordination. The current experimental and theoretical work provides evidence that the mechanism of frequency adaptation underpins memory of shared behavior between social partners. It supports the idea that, based on experiments of social interaction, social behavior can be predicted (with experimentally–verified models) and reproduced (with those models animating interactive virtual partners, Dumas et al., 2014; Kelso, 2009; Kostrubiec et al., 2015).

The current study has the potential to extend the conventional taxonomy of memory (e.g., Squire & Wixted, 2011) to the social realm. People may learn by intentionally observing and modifying their behavior, but also while simply behaving spontaneously with others. By socially coordinating, new behavior can be learned and then performed on one’s own, such as learning a dance. Moving with an instructor stabilizes new behavior between teacher and learner until the learner is able to perform on their own.

The basis for individual differences in coupling and adaptation likely stem from different interpersonal dispositions such as friendliness (willingness to couple) and likability of the partner (Miles, Lumsden, Richardson, & Macrae, 2011; Zhao et al., 2015). How such factors map onto the kind of social coordination and memory observed and modeled here is an intriguing subject for future studies of social coordination and its persistent effects on individuals.

Experiments have shown that bi-directional social interactions can influence future individual or social behavior. For example, there is greater recall of information about others who have moved with a joint rhythm (Miles, Nind, Henderson, & Macrae, 2010; Woolhouse, Tidhar, & Cross, 2016). Pairs of people jointly solve a labyrinth game in less time when they had previously coordinated together by rocking their chairs in synchrony versus those who did not rock in synchrony (Valdesolo, Ouyang, & DeSteno, 2010). In addition, it has been reported that people’s motives, attitudes, and feelings affect who coordinates with whom and by how much (Lumsden, Miles, Richardson, Smith, & Macrae, 2012; Miles, Griffiths, Richardson, & Macrae, 2010; Miles et al., 2011). The converse is also the case, namely, that social coordination can lead to greater pro-sociality, influence self–esteem, and other factors (Hove & Risen, 2009; Launay, Dean, & Bailes, 2013; Lumsden, Miles, & Macrae, 2014; Miles, Nind, & Macrae, 2009; Reddish, Bulbulia, & Fischer, 2014; Rennung & Göritz, 2016). Quantitative studies of social coordination may also be supplemented by insights from phenomenological studies of first–person experience of social coordination, essentially—remembrances of recent interactions (Fairhurst, Janata, & Keller, 2013; Lakens & Stel, 2011; Limerick, Coyle, & Moore, 2014; Llobera et al., 2016; Salmela & Nagatsu, 2016).

The present paper offers an entry point to quantify the lasting effects of social interactions, research which can potentially extend into a deeper understanding of psychotherapeutic outcomes (cf. Ramseyer & Tschacher, 2011; Tschacher, Haken, & Kyselo, 2015). Social interactions are associated with improvement in health and well–being (van Harmelen et al., 2016; Kim, Benjamin, Fowler, & Christakis, 2016), while social isolation is associated with degradation of mental health (e.g., solitary confinement). In doctor–patient relationships, social interactions can affect health treatment outcomes (Benedetti, 2013; Wager & Atlas, 2015; for electrocorticography of interacting with a doctor or a “darling,” see Derix, Iljina, Schulze-Bonhage, Aertsen, & Ball, 2012). Moving with others can even elevate pain thresholds (Cohen, Ejsmond-Frey, Knight, & Dunbar, 2010; Colloca & Benedetti, 2009; Tarr, Launay, Cohen, & Dunbar, 2015). The coordination dynamics of social memory suggests some of the key variables and dynamics necessary for understanding how health and social life relate and how the benefits of social interaction might persist.

All or nearly all mental illnesses are identified by their impact on social interaction (Schilbach, 2016). Of interest are dynamical diseases in behavior, so-called “functional abnormalities” that can be understood using dynamical systems modeling. Quantitative models have been proposed to capture the therapeutic alliance, a construct associated with positive psychotherapy outcomes (Beuter & Vasilakos, 1995; Glass & Mackey, 1988; Glass, 2015; Koole & Tschacher, 2016; Tschacher et al., 2015), which suggest that increased incidence of synchrony between patient and psychotherapist over time is a marker of improvement. For instance, changes in gait characteristics in patients with mild depression may indicate the effectiveness of patient–therapist interactions over the course of cognitive–behavioral therapy sessions (e.g., Michalak, Troje, & Heidenreich, 2011).

The current work on social memory makes a conceptual contribution to the so-called causal loops of Coordination Dynamics (Kelso & Engstrøm, 2006; Nordham & Kelso, 2016; Tschacher & Haken, 2007; Zhang, Nordham, & Kelso, 2015), in which control parameters change the order of a system, e.g., the oil in a heated pan creates convection rolls (order parameter) in response to the temperature difference above and below the pan (control parameter). In turn, the order of the system can change the control parameter, i.e. the rolls in the oil effectively transfer heat, thus decreasing the temperature difference. Likewise, as shown empirically and theoretically here, the individual (quantified by the frequency difference) affects the interpersonal (social coordination pattern) and, in a complementary fashion, the interpersonal (coordination pattern) affects the individual (frequency difference). In this way, social interactions can make people more similar, at least in the short term.

In summary, in the present work, the occurrence of phase coupling and frequency adaptation were shown to enhance social memory both empirically and theoretically. To end on a speculative though suggestive note, this says that if you want to form a lasting relationship, you should choose a partner whose intrinsic frequency is similar to your own. Similar intrinsic frequencies have greater potential to couple, and thus—through coupling and adaptation—to create a more lasting social bond.