Comparing the accuracy of several network-based COVID-19 prediction algorithms

Abstract

Researchers from various scientific disciplines have attempted to forecast the spread of coronavirus disease 2019 (COVID-19). The proposed epidemic prediction methods range from basic curve fitting methods and traffic interaction models to machine-learning approaches. If we combine all these approaches, we obtain the Network Inference-based Prediction Algorithm (NIPA). In this paper, we analyse a diverse set of COVID-19 forecast algorithms, including several modifications of NIPA. Among the algorithms that we evaluated, the original NIPA performed best at forecasting the spread of COVID-19 in Hubei, China and in the Netherlands. In particular, we show that network-based forecasting is superior to any other forecasting algorithm.

1. Introduction

In December 2019, SARS-CoV-2, the virus that causes coronavirus disease 2019 (COVID-19), emerged in the Chinese province of Hubei. The number of COVID-19 cases in China rose dramatically to almost 80,000 by the end of February 2020. From China, COVID-19 quickly spread throughout the whole world, with almost ten million cases by the end of June 2020. Many countries imposed nation-wide lockdowns to slow down the spread of COVID-19. A reliable forecast of the pandemic outbreak is key for targeted disease countermeasures and for the appropriate design of exit strategies to lift lockdowns.

Unfortunately, just as weather forecasts, the prediction of epidemic outbreaks is subject to fundamental limits (Moran et al., 2016). One aspect is the limited availability of data, because epidemic time series are relatively short, and carrying out medical tests on a large scale is challenging. Also, the final number of infected cases is highly sensitive to initial perturbations (Prasse, Achterberg & Van Mieghem, 2020). Nonetheless, many methods have been developed and applied to forecast the spread of COVID-19. Perhaps the simplest approach is based on fitting the number of infections to a sigmoid curve, such as the logistic function (Roosa et al., 2020, Verhulst, 1845), Hill function (Hill, 1910), or Gompertz function (Gompertz, 1825). Using nonlinear regression, the parameters of the sigmoid curve can be estimated. For the comparison of prediction algorithms in this work, we focus on the logistic function. The logistic function is of particular interest, because the logistic function is the (approximate) solution for the number of infected cases (Van Mieghem, 2016) in the Susceptible-Infected-Susceptible (SIS) epidemic model, and for the number of removed cases in the Susceptible-Infected-Removed (SIR) epidemic model (Kermack and McKendrick, 1927, Prasse, Achterberg and Van Mieghem, 2020).

By fitting the number of infected cases to a sigmoid curve, we implicitly assume that the spread in a particular region is independent of other regions, which contrasts with the strong interconnectedness of our modern world. The interaction between different regions, which is due to the movement of people, is taken into account by network-based techniques.

The interaction can be described by a network $G$ with $N$ nodes. Each node $i$ in the network $G$ represents a particular region (country, province, municipality, or city), and the link $a_{ij}\in \{0,1\}$ represents the existence of an interaction from region $j$ to region $i$, specified by a link weight ${\beta }_{ij}$ denoting the infection probability from region $j$ to region $i$. The self-infection probability within a region $i$ is given by ${\beta }_{ii}$, which we expect to be dominant over the other infection probabilities, because the interaction within a region is stronger than the interaction with other regions. The $N\times N$ infection probability matrix $B$, with elements ${\beta }_{ij}$ is, however, unknown and must be derived from past observations of the epidemic. We address this issue in more detail in Section 2.

Throughout this work, we often use “the number of infected cases”, which we understand as “the number of cases reported by local authorities”. Asymptomatic individuals, who do not feel sick and even do not know that they are infected and infectious, are not reported and can infect others unwittingly. To gain an understanding of the percentage of asymptomatic cases, one possibility is to test the population at random with, for example, blood tests. For COVID-19, the fraction of asymptomatic cases is estimated to be as large as 80% (Day, 2020). Since the number of asymptomatic cases cannot be determined on a daily basis, we confine ourselves to the number of reported cases in this work.

Many scientific disciplines have investigated and forecasted the spread of COVID-19. Statistical approaches are commonly based on Kalman filtering (Yang, Yi et al., 2020) or consider Bayesian approaches (Lorch et al., 2020). Network-based approaches consider aeroplane networks, daily commute traffic, or cell phone traffic (Chang et al., 2020). Data scientists apply machine-learning algorithms, like the adaptive neuro-fuzzy inference system (Al-qaness, Ewees, Fan, & Abd El Aziz, 2020) or Long Short-Term Memory (LSTM) (Yang, Zeng et al., 2020). Mathematicians have performed parameter estimation on compartmental models such as the SIR model (Kergassner et al., 2020, Yang, Zeng et al., 2020) or the Susceptible-Exposed-Infected-Removed (SEIR) model (He, Peng, & Sun, 2020).

Most epidemic models forecast the number of infected cases as a point forecast (generally: the mean of a distribution) rather than a complete distribution. All models in this work were designed to provide point forecasts, but can be generalised to provide prediction intervals. We discuss this topic further in Section 2.

The focus of this work is the comparison of a diverse set of methods for forecasting the spread of COVID-19, ranging from fitting closed-form epidemic curves and comprehensive machine-learning algorithms to network-based approaches. We focus on the spread of COVID-19, but we emphasise that all methods can be applied to general epidemic outbreaks. We show that pure machine-learning and network-agnostic algorithms or epidemiological models are inferior to algorithms that combine multiple approaches and rely on the underlying network topology. In particular, the Network Inference-based Prediction Algorithm (NIPA) is superior to any other algorithm that we evaluated. In Section 2, we explain eight forecast algorithms for predicting the future number of COVID-19 cases. In Section 3, we demonstrate their performance in two selected regions—Hubei, China and the Netherlands—and discuss the strengths and weaknesses of each algorithm. Finally, we summarise our findings in Section 4.

2. Prediction algorithms

The spread of COVID-19 can be measured in terms of the daily number of reported cases. We model the course of the epidemic with an SIR compartmental model, where each individual is either susceptible (healthy), infected (can infect the susceptible), or removed (recovered or died). We denote the (discrete) time by $k=1,\dots ,n$, where $n$ is the total number of observation days. The first COVID-19 case was reported on day $k=1$. Given that nearly all governments report their epidemic data once a day, we take a time step of one day as a natural choice and investigate the effect of the time step on the prediction accuracy in Appendix G. The SIR epidemic model with time-varying spreading parameters is given by:

Definition 1 SIR Epidemic Model (Kermack and McKendrick, 1927, Prasse and Van Mieghem, 2020a, Youssef and Scoglio, 2011) —

The viral state $v_i\left[k\right]={({\mathcal{S}}_i\left[k\right],{\mathcal{I}}_i\left[k\right],{\mathcal{R}}_i\left[k\right])}^T$ of region $i$ evolves in discrete time $k=1,2,\dots ,n$ according to

$${\mathcal{I}}_i[k+1]=(1-{\delta }_i){\mathcal{I}}_i\left[k\right]+(1-{\mathcal{I}}_i\left[k\right]-{\mathcal{R}}_i\left[k\right])\times \sum _{j=1}^N{\beta }_{ij}\left[k\right]{\mathcal{I}}_j\left[k\right],$$ (1)

$${\mathcal{R}}_i[k+1]={\mathcal{R}}_i\left[k\right]+{\delta }_i{\mathcal{I}}_i\left[k\right],$$ (2)

and the fraction of susceptible individuals follows as

$${\mathcal{S}}_i\left[k\right]=1-{\mathcal{I}}_i\left[k\right]-{\mathcal{R}}_i\left[k\right].$$ (3)

Here, ${\beta }_{ij}\left[k\right]\ge 0$ denotes the infection probability from region $j$ to region $i$ at time $k$, and ${\delta }_i>0$ denotes the curing probability of region $i$.

The spread of COVID-19 cannot be described exactly by the SIR equations 1, (2) and (3). The COVID-19 pandemic evolves in continuous time, whereas the SIR model evolves in discrete time, with a time step of one day. Additionally, the SIR model is unable to describe phenomena like personal social distancing, nation-wide lockdowns, and the availability of vaccinations. Each of these model assumptions introduces model errors. Prior to the introduction of several forecasting algorithms, we explain how model errors can be used to obtain prediction intervals for the forecasted number of infected cases.

As  described  in  Prasse, Achterberg, Ma and Van Mieghem (2020), we obtain the fraction of susceptible ${\mathcal{S}}_i\left[k\right]$, infectious ${\mathcal{I}}_i\left[k\right]$, and removed ${\mathcal{R}}_i\left[k\right]$ individuals in region $i$ from the observed infections $y_i\left[k\right]$. We aim to find the best possible forecast ${\hat{y}}_i\left[k\right]$ for the cumulative number of infected cases $y_i\left[k\right]$ for region $i$ and time $k$. In this work, we discuss eight prediction methods.

2.1. Potential generalisation to prediction intervals

Before introducing the different prediction methods, we emphasise that this work focuses on short-term point forecasts. Long-term epidemic behaviour is very random, and providing forecast intervals is essential to give a complete picture of the long-term viral spread (Cirillo & Taleb, 2020). Extending the point forecast methods in this work to prediction intervals is outside the scope of this work. Nonetheless, we consider it valuable to conceptually discuss an extension of the SIR equation (1) to allow for the computation of prediction intervals. A real epidemic does not follow the SIR model (1) exactly. Instead, the infection state ${\mathcal{I}}_i\left[k\right]$ evolves from time $k$ to $k+1$ as

$${\mathcal{I}}_i[k+1]=(1-{\delta }_i){\mathcal{I}}_i\left[k\right]+(1-{\mathcal{I}}_i\left[k\right]-{\mathcal{R}}_i\left[k\right])\times \sum _{j=1}^N{\beta }_{ij}\left[k\right]{\mathcal{I}}_j\left[k\right]+w_i\left[k\right],$$ (4)

where $w_i\left[k\right]$ denotes the model error of region $i$ at time $k$; see also Appendix A. Equation (4) can be used as a basis for prediction intervals with a Monte Carlo approach. We define the $N\times 1$ error vector as $w\left[k\right]={(w_1\left[k\right],\dots ,w_N\left[k\right])}^T$ and the $N\times 1$ infection vector as $\mathcal{I}\left[k\right]={({\mathcal{I}}_1\left[k\right],\dots ,{\mathcal{I}}_N\left[k\right])}^T$ for all times $k$. Then, based on Eq. (4), past observations $\mathcal{I}\left[1\right],\dots ,\mathcal{I}\left[n\right]$, and errors $w\left[1\right],\dots ,w[n-1]$, the point forecast algorithms provide an estimate of the viral state $\mathcal{I}\left[k\right]$ at future times $k>n$.

Conceptually, a prediction interval for the future viral state ${\mathcal{I}}_i\left[k\right]$ can be obtained in two steps. First, we obtain random samples from the distribution of the model errors $w\left[1\right],\dots ,w[n-1]$. Second, for each sample of errors $w\left[1\right],\dots ,w[n-1]$, we obtain a point forecast of the future viral states $\mathcal{I}\left[k\right]$. The prediction intervals for the future viral state $\mathcal{I}\left[k\right]$ can be obtained from the ensemble of point forecasts.

The details of the outlined method for obtaining prediction intervals are beyond the scope of this paper. Two particular challenges are the determination of the distribution of the model errors $w\left[k\right]$ and the implementation of a computationally efficient sampling method.

2.2. Sigmoid curves

The logistic function is a well-known example of an epidemiological sigmoid curve (Van Mieghem, 2016, Verhulst, 1845). We assume the cumulative number of infected cases $y_i\left[k\right]$ in region $i$ at time $k$ to follow a logistic function:

$$y_i\left[k\right]=\frac{y_{\infty ,i}}{1+e^{-K_i(k-t_{0,i})}},$$ (5)

where $y_{\infty ,i}$ is the long-term fraction of infections, $K_i$ is the logistic growth rate, and $t_{0,i}$ is the inflection point, also known as the epidemic peak. The parameters $y_{\infty ,i}$, $K_i$, and $t_{0,i}$ are estimated for each region separately using a nonlinear curve fitting procedure, which is explained in Appendix F. Other sigmoid curves, like the Hill function and Gompertz function, are also discussed in Appendix F.

2.3. Long short-term memory

Recurrent neural networks (Elman, 1990) (RNNs) have been used in various tasks related to sequences (Goodfellow, Bengio, & Courville, 2016), time series analysis and forecasting, speech recognition or natural language processing (Young, Hazarika, Poria, & Cambria, 2018), and they have been demonstrated to achieve state-of-the-art performance. LSTM networks (Hochreiter & Schmidhuber, 1997) are specific types of RNNs that resolve the long-standing problem of long-term dependencies. LSTM introduces additional input, output, and optional forget gates as interfaces with additional weights on the top of standard input data and hidden weights in the standard RNN unit. There are several variations (Gers and Schmidhuber, 2001, Gers et al., 2000) of LSTM networks, such as LSTMs with or without a forget gate and a “peephole connection”, (Jozefowicz, Zaremba, & Sutskever, 2015). For the internal mechanism between the gates and the exact mathematical relations, we refer the reader to Gers et al. (2000) or Yu, Si, Hu, and Zhang (2019). Here, we utilise the most common mechanism—an LSTM with a forget gate. In the simulations, we use an LSTM with sequence and hidden sizes both equal to four in a single LSTM layer (e.g., it is possible to stack a few LSTM layers, which leads to more overfitting), a learning rate of 0.1, and the Adam optimiser (Kingma & Ba, 2014), with mean squared error loss in 2000 epochs of training.

2.4. Network inference-based prediction algorithm (NIPA)

Network-based approaches take into account the interactions between different regions. However, the contact network $G$ is unknown (and consequently also the infection probability matrix $B$) and must be inferred from the epidemic outbreak. NIPA was originally proposed in Prasse and Van Mieghem (2020a), and an adaption of NIPA was applied to the spread of COVID-19 in Hubei, China (Prasse, Achterberg, Ma et al., 2020) and Italy (Pizzuti, Socievole, Prasse, & Van Mieghem, 2020). NIPA consists of two steps. First, the underlying infection matrix $B$ is inferred from the epidemic outbreak. Second, the infection matrix $B$ and the estimated curing rates ${\delta }_i$ for node $i$ are used to forecast the outbreak by iterating the SIR model on the estimated infection matrix $B$. Even though NIPA successfully forecasted the spread of COVID-19 in the Chinese province of Hubei, the underlying infection matrix $B$ could not be inferred (Prasse & Van Mieghem, 2020b).

2.5. NIPA applied to each region separately

As a benchmark model, we apply NIPA to each region separately, which we name NIPA separate. NIPA separate is a machine-learning method based on the SIR model, but it does not consider the interaction between different regions.

2.6. NIPA static prior

The formulation of NIPA can be extended to include knowledge of the underlying contact network. We use a time-independent traffic network (with the corresponding traffic intensity matrix $M$) to obtain a prior for the infection probability matrix $B$ as

$$B_{\text{prior}}=diag\left(c_1,\dots ,c_N\right)M.$$ (6)

We explain our motivation for the prior infection matrix $B_{\text{prior}}$ in Appendix B. The positive scalars $c_1,\dots ,c_N$ are unknown and are set by cross-validation. We assume that the true infection matrix $B$ is normally distributed around the prior infection matrix $B_{\text{prior}}$. Based on the prior infection matrix $B_{\text{prior}}$ and observations of the spread of COVID-19, we obtain the Bayesian estimate $B_{\text{posterior}}$ by solving the optimisation problem

$$B_{\text{posterior}}=\underset{B}{argmax}Pr\left[B|y_{}\left[1\right],\dots ,y_{}\left[n\right]\right]$$ (7)

$$\text{s.t.}\sum _{j=1}^N{\beta }_{ij}\le 1,i=1,\dots ,N,$$

where $y_{}\left[k\right]$ is the observed $N\times 1$ infection vector $y_{}\left[k\right]={\left(y_1\left[k\right],\dots ,y_N\left[k\right]\right)}^T$ at all times $k=1,\dots ,n$. Using the estimated infection matrix $B_{\text{posterior}}$ and the estimated curing rates ${\delta }_i$ for region $i$, we forecast the outbreak by iterating the SIR model. For details on NIPA static prior, see Appendix C.

Table 1.

All algorithms discussed in this paper. *If the algorithm is based on a phenomenological epidemic process, like the SIR model. **If the algorithm is able to forecast small perturbations in the global trend. ***If the spread between different regions is considered.

Algorithm	Epidemiology*	Adaptive**	Network***
NIPA	✓	✓	✓
NIPA separate	✓	✓	×
NIPA static prior	✓	✓	✓
NIPA dynamic prior	✓	✓	✓
Logistic function	✓	×	×
Hill function	✓	×	×
Gompertz function	✓	×	×
LSTM	×	✓	×

2.7. NIPA dynamic prior

During the COVID-19 pandemic, many countries have imposed some kind of lockdown, in which the free movement of people is significantly restricted. Thus, the true contact network $G$ is not static but varies over time. We use a time-varying traffic matrix $M\left[k\right]$ as an approximation for the prior infection matrix $B_{\text{prior}}\left[k\right]$, whose entries equal

$$B_{\text{prior}}\left[k\right]=diag\left(c_1,\dots ,c_N\right)M\left[k\right]$$ (8)

for all times $k$. The positive scalars $c_1,\dots ,c_N$ are unknown and are set by hold-out validation. We propose a Bayesian approach called NIPA dynamic prior to estimate the true infection matrix $B\left[k\right]$ from the time series of infected cases $y_i\left[k\right]$ and the prior infection matrix $B_{\text{prior}}\left[k\right]$. Using the estimated time-varying infection matrix $B_{\text{posterior}}\left[k\right]$ and the curing rates ${\delta }_i$ for each region $i$, we forecast the outbreak by iterating the SIR model. Appendix D explains the technical details of NIPA dynamic prior.

One challenge to NIPA dynamic prior is the unavailability of the contact network in the future. Hence, we assume that the traffic matrix will remain constant after the last observation point $n$: $B_{\text{prior}}[n+k]=B_{\text{prior}}\left[n\right]$ for all $k>0$. We summarise all prediction algorithms in Table 1.

3. Evaluation of the prediction performance

We evaluate the prediction accuracy of the methods discussed in Section 2 by forecasting the spread of COVID-19 in a selected number of regions. We set the maximal forecast horizon to six days, because of the difficulty of predicting epidemic outbreaks (Prasse, Achterberg & Van Mieghem, 2020).

Each prediction algorithm produces a forecast ${\hat{y}}_i\left[k\right]$ for the cumulative number of infected cases $y_i\left[k\right]$ for region $i$ at time $k$. To quantify the prediction error at time $k$, we use the symmetric mean absolute percentage error (sMAPE)

$$e_{\text{sMAPE}}\left[k\right]=\frac{1}{N}\sum _{i=1}^N\frac{|y_i\left[k\right]-{\hat{y}}_i\left[k\right]|}{(y_i\left[k\right]+{\hat{y}}_i\left[k\right])/2},$$ (9)

which  is  commonly  used  in  forecasting (Hyndman & Koehler, 2006). Furthermore, we quantify the percentage error (PE) as follows:

$$e_{\text{PE},i}\left[k\right]=\frac{y_i\left[k\right]-{\hat{y}}_i\left[k\right]}{y_i\left[k\right]},$$ (10)

for region $i$ and time $k$ to investigate over- and underestimations. We consider the spread of COVID-19 in two regions: the cities in Hubei, China, and the provinces in the Netherlands. These regions cannot be regarded as full representatives of the spread of COVID-19, let alone general infectious diseases. Rather, these regions illustrate the strengths and weaknesses of our methods.

3.1. Hubei, China

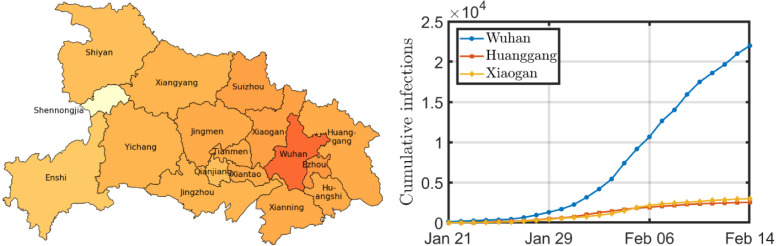
We evaluate the prediction accuracy first in the Chinese province Hubei. In December 2019, the first cases of COVID-19 were detected in Wuhan, the capital of Hubei. The first case outside Wuhan was reported on January 21. From January 24 onwards, the whole province Hubei was under lockdown, prohibiting any non-urgent travel. On February 15, the local government in Hubei changed the diagnosing policy, causing an erratic increase in the number of reported cases on February 15. Therefore, we restrict ourselves to the period from January 21 to February 14. The reported cases are provided by the  Health Commission of Hubei (2020). The majority of COVID-19 patients were reported in Wuhan, as shown in Fig. 1. We removed the region Shennongjia from our analysis, because of the small number of infections in that region.

Fig. 1.

The figure on the left shows a geographical map of Hubei. The darker the city, the more infections per 100,000 inhabitants on February 14. The three cities with the most infections on February 14 are displayed on the right.

For NIPA static prior, we require a traffic network describing the interactions between the cities in Hubei. The Chinese company Baidu provides an estimate of the number of commuters between all cities in Hubei on a daily basis (Baidu Migration website, 2020). The static prior is set proportional to the traffic network on January 21, which corresponds to day $k=1$.

Fig. 2 shows the prediction accuracy over time for different forecast algorithms. The horizontal axis shows the date $d$. We forecasted the disease several days ahead, using all available information from January 22 until $d$. For example, the right-most point in Fig. 2(a) includes data from January 22 to February 13 to forecast the situation on February 14.

Fig. 2.

Prediction accuracy for the situation in Hubei, China. The subfigures show the prediction accuracy for a forecast horizon of (a) one day, (b) two days, (c) three days, (d) four days, (e) five days, and (f) six days for the prediction algorithms from Section 2.

The sMAPE error in Fig. 2 tends to decrease as time evolves, because a growing amount of data is available. Furthermore, the total number of infected cases quickly increases, whereas the daily infected cases increase at a lower rate, indicating sub-exponential growth (Maier and Brockmann, 2020, Prasse, Achterberg and Van Mieghem, 2020). Sub-exponential growth will inevitably reduce the sMAPE error, because sMAPE is a relative error metric. On the other hand, the prediction accuracy decreases rapidly if the forecast horizon is enlarged. In particular, the number of cases five and six days ahead around February 1 cannot be predicted accurately, which is illustrated by Fig. 2, Fig. 2, respectively.

In general, the logistic function performs worse than the other algorithms. There may be several reasons for this. First, by fitting a logistic curve, we assume the number of cases to follow the SIR model closely (Kermack and McKendrick, 1927, Prasse, Achterberg and Van Mieghem, 2020). Hence, we do not allow any individual or governmental responses to COVID-19, which typically flattens the (logistic) curve. Second, the logistic function ignores the spread between regions, which further deteriorates the prediction accuracy. Third, the logistic function is symmetric around the epidemic peak at $k=t_0$; the increase and decrease in the number of cases around the peak is equal. Most epidemic outbreaks of COVID-19 show a rapid increase and a more gradual decrease in the daily number of cases. A possible reason for this is that most lockdowns are enforced immediately, whereas lockdown measures are lifted gradually. Occasionally, the Hill function (Hill, 1910) and Gompertz function (Gompertz, 1825) are used to predict epidemic outbreaks, because they allow asymmetry around the epidemic peak. In this work, we focus on the logistic function because of its relation to the solution of the SIR and SIS models, and we discuss the Hill function and the Gompertz function in Appendix F.

The performance of LSTM is fairly good, but LSTM fails to find an accurate forecast around January 31. Since the time series is the shortest at the left-most part of Fig. 2, less data is available to train the LSTM. Pure machine-learning algorithms are known to yield a lower prediction accuracy than other methods if the time series is short (Makridakis, Spiliotis, & Assimakopoulos, 2020).

The prediction accuracy of all NIPA methods in Fig. 2 is similar, although NIPA static prior is considerably worse around February 4 for predictions of three or more days ahead. A possible reason is that the impact of the nation-wide lockdown on January 24 is captured incorrectly by the static prior, whereas the original NIPA method has more freedom to adjust its contact network accordingly and NIPA dynamic prior receives a more tailored, time-varying prior during the lockdown situation. Another reason is that the prior network (dynamic or static) may deviate significantly from the true infection matrix. Under ideal circumstances, namely when the epidemic outbreak exactly follows the SIR model, we show that NIPA static prior outperforms NIPA in Appendix E.

Fig. 2 also shows that the negligence of the network interaction by the NIPA separate model decreases the prediction accuracy compared to NIPA. Hence, a network-based approach appears beneficial for forecasting. We summarise the results in Section 4.

Another interesting topic is forecast bias: the tendency to systematically overestimate or underestimate the true number of infected cases. Using the Percentage Error (PE), we estimate the bias for all prediction algorithms for region $i$ at time $k$. The surface error plots in Fig. 3 show the PE as a function of time for a four-days-ahead prediction. The logistic function and LSTM show the largest deviation around the mean, especially around February 1, which is in agreement with Fig. 2. Furthermore, Fig. 3 illustrates that the logistic function and LSTM systematically underestimate the true number of cases. On the other hand, NIPA static prior appears to overestimate the true number of cases. A possible reason for this is the following. The static network is taken to be proportional to the traffic flow before the lockdown measures. When a lockdown is introduced, the static prior remains constant, so the algorithm overestimates the true result. After some time, the newly collected data shows evidence that the prior is not very accurate, so NIPA static prior ignores the prior and uses the data instead, which improves the forecast accuracy again.

Fig. 3.

Surface error plots for four-days-ahead forecasts versus time. The subfigures show (a) NIPA, (b) NIPA separate, (c) NIPA static prior, (d) NIPA dynamic prior, (e) logistic function, and (f) LSTM.

3.2. The Netherlands

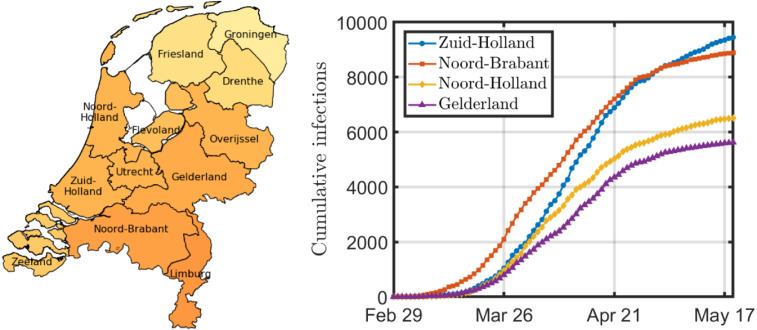
As a second case study, we regard the spread of COVID-19 in the Netherlands. The first patient, who had visited Italy the week before, was diagnosed on February 27. After February 27, the number of cases grew rapidly, as depicted in Fig. 4. The epidemic peak was observed at the end of March, and the daily number of cases subsequently dropped. We consider the spread of COVID-19 at a provincial level, for which data is available from the Dutch National Institute for Public Health and the Environment, called RIVM (RIVM, 2020). The Netherlands is subdivided into 12 provinces, for which the RIVM reports the daily number of new infections. Since the number of infected cases increased more gradually in the Netherlands than in Hubei, China, the total epidemic period is longer and more data points are available. A more gradual increase in the number of cases should be beneficial for the prediction accuracy.

Fig. 4.

The figure on the left shows a geographical map of the Netherlands. The darker the province, the more infections per 100,000 inhabitants on May 19. The four provinces with the most infections on May 19 are displayed on the right.

For NIPA static prior, we require a traffic network as an approximation for the interaction between the provinces. Statistics Netherlands (Centraal Bureau voor de Statistiek) reports the number of people $m_{ij}$ working in province $i$ and living in province $j$, averaged over one year (CBS, 2018). We use the Google Mobility Data “Workplaces” to estimate the time-varying traffic network for each province in the Netherlands (Google LLC, 2020). Google reports the percentage decrease of traffic $p_i\left[k\right]$ on day $k$ in province $i$ compared to an ordinary day between January 3 and February 6, 2020. During the lockdown, we expect $p_i\left[k\right]<1$ because of the lockdown measures. Then, we construct the time-dependent traffic matrix as follows: $m_{ij}\left[k\right]=m_{ij}\cdot p_i\left[k\right]$.

The prediction accuracy for the Netherlands is outlined in Fig. 5. Before April 1, the situation in the Netherlands is similar to Hubei, where the NIPA methods perform the best, but there are large deviations in the prediction accuracy. After April 1, the accuracy of the NIPA methods is nearly identical to each other. In other words, the influence of the initial static/dynamic network on the prediction is small. The main reason for this is that the NIPA algorithms are trained on a growing amount of infection data as time advances. Among the best performing methods over the whole period are original NIPA and NIPA separate, whereas the logistic function and LSTM show the worst performance.

Fig. 5.

Prediction accuracy for the situation in the Netherlands. The subfigures show the prediction accuracy (a) one day ahead, (b) two days ahead, (c) three days ahead, (d) four days ahead, (e) five days ahead, and (f) six days ahead.

The prediction accuracy of NIPA separate and NIPA are comparable, except at the left-hand side of Fig. 5. A possible reason for this is that the spread of the coronavirus was initially dominated by interprovincial interactions. After imposing the lockdown at the end of March, the interaction between provinces decreased significantly, so the spread of the coronavirus mainly took place within each province.

4. Conclusion

We compared the prediction accuracy of eight algorithms designed to forecast the spread of COVID-19. We summarise the results in Table 2. The error in Table 2 was obtained by averaging over all sMAPE forecast errors for forecast horizons between one and six days. Fitting a sigmoid curve, like the logistic function, performed the worst among the methods considered. The main reasons for the low prediction accuracy are the imposed symmetry around the epidemic peak and the negligence of the interaction between regions. Other sigmoid curves, such as the Hill function and the Gompertz function, performed slightly better than the logistic function, but performed worse than most other algorithms. The LSTM machine-learning algorithm is not based on any phenomenological epidemic processes, nor does it consider provincial interactions. Table 2 shows that the prediction accuracy of LSTM is comparable to the Hill and Gompertz functions.

Table 2.

The performance of all algorithms discussed in this paper. The Netherlands is abbreviated as NL. *As input, each algorithm requires the population size $N_i$ of each region $i$ and a time series of the infected cases $y_i\left[k\right]$ in each region $i$ at any time $k$.

Algorithm	Additional input*	Error (Hubei)	Error (NL)	Bias
NIPA	–	0.122	0.0381
NIPA separate	–	0.129	0.0487
NIPA static prior	Static traffic network	0.135	0.0384	Over
NIPA dynamic prior	Dynamic traffic network	0.129	0.0429
Logistic function	–	0.186	0.0735	Under
Hill function	–	0.142	0.0531
Gompertz function	–	0.141	0.0528
LSTM	–	0.160	0.0570	Under

The Network Inference-based Prediction Algorithm (NIPA) is a combination of machine learning and phenomenological epidemiology (SIR model), and it considers the interaction between different regions. Table 2 illustrates that the prediction accuracy of NIPA is better than that of any other algorithm. Applying NIPA for each region separately (NIPA separate) yielded a forecast error comparable to that of LSTM. We thus conclude that a network-based approach is beneficial for accurate forecasts. We also showed that choosing a time-varying or static prior close to the true contact network may improve the forecast accuracy of NIPA. Surprisingly, the inclusion of a time-varying or static prior in NIPA on real infection data does not improve the forecast accuracy for the considered regions. Among several reasons, the chosen prior might be an inaccurate estimate of the true contact network.

In a practical setting, such as the current COVID-19 pandemic, policymakers might prefer to anticipate to worst-case prediction of the number of infected cases. In that case, an asymmetric error metric that penalises underestimations more significantly than overestimations may be more suitable.

Appendix A. SIR epidemic model

The SIR epidemic model is defined in Definition 1. The COVID-19 pandemic does not exactly follow the SIR epidemic model. Instead, at any time $k$, the fraction of COVID-19 infections in region $i$ obeys

$${\mathcal{I}}_i[k+1]=\left(1-{\delta }_i\right){\mathcal{I}}_i\left[k\right]+{\mathcal{S}}_i\left[k\right]\sum _{j=1}^N{\beta }_{ij}\left[k\right]{\mathcal{I}}_j\left[k\right]+w_i\left[k\right].$$ (A.1)

Here, $w_i\left[k\right]$ denotes the model error of region $i$ at time $k$. Under Assumption 2, the model errors $w_i\left[k\right]$ are identically distributed at any time $k$ and for any region $i$:

Assumption 2

The model error $w_i\left[k\right]$ is normally distributed as

$$w_i\left[k\right]\sim \mathcal{N}\left(0,{\sigma }_w^2\right).$$ (A.2)

Furthermore, the model errors $w_i\left[k\right]$, $w_j\left[\tilde{k}\right]$ are stochastically independent for all times $k\ne \tilde{k}$ and regions $i\ne j$.

Assumption 3

For any node $i$, the curing probabilities satisfy ${\delta }_i\le 1$, and, at time $k\in \mathbb{N}$, the infection probabilities ${\beta }_{ij}\left[k\right]$ satisfy

$$\sum _{j=1}^N{\beta }_{ij}\left[k\right]\le 1.$$ (A.3)

Under Assumption 3, the fractions ${\mathcal{S}}_i\left[k\right]$, ${\mathcal{I}}_i\left[k\right]$, and ${\mathcal{R}}_i\left[k\right]$ remain in $[0,1]$ at any time $k$, as stated by Lemma 4, which is inspired by Paré, Liu, Beck, Kirwan, and Başar (2020, Lemma 1) and has been proved for time-invariant infection probabilities ${\beta }_{ij}$ in Prasse, Achterberg, Ma et al. (2020).

Lemma 4 Prasse, Achterberg, Ma et al., 2020 —

Suppose that ${\mathcal{I}}_i\left[1\right]\ge 0$ , ${\mathcal{R}}_i\left[1\right]\ge 0$ and ${\mathcal{I}}_i\left[1\right]+{\mathcal{R}}_i\left[1\right]\le 1$ for any node $i$ . Then, under Assumption 3 , it holds that ${\mathcal{I}}_i\left[k\right]\ge 0$ , ${\mathcal{R}}_i\left[k\right]\ge 0$ and ${\mathcal{I}}_i\left[k\right]+{\mathcal{R}}_i\left[k\right]\le 1$ at any time $k\in \mathbb{N}$ for any node $i$ .

Proof

We prove Lemma 4 by induction. Suppose that at time $k$ for any node $i$ it holds that

$${\mathcal{I}}_i\left[k\right]\ge 0$$ (A.4)

and

$${\mathcal{R}}_i\left[k\right]\ge 0$$ (A.5)

and

$${\mathcal{I}}_i\left[k\right]+{\mathcal{R}}_i\left[k\right]\le 1.$$ (A.6)

Under Assumption 3, it holds that $0\le {\delta }_i\le 1$ and ${\beta }_{ij}\ge 0$. Thus, we obtain from the SIR governing equation (1), (A.6) that both ${\mathcal{I}}_i[k+1]$ and ${\mathcal{R}}_i[k+1]$ equal a sum of positive addends, which implies that

$${\mathcal{I}}_i[k+1]\ge 0$$ (A.7)

and

$${\mathcal{R}}_i[k+1]\ge 0.$$ (A.8)

Furthermore, we obtain for any node $i$ that

$${\mathcal{I}}_i[k+1]+{\mathcal{R}}_i[k+1]={\mathcal{I}}_i\left[k\right]+{\mathcal{R}}_i\left[k\right]+(1-{\mathcal{I}}_i\left[k\right]-{\mathcal{R}}_i\left[k\right])\sum _{j=1}^N{\beta }_{ij}\left[k\right]{\mathcal{I}}_j\left[k\right].$$ (A.9)

From (A.4), (A.5), and (A.6), we obtain that ${\mathcal{I}}_i\left[k\right]+{\mathcal{R}}_i\left[k\right]\in [0,1]$. Since (A.5), (A.6) imply that ${\mathcal{I}}_i\left[k\right]\le 1$, it holds that

$$\sum _{j=1}^N{\beta }_{ij}\left[k\right]{\mathcal{I}}_j\left[k\right]\le 1$$ (A.10)

under Assumption 3. Thus, ${\mathcal{I}}_i[k+1]+{\mathcal{R}}_i[k+1]\le 1$, since the right side of (A.9) is a convex combination of 1 and ${\sum }_{j=1}^N{\beta }_{ij}\left[k\right]{\mathcal{I}}_j\left[k\right]\in [0,1]$.  □

Appendix B. Motivation for the static and dynamic prior

We intend to give a short motivation for the static prior in Eq. (6). Suppose that each individual has on average $〈d〉$ contacts (here, $〈\cdot 〉$ denotes the average) in the population. If a person is infected and that person’s neighbours are healthy, the person can infect any of its neighbours independently with probability $p$. Hence, the total number of infections follows a Binomial distribution

$$Pr\left[m\right]=\left(\genfrac{}{}{0ex}{}{〈d〉}{m}\right)p^m{(1-p)}^{〈d〉-m}.$$ (B.1)

In case $〈d〉$ is large and $\lambda \equiv p〈d〉$ is small, we can approximate (B.1) by a Poisson distribution

$$Pr\left[m\right]=e^{-\lambda }\frac{{\lambda }^m}{m!}.$$ (B.2)

If there are $N$ visiting, infected individuals that may all infect the population independently, the resulting distribution is the sum of independent, identically distributed Poisson distributions, which is again a Poisson distribution with $〈m〉=N\lambda$.

We denote the number of people living in region $j$ and travelling for work to region $i$ by $m_{ij}$. Each individual has $〈d〉$ contacts and can infect each individual with probability $p$. Then, region $j$ has on average $m_{ij}〈d〉p$ new infections, provided that no two individuals who visit the same region $j$ have contact with the same people. In particular, the fraction of new infections that region $i$ gets from region $j$ is given by

$${\beta }_{ij}=\frac{m_{ij}〈d〉p}{N_i}.$$ (B.3)

If we define $c_i=\frac{〈d〉p}{N_i}$, we obtain Eq. (6).

Appendix C. Details on NIPA static prior

We assume that the infection matrix $B$ is normally distributed around the prior $B_{\text{prior}}$, whose elements equal $b_{\text{prior},ij}=c_i{m}_{ij}$:

Assumption 5

Every non-diagonal element ${\beta }_{ij}$, where $i\ne j$, of the matrix $B$ is normally distributed as

$$Pr\left[{\beta }_{ij}\right]=\left\{\begin{array}{c}{\alpha }_i\frac{1}{\sqrt{2\pi }{\sigma }_i}exp\left(-\frac{1}{2{\sigma }_i^2}{\left({\beta }_{ij}-c_i{m}_{ij}\right)}^2\right)\hfill \\ \text{if}0\le {\beta }_{ij}\le 1,\hfill \\ 0\text{otherwise}.\hfill \end{array}\right)$$ (C.1)

Here, $c_i$ denotes the proportionality constant, and the constant ${\alpha }_i$ is set such that

$${\int }_{\mathbb{R}}Pr\left[{\beta }_{ij}\right]d{\beta }_{ij}=1.$$ (C.2)

The normal distribution (C.1) is cut off for values outside of the interval $[0,1]$, since the infection probability ${\beta }_{ij}$ cannot be outside the interval $[0,1]$. The standard deviation ${\sigma }_i$ is a measure of the accuracy of the prior distribution (C.1). Both the proportionality constant $c_i$ and the standard deviation ${\sigma }_i$ are unknown. Assumption 5 implies that the diagonal elements ${\beta }_{ii}$ of the matrix $B$ are uniformly distributed in the interval $[0,1]$.

We obtain the estimate $B_{\text{posterior}}$ of the contact network by a Bayesian (or maximum a posteriori) approach. Given the observed $N\times 1$ infection vector $\mathcal{I}\left[k\right]={({\mathcal{I}}_1\left[k\right],\dots ,{\mathcal{I}}_N\left[k\right])}^T$ at all times $k=1,\dots ,n$, we pose the optimisation problem

$$B_{\text{posterior}}=\underset{B}{argmax}Pr\left[B|\mathcal{I}\left[1\right],\dots ,\mathcal{I}\left[n\right]\right]$$ (C.3)

$$\text{s.t.}\sum _{j=1}^N{\beta }_{ij}\le 1,i=1,\dots ,N.$$

With the constraint in (C.3), we ensure that the predictions of the infections satisfy $0\le {\mathcal{I}}_i\left[k\right]\le 1$; see Lemma 4 in Appendix A. We define the $(n-1)\times 1$ vector $V_i$ and the $(n-1)\times N$ matrix $F_i$ as follows (Prasse, Achterberg, Ma et al., 2020):

$$V_i=\left(\begin{array}{c}\hfill {\mathcal{I}}_i\left[2\right]-(1-{\delta }_i){\mathcal{I}}_i\left[1\right]\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathcal{I}}_i\left[n\right]-(1-{\delta }_i){\mathcal{I}}_i[n-1]\hfill \end{array}\right)$$ (C.4)

and

$$F_i=\left(\begin{array}{ccc}\hfill {\mathcal{S}}_i\left[1\right]{\mathcal{I}}_1\left[1\right]\hfill & \hfill ...\hfill & \hfill {\mathcal{S}}_i\left[1\right]{\mathcal{I}}_N\left[1\right]\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\mathcal{S}}_i[n-1]{\mathcal{I}}_1[n-1]\hfill & \hfill ...\hfill & \hfill {\mathcal{S}}_i[n-1]{\mathcal{I}}_N[n-1]\hfill \end{array}\right).$$ (C.5)

We obtain the Bayesian estimate $B_{\text{posterior}}$ by solving a constrained linear least-squares problem. Proposition 6 is an adaptation of the Bayesian interpretation in Prasse and Van Mieghem (2020b).

Proposition 6

Under Assumption 2, Assumption 5 , the Bayesian estimation problem (C.3) is equivalent to solving the optimisation problem

$$\underset{{\beta }_{i1},\dots ,{\beta }_{iN}}{min}{‖V_i-F_i\left(\begin{array}{c}\hfill {\beta }_{i1}\hfill \\ \hfill ⋮\hfill \\ \hfill {\beta }_{iN}\hfill \end{array}\right)‖}_2^2+{\rho }_i\sum _{j=1,j\ne i}^N{\left({\beta }_{ij}-c_i{m}_{ij}\right)}^2$$$$\text{s.t.}0\le {\beta }_{ij}\le 1,j=1,\dots ,N,\sum _{j=1}^N{\beta }_{ij}\le 1,$$ (C.6)

for any region $i$ , where the penalisation parameter equals ${\rho }_i={\sigma }_w^2/{\sigma }_i^2$ .

Proof

The objective function of the optimisation problem (C.3) is equivalent to

$$\hat{B}=\underset{B}{argmax}log\left(Pr\left[B\right]\right)+\sum _{k=2}^{n}log\left(Pr\left[\mathcal{I}\left[k\right]|\mathcal{I}[k-1],B\right]\right).$$ (C.7)

In the following, we rewrite the two terms in (C.7). First, with (C.1), it holds that

$$log\left(Pr\left[B\right]\right)=\left\{\begin{array}{c}\sum _{i=1}^N\sum _{j=1}^{N}log\left({\alpha }_i\right)\hfill \\ -log\left(\sqrt{2\pi }{\sigma }_i\right)-\frac{1}{2{\sigma }_i^2}{\left({\beta }_{ij}-c_i{m}_{ij}\right)}^2\hfill \\ \text{if}0\le {\beta }_{ij}\le 1\forall i,j,\hfill \\ -\infty \text{otherwise}.\hfill \end{array}\right)$$ (C.8)

Neither the term $log\left({\alpha }_i\right)$ nor the term $log\left(\sqrt{2\pi }{\sigma }_i\right)$ depend on the matrix $B$. Furthermore, the prior $log\left(Pr\left[B\right]\right)$ is finite only if $0\le {\beta }_{ij}\le 1$ for all regions $i,j$. Thus, the optimisation problem (C.7) is equivalent to

$$\hat{B}=\underset{B}{argmax}\sum _{i=1}^N\sum _{j=1}^N-\frac{1}{2{\sigma }_i^2}{\left({\beta }_{ij}-c_i{m}_{ij}\right)}^2+\sum _{k=2}^{n}log\left(Pr\left[\mathcal{I}\left[k\right]|\mathcal{I}[k-1],B\right]\right)$$$$\text{s.t.}0\le {\beta }_{ij}\le 1,i=1,\dots ,N,$$$$j=1,\dots ,N.$$ (C.9)

Second, since the model errors $w_i\left[k\right]$ are stochastically independent for different regions $i$, we can rewrite the second term in the objective of (C.9) as

$$log\left(Pr\left[\mathcal{I}\left[k\right]|\mathcal{I}[k-1],B\right]\right)=\sum _{i=1}^{N}log\left(Pr\left[{\mathcal{I}}_i\left[k\right]|\mathcal{I}[k-1],B\right]\right)$$ (C.10)

$$=\sum _{i=1}^{N}log\left(Pr\left[w_i\left[k\right]={\Delta }_i\left[k\right]\right]\right),$$ (C.11)

where the second equality follows from (A.1), and by defining

$${\Delta }_i\left[k\right]={\mathcal{I}}_i\left[k\right]-\left(1-{\delta }_i\right){\mathcal{I}}_i[k-1]+{\mathcal{S}}_i[k-1]\sum _{j=1}^N{\beta }_{ij}{\mathcal{I}}_j[k-1].$$ (C.12)

Under Assumption 2, the model error $w_i\left[k\right]$ follows the normal distribution. Thus, it holds that

$$log\left(Pr\left[w_i\left[k\right]={\Delta }_i\left[k\right]\right]\right)=-log\left(\sqrt{2\pi }{\sigma }_w\right)-\frac{1}{2{\sigma }_w^2}{\Delta }_i^2\left[k\right].$$ (C.13)

The term $log\left(\sqrt{2\pi }{\sigma }_w\right)$ is independent of the matrix $B$. Thus, it follows from (C.10), (C.13) that the second term in the objective of (C.9) can be replaced by

$$\sum _{i=1}^N\sum _{k=2}^n\frac{1}{2{\sigma }_w^2}{\Delta }_i^2\left[k\right]=\sum _{i=1}^N\frac{1}{2{\sigma }_w^2}{‖V_i-F_i\left(\begin{array}{c}\hfill {\beta }_{i1}\hfill \\ \hfill ⋮\hfill \\ \hfill {\beta }_{iN}\hfill \end{array}\right)‖}_2^2,$$ (C.14)

where the equality follows from the definition of the vector $V_i$ and the matrix $F_i$ in (C.4), (C.5), respectively. Hence, the optimisation problem (C.9) becomes

$$\hat{B}=\underset{B}{argmin}\sum _{i=1}^N\frac{1}{2{\sigma }_w^2}{‖V_i-F_i\left(\begin{array}{c}\hfill {\beta }_{i1}\hfill \\ \hfill ⋮\hfill \\ \hfill {\beta }_{iN}\hfill \end{array}\right)‖}_2^2+\sum _{i=1}^N\frac{1}{2{\sigma }_i^2}\sum _{j=1}^N{\left({\beta }_{ij}-c_i{m}_{ij}\right)}^2$$$$\text{s.t.}0\le {\beta }_{ij}\le 1,i=1,\dots ,N,$$$$j=1,\dots ,N.$$ (C.15)

The problem (C.15) can be optimised independently for any region $i$. Thus, we obtain, after multiplication with $2{\sigma }_w^2$, the equivalent optimisation problem for any region $i$ as

$$\underset{{\beta }_{i1},\dots ,{\beta }_{iN}}{min}{‖V_i-F_i\left(\begin{array}{c}\hfill {\beta }_{i1}\hfill \\ \hfill ⋮\hfill \\ \hfill {\beta }_{iN}\hfill \end{array}\right)‖}_2^2+\frac{{\sigma }_w^2}{{\sigma }_i^2}\sum _{j=1}^N{\left({\beta }_{ij}-c_i{m}_{ij}\right)}^2$$$$\text{s.t.}0\le {\beta }_{ij}\le 1,j=1,\dots ,N.$$ (C.16)

By identifying ${\rho }_i={\sigma }_w^2/{\sigma }_i^2$, we obtain that (C.16) with the constraint ${\sum }_{j=1}^N{\beta }_{ij}\le 1$ is equivalent to the constrained linear least-squares problem (C.6).  □

The first term in the objective of (C.6) measures the fit to the observed epidemic data. The second term measures the deviation of the infection rates ${\beta }_{ij}$ from the prior (C.1). The scalar parameter ${\rho }_i$ balances the two terms: if the prior (C.1) is very accurate or the model errors $w_i\left[k\right]$ are large, then ${\rho }_i$ should be large. The optimal value of the parameter ${\rho }_i$ is equivalent to the ratio of the unknown variances ${\sigma }_w^2$ and ${\sigma }_i^2$ of the model errors $w_i\left[k\right]$ and the prior (C.1), respectively. The optimisation problem (C.6) is convex and can be solved efficiently (Boyd & Vandenberghe, 2004). To obtain the solution to (C.6) numerically, we make use of the Matlab command lsqlin. We stress the similarity of the optimisation problem (C.6) to the least absolute shrinkage and selection operator (LASSO) of Tibshirani (Tibshirani, 1996), which is the basis of NIPA without prior (Prasse, Achterberg, Ma et al., 2020). Instead of the second least-squares term in the objective of (C.6), LASSO considers the ${\ell }_1$-norm penalisation term

$${\rho }_i\sum _{j=1,j\ne i}^N\left|{\beta }_{ij}\right|.$$ (C.17)

In fact, NIPA without prior can also be interpreted as a Bayesian estimation approach (Prasse & Van Mieghem, 2020b).

C.1. Pseudocode

To solve the optimisation problem (C.6) for the infection rates ${\beta }_{i1}$, …, ${\beta }_{iN}$, we must specify three unknown variables. First, we must specify the curing rate ${\delta }_i$ of region $i$, which determines the fractions ${\mathcal{S}}_i\left[k\right]$ and ${\mathcal{R}}_i\left[k\right]$ of susceptible and recovered individuals, respectively (Prasse, Achterberg, Ma et al., 2020). Second, we must specify the parameter ${\rho }_i$. Third, the proportionality constant $c_i$ of the prior (C.1) is also unknown. We perform cross-validation to set the three unknown variables ${\delta }_i$, ${\rho }_i$, $c_i$.

NIPA static prior is similar to NIPA without prior, except for two alterations. First, we solve the constrained linear least-squares problem (C.6) instead of LASSO. Second, in addition to the parameter ${\rho }_i$ and the curing rate ${\delta }_i$, for Bayesian NIPA there is one more unknown variable, namely the proportionality constant $c_i$, which is a parameter of the prior distribution (C.1). To determine the constant $c_i$, we consider 50 logarithmically equidistant candidate values in the set $\Psi =\{c_{\text{min}},\dots ,c_{\text{max}}\}$. The minimal and the maximal values are set to $c_{\text{min}}=0.01$ and $c_{\text{max}}=100$, respectively. We set the value of $c_i$ by cross-validation. To obtain the epidemic outbreak prediction of Bayesian NIPA, we execute (Prasse, Achterberg, Ma et al., 2020 Algorithm 1), where (Prasse, Achterberg, Ma et al., 2020 Algorithm 2) is replaced by Algorithm 1 stated below.

Appendix D. Details on NIPA dynamic prior

We assume that the time-varying infection rates ${\beta }_{ij}\left[k\right]$ are proportional to the known population flow $m_{ij}\left[k\right]$. More precisely, we assume that the infection rates ${\beta }_{ij}\left[k\right]$ for all regions $i,j$, when $i\ne j$, equal

$${\beta }_{ij}\left[k\right]=c_i{m}_{ij}\left[k\right]$$ (D.1)

for some unknown proportionality constant $c_i>0$. Furthermore, we assume that the self-infection probabilities ${\beta }_{ii}$ do not change over time $k$. With (D.1), the SIR model in Definition 1 yields that

$${\mathcal{I}}_i[k+1]=(1-{\delta }_i){\mathcal{I}}_i\left[k\right]+{\beta }_{ii}{\mathcal{S}}_i\left[k\right]{\mathcal{I}}_i\left[k\right]+c_i{\mathcal{S}}_i\left[k\right]\sum _{j=1,j\ne i}^N{m}_{ij}\left[k\right]{\mathcal{I}}_j\left[k\right]+w_i\left[k\right].$$ (D.2)

D.1. Maximum-likelihood estimation

To predict the infectious state ${\mathcal{I}}_i\left[k\right]$ with (D.2), we must estimate the constants $c_i$, the self-infection probabilities ${\beta }_{ii}$, and the curing rates ${\delta }_i$. We define the $N\times 1$ vectors $c={(c_1,\dots ,c_N)}^T$ and $b={({\beta }_{11},\dots ,{\beta }_{NN})}^T$. We pose the estimation problem in a maximum-likelihood sense as

$$\underset{c,b}{max}Pr\left[\mathcal{I}\left[1\right],\dots ,\mathcal{I}\left[n\right]|c,b\right]$$$$\text{s.t.}{c}_i\ge 0,i=1,\dots ,N,$$$${\beta }_{ii}\ge 0,i=1,\dots ,N,$$$${\beta }_{ii}+c_i\sum _{j=1,j\ne i}^N{m}_{ij}\left[k\right]\le 1$$$$i=1,\dots ,N,k=1,\dots ,n.$$ (D.3)

The last constraint in (D.3) ensures that the predictions of the infections satisfy ${\mathcal{I}}_i\left[k\right]\le 1$; see Lemma 4. From the maximum-likelihood problem (D.3) we derive, for any region $i$, the LASSO optimisation problem as

$$\underset{c_i,{\beta }_{ii}}{min}\sum _{k=1}^{n-1}\left({\mathcal{I}}_i[k+1]-(1-{\delta }_i){\mathcal{I}}_i\left[k\right]\right)$$$${\left(-{\beta }_{ii}{\mathcal{S}}_i\left[k\right]{\mathcal{I}}_i\left[k\right]-c_i{\mathcal{S}}_i\left[k\right]\sum _{j=1,j\ne i}^N{m}_{ij}\left[k\right]{\mathcal{I}}_j\left[k\right]\right)}^2$$$$+{\rho }_i({\beta }_{ii}+c_i)$$$$\text{s.t.}{c}_i\ge 0,$$$${\beta }_{ii}\ge 0,$$$${\beta }_{ii}+c_i\sum _{j=1,j\ne i}^N{m}_{ij}\left[k\right]\le 1,k=1,\dots ,n.$$ (D.4)

Here, we denote the regularisation parameter by ${\rho }_i\ge 0$, which aims to avoid overfitting. The greater the parameter ${\rho }_i$, the smaller the estimates of the coefficients ${\beta }_{ii},c_i$. If the regularisation parameter ${\rho }_i=0$, then solving the LASSO (D.4) for any node $i$ is equivalent to solving the maximum-likelihood problem (D.3). (The equivalence of the optimisation problem (D.3) and the LASSO (D.4) can be derived analogously to Proposition 6.)

To solve the optimisation problem (D.4) for the constants $c_i$ and ${\beta }_{ii}$, we must specify two unknown variables. First, we must specify the curing rate ${\delta }_i$ of region $i$, which determines the fractions ${\mathcal{S}}_i\left[k\right]$ and ${\mathcal{R}}_i\left[k\right]$ of susceptible and recovered individuals, respectively (Prasse, Achterberg, Ma et al., 2020). Second, we must specify the parameter ${\rho }_i$. We perform hold-out cross-validation to set the unknown variables ${\delta }_i$ and ${\rho }_i$: The training set consists of the first 80% of the observations, and the validation set equals the last 20% of the observations. In pseudocode, NIPA dynamic prior is given by Algorithm 2.

Appendix E. NIPA static prior under perfect conditions

The original NIPA method is known to provide accurate predictions when the epidemic perfectly follows the SIR model (Prasse, Achterberg, Ma et al., 2020 Supplementary Material 1). Here, we intend to show that NIPA static prior performs even better if the prior matrix is close to the real infection matrix.

Suppose we generate data from an SIR epidemic as in Definition 1. We use a network with $N=10$ nodes with an equal curing rate $\delta$ for each node: ${\delta }_i=0.2$ for all $i$. We set the curing rate ${\delta }_i$ in the NIPA algorithms to the exact curing rates ${\delta }_i=0.2$, such that both NIPA and NIPA static prior will always estimate the curing rates correctly. We consider infection probabilities ${\beta }_{ij}$ that are uniformly distributed in the interval $(0,1)$. The effective reproduction number $R_0$ can be computed as (Van den Driessche & Watmough, 2002)

$$R_0=\text{maximum eigenvalue of }\left(B\cdot diag\left(\frac{1}{{\delta }_1},\dots ,\frac{1}{{\delta }_N}\right)\right).$$ (E.1)

We normalise $B$ element-wise such that the basic reproduction number $R_0$ equals 2.0. Furthermore, we set the population size $N_i$ for each region $i$ to a uniformly distributed number in the interval $[10^5,10^6]$ and start with an initial $y_1\left[1\right]=100$ infected cases in node 1, and zero infected cases in the other nodes. Most importantly, we set the prior infection matrix $B_{\text{prior}}$ to the exact infection matrix $B$, multiplied by some noise

$$B_{\text{prior},ij}={\beta }_{ij}{w}_{ij}.$$ (E.2)

Here, $w_{ij}$ is uniformly distributed in the interval $[1,2]$. The other parameters are the same as in the main article.

The result in Fig. E.6 is clear: NIPA static prior is able to capture the dynamics much better than NIPA. Hence, we conclude that NIPA static prior in combination with a good prior yields better prediction accuracy than the original NIPA method.

Fig. E.6.

The prediction for (a) NIPA and (b) NIPA static prior with generated SIR data based on Definition 1 on a 10-node network.

Appendix F. Sigmoid curves

In epidemiology, sigmoid curves are commonly used to forecast the future number of infected cases.

The logistic function

was developed by Verhulst in 1845 to explain the growth of the population in a specific region (Verhulst, 1845). The logistic function is the most often used sigmoid curve in epidemiology, because the logistic function is the (approximate) solution of the SIS and SIR model (Prasse, Achterberg & Van Mieghem, 2020). The logistic function assumes the cumulative number of infected cases $y_i\left[k\right]$ in region $i$ and time $k$ to follow

$$y_i\left[k\right]=\frac{y_{\infty ,i}}{1+e^{-K_i(k-t_{0,i})}},$$ (F.1)

where $y_{\infty ,i}$ is the long-term fraction of infections, $K_i$ is the logistic growth rate, and $t_{0,i}$ is the inflection point, which is also known as the epidemic peak.

The Hill function

was introduced in 1910 to describe the binding of molecules to surfaces (Hill, 1910). Later, it was successfully applied to describe the spread of epidemics (Kiskowski & Chowell, 2016). The Hill function assumes the cumulative number of infected cases $y_i\left[k\right]$ in region $i$ at time $k$ to follow

$$y_i\left[k\right]=\frac{y_{\infty ,i}}{1+{\left(\frac{K_i}{k-t_{0,i}}\right)}^{n_i}},$$ (F.2)

where $y_{\infty ,i}$ is the long-term fraction of infections, $K_i$ is the Hill growth rate, $n_i$ is the Hill coefficient, and $t_{0,i}$ is the inflection point, also known as the epidemic peak.

The Gompertz function

was introduced in 1825 to describe human mortality in a general population (Gompertz, 1825). Later, the Gompertz function was also used to describe the spread of epidemics (Winsor, 1932). The Gompertz function assumes the cumulative number of infected cases $y_i\left[k\right]$ in region $i$ at time $k$ to follow

$$y_i\left[k\right]=y_{\infty ,i}{e}^{-c_i{e}^{-a_{i}k}},$$ (F.3)

where $y_{\infty ,i}$ is the long-term fraction of infections, $c_i$ is a displacement factor (comparable to the inflection point), and $a_i$ is the Gompertz growth rate.

We describe the curve-fitting procedure here for the logistic function, but the parameters for any curve can be estimated analogously. Suppose that we have a time series of the cumulative number of reported cases $y_{\text{rep},i}\left[k\right]$ for time $k=1,\dots ,n$ and for any region $i$. Then, we minimise the mean squared error for each region separately:

$$({\hat{y}}_{\infty ,i},{\hat{K}}_i,{\hat{t}}_{0,i})=\underset{(y_{\infty ,i},K_i,t_{0,i})}{min}\sum _{k=1}^n{\left(y_{\text{rep},i}\left[k\right]-\frac{y_{\infty ,i}}{1+e^{-K_i(k-t_{0,i})}}\right)}^2,$$$$\text{s.t.}0\le y_{\infty ,i}\le N_i,$$$$K_i\ge 0,$$$$t_{0,i}\ge 0,$$ (F.4)

where $N_i$ is the population of region $i$. We evaluate the nonlinear minimisation problem (F.4) by the command $GlobalSearch$ in Matlab. As initial conditions, we provide $y_{\infty ,i}=y\left(t_{\text{obs}}\right),K_i=1,t_{0,i}=t_{\text{obs}}$. The parameters $(y_{\infty ,i},K_i,n_i,t_{0,i})$ for the Hill function and $(y_{\infty ,i},c_i,a_i)$ for the Gompertz function can be estimated analogously.

Appendix G. Influence of the time step on the prediction accuracy

In the discrete-time SIR model (1), we use the time step $\Delta t=1$ day. By approximating a continuous-time process (the COVID-19 pandemic) by a discrete-time process (SIR model) we make a model error. We investigate the influence of the time step on the prediction accuracy by comparing the NIPA prediction accuracy for various time steps, ranging from $\Delta t=0.5$ days to $\Delta t=3$ days. Since the number of infected cases is (generally) reported once a day, the data for the time step $\Delta t=0.5$ days is obtained by linearly interpolating the number of cumulative cases $y_i\left[k\right]$. For time steps $\Delta t=1$ day and $\Delta t=0.5$ days, we smooth the raw data before calling the NIPA algorithm (Prasse, Achterberg, Ma et al., 2020).

For time steps $\Delta t=2$ days and $\Delta t=3$ days, there are two possible methods. Method (A) assumes that the cumulative number of cases $y_i\left[k\right]$ is reported every two (or three) days, and is unreported on the intermediate days. Then, we smooth the remaining data before the NIPA algorithm is used. In fact, we have omitted the data on the intermediate days. In contrast, method (B) first smooths all raw data. Thereafter, we only use the cumulative number of cases $y_i\left[k\right]$ every two or three days for a time step of two or three days, respectively. The main difference is that method (A) completely neglects the data on intermediate days, whereas method (B) first applies a smoother, and then neglects the intermediate data.

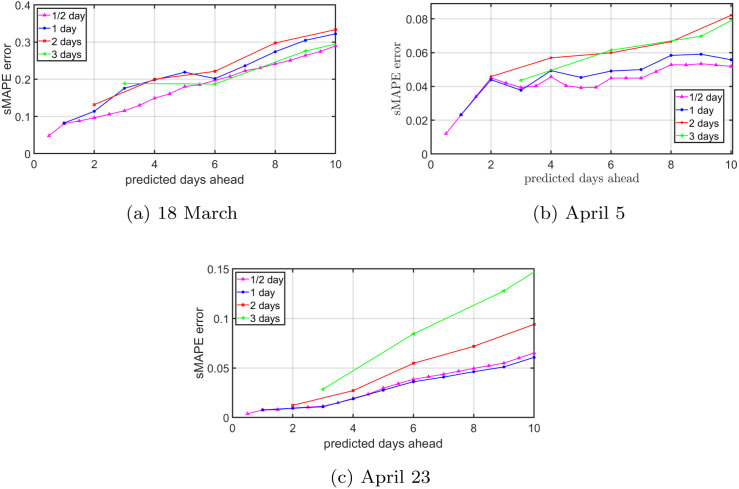
Fig. G.7, Fig. G.8 show an exemplary situation from the Netherlands for three initial dates. The configuration for the time steps $\Delta t=1$ day and $\Delta t=0.5$ days is equal in both figures. At the beginning of the COVID-19 outbreak, as shown in Fig. G.7(a) for method (A) and Fig. G.8(a) for method (B), the prediction accuracy is similar for all time steps. The small amount of available data and the rapidly increasing number of cases hampers accurate forecasting. As the epidemic evolves, method (A) and method (B) start to deviate. By omitting data, as in method (A), the sMAPE error in Fig. G.7 increases more quickly for time steps of two and three days than for smaller time steps. Hence, removing data causes the prediction accuracy to decrease. On the other hand, method (B) in Fig. G.8 shows similar behaviour for all time steps. We conclude that if the amount of data is unchanged, the choice of the time step has limited effect on the prediction accuracy.

Fig. G.7.

(Method A: First remove, then smooth.) The NIPA prediction accuracy for the situation in the Netherlands for varying time steps $\Delta t$. The subplots show the forecast for (a) March 18, (b) April 5, and (c) April 23. For the time step $\Delta t=2$ days and $\Delta t=3$ days, the data is first removed and then smoothed.

Fig. G.8.

(Method B: First smooth, then remove.) The NIPA prediction accuracy for the situation in the Netherlands for varying time steps $\Delta t$. The subplots show the forecast for (a) March 18, (b) April 5, and (c) April 23. For the time step $\Delta t=2$ days and $\Delta t=3$ days, the data is first smoothed and then removed.