Stereolithographic 3D Printing for Deterministic Control over Integration in Dual-Material Composites

Abstract

This work introduces a rapid and facile approach to predictably control integration between two materials with divergent properties. Programmed integration between photopolymerizable soft and stiff hydrogels was investigated for their promise in applications such as tissue engineering where heterogeneous properties are often desired. Spatial control afforded by grayscale 3D printing was leveraged to define regions at the interface that permit diffusive transport of a second material in-filled into the 3D printed part. The printing parameters (i.e., effective exposure dose) for the resin were correlated directly to mesh size to achieve controlled diffusion. Applying this information to grayscale exposures led to a range of distances over which integration was achieved with high fidelity. A prescribed finite distance of integration between soft and stiff hydrogels led to a 33% increase in strain to failure under tensile testing and eliminated failure at the interface. The feasibility of this approach was demonstrated in a layer-by-layer 3D printed part fabricated by stereolithography, which was subsequently infilled with a soft hydrogel containing osteoblastic cells. In summary, this approach holds promise for applications where integration of multiple materials and living cells is needed by allowing precise control over integration and reducing mechanical failure at contrasting material interfaces.

Graphical Abstract

This work leverages grayscale 3D printing to predictably control integration between two materials with divergent properties. A prescribed distance of integration between soft and stiff hydrogels eliminated failure at the interface. This approach holds promise for applications where composites require integration of multiple materials that minimize the risk of mechanical failure at material interfaces.

1. INTRODUCTION

Devices employed in biomedical,^[1–3] soft electronics,^[4] opto-electronics^[5,6] and robotics^[7–10] must often integrate soft functional materials with stiffer structural components. Integrating a broad spectrum of available materials affords large variations in properties with multiple functionalities to meet the demands of many applications.^[11–14] However, large internal stresses concentrate at the interface across materials with divergent properties, leaving the interface vulnerable to mechanical failure.^[15,16] Moreover, applications that use hydrated polymeric materials, such as hydrogels, are faced with the added challenge of differential swelling between heterogenous materials that introduces additional localized stress.^[17] These interfacial stresses lead to delamination and create points of failure. Consequently, application of soft and stiff composite materials demands improved methods to create robust interfaces between materials with strongly contrasting mechanical properties and/or swelling behavior.^[18–20]

Stability and function of composite materials depends on the robustness of the interface between the constituent materials. Adhesives are efficient at bonding materials of similar modulus. Examples include stiff-to-stiff materials such as metal implants that are bonded to bone via bone cement and soft-to-soft materials such as soft tissues that are bonded together via fibrin glue. However, they are often inadequate for heterogenous materials where stress concentrations develop.^[21] Nature has developed alternatives to adhesives by integrating two dissimilar materials across defined interfacial regions. This elegantly overcomes the mismatch in properties across heterogeneous materials and minimizes failure at the interface.^[22–25] For example, squid beaks have a soft base that transitions to a hard tip by modulating the amount of water, chitin and proteins.^[26] Teeth exhibit a transition from hard enamel to soft dentin, which is achieved by changes in fibre density and orientation across the dentino-enamel junction and provides a mechanism to dissipate load during mastication.^[27] Another example is in articulating joints and intervertebral discs where soft cartilage transitions to stiff bone. This transition is characterized by a wavy interface that interconnects vertically aligned collagen fibers, which together resist failure under shear and tensile stress.^[28–30]

There is a need to engineer solutions that can mimic bio-inspired interfaces and, depending on the function of the device, prescribe programmable interfacial regions between two materials.^[31,32] This would increase the range of material properties that can reliably be combined. For example, in the context of tissue engineering, composite materials have emerged as an important class of materials that can achieve improved mechanical properties, enhanced degradation behavior and rates, and superior bioactivity over single materials.^[33,34] For engineering tissues subjected to mechanical forces, composite scaffolds have been designed with stiff materials embedded with soft hydrogels to meet the simultaneous demand for in vivo function and for cell and tissue growth.^[35–38] To this end, 3D printing methods have been employed to create mechanically supportive structures into which soft materials are incorporated.^[39,40] Examples include regenerative strategies for cartilage,^[41,42] bone,^[43,44] the cartilage-bone junction^[45], and the tendon-bone junction^[46] where the inclusion of 3D printed structures provides mechanical support. However, studies have reported that the presence of a weak interface between two dissimilar materials and even between two similar materials reduces the overall mechanical properties.^[47] Thus, integration of multiple materials into a composite must be a key component to the design.

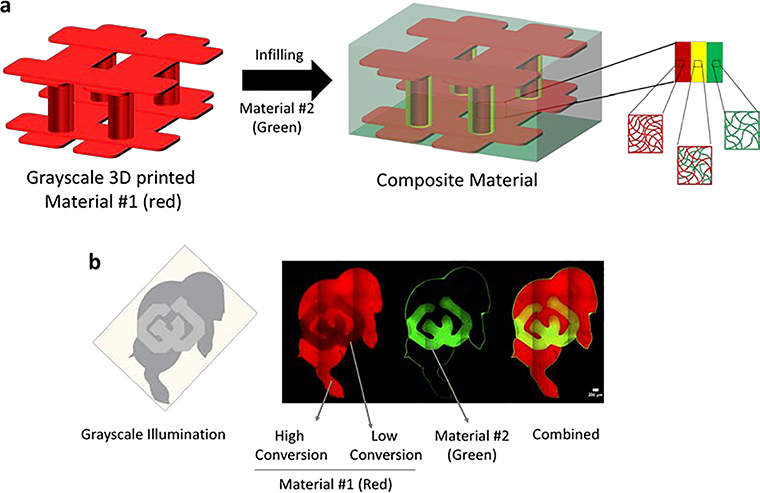
In this work, we leverage stereolithography (SLA)-based 3D printing to achieve precise spatial control over the 3D printed material properties as a means to define the degree to which a second material integrates into the 3D printed part. SLA was chosen because it renders excellent process control to produce complex and overhanging structures with high resolution (<20μm).^[48,49] The overarching goal for this work is to produce a dual-material part with a robust interfacial region between a 3D printed part and its infill (Figure 1a). In our approach, a 3D printed structure is formed by photopolymerization using SLA, followed by a second process that introduces a second photopolymerizable material. Precise grayscale illumination controls conversion during the printing process to yield a 3D printed part with spatially defined crosslink density. The local crosslink density and swelling properties define the mesh size of the crosslinked network, which in turn controls transport of the second material into the 3D printed part, defining the region of integration between two materials (Figure 1b). The objectives for this study were two-fold. The first objective was to establish a link between polymerization kinetics, defined by the printing parameters (i.e., exposure dose), and the resultant material properties (e.g., mesh size) to prescribe predictively regions of integration between two materials. The second objective was to demonstrate deterministic and spatial control over integration between two materials, evaluate the interfacial mechanical properties, and apply it to 3D printing in SLA with an integrated cell-laden soft hydrogel.

Figure 1.

Schematic of a 3d printed stiff material #1 containing pillars bound by an upper and lower lattice that is formed by stereolithography (SLA) (red) and then is infilled with a soft material #2 (green). During 3D printing, a thin shell around the columns is intentionally polymerized at low conversion to create regions that allow transport of the soft polymer into the 3D printed structure. This defines the region of integration (yellow). In the absence of these regions, transport of the soft material is prevented and an abrupt interface forms. When partially converted regions are patterned, transport of the soft material is achieved and an interpenetrating network forms between the soft and stiff materials (i.e., polymers) creating a strong interfacial bond. b) Demonstration of controlled selective transport in Ralphie (the buffalo mascot of the University of Colorado at Boulder). The gray scale image representing the energy dose distribution (left) was used to print a stiff polymer tagged with a red fluorophore containing regions of high and low conversion. Interpenetration of the soft polymer tagged with a green fluorophore was restricted to regions of low conversion and absent in regions of high conversion. The confocal fluorescence microscopy image demonstrates the controlled integration of the two within the block letters ‘CU’.

2. RESULTS AND DISCUSSION

2.1. Hydrogel Chemistry and Resulting Stiffness

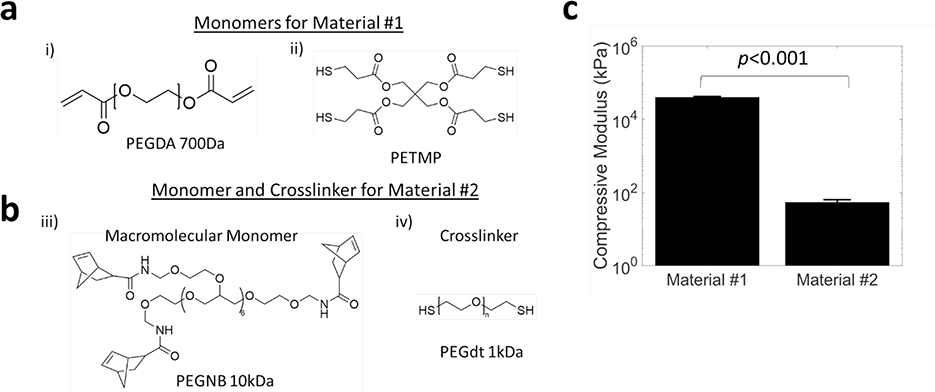
Two photopolymerizable “thiol-ene” and “thiol-acrylate” based poly(ethylene glycol) hydrogel materials with starkly different properties were investigated (Figure 2a,b). In this work, we 3D print the stiff hydrogel as material #1 and then infill with the soft hydrogel as material #2. The stiff material was prepared from poly(ethylene glycol) diacrylate (PEGDA700) with a low percentage of pentaerythritol tetrakis(3-mercaptopropionate) (PETMP), a four-arm thiol monomer. PETMP helps decrease oxygen inhibition time^[50] and therefore polymerization time, and introduces additional crosslink points to enhance stiffness.^[51] A PEG acrylate-based resin was selected for its wide use in additive manufacturing. Material #1 is photopolymerized via free-radical mediated reaction using 405nm light. The soft material was prepared from a light activated “thiol-ene” PEG hydrogel, with 8-arm PEG norbornene (PEGNB) as the macromolecular monomer and PEG dithiol as the crosslinker in phosphate buffered saline (PBS). This hydrogel was selected due to its promise in biological applications, minimal side products and demonstrated cytocompatibility and biocompatibility.^[52,53] At complete conversion, the stiff hydrogel (material #1) yielded a compressive modulus of 40 (2) MPa (average (std dev)) (Figure 2c). At complete conversion, the soft hydrogel (material #2) yielded a compressive modulus of 54 (9) kPa (Figure 2c), with three orders of magnitude modulus difference. The modulus for the soft hydrogel (material #2) was chosen based on several studies including our own work and others using hydrogels for 3D models of cell culture and for tissue engineering scaffolds of bone^[54–56], cartilage^[57–59] and tendons.^[60] The modulus for stiff material (material #1) was chosen to give a large differential in stiffness. Moreover, the volume fraction of the 3D printed stiff material can be varied to tune the final modulus of the scaffold. For example, a 5% volume fraction will yield 2 MPa, based on composite theory, when combined with the soft hydrogel, creating a composite scaffold matching the modulus of cartilage^[61].

Figure 2.

Chemical structures of a) monomers for material #1 and b) macromolecular monomer and crosslinker for material #2 and c) their corresponding compressive moduli. Data presented as mean with standard deviation as error bars for n=5.

2.2. Correlation of Material Property to Printing Parameters to Control Diffusive Transport

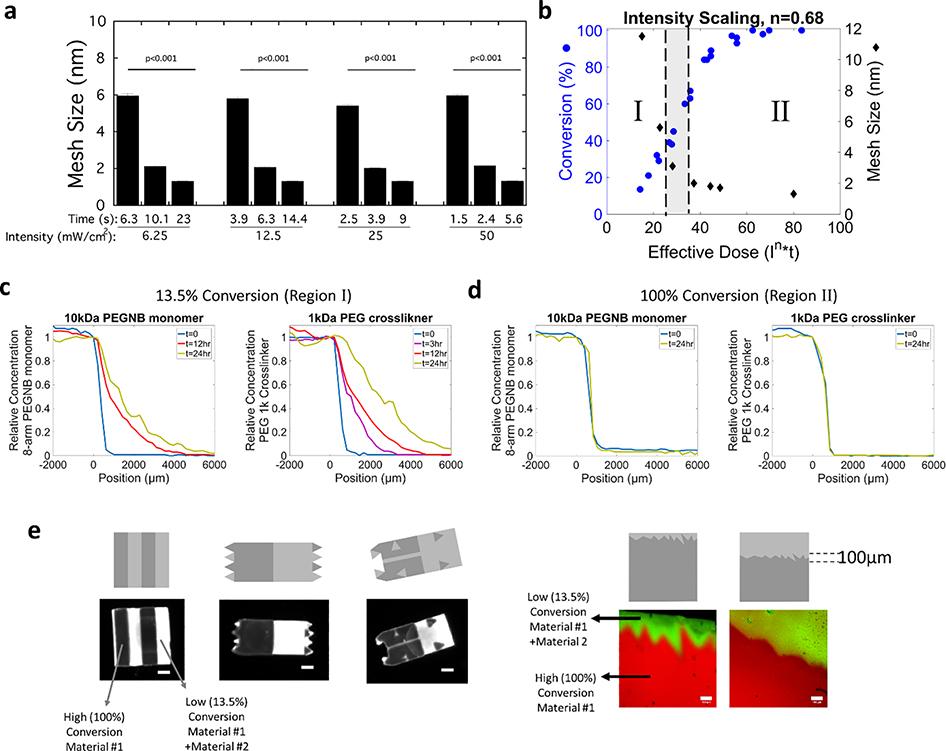
To apply grayscale illumination as a means to spatially control the local properties for material integration, the hydrogel properties of material #1 were first evaluated as a function of light intensity and exposure time (Figure S1). Since we are interested in controlling diffusive transport to facilitate integration, the mesh size, which is defined as the average distance between two adjacent crosslinks and describes the maximum size of a solute molecule that can diffuse into the swollen crosslinked polymer, is the relevant parameter. The mesh size of material #1 was determined under different exposure conditions (Figure 3a). The light intensity was varied from 6.25 mW/cm² to 50 mW/cm² and for each light intensity, exposure time was also varied (as shown in Figure 3a). Mesh size was calculated from the experimentally determined swelling ratio and the crosslink density following the method described by Canal and Peppas.^[62] The crosslink density was determined from experimentally measured compressive modulus and swelling ratio following methods described previously,^[63] which combines Flory-Rehner theory and theories of mixture and poroelasticity. Under these exposure conditions, the mesh size decreased from 6 nm to 1.3 nm. These results demonstrate that similar mesh sizes are achieved with different combinations of light intensities and exposure times. Since effective energy dose (i.e., combination of light intensity and exposure time) defines the polymer network structure during 3D printing, these findings indicate that the 3D printing parameters can be tuned while achieving the same mesh size.

Figure 3.

a) Assessment of mesh size of bulk printed material #1 as a function of incident light intensities and exposure times. Data presented as mean with standard deviation as error bars for n=4. p-values represent the effect of time for each light intensity. b) Conversion for material #1 and the corresponding mesh size of material #1 as a function of effective dose. When in region I, the mesh size of material #1 is larger than the size of diffusing monomers of material #2 enabling their transport and integration. When in region II, the mesh size of material #1 is smaller than the diffusing monomers of material #2 and hence transport and integration is inhibited, and instead a sharp interface forms. c-d) Concentration profiles as measured by fluorescence for a fluorescently labeled 10k PEGNB monomer and 1k PEG crosslinker into material #1 at c) ~13.5% conversion and at d) 100% conversion. e) Illustrations of the fidelity of spatial control over low and high conversion for material #1 that subsequently directs the transport of monomer and crosslinker of material #2, followed by a second polymerization. Examples include undulating boundaries and site-specific integration and a jagged interface with a small (left) or large (right) region of integration region. Grayscale digital projected images are shown followed by the spatially patterned material #1, the location of material #2 and the composite material. Images were acquired on a Versadoc Imager (left) or by confocal microscopy (right). Scale bars for the black and white images on the left is 1mm and the scale bars for the confocal microscopy images of the jagged interface on the right is 100μm.

To correlate material properties to an effective dose, we derived a relationship for SLA printing parameters of light intensity and exposure time (i.e., exposure dose) to conversion of the polymerizing species (i.e., the disappearance of the acrylate carbon-carbon double bond in material #1). The conversion of material #1 was characterized by FTIR at various intensities and exposure times. The rate of polymerization (R_p) is related to the rate of initiation (R_i), which is in turn related to the incident light intensity (I_o) and initiator concentration ([In]) through the steady state approximation given by the power law relationship:

$$R_p\approx R_i^{\alpha }\approx {\left(I_o\left[In\right]\right)}^{\alpha }$$ (1)

Accounting for the three distinct events of oxygen inhibition, light-induced polymerization, and dark polymerization,^[64] the scaling factor α for this resin was previously determined to be 0.68 (0.01).^[65] With this scaling factor, conversion as a function of effective dose ($I_o^{\alpha }$ x time) reduces to a single master curve (Figure 3b). From this curve, conversion is predicted at any intensity and time for material #1. The mesh size was determined as a function of effective dose and shown on the same plot with conversion (Figure 3b). When combined, the mesh size of material #1 can now be prescribed by effective dose using this master curve (Figure 3b). Importantly, a similar master curve can be generated for any 3D printed resin and subsequently regions defined for any filler based on the size of its precursors. In essence, the master curve can be utilized to define regions of integration across a wide variety of materials.

To enable regions of integration to be predictably prescribed, we next characterized diffusion of the monomers for material #2 into a bulk printed material #1. The latter was prepared at two effective doses, one that yielded a large mesh size (11 nm) at 13.5% conversion and the second that yielded a small mesh size (1.3 nm) at 100% conversion. Using a 1D experimental set-up (Figure S2) with material #1 swollen to equilibrium, diffusion of monomer and crosslinker labeled with a green fluorophore was monitored in time and space. For the 13.5% conversion case, the concentration profiles of fluorescent PEGNB and the fluorescent PEG crosslinker based on fluorescence versus position shows increasing concentration as a function of time. The profiles were consistent with Fickian diffusion and from the plots, diffusivity, D_g, of each monomer in the material #1 was estimated to be 25×10⁻⁸ cm²/s for PEGNB and 72×10⁻⁸ cm²/s for the PEG crosslinker (Figure 3c). On the contrary for the 100% conversion case of material #1, there was no diffusion of 8-arm PEGNB or PEG crosslinker observed into material #1 evident by a lack of change in the relative concentration as a function of position from 0 to 24hrs (Figure 3d). By controlling the mesh size of material #1, it is possible to prescribe selectively ‘OFF’ regions that restrict diffusion and produce a sharp interface or ‘ON’ regions that permit diffusion and support integration of one material into a second material.

With the knowledge of the mesh size for material #1 and diffusivity, D_g, of each monomer into the hydrogel network for the 13.5% conversion condition, the hydrodynamic radius (r_h) for PEG crosslinker and for PEGNB monomer was estimated. The radius of each monomer was determined to be 2.2 and 4.7 nm, respectively (see SI). The ratio $\frac{{\mathrm{r}}_{\mathrm{h}}}{\mathrm{\xi }}$ can then be used to more broadly define the ‘ON’ regions and the ‘OFF’ regions. In other words, when $\frac{{\mathrm{r}}_{\mathrm{h}}}{\mathrm{\xi }}<1$, material #1 will support transport of the monomer and crosslinker, defined as Region I in Figure 3b. However, when $\frac{{\mathrm{r}}_{\mathrm{h}}}{\mathrm{\xi }}>1$, material #1 will restrict their transport, defined as Region II in Figure 3b. An intermediate region exists, which is shown in gray in Figure 3b, and describes the region where transport is expected for the crosslinker, but not the PEGNB monomer. It is important to point out that while the exact value of the mesh size depends on the accuracy of the Canal and Peppas model^[62] as applied to this particular hydrogel system, the ratio $\frac{{\mathrm{r}}_{\mathrm{h}}}{\mathrm{\xi }}$, which relies on the experimentally determined Fickian diffusion experiments, provides an accurate depiction of the ‘ON’ and ‘OFF” regions for this system.

The fidelity of spatial control to create regions that support integration and regions that do not support integration was demonstrated by utilizing grayscale patterning of a single layer of printed material #1 in several arbitrary patterns (Figure 3e). The grayscale digital image that was used to create the pattern and achieve regions at 100% conversion and other regions at 13.5% conversion is shown in each case. The variable intensity of the red fluorescence qualitatively demonstrates the fidelity of the pattern, where high intensity correlates to regions at 100% conversion and low intensity correlates to regions at 13.5% conversion. Subsequently, material #1 was soaked in a bath of fluorescently labeled crosslinkers combined with the PEGNB monomers for 48 hours. Material #1 was then briefly rinsed, exposed to light, and then rinsed thoroughly to remove any unreacted monomers. Material #2 integrated into material #1, but only in the regions corresponding to the 13.5% conversion. Patterns of alternating high and low conversion regions and patterns of high and low regions intermixed into arbitrary patterns demonstrate the fidelity of spatial control. For example, in the same hydrogel construct material #2 was localized to a low conversion channel that was patterned to be 200-μm in width and 2-mm in length within a high conversion matrix. Other examples show areas of high conversion that were in the shape of triangles embedded in a low conversion matrix. Extending this idea, we were inspired by the wavy tide mark at the osteochondral interface between the deep zone of cartilage and calcified cartilage. To imitate this tide mark, a jagged interface was patterned between fully and partially converted regions of material #1, followed by in-diffusion and polymerization of material #2. The grayscale patterns were recapitulated in the hydrogel with high fidelity. These examples show the spatial control afforded by grayscale patterning that prescribe the ‘ON’ regions to support integration and the ‘OFF’ regions to prevent integration between two materials.

2.3. Demonstration of Spatial Control over Integration

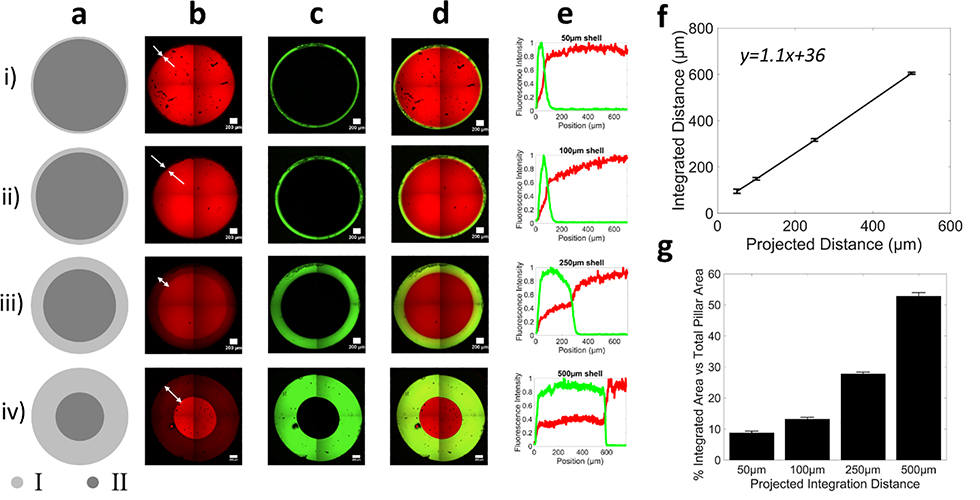
In the next series of experiments, the above findings were applied to design a grayscale illumination pattern to demonstrate deterministic control of spatially variable conversion in circular pillars for controlled integration of two materials. Material #1 was patterned into circular pillars that were 2mm in diameter with an inner core that was prescribed at 100% conversion and an outer shell that was prescribed at 13.5% conversion (Figure 4). The shell was designed to permit transport and integration of material #2 while the core was designed to prevent transport. This approach allows the core to maintain its overall mechanical properties, while the shell allows integration of the second material. The percentage area of the shell in the total column varied from 9% (0.5%) to 53% (1%), demonstrating a highly tunable approach to vary the core-shell diameters to control integration distances and maintain required mechanical stability (Figure 4g). Extended diffusion times (48 hours) were chosen to allow the precursors to diffuse fully into material #1 and reach equilibrium. The shell width, and hence integration distance, was patterned from 50 μm to 500 μm (Figure 4a-d). Representative fluorescent intensity line profiles for material #1 and material #2 illustrate the integration region where both red and green fluorescence overlap (Figure 4e). The distance over which material #2, after in-diffusing for 48 hours and photopolymerized, integrated into material #1 correlated to the prescribed shell pattern, (Figure 4f). The slope of the line in Figure 4f was greater than one, which is attributed to the swelling of material #1 in an aqueous solvent (i.e., PBS). Through simple spatial control over conversion, the distance of integration is readily tunable. This approach demonstrates that composite materials with pre-defined interfaces can be created on demand and in a single step during the printing process and without any additional fabrication steps.

Figure 4.

Grayscale illumination to spatially control the local properties of material #1 (red) to control integration of material #2 (green). a) Digital projected image of illumination pattern showing a core at high (~100%) and a shell at low (13.5%) conversion. Region I shell thickness is 50 μm in (i),100 μm in (ii), 250μm in (iii) and 500 μm in (iv) for 2 mm diameter hydrogel pillars. Representative confocal microscopy images of b) material #1, c) material #2, and d) the composite image. Representative confocal microscopy images were stitched from four images and it recapitulates the digital image. e) Line profiles of each fluorescence intensity across the integration region. In all cases, no integration is observed in the core. f) The projected distance for different shell patterns predicts the true thickness of the interfacial region. g) Percentage area of shell and core in the pillars, where the percentage integrated area corresponds to the shell area. Data are presented as mean with standard deviation as error bars for n=5.

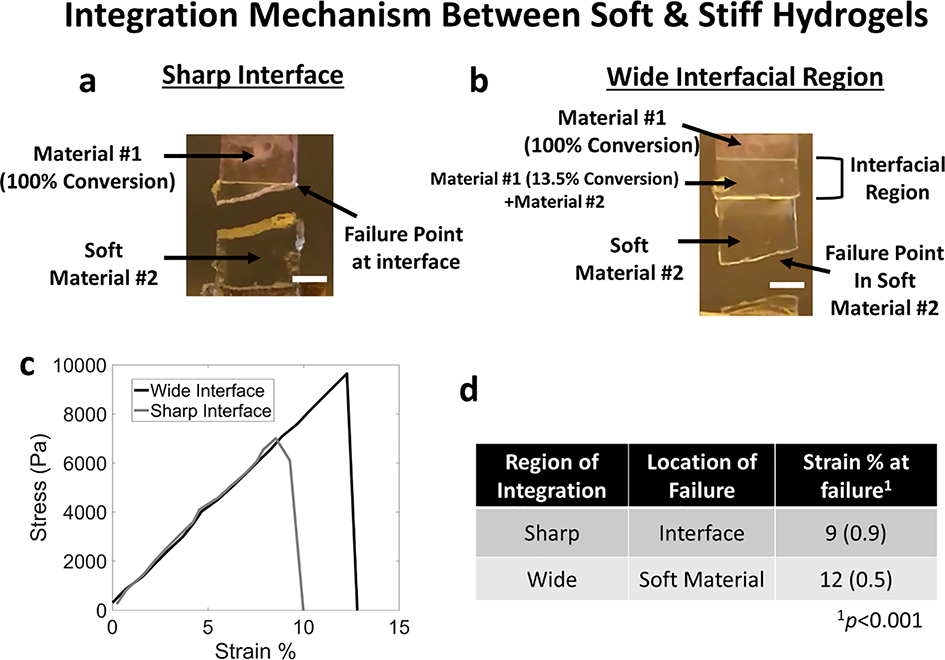
2.4. Characterization of the Failure of a Composite Material with Different Interfacial Properties

Mechanical failure of a composite material comprised of these two heterogenous hydrogel materials was probed as a function of their integration when pulled under tension to failure (Figure 5). In one case, a rectangular sample was designed with a sharp interface consisting of a 7-mm in length material #1, which was photopolymerized to 100% conversion followed by introducing material #2 and polymerizing again to create a 14-mm long sample. In the second case, material #1 was patterned with a 6-mm long region at 100% conversion adjacent to a 1-mm long region at 13.5% conversion. Material #2 was introduced, in-diffused for 48 hours, and photopolymerized to create 14-mm long sample. In the first case, the failure of the composite material occurred at the interface (Figure 5a). In the second case, failure of the composite material occurred in the soft material #2 (Figure 5b). Videos of the mechanical tests are provided in the Supplementary Information. The stress-strain plot for two samples of each condition is shown in Figure 5c. Samples with a prescribed sharp interface failed at a lower (p<0.001) strain [9% (0.9%)] when compared to a prescribed wide interface case [12% (0.5%)] (Figure 5d). We note that the wider interface also withstood higher peak stresses before failure when compared to the sharp interface. The results demonstrate that a prescribed interfacial region that interlocks two materials with divergent properties led to enhanced mechanical robustness across the interface and instead failure occurred in the weaker material (i.e., material #2).

Figure 5.

Tensile tests were performed to failure for a composite material composed of material #1 and #2 with (a) a sharp interface and (b) a programmed integrated region. Digital photographs are shown for a representative sample after failure. c) Representative stress vs strain plot for a composite material with a sharp interface (grey) or wide interface (black). d) Tabulated summary of findings. Data are presented as mean and standard deviation for n=3–4. Scale bar: 2mm

2.5. Demonstration of 3D control over Integration in 3D Printed Parts by SLA

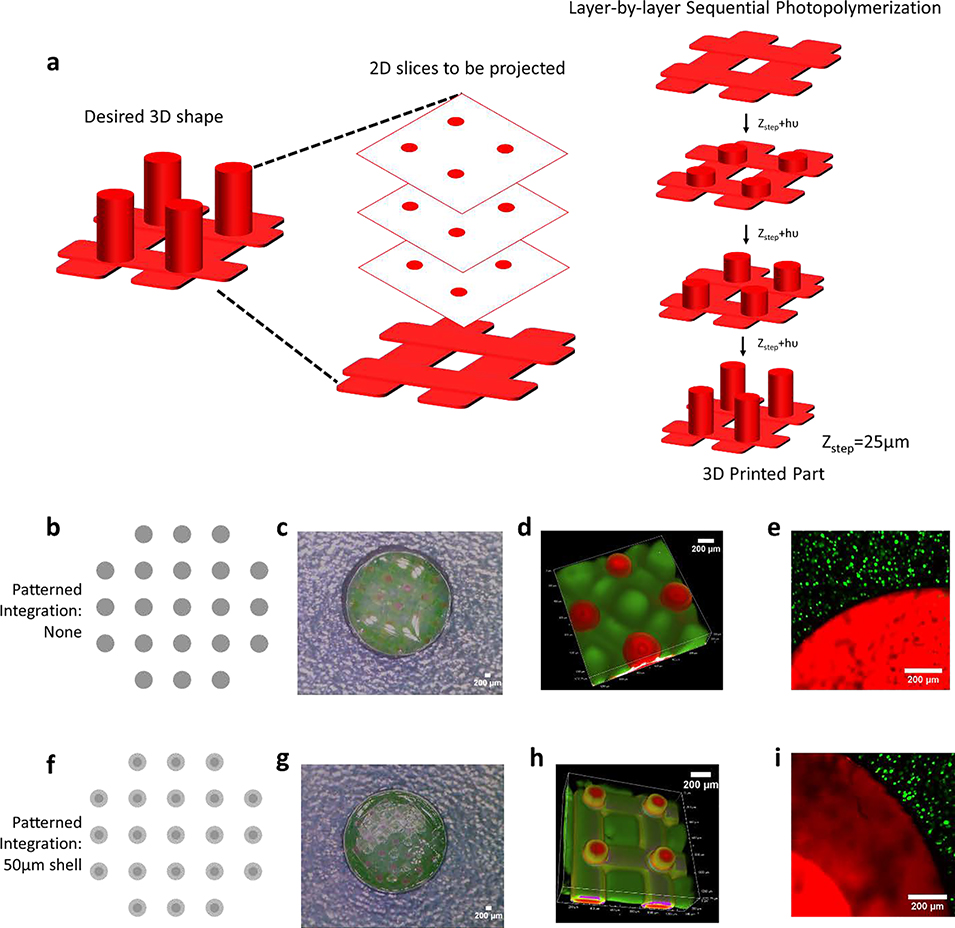
In the final series of experiments, to demonstrate the ability to apply these concepts to a 3D printed part, material #1 was printed using SLA and then infilled with material #2. Layer-by-layer printing was used to form a structure similar to Figure 1a, where two lattices of 125-μm thickness each were separated by cylindrical pillars of 200-μm diameter and 1.25-mm height (Figure 6a). We employed our recent dual cure approach that uses a thermal post-cure to achieve isotropic properties across each layer of the 3D printed parts.^[65] Two cases are shown to demonstrate control over integration in 3D. In the first, the exposure dose was spatially uniform across the 200-μm diameter printed pillars (Figure 6b-d). In the second, the 200-μm diameter pillars were printed with a 100-μm diameter high conversion core and 50-μm low conversion outer shell (Figure 6f-h). In both cases, in-diffusion of monomers of material #2 into the 3D printed part was followed by polymerization of material #2. The results demonstrate the ability to achieve either a sharp interface or wide (~100 μm) interfacial region between the two materials spanning three-orders of magnitude in stiffness (i.e., 40 MPa for material #1 and 53 kPa for material #2) within a 3D printed part.

Figure 6.

A 3D printed stiff scaffold structure (fluorescently labelled red) with soft infilled hydrogel (fluorescently labelled green). a) Schematic illustrating layer-by-layer printing. Top lattice not shown for clarity purpose. b) The scaffold includes a lattice base off of which pillars each with a diameter of 200μm, were patterned with material #1 either at high (100%) conversion (b-d) or with a 50μm shell of low (13.5%) conversion (f-g) shown by digital photograph, grayscale digital projected image, and confocal microscopy images. Cells encapsulated in material #2 is infilled into material #1 with (e) sharp interface and (i) wide interfacial region.

Lastly, we demonstrate feasibility of this approach for cell encapsulation towards applications in tissue engineering. After desired integration between the 3D printed part and material #2 is achieved, MC3T3-E1 pre-osteoblast cells were combined with the solution of material #2 precursors, and was subsequently infilled into the 3D printed part and then photopolymerized. The encapsulated pre-osteoblast cells had excellent cell viability with no observable adverse effects by introducing a region of integration into the 3D printed part (Figure 6e, 6i). The cells, which were localized to material #2, were uniformly distributed in material #2. This example demonstrates the ability to encapsulate cells in a soft hydrogel (i.e., material #2), which is then embedded in a stiff structure, thus providing enhanced mechanical support. Moreover, the patterned region enables integration between the two materials, achieving a robust interface that minimizes failure. Overall, we demonstrate control over integration distance, that reduces points of failure, while maintaining excellent cell viability.

This work investigated integration of two selected materials, one that is used to create a 3D printed material and one that is used as the infill, and that vary in mechanical properties. However, the principles described herein are readily adapted to a range of material properties and are not limited to the two materials investigated in this study. For example, the hydrogel mechanical properties for the soft hydrogel are easily tunable by varying the monomer concentration, molecular weight, and architecture (4-arm vs 8-arm PEG) and /or by changing the solvent content. In the thiol-ene hydrogel formulation used herein, changing the solvent content can result in moduli that span ~5kPa to ~250kPa.^[66,67] Under this scenario, the monomers themselves would not change and therefore their transport properties into the material #1 would be unchanged. Thus, the spatial patterning of material #1 used in this study to control ‘ON’ and ‘OFF’ diffusion of material #2 would apply to a wide range of properties for the soft material. More broadly, the methods described in this study are easily translatable to any material. A master curve (i.e., Figure 3b) can be generated for any material used in 3D printing. From this master curve, the printing parameters can be selected based on the ratio, $\frac{{\mathrm{r}}_{\mathrm{h}}}{\mathrm{\xi }}$, to prescribe a well-defined region in the 3D printed part that permits integration with the infilled material. Thus, we present an approach that can be adapted across a wide range of material properties (e.g., mechanics) that leverages the spatial control of 3D printing to prescribe regions of integration between two materials.

This study was motivated by the increasing demand for 3D printing in tissue engineering.^[68,69] In particular, 3D printed structures that are infilled with a cell-laden hydrogel enable the design of cell-laden hydrogel to be independent of the structural and/or mechanical needs of the scaffold for in vivo applications.^[39] For example, cartilage and bone require high modulus to support the mechanical forces applied during physical activity. However, scaffold environments that are conducive to differentiation and neotissue growth often require low modulus materials.^[59,70] Other examples of high moduli tissues include periodontal tissue engineering where 3D printing is being investigated.^[71,72] Applications such as skin, skeletal muscle, and blood vessels require high strength and elastic materials to recapitulate the tissues mechanical response in vivo,^[73] but these environments may not be optimal for promoting the desired cellular response.^[74] Beyond tissue engineering, applications such as soft electronics that also applies 3D printing to create composite materials, requires good integration between conductive inks and substrates.^[75] Ultimately for these composite materials to be functional in their intended application, integration of the 3D printed material part and its infilled material is critical to preventing failure at the interface and to their long-term success.

3. CONCLUSIONS

In summary, we describe a simple and highly tunable approach to create a region of integration between a 3D printed part and its infilled material. Spatial control over integration is achieved by controlling conversion of the resin during SLA-based 3D printing. A master curve was generated for this particular resin, linking the printing parameters (i.e., effective exposure dose) to mesh size. This approach can be applied to any resin and infilled material to spatially define regions for integration. Moreover, we demonstrate the feasibility for use in tissue engineering whereby cells can be readily entrapped into a soft hydrogel that is embedded into a stiff 3D printed structure. In summary, with the flexibility afforded by SLA, our approach can readily be extended to a variety of crosslinked polymeric materials with complex geometries and pave the way for new generation of materials with highly contrasting properties within a composite material for tissue engineering as well as other applications.

4. EXPERIMENTAL SECTION

4.1. Materials

Poly(ethylene glycol) diacrylate (PEGDA, MW=700 Da), a tetrafunctional thiol, pentaerythritol tetrakis(3-mercaptopropionate) (PETMP), the photoinitiator, diphenyl(2,4,6-trimethylbenzoyl) phosphine oxide (TPO), poly(ethylene glycol) dithiol (PEGdt, MW=1 kDa) were purchased from Sigma-Aldrich. The 8-arm PEG-amine (MW= 10 kDa) was purchased from JenKem USA. The photoinitiator, I2959, was obtained from BASF. PolyFluor 570, Methacryloxyethyl thiocarbamoyl rhodamine B was obtained from Polysciences Inc. AlexaFluor 488 C5 Maleimide was obtained from ThermoFisher Scientific. AlexaFluor 488 Carboxylic Acid, 2,3,5,6-Tetrafluorophenyl Ester, 5-isomer was obtained from ThermoFisher Scientific. Dulbecco’s phosphate buffered saline (PBS) was obtained from Corning. 2-(1H-7-azabenzotriazol-1-yl)-1,1,3,3-tetramethyluronium hexafluorophosphate methanaminium (HATU) was purchased from AK Scientific Inc. N,N-diisopropylethylamine (DIPEA), Dimethylformamide (DMF) and Dichloromethane (DCM) were purchased from Sigma-Aldrich

4.2. Material Preparation

Material #1 was formed from neat PEGDA 700 (98.95 wt%) and PETMP (1wt%) with TPO as the photoinitiator (0.05 wt%). Free-radical polymerization was initiated using 400–500nm light at prescribed intensities between 6.25 mW/cm² to 50 mW/cm². Fluorescent material #1 was formed by adding 0.1 mM rhodamine methacrylate to the precursor solution. Material #2 was formed from 8-arm poly(ethylene glycol) (10 kDa) endcapped with norbornene (5 wt%) (PEGNB) and PEGdt (stoichiometric ratio of 1 thiol to 1 ene) in PBS, I2959 as the photoinitiator (0.05 wt%) at 25 mW/cm² using a 320–500 nm light for 3 minutes. PEGNB was synthesized from 8-arm PEGamine that was reacted overnight, at room temperature under inert atmosphere with 5-norbornene-2-carboxylic acid with HATU and DIPEA in DMF/DCM. The PEGNB product was precipitated in diethylether and then filtered, dialyzed and lyophilized. Fluorescent monomers for material #2 were prepared by using AlexaFluor 488 C5 Maleimide (0.01 mM) for the PEGdt or AlexaFluor 488 TFP ester (0.01 mM) for PEGNB.

4.3. Material Property Characterization

The compressive modulus and swelling ratios of material #1 were measured at different light intensity and exposure times. Material #1 at different degrees of conversion were swollen to equilibrium in PBS and were subjected to unconfined compression at a constant strain rate of 0.02 mm/s with a 250 N load cell. Material #2 swollen to equilibrium in PBS were subjected to unconfined compression with a 10N load cell. The modulus reported is the slope of the stress vs strain curve between 10% and 15% strain. The equilibrium volumetric swelling ratios were determined from the equilibrium swollen mass, dry polymer mass after lyophilization, and the densities of the polymer and solvent. Crosslinking density,ρ_x and polymer-solvent interaction parameter, χ₁₂ were determined following methods described elsewhere that combine Flory-Rehner theory with theories of mixture and poroelasticity.^[63] The mesh size was estimated following Canal and Peppas,^[62]

$$\mathrm{\xi }={\mathrm{Q}}^{1/3}{\mathrm{C}}_{\mathrm{n}}^{1/2}{\mathrm{n}}^{1/2}\mathrm{l}$$ (2)

where Q is the equilibrium volumetric swelling ratio, C_n is the characteristic ratio of the polymer assumed to be 4^[76], l is the average bond length assumed to be 1.54 Å^[76] and n is the number of bonds between crosslinks, which was determined from the crosslinking density.

4.4. Fourier Transform Infrared Spectroscopy (FTIR)

Thermo Scientific Nicolet 6700 FTIR spectrometer equipped with simultaneous light irradiation was used to monitor real-time conversion in material #1. The precursor solution for material #1 was placed in 880 μm thick circular silicone mold with a diameter of 1cm and between glass slides. The disappearance of the peak associated with the carbon-carbon double bond in the acrylate at 6100 cm⁻¹−6200 cm⁻¹ was monitored over time under 400–500 nm light at a prescribed light intensity (6.25–50 mW/cm²) and exposure time and during dark polymerization. The area under the curve (6100–6200 cm⁻¹) before and after the light exposure was monitored and the conversion (C) as a function of time was calculated based on the disappearance of the acrylate by

$$C_{acrylate}=1-\frac{A_{final}}{A_{initial}}$$ (1)

The exposed sample was continued to be monitored under FTIR until dark polymerization ceased.

4.5. Digital Light Projection for SLA

A custom-built projection SLA system equipped with a LED (λ=405 nm, SOLIS-405C, Thorlabs) light source and spatial light modulator (1920×1152 Analog SLM, Meadowlark Optics) as the dynamic photomask was used. The optical resolution on the sample plane is 5 μm.

4.6. One dimensional (1-D) diffusion experiments

Rectangular PEGDA gels (20mmx5mmx1mm) were made between two glass slides to yield either partial conversion (13.5%) or full conversion (~100%) using the SLA system. The gel was maintained between the two glass slides and soaked in ethanol to remove unreacted monomers and then the reservoirs on either end of the hydrogel were filled with diH₂O for 48 hr at room temperature. Water swollen hydrogels were placed in a VersaDoc MP 4000 Molecular Imaging System (Bio- Rad; Hercules, CA) and one reservoir was replaced with either an aqueous solution of 0.01 mM Alexa Fluor 488 C5 Maleimide pre-reacted with 1 kDa PEG crosslinker or 0.01 mM Alexa Fluor 488 TFP ester pre-reacted with 10 kDa 8-arm PEGNB. Images were acquired at multiple time points. From these images, Image J was used to plot concentration profiles of fluorescence intensity as a function of distance into the gel. These profiles were fit to the solution of Fick’s second law in 1-D via the curve fitting tool in MATLAB (The Mathworks, Inc., Natick, MA) to extract approximate diffusivities for the two conversions investigated.

4.7. Mechanical failure testing

Rectangular samples (7 mm x 4 mm x 1 mm) of patterned material #1 were fabricated (Case 1: Material #1 was fully converted throughout, Case 2: Material #1 had a 1 mm patterned region of partial conversion (13.5%)). After the solvent soak in 70% ethanol for 48 hours and subsequent swelling in PBS, material #1 was immersed in the precursor solution of material #2 for 48 hours. Thereafter, material #2 was photopolymerized alongside material #1 to form a 14 mm x 4 mm x 1 mm rectangular composite sample for the interface testing. The composite samples with different levels of integration were superglued to thin cardboard pieces that were then held by the clamps. This was done to prevent slipping of the hydrated hydrogels at the clamp. The samples were subjected to a constant strain pulling rate of 0.1 mm/s applied by a mechanical tester to failure and force versus distance was measured. Videos were acquired during testing for Case #1 (Supplemental Video S1) and Case #2 (Supplemental Video S2). The initial and final frames of the video were separated into still photographs. Stress was determined by normalizing force to the cross-sectional area of material #1 after equilibrium swelling. Strain was determined from the initial length of the specimen exposed between the cardboard. The strain at failure, which is defined when the slope changes sign, i.e. at the peak stress value, was compared between the two conditions.

4.8. Imaging of composite materials

Patterned material #1 was soaked in 70% Ethanol for 48 hours followed by equilibrium swelling in diH₂O or PBS. Depending on the experiment, the precursor solution for material #2 was introduced either into one side of the reservoirs in the 1D experiment or by submerging the material #1 in the precursor solution of material #2. The submerged samples were later photopolymerized to lock the material #2 in place. The composite samples were swelled to equilibrium in diH₂O and then imaged. For the experiments in Figure 7b, images were acquired VersaDoc MP 4000 Molecular Imaging System. For all other experiments, images were acquired using confocal fluorescence microscopy (Zeiss LSM5 Pascal system) with a water immersed 10X objective lens. NIH ImageJ software was used to determine distances of overlapping fluorescence.

4.9. 3D printing overhanging structures using SLA

PEGDA 700 and PETMP were mixed at 99:1 wt% with 0.25 wt% TPO as a photoinitiator, 0.8 wt% Tinuvin1 CarboProtect1 as a photoabsorber and 0.05 wt% AIBN as a thermal initiator. The CAD design was composed of 200 μm diameter pillar structures connected by a lattice on top and bottom. Each pillar was composed of either a uniform grayscale of 149 or a 100 μm core of gray scale 149 and a 50 μm thick shell of gray scale 185 in order to vary intensity on the x-y plane. The irradiation intensity of gray level 149 was I = 30 mW/cm² and the intensity of gray level 185 was I = 10 mW/cm², as measured by a power meter (Model 2936-C, Newport) at λ=405 nm. The structure was sliced into sixty 25 μm layers to form a structure with a height of 1.5 mm before swelling. Each layer was exposed for 10 s. The bottom lattice was exposed for five layers creating a 125 μm thick lattice. The subsequent 54 exposures created the pillars, and the last layer exposed the lattice for the top, creating an overhanging feature of 125 μm in length. The structures were soaked in 100% ethanol after 3D printing for t = 1 min followed by placing in an oven at a temperature 105 +/−5 °C under vacuum for 1 h. Each construct was subsequently soaked in 70% ethanol for 48 hr.

4.10. MC3T3-E1 Cell Experiment

The murine pre-osteoblast cell-line, MC3T3-E1 was used. The cells were expanded in growth media (α-minimum essential media, Gibco) supplemented with 10% fetal bovine serum (Atlanta Biologics) and 1% Penicillin-Streptomycin (Corning) at 37°C and 5% CO₂. Cells were passaged at 90% confluency with 0.25% Trypsin-EDTA (Gibco). The cells (passage 6) were encapsulated in the soft hydrogel precursor solution, at 10 million cells/mL, infilled in the 3D printed structures and photopolymerized as described above. The cell-laden composite hydrogels were cultured in media (FBS, α-MEM, Pen-Strep) for 24hr. Live cells were stained using Calcein AM and visualized using confocal fluorescence microscopy. All procedures with cells were performed under aseptic conditions, inside biosafety cabinet using sterilized equipment. The 3D printed structures (material #1) were sterilized by soaking the structures in 70% ethanol overnight. All the precursors for material #2 were sterile filtered by passing it through a 0.22μm sterile filter.

4.11. Statistics

Statistical comparisons for compressive modulus between the two materials and the strain at failure for two different interfacial properties were preformed using an unpaired two-sample t-test assuming equal variance. Statistical comparisons for mesh size and the effect of projected distances on integration distances were performed using linear regression analysis. Data are reported by the mean with standard deviation presented parenthetically in the text after them or as error bars in the plots. Statistical significance was set at p<0.05 and p-values below this value are given to indicate the level of significance.