Abstract
A local disruption can propagate to forward and downward through the material flow and eventually influence the entire supply chain network (SCN). This phenomenon of ripple effect, immensely existing in practice, has received great interest in recent years. Moreover, forward and backward disruption propagations became major stressors for SCNs during the COVID-19 pandemic triggered by simultaneous and sequential supply and demand disruptions. However, current literature has paid less attention to the different impacts of the directions of disruption propagation. This study examines the disruption propagation through simulating simple interaction rules of firms inside the SCN. Specifically, an agent-based computational model is developed to delineate the supply chain disruption propagation behavior. Then, we conduct multi-level quantitative analysis to explore the effects of forward and backward disruption propagation, moderated by network structure, network-level health and node-level vulnerability. Our results demonstrate that it is practically important to differentiate between forward and backward disruption propagation, as they are distinctive in the associated mitigation strategies and in the effects on network and individual firm performance. Forward disruption propagation generally can be mitigated by substitute and backup supply and has greater impact on firms serving the assembly role and on the supply/assembly networks, whereas backward disruption propagation is normally mitigated by flexible operation and distribution and has bigger impact on firms serving the distribution role and on distribution networks. We further analyze the investment strategies in a dual-focal supply network under disruption propagation. We provide propositions to facilitate decision-making and summarize important managerial implications.
Keywords: Ripple Effect, Forward disruption propagation, Backward disruption propagation, Supply chain network, Resilience investment
1. Introduction
In today's tightly coupled supply chains, a disruption at either the supplier side or the customer side can easily wreak havoc across the entire supply chain network (SCN). During the COVID-19 pandemic, the global supply chains face both supply shortage and demand shrink which might lead to simultaneous or sequential forward and backward propagations of disruptions (Ivanov & Dolgui, 2020a; Queiroz, Ivanov, Dolgui & Fosso Wamba, 2020; Ivanov & Das, 2020; Paul & Chowdhury, 2020). For instance, the pandemic caused the operations suspension in China in February and March 2020, which further disrupted US and European manufacturers and retailers because of supply shortage (Ivanov, 2020a; Thomas, 2020). Additionally, the stay-at-home order during the COVID-19 pandemic has caused demand disruption to the travel and tourism-related industries. Then the disruption diffuses to airline companies, hotels, and restaurants and further negatively influences their associated supply companies (CRS Insight, 2020). The diffusion of an operational disruption beyond its origin and across the entire network is termed as disruption propagation (Basole & Bellamy, 2014; Bierkandt, Wenz, Willner & Levermann, 2014; Garvey, Carnovale & Yeniyurt, 2015; Scheibe & Blackhurst, 2018), also known as the ripple effect (Dolgui, Ivanov & Sokolov, 2018; Ivanov, Sokolov & Dolgui, 2014b; Ghadge, Dani, Chester, & Kalawsky, 2013).
The propagating effects make the impacts of a local disruption unpredictable, hence hard to prepare for and manage. Traditional supply chain risk management normally starts with risk identification and ends with different strategies to manage the identified risks (Craighead, Blackhurst, Rungtusanatham & Handfield, 2007). This approach is effective in coping with existing or anticipated disruptions, but less effective in handling abrupt or unexpected ones. For the latter, it is important for firms to build resilience that allows the firms to best prepare for, quickly respond to, and recover from unexpected disruptions (Chowdhury & Quaddus, 2017; Sawik, 2020; Yoon, Talluri, Yildiz & Ho, 2018; Dubey et al., 2019; Pettit, Fiksel & Croxton, 2010; Baghersad & Zobel, 2021). In practice, choosing the optimal level of resilience is a critical decision to make, as over-capacity incurs unnecessary costs while under-capacity exposes firms to risks (Fiksel, Polyviou, Croxton & Pettit, 2015).
A comprehensive understanding of supply chain disruption propagation and how it affects both individual firms and the whole supply chain can support various levels of decision-making in terms of resilience investment. From the preceding examples, disruptions can either propagate from the supplier side (forward disruption propagation), or the buyer side (backward disruption propagation) (Li & Zobel, 2020; Wenz, Willner, Bierkandt & Levermann, 2014). Also, in practice, mitigation strategies associated with disruptions from the supplier side and the demand side are distinctive. For example, Kroger provides additional distribution channels, such as the service of ordering online and curbside pick-up, and contracts with Instacart for grocery delivery service, to manage the demand disruption during the COVID-19 pandemic. Comparatively, to mitigate the supply disruption, firms normally increase stock level or look for substitute supply or backup suppliers.
Therefore, to effectively mitigate the disruption risks, it is critical to understand how different types of disruption propagation influence both the individual firm and the whole supply chain network. At the firm level, the impact of a local disruption varies with the firm's resilience and its position in the SCN. This causes differences in firm vulnerability across the supply chain. Understanding each firm's vulnerability level can guide proper firm-level resilience investment. At the network-level, the whole SCN performance is the integrated performance of individual firms inside the supply network, which can be measured by network health – the number of healthy (i.e., undisrupted) firms at a specific time point (Basole & Bellamy, 2014; Li & Zobel, 2020). Investigating how a local disruption affects the network health allows supply chain managers to allocate resources optimally across the SCN, effectively manage disruption propagation, and achieve better network performance.
Although the supply chain research has shown an increasing interest in disruption propagation (Basole & Bellamy, 2014; Dolgui et al., 2018; Marchese & Paramasivam, 2013), current literature is still limited in the following two aspects. First, the majority of current studies either focus on one specific direction of disruption propagation – forward propagation along the material flow (Bierkandt et al., 2014; Han & Shin, 2016) or backward propagation in a reverse direction of the material flow (Wenz et al., 2014) – or treat them with no difference (Basole & Bellamy, 2014; Li, Zobel, Seref & Chatfield, 2020). Although a limited number of studies have considered both forward and backward disruption propagation (Garvey et al., 2015; Hosseini & Ivanov, 2019; Ojha, Ghadge, Tiwari & Bititci, 2018) using the Bayesian network approach in a simple supply chain structure context, the forward and backward propagations remain diversely separately perspectives. As these two types of disruption propagation mechanisms are distinctive in practice, we are motivated to consider both directions of the ripple effect and examine their marginal and joint effects on firm and SCN performance from a complex network perspective. Second, despite the mature literature on supply chain resilience, very few studies have examined the interplay of resilience investment between dual focal firms that share a common supply base subject to risk and disruption propagation. Viewing firms embedded in a SCN, we address the research gaps by answering the following two research questions (RQs).
RQ1: How does forward and backward disruption propagation affect network-level health and node-level vulnerability?
RQ2: How can a focal firm's resilience investment in its SCN influence this focal firm itself and other focal firms in the network, given the existence of shared supply base?
To address these questions, we first introduce a theoretical framework that illustrates the disruption propagation mechanism, which articulates the interplay between node-level influencing factors, network structure, disruption propagation, and associated investments. In this framework, we identify the origins and mechanisms of forward and backward disruption propagation. As forward and backward disruption propagation are associated with distinctive mitigation strategies, differentiating them can support effective decision-makings, especially in limited resources. We use the agent-based simulation to model the disruption propagation behavior and then conduct multi-level quantitative analyses based on the simulation data. Our results show that the impacts of forward and backward disruption propagation, both on network-level health and node-level vulnerability, are distinctive and moderated by the network structure. Thus, to effectively mitigate the disruption, practitioners should consider the resilience capacities related to different types of disruption propagation and network structure. Additionally, we perform a game theoretical analysis to evaluate the influence of one focal firm's resilience investment on other focal firms. In contrast with the commonly used ego network, which includes only one focal firm, we investigate a supply network of dual focal firms that have commonly observed shared supply base (Wang, Li, Wu, & Anupindi, 2020). Our results show that examining the broader industrial network beyond a firm's ego network and enhancing supply chain visibility can support better decision-makings to mitigate disruption risks. In this sense, we extend the traditional “triad” structure (Choi & Wu, 2009) that has one buyer and two suppliers to two buyers and one shared supply base. The game theoretical analysis indicates that one focal firm's investment decision should consider the benefit-cost ratios of both its own and the other focal firm.
The remainder of the paper is organized as follows. Section 2 presents a review of the literature on supply chain disruption propagation. The disruption propagation mechanism is described in detail in Section 3. We design the experiment in Section 4. We perform the empirical analysis and provide the propositions derived from the results in Section 5. Section 6 summarizes the managerial implications. We conclude the paper with a discussion on the contributions and limitation in Section 7.
2. Literature review
Supply chain disruption propagation, also known as the ripple effect, has drawn increasing academic interest recently, due to the significant global economic loss caused by various disruption events such as the 2011 Thailand Flood, the 2012 Japan Earthquake, and the 2020 COVID-19 Pandemic (Ivanov, 2020a). Disruption propagation / ripple effect refers to that an operational failure at one entity of the SCN causes operational failures of other business entities (Dolgui et al., 2018; Ivanov, Pavlov & Sokolov, 2014a; Li & Zobel, 2020; Nguyen & Nof, 2019). This concept is different from the bullwhip effect (Dolgui, Ivanov & Rozhkov, 2020; Lee, Padmanabhan & Whang, 1997), as the bullwhip effect is triggered by small demand vulnerabilities but does not necessarily imply a severe operational failure (Chatfield, Hayya & Cook, 2013; Wang & Disney, 2016). Within the research scope of operational failure, there are studies on the ripple effect that mainly focus on downward disruption propagation from the supplier side (Ivanov, 2018; Ivanov et al., 2014b), the snowball effects where impacts can transmit and get amplified towards a larger number of firms in the supply chain (Swierczek 2016 ; 2014), the backward disruption propagation that means disruptional effects diffuse backwards opposite to the direction of the material flows (Wenz et al., 2014), as well as the general disruption propagation both from supplier and demand sides (Basole & Bellamy, 2014; Li & Zobel, 2020; Li et al., 2020; Zhao, Zuo & Blackhurst, 2019).
Various approaches have been adopted in the current studies on disruption propagation. First of all, modeling and simulation methods are widely used in this field (Ivanov, 2017; Macdonald, Zobel, Melnyk, & Griffis, 2018), including agent-based simulation from a complex network perspective (Basole & Bellamy, 2014; Li & Zobel, 2020; Li et al., 2020; Tang, Jing, He & Stanley, 2016; Zhao et al., 2019), investigating risk propagation using Bayesian network approaches (Garvey & Carnovale, 2020; Garvey et al., 2015; Hosseini & Ivanov, 2019; Hosseini, Ivanov & Dolgui, 2019; Ojha et al., 2018), numerical models to simulate indirect effects in the global supply chain using the input-output model (Bierkandt et al., 2014; Wenz et al., 2014), the entropy approach to study the vulnerability of cluster SCN during the cascading failures (Zeng & Xiao, 2014), and other operations research methods (Ivanov et al., 2014a; Kinra, Ivanov, Das & Dolgui, 2020; Liberatore, Scaparra & Daskin, 2012; Pavlov, Ivanov, Pavlov & Slinko, 2019; Sinha, Kumar & Prakash, 2020).
Second, there are qualitative studies investigating disruption propagation from different aspects. Ivanov (2018) and Dolgui et al. (2018) addressed the ripple effect, analyzed major recent publications, and delineated research perspectives in the domain. Scheibe & Blackhurst (2018) provided theoretical insights into the risk propagation using the grounded theory case study approach. Deng, Yang, Zhang, Li and Lu (2019), through a case study as well, explored risk propagation mechanisms and put forward the feasible countermeasures for perishable product supply chain to improve sustainability. At last, there are also several related empirical studies. Goto, Takayasu and Takayasu (2017) derived a stochastic function of risk propagation from comprehensive data of bankruptcy events in Japan from 2006 to 2015. Świerczek (2014) explored the relationship between supply chain integration and the snowball effect. Zhang, Chen and Fang (2018) surveyed 31 Chinese firms involved in the auto-industry and explored the transmission of a supplier's disruption risk along the supply chain.
The aforementioned studies have greatly enriched our understanding of the disruption propagation / ripple effect phenomenon. However, the literature falls short in two aspects. First, although a firm's operational failure can result from either its suppliers’ or customers’ disruption in practice, to the best of our knowledge, there are no recent studies considering the different impacts of forward and backward disruption propagation on the supply chain. A study considering both directions of disruption propagation is more comprehensive and realistic. Understanding disruption propagation comprehensively is crucial to the identification of effective techniques for supply chain risk management. Second, there are limited studies on the disruption propagation from a complex network perspective (Basole & Bellamy, 2014; Li et al., 2020). The majority of the current studies still focus on a simple supply chain structure, such as an ego network. Research based on simple structures could not fully grasp the interaction between the network structure and disruption propagation (Li et al., 2020; Mizgier, Jüttner & Wagner, 2013; Zhao et al., 2019). For example, studies based on a single firm's ego network ignore the influence of disruptions originated outside of the ego network.
Motivated by the research gaps, we study the forward and backward disruption propagation and contribute to the literature in the following aspects. First, this study comprehensively delineates the disruption propagation mechanism, which differentiates between forward and backward disruption propagation and identifies the influential factors in detail. In the analysis, we find that forward and backward disruption propagation influences node vulnerability and network health in distinctive ways. Thus, investment strategies to reduce both directions of propagation may differ significantly in practice. Second, this study investigates disruption propagation from a complex network perspective. Extending the traditional perspective of a firm's ego network, we examine a realistic industrial network with two focal firms. The industrial network more realistically reflects how network structure interacts with disruption propagation and how one focal firm should make resilience investment decisions subject to other focal firms’ actions. Based on the analysis of the industrial network, this study proposes to develop effective strategies for one focal firm to benefit from other focal firms’ resilience investment.
3. Modeling disruption propagation
Disruptions can diffuse along the material flow as well as in a reverse direction. Such a complex behavior of disruption propagation in the SCN can originate from simple interaction rules among firms. To capture the disruption propagation, we characterize the basic interaction rules first in this section.
3.1. Dyadic buyer-supplier relationship
In a dyadic buyer (j)-supplier (i) relationship, a disruption can diffuse either from a supplier to a buyer or from a buyer to a supplier. The forward disruption propagation refers to the disruption diffusion from supplier i to buyer j, along the material flow (Bierkandt et al., 2014). The rate of forward disruption diffusion, , is defined as the probability of a disrupted buyer at the time point t + 1 if the supplier is disrupted at time t. The forward disruption diffusion is a probability because one firm's disruption may not necessarily lead to another firm's disruption (Li & Zobel, 2020). For example, the same fire in Philips’ plant had almost no impact on Nokia but caused huge loss to Ericsson (Norrman & Jansson, 2004).
This rate of forward disruption diffusion is affected by the following factors.
-
-
The nature of the supplier's disruption. This includes the type, severity, and length of the disruption. For example, a disruption caused by cyber-attacks may influence the buyer differently from one caused by the adverse weather.
-
-
The dependence of the buyer on the supplier. If the buyer is highly dependent on the supplier (for example, the buyer sources the key components solely from this supplier), the buyer tends to be more easily disrupted by the supplier.
-
-
The buyer's resilience capacity. If the buyer has a higher resilience capacity such as the higher safety stock, better supply chain visibility, or a quicker response plan, it is less likely to be impacted by a supplier's disruption.
Comparatively, backward disruption propagation refers to the disruption diffusion from buyer j back to supplier i, which passes through the adverse direction of the material flow (Wenz et al., 2014). When the buyer suffers a disruption, the supplier may suspend its operations to avoid producing too many supplies that the buyer does not need. For example, when HP and Dell faced production disruption during the 2011 Thailand flood, the operations of Intel that is HP and Dell's supplier were also disrupted due to a lack of demand (Intel, 2011).
The rate of backward disruption diffusion, , is affected by the following factors.
-
-
The nature of the buyer's disruption, including the type, severity, and length of the disruption.
-
-
The dependence of the supplier on the buyer. If the supplier is highly dependent on the buyer (for example the majority of the supplier's revenue comes from the buyer), the supplier tends to have a higher disruption diffusion rate from the buyer's disruption.
-
-
The supplier's resilience capacity. The higher resilience capacity the supplier has (such as higher operational flexibility and supply chain visibility), the supplier is less likely to be impacted by the buyer disruption.
Forward and backward disruption propagation differ in two main aspects. First, the disruption propagation rates are different as the resilience capacities against forward and backward disruption propagation are distinctive. The resilience capacity against backward disruption propagation mainly relies on its operation and distribution flexibility, while the resilience capacity against forward disruption propagation largely depends on the availability of substitute resources. Second, the dependence between the buyer and the supplier is mostly asymmetric in reality. For example, a small supplier whose major business comes from Walmart is highly dependent on Walmart, but not vice versa. Based on these differences, forward and backward disruption propagation should be modeled and evaluated differently to provide better decision-making to improve supply chain resilience.
3.2. Node status transition probability
In a directed SCN with multiple suppliers and buyers, the disruption probability of one particular business entity depends on its relationship with all disrupted neighbors, including both suppliers and buyers. We assume every node in the SCN has two states, namely healthy (H) and disrupted (D). The disruption status of a node means that the firm suspends its operations due to reasons including but not limited to inventory stockout, labor strike, extreme weather and earthquakes. There is uncertainty that a healthy node i at time t can become disrupted at time t + 1 under the influence of its disrupted suppliers and buyers at time t. For example, a firm with ample safety stock that faces a supplier disruption may less likely become disrupted than a firm with a low safety stock level. To take this into consideration, we model the status transition as a probability.
For a firm with multiple disrupted neighbors, we assume the disruption impact from suppliers and buyers are independent. We acknowledge that this assumption cannot grasp the full picture, as the impacts of disruptions may be interdependent in practice (Ackermann, Howick, Quigley, Walls & Houghton, 2014; Garvey & Carnovale, 2020; Garvey et al., 2015; Qazi, Quigley, Dickson & Ekici, 2017). However, the assumption of independence also provides two main benefits. First, this assumption holds in many real cases, so the derived results have important practical implications. For instance, a firm has several suppliers who have their own manufacturing. The quality of the suppliers’ products (i.e., components) determines the final product quality. As the quality of one product is not affected by other suppliers’ products, disruption impacts from suppliers are independent in this sense. Second, this assumption is widely used in the risk management literature (Qazi et al., 2017; Zhao & Freeman, 2019), as it makes the model tractable. If the risk dependence estimation becomes complicated and difficult, more errors can occur, and relying on incorrect estimation can be costly in practice (Zhao & Freeman, 2019). Future studies can build on and relax the assumption of independence. In this way, for a given node, the transition probability from healthy status to disrupted status is:
| (3.1) |
where stands for node i’s transition probability from being healthy at time t to being disrupted at t + 1; and stands for disrupted suppliers and disrupted customers of node i, respectively; represents the probability of forward propagation from supplier k to node i at time t; and indicates the probability of backward propagation from customer j to node i at time t.
A disrupted node can recover and become healthy. Let be the recovery probability of node i from being disrupted at time t to being healthy at time t + 1, regardless of the statuses of suppliers and buyers. Assuming the recovery is independent from the influences of suppliers and buyers, we model the transition probability of node i from being disrupted at time t to being healthy at t + 1 as:
| (3.2) |
Formula (3.2) implies that when some of its suppliers and buyers are disrupted, supplier i’s ability to recover will be discounted, and its recovery process will slow down.
3.3. Disruption propagation mechanism
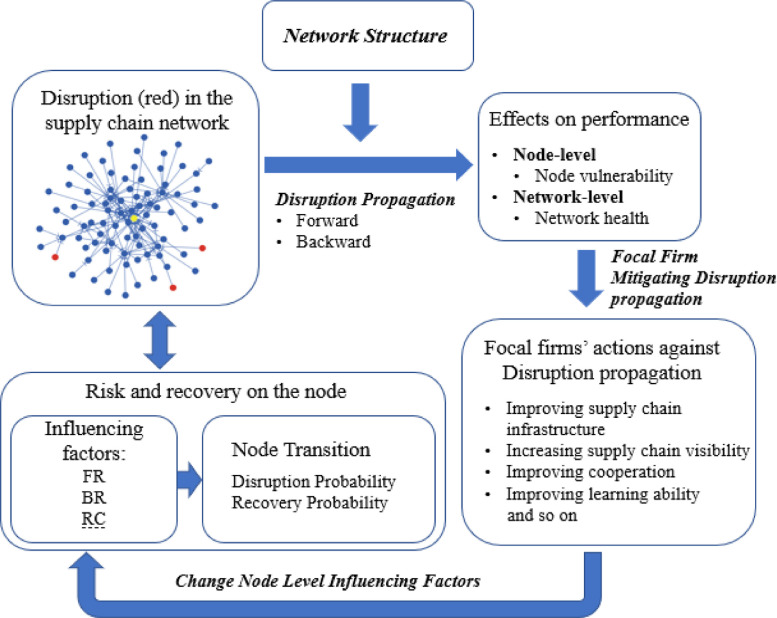
The complex disruption propagation behavior within the SCN emerges from the aforementioned interaction rules among nodes. Fig. 1 depicts the disruption propagation mechanism. Each individual node has its own specific FR, BR, and RC values based on its dependency with the neighbors and its resilience capacity. These node-level influencing factors interact with the network structure, determine the nodes’ transition probabilities, and ultimately shape the disruption propagation across the SCN.
Fig. 1.
Disruption propagation mechanism.
Disruption propagation exerts effects on both node and network levels. At the node level, some nodes have more frequent disruptions than others during the disruption propagation process. Supply chain managers should therefore be more concerned with those nodes. At the network level, the disruption varies with and is moderated by different node-level factors and the network structure. Given a network structure, supply chain managers can control and mitigate the disruption propagation at both node and network levels through proper investment that can change node-level factors of FR, BR and RC. Based on the framework, we investigate the impacts of disruption propagation at both node and network levels by designing experiments that interact node-level factors with the network structure in the next section.
4. Experimental design
The purpose of this study is to investigate how FR and BR influence the ripple effect differently. Given a SCN , consisting of the Set of nodes and of directed edges. Each node has two possible status: 1 represents healthy and 0 represents disrupted. The transition probability of each node is determined by the current status of itself and all of its neighbors’ current status as Eq (3.1) and Eq (3.2). To formulate such a problem, the model is set up as locally interacting Markov chains, also known as probabilistic cellular automata (PCA) (Fernández, Louis & Nardi, 2018). The state space of such a model is the tensor product of the statuses of all the local Markov chains, which is huge in our context. For example, for an individual node with 3 suppliers and 2 customers, there are in total combinations of statuses. Enumerating the transition probabilities for all the possibilities is challenging. This might work for a small sized network, but it will eventually become infeasible when the size or complexity of the network grows (Garvey & Carnovale, 2020). In fact, the area of PCA acknowledges its complexity and suggests that it is used as a flexible modeling, such as agent-based modeling, and simulation framework in an applied context (Fernández et al., 2018).
Therefore, we implement agent-based simulation (ABS) in this study for the following benefits. Firstly, ABS allows us to re-create and predict the performance of complex systems or phenomenon through simulating the simultaneous interactions of agents (Basole & Bellamy, 2014; Li & Zobel, 2020; Zhang, Adomavicius, Gupta & Ketter, 2020), and the SCN is such a complex system. Second, ABS allows us to explore and investigate separate effects of factors and interactions among factors through numerical experiments under a variety of settings (Zhang et al., 2020). Moreover, ABS provides a visual and easy-to-understand approach that both researchers and practical audience can comprehend, which leads to a broader practical prospect of application. This approach can also be extended to other purposes. For example, it can easily extend to the heterogeneous setting of FR, BR and RC to observe the behavior of a detailed SCN.
To explore the disruption propagation within the SCN, we conduct our main analysis using the Japan automotive industry SCN with two focal firms. To make sure the findings can apply to boarder types of networks, we generate two comparable random networks as the robustness check. Compared with studies using one focal firm's ego network, our setup allows us to compare the impacts of disruption propagation on different focal firms, as well as other entities inside the SCN.
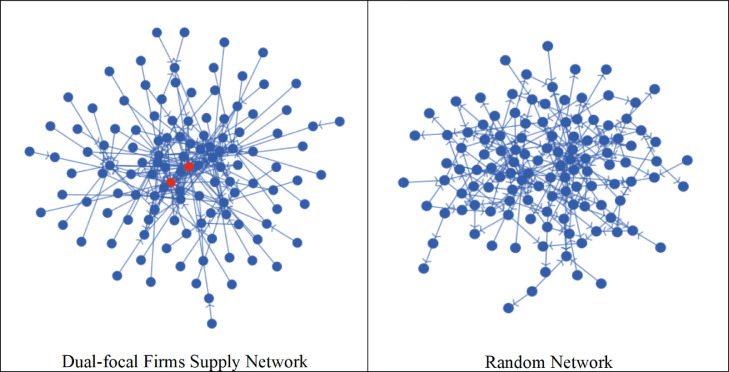
We choose Honda and Toyota as the focal firms. Both of them are the largest automobile makers in Japan. Their supply chains are typical and highly interacting complex networks exposed to various disruption risks (Wagner and Bode, 2006, Wagner and Bode, 2008). We construct the supply network using the Bloomberg SPLC database and select the first- and second-tier suppliers of the focal firms. We select only COGS (Cost of Goods Sold), which refers to direct costs of producing the goods sold, relationships where the percentage of COGS is over 0.5%, in order to get the most significant material flows. This gives us a network with 121 nodes and 193 links. There are 63 common suppliers at both tiers 1 and 2 for Toyota and Honda. Fig. 2 illustrates this network where the two red nodes stand for the two focal firms.
Fig. 2.
Dual-focal firms supply network and random network.
We conduct experiments on the automobile supply network to discover how the node-level factors result in the disruption propagation and cause disruption at both node and network levels. “Experimentation is a powerful methodology that enables researchers to establish causal claims empirically” (Imai, Tingley & Yamamoto, 2013). By designing and implementing experiments, we are able to mitigate the concern of endogeneity (Antonakis, Bendahan, Jacquart & Lalive, 2014), which is usually a challenging of causal inference in studies using observational data (Ho, Lim, Reza & Xia, 2017). In this study, we integrate experimental design with the agent-based simulation to obtain the data for analysis. Agent-based simulation is capable to simulate interactive agents’ behaviors in an attempt to understand complex phenomena (Basole & Bellamy, 2014; Li et al., 2020; Nair & Vidal, 2011; K. Zhao et al., 2019).
For the simulation, we set the initial disruption probability at 5%, which indicates the initial disruption is small and regional. For the node-level influencing factors, we focus on the aforementioned forward disruption diffusion rate , backward disruption diffusion rate , and recovery rate . Due to companies’ distinctive resilience capacities and different dependency levels between firms, disruption propagation varies by firm, time, and network in reality. However, we assume a homogeneous setting in which the values of the three parameters , , and are constant across agents and over time in our analysis. This is because although heterogeneous local settings can provide more accurate estimation of one particular case, it also offsets general findings of these influencing factors. As our main research objective is to investigate how these factors influence disruption propagation, we assume homogeneous node-level factors to avoid noises of other factors (Li & Zobel, 2020). Therefore, we denote , , and by , , and . Based on formulas (3.1) and (3.2), for a node that has n disrupted suppliers and m disrupted customer, the integrated disruption probability at time t is for a healthy node, and the recovery probability at time t is for a disrupted node.
We conduct a full factorial design. The value combinations of FR, BR, and RC serve as experiment treatments. We control over the parameters as listed in Table 1 . The parameter settings represent three different levels for each parameter: low, medium, and high. The networks receive one treatment condition at a time. To control for the impact of the random disruption, we conduct each experimental run of a treatment condition 50 times. Each time we collect the status of each node (disrupted or healthy) at every time point. By averaging across the 50 times, we obtain node-level vulnerability and network-level health defined in Section 5.
Table 1.
Parameters in the analysis.
| Parameter | Associated Investment Examples | Setting |
|---|---|---|
| FR | Increasing safety stock Increasing supply chain visibility Increasing backup resources |
{0.2, 0.5, 0.8} |
| BR | Increasing production flexibility Effective demand management efforts Increasing supply chain visibility |
{0.2, 0.5, 0.8} |
| RC | Implementing effective risk mitigation plan | {0.2, 0.5, 0.8} |
In addition to the main analysis, to increase the robustness of the findings, we create two random networks with the same number of nodes and links and compare their results to the results of the Japanese automotive industry network. We find the results of the two random networks are consistent with each other. For the simplicity of presentation, we only report results of one random network. Fig. 2 shows the plot of the reported random network.
5. Analysis and discussion
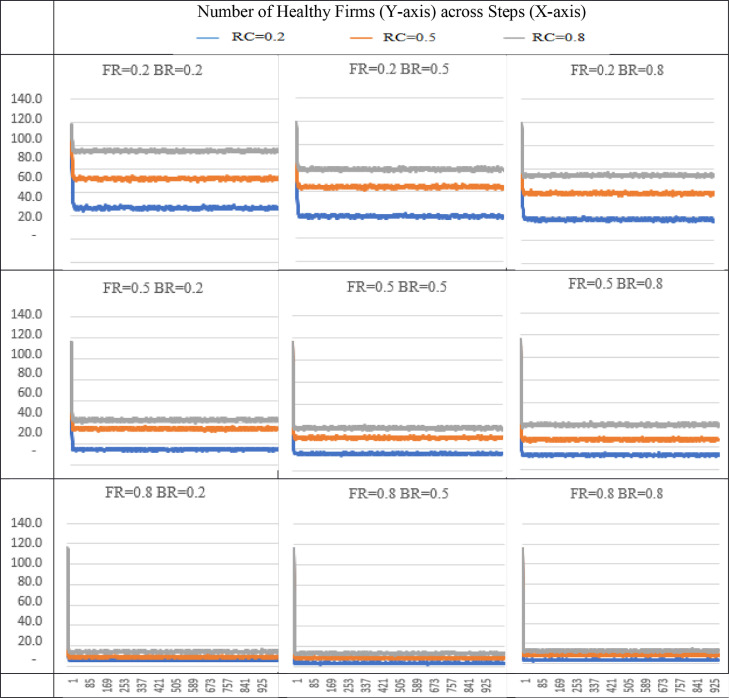
To begin, we visualize the network-level disruption propagation behavior in Fig. 3 using the number of healthy firms (Basole & Bellamy, 2014) with respect to different settings of parameters. We set the max period to be 1000, which is long enough for disruption propagation to reach a steady state.
Fig. 3.
Visualization of disruption propagation.
From Fig. 3, first, we can observe that a small initial disruption can cause significant turmoil in the whole supply chain network. With an initial disruption probability at p = 0.05, the number of healthy nodes decreases in all scenarios. This means that more firms become disrupted after the initial disruption. Second, the number of healthy nodes becomes steady after around 50 steps, which signifies that, for a given set of parameters, the disruption propagation tend to reach a steady state after a fixed number of periods (Basole & Bellamy, 2014). Thus, in the following analysis, we only focus on the steady state found from time stamps 101 to 1000. Third, as expected, both forward and backward disruption diffusion rates are negatively associated with the number of healthy nodes, and the recovery rate is positively associated with it. However, it is still unclear how these influencing factors interact with the network structure to determine the performance of the supply chain and individual firms. It is also unclear how the resilience investment can improve the supply chain performance. To explore these questions, we conduct the following analyses.
5.1. Network-level performances
First, we investigate how the node influencing factors determine the SCN performance. We use two network-level ripple effect performances: network health and propagation period. Network health describes the overall health status of the SCN. We follow Basole and Bellamy (2014) and measure it using the number of healthy nodes at the stable status, which is operationalized as the average number of healthy nodes from step 101 to 1000 in our case. Propagation period is the number of periods the SCN used to disperse the disruption risks to a steady status, which describes the propagation speed that lower propagation period means quicker propagation speed.
To rigorously demonstrate the effects of node-level influencing factors on network health and propagation period, we perform the OLS regression analysis using the model 5.1.1 and model 5.1.2. The dependent variable, network health or propagation period, has been log-transformed to conform to the OLS regression assumptions. To mitigate multi-collinearity due to the interaction effects, we have standardized the independent variables in the analysis. The variance inflation factors (VIF) analysis reveals that VIFs for all variables (including the interaction terms) are below 4, which is lower than the critical value of 10 (Kutner, Nachtsheim, Neter & Li, 2005), indicating that multicollinearity is not a concern.
| (5.1.1) |
| (5.1.2) |
The subscript i stands for each observation. Table 2 shows the results.
Table 2.
Regression results for the automotive industry network and random network.
| Dependent Variable | Network Health |
Propagation Period |
||
|---|---|---|---|---|
| (Auto Industry Network) | (Random Network) | (Auto Industry Network) | (Random Network) | |
| Model (1) | Model (2) | Model (3) | Model (4) | |
| FR | −0.062*** | −0.656*** | −0.930*** | −6.001*** |
| (0.006) | (0.009) | (0.208) | (0.458) | |
| BR | −0.839*** | −0.667*** | −5.427*** | −7.037*** |
| (0.006) | (0.009) | (0.208) | (0.458) | |
| RC | 0.413*** | 0.535*** | −2.899*** | −1.183** |
| (0.006) | (0.009) | (0.208) | (0.458) | |
| Constant | 3.114*** | 2.759*** | 11.902*** | 18.026*** |
| (0.006) | (0.009) | (0.187) | (0.412) | |
| Obs. | 1350 | 1350 | 1350 | 1350 |
| Adj. R2 | 0.949 | 0.917 | 0.389 | 0.220 |
| F Stat | 8620.4*** | 4958.4*** | 299.2*** | 138.1*** |
Standard errors in parentheses.
* p < 0.05, ** p < 0.01, *** p < 0.001.
For this auto supply network, we find that backward risk diffusion rate reduces supply network health and propagation period (equivalent to increase propagation speed) at a higher rate than forward risk diffusion rate, as the absolute value of the coefficient of is much higher than that of . To demonstrate the significant difference between the coefficients of and , we conduct a linear hypothesis test (F-test, null hypothesis: ). The result supports the significant difference between the effects of and (F = 10,845***, df = (1, 1342)). Although this result is based on one specific SCN, it indicates that it is necessary and important to separate backward and forward disruption diffusion rates when investigating the impacts of the disruption propagation behavior. From a practical perspective, evaluating their impacts separately can support effective decision-making as investments on decreasing forward disruption diffusion can be very different from decreasing backward diffusion. Thus, we formulate the following proposition:
Proposition 1a
Forward and backward disruption propagation can reduce supply network health at different rates.
Proposition 1b
Forward and backward disruption propagation can increase propagation speed (decrease propagation period) at different rates.
We conduct further analysis to look into the reasons that make the impacts of and vary. As the settings of and are the same, the firm disruption probability and recoverability is determined by the number of disrupted suppliers n and the number of disrupted customers m at each period. While the number of disrupted suppliers and customers largely depend on the network structure, we believe this difference in effects, both for network health and propagation period, may come from the network configuration. With this in mind, we compare the results of the automobile industry network with the results of the comparable random network. Table 2 also shows that for the random network, the coefficients of and are very close, which indicates the impacts of and are not differentiable.
The auto supply network is a typical supply network with the characteristic that a majority of nodes have higher out-degree than in-degree and very few nodes has higher in-degree than out-degree. Thus, the majority nodes are subject to higher impacts of and few nodes are subject to higher impacts of . As a result, the overall supply network is subject to higher impacts from than . Comparatively, the random network has most nodes with balanced in-degree and out-degree, so the impacts of and on the network are similar. Thus, we can derive the difference in the impacts of and comes from the network configuration, which is the distribution of in-degrees and out-degrees across nodes in the network. In general, a typical supply network is subject to higher impact of , a balanced network such as random network is subject to balanced impact of and , and a typical distribution network is subject to higher impact of . Below we propose the following.
Proposition 2a
Network configuration, i.e., the distribution of in-degrees and out-degrees across nodes in the network, leads to different effects of forward vs. backward disruption propagation on network health.
Proposition 2b
Network configuration, i.e., the distribution of in-degrees and out-degrees across nodes in the network, leads to different effects of forward vs. backward disruption propagation on propagation speed.
5.2. Node-Level vulnerability
In practice, supply chain managers not only concern about the performance of their supply networks, but also pay great attention to the performance of individual suppliers. In this section, we use node vulnerability to describes how vulnerable an individual node is when exposed to disruption risks inside the SCN. In a specific network, some firms are more vulnerable than others, thus the supply chain manager should be more cautious of the vulnerable nodes and make proper investment to decrease their vulnerability. In our context, we measure node vulnerability as the percent of disrupted periods for a node after disruption propagation becomes stable.
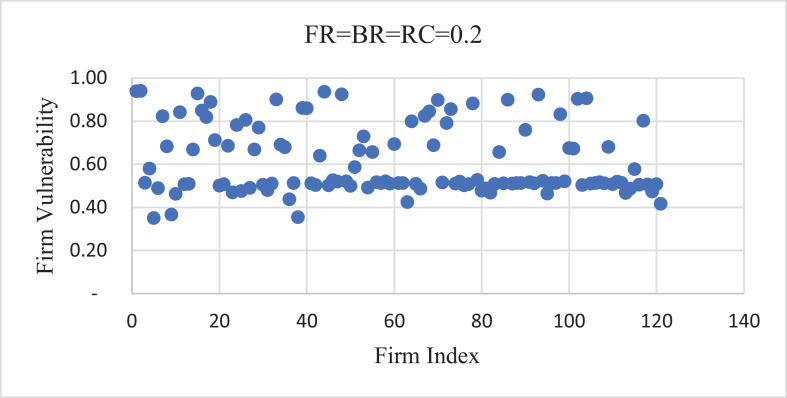
Fig. 4 depicts the overlay plot of node vulnerability when , where the dots stand for suppliers. Fig. 4 shows that some firms have higher vulnerability than other firms for this particular network in the scenario. Examining other scenarios of different values of FR, BR and RC, we find that the variation of node vulnerability is not in a consistent scale, that is, the variation of node vulnerability is high in the scenario of high FR and BR. Nonetheless, we find some nodes are consistently vulnerable across all scenarios. Table 3 lists the firms whose vulnerability is above 90% of all the scenarios, as well as their centrality information. Compared with the average degree of the supply network that is 1.60, average betweenness centrality of 30.24, and average closeness centrality of 0.369, these highly vulnerable firms have higher centrality measures in the supply network. Considering that the scale of node vulnerability varies at different scenarios, we conjecture that node position in the network and node-level influencing factors can interact and affect node vulnerability.
Fig. 4.
Firm vulnerability scatter plot.
Table 3.
Most vulnerable firms list.
| Company name | Number of Scenarios this company has high vulnerability (>90%) (Total 27 scenarios) |
In-Degree | Out-Degree | Betweenness-Centrality | Closeness-Centrality |
|---|---|---|---|---|---|
| Toyota Motor Corp | 27 | 22 | 5 | 1009 | 0.5 |
| Honda Motor Corp | 27 | 23 | 2 | 204.8 | 1 |
| Daihatsu Motor Corp | 27 | 21 | 1 | 149 | 0.3409 |
| Denso Corp | 27 | 7 | 7 | 177.9 | 0.5357 |
| Nippon Steel & Sumi | 27 | 14 | 3 | 270.3 | 0.4545 |
| Toyoda Gosei Corp | 24 | 7 | 8 | 584.9 | 0.5769 |
| Mitsui OSK Lines | 20 | 10 | 2 | 221 | 0.3409 |
| JTEKT Corp | 20 | 6 | 3 | 57.3 | 0.4286 |
Identifying the most vulnerable firms and understanding what contributes to the node vulnerability can support decision-making against disruptions in practice. For a given SCN, changing a node's centrality is usually difficult, especially in a short time frame, as the centrality is determined by the node's market position, business nature, and competitor status. In this sense, to decrease the node vulnerability, supply chain managers can and are more interested in adjusting node-level influencing factors that interact with the centrality to affect node vulnerability. This requires us to understand how node-level influencing factors interact with the network structure to impact the node vulnerability.
We investigate the following OLS regression model and present in Table 4 the results of both the auto industry network and a random network. In this analysis, we introduce two new variables to describe the node position in a network. The first variable is total degree () as the measure of centrality. A robustness check shows the results using are consistent with those using betweenness or closeness centrality. The second variable is degree difference (), which describes the net flow direction of the node. A positive means higher in-flow and negative means higher out-flow.
Table 4.
Regression results for node vulnerability analysis.
| Dependent Variable | Node Vulnerability (Auto Industry Network) |
Node Vulnerability (Random Network) |
||
|---|---|---|---|---|
| Model (5) | Model (6) | Model (7) | Model (8) | |
| FR | 0.026*** | 0.026*** | 0.142*** | 0.142*** |
| (0.003) | (0.002) | (0.003) | (0.003) | |
| BR | 0.222*** | 0.222*** | 0.152*** | 0.152*** |
| (0.003) | (0.002) | (0.003) | (0.003) | |
| RC | −0.100*** | −0.100*** | −0.116*** | −0.116*** |
| (0.003) | (0.002) | (0.003) | (0.003) | |
| TD | 0.220*** | 0.220*** | 0.122*** | 0.122*** |
| (0.005) | (0.005) | (0.003) | (0.003) | |
| DD | −0.103*** | −0.103*** | −0.007* | −0.007** |
| (0.005) | (0.005) | (0.003) | (0.003) | |
| FR * TD | 0.009 | −0.024*** | ||
| (0.005) | (0.003) | |||
| BR * TD | −0.079*** | −0.006* | ||
| (0.005) | (0.003) | |||
| FR * DD | −0.0002 | 0.045*** | ||
| (0.005) | (0.003) | |||
| BR * DD | 0.021*** | −0.046*** | ||
| (0.005) | (0.003) | |||
| Constant | 0.618*** | 0.618*** | 0.699*** | 0.699*** |
| (0.003) | (0.002) | (0.003) | (0.003) | |
| Number of observations | 3267 | 3267 | 3267 | 3267 |
| Adj. R2 | 0.790 | 0.828 | 0.708 | 0.755 |
| F Statistic | 2452.3*** (df = 5; 3261) |
1749.5*** (df = 9; 3257) |
1582.5*** (df = 5; 3261) |
1118.1*** (df = 9; 3257) |
Standard errors in parentheses.
* p < 0.05, ** p < 0.01, *** p < 0.001.
Table 4 clearly shows that both node-level factors and node position contribute to the node vulnerability. Specifically, nodes with higher centrality () tend to have higher vulnerability. Forward and backward disruption diffusion rates (FR and BR) positively impact node vulnerability. Recovery rate (RC) negatively influences node vulnerability. Besides, there is another interesting observation that the impacts of forward and backward risk diffusion rates on node vulnerability vary by the degree difference . A node with a positive is more serving as an assembly role in the network, and then its vulnerability is more due to forward propagation (coefficient of is positive). Practically, firms who play an important assembly role have more connections with suppliers than with customers. Thus, those firms are more vulnerable to disruption propagation from the supplier side than from the customer side. Therefore, to decrease the vulnerability, they should increase the safety stock level, build close relationships with suppliers, and invest in backup resources against forward disruption propagation.
Comparatively, a node with a negative has more links with customers and is more like to fulfill the tasks of distribution in the network. Thus, its disruption mostly stems from backward propagation (coefficient of is negative). These firms should invest in monitoring market information closely and increasing production and operation flexibility against backward disruption propagation. Based on the above analysis, we present the following propositions.
Proposition 3
Node-level influencing factors and the node's structural position in the supply network can interact and contribute to the node vulnerability.
Proposition 4a
A node with a positive degree difference (higher indegree than outdegree) is affected more by forward disruption propagation than by backward propagation. Nodes with positive degree differences (out-degree higher than in-degree) should invest in alternative supply and sourcing.
Proposition 4b
A node with a negative degree difference (higher outdegree than indegree) is affected more by backward disruption propagation than by forward propagation. Nodes with negative degree differences (out-degree lower than in-degree) should invest in operational and product flexibility.
5.3. Resilience investment
The purpose of understanding disruption propagation is to support effective decision-making of resilience investment against disruptions. In practice, the network-level resilience investment is usually initiated by focal firms, such as improving supply chain infrastructure, enhancing supply chain visibility, and improving cooperative and learning abilities. Such kinds of investment can influence , and on every node inside the focal firm's ego network. In a dual-focal supply network, one focal firm's investment can influence both itself and the other focal firm, because of the existence of the shared supply base. Thus, the investment decision of one focal firm may be subject to the influence of the other focal firm. In this section, we aim to discover how the investment of one focal firm influences itself, the other focal firm, and the overall SCN health. Then we discuss the implications about investment decisions of focal firms in a competitive environment.
We consider three types of investment: Honda-initiated investment, Toyota-initiated investment, and collaborative investment. The Honda- and Toyota-initiated investment only influences the suppliers in their own ego supply chains, whereas the collaborative investment requires the collaboration of both focal firms and can influence the whole auto industry supply network. We set up a benchmark setting of . Under this setting, there is enough room for improvement (i.e., to reduce FR and BR) from the perspectives of both network and individual nodes. We assume the investment can decrease forward and backward disruption diffusion rates in the same pattern. For a given investment level, we have and . The investment level ranges from 0 to 1.
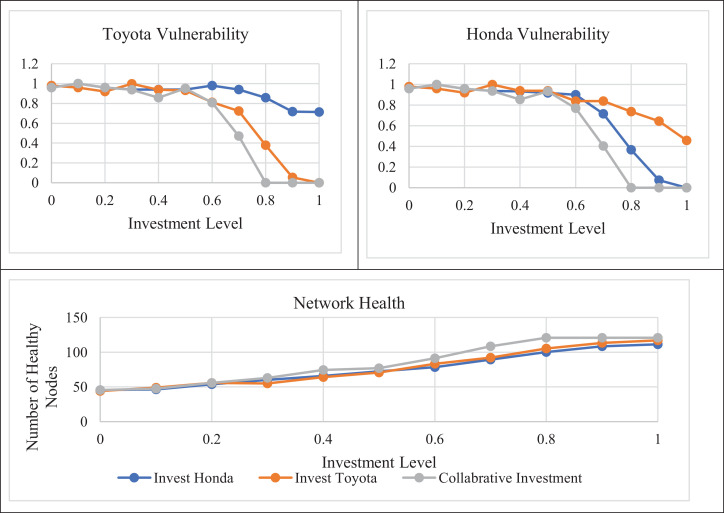
Our numerical results are shown in Fig. 5 , which depicts how different investments influence the focal firm's vulnerability and the health of the whole supply network. From the perspective of network health, there is little difference between benefits from a Honda initiated investment and from a Toyota initiated investment. Unsurprisingly, the collaborative investment has better performance than Honda or Toyota initiated investments, even though the marginal benefits vary by investment levels. From the perspective of focal firms, both Honda and Toyota can benefit from the other focal firm's investment, no matter whether they choose to invest in their own ego supply networks. This benefit comes from the fact that they have common suppliers. Thus, one focal firm's investment can affect the disruption diffusion rates on the other firm's supply network by influencing common suppliers.
Fig. 5.
Focal firms’ vulnerability and Network health.
From Fig. 5, we further notice two factors that can affect the ability for a focal firm to benefit from the other focal firm's investment: the focal firm's relationship to the shared supply base and the investment level. First, the focal firm's relationship to the shared supply network affects the gain from the other's investment. For example, suppose both Honda and Toyota can choose to invest at level 0.8. As shown in Table 5 , Honda's gain from Toyota's investment (0.96 - 0.74 = 0.22) is different from Toyota's gain from Honda's investment (0.96 - 0.86 = 0.1). Having controlled the investment level and the disruption diffusion rates, we tease out the only variant – the focal firm's relationship to the shared supply network – as the contributing factor to such a difference in two firms’ benefits. We advocate future research on the mechanisms of this interesting phenomenon.
Table 5.
Focal firm vulnerability changes with investment level at 0.8.
| Toyota vulnerability |
|||
|---|---|---|---|
| Not invest | Invest | ||
| Honda vulnerability | Not invest | (0.96,0.96) | (0.74,0.38) |
| Invest | (0.37,0.86) | (0,0) | |
Second, the investment level affects a firm's gain from the other's investment. From Fig-ure 5, in this same industrial network with fixed network topology, low investment level (<=0.6) exhibits different patterns of vulnerability reduction to high investment level (> 0.6). In low investment level, the gains from these three types of investments are indistinctive for both focal firms. Comparatively, in high investment level, the marginal benefits in all scenarios become significantly larger. This observation shows that there is curvilinear effect for the investment level, and that investment return increases after a certain point, which indicates that finding out the turning point in practice can greatly improve the investment effectiveness. Based on the preceding rationale, we propose:
Proposition 5a
In the industrial supply network, focal firms can benefit from other focal firms’ resilience investment.
Proposition 5b
The focal firm's gain from the other focal firm's investment is affected by the focal firm's relationship to the shared supply base and the other focal firm's investment level.
Third, we investigate the boundary conditions in which the focal firm's investment pays off by introducing the cost of investment. The cost structure is presumably linear, which is parsimonious yet reasonable. We transform the investment benefit to an economic value so that the gain and cost are comparable. Specifically, we use and as scalars to linearly monetize the vulnerability reductions for Honda and Toyota. The corresponding unit investment costs for each node inside their ego network are and . In our example, there are 96 nodes in Honda's ego supply network and 91 nodes in Toyota's ego supply network. The payoff becomes the benefit minus the cost. Table 6 is derived from Table 5 and presents the pay-off with an investment level of 0.8. For instance, under the investment of Toyota payoff comes from the difference between investment and non-investment of Toyota vulnerability in Table 5 (i.e., 0.96 – 0.74).
Table 6.
Payoff table with investment level = 0.8.
| Toyota payoff |
|||
|---|---|---|---|
| Not invest | Invest | ||
| Honda payoff | Not invest | (0, 0) | (0.22, 0.58 – 91) |
| Invest | (0.59 – 96, 0.1) | (0.74 – 96, 0.86 – 91) | |
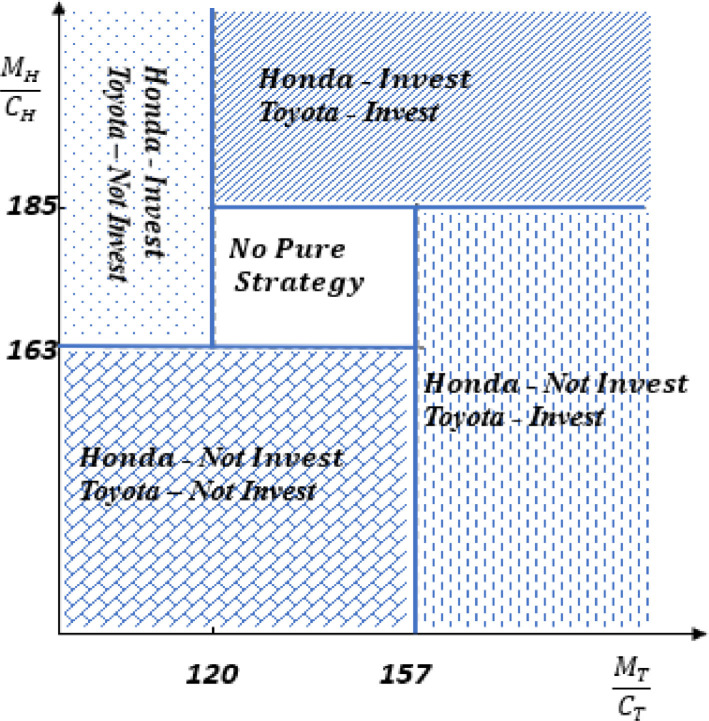
We can derive the strategy space through game theoretical analysis. Fig. 6 shows the strategies. It shows that when Honda always choose to invest, and when , Honda always choose not to invest no matter Toyota's decision. Similarly, when , Toyota always choose to invest, and when , Toyota always choose not to invest regardless of Honda's decision. However, when , Honda's decision is dependent on the value of . And , Toyota's decision is also dependent on the value of . This indicates that the investment decision made by one focal firm should not only consider its benefit-cost ratio, but also consider the other focal firm's benefit-cost ratio. Therefore, looking at the whole supply chain can support better decision-making than only focusing on one firm's ego supply network. Here we propose:
Fig. 6.
Space of dual focal firms’ resilience investment strategies.
Proposition 6a
The investment decision made by one focal firm should consider the benefit-cost ratio of both itself and the other focal firm(s).
Proposition 6b
The focal firm can benefit from examining the industrial or competitors’ SCNs as opposed to focusing on its own ego SCN.
6. Managerial implications
In the foregoing analysis, we show that differentiating between the forward and backward disruption propagation can support effective decision-making to improve supply chain resilience as well as to reduce firm vulnerability. In this section, we provide the following managerial implications that intend to guide managers to better mitigate propagating disruptions based on the simulation findings.
-
1.
Managers should clarify the origin of the disruption and differentiate between the forward and backward disruption propagation.
Our reasoning and analytical results show that forward and backward disruption propagation is distinctive in the following aspects: the origin, the mechanisms, the impacts on firm vulnerability and network health, and the mitigation strategies of the disruption. In this sense, the first and foremost step is to clarify the origin and differentiate between the two kinds of disruption propagation. For example, the 2012 Japan earthquake caused disruptions to many Japanese suppliers of major automobile firms in the U.S. The disruption originated from the supply side and soon wreaked havoc across the global automobile industry through the forward propagation. On the contrary, the COVID-19 pandemic has left no rung of the fashion supply chain unharmed, mainly due to the demand-side disruption and backward propagation. Through clarifying the origins and the types of disruption propagation, effective mitigation and restore strategies can be established. This implication aligns with emphasizing knowledge of disruption origin and severity in previous literature (Craighead et al., 2007; Pettit et al., 2010; Gupta, Ivanov & Choi, 2020), and also introduces the practical importance of differentiating forward and backward disruption propagation that is largely neglected in the literature (Otto, Willner, Wenz, Frieler & Levermann, 2017).
-
2.
Managers need to consider different mitigation methods associated with forward and backward disruption propagation.
The analysis reveals that the forward propagation causes more damage to the firms serving as an assembly entity while backward propagation results in more loss to firms serving as a distribution entity. The mitigation methods associated with forward and backward disruption propagation are different in the sense that safety stock and backup supply are used to mitigate forward disruption propagation while flexible operation and demand management are generally used to manage backward disruption propagation. Moreover, because resources to mitigate and recover from disruptions are limited, firms often invest more heavily in one kind of strategy that targets a specific source or direction of disruption. For example, automobile companies who suffered from the Japan earthquake have developed supplier relationship and business continuity programs that help them ensure a smooth supply, whereas fashion brands during the pandemic are implementing omni-channel retailing to promote the demand level. This implication further enhances the practical importance of differentiating between forward and backward disruption propagation. Hence, an appropriate and targeted strategy is critical and can potentially save firms millions of dollars (Fiksel et al., 2015; Ivanov et al., 2014a).
-
3.
Managers should consider the network topology of the industry and the structural position of the firm in the network, to cope with forward and backward disruption propagation.
The simulation findings demonstrate that the network structural properties moderate the impact of forward and backward disruption propagation on operational performance at both industry and firm levels. At the network-level, a supply network or an assembly network is more exposed to forward disruption propagation whereas a distribution or logistics network is more exposed to backward disruption propagation. At the node-level, firms with a higher degree centrality are more vulnerable. Specifically, a positive degree difference (higher in-degree than out-degree) is more vulnerable to forward disruption propagation, whereas a negative degree difference is more influenced by backward disruption propagation. In order to accurately assess the influence of the disruption on firms and the industry, managers should take a comprehensive consideration of the SCN structure.
Echoing and extending the current literature that has put great emphasis on the impact of SCN structure on disruption propagation (Basole & Bellamy, 2014; Li & Zobel, 2020; Li et al., 2020), this implication supplements the current literature by explicating how the different directions of disruption propagation, interacted with network structure, influence both the firm vulnerability and network health. This research also implies that a more comprehensive understanding of network structure and how it intertwined with other factors is critical to determine the supply chain performance.
-
4.
Managers should integrate into account the information beyond the focal firm's ego network.
Researchers and practitioners widely acknowledge the phenomenon of common suppliers shared by multiple ego networks of buying firms. We observe in the simulation that a small local disruption can propagate to other suppliers and even suppliers outside the focal firm's ego network in the SCN. Thus, focusing only on one firm's ego network underestimates the effect of disruption risks. Information beyond the ego network allows practitioners to better evaluate the effect of operational risks and prepare for more effective mitigation in advance. Moreover, our analysis indicates that one supply chain can benefit from the resilience investment in other supply chains. Information beyond one focal firm's ego network can introduce benefits regarding how to take advantage of other focal firms’ resilience investment. This implication aligns with the advocation of looking at suppliers in deeper tiers (Simchi-Levi et al., 2015; Simchi-Levi, Schmidt & Wei, 2014; Zhao et al., 2019; Hosseini, Ivanov & Blackhurst, 2020), increasing supply chain visibility (Basole & Bellamy, 2014; Ivanov, Dolgui & Sokolov, 2019), and improving information accuracy (Li, Zobel & Russell, 2017).
-
5.
Managers of a focal firm should consider the cost-performance of the resilience investment for not only that focal firm but also other focal firms (buyers).
Due to the existence of common suppliers of multiple ego supply networks, one focal firm's resilience investment decisions can affect and be affected by other focal firms. Our results present the boundary conditions under which resilience investment achieves its best outcome. Fig. 6 provides an example of applying the “benefit-cost ratio” that is similar to the concept of cost-performance to determine when a firm will be better off through other firm's resilience investment. In general, there is a threshold, beyond which managers of the focal firm should think to build their own firm's resilience, regardless of other firms’ risk strategies. It is critical for managers to map out the network, quantify the cost-performance, and figure out the threshold based on supply networks and real contexts of disruption risks.
Although it is widely accepted that supply chains consist of highly interactive business entities (Christopher & Peck, 2004; Simchi-Levi et al., 2014) and common supply base exists in different supply chains (K. Zhao et al., 2019), to the best of our knowledge, current literature has not considered the influence of common supply base on the impact and outcome of resilience investment. This implication highlights the importance of considering and incorporating common supply base and other focal firm's resilience investment into the decision-makings process. To this end, further analysis of the ripple effect in the settings of intertwined supply networks, viable and reconfugurable supply chains is a promising and understudied research direction (Wang, Dou, Muddada & Zhang, 2018; Ivanov, 2020b; Ivanov & Dolgui, 2020b; Dolgui, Ivanov & Sokolov, 2020b).
7. Conclusion
This study explores disruption propagation that can originate from either supply or demand side and can diffuse in both directions. First, we propose a theoretical framework for disruption propagation mechanism, in which network structure, node-level disruption diffusion rate, recovery rate and firms’ investment influence the supply chain disruption propagation behavior. Next, we design an experiment and investigate how node-level influencing factors, especially forward and backward disruption diffusion rates, interact with the network structure and determine the firm vulnerability and network health. Finally, we analyze how one focal firm's investment influences itself, the other focal firm, and the overall SCN. Based on the analysis, we generate several important managerial implications.
The results are threefold. First, at the network-level, forward and backward disruption diffusion rates do exert different effects on network health, moderated by the network structure. Generally, forward disruption diffusion rate has a more severe effect on a supply network, while backward disruption diffusion rate has more impact on a distribution network. Second, at the node-level, we find that both node-level influencing factors and node position contribute to node vulnerability. Higher centrality leads to higher node vulnerability. The nodes with higher in-degree than out-degree are more sensitive to forward disruption propagation, and vice versa. Finally, for a network with two focal firms, one focal firm can benefit from the other's investment. The benefit is influenced by the relationship between the focal firm and the overlapped supply network, as well as the investment level. We delineate the relationship between the focal firms’ benefit-cost ratio and their strategy space, which implies that one focal firm's investment decision should consider both focal firms’ benefit-cost ratios.
This study contributes in many ways. Theoretically, our study is among the first to consider the difference in the effects of forward and backward disruption propagation, and map them to corresponding resilience investments. Moreover, this work extends the understanding of “triad” disruption propagation by using a network with multiple focal firms. Practically, this study implies that firms should manage forward and backward propagation differently because of their distinctive origins, associated investments, and effects on node vulnerability and network health. Also, a focal firm's interest is to map out not only its ego network, but also the industrial network. When making resilience investment decisions, one focal firm should consider the counterparts’ decisions, its relationship to the shared network, and risk characteristics.
There are several limitations of this study, which can be extended in future work. The first limitation is related to the effects of network structure on disruption propagation. Our analysis is based on one realistic SCN and two comparable random networks. It is enough to investigate the influence of node-level factors on disruption propagation, but has its limitation on addressing the effects of network structure, which requires a sufficient number of samples of various network structures. Considering network structure plays a critical role in disruption propagation, future studies based on a large number of network structure samples are required for further understanding of disruption propagation. The second is about the assumption of the risk independency. As disruption impacts may be interdependent in reality, future studies could relax this assumption and investigate how the interdependency of risks can influence the supply chain resilience. The third is the homogeneous setting of node-level factors required by the experiment design. Although a homogenous setting allows us to effectively investigate the impacts of these factors on the ripple effect, this setting reduces the proximity to the real-world situation, as agents in a real supply chain are essentially different in terms of disruption prevention and response activities. Future studies can relax this setting and individualize the agent parameter value to model a more realistic ripple effect given the supply chain structure. The fourth limitation is about the curvilinear effect of investment levels. Our work shows that the effect exists in our specific setting. To derive the general curvilinear effect and the rules of the turning point that can be broadly applied, a well-designed experiment including different settings of network configurations and various FR, BR, and RC levels should be implemented in a future study.
Acknowledgements
We thank three anonymous reviewers for their precious time, valuable comments, and suggestions which helped us to improve the paper immensely.
References
- Ackermann F., Howick S., Quigley J., Walls L., Houghton T. Systemic risk elicitation: Using causal maps to engage stakeholders and build a comprehensive view of risks. European Journal of Operational Research. 2014;238(1):290–299. doi: 10.1016/j.ejor.2014.03.035. [DOI] [Google Scholar]
- Antonakis J., Bendahan S., Jacquart P., Lalive R. Causality and endogeneity: Problems and solutions. The Oxford Handbook of Leadership and Organizations. 2014 doi: 10.1093/oxfordhb/9780199755615.013.007. [DOI] [Google Scholar]
- Baghersad M., Zobel C.W. Assessing the extended impacts of supply chain disruptions on firms: an empirical study. International Journal of Production Economics. 2021;231 doi: 10.1016/j.ijpe.2020.107862. [DOI] [Google Scholar]
- Basole R.C., Bellamy M.A. Supply network structure, visibility, and risk diffusion: A computational approach. Decision Sciences. 2014;45(4):753–789. doi: 10.1111/deci.12099. [DOI] [Google Scholar]
- Bierkandt R., Wenz L., Willner S.N., Levermann A. Acclimate—A model for economic damage propagation. Part 1: Basic formulation of damage transfer within a global supply network and damage conserving dynamics. Environment Systems and Decisions. 2014;34(4):507–524. doi: 10.1007/s10669-014-9523-4. [DOI] [Google Scholar]
- Chatfield D.C., Hayya J.C., Cook D.P. Stockout propagation and amplification in supply chain inventory systems. International Journal of Production Research. 2013;51(5):1491–1507. doi: 10.1080/00207543.2012.697205. [DOI] [Google Scholar]
- Choi T.Y., Wu Z. Triads in supply networks: Theorizing buyer-supplier-supplier relationships. Journal of Supply Chain Management. 2009;45(1):8–25. doi: 10.1111/j.1745-493X.2009.03151.x. [DOI] [Google Scholar]
- Chowdhury M.M.H., Quaddus M. Supply chain resilience: Conceptualization and scale development using dynamic capability theory. International Journal of Production Economics. 2017;188:185–204. doi: 10.1016/j.ijpe.2017.03.020. [DOI] [Google Scholar]
- Christopher M., Peck H. Building the resilient supply chain. International Journal of Logistics Management. 2004;15(2):1–13. [Google Scholar]
- Craighead C.W., Blackhurst J., Rungtusanatham M.J., Handfield R.B. The severity of supply chain disruptions: Design characteristics and mitigation capabilities. Decision Sciences. 2007;38:131–156. [Google Scholar]
- CRS Insight . 2020. U.S. travel and tourism and COVID-19.https://crsreports.congress.gov/product/pdf/IN/IN11325 Retrieved from. [Google Scholar]
- Deng X., Yang X., Zhang Y., Li Y., Lu Z. Risk propagation mechanisms and risk management strategies for a sustainable perishable products supply chain. Computers and Industrial Engineering. 2019;135:1175–1187. doi: 10.1016/j.cie.2019.01.014. [DOI] [Google Scholar]
- Dolgui A., Ivanov D., Rozhkov M. Does the ripple effect influence the bullwhip effect? An integrated analysis of structural and operational dynamics in the supply chain†. International Journal of Production Research. 2020;58(5):1285–1301. doi: 10.1080/00207543.2019.1627438. [DOI] [Google Scholar]
- Dolgui A., Ivanov D., Sokolov B. Ripple effect in the supply chain: An analysis and recent literature. International Journal of Production Research. 2018;56(1–2):414–430. doi: 10.1080/00207543.2017.1387680. [DOI] [Google Scholar]
- Dolgui A., Ivanov D., Sokolov B. Reconfigurable supply chain: The X-Network. International Journal of Production Research. 2020;58(13):4138–4163. [Google Scholar]
- Dubey R., Gunasekaran A., Childe S.J., Papadopoulos A., Blome C., Luo Z. Antecedents of resilient supply chains: An empirical study. IEEE Transactions on Engineering Management. 2019;66(1):8–19. [Google Scholar]
- Fernández R., Louis P.-.Y., Nardi F.R. Overview: PCA models and issues. In: Louis P.-Y., Nardi F.R., editors. Probabilistic cellular automata. Springer; 2018. [Google Scholar]
- Fiksel J., Polyviou M., Croxton K.L., Pettit T.J. From risk to resilience: Learning to deal with disruption. MIT Sloan Management Review. 2015;56(2):79–86. [Google Scholar]
- Garvey M.D., Carnovale S. The rippled newsvendor: A new inventory framework for modelling supply chain risk severity in the presence of risk propagation. International Journal of Production Economics. 2020;228 doi: 10.1016/j.ijpe.2020.107752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garvey M.D., Carnovale S., Yeniyurt S. An analytical framework for supply network risk propagation: A Bayesian network approach. European Journal of Operational Research. 2015;243(2):618–627. doi: 10.1016/j.ejor.2014.10.034. [DOI] [Google Scholar]
- Ghadge A., Dani S., Chester M., Kalawsky R. A systems thinking approach for modelling supply chain risk propagation. Supply Chain Management: An International Journal. 2013;18(5):523–538. [Google Scholar]
- Goto H., Takayasu H., Takayasu M. Estimating risk propagation between interacting firms on inter-firm complex network. PLoS ONE. 2017;12(10) doi: 10.1371/journal.pone.0185712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta V., Ivanov D., Choi T.-M. Competitive pricing of substitute products under supply disruption. Omega. 2020 doi: 10.1016/j.omega.2020.102279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han J., Shin K. Evaluation mechanism for structural robustness of supply chain considering disruption propagation. International Journal of Production Research. 2016;54(1):135–151. doi: 10.1080/00207543.2015.1047977. [DOI] [Google Scholar]
- Ho T.H., Lim N., Reza S., Xia X. OM forum - Causal inference models in operations management. Manufacturing and Service Operations Management. 2017;19(4):509–525. doi: 10.1287/msom.2017.0659. [DOI] [Google Scholar]
- Hosseini S., Ivanov D. A new resilience measure for supply networks with the ripple effect considerations: A Bayesian network approach. Annals of Operations Research. 2019:1–27. doi: 10.1007/s10479-019-03350-8. [DOI] [Google Scholar]
- Hosseini S., Ivanov D., Blackhurst J. Conceptualization and measurement of supply chain resilience in an open-system context. IEEE Transactions on Engineering Management. 2020 doi: 10.1109/TEM.2020.3026465. [DOI] [Google Scholar]
- Hosseini S., Ivanov D., Dolgui A. Ripple effect modelling of supplier disruption: Integrated Markov chain and dynamic Bayesian network approach. International Journal of Production Research. 2019 doi: 10.1080/00207543.2019.1661538. [DOI] [Google Scholar]
- Imai K., Tingley D., Yamamoto T. Experimental designs for identifying causal mechanisms. Journal of the Royal Statistical Society. Series A: Statistics in Society. 2013;176(1):5–51. doi: 10.1111/j.1467-985X.2012.01032.x. [DOI] [Google Scholar]
- Intel . 2011. 2011 Annual report - Intel Corporation. [Google Scholar]
- Ivanov D. Simulation-based ripple effect modelling in the supply chain. International Journal of Production Research. 2017;55(7):2083–2101. doi: 10.1080/00207543.2016.1275873. [DOI] [Google Scholar]
- Ivanov D. Supply Chain Risk Management: Bullwhip Effect and Ripple Effect. In: Ivanov D., editor. Structural dynamics and resilience in supply chain risk management. Springer International Publishing; Cham: 2018. pp. 19–44. [Google Scholar]
- Ivanov D. Predicting the impacts of epidemic outbreaks on global supply chains: A simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transportation Research Part E: Logistics and Transportation Review. 2020 doi: 10.1016/j.tre.2020.101922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanov D. Viable Supply Chain Model: Integrating agility, resilience and sustainability perspectives – lessons from and thinking beyond the COVID-19 pandemic. Annals of Operations Research. 2020 doi: 10.1007/s10479-020-03640-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanov D., Das A. Coronavirus (COVID-19 / SARS-CoV-2) and supply chain resilience: A research note. International Journal of Integrated Supply Management. 2020;13(1):90–102. [Google Scholar]
- Ivanov D., Dolgui A. OR-Methods for coping with the ripple effect in supply chains during COVID-19 pandemic: Managerial insights and research implications. International Journal of Production Economics. 2020 doi: 10.1016/j.ijpe.2020.107921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanov D., Dolgui A. Viability of intertwined supply networks: extending the supply chain resilience angles towardsl survivability. a position paper motivated by COVID-19 Outbreak. International Journal of Production Research. 2020;58(10):2904–2915. [Google Scholar]
- Ivanov D., Dolgui A., Sokolov B. The impact of digital technology and Industry 4.0 on the ripple effect and supply chain risk analytics. International Journal of Production Research. 2019;57(3):829–846. doi: 10.1080/00207543.2018.1488086. [DOI] [Google Scholar]
- Ivanov D., Pavlov A., Sokolov B. Optimal distribution (re)planning in a centralized multi-stage supply network under conditions of the ripple effect and structure dynamics. European Journal of Operational Research. 2014;237(2):758–770. doi: 10.1016/j.ejor.2014.02.023. [DOI] [Google Scholar]
- Ivanov D., Sokolov B., Dolgui A. The Ripple effect in supply chains: Trade-off ‘efficiency-flexibility-resilience’ in disruption management. International Journal of Production Research. 2014;52(7):2154–2172. doi: 10.1080/00207543.2013.858836. [DOI] [Google Scholar]
- Kinra A., Ivanov D., Das A., Dolgui A. Ripple effect quantification by supply risk exposure assessment. International Journal of Production Research. 2020;58(19):5559–5578. [Google Scholar]
- Kutner M., Nachtsheim C., Neter J., Li W. McGraw Hill; 2005. Applied statistical linear models. [Google Scholar]
- Lee H.L., Padmanabhan V., Whang S. Information Distortion in a Supply Chain: The Bullwhip Effect. Management Science. 1997;43(4):546–558. doi: 10.1287/mnsc.43.4.546. [DOI] [Google Scholar]
- Li Y., Zobel C.W. Exploring supply chain network resilience in the presence of the ripple effect. International Journal of Production Economics. 2020;228 doi: 10.1016/j.ijpe.2020.107693. [DOI] [Google Scholar]
- Li Y., Zobel C.W., Russell R.S. Value of supply disruption information and information accuracy. Journal of Purchasing and Supply Management. 2017;23(3):191–201. doi: 10.1016/j.pursup.2016.12.001. [DOI] [Google Scholar]
- Li Y., Zobel C.W., Seref O., Chatfield D. Network characteristics and supply chain resilience under conditions of risk propagation. International Journal of Production Economics. 2020;223 doi: 10.1016/j.ijpe.2019.107529. [DOI] [Google Scholar]
- Liberatore F., Scaparra M.P., Daskin M.S. Hedging against disruptions with ripple effects in location analysis. Omega. 2012;40(1):21–30. doi: 10.1016/j.omega.2011.03.003. [DOI] [Google Scholar]
- Macdonald J.R., Zobel C.W., Melnyk S.A., Griffis S.E. Supply chain risk and resilience: theory building through structured experiments and simulation. International Journal of Production Research. 2018;56(12):4337–4355. doi: 10.1080/00207543.2017.1421787. [DOI] [Google Scholar]
- Marchese K., Paramasivam S. Deloitte Development LLC; 2013. The ripple effect. how manufacting and retail executive view the growing challenge of supply chain risk.http://scholar.google.com/scholar?hl=en&btnG=Search&q=intitle:NO+Title#0%5Cnhttp://eric.ed.gov/?id=EJ745598 Retrieved from. [Google Scholar]
- Mizgier K.J., Jüttner M.P., Wagner S.M. Bottleneck identification in supply chain networks. International Journal of Production Research. 2013;51(5):1477–1490. doi: 10.1080/00207543.2012.695878. [DOI] [Google Scholar]
- Nair A., Vidal J.M. Supply network topology and robustness against disruptions – An investigation using multi-agent model. International Journal of Production Research. 2011 [Google Scholar]
- Nguyen W.P.V., Nof S.Y. Collaborative response to disruption propagation (CRDP) in cyber-physical systems and complex networks. Decision Support Systems. 2019;117:1–13. doi: 10.1016/j.dss.2018.11.005. [DOI] [Google Scholar]
- Norrman A., Jansson U. Ericsson's proactive supply chain risk management approach after a serious sub‐supplier accident. International Journal of Physical Distribution &Logistics management. 2004;34(5):434–456. doi: 10.1108/09600030410545463. [DOI] [Google Scholar]
- Ojha R., Ghadge A., Tiwari M.K., Bititci U.S. Bayesian network modelling for supply chain risk propagation. International Journal of Production Research. 2018;56(17):5795–5819. doi: 10.1080/00207543.2018.1467059. [DOI] [Google Scholar]
- Otto C., Willner S.N., Wenz L., Frieler K., Levermann A. Modeling loss-propagation in the global supply network: The dynamic agent-based model acclimate. Journal of Economic Dynamics and Control. 2017;83:232–269. doi: 10.1016/j.jedc.2017.08.001. [DOI] [Google Scholar]
- Paul S.K., Chowdhury P. A production recovery plan in manufacturing supply chains for a high-demand item during COVID-19. International Journal of Physical Distribution & Logistics Management. 2020 doi: 10.1108/IJPDLM-04-2020-0127. [DOI] [Google Scholar]
- Pavlov A., Ivanov D., Pavlov D., Slinko A. Optimization of network redundancy and contingency planning in sustainable and resilient supply chain resource management under conditions of structural dynamics. Annals of Operations Research. 2019:1–30. doi: 10.1007/s10479-019-03182-6. [DOI] [Google Scholar]
- Pettit T.J., Fiksel J., Croxton K.L. Ensuring supply chain resilience: Development of a conceptual framework. Journal of Business Logistics. 2010;31(1):1–21. [Google Scholar]
- Qazi A., Quigley J., Dickson A., Ekici Ş.Ö. Exploring dependency based probabilistic supply chain risk measures for prioritising interdependent risks and strategies. European Journal of Operational Research. 2017;259(1):189–204. doi: 10.1016/j.ejor.2016.10.023. [DOI] [Google Scholar]
- Queiroz M.M., Ivanov D., Dolgui A., Fosso Wamba S. Impacts of epidemic outbreaks on supply chains: Mapping a research agenda amid the COVID-19 pandemic through a structured literature review. Annals of Operations Research. 2020 doi: 10.1007/s10479-020-03685-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawik T. 2nd Edition. Springer; New York: 2020. Supply Chain Disruption Management. [Google Scholar]
- Scheibe K.P., Blackhurst J. Supply chain disruption propagation: A systemic risk and normal accident theory perspective. International Journal of Production Research. 2018;56(1–2):43–59. doi: 10.1080/00207543.2017.1355123. [DOI] [Google Scholar]
- Simchi-Levi D., Schmidt W., Wei Y. From Superstorms to Factory Fires. Harvard Business Review. 2014;92(1/2):96–101. [Google Scholar]
- Simchi-Levi D., Schmidt W., Wei Y., Zhang P.Y., Combs K., Ge Y. Identifying risks and mitigating disruptions in the automotive supply chain. Interfaces. 2015;45(5):375–390. doi: 10.1287/inte.2015.0804. [DOI] [Google Scholar]
- Sinha P., Kumar S., Prakash S. Measuring and mitigating the effects of cost disturbance propagation in multi-echelon apparel supply chains. European Journal of Operational Research. 2020;282(1):148–160. doi: 10.1016/j.ejor.2019.09.015. [DOI] [Google Scholar]
- Świerczek A. The impact of supply chain integration on the “snowball effect” in the transmission of disruptions: An empirical evaluation of the model. International Journal of Production Economics. 2014;157:89–104. doi: 10.1016/j.ijpe.2013.08.010. [DOI] [Google Scholar]
- Swierczek A. The “snowball effect” in the transmission of disruptions in supply chains: The role of intensity and span of integration. International Journal of Logistics Management. 2016 doi: 10.1108/IJLM-08-2015-0133. [DOI] [Google Scholar]
- Tang L., Jing K., He J., Stanley H.E. Complex interdependent supply chain networks: Cascading failure and robustness. Physica A: Statistical Mechanics and Its Applications. 2016;443:58–69. doi: 10.1016/j.physa.2015.09.082. [DOI] [Google Scholar]
- Thomas L. Coronavirus wreaks havoc on retail supply chains globally, even as China's factories come back online. CNBC. 2020 https://www.cnbc.com/2020/03/16/coronavirus-wreaks-havoc-on-retail-supply-chains-globally.html Retrieved from. [Google Scholar]
- Wagner S.M., Bode C. An empirical investigation into supply chain vulnerability. Journal of purchasing and supply management. 2006;12(6):301–312. doi: 10.1016/j.pursup.2007.01.004. [DOI] [Google Scholar]
- Wagner S.M., Bode C. An empirical examination of supply chain performance along several dimensions of risk. Journal of Business Logistics. 2008;29(1):307–325. [Google Scholar]
- Wang X., Disney S. The bullwhip effect: Progress, trends and directions. European Journal of Operational Research. 2016;250(3):691–701. doi: 10.1016/j.ejor.2015.07.022. [DOI] [Google Scholar]
- Wang J., Dou R., Muddada R.R., Zhang W. Management of a holistic supply chain network for proactive resilience: Theory and case study. Computers and Industrial Engineering. 2018;125:668–677. [Google Scholar]
- Wang Y., Li J., Wu D., Anupindi R. When ignorance is not bliss: An empirical analysis of subtier supply network structure on firm risk. Management Science. 2020 doi: 10.1287/mnsc.2020.3645. [DOI] [Google Scholar]
- Wenz L., Willner S.N., Bierkandt R., Levermann A. Acclimate—A model for economic damage propagation. Part II: A dynamic formulation of the backward effects of disaster-induced production failures in the global supply network. Environment Systems and Decisions. 2014;34(4):525–539. doi: 10.1007/s10669-014-9521-6. [DOI] [Google Scholar]
- Yoon J., Talluri S., Yildiz H., Ho W. Models for supplier selection and risk mitigation: A holistic approach. International Journal of Production Research. 2018;56(10):3636–3661. [Google Scholar]
- Zeng Y., Xiao R. Modelling of cluster supply network with cascading failure spread and its vulnerability analysis. International Journal of Production Research. 2014;52(23):6938–6953. doi: 10.1080/00207543.2014.917769. [DOI] [Google Scholar]
- Zhang Jiantong, Chen X., Fang C. Transmission of a supplier's disruption risk along the supply chain: A further investigation of the Chinese automotive industry. Production Planning and Control. 2018;29(9):773–789. doi: 10.1080/09537287.2018.1470268. [DOI] [Google Scholar]
- Zhang Jingjing, Adomavicius G., Gupta A., Ketter W. Consumption and performance: Understanding longitudinal dynamics of recommender systems via an agent-based simulation framework. Information Systems Research. 2020 doi: 10.1287/ISRE.2019.0876. [DOI] [Google Scholar]
- Zhao K., Zuo Z., Blackhurst J.V. Modelling supply chain adaptation for disruptions: An empirically grounded complex adaptive systems approach. Journal of Operations Management. 2019;65(2):190–212. doi: 10.1002/joom.1009. [DOI] [Google Scholar]
- Zhao M., Freeman N.K. Robust sourcing from suppliers under ambiguously correlated major disruption risks. Production and Operations Management. 2019;28(2):441–456. doi: 10.1111/poms.12933. [DOI] [Google Scholar]