Abstract
Objectives
The aim of this study was to assess the performance and impact of multilevel modelling (MLM) compared with ordinary least squares (OLS) regression in trial-based economic evaluations with clustered data.
Methods
Three thousand datasets with balanced and unbalanced clusters were simulated with correlation coefficients between costs and effects of − 0.5, 0, and 0.5, and intraclass correlation coefficients (ICCs) varying between 0.05 and 0.30. Each scenario was analyzed using both MLM and OLS. Statistical uncertainty around MLM and OLS estimates was estimated using bootstrapping. Performance measures were estimated and compared between approaches, including bias, root mean squared error (RMSE) and coverage probability. Cost and effect differences, and their corresponding confidence intervals and standard errors, incremental cost-effectiveness ratios, incremental net-monetary benefits and cost-effectiveness acceptability curves were compared.
Results
Cost-effectiveness outcomes were similar between OLS and MLM. MLM produced larger statistical uncertainty and coverage probabilities closer to nominal levels than OLS. The higher the ICC, the larger the effect on statistical uncertainty between MLM and OLS. Significant cost-effectiveness outcomes as estimated by OLS became non-significant when estimated by MLM. At all ICCs, MLM resulted in lower probabilities of cost effectiveness than OLS, and this difference became larger with increasing ICCs. Performance measures and cost-effectiveness outcomes were similar across scenarios with varying correlation coefficients between costs and effects.
Conclusions
Although OLS produced similar cost-effectiveness outcomes, it substantially underestimated the amount of variation in the data compared with MLM. To prevent suboptimal conclusions and a possible waste of scarce resources, it is important to use MLM in trial-based economic evaluations when data are clustered.
Electronic supplementary material
The online version of this article (10.1007/s40273-020-00946-y) contains supplementary material, which is available to authorized users.
Key Points for Decision Makers
| Ignoring clustering of data in the analysis of trial-based economic evaluations overestimates the probability of cost effectiveness. |
| It is recommended to use multilevel modelling for trial-based economic evaluations with clustered data. |
| Further research should investigate how to best combine multilevel modelling with resampling approaches. |
Introduction
Because resources available for healthcare are scarce, policy makers need to decide which healthcare interventions to reimburse and which not to [1]. Policy makers increasingly use information from economic evaluations, which assess whether the additional costs of a new intervention are justified by its additional effects compared with one or more alternative interventions [1, 2]. In many countries, the results of economic evaluations are even established as a formal decision criterion for the reimbursement and/or pricing of healthcare interventions [1].
Economic evaluations are often performed alongside a randomized controlled trial. Ideally, participants of such so-called trial-based economic evaluations are randomized to an intervention or control group at the individual level. Sometimes this is not possible, and clusters of patients (e.g. at the hospital or general practice level) are randomized instead. Participants within clusters are likely to be more similar than participants between clusters and, consequently, cost and effect data are considered to be clustered [3–6]. This is due to the fact that participant and/or healthcare provider characteristics influencing costs and effects are similar within a cluster and highly likely to vary across clusters due to variations in disease severity, training level of healthcare providers, adherence to treatment protocols by healthcare providers or type of hospital [6].
Statistical methods such as ordinary least squares (OLS) regression assume that outcomes among participants are independent and such methods are, therefore, likely to underestimate the total amount of sampling variability when data are clustered [7]. Ignoring the clustered nature of data results in inaccurate estimates of statistical uncertainty [8–10], and consequently may lead to suboptimal conclusions [11–14]. Typically, multilevel modelling (MLM) results in larger standard errors (SEs) than OLS, because in MLM information provided by participants belonging to the same cluster contributes less than 100% new information [4]. The more alike participants are within a cluster, which is quantified using the intraclass correlation coefficient (ICC), the less new information is provided by a participant belonging to that same cluster. Despite the fact that statistical methods for dealing with clustered data are available and their use in effectiveness studies is well established [8, 15–17], these methods are hardly used in trial-based economic evaluations [5, 18]. In addition, no clear recommendations on how to deal with clustered data are available in pharmacoeconomic guidelines [19].
Methods that can be used to deal with clustered data in trial-based economic evaluations [20–22] include MLM, two-stage bootstrapping (2SB), seemingly unrelated regression (SUR) and generalized estimating equations (GEE) with robust SEs [23–27]. Of these, simulation studies found MLM to be the preferred method, as MLM resulted in more precise point estimates and better statistical performance compared with the other methods [5, 25, 28]. So far, studies evaluating the relative performance of methods for analyzing clustered data in trial-based economic evaluations mainly assumed a normal distribution for costs and effects or used other approaches, such as Bayesian statistical methods [20, 22, 24, 25, 27]. Although Bayesian methods may also be used for analyzing clustered data, we focused on frequentist statistical methods in our study, because they are better known by the majority of (applied) researchers and are easier to implement in standard statistical software packages. Therefore, we think that frequentist methods are currently most likely to improve practice. Also, most papers only assessed the impact of the different methods on cost and effect differences and/or incremental cost-effectiveness ratios (ICERs), but not on the joint uncertainty surrounding costs and effects. Therefore, the aim of this study was to assess the performance and show the impact on cost-effectiveness outcomes of using MLM compared with OLS in trial-based economic evaluations using clustered data.
Methods
The performance and impact of MLM compared with OLS in trial-based economic evaluations using clustered data was assessed using simulated data.
Data Generation Mechanisms
Datasets were simulated using simstudy [29] in R [30]. In order to estimate the key performance measure, coverage probability, with an acceptable degree of imprecision (i.e. to reach a maximal Monte Carlo SE of 0.5), 3000 datasets were used [31]. The coverage probability refers to the probability that the true value falls within the estimated confidence intervals (CIs) (see Sect. 2.4). Moreover, simulation studies are empirical experiments, in which performance measures such as the aforementioned coverage probability are estimated, which means that these estimates of performance measures are subject to error. Monte Carlo SEs quantify this simulation error by providing an estimate of the SE of performance measures as a result of using a finite number of simulations (nsims) [31]. Both balanced and unbalanced clusters were simulated. For the balanced clusters (i.e. all clusters of equal size), 30 clusters were simulated with 30 individuals per cluster. To simulate 30 unbalanced clusters (i.e. clusters are not equal in size), a zero-truncated Poisson distribution was used with a mean of 30 individuals per cluster. Clusters were equally randomized to an intervention or control group. Thirty clusters were simulated, as a total of 20 clusters or more is suggested for asymptotic assumptions to hold, which means that the sample size (i.e. observations at both cluster and individual levels) needs to be sufficiently large [32, 33].
In all scenarios, costs were expressed in Euros (€) and effects were expressed in quality-adjusted life-years (QALYs). A cost difference (∆C) of €100 and an effect difference (∆E) of 0.05 were specified as true reference values. The latter is in line with the minimally clinically important difference for QALYs [34]. QALYs were assumed to be normally distributed [35, 36]. Cost data in trial-based economic evaluations typically have a distribution that is heavily right skewed [37] with a point mass at zero costs and a small number of outliers [38]. To account for this, costs were simulated using a gamma distribution.
Correlation Structures
We accounted for two types of correlations that are present in trial-based economic evaluations with clustered cost and effect data, which are graphically presented in Fig. 1. First, the correlation between costs and effects is depicted as Corr(Costs, QALYs) in Fig. 1 [39, 40]. This correlation can range from − 1, meaning that higher costs are associated with worse effects, to 1, meaning that higher costs are associated with better effects. If data are clustered, this type of clustering may exist at both the individual level and the cluster level. Datasets were simulated with a correlation between costs and effects of − 0.5, 0, and 0.5, at both the individual level and the cluster level [6].
Fig. 1.
Correlation structures in cluster-randomized trials with unbalanced clusters. Corr(Costs, QALYs) correlation between costs and effects, QALY quality-adjusted life-year
Second, the intraclass correlation coefficient (ICC) is a measure of the correlation between the observations of participants belonging to the same cluster, and is estimated using the between-cluster variance and within-cluster variance (see Fig. 1) [4]. The ICC provides an indication of how much the observations from participants within a cluster are similar. This correlation can range from 0, meaning that none of the observations from participants within a cluster are alike, to 1, meaning that all the observations from participants within a cluster are the same [41]. When the ICC is 0, all the observations within the cluster are unique, and the effective sample size is equal to the number of participants. In a situation where all the observations within a cluster are similar (i.e. ICC = 1), the effective sample size is reduced to the number of clusters [4, 41, 42]. The ICC was set at 0.05, 0.10, 0.20 and 0.30 for both costs and effects. Although in empirical studies, ICCs are typically smaller than 0.20 [4], a higher ICC was also used to evaluate whether the applied methods are robust in situations with larger ICCs. For a detailed explanation of how the ICC was specified, we refer the reader to Online Resource 1 (see electronic supplementary material [ESM]).
An overview of all parameter ranges, as well as their motivation, can be found in Table 1. In total, 3000 datasets for each of the 24 different scenarios were simulated (Online Resource 2, see ESM). The range of values for the different parameters are based on values typically found in trial-based economic evaluations. The simulation code is provided in Online Resource 3 (see ESM).
Table 1.
Brief description of parameter values and motivation
| Parameters | Value | Motivation |
|---|---|---|
| Cost difference (∆C) | Specified using the following equation: Costs = 1100 + 100 × (treatment arm), resulting in ∆C ≈ €100 | A cost difference between treatment arms of €100 is likely to appear in ‘real-life’ situations |
| Effect difference (∆E) | Specified using the following equation: QALY = 0.60 + 0.05 × (treatment arm), resulting in ∆E ≈ 0.05 | Minimally important difference in utilities across different medical conditions range from 0.01 to 0.14 [34, 43–45] |
| Correlation | The correlation between costs and effects was set at three different values; negative correlation (− 0.5), no correlation (0) and positive correlation (0.5) | Within each arm of the trial it is likely that costs and QALYs are correlated, as these come from the same participants [6, 21, 46] |
| Intracluster correlation coefficient (ICC) | Four different values were specified for the ICC by manipulating the between-cluster and within-cluster variances. Beginning with a low ICC (0.05), this was increased to values of 0.10, 0.20 and 0.30 | In empirical data, the ICC typically does not surpass 0.20 [4] |
| Cluster size | Balanced and unbalanced clusters were simulated with on average 30 participants per cluster | In practice, unbalanced clusters are more common than balanced clusters and are considered as having less power than equal-sized trials with balanced clusters [47] |
QALY quality-adjusted life-year
Data Analysis
Two statistical approaches were used to estimate the cost effectiveness of the intervention compared with the control. The first approach was OLS, which does not take into account the hierarchical structure of the data. Two OLS models were specified, one for costs and one for effects (formulas 1 and 2):
| 1 |
| 2 |
where and are the observed costs and QALYs of participant i, and refer to the models’ intercept, β1c and β1e refer to the regression coefficient for the independent variable ‘treatment arm’ [i.e. the mean difference in costs (∆C) and QALYs (∆E) between treatment groups], and and refer to the unexplained variance at the individual level.
The second approach was MLM, which does take into account the hierarchical structure of the data. Two MLMs were specified, one for costs and one for effects (formulas 3 and 4), assuming a two-level structure and using maximum likelihood estimation [4]:
| 3 |
| 4 |
where and are the observed costs and QALYs of participant i in cluster j, and refer to the models’ intercept; β1jc and β1je refer to the regression coefficient for the variable ‘treatment arm’ (i.e. the mean difference in costs [∆C] and QALYs [∆E] between treatment groups); and refer to the unexplained variance at the individual level; and and refer to the unexplained variance (random effects) at the cluster level [4].
For effects, normal-based 95% CIs were estimated. For costs, 95% CIs were estimated using bias-corrected and accelerated (BCa) bootstrapping with 2000 replications [48]. OLS was combined with bootstrapping at the individual level, and the bootstrap procedure was stratified for treatment arm. MLM was combined with cluster bootstrapping, which is recommended for resampling clustered data [49]. In this approach, whole clusters instead of individuals are resampled, which maintains the hierarchical structure of the data.
ICERs were calculated by dividing the difference in costs by the difference in effects (i.e. ∆C/∆E) [50]. The incremental net monetary benefit (INMB) was estimated as
| 5 |
where λ refers to the ceiling ratio (i.e. the maximum amount of money decision makers are willing to pay per unit of effect gained) for cost effectiveness. In this study, the British threshold of 23, 300 €/QALY was used.
The joint uncertainty surrounding costs and effects was summarized using cost-effectiveness acceptability curves (CEACs) [51], which were estimated using the parametric p-value approach for INMBs [52]. CEACs show the probability of an intervention being cost effective in comparison with control for a range of different ceiling ratios [51, 53]. Online Resource 4 contains a ready-to-use Stata® script for conducting trial-based economic evaluations with clustered data (see ESM).
Comparison of Methods
The performance of the two statistical approaches was compared using different performance measures [31]. These performance measures were estimated for cost differences, effect differences and INMBs using a threshold of 23,300 €/QALY.
- Empirical bias: the mean difference between the estimated value in the simulated datasets ( and the true value ():
which indicates how far the estimated value is from the true value. Values closer to zero imply less bias.6 - Root mean squared error (RMSE): the square root of the quadratic mean difference between the estimated values ( and the true values ():
which integrates the squared bias and variance in one performance measure. A RMSE of 0 indicates a perfect fit to the data, and lower RMSEs, thus, indicate better performance.7 - Coverage probability: the percentage of times that the true value () is covered in the 95% CI around the estimated value (:
8
Coverage probabilities (expressed in %) close to the nominal level of 1 − α (α = 0.05), together with narrow CI width, indicate higher power and greater accuracy. Coverage probabilities below 90% indicate an increased chance of type-I error (i.e. ‘false positive’), while coverage probabilities above 97% indicate an increased chance of type-II error (i.e. ‘false negative’) [54].
To assess the impact of using MLM versus OLS on cost-effectiveness outcomes, cost and effect differences between groups including their CIs and SEs, as well as ICERs, INMBs and the probabilities of cost effectiveness were compared.
R [30] (version 3.5.2) was used to simulate datasets and the cost-effectiveness analyses were performed in StataSE 16® (StataCorp LP, CollegeStation, TX, USA).
Results
In Table 2, performance measures are summarized for OLS and MLM. Table 3 summarizes the cost-effectiveness outcomes as estimated by OLS and MLM. Both tables present estimates for all 24 scenarios.
Table 2.
Performance measures for all scenarios (Monte Carlo SE in parentheses)
| ICC | Method | Costs (true ∆C = €100) | QALYs (true ∆E = 0.05) | INMB (true INMB = 1065) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias (SE) | RMSE (SE) | Coverage probability (SE) | Bias (SE) | RMSE (SE) | Coverage probability (SE) | Bias (SE) | RMSE (SE) | Coverage probability (SE) | ||
| Unbalanced clusters | ||||||||||
| Negative correlation (ρ = − 0.5) | ||||||||||
| 0.05 | OLS | − 4.12 (2.21) | 120.90 (19.58) | 77.7% (0.76) | 0.000060 (0.00045) | 0.025 (0.0040) | 79.2% (0.74) | 5.52 (11.75) | 643.24 (104.81) | 79.0% (0.74) |
| MLM | − 4.39 (2.19) | 120.18 (19.49) | 87.6% (0.60) | 0.00015 (0.00045) | 0.024 (0.0040) | 92.7% (0.48) | 7.96 (11.69) | 639.98 (104.28) | 91.8% (0.50) | |
| 0.10 | OLS | − 3.97 (1.97) | 107.75 (17.29) | 66.0% (0.86) | 0.00031 (0.00072) | 0.039 (0.0064) | 65.8% (0.87) | 11.25 (17.83) | 976.52 (158.58) | 65.8% (0.87) |
| MLM | − 4.21 (1.95) | 106.70 (17.16) | 86.3% (0.63) | 0.00049 (0.00071) | 0.039 (0.0063) | 93.1% (0.46) | 15.65 (17.67) | 967.66 (157.08) | 92.3% (0.49) | |
| 0.20 | OLS | − 3.84 (1.85) | 101.15 (16.14) | 52.8% (0.91) | 0.00053 (0.00082) | 0.045 (0.0073) | 53.2% (0.91) | 16.27 (20.23) | 1108.08 (179.37) | 53.2% (0.91) |
| MLM | − 4.02 (1.82) | 99.88 (15.98) | 85.9% (0.63) | 0.00074 (0.00081) | 0.045 (0.0072) | 93.1% (0.46) | 21.20 (19.99) | 1094.80 (177.04) | 92.8% (0.48) | |
| 0.30 | OLS | − 3.77 (1.80) | 98.52 (15.68) | 43.4% (0.90) | 0.00087 (0.0012) | 0.063 (0.010) | 46.1% (0.91) | 23.97 (27.88) | 1527.11 (246.60) | 46.1% (0.91) |
| MLM | − 3.89 (1.77) | 97.16 (15.51) | 85.8% (0.64) | 0.0011 (0.0011) | 0.062 (0.010) | 93.0% (0.47) | 30.46 (27.51) | 1506.83 (242.98) | 92.8% (0.48) | |
| No correlation (ρ = 0) | ||||||||||
| 0.05 | OLS | − 4.12 (2.21) | 120.90 (19.58) | 77.7% (0.76) | − 0.00044 (0.00044) | 0.024 (0.0038) | 79.7% (0.73) | − 6.18 (10.53) | 576.69 (91.69) | 80.3% (0.73) |
| MLM | − 4.39 (2.19) | 120.18 (19.49) | 87.6% (0.60) | − 0.00038 (0.00044) | 0.024 (0.0038) | 93.8% (0.44) | − 4.39 (10.48) | 573.88 (91.21) | 93.5% (0.45) | |
| 0.10 | OLS | − 3.97 (1.97) | 107.75 (17.29) | 66.0% (0.86) | − 0.00050 (0.00070) | 0.038 (0.0061) | 65.8% (0.87) | − 7.68 (16.54) | 905.56 (143.34) | 65.5% (0.87) |
| MLM | − 4.21 (1.95) | 106.70 (17.16) | 86.3% (0.63) | − 0.00035 (0.00070) | 0.038 (0.0060) | 93.5% (0.45) | − 3.99 (16.39) | 897.52 (142.03) | 93.2% (0.46) | |
| 0.20 | OLS | − 3.84 (1.85) | 101.15 (16.14) | 52.8% (0.91) | − 0.00039 (0.00081) | 0.044 (0.0070) | 52.3% (0.91) | − 5.12 (19.96) | 1038.39 (164.42) | 52.1% (0.91) |
| MLM | − 4.02 (1.82) | 99.88 (15.98) | 85.9% (0.63) | − 0.00020 (0.00080) | 0.044 (0.0069) | 93.65 (0.45) | − 0.57 (18.74) | 1026.18 (162.49) | 93.0% (0.46) | |
| 0.30 | OLS | − 3.77 (1.80) | 98.52 (15.68) | 43.4% (0.90) | − 0.00040 (0.0011) | 0.062 (0.0098) | 44.3% (0.91) | − 5.50 (26.50) | 1451.37 (229.84) | 44.7% (0.91) |
| MLM | − 3.89 (1.77) | 97.16 (15.51) | 85.8% (0.64) | − 0.00013 (0.0011) | 0.061 (0.0097) | 93.2% (0.46) | 0.82 (26.16) | 1432.44 (226.89) | 93.2% (0.46) | |
| Positive correlation (ρ = 0.5) | ||||||||||
| 0.05 | OLS | − 4.12 (2.21) | 120.90 (19.58) | 77.7% (0.76) | − 0.00083 (0.00043) | 0.024 (0.0038) | 80.3% (0.73) | − 15.12 (9.32) | 510.39 (80.52) | 80.7% (0.72) |
| MLM | − 4.39 (2.19) | 120.18 (19.49) | 87.6% (0.60) | − 0.00080 (0.00043) | 0.024 (0.0038) | 93.4% (0.45) | − 14.29 (9.27) | 508.03 (80.08) | 94.1% (0.43) | |
| 0.10 | OLS | − 3.97 (1.97) | 107.75 (17.29) | 66.0% (0.86) | − 0.0012 (0.00069) | 0.038 (0.0061) | 67.7% (0.85) | − 23.50 (15.35) | 840.86 (133.58) | 67.8% (0.85) |
| MLM | − 4.21 (1.95) | 106.70 (17.16) | 86.3% (0.63) | − 0.0011 (0.00069) | 0.038 (0.0060) | 93.4% (0.45) | − 21.46 (15.21) | 833.45 (132.48) | 93.8% (0.44) | |
| 0.20 | OLS | − 3.84 (1.85) | 101.15 (16.14) | 52.8% (0.91) | − 0.0012 (0.00080) | 0.044 (0.0070) | 53.8% (0.91) | − 24.12 (17.80) | 975.01 (155.44) | 53.2% (0.91) |
| MLM | − 4.02 (1.82) | 99.88 (15.98) | 85.9% (0.63) | − 0.0011 (0.00079) | 0.043 (0.0069) | 93.9% (0.46) | − 21.21 (17.59) | 963.54 (153.88) | 93.7% (0.44) | |
| 0.30 | OLS | − 3.77 (1.80) | 98.52 (15.68) | 43.4% (0.90) | − 0.0016 (0.0011) | 0.061 (0.0098) | 46.1% (0.91) | − 32.49 (25.29) | 1385.25 (221.34) | 45.6% (0.90) |
| MLM | − 3.89 (1.77) | 97.16 (15.51) | 85.8% (0.64) | − 0.0014 (0.0011) | 0.061 (0.0097) | 93.4% (0.45) | − 28.13 (24.96) | 1367.13 (218.92) | 93.6% (0.45) | |
| Balanced clusters | ||||||||||
| Negative correlation (ρ = − 0.5) | ||||||||||
| 0.05 | OLS | 1.21 (2.17) | 118.63 (19.21) | 79.4% (0.74) | − 0.000011 (0.00043) | 0.024 (0.0038) | 81.2% (0.71) | − 1.47 (11.33) | 620.43 (99.40) | 80.5% (0.72) |
| MLM | 1.21 (2.17) | 118.63 (19.21) | 87.6% (0.60) | − 0.000011 (0.00043) | 0.024 (0.0038) | 93.4% (0.45) | − 1.47 (11.33) | 620.43 (99.40) | 92.9% (0.47) | |
| 0.10 | OLS | 1.11 (1.92) | 105.11 (17.04) | 67.2% (0.86) | − 0.00000024 (0.00069) | 0.038 (0.0060) | 68.7% (0.85) | − 1.17 (17.08) | 935.20 (150.07) | 68.3% (0.85) |
| MLM | 1.11 (1.92) | 105.11 (17.04) | 87.2% (0.61) | − 0.00000024 (0.00069) | 0.038 (0.0060) | 93.4% (0.45) | − 1.17 (17.08) | 935.20 (150.07) | 92.8% (0.47) | |
| 0.20 | OLS | 1.03 (1.80) | 98.46 (15.97) | 54.5% (0.91) | 0.000010 (0.00078) | 0.043 (0.0069) | 55.6% (0.91) | − 0.80 (19.30) | 1056.89 (170.14) | 55.9% (0.91) |
| MLM | 1.03 (1.80) | 98.46 (15.97) | 86.8% (0.62) | 0.000010 (0.00078) | 0.043 (0.0069) | 93.4% (0.45) | − 0.80 (19.30) | 1056.89 (170.14) | 93.3% (0.46) | |
| 0.30 | OLS | 0.99 (1.75) | 95.85 (15.56) | 45.9% (0.91) | 0.000024 (0.0011) | 0.060 (0.0097) | 48.6% (0.91) | − 0.44 (26.54) | 1453.49 (234.41) | 48.5% (0.91) |
| MLM | 0.99 (1.75) | 95.85 (15.56) | 86.7% (0.62) | 0.000024 (0.0011) | 0.060 (0.0097) | 93.5% (0.45) | − 0.44 (26.54) | 1453.49 (234.41) | 93.3% (0.46) | |
| No correlation (ρ = 0) | ||||||||||
| 0.05 | OLS | 1.21 (2.17) | 118.63 (19.21) | 79.4% (0.74) | 0.00019 (0.00042) | 0.023 (0.0037) | 81.4% (0.71) | 3.28 (10.13) | 554.87 (88.50) | 81.3% (0.71) |
| MLM | 1.21 (2.17) | 118.63 (19.21) | 87.6% (0.60) | 0.00019 (0.00042) | 0.023 (0.0037) | 94.0% (0.43) | 3.28 (10.13) | 554.87 (88.50) | 93.3% (0.46) | |
| 0.10 | OLS | 1.11 (1.92) | 105.11 (17.04) | 67.2% (0.86) | 0.00031 (0.00067) | 0.037 (0.0058) | 69.3% (0.84) | 6.02 (15.77) | 863.79 (137.79) | 68.4% (0.85) |
| MLM | 1.11 (1.92) | 105.11 (17.04) | 87.2% (0.61) | 0.00031 (0.00067) | 0.037 (0.0058) | 94.1% (0.43) | 6.02 (15.77) | 863.79 (137.79) | 93.9% (0.44) | |
| 0.20 | OLS | 1.03 (1.80) | 98.46 (15.97) | 54.5% (0.91) | 0.00034 (0.00077) | 0.042 (0.0067) | 56.3% (0.91) | 6.90 (17.98) | 984.90 (157.60) | 56.7% (0.90) |
| MLM | 1.03 (1.80) | 98.46 (15.97) | 86.8% (0.62) | 0.00034 (0.00077) | 0.042 (0.0067) | 94.0% (0.43) | 6.90 (17.98) | 984.90 (157.60) | 93.8% (0.44) | |
| 0.30 | OLS | 0.99 (1.75) | 95.85 (15.56) | 45.9% (0.91) | 0.00047 (0.0011) | 0.059 (0.0094) | 48.7% (0.91) | 9.85 (25.08) | 1373.24 (220.15) | 48.8% (0.91) |
| MLM | 0.99 (1.75) | 95.85 (15.56) | 86.7% (0.62) | 0.00047 (0.0011) | 0.059 (0.0094) | 93.8% (0.44) | 9.85 (25.08) | 1373.24 (220.15) | 93.8% (0.44) | |
| Positive correlation (ρ = 0.5) | ||||||||||
| 0.05 | OLS | 1.21 (2.17) | 118.63 (19.21) | 79.4% (0.74) | 0.00035 (0.00042) | 0.021 (0.0.0037) | 81.9% (0.70) | 6.83 (9.02) | 493.90 (78.22) | 82.1% (0.70) |
| MLM | 1.21 (2.17) | 118.63 (19.21) | 87.6% (0.60) | 0.00035 (0.00042) | 0.021 (0.0.0037) | 94.6% (0.41) | 6.83 (9.02) | 493.90 (78.22) | 94.8% (0.40) | |
| 0.10 | OLS | 1.11 (1.92) | 105.11 (17.04) | 67.2% (0.86) | 0.00053 (0.00067) | 0.037 (0.0058) | 69.8% (0.84) | 11.30 (14.75) | 808.07 (128.26) | 69.7% (0.84) |
| MLM | 1.11 (1.92) | 105.11 (17.04) | 87.2% (0.61) | 0.00053 (0.00067) | 0.037 (0.0058) | 94.3% (0.42) | 11.30 (14.75) | 808.07 (128.26) | 94.5% (0.42) | |
| 0.20 | OLS | 1.03 (1.80) | 98.46 (15.97) | 54.5% (0.91) | 0.00058 (0.00077) | 0.042 (0.0067) | 56.2% (0.91) | 12.48 (17.03) | 932.44 (148.53) | 56.5% (0.91) |
| MLM | 1.03 (1.80) | 98.46 (15.97) | 86.8% (0.62) | 0.00058 (0.00077) | 0.042 (0.0067) | 94.2% (0.43) | 12.48 (17.03) | 932.44 (148.53) | 94.1% (0.43) | |
| 0.30 | OLS | 0.99 (1.75) | 95.85 (15.56) | 45.9% (0.91) | 0.00078 (0.0011) | 0.059 (0.0094) | 48.2% (0.91) | 17.24 (24.15) | 1322.74 (211.27) | 48.4% (0.91) |
| MLM | 0.99 (1.75) | 95.85 (15.56) | 86.7% (0.62) | 0.00078 (0.0011) | 0.059 (0.0094) | 94.1% (0.43) | 17.24 (24.15) | 1322.74 (211.27) | 94.1% (0.43) | |
Coverage probabilities are presented in percentages (%). Bold text indicates coverage probabilities < 90%
ICC intraclass correlation coefficients, INMB incremental net monetary benefit, MLM multilevel modelling, OLS ordinary least squares, QALY quality-adjusted life-year, RMSE root mean squared error, SE standard error
Table 3.
Average cost-effectiveness outcomes and statistical uncertainty estimates over 3000 simulated datasets with true ∆C = €100, true ∆E = 0.05 and true INMB = 1065
| ICC | Method | ∆C (95% CI), € | SE ∆C | ∆E (95% CI), QALY | SE ∆E | ICER, €/QALY | INMB (95% CI) At a ceiling ratio = 23, 300 €/QALY |
SE INMB |
|---|---|---|---|---|---|---|---|---|
| Unbalanced clusters | ||||||||
| Negative correlation (ρ = − 0.5) | ||||||||
| 0.05 | OLS | 96 (− 51 to 243) | 75 | 0.050 (0.019 to 0.081) | 0.016 | 1915 | 1071 (269 to 1873) | 409 |
| MLM | 96 (− 88 to 280) | 94 | 0.050 (0.0049 to 0.095) | 0.023 | 1906 | 1073 (− 81 to 2227) | 589 | |
| 0.10 | OLS | 96 (− 6 to 198) | 52 | 0.050 (0.013 to 0.087) | 0.019 | 1909 | 1076 (145 to 2007) | 475 |
| MLM | 96 (− 65 to 257) | 82 | 0.050 (− 0.023 to 0.12) | 0.037 | 1897 | 1081 (− 675 to 2837) | 896 | |
| 0.20 | OLS | 96 (23 to 169) | 37 | 0.050 (0.017to 0.083) | 0.017 | 1903 | 1081 (285 to 1877) | 406 |
| MLM | 96 (− 53 to 245) | 76 | 0.051 (− 0.031 to 0.13) | 0.042 | 1892 | 1086 (− 903 to 3075) | 1015 | |
| 0.30 | OLS | 96 (37 to 155) | 30 | 0.051 (0.014 to 0.088) | 0.019 | 1892 | 1089 (176 to 2002) | 466 |
| MLM | 96 (− 49 to 241) | 74 | 0.051 (− 0.065 to 0.17) | 0.059 | 1879 | 1095 (− 1653 to 3843) | 1402 | |
| No correlation (ρ = 0) | ||||||||
| 0.05 | OLS | 96 (− 51 to 243) | 75 | 0.050 (0.019 to 0.081) | 0.016 | 1935 | 1059 (320 to 1798) | 377 |
| MLM | 96 (− 88 to 280) | 94 | 0.050 (0.0049 to 0.095) | 0.023 | 1927 | 1061 (− 9 to 2131) | 546 | |
| 0.10 | OLS | 96 (− 6 to 198) | 52 | 0.049 (0.012 to 0.086) | 0.019 | 1940 | 1057 (173 to 1941) | 451 |
| MLM | 96 (− 65 to 257) | 82 | 0.050 (− 0.023 to 0.12) | 0.037 | 1929 | 1061 (− 621 to 2743) | 858 | |
| 0.20 | OLS | 96 (23 to 169) | 37 | 0.050 (0.017 to 0.083) | 0.017 | 1938 | 1060 (300 to 1820) | 388 |
| MLM | 96 (− 53 to 245) | 76 | 0.050 (− 0.032 to 0.13) | 0.042 | 1927 | 1064 (− 853 to 2981) | 978 | |
| 0.30 | OLS | 96 (37 to 155) | 30 | 0.050 (0.013 to 0.087) | 0.019 | 1940 | 1060 (174 to 1946) | 452 |
| MLM | 96 (− 49 to 241) | 74 | 0.050 (− 0.066 to 0.17) | 0.059 | 1927 | 1066 (− 1609 to 3741) | 1365 | |
| Positive correlation (ρ = 0.5) | ||||||||
| 0.05 | OLS | 96 (− 51 to 243) | 75 | 0.049 (0.018 to 0.080) | 0.016 | 1950 | 1050 (380 to 1720) | 342 |
| MLM | 96 (− 88 to 280) | 94 | 0.049 (0.0039 to 0.094) | 0.023 | 1943 | 1051 (67 to 2035) | 502 | |
| 0.10 | OLS | 96 (− 6 to 198) | 52 | 0.049 (0.012 to 0.086) | 0.019 | 1967 | 1042 (209 to 1875) | 425 |
| MLM | 96 (− 65 to 257) | 82 | 0.049 (− 0.024 to 0.12) | 0.037 | 1959 | 1044 (− 557 to 2645) | 817 | |
| 0.20 | OLS | 96 (23 to 169) | 37 | 0.049 (0.016 to 0.082) | 0.017 | 1970 | 1041 (316 to 1766) | 370 |
| MLM | 96 (− 53 to 245) | 76 | 0.049 (− 0.033 to 0.13) | 0.042 | 1962 | 1044 (− 798 to 2886) | 940 | |
| 0.30 | OLS | 96 (37 to 155) | 30 | 0.048 (0.011 to 0.085) | 0.019 | 1987 | 1033 (176 to 1890) | 437 |
| MLM | 96 (− 49 to 241) | 74 | 0.049 (− 0.065 to 0.16) | 0.058 | 1976 | 1037 (− 1564 to 3638) | 1327 | |
| Balanced clusters | ||||||||
| Negative correlation (ρ = − 0.5) | ||||||||
| 0.05 | OLS | 101 (− 46 to 248) | 75 | 0.050 (0.019 to 0.081) | 0.016 | 2025 | 1064 (264 to 1864) | 408 |
| MLM | 101 (− 81 to 283) | 93 | 0.050 (0.0050 to 0.095) | 0.023 | 2025 | 1064 (− 79 to 2207) | 583 | |
| 0.10 | OLS | 101 (− 1 to 203) | 52 | 0.050 (0.013 to 0.087) | 0.019 | 2022 | 1064 (135 to 1993) | 474 |
| MLM | 101 (− 58 to 260) | 81 | 0.050 (− 0.021 to 0.12) | 0.036 | 2022 | 1064 (− 680 to 2808) | 890 | |
| 0.20 | OLS | 101 (28 to 174) | 37 | 0.050 (0.017 to 0.083) | 0.017 | 2020 | 1064 (270 to 1858) | 405 |
| MLM | 101 (− 48 to 250) | 76 | 0.050 (− 0.032 to 0.13) | 0.042 | 2020 | 1064 (− 912 to 3040) | 1008 | |
| 0.30 | OLS | 101 (42 to 160) | 30 | 0.050 (0.013 to 0.087) | 0.019 | 2019 | 1065 (154 to 1976) | 465 |
| MLM | 101 (− 44 to 246) | 74 | 0.050 (− 0.064 to 0.16) | 0.058 | 2019 | 1065 (− 1663 to 3793) | 1392 | |
| No correlation (ρ = 0) | ||||||||
| 0.05 | OLS | 101 (− 46 to 248) | 75 | 0.050 (0.019 to 0.081) | 0.016 | 2016 | 1068 (331 to 1805) | 376 |
| MLM | 101 (− 81 to 283) | 93 | 0.050 (0.0050 to 0.095) | 0.023 | 2016 | 1068 (2 to 2134) | 544 | |
| 0.10 | OLS | 101 (− 1 to 203) | 52 | 0.050 (0.013 to 0.087) | 0.019 | 2010 | 1071 (189 to 1953) | 450 |
| MLM | 101 (− 58 to 260) | 81 | 0.050 (− 0.021 to 0.12) | 0.036 | 2010 | 1071 (− 601 to 2743) | 853 | |
| 0.20 | OLS | 101 (28 to 174) | 37 | 0.050 (0.017 to 0.083) | 0.017 | 2007 | 1072 (312 to 1832) | 388 |
| MLM | 101 (− 48 to 250) | 76 | 0.050 (− 0.032 to 0.13) | 0.042 | 2007 | 1072 (− 784 to 2928) | 947 | |
| 0.30 | OLS | 101 (42 to 160) | 30 | 0.050 (0.013 to 0.087) | 0.019 | 2001 | 1075 (191 to 1959) | 451 |
| MLM | 101 (− 44 to 246) | 74 | 0.050 (− 0.064 to 0.16) | 0.058 | 2001 | 1075 (− 1589 to 3739) | 1359 | |
| Positive correlation (ρ = 0.5) | ||||||||
| 0.05 | OLS | 101 (− 46 to 248) | 75 | 0.050 (0.019 to 0.081) | 0.016 | 2010 | 1072 (402 to 1742) | 342 |
| MLM | 101 (− 81 to 283) | 93 | 0.050 (0.0050 to 0.095) | 0.023 | 2010 | 1072 (92 to 2052) | 500 | |
| 0.10 | OLS | 101 (− 1 to 203) | 52 | 0.051 (0.014 to 0.088) | 0.019 | 2001 | 1076 (243 to 1909) | 425 |
| MLM | 101 (− 58 to 260) | 81 | 0.051 (− 0.020 to 0.12) | 0.036 | 2001 | 1076 (− 519 to 2671) | 814 | |
| 0.20 | OLS | 101 (28 to 174) | 37 | 0.051 (0.018 to 0.084) | 0.017 | 1998 | 1077 (354 to 1800) | 933 |
| MLM | 101 (− 48 to 250) | 76 | 0.051 (− 0.031 to 0.13) | 0.042 | 1998 | 1077 (− 760 to 2914) | 937 | |
| 0.30 | OLS | 101 (42 to 160) | 30 | 0.051 (0.014 to 0.088) | 0.019 | 1989 | 1082 (227 to 1937) | 436 |
| MLM | 101 (− 44 to 246) | 74 | 0.051 (− 0.063 to 0.17) | 0.058 | 1989 | 1082 (− 1511 to 3675) | 1323 | |
CI confidence interval, ICC intracluster correlation coefficient, ICER incremental cost-effectiveness ratio, INMB incremental net monetary benefit, MLM multilevel modelling, OLS ordinary least squares regression, QALY quality-adjusted life-year, SE standard error, ∆C cost difference, ∆E effect difference
Performance Measures
For all outcomes, bias and RMSE were roughly similar for MLM and OLS. However, for all outcomes, MLM resulted in coverage probabilities closer to nominal levels compared with OLS (Table 2). The differences between MLM and OLS in terms of coverage probabilities became more pronounced with increasing ICCs (Table 2).
Cost-Effectiveness Outcomes
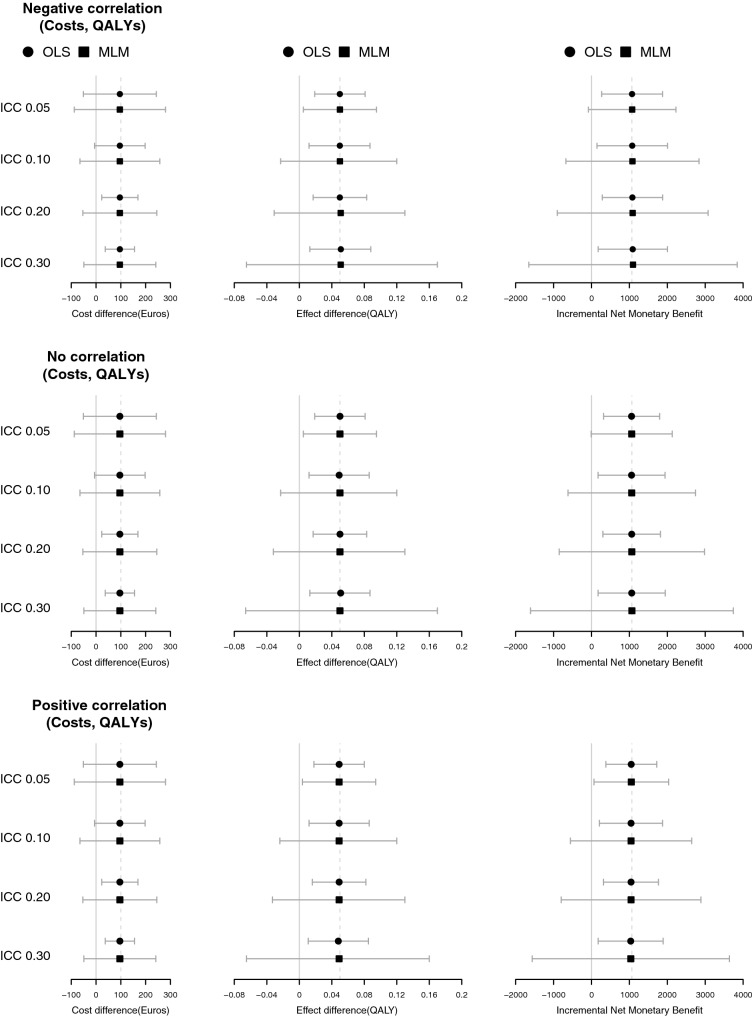
Table 3 shows that cost differences, effect differences, ICERs and INMBs were exactly similar for OLS and MLM when clusters were balanced, and only slightly differed between the two methods with unbalanced clusters. In all scenarios, the CI width increased considerably when using MLM instead of OLS for cost and effect differences as well as INMBs. This increase in CI width was found to increase with increasing ICCs (Table 3). In several scenarios, QALY and cost differences between groups and INMBs were not statistically significant when using MLM, whereas they were significant when using OLS. This is graphically illustrated in Fig. 2. MLM and OLS also resulted in different CEACs, with the difference in probabilities of the intervention being cost effective compared with control becoming larger with higher ICCs (Fig. 3).
Fig. 2.
Graphical presentation of confidence interval width and mean point estimates with increasing ICCs and correlation for costs, QALYs and INMBs with unbalanced clusters. ICC intracluster correlation coefficient, INMB incremental net monetary benefit, MLM multilevel modelling, OLS ordinary least squares regression, QALY quality-adjusted life-year
Fig. 3.
Cost-effectiveness acceptability curves for different ICCs with negative correlation (ρ = − 0.5). ICC intracluster correlation coefficient, MLM multilevel modelling, OLS ordinary least squares regression, P(CE) probability of cost-effectiveness, QALY quality-adjusted life-year
Discussion
Using MLM instead of OLS in trial-based economic evaluations with clustered data showed better statistical performance, specifically in terms of coverage probabilities that were closer to the nominal level of 1 − α. Regarding cost-effectiveness outcomes, using MLM instead of OLS had a large impact on the level of statistical uncertainty surrounding cost differences, effect differences and INMBs. Generally, MLM resulted in a larger amount of statistical uncertainty than OLS, especially for higher ICCs. In some scenarios, this even resulted in cost and/or effect differences being statistically significant when using OLS, but statistically non-significant when using MLM. The impact of using MLM instead of OLS on the CEACs was substantial. These findings indicate that ignoring the clustered nature of data in economic evaluations alongside cluster randomized trials is inappropriate. Thus, if data are clustered in a trial-based economic evaluation, researchers are highly encouraged to use MLM over OLS.
The rationale behind using MLM when data are clustered is to accurately estimate the amount of variation in the data, which is typically underestimated when using OLS to analyze such data [4, 55]. Even at a relatively small ICC (i.e. 0.05), the amount of statistical uncertainty was found to be considerably larger when using MLM instead of OLS. In line with previous studies, we also found that the degree of underestimation in statistical uncertainty increased with larger ICCs [4, 55, 56]. The underestimation of statistical uncertainty when using OLS may increase the probability of falsely rejecting the null-hypothesis (type-1 error), meaning that researchers may incorrectly claim that an intervention is cost effective when in truth this is not the case. This is emphasized by the fact that the estimated coverage probabilities of OLS were further from the nominal level of 0.95 than MLM. Thus, ignoring clustering of data in economic evaluations alongside cluster randomized trials may lead to suboptimal conclusions.
It is worth noting that point estimates of the differences in costs and effects between treatment groups only differed between MLM and OLS when clusters were unbalanced. This is due to the fact that, if clusters are unbalanced, a heterogeneous treatment effect is present between clusters, whereas this is not the case if clusters are balanced [4]. However, the identified differences between statistical approaches were relatively small, which is likely the result of the moderate degree of imbalance that was generated in the simulated clusters [57–59].
Due to the higher levels of statistical uncertainty as estimated by MLM compared with OLS, the probability of cost effectiveness was lower for MLM compared with OLS. At larger ICCs (i.e. ICC = 0.30), the maximum difference in the probability of cost effectiveness between both methods was relatively large (i.e. 0.27), which might have implications on reimbursement decisions. Even at a small ICC (ICC = 0.05), a notable difference in the probability of cost effectiveness was apparent (i.e. max 0.08).
Although point estimates were roughly similar between MLM and OLS, MLM was found to estimate the amount of variation in the simulated data more appropriately with coverage probabilities closer to the nominal level of 0.95 than OLS. For effect differences and INMBs, coverage probabilities reached nominal levels. For cost differences, this was not the case, which is likely due to the highly skewed nature of cost data. Previous research showed that when sampling from a skewed distribution, coverage probabilities tend to be substantially lower than the nominal 1-α, and this effect will increase if sampling is done from more heavy-tailed distributions [60].
Comparison with Other Studies
Previous studies also found MLM to be preferred over OLS [24, 25, 27]. However, these studies assumed a normal distribution for costs and effects. Although some authors [40, 61–63] showed that MLMs assuming a normal distribution can adequately handle skewed distributions, the current study extends the multilevel framework by providing insight into how a frequentist MLM combined with a cluster-bootstrap that accounts for the skewed distribution of costs performs in comparison to a naïve analysis such as a bootstrapped OLS. Ren et al. [49] showed that bootstrapping at the cluster level is preferred over bootstrapping at the individual level when resampling clustered data. The main reason for this is that resampling at the cluster level accurately reflects the original sample information.
Strengths and Limitations and Implications for Further Research
A strength of this study was the comparison of both the performance and impact of MLM and OLS for a wide range of scenarios. Based on empirical datasets, different parameters were specified and varied to simulate data that resembled ‘real’ data as closely as possible. One of the main advantages of this method is that it avoids the need for a large number of empirical datasets, which is generally not feasible [64]. A second strength is that the multilevel framework for trial-based economic evaluations alongside cluster-randomized trials is extended by accounting for the right skewed nature of cost data using a non-parametric cluster-bootstrap. Also, to the best of our knowledge, this is the first study that assessed the impact of adjusting for the clustered nature of cost data in trial-based economic evaluations on the resulting cost differences, effect differences, ICERs and CEACs.
This study also has some limitations. First, when simulating effects, QALYs were assumed to be normally distributed, although they may sometimes be left skewed. This was done because it enabled precise specification of variances and correlations between costs and effects. Second, no other methods than OLS and MLM were considered. MLM was chosen because previous studies evaluating the performance of different methods to deal with clustered data [20–27] concluded that MLM was one of the most appropriate methods [25]. Third, although efforts were made to simulate data as appropriately as possible, it is possible that empirical cost and effect data still have certain characteristics that we did not simulate in the current study, for example baseline imbalances and missing data. Fourth, although within the statistical literature, different bootstrapping techniques have been discussed and recommended [6, 20, 23, 49, 65], there is a lack of consensus on how to combine bootstrapping techniques with a cluster-adjusting analysis such as MLM. In the current study, the resampling approach of Ren et al. [49] was used, but coverage probabilities for costs did not reach nominal levels. Future research should, therefore, investigate which bootstrap approach is most optimal in situations with right-skewed cost data and take other characteristics into account in the simulations.
Conclusion
Although OLS produced roughly similar point estimates to MLM in trial-based economic evaluations with clustered data, it substantially underestimated the amount of variation compared with MLM. In all scenarios, OLS overestimated the probability of cost effectiveness compared with MLM. To prevent suboptimal conclusions, it is important to use MLM in trial-based economic evaluations when data are clustered.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Author contributions
ME: study rationale and design, writing the manuscript, analysis, interpretation and reflection, rewriting the manuscript. JMVD: study rationale and design, interpretation and reflection, reviewing the manuscript. KSG: analysis, interpretation and reflection, reviewing the manuscript. MWH: interpretation and reflection, reviewing the manuscript. MWT: interpretation and reflection, reviewing the manuscript. JEB: study rationale and design, interpretation and reflection, reviewing the manuscript. All authors have participated in the planning, execution, interpretation and/or reporting of the study and all of them approved the final version of the manuscript.
Declarations
Funding
No financial support for this study was provided.
Conflict of interest
The authors declare that there is no conflict of interest.
Availability of data and material
Data can be generated using the provided simulation code.
Code availability
Analysis can be performed using the provided software code (Stata®).
Contributor Information
Mohamed El Alili, Email: m.elalili@vu.nl.
Johanna M. van Dongen, Email: j.m.van.dongen@vu.nl
Keith S. Goldfeld, Email: keith.goldfeld@nyulangone.org
Martijn W. Heymans, Email: mw.heymans@amsterdamumc.nl
Maurits W. van Tulder, Email: maurits.van.tulder@vu.nl
Judith E. Bosmans, Email: j.e.bosmans@vu.nl
References
- 1.Drummond M, Sculper M, Claxton K, Stoddart G, Torrance G. Methods for the economic evaluation of Health Care Programmes. 4. Oxford: Oxford University Press; 2015. [Google Scholar]
- 2.Petrou S, Gray A. Economic evaluation alongside randomised controlled trials: design, conduct, analysis, and reporting. BMJ. 2011;342:d1548. doi: 10.1136/bmj.d1548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Manca A, Rice N, Sculpher MJ, Briggs AH. Assessing generalisability by location in trial-based cost-effectiveness analysis: the use of multilevel models. Health Econ. 2005;14(5):471–485. doi: 10.1002/hec.914. [DOI] [PubMed] [Google Scholar]
- 4.Twisk JW. Applied multilevel analysis: a practical guide for medical researchers. Cambridge: Cambridge University Press; 2006. [Google Scholar]
- 5.Gomes M, Grieve R, Nixon R, Edmunds WJ. Statistical methods for cost-effectiveness analyses that use data from cluster randomized trials: a systematic review and checklist for critical appraisal. Med Decis Mak. 2012;32(1):209–220. doi: 10.1177/0272989X11407341. [DOI] [PubMed] [Google Scholar]
- 6.Flynn T, Peters T. Conceptual issues in the analysis of cost data within cluster randomized trials. J Health Serv Res Policy. 2005;10(2):97–102. doi: 10.1258/1355819053559065. [DOI] [PubMed] [Google Scholar]
- 7.McNeish DM. Analyzing clustered data with OLS regression: the effect of a hierarchical data structure. Mult Linear Regres Viewp. 2014;40(1):11–16. [Google Scholar]
- 8.Campbell MJ, Donner A, Klar N. Developments in cluster randomized trials and statistics in medicine. Stat Med. 2007;26(1):2–19. doi: 10.1002/sim.2731. [DOI] [PubMed] [Google Scholar]
- 9.Donner A, Klar N. Design and analysis of cluster randomization trials in health research. England: Arnold London; 2000. [Google Scholar]
- 10.Hayes R, Moulton L. Cluster randomised trials. Boca Raton: Taylor & Francis; 2009. [Google Scholar]
- 11.Austin PC. A comparison of the statistical power of different methods for the analysis of cluster randomization trials with binary outcomes. Stat Med. 2007;26(19):3550–3565. doi: 10.1002/sim.2813. [DOI] [PubMed] [Google Scholar]
- 12.Feng Z, McLerran D, Grizzle J. A comparison of statistical methods for clustered data analysis with Gaussian error. Stat Med. 1996;15(16):1793–1806. doi: 10.1002/(SICI)1097-0258(19960830)15:16<1793::AID-SIM332>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
- 13.Nixon RM, Thompson SG. Baseline adjustments for binary data in repeated cross-sectional cluster randomized trials. Stat Med. 2003;22(17):2673–2692. doi: 10.1002/sim.1483. [DOI] [PubMed] [Google Scholar]
- 14.Ukoumunne OC, Thompson SG. Analysis of cluster randomized trials with repeated cross-sectional binary measurements. Stat Med. 2001;20(3):417–433. doi: 10.1002/1097-0258(20010215)20:3<417::aid-sim802>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- 15.Omar RZ, Thompson SG. Analysis of a cluster randomized trial with binary outcome data using a multi-level model. Stat Med. 2000;19(19):2675–2688. doi: 10.1002/1097-0258(20001015)19:19<2675::aid-sim556>3.0.co;2-a. [DOI] [PubMed] [Google Scholar]
- 16.Spiegelhalter DJ. Bayesian methods for cluster randomized trials with continuous responses. Stat Med. 2001;20(3):435–452. doi: 10.1002/1097-0258(20010215)20:3<435::aid-sim804>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- 17.Turner RM, Omar RZ, Thompson SG. Bayesian methods of analysis for cluster randomized trials with binary outcome data. Stat Med. 2001;20(3):453–472. doi: 10.1002/1097-0258(20010215)20:3<453::aid-sim803>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- 18.El Alili M, van Dongen JM, Huirne JAF, van Tulder MW, Bosmans JE. Reporting and analysis of trial-based cost-effectiveness evaluations in obstetrics and gynaecology. Pharmacoeconomics. 2017;35(10):1007–1033. doi: 10.1007/s40273-017-0531-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.van Dongen JM, El Alili M, Varga AN, Guevara Morel AE, Jornada Ben A, Khorrami M, et al. What do national pharmacoeconomic guidelines recommend regarding the statistical analysis of trial-based economic evaluations? Expert Rev Pharmacoecon Outcomes Res. 2020;20(1):27–37. doi: 10.1080/14737167.2020.1694410. [DOI] [PubMed] [Google Scholar]
- 20.Bachmann MO, Fairall L, Clark A, Mugford M. Methods for analyzing cost effectiveness data from cluster randomized trials. Cost Eff Resour Alloc. 2007;5:12. doi: 10.1186/1478-7547-5-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Flynn TN, Peters TJ. Cluster randomized trials: another problem for cost-effectiveness ratios. Int J Technol Assess Health Care. 2005;21(3):403–409. doi: 10.1017/s0266462305050531. [DOI] [PubMed] [Google Scholar]
- 22.Grieve R, Nixon R, Thompson SG. Bayesian hierarchical models for cost-effectiveness analyses that use data from cluster randomized trials. Med Decis Mak. 2010;30(2):163–175. doi: 10.1177/0272989X09341752. [DOI] [PubMed] [Google Scholar]
- 23.Davison AC, Hinkley DV. Bootstrap methods and their application. Cambridge: Cambridge University Press; 1997. [Google Scholar]
- 24.Goldstein H. Multilevel statistical models. New York: Wiley; 2011. [Google Scholar]
- 25.Gomes M, Ng ES, Grieve R, Nixon R, Carpenter J, Thompson SG. Developing appropriate methods for cost-effectiveness analysis of cluster randomized trials. Med Decis Mak. 2012;32(2):350–361. doi: 10.1177/0272989X11418372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hardin JW. Generalized estimating equations (GEE) New York: Wiley Online Library; 2005. [Google Scholar]
- 27.Leyland AH, Goldstein H. Multilevel modelling of health statistics. New York: Wiley; 2001. [Google Scholar]
- 28.Gomes M, Grieve R, Nixon R, Ng ES, Carpenter J, Thompson SG. Methods for covariate adjustment in cost-effectiveness analysis that use cluster randomised trials. Health Econ. 2012;21(9):1101–1118. doi: 10.1002/hec.2812. [DOI] [PubMed] [Google Scholar]
- 29.Goldfeld, K. S. simstudy: Simulation of study data (2018). R package version 0.1.16 retrieved from https://cran.r-project.org/web/packages/simstudy/index.html.
- 30.Team RC. R: a language and environment for statistical computing. Vienna: R Foundation for statistical computing; 2017. [Google Scholar]
- 31.Morris TP, White IR, Crowther MJ. Using simulation studies to evaluate statistical methods. Stat Med. 2019;38(11):2074–2102. doi: 10.1002/sim.8086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.O'Hagan A, Stevens JW. Assessing and comparing costs: how robust are the bootstrap and methods based on asymptotic normality? Health Econ. 2003;12(1):33–49. doi: 10.1002/hec.699. [DOI] [PubMed] [Google Scholar]
- 33.Donner A. Some aspects of the design and analysis of cluster randomization trials. J R Stat Soc: Ser C (Appl Stat) 2002;47(1):95–113. [Google Scholar]
- 34.Coretti S, Ruggeri M, McNamee P. The minimum clinically important difference for EQ-5D index: a critical review. Expert Rev Pharmacoecon Outcomes Res. 2014;14(2):221–233. doi: 10.1586/14737167.2014.894462. [DOI] [PubMed] [Google Scholar]
- 35.Whitehead SJ, Ali S. Health outcomes in economic evaluation: the QALY and utilities. Br Med Bull. 2010;96(1):5–21. doi: 10.1093/bmb/ldq033. [DOI] [PubMed] [Google Scholar]
- 36.Barrie S. QALYs, euthanasia and the puzzle of death. J Med Ethics. 2015;41(8):635. doi: 10.1136/medethics-2014-102060. [DOI] [PubMed] [Google Scholar]
- 37.Mihaylova B, Briggs A, O'Hagan A, Thompson SG. Review of statistical methods for analysing healthcare resources and costs. Health Econ. 2011;20(8):897–916. doi: 10.1002/hec.1653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gilleskie DB, Mroz TA. A flexible approach for estimating the effects of covariates on health expenditures. J Health Econ. 2004;23(2):391–418. doi: 10.1016/j.jhealeco.2003.09.008. [DOI] [PubMed] [Google Scholar]
- 39.Polsky D, Glick HA, Willke R, Schulman K. Confidence intervals for cost-effectiveness ratios: a comparison of four methods. Health Econ. 1997;6(3):243–252. doi: 10.1002/(sici)1099-1050(199705)6:3<243::aid-hec269>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 40.Willan AR, Briggs AH, Hoch JS. Regression methods for covariate adjustment and subgroup analysis for non-censored cost-effectiveness data. Health Econ. 2004;13(5):461–475. doi: 10.1002/hec.843. [DOI] [PubMed] [Google Scholar]
- 41.Aarts E, Dolan CV, Verhage M, van der Sluis S. Multilevel analysis quantifies variation in the experimental effect while optimizing power and preventing false positives. BMC Neurosci. 2015;16:94. doi: 10.1186/s12868-015-0228-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Killip S, Mahfoud Z, Pearce K. What is an intracluster correlation coefficient? Crucial concepts for primary care researchers. Ann Fam Med. 2004;2(3):204–208. doi: 10.1370/afm.141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Walters SJ, Brazier JE. Comparison of the minimally important difference for two health state utility measures: EQ-5D and SF-6D. Qual Life Res. 2005;14(6):1523–1532. doi: 10.1007/s11136-004-7713-0. [DOI] [PubMed] [Google Scholar]
- 44.Kim S-K, Kim S-H, Jo M-W, Lee S-I. Estimation of minimally important differences in the EQ-5D and SF-6D indices and their utility in stroke. Health Qual Life Outcomes. 2015;13:32. doi: 10.1186/s12955-015-0227-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pickard AS, Neary MP, Cella D. Estimation of minimally important differences in EQ-5D utility and VAS scores in cancer. Health Qual Life Outcomes. 2007;5:70. doi: 10.1186/1477-7525-5-70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gray AM, Clarke PM, Wolstenholme JL, Wordsworth S. Applied methods of cost-effectiveness analysis in healthcare. Oxford: Oxford University Press; 2011. [Google Scholar]
- 47.Eldridge SM, Ashby D, Kerry S. Sample size for cluster randomized trials: effect of coefficient of variation of cluster size and analysis method. Int J Epidemiol. 2006;35(5):1292–1300. doi: 10.1093/ije/dyl129. [DOI] [PubMed] [Google Scholar]
- 48.Barber JA, Thompson SG. Analysis of cost data in randomized trials: an application of the non-parametric bootstrap. Stat Med. 2000;19(23):3219–3236. doi: 10.1002/1097-0258(20001215)19:23<3219::aid-sim623>3.0.co;2-p. [DOI] [PubMed] [Google Scholar]
- 49.Ren S, Lai H, Tong W, Aminzadeh M, Hou X, Lai S. Nonparametric bootstrapping for hierarchical data. J Appl Stat. 2010;37(9):1487–1498. [Google Scholar]
- 50.Glick H, Doshi JA, Sonnad SS, Polsky D. Economic evaluation in clinical trials. 2. Oxford: Oxford University Press; 2015. [Google Scholar]
- 51.Fenwick E, O'Brien BJ, Briggs A. Cost-effectiveness acceptability curves—facts, fallacies and frequently asked questions. Health Econ. 2004;13(5):405–415. doi: 10.1002/hec.903. [DOI] [PubMed] [Google Scholar]
- 52.Hoch JS, Dewa CS. Advantages of the net benefit regression framework for economic evaluations of interventions in the workplace: a case study of the cost-effectiveness of a collaborative mental health care program for people receiving short-term disability benefits for psychiatric disorders. J Occup Environ Med. 2014;56(4):441–445. doi: 10.1097/JOM.0000000000000130. [DOI] [PubMed] [Google Scholar]
- 53.van Hout BA, Al MJ, Gordon GS, Rutten FF. Costs, effects and C/E-ratios alongside a clinical trial. Health Econ. 1994;3(5):309–319. doi: 10.1002/hec.4730030505. [DOI] [PubMed] [Google Scholar]
- 54.Diaz-ordaz K, Kenward M, Gomes M, Grieve R. Multiple imputation methods for bivariate outcomes in cluster randomised trials. Stat Med. 2016;35(20):3482–96. [DOI] [PMC free article] [PubMed]
- 55.Huang FL. Multilevel modeling myths. Sch Psychol Q. 2018;33(3):492. doi: 10.1037/spq0000272. [DOI] [PubMed] [Google Scholar]
- 56.Huang FL. Multilevel modeling and ordinary least squares regression: how comparable are they? J Exp Educ. 2018;86(2):265–281. [Google Scholar]
- 57.Astin AW, Denson N. Multi-campus studies of college impact: which statistical method is appropriate? Res High Educ. 2009;50(4):354–367. [Google Scholar]
- 58.Huang FL. Alternatives to multilevel modeling for the analysis of clustered data. J Exp Educ. 2016;84(1):175–196. [Google Scholar]
- 59.Lai MH, Kwok O-M. Examining the rule of thumb of not using multilevel modeling: the “design effect smaller than two” rule. J Exp Educ. 2015;83(3):423–438. [Google Scholar]
- 60.Wilcox R. Chapter 11—more regression methods. In: Wilcox R, editor. Introduction to robust estimation and hypothesis testing. 3. Boston: Academic Press; 2012. pp. 533–629. [Google Scholar]
- 61.Briggs A, Nixon R, Dixon S, Thompson S. Parametric modelling of cost data: some simulation evidence. Health Econ. 2005;14(4):421–428. doi: 10.1002/hec.941. [DOI] [PubMed] [Google Scholar]
- 62.Nixon RM, Wonderling D, Grieve RD. Non-parametric methods for cost-effectiveness analysis: the central limit theorem and the bootstrap compared. Health Econ. 2010;19(3):316–333. doi: 10.1002/hec.1477. [DOI] [PubMed] [Google Scholar]
- 63.Pinto EM, Willan AR, O'Brien BJ. Cost-effectiveness analysis for multinational clinical trials. Stat Med. 2005;24(13):1965–1982. doi: 10.1002/sim.2078. [DOI] [PubMed] [Google Scholar]
- 64.Law AM, Kelton WD, Kelton WD. Simulation modeling and analysis. New York: McGraw-Hill; 1991. [Google Scholar]
- 65.Van der Leeden R, Meijer E, Busing FM. Resampling multilevel models. Handbook of multilevel analysis. Berlin: Springer; 2008. pp. 401–433. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.