Joint prediction and time estimation of COVID-19 developing severe symptoms using chest CT scan

Graphical abstract

Abstract

With the rapidly worldwide spread of Coronavirus disease (COVID-19), it is of great importance to conduct early diagnosis of COVID-19 and predict the conversion time that patients possibly convert to the severe stage, for designing effective treatment plans and reducing the clinicians’ workloads. In this study, we propose a joint classification and regression method to determine whether the patient would develop severe symptoms in the later time formulated as a classification task, and if yes, the conversion time will be predicted formulated as a classification task. To do this, the proposed method takes into account 1) the weight for each sample to reduce the outliers’ influence and explore the problem of imbalance classification, and 2) the weight for each feature via a sparsity regularization term to remove the redundant features of the high-dimensional data and learn the shared information across two tasks, i.e., the classification and the regression. To our knowledge, this study is the first work to jointly predict the disease progression and the conversion time, which could help clinicians to deal with the potential severe cases in time or even save the patients’ lives. Experimental analysis was conducted on a real data set from two hospitals with 408 chest computed tomography (CT) scans. Results show that our method achieves the best classification (e.g., 85.91% of accuracy) and regression (e.g., 0.462 of the correlation coefficient) performance, compared to all comparison methods. Moreover, our proposed method yields 76.97% of accuracy for predicting the severe cases, 0.524 of the correlation coefficient, and 0.55 days difference for the conversion time.

1. Introduction

Coronavirus disease (COVID-19) is an infectious disease caused by the severe-acute respiratory symptom Coronavirus 2 (SARS-Cov2), and has resulted in more than 1.3 million confirmed cases and about 75k deaths worldwide as of April 7, 2020 (JHU, 2020). Due to its rapid spread, infection cases are increasing with the high fatality rate (e.g., up to 5.7%). Statistical models and machine learning methods have been developing to analyze the transmission dynamics and conduct early diagnosis of COVID-19 (del Rio, Malani, 2020, Li, Guan, Wu, Wang, Zhou, Tong, Ren, Leung, Lau, Wong, et al., 2020). For example, (Wu et al., 2020) employed the susceptible-exposed-infectious-recovered model to estimate the number of the COVID-19 cases in Wuhan based on the number of exported COVID-19 cases which moved from Wuhan to other cities in China.

The increasing number of confirmed COVID-19 cases results in the lack of the clinicians and the increase of the clinicians’ workloads. Many laboratory techniques have been used to confirm the suspected COVID-19 cases by clinicians (Jung et al., 2020), including real-time reverse transcription polymerase chain reaction (RT-PCR) (Corman, Bleicker, Brünink, Drosten, Zambon, 2020, Ai, Yang, Hou, Zhan, Chen, Lv, Tao, Sun, Xia, 2020), non-PCR tests (e.g., isothermal nucleic acid amplification technology (Craw and Balachandran, 2012)), non-contrast chest computed tomography (CT) and radiographs (Lee et al., 2020), and so on. It is well known that manual identification of COVID-19 is time-consuming and increases the infection risk of the clinicians (Kong and Agarwal, 2020). Moreover, laboratory tests are usually prohibited for all suspected cases due to the limitation of the test kits (Kong, Agarwal, 2020, Ng, Lee, Yang, Yang, Li, Wang, Lui, Lo, Leung, Khong, et al., 2020). Also, RT-PCR has been widely used to confirm COVID-19, but easily results in low sensitivity (Chaganti et al., 2020). As a good alternative, artificial intelligence techniques on the available data from laboratory tests have been playing important roles on the confirmation and follow-up of COVID-19 cases. For example, (Alom et al., 2020) employed the inception residual recurrent convolutional neural network (CNN) and transfer learning on X-ray and CT scan images to detect COVID-19 and segment the infected regions of COVID-19. (Ozkaya et al., 2020) first applied CNN to fuse and rank deep features for the early detection of COVID-19, and then used support vector machine (SVM) to conduct binary classification using the obtained deep features.

Imaging data is playing an important role in the diagnosis of all kinds of pneumonia diseases including COVID-19 (Shi et al., 2020a), so CT has been popularly used and applied to help monitor imaging changes and measure the disease severity such as in China (Zhao, Zhong, Xie, Yu, Liu, 2020, Chaganti, Balachandran, Chabin, Cohen, Flohr, Georgescu, Grenier, Grbic, Liu, Mellot, Murray, Nicolaou, Parker, Re, Sanelli, Sauter, Xu, Yoo, Ziebandt, Comaniciu). For example, (Chaganti et al., 2020) designed an automated system to quantify the abnormal tomographic patterns appeared in COVID-19 and (Li et al., 2020a) employed CNNs with the imaging features of radiographs and CT images for identifying COVID-19.

In this work, we investigate a new early diagnosis method to predict whether the mild confirmed cases (i.e., non-severe cases) of COVID-19 would develop severe symptoms in the later time and estimate the time interval. However, it is challenging due to many issues, such as small infected lesions in the chest CT scan at the early stage, appearances similar to other pneumonia, the data set with high-dimensional features and small-sized samples, and imbalanced group distribution.

First, the infected lesions in the chest CT scan at the early stage are usually small and their appearances are quite similar to that of other pneumonia. Given the early stage of COVID-19 with minor imaging signs, it is difficult to predict its future progression status. Conventional severity assessment methods can easily distinguish a severe sign of the image from the mild sign, since the changes of CT data are correlated with the disease severity, e.g., the lung involvement and abnormalities increase while the symptoms become severe. However, the infected volume of the non-severe COVID-19 cases is usually mild. For example, (Guan et al., 2020) showed that 84.4% of non-severe patients had mild symptoms and more than 95% severe cases had severe symptoms on CT changes. On the other hand, the clinicians have few prior knowledge about whether or when the non-severe cases convert to severe cases, so early diagnosis and conversion time prediction could reduce the clinicians’ workloads or even save patients’ levies.

Second, the collected data set usually has a small number of samples (i.e., small-sized samples) and high-dimensional features. Due to all kinds of reasons, such as data protection, data security, and the scenario of acute infectious diseases, a small number of subjects are available for early diagnosis of COVID-19. The limited samples or subjects are difficult to build an effective artificial intelligence model. Moreover, high-dimensional features for each imaging data are often extracted, by considering to capture the comprehensive changes of the disease. Hence, both of scenarios often result in the issue of over-fitting and the issue of curse of dimensionality (Hu, Zhu, Zhu, Gan, 2020, Zhu, Suk, Shen, 2014).

Third, the class or group distribution of the data set is generally imbalanced. In particular, the number of severe cases is much smaller than the number of non-severe cases, e.g., about 20% reported2 Such a scenario poses a challenge for most classification methods because they were designed under the assumption that each class has an equal number of samples (Adeli et al., 2020). As a result, previous classification techniques output poor predictive performance, especially for the minority class (Adeli et al., 2020w, Zhu, Zhu, Zheng, 2020).

In this work, we propose a novel joint regression and classification method to identify the severe COVID-19 cases from the non-severe cases and predict the conversion time from a non-severe case to the severe case in a unified framework. Specifically, we employ the logistic regression for the binary classification task and the linear regression for the regression task. Moreover, we employ an ℓ_2,1-norm regularization term on both the classification coefficient matrix and the regression coefficient matrix to consider the correlation between the two tasks as well as select the useful features for disease diagnosis and conversion time prediction. We further design a novel method to learn the weights of the samples, i.e., automatically learning the weight of each sample so that the important samples have large weights and the unimportant samples have small or even zero weights. Moreover, the samples with zero weights in each class are excluded to the process of the construction of the joint classification and regression, thus the problem of imbalance classification can be solved.

Different from previous literature, the contribution of our proposed method is listed as follows.

First, our method considers the issues, including imbalance classification, feature selection, and sample weight, in the same framework. Moreover, our method takes into account the correlation between the classification task and the regression task. In the literature, few study has focused on exploring the above issues simultaneously. For example, the studies separately conduct feature selection (Zhu et al., 2017b) and sample weight (Hu, Zhu, Zhu, Gan, 2020, Zhu, Yang, Zhang, Zhang, 2019), while (Zhu et al., 2014) proposed to conduct joint classification and regression. Recently, a few studies simultaneously conduct feature selection and sample selection (Adeli et al., 2020w, Hu, Zhu, Zhu, Gan, 2020).

Second, a few machine learning methods were proposed to conduct the diagnosis of COVID-19 disease. For example, (Tang et al., 2020) employed random forest to detect the severe cases from the confirmed cases based on the CT scan data. (Shi et al., 2020a) conducted the same task by a two-step strategy, i.e., automatically categorizing all subjects into groups followed by random forests in each group for classification. However, previous literature did not take into account any of the above issues. Recently, deep learning techniques (Alom, Rahman, Nasrin, Taha, Asari, Ozkaya, Ozturk, Barstugan, Li, Qin, Xu, Yin, Wang, Kong, Bai, Lu, Fang, Song, et al., 2020) have been employed to conduct early diagnosis of COVID-19, but lacking the interpretability. To our knowledge, this is the first study simultaneously detecting the severe cases and predicting the conversion time, which have widely applications because the severe cases could endanger patients’ lives and correctly predicting of the conversion time makes the clinicians take care the patients early or even save the patients’ lives.

2. Related work

AI technologies have widely been applied in the study of COVID-19 disease with the medical imaging data including X-ray and Computed Tomography (CT), in the applications of segmentation (Fan, Zhou, Ji, Zhou, Chen, Fu, Shen, Shao, 2020, Xie, Jacobs, Charbonnier, van Ginneken, 2020) and diagnosis (Kang, Xia, Yan, Wan, Shi, Yuan, Jiang, Wu, Sui, Zhang, et al., 2020, Ouyang, Huo, Xia, Shan, Liu, Mo, Yan, Ding, Yang, Song, et al., 2020). In this study, we give a brief review of the COVID-19 diagnosis and prognosis.

In the past few months, a large number of computer-aided diagnosis methods have been designed for the COVID-19 diagnosis. For example, (Chen et al., 2020) and (Bhandari et al., 2020) employed the logistic regression model to conduct COVID-19 disease diagnosis. (Hassanien et al., 2020) proposed to first use the multi-level threshold method to pre-process the images of COVID-19 patients, and then utilize SVM to distinguish the COVID-19 patients from normal cases. (Shaban et al., 2020) proposed a hybrid feature selection method to find informative features from chest CT images before using the kNN classifier to conduct COVID-19 disease diagnosis. Considering that deep learning methods always outperform traditional machine learning methods in real applications, (Song et al., 2020) proposed a CT diagnosis system based on the ResNet model to identify COVID-19 patients from healthy people. (Fan et al., 2020) proposed to first employ a deep segmentation network to automatically identify infected regions in chest CT scans, and then conduct the COVID-19 diagnosis by a semi-supervised way. (Xie et al., 2020b) designed two diverse relational U-networks to segment pulmonary lobes with CT images to output the high-level convolution features for COVID-19 diagnosis.

Considering the fact that mild patients may quickly deteriorate into the severe/critical stage, it is crucial to predict the development of patients disease. To do this, machine learning methods have widely been proposed to construct predict models to evaluate patients’ conditions. For example, (Yan et al., 2020) employed the XGBoost classifier to select informative features first and then predict the survival rates as well as the maximum number of days for severe patients. (Chakraborty and Ghosh, 2020) proposed to forecast the number of daily confirmed COVID-19 patients from different countries and (Salgotra et al., 2020) designed a gene expression programming-based method to predict the number of confirmed COVID-19 patients. (Petropoulos and Makridakis, 2020) employed the exponential smoothing method to forecast the confirmed COVID-19 cases and (Xie et al., 2020a) proposed a multivariable logistic regression model to predict the inpatient mortality of the COVID-19 patients. In addition, deep learning methods are also investigated to design prediction model. For example, (Arora et al., 2020) employed the recurrent neural network and the long-short term memory (LSTM) network to predict the number of confirmed COVID-19 cases in India. (Ibrahim et al., 2020) proposed a LSTM model to forecast the number of infected COVID-19 cases.

The literature demonstrated that each task can provide the complementary information to other tasks in multi-task learning (Zhu et al., 2014), so the framework integrating the classification task with the regression task has been designed to conduct diagnosis analysis as well as forecast the disease trend in the future. For example, (Wang et al., 2020) proposed a fully deep learning method on the original chest CT images to conduct the COVID-19 diagnosis and the prognostic analysis. (Bai et al., 2020) proposed a LSTM model to identify the severe patients and predict the patients with potential malignant progression (Bai et al., 2020). However, to the best of our knowledge, this work is the first study to simultaneously distinguish the severe cases from the mild cases and predict the conversion time from the mild cases to the severe cases.

3. Materials and image preprocessing

This study investigated the chest CT images of 408 confirmed COVID-19 patients. The demographic information is summarized in Table 1 . If a patient has multiple scans over time, the first scan is used. All CT images was provided by Shanghai Public Health Clinical Center and Sicuan University West China Hospital. Informed consents were waived and all private information of patients was anonymized. Moreover, the ethics of committees of these two institutes approved the protocol of this study.

Table 1.

Demographic information of all subjects. The numbers in parentheses denote the number of subjects in each class. It is noteworthy that 52 cases were converted to severe on average 5.64 days and 34 cases were severe at admission.

	Severe cases	Non-severe cases
	(86)	(322)
Female/male	35/51	160/162
Age	55.43  ±  16.35	49.30  ±  15.70

All patients were confirmed by the national centers for disease control (CDC) based on the positive new Coronavirus nucleic acid antibody. Moreover, patients with large motion artifacts or pre-existing lung cancer conditions on the CT scans were excluded from this study.

3.1. Image acquisition parameters

All patients underwent the thin-section CT scan by the scanners including SCENARIA 64 from Hitachi, Brilliance 64 from Philips, uCT 528 from United Imaging. The CT protocol is listed as follows: kV: 120, slice thickness: 1-1.5 mm, and breath hold at full inspiration. More details about both the image acquisition and the image pre-processing can be found in (Shan, Gao, Wang, Shi, Shi, Han, Xue, Shen, Shi, 2020, Shi, Xia, Shan, Wu, Wei, Yuan, Jiang, Gao, Sui, Shen, 2020). Moreover, we used the mediastinal window (with window width 350 hounsfield unit (HU) and window level 40 HU) and the lung window (with window width 1200 HU and window level-600 HU) for reading analysis.

3.2. Image pre-processing

We utilized the disease characteristics, i.e., infection locations and spreading patterns, to extract handcrafted features of each COVID-19 chest CT image. To do this, we used the COVID-19 chest CT analysis tool developed by Shanghai United Imaging Intelligence Co. Ltd., and followed the literature (Shan et al., 2020) to calculate the quantitative features.

First, the COVID-19 chest CT analysis tool designed a deep learning method named VB-net to automatically segment infected lung regions and lung fields bilaterally. The infected lung regions were mainly related to manifestations of pneumonia, such as mosaic sign, ground glass opacification, lesion-related signs, and interlobular septal thickening.

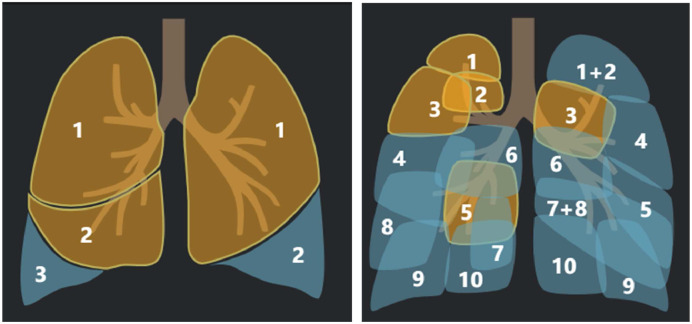
Second, after the segmentation process, the lung fields included the left lung and the right lung, 5 lung lobes, and 18 pulmonary segments, as shown in Fig. 1 . Specifically, the left lung included superior lobe and inferior lobe, while the right lung included superior lobe, middle lobe, and inferior lobe. Moreover, the left lung has 8 pulmonary segments and the right lung has 10 pulmonary segments. As a result, we had 26 regions of interest (ROIs) for each CT images.

Fig. 1.

The visualization of the segments of a chest CT scan image, i.e., 5 lung lobes (left) and 18 pulmonary segments.

Third, we partitioned each segment to five parts based on the HU ranges, i.e., $H{U}_{[-\infty ,-700]},$ $H{U}_{[-700,-500]},$ $H{U}_{[-500,-200]},$ $H{U}_{[-200,50]},$ and HU _[50,∞]. Specifically, $H{U}_{[-\infty ,-700]}$ indicates the parts with the HU range between $-\infty$ and -700, $H{U}_{[-700,-500]}$ indicates the parts with the HU range between -700 and -500, $H{U}_{[-500,-200]}$ indicates the parts with the HU range between -500 and -200, $H{U}_{[-200,50]}$ indicates the parts with the HU range between -200 and 50, and HU _[50,∞] indicates the parts with the HU range between 50 and ∞. As a result, each CT image was partitioned to 130 parts (i.e., $390=26*5$).

In this study, we extracted three kinds of handcrafted features from each part, i.e., density feature, volume feature, and mass feature. Specifically, we obtained the volume feature as the total volume of infected region and the density feature by calculating the averaged HU value within the infected region. We further followed (Song et al., 2014) to define the mass feature to simultaneously reflect the volume and density of subsolid nodule because the mass feature has been demonstrated to have potentially superior reproducibility to 3D volumetry, i.e., $Mass=(Density+1000)\times Volume\times 0.001$.

Finally, each CT image is represented by 390-dimension handcrafted features in this study.

4. Method

In this paper, we denote matrices, vectors, and scalars, respectively, as boldface uppercase letters, boldface lowercase letters, and normal italic letters. Specifically, we denote a matrix as $\mathbf{X}=[{\mathbf{x}}_1,\dots ,{\mathbf{x}}_n]$. The i-th row and j-th column of X are denoted as x ⁱ and x _j, respectively. We further denote the Frobenius norm and the ℓ_2,1-norm of a matrix X as ${\parallel \mathbf{X}\parallel }_F=\sqrt{{\sum }_i{\parallel {\mathbf{x}}^i\parallel }_2^2}=\sqrt{{\sum }_j{\parallel {\mathbf{x}}_j\parallel }_2^2}$ and ${\parallel \mathbf{X}\parallel }_{2,1}={\sum }_i{\parallel {\mathbf{x}}^i\parallel }_2={\sum }_i\sqrt{{\sum }_j{x}_{ij}^2},$ respectively. We also denote the transpose operator, the trace operator, and the inverse of a matrix X as X ^T, tr(X), and ${\mathbf{X}}^{-1},$ respectively.

4.1. Sparse logistic regression

In the classification problem, given the feature matrix $\mathbf{X}\in {\mathbb{R}}^{d\times n}$ including n samples ${\mathbf{x}}_i\in {\mathbb{R}}^d$ ($i=1,\dots ,n$) and their corresponding labels $y_i\in \{-1,+1\},$ the logistic regression is employed to distinguish the severe cases (i.e., $y_i=+1$) from the confirmed COVID-19 cases (i.e., $y_i=-1$). Specifically, by denoting $\mathbf{w}\in {\mathbb{R}}^d$ as the coefficient vector, the logistic loss function is defined as

$$\underset{\mathbf{w}}{min}\sum _{i=1}^n\log (1+exp(-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i\right)))+{\lambda }_1{\parallel \mathbf{w}\parallel }_2^2$$ (1)

where λ ₁ is a tuning parameter, and the ℓ₂-norm regularization term on the coefficient vector w is used to control the complexity of the logistic regression. Eq. (1) conducts the classification task without taking into account the issues, such as feature selection, sample weight, and imbalance classification.

First, in real applications, clinicians have prior knowledge on the regions of the CT scan data which are possible related to the disease, but we cannot only extract the features from these regions because they may cooperate with other regions to influence the disease. As a result, we extract the features from all imaging data to obtain the high-dimensional data, which captures the comprehensive changes of confirmed COVID-19 cases but increases the store and computation costs as well as easily results in the issue of curse of dimensionality (Zhu, Zhu, Zheng, 2020, Shen, Zhu, Zheng, Zhu, 2020). To address this issue, we design machine learning models to automatically recognize the features related to the disease by taking into account the correlation among the features. Specifically, we replace the ℓ₂-norm on the coefficient vector w (i.e., ${\parallel \mathbf{w}\parallel }_2^2$) by the ℓ₁-norm (i.e., ‖w‖₁ and ${\parallel \mathbf{w}\parallel }_1={\sum }_{i=1}^d\left|w_i\right|$), which outputs sparse elements to make the corresponding features (i.e., the rows in X) not involving the classification task, i.e., 

$$\underset{\mathbf{w}}{min}\sum _{i=1}^n\log (1+exp(-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i\right)))+{\lambda }_2{\parallel \mathbf{w}\parallel }_1$$ (2)

where λ ₂ is a tuning parameter.

4.2. Balanced and sparse logistic regression

In binary classification, the issue of imbalance classification easily results in the classification results bias to the majority class, i.e., outputting high false negatives. In the literature, both re-sampling methods and cost-sensitive learning methods (Zhu et al., 2019) have been used for solve the issue of imbalance classification.

Recently, robust loss functions has been widely designed to reduce the influences of outliers by taking into account the sample weight in robust statistics (Zhu et al., 2020b). Specifically, robust loss functions use a weight vector $\mathit{\alpha }\in {\mathbb{R}}^{1\times n}$ to automatically output small weights to the samples with large estimation errors and large weights to the samples with small estimation errors. As a consequence, the samples with large estimation errors are regarded as outliers and their influences are reduced. In the literature, a number of robust loss functions have been developed, including ${\ell }_1-{\ell }_2$ function, Cauchy function, and Geman–McClure estimator, and so on (Hu, Zhu, Zhu, Gan, 2020, Zhu, Gan, Lu, Li, Zhang, 2020). However, the robust loss function was not designed to explore the issue of the imbalance classification.

In this paper, motivated by the robust loss functions assigning weights to the samples, we propose a new method to assign a weight to each sample as well as to solve the problem of imbalance classification. By regarding that different samples have different contributions to the construction of the classification model, our method expects to assign large weights to the important samples and small weights to the unimportant samples. Moreover, by regarding of the problem of imbalance classification, our method expects to set different numbers of zero weights to different classes so that there is a balance of the sample number between the positive class and the negative class. To do this, we employ an ℓ₀-norm constraint on the weight vector α to have the following loss function:

$$\begin{array}{cc}& \underset{\mathit{\alpha },\mathbf{w}}{\min }\sum _{i=1}^n{\alpha }_i\log (1+exp(-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i\right)))+{\lambda }_2{\parallel \mathbf{w}\parallel }_1\hfill \\ & s.t.,\parallel {\mathit{\alpha }}_{-1}{\parallel }_0=k_{-}and{\parallel {\mathit{\alpha }}_{+1}\parallel }_0=k_{+}\hfill \end{array}$$ (3)

where ${\mathit{\alpha }}_{-1}$ indicates the weight set of all negative samples and ${\mathit{\alpha }}_{+1}$ indicates the weight set of all positive samples. The constraint ‘$\parallel {\mathit{\alpha }}_{-1}{\parallel }_0=k_{-}$’ indicates that the number of non-zero elements in the negative class is $k_{-}$. Specifically, after receiving the estimation value for each sample, i.e., $log(1+\exp (-\left(y_i{\mathbf{w}}^T{\mathbf{x}}_i\right))),$ we first sort the estimation values of all samples in the same class with an increase order, and then keep the original weights to the weights of the $k_{-}$ negative samples with the smallest estimation values and 0 to the weights of the left negative samples. In this way, either the negative samples or the positive samples with zero weights will not be involved the process of the classification model.

Our method in Eq. (3) has at least two advantages, i.e., automatically selecting important samples (i.e., reducing the influence of the outliers) to learn the classification model and adjusting the number of selected samples for each class by tuning the values of $k_{-}$ and $k_{+}$ (e.g., $k_{-}=k_{+}$) to solve the imbalance classification problem. In particular, our method in Eq. (3) employs the ℓ₀-norm constraint for each class to output exactly predefined non-zero elements. On the contrary, self-paced learning uses the ℓ₁-norm constraint for all samples or other robust loss functions (Zhu, Zhu, Zheng, 2020, Hu, Zhu, Zhu, Gan, 2020) to estimate the sample weight without guaranteeing the exact number of non-zero elements. As a result, compared to self-paced learning only considering the sample weight to reduce the influence of outliers, our method takes into account the sample weight to remove outliers not to involve the process of the model construction as well as solve the problem of imbalance classification.

4.3. Joint logistic regression and linear regression

Besides distinguishing the severe cases from the non-severe cases, predicting the conversion time converting a non-severe case to a severe case is also important because it may be related to the patients’ lives. To do this, a naive solution is to separately conduct a classification task to diagnose the severe cases and a regression task to predict the conversion time. Obviously, the separate strategy ignores the correlation among two tasks. In this paper, by regarding the prediction of conversion time as a regression task, we define a ridge regression to linearly characterize the correlation between the feature matrix X and the vector of the conversion time $\mathbf{z}\in {\mathbb{R}}^{1\times n}$ by

$$\underset{\mathbf{v}}{\min }\parallel {\mathbf{v}}^T{\mathbf{X}-\mathbf{z}\parallel }_2^2+{\lambda }_3{\parallel \mathbf{v}\parallel }_2^2$$ (4)

where $\mathbf{v}\in {\mathbb{R}}^d$ is the coefficient vector for the regression task and λ ₃ is a tuning parameter.

Similar to the classification task in Eq. (3), the regression task in Eq. (4) still needs to consider the issues, such as feature selection, sample weight, and imbalance classification. Moreover, in this study, we conduct joint classification and regression (i.e., multi-task learning) by simultaneously considering a classification task and a regression task in the same framework. We expect that each task could obtain information from another task so that the model effectiveness of each of them can be improved by the shared information. Specifically, we employ the ℓ_2,1-norm regularization term with respect to both the variable w and the variable v to obtain the following objective function:

$$\begin{array}{cc}& \underset{\mathit{\alpha },\mathbf{w},\mathbf{v},\mathit{\beta }}{\min }\sum _{i=1}^n{\alpha }_i\log (1+exp(-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i\right)))\hfill \\ & +\gamma \parallel \mathit{\beta }({\mathbf{v}}^T\mathbf{X}-\mathbf{z}){\parallel }_2^2+\lambda {\parallel [\mathbf{w},\mathbf{v}]\parallel }_{2,1}\hfill \\ & s.t.,\parallel {\mathit{\alpha }}_{-1}{\parallel }_0=k_{-}and{\parallel {\mathit{\alpha }}_{+1}\parallel }_0=k_{+},\hfill \\ & \parallel {\mathit{\beta }}_{-1}{\parallel }_0=k_{-}and{\parallel {\mathit{\beta }}_{+1}\parallel }_0=k_{+}\hfill \end{array}$$ (5)

where $\mathit{\beta }\in {\mathbb{R}}^{1\times n}$ is the sample weight vector for the regression task and $[\mathbf{w},\mathbf{v}]\in {\mathbb{R}}^{d\times 2}$. γ and λ are tuning parameters. ‖[w, v]‖_2,1 indicates that the selected features are obtained by the classification and regression model. Moreover, the selected features are their shared or common information benefiting each of them (Evgeniou and Pontil, 2004).

Eq. (5) needs a tuning parameter γ to have a magnitude or importance trade-off between two tasks. However, the process of tuning parameter is time-consuming and needs prior knowledge. In this work, we use a squared root operator on the second term of Eq. (5) to automatically obtain their weights. It is noteworthy that we keep the parameter λ to be tuned because it controls the sparsity of the term ‖[w, v]‖_2,1 and the sparsity will be changed based on the data distribution (Evgeniou, Pontil, 2004, Zhu, Li, Zhang, Xu, Yu, Wang, 2017). Hence, the final objective function of our proposed joint classification and regression method is:

$$\begin{array}{cc}& \underset{\mathit{\alpha },\mathbf{w},\mathbf{v},\mathit{\beta }}{\min }\sum _{i=1}^n{\alpha }_i\log (1+exp(-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i\right)))\hfill \\ & +\sqrt{{\sum }_{i=1}^n{\beta }_i{\parallel {\mathbf{v}}^T{\mathbf{x}}_i-z_i\parallel }_2^2}+\lambda {\parallel [\mathbf{w},\mathbf{v}]\parallel }_{2,1}\hfill \\ & s.t.,\parallel {\mathit{\alpha }}_{-1}{\parallel }_0=k_{-}and{\parallel {\mathit{\alpha }}_{+1}\parallel }_0=k_{+},\hfill \\ & \parallel {\mathit{\beta }}_{-1}{\parallel }_0=k_{-}and{\parallel {\mathit{\beta }}_{+1}\parallel }_0=k_{+}\hfill \end{array}$$ (6)

To solve the optimization problem in Eq. (6), i.e., optimizing the variables v and β, we compute the derivatives of the square root in Eq. (6) and obtain the following formulation

$$\begin{array}{c}\hfill \{\begin{array}{c}\underset{\mathit{\alpha },\mathbf{w},\mathbf{v},\mathit{\beta }}{\min }\sum _{i=1}^n{\alpha }_i\log (1+exp(-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i\right)))\left(7\mathrm{a}\right)\hfill \\ +\gamma \sum _{i=1}^n{\beta }_i\parallel {\mathbf{v}}^T{\mathbf{x}}_i-z_i{\parallel }_2^2+\lambda {\parallel [\mathbf{w},\mathbf{v}]\parallel }_{2,1}\hfill \\ s.t.,\parallel {\mathit{\alpha }}_{-1}{\parallel }_0=k_{-}and{\parallel {\mathit{\alpha }}_{+1}\parallel }_0=k_{+},\hfill \\ \parallel {\mathit{\beta }}_{-1}{\parallel }_0=k_{-}and{\parallel {\mathit{\beta }}_{+1}\parallel }_0=k_{+}\hfill \\ \gamma =\frac{1}{2\sqrt{\parallel \mathit{\beta }({\mathbf{v}}^T\mathbf{X}-\mathbf{z}){\parallel }_2^2}}.\left(7\mathrm{b}\right)\hfill \end{array}\end{array}$$

The values of γ in Eq. (7b) is automatically obtained without the tuning process and can be regarded as the weight of the tasks. Specifically, if the prediction error is small, the value of γ is large, i.e., the regression task is more important than the classification task. Hence, the optimization of the value of γ automatically balances the contributions of two tasks. As a result, the optimization of Eq. (6) is changed to optimize Eq. (7a).

4.4. Optimization

In this paper, we employ the alternating optimization strategy (Bezdek and Hathaway, 2003) to optimize the variables w, α, v, and β, in Eq. (7a). We list the pseudo of our optimization method in Algorithm 1 and report the details as follows.

Algorithm 1.

The pseudo of our optimization method.

(i) Update w by fixing α, β and v

After other variables are fixed, the objective function with respect to w in Eq. (7a) becomes

$$\underset{\mathbf{w}}{\min }\sum _{i=1}^n{\alpha }_i\log (1+exp(-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i\right)))+\lambda tr\left({\mathbf{w}}^T\mathbf{D}\mathbf{w}\right)$$ (8)

where $\mathbf{D}\in {\mathbb{R}}^{d\times d}$ is a diagonal matrix and the value of its i-th diagonal element is $\frac{1}{{2\parallel [\mathbf{w},\mathbf{v}]}^i{\parallel }_2}$. To solve the imbalance classification problem, we set $k_{-}=k_{+}=k$ to obtain 2k samples for the training process. Hence, Eq. (8) becomes

$$\underset{\mathbf{w}}{\min }\sum _{i=1}^{2k}{\alpha }_i\log (1+exp(-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i\right)))+\lambda tr\left({\mathbf{w}}^T\mathbf{D}\mathbf{w}\right).$$ (9)

By setting $y_i\in \{-1,1\}$ and $h_w\left({\mathbf{x}}_i\right)=\frac{1}{1+exp(-\left({\mathbf{w}}^T{\mathbf{x}}_i\right))},$ Eq. (9) becomes

$$\begin{array}{cc}& \underset{\mathbf{w}}{\min }\sum _{i=1}^{2k}{\alpha }_i(-\frac{1+y_i}{2}log\left(h_w\left({\mathbf{x}}_i\right)\right)-\frac{1-y_i}{2}log(1-h_w\left({\mathbf{x}}_i\right)))\hfill \\ & +\lambda tr\left({\mathbf{w}}^T\mathbf{D}\mathbf{w}\right).\hfill \end{array}$$ (10)

In this paper, we employ the Newton’s method (Liu and Nocedal, 1989) to minimize Eq. (10) by the following update rules

$$\mathbf{w}=\mathbf{w}-\mathbf{a}{\mathbf{B}}^{-1}$$ (11)

where $\mathbf{a}\in {\mathbb{R}}^d$ and $\mathbf{B}\in {\mathbb{R}}^{d\times d}$ are defined as

$$\begin{array}{c}\hfill \{\begin{array}{c}\mathbf{a}=\sum _{i=1}^{2k}{\alpha }_i(h_w\left({\mathbf{x}}_i\right)-\frac{1+y_i}{2}){\mathbf{x}}_{\mathbf{i}}+2\lambda \mathbf{Dw}\hfill \\ \mathbf{B}=\sum _{i=1}^{2k}{\alpha }_i{h}_w\left({\mathbf{x}}_i\right)(1-h_w\left({\mathbf{x}}_i\right)){\mathbf{x}}_i{\mathbf{x}}_i^T+2\lambda \mathbf{D}\hfill \end{array}\end{array}$$ (12)

(ii) Update v by fixing α, β and w

The objective function with respect to v in Eq. (7a) is

$$\underset{\mathbf{v}}{\min }\sum _{i=1}^n{\beta }_i{\parallel {\mathbf{v}}^T{x}_i-z_i\parallel }_F^2+\frac{\lambda }{\gamma }tr\left({\mathbf{v}}^T\mathbf{D}\mathbf{v}\right).$$ (13)

By letting $\mathbf{G}=[{\beta }_1{\mathbf{x}}_1,\dots ,{\beta }_n{\mathbf{x}}_n]\in {\mathbb{R}}^{d\times n}$ and $\mathbf{m}=[{\beta }_1{z}_1,\dots ,{\beta }_n{z}_n]\in {\mathbb{R}}^{1\times n},$ we have

$$\underset{\mathbf{v}}{\min }{\parallel {\mathbf{v}}^T\mathbf{G}-\mathbf{m}\parallel }_2^2+\frac{\lambda }{\gamma }tr\left({\mathbf{v}}^T\mathbf{D}\mathbf{v}\right)$$ (14)

Eq. (14) has a closed-form solution, i.e., 

$$\mathbf{v}={(\mathbf{G}{\mathbf{G}}^T+\frac{\lambda }{\gamma }\mathbf{D})}^{-1}\mathbf{Gm}$$ (15)

(iii) Update α and β by fixing v and w

By denoting the estimation value of the classification task for the i-th sample as $l_1^i=\log (1+exp(-y_i{\mathbf{w}}^T{\mathbf{x}}_i))$ ($i=1,\dots ,n$), we sort the values $l_1^i$ ($i=1,\dots ,n$) with an increase order for each class to denote the weight set of k negative samples with the smallest estimation values as $I_{-}=\{{\widehat{\alpha }}_{\left[1\right]}^{-},\dots ,{\widehat{\alpha }}_{\left[k\right]}^{-}\}$ (where ${\widehat{\alpha }}_{\left[i\right]}^{-}<{\widehat{\alpha }}_{\left[j\right]}^{-}$ if [i] < [j]) and the weight set of k positive samples with the smallest estimation values as $I_{+}=\{{\widehat{\alpha }}_{\left[1\right]}^{+},\dots ,{\widehat{\alpha }}_{\left[k\right]}^{+}\}$ (where ${\widehat{\alpha }}_{\left[i\right]}^{+}<{\widehat{\alpha }}_{\left[j\right]}^{+}$ if [i] < [j]), and then we have

$$\begin{array}{c}\hfill {\widehat{\alpha }}_{\left[i\right]}=\{\begin{array}{cc}{\alpha }_j\left[i\right]\in I_{-}\cup I_{+}and\left[i\right]\bowtie j\hfill & \\ 0others\hfill \end{array}\end{array}$$ (16)

where $\{1,\dots ,n\}$ is the index of the original order before the sorting and $\left\{\right[1],\dots ,[n\left]\right\}$ is the index of the increase order after the sorting. [i]⋈j indicates that the j-th index in the original order is matched with the [i]-th index in the increase order.

By denoting the estimation value of the regression task for the i-th sample as $l_2^i={\parallel {\mathbf{v}}^T{\mathbf{x}}_i-z_i\parallel }_2^2$ ($i=1,\dots ,n$), we sort the values $l_2^i$ ($i=1,\dots ,n$) with an increase order for each class to denote the weight set of k negative samples with the smallest estimation values as $Q_{-}=\{{\widehat{\beta }}_{\left[1\right]}^{-},\dots ,{\widehat{\beta }}_{\left[k\right]}^{-}\}$ (where ${\widehat{\beta }}_{\left[i\right]}^{-}<{\widehat{\beta }}_{\left[j\right]}^{-}$ if [i] < [j]) and the weight set of k positive samples with the smallest estimation values as $Q_{+}=\{{\widehat{\beta }}_{\left[1\right]}^{+},\dots ,{\widehat{\alpha }}_{\left[k\right]}^{+}\}$ (where ${\widehat{\beta }}_{\left[i\right]}^{+}<{\widehat{\beta }}_{\left[j\right]}^{+}$ if [i] < [j]), and then we have

$$\begin{array}{c}\hfill {\widehat{\beta }}_{\left[i\right]}=\{\begin{array}{cc}{\beta }_j\left[i\right]\in Q_{-}\cup Q_{+}and\left[i\right]\bowtie j\hfill & \\ 0others\hfill \end{array}\end{array}$$ (17)

4.5. Convergence analysis

Algorithm 1 involves to optimize five variables (i.e., w, α, v, β, and γ). By denoting w ^t, α ^t, v ^t, β ^t, and γ^t, respectively, as the t-th iteration results of w, α, v, β, and γ, we denote the objective function value of the t-th iteration of Eq. (6) as J(w ^t, α ^t, v ^t, β ^t, γ^t).

By fixing α ^t, v ^t, β ^t, and γ^t, we employ the Newton’s method to optimize w and the Newton’s method can achieve the convergence, so we have

$$J({\mathbf{w}}^{t+1},{\mathit{\alpha }}^t,{\mathbf{v}}^t,{\mathit{\beta }}^t,{\gamma }^t)\le J({\mathbf{w}}^t,{\mathit{\alpha }}^t,{\mathbf{v}}^t,{\mathit{\beta }}^t,{\gamma }^t)$$ (18)

The optimizations of the variables (i.e., α, v, β, and γ) have closed-form solutions, so we have

$$J({\mathbf{w}}^{t+1},{\mathit{\alpha }}^{t+1},{\mathbf{v}}^t,{\mathit{\beta }}^t,{\gamma }^t)\le J({\mathbf{w}}^{t+1},{\mathit{\alpha }}^t,{\mathbf{v}}^t,{\mathit{\beta }}^t,{\gamma }^t)$$ (19)

$$J({\mathbf{w}}^{t+1},{\mathit{\alpha }}^{t+1},{\mathbf{v}}^{t+1},{\mathit{\beta }}^t,{\gamma }^t)\le J({\mathbf{w}}^{t+1},{\mathit{\alpha }}^{t+1},{\mathbf{v}}^t,{\mathit{\beta }}^t,{\gamma }^t)$$ (20)

$$J({\mathbf{w}}^{t+1},{\mathit{\alpha }}^{t+1},{\mathbf{v}}^{t+1},{\mathit{\beta }}^{t+1},{\gamma }^t)\le J({\mathbf{w}}^{t+1},{\mathit{\alpha }}^{t+1},{\mathbf{v}}^{t+1},{\mathit{\beta }}^t,{\gamma }^t)$$ (21)

$$J({\mathbf{w}}^{t+1},{\mathit{\alpha }}^{t+1},{\mathbf{v}}^{t+1},{\mathit{\beta }}^{t+1},{\gamma }^{t+1})\le J({\mathbf{w}}^{t+1},{\mathit{\alpha }}^{t+1},{\mathbf{v}}^{t+1},{\mathit{\beta }}^{t+1},{\gamma }^t).$$ (22)

By integrating the inequalities, i.e., Eqs. (18)-(22), we obtain

$$J({\mathbf{w}}^{t+1},{\mathit{\alpha }}^{t+1},{\mathbf{v}}^{t+1},{\mathit{\beta }}^{t+1},{\gamma }^{t+1})\le J({\mathbf{w}}^t,{\mathit{\alpha }}^t,{\mathbf{v}}^t,{\mathit{\beta }}^t,{\gamma }^t).$$ (23)

According to Eq. (23), the objective function values in Eq. (6) gradually decrease with the increase of iterations until Algorithm 1 converges. Hence, the convergence proof of Algorithm 1 to optimize Eq. (6) is completed.

5. Experiments

We experimentally evaluated our method, compared to state-of-the-art classification and regression methods, on a real COVID-19 data set with the chest CT scan data, in terms of binary classification and regression performance.

5.1. Experimental setting

We selected SVM and Ridge regression, respectively, as the baseline methods for the classification task and the regression task. Other comparison methods include ℓ₁-SVM (L1SVM) (Chang and Lin, 2011), random forest (Liaw and Wiener, 2002), Sample-Feature Selection (SFS) (Adeli et al., 2020), ℓ₁-SVR (Chang and Lin, 2011) (L1SVR), Least Absolute Shrinkage and Selection Operator (Lasso) (Tibshirani, 1996), Matrix-Similarity Feature Selection (MSFS) (Zhu et al., 2014), and three deep learning methods (e.g., Hyperface (Ranjan et al., 2017), COVID-CAPS (Afshar et al., 2020), and CNN combine with Extreme learning machine (CNNE) (Duan et al., 2018)). We summarize the details of all comparison methods in Table 2 . It is noteworthy that random forest can be used for feature selection, sample selection, and imbalance classification. However, in this study, we only used random forest to consider the problem of imbalance classification.

Table 2.

The summarization of all methods. The first block and the second block, respectively, list the classification methods and the regression methods, while all multi-task methods are listed in the third block. Note that, FS: feature selection, SW: sample weight, IMB: imbalance classification, CLASS: classification, and REG: regression.

Methods	FS	SW	IMB	CLASS	REG
SVM (Chang and Lin, 2011)				√
L1SVM (Chang and Lin, 2011)	√			√
Random forest (Liaw and Wiener, 2002)			√	√
SFS (Adeli et al., 2020)	√	√	√	√
Ridge regression					√
L1SVR (Chang and Lin, 2011)	√				√
Lasso (Tibshirani, 1996)	√				√
Random forest (Liaw and Wiener, 2002)	√		√		√
MSFS (Zhu et al., 2014)	√			√	√
Hyperface (Ranjan et al., 2017)				√	√
COVID-CAPS (Afshar et al., 2020)			√	√	√
CNNE (Duan et al., 2018)				√	√
Proposed	√	√	√	√	√

In our experiments, we repeated the 5-fold cross-validation scheme 20 times for all methods to report the average results as the final results. In the model selection, we set $\lambda \in \{{10}^{-3},{10}^{-2},\dots ,{10}^3\}$ in Eq. (6), and fixed $k=50$ for solving the problem of imbalance classification for our method. We followed the literature to set the parameters of the comparison methods so that they outputted the best results.

The evaluation metrics include accuracy, specificity, sensitivity, and area under the ROC curve (AUC) for the classification task, as well as correlation coefficient (CC) and root mean square error (RMSE) for the regression task.

5.2. Classification results

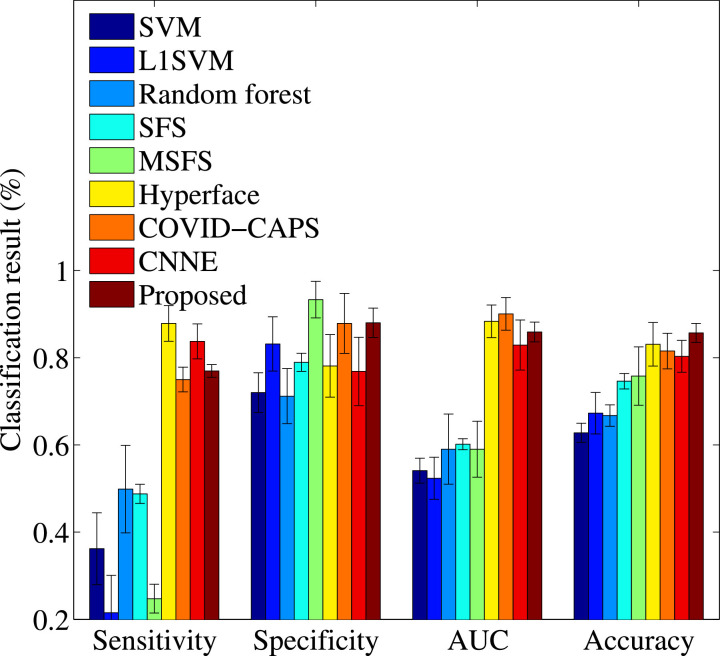
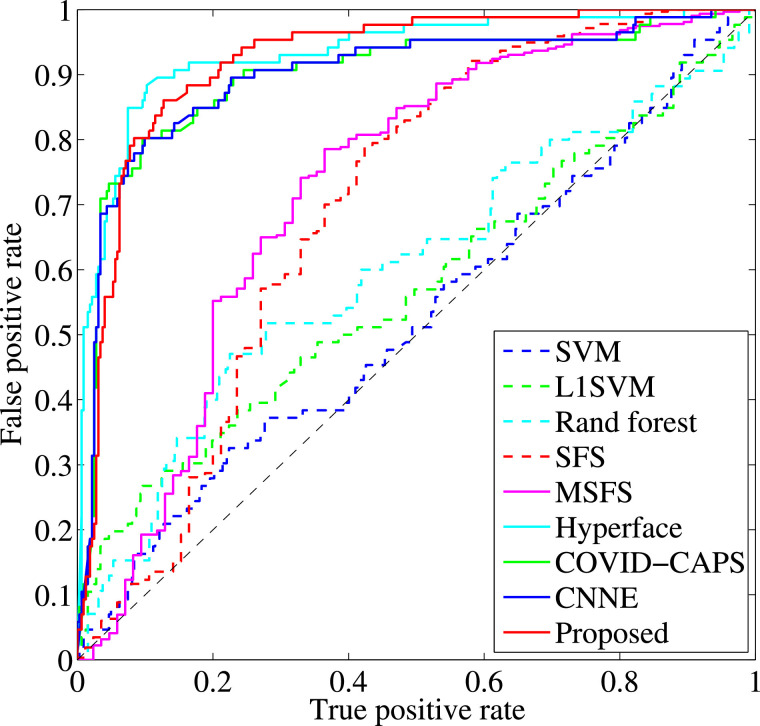
We report the classification performance and the Receiver Operating Characteristic (ROC) curves, respectively, of all methods in Fig. 2 and Fig. 3 . We also report the classification performance of our proposed method using single-task learning and multi-task learning in Table 3 . Based on the results, we conclude our observations as follows.

Fig. 2.

Classification results of all methods.

Fig. 3.

ROC curves of all methods.

Table 3.

Classification results (%) of three methods. Proposed W/O Regression indicates Eq. (3).

Methods	SFS (Adeli et al., 2020)	Proposed w/o Regression	Proposed
Accuracy	78.18  ±  3.71	83.25  ±  2.44	85.69  ±  2.20
Sensitivity	50.65  ±  6.33	70.73  ±  3.36	76.97  ±  3.36
Specificity	86.31  ±  2.69	86.60  ±  3.45	88.02  ±  1.45
AUC	73.88  ±  6.66	81.74  ±  3.30	85.91  ±  2.27

First, it could be observed that the proposed method achieved the best classification performance, followed by Hyperface, COVID-CAPS, CNNE, MSFS, SFS, L1SVM, Random forest, and SVM. Specifically, our proposed method improves on average by 32.80% and 2.61%, respectively, compared to the worst comparison method (i.e., SVM) and the best comparison methods (i.e., Hyperface), in terms of all four evaluation metrics. The reason is the fact that our method takes into account the issues in the same framework, such as feature selection removing the redundant features, sample weight reducing the influence of the outliers, imbalance classification reducing the issue of high false negatives, and joint classification and regression utilizing the share information between two tasks to improve the model effectiveness of each of them.

Second, it is important to conduct dimensionality reduction (including feature selection) for analyzing the high-dimensional data, which easily results in the issue of curse of dimensionality (Shen et al., 2020). In the literature, many studies showed that the classification model on the high-dimensional data will output low performance (Zhu et al., 2014). Fig. 2 verified the above statement. In our experiments, only SVM does not consider the issue of high-dimensional data and achieves the worst classification performance. More specifically, the best comparison method (i.e., Hyperface) improves by 26.32% and the worst comparison method (i.e., Random forest) improves by 4.52%, for all evaluation metrics, compared to the baseline SVM.

Third, it is useful to use joint classification and regression framework for detecting the severe cases from mild confirmation cases. As shown in Table 3 and Fig. 2, our proposed method conducting joint classification and regression achieves better classification performance, compared to the single-task based classification methods, e.g., random forest, L1SVM, SFS, and SVM. Moreover, the methods (e.g., MSFS, Hyperface, COVID-CAPS, and our method) are joint models. However, our method outperforms other joint models since our proposed method takes into account one more constraint. In particular, we conducted single-task classification using Eq. (3), i.e., our proposed method without considering the regression task, Proposed w/o Regression in Table 3. As a result, Proposed w/o Regression outperforms SFS since both of them take into account three following constraints, such as feature selection, sample weight, and imbalance classification.

5.3. Regression results

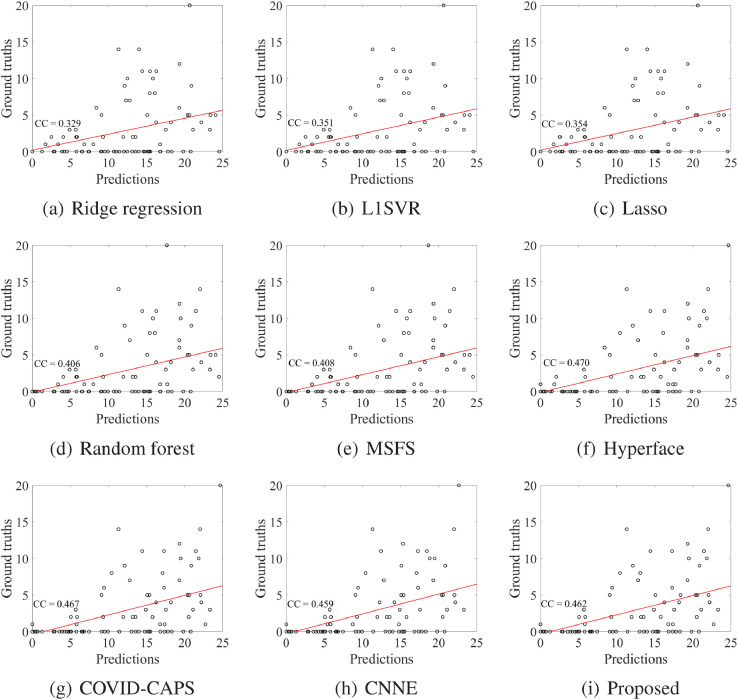
We evaluated the regression performance through the prediction of conversion time from the non-severe case to the severe case. We reported the regression results (i.e., correlation coefficient (CC) and RMSE) of all methods in Table 4 and scatter plots of all methods in Fig. 4 .

Table 4.

Regression results of all methods.

Methods	CC	RMSE
Ridge regression	0.329  ±  0.158	20.02  ±  9.724
L1SVR (Chang and Lin, 2011)	0.351  ±  0.085	10.49  ±  2.072
Lasso (Tibshirani, 1996)	0.354  ±  0.165	9.92  ±  9.571
Random forest (Liaw and Wiener, 2002)	0.406  ±  0.188	13.22  ±  6.762
MSFS (Zhu et al., 2014)	0.408  ±  0.092	9.29  ±  1.104
Hyperface (Ranjan et al., 2017)	0.470  ±  0.026	7.58  ±  0.719
COVID-CAPS (Afshar et al., 2020)	0.467  ±  0.023	7.89  ±  0.451
CNNE (Duan et al., 2018)	0.459  ±  0.033	8.61  ±  0.084
Proposed	0.462  ±  0.056	7.35  ±  1.087

Fig. 4.

Scatter plots and the corresponding correlation coefficients (CCs) of all methods for predicting the severe cases.

First, the regression performance of the methods without dimensionality reduction (e.g., Ridge regression) is worse than the methods with dimensionality reduction, e.g., Lasso, L1SVR, MSFS, Hyperface, COVID-CAPS, CNNE, and our proposed method. Moreover, our method outperforms the traditional machine learning methods such as Ridge regression, L1SVR, Lasso, Random forst, and MSFS. For example, our method receives the best performance for correlation coefficient (e.g., 0.462) and RMSE (e.g., 7.351). However, some deep learning methods (e.g., Hyperface and COVID-CAPS) are better than our proposed method a little bit, in terms of correlation coefficient.

Second, similar to the results of the classification task, the results of the regression task show the advantages of the considerations, such as feature selection, sample weight, imbalance classification, and joint classification and regression. In particular, our proposed method considering all four considerations improves 0.054 and 1.940, respectively, in terms of correlation coefficient and RMSE, compared to MSFS which takes two considerations into account, such as feature selection, and joint classification and regression.

5.4. Ablation analysis

In this section, we evaluate the effectiveness of each part in our proposed joint model by analyzing the following scenarios, i.e., the effectiveness of each part in the joint model, the parameter sensitivity of λ in Eq. (6), and the convergence analysis of Algorithm 1. As a result, we report the results of our proposed method only conducting the classification task (i.e., Proposed w/o Regression in Eq. (3)) in Table 3 and the results of our proposed method only conducting the regression task (i.e., Lasso) in Table 4. We also list the variations of all evaluation metrics on our proposed method with different values of λ in Table 5 and the variations of the objective function values of Eq. (6) in Fig. 5 .

Table 5.

The results of all evaluation metrics with different values of λ.

λ	Accuracy	Sensitivity	Specificity	AUC	CC	RMSE
0.001	81.59 ± 1.79	75.92 ± 2.09	83.11 ± 2.19	82.99 ± 3.43	0.423 ± 0.026	9.58 ± 0.719
0.01	83.57 ± 2.21	78.31 ± 2.31	84.98 ± 1.91	83.28 ± 4.14	0.451 ± 0.053	8.88 ± 1.217
0.1	82.15 ± 2.08	73.16 ± 2.83	84.56 ± 2.89	83.21 ± 3.55	0.449 ± 0.043	8.11 ± 1.191
1	84.57 ± 3.25	77.11 ± 3.06	86.75 ± 2.85	84.65 ± 3.74	0.428 ± 0.039	9.35 ± 1.084
10	85.69 ± 2.20	76.97 ± 3.36	88.02 ± 1.45	85.91 ± 2.27	0.462 ± 0.056	7.35 ± 1.087
100	84.21 ± 2.74	77.12 ± 3.50	86.11 ± 3.06	83.65 ± 4.52	0.448 ± 0.071	7.68 ± 1.464
1000	83.44 ± 3.74	78.53 ± 3.55	84.55 ± 2.80	83.78 ± 3.82	0.439 ± 0.081	8.49 ± 1.641

Fig. 5.

The variations of the objective function values of Eq. (6) at different iterations.

Based on Tables 3 and 4, our joint model separately considering either the classification task or the regression task outperforms some comparison methods. For example, Proposed w/o Regression is better than SFS, which was designed to conduct the classification task only. Lasso outperforms two classic regression methods, i.e., Ridge regression and L1SVR. This demonstrates that our joint models work well even they conduct one task only.

Table 5 shows that the proposed method is sensitive to the parameters’ setting since different values of λ lead to different performances. This indicates importance of turning the parameter for our proposed method. To do this, the cross-validation scheme is a good method for tuning the parameter. For example, the best performance for both the classification task and the regression task can be easily obtained while setting λ = 10 by the 5-fold cross-validation scheme.

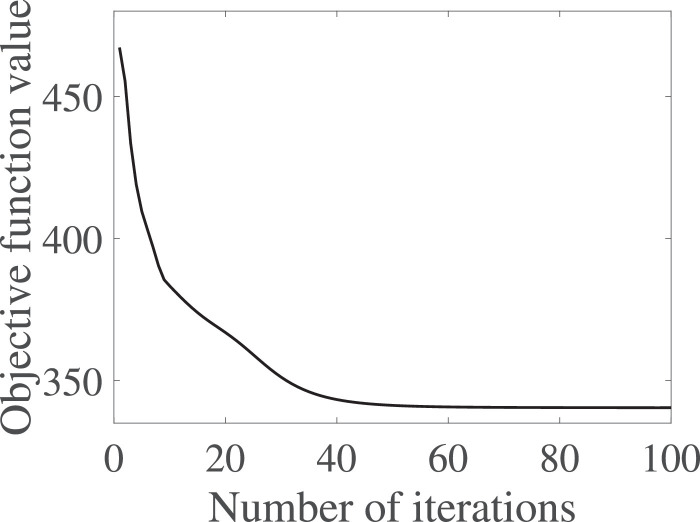
We proposed Algorithm 1 to optimize our objective function Eq. (6) and theoretically proved its convergence. We experimentally verified the convergence of Algorithm 1 by investigating the variations of the objective function values of Eq. (6) at different iteration times. We reported the results in Fig. 5 while setting the stop criteria of Algorithm 1 as $\frac{{\parallel obj(t+1)-obj\left(t\right)\parallel }_2^2}{obj\left(t\right)}\le {10}^{-4},$ where obj(t) is the objective function value of Eq. (6) in the t-iteration. We have two observations from Fig. 5. On one hand, Algorithm 1 sharply reduced the objective function values in the first several iterations and then began to be stable. On the other hand, Algorithm 1 achieves its convergence within tens of iteration times. Hence, Algorithm 1 solving our objective function in Eq. (6) achieves fast convergence.

6. Discussion

6.1. Imbalance classification

In the classification task, our method investigates the issues, i.e., feature selection, sample weight, imbalance classification, and joint classification and regression. As a result, our method outperforms all comparison methods only focusing on part of four issues. Moreover, our solution for each issue is shown reasonable and feasible. An interesting question is which issue dominates the COVID-19 analysis with chest CT scan data. There is not theoretical answer. However, based on our experimental results, the problem of imbalance classification should be the first issue to be considered due to the following reasons.

First, it is necessary to take into account the problem of imbalance classification. In our experiments, random forest outperforms L1SVM (e.g., improving by 6.84% on average for all evaluation metrics) because random forest considers the problem of imbalance classification and L1SVM takes into account the issue of high-dimensional data. Moreover, the only difference between SFS and MSFS is that SFS considers the problem of imbalance classification and MSFS conducts a joint classification and regression. As a result, SFS beats MSFS a little bit, i.e., 1.26% improvement in terms of all evaluation metrics.

Second, in Fig. 2, the sensitivities of the methods (e.g., SVM, L1SVM, and MSFS) are low, e.g., 23.86%, 26.73%, and 47.45% respectively. The reason is that their classifiers could directly predict the samples of the minority class with the label of the majority class to output high accuracy, e.g., 67.35%, 75.26%, and 86.31%, respectively. On the contrary, the methods (e.g., random forest, SFS, and our Proposed w/o Regression) consider the issue of imbalance classification to output the high sensitivities, e.g., 49.61%, 50.65%, and 70.73%, respectively.

6.2. Top selected regions

In this section, we list the top selected features (i.e., the chest regions) of our proposed method in Table 6 , which could help the clinicians to improve the efficiency and the effectiveness of the disease diagnosis. To do this, we first obtained the totally selected number for each feature across 100 experiments, i.e., repeating the 5-fold cross validation scheme 20 times, and then reported top 22 selected features (i.e., regions), each of which was selected at least 90 out of 100 times. We list our observations as follows.

Table 6.

Regions distribution at different HU ranges for the top selected regions.

Hu ranges	left lung (6)	right lung (16)
$[-\infty ,-700]$	0	2
$[-700,-500]$	1	8
$[-500,-200]$	2	5
$[-200,50]$	1	0
[50, ∞]	2	1

First, most selected features (i.e., 17 out of 22) are in the HU range of $[-700,-200],$ corresponding to the regions of ground glass opacity which has been demonstrated related to the severity of COVID-19 (Tang et al., 2020). Second, the region number in the right lung is larger than the number in the left lung, i.e., 16 vs. 6. The possible reason is that the virus might easily infect the regions in the right lung (Shi et al., 2020b). Third, we extracted 3 kinds of handcrafted features, i.e., the density features, the mass features, and the volume features, from each part. Moreover, the mass feature is related to both the density feature and the volume feature. Based on the results, our method selected 4 and 7 density features, respectively, from the left lung and the right lung, and 2 and 6 mass features, respectively, from the left lung and the right lung. However, our method only selected 3 volume feature from the right lung. Hence, we would have the conclusion that the density feature is the most important in our experiments, followed by the mass feature and the volume feature.

6.3. Importance of prediction and time estimation of severe cases

To our knowledge, this study is the first work to simultaneously predict and estimate the conversion time of COVID-19 developing to severe symptoms using the chest CT scan data.

First, our method obtains higher sensitivity, i.e., 76.97%, compared to (Tang et al., 2020), i.e., 74.5% of sensitivity. That is, our method achieves higher accuracy for classifying the severe cases than (Tang et al., 2020). The reason could contribute to that 1) our method designs a novel solution for the problem of imbalance classification, and 2) the regression information in our proposed joint model improves the classification performance.

Second, as shown in Fig. 4, the correlation coefficient (i.e., 0.524) between our predictions and the corresponding ground truths for the severe cases is larger than the value (i.e., 0.462) in Table 4 which measures the correlation between our predictions and the corresponding ground truths for all subjects. Moreover, our proposed method yields the averaged conversion time (i.e., 4.59  ±  0.223 days, which has 0.55 days different from the ground truth of the conversion time, i.e., 5.64 ± 4.30 days) from all non-serve cases to the severe stage, with the least estimation error (i.e., 6.01  ±  1.22), compared to all comparison methods. The possible reason should be that the classification information could improve the effectiveness of the regression task in our proposed joint model. Hence, our proposed method imply that our proposed method is good at predicting the conversion time from the non-severe stage to the severe stage. In real applications, correctly classifying severe cases is more important than correctly classifying the non-severe cases because the former could reduce the clinicians workloads. In particular, the correct prediction of the conversion time could help the clinicians designing effective treatment plan for the potential severe cases in time or even save the patients’ lives.

6.4. Limitations

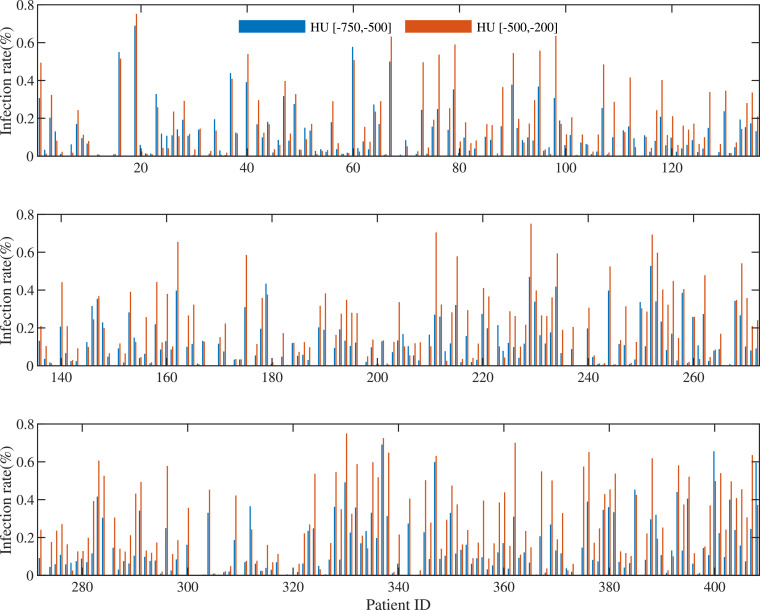
Recently, many studies focused on the study of early diagnosis of COVID-19. For example, (Shi et al., 2020a) conducted binary classification on 1658 confirmed cases and 1027 community acquired pneumonia cases to achieve 90.7% of sensitivity and 87.9% of accuracy. (Tang et al., 2020) focused on detecting 121 non-severe cases from 55 severe cases to yield 74.5% of sensitivity and 87.5% of accuracy. Compared to (Tang, Zhao, Xie, Zhong, Shi, Liu, Shen, 2020, Shi, Xia, Shan, Wu, Wei, Yuan, Jiang, Gao, Sui, Shen, 2020), this study only yielded an accuracy of 85.91%, which seems lower than that reported in previous work. However, the task in this paper tried to solve is more different, as we predict whether the patient would develop severe symptoms from the mild symptoms. This would result in the problem of imbalance classification since only a small portion of patients would convert severe based on the prevalence rate. First, the problem of imbalance classification of our data set is bias, i.e., 86 severe cases vs. 322 non-severe cases. This makes difficult to construct effective classification models. Second, the difference of infected volumes between the severe cases and the non-severe cases is small, as shown in Fig. 6 , while the corresponding difference is distinguished in (Tang et al., 2020), thus the latter can easily conduct classification. With the increase of available the data of severe cases, the accuracy of our method could be further improved. In our future work, we plan to generate new samples for the minority class to lessen the problem of imbalance classification, as well as design new deep transfer learning methods using other data sources (e.g., X-ray data) to solve the issue of small-sized sample and high-dimensional features.

Fig. 6.

Ratios of infected volumes in the HU ranges of [-700,-500] and [-500, -200], where patient IDs 1–322 are non-severe cases and patient IDs (323–408) are severe cases.

This study only focused on binary classification, i.e., severe cases vs. non-severe cases. In our future work, we plan to conduct multi-class classification on four types of COVID-19 diagnosis, i.e., mild, common, severe, and critical.

7. Conclusion

In this paper, we proposed a new method to jointly conduct disease identification and conversion time prediction, by taking into account the issues, such as high-dimensional data, small-sized sample, outlier influence, and imbalance classification. To do this, we designed a sparsity regularization term to conduct feature selection and learn the shared information between two tasks, and proposed a new method to take into account the sample weight and the issue of imbalance classification. Finally, experimental results showed that our proposed method achieved the best performance for detecting the severe case from non-severe cases and the conversion time from the mild confirmed case to the severe case with the CT data in a real data set, compared to the comparison methods.

In the future, we can use registration techniques (Luan, Qi, Xue, Chen, Shen, 2008, Fan, Rao, Hurt, Giannetta, Korczykowski, Shera, Avants, Gee, Wang, Shen, 2007, Xue, Shen, Davatzikos, 2006) to align the longitudinal images of the same patients for more accurate measurement of local infection changes for helping patient management.

CRediT authorship contribution statement

Xiaofeng Zhu: Conceptualization, Methodology, Software, Writing - original draft. Bin Song: Validation, Resources, Data curation. Feng Shi: Methodology, Investigation, Writing - original draft. Yanbo Chen: Software, Validation, Investigation. Rongyao Hu: Formal analysis, Investigation, Methodology, Writing - original draft. Jiangzhang Gan: Methodology, Software, Writing - review & editing. Wenhai Zhang: Data curation, Visualization. Man Li: Data curation, Visualization. Liye Wang: Resources, Data curation, Visualization. Yaozong Gao: Methodology, Writing - review & editing. Fei Shan: Resources, Data curation, Supervision, Writing - review & editing. Dinggang Shen: Writing - review & editing, Supervision, Project administration.

Declaration of Competing Interest

F.S., Y.C., W.Z., M.L., L.W., Y.G., and D.S. are employees of Shanghai United Imaging Intelligence Co., Ltd. The company has no role in designing and performing the surveillances and analyzing and interpreting the data. All other authors report no conflicts of interest relevant to this article.