Heterotrophic eukaryotes show a slow-fast continuum, not a gleaner–exploiter trade-off

Significance

Organisms must allocate energy and resources to all basic life functions, and this leads to inescapable trade-offs. These trade-offs govern the species composition and functioning of ecosystems. We show that perhaps the most commonly assumed trade-off in ecology—between relative performance at low and high resource (food) levels—does not exist. Instead, species that do better at low resource levels also do better at high resource levels. Models predicting how communities respond to environmental change will need to be reevaluated in light of this. Our results also imply that the most important trade-off in nature is probably that between the ability to grow fast and to survive the threat of predation.

Abstract

Gleaners and exploiters (opportunists) are organisms adapted to feeding in nutritionally poor and rich environments, respectively. A trade-off between these two strategies—a negative relationship between the rate at which organisms can acquire food and ingest it—is a critical assumption in many ecological models. Here, we evaluate evidence for this trade-off across a wide range of heterotrophic eukaryotes from unicellular nanoflagellates to large mammals belonging to both aquatic and terrestrial realms. Using data on the resource acquisition and ingestion rates in >500 species, we find no evidence of a trade-off across species. Instead, there is a positive relationship between maximum clearance rate and maximum ingestion rate. The positive relationship is not a result of lumping together diverse taxa; it holds within all subgroups of organisms we examined as well. Correcting for differences in body mass weakens but does not reverse the positive relationship, so this is not an artifact of size scaling either. Instead, this positive relationship represents a slow–fast gradient in the “pace of life” that overrides the expected gleaner–exploiter trade-off. Other trade-offs must therefore shape ecological processes, and investigating them may provide deeper insights into coexistence, competitive dynamics, and biodiversity patterns in nature. A plausible target for study is the well-documented trade-off between growth rate and predation avoidance, which can also drive the slow–fast gradient we observe here.

Trade-offs represent fundamental challenges that organisms face when acquiring and allocating resources to growth, defense, and reproduction. If trade-offs did not exist, the equilibrium outcome would be a single “Darwinian demon” (or a single species in ecological competition) that succeeds in all conditions. Because this contradicts both logic and patterns in nature, we know that trade-offs must exist (1–3). They are therefore a core assumption in ecological and evolutionary models, and they govern the composition and dynamics of biological communities (4–6). One commonly assumed form is the trade-off between the capacities for searching for food and for acquiring and processing food, called the “gleaner–exploiter” or “gleaner–opportunist trade-off” (7), or the “oligotroph–copiotroph trade-off” in microbial ecology (8, 9). This trade-off is expected because resources are limited, and there are high energetic and material costs associated with construction, maintenance, and operation of structures to search for and process food. Organisms living in low-resource environments are expected to be gleaners that can rapidly search large areas or volumes for resources, that is, they have a high maximum clearance rate (or “attack rate” in the terrestrial literature). Conversely, organisms in resource-rich environments are expected to be exploiters that ingest, assimilate, and process resources at high rates (high maximum ingestion rate). As the two strategies lead to greater relative success under different conditions, the gleaner–exploiter trade-off can enable coexistence between competing species when combined with spatial or temporal heterogeneity in resource availability (2, 10–13). This idea enjoys broad acceptance in ecology and continues to shape the way we model ecological interactions and ecosystem processes (14, 15); it has even been discussed as the “well-known trade-off between attack rates and the conversion of prey into predator biomass” (7). However, there is surprisingly little experimental or observational evidence that such a trade-off exists. This represents a major gap in our understanding of ecological processes and their drivers.

Here, we explore whether the gleaner–exploiter trade-off exists in eukaryotic heterotrophic consumers. The gleaner–exploiter trade-off may be investigated both within and across species, and the patterns observed may be different at the two scales. We focus on exploring patterns across species here, though we briefly examine intraspecific variation as well.

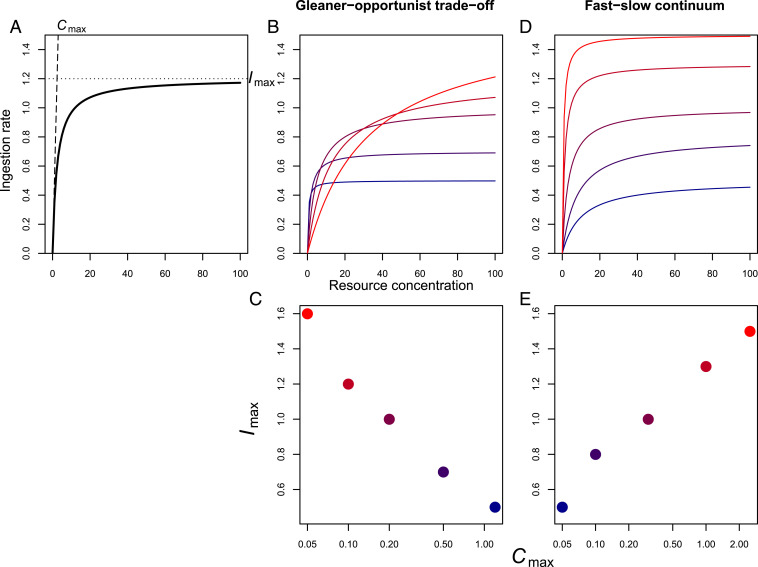
Resource acquisition and consumption are measured in experiments that quantify the number of prey consumed per predator per unit time, across gradients in prey density. This relationship is a saturating function because at high prey density the predator is limited by the rate at which it can handle, ingest, and assimilate food (Fig. 1A). Holling type II, Holling type III, and Ivlev functions all describe this saturating relationship, and they are all characterized by two parameters: the predator’s maximum ingestion rate (I_max) and its maximum clearance rate (C_max, also known as attack rate) (16). Increasing the maximum ingestion rate parameter improves performance under high-resource conditions. Increasing the maximum clearance rate parameter improves performance under low-resource conditions. The putative gleaner–exploiter trade-off can therefore be restated as a negative relationship between these parameters (Fig. 1 B and C). We make the assumption that organisms with high ingestion rates also have high assimilation rates and support this with data. Hereafter, we discuss ingestion and assimilation as a joint process.

Fig. 1.

(A) A typical functional response curve relating resource uptake rate to resource concentration. The functional response curve is characterized by two parameters, I_max and C_max. C_max is the initial slope of the curve and is equal to the maximum volume or area that the consumer can clear for resources per unit time. I_max is the uptake rate at which the curve saturates. For both parameters, higher values imply better performance: C_max reflects performance at low resource concentrations and I_max at high concentrations. (B and C) The variation in functional response curves between species implied by a gleaner–opportunist trade-off (B) and the consequent negative relationship between C_max and I_max (C). (D and E) In contrast, D shows the variation in functional response curves between species implied by a slow-fast gradient in the pace of life and E shows the consequent positive relationship between C_max and I_max. Colors of dots in C and E refer to the corresponding curves in B and D.

To evaluate whether the gleaner–exploiter trade-off exists, we used C_max and I_max estimates from organisms ranging from unicellular nanoflagellates to large mammals, across a range of terrestrial and aquatic systems. These data were obtained from measurements of functional response curves (Fig. 1A) compiled in two published datasets (16, 17). Together, these provided us with more than 1,300 estimates of each rate from >500 species belonging to a wide range of taxonomic groups (see Materials and Methods for details). C_max was expressed in dimensions of volume per time or area per time depending on whether the taxa scanned volumes or surfaces for prey. We refer to these as volume and surface feeders, respectively. We analyzed these C_max and I_max values as well as body mass-corrected versions that we call specific C_max and specific I_max.

Results

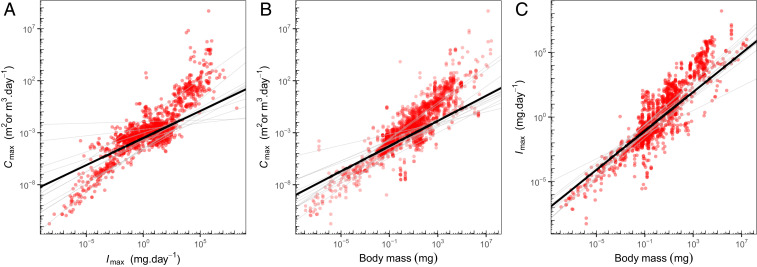
C_max and I_max are strongly and positively related to each other (Fig. 2A and SI Appendix, Table S1), and this relationship holds across taxonomic groups, habitats, and feeding dimensionalities (SI Appendix, Fig. S1). However, both rates are strongly associated with organism body mass; larger individuals have higher clearance rates and can ingest more prey than small ones (Fig. 2 B and C and SI Appendix, Tables S2 and S3). So the positive relationship between C_max and I_max simply reflects the size-scaling of traits expected from the metabolic theory of ecology. This confounding effect of body mass can be addressed in three ways: 1) by including body mass in the regression as a covariate (i.e. multiple regression), 2) by first size-correcting the trait estimates (i.e., dividing by organismal body mass) and then regressing specific C_max and specific I_max estimates against each other, or 3) by calculating the residuals of the regressions of each of the traits against body mass, and regressing them against each other. All three approaches gave us consistent results, so we present the results based on size correction alone here, as this presentation is more familiar to many readers (see SI Appendix, Fig. S2 and Tables S4–S6 for results from all three approaches).

Fig. 2.

Relationships between C_max, I_max, and body mass. C_max and I_max are strongly positively associated (A) (marginal R² = 72%, conditional R² = 96%), but this relationship reflects their strong dependence on body mass (B and C) (marginal R² = 64 and 72%, conditional R² = 94 and 92%, for C_max and I_max, respectively). The size dependence of both traits is close to isometric based on OLS regression, but accounting for nonindependence with random effects for species and taxonomic group identity reduces the slopes to 0.75 for I_max and 0.6 for C_max. Black lines represent across-group patterns captured in the models by fixed effects, while gray lines represent phylum-level variation captured with random slopes and intercepts. Species-level variation is also captured by random intercepts. Variation in the relationships across environments (aquatic/terrestrial) and feeding dimension (surface/volume feeders) is minimal, and is shown in SI Appendix, Fig. S1.

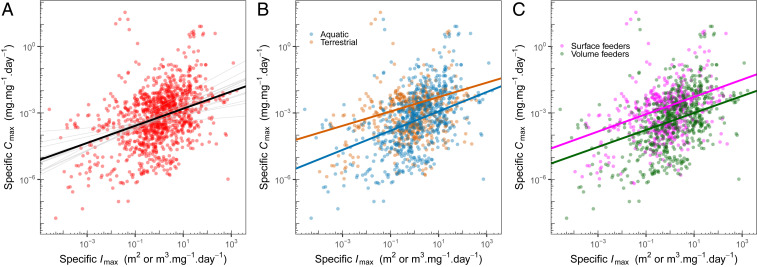
Specific C_max and specific I_max are also positively associated (Fig. 3A and SI Appendix, Table S4), contrary to the expectation of the gleaner–exploiter trade-off. In other words, size correction does not reveal a trade-off. The relationship between specific C_max and specific I_max is relatively weak (marginal R² of 12%), partly because the species and phylum random effects account for most of the variation (conditional R² of 81%). However, the relationship remains robust across taxonomic groups and model specifications (Fig. 3 and SI Appendix, Fig. S3). Every phylum exhibited a positive relationship both in the models with all phyla (SI Appendix, Fig. S3) and when investigated separately, so this is not driven by patterns in a subset of the data. Habitat of origin (terrestrial/aquatic) and feeding dimensionality (surface/volume) also have minimal effect on the relationship between C_max and I_max, whether size-corrected or not (Fig. 3 and SI Appendix, Tables S7–S12).

Fig. 3.

Specific C_max (i.e., size-corrected C_max) is positively related to specific I_max. (A) This positive relationship holds across species and phyla (black line, representing fixed effects in the model) and also within all phyla examined (gray lines, captured in the model by random slope and intercept terms). (B) Variation between habitats has little effect on the relationship. (C) The same is true for feeding dimensionality. Note that within-phylum patterns (random effects) are not shown in B and C for clarity but were accounted for in the model. SI Appendix, Fig. S3 shows an alternate visualization of A with points colored by group identity.

Discussion

The assumption of a trade-off between capacities to acquire and process resources has played a major role in the development of ecological theory, particularly in the context of species coexistence and diversity (1, 2, 18). The logic behind this trade-off is simple. Resource acquisition requires flagella, feeding appendages, a motor apparatus, and/or systems to sense, search for, and capture prey. Converting acquired food to energy requires a gut or specialized cellular organelles to digest and assimilate it. Maintaining and operating these machineries for acquisition and subsequent processing requires investments in material and energy. If a larger capacity to acquire food is needed, the cost must be paid for by reducing allocation to the machinery for processing, and vice versa. This trade-off has been demonstrated in a few specific taxa (19).

However, our analysis here contradicts this expectation across a very large range of eukaryotic heterotrophs. We find instead that the relationship between capacities to search for and process resources is positive, even when adjusted to account for differences in body mass. Surprisingly, organisms that efficiently search for resources when these are scarce are also most effective at ingesting and utilizing resources when they are abundant (Figs. 2 and 3). Moreover, this pattern holds across a wide range of taxonomic groups, terrestrial and aquatic environments, and surface and volume feeders (Fig. 3 and SI Appendix, Fig. S3). The taxonomic groups in our dataset span a wide range of ecological strategies and life histories, yet none exhibits any sign of the expected trade-off. And despite dramatic differences between terrestrial and aquatic environments in food concentration and spatial and temporal heterogeneity in both environmental variability and food availability, the patterns we describe differ only to a small degree. In short, the absence of a trade-off is a general pattern, not driven by data imbalances or particular groups. We note that there is also a positive relationship between affinity (equivalent to clearance rate) and maximum uptake rate of dissolved nutrients in microbial osmotrophs (bacteria and phytoplankton) (SI Appendix, Fig. S6) despite similar claims of a gleaner–exploiter trade-off in these taxa (20, 21). The explanation here is specific to microbial osmotrophs, however: both affinity and maximum uptake rate increase with the density of uptake sites (porters) on the cell surface (22), and a positive relationship is therefore to be expected.

What does the positive relationship between acquisition and ingestion imply for our understanding of nature? It represents additional evidence for a dominant slow–fast gradient in organismal strategies (Fig. 1 D and E) (23, 24). Indeed, the huge diversity of animal and plant life-history strategies can to a large extent be explained by a slow–fast gradient in the “pace of life” (25, 26). The pace-of-life syndrome describes the suite of correlated, coevolved traits that jointly constitute a single axis of biological variation across the tree of life. In this framework, physiology, behavior, life history, and morphology have all coevolved to satisfy the fundamental trade-off between current and future reproduction. In other words, traits and behaviors that favor success in the short term come at the cost of longevity and success in future reproductive possibilities. Strong environmental variation that keeps population sizes low favors “fast” life strategies that can rapidly reproduce and colonize ephemeral habitats. “Slow” traits such as high competitive ability are favored in stable environments, where population densities are large and density-dependent effects are strong.

The food acquisition and processing traits that we describe here likely represent important components of the slow–fast trait continuum. Foraging activity inevitably leads to elevated predation risks (27, 28). Fast life-history strategies that acquire more resources at both low and high resource concentrations come at the cost of a greater predation risk. Slow strategies that are poor at resource acquisition at all resource concentrations benefit from lower mortality. This implies a trade-off between food acquisition and mortality, which is well-documented in some taxa (29). Indeed, this trade-off may well cause the emergence of the slow-fast gradient (30–32). And far from being specific to heterotrophs or even motile organisms, this pattern resembles the trade-off in plants between acquisition and conservation of resources (acquisitive–conservative or leaf economic spectrum). Plants that acquire nutrients and grow slowly are better at conserving these by avoiding predation and tissue losses, leading to a similar slow–fast continuum (33–35).

We foresee four possible objections to our conclusions: 1) Trade-offs may apply at an intraspecific level but not an interspecific level, 2) trade-offs may be concealed by variation in resource acquisition (36), 3) our assumption that—all else being equal—increases in maximum ingestion rate are associated with increases in maximum assimilation rate may be untrue, and 4) we have not accounted for relatedness appropriately in our analyses. We address these in turn.

We first consider the possibility that gleaner–exploiter trade-offs exist at a narrower taxonomic scale than the broad groups we examined. Although we cannot address this definitively across a wide range of taxa, our dataset does contain multiple estimates from a small number of species. We therefore examined the six species for which we have 20 measurements or more of specific maximum clearance rate and specific maximum ingestion rate (SI Appendix, Fig. S4). In five of these species, we again find a positive relationship, consistent with our overall findings. In the sixth species, Scolothrips takahashii, we find a very weak and nonsignificant negative relationship [CIs: −0.42, 0.2]. This analysis is complicated by measurements on different life stages for some species, and the existence of unsuccessful individuals that gain few resources. This brings us to the second objection.

Intraspecific trade-offs may be concealed if variation in resource allocation between individuals in a population is much smaller than variation in resource acquisition (3, 34, 36, 37). Individuals within a population that acquire fewer resources also have fewer offspring on average. Including these low-fitness individuals in analyses can drive a positive relationship between traits at the population level; this is misleading because the strategies of the next generation are determined by the individuals that have more offspring. Therefore, a more careful examination would be needed to conclusively establish the absence of intraspecific trade-offs. However, this argument is much weaker when applied to comparisons across species (36), the focus of this paper. Species (generally speaking) can be expected to reproduce themselves to the next generation and are not subject to the bias introduced by low-fitness individuals in intraspecific comparisons. Additionally, this objection applies most strongly to field populations; controlled laboratory studies are able to minimize variation in resource availability. However, only 22 data points in our dataset are from field studies. Therefore, we believe that the positive trait relationship across species cannot be attributed to this mechanism.

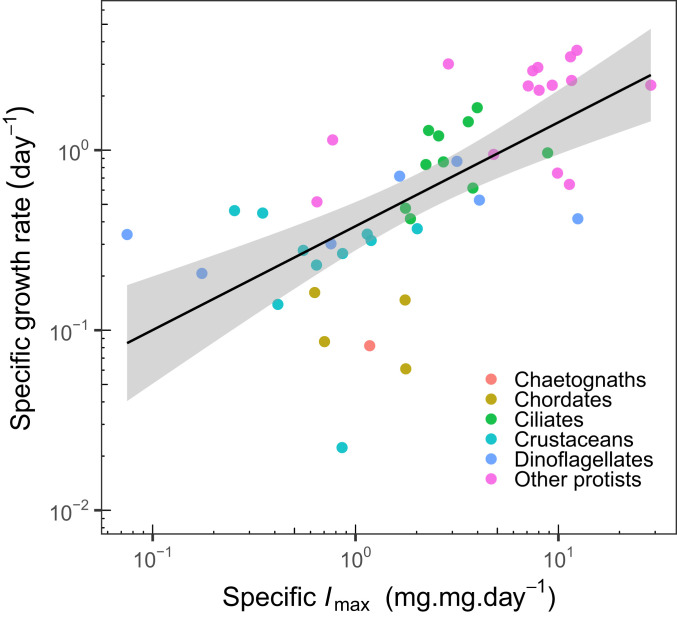
Third, we may be incorrect in our assumption that maximum ingestion rates and maximum assimilation rates are positively associated, and therefore in our consequent decision to treat these as a single process. A direct test of this across species is unfortunately not possible because of a lack of data on assimilation rates, although this has in one case been demonstrated within a species (38). However, we can assess this indirectly. Ingesting and assimilating food necessarily implies some somatic growth. If an organism has a high ingestion rate and a low assimilation rate, it has a low resource-use efficiency and a relatively low growth rate. In contrast, a high ingestion rate and a high assimilation rate implies a high resource-use efficiency and a high growth rate (in the presence of sufficient food). Therefore, we can test our underlying assumption by checking for a positive association between maximum specific ingestion rates and specific growth rates (or, alternatively, a lack of association with resource-use efficiencies). We find support for this assumption in a small but reasonably diverse dataset of 47 taxa (Fig. 4 and SI Appendix, Table S13).

Fig. 4.

Higher specific maximum ingestion rates are associated with higher maximum specific growth rates (P < 0.001, R² = 0.42), lending support to our assumption that maximum ingestion rates and maximum assimilation rates are positively associated. This used an OLS regression. Taxonomic group variation was ignored because only six groups were present, and three of those had fewer than three points.

Finally, our use of random effects for species and for high-level taxonomic groups (broadly corresponding to phyla) is an imperfect proxy for nonindependence due to phylogenetic relatedness. At present, the data and methods available are insufficient to fit an appropriate evolutionary model that accounts for the complexities of trait evolution across this broad taxonomic and trait range (Materials and Methods). A gleaner–exploiter trade-off may therefore occur at intermediate taxonomic/phylogenetic scales (as we have accounted for variation at the phylum and at the species level, however imperfectly). We cannot rule out this scenario but it appears unlikely to us. A more plausible version of this argument is that specific clades, defined at intermediate taxonomic scales such as family or class, may exhibit a gleaner–exploiter trade-off. However, these clades would be exceptions to the general rule, which is the focus of our argument.

We have shown that there is no evident trade-off between acquisition and ingestion/assimilation capacities across species; in other words, the gleaner–exploiter trade-off does not exist. But some trade-off must exist, and our theoretical understanding of ecological processes relies on understanding its nature. Our work therefore suggests that other trade-offs deserve more attention, both empirical and theoretical. Out of the wide variety of putative trade-offs that relate important biological traits (predation rates, defense, competitive ability, colonization, abiotic tolerances, and others), one of the best documented is that between foraging and predation risk (29). Our findings lend indirect support to the importance of this trade-off, which can contribute to the emergence of the slow-fast gradient we observe in our data (30–32). The fundamental foraging–predation risk trade-off may therefore be a more important determinant of the composition, diversity, and dynamics of biological communities than the gleaner–exploiter trade-off. Much remains unknown about how it influences community dynamics and ecosystem processes (39), and its implications deserve further investigation. The slow–fast gradient in the pace of life represents an additional, interesting dimension of biological variation, but one that is unlikely to directly contribute to patterns of coexistence.

Materials and Methods

We synthesized two datasets of resource acquisition and ingestion measurements compiled from the literature (16, 17). Both compilations are mainly composed of data from laboratory experiments, but a few field experiments (n = 22) are included in ref. 17. We describe the datasets and processing steps taken below.

Data.

Data sources and description.

The Kiørboe and Hirst dataset (16) focuses on aquatic organisms, specifically pelagic ones. It provides 873 estimates of C_max, 337 estimates of I_max, and 151 cases where both parameters were estimated simultaneously in the same species. The taxa encompass heterotrophic protists (nanoflagellates, dinoflagellates, ciliates), crustaceans (copepods, krill), chaetognaths, tunicates (salps), planktivorous fish, and gelatinous plankton (cnidarians and ctenophores).

The Uiterwaal et al. dataset (17) focuses on heterotrophic eukaryotes. It includes organisms from both aquatic and terrestrial environments, ranging in size from microscopic flagellates to large mammals. The aquatic groups present include insects in addition to all those in the Kiørboe and Hirst dataset. The terrestrial taxa are primarily insects and arachnids, but also include birds, mammals, and reptiles. It therefore includes taxa from the Kiørboe and Hirst dataset, but contains many more data points (2,083).

Together, the datasets contained a diversity of taxonomic groups that we modeled at the phylum level: arthropods, chaetognaths, chordates, ciliates, cnidarians, crustaceans, ctenophores, dinoflagellates, molluscs, platyhelminths, rotifers, tardigrades, as well as “other protists.” Modeling other protists as separate taxa was not feasible because of the poor representation of some of the taxa.

Data-processing steps.

• 1)Uiterwaal et al. (17) estimated a handling time parameter (time per unit resource consumed) by fitting a Holling type II function to data on foraging rate as a function of resource availability. We converted handling time to maximum ingestion rate by taking its inverse, thereby expressing it in dimensions of mass per time.
• 2)The two datasets expressed body mass in different units. To make the two datasets comparable, we converted carbon mass to fresh weight by assuming a carbon content of 10% of the wet mass (40); that is, carbon mass was multiplied by a factor of 10.
• 3)To enable comparison, all estimates were temperature-corrected to reflect their estimated value at 15 °C, assuming a Q₁₀ of 2.8 (41). Temperature correction is somewhat questionable in the case of warm-blooded animals, but 1) these represented a very small number of individuals (27 mammals, 20 birds), and 2) across the dataset, log₁₀-transformed uncorrected and temperature-corrected C_max values had a correlation of 0.98, while the same comparison for I_max values yielded a correlation of 0.97, making any such changes relatively unimportant.
• 4)We calculated mass-corrected maximum ingestion rates and maximum clearance rates by dividing the values by the species’ body mass.

Data-exclusion rules.

• 1)Cases without temperature information from ref. 17 were excluded.
• 2)Cases where there were no estimates of the mass of individual prey were excluded except for the model and plot of the absolute clearance rate and ingestion rate against each other (Fig. 2).
• 3)Most species were aquatic or terrestrial, but two species were listed as being of “mixed” habitat. These were excluded.
• 4)Most terrestrial organisms were surface feeders (two-dimensional [2D] environment), while most aquatic were volume feeders (3D environment). However, in some cases, predator–prey interactions were classified as occurring in a 2.5D environment in ref. 17, for example, insects crawling on whole plants or spiders on webs. These data were excluded as they are difficult to interpret and compare with observations in 2D and 3D space.
• 5)When specific maximum ingestion rates are plotted against body mass, there is a cloud of points that separates clearly from the bulk of the data (SI Appendix, Fig. S5). These points have unrealistically high specific ingestion rates, exceeding 10³⋅d⁻¹, namely organisms consuming more than 1,000 times their own body mass per day. These values are highly implausible, and so the data almost certainly represent errors. They were therefore excluded.
• 6)We excluded all points from a single study (42) that ref. 17 noted were of poor quality.
• 7)Data from a few studies were present in both datasets. Because some of the source studies themselves represented compilations of earlier datasets, we could not simply exclude cases where the source paper was identical. To be conservative, we excluded all species from ref. 17 that were also present in ref. 16 before merging.

After removing data according to the above criteria, we were left with 2,457 data points with 2,114 estimates of maximum clearance rate, 1,392 estimates of maximum ingestion rate, and 1,206 cases where both rates were estimated in the same species; 1,206 is therefore the sample size for our primary results about the relationship between the two traits, although the regressions of the individual traits against body size had more (details in SI Appendix, Tables S1–S13). We additionally had 47 data points from ref. 16 for which estimates of both specific growth rate and maximum specific ingestion rate were available.

Analysis.

Details of all models fitted are in SI Appendix, Tables S1–S13 and code to reproduce all analyses, tables, and plots can be found at DOI: 10.5281/zenodo.4002083.

Modeling approach.

Relationships between pairs of continuous variables can be addressed well through a regression framework. However, the present dataset possesses features to which ordinary least-squares (OLS) regression is not well-suited.

• 1)Nonindependence of points due to taxonomic relatedness. The 2,457 data points in our dataset arose from measurements on just 510 species. Points from the same species are expected to be more similar to each other than those from other species. The same argument applies to closely related species. We addressed this by using linear mixed-effects models with random effect terms (details in Model fitting) for species identity and for taxonomic group. These taxonomic groups broadly corresponded to phyla, with the exception of varied protists that were grouped together for simplicity and model robustness. The taxonomic groups we used were arthropods, chaetognaths, chordates, ciliates, cnidarians, crustaceans, ctenophores, dinoflagellates, molluscs, platyhelminths, rotifers, tardigrades, and other protists. We note that this nonindependence could also be addressed through a phylogenetic regression framework, but the gains from the additional complexity are expected to be limited unless an accurate evolutionary model is fit, namely one that takes into account correlated trait evolution, variation in evolutionary rates across the phylogeny, evolutionary jumps in trait value, and other features expected across this broad phylogenetic and taxonomic range. This remains technically challenging despite substantial advances in recent years (43–45), and the data required to do so across our dataset do not exist. As our results were robust to a variety of different modeling approaches, we believe this is unlikely to alter our conclusions.
• 2)Many of the relationships we investigate here are reversible, in the sense that either variable could be plotted on the x-axis. However, switching the axes leads to substantially different predictions because of the way residuals are calculated in standard regression fitting; regression slopes are biased toward 0. Standardized major-axis (SMA) regression is a solution to this problem, although it tends to produce slope estimates that are biased upward in realistic conditions (46). Unfortunately, it is presently not possible to do SMA regression with random effects, to our knowledge. As we believe the latter to address a more important problem for our analysis, we did not use SMA regression. As our primary conclusion is that the relationship is not negative and SMA regression estimates are more steeply positive, any bias introduced by avoiding SMA regression is in the direction of making our analyses more conservative.

Model fitting.

Most results in the paper are based on linear mixed-effects models with log₁₀-transformed rates and body mass estimates. The models used both 1) random intercepts for species identity, and 2) random intercepts and slopes for phylum identity.

For the relationship between specific growth rate and maximum specific ingestion rate (Fig. 4), only 2 out of the 47 points belonged to the same species and very few taxonomic groups were represented, making a mixed-effects model unsuitable. OLS regression was used in this case instead.

Model checking.

As a test of robustness, we fit all models (except that in Fig. 4) with OLS regression, SMA regression, and linear mixed-effects models with different random-effects structures (random intercepts for species only, random intercepts for species and phylum, random intercepts for species and phylum plus random slopes for phylum). These sets of models gave slightly different parameter estimates, but no analysis led to a different conclusion. We therefore present the results from the models we believe to be most appropriate: linear mixed-effects models with random intercepts for species and phylum identity in addition to random slopes for phylum identity. In one case, the model returned a singular fit. Deeper investigation using Bayesian hierarchical models with weakly informative priors showed that these had negligible influence on parameter estimates and inferences, but we present the Bayesian hierarchical model results in this case because its estimates are more reliable.

We used two common metrics for assessing the variance explained in mixed models, the marginal R² and conditional R² (47). The marginal R² quantifies the variance explained by the fixed effects alone, while the conditional R² quantifies the variance explained by the full model, namely fixed and random effects jointly.

Tools used.

We used the R statistical environment v. 3.6.2, along with the packages dplyr and janitor for data handling, lmodel2 for SMA regression, lme4 for mixed-effects modeling, rstanarm for Bayesian hierarchical modeling, MuMIn for estimates of variance explained in the mixed models, pbkrtest for mixed-model hypothesis testing, ggplot2, ggtext, and cowplot for plotting, and sjPlot for generating tables.

Data Availability.

Data (DOI: 10.5281/zenodo.4002028) and code (DOI: 10.5281/zenodo.4002083) for all analyses and plots presented in this paper are available on GitHub.