Stick–slip model for actin-driven cell protrusions, cell polarization, and crawling

Significance

Spreading and crawling cells display rich nonlinear dynamics, which include periodic phases of growth and retraction of cellular protrusion, traveling waves along the cell edges, and spontaneous cell polarization and crawling. Using a theoretical model combining the mechanosensitivity of cell–substrate adhesion kinetics and linear cell viscoelastic mechanics, I show that the force-sensitive unbinding of adhesion bonds leads to stick–slip dynamics that recapitulate these dynamics’ features. The model also highlights the role of the cell membrane tension in controlling spontaneous symmetry breaking and the transition between spreading and crawling. This suggests that purely mechanical feedback loops, in addition to those involved in biochemical signaling networks, are key regulators of cell crawling.

Abstract

Cell crawling requires the generation of intracellular forces by the cytoskeleton and their transmission to an extracellular substrate through specific adhesion molecules. Crawling cells show many features of excitable systems, such as spontaneous symmetry breaking and crawling in the absence of external cues, and periodic and propagating waves of activity. Mechanical instabilities in the active cytoskeleton network and feedback loops in the biochemical network of activators and repressors of cytoskeleton dynamics have been invoked to explain these dynamical features. Here, I show that the interplay between the dynamics of cell–substrate adhesion and linear cellular mechanics is sufficient to reproduce many nonlinear dynamical patterns observed in spreading and crawling cells. Using an analytical formalism of the molecular clutch model of cell adhesion, regulated by local mechanical forces, I show that cellular traction forces exhibit stick–slip dynamics resulting in periodic waves of protrusion/retraction and propagating waves along the cell edge. This can explain spontaneous symmetry breaking and polarization of spreading cells, leading to steady crawling or bipedal motion, and bistability, where persistent cell motion requires a sufficiently strong transient external stimulus. The model also highlights the role of membrane tension in providing the long-range mechanical communication across the cell required for symmetry breaking.

Cell crawling is ubiquitous in many biological processes from development to cancer. It is inherently a problem of mechanics, in which forces generated by the cytoskeleton are transmitted to the environment through transient adhesion to allow for cell translocation (1). The cytoskeleton is a highly dynamical active gel able to exert pushing forces through the polymerization of actin filaments and contractile forces through the interaction between actin and myosin motors. In a schematic description of cell crawling, the protrusion of the cell front is driven by actin polymerization while actomyosin contraction retracts the cell rear (2). In their physiological context, cells often polarize and crawl in response to external cues, such as gradients of chemoattractants or of mechanical properties of their environment (3, 4). However, many cells also crawl as a result of spontaneous symmetry breaking and exhibit periodic and/or propagating waves of activity (5). Even cell fragments devoid of nucleus show spontaneous symmetry breaking and bistability and can be driven into a persistent motile state by transient mechanical stimuli (6).

These nonlinear features call for a description of motile cells as self-organized systems in which feedback loops lead to dynamical phase transitions (7–9). Many such descriptions have been proposed, most of which focus on the behavior of the cytoskeleton itself. One class of models, which include bistability, polarization, and wave propagation, is based on the existence of feedback loops within the biochemical network of proteins regulating cytoskeletal activity, such as Rac GTPases which activate actin polymerization and protrusion or Rho GTPases which activate actomyosin contractility (10–12). This includes possible mechanical feedback, for instance through modulations of the cell membrane tension (13, 14). Another class of models focuses on the mechanics of the cytoskeleton, an active viscoelastic gel made of polar filaments which can spontaneously form asters and vortices (15). Symmetry breaking (16) and spontaneous motility (17) can be obtained by coupling filament orientation to the cell boundary, and waves can arise from the reaction–diffusion dynamics of actin nucleators and inhibitors (18). Modulations of the myosin distribution by the actin flow have also been studied extensively and can lead to instabilities (19) and spontaneous polarization and motion (20–24). In fast-moving, crescent-shaped cells such as keratocytes and cell fragments, the actin cytoskeleton often forms a branched network at the cell front and contractile bundles enriched in myosin at the back. A switch-like transition between these two structures has been described using phenomenological models (25, 26). Finally, many models have also addressed the shape, dynamics, and speed of motile cells through feedback between shape and the rate of actin polymerization and depolymerization (27–31).

The models above generally treat force transmission with the substrate as a simple linear friction. The present work focuses on the nonlinear dynamics of cell–substrate adhesion. More specifically, it concentrates on so-called mesenchymal cell motility on a flat substrate, where a thin protrusion called the lamellipodium forms the leading edge of spreading and crawling cells, powered by actin polymerization (32). Polymerization is often offset by a retrograde flow of actin away from the cell edge, driven by actomyosin contraction and the cell membrane tension. According to the “molecular clutch” model (33, 34), these retrograde forces are balanced by frictional traction forces resulting from the transient linkage between actin filaments and the substrate through the binding and unbinding of adhesion molecules such as integrins. This linkage involves a myriad of regulatory proteins (35), many of which are mechanosensitive (34, 36–38). The lifetime of individual bonds can decrease [slip bonds (39, 40)] or increase [catch bonds (41–44)] under force. As detailed below, this can lead to stick–slip dynamics, which are well known in the context of materials science (45, 46) and also in the cellular context (47, 48). This provides a natural explanation for the existence of two (slipping and gripping) states of actin flow dynamics (49, 50), for the biphasic relationship between actin flow and traction force (51–54), and for the traction force dependence on substrate stiffness (55, 56).

A stick–slip transition has been extensively discussed in the context of cell protrusion and motility, either using a discontinuous version of the stick–slip transition where adhesion sites break beyond a critical force (57–62) or quantitatively accounting for the dynamics of the transition in a population of stochastic bonds (47, 63–65). However, we are still in need of a simple analytical understanding of the interplay between the stick–slip dynamics and other dynamical processes within the cell, which has thus far mostly been studied through computer simulations. The present work offers such a description within a linear cell mechanics framework based on simple elastic or viscoelastic constitutive relationships. It mostly focuses on one-dimensional (1D) cells, although lateral propagating waves are also discussed. Even this simplified model displays a rich dynamical behavior, including protrusion/retraction waves, spontaneous polarization or bistability, and unsteady motion. This can be used as a firm basis to understand more complicated systems with multiple interacting feedback loops.

Model and Results

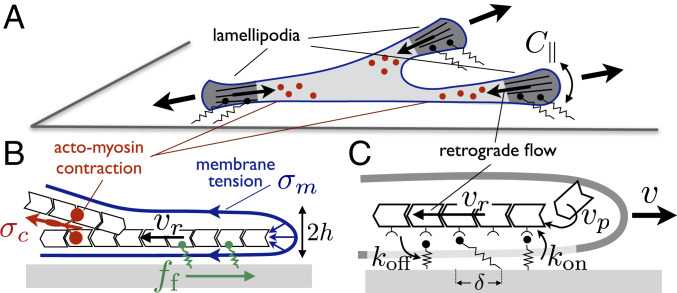
Actin filaments polymerizing against the cell membrane and actomyosin contraction create an actin retrograde flow away from the cell edge. This flow correlates with high substrate traction stress and is often concentrated in the lamellipodium, near the cell edges (51, 66) (Fig. 1A). According to the molecular clutch model, traction stress is akin to a friction force exerted by adhesion molecules transiently bound to moving filaments (Fig. 1C). The retrograde velocity is fixed by the force balance (sketched in Fig. 1B) between this friction force and the “retrograde force” from the cytoskeleton tension ${\sigma }_c$—mostly due to the actomyosin contraction—and the membrane tension ${\sigma }_m$ (67). The latter force is the membrane Laplace pressure integrated over the lamellipodium thickness $2h$: $2h{\sigma }_{m}C$, where the total curvature $C=1/h+C_{\Vert }$ is the sum of the curvature along the lamellipodium height $1/h$ and the curvature along the cell edge $C_{\Vert }$ (Fig. 1A). Assuming a uniform retrograde flow velocity $v_r$ over the lamellipodium for simplicity and calling $f_{\text{f}}\left(v_r\right)$ the friction force per unit length along the cell edge, integrated over the lamellipodium depth, the local force balance reads

$$f_{\text{f}}\left(v_r\right)={\sigma }_c+2{\sigma }_m\left(1+h{C}_{\Vert }\right).$$ [1]

Fig. 1.

Sketch of the model. (A) A 2D cell with three protrusions, showing the local cell edge curvature $C_{\Vert }$. (B) Force balance at the cell edge between the friction force $f_{\text{f}}$ and the retrograde force from membrane tension ${\sigma }_m$ (blue arrows at the tip show the local Laplace pressure) and actomyosin contraction ${\sigma }_c$. (C) Binding/unbinding cycle of adhesive linkers on a moving actin filament polymerizing near the cell edge.

Mechanosensitive Adhesion and Stick–Slip Dynamics.

The traction force is mediated by protein linkers binding to and unbinding from actin filaments with rates $k_{\text{on}}$ and $k_{\text{off}}$ (Fig. 1C). Both rates might depend on the force $f_b$ felt by a given linker. In the following, I concentrate on the mechanosensitive off rate and define the dimensionless, force-dependent off rate $r\left(f_b\right)=k_{\text{off}}/k_{\text{off}}^0$, where $k_{\text{off}}^0$ is the off rate under zero force. Similarly, the dimensionless on rate is $r_{\text{on}}=k_{\text{on}}/k_{\text{off}}^0$ and the dimensionless time is $\overline{t}=k_{\text{off}}^{0}t$. The stochastic friction force is proportional to the fraction of available linkers attached to actin filaments at a given time, called $n$, multiplied by their average extension $\delta \sim v_r/r$ (Fig. 1C and SI Appendix, section S2). The kinetic equation for the fraction of bound linkers and the total substrate friction force reads (45, 47, 68, 69)

$$\frac{\partial n}{\partial \overline{t}}=r_{\text{on}}-\left(r_{\text{on}}+r\right)n\hspace{1em}\mathrm{a}\mathrm{n}\mathrm{d}\hspace{1em}{f}_{\text{f}}\left(v_r\right)=\left({\alpha }_0+{\alpha }_1\frac{n}{r}\right)v_r,$$ [2]

where ${\alpha }_1$ is the coefficient of stochastic friction and ${\alpha }_0$ is a bare friction coefficient characterizing other (linear) viscous dissipation between the actin flow and the substrate. The former can be expressed in terms of the linkers density $\rho$ and stiffness $k_b$ as ${\alpha }_1=\rho l_{\mathrm{l}}{k}_b/k_{\text{off}}^0$, where $l_{\mathrm{l}}$ is the lamellipodium width.

For constant binding and unbinding rates, the stochastic friction force is linear with the retrograde velocity (68). For slip bonds, generic thermodynamic arguments suggest that the off rate increases exponentially with the force per bond $f_b$: $r=e^{\left|f_b\right|/f_b^{*}}$, where $f_b^{*}$ is a characteristic molecular force scale (37, 70). The retrograde velocity can thus be directly related to the off rate: $v_r=v_{\beta }r\log r$, where $v_{\beta }=k_{\text{off}}^0{f}_b^{*}/k_b$ is a velocity scale characterizing the mechanosensitivity of unbinding. The steady-state friction force is nonlinear with the retrograde velocity and reads

$${f_{\text{f}}}^{*}={\alpha }_0{v}_{\beta }\left(r+{\overline{\alpha }}_1\frac{r_{\text{on}}}{r_{\text{on}}+r}\right)\log r;\hspace{0.17em}\hspace{0.17em}{v}_r=v_{\beta }r\log r,$$ [3]

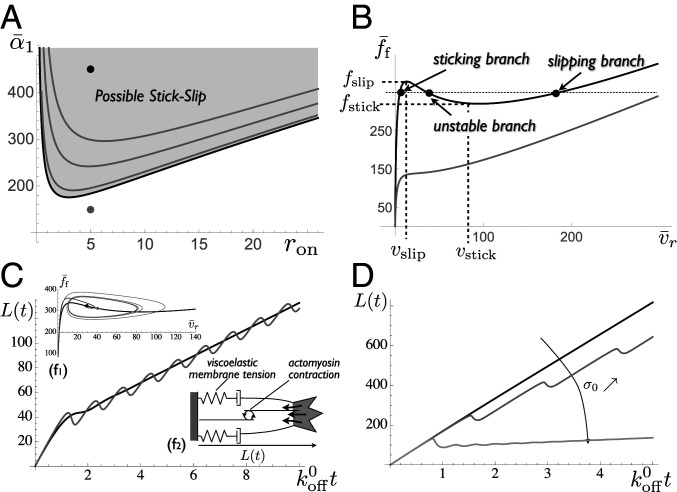
where ${\overline{\alpha }}_1\equiv {\alpha }_1/{\alpha }_0$. This defines a regime of high friction for small retrograde velocity when most linkers are bound and low friction dominated by the viscous drag ${\alpha }_0$ for large velocity when most linkers are unbound. Remarkably, the force–velocity relationship Eq. 3 is nonmonotonous for a broad range of parameters, with an abrupt transition between the two regimes (Fig. 2 A and B), equivalent to a stick–slip transition (46). This occurs when the ratio of stochastic to viscous friction ${\overline{\alpha }}_1$ is large, which is expected for crawling cells. In this regime, one may define characteristic values of the force and retrograde velocity (Fig. 2B). The high-friction regime exists for small forces $f_{\text{f}}<f_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}$ and small retrograde velocity $v_r<v_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}$, and the low-friction regime exists for large force $f_{\text{f}}>f_{\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{k}}$ and large velocity $v_r>v_{\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{k}}$.

Fig. 2.

Stick–slip dynamics of cellular protrusions. (A) Possible stick–slip region in the parameter space $\left\{r_{\text{on}},{\overline{\alpha }}_1={\alpha }_1/{\alpha }_0\right\}$ for an elastic protrusion of dimensionless stiffness ${\overline{k}}_{\sigma }=k_{\sigma }/\left({\alpha }_0{k}_{\text{off}}^0\right)$. The shaded region corresponds to a nonmonotonous friction force. Black line, stick–slip boundary for infinitely fast linker kinetics (${\overline{k}}_{\sigma }\to 0$); gray lines, boundaries for ${\overline{k}}_{\sigma }=1,\hspace{0.17em}5$, and 10 (Eq. 6). (B) Force/velocity relationship in and out of the stick–slip region (for $r_{\text{on}}=5$ and ${\overline{\alpha }}_1=150$ [gray] or 450 [black]). Characteristic values of the retrograde velocity (${\overline{v}}_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}$ and ${\overline{v}}_{\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{k}}$) and force (${\overline{f}}_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}$ and ${\overline{f}}_{\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{k}}$) are defined. (C and D) Growth of a 1D viscoelastic protrusion (sketched) for ${\overline{\alpha }}_1=400$ and $r_{\text{on}}=5$. (C) Protrusion length with time for two viscoelastic relaxation times and the same average speed: black, ${\overline{\tau }}_{\sigma }=0.2$ and ${\overline{\sigma }}_0=300$; and gray, ${\overline{\tau }}_{\sigma }=1$ and ${\overline{\sigma }}_0=214$ (with $r_p=15$). (D) Protrusion length with time for different homeostatic tension (with ${\overline{\tau }}_{\sigma }=0.5$ and $r_p=45$).

Catch-bond effects lead to a biphasic dependence of the unbinding rate, decreasing under small force and increasing under larger force (56, 71). This strongly amplifies the stick–slip behavior (SI Appendix, section S2 and Fig. S1). This could be of strong physiological relevance, but does not qualitatively change the results described below and the following analysis concentrates on slip bonds.

Dynamics of Protrusion Powered by Actin Polymerization.

We first focus on the dynamics of a unidimensional cellular protrusion or a cell front moving at uniform velocity ($C_{\Vert }=0$ in Eq. 1). The protrusion length $L\left(t\right)$ grows through a balance between actin polymerization at a velocity $v_p$ at the protrusion tip and actin retrograde flow: ${\partial }_{t}L=v_p-v_r$ (Fig. 1C). The retrograde force from membrane tension and actomyosin contraction may evolve in time. The cell membrane tension has a viscoelastic behavior. It increases (up to fourfold) following the formation of cell protrusions or cell spreading and relaxes at longer times (13, 72, 73), through the flattening of membrane invaginations such as caveolae (74, 75) or via endocytosis and exocytosis (76, 77). Disregarding spatiotemporal modulation of actomyosin activity, the total tension $\sigma ={\sigma }_c+2{\sigma }_m$ is described as a generic Maxwell fluid with a short-time elastic behavior characterized by an effective stiffness $k_{\sigma }$ and a long-time viscous relaxation toward a homeostatic tension ${\sigma }_0$ with a relaxation time ${\tau }_{\sigma }$:

$${\partial }_t\sigma +\frac{\sigma -{\sigma }_0}{{\tau }_{\sigma }}=k_{\sigma }{\partial }_{t}L=k_{\sigma }\left(v_p-v_{\beta }r\log r\right).$$ [4]

Elastic protrusions.

In the elastic regime (${\tau }_{\sigma }\to \infty$), the retrograde velocity balances the polymerization velocity for a stationary protrusion length $L^{*}$ satisfying $\sigma \left(L^{*}\right)={f_{\text{f}}}^{*}\left(r_p\right)$, where $r_p$ is the stationary off rate: $v_{\beta }{r}_p\log r_p=v_p$. Linear stability analysis of a perturbation around the steady state, $r=r_p+\delta r{e}^{\lambda t},n=n_p+\delta n{e}^{\lambda t}$ (with $n_p=r_{\text{on}}/\left(r_{\text{on}}+r_p\right)$) yields an equation for the dimensionless growth rate $\overline{\lambda }=\lambda /k_{\text{off}}^0$ (SI Appendix, section S3),

$${\overline{\alpha }}_1\frac{n_p}{r_p}+\left(\log r_p+1\right)\left(1+\frac{{\overline{k}}_{\sigma }}{\overline{\lambda }}\right)=\frac{n_p{\overline{\alpha }}_1\log r_p}{\left(\overline{\lambda }+r_p+r_{\mathrm{o}\mathrm{n}}\right)},$$ [5]

where the dimensionless stiffness ${\overline{k}}_{\sigma }=k_{\sigma }/\left({\alpha }_0{k}_{\text{off}}^0\right)$ compares the dynamics of cell tension variations to the kinetics of linkers binding and unbinding. The system undergoes a supercritical Hopf bifurcation ($\mathrm{R}\mathrm{e}\left(\lambda \right)>0$), leading to a stable limit cycle (78), when

$$\frac{{\overline{\alpha }}_1}{{\overline{\alpha }}_{\mathrm{1,0}}^{*}}-1>\frac{{\overline{k}}_{\sigma }}{r_{\text{on}}+r_p};\hspace{0.17em}\hspace{0.17em}{\overline{\alpha }}_{\mathrm{1,0}}^{*}=\frac{r_p{\left(r_p+r_{\text{on}}\right)}^2\left(\log r_p+1\right)}{r_{\text{on}}\left(r_p\log r_p-r_p-r_{\text{on}}\right)}.$$ [6]

If ${\overline{k}}_{\sigma }\to 0$, this condition means that the fixed point lies in the unstable branch of the force/velocity curve ($v_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}<v_p<v_{\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{k}}$ in Fig. 2B). The stick–slip range is reduced for finite values of ${\overline{k}}_{\sigma }$ (Fig. 2A). If Eq. 6 is satisfied, the elastic protrusion undergoes permanent oscillations, alternating between phases of growth (high friction and low retrograde velocity) and retraction (low friction and high retrograde velocity). The oscillation period depends on the difference between the slipping and the sticking forces and thus increases with the substrate adhesion strength ${\overline{\alpha }}_1$ (SI Appendix, Fig. S2). Under physiological conditions, for which one can estimate $r_{\text{on}}\simeq 10$, $v_{\beta }=1\hspace{0.17em}\mathrm{n}\mathrm{m}/\mathrm{s}$, ${\alpha }_0{v}_{\beta }=0.1\hspace{0.17em}\mathrm{\mu }\mathrm{N}/\mathrm{m}$, ${\overline{\alpha }}_1\simeq 10^3$, and ${\overline{k}}_{\sigma }\simeq 1$ (SI Appendix, Table S1), stick–slip is expected for a broad range of polymerization velocity $v_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}\simeq 15\hspace{0.17em}\mathrm{n}\mathrm{m}/\mathrm{s}<v_p<v_{\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{k}}\simeq 270\hspace{0.17em}\mathrm{n}\mathrm{m}/\mathrm{s}$. Note that although the present model considers a homogeneous distribution of bonds over the lamellipodium width $l_{\mathrm{l}}$, the maximum stochastic friction force density $f_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}/l_{\mathrm{l}}\simeq 100\hspace{0.17em}\mathrm{P}\mathrm{a}$ and the retrograde velocity at which it occurs $v_r\simeq 10\hspace{0.17em}\mathrm{n}\mathrm{m}/\mathrm{s}$ are consistent with those measured for focal adhesions (51). The present model is thus also relevant to qualitatively describe these dense adhesive structures, although additional cooperativity, e.g., in the binding process, is likely to be involved in their formation and maturation.

Viscoelastic protrusion.

At long time ($t\gg {\tau }_{\sigma }$), the tension is that of a viscous fluid, $\sigma ={\sigma }_0+{\alpha }_{\sigma }{\partial }_{t}L$ with ${\alpha }_{\sigma }=k_{\sigma }{\tau }_{\sigma }$, and the protrusion’s average length varies linearly with time. The short-time elastic response, including the stick–slip instability described above, nevertheless persists if tension relaxation is slower than the linkers kinetics ($k_{\text{off}}^0{\tau }_{\sigma }>1$; SI Appendix, section S3). The protrusion then alternates phases of growth and retraction with an average net growth (Fig. 2C). Oscillations of the cell edge are observed in a limited range of values for the homeostatic cell tension ${\sigma }_0$. Indeed, as for elastic protrusions, stick–slip of viscoelastic protrusions requires that the steady-state retrograde velocity lies within the decreasing branch of the force–velocity curve (Fig. 2B). This velocity can be modulated by factors affecting ${\sigma }_0$, in particular as actomyosin contraction (Fig. 2D).

Viscoelastic protrusion; Kelvin–Voigt model.

For very large strain, the membrane reservoir should eventually become unable to provide the membrane area needed to regulate membrane tension leading to an elastic behavior with a different stiffness $k_{\sigma }^{\prime }$ and to a saturation of the protrusion length. This can be accounted for by the so-called Kelvin–Voigt viscoelastic model: $\sigma ={\sigma }_0+k_{\sigma }^{\prime }L+{\alpha }_{\sigma }{\partial }_{t}L$. This is dynamically equivalent to a purely elastic protrusion with a larger bare friction parameter ${\alpha }_0^{\prime }={\alpha }_0+{\alpha }_{\sigma }$. For single protrusions, the bare friction coefficient may thus be thought of as including viscous dissipation within the cell itself. The stability threshold Eq. 6 is still valid, but with ${\overline{\alpha }}_1={\alpha }_1/{\alpha }_0^{\prime }$ and ${\overline{k}}_{\sigma }=k_{\sigma }^{\prime }/\left({\alpha }_0^{\prime }{k}_{\text{off}}^0\right)$.

Symmetry Breaking and Crawling of an Elastic Cell.

We consider the dynamics of a simple 1D cell with a polymerization-driven protrusion at the two cell ends (Fig. 3). In a first instance, let us assume a uniform elastic cell tension so that the two cell ends experience an instantaneous mechanical coupling and feel the same tension. The dimensionless off rates $r_i$ and the fractions of bound linkers $n_i$ at the two cell ends ($i=\left\{\mathrm{1,2}\right\}$) satisfy the equations

$$\frac{\partial n_i}{\partial \overline{t}}=r_{\text{on}}-\left(r_{\text{on}}+r_i\right)n_i;\left(1+{\overline{\alpha }}_1\frac{n_i}{r_i}\right)r_i\log r_i=\overline{\sigma }$$

$$\frac{\partial \overline{\sigma }}{\partial \overline{t}}={\overline{k}}_{\sigma }\left(2{\overline{v}}_p-r_1\log r_1-r_2\log r_2\right)$$ [7]

with $\overline{\sigma }=\sigma /\left({\alpha }_0{v}_{\beta }\right)$ and $\overline{v}=v/v_{\beta }$. The cell size satisfies ${\partial }_{t}L=v_1+v_2$, and the cell velocity is $v_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}=\left(v_1-v_2\right)/2$. Static spreading corresponds to the retrograde velocity matching the polymerization velocity at both ends ($v_1=v_2=0$, or $r_1=r_2=r_p$). Two independent modes of fluctuation exist around this state: the symmetric mode, where both ends protrude and retract in synchrony ($v_1=v_2$), and the antisymmetric mode, where one end retracts while the other protrudes ($v_1=-v_2$), leading to net cell translocation. The former is akin to two symmetric elastic protrusions and is unstable under the condition given by Eq. 6 with $k_{\sigma }\to 2k_{\sigma }$. The latter occurs without membrane stretching and corresponds to $k_{\sigma }=0$.

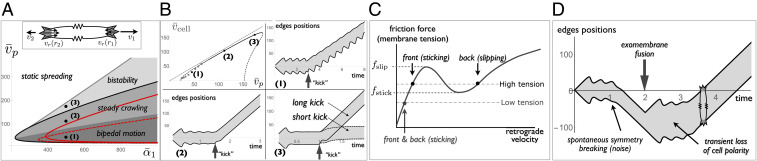
Fig. 3.

Polarization and crawling of a 1D elastic cell. (A) (Top) Sketch of a 1D cell with protrusions at both ends coupled through the elastic cell tension (springs with a dimensionless stiffness ${\overline{k}}_{\sigma }$). (Bottom) Crawling phase diagram with the adhesion parameter ${\overline{\alpha }}_1$ and the polymerization velocity ${\overline{v}}_p$. The symmetric spreading state is oscillatory within the thick solid lines (Eq. 6, black for ${\overline{k}}_{\sigma }\to 0$ and red for ${\overline{k}}_{\sigma }=10$). A crawling state exists within the regions shaded gray. Three regions can be distinguished: a steady crawling state, where the cell moves without changing its shape, coexists with the static spreading state in the bistability region, and coexists with the oscillatory spreading state in the steady crawling region. In the bipedal motion region, no true steady state exists and a bipedal crawling state—where the cell’s leading and trailing edges follow different limit cycles—coexists with the oscillatory spreading state. The dashed red line is the boundary between steady crawling and bipedal motion for ${\overline{k}}_{\sigma }=10$. (B) (Top) Variation of the cell velocity with the polymerization velocity. The solid part of the curve corresponds to steady crawling and the dashed parts are unstable steady states. Gray dots correspond to bipedal motion. The other panels are examples of “kymographs” showing the position of the two cells ends as a function of time in the three different regimes. The cell is first allowed to spread isotropically and is given an asymmetric “kick” which transiently removes all bound linkers on one side of the cell at a prescribed time (arrows). In the bistable region, the binder may rebind immediately after the kick (short kick) or after a short delay $\mathrm{\Delta }t=0.05/k_{\text{off}}^0$ (long kick). (C) Role of membrane tension on cell polarity. The coexistence of a sticking and a slipping regime, necessary for cell polarization, requires high enough tension. The slipping state is inaccessible if membrane tension is decreased. (D) Cell edge position as a function of time. Isotropic spreading starts at $t=0$ and is followed by a spontaneous breaking of symmetry due to intrinsic noise on $r_{\text{on}}$. Membrane tension is abruptly halved at $t=2/k_{\text{off}}^0$, e.g., following the fusion of exocellular vesicles, resulting in a transient loss of cell polarity. High tension is restored after further spreading, leading to a new symmetry-breaking event. Parameters: $r_{\text{on}}=10$, (B) ${\overline{\alpha }}_1=500$ and ${\overline{k}}_{\sigma }=10$, (D) ${\overline{v}}_p=100$, and $r_{\text{on}}$ is a Gaussian random variable varying within $1\%$ around $r_{\text{on}}=10$.

In the stick–slip regime, the local force balance $f_{\text{f}}=\sigma$ admits three solutions, corresponding to the three branches of the force–velocity curve (labeled sticking branch, unstable branch, and slipping branch in Fig. 2B). For an elastic cell with a uniform tension, a steady crawling state exists in a limited range of polymerization velocity where the retrograde velocities $v_{r,1}$ and $v_{r,2}$ at the two cell ends are on different branches and satisfy $f_{\text{f}}\left(v_{r,1}\right)=f_{\text{f}}\left(v_{r,2}\right)$ and $v_{r,1}+v_{r,2}=2v_p$. The conditions for the existence of such a solution, together with the stability boundary for static spreading (Eq. 6), lead to the crawling phase diagram shown in Fig. 3A. Linear stability analysis (SI Appendix, section S4 and Fig. S5) shows that steady crawling with the cell front on the sticking branch and the rear on the slipping branch of the $f_{\text{f}}\left(v_r\right)$ curve is always stable. It coexists with a stable static state in the “bistability” region and with an oscillatory spreading state in the “steady crawling” region of the phase diagram. For smaller values of the polymerization velocity, steady crawling corresponds to the cell front on the sticking branch and the rear on the unstable branch of the $f_{\text{f}}\left(v_r\right)$ curve. This state is unstable if ${\overline{k}}_{\sigma }\to 0$, and one or both cell ends follow a limit cycle, resulting in an unsteady motion with a delay between protrusion of the front and retraction of the rear. This is the “bipedal” region of the phase diagram, in reference to the bipedal motion of keratocytes (58) which has been discussed in earlier theoretical works (58, 60, 61, 79). Bipedal motion always coexists with the oscillatory spreading state. The boundary between steady crawling and bipedal motion depends on the value of the dimensionless cell stiffness ${\overline{k}}_{\sigma }$ as shown in Fig. 3A.

Spontaneous cell polarization and crawling can be triggered externally, e.g., by an asymmetric mechanical perturbation. Fig. 3B shows the result of a kick, a transient increase of the retrograde force leading to complete linkers detachment at one end of the cell. In the steady crawling and bidepal phases, a short kick applied to the oscillatory symmetric state is often sufficient to elicit cell polarization and motion. The timing of the kick has an impact and symmetry breaking is triggered more efficiently if the kick is applied during the spreading rather than the retracting phase of the symmetric oscillatory cycle. Close to the bistability boundary, a short kick leads to small cell translocation but permanent polarization requires a longer kick. Examples of these behaviors, together with the relationship between cell velocity and the polymerization velocity in the different crawling regimes, are shown in Fig. 3B.

The transition between states can also result from intracellular noise. All of the model parameters, such as the polymerization velocity, actomysoin contractility, and membrane tension, are subject to active and thermal fluctuations, whose amplitude affects the persistency of cellular behavior (24). Fig. 3D shows examples of spontaneous cell polarization triggered by fluctuations of the on rate $r_{\mathrm{o}\mathrm{n}}$, assumed to be Gaussian and uncorrelated in time for simplicity. With this choice of parameters, the symmetric state is only weakly stable and small fluctuations ($1\%$) are sufficient to trigger symmetry breaking.

The cell tension $\sigma$ plays an important role in cell polarization. The existence of a motile state requires that the tension is sufficiently high to access the unstable branch of the force–velocity curve: $f_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}<\sigma <f_{\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{k}}$ (Fig. 3C). Such a level of tension is naturally reached during spreading if $v_p>v_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}$, allowing the cell to spontaneously polarize and crawl (see Fig. 3D in the presence of intracellular noise). If the membrane tension of the crawling cell is abruptly decreased below $f_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{p}}$, e.g., after the fusion of extracellular vesicles with the cell membrane as in ref. 80, the slipping state is temporarily inaccessible and the cell becomes unpolarized, with both ends in the sticking regime. The cell then spreads further and membrane tension increases, eventually triggering a new event of spontaneous cell polarization (Fig. 3D). The steady-state tension is thus entirely determined by the polymerization velocity and the adhesion strength and not by the amount of available membrane area, in agreement with experimental observations (80).

An alternative model in which the linear viscous force at high retrograde flow speed (parameter ${\alpha }_0$) is due to the viscoelasticity of the cytoskeleton rather than to substrate friction is studied in SI Appendix, section S5 and Fig. S6. In this case, the unstable branch persists up to $v_r\to \infty$ and the bistability region disappears.

Persistent Tension Gradients.

In the elastic model above, propagation of mechanical stress across the cell is instantaneous, and the cell tension is uniform. In moving keratocytes, membrane tension is typically higher at the front than at the back of the cell (81). The cell membrane being fluid, persistent tension gradients are necessarily generated by viscous dissipation—e.g., through friction between the cell membrane and the substrate (82, 83). Membrane tension is thus a local quantity, characterized by two parameters: an elastic stiffness $k$—the local equivalent of the global stiffness $k_{\sigma }$ with the expected scaling $k_{\sigma }=k/L$ where $L$ is the cell length—and a local friction coefficient $\zeta$. Calling $u\left(z\right)$ the local membrane displacement and combining the constitutive relationship ${\sigma }_m=k{\partial }_{z}u$ with the local membrane force balance, $\zeta \dot{u}={\partial }_z{\sigma }_m$, yields a diffusion equation for the membrane tension

$${\partial }_t{\sigma }_m\left(z\right)=\frac{k}{\zeta }{\partial }_z^2{\sigma }_m\left(z\right),$$ [8]

with a diffusion coefficient $D=k/\zeta$. A $20\%$ difference between the front and rear membrane tensions of keratocytes crawling at a velocity $v\simeq 0.1\hspace{0.17em}\mathrm{\mu }\mathrm{m}/\mathrm{s}$ (81) yields an estimate of $\zeta \simeq 10\hspace{0.17em}\mathrm{P}\mathrm{a}.\mathrm{s}/\mathrm{\mu }\mathrm{m}$ and $D\simeq 1\hspace{0.17em}\mathrm{\mu }{\mathrm{m}}^2/\mathrm{s}$ (SI Appendix, Table S1). Diffusive propagation of mechanical tension is also expected within the cytoskeleton due to its poroelastic nature, with similar values for the diffusion coefficient (84). Eq. 8 may thus be assumed to describe the spatiotemporal variation of the total tension $\sigma =2{\sigma }_m+{\sigma }_c$.

Tension gradients generated by periodic protrusion/retraction cycles of a cell edge with a period $\tau$ (of order $20\hspace{0.17em}\mathrm{s}$ in ref. 85) decay over a length scale $\sqrt{D\tau }\simeq 5\hspace{0.17em}\mathrm{\mu }\mathrm{m}$. Cell edges much farther apart are essentially mechanically independent. To account for this, the tension appearing in the force balance Eq. 8 must be replaced by the tension at either end of the cell $\sigma \left(\pm L/2\right)$ calculated with Eq. 8, supplemented with the boundary conditions ${\dot{u}}_{\mathrm{1,2}}=\dot{u}\left(\pm L/2\right)=\pm \left(v_p-v_{r\left(\mathrm{1,2}\right)}\right)$ (Fig. 4A). Linear expansion of the dynamical equations (SI Appendix, section S6) shows that the growth rate equation Eq. 5 still holds, albeit with rate-dependent effective stiffnesses ${\overline{k}}_{\sigma ,\lambda }^{\pm }$ for symmetric ($+$) and antisymmetric ($-$) perturbations given by

$${\overline{k}}_{\sigma ,\lambda }^{\pm }=\overline{k}\sqrt{\overline{\lambda }/\overline{D}}\left(\coth \sqrt{\overline{\lambda }/\overline{D}}\pm \frac{1}{\sinh \sqrt{\overline{\lambda }/\overline{D}}}\right),$$ [9]

with $\overline{k}=k/\left(L{\alpha }_0{k}_{\text{off}}^0\right)$, $\overline{\zeta }=\zeta L/{\alpha }_0$, $\overline{\lambda }=\lambda /k_{\text{off}}^0$, and $\overline{D}=\overline{k}/\overline{\zeta }$.

Fig. 4.

Symmetry breaking with tension gradients. (A) Sketch of a 1D cell with protrusions at both ends, coupled by elastic elements experiencing friction from the substrate. (B) Stability phase diagram of static spreading with the inverse substrate friction $1/\overline{\zeta }={\alpha }_0/\left(\zeta L\right)$ and stiffness $\overline{k}=k/\left(L{\alpha }_0{k}_{\text{off}}^0\right)$, normalized by their asymptotic values for $\overline{D}\to \infty$ (Eq. 10). Parameters are such that the $\overline{\zeta }\to 0$ limit is in the steady-crawling region of Fig. 3A. A small perturbation (the removal of $10\%$ of the bound linkers at one end of a cell initially at the symmetric stationary state) leads to permanent cell polarization and crawling above the red line. Below this line, the end state is symmetric. The green line shows the effect of increasing the cell length, all other dimensional parameters being unchanged. (C) Example of cell trajectories for the parameters given by the different symbols in B. Dashed lines are the trajectories for $\overline{D}\to \infty$. For $r_{\text{on}}=10,\hspace{0.17em}{\overline{\alpha }}_1=500,\hspace{0.17em}{\overline{v}}_p=100$ (corresponding to ${\overline{k}}_{\infty }\simeq 10$ and ${\overline{\zeta }}_{\infty }\simeq 1$).

Linear stability analysis of static spreading must be performed numerically and leads to the phase diagram shown in Fig. 4B. Asymptotic behaviors are derived in SI Appendix, section S6. In the limit of high friction, $\overline{D}\ll 1$, tension variation near the tip of a moving protrusion relaxes over a very short length scale $\sqrt{D\left|\lambda \right|}\ll L$, leading to a large effective stiffness ${\overline{k}}_{\sigma ,\lambda }\sim \sqrt{\overline{k}\overline{\zeta }/\left|\overline{\lambda }\right|}$. Protrusions are unstable below a threshold effective stiffness, leading to the scaling $\overline{k}\sim 1/\overline{\zeta }$ for the stability boundary of both types of perturbations. In the limit of low friction, $\overline{D}\gg 1$, symmetric perturbations are unstable below a threshold stiffness ${\overline{k}}_{\infty }$ and antisymmetric perturbations are unstable below a threshold friction ${\overline{\zeta }}_{\infty }$, given by

$${\overline{k}}_{\infty }=\frac{r_{\text{on}}+r_p}{2}\left(\frac{{\overline{\alpha }}_1}{{\overline{\alpha }}_1^{*}\left(0\right)}-1\right),\hspace{0.17em}{\overline{\zeta }}_{\infty }=2\left(\frac{{\overline{\alpha }}_1}{{\overline{\alpha }}_1^{*}\left(0\right)}-1\right)$$ [10]

with ${\overline{\alpha }}_{\mathrm{1,0}}^{*}$ given by Eq. 6.

In regions of the phase diagram where both the symmetric and antisymmetric perturbations are unstable, the end state may be the polarized crawling state or the oscillatory spreading state, depending on initial conditions. Under high friction the stability criterion is the same for symmetric and antisymmetric fluctuations because the two protrusions are independent. This means that fluctuations are unlikely to lead to persistent cell polarization. Numerical solutions of the coupled equations for linkers kinetics and diffusion of the cell tension are shown in Fig. 4 for cells initially in the static spreading state with $10\%$ of bound linkers removed at one end of the cell—a moderate kick compared to Fig. 3B. This asymmetric kick leads to persistent polarization and crawling if the dimensionless friction coefficient $\overline{\zeta }=\zeta L/{\alpha }_0$ is below a threshold value that depends on the dimensionless stiffness. If the lamellipodium size is uncorrelated with the cell size, so that both ${\alpha }_1$ and ${\alpha }_0$ are independent of $L$, polarization is predicted to occur below a threshold cell size (Fig. 4B).

Lateral Traveling Waves.

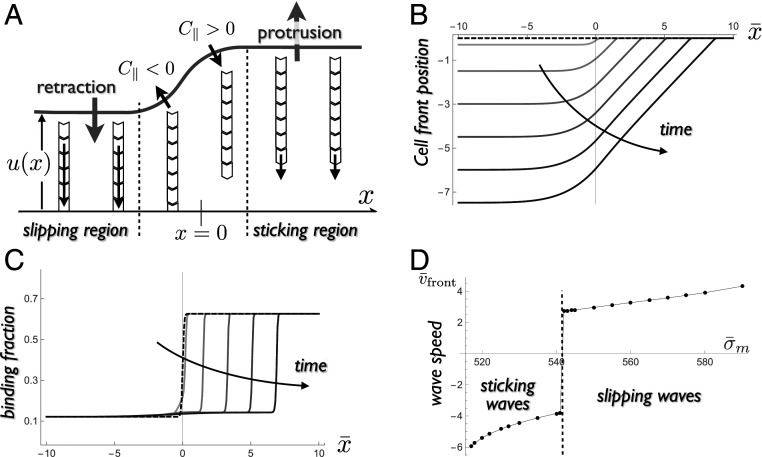
In this section, the 1D stick–slip model is extended to a two-dimensional (2D) situation to discuss the occurrence of traveling waves along the edge of cells. Traveling waves are ubiquitous in motile cells (86–88) and have been discussed in the context of the active mechanics of the cytoskeleton or the reaction–diffusion dynamics of biochemical cytoskeleton regulators (5). The abrupt nature of the switch between high- and low-friction states suggests the possibility for traveling waves of purely mechanical origin. To see this, we restrict ourselves to small cell edge deformations. Let us consider an initially flat cell edge where regions in the sticking and slipping state coexist. In Fig. 5A, half the edge ($x>0$) is in the sticking state and the other half ($x<0$) in the slipping state at $t=0$, where $x$ is the coordinate along the cell edge. As the spreading velocity is different in these two regions, a kink forms and grows at the boundary between them, with a positive curvature in the sticking region and a negative curvature in the slipping region. Calling $u\left(x\right)$ the position of the cell front, and assuming small deformation (${\partial }_{x}u\ll 1$), the membrane force in Eq. 1 reads $2{\sigma }_m\left(1+h{C}_{\Vert }\right)\simeq 2{\sigma }_m\left(1-h{\partial }_x^{2}u\left(t\right)\right)$. The positive (negative) curvature increases (decreases) the retrograde force. Since the curvature increases with time, one side of the boundary between the two states (or sometimes both; SI Appendix, section S7 and Fig. S7) eventually undergoes the stick–slip transition leading to a lateral movement of the boundary.

Fig. 5.

Traveling wave. (A) Sketch of the cell edge at an interface between a region of fast retrograde flow (slipping) and a region of slow retrograde flow (sticking). The edge curvature modifies the force driving actin retrograde flow. Positive (negative) curvature reduces (increases) the driving force, triggering a transition between the sticking and slipping states and the lateral motion of the interface. (B) Evolution of the cell edge profile relative to the protrusive side with time. (C) Evolution of the fraction of bound linkers with time (for equal time steps up to $t=2.8/k_{\text{off}}^0$). A traveling wave moves at a constant velocity, toward the sticking region (slipping wave) in this particular example (examples of sticking waves are shown in SI Appendix, Fig. S7). (D) The front velocity depends on membrane tension, with an abrupt transition between a sticking wave ($v_{\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{t}}<0$) and a slipping wave ($v_{\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{t}}>0$) observed at a particular value of the membrane tension. Parameters: $r_{\text{on}}=10,{\overline{\alpha }}_1=500,\hspace{0.17em}{\overline{v}}_p=100$, and ${\overline{\sigma }}_m=285$.

At lowest order in edge deformation, the evolution of the edge profile is given by ${\partial }_{t}u\left(x\right)=v_p-v_{\beta }r\left(x\right)\log r\left(x\right)$, with a position-dependent retrograde velocity obtained from Eqs. 1 and 2:

$$\frac{\partial r\left(\overline{x}\right)}{\partial \overline{t}}=\frac{{\partial }_{\overline{x}}^2\left(r\left(\overline{x}\right)\log r\left(\overline{x}\right)\right)-{\overline{\alpha }}_1\log r\left(\overline{x}\right)\dot{n}\left(\overline{x}\right)}{\log r\left(\overline{x}\right)+1+{\overline{\alpha }}_{1}n\left(\overline{x}\right)/r\left(\overline{x}\right)}$$ [11]

with the local linker’s kinetics still given by Eq. 2. Here, the dimensionless spatial coordinate is $\overline{x}=x\sqrt{{\alpha }_0{k}_{\text{off}}^0/\left(2{\sigma }_{m}h\right)}$. Eqs. 1 and 2 support traveling waves in the stick–slip regime, as can be seen from the evolution of the edge profile and the density of the bound linker (Fig. 5 B and C). The front velocity scales as $v_{\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{t}}=\sqrt{2{\sigma }_{m}h{k}_{\text{off}}^0/{\alpha }_0}{\overline{v}}_{\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{t}}\left({\overline{\sigma }}_m,{\overline{\alpha }}_1,r_{\text{on}}\right)$, where ${\overline{v}}_{\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{t}}$ is a dimensionless function of dimensionless parameters. Fig. 5D shows how ${\overline{v}}_{\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{t}}$ depends on the membrane tension ${\overline{\sigma }}_m$. The most remarkable feature is a transition from a sticking wave to a slipping wave (a change of sign of $v_{\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{t}}$) above a threshold tension. This is because the slipping state is more stable at high tension. The dependence with the two other parameters is less interesting (SI Appendix, section S7). Using physiological parameters (SI Appendix, Table S1), $v_{\mathrm{f}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{t}}\sim 0.1\hspace{0.17em}\mathrm{\mu }\mathrm{m}/\mathrm{s}$, which agrees with the order of magnitude observed in mouse embryonic fibroblasts and T cells (87).

Discussion

Many of the molecular players involved in cell motility have been identified, but we are still searching for the basic principles underlying their organization in space and time. A growing body of evidence shows that mechanics plays a key role in organizing cell motility, be it the active mechanics of the cytoskeleton, the tension of the cell membrane, or the stiffness of the substrate. I propose a simple model of cell spreading and crawling based on the interplay between actin polymerization and cell–substrate adhesion mediated by mechanosensitive stochastic linkers. Despite its simplicity, the model reproduces a number of cellular behaviors reported in the literature: 1) the stick–slip behavior of the cell front (85, 86), 2) spontaneous symmetry breaking or bistability of cells and cell fragments (6, 89), 3) the crucial role of membrane tension in regulating this process (80), and 4) the existence of slipping or sticking lateral waves propagating along the cell edge (86–88). The model also uncovers the few dimensionless parameters controlling the transition between different dynamical behaviors.

A number of simplifying assumptions are made regarding the mechanics and dynamics of the cytoskeleton. The rate of actin polymerization and the distribution of actomyosin contractile stress, assumed constant and uniform here, do vary across the cell. Transient loss of adhesion can locally increase the actin density and lead to the formation of ruffles or actin arcs stabilized by actomyosin contraction (90). As discussed in the Introduction, modulation of these parameters through feedback loops can also lead to some of the dynamical features explained here. It is nevertheless important to study individually the different modules that can be combined to regulate the behavior of crawling cells. The present simplifications allow us to precisely focus on the role of mechanosensitive adhesion.

The dynamics of cellular protrusions driven by actin polymerization result from a balance between actomyosin contraction and membrane tension, which generate an actin retrograde flow, and the traction force generated by stochastic adhesion bonds transiently linking actin filaments with the substrate. Collective effects within the population of mechanosensitive bonds lead to a nonmonotonic relationship between the steady-state traction force and the retrograde flow velocity (Fig. 2B). This defines a range of polymerization velocity within which protrusions may exhibit stick–slip dynamics, alternating phases of growth with a weak retrograde flow and retraction with a strong retrograde flow. Whether such instability develops depends on the way the tension at the tip of a protrusion varies with the protrusion length and growth rate. For simple elastic cells with a uniform tension, this is characterized by a dimensionless effective stiffness ${\overline{k}}_{\sigma }=k_{\sigma }/\left({\alpha }_0{k}_{\text{off}}^0\right)$, which compares the rates of variation of the cell tension and of the density of attached bonds. Tension variations during growth and retraction attenuate the collective effects among the adhesion bonds, so that single protrusions display stick–slip dynamics if ${\overline{k}}_{\sigma }$ is below a threshold value, that is, if the cell (and in particular the cell membrane) is sufficiently soft.

For purely elastic protrusions, the protrusion length averaged over the periods of growth and retraction remains constant. If the cell tension is viscoelastic with a long-time viscous behavior, the short-time periodic stick–slip behavior superimposes on a slower long-time growth (Fig. 2 C and D), leading to dynamics that strongly resemble, both in shape and in time scale (period $\sim 20\hspace{0.17em}\mathrm{s}$), the periodic oscillations of the edge of spreading fibroblasts (85, 86). The periodic buckling of the lamellipodium proposed in ref. 85 to explain these observations is not incompatible with the present explanation. Indeed, buckling, along with actin arcs and ruffles, can constitute a nonlinear response to the abrupt actin unbinding from the substrate, which is at the origin of the oscillations proposed here. Importantly, oscillations of the leading edge are observed within a finite range of cell homeostatic tension (Fig. 2D). They can be suppressed by myosin inhibition, as observed in refs. 85 and 86, but also by myosin overexpression, which is a falsifiable prediction of the present model. The oscillatory behavior of cellular protrusions can also be modulated by factors regulating membrane tension, such as microtubules, the fusion protein SNARE, or dynamin.

Spontaneous cell polarization and crawling are studied using a simple 1D model where two polymerization-driven protrusions form at both ends of the cell and are mechanically coupled by the cell tension. This simplified geometry allows us to disregard the complex interplay between the cell shape and the local force balance in 2D motility (28). It is appropriate for cells confined on adhesive tracks (91) and is also relevant for motility in physiological 3D matrices, which appears closer in many ways to 1D than to 2D motility (92).

In addition to the local balance between the traction force and the cell tension at each cell end, the net force exerted by the cell on the substrate must vanish by virtue of Newton’s third law. This is naturally satisfied for a symmetric cell, which can either settle into a static spreading state where the retrograde flow compensates the polymerization velocity at both ends or settle into an oscillatory state alternating phases of symmetric spreading and retraction around a fixed length, without net cell translocation. Crucially, the nonmonotonic nature of the force–velocity relationship allows for a state of broken symmetry, in which the cell is polarized and motile with the leading edge in the sticking state and the trailing edge in a slipping state. Depending on the parameters, the crawling state can be a true steady state where the cell moves without changing its shape or an unsteady moving state where the leading and trailing edges display asynchronous oscillation reminiscent of the bipedal motion of keratocytes (58).

If the cell tension equilibrates fast and is uniform, the motility behavior is mostly determined by the polymerization velocity and the strength of adhesion (Fig. 3). Under low adhesion, the cell is in the static spreading state and cannot crawl. Upon increasing the adhesion strength, a region of bistability emerges, where the transition from a (meta)stable static state and a steady crawling state needs to be triggered by large fluctuations or external (i.e., mechanical) perturbations. For larger adhesion strength, the static state is unstable and the polarized state competes with an oscillatory spreading state. Finally, for even larger adhesion, crawling is unsteady and the leading and trailing edges of the cell display asynchronous oscillations. The value of the effective cell stiffness ${\overline{k}}_{\sigma }$ modifies the boundaries between static and oscillatory spreading and between steady and bipedal crawling (Fig. 3). A large effective stiffness, which corresponds to a small cell length, increases the bistability region. This could explain why small cell fragments are prone to bistability (6). Symmetry breaking is often explained by the redistribution of actomyosin contraction to the back of the cell (6, 20–25, 89), and myosin activity does increase the probability of symmetry breaking and the velocity of cells and cell fragments in 2D (6, 89). It is noteworthy, however, that a majority of keratocyte fragments in ref. 6 are polarized and motile even in the presence of drugs inhibiting myosin activity. This suggests that the mechanosensitive adhesion switch described here can be sufficient to elicit the excitable behavior of crawling cells, which is enhanced through the feedback between actin flow and myosin distribution.

The model identifies the cell tension, and in particular the tension of the cell membrane, as key to the coordination between the two cell edges. Remarkably, a sudden decrease of membrane tension provoked by the fusion of extracellular vesicles leads to the formation of multiple lamellipodia that significantly hampers the cell’s ability to polarize and crawl (80). The present model recapitulates this behavior, including the resumption of persistent polarization and directed motion after further cell spreading, with tension values similar to those before vesicle fusion. Multiple lamellipodia form under low tension because the slipping state exists only under high enough tension, so that both ends of the cell are in a protrusive state under low tension. The homeostatic tension of crawling cells is determined by a balance between cytoskeletal forces and adhesion rather than by the available membrane area, in agreement with the conclusion of ref. 80. An increase of membrane tension upon cell spreading may thus be the force driving the cell into bistability, allowing for the existence of a polarized, motile state.

While spontaneous symmetry breaking and motion upon spreading are common for cell fragments (6) and some cell types such as keratocytes (89), other cell types form and retract uncoordinated protrusions without global symmetry breaking. This is not easily explained if the cell tension is uniform since cells with dynamic protrusions also possess a metastable crawling state (Fig. 3). The absence of symmetry breaking could be a matter of time scale or related to the difference between 1D and 2D geometries. I propose instead that it is due to finite relaxation time of tension heterogeneities across the cell. Membrane tension is larger at the front than at the rear of fast-moving cells such as keratocytes (81), likely due to membrane friction with the substrate or with elements of the cytoskeleton (82, 83). As a consequence, tension relaxes in a diffusive manner, and dynamic protrusions farther than a few micrometers apart are mechanically independent. This fundamentally affects the crawling phase diagram (Fig. 4) and spontaneous symmetry breaking is limited to cells with low friction or equivalently to small cell size.

The extension of the present model to 2D geometry is not expected to alter our main conclusion. One interesting feature that can emerge, however, is the propagation of lateral waves of protrusion/retraction along the cell edge (86–88). The lateral curvature of the cell edge affects the force on the actin filaments and can induce a stick–slip transition. I show that this leads to propagating waves at the interface between sticking and slipping regions at the edge of the cell, with a velocity ($\sim 0.1\hspace{0.17em}\mathrm{\mu }\mathrm{m}/\mathrm{s}$) comparable to that of lateral waves observed in mouse embryonic fibroblasts and T cells (87). The velocity of these “stick–slip waves” is not controlled by the polymerization velocity, but rather by a balance between membrane tension and substrate friction. Such waves constitute an alternative to reaction–diffusion waves of cytoskeleton regulators (5) for rapid transmission of mechanical signals across the cell during migration.

To conclude, the stick–slip mechanism described here, which bestows motile cells with dynamical behaviors typical of excitable systems and can reproduce a diversity of experimental behavior, is intimately linked to the interplay between the time scale of formation and disruption of cell adhesion and the viscoelastic and diffusive time scale of cell tension variation. Its full understanding requires a proper treatment of both dynamical processes such as the ones proposed here. This adds a knob to the cell toolkit, that also includes diffusion/reaction of signaling molecules and active cytoskeleton mechanics, to confer robustness and sensitivity to crawling cells.

Data Availability.

All study data are included in this article and SI Appendix.