Tunable layered-magnetism–assisted magneto-Raman effect in a two-dimensional magnet CrI₃

Significance

The two-dimensional (2D) magnetic semiconductor CrI₃ hosts a variety of strong and tunable magneto-optical effects and allows for the development of novel magneto-optical devices. While the elastic magneto-optical effects in CrI₃ are well understood, its recently discovered inelastic magneto-Raman effect remains to have case-specific interpretations varying upon the thickness of CrI₃. We perform comprehensive Raman measurements on 2D CrI₃ with polarization, temperature, layer number, and magnetic field dependence. We resolve a Davydov-split–induced N-fold multiplet in N-layer CrI₃ and reveal the distinct magneto-Raman behaviors of individual phonons within the multiplet. Our results discover a layered-magnetism–coupled phonon scattering mechanism that explains the rich magneto-Raman effect in CrI₃ of arbitrary thickness and elucidates the spin–phonon coupling physics in layered magnets.

Abstract

We used a combination of polarized Raman spectroscopy experiment and model magnetism–phonon coupling calculations to study the rich magneto-Raman effect in the two-dimensional (2D) magnet CrI₃. We reveal a layered-magnetism–assisted phonon scattering mechanism below the magnetic onset temperature, whose Raman excitation breaks time-reversal symmetry, has an antisymmetric Raman tensor, and follows the magnetic phase transitions across critical magnetic fields, on top of the presence of the conventional phonon scattering with symmetric Raman tensors in N-layer CrI₃. We resolve in data and by calculations that the first-order A_g phonon of the monolayer splits into an N-fold multiplet in N-layer CrI₃ due to the interlayer coupling $\left(N\ge 2\right)$ and that the phonons within the multiplet show distinct magnetic field dependence because of their different layered-magnetism–phonon coupling. We further find that such a layered-magnetism–phonon coupled Raman scattering mechanism extends beyond first-order to higher-order multiphonon scattering processes. Our results on the magneto-Raman effect of the first-order phonons in the multiplet and the higher-order multiphonons in N-layer CrI₃ demonstrate the rich and strong behavior of emergent magneto-optical effects in 2D magnets and underline the unique opportunities of spin–phonon physics in van der Waals layered magnets.

Two-dimensional (2D) CrI₃ of few-layer form features a layered-antiferromagnetic (AFM) order where the spins align along the out-of-plane direction ferromagnetically within each layer and antiferromagnetically between adjacent layers (1–5). It undergoes a layered-AFM to ferromagnetic (FM) phase transition upon applying a moderate magnetic field (1–7), or electric field (8–10), or electrostatic doping (11), or hydrostatic pressure (12, 13). The strong coupling between spin and charge degrees of freedom in 2D CrI₃ allows magneto-optical effects manifested in a variety of ways including large magneto-optical Kerr effect (5) and magnetic circular dichroism (8–13), spontaneous helical photoluminescence (14), giant nonreciprocal second harmonic generation (15), and anomalous magneto-optical Raman effect (7, 16–19). All of these magneto-optical effects can be tuned across the layered-AFM to FM phase transition, making 2D CrI₃ a promising candidate for applications in magnetic sensors, optical modulation, and data storage.

Among all magneto-optical effects in CrI₃, the magneto-optical Raman effect is of particular interest for two reasons. First, among all known magnets, the largest magnetism-induced optical rotation is observed for the linearly polarized, inelastically scattered light off the A_g phonon mode (∼129 cm⁻¹) in the FM phase of CrI₃ (16). Second, different phonon modes exhibit distinct magneto-optical behavior that the A_g mode emerges whereas its neighboring strongest antisymmetric mode (∼127 cm⁻¹) disappears in the linear crossed polarization channel across the layered-AFM to FM transition (7, 16–18). However, the physical origin of the magneto-optical Raman effect remains elusive with diverse proposals ranging from Davydov split for bilayer CrI₃ (16, 18), to zone-folded phonon for few-layer CrI₃ (17), to coupled magnetism–phonon scattering for bulk CrI₃ (7), none of which can be trivially generalized to explain CrI₃ of arbitrary thickness.

In this work, we systematically examine the magneto-optical Raman effect for N-layer CrI₃ (N = 1 to 4) by performing polarization, temperature, and magnetic field-dependent micro-Raman spectroscopy measurements and unambiguously identify the layered-magnetism–assisted phonon scattering as the origin applicable for CrI₃ of any thickness. N-layer CrI₃ crystalline flakes were exfoliated from high-quality CrI₃ single crystals, sandwiched between hexagonal boron nitride (hBN) thin flakes, and then placed onto SiO₂/Si substrates inside a high-purity (>99.999%) nitrogen-filled glovebox. Micro-Raman spectroscopy measurements in the backscattering geometry were carried out with a 633-nm excitation laser resonant with the charge-transfer transition (14), inside a vacuum cryostat at a base pressure lower than $7\times {10}^{-7}$ mbar, and under an out-of-plane magnetic field $\left(B_{\perp }\right)$ up to 2.2 T.

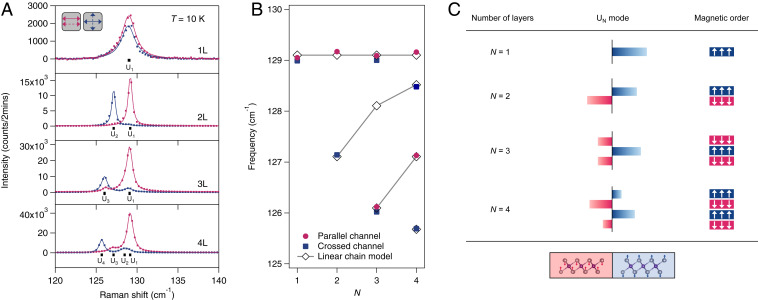
We start with resolving in N-layer CrI₃ the interlayer coupling-induced split of the A_g mode of monolayer CrI₃ (20, 21). Fig. 1A shows Raman spectra in both parallel and crossed linear polarization channels taken at T = 10 K and $B_{\perp }=0$ T on 1L to 4L CrI₃ (see full-range spectra in both channels and comparison to off-resonance 532-nm excitations in SI Appendix, section I and Figs. S1 and S2, respectively). It has been established for CrI₃ that the modes in the crossed channel in Fig. 1A correspond to antisymmetric Raman tensor $\left({\text{R}}_{\text{AS}}\right)$ whereas those in the parallel channel are for symmetric Raman tensor of A_g symmetry $\left({\text{R}}_{\mathrm{S}}\right)$ (19). We highlight three key observations that have not been reported in previous work (7, 16–19, 22, 23) and summarize them in Fig. 1B with fitted mode frequencies vs. N. First, the number of modes increases proportional to the number of layers (with an exception for N = 3 that is explained in SI Appendix, section II). Second, the highest frequency remains constant while the lowest frequency decreases with increasing N, leading to a greater frequency separation between them. Third, the parallel and crossed channels show modes of the same frequencies for odd N whereas they select modes with distinct frequencies for even N. To interpret the A_g mode splitting, we take a simple linear chain model of N-layer CrI₃, as introduced in few-layer transition metal dichalcogenides (24–27),

$$H=H_0+\frac{1}{2}{\displaystyle \sum _{i=2}^{N}k{\left(u_{i-1}-u_i\right)}^2},\text{with}\hspace{0.17em}{H}_0={\displaystyle \sum _{i=1}^N\left(\frac{1}{2}m{\dot{u}}_i^2+\frac{1}{2}{k}_0{u}_i^2\right)},$$

where $H_0$ represents the original A_g mode at frequency ${\omega }_0=\sqrt{k_0/m}$ within individual layers, $u_i$ represents the displacement field in the ith layer, and $k$ stands for the coupling constant between adjacent layers, equivalent to a coupling frequency $\omega =\sqrt{k/m}.$ Diagonalizing H leads to N nondegenerate eigenfrequencies ${\text{Ω}}_i\left({\omega }_0,\omega \right)$ and their corresponding eigenmodes ${\overrightarrow{U}}_i$ (i = 1, 2, …, N) (i.e., Davydov splitting), with i = 1 being the highest-frequency mode and i = N being the lowest-frequency mode. By choosing ${\omega }_0=129.10\pm 0.10$ cm⁻¹ and $\omega =15.98\pm 0.55$ cm⁻¹, the calculated frequencies ${\text{Ω}}_i$ (solid lines with open diamonds) match well with all of the experimental values (red solid squares and blue solid circles), as highlighted by the fan diagram in Fig. 1B. See detailed calculations of ${\text{Ω}}_i$ and ${\overrightarrow{U}}_i$ in SI Appendix, section II and Tables S1 and S2.

Fig. 1.

(A) Raman spectra of 1L to 4L CrI₃ acquired in linear parallel (red) and crossed (blue) channels at 10 K. The solid curves are fits to the raw data (dots). The vertical bars underneath individual spectra denote the fitted frequencies and $U_i$ (i = 1, …, N) labels the corresponding modes in N-layer CrI₃. (B) Plot of the fitted frequencies of the modes in A as a function of layer number N. Red solid circles and blue solid squares correspond to modes extracted from the linear parallel and crossed channels, respectively. Solid curves with open diamonds are fits to the Davydov-split frequencies calculated from the linear chain model. (C) Atomic displacement of the lowest-frequency mode $U_N$ along with the layered-AFM order to illustrate that ${\overrightarrow{U}}_i$ and $\overrightarrow{M}$ share the same parity and that ${\overrightarrow{U}}_i·\overrightarrow{M}$ is maximized at i = N. The rectangular bar represents the atomic displacement amplitude and phase for individual layers, by its length and color (red and blue for opposite phase), respectively.

Because N-layer CrI₃ is structurally centrosymmetric, its N-calculated eigenmodes have alternating parities, with the highest-frequency mode always parity even as a result of equal, in-phase atomic displacement between layers (i.e., ${\overrightarrow{U}}_1=\left(\mathrm{1,1},\dots ,1\right)/\sqrt{N}$). In the parallel channel where only modes with even parity and symmetric Raman tensor ${\text{R}}_{\mathrm{S}}$ can be detected, we expect to see every other mode starting with the highest-frequency one (i = 1, 3, 5, …). This expectation is indeed consistent with our data that $U_1$ for N = 1 and 2 and $U_{\mathrm{1,3}}$ for N = 3 and 4 are observed in the linear parallel channel in Fig. 1 A and B. In contrast to the structure of N-layer CrI₃, the layered-AFM order is centrosymmetric for odd N and noncentrosymmetric for even N. Therefore, it should couple to parity-even phonon modes for odd N and parity-odd phonons for even N to make the coupled layered-AFM–phonon entity parity even and thus Raman active. Due to the broken time-reversal symmetry from the magnetism, this layered-AFM–assisted phonon scattering corresponds to antisymmetric Raman tensor ${\text{R}}_{\text{AS}}$ and can appear only in the linear crossed channel. We anticipate observing in the linear crossed channel every other mode from the lowest-frequency one (i = N, $N-2,$ $N-4,$ …), because ${\overrightarrow{U}}_N$ always has the same parity as the layered AFM for any N. The result in Fig. 1 A and B corroborates with this prediction that $U_1$ for N = 1, $U_2$ for N = 2, $U_{\mathrm{3,1}}$ for N = 3, and $U_{\mathrm{4,2}}$ for N = 4 are present in the linear crossed channel. The coupling efficiency between a phonon mode and the layered-AFM order can be evaluated by the projection ${\overrightarrow{U}}_i·\overrightarrow{M}$ of the eigenmode vector ${\overrightarrow{U}}_i$ onto the pseudovector (i.e., axial vector) for the layered-AFM $\overrightarrow{M}=\left(1,-1,\mathrm{..},{\left(-1\right)}^{N-1}\right)$ with +1 for spin up and −1 for spin down in a single layer. In particular, for any N > 1, the lowest-frequency mode ${\overrightarrow{U}}_N$ features out-of-phase atomic displacement between adjacent layers and matches best the pattern of alternating spin orientations in the layered-AFM state (Fig. 1C), yielding the strongest coupling strength of ${\overrightarrow{U}}_i·\overrightarrow{M}$ and thus the most intense signal among the modes in the linear crossed channel (Fig. 1A). See the computed ${\overrightarrow{U}}_i·\overrightarrow{M}$ in the layered-AFM state of 1L to 4L CrI₃ in SI Appendix, Table S3.

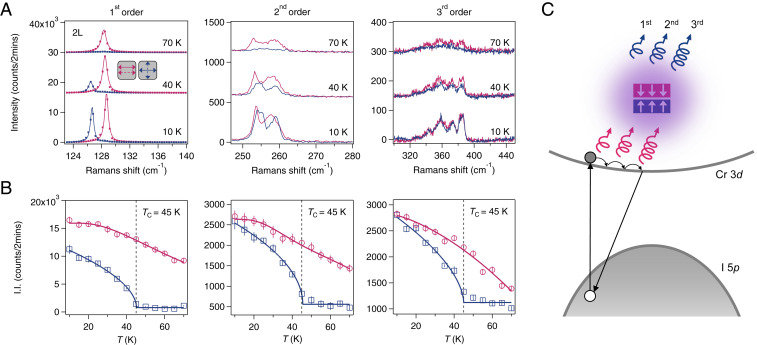
So far we have established the physical origin of the N-fold multiplet for N-layer CrI₃ as a combined effect of Davydov splitting and layered-AFM–phonon coupling, leading to the conventional phonons of ${\text{R}}_{\mathrm{S}}$ in the linear parallel channel (24–27) and the layered-AFM–coupled phonons of ${\text{R}}_{\text{AS}}$ in the linear crossed channel (7, 19). We note that a magnetism-induced symmetric E_g phonon mode splitting was previously reported in 2D Cr₂Ge₂Te₆ (28). Here, the structural and magnetic nature of modes in the linear parallel and crossed channel, respectively, is further supported by their distinct temperature dependence in these two channels. Taking 2L CrI₃ as an example, the crossed-channel signal emerges below the magnetic transition temperature T_C = 45 K whereas the parallel channel signal is present above T_C and increases only slowly below T_C, as illustrated by representative spectra taken at 70, 40, and 10 K in Fig. 2A. Such a behavior extends beyond the first-order phonons (Fig. 2 A, Left) to the second- and third-order ones (Fig. 2 A, Center and Right, respectively). For all three orders, the temperature dependence of integrated intensity (I.I.) in the linear crossed channel fits well with an order parameter-like function $I_0+I\sqrt{T_{\mathrm{C}}-T}$ (blue curves in Fig. 2B), in contrast to those in the linear parallel channel following a smooth anharmonic decay behavior (29) (red curves in Fig. 2B). As pictorially summarized in Fig. 2C, we propose that a multiphonon process (30, 31) leads to conventional first-, second-, and third-order phonon modes (red) in the linear parallel channel, and their coupling with the layered-AFM order results in the magnetic counterparts (blue) in the linear crossed channel.

Fig. 2.

(A) First-, second-, and third-order Raman spectra of 2L CrI₃ in the linear parallel (red) and crossed (blue) channels at selected temperatures of 70, 40, and 10 K. Spectra are vertically offset for clarity. First-order spectra show raw data points and fitting curves, and second- and third-order spectra are raw spectra. (B) Temperature dependence of integrated intensity (I.I.) of first-, second-, and third-order Raman modes in the parallel (red circles) and crossed (blue squares) channels. Solid curves are fits to the anharmonic decay model in the parallel channel (red curves) and the order parameter-like function $I_0+I\sqrt{T_{\mathrm{C}}-T}$ in the crossed channel (blue curves). Critical temperature T_C = 45 K is marked by a dashed vertical line in each panel. (C) Schematic illustration of the single- to multiphonon scattering (red) and its layered-AFM–assisted counterpart (blue). The springs with one to three windings represent first- to third-order process.

We then proceed to explore the magnetic field dependence of the layered-magnetism–assisted phonon modes in N-layer CrI₃. From here on, we chose circularly polarized light to perform Raman measurements to prevent any artifacts from the Faraday rotation of light from passing through optical components in a stray magnetic field. In this work, we focus on two representative thicknesses, 2L and 4L CrI₃, having one and two critical magnetic transitions, respectively (Raman spectra of 3L CrI₃ at 0 T in SI Appendix, section II and Fig. S3). We note that the mechanism described below is applicable for arbitrary N-layer CrI₃.

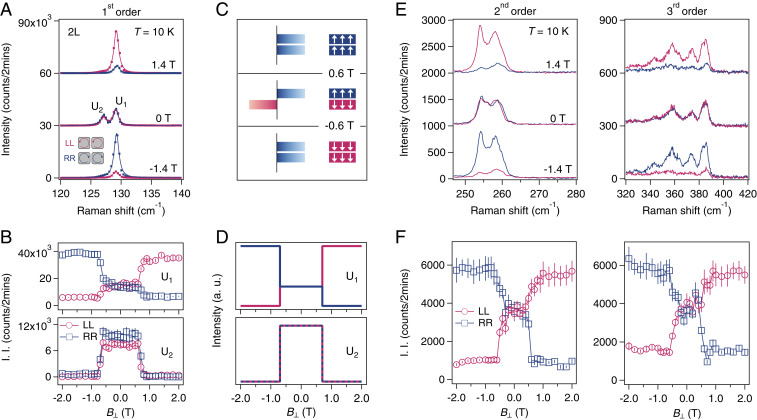
The 2L CrI₃ undergoes a layered-AFM to FM transition at a critical magnetic field $B_c=\pm 0.6\hspace{0.17em}\mathrm{T}$ (5). Fig. 3A presents Raman spectra of first-order modes taken at $B_{\perp }=0\hspace{0.5em}\mathrm{T}$ and $\pm 1.4\hspace{0.5em}\mathrm{T,}$ below and above $B_c,$ respectively, at 10 K in both LL and RR channels, where LL(RR) stands for the polarization channel with the incident and scattered light being left(right)-hand circularly polarized. At 0 T, both modes ($U_1$ and $U_2$) of 2L CrI₃ are present in Raman spectra that are identical in LL and RR channels. At $\pm 1.4\hspace{0.5em}\mathrm{T,}$ only the high-frequency mode $\left(U_1\right)$ survives, and it shows giant Raman circular dichroism of $\pm 78\%$ $\left(\frac{\mathrm{I}.\mathrm{I}{.}_{\mathrm{L}\mathrm{L}}-\mathrm{I}.\mathrm{I}{.}_{\mathrm{R}\mathrm{R}}}{\mathrm{I}.\mathrm{I}{.}_{\mathrm{L}\mathrm{L}}+\mathrm{I}.\mathrm{I}{.}_{\mathrm{R}\mathrm{R}}}\right).$ See the comparison of selection rules between linear and circular polarization bases for 2L CrI₃ in SI Appendix, Table S5. The magnetic field dependence of the $U_2$ integrated intensity clearly shows its disappearance at $B_c,$ whereas that of $U_1$ increases (decreases) abruptly in the LL (RR) channel at $B_c,$ as shown in Fig. 3B. Fig. 3 E and F shows the magnetic field dependence of the second- and third-order modes of 2L CrI₃. Both of them mimic the magnetic field dependence of $U_1$ with a reduction of circular dichroism above $B_c,$ $\pm 71\%$ for the second order and $\pm 50\%$ for the third order. This observation suggests the participation of $U_1$ in the second- and third-order multiphonon process.

Fig. 3.

(A) Raman spectra of 2L CrI₃ in cocircularly polarized channels, LL (red) and RR (blue), in selected out-of-plane magnetic field $\left(B_{\perp }\right)$ of 1.4, 0, and $-1.4\hspace{0.5em}\mathrm{T}\mathrm{.}$ Dots are raw data points and solid curves are fitting curves. (B) Magnetic field dependence of integrated intensities (I.I.) of the two modes of 2L CrI₃, $U_1$ and $U_2,$ in both LL (red circles) and RR (blue squares) channels. (C) List of phonon modes in 2L CrI₃ that have finite coupling strength ${\overrightarrow{U}}_i·\overrightarrow{M}$ for individual magnetic orders at $B_{\perp }$ above and between $B_c=\pm 0.6\hspace{0.5em}\mathrm{T,}$ the critical magnetic field for the layered-AFM to FM transition. (D) Calculated $B_{\perp }$ dependence of $U_1$ and $U_2$ of 2L CrI₃. (E) Second- and third-order Raman modes (raw spectra) acquired in the same condition as A. (F) $B_{\perp }$ dependence of I.I. of second- and third-order modes of 2L CrI₃.

We refer to the layered-magnetism–phonon coupling that we have developed above to understand the magnetic field dependence of the two first-order modes ($U_1$ and $U_2$) of 2L CrI₃. For each mode $U_i,$ its Raman tensor ${\text{R}}^i$ is composed of the conventional structural $\left({\text{R}}_{\mathrm{S}}^i\right)$ and the layered-magnetism–assisted magnetic $\left({\text{R}}_{\text{AS}}^i\right)$ contributions; i.e., ${\text{R}}^i={\text{R}}_{\mathrm{S}}^i+{\lambda }_i{\text{R}}_{\text{AS}}^i,$ where ${\text{R}}_{\mathrm{S}}^i$ is magnetic field independent and is present only for parity-even modes, ${\text{R}}_{\text{AS}}^i\propto {\overrightarrow{U}}_i·\overrightarrow{M}$ reflects the magnetic origin and selects the zero-momentum component, and ${\lambda }_i$ is the ratio of the magnetic to structural contribution for the ith mode that depends on microscopic parameters such as spin–orbit coupling. Here, $\overrightarrow{M}$ changes from $\left(1,-1\right)$ to $\left(\pm 1,\pm 1\right)$ across the layered-AFM to FM transition at $B_c=\pm 0.6\hspace{0.5em}\mathrm{T}$ with the fully polarized FM spin moments pointing upward/downward. Specifically, for the parity-even high-frequency mode of ${\overrightarrow{U}}_1=\frac{1}{\sqrt{2}}\left(\mathrm{1,1}\right),$ ${\text{R}}_{\mathrm{S}}^1=\left(\begin{array}{cc}{a}_1& 0\\ 0& a_1\end{array}\right)$ at all magnetic fields and ${\text{R}}_{\text{AS}}^1={\overrightarrow{U}}_1·\overrightarrow{M}\left(\begin{array}{cc}0& -a_1\\ +a_1& 0\end{array}\right)=0$ below $B_c$ and $\left(\begin{array}{cc}0& \mp \sqrt{2}{a}_1\\ \pm \sqrt{2}{a}_1& 0\end{array}\right)$ above $B_c=\pm$ 0.6 T (Fig. 3 C, Top and Bottom), whereas for the parity-odd low-frequency mode of ${\overrightarrow{U}}_2=\frac{1}{\sqrt{2}}\left(1,-1\right),$ ${\text{R}}_{\mathrm{S}}^2=0$ always and ${\text{R}}_{\text{AS}}^2=\left(\begin{array}{cc}0& -\sqrt{2}{a}_2\\ +\sqrt{2}{a}_2& 0\end{array}\right)$ below $B_c$ and 0 otherwise (Fig. 3C, Middle), where $=\sqrt{-1}$ to account for the broken time-reversal symmetry and $a_i$ stands for the Raman scattering strength of the ith mode (see the calculated magnetic field dependence of $U_1$ and $U_2$ in SI Appendix, Tables S4 and S5). This model faithfully reproduces the magnetic field dependence of both first-order modes of 2L CrI₃ in LL and RR channels by tuning only ${\lambda }_i$ and $a_i$ (Fig. 3D).

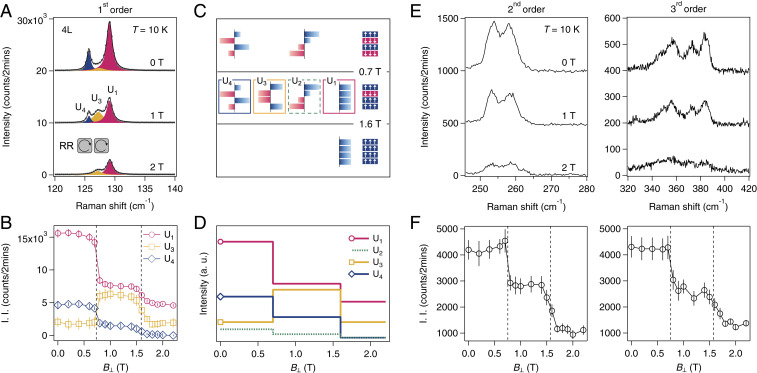
Different from 2L CrI₃, N-layer CrI₃ (N > 2) undergoes two spin–flip transitions with increasing $B_{\perp },$ one at $B_{c1}=\pm 0.7\hspace{0.5em}\mathrm{T}$ for spins in surface layers and the other at $B_{c2}=\pm 1.6\hspace{0.5em}\mathrm{T}$ for spins in interior layers (1, 2). For simplicity but without losing any generality, we pick 4L CrI₃ and focus on measurements with the upward magnetic field and in the RR polarization channel. Fig. 4A shows Raman spectra of first-order modes taken at $B_{\perp }=0\hspace{0.17em}\mathrm{,}$ 1, and 2 T, below $B_{c1},$ between $B_{c1}$ and $B_{c2},$ and above $B_{c2},$ respectively, at 10 K and in the RR channel. At 0 T, we can reliably resolve only three of the fourfold multiplet of 4L CrI₃, namely, $U_1,$ $U_3,$ and $U_4$ as fitted by the red, orange, and blue Lorentzian profiles, respectively. This is because $U_2$ is spectrally so close to $U_1$ but has a much weaker intensity (Fig. 1A), thus getting overwhelmed by the strong $U_1$ in the RR channel. We observe both $U_1$ and $U_4$ decrease subsequently at 1 and 2 T to finite and zero intensity, respectively, whereas $U_3$ increases at 1 T and then decreases at 2 T. The detailed magnetic field dependence of the $U_1,$ $U_3,$ and $U_4$ integrated intensity is shown in Fig. 4B, displaying the contrasting trends of $U_3$ to $U_1$ and $U_4,$ and those of the second- and third-order modes are shown in Fig. 4 E and F, closely mimicking that of $U_1.$

Fig. 4.

(A) Raman spectra of 4L CrI₃ in the RR channel in selected $B_{\perp }$ of 0, 1, and 2 T. Gray dots are raw data points and black curves are fits to multiple Lorentzian functions. Lorentzian profiles in red, orange, and blue correspond to $U_1,$ $U_3,$ and $U_4$ modes of 4L CrI₃. (B) $B_{\perp }$ dependence of I.I. of $U_1$ (red circles), $U_3$ (orange squares), and $U_4$ (blue diamonds). Vertical dashed lines mark the critical magnetic fields for spin–flip transitions, $B_{c1}=0.7\hspace{0.5em}\mathrm{T}$ and $B_{c2}=1.6\hspace{0.5em}\mathrm{T}.$ (C) List of phonon modes in 4L CrI₃ that have finite coupling strength ${\overrightarrow{U}}_i·\overrightarrow{M}$ for magnetic orders below $B_{c1},$ between $B_{c1}$ and $B_{c2},$ and above $B_{c2}.$ The dashed green box marks $U_2$ that is not observed in A due to its weak intensity and closeness to $U_1.$ Solid boxes of red, orange, and blue color highlight $U_1,$ $U_3,$ and $U_4,$ respectively. (D) Calculated $B_{\perp }$ dependence of $U_1$ (red), $U_2$ (green), $U_3$ (orange), and $U_4$ (blue) of 4L CrI₃. (E and F) $B_{\perp }$ dependence of second- and third-order modes of 4L CrI₃.

We carry out a similar analysis as we have done for 2L CrI₃ above, but add an additional intermediate magnetic phase $\overrightarrow{M}=\left(1,-\mathrm{1,1,1}\right)$ between the layered AFM of $\left(1,-\mathrm{1,1},-1\right)$ and the fully spin-polarized FM of $\left(\mathrm{1,1,1,1}\right).$ While the structural contribution $\left({\text{R}}_{\mathrm{S}}^i\right)$ is present only for parity-even modes, $U_1$ and $U_3,$ and remains magnetic field independent, the layered-magnetism–coupled magnetic contribution $\left({\text{R}}_{\text{AS}}^i\right)$ varies proportionally to ${\overrightarrow{U}}_i·\overrightarrow{M}$ as $\overrightarrow{M}$ changes as a function of $B_{\perp }.$ Fig. 4C lists the modes that have finite coupling to every layered magnetic order and thus nonzero ${\text{R}}_{\text{AS}}^i,$ according to which the magnetic contribution of $U_1$ appears above $B_{c1},$ that of $U_3$ emerges between $B_{c1}$ and $B_{c2},$ and $U_{\mathrm{2,4}}$ is present only below $B_{c2}$ (see the calculated magnetic field dependence of $U_1,$ $U_2,$ $U_3,$ and $U_4$ in SI Appendix, Tables S6 and S7). By adjusting ${\lambda }_i$ and $a_i,$ the ratio of the magnetic to structural contribution and the overall strength of the ith mode, we successfully show the consistency between the experimental and calculated magnetic field dependence of $U_{\mathrm{1,3,4}}$ and predict that of $U_2$ despite its invisibility in our experiment (Fig. 4D).

In conclusion, we have established the Davydov splitting of the A_g mode of a monolayer into an N-fold multiplet in N-layer CrI₃ and discovered, distinct from nonmagnetic few-layer atomic crystals (24–27), a unique layered-magnetism–assisted phonon scattering mechanism in the magnetic phases of CrI₃. We find this mechanism extends beyond first-order phonons to the multiphonon modes and further resolve the distinct magnetic field dependence for different first-order modes within the N-fold multiplet in N-layer CrI₃. Our calculations based on the combination of Davydov splitting and layered-magnetism–phonon coupling successfully explain the selection rules for individual split modes and capture the rich behavior of their distinct magnetic field dependence, effective for 2D CrI₃ of arbitrary thickness.

Materials and Methods

Sample Fabrication.

CrI₃ single crystals were grown by the chemical vapor transport method, as detailed in ref. 19. The 1L to 4L CrI₃ samples were exfoliated in a nitrogen-filled glovebox. Using a polymer-stamping transfer technique inside the glovebox, 1L to 4L CrI₃ flakes were then sandwiched between two few-layer hBN flakes and transferred onto SiO₂/Si substrates for Raman spectroscopy measurements.

Micro-Raman Spectroscopy.

Micro-Raman spectroscopy measurements were carried out using a 633-nm excitation laser. The incident beam was focused by a 40× objective down to ∼3 μm in diameter at the sample site, and the power was kept at 80 μW. The scattered light was collected by the objective in a backscattering geometry, then dispersed by a Horiba LabRAM HR Evolution Raman spectrometer, and finally detected by a thermoelectric cooled CCD camera. A closed-cycle helium cryostat is interfaced with the micro-Raman system for the temperature-dependent measurements. All thermal cycles were performed at a base pressure that is lower than 7 × 10⁻⁷ mbar. In addition, a cryogen-free magnet is integrated with the low-temperature cryostat for the magnetic field-dependent measurements. In this experiment, the magnetic field was applied along the out-of-plane direction and covered a range of 0 to 2.2 T.

Data Availability.

All study data are included in this article and SI Appendix.