Abstract
This paper assesses the role of gold as a safe haven or hedge against crude oil price risks. We employ the asymmetric VARMA-GARCH model, using daily data from January 2016 to August 2020. To account for the impact of COVID-19 pandemic, we partitioned the data into two to reflect the periods before and during the pandemic. Our empirical results find gold as a significant safe haven against oil price risks. The optimal portfolio and hedging analyses conducted also validate the hedging effectiveness of gold against risk associated with oil. The robustness of our results is further confirmed using three other prominent precious metals - silver, platinum, and palladium. In sum, our results are useful for investors and portfolio managers that are desirous of using gold and other precious metals as portfolio rebalancing tools to minimize or circumvent risks associated with volatile oil returns.
Keywords: Gold, Oil, Safe haven, Hedging, VARMA GARCH
1. Motivation
This paper investigates whether gold can continue to show its impressive run as a safety net for investors against oil market risks induced by the COVID-19 pandemic. The prospect of gold to provide cover for investors in the global crude oil market in the face of the pandemic has not been explored.1 This research objective is significant, given that the financial markets, including the crude oil market are vulnerable to pandemics. With increased financialisation, the global financial and commodity markets have been empirically shown to be negatively impacted by SARS, EBOLA, & COVID-19 pandemics [see Chen et al., 2009; Ichev and Marinč, 2018; Akhtaruzzaman et al., 2020; Ji et al., 2020; Shehzad et al., 2020; Salisu et al., 2020]. Particularly, the COVID-19 pandemic has led to global economic slowdown, dropping West Texas intermediate oil price below zero in April 2020, accompanied by a fall in the world industrial production index by about 4.5% in the first quarter of 2020 [see Gharib et al., 2020; Bakas and Triantafyllou, 2020]. Further, the crude oil market has witnessed some of its highest uncertainties partly due to the COVID-19 pandemic and partly due to political manoeuvres among oil producers during the period (see Ali et al., 2020).
The scenario described as “crash in the global oil price due to the COVID-19 pandemic” justifies our search for a safe asset in the face of mounting global panic and increased risk aversion in the global financial markets [see also, Zhang et al., 2020; Salisu et al., 2020]. The first motivation for the choice of gold for this hedging purpose is consequent on its low variability, and its ability to preserve wealth during inflation and safeguard investment during financial crises/uncertainties [see Tully and Lucey, 2007; Shafiee and Topal, 2010; Narayan et al., 2010; Wang, 2013; Bildirici and Turkmen, 2015; Jebran et al., 2017; Uzo-Peters et al., 2018; Jin et al., 2019; Wei et al., 2019]. The second motivation to support our choice of gold rests on the inferences from Selmi et al. (2018) that gold is a worthy hedging asset when facing severe oil price movements. The third and strongest motivation for the study emanates from Ji et al. (2020), who find strong hedging role for gold during COVID-19 pandemic when other potential asset classes are less effective.2
The research objective to look at the efficacy of gold as a good hedge against oil price risk is not arbitrary. Theoretically, it develops from an established age-long relationship between crude oil and gold [see Soytas et al., 2009; Narayan et al., 2010; Zhang and Wei, 2010; Ewing and Malik, 2013; Gil-Alana et al., 2017; Bildirici and Sonustun, 2018; Bedoui et al., 2019; Chen and Xu, 2019] as the two biggest, commonly traded assets in the global financial/commodity markets. From the perspective of investors, when oil price risks increase financial markets’ uncertainty as argued earlier during the pandemic, it is incumbent on investors to seek protection in gold as against other assets that contribute to spiral in financial contagions like oil, cryptocurrencies, and stocks [see Yaya et al., 2016; Corbet et al., 2020; Conlon et al., 2020]. From a policy stance, the global linkage of gold and crude oil markets would indicate that the two prices be considered with an economic lens and within the spectrum of the energy & financial policies of net buying and selling economies [see Kanjilal and Ghosh, 2017; Seyyedi, 2017; Aguilera and Radetzki, 2017; Sephton and Mann, 2018].
Following the introduction, the second section deals with theoretical construction for hedging oil price risks with gold. The methodology section describes the data, the estimable model and the estimation technique in Section 3. Section 4 discusses the results and Section 5 concludes the study.
2. The link between gold and crude oil markets: some highlights
The theoretical construction for linking the crude oil and gold markets has been argued to stem from the age-long connection between the crude oil and gold markets, and the gold and oil prices – both having global effects on the macroeconomic fundamentals of wide-ranging countries [see Soytas et al., 2009; Narayan et al., 2010; Zhang and Wei, 2010; Ewing and Malik, 2013; Gil-Alana et al., 2017; Bildirici and Sonustun, 2018; Bedoui et al., 2019; Chen and Xu, 2019]. Crude oil is a major source of energy globally and is therefore shown to significantly influence global macroeconomic dynamics, including economic growth, inflation, and stock market fundamentals of many countries [see Aguilera and Radetzki, 2017; Ansari and Sensarma, 2019]. The gold market has also grown in size globally due to increase in its financial features especially post Bretton Woods, and therefore conveys price information across the global economy [see Zhang and Wei, 2010; Beckmann et al., 2018].
With this connection, the theoretical linkage for the role of gold as a good hedge against oil price risk is straightforward. The nexus can be observed in two ways. First, oil price shock is associated with rising inflationary pressures [see for example, Hooker, 2002; Hunt, 2006; Zhang and Wei, 2010; Aguilera and Radetzki, 2017]. When this happens, it becomes a smart investment decision to look for a safe haven, given existing pieces of evidence that gold provides cover against inflation risks [see for example, Shafiee and Topal, 2010; Jain and Ghosh, 2013; Batten et al., 2014; Bildirici and Turkmen, 2015; Jin et al., 2019]. Second, in periods of high financial markets uncertainties like the one brought about by the COVID-19 pandemic (see Bakas and Triantafyllou, 2020), risk aversion rises because investors are more concerned with cutting investment losses [see Tversky and Kahneman, 1991; Hwang and Satchell, 2010]; the risk aversion motivates investors to look for alternatives to oil in their portfolio choices in the form of safe investment in gold [see Yaya et al., 2016; Conlon et al., 2020]. This second view is based on the submission that gold market retains its low variability [see Qadan, 2019] in the face of high uncertainty in the mainstream financial markets during pandemics.
2.1. Theoretical note
The ability of gold to serve as a hedge or safe haven can be viewed theoretically from the modern theory of Optimal Asset Selection propounded by Markowitz in 1952 (Adewuyi et al., 2019; Elie et al., 2019; Shahzad et al., 2019; Reboredo, 2013). According to this theory, expected returns (mean) and variance (risk) of the portfolio are the key determinants of portfolio selection. The theory further states that investment in a financial asset is a function of its correlation to other alternative assets like gold, bond, metals etc. in order to minimize risk and achieve diversification of assets. The Markowitz model was modified into Capital Asset Pricing Model (CAPM) by establishing a linear relationship between the expected rate of returns on an asset and its associated risks (Arfaoui and Rejeb, 2017; Hoang et al., 2015; Hood and Malik, 2013; Reboredo and Rivera-Castro, 2014; Reboredo and Ugolini, 2015). The expected rate of returns on a set of risky assets is the aggregate of the expected rate of returns on the assets that are uncorrelated with the market, and a premium of the risk that the investor must incur for holding the assets. The CAPM calibrated international pieces of evidence into its model through the International Capital Asset Pricing Model (ICAPM) by calibrating international market risk factors into its risk-return optimal assets selection, allocation, and portfolio diversification. The ICAPM affords investors the opportunities to move investment from local horizon like stock to global space via trading in gold, oil etc., mirroring events in the domestic economic viz-a-viz international economic space, with huge potential for arbitrage opportunities for investors. As pointed out by (Adewuyi et al., 2019; Arfaoui and Rejeb, 2017; Elie et al., 2019), gold seems to be the best investment alternatives (hedge or safe haven) in a period of crumbling economic outlook characterized by stock market crash, unfavorable exchange rates and weak commodities outlook. It is therefore expedient to note that return on gold (as determined by the demand for gold) is dependent on the returns on alternative investments like oil, bond etc. and the global risk factor. Therefore, risk-return (mean-variance) analysis in the global space is key to examining the expected returns and risk (variance) associated with gold and oil.
3. Data and model
3.1. Data and preliminary tests
Following this study's objectives as earlier discussed, we collected data for the two main variables of interest, namely the global gold and crude oil prices. The gold price is measured using the London Bullion Market Association (LBMA) gold fixing Price in U.S. Dollars per troy ounce. Crude oil price is proxied using the London Brent crude oil price. Daily data on gold and oil prices were collected from the US Federal Reserve Bank of St. Louis (fredstat) economic database, spanning January 2016 and August 2020. For robustness purposes, our empirical analyses are extended to evaluate the volatility spillovers and effectiveness of other prominent precious metals in hedging oil price risks. Specifically, we collected data on three other precious metals: silver, platinum, and palladium. Furthermore, we extend the analyses to account for the Covid-19 pandemic effects by extending the data sample to two additional sub-samples: (i) before COVID-19, which covers the period before the emergence of COVID-19 (ii) Covid-19 period-that is, since the first declaration of the emergence of the virus till date.3
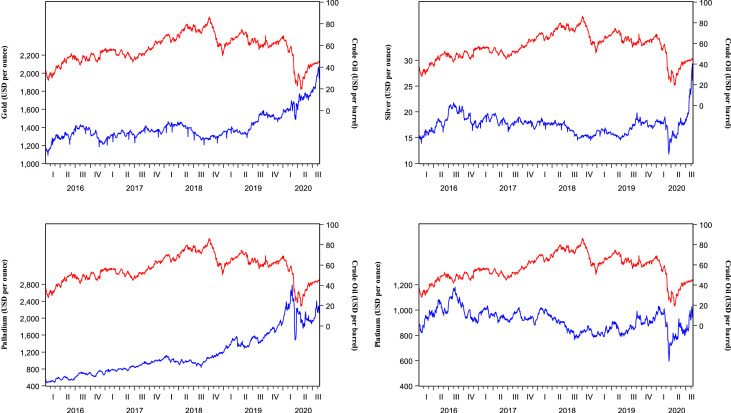
The descriptive analysis of the returns4 for gold and crude oil prices are summarised in Table 1 . The summary statistics considered include mean, maximum, minimum, standard deviation, skewness, and kurtosis. The mean of the summary statistics indicates positive average gold stock returns across the three sub-periods considered, while the average crude oil returns is positive before the emergence of COVID-19 but negative during the pandemic period. The positive average gold returns since the outbreak of COVID-19 and its effects on the global financial and commodities markets could be suggestive of a relatively average improved performance, same as for palladium and silver markets. On the other hand, the crude oil as well as platinum price returns experienced an overall average decline since the outbreak of COVID-19. The standard deviation which depicts a more volatile crude oil returns than gold and returns for the three other metals is considered. Lastly, all the series returns are negatively skewed for the full sample during the pandemic, while oil is positive before the outbreak. The high kurtosis values suggest that all the series are leptokurtic. Furthermore, we extend the summary statistics to explore the co-movement between crude oil and the four commodities considered. The graphical illustration presented in Fig. 1 suggests that there is co-movement between each commodity price series and crude oil prices, and this is stronger and more noticeable since the outbreak of COVID-19.
Table 1.
Summary statistics for crude oil and precious metals returns.
| Gold | Oil | Palladium | Platinum | Silver | |
| Full sample | |||||
| Mean | 0.0455 | 0.0166 | 0.1178 | 0.0067 | 0.0472 |
| Maximum | 7.5669 | 19.0774 | 18.6270 | 9.9314 | 7.9842 |
| Minimum | −7.8239 | −27.9762 | −22.9172 | −13.6136 | −12.3536 |
| Standard deviation | 1.3532 | 2.7630 | 2.0784 | 1.5572 | 1.8916 |
| Skewness | −0.0360 | −1.2775 | −0.8709 | −0.6784 | −0.4476 |
| Kurtosis | 13.1432 | 24.6703 | 23.3954 | 14.7637 | 9.7337 |
| Pre-COVID-19 sample | |||||
| Mean | 0.0300 | 0.0592 | 0.1203 | 0.0088 | 0.0194 |
| Maximum | 7.5669 | 13.6392 | 5.2944 | 3.7523 | 7.9842 |
| Minimum | −7.8239 | −8.1057 | −7.6931 | −4.5973 | −7.5583 |
| Standard deviation | 1.3339 | 2.0845 | 1.6303 | 1.1849 | 1.6605 |
| Skewness | −0.0231 | 0.2029 | −0.4303 | −0.0081 | −0.1901 |
| Kurtosis | 14.7462 | 6.8605 | 4.7422 | 3.8010 | 8.7647 |
| COVID-19 sample | |||||
| Mean | 0.1445 | −0.2361 | 0.0911 | −0.0114 | 0.2305 |
| Maximum | 5.6117 | 19.0774 | 18.6270 | 9.9314 | 7.1035 |
| Minimum | −4.7960 | −27.9762 | −22.9172 | −13.6136 | −12.3536 |
| Standard deviation | 1.4768 | 5.3825 | 3.8948 | 3.0155 | 2.9873 |
| Skewness | −0.1312 | −1.2596 | −0.7740 | −0.6853 | −0.7723 |
| Kurtosis | 5.8595 | 11.6869 | 13.3700 | 7.3272 | 6.5156 |
Fig. 1.
Co-movements between crude oil prices and precious metal prices.
Following the descriptive statistics discussion, we evaluate the choice of appropriate GARCH model to be used for the empirical analyses. These formal pre-tests include serial correlation, conditional heteroscedasticity, asymmetry and constant conditional correlation (CCC) tests. The serial correlation test is carried out using the Ljung-Box Q-statistics, and the ARCH-LM test is employed to evaluate the conditional heteroscedasticity. We test for asymmetry using the Engle and Ng sign and bias tests and the CCC test is carried out using the Engle-Sheppard test. The results are summarised in Table 2 .
Table 2.
Conditional heteroscedasticity, autocorrelation and asymmetry tests).
| Pane 2a: Conditional Heteroscedasticity and Autocorrelation Tests | ||||||
|---|---|---|---|---|---|---|
| Full sample | Pre-COVID-19 sample | COVID-19 sample | ||||
| Gold | Oil | Gold | Oil | Gold | Oil | |
| ARCH LM (6) | 25.227*** (0.000) | 15.109*** (0.000) | 17.263*** (0.000) | 9.614*** (0.000) | 2.330** (0.035) | 2.107* (0.056) |
| ARCH LM (12) | 12.768*** (0.000) | 16.124*** (0.000) | 8.878*** (0.000) | 7.021*** (0.000) | 1.847** (0.047) | 1.820* (0.051) |
| LB(6) | 17.140*** (0.004) | 5.373 (0.372) | 31.080*** (0.000) | 3.202 (0.0.669) | 10.900* (0.053) | 2.301 (0.806) |
| LB(12) | 22.838** (0.018) | 20.147** (0.043) | 33.346*** (0.000) | 13.229 (0.279) | 17.840* (0.085) | 9.663 (0.561) |
| LB2(6) | 133.81*** (0.000) | 113.48*** (0.000) | 102.88*** (0.000) | 79.681*** (0.000) | 20.701*** (0.002) | 13.103** (0.041) |
| LB2(12) | 137.28*** (0.000) | 316.83*** (0.000) | 112.05*** (0.000) | 144.82*** (0.000) | 41.764*** (0.000) | 30.028*** (0.003) |
| Pane 2b: Asymmetry test and CCC test | ||||||
| Sign bias | 1.042 (0.298) | 1.176 (0.240) | 3.371*** (0.000) | 1.995** 0.046 | 0.022 (0.983) | 0.115 (0.909) |
| Negative bias | 1.222 (0.222) | 1.850* (0.065) | 8.134*** (0.000) | 0.724 (0.469) | 0.502 (0.616) | 1.053 (0.294) |
| Positive bias | 1.233 (0.218) | 0.023 (0.982) | 0.539 (0.590) | 0.459 (0.646) | 0.787 (0.423) | 0.517 (0.606) |
| Joint bias | 3.014 (0.390) | 9.893** (0.020) | 66.690*** (0.000) | 4.685 (0.196) | 0.876 (0.831) | 2.477 (0.480) |
| ES test | 0.084 (0.959) | 0.073 (0.964) | 0.171 (0.918) | |||
| Model Choice | Asymmetry CCC | Asymmetry CCC | Symmetry CCC | |||
Note: The ARCH LM tests refer to the Engle (1982) test for conditional heteroscedasticity while the LB and LB2 imply the Ljung-Box tests for autocorrelations involving the standardized residuals in levels and squared standardized residuals respectively. The null hypothesis for the ARCH LM test is that the series has no ARCH effects (that is, it is not volatile) while LB test for null hypothesis is that the series is not serially correlated; ES test imply the Engle-Sheppard CCC test; the values in parentheses – ( ) denote the computed probability values.
The ARCH-LM tests indicate evidence of statistically significant conditional heteroscedasticity in both gold and oil price returns across the three estimation sub-samples. By implication, estimators that account for such ARCH effects is preferred. In addition, the Ljung-Box serial correlation tests also support the evidence of statistically significant serial correlation. The additional formal pre-tests including the Engle-Ng sign and joint size bias tests indicate statistically significant estimates for both the full sample and pre-COVID periods. Hence, it supports evidence of significant asymmetric effects on gold and crude oil price returns. During the COVID-19 period however, the asymmetric effect is not evident. Hence the estimation for the COVID-19 sample statistically supports the symmetric variant of the VARMA-GARCH model. Lastly, the Engle-Sheppard tests across the three data samples considered are not statistically significant, and these therefore provide statistical evidence of constant conditional correlations between the two commodity sectors. The summary of the preferred model for each data sample is summarised on the last row of Table 2.
Note: The returns series are computed as log return which is defined as where denotes the crude oil and precious metals prices at period t. The precious metals comprise gold, palladium, platinum and silver.
3.2. The empirical model
Based on the results of the preliminary tests presented and discussed in the preceding section, the study favours both the symmetric and asymmetric variant of the VARMA–CCC-GARCH model as proposed by Ling and McAleer (2003) and extended by McAleer et al. (2009). The VARMA–CCC-GARCH model remains a prominent instrument when modelling interdependencies and spillovers among financial time series both with or without asymmetric shock effects (see also (Al-Maadid et al., 2017; Salisu and Mobolaji, 2013; Salisu and Oloko, 2015). The symmetric variant of the model specifies a conditional mean equation with vector autoregressive moving average (VARMA) and a conditional variance equation within a multivariate GARCH process framework, while the asymmetric variant assumes asymmetric effects for equal magnitude of positive and negative shocks. Besides, the preference for the model and its strength lie in its capturing of both the symmetric and asymmetric effects that could exist in the financial asset returns, and which structurally the CCC and DCC models may not capture (McAleer et al., 2009). The conditional mean equation for the bivariate VARMA(1,1)–CCC–AGARCH(1,1) model, which captures the spillovers between gold and oil price returns is specified respectively as:
| [1] |
| [2] |
where and denote gold and oil price returns in period respectively; and are constant terms, and are coefficients of the lagged terms of own-returns respectively for gold and crude oil and both explains own-returns shock spillovers, and are respectively coefficients of lagged terms of cross-returns for gold and crude oil. Both coefficients explain the cross shock spillovers between gold and crude oil price returns; and are independently and identically distributed errors. The conditional variance equations provide the computation of the volatility spillover effects across the two assets; besides, the conditional variance equations show that conditional variance for each sector is dependent on its immediate past values and innovations as well as past values and innovations from the other sector. They are specified in Eqs. [3], [4] for gold and crude oil respectively:
| [3] |
| [4] |
Finally, the conditional covariance is expressed as:
| [5] |
where is the conditional constant correlations between gold and oil price returns. The estimation procedure as well as the statistical and structural properties of the model, which provides both the necessary and sufficient conditions, are provided in Ling and McAleer (2003) (see also Salisu and Mobolaji (2013) and Salisu and Oloko (2015). Some of the relevant statistics which establish the goodness of fit of the models, are determined using the minimum values of Akaike Information Criterion (AIC) and Schwartz Bayesian Criterion (SBC). In addition, relevant post estimation diagnostics include the Ljung–Box statistic, used to test for autocorrelation with the null hypothesis that there is no autocorrelation; the McLeod–Li statistics employed to test for ARCH effects, with the underlying null hypothesis that there are no ARCH effects in the model. The estimated model is robust when the null hypothesis of both the Ljung–Box and McLeod–Li statistics are not rejected. The estimated results are presented and discussed in the next section.
4. Results and discussion
4.1. Main results
The results of the bivariate asymmetric and symmetric VARMA–CCC–GARCH models are summarised in Table 3 for both the mean equation and variance equation estimates. As noted in the data section, the estimated results are summarised into three components based on the three data samples. The mean equation results show that there are statistically significant spillovers between gold returns and crude oil sector returns across the three sub-sample estimations. However, while the coefficients are positive, the estimated results during COVID-19 pandemic show negative coefficient of returns spillovers from gold to oil price returns. Intuitively, the returns spillover estimate suggests that one percent increase gold price returns since the outbreak of the pandemic will lead to a decline of about 0.39 percent in oil price returns in the subsequent period.
Table 3.
Returns and volatility spillovers between gold and oil price returns.
| Variables | Full sample | Pre-COVID-19 sample | COVID-19 sample | |
|---|---|---|---|---|
| Mean Equation | ||||
| −0.0689*** (0.000) | −0.0830*** (0.000) | 0.2789*** (0.000) | ||
| 0.0301*** (0.000) | 0.0729*** (0.000) | 0.1622*** (0.000) | ||
| −0.0076*** (0.000) | 0.0407*** (0.000) | −0.0458*** (0.000) | ||
| −0.0379*** (0.000) | −0.0453*** (0.000) | 0.1223*** (0.000) | ||
| 0.0036*** (0.000) | 0.0009*** (0.000) | 0.0027*** (0.000) | ||
| 0.0474*** (0.000) | 0.0600*** (0.000) | −0.3918*** (0.000) | ||
| Variance Equation | ||||
| 0.9525*** (0.000) | 0.9599*** (0.000) | −0.0060*** (0.000) | ||
| 0.0872*** (0.000) | 0.0841*** (0.000) | −2.6889*** (0.000) | ||
| −0.0191*** (0.000) | 0.0044*** (0.000) | 0.1297*** (0.000) | ||
| 0.0005*** (0.000) | 0.0078*** (0.000) | 0.0030*** (0.000) | ||
| −0.0078*** (0.000) | −0.0019*** (0.000) | −0.3422*** (0.000) | ||
| 0.0156*** (0.000) | 0.0064*** (0.000) | 0.0557*** (0.000) | ||
| 0.0030*** (0.000) | −0.0450*** (0.000) | 0.9698*** (0.000) | ||
| 0.0360*** (0.000) | 0.0440*** (0.000) | −0.0096*** (0.000) | ||
| 0.0412*** (0.000) | −0.0071*** (0.000) | 3.2434*** (0.000) | ||
| 0.8810*** (0.000) | 0.9262*** (0.000) | 0.7497*** (0.000) | ||
| 0.5131*** (0.000) | 0.4768*** (0.000) | |||
| 0.1584*** (0.000) | 0.0966*** (0.000) | |||
| 0.0153*** (0.000) | −0.0008 (0.9819) | 0.1017*** (0.000) | ||
| Model diagnostics | ||||
| AIC | 7.490 | 7.224 | 8.997 | |
| SBC | 7.571 | 7.315 | 9.326 | |
| Hannan-Quinn | 7.520 | 7.259 | 9.130 | |
Note: Parameters in mean and variance equations are as defined in the model given in equations [1] to [4[; the subscripts 1 and 2 respectively indicate health and crude oil sectors returns respectively; the asterisks ***, ** and *denote statistical significance at 1%, 5% and 10% level. The values in parentheses – ( ) denote the computed probability values. Best model is selected based on minimum values of Akaike Information Criterion (AIC) and Schwartz Bayesian Criterion (SBC). Note that AIC and SBC are not comparable for the different partitions.
The volatility spillovers between the two commodities price returns further confirm that there are significant volatility effects. The estimated coefficient of the variance equation is summarised in Table 3 and it shows that all the parameters of the ARCH and GARCH terms are statistically significant. The own shocks for the gold and crude oil returns is positive and statistically significant both before and during the pandemic period. The coefficients of the cross-returns spillovers between gold and crude oil returns (, ) show that the current conditional volatility for each of the market significantly affects the immediate returns in the other market. However, while it is positive from oil to gold markets, the reverse is the case from gold to crude oil returns across the three samples. This finding is consistent with previous studies which established that crude oil firms are severely exposed to event-related risks such as the 9/11 attacks in the US and the global financial crisis of 2008 (see also (Kim et al., 2013; Lee and Jang, 2011; Li et al., 2020; Paraskevas and Quek, 2019; Park et al., 2017; Shrydeh et al., 2019).
As expected, the own-volatility transmission for each of the market is positive and statistically significant for both returns before and during the pandemic. In addition, the cross-sector volatility spillover effects between gold and crude oil returns (, ) show that the current conditional volatility for each of the market significantly depends on immediate past values and innovations from the other market. However, the signs and magnitude of the bi-directional volatility transmissions vary across the three data partitions; though it is positive and significant for the full sample estimates. This indicates that conditional volatility of the gold returns responds positively to past shocks of crude oil returns before the pandemic, and vice versa. On the contrary, the signs are interchanged for the crude oil conditional volatility response to lagged conditional variance in gold market, with a negative response before the pandemic changing to positive during the outbreak of COVID-19. In terms of asymmetric shock effects, the results show evidence of positive and significant asymmetric shock effects for both commodities for full sample and pre-COVID.
The post-estimation diagnostics rendered using the Ljung–Box statistic and McLeod–Li tests are summarised in Table 4 . The results show the robustness of estimates. Although the results of the Ljung-Box tests indicate the rejection of the null hypothesis of no serial correlation at six lags for the full sample and pre-COVID estimation; the null hypothesis cannot be rejected when higher lags are considered, indicating the suitability of the model and estimates. Similarly, the adequacy of the ARCH and GARCH terms are supported by the McLeod test which shows that there are no remaining ARCH effects.
Table 4.
Post estimation diagnostics.
| Full Sample | Pre-COVID-19 sample | COVID-19 sample | ||||
|---|---|---|---|---|---|---|
| Gold | Crude oil | Gold | Crude oil | Gold | Crude oil | |
| Ljung-Box Q(6) | 23.624*** (0.001) | 2.818 (0.831) | 38.551*** (0.000) | 0.718 (0.994) | 8.272 (0.219) | 2.522 (0.866) |
| Ljung-Box Q(12) | 27.565*** (0.006) | 9.193 (0.686) | 42.500*** (0.000) | 7.214 (0.843) | 18.343 (0.106) | 5.896 (0.921) |
| McLeod-Li(6) | 2.116 (0.909) | 8.486 (0.205) | 3.046 (0.803) | 3.805 (0.703) | 4.207 (0.649) | 1.533 (0.957) |
| McLeod-Li(12) | 5.717 (0.930) | 10.021 (0.614) | 6.632 (0.881) | 5.091 (0.955) | 7.495 (0.823) | 4.095 (0.982) |
Note: The Ljung-Box and McLeod tests provide the empirical statistics respectively for the serial correlation and remaining conditional heteroscedasticity of orders 6 and 12 for robustness purposes.
4.2. Hedging effectiveness and optimal portfolio between gold and oil returns
This section discusses the optimal portfolio weights and hedging effectiveness of gold for crude oil returns using the conditional variance and covariance estimates obtained from the main estimation. The significant of returns and volatility spillovers between the gold and crude oil returns is suggestive of volatility and risk susceptibilities to investors’ assets in the global financial and commodity markets. The outbreak of COVID-19 pandemic further amplifies these associated volatilities and risks susceptibilities. It is therefore imperative for investors to mitigate such risks by engaging in portfolio rebalancing and hedging, through engagement in future contract and without jeopardising their expected returns.
We estimate the optimal portfolio weights (OPW) to evaluate the optimal proportion of gold and crude oil assets that should form a rational investor's portfolio. Following Kroner and Ng (1998) and Arouri et al. (2011), we construct the optimal portfolio weight of holding the two assets using the conditional variance and covariances defined as:
| [6] |
and,
| [7] |
where denotes the weight of gold asset in a one-dollar gold/crude oil stock portfolio at time , and is the conditional covariance between the gold and crude oil returns at time . Consequently, the optimal weight of gold in the two asset classes considered can be evaluated as . Furthermore, we construct the optimal hedge ratio (OHR) to evaluate the hedging effectiveness of gold against crude oil returns. Following Kroner and Sultan (1993) the risk of a crude oil investment portfolio is minimised if a long position of one dollar in crude oil asset can be hedged by a short position of dollars in gold (see also Arouri et al., 2011; Salisu and Mobolaji (2013); Salisu and Oloko (2015)). The formulation of the OHR between these two assets is defined as:
| [8] |
The results of the optimal portfolio weights and optimal hedge ratio computed for the sample partitions are summarised in Table 5 . The results indicate that optimal weight of gold assets in a one-dollar gold–crude oil stock portfolio is about 36% before the outbreak of COVID-19 but increased to almost 100% during the outbreak. On the other hand, the values of the hedge ratios suggest that risks associated with crude oil stocks can be hedged by taking a short position in gold assets (See also (Baur and Lucey, 2010). The estimated OHR for the COVID-19 sample shows that the hedging effectiveness of gold against crude oil returns increased with the outbreak of COVID-19. For example, while the estimated OHR for the pre-COVID-19 sample is about −0.001, that of COVID-19 sample is positive and about 0.0002.
Table 5.
Optimal portfolio weights and hedge ratios.
| Full sample | Pre-COVID-19 sample | COVID-19 sample | |
|---|---|---|---|
| 0.8392 | 0.3627 | 1.0002 | |
| 0.0068 | −-0.0010 | 0.0002 |
Notes: The table reports average optimal weights and hedge ratios in a gold-crude oil portfolio.
4.3. Robustness checks
We extend the empirical estimation by investigating the role of other prominent precious metals on the portfolio choice and their hedging effectiveness against crude oil risks, especially during the COVID-19 outbreak. Essentially, we consider three other prominent commodities: silver, platinum, and palladium. We commence estimating the appropriate bivariate VARMA-GARCH models for both the mean and variance equations between each metal and crude oil price returns.5 The estimated results for the three metals - palladium, platinum and silver, show evidence of statistically significant bidirectional returns and volatility spillover transmission with crude oil prices; thus indicating that the trio, as also established for gold returns, could serve as safe havens for rising risks in the crude oil returns (see Table A1, Table A2 in the appendix). In addition, the estimated OPW and OHR results as summarised in Table A3 of the Appendix section, indicate that optimal weight of each of the considered metals in a one-dollar investment portfolio is at 100, 0.96, and 1.01 for palladium, platinum and silver respectively. These results, as also established in the case of gold, are suggestive that each of the precious metals are optimal investment safe haven for crude oil investment risks since the outbreak of COVID-19. In addition, the computed hedge ratios further establish that risks associated with crude oil returns can be hedged by taking a short position in either of these assets (see also (Bhatia et al., 2020; Dutta et al., 2019; Hernandez et al., 2019; Yıldırım et al., 2020).
Table A1.
Returns and volatility spillovers between metals and oil price returns during pandemics
| Variables | Palladium | Platinum | Silver | ||
| Mean Equation | |||||
| 0.3588*** (0.005) | −0.0069*** (0.000) | 0.2610*** (0.000) | |||
| 0.1301 (0.542) | 0.0011*** (0.000) | −0.0504*** (0.000) | |||
| 0.0490 (0.418) | 0.0404*** (0.000) | 0.0361*** (0.000) | |||
| 0.2032*** (0.000) | 0.2297*** (0.000) | 0.1356*** (0.000) | |||
| 0.1091*** (0.000) | −0.0110*** (0.000) | 0.0283*** (0.000) | |||
| −0.0350*** (0.000) | −0.0223*** (0.000) | 0.0054*** (0.000) | |||
| Variance Equation | |||||
| 1.4084*** (0.005) | 1.9713*** (0.000) | 0.5792*** (0.000) | |||
| 0.1455 (0.584) | 0.8536*** (0.000) | 0.9723*** (0.000) | |||
| 1.0652*** (0.000) | 0.1258*** (0.000) | 0.2197*** (0.000) | |||
| 0.1141*** (0.002) | −0.0135*** (0.000) | −0.0072*** (0.000) | |||
| −0.0501 (0.116) | −0.0451*** (0.000) | −0.0087*** (0.000) | |||
| 0.4148*** (0.000) | 0.5649*** (0.000) | 0.6624*** (0.000) | |||
| 0.0864* (0.056) | 0.5123*** (0.000) | 0.6963*** (0.000) | |||
| 0.0165 (0.436) | 0.0392*** (0.000) | 0.0110*** (0.000) | |||
| 0.1039*** (0.001) | −0.0236*** (0.000) | −0.0131*** (0.000) | |||
| 0.6280*** (0.000) | 0.6075*** (0.000) | 0.5273*** (0.000) | |||
| 0.2244*** (0.001) | 0.3022*** (0.000) | 0.2663*** (0.000) | |||
| Model diagnostics | |||||
| AIC | 10.827 | 10.462 | 10.393 | ||
| SBC | 11.157 | 10.791 | 10.723 | ||
| Hannan-Quinn | 10.961 | 10.596 | 10.527 | ||
Note: Parameters in mean and variance equations are as defined in the model given in equations [1] to [4[; the subscripts 1 and 2 respectively indicate health and crude oil sectors returns respectively; the asterisks ***, ** and *denote statistical significance at 1%, 5% and 10% level. The values in parentheses – ( ) denote the computed probability values. Best model is selected based on minimum values of Akaike Information Criterion (AIC) and Schwartz Bayesian Criterion (SBC). Note that AIC and SBC are not comparable for the different partitions.
Table A2.
Post Estimation Diagnostics
| Palladium | Platinum | Silver | |
|---|---|---|---|
| Ljung-Box Q(6) | 5.2051 (0.5178) | 2.3646 (0.883) | 5.7490 (0.4519) |
| Ljung-Box Q(12) | 7.0236 (0.8561) | 13.600 (0.327) | 24.084* (0.0198) |
| McLeod-Li(6) | 6.2011 (0.4010) | 1.9854 (0.921) | 2.4685 (0.8720) |
| McLeod-Li(12) | 18.893* (0.0911) | 5.234 (0.950) | 11.3248 (0.5013) |
Note: The Ljung-Box and McLeod tests provide the empirical statistics respectively for the serial correlation and remaining conditional heteroscedasticity of orders 6 and 12 for robustness purposes.
Table A3.
Optimal portfolio weights and hedge ratios
| Palladium | Platinum | Silver | |
|---|---|---|---|
| 1.0006 | 0.9556 | 1.0062. | |
| 0.0498 | 0.1219 | 0.0646. |
Notes: The table reports average optimal weights and hedge ratios in a precious metal and crude oil asset portfolio using the variance and covariance estimates of the VARMA–CCC–GARCH models after accounting for exogenous factors including exchange rate and gold EMV volatilities.
The results from the study offers some significant implications. For instance, the results reveal that it is better off to calibrate gold in asset portfolio so as to maximize the expected utilities of risk-averse investors, especially when faced with significant upward shifts (or stability) in gold prices when compared with nose-diving oil prices. Furthermore, the ability of gold to hedge or serve as a safe haven suggests tilting towards gold in order to abate the growing concern about energy security and climate change related issues associated with oil. For policymakers, the findings suggest that policy should be tailored towards reducing the adverse effect of oil price volatility, which could be done by promoting the consumption of clean energy in place of fossil fuels.
5. Conclusion
This paper empirically evaluates the safe haven and hedging properties of gold during oil price crisis. To accommodate the statistical features of the series such as conditional heteroscedasticity and conditional correlations between gold and oil markets, we employ the VARMA-GARCH model and its asymmetric variants. This model allows us to evaluate the returns and volatility spillover transmission between gold and crude oil returns. The impact of the COVID-19 outbreak is further accounted for in the empirical exercise by partitioning the data sample into two to reflect the periods before and during the pandemic. The estimated results show statistically significant bidirectional returns and volatility spillovers between the gold and crude oil returns. The computed optimal weight and hedge ratios further validate the hedging effectiveness of gold against risks associated with crude oil, particularly during the pandemic period. We extend the estimation to investigate whether other precious metals such as palladium, platinum and silver will exhibit similar features as gold, and our results are in the affirmative, albeit with lower magnitudes. Summarily, we find that a diversified asset portfolio may improve the risk-adjusted return performance. Future studies that extend the safe haven and hedging properties of precious metals to risk associated with other financial assets such as stock market, foreign exchange market, bond market, and real estate, particularly during pandemics will further enrich the extant literature.
Footnotes
For robustness, we explore the hedging effectiveness of other precious metals like silver, platinum and palladium (see Agyei-Ampomah et al., 2014; Lucey and Li, 2015; Qadan, 2019).
In this vein, the choice of gold is further underscored from the perspectives of Conlon and McGee (2020), Corbet et al. (2020), Conlon et al. (2020) showing that other potential hedging assets like digital money and oil lose their hedging powers during the COVID-19 pandemic.
WHO's Country Office in the People's Republic of China picked up a media statement by the Wuhan Municipal Health Commission from their website on cases of ‘viral pneumonia’ in Wuhan, People's Republic of China. See https://promedmail.org/promed-post/?id=6864153%20#COVID19.
Returns are computed from the price series for each of the commodity as.
The results are summarised in the Appendix section.
References
- Adewuyi Adeolu, Awodumi Olabanji, Abodunde Temitope. Analysing the gold-stock nexus using VARMA-BEKK-AGARCH and Quantile regression models: New evidence from South Africa and Nigeria. Resour. Pol. 2019;61(C):348–362. [Google Scholar]
- Aguilera R.F., Radetzki M. The synchronized and exceptional price performance of oil and gold: explanations and prospects. Resour. Pol. 2017;54:81–87. [Google Scholar]
- Agyei-Ampomah S.A.M., Gounopoulos D., Mazouz K. Does gold offer a better protection against losses in sovereign debt bonds than other metals? J. Bank. Finance. 2014;40:507–521. [Google Scholar]
- Akhtaruzzaman M., Boubaker S., Sensoy A. Financial contagion during COVID–19 crisis. Finance Res. Lett. 2020 doi: 10.1016/j.frl.2020.101604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ali M., Alam N., Rizvi S.A.R. Coronavirus (COVID-19) - an epidemic or pandemic for financial markets. Journal of Behavioral and Experimental Finance. 2020;27:100341. doi: 10.1016/j.jbef.2020.100341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Al-Maadid A., Caporale G.M., Spagnolo F., Spagnolo N. Spillovers between food and energy prices and structural breaks. International Economics. 2017;150:1–18. doi: 10.1016/j.inteco.2016.06.005. [DOI] [Google Scholar]
- Ansari M.G., Sensarma R. US monetary policy, oil and gold prices: which has a greater impact on BRICS stock markets? Econ. Anal. Pol. 2019;64:130–151. [Google Scholar]
- Arfaoui Mongi, Rejeb Aymen Ben. Oil, gold, US dollar and stock market interdependencies: a global analytical insight. Eur. J. Manag. Bus. Econ. 2017;26(3):278–293. [Google Scholar]
- Arouri M.E.H., Jouini J., Nguyen D.K. Volatility spillovers between oil prices and stock sector returns: implications for portfolio management. J. Int. Money Finance. 2011;30(7):1387–1405. [Google Scholar]
- Bakas D., Triantafyllou A. Commodity price volatility and the economic uncertainty of pandemics. Econ. Lett. 2020;193:109283. [Google Scholar]
- Batten J.A., Ciner C., Lucey B.M. On the economic determinants of the gold–inflation relation. Resour. Pol. 2014;41:101–108. [Google Scholar]
- Baur D.G., Lucey B.M. Is gold a hedge or a safe haven? An analysis of stocks, bonds and gold. Financ. Rev. 2010;45(2):217–229. doi: 10.1111/j.1540-6288.2010.00244.x. [DOI] [Google Scholar]
- Beckmann J., Berger T., Czudaj R. Quantitative Finance; 2018. Gold Price Dynamics and the Role of Uncertainty. [DOI] [Google Scholar]
- Bedoui R., Braiek S., Guesmi K., Chevallier J. On the conditional dependence structure between oil, gold and USD exchange rates: nested copula based GJR-GARCH model. Energy Econ. 2019;80:876–889. [Google Scholar]
- Bhatia V., Das D., Kumar S.B. Hedging effectiveness of precious metals across frequencies: evidence from Wavelet based Dynamic Conditional Correlation analysis. Phys. Stat. Mech. Appl. 2020;541:123631. doi: 10.1016/j.physa.2019.123631. [DOI] [Google Scholar]
- Bildirici M., Turkmen C. Nonlinear causality between oil and precious metals. Res. Pol. 2015;46:202–211. [Google Scholar]
- Bildirici M.E., Sonustun F.O. The effects of oil and gold prices on oil-exporting countries. Energy Strategy Reviews. 2018;22:290–302. [Google Scholar]
- Chen C.D., Chen C.C., Tang W.W., Huang B.Y. The positive and negative impacts of the SARS outbreak: a case of the Taiwan industries. J. Develop. Area. 2009:281–293. [Google Scholar]
- Chen R., Xu J. Forecasting volatility and correlation between oil and gold prices using a novel multivariate GAS model. Energy Econ. 2019;78:379–391. [Google Scholar]
- Conlon T., Corbet S., McGee R.J. Are cryptocurrencies a safe haven for equity markets? An international perspective from the COVID-19 pandemic Research in International Business and Finance. 2020;54:101248. doi: 10.1016/j.ribaf.2020.101248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conlon T., McGee R. Safe haven or risky hazard? Bitcoin during the COVID-19 bear market. 2020. https://ssrn.com/abstract=3560361 Available at SSRN: [DOI] [PMC free article] [PubMed]
- Corbet S., Larkin C., Lucey B. The contagion effects of the COVID-19 pandemic: evidence from gold and cryptocurrencies. Finance Res. Lett. 2020;35:101554. doi: 10.1016/j.frl.2020.101554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dutta A., Bouri E., Roubaud D. Nonlinear relationships amongst the implied volatilities of crude oil and precious metals. Resour. Pol. 2019;61:473–478. doi: 10.1016/j.resourpol.2018.04.009. [DOI] [Google Scholar]
- Elie Bouri, Naji Jalkh, Dutta Anupam, Uddin Gazi. Gold and crude oil as safe-haven assets for clean energy stock indices: blended copulas approach. Energy. 2019;178(C):544–553. [Google Scholar]
- Engle R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica. 1982;50(4):987–1007. [Google Scholar]
- Ewing B.T., Malik F. Volatility transmission between gold and oil futures under structural breaks. Int. Rev. Econ. Finance. 2013;25:113–121. [Google Scholar]
- Gharib C., Mefteh-Wali S., Jabeur S.B. The bubble contagion effect of COVID-19 outbreak: evidence from crude oil and gold markets. Finance Res. Lett. 2020 doi: 10.1016/j.frl.2020.101703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gil-Alana L.A., Yaya O.S., Awe O.O. Time series analysis of co-movements in the prices of gold and oil: fractional cointegration approach. Resour. Pol. 2017;53:117–124. [Google Scholar]
- Hernandez J.A., Shahzad S.J.H., Uddin G.S., Kang S.H. Can agricultural and precious metal commodities diversify and hedge extreme downside and upside oil market risk? An extreme quantile approach. Resour. Pol. 2019;62:588–601. doi: 10.1016/j.resourpol.2018.11.007. [DOI] [Google Scholar]
- Hoang Thi-Hong-Van, Lean Hooi Hooi, Wong Wing-Keung. Is gold good for portfolio diversification? A stochastic dominance analysis of the Paris stock exchange. Int. Rev. Financ. Anal. 2015;42(C):98–108. [Google Scholar]
- Hood Matthew, Malik Farooq. Is gold the best hedge and a safe haven under changing stock market volatility? Rev. Financ. Econ. 2013;22(2):47–52. [Google Scholar]
- Hooker M.A. Are oil shocks inflationary? Asymmetric and nonlinear specifications versus changes in regime. J. Money Credit Bank. 2002;34:540–561. [Google Scholar]
- Hunt B. Oil price shocks and the U.S. stagflation of the 1970s: some Insights from GEM. Energy J. 2006;27:61–80. [Google Scholar]
- Hwang S., Satchell S.E. How loss averse are investors in financial markets? J. Bank. Finance. 2010;34(10):2425–2438. [Google Scholar]
- Ichev R., Marinč M. Stock prices and geographic proximity of information: evidence from the Ebola outbreak. Int. Rev. Financ. Anal. 2018;56:153–166. doi: 10.1016/j.irfa.2017.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain A., Ghosh S. Dynamics of global oil prices, exchange rate and precious metal prices in India. Resour. Pol. 2013;38:88–93. [Google Scholar]
- Jebran K., Chen S., Saeed G., Zeb A. Dynamics of oil price shocks and stock market behavior in Pakistan: evidence from the 2007 financial crisis period. Financ. Innovat. 2017;3:2. doi: 10.1186/s40854-017-0052-2. [DOI] [Google Scholar]
- Ji Q., Zhang D., Zhao Y. Searching for safe-haven assets during the COVID-19 pandemic. Int. Rev. Financ. Anal. 2020;71:101526. doi: 10.1016/j.irfa.2020.101526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin J., Yu J., Hu Y., Shang Y. Which one is more informative in determining price movements of hedging assets? Evidence from Bitcoin, gold and crude oil markets. Physica A. 2019;527:121121. [Google Scholar]
- Kanjilal K., Ghosh S. Dynamics of crude oil and gold price post 2008 global financial crisis – new evidence from threshold vector error-correction model. Resour. Pol. 2017;52:358–565. [Google Scholar]
- Kim Y.H., Kim M.C., O'Neill J.W. Advertising and firm risk: a study of the restaurant industry. J. Trav. Tourism Market. 2013;30(5):455–470. doi: 10.1080/10548408.2013.803392. [DOI] [Google Scholar]
- Kroner K.F., Ng V.K. Modeling asymmetric comovements of asset returns. Rev. Financ. Stud. 1998;11(4):817–844. https://econpapers.repec.org/RePEc:oup:rfinst:v:11:y:1998:i:4:p:817-844 [Google Scholar]
- Kroner Kenneth F, Sultan Jahangir. Time-varying distributions and dynamic hedging with foreign currency futures. J. Financ. Quant. Anal. 1993;28(4):535–551. [Google Scholar]
- Lee S.K., Jang S. Foreign exchange exposure of US tourism-related firms. Tourism Manag. 2011;32(4):934–948. doi: 10.1016/j.tourman.2010.08.008. [DOI] [Google Scholar]
- Li J., Feng Y., Li G., Sun X. Tourism companies' risk exposures on text disclosure. Ann. Tourism Res. 2020;84:102986. doi: 10.1016/j.annals.2020.102986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ling S., McAleer M. Asymptotic theory for a vector ARMA-GARCH model. Econom. Theor. 2003;19(2):280–310. doi: 10.1017/S0266466603192092. [DOI] [Google Scholar]
- Lucey B.M., Li S. What precious metals act as safe havens, and when? Some US evidence. Appl. Econ. Lett. 2015;22(1):35–45. [Google Scholar]
- McAleer M., Hoti S., Chan F. Structure and asymptotic theory for multivariate asymmetric conditional volatility. Econom. Rev. 2009;28(5):422–440. doi: 10.1080/07474930802467217. [DOI] [Google Scholar]
- Narayan P.K., Narayan S., Zheng X. Gold and oil futures markets: are markets efficient? Appl. Energy. 2010;87:3299–3303. [Google Scholar]
- Paraskevas A., Quek M. When Castro seized the Hilton: risk and crisis management lessons from the past. Tourism Manag. 2019;70:419–429. doi: 10.1016/j.tourman.2018.09.007. [DOI] [Google Scholar]
- Park S., Song S., Lee S. Corporate social responsibility and systematic risk of restaurant firms: the moderating role of geographical diversification. Tourism Manag. 2017;59:610–620. doi: 10.1016/j.tourman.2016.09.016. [DOI] [Google Scholar]
- Qadan M. Risk appetite and the prices of precious metals. Resour. Pol. 2019;62:136–153. [Google Scholar]
- Salisu A.A., Mobolaji H. Modeling returns and volatility transmission between oil price and US–Nigeria exchange rate. Energy Econ. 2013;39:169–176. [Google Scholar]
- Salisu A.A., Oloko T.F. Modelling spillovers between stock market and FX market: evidence for Nigeria. J. Afr. Bus. 2015;16(1–2):84–108. doi: 10.1080/15228916.2015.1061285. [DOI] [Google Scholar]
- Reboredo Juan. Is gold a safe haven or a hedge for the US dollar? Implications for risk management. J. Bank. Finance. 2013;37(8):2665–2676. [Google Scholar]
- Reboredo Juan, Rivera-Castro Miguel. Gold and exchange rates: downside risk and hedging at different investment horizons. Int. Rev. Econ. Finance. 2014;34(C):267–279. [Google Scholar]
- Reboredo J.C., Ugolini A. Downside/upside price spillovers between precious metals: a vine copula approach. N. Am. J. Econ. Finance. 2015;34:84–102. [Google Scholar]
- Salisu A.A., Akanni L., Raheem I. The COVID-19 global fear index and the predictability of commodity price returns. Journal of Behavioral and Experimental Finance. 2020;27:100383. doi: 10.1016/j.jbef.2020.100383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selmi R., Mensi W., Hammoudeh S., Bouoiyour J. Is Bitcoin a hedge, a safe haven or a diversifier for oil price movements? A comparison with gold. Energy Econ. 2018;74:787–801. [Google Scholar]
- Sephton P., Mann J. Gold and crude oil prices after the great moderation. Energy Econ. 2018;71:273–281. [Google Scholar]
- Seyyedi S. Analysis of the interactive linkages between gold prices, oil prices, and the exchange rate in India. Global Econ. Rev. 2017;46(1):65–79. [Google Scholar]
- Shafiee S., Topal E. An overview of global gold market and gold price forecasting. Res. Pol. 2010;35:178–189. [Google Scholar]
- Shahzad Syed Jawad Hussain, Rehman Mobeen Ur, Jammazi Rania. Spillovers from oil to precious metals: quantile approaches. Resour. Pol. 2019;61(C):508–521. [Google Scholar]
- Shehzad K., Xiaoxing L., Kazouz H. COVID-19's disasters are perilous than Global Financial Crisis: a rumor or fact? Finance Res. Lett. 2020 doi: 10.1016/j.frl.2020.101669. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shrydeh N., Shahateet M., Mohammad S., Sumadi M. The hedging effectiveness of gold against US stocks in a post-financial crisis era. Cogent Economics and Finance. 2019;7(1) doi: 10.1080/23322039.2019.1698268. [DOI] [Google Scholar]
- Soytas U., Sari R., Hammoudeh S., Hacihasanoglu E. World oil prices, precious metal prices and macroeconomy in Turkey. Energy Pol. 2009;37:5557–5566. [Google Scholar]
- Tully E., Lucey B.M. A power GARCH examination of the gold market. Res. Int. Bus. Finance. 2007;21:316–325. [Google Scholar]
- Tversky A., Kahneman D. Loss aversion in riskless choice: a reference-dependent model. Q. J. Econ. 1991;106(4):1039–1061. [Google Scholar]
- Uzo-Peters A., Laniran T., Adenikinju A. Brent prices and oil stock behaviors: evidence from Nigerian listed oil stocks. Financ. Innovat. 2018;4:8. doi: 10.1186/s40854-018-0092-2. [DOI] [Google Scholar]
- Wang K.M. Can gold effectively hedge risks of exchange rate? J. Bus. Econ. Manag. 2013;14:833–851. [Google Scholar]
- Wei Y., Qin S., Li X., Zhu S., Wei G. Oil price fluctuation, stock market and macroeconomic fundamentals: evidence from China before and after the financial crisis. Finance Res. Lett. 2019;30:23–29. [Google Scholar]
- Yaya O.S., Tumala M.M., Udomboso C.G. Volatility persistence and returns spillovers between oil and gold prices: analysis before and after the global financial crisis. Resour. Pol. 2016;49:273–281. [Google Scholar]
- Yıldırım D.C., Cevik E.I., Esen O. Time-varying volatility spillovers between oil prices and precious metal prices. Resour. Pol. 2020;68:101783. doi: 10.1016/j.resourpol.2020.101783. [DOI] [Google Scholar]
- Zhang D., Hu M., Ji Q. Financial markets under the global pandemic of COVID-19. Finance Research Letters. 2020:101528. doi: 10.1016/j.frl.2020.101528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Wei Y. The crude oil market and the gold market: evidence for cointegration, causality and price discovery. Resour. Pol. 2010;35:168–177. [Google Scholar]